巧借Excel在AutoCAD中设计凸轮轮廓曲线
巧借Excel在AutoCAD中设计凸轮轮廓曲线

巧借Excel在AutoCAD中设计凸轮轮廓曲线摘要:本文介绍一种借用EXCEL应用程序来计算并保存数据,并与CAD精确绘图巧妙地结合,设计凸轮轮廓曲线的方法,该方法也可用于其它二维或三维曲线的绘制中。
论文毕业论文关键词:凸轮轮廓曲线 AutoCAD 图解法1.问题的提出本文以设计二维凸轮轮廓曲线为例,介绍一种一般操作者就能方便做到的,借用EXCEL应用程序来计算并保存数据,并与AutoCAD精确绘图巧妙地结合,绘制二维或三维非规则曲线的方法,以供大家参考。
2.概述在凸轮机构中,最常用的就是平面凸轮机构,要设计平面凸轮的轮廓曲线。
设计方法通常有图解法和解析法两种。
作图法简便易行、直观,作图误差较大,精度较低,适用于低速对从动件运动规律要求不高的一般精度凸轮设计;对于精度要求高的高速凸轮、靠模凸轮等,必须用解析法列出凸轮的轮廓曲线方程,用计算机辅助设计精确地设计凸轮机构。
我们沿用原有的图解法思路,使用CAD作为工具,两者的联合运用,能产生意想不到的更简单、直接、方便的处理方法。
在这种基于AutoCAD的图解法基础上,利用AutoCAD与其它文档交换信息和数据的功能,对于一些计算量较大输入点较多的图形,与EXCEL应用程序相结合,使作图更加简便快捷。
如设计下面的偏置滚子从动件盘形凸轮轮廓曲线,已知偏距e=10㎜,基圆半径r0=40㎜,行程h=25㎜,滚子半径rT=10㎜。
凸轮以角速度ω顺时针转动,从动件的运动规律为:运动阶段1,推程Φ=180°、凸轮转角φ(°)为0~180,运动形式:等加速-等减速运动,运动方程方程:s=(2h/Φ2)φ2=(2*25/1802)φ(0≤φ≤90)或s=h-2h(Φ-φ)2/Φ2=25-2*25*(180-φ)2/1802(90≤φ≤180)运动阶段2,远休止ΦS=30°、凸轮转角φ(°)为180~210,运动形式:静止不动,运动方程方程: s=h=25(180≤φ≤210)运动阶段3,回程Φ=90°、凸轮转角φ(°)为210~300,运动形式:等加速-等减速运动,运动方程方程: s= h-(2h/Φ’2)/φ’2=25-(2*25/180)2/(φ-210)2(180≤φ≤210)或s=2h(Φ’-φ’)2/Φ’2=2*25*(90-(φ-210))2/902(180≤φ≤210)运动阶段4,远休止ΦS=60°、凸轮转角φ(°)为300~360,运动形式:静止不动,运动方程方程: s=0(300≤φ≤360)3、解题思路要使基于CAD技术的图解法充分发挥软件精确、高效绘图的作用,就要首先改进原来的作图方法。
巧用Excel在AutoCAD中精确绘制公式曲线曲面

图 1 渐开线形成果原理图 图 2 AutoCAD 中得到的渐开线齿轮轮廓
第二步打开 AutoCAD ,绘制齿轮的齿顶圆 、分度圆 、齿根圆 ,并点击工具栏“Spline”样条曲线 ,把 Excel 电 子表格中极坐标列数据复制到 AutoCAD 命令行中 ,即可生成一条齿轮渐开线 ,再经过镜像 、旋转 、阵列等命 令得到一个完整的渐开线齿轮轮廓如图 2 所示. 此渐开线齿轮齿廓可在 AutoCAD 环境下对它进行拉伸形成齿轮三维立体模型[324 ] . 也可对它进行其它 的分析和计算等.
向径/ mm 46. 984 6 46. 985 1 46. 986 6 46. 988 9 46. 992 4 46. 996 8 47. 002 1 47. 008 4 47. 015 6 47. 023 8 47. 033 1 47. 043 2 47. 054 4 47. 066 5 47. 079 6 47. 093 7
顶圆半径
ra
=
m(z
+
2
h
3 a
)
/
2
=
52
,
基圆半径
rb =
rcosα =
m zcosα/ 2 = 46. 98 ( r 为分度圆半径) ,齿顶圆压力角αa = arc2
cos ( rb/ ra) = 25. 37°. 为了得到足够长度的渐开线 , 这里取最
大压力角 αmax = 26°;根据精度要求在渐开线上取分段数 ,这
第 20 卷 第 2 期 2009 年 6 月
广 西 工 学 院 学 报
Vol120 No12
J OU RNAL OF GUAN GXI UN IV ERSIT Y OF TECHNOLO GY
利用CAD画凸轮机构
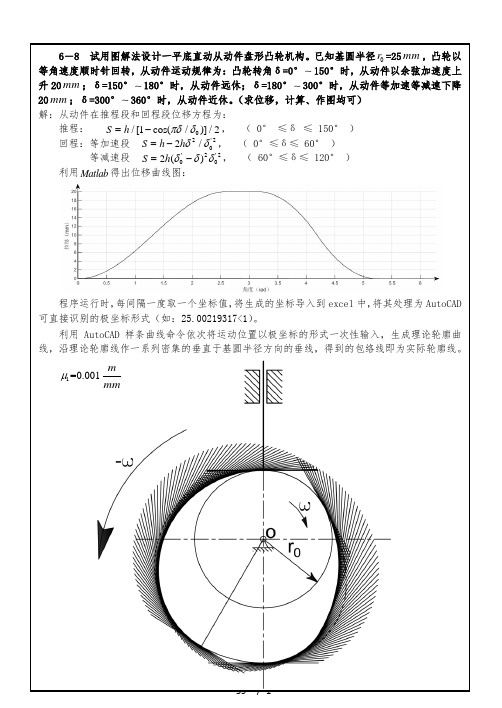
利用CAD 画凸轮机构 - 59 - / 1
6-8 试用图解法设计一平底直动从动件盘形凸轮机构。
已知基圆半径0r =25mm ,凸轮以等角速度顺时针回转,从动件运动规律为:凸轮转角δ=0°150°时,从动件以余弦加速度上升20mm ;δ=150°180°时,从动件远休;δ=180°300°时,从动件等加速等减速下降20mm ;δ=300°360°时,从动件近休。
(求位移,计算、作图均可) 解:从动件在推程段和回程段位移方程为: 推程: 0/[1cos(/)]/2S h πδδ=-, ( 0° ≤δ ≤ 150° ) 回程:等加速段 2'202/S h h δδ=-, ( 0°≤δ≤ 60° ) 等减速段 '2'2002()S h δδδ=-, ( 60°≤δ≤ 120° ) 利用Matlab 得出位移曲线图: 程序运行时,每间隔一度取一个坐标值,将生成的坐标导入到excel 中,将其处理为AutoCAD 可直接识别的极坐标形式(如:25.00219317<1)。
利用AutoCAD 样条曲线命令依次将运动位置以极坐标的形式一次性输入,生成理论轮廓曲线,沿理论轮廓线作一系列密集的垂直于基圆半径方向的垂线,得到的包络线即为实际轮廓线。
1=0.001μm mm。
EXCEL和CAD结合自动生成曲线的简单方法

可能很多人都困惑如何能方便地在CAD中划曲线。
下面这个方法是本人毕业设计时琢磨出来了,划型线非常方便。
希望大家广泛传播,减轻大家划曲线的工作量。
假如3个点的坐标为 1,2 3,4 5,6
在excel 单元格中
A B C D E
spline 1,2 3,4 5,6 ( 输入2个空格)
复制整行,粘贴到CAD命令栏内,曲线就自动生成了。
(spline 也可以换成_spline)
多个曲线时,如上所示,下一行在EXCEL中也这样排列,然后把几行一起复制粘贴到CAD 命令栏中,几条曲线就自动生成了。
单元格中的点,比如"1,2" 可以用 EXCEL 文字结合命令组合,如下所示:
A B C
1 1
2 (=A1&","&B1)
这样可以结合成点坐标,然后按照上面提到的spline 输入格式可以自动生成曲线。
这个原理其实就是利用CAD本身的输入规则,在EXCEL中排列好,粘贴到CAD命令栏,就相当于输入数据,最后的空格也是和在CAD中
画曲线后两端的自动取曲率是一样的。
一种凸轮廓线的设计方法

一种凸轮廓线的设计方法
方法一:使用CAD软件来设计凸轮廓线
1、选择CAD软件,打开新的工程,创建一个新的图形;
2、根据规定的要求,在图形中绘制凸轮廓线,可以直接使用绘图工具进行绘制,也可以使用数学函数来生成凸轮廓线;
3、如果需要对凸轮廓线进行修改,可以使用CAD软件中的编辑工具来修改;
4、保存凸轮廓线,并将其导出为可以使用的文件格式。
方法二:使用绘图工具来设计凸轮廓线
1、选择一款绘图工具,打开新的工程,创建一个新的图形;
2、根据规定的要求,使用绘图工具在图形中绘制凸轮廓线;
3、如果需要对凸轮廓线进行修改,可以使用绘图工具中的编辑工具来修改;
4、保存凸轮廓线,并将其导出为可以使用的文件格式。
CAD精确绘制盘形凸轮曲线的方法

CAD精确绘制盘形凸轮曲线的方法2003年6月第16卷第2期十堰职业技术学院JournalofShiyanTechnicalInstituteJune,2003V oI.16NO.2CAD精确绘制盘形凸轮曲线的方法鲁春发,莫足琴(十堰职业技术学院计算机工程系,湖北十堰442000)[摘要]通过对凸轮轮廓曲线的几何分析,运用应用程序Excel和AutoCAD精确地绘制出了凸轮的轮廓曲线,解决了AutoCAD2000中不能画凸轮的问题,使AutoCAD2000的功能得到了扩展.[关键词]Excel;CAD;凸轮;轮廓曲线[中图分类号]TH122[文献标识码]A[文章编号]1008-4738(2003)02-0060-02l引言我们在设计盘形凸轮机构时,通常采用图解法或解析法进行凸轮轮廓曲线的设计,图解法作图误差较大,精度低,而传统的解析法又比较繁琐,现在,计算机的普及为我们精确地绘制盘形凸轮机构凸轮的轮廓曲线提供了便捷工具.我们可采用常用的应用程序Excel和AutoCAD绘制出盘形凸轮的轮廓曲线.2尖顶从动件盘形凸轮轮廓曲线上点的直角坐标的确定方法如图1所示,当凸轮逆时针转动,从动件的尖顶从岛点转到B点转过角度时,尖顶从动件盘形凸轮轮廓曲线上B点的直角坐标,y^可根据盘形凸轮的回转中心0点的坐标(,),基圆的半径凡,偏心距e(右偏,图中OA的长度)及从动杆的运动规律F()来确定(=Bo0C).由图中我们可知:珈._,x图1=Xo+c+BC×sin(BCE)y^=yd+YC+BC×c∞(LBCE)其中:BC=F(),LBCE=LDCE—LDCB=一arcsin(e/Rb)(如从动杆为左偏,则将式中的"一"号改为"+"号即可),Xc=凡×sin(),Yc=R6×C05().所以.尖顶从动件盘形凸轮轮廓曲线上曰点的直角坐标可表示为:五=+R^×sin()+F()×sin(一arcsin(e/Rb))Yb=y0+R^×C05()+F()×C05(一arcsin(e/Rb))3软件应用3.1用Excel计算出尖顶从动件盘形凸轮轮廓曲线上B点的直角坐标打开一张Excel工作表将A列置为凸轮转动的角度,可每5.算一个值(此值设置得愈小,算出的坐标值愈多,则描绘出的凸轮轮廓曲线愈精确,当然花的时间也相应多些),共72个值,Al输人标题,A2,A3分别输入0,5二值后同时选中A2,A3两单元格,将鼠标指向选中的单元格右下角的十字光标,按住鼠标左键往下拖动到A73单元格后松开鼠标即输入完所需的数据;将B列置为F(),B1输入标题F(),从JB2开始按从动杆的运动规律分段输人运动规律函数,将鼠标指向输人函数的单元格右下角的十字光标,按住鼠标左键分段往下拖动即计算完并显示出所需的数据(下面各列数据的计算和显示均用此法);将C列置为,将D列置为,为了坐标值不出现负值以方便绘图时点的输人,可将坐标,yD设置得稍微大些;将E列置为基圆半径R,将F列置为偏心距e;将G列置为偏角LBCD,LBCD=arcsin(e/Rb)=arcsin(F/E);将H列置为偏心距以=Xo+R^×sin()+F()×sin(一arcsin(e/瞄))=C+E×sin(3.1415926×A/180)+B×sin(3.1415926×A/180一G)将,列置为偏心距y^y^=ro+R^×cos()+F()×C05(一arcsin(e/瞄))=D+E×C05(3.1415926×A/180)+B×C05(3.1415926×A/180一G)直接用已知条件给出的数值代替表中的符号.Excel工作表就能快速准确地显示出尖顶从动件盘形凸轮轮廓曲线[收稿日期]2002—11-30[作者简介]鲁春发(1964一),男,十堰职业技术学院计算机工程系党总支书记,高级实验师;莫足琴(1973一),女,十堰职业技术学院计算机工程系助理实验师.一6o一CAD精确绘制盘形凸轮曲线的方法上各点的直角坐标.此方法还有一个好处是在设计不同的凸轮轮廓曲线时只需将从动杆的运动规律函数F('p)改变一下,其它地方均无需改动,即可得出另一个尖顶从动件盘形凸轮轮廓曲线上各点的直角坐标值.3.2用AutoCAD绘制凸轮轮廓曲线打开AutoCAD应用程序,输人"样条曲线"命令,在命令行中输人用Excel工作表算出的值,输完后即得到了尖顶从动件盘形凸轮轮廓曲线.如果是滚子从动件盘形凸轮,则先按上述方法绘制出尖顶从动件盘形凸轮轮廓曲线后,利用AutoCAD应用程序中的偏移工具进行绘制,方法是:1)输人"偏移"命令;2)给出偏移的距离(即滚子的半径);3)选择要偏移的实体(即尖顶从动件盘形凸轮轮廓曲线);4)指定偏移的方位(用鼠标点击尖顶从动件盘形凸轮轮廓曲线的内侧即可).此时CAD自动绘出滚子从动件盘形凸轮的轮廓曲线.4应用举例例如:设计一偏置滚子移动从动件盘形凸轮机构.已知凸轮的基圆半径为r5:40rata,滚子半径I"t=12mm,从动件偏在凸轮转动中心0的右边,其偏距e=18mm.凸轮以逆时针方向回转,当凸轮转过.=180.时,从动件按余弦加速度规律上升36ram;当凸轮再转过=20.时,从动件停留在最高位置不动;当凸轮又转过,=120.时,从动件按等加速等减速运动规律退回原处;当凸轮再转过轨=4o.时,从动件停留在最低位置不动.设计这一凸轮轮廓曲线时,首先列出凸轮理论轮廓各段曲线上点的坐标方程:0.~180.:F()=36/2×(1一cos~o)180.一200.:,(p)=36200.一320.:分等加速和等减速两部分等加速部分(200.~260.):F(p)=36—36X2/120X(p一200)等减速部分(260.一320.):F(p)=36X2/120X(320一妒)320.一360.:F(p)=0将上述函数表达式分段代人设计好的F~eel工作表,同时用已知条件代替表格中的符号,Excel工作表即显示出各点的直角坐标(见图2,此处仅显示部分坐标点的值).为方便点的输人,可用"格式"菜单中的"单元格"选项将H列和I 列单元格数值的小数位设置成一位,使坐标值保留一位小数.打开AutoCAD应用程序,输人"样条曲线"命令,在命令行分别输人72个点的直角坐标值,即得出凸轮的理论轮廓曲线.强萄需麓甏%鐾…墼糊黼瞄圄鲴..一1.2蠲镕目目嘲r(由)-x?'Y●,Rb'B,膏轴Yho0.0O0.8o80.408O.'','58O,0.t2O.O:50.06880804OI8O.4''7'S83.5l19.9O.273808o40I80.4''々'586.9ll9.70.6l3808O40I8O.4''7'590.2lI9.21.0868O8o哇0I8O.4''7'S93.6ll8.7251.6e080曩0l8O.4667'S96.7.嘉蠹囊02.4l0o8O哇0l8O.4''76510o.1l7.353,.8O.4''76S1O3.4ll6.0404.2O.6'7'SlO6.7lI4.7鬓.27280I0.06'7'5lo9.9ll3.3糍5o6.8t)_辱o,l80.4''7'SllS.2ll1.6 墨嚣s5y.6r,6808ol18O.'67'Sll6.tlO9.76().18O.66了'5ll9.6lO7.S651.39380l8O.4''7'5I22.7lO5.1图输人"偏移"命令,在命令行输人滚子的半径l2,然后用鼠标点击理论轮廓曲线的内侧,即得到了要设计的偏置滚子移动从动件盘形凸轮机构凸轮的实际轮廓曲线(见图3).5小结目前中还没有画凸轮轮廓曲线的功能,采用绘制机械图时还不能准确地画出凸轮轮廓曲线,用上述方法不仅可绘制出凸轮轮廓曲线,而且非常准确,特别是对滚子从动件,直接运用图中的"偏移"命令,快速准确,省去了手工绘图时必须画圆的包络线的麻烦.另外用计算尖顶从动件盘形凸轮轮廓曲线上点的直角坐标时,一旦设置好后可保存在电脑中,以后再设计凸轮轮廓曲线时只需将其调出,将运动规律函数及其它参数修改一下即可,对经常从事机械设计者非常适用.咖CADLU一.一(..,,,)c鲫applyap.c舢●:;;curve一6l一¨一秘-.|断一。
基于AutoCAD的凸轮外形轮廓曲线设计

0
1
00 ■
【
s :
“ 3 0 ・0
_ ; 々
.
} } ’ 0… ∞
一
…
{ ∞
) 0
。
一 0
0, ∞…
c
L
t:
¨
∞
… {
】 J
《
j , ‘ 1
0
s 4 ∞
l
≯
0{ 0 i
‘ e { } i … { …
1 々
-
“ 。 ”
一 ^ … 1^ 一 } £ ∞
0
L_ ' f
, } , l
{ ’ 0 I J 0 【
§
《
’ 【
{
“0 0 0 ∞
t
-
L
1_ _ …
f
一
…Leabharlann n ,_
~ … %
1引言
’
凸轮 机 构 是 机 械 传 动 中 的一 种 常 用机 根 据 凸轮 精 度 要 求 可 将 凸轮 转 角 分 成 构 , 自动 化 和 半 自动 化 机 械 中 应 用 非 常 , 分 , 取 值越 大 , 廓 曲线越 精 确 。 本例 在 l 等 n 轮 广 泛 。 根据 使 用 要 求 确 定 了 凸轮 机 构 的类 中取 , 1 0 利 用 E c l l O, = x e 的快 速 制表 和 数据 型 、基 本 参 数 以 及 从 动件 运 动 规 律 后 , 即 计 算 功 能 完 成坐 标 的 计 算 , 体 如 下 : 具 可 进 行 凸轮 外 形 轮 廓 曲线 的 设 计 , 计 凸 设 () E c l A 列第 一 行 A1 1在 x e 中 中输 入 轮 外 形 轮 廓 曲 线 的 方 法 有 作 图 法 和 解 析 “ 角 ( ” A2中输 入 “ ” 由于 推 程 角 转 p , 0, 法 , 者 所 依 据 的 设 计 原 理 基 本 相 同 。 作 两 9 。 ,=10所 以 A 0 / 0 I 2中输 入 “ .” 利用 09 , 图法 简便 、直 观 , 作 图误 差 较 大 , 以 获 但 难 E cl x e 的等差数 列 快速 输入 法 , 可以快 速在 得 凸轮 外 形 轮 廓 曲线 上 各 点 的 精 确 坐 标 , A 列 依次 生 成 0 0 , 长 为 0 9 等差 ~9 。 步 .的 所 以 按 照 作 图法 所 得 轮 廓 数 据 加 工 的 凸轮
应用EXCEL在CAD中绘制曲线

应用EXCEL在CAD中绘制曲线随着计算机技术的不断发展和CAD软件的不断完善,现在在CAD中绘制曲线已经不再像是几十年前那样需要手动勾画了。
使用软件可以完成绘制所有类型的曲线,让绘制曲线的过程更加快速简便。
本文将从应用EXCEL在CAD中绘制曲线入手,为大家详细介绍如何利用软件这一工具在CAD中绘制高质量的曲线。
一、前置知识在学习如何利用EXCEL绘制曲线前,我们需要先了解一些基本的CAD曲线绘制知识,以便更好地运用EXCEL工具。
1.1 CAD中的曲线类型1.1.1 直线直线是CAD中最简单的曲线,可以通过给定两个点来绘制。
直线子命令可以通过选择“直线”工具栏上的图标或输入“line”来启动。
在CAD中,直线通常是由图形的边缘或边缘之间组成的。
1.1.2 圆圆是CAD中最基本的弧线。
绘制圆时,可以将其中心点和半径指定到指定的位置,也可以使用两个点定义其直径。
圆子命令可以通过选择“圆”工具栏上的图标或输入“circle”来启动。
1.1.3 椭圆椭圆是由半长轴和半短轴决定的圆形变体。
与圆不同,椭圆在CAD中无法通过设置半径来确定。
可以使用两个点或关键点、与两个轴线相交的点、中心点和两个轴线的长度来创建椭圆。
椭圆子命令可以通过选择“椭圆”工具栏上的图标或输入“ellipse”来启动。
1.1.4 弧弧是由圆弧的圆心、半径和起始和结束角度定义的。
可以通过向圆弧添加关键点来创建更复杂的弧。
弧度量采用角度制方式,可以通过键入一个角度度数、长度或一个关键点位置来创建。
圆弧子命令可以通过选择“圆弧”工具栏上的图标或输入“arc”来启动。
1.1.5 曲线CAD中的曲线通常是由控制点定义的NURBS曲线。
控制点是影响曲线形状的点,曲线从一个控制点移动到另一个控制点。
曲线的精度通常通过指定控制点的数量来控制。
例如,如果只有少量控制点,则曲线将是基本的弧线。
如果有非常多的控制点,曲线可以非常复杂。
在CAD中,曲线子命令可以通过选择“曲线”工具栏上的图标或输入“spline”来启动。
用作图法绘制凸轮靠模的轮廓曲线

用作图法绘制凸轮靠模的轮廓曲线徐建军;包轩庭【摘要】This paper proposes a method of using a drawing to determine the profile curve of cam profile model⁃ing. It is a simpler solution to grinding cam, which has a spline curve contour.% 提出了一种用作图法来确定凸轮靠模轮廓曲线的方法,比较简便地解决了轮廓为样条曲线的凸轮的磨削问题。
【期刊名称】《常熟理工学院学报》【年(卷),期】2012(000)010【总页数】3页(P79-81)【关键词】凸轮;靠模;作图法【作者】徐建军;包轩庭【作者单位】常熟职业教育中心校,江苏常熟 215500;常熟理工学院机械工程学院,江苏常熟 215500【正文语种】中文【中图分类】TS913某工业缝纫机厂在生产中需要加工一款凸轮,其轮廓形状见图1,该凸轮的轮廓曲线由样条曲线构成,该曲线是通过三坐标测量仪对凸轮实物采样若干个点后,用计算机辅助设计软件绘制而成.其加工工艺为:粗加工采用线切割加工,精加工为磨削加工.由于批量不大,为了降低生产成本,企业没有添置专用的凸轮磨床,而是对普通的外圆磨床进行改造,采用靠模进行仿形磨削,因此需要确定该凸轮靠模的轮廓曲线.凸轮的精加工在外圆磨床上采用仿形磨削完成.通过靠模控制砂轮架做前后运动,从而控制砂轮仿形磨削加工出凸轮.靠模导轮安装在砂轮架上,导轮的中心和砂轮回转中心等高,然后通过强力弹簧将导轮紧压在靠模上.靠模和凸轮安装在同一芯轴上,通过电机驱动芯轴回转,从而实现仿形磨削.由图2可知,假设采用标准形状的凸轮作为靠模,在磨削凸轮的升程段和降程段时,由于导轮和砂轮的直径不同,导致导轮与靠模的接触点与砂轮的实际切削点位置不同.如图2所示,凸轮和靠模的回转中心是O1,导轮的回转中心是O2,砂轮的回转中心是O3,三点处于同一水平面内.砂轮与凸轮的接触点是A点,导轮与靠模(凸轮标准廓形)的接触点是B点.因而在磨削时会产生过切,造成加工后得到的凸轮形状与标准形状相差甚远.所以,需要按照现有的凸轮轮廓曲线,并根据导轮和砂轮的直径,确定靠模的轮廓曲线.3.1 常用方法凸轮靠模形状的确定,一般采用数学计算法和反靠法两种方法.数学计算法是以凸轮型面参数方程、机床的结构参数以及砂轮直径等数据为计算的原始资料,在分析磨削过程中的几何关系变化规律的基础上,推导出导轮中心的极坐标方程,然后运用包络法求得靠模的型面参数方程.但对本例而言,由于只有凸轮实物,没有凸轮的型面参数方程等其他相关信息,因此无法应用数学计算法来确定靠模的轮廓曲线.反靠法是将凸轮磨床上的砂轮换成与砂轮直径相等的导轮,将导轮换成与导轮直径相等的砂轮,将头尾座顶针间的凸轮轴换装上标准凸轮(原始靠模),并借助于弹簧拉力使导轮靠紧旋转主轴上的标准凸轮,驱动砂轮磨削出凸轮靠模.但其制作精度受机床的系统刚性和几何精度、弹簧张力的变化、磨削冲击等诸多因素影响,往往一次反靠无法得到符合精度要求的靠模.因此,反靠法尽管可以应用于本例中的凸轮靠模制作,但其制作精度不够高,且制作周期较长,因此需考虑更为精确、便捷的方法.3.2 绘图法通过了解磨床的工装改造、夹具和分析凸轮的磨削过程,根据凸轮轮廓曲线是通过点阵拟合的样条曲线这一特点,采用了作图法来确定靠模的轮廓曲线的方法.在分析砂轮的运动规律时,假设凸轮不动,导轮和砂轮绕凸轮旋转.在不考虑砂轮磨损的情况下,砂轮的直径是一个固定值,则将凸轮的轮廓曲线向外偏距一个砂轮半径值,得到的曲线即砂轮中心的运动轨迹,而导轮固定在砂轮架上,其回转中心和砂轮的回转中心也是一个固定值.如图3所示,从凸轮的回转中心O1出发作一条直线,另一个端点O3落在砂轮的运动中心轨迹上,然后将该直线缩短一个导轮和砂轮的中心距的长度,得到O2点,该点即导轮的回转中心.重复上述操作,得到一系列的导轮中心点,然后以各点为圆心,根据导轮直径绘制若干个导轮圆,这一系列的导轮圆所构成的内侧的包络线即为所需要的靠模的轮廓轨迹曲线.通过上述操作,得到的凸轮靠模的轮廓曲线如图4所示.通过绘图法得到靠模轮廓曲线后,将其导入线切割编程软件,生成加工程序,再将毛坯材料经过热处理后,用线切割加工即可得到比较精确的凸轮靠模.对于该类通过逆向建模得到的凸轮,由于无法采用科学计算法来计算靠模轮廓曲线,本文提出了一种用作图法来确定其磨削靠模的轮廓曲线方法,是一种比较快捷、精确的方法,其靠模的精度取决于绘图时导轮中心点的密度和线切割加工的制造精度.在企业的实际生产中,由于凸轮的粗加工采用了线切割加工,因此磨削余量较小且均匀,同时采用较硬的砂轮后,砂轮磨损较少,在加工中能很好地保证凸轮的磨削精度;将磨削后的凸轮装配到工业缝纫机后,能使缝纫机精准地完成相应的运动,获得了较好的效果.【相关文献】[1]涂鲜,颉谭成.凸轮靠模廓形的设计[J].制造技术与机床,2004(12).[2]刘兴富.凸轮靠模轮廓曲线的设计制造与检测[J].江苏机械制造与自动化,2000(05).[3]袁礼彬.基于AutoCAD的靠模轮廓曲线设计[J].工具技术,2011(01).[4]张棉好,徐洪,刘智强.参数化凸轮轮廓曲线的设计[J].现代制造工程,2005(09).[5]张恭潜.圆族包络法加工摇摆式凸轮磨靠模及靠模廓线特征[J].内燃机,2010(04).[6]孙敦兴.平动式凸轮靠模设计及其轮廓曲线加工误差[J].制造技术与机床,1981(10).[7]周腾芳,郭仲衡.凸轮靠模的计算[J].现代制造工程,1983(08).[8]王联京.在外圆磨上用纵摆夹具磨圆弧[J].现代制造工程,1979(02).。
巧借Excel在AutoCAD中设计凸轮轮廓曲线

是 计算 ,为 了得到更 为准确的 曲线 ,
取点要尽 量多 ,求这些点 的极坐标值 是 一个很 大的计算量 ,如 何计算 ,计
轮转角 中( 为 2 。) 0~3 1 0,运动形 算后数据保存在哪里?其次是绘制曲线 0 方程 : s = h一 2 ( h/中’2 / 中’ ) ≤中≤2 0)或 s 2 中’一 中’2 1 = h( )/
( 0 ≤ 中≤ 36 3 0 0)
= A 1t 的 图解法基础上 ,利用 式 :静止 不 动 ,运 动方 程 方 程 : s 0 和 保 存 数 据 。 oCAD . 1
A tC u o AD与其它文档交换信息和数据
按从 动 件 的运 动规 律 所给 数据 ,
路 ,使用 CAD作为T具 ,两者的联合 ( 0 ≤ 中≤ 21 1 8 0)
运用, 能产生意想不到的更简单、 直接 、
方 便 的 处 理 方 法 。 在 这 种 基 干
用程序 ,可以执行计算 、分析信 息并
凸轮转角 中( 为 3 0~3 0 。) 0 6 ,运动形 管理表 格等 ,我们就 用 匕来进行 计算
I8 2
维普资讯
由于 凸轮轮廓 曲线要对麻推 程运 动角 ( ) 中’、近休止角( ’ ) ( S四个部分。根据 p
计 凸轮机 构 。我们沿 用 原有 的 图解法 思
要输二十 多次 ,非常 费时而且很容 易 出错 。
4
.
2 一 2 2 / 8 )/ 中 l) 10 凸轮等 ,必须用解析法列出凸轮的轮廓 2 5 (* 5 102 ( 2 O2 (8
解 决 办法
41 . 数据的计算
E E XC L是 我 们大 家 比较 熟悉 的应
维普资讯
基于Matlab和Excel设计凸轮轮廓曲线

基于Matlab和Excel设计凸轮轮廓曲线
吴晓明;雷亚勇
【期刊名称】《现代制造工程》
【年(卷),期】2007(000)001
【摘要】提出一种基于解析法设计凸轮轮廓线的原理,以Matlab为平台,Excel为中间站,通过人机交互式作图,实现了在AutoCAD中的凸轮轮廓的绘制.
【总页数】3页(P53-54,131)
【作者】吴晓明;雷亚勇
【作者单位】燕山大学机械工程学院,秦皇岛,066004;燕山大学机械工程学院,秦皇岛,066004
【正文语种】中文
【中图分类】TP391
【相关文献】
1.基于MATLAB软件的凸轮轮廓曲线设计及从动件运动学仿真 [J], 李霞;刘本学;张三川
2.基于Matlab和Pro/E的凸轮轮廓曲线精确设计 [J], 陈韵
3.基于Matlab和Pro/E的凸轮轮廓曲线设计及从动件运动学仿真 [J], 肖帮东;黄浩;徐中
4.基于MATLAB语言的凸轮轮廓曲线的解析法设计 [J], 杜韧;冯伟娜;刘昭;刘宏伟;毕珊珊
5.基于AutoCAD与Excel的凸轮轮廓曲线设计 [J], 郑彬;尧遥
因版权原因,仅展示原文概要,查看原文内容请购买。
凸轮轮廓曲线在AutoCAD中的快速生成

( n tt t fTe h o o y. I s iu e o c n lg CAE M in a g 6 1 0 Ch n ) P. a y n 2 9 0. i a
摘 要 : 于 Auo AD在 凸轮 图解 法设 计 中 的 基 tC 成功应 用, 结合 E c l x e 强大 的制表 与 计算 功 能 , 出 给
E c l 确 计 算 和 快 速 制 表 能 力 , 利 用 Auo AD xe精 在 tC
档 中, 然后 打开 Auo AD, tC 绘制 凸轮 基 圆 , 将用 户坐 标 系 调整 到凸轮 圆心 , 并且 以从 动 件 与 凸轮 中心 的 连 线 为 X轴 , 图 3所示 。在命 令 框 输 入“ l e 或 如 pi ” n
维普资讯
凸轮轮 廓 曲线在 Auo A tC D中的快速生成
廖 海 平 , 翠 华 曾
( 国工程 物 理研 究院 工学 院, 中 四川 绵 阳 6 1 0 ) 2 9 0
Fa tDr wi g Co t r Cur eofCa wih Aut CAD s a n n ou v m t o
了一 种 E c l Auo AD 相 结 合 快 速 生 成 凸轮 曲 xe 与 tC
线 的方 法 。
制 程序 , 但这 种方 法 对 于 一 般 的工 程 技 术人 员 来 说
存 在一 定 的难度 且通 用性 较差 。
1 使 用 Auo tCAD绘 制 凸轮 轮 廓 曲线 的 一般 步 骤
要求 的 近 似 凸 轮 轮 廓 曲线 。其 一 般 的步 骤 如 下 所
述 一 。引。
a 根据 凸轮轮 廓 曲 线 各段 的不 同 精度 要 求 , . 确 定极 坐标 辐射 线 的疏 密程度 。
AutoCAD借力Excel巧绘曲线
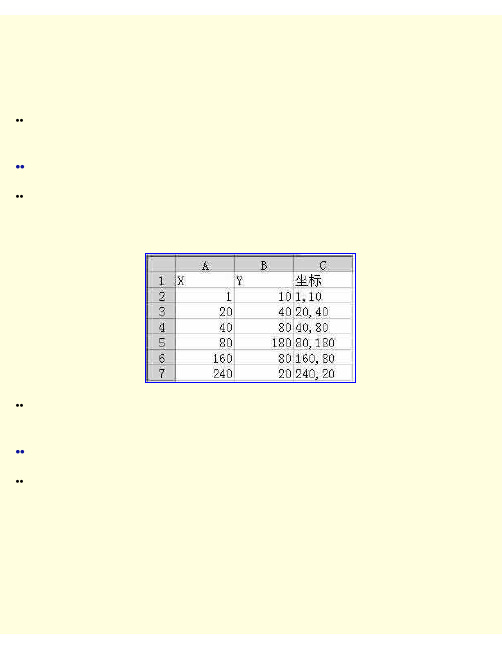
Auto CAD社区(22):借力Excel巧绘曲线
阿@2004年6月7日 第22期
••笔者在作图时经常需要根据多个坐标点绘制曲线,而输入坐标点的工作非常繁琐。
后来,笔者发现了下面的简便方法。
••1.编制Excel工作表
••启动Excel,在A列中输入X坐标,在B列中输入Y坐标,然后在C列中输入公式得到坐标点,具体方法为:在C2中输入公式“=A2&“,”&B2”,然后用填充柄将C2中的公式复制到C列中相关的单元格内(图1)。
••选中C2:C7单元格区域,单击工具栏中的“复制”按钮,把这些坐标值复制到“剪贴
板”中。
••2.绘制曲线
••启动AutoCAD,在命令行中键入“spline”,按回车键,在“[对象(O)]:”提示信息后,单击右键,选择“粘贴”命令,就可以得到曲线了(图2)。
••把坐标值编辑为Excel文件,一是便于修改,二是可以反复利用这些坐标值,非常方便。
基于EXCEL和SolidWorks设计凸轮轮廓及运动学分析

基于EXCEL和SolidWorks设计凸轮轮廓及运动学分析李建莉【摘要】通过对凸轮从动件运动规律的分析,在EXCEL中利用Akima插值法生成平面凸轮轮廓位移数据点.在SolidWorks中通过调用EXCEL处理的平面凸轮轮廓数据点生成具有封闭连续轮廓曲线的凸轮,再利用SolidWorks中的COSMOS/Motion插件进行凸轮运动仿真,生成相应的位移曲线图,与在EXCEL中生成凸轮轮廓位移图进行对比,从而为凸轮轮廓设计及运动学分析提供借鉴.【期刊名称】《机械工程师》【年(卷),期】2017(000)009【总页数】3页(P83-84,87)【关键词】EXCEL;SolidWorks;凸轮轮廓;运动仿真【作者】李建莉【作者单位】兰州资源环境职业技术学院,兰州730021【正文语种】中文【中图分类】TP391.7SolidWorks中的COSMOS/Motion 插件是一个虚拟原型机仿真工具,能够帮助设计人员在设计前期判断设计是否能达到预期目标,SolidWorks Motion可以根据表格数据或输入诸如STEP等函数的方式来创建凸轮轮廓。
可以通过运动驱动从动件,利用反向的操作,由从动件的运动生成凸轮轮廓。
本文中将以对心尖顶直动从动件盘形凸轮为载体,根据输入从动件的一组位移数据来生成凸轮的轮廓。
为了生成这个凸轮,研究解决3个关键问题:定义从动件的运动;生成跟踪路径;将曲线作为草图输出并生成实体造型。
由得到的凸轮轮廓,利用SolidWorks Motion进行运行仿真,输出运动轮廓位移曲线,将得到位移曲线和EXCEL中生成位移曲线进行对比,由此分析为凸轮轮廓设计另辟蹊径。
根据凸轮的用途和工况,选择不同的曲线类型。
设计一个对心顶尖推动盘形凸轮的实际轮廓线。
凸轮的轮廓形状决定了从动件的运动轨迹,反之,从动件的不同运动轨迹也要求凸轮具有不同形状的轮廓。
当从动件运动过程分为“升-停-升-降-停-降”,在实际生产加工中,往往不知道精确的凸轮轮廓线方程,只能得到一些离散点。
基于AutoCAD与Excel的凸轮轮廓曲线设计

引言在各种机器中,常常采用凸轮从动件系统,如汽车发动机的气门是靠凸轮开启的,在许多制造消费品的机器上,也采用各式各样的凸轮。
与连杆机构相比较,凸轮机构较易实现所规定的运动规律[1]。
尤其原动件连续运动而从动件作间歇运动时,采用凸轮机构最为方便[2]。
但凸轮的设计必须依靠精确的凸轮轮廓线来满足从动件的各种预期的运动规律。
凸轮机构的设计,关键是获得精确的凸轮轮廓曲线来满足从动件各种预期的运动规律,以实现机械的自动化,而凸轮曲线特性优良与否直接影响到凸轮机构的效率、精度以及寿命[3]。
凸轮轮廓线的设计一般分为图解法和解析法。
解析法精度较高,但计算繁琐;图解法虽然直观、方便,但手工作图误差较大,一般用于低速和不重要的场合[4]。
通过运用解析法可以精确地计算出轮廓线上的各点坐标,然后绘制成图。
AutoCAD 具有完备的二维绘图[5]。
Excel 程序可以使不具备一定编写程序能力的工程技术人员非常方便地进行机械设计计算[6]。
1凸轮轮廓线的解析法设计凸轮指的是机械的回转或滑动件(如轮或轮的突出部分),它把运动传递给紧靠其边缘移动的滚轮或在槽面上自由运动的针杆,或者它从这样的滚轮和针杆中承受力。
凸轮随动机构可设计成在其运动范围内能满足几乎任何输入输出关系,对某些用途来说,凸轮和连杆机构能起同样的作用,对于两者都可以用的工作,凸轮比连杆机构易于设计,并且凸轮还能做许多连杆机构所不能做的事情,从另一方面来说,凸轮机构比连杆机构易于制造。
用解析法设计凸轮的轮廓曲线,其基本方法就是根据从动件的运动规律和已知的机构参数,利用已有的运动方程式,运用Excel 软件计算出从动件的行程位置及凸轮的工作廓线的极坐标值。
但无论是采用图解法还是解析法,设计凸轮轮廓曲线方法的基本原理都是反转法,即给整个凸轮机构加上一个与凸轮转动角速度ω大小相等、方向相反的角速度-ω,不影响各构件之间的相对运动。
根据相对运动原理,此时凸轮将固定不动,从动件一方面随其导路以-ω绕轴转动,另一方面又相对其导路按预定的运动规律移动,从动件在这种复合运动中其尖顶始终与凸轮轮廓相接触。
凸轮型线绘制方法

凸轮型线绘制方法
1、第一步:在EXECL里录入型线数据;如图
A列为极经、B列为<、C列为角度;
将其按图号另存为TXT文件;
2:第二步:打开前步之TXT文件,将其中空格复制下来进行全部替换,(注意”替换为”栏中不输入任何字符),如图:
再将首行输入“SPLINE”,大小写即可,(整个文件中不应该有空格和其他字符),如图:
3、第三步:将此文件后缀名更改为“.scr”,此文件可用记事本打开,如图
4、第四步:打开CAD,键入命令“scr”,读取上步所做的scr脚本文件,即可
绘制出所需型线。
(注意:此型线的原点原点为CAD的坐标零点,即“0,0”点,最好在型线绘制前将型面基圆绘出,同时将“对象捕捉”功能关闭)
5、注意,图纸上型线数据有可能是滚轮中心数据,也有可能是型面轮廓数据,要注意区分,后者可以通过在CAD中将滚轮中心轮廓向内偏移滚轮半径得到。
基于Excel的盘形凸轮线切割加工

基于Excel的盘形凸轮线切割加工
周敬勇;郑慧玲;杨光明;张啸
【期刊名称】《科技广场》
【年(卷),期】2017(000)003
【摘要】本文根据给定的凸轮运动规律,利用Excel生成盘形凸轮轮廓的X、Y点阵坐标,然后将数据点导入到Auto-CAD中,再将生成的工程图,保存为dwg格式文件,最后将dwg文件导入到电火花线切割加工机床,按要求设定好加工工艺参数,直接驱动机床加工出盘型凸轮.
【总页数】5页(P97-101)
【作者】周敬勇;郑慧玲;杨光明;张啸
【作者单位】合肥职业技术学院, 安徽合肥 238000;井冈山大学机电工程学院, 江西吉安 343009;合肥职业技术学院, 安徽合肥 238000;合肥职业技术学院, 安徽合肥 238000
【正文语种】中文
【中图分类】TP391;TH112
【相关文献】
1.盘形凸轮的测绘与数控线切割加工 [J], 李文君
2.盘形凸轮的测绘与数控线切割加工 [J], 李文君
3.基于ADAMS/View的负半径滚子推杆盘形凸轮轮廓设计及运动仿真 [J], 高玉鸿;沈承楠
4.基于Excelize函数库实现Excel文件的自动读写操作 [J], 李琨;石晓明;贾立伟
5.基于Excelize函数库Excel多关键字排序算法的设计与实现 [J], 李琨;贾立伟;石晓明
因版权原因,仅展示原文概要,查看原文内容请购买。
运用AutoCAD设计凸轮轮廓曲线

运用AutoCAD设计凸轮轮廓曲线
齐真;黄皓
【期刊名称】《机电技术》
【年(卷),期】2009(032)003
【摘要】本文介绍了利用AutoCAD设计凸轮轮廓曲线的方法,该方法可提高设计精度和效率,同时也解决了手工绘制凸轮轮廓曲线误差较大的问题.
【总页数】3页(P10-12)
【作者】齐真;黄皓
【作者单位】武汉职业技术学院;武汉职业技术学院
【正文语种】中文
【中图分类】TP391.72;TH132.47
【相关文献】
1.基于AutoCAD的凸轮轮廓曲线的设计 [J], 赵亮培
2.AutoCAD中凸轮轮廓曲线的绘制与设计 [J], 肖辉进;曾强
3.基于AutoCAD凸轮轮廓曲线设计 [J], 张惠茹
4.基于AutoCAD的凸轮轮廓曲线设计方法研究 [J], 黄永玉;张建育
5.基于AutoCAD与Excel的凸轮轮廓曲线设计 [J], 郑彬;尧遥
因版权原因,仅展示原文概要,查看原文内容请购买。
用AUTO LISP设计凸轮轮廓

用AUTO LISP设计凸轮轮廓
陈启梁
【期刊名称】《化工装备技术》
【年(卷),期】1989(010)004
【摘要】本文讨论用Auto LISP语言开发机械CAD的方法。
以对心滚子凸轮为例,提出编写绘制其轮廓曲线源程序的方法。
程序首先输入参数并对它进行处理,接着计算理论的和实际的轮廓,最后调用Auto CAD的命令函数绘制轮廓曲线。
【总页数】5页(P12-16)
【作者】陈启梁
【作者单位】无
【正文语种】中文
【中图分类】TH112.2
【相关文献】
1.Auto CAD环境下的凸轮轮廓的图解法设计 [J], 张晓伟
2.基于Auto LISP的膨胀弯设计流程程序化 [J], 周大林;潘东民
3.基于Auto Lisp的蜗轮蜗杆传动的软件设计 [J], 李滟泽
4.Auto Lisp程序设计语言及其应用讲座(四):第八节 Lisp表处理函数 [J], 茹志富
5.Auto CAD环境下的凸轮轮廓的图解法设计 [J], 张晓伟
因版权原因,仅展示原文概要,查看原文内容请购买。
利用CAD画凸轮机构
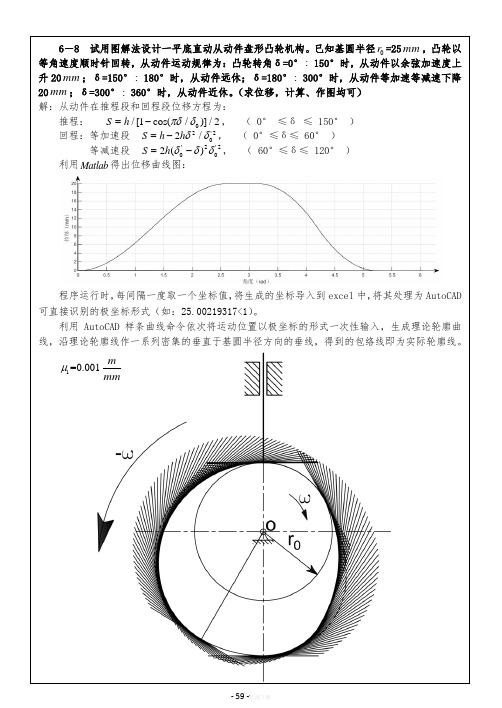
精品文档
6-8 试用图解法设计一平底直动从动件盘形凸轮机构。
已知基圆半径0r =25mm ,凸轮以等角速度顺时针回转,从动件运动规律为:凸轮转角δ=0°:150°时,从动件以余弦加速度上升20mm ;δ=150°:180°时,从动件远休;δ=180°:300°时,从动件等加速等减速下降20mm ;δ=300°:360°时,从动件近休。
(求位移,计算、作图均可) 解:从动件在推程段和回程段位移方程为: 推程: 0/[1cos(/)]/2S h πδδ=-, ( 0° ≤δ ≤ 150° ) 回程:等加速段 2'202/S h h δδ=-, ( 0°≤δ≤ 60° ) 等减速段 '2'2002()S h δδδ=-, ( 60°≤δ≤ 120° ) 利用Matlab 得出位移曲线图: 程序运行时,每间隔一度取一个坐标值,将生成的坐标导入到excel 中,将其处理为AutoCAD 可直接识别的极坐标形式(如:25.00219317<1)。
利用AutoCAD 样条曲线命令依次将运动位置以极坐标的形式一次性输入,生成理论轮廓曲线,沿理论轮廓线作一系列密集的垂直于基圆半径方向的垂线,得到的包络线即为实际轮廓线。
1=0.001μm mm
精品文档
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧借Excel在AutoCAD中设计凸轮轮廓
曲线
摘要:本文介绍一种借用EXCEL应用程序来计算并保存数据,并与CAD精确绘图巧妙地结合,设计凸轮轮廓曲线的方法,该方法也可用于其它二
维或三维曲线的绘制中。
论文毕业论文关键词:凸轮轮廓曲
线 AutoCAD 图解法1.问题的提出本文以设计二维凸轮轮廓曲线为例,
介绍一种一般操作者就能方便做到的,借用EXCEL应用程序来计算并保存数据,并与AutoCAD精确绘图巧妙地结合,绘制二维或三维非规则曲线的方法,以供大家参考。
2.概述在凸轮机构中,最常用的就是平面凸轮机构,要设计平面凸轮的轮廓曲线。
设计方法通常有图解法和解析法两种。
作图法简便易行、直观,作图误差较大,精度较低,适用于低速对从动件运动规律要求不高的一般精度凸轮设计;对于精度要求高的高速凸轮、靠模凸轮等,必须用解析法列出凸轮的轮廓曲线方程,用计算机辅助设计精确地设计凸轮机构。
我们沿用原有的图解法思路,使用CAD作为工具,两者的联合运用,能产生意想不到的更简单、直接、方便的处理方法。
在这种基于AutoCAD的图解法基础上,利用AutoCAD与其它文档交换信息和数据的功能,对于一些计算量较大输入点较多的图形,与EXCEL应用程序相结合,使作图更加简便快捷。
如设计下面的偏置滚子从动件盘形凸轮轮廓曲线,已知偏距e=10㎜,基圆半径r0=40㎜,行程h=25㎜,滚子半径rT=10㎜。
凸轮以角速度ω顺时针转动,从动件的运动规
律为:运动阶段1,推程Φ=180°、凸轮转角φ(°)为0~180,运动形式:等加速-等减速运动,运动方程方程:s=(2h/Φ2)φ2=(2*25/1802)φ
(0≤φ≤90)或s=h-2h(Φ-φ)2/Φ2=25-2*25*(180-
φ)2/1802(90≤φ≤180)运动阶段2,远休止ΦS=30°、凸轮转角φ(°)为180~210,运动形式:静止不动,运动方程方程: s=h=25
(180≤φ≤210)运动阶段3,回程Φ=90°、凸轮转角φ(°)为210~300,运动形式:等加速-等减速运动,运动方程方程: s= h-(2h/Φ’2)/φ’2=25-(2*25/180)2/(φ-210)2(180≤φ≤210)或s=2h(Φ’-
φ’)2/Φ’2=2*25*(90-(φ-210))2/902(180≤φ≤210)运动阶段4,远休
止ΦS=60°、凸轮转角φ(°)为300~360,运动形式:静止不动,运动方程
方程: s=0(300≤φ≤360)3、解题思路要使基于CAD技术的图解法充分发挥软件精确、高效绘图的作用,就要首先改进原来的作图方法。
图解法和解析法其本质完全相同,只是求解手段、求解过程不同,这里我们不用作图法确定曲线上点的方法,而是直接利用解析法里凸轮轮廓曲线的极坐标方程,求出凸轮轮廓曲线上若干个点(越多曲线越准确)的极坐标值(ρ,θ),再用spline (绘制样条曲线)命令,输入各点坐标值,作出凸轮的轮廓曲线。
如果是滚子从动件,得到理论轮廓线后,直接用offset(偏移)命令,输入滚子半径即可得到凸轮的实际轮廓曲线。
这里有两个问题需要解决。
首先是计算,为了得到更为准确的曲线,取点要尽量多,求这些点的极坐标值是一个很大的计算量,如何计算,计算后数据保存在哪里?其次是绘制曲线时点的坐标的输入,如果一个个
输入要输二十多次,非常费时而且很容易出错。
4、解决办法4.1数据的计算EXCEL是我们大家比较熟悉的应用程序,可以执行计算、分析信息并管理表格等,我们就用它来进行计算和保存数据。
按从动件的运动规律所给数据,由于凸轮轮廓曲线要对应推程运动角(Φ)、远休止角(ΦS)、回程运动角(Φ’)、近休止角(Φ’S)四个部分。
根据运动规律,推程运动角(Φ)和回程运动角(Φ’)对应的是不规则的二维曲线,远休止角(ΦS)和近休止角(Φ’S)对应的是正圆弧,我们都用SPLINE命令绘制。
为使曲线尽量准确,各段都要均分为若干份。
推程运动角(Φ)和回程运动角(Φ’)因为对应角都较大各分成8分共16个点;远休止角(ΦS)较小分成2份共,近休止角(Φ’S)分成4份共6个点,合计共取22个点。
先把这些数据输入EXCEL表格,按从动件的运动规律所给数据计算各点对应于基圆的位移值S、运动过程中通过各分点的导路方向与基圆半径的夹角β及起始位置点B0对应的夹角β0,凸轮轮廓曲线上各点对应极半径ρ和夹角θ等,最后才能合成各点的极坐标值。
这个过程计算量比较大,但无论采用何种方法设计,初始数据的取得都要经过计算,计算过程中所用公式及各参数的含义请参阅相关资料,因篇幅有限,这里不多作说明。
4.2极坐标的合成如图2所示,经过计算得到极半径ρ和夹角θ的值后,要合并成极坐标(ρ<θ)的形式。
使用连接运算符即“与”号(&)连接F列和G列两个数字串,两数字串中间还要用表示角度的符号“<”连接,操作方法如下:在H2单元格内输入公式“=A2&“<”&B2”,并按下Enter键,H2中就出现了一对极坐标值,再用鼠标拖动的方法将H2的的公式进行复制,就可以得到一组极坐标值。
这就是我们需要的凸轮轮廓曲线上各点的极坐标,将数据保存备用。
如果引号中间括起的是“,”号,就可以得到直角坐标的形式,在以直角坐标绘制曲线时可用。
以此类推开去,这样合并或连接,可得到任何你需要的数据。
4.3数据的输入,理论轮廓曲线的形成选出凸轮轮廓曲线上的点的极坐标值,即图中H列数据,将其复制到剪贴板上,可用Excel中的复制按钮或者直接按下
Ctrl+C键来完成此工作。
打开AutoCAD,在命令行处键入spline(绘制样条曲线)命令,出现提示:"输入第一点或[对象(O)]",在此位置处点击鼠标右键,从弹出的菜单中选择“粘贴”菜单项,这样在Excel中的极坐标值就传送到了AutoCAD中,并自动连接成曲线,单击鼠标右键或按下Enter键,取消继续画线状态,你需要的曲线就立刻出现在你面前,既简捷又不会出错,比一次次输入点的坐标值不知要快上了多少倍。
4.4实际轮廓曲线的形成如果是尖顶从动件,上面的曲线即为所求凸轮的轮廓曲线。
对于滚子从动件,我们得到理论轮廓线后,直接用offset(偏移)命令,出现提示:“指定偏移距离或[通过(T)]<通过>:”,输入滚子半径rT=10㎜,选择轮廓曲线作为偏移对象,指定内侧为偏移方向,即可得到凸轮的实际轮廓曲线。
4.5其它需要解决的问题如果需要表示曲线及基圆上各分点等,可以依照上述方法推广,在EXCEL表格中得出各分点的极坐标,在CAD中设置点样式用绘制点的命令一次输入各点坐标值即可。
凸轮的基圆、偏距圆等,用相应命令绘制,非常简单,不必多说。
该方法还可推广到绘制其它二维或三维曲线。
如渐开线、阿基米德螺旋线、摆线等二维曲线。
三维曲线如绘制三维螺旋线也属此类问题,可以先在EXCEL表格中得到螺旋线的柱面坐标值如图3所示,这用上面的方法也不难得到,然后再用spline命令将在EXCEL表格中得到的各分点坐标值粘贴过来就可完成三维螺旋线的绘制,如果需要多圈,再复制或阵列即可。
上述方法方便快捷,简单易行,不需任何编程,对.于不太熟悉CAD二次开发的用户是一种快速绘制二维或
三维曲线的好办法。
参考文献:[1]陈立德机械设计基础 (第2版) 北京高等教育出版社[M] 2004.7 62-72[2]张帆等 AutoCAD辅助设计专家北京清华大学出版社[M] 2005.2 366-369[3]王有良、唐跃
刚 AutoCAD开发与应用[J] 山东大学学报 2005,。
