解析几何第四版吕林根课后习题答案第三章
解析几何第四版吕林根 期末复习 课后习题(重点)详解

第一章 矢量与坐标§1.3 数量乘矢量4、 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线,又∵B 为公共点,从而A 、B 、D 三点共线.6、 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点,证明:三中线矢量AL , BM ,可 以构成一个三角形.证明: )(21AC AB AL +=)(21+=)(21CB CA CN +=0)(21=+++++=++∴7.、设L 、M 、N 是△ABC 的三边的中点,O 是任意一点,证明 ++=OL +OM +ON .[证明] += MB OM OB += NC ON OC +=)(OM +++++=++∴ =)(CN BM AL ON OM OL ++-++ 由上题结论知:0=++CN BM AL ON OM OL OC OB OA ++=++∴ 从而三中线矢量BM ,,构成一个三角形。
8.、如图1-5,设M 是平行四边形ABCD 的中心,O 是任意一点,证明OA +OB ++OD =4OM .[证明]:因为OM =21(OA +), OM =21(OB +), 所以 2OM =21(OA +OB +OC +) 所以OA +OB ++OD =4OM .10、 用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.图1-5证明 已知梯形ABCD ,两腰中点分别为M 、N ,连接AN 、BN . →→→→→→++=+=DN AD MA AN MA MN ,→→→→→→++=+=CN BC MB BN MB MN ,∴ →→→+=BC AD MN ,即§1.4 矢量的线性关系与矢量的分解3.、设一直线上三点A , B , P 满足AP =λ(λ≠-1),O 是空间任意一点,求证:OP =λλ++1[证明]:如图1-7,因为=-OA ,PB =OB -,所以 -OA =λ (OB -),(1+λ)OP =+λ,从而 OP =λλ++1OB.4.、在ABC ∆中,设,1e =2e =.(1) 设E D 、是边BC 三等分点,将矢量,分解为21,e e 的线性组合; (2)设AT 是角A 的平分线(它与BC 交于T 点),将分解为21,e e 的线性组合解:(1)()12123131,e e e e -==-=-= , 2111231323131e e e e e BD AB AD +=-+=+=,同理123132e e AE +=(2)因为||||TC =||11e e ,且 BT 与方向相同, 所以 BT ||21e e .由上题结论有AT ||||1||212211e e e e e +||||212112e e e e e e +.5.在四面体OABC 中,设点G 是ABC ∆的重心(三中线之交点),求矢量对于矢量,,,的分解式。
解析几何第四版吕林根课后习题答案第三章

解析几何第四版吕林根课后习题答案第三章第三章平面与空间直线§3.1 平面的方程1.求下列各平面的坐标式参数方程和一般方程:( 1 )通过点M 1 (3,1, 1) 和点 M 2 (1, 1,0) 且平行于矢量{ 1,0,2} 的平面( 2 )通过点M 1(1, 5,1) 和 M 2 (3,2,2) 且垂直于xoy坐标面的平面;( 3)已知四点A(5,1,3) , B(1,6,2), C (5,0,4)D ( 4,0,6) 。
求通过直线AB且平行于直线CD 的平面,并求通过直线AB 且与ABC 平面垂直的平面。
解:(1)M1M 2{2,2,1} ,又矢量{1,0,2} 平行于所求平面,故所求的平面方程为:x32u vy12uz1u2v一般方程为: 4x 3y2z70( 2)由于平面垂直于xoy 面,所以它平行于z 轴,即 { 0,0,1} 与所求的平面平行,又M 1M 2{ 2,7, 3} ,平行于所求的平面,所以要求的平面的参数方程为:x 12uy 5 7uz 1 3u v一般方程为:7( x 1) 2( y 5) 0 ,即 7x 2 y 170 。
(3)(ⅰ)设平面通过直线AB ,且平行于直线CD :AB{ 4,5, 1} , CD { 1,0,2}从而的参数方程为:x54u vy15uz3u2v一般方程为:10 x9 y 5z 74 0 。
(ⅱ)设平面通过直线 AB ,且垂直于ABC 所在的平面AB{ 4,5, 1} AB AC { 4,5, 1} { 0, 1,1} {4,4,4} 4{1,1,1}均与平行,所以的参数式方程为:x54u vy15u vz3u v一般方程为: 2x y3z 2 0 .2.化一般方程为截距式与参数式:: x 2y z 40 .解:与三个坐标轴的交点为:( 4,0,0), (0 2,0), (0,0,4) ,所以,它的截距式方程为:x y z1. 424又与所给平面方程平行的矢量为:{ 4,2,0}, { 4,0,4} ,所求平面的参数式方程为:x 4 2u vy uz v3. 证明矢量v{ X ,Y, Z} 平行与平面Ax By Cz D 0 的充要条件为:AX BY CZ 0.证明:不妨设 A 0,则平面 Ax By Cz D0的参数式方程为:x D B Cv AuyA A uz v故其方位矢量为:{B,1,0}, {,0,1} ,A A从而 v 平行于平面 Ax By Cz D0 的充要条件为:B Cv ,{,1,0}, {,0,1} 共面A AX Y ZB 0 01AC 1AAX BY CZ0 .4. 已知连接两点 A(3,10, 5), B(0,12, z) 的线段平行于平面 7x 4 y z 10 ,求 B 点的 z坐标 .解:AB { 3,2,5 z}而 AB 平行于 7 x 4 y z 1 0由题 3知:( 3)72 4( z 5) 0从而 z18 .5. 求下列平面的一般方程 .⑴通过点 12, 1,1 和3, 2,1 且分别平行于三坐标轴的三个平面;⑵过点3,2, 4 且在 x 轴和 y 轴上截距分别为2 和 3的平面 ;⑶与平面 5x y 2z 30 垂直且分别通过三个坐标轴的三个平面;⑷已知两点 1 3, 1,2,24, 2, 1,求通过1 且垂直于1 ,2的平面 ;⑸原点在所求平面上的正射影为2,9, 6 ;⑹求过点13, 5,1 和24,1,2 且垂直于平面 x 8 y 3z 1 0的平面 . 解: 平行于 x 轴的平面方程为x 2y1 z 11 1 0 0 . 即 z1 0 .1同理可知平行于y 轴 , z 轴的平面的方程分别为z 1 0, xy 1 0 .⑵设该平面的截距式方程为x y z 1, 把点3,2,2423c4 代入得 c19故一般方程为 12 x 8y 19 z 24 0 .⑶若所求平面经过x 轴,则0,0,0 为平面内一个点 ,5,1, 2 和 1,0,0 为所求平面的方位矢量,x 0 y 0 z 0∴点法式方程为51 2 01∴一般方程为 2 y z0 .同理经过 y 轴 , z 轴的平面的一般方程分别为2x 5z 0, x 5 y 0 .⑷1 21, 1, 3 .12 垂直于平面,∴该平面的法向量 n1, 1, 3 , 平面通过点13, 1,2 , 因此平面的点位式方程为x 3y 13 z20.化简得 xy 3z 2 0 .(5)op 2,9, 6 .pop4 81 36 11.opp n 0 11 cos , cos , cos2,9,6 .∴ cos2,cos9,cos 6 .11则该平面的法式方程为2 96z 11 0.:xy1111 11既 2x 9 y 6z 121 0. (6)平面 x8y3z 1 0 的法向量为 n 1, 8,3 ,M 1M 21,6,1 ,点从 4,1,2x 4 y 1 z 28 31 8 3 0,则 A写出平面的点位式方程为626,16 11B3 1 2, C1 3 14, D26474 ,1 11 1则一般方程 Ax ByCz D 0, 即: 13 x y 7 z 37 0.6.将下列平面的一般方程化为法式方程。
《解析几何》(第四版)吕林根 许子道 编第3章平面与空间直线3.2平面与点的相关位置

容易看出,点与平面间的离差 :
(3.2-1)
当且仅当点
M
和原点在平面
0
的不同侧
(图3
4),
0; 在同一侧(图3 5) 0;
当且仅当点
M
在平面
0
上时,
0.
z
R
M0
P
n
r0
o
q
Q
y
zபைடு நூலகம்
P
o n
R
q
r0
Q
M0
y
x
图3-4
x
图3-5
显然, 即是点M0与平面间的距离d,即
d,
定理3.2.1
MM , M 为垂足,
M
P为上任一点, 则总有
图3-3
MM MP ,
当且仅当点P与M 重合
P
M
时,式中等号成立,所以MM 为点M与平面的距离.
点关于平面的离差
定义3.2.2 若自点M0到平面引垂线,其垂足为
Q, 则QM0在的单位法向量n上的射影叫点M0与
间的离差, 记作
Pr
j
n
QM
0
间的离差与距离, 求出该平面的法式方程,问题迎刃而解.
例 1 求两平面 z x 2y 1, 3x 6y 3z 4间的距离.
解 先判断两平面是否平行.
n1
(1,2, 1),
n2
(3,6,
3),
1 2 1 3 6 3 n1 // n2 .
在第一个平面内任取一点,比如(0,0,1),
则点M
1,
M
2在由
1
,
所构成的相邻的二面角
2
内;
如图(3 8).
解析几何_吕林根_许子道_第四版_课后习题解答
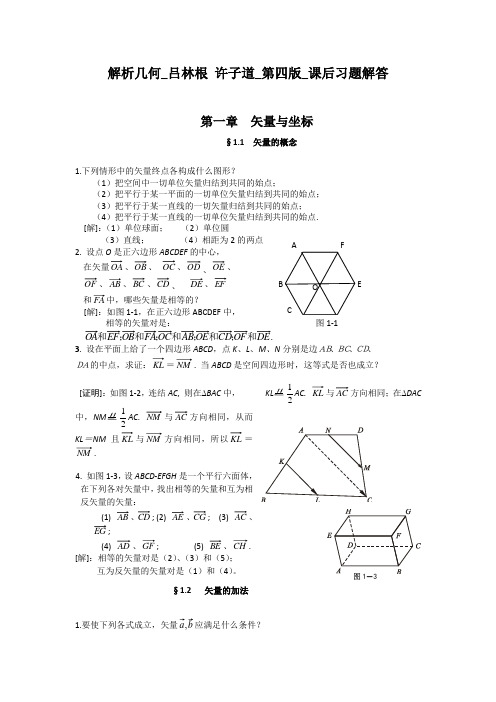
解析几何_吕林根 许子道_第四版_课后习题解答第一章 矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点; (3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点. [解]:(1)单位球面; (2)单位圆(3)直线; (4)相距为2的两点2. 设点O 是正六边形ABCDEF 的中心,在矢量OA 、OB 、 OC 、OD 、OE 、 OF 、AB 、BC 、CD 、 DE 、EF 和FA 中,哪些矢量是相等的?[解]:如图1-1,在正六边形ABCDEF 中,相等的矢量对是: 图1-1 .DE OF CD OE AB OC FA OB EF OA 和;和;和;和;和3. 设在平面上给了一个四边形ABCD ,点K 、L 、M 、N 分别是边AB、BC、CD、DA的中点,求证:KL =NM . 当ABCD 是空间四边形时,这等式是否也成立?[证明]:如图1-2,连结AC , 则在∆BAC 中,21AC. KL 与AC 方向相同;在∆DAC 中,21AC . NM 与AC 方向相同,从而KL =NM 且KL 与NM 方向相同,所以KL =NM .4. 如图1-3,设ABCD -EFGH 是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB 、CD ; (2) AE 、CG ; (3) AC 、EG ;(4) AD 、GF ; (5) BE、CH . [解]:相等的矢量对是(2)、(3)和(5); 互为反矢量的矢量对是(1)和(4)。
§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件?E(1=+ (2+=+ (3-=+ (4+=- (5=[解]:(1)b a ,-=+(2)b a ,+=+(3≥且b a ,-=+ (4)b a ,+=(5)b a ,≥-=-§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解 ⑴→→→→→→→→→→→→→→-=+-+---+=-⋅+--⋅-ay b x b y a y b x a x b y a y b x a x b a y x b a y x 22)()()()(⑵ →→→→→→→→→→+=+-+-+=+3132132142232e e e e e e e e b a ,→→→→→→→→→→→-+-=+---+=-321321321342)223(2e e e e e e e e e b a , →→→→→→→→→→→-+-=+---+=-3213213217103)223(2)2(323e e e e e e e e e b a . 2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF .解 →→→→→→→→→→→-+=-+-+=+=c b a c a c b a AB CD EF 533)2(21)865(212121.3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线,又∵B 为公共点,从而A 、B 、D 三点共线.4 在四边形ABCD 中,→→→+=b a AB 2,→→→--=b a BC 4,→→→--=b a CD 35,证明ABCD 为梯形.证明∵→→→→→→→→→→→→→=--=-+--++=++=BC b a b a b a b a CD BC AB AD 2)4(2)35()4()2( ∴→AD ∥→BC ,∴ABCD 为梯形.6. 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点,证明:三中线矢量AL , BM ,CN 可 以构成一个三角形.[证明]: )(21AC AB AL +=)(21BC BA BM +=)(21CB CA CN +=0)(21=+++++=++∴CB CA BC BA AC AB CN BM AL从而三中线矢量CN BM AL ,,构成一个三角形。
《解析几何》(第四版)吕林根 许子道 编第3章平面与空间直线3.1平面的方程

M0 b
e3
r0
r
o e1
e2
M a
y
程,u, v为参数.
图3-1
若设点
M0 r0
(x0 , y0
x0 ,
, z0 y0 ,
), M
z0 ,
(x , r
y, x
z), 则 , y, z
,
再设
a
X 1 , Y1 ,
Z1,
b X 2 ,Y2 , Z2,
则由(3.11)得
x y
x0 y0
并设点
M (x, y, z)为上任一点(图3 2), 则
r
x
,
y,
z
OM
,
ri
OM i
xi ,
yi , zi ,
(i 1,2,3)
a M1M 2 r2 r1
x2
x1,
y2
y1,
z2
z1,
b M1M3 r3 r1
x3 x1, y3 y1, z3 z1,
x
z
M2
e3
rM1 r12r3 r
o e1
e2
M3 M
y
图3-2
故平面的向量式参数方程 r r1 u(r2 r1) v(r3 r1),
(3.1-5)
坐标式参数方程
x y
x1 y1
u ( x2 u( y2
x1 ) y1 )
v( x3 v( y3
x1 ) , y1 ) ,
z z1 u(z2 z1) v(z3 z1).
过z轴( y轴或x轴); (3) A, B,C中有两个为0,则 D 0, B C 0(A C 0 或 A B 0) 平面
(3.110)平行于yz面(xz面或xy面); D 0, B C 0(A C 0 或 A B 0) 平面
3-1解析几何吕林根第四版

R(0,0,c)(其中a 0,b 0,c 0),求此平面方程.
z
将 A D, B D, C D,
c
a
b
c
代入所设方程
Ax By Cz D 0,
o
xa
y
b
得
x y z 1 平面的截距式方程
a bc
x轴上截距 y轴上截距 z 轴上截距
5. 平面的截距式方程
若已知三点为平面与三坐标的交点 M1 a,0,0, M2 0,b,0,
化简得
n1
n2
2x 3 y z 6 0.
nr
例 求过点(1,0,-1), 且平行于向量 n1 {2,1,1} 和 n1 {1, 1, 0} 的平
面方程.
解 取所求平面法向量 n n1 n2 {1,1, 3},
所求平面方程为
1 ( x 1) 1 ( y 0) 3 ( z 1) 0, n1
为所求平面之法向.
故得平面方程为: r
( x x1, y y1, z z1) n 14( x 2) 9( y 1) (z 4)
14x 9 y z 15 0
或
r ( x x2, y y2, z z2) n
14( x 1) 9( y 3) (z 2)
14x 9 y-z 15 0
所以, 点B与C分居在平面的两侧.
的方位向量。
ur uur ur
uuuuur ur
在空间取仿射坐标系 O;e1, e2, e3 ,并设点 M0 的向 OM0 r0 ,平面
z
uuuur r
上任意一点 M 的向径为 OM r ,
b
r ur r r
M0
a
M
则平面 的向量式参数方程为 r r0 ua vb
《解析几何》(第四版)吕林根 许子道 编第3章平面与空间直线3.1平面的方程

x0 y0 z0 D X1 Y1 Z1 ,
因a,
b 不共线,
X2 所以A,
B,
Y2 Z2 C不全为零
,
这表明
:
任一平面都可用关于 x, y, z的三元一次方程表示 .
反之,可证 : 任一关于x, y, z的一次方程 (3.110)都表示平面.
事实上,因A, B, C不全为零,不妨设A 0,则(3.110)
在空间,
取仿射坐标系
O;e1
,
e2
,
e3
,
并设点
M
的向径
0
OM
0
r0
,
平面上任一点
M的向径OM
r
(图3
1),
则
a,
点 M在平面上 M
b不共线,由 定理 1.4.2知
0M
, a, z
b共面.
又 即
MM0 M0 Muarvrb0 ,, r r0 ua vb.
(3.1-1)
平面 的向量式参数方 x
2 11 3 3 2
问题:说明上式的由来 .
将方程组(*)变形为
A 5B D, 3A 2B D.
由克莱姆法则 , 有
D 5 5 1
D 2 2 1
A
D,
1 5 1 5
32 32
1 D 1 1 B 3 D 1 3 D,
1 5 1 5 32 32
5 1 1 1
2 1 13
A:B:D
D:
616
化简得 1 1 1 , 令 1 1 1 t 6a b 6c 6a b 6c
a 1 , b 1, c 1 ,
6t
t
6t 代入体积式
1 1 1 1 1 t 1 ,
解析几何第三章习题及解答

第三章 常见曲面习题3.11.证明:如果2220a b c d ++->,那么由方程2222220x y z ax by cz d ++++++=给出的曲面是一球面,求出它的球心坐标和半径。
证明:将方程配方得222222()()()x a y b z c a b c d +++++=++-,由2220a b c d ++->,得到方程表示球心是(,,)a b c ---2.求过三点(3,0,0),(0,2,0),(0,0,1)的圆的方程。
解:空间中的圆可由过三点(3,0,0),(0,2,0),(0,0,1)的一个球面和一个平面的交线表示,设过该三点的球面方程为2220x y z ax by cz d ++++++=,得到930,420,10a d b d c d ++=⎧⎪++=⎨⎪++=⎩球面方程为22294(1)032d dx y z x y d z d ++++---++=,其中d 任意。
过该三点的平面方程是132x yz ++=,所以所求圆的方程可以为 2226()2(9)3(4)6(1)60,23660x y z d x d y d z d x y z ⎧++-+-+-++=⎨++-=⎩ 其中d 任意。
3.证明曲线24224324,1,(,)1,1t x t t t y t t t t z t t ⎧=⎪++⎪⎪=∈-∞+∞⎨++⎪⎪=⎪++⎩在一球面上,并此球面方程。
证明:因为曲线满足2322222224242422242424()()()111()(1)11tt t x y z t t t t t t t t t t y t t t t++=++++++++=++==++++即22211()24x y z +-+=,所以曲线在一个球面上。
4.适当选取坐标系,求下列轨迹的方程(1)到两定点距离之比等于常数的点的轨迹; (2)到两定点距离之和等于常数的点的轨迹; (3)到定平面和定点等距离的点的轨迹。
解析几何第四版吕林根课后习题答案

第三章 平面与空间直线§ 平面的方程1.求下列各平面的坐标式参数方程和一般方程:1通过点)1,1,3(1-M 和点)0,1,1(2-M 且平行于矢量}2,0,1{-的平面2通过点)1,5,1(1-M 和)2,2,3(2-M 且垂直于xoy 坐标面的平面;3已知四点)3,1,5(A ,)2,6,1(B ,)4,0,5(C )6,0,4(D ;求通过直线AB 且平行于直线CD 的平面,并求通过直线AB 且与ABC ∆平面垂直的平面; 解: 1 }1,2,2{21--=M M ,又矢量}2,0,1{-平行于所求平面, 故所求的平面方程为: 一般方程为:07234=-+-z y x2由于平面垂直于xoy 面,所以它平行于z 轴,即}1,0,0{与所求的平面平行,又}3,7,2{21-=M M ,平行于所求的平面,所以要求的平面的参数方程为:一般方程为:0)5(2)1(7=+--y x ,即01727=--y x ; 3ⅰ设平面π通过直线AB,且平行于直线CD : }1,5,4{--=AB ,}2,0,1{-=CD 从而π的参数方程为:一般方程为:0745910=-++z y x ;ⅱ设平面π'通过直线AB,且垂直于ABC ∆所在的平面∴ }1,5,4{--=AB , }1,1,1{4}4,4,4{}1,1,0{}1,5,4{==-⨯--=⨯AC AB均与π'平行,所以π'的参数式方程为: 一般方程为:0232=--+z y x . 2.化一般方程为截距式与参数式:042:=+-+z y x π.解: π与三个坐标轴的交点为:)4,0,0(),0,20(),0,0,4(--, 所以,它的截距式方程为:1424=+-+-z y x . 又与所给平面方程平行的矢量为:}4,0,4{},0,2,4{-,∴ 所求平面的参数式方程为:3.证明矢量},,{Z Y X v =平行与平面0=+++D Cz By Ax 的充要条件为:0=++CZ BY AX .证明: 不妨设0≠A ,则平面0=+++D Cz By Ax 的参数式方程为: 故其方位矢量为:}1,0,{},0,1,{AC A B --,从而v 平行于平面0=+++D Cz By Ax 的充要条件为:v ,}1,0,{},0,1,{ACA B --共面⇔ ⇔0=++CZ BY AX . 4. 已知连接两点),12,0(),5,10,3(z B A -的线段平行于平面0147=--+z y x ,求B 点的z 坐标.解: }5,2,3{z AB +-= 而AB 平行于0147=--+z y x 由题3知:0)5(427)3(=+-⨯+⨯-z 从而18=z .5. 求下列平面的一般方程.⑴通过点()1,1,21-M 和()1,2,32-M 且分别平行于三坐标轴的三个平面; ⑵过点()4,2,3-M 且在x 轴和y 轴上截距分别为2-和3-的平面;⑶与平面0325=+-+z y x 垂直且分别通过三个坐标轴的三个平面; ⑷已知两点()()1,2,4,2,1,321--M -M ,求通过1M 且垂直于21,M M 的平面; ⑸原点O 在所求平面上的正射影为()6,9,2-P ;⑹求过点()1,5,31-M 和()2,1,42M 且垂直于平面0138=-+-z y x 的平面.解:平行于x 轴的平面方程为001011112=--+-z y x .即01=-z .同理可知平行于y 轴,z 轴的平面的方程分别为01,01=-+=-y x z . ⑵设该平面的截距式方程为132=+-+-c z y x ,把点()4,2,3-M 代入得1924-=c 故一般方程为02419812=+++z y x .⑶若所求平面经过x 轴,则()0,0,0为平面内一个点,{}2,1,5-和{}0,0,1为所求平面的方位矢量,∴点法式方程为001215000=----z y x ∴一般方程为02=+z y .同理经过y 轴,z 轴的平面的一般方程分别为05,052=-=+y x z x . ⑷{}2121.3,1,1M M --=M M →垂直于平面π,∴该平面的法向量{}3,1,1--=→n ,平面∂通过点()2,1,31-M , 因此平面π的点位式方程为()()()02313=--+--z y x . 化简得023=+--z y x . 5 {}.6,9,2-=→op∴ .116cos ,119cos ,112cos -===∂γβ 则该平面的法式方程为:.011116119112=--+z y x既 .0121692=--+z y x6平面0138=-+-z y x 的法向量为{}3,8,1-=→n ,{}1,6,121=M M ,点从()2,1,4写出平面的点位式方程为0161381214=----z y x ,则,261638-=-=A74282426,141131,21113-=++⨯-=====D C B ,则一般方程,0=+++D Cz By Ax 即:.037713=---z y x 6.将下列平面的一般方程化为法式方程; 解:.3-=D∴将已知的一般方程乘上.301=λ得法式方程.030330530230=-+-z y x()∴-=∴=.21.12λD 将已知的一般方程乘上.21-=λ得法式方程.0212121=-+-y x()∴-=∴=.1.2.3λD 将已知的一般方程乘上.1-=λ得法式方程.02=--x().91.0.4±=∴=λD 即91=λ或91-=λ将已知的一般方程乘上91=λ或.91-=λ得法式方程为0979494=+-z y x 或.0979494=-+-z y x 7.求自坐标原点自以下各平面所引垂线的长和指向平面的单位法矢量的方向余弦;解:().71.35.1=-=λD 化为法式方程为05767372=-++z y x 原点指向平面π的单位法矢量为,76,73,72⎭⎬⎫⎩⎨⎧=u 它的方向余弦为.76cos ,73cos ,72cos ===γβα原点o 到平面π的距离为.5=-=D P λ().31.21.2-==λD 化为法式方程为-07323231=--+-z y x 原点指向平面π的单位法矢量为,32,32,310⎭⎬⎫⎩⎨⎧--=n 它的方向余弦为122cos ,cos ,cos .333αβγ=-==-原点o到平面π的距离7.p D λ=-= 第20页8.已知三角形顶点()()()0,7,0,2,1,1,2,2,2.A B C --求平行于ABC 所在的平面且与她相距为2各单位的平面方程;解:设,.AB a AC b ==点()0,7,0.A -则{}{}2,6,1,2,9,2a b ==写出平面的点位式方程72610292x y z += 设一般方程0. 3.2,6,140.Ax By Cz D A B C D +++=∴====-< 则1. 2.7p D λλ==-=相距为2个单位;则当4p =时28.D =-当0p =时0.D =∴所求平面为326280.x y z -+-=和3260.x y z -+=9.求与原点距离为6个单位,且在三坐标轴,ox oy 与oz 上的截距之比为::1:3:2a b c =-的平面;解:设,3,2.0.a x b x c x abc =-==≠∴设平面的截距方程为 1.x y z a b c++= 即.bcx acy abz abc ++= 又原点到此平面的距离 6.d =6.=∴所求方程为7.32y zx -++= 10.平面1x y z a b c++=分别与三个坐标轴交于点,,.A B C 求ABC 的面积;解 (,0,0)A a , (0,,0)B b ,(0,0,)C c {},,0AB a b =-,{},0,AC a c =-.{},,AB AC bc ca ab ⨯=;2AB AC b ⨯=.∴S ABC11.设从坐标原点到平面的距离为;求证1.p p =∴= 从而有22221111.p a b c =++ § 平面与点的相关位置1.计算下列点和平面间的离差和距离: 1)3,4,2(-M , :π 0322=++-z y x ; 2)3,2,1(-M , :π 0435=++-z y x . 解: 将π的方程法式化,得:01323132=--+-z y x ,故离差为:311332431)2()32()(-=-⨯-⨯+-⨯-=M δ,M 到π的距离.31)(==M d δ2类似1,可求得0354353356355)(=-++-=M δ,M 到π的距离.0)(==M d δ2.求下列各点的坐标:1在y 轴上且到平面02222=--+z y 的距离等于4个单位的点; 2在z 轴上且到点)0,2,1(-M 与到平面09623=-+-z y x 距离相等的点; 3在x 轴上且到平面01151612=++-z y x 和0122=--+z y x 距离相等的点;解:1设要求的点为)0,,0(0y M 则由题意∴ 610=-y ⇒50-=y 或7.即所求的点为0,-5,0及0,7,0; 2设所求的点为),0,0(0z 则由题意知: 由此,20-=z 或-82/13; 故,要求的点为)2,0,0(-及)1382,0,0(-; 3设所求的点为)0,0,(0x ,由题意知: 由此解得:20=x 或11/43; 所求点即2,0,0及11/43,0,0;3.已知四面体的四个顶点为)4,1,1(),5,11,2(),3,5,3(),4,6,0(---C B A S ,计算从顶点S 向底面ABC 所引的高; 解:地面ABC 的方程为: 所以,高335426=+⨯--=h ;4.求中心在)2,5,3(-C 且与平面01132=+--z y x 相切的球面方程; 解:球面的半径为C 到平面π:01132=+--z y x 的距离,它为:142142814116532==+++⨯=R ,所以,要求的球面的方程为:56)2()5()3(222=++++-z y x .即:0184106222=-++-++z y x z y x .5.求通过x 轴其与点()5,4,13M 相距8个单位的平面方程;解:设通过x 轴的平面为0.By Cz +=它与点()5,4,13M 相距8个单位,从而228.481041050.B BC C =∴--=因此()()1235430.B C B C -+=从而得12350B C -=或430.B C +=于是有:35:12B C =或():3:4.B C =-∴所求平面为35120y z +=或340.y z -=6. 求与下列各对平面距离相等的点的轨迹. ⑴053407263=--=--+y x z y x 和; ⑵062901429=++-=-+-z y x z y x 和. 解: ⑴ ()0726371:1=--+z y x π 令()()53451726371--=--+y x z y x化简整理可得:0105113=+-z y x 与07010943=--+z y x . ⑵对应项系数相同,可求42614221'-=+-=+=D D D ,从而直接写出所求的方程:0429=-+-z y x .9 判别点M2 -1 1和N 1 2 -3在由下列相交平面所构成的同一个二面角内,还是在相邻二面角内,或是在对顶的二面角内 11:3230x y z π-+-=与2:240x y z π--+= 21:2510x y z -+-=与2:32610x y z π-+-= 解:1将M2 -1 1,N1 2 -3代入1π,得: 6123032630++-〉⎧⎨---〈⎩则M,N 在1π的异侧 再代入2π,得:221470143440+-+=〉⎧⎨-++=〉⎩∴MN 在2π的同侧 ∴MN 在相邻二面角内2将M2 -1 1N1 2 -3代入1π,得:4151902215180++-=〉⎧⎨---=-〈⎩则MN 在1π的异侧; 再代入2π,得:662113034181200++-=>⎧⎨---=-<⎩则MN 在2π的异侧∴ MN 在对顶的二面角内10 试求由平面1π:2230x y z -+-=与2π:32610x y z +--=所成的二面角的角平分方程,在此二面角内有点1, 2, -3解:设px y z 为二面角的角平分面上的点,点p 到12ππ的距离相等=5332190(1)234240(2)x y z x y z +--=⎧⎨---=⎩把点p 代入到12ππ上,10δ< 20δ> 在1上取点1850 0代入12ππ,''1200δδ>>; 在2上取点0 0 -6代入12ππ,""1200δδ<>∴2为所求,∴解平面的方程为:34240x y z ---=两平面的相关位置1.判别下列各对直线的相关位置: 10142=+-+z y x 与0324=--+z y x ; 20522=---z y x 与013=--+z y x ; 305426=--+z y x 与029639=--+z y x ;解:1 )1(:21:41)4(:2:1-=-, ∴ 1中的两平面平行不重合; 2 )1(:3:1)2(:)1(:2-≠--, ∴ 2中两平面相交; 3 )6(:3:9)4(:2:6-=-, ∴ 3中两平面平行不重合;2.分别在下列条件下确定n m l ,,的值:1使08)3()1()3(=+-+++-z n y m x l 和016)3()9()3(=--+-++z l y n x m 表示同一平面;2使0532=-++z my x 与0266=+--z y lx 表示二平行平面; 3使013=+-+z y lx 与027=-+z y x 表示二互相垂直的平面; 解:1欲使所给的二方程表示同一平面,则: 即:从而:97=l ,913=m ,937=n ; 2欲使所给的二方程表示二平行平面,则: 所以:4-=l ,3=m ;3欲使所给的二方程表示二垂直平面,则: 所以: 71-=l ;3.求下列两平行平面间的距离: 10218419=++-z y x ,0428419=++-z y x ; 207263=--+z y x ,014263=+-+z y x ; 解:1将所给的方程化为: 所以两平面间的距离为:2-1=1;2同1可求得两平行平面间的距离为1+2=3; 4.求下列各组平面所成的角: 1011=-+y x ,083=+x ;2012632=-+-z y x ,0722=-++z y x ; 解:1设1π:011=-+y x ,2π:083=+x∴ 4),(21πππ=∠或43π; 2设1π:012632=-+-z y x ,2π:0722=-++z y x218cos ),(121-=∠ππ或218cos ),(121--=∠πππ; 5. 求下列平面的方程:1 通过点()1,0,01M 和()0,0,32M 且与坐标面xOy 成060角的平面;2 过z 轴且与平面0752=--+z y x 成060角的平面. 解 ⑴ 设所求平面的方程为.113=++z b y x 又xoy 面的方程为z=0,所以21113110103160cos 222=+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⋅+⋅=b b ο 解得203±=b ,∴所求平面的方程为12633=+±+z yx , 即03326=-+±z y x⑵设所求平面的方程为0=+By Ax ;则21514260cos 22=+++±+=B A BA ο 3,038322BA B AB A =∴=-+或B A 3-= ∴所求平面的方程为03=+y x 或03=-y x .§ 空间直线的方程1.求下列各直线的方程:1通过点)1,0,3(-A 和点)1,5,2(-B 的直线; 2通过点),,(0000z y x M 且平行于两相交平面i π:)2,1(=i 的直线;3通过点)3,51(-M 且与z y x ,,三轴分别成︒︒︒120,45,60的直线;4通过点)2,0,1(-M 且与两直线11111-+==-z y x 和01111+=--=z y x 垂直的直线; 5通过点)5,3,2(--M 且与平面02536=+--z y x 垂直的直线; 解:1由本节—6式,得所求的直线方程为: 即:01553-=-=+z y x ,亦即01113-=-=+z y x ; 2欲求直线的方向矢量为: 所以,直线方程为:221102211022110B A B A z z A C A C y y C B C B x x -=-=-; 3欲求的直线的方向矢量为:{}⎭⎬⎫⎩⎨⎧-=︒︒︒21,22,21120cos ,45cos ,60cos ,故直线方程为:132511--=+=-z y x ; 4欲求直线的方向矢量为:{}{}{}2,1,10,1,11,1,1---=-⨯-, 所以,直线方程为:22111+==-z y x ; 5欲求的直线的方向矢量为:{}5,3,6--, 所以直线方程为:553362-+=--=-z y x ; 2.求以下各点的坐标: 1在直线381821-=-=-z y x 上与原点相距25个单位的点; 2关于直线⎩⎨⎧=+-+=+--03220124z y x z y x 与点)1,0,2(-P 对称的点;解:1设所求的点为),,(z y x M ,则: 又222225=++z y x即:222225)38()8()21(=+++++t t t ,解得:4=t 或762-所以要求的点的坐标为:)7130,76,7117(),20,12,9(---; 2已知直线的方向矢量为:{}{}{}3,6,62,1,24,1,1-=-⨯--,或为{}1,2,2-, ∴过P 垂直与已知直线的平面为:0)1(2)2(2=++--z y x ,即0322=-+-z y x ,该平面与已知直线的交点为)3,1,1(,所以若令),,(z y x P '为P 的对称点,则:221x +=,201y +=,213z+-= ∴7,2,0===z y x ,即)7,2,0(P ';3.求下列各平面的方程: 1通过点)1,0,2(-p ,且又通过直线32121-=-=+z y x 的平面; 2通过直线115312-+=-+=-z y x 且与直线 平行的平面; 3通过直线223221-=-+=-z y x 且与平面0523=--+z y x 垂直的平面; 4通过直线⎩⎨⎧=-+-=+-+014209385z y x z y x 向三坐标面所引的三个射影平面;解:1因为所求的平面过点)1,0,2(-p 和)2,0,1(-'p ,且它平行于矢量{}3,1,2-,所以要求的平面方程为: 即015=-++z y x ;2已知直线的方向矢量为{}{}{}5,3,11,2,11,1,2-=-⨯-, ∴平面方程为:即015211=-++z y x3要求平面的法矢量为{}{}{}13,8,11,2,32,3,2-=-⨯-,∴平面的方程为:0)2(13)2(8)1(=--+--z y x ,即09138=+--z y x ; 4由已知方程⎩⎨⎧=-+-=+-+014209385z y x z y x分别消去x ,y ,z 得到:0231136=+-z y ,079=+-z x ,06411=+-y x此即为三个射影平面的方程;4.化下列直线的一般方程为射影式方程与标准方程,并求出直线的方向余弦: 1⎩⎨⎧=---=+-+0323012z y x z y x 2⎩⎨⎧=+--=-+064206z y x z x3⎩⎨⎧==-+20x z y x解:1直线的方向数为:)5(:1:)3(1312:3221:2111--=------∴射影式方程为: ⎪⎩⎪⎨⎧-+-=--+--=59515253z y z x , 即⎪⎩⎪⎨⎧--=+=59515253z y z x ,标准方程为:z y x =-+=-51595352, 方向余弦为:35353553cos ±=±=α,35153551cos =-±=β,3555351cos ±=±=γ;2已知直线的方向数为:)4(:3:44201:2111:1410-=----,射影式方程为:⎪⎩⎪⎨⎧--+-=--+-=4184342444z y z x , 即⎪⎩⎪⎨⎧+-=+-=29436z y z x 标准方程为:z y x =--=--432916, 方向余弦为:4144411cos =-±=α,41344143cos =-±=β, 4144411cos ±=±=γ;3已知直线的方向数为:1:1:0)1(:)1(:00111:1011:0011=--=--, ∴射影式方程为: ⎩⎨⎧-==22z y x ,标准式方程为:z y x =+=-1202, 方向余弦为:0cos =α,21cos ±=β,21cos ±=γ;5. 一线与三坐标轴间的角分别为,,αβγ.证明222sin sin sin 2.αβγ++= 证 ∵222cos cos cos 1αβγ++=, ∴2221sin 1sin 1sin 1αβγ-+-+-=,即222sin sin sin 2.αβγ++=§ 直线与平面的相关位置1.判别下列直线与平面的相关位置:137423zy x =-+=--与3224=--z y x ; 2723z y x =-=与8723=+-z y x ; 3⎩⎨⎧=---=-+-01205235z y x z y x 与07734=-+-z y x ; 4⎪⎩⎪⎨⎧-=+-==4992t z t y t x 与010743=-+-z y x ; 解:1 0)2(3)2()7(4)2(=-⨯+-⨯-+⨯-, 而017302)4(234≠=-⨯--⨯-⨯,, 所以,直线与平面平行; 2 0717)2(233≠⨯+-⨯-⨯ 所以,直线与平面相交,且因为772233=--=, ∴ 直线与平面垂直;3直线的方向矢量为:{}{}{}1,9,51,1,22,3,5=--⨯-,0179354=⨯+⨯-⨯,而点)0,5,2(--M 在直线上,又07)5(3)2(4=--⨯--⨯, 所以,直线在平面上; 4直线的方向矢量为{}9,2,1-,∴直线与平面相交;2.试验证直线l :21111-=-=-z y x 与平面π:032=--+z y x 相交,并求出它的交点和交角;解: 032111)1(2≠-=⨯-⨯+-⨯∴ 直线与平面相交;又直线的坐标式参数方程为: ⎪⎩⎪⎨⎧+=+=-=t z t y t x 211设交点处对应的参数为0t ,∴10-=t ,从而交点为1,0,-1;又设直线l 与平面π的交角为θ,则:21662111)1(2sin =⨯⨯-⨯+-⨯=θ, ∴ 6πθ=;3.确定m l ,的值,使: 1直线13241zy x =+=-与平面0153=+-+z y lx 平行; 2直线⎪⎩⎪⎨⎧-=--=+=135422t z t y t x 与平面076=-++z my lx 垂直;解:1欲使所给直线与平面平行,则须: 即1=l ;2欲使所给直线与平面垂直,则须: 所以:8,4-==m l ;4.决定直线⎩⎨⎧=++=++00222111z C y B x A z C y B x A 和平面0)()()(212121=+++++z C C y B B x A A 的相互位置;解:在直线上任取),,(1111z y x M ,有:这表明1M 在平面上,所以已给的直线处在已给的平面上;5.设直线与三坐标平面的交角分别为.,,υμλ证明.2cos cos cos 222=++υμλ 证明 设直线与X,Y,Z 轴的交角分别为.,,γβα而直线与yoz,zox,xoy 面的交角依次为.,,γμλ那么,υπγμπβλπα-=-=-=2,2,2.而.1cos cos cos 222=++γβα∴.12cos 2cos 2cos 222=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-υπμπλπ从而有.2cos cos cos 222=++υμλ 6.求下列球面的方程1与平面x+2y+3=0相切于点()3,1,1-M 且半径r=3的球面;2 与两平行平面6x-3y-2z-35=0和6x-3y-2z+63=0都相切且于其中之一相切于点()1,1,5--M 的球面.解: ⑴⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=+=+=t z t y t x 323321311为过切点M 且垂直与已知平面的直线,显见32,32,31是这条直线的方向余弦. 取3=t ,则得3,2==y x ; 取3-=t ,则得5,1,0-=-==z y x .故所求球面有两个:()()()9132222=++-+-z y x ,与()()951222=++++z y x . ⑵t z t y t x 21,31,65--=--=+=为过点M 且垂直于两平面的直线,将其代入第二个平面方程,得2-=t ,反代回参数方程,得3,5,7==-=z y x .设球之中心为C ,半径为r ,则()()()()49112115,1,2,12222=--+--++=-r C .故所求球面方程为()()()49121222=-+-++z y x .空间直线的相关位置1.直线方程⎩⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A 的系数满足什么条件才能使:1直线与x 轴相交; 2直线与x 轴平行; 3直线与x 轴重合; 解:1所给直线与x 轴相交⇔ ∃ 0x 使0101=+D x A 且0202=+D x A⇔02211=D A D A 且 1A ,2A 不全为零;2 x 轴与平面01111=+++D z C y B x A 平行 又x 轴与平面02222=+++D z C y B x A 平行,所以 即021==A A ,但直线不与x 轴重合,∴ 21,D D 不全为零;3参照2有021==A A ,且021==D D ; 2.确定λ值使下列两直线相交: 1⎩⎨⎧=-++=-+-01540623z y x z y x λ与z 轴;2λ12111-=+=-z y x 与z y x ===+11; 解:1若所给直线相交,则有类似题1: 从而 5=λ;2若所给二直线相交,则 从而:45=λ;3.判别下列各对直线的相互位置,如果是相交的或平行的直线求出它们所在的平面;如果是异面直线,求出它们之间的距离;1⎩⎨⎧=-+=+-0623022y x z y x 与⎩⎨⎧=-+=--+01420112z x z y x ;2131833-=--=-z y x 与462733-=+=-+z y x ; 3⎪⎩⎪⎨⎧--=+==212t z t y tx 与5217441-+=-=-z y x ; 解:1将所给的直线方程化为标准式,为:-2:3:4=2:-3:-4 ∴二直线平行;又点)0,43,23(与点7,2,0在二直线上,∴矢量⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧--0,45,2110,432,237平行于二直线所确定的平面,该平面的法矢量为:{}{}19,22,50,45,2114,3,2--=⎭⎬⎫⎩⎨⎧⨯-,从而平面方程为:0)0(19)2(22)7(5=-+---z y x , 即 0919225=++-z y x ;2因为0270423113637833≠-=---++=∆,∴二直线是异面的;二直线的距离:{}{}30327031562704,2,31,1,34231133156222==++=-⨯----=d ;3因为0574121031=--=∆,但是:1:2:-1≠4:7:-5所以,两直线相交,二直线所决定的平面的法矢量为{}{}{}1,1,35,7,412,1--=-⨯-,∴平面的方程为:33++-z y x ;4.给定两异面直线:01123-==-z y x 与10211zy x =-=+,试求它们的公垂线方程;解:因为{}{}{}1,2,11,0,10,1,2--=⨯, ∴公垂线方程为:即⎩⎨⎧=--+=-+-022220852z y x z y x ,亦即⎩⎨⎧=--+=-+-010852z y x z y x ;5.求下列各对直线间的角 1 .61932256231+=-=-=+=-z y x z y x 与 2.02302640220243⎩⎨⎧=+-=--+⎩⎨⎧=-+=--z y z y x z y x z y x 与解 1 777236814436912546cos 222222212121212121±=++++++±=++++++±=z y x z y x z z y y x x θ ∴ .7772arccos 7772arccos -=πθ或(2) 直线43412630230264,11210:0220243+=+=⎩⎨⎧=+-=--+=⎩⎨⎧==-+=--z y x z y z y x zy x z y x z y x 的对称式方程为:的对称式方程为 ∴ .19598arccos 19598arccos-=πθ或 6. 设d 和d '分别是坐标原点到点(,,)M a b c 和(,,)M a b c ''''的距离,证明当aa bb cc dd ''''+++时,直线MM '通过原点.证 {},,OM a b c =,{},,OM a b c ''''=,OM OM aa bb cc ''''⋅=++,而当OM OM OM OM ''⋅=⋅,cos(,)OM OM dd ''=时,必有cos(,)1OM OM '=,∴//OM OM ',∴当aa bb cc dd ''''+++时, 直线MM '通过原点.7.求通过点()2,0,1-P 且与平面0123=-+-z y x 平行,又与直线12341zy x =--=-相交的直线方程.解 设过点()2,0,1-P 的所求直线为∵ 它与已知平面0123=-+-z y x 平行,所以有023=+-z y x 1 又∵ 直线与已知直线相交,那么必共面. ∴ 又有 即 7x+|8y-12z=02由1,2得 31:50:48713:71232:12821::-=----=Z Y X而 ()1:2:431:50:4-≠- ∴ 所求直线的方程为.3125041+==--z y x 8. 求通过点()1,0,4-P 且与两直线⎩⎨⎧=-+=--⎩⎨⎧=--=++4423,221z y x z y x z y x z y x 与都相交的直线方程.解 设所求直线的方向矢量为{}z y x v ,,=→, 则所求直线可写为.14Zz Y y X x +==- ∵ 直线1l 平行于矢量{}{}{}3,3,01,1,21,1,121-=--⨯=⨯→→n n ∴矢量{}3,3,0-=→v 为直线1l 的方向矢量. 由于02111≠-因此令y=o 解方程组得x=1,z=o∴ 点1,o,o 为直线1l 上的一点. ∴ 直线1l 的标准方程为62155+=-=-z y x . ∵ (){}.3,3,01.0,0,1,1121-=→v M l l l l 方向矢量为过点都相交且与∴ 有0330103,,11=--=⎪⎭⎫⎝⎛→→→ZYXv v p m即 X+3Y+3Z=0. 即 X-13Y-3Z=0. 得 X:Y:Z=30:6:-16 又∵ ,3:3:016:6:30-≠- 即 .1→→v v 不平行6:1:516:6:30≠-, 即 .2→→v v 不平行 ∴ 所求直线方程为: 9. 求与直线137182-=-=+z y x 平行且和下列两直线相交的直线. ⑴⎩⎨⎧+=-=⎩⎨⎧+=-=5342,3465y z x z x z x z ⑵⎪⎩⎪⎨⎧=-=+=⎪⎩⎪⎨⎧=+=-=t z t y t x t z t y t x 74105,5332 解 ⑴ 在两直线上分别取两点()(),4,3,0,39,0,921--M M 第一条直线的方向矢量为{}0,1,01→v , 第二条直线的方向矢量为{}6,2,32→v , 作两平面:即 ,03198;03038=---=+-z y x z x将其联立即为所求直线的方程⑵021532,017813253=++-=-+z y x z y x 即1017,0178145710=---=+-z y x z y x 即212联立: .017021532⎩⎨⎧=---=++-z y x z y x这就是所要求的直线方程. 10. .求过点()0,1,2P 且与直线垂直225235:-+==-z y x l 相交的直线方程. 解 设所求直线的方向矢量为{}Z Y X v ,,0=→则所求直线0l 可写为.012Zz Y y X x -=-=- ∴ 3X+2Y-2Z=0 1 即 50X-69Y+6Z=0 2 由1,2得 311:131:120::=Z Y X ∴所求直线0l 为:§ 空间直线与点的相关位置1.直线⎩⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A 通过原点的条件是什么解:已知直线通过原点⇔ 故条件为021==D D ; 2.求点)1,3,2(-p 到直线⎩⎨⎧=++-=++-0172230322z y x z y x 的距离;解:直线的标准方程为:所以,p 到直线的距离为:1534532025)2(1212392292421243222222===-++-+--+-=d ; § 平面束1.求通过平面0134=-+-z y x 和025=+-+z y x 的交线且满足下列条件之一的平面:1通过原点; 2与y 轴平行; 3与平面0352=-+-z y x 垂直;解:1设所求的平面为:0)25()134(=+-++-+-z y x z y x λ 欲使平面通过原点,则须:021=+-λ,即21=λ, 故所求的平面方程为: 即:0539=++z y x ; 2同1中所设,可求出51=λ;故所求的平面方程为:0)25()134(5=+-++-+-z y x z y x 即:031421=-+z x ;3如1所设,欲使所求平面与平面0352=-+-z y x 垂直,则须: 从而:3=λ,所以所求平面方程为:05147=++y x ;2.求平面束0)42()53(=+--+-+z y x y x λ,在y x ,两轴上截距相等的平面; 解:所给的方程截距式为: 据要求:λλλλ--=+-345145 ⇒ 1=λ; 所以,所求的平面为:01222=--+z y x ;3.求通过直线⎩⎨⎧=+-=++0405z x zy x 且与平面01284=+--z y x 成4π角的平面;解:设所求的平面为:0)4()5(=+-+++z x z y x λμ 则:22)8()4(1)()5()()8()()4(5)(222222=-+-+-+++-⨯-+-⨯++±λμμλμλμμλμ 从而 ,1:0:=λμ或3:4- 所以所求平面为:04=+-z x或012720=-++z y x ;4.求通过直线32201-=+=+zy x 且与点)2,1,4(p 的距离等于3的平面; 解:直线的一般方程为:设所求的平面的方程为0)223()1(=++++z y x μλ, 据要求,有:∴有λμμλμλ908125)13(92222++=+∴ 1:6:-=μλ或8:3即所求平面为:0)223()1(6=++++-z y x或 0)223(8)1(3=++++z y x即:04236=+--z y x 或01916243=+++z y x ;5. 求与平面0432=-+-z y x 平行且满足下列条件之一的平面. ⑴通过点()3,2,1-; ⑵y 轴上截距为3-; ⑶与原点距离为1.解: ⑴设所求的平面为032=-+-λz y x ,将点()3,2,1-的坐标代入方程得14=λ,则所求平面方程为01432=-+-z y x .⑵设所求的平面为λ=+-z y x 32.6,32,132=-=-=-=-=λλλλλ得令zyx.故所求平面为0632=-+-z y x .⑶设所求的平面为032=++-λz y x ,将其法化为()032141=++-±λz y x ,将原点的坐标代入得141±=λ,故所求平面为014132=±+-z y x .6.设一平面与平面x+3y+2z=0平行,且与三坐标平面围成的四面体体积为6,求这平面的方程;解 设所求平面方程为:x+3y+2z+0=λ 原点到该平面的距离为.14222λ=++=CB A D d∴ λλλ21,31,---分别叫做平面在三坐标轴上的截距. 四面体体积.31Sh V = ∴ )21)(31)((21316λλλ---=∴ .6±=λ∴ 这个平面的方程为0623=±++z y x8.直线⎩⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A 的系数满足什么条件才能使直线在坐标平面XOZ 内解 坐标平面XOZ 属于平面束化简为()()()()021212121=+++++++mD lD z mC lC y mB lB x mA lA 设平面XOZ 面.0,0,0≠≠=z x y有⎪⎩⎪⎨⎧=+=+=+000212121mD lD mC lC mA lA ∴.212121D D C C A A ==。
解析几何第四版吕林根课后习题答案一至三章

PA1 PO PA2 PO PAn PO 0
即
PA1 PA2 PAn n PO
§1.4 向量的线性关系与向量的分解
1.在平行四边形 ABCD 中, (1)设对角线 AZ a, BD b, 求 AB, BC , CD, DA. 解: AB
解?a?b?b?a?b?a?b?a?b?a?b?a?b?a?????????????????yxyyxxyyxxyxyx22?e?e?e?e?e?e?e?e?b?a?????????3132132142232?e?e?e?e?e?e?e?e?e?b?a???????????3213213213422232?e?e?e?e?e?e?e?e?e?b?a???????????321321321710322322323
OA OB + OC = OL + OM + ON .
7. 设 L、M、N 是△ABC 的三边的中点,O 是任意一点,证明 [证明] OA OL LA
OB OM MB OC ON NC OA OB OC OL OM ON ( LA MB NC )
1 1 1 1 b a , BC b a , CD b a , DA b a .设边 BC 和 CD 的 2 2 2 2
(2)中点 M 和 N,且 AM P, AN q 求 BC , CD 。 解: AC
1 1 q P , BC 2MC 2 q P P q 3P 2 2
解析几何第三章答案

解析几何第三章答案第3章平面与空间直线§ 3.1平面的方程1.求下列各平面的坐标式参数方程和一般方程:(1)通过点)1,1,3(1-M 和点)0,1,1(2-M 且平行于矢量}2,0,1{-的平面(2)通过点)1,5,1(1-M 和)2,2,3(2-M 且垂直于xoy 坐标面的平面;(3)已知四点)3,1,5(A ,)2,6,1(B ,)4,0,5(C )6,0,4(D 。
求通过直线AB 且平行于直线CD 的平面,并求通过直线AB 且与ABC ?平面垂直的平面。
解:(1) }1,2,2{21--=M M ,又矢量}2,0,1{-平行于所求平面,故所求的平面方程为:++-=-=--=v u z u y vu x 212123一般方程为:07234=-+-z y x(2)由于平面垂直于xoy 面,所以它平行于z 轴,即}1,0,0{与所求的平面平行,又}3,7,2{21-=M M ,平行于所求的平面,所以要求的平面的参数方程为:+-=+-=+=v u z u y u x 317521 一般方程为:0)5(2)1(7=+--y x ,即01727=--y x 。
(3)(ⅰ)设平面π通过直线AB ,且平行于直线CD : }1,5,4{--=,}2,0,1{-= 从而π的参数方程为:+-=+=--=v u z uy vu x 235145 一般方程为:0745910=-++z y x 。
(ⅱ)设平面π'通过直线AB ,且垂直于ABC ?所在的平面∴}1,5,4{--=, }1,1,1{4}4,4,4{}1,1,0{}1,5,4{==-?--=?均与π'平行,所以π'的参数式方程为:+-=++=+-=v u z v u y v u x 35145 一般方程为:0232=--+z y x .2.化一般方程为截距式与参数式: 042:=+-+z y x π. 解:π与三个坐标轴的交点为:)4,0,0(),0,20(),0,0,4(--,所以,它的截距式方程为:1424=+-+-z y x . 又与所给平面方程平行的矢量为:}4,0,4{},0,2,4{-,∴所求平面的参数式方程为:=-=++-=v z uy v u x 24 3.证明矢量},,{Z Y X v =平行与平面0=+++D Cz By Ax 的充要条件为:0=++CZ BY AX . 证明:不妨设0≠A ,则平面0=+++D Cz By Ax 的参数式方程为:==---=v z uy v A C u A B A D x 故其方位矢量为:}1,0,{},0,1,{ACA B --,从而平行于平面0=+++D Cz By Ax 的充要条件为:v ,}1,0,{},0,1,{ACA B --共面?01001=--AC A B Z Y X ? 0=++CZ BY AX .4.已知:连接两点),12,0(),5,10,3(z B A -的线段平行于平面0147=--+z y x ,求B 里的坐标z .解:}5,2,3{z +-= 而AB 平行于0147=--+z y x 由题3知:0)5(427)3(=+-?+?-z 从而18=z .§ 3.2 平面与点的相关位置1.计算下列点和平面间的离差和距离:(1))3,4,2(-M ,:π0322=++-z y x ;(2))3,2,1(-M ,:π 0435=++-z y x .解:将π的方程法式化,得:01323132=--+-z y x ,故离差为:311332431)2()32()(-=-?-?+-?-=M δ,M 到π的距离.31)(==M d δ(2)类似(1),可求得0354353356355)(=-++-=M δ,M 到π的距离.0)(==M d δ2.求下列各点的坐标:(1)在y 轴上且到平面02222=--+z y 的距离等于4个单位的点;(2)在z 轴上且到点)0,2,1(-M 与到平面09623=-+-z y x 距离相等的点;(3)在x 轴上且到平面01151612=++-z y x 和0122=--+z y x 距离相等的点。
解析几何第四版吕林根 期末复习 课后习题(重点)详解

第一章 矢量与坐标§ 数量乘矢量4、 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线,又∵B 为公共点,从而A 、B 、D 三点共线.6、 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点,证明:三中线矢量AL , BM , CN 可 以构成一个三角形. 证明: )(21AC AB AL +=Θ )(21+=)(21CB CA CN +=0)(21=+++++=++∴7.、设L 、M 、N 是△ABC 的三边的中点,O 是任意一点,证明 OB OA ++OC =OL ++.[证明] LA OL OA +=Θ MB OM OB += NC ON OC +=)(OM +++++=++∴ =)(CN BM AL ON OM OL ++-++ 由上题结论知:0=++ ON OM OL OC OB OA ++=++∴ 从而三中线矢量,,构成一个三角形。
8.、如图1-5,设M 是平行四边形ABCD 的中心,O 是任意一点,证明OA +OB ++OD =4OM .[证明]:因为OM =21(OA +), OM =21(OB +OD ), 所以 2=21(OA +OB +OC +) 所以OA +OB ++OD =4OM .10、用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.图1-5证明 已知梯形ABCD ,两腰中点分别为M 、N ,连接AN 、BN . →→→→→→++=+=DN AD MA AN MA MN ,→→→→→→++=+=CN BC MB BN MB MN ,∴ →→→+=BC AD MN ,即§ 矢量的线性关系与矢量的分解3.、设一直线上三点A , B , P 满足AP =(-1),O 是空间任意一点,求证:OP =λλ++1[证明]:如图1-7,因为=-OA ,PB =OB -,所以 -OA = (OB -),(1+)OP =+,从而 OP =λλ++1OB.4.、在ABC ∆中,设,1e =2e =.(1) 设E D 、是边BC 三等分点,将矢量,分解为21,e e 的线性组合; (2)设AT 是角A 的平分线(它与BC 交于T 点),将分解为21,e e 的线性组合 解:(1)()12123131,e e e e -==-=-=Θ, 2111231323131e e e e e BD AB AD +=-+=+=,同理123132e e AE +=(2)因为||||TC ||11e e , 且 BT 与方向相同, 所以 BT ||21e e .由上题结论有AT ||||1||212211e e e e e +||||212112e e e e e e +.5.在四面体OABC 中,设点G 是ABC ∆的重心(三中线之交点),求矢量对于矢量,,,的分解式。
解析几何第四版课后答案第三章中医谈方论药第三章答案

解析几何第四版课后答案第三章中医谈方论药第三章答案中医谈方论药第三章答案第三章单元测试 1以下哪一部书是李克绍先生的学术代表作 ( ) A.《胃肠病漫话》 B.《伤寒论串讲》 C.《伤寒解惑论》 D.《伤寒论语释》 2以下哪一项不属于《伤寒解惑论》中提出九种治学方法。
( ) A.关于“要理解当时医学上的名词术语” B.关于“读于无字处和语法上的一些问题” C.关于“内容不同的条文要有不同的阅读法” D.关于“要理解寒温之争” 3丁元庆教授认为,《伤寒解惑论》中提出的哪一项既是标准也是方向?( ) A.关于“要和《内经》《本草经》《金匮要略》结合起来”B.关于“要与临床相结合” C.关于“对传统的错误看法要敢破敢立” D.关于“对原文要一分为二” 4以下哪段话是李克绍先生所说:( ) A.“胸中有万卷书,笔底无半点尘,始可著书;胸中无半点尘,目中无半点尘者,才许作古文疏注。
” B.“能否理论联络实际,在临床医疗中能否灵敏运用,这是检验学习《伤寒论》成功与否的重要标志。
” C.“《伤寒论》言证候不谈病机,述病理而少及生理,出方剂而不言药理” D.“医者书不熟那么理不明,理不明那么识不清,临证游移,漫无定见,药证不合,难以奏效。
”5以下哪段话,是湖北叶发正研究员在《伤寒学术史》中对李克绍先生的评价:( ) A.“他的论著享誉海内外,称得起现代的伤寒著名学家。
”B.“高山仰止,景行行止” C.“他对《伤寒论》的研究创当代《伤寒论》注疏之新风,其见解独特、基于临床、前后照应、逻辑严密;他活泼泼地注疏通解了活泼泼的《伤寒论》。
” D.“先生最反对学术上人云亦云,不求甚解,认为这是自欺欺人的不良学风。
先生读书也看前人注解,但决不盲从。
”6以下哪一项,不是丁元庆教授对急性口僻的辨治分析^p :( ) A.口僻发生在面部,表现为口眼歪斜。
面部是足阳明胃经循行之地。
B.阳明炽热内盛,炙灼足阳明人迎脉,形成人迎脉积。
2-3解析几何吕林根第四版

把曲线投影到yoz平面内,得
2 y2 z2 9
,
x 0
写出投影曲线的参数方程:
y
3 cos 2 ,(0 2 )
z 3 sin
再写出原空间曲线的 参数方程:
x
3 cos
2
y
3
cos ,(0 2 ).
2
z 3 sin
例8:有两条相互直交的直线 l1 与 l2 ,其中l1 绕l2作螺旋运动, 即一方面 l1 绕 l2 等速转动,另一方面又沿着l2 作等速直线运动 ,在运动中 l1 永远保持与 l2直交,这样由 l1 划出的曲面叫做螺旋 面,试建立螺旋面方程。
的角速度为,那么在t秒后质点从
起点A运动到P 的位置,P在xoy面
上的射影为Q, 设直线运动的速度
v与角速度之比为b,即 v b.
t
o
P
•
xA
Q
y
r uuur
uuur
ur
则 R(i,OQ) t, QP btk,所以有
r uuur uuur uuur r
r
ur
r OP OQ QP ia cost ja sint kb(t - t )
解: 取l2 为OZ轴,设 l1 的初始位置与OX轴重合,转动角为
r uuur uuuur uuur 则 r OM MN NP
uuur
r
r
而 OM ON cost i OP cost i
uuuur
r
r
MN ON sint j OP sint j
z
O l1
l2 r r
uuur ur
NP vt k
交线为椭圆.
二、空间曲线的参数方程
设向量函数
《解释几何第四版》讲解与习题第三章平面与空间直线

平面内两点确定一条直线
在平面内,任意两点可以确定一条且 仅有一条直线。
直线的基本性质
01
02
03
直线是无限延长的
直线在平面内是无限延长 的,没有终点。
两点之间线段最短
在平面上,任意两点之间 的线段是最短的路径。
直线的方向性
直线具有一个固定的方向, 或者沿两个方向无限延长。
点与直线的位置关系
点在直线上
空间几何体的对称性
02
空间几何体可能具有对称性,如中心对称、轴对称或面对称等。
空间几何体的角与距离
03
空间几何体中涉及的角度和距离是重要的几何量,它们对于研
究几何体的性质和关系至关重要。
空间几何体的表面积和体积
1 2
表面积的计算
根据几何体的形状和尺寸,可以计算其表面积, 这对于材料用量、表面热交换等实际问题有重要 意义。
《解释几何第四版》讲 解与习题第三章平面与 空间直线
目录 CONTENT
• 平面几何基础 • 空间几何基础 • 平面与空间直线的关系 • 平面与空间直线在解题中的应用 • 习题解析
01
平面几何基础
平面的基本性质
平面是无限延展的
平面内三点确定一个平面
平面在三维空间中是无限延展的,没 有边界。
在平面内,任意三个不共线的点可以 确定一个且仅有一个平面。
体积的计算
对于封闭的空间几何体,可以计算其体积,这对 于质量、密度、重心等物理量有直接影响。
3
表面积和体积的关系
某些空间几何体的表面积和体积之间存在特定的 关系,如球体的表面积与其半径成正比,而体积 与其半径的立方成正比。
空间几何体的投影
正投影
当光线与投影面垂直时,物体在 投影面上的投影称为正投影,这 种投影能够真实反映物体的形状
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章平§3.1平面的方程1.求下列各平面的坐标式参数方程和一般方程:(1)通过点M J QI-I)和点M2(1,—1,0)且平行于矢量{—1,0,2}的平面(2)通过点M^l,—5,1)和M 2 (3,2,—2)且垂直于xoy坐标面的平面;(3)已知四点A(5,1,3) , B(1,6,2) , C(5,0,4) D(4,0,6)。
求通过直线AB且平行于直线CD的平面, 并求通过直线AB且与MBC平面垂直的平面。
解:(1) M1M2 ={_2,_2,1},又矢量{—1,0,2}平行于所求平面,故所求的平面方程为:般方程为:4x -3y+2Z -7 =0(2)由于平面垂直于xoy面,所以它平行于z轴,即{0,0,1}与所求的平面平行,又M 1M 2 ={2,7,-3},平行于所求的平面,所以要求的平面的参数方程为:般方程为:7(x—1)—2(y+5)=0,即7x—2y-17 = 0。
(3)( i)设平面兀通过直线AB,且平行于直线CD :AB={m,5,—1},CD ={-1,0,2}从而兀的参数方程为:般方程为:10x +9y + 5z-74=0。
(ii)设平面兀'通过直线AB,且垂直于MBC所在的平面AB ={75,-1},ABX AC ={-4,5,-1}x{0T,1} ={4,4,4} =4{1,1,1}均与兀’平行,所以兀’的参数式方程为:般方程为:2X+ y -3z - 2 = 0 .2.化一般方程为截距式与参数式:兀:X +2y-z+4 =0.解:兀与三个坐标轴的交点为:(—4,0,0), (0—2,0), (0,0,4),所以,它的截距式方程为:△+丄+2 =1又与所给平面方程平行的矢量为:{4, —2,0},-4 -2 4又与所给平面方程平行的矢量为:{4, —2,0},1二所求平面的参数式方程为:3.证明矢量v={X,Y,Z}平行与平面 Ax + By+Cz + D=0的充要条件为: AX + BY + CZ = 0.证明:不妨设A H O, 则平面Ax +By +Cz + D =0的参数式方程为:BC故其方位矢量^:^-,1,0},^-,0,1},从而v 平行于平面 Ax + By + Cz + D = 0的充要条件为:- B Cv ,{-—,1,0}, {——,0,1}共面 UA A二 AX +BY +CZ =0.4.已知连接两点 A(3,10,—5), B(0,12,z)的线段平行于平面 7x + 4y-z-1= 0,求B 点的z 坐标.而 AB 平行于 7x +4y -z-1 =0由题 3 知: (-3) X 7 + 2x4 - (z+5) = 0 从而Z = 18.5.求下列平面的一般方程 ⑴通过点M 1 (2^1,1跑M 2 (3,—2,1)且分别平行于三坐标轴的三个平面 ⑵过点M (3,2,7 且在X 轴和y 轴上截距分别为-2和-3的平面;⑶与平面5x +y -2z + 3 =0垂直且分别通过三个坐标轴的三个平面 ⑷已知两点M r (3,—1,22(4,-2,-1 ),求通过M 1且垂直于M 2的平面;⑸原点0在所求平面上的正射影为P(2,9,—6);⑹求过点M 1 (3^5,1 )和同2 (4,1,2 )且垂直于平面X —8y+3z —1=0的平面.—=1,把点 M (3,2, V ”弋入得 C =-迢 -2 -3 C19解:平行于X 轴的平面方程为X-2 y+1 1 -1Z —1=0.即 Z —1 =0.同理可知平行于y 轴,z 轴的平面的方程分别为 Z -1 = 0,x + y -1 =0 .解:AB ={—3,2,5+ z}⑵设该平面的截距式方程为3 1 11故一般方程为 12x +8y + 19z +24=0.⑶若所求平面经过X 轴,则(0,0,0 )为平面内一个点,fe ,1, _2}和丸0,0}为所求平面的方位矢量,•••一般方程为2y+ z=0.同理经过y 轴,z 轴的平面的一般方程分别为 2x+ 5z=0,x-5y = 0.⑷M =《,-1,-3九跑2垂直于平面兀, •••该平面的法向量=勺,—1,—3)平面C 通过点M )3,—1,2 ),因此平面兀的点位式方程为(x -3)-(y +1)-3(z -2)=0. 化简得 x-y -3z + 2 =0.(5) op = {2,9,-6}C 2 n 9 甘 6 •- cosc = —,cosP = — ,cosY = ——.11 11 112 9 6则该平面的法式方程为:二X +旦y -2z-11 =0.11 11 11既 2x +9y —6z —121 =0.(6)平面 X —8y +3z -1 =0 的法向量为 n = £,—8,3}, M 1M 2= 14,D = —26^4 + 2 + 28 = —74 , 则一般方程 Ax+By+Cz + D =0,即:13x - y-7z-37= 0. 6.将下列平面的一般方程化为法式方程。
解:寫D = -3.•••点法式方程为X -0 y-05 1Z —0 -2 =0写岀平面的点位式方程为X —4 y-1 -8z-2-8 6= —26,= 2,C =7301x y+7z 2 6 1一般方程乘上A =1 9 =-1 .得法式方97 一一z =0. 97 .求自坐标原点自以下各平面所引垂线的长和指向平面的单位法矢量的方向余弦。
1解:(1)D = —35.几=—.化为法式方程为7+ 3y+6z — 5 = 0原点指向平面 兀的单位法矢量为77它的方向余弦为17 7 7j 2co 糅=-,Co^=3,co^-.原点0到平面兀的距离为 77P = -)D = 5.1(2»=21.「—3.化为法式方程为1 --x 3+ Zy — 2Z -7=0原点指向平面 兀的单位法矢量为 3 3 「 ,2,-2|它的方向余弦为1 3 3 3 J1 2 2cosa = —一 ,cos P = —,cos Y = —一.原点o 到平面兀的距离p = -A D = 7.第20页8•已知三角形顶点 A(0,—7,0),B(2,—1,1),C( 2,2,2求平行于L ABC 所在的平面且与她相距为 2各单位的平面方程。
设AB=a,AC =b.点A(0,—7,0 ).则a = {2,6,1},b={2,9,2}写岀平面的点位式方程设一般方程Ax +By +Cz +D =0,・.A =3.B = 2,C = 6,D = —14 c 0.几=-斗.得法式方程421X + 1±1 1=0.”・.A =—.即几=—或 Z =9 9”将已知的一般方程乘上扎=丄.得法式方程V 30 7302yj 303=0.= 2.”・.A = —1.”・.将已知的一般方程乘上扎=—1.得法式方程 -x-2 = 0.1则几=7.p—2.相距为2个单位。
则当P =4时D = —28.当P =0时D =0.”所求平面为 3x -2y +6z -28 =0.和 3x -2y + 6z = 0. 9.求与原点距离为 6个单位,且在三坐标轴 OX,oy 与oz 上的截距之比为 a: b: C = —1:3: 2的平面。
解:设a = —x,b =3x, c = 2x.T abc 工0「设平面的截距方程为 -+丄+兰=1.a b c即 bcx +acy + abz =abc.又•「原点到此平面的距离 d = 6._______ = 6.J(b 2c 2 +a 2c 2 +a 2b 2 図2y z”".所求方程为 —x +—+— =7.3 2x y z10.平面—+丄+ — =1分别与三个坐标轴交于点A ,B ,C.求L ABC 的面积。
a b C解 A(a, 0, 0 )B(0,b,0),C(0,0, C ) TB ={—a, b,0},7C ={—a,0, C }.A^xA? ={bc,ca,ab}; c 2+c 2a 2 +a 2b 2.SLABC = 1j b 2c 2 +c 2a 2 +a 2b 211.设从坐标原点到平面的距离为。
求证证明:由题知:-1+丄c1 1 1=—+— + —2 .2 2 -§3.2平面与点的相关位置(1)M (—2,4,3),兀:2x -y +2z +3 =0 ; (2)M (12—3),兀:5x-3y +z +4 =0.将兀的方程法式化,得:解:2+1 2 c-—x+—y- — zT = 0 ,3 3 3—6 —2咒4 +5=3。
—6 —2咒4 +5=3。
2 1 2 1故离差为: 6(M ) =(-—)x(_2) +-X 4-—X 3-1 =--3 3 3 31 M 到兀的距离d = ^M )=—. 3(2)类似(1),可求得6(M ) = + 6+ ___________ =0 ()V35 735 V35 735 ,M 到兀的距离d = 3(M) =0.2.求下列各点的坐标:(1)在y 轴上且到平面2+ 2y-2z-2=0的距离等于4个单位的点;(2)在z 轴上且到点 M(1,—2,0)与到平面3x —2y + 6z —9 = 0距离相等的点; 12x-16y+15Z + 1 =0 和 2x + 2y -z-1 =0距离相等的点。
y 0 = —5 或 7.(2)设所求的点为(0,0,Z 0)则由题意知:由此,Z 0 = -2 或-82/13。
82故,要求的点为(0,0,—2)及(0,0,——)。
13 (3)设所求的点为(x 0,0,0),由题意知:由此解得:X 0 = 2或11/43。
所求点即(2,0,0)及(11/43,0,0)。
3.已知四面体的四个顶点为 S(0,6,4), A(3,5,3), B(—2,11,—5), C(1, —1,4),计算从顶点S 向底面ABC 所 引的高。
解:地面ABC 的方程为: 所以,高h =4.求中心在C(3,—5,2)且与平面2x — y —3z +11 = 0相切的球面方程。
解:球面的半径为 C 到平面兀:2x-y —3z+11=0的距离,它为:(3)在x 轴上且到平面 解:(1)设要求的点为M (0, y 0,0)则由题意 即所求的点为(0,-5,0)及(0,7,0)。
2X3 + 5+6 +11V14(X -3)2 +(y +5)2+(z + 2)=56.即:X 2+y 2+ z 2-6x +10y + 4z-18=0.从而得 12B-35C =0或4B+3C=0.于是有 B:C =35:12或 B:C=3:(-4). 所求平面为 35y+12z=0或 3y —4z=0.6.求与下列各对平面距离相等的点的轨迹 ⑴ 3x +6y -2z-7 =0和4x-3y -5 =0; ⑵ 9x —y +2z —14 =0禾口9x — y + 2z +6 =0. 解:⑴兀/一卩乂 +6y -2z -7)=0令1(3x +6y -2z -7)<(4x —3y —5)化简整理可得:13x —51y +10Z =0与43x +9y —10z —70 =0.D " +D 2 -14 + 6⑵对应项系数相同,可求 D = ------------------ = ------- =-4,从而直接写岀所求的方2 2程:9x - y + 2z —4 =0 .9判别点M ( 2 -1 1)和N (1 2 -3 )在由下列相交平面所构成的同一个二面角内,还是在相邻二 面角内,或是在对顶的二面角内?(1)— y + 2z —3=0 与兀 2:x —2y —z +4=0(2)1: 2x — y + 5z —1 = 0与兀2 :3x —2y+6Z-1 =0解:(1)将 M( 2 -1 1),N( 1 2 -3)代入.1,得:Pr 十 2一3]0.3 - 2- 6- 3(0所以, 要求的球面的方程为:5.求通过x 轴其与点M (5,4,13 )相距8个单位的平面方程。
