11光子晶体波导
新型光子晶体波导的研究与应用

新型光子晶体波导的研究与应用光子晶体是一种具有禁带结构的材料,它能够控制和操控光的传播。
新型光子晶体波导是在光子晶体基础上,通过改变光子晶体结构或引入光子晶体结构中的缺陷来实现光的传导的一种结构。
近年来,新型光子晶体波导已经引起了广泛的研究关注,并且在光通信、传感等领域有着广泛的应用潜力。
新型光子晶体波导的研究主要包括波导的设计与制备、性能的调控以及在光学器件中的应用等方面。
首先,波导的设计与制备是新型光子晶体波导研究的基础。
波导的设计需要考虑光子晶体的禁带性质,以及波导的带宽、损耗等性能指标。
制备新型光子晶体波导需要考虑制备工艺和材料选择等方面的问题,例如采用自组装技术制备二维或三维光子晶体结构,或者通过纳米加工等方法制备相应的波导结构。
其次,对新型光子晶体波导的性能进行调控是关键的研究方向。
通过调控波导的尺寸、形状、结构等参数,可以实现对波导的传输特性、耦合特性等性能进行调控。
例如,可以通过改变波导的宽度或高度来实现波导的模场大小调控,或者通过改变波导的结构来实现波导的色散特性调控。
此外,还可以通过引入光子晶体中的缺陷来实现波导的功能化,如引入缺陷态来实现光隔离、光放大等功能。
最后,新型光子晶体波导在光学器件中有着广泛的应用潜力。
光子晶体波导可以用于实现光的耦合、分光、传输等功能,因此在光通信、光传感等领域有着重要的应用价值。
例如,可以将新型光子晶体波导应用于光分路器、光开关、光放大器等光学器件中,以实现高性能的光学功能。
同时,新型光子晶体波导还可以用于传感领域,通过改变波导结构或引入敏感材料来实现对物理量、化学量的传感,例如温度、压力、湿度等。
总结起来,新型光子晶体波导的研究与应用是一个多学科交叉的领域,涉及材料科学、光学等多个学科的知识。
随着对光子晶体的深入研究,新型光子晶体波导的性能也将得到进一步的改善和优化,将有望在光通信、传感等领域实现更多的应用。
光子晶体中的能带结构与光学波导效应

光子晶体中的能带结构与光学波导效应引言随着人类对光学科学的不断深入研究,光子晶体作为一种新兴材料,引起了广泛的关注。
光子晶体是一种具有周期性结构的介质,在此结构中光的传播被限制或操控,从而产生一系列独特的光学效应。
其中,能带结构和光学波导效应是光子晶体中最为重要的两个方面。
本文将详细介绍光子晶体中的能带结构和光学波导效应,并探讨其在光学应用中的潜在价值。
光子晶体的基本概念光子晶体,又称为光子晶格或光子带隙材料,是一种具有调制折射率的周期性结构。
与电子晶体类似,光子晶体中也存在能带结构,即光子带隙。
光子晶体的制备方法多种多样,可以根据不同的应用需求选择不同的制备方法。
典型的制备方法包括自组装、纳米加工以及溶胶凝胶等。
光子晶体的周期性结构导致了光子能量的禁带结构,其中的带隙区域在光学波长尺寸范围内,可以对特定波长的光进行完全或部分的反射或禁闭。
这种能带结构的调控使得光子晶体能够在光学通信、光学传感、光电子器件等领域发挥重要作用。
光子晶体中的能带结构光子晶体中的能带结构指的是光子晶体中光的能量在空间中的分布状态。
光子晶体的能带结构如同电子在晶体中的能带结构一样,可以分为导带和禁带。
导带中的光子能够在光子晶体中自由传播,而禁带中的光子能量被禁止传播,因此禁带区域内的光子形成了光子带隙。
光子晶体中的能带结构可以通过调节晶格结构、折射率的变化以及周期性的改变等方式进行调控。
通过控制光子晶体的周期性结构,可以改变能带结构的宽度和位置,从而实现对特定波长的光进行选择性的传播或反射。
通过调节光子晶体的尺寸和结构参数,可以实现对带隙位置和宽度的调控。
光子晶体中的能带结构对光的传播产生重要影响。
当光的波长与光子晶体中的禁带结构相匹配时,光将无法通过光子晶体,从而形成光学隔离效应。
这种能带结构的特性在光学通信和光学传感中具有广泛的应用潜力。
光子晶体中的光学波导效应光学波导效应是指在光子晶体中通过调节结构参数,使得光在材料内部进行导波传输的现象。
光子晶体波导
光⼦子晶体
⼆二维光⼦子晶体慢光耦合谐振腔阵列结构 (三⾓角晶格柱阵列、⾮非线性效应电光聚合物填充)
光⼦子晶体波导与微腔集成结构电光传感器(PWE、FDTD)
光⼦子晶体W1波导
光⼦子晶体微纳集成级联传感器阵列结构
光⼦子晶体微纳集成并联传感器阵列结构(减少串扰)
⾼高性能光⼦子晶体波导微腔集成结构传感器
多束光⼦子晶体纳⽶米束微腔并⾏行排列(FDTD)
⾼高Q值
⾼高折射率灵敏度实验测试(PBS溶液蛋⽩白质分⼦子检测)光⼦子晶体微位移、压⼒力传感器
光⼦子晶体特性
⾼高灵敏度⾼高分辨率集成度⾼高抗干扰分析⽅方法
平⾯面波展开法(PWE)
时域有限差分法(FDTD)研究分类
光⼦子晶体波导、微腔(不同缺陷结构平板光⼦子晶体)
光⼦子晶体波导与微腔集成能带特性光场分布特性导光特性(波导)
局域特性(微腔)空间分布结构分类
⼀一维光⼦子晶体
⼆二维光⼦子晶体(重点)
三维光⼦子晶体
控光特性光场传输机制
透射特性
⾼高性能参数FOM
⾼高Q值
⾼高灵敏度光⼦子晶体槽波导
⾼高性能参数FOM
光⼦子晶体槽波导微位移传感器
光⼦子晶体微机械压⼒力传感器及相应的集成传感阵列
响应时间少光⼦子带隙(重要)光⼦子晶体波导传感器(线缺陷)光⼦子晶体微腔传感器(点缺陷)光⼦子晶体集成阵列传感器(点、线缺陷)
光⼦子晶体W1波导光⼦子晶体槽波导
实现⽆无标签检测
光⼦子晶体能带结构光波传输特性光场局域特性导光透射特性
光⼦子晶体波导
光⼦子晶体槽波导电光传感器结构(创新)
平坦波导实现超低速慢光传输控光局域特性
阻断特定频率光⼦子电光调制波尔斯效应。
光子晶体光波导的发展与应用

光子晶体光波导的发展与应用光子晶体光波导的发展与应用:随着光通信、光计算、光信息处理的发展,全光型信息处理器件,如光控开关、光学双稳态器件、光逻辑门、光放大器、光耦合器、光前激光器等应用越来越广泛。
光波导作为微光学线路中的基本连接器件,在光纤通信、集成光学、变折射率光学和光前传感器领域中具有重要的应用价值。
如在光电子集成电路中,高速率和大容量密集比分复用网络系统,需要重点解决高速传输、复用和接复用、光分叉、光交叉互连、光波导开关以及高速光调制等,这些器件都离不开高性能和高可靠性的各类光波导结构与器件。
随着通信和信息处理系统中传输容量的迅速增加,光信号并行化处理程度的不断扩大,数据传输速率达到Tbit/s。
传统光波导光顺号较大,传输稳定性也不是很理想,进一步减小损耗、提高稳定性也受到诸多的限制。
光子晶体光波导具有传输速率快、损耗率低、稳定性好等特点,可以满足日益增长的信息传输要求。
另外,光子晶体的主要特点是设计灵活,通过改变其结构和参数,可以方便的制备各种类型的光波导及各类新型的光学器件,这些器件将成为下一代电子信息产业和光集成电路的主要器件并发挥着重要作用。
一般来说,用于传输电磁波的光波导主要有两种,一种是金属性的电磁波导,主要传到微波电磁波;另一种是大量光信号快速传输的载体,已成为改变折射率光学的生长点,也是许多器件非线性光波导的构筑基础。
传统介质光波导的导光机制是应用光的全反射原理,对光的束缚能力很微弱,即使在仅有5°的弯曲的情况下一般光场就有超过50%的辐射损耗,因此,对传统来说弯曲损耗是一个相当严重的问题,已成为集成电路的发展瓶颈。
为了降低损耗,需增加弯曲处的曲率半径,这不仅增加了波导的体积,也增加了成本。
光子晶体对光的传播具有较强、灵活的控制能力,不仅对直线式传导,而且对锐利的直角,其传导的效率也很高。
如果在PC结构中引入一个线缺陷,创建一个导光的通道,称为光子晶体光波导(PCW)。
光子晶体光波导

四、光子晶体滤波器
0 90 利用点、线缺陷设计 转角的滤波器、直通道滤波器及多通
道滤波器
1、一个点缺陷构成空腔,线缺陷构成输入/输出波导
2、两个点缺陷和线缺陷波导构成的PC滤波器
3、多通道分束滤波器
由以上可知:通过控制点缺陷的位置和线缺陷的方向可以 控制滤波的频率和方向,通过设计点缺陷的几何形状达到 调谐滤波器频率的目的。
a为横向强度分布,b-i分别为探测器距输出端不同距离的 光束横向强度分布图,可知随探测器长度增加,光束剖面 没有产生显著扩展,因为光在波导中没有任何限制。
用FDTD模拟光波的传播, 其在不用PC输出结构的 输出端强度分布图,可 知,光束发射方向对PC 端的发射结构有依赖性
a图是在PC中增加一个点缺陷,光在其表面的发射角和发射 方向;b图是光通过无点缺陷的PC波导表面射出时,方向 呈半球形发射,发散角很大。 由以上可知:在PC表面引入点缺陷后,输出光束的发散角显 著减小,有效控制了光的发射方向。
a中在 f1 87GHz 和 f 2 101 GHz 处,两波导透过率几乎相等, 说明在90处损失几乎为零。
b 、c分别为折角波导和直角 波导的理论模拟、实验测量 的透射图,在 f1 87GHz 和 f 2 101 GHz 处理论和实验数 据几乎重叠,而直角波导的 透射率超过了80%。
光子晶体光波导及光学器件
汇报人:徐婷
光子晶体光波导
传统光波导
传输速率快 损耗率低 稳定性好 设计灵活、改变其 结构和参数便于制 备各种类型光波导
损耗大
传输稳定性差
光波难以弯曲, 使光学元件集成 化变得困难
一、光子晶体光波导
1、一维PCW
空气缺陷层
ห้องสมุดไป่ตู้
光子晶体波导

光子晶体波导光子晶体波导是一种利用光子晶体结构产生波导效应的光学器件。
所谓光子晶体是指一类具有周期性结构的光学介质材料,其晶格常数与光波长相当,因此对光具有特殊的衍射和散射特性。
光子晶体波导利用这一特性,在光子晶体内部形成能够在其中传播的光波,实现光信号的分支和转导。
下面我们将对光子晶体波导的原理、制备和应用进行详细介绍。
一、光子晶体波导的原理光子晶体波导的波导效应来源于光子晶体的色散特性和布拉格散射效应。
所谓色散效应是指在介质内传播的光的波长和相速度与外界的介质相关,并表现出色散的特性。
而布拉格散射则是指光的波长和晶格周期匹配,从而在晶格结构内衍射出特定方向和波长的滞留波,形成反射和散射的效应。
当这两种效应同时存在时,就会在光子晶体的特定方向、波长和振幅范围内产生波导效应。
光子晶体波导的波导效应可以通过折射率分布、色散和光学模式的分析来解释。
对于具有正六边形晶格结构的光子晶体,其折射率分布表现为一层层相互封闭的带隙结构,其垂直与晶格面的平面波模式不能通过光子晶体传播。
而在带隙之外,光子晶体则存在一系列模式,其中有一种由于波导介质的折射率高于周围介质,从而能够在其中传播,形成光子晶体波导结构。
二、光子晶体波导的制备光子晶体波导的制备可以通过多种方法实现。
其中,溶胶-凝胶法、原子层沉积法、纳米压印法和自组装法是较为常用的方法。
溶胶-凝胶法是一种简单有效的光子晶体波导制备方法,其主要是通过在介质表面形成刻蚀或沉积波导结构的方法,形成光子晶体波导。
溶胶-凝胶法利用的是溶胶和凝胶的化学反应原理,将有机或无机前体分散在水或有机溶液中,形成胶体,之后通过升温凝胶,形成毛细管结构。
再通过腐蚀、烧结等处理,形成该结构的波导结构。
原子层沉积法是一种通过将材料在表面上依次沉积的方法制备光子晶体波导。
通过不断沉积厚度固定的单层光子晶体材料,形成多次反射和散射,最终形成波导结构。
这种方法可获得具有更加精细的结构和表面光滑的光子晶体,但其制备时间和成本相应较高。
光子晶体波导中的色散与光学调制研究

光子晶体波导中的色散与光学调制研究光子晶体波导是一种具有周期性结构的光学器件,它可以通过调控光的传播速度和光的传播路径来实现对光的调制。
在光子晶体波导中,色散是一个重要的性质,它决定了光的频率与波导中的传播速度之间的关系。
本文将探讨光子晶体波导中的色散与光学调制的研究进展。
首先,我们需要了解什么是色散。
色散是指不同频率的光在介质中传播时速度不同的现象。
在光子晶体波导中,色散可以通过调控波导的结构来实现。
一种常见的方式是通过改变波导的周期性结构,从而改变波导中的等效折射率。
当波导的周期性结构发生变化时,波导中的光的传播速度也会发生变化,从而产生色散效应。
光子晶体波导中的色散可以分为正常色散和反常色散两种情况。
正常色散是指随着光的频率增加,光的传播速度减小的现象。
反常色散则是指随着光的频率增加,光的传播速度增加的现象。
这两种色散现象在光子晶体波导中都可以实现,具体取决于波导的结构和材料的选择。
在光子晶体波导中,色散的调制可以通过多种方式实现。
一种常见的方式是通过外加电场来改变波导的等效折射率。
当外加电场改变波导的周期性结构时,波导中的光的传播速度也会发生变化,从而实现对光的调制。
另一种方式是通过光子晶体波导中的非线性效应来实现光的调制。
非线性效应是指当波导中的光强度较大时,光与介质之间的相互作用会导致光的频率发生变化。
通过调控波导中的非线性效应,可以实现对光的频率和相位的调制。
光子晶体波导中的色散和光学调制的研究具有广泛的应用前景。
一方面,光子晶体波导中的色散可以用于实现光的分离和滤波,从而实现光的多路复用和调制。
另一方面,光子晶体波导中的光学调制可以用于实现光的调制和调制解调器的设计。
这些应用对于光通信和光电子技术的发展具有重要的意义。
目前,光子晶体波导中的色散和光学调制的研究已经取得了一些重要的进展。
研究人员通过改变波导的结构和材料的选择,实现了正常色散和反常色散的调制。
同时,他们还通过外加电场和非线性效应实现了光的调制。
光子晶体缺陷波导
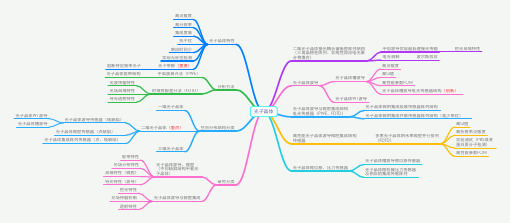
光子晶体是一种介电常数随空间周期性变化的光学微结构,从晶体结构来说,晶体内部的原子是周期性有序排列的。
当电磁波在其中传播时,受到多重散射耦合,散射波之间的干涉作用使光子晶体产生了类似于电子晶体的能带结构,这就是光子带隙。
带隙会让光在一定频率范围内的光子在光子晶体内的某些方向上是严格禁止传播的。
但是在光子晶体中引入杂质和缺陷时,与缺陷态频率符合的光子会被局限在缺陷位置而不能向空间传播的光子会被局限在缺陷位置,而不能向空间传播。
光子晶体缺陷的存在,在带隙中产生缺陷模,这个缺陷模对应的光波就能不受带隙限制。
利用光子晶体缺
陷态的特点,可以制作光波导。
一般的光纤波导中,波导大拐弯时,会漏掉部分光波能量,使传输效率降低。
而光子晶体弯曲波导中,利用不同方向缺陷模共振匹配原理。
原则上只要达到模式匹配,不管拐多大弯,都能达到很高的传输效率。
11光子晶体波导

厄米算符
ˆ iK 1 iK A K
r
ˆ 的本征值方程 算符A K
ˆ H H A K K c2 K
2
本征值为 2 / c 2
波矢作为自由参数解得本征值和本征模场
12
第11章 光子晶体波导
11.1 光子晶体理论
11.1.2 平面波展开法
倒格子基矢: 一组与三维位置空间基矢正交的矢量 定义
b1 2π a2 a3 Ω b2 2π a3 a1 Ω b3 2π a1 a2 Ω 由 b1 b2 b3
ai b j 2 ij
图11.4基矢与倒格子基矢
倒格子:
构成的新点阵
h1、h2、h3为整数
倒格矢: 任一倒格点 G h1b1 h2b2 h3b3 倒格矢与晶格矢满足
( r ) e iK r u( r )
满足周期算符本征方程的本征函数,必由一个平面波因子和 一个周期函数组成,即Bloch 波。 K Bloch 波矢
(r ) 是一个周期性调幅的平面波
11
第11章 光子晶体波导
11.1 光子晶体理论
11.1.2 平面波展开法 本征值方程
2 ˆ FH H 2
对一维和二维问题,矢量方程可分离成两个独立的TE和 TM模方程,每种 模 式 场 只有三个分量不为零 。 三维问题 的 解为混合模,但结构如果具有镜像对称性,则波矢一定在反 射面内,这时模式分为奇模和偶模,分别类似于TM模和TE 模。因此为简单起见只需要分析偏振模式就可以了。 设磁场沿z方向,将 H K 在倒格子空间按分立的傅里叶级数展开 H K z0 hm e iG r H iK 1 iK H c
光子晶体波导慢光技术

V01.44.No.10Oct.2007图l二维光子晶体波导的能带图导硅芯片控制光速传播的影响最大f1引。
2光子晶体波导慢光的产生如果介质的折射率为n,则光在介质中的传输速度为c/n,因此n表示光速的减慢程度。
假设这里是单频连续波,对光脉冲信号,用群折射率来代替n,则群速度的表达式可以写为%=c/ng,%由(dk/dto)一给出,其中光波的角频率为∞,k为波数。
在真空中,Yg=C,因为忌:to/c,在反常色散材料中%变得非常大。
图l为光子晶体波导光子带结构,水平轴为主传播方向,纵轴方向为归一化频率toa/r2兀c1=a肛。
这里,a是晶格常数,而A是真空中对应角频率tO的波长。
实线代表波导模,它表示光在禁带和泄漏线之间传播,泄漏线以上的区域为泄漏区,进入这个区域的光将在垂直方向泄露f如果在光子晶体波导表面为空气,则有oJ/c:尼1。
如果光子晶体平板是200~300nltl厚,晶格常数a是400~500nnl,那么光的传播波长可以在1.55gm附近。
要注意波导带的梯度在带边Ⅵ兀Vw.opticsjournal.net变为0。
从群速度公式可以看到,在这种情况下群速度%=0。
这种现象的产生是由于光在光子晶体中传播时不断向前向后发生布拉格反射造成的。
在布拉格光栅和多层堆栈结构里也观察到了类似的现象。
图2显示了光子晶体波导的透射谱曲线【i4J。
在这个透射谱中由于法布里一珀罗fF—n谐振而引起振荡,透射谱的峰一峰值间隔△旯朝着带边越来越小。
如果取波导长度为L,那么群折射率n。
可以由2V(2L52)给定。
根据这个方程可以估算出n。
,图2中在带边附近将超过100。
然而当n。
变得非常大的时候,透过率也将变得很低,因此慢光很难被观察到。
3测量波导中慢光的主要手段在实验上观察光子晶体平板波导色散现象仍然十分困难【15I。
早期,群速度和色散的相关报道都采用间接测量方式[IIJ,并通常采用相干结构测量。
由于受衍射极限的限制,传统的显微镜无法对波导内的光脉冲进行直接观察。
光子晶体波导与光导效应

光子晶体波导与光导效应光子晶体(photonic crystal)是一种周期性的材料结构,它的晶格常数与可见光波长相近,能够引起光的衍射现象。
光子晶体波导则是在光子晶体中引入一条缺陷,将光线限制在缺陷区域内传输的一种波导结构。
光子晶体波导的出现对于光导效应的研究起到了重要的推动作用。
光导效应(light guidance effect)是指在特定的光传输系统中,光线可以通过特定的路径传输,而不发生衍射和散射,实现高效率的能量传输。
在光导效应中,光线的波长决定了传输的特性,而在传统的光纤通信中,主要依靠衍射和反射来实现光的传输。
然而,随着科学技术的发展,光子晶体波导的出现使得光导效应得到了更好的实现。
光子晶体波导的设计和制备是一个复杂的过程。
首先需要确定想要传输的光波的波长范围,然后选择相应的光子晶体结构。
一般而言,光子晶体波导有平面型和三维型两种常见的结构。
平面型光子晶体波导是在二维平面上设计制备的,而三维型光子晶体波导则需要在三维空间中进行设计制备。
光子晶体波导的性能主要取决于两个方面:材料的折射率差和结构的周期性。
折射率差越大,能够限制光线的范围越大,光的传输损耗越小。
而结构的周期性则决定了光子晶体波导的带隙宽度和带隙中心。
带隙宽度决定了光波的传输范围,而带隙中心决定了波导模式的传输速度和方向。
在光子晶体波导中,光的传输主要通过两种方式:布拉格反射和全内反射。
布拉格反射是当光波传播方向与晶体周期平行时,根据布拉格衍射原理,光波被周期性结构反射回来。
而全内反射是当光波传播方向与晶体周期垂直时,根据全内反射原理,光波被晶体表面的折射率差折射回来。
光子晶体波导在通信、传感和光子集成电路等领域具有广泛的应用前景。
在通信领域,光子晶体波导可以用于光纤通信系统的端口耦合和分光器件的设计。
在传感领域,光子晶体波导可以用于设计和制备高灵敏度的光传感器,例如生物传感器、环境传感器等。
在光子集成电路领域,光子晶体波导可以用于光子芯片的制备,实现光电器件和电子器件的高度集成。
科研创新训练--光子晶体波导comsol
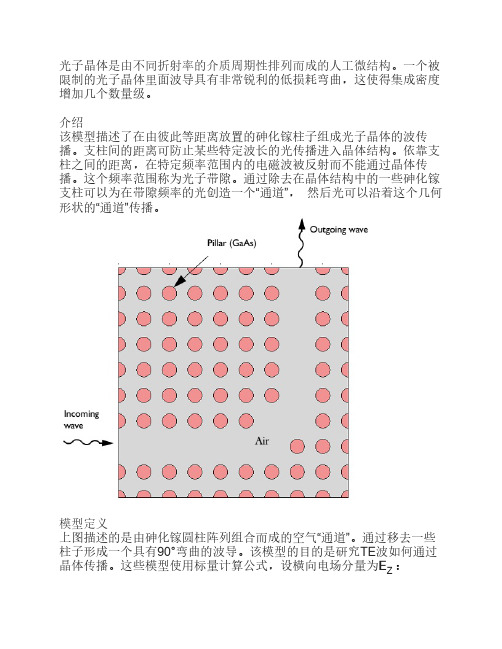
砷化镓 1. 在模型建立器中,展开材料>砷化镓பைடு நூலகம்点,然后单击折射率 2. 在属性组设置窗口中,找到局部性质部分。 3. 在局部性质表中,输入以下设置:
4. 找到输出属性与模型输入部分。找到输出属性分段。在该表中, 输入以下设置
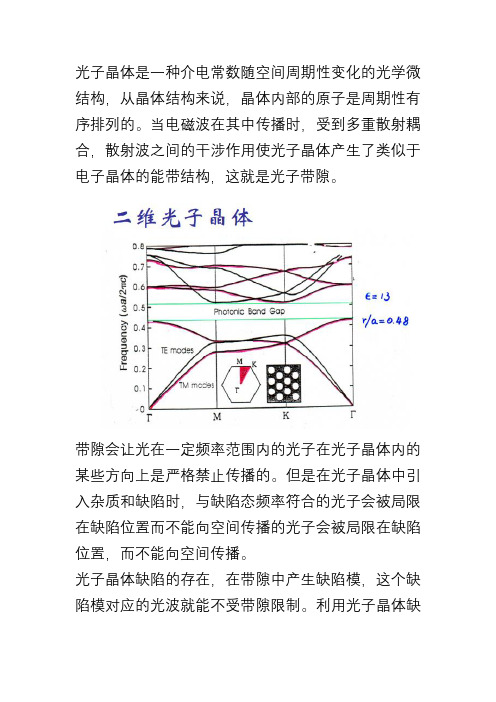
模型定义 上图描述的是由砷化镓圆柱阵列组合而成的空气“通道”。通过移去一些 柱子形成一个具有90°弯曲的波导。该模型的目的是研究TE波如何通过 晶体传播。这些模型使用标量计算公式,设横向电场分量为EZ :
其中,n是折射率,k0是自由空间波数。 由于没有物理边界,可以在所有边界使用散射边界条件。设振幅EZ在入 射波的边界上为1。 结果和讨论 图1包含了电场的z分量的曲线图。它清楚地展示了光波通过波导的传 播。
1.55。 6. 在曲率因子编辑字段中,键入0.65。 7. 单击建立全部按钮
研究 第1步:频域
1. 在模型建立器窗口中,展开研究1的节点,然后单击步阶1:频 域。
2. 在频域的设置窗口中,找到研究设定部分 3. 在频率编辑字段中,键入3e8/1e-6 3e8/1.2e-6。这将让你得到一
个自由空间波长为1微米和一个自由空间波长为 1.2微米的解 4. 在研究工具栏上,单击计算
材料2 1. 在主页面上,单击新材料 2. 右键单击材料2和选择重命名
3. 去重命名材料对话框,并在新名称编辑字段中键入空气 4. 单击确定 5. 仅仅选择域2 6. 在材质的设置窗口中,单击材料属性部分 7. 在材质属性树中,选择电磁模型>折射率>折射率(n) 8. 单击新增至材料 9. 找到材料目录部分。在该表中,输入以下设置
光子晶体波导的非线性效应研究

光子晶体波导的非线性效应研究光子晶体波导是一种基于光子晶体结构的光学波导器件,其特点是具有高度指向性和可调谐性。
光子晶体波导的非线性效应是其重要的性能之一,研究这种非线性效应能够扩展其应用领域并提高其性能。
非线性效应是指光的电荷和极化率与光强之间的关系不是线性的。
光子晶体波导的非线性效应可以通过在光子晶体中引入材料的二阶或高阶非线性极化来实现。
通过控制非线性材料的位置和分布,可以调节光子晶体波导的非线性效应。
光子晶体波导的非线性效应主要包括自相位调制、自频移效应和非线性光激发效应。
自相位调制是指光子晶体波导的折射率会随着光的强度发生变化。
当光子晶体波导处于正常色散情况下时,当光的强度增大时,折射率也会随之增大,从而引起相位的变化。
这种自相位调制效应可以用于光通信中的光波长转换和光开关等应用。
自频移效应是指光子晶体波导中的光会随着传输距离的增加而发生频率的变化。
这种效应可以通过调节光子晶体波导的尺寸和折射率来实现。
自频移效应可以用于光时钟和光频率转换等应用。
非线性光激发效应是指通过外界激励使光子晶体波导中的非线性极化发生变化,从而产生新的频率成分。
这种效应可以通过在光子晶体波导中引入非线性材料或外部控制光束进行实现。
非线性光激发效应可以用于光频率梳、光调制和光源等应用。
光子晶体波导的非线性效应研究需要综合使用光学理论分析、电磁场模拟和实验验证等方法。
首先,可以通过光学理论分析对光子晶体波导的结构进行设计和优化。
其次,通过电磁场模拟可以模拟和分析光子晶体波导中的光场分布和非线性效应。
最后,通过实验验证可以验证和优化光子晶体波导的非线性效应。
光子晶体波导的非线性效应研究具有重要的科学意义和广阔的应用前景。
它不仅可以在光通信、光传感和量子通信等领域发挥作用,还可以为光电子集成和光量子计算等领域提供基础支持。
因此,加强光子晶体波导的非线性效应研究,对于推动光子学科学的进展和实现新的光学器件和系统具有重要意义。
光子晶体光纤中的光子波导与耦合效应研究

光子晶体光纤中的光子波导与耦合效应研究光子晶体光纤是一种具有周期性折射率分布的光纤结构,得益于其特殊的光导特性,它在光子学领域中具有广泛的应用前景。
其中,光子波导与耦合效应是光子晶体光纤研究的重要内容。
光子波导是指在光子晶体光纤中存在的具有较低折射率的区域,光信号主要通过该区域传输。
光子波导的存在使得光子晶体光纤具有了优异的光导特性,能够有效地限制光信号的传播方向和范围。
通过调控光子波导的形状和尺寸,可以实现对光信号的控制和调制,从而实现更加灵活多样的光传输功能。
而光子波导与耦合效应是指光子波导之间的光信号相互作用和传输现象。
光子波导与耦合效应可以用来实现光信号在光子晶体光纤中的传输和切换。
例如,在一个光子波导中注入光信号,通过控制光信号与相邻光子波导之间的耦合强度,可以使光信号从一个光子波导传输到另一个光子波导中。
这种光子波导与耦合效应被广泛应用于光子晶体光纤中的光调制和光开关等光学器件的设计与制备。
针对光子波导与耦合效应的研究,科学家们通过数值模拟和实验方法进行探索。
其中,光子晶体光纤光学器件的设计和优化是非常关键的一环。
设计合理的光子晶体光纤结构和波导参数可以实现较强的光导功能和稳定的光传输特性。
通过结合光学材料的特性,科学家们可以制备不同类型的光子波导结构,如点缺陷波导、线缺陷波导等,以实现不同的光学功能和应用需求。
另外,光子晶体光纤中的光子波导与其他光纤之间的耦合效应也是研究的重要内容。
由于光纤之间存在不同结构和折射率的差异,光信号在耦合过程中会发生模式耦合和能量损耗等现象。
通过研究光子波导与其他光纤之间的耦合效应,可以优化光信号的传输效率和稳定性,并为光子晶体光纤的实际应用提供参考和指导。
总的来说,光子晶体光纤中的光子波导与耦合效应是光子晶体光纤研究的重要方向。
科学家们通过设计合理的光子晶体光纤结构和优化波导参数,以及研究光子波导与其他光纤之间的耦合效应,不断推动着光子晶体光纤在光通信、传感和光学器件等领域的应用。
光子晶体与光波导

光子晶体与光波导光子晶体与光波导是光子学领域中两个关键概念,它们在光学器件的设计与应用中具有重要作用。
光子晶体是一种具有周期性折射率分布的材料,它通过光子之间的布拉格散射来调控光的传播。
而光波导则是一种用于在光学器件中引导光传播的结构。
一、光子晶体光子晶体是一种周期性变化折射率的材料,其结构类似于晶体学中的晶格。
它通过周期性的折射率分布,在特定的频率范围内形成禁带(光子禁带),使禁带内的光无法传播。
而禁带之外的光则可以在光子晶体中传播。
光子晶体可以根据其周期性分布的不同,分为一维、二维和三维光子晶体。
1. 一维光子晶体一维光子晶体是最简单的光子晶体结构。
它具有周期性的折射率变化,常见的例子是光纤光栅。
一维光子晶体通过周期性的折射率变化,可以在特定的频率范围内抑制光的传播,形成光子禁带。
这使得一维光子晶体在光滤波、光调制和光传感等领域中得到广泛应用。
2. 二维光子晶体二维光子晶体是由周期性排列的柱状或球形结构组成的。
它的周期性分布使得特定频率的光无法传播,形成二维光子禁带。
二维光子晶体可以通过调控结构尺寸和材料折射率来改变光子禁带的频率范围。
二维光子晶体在激光器、光波导和光传感器等领域中有着重要的应用。
3. 三维光子晶体三维光子晶体是一种具有立体结构的光子晶体,可以在三个空间方向上调控光的传播。
它通过周期性的结构分布,形成三维光子禁带,具有非常广阔的应用前景。
三维光子晶体在光学传感、激光器、全息成像等领域中发挥着重要的作用。
二、光波导光波导是一种用于引导光传播的结构。
它可以将光能量从一个地方传输到另一个地方,实现光的灵活控制和调制。
常见的光波导结构包括平板波导、光纤波导和光子晶体波导。
1. 平板波导平板波导是一种将光能限制在一个平面内传播的波导结构。
它通常由两个具有不同折射率的材料层组成,利用折射率的差异来引导光传播。
平板波导广泛应用于光通信和光集成电路等领域。
2. 光纤波导光纤波导是一种利用光纤结构传输光能的波导结构。
光子晶体波导

2007年意大利Trento大学F. Riboli,P. Bettotti等人研究了基于硅狭缝波导的一维光子晶体中的带隙特性和慢光效应。
该研究组还数值分析了耦合谐振腔光波导的特性,采用5个耦合腔级联的系统的群速率约为C/100,这种结构能够提高非线性相位的灵敏度。
(Band gap characterization and slow light effects in one dimensional photonic crystals based on silicon slot-waveguides----- F. Riboli,P. Bettotti,L. Pavesi)2010年北京邮电大学Xuan Zhang等人研究了狭缝光子晶体波导的特性并进行了结构优化。
通过调整第一行与第二行的空气狭缝的宽度和空孔的半径研究导模的特性。
研究发现当增加空气槽的宽度和空气孔半径时导模转移至高频。
文中通过分析场分布和传输特性优化波导。
这种波导可应用于传感器、补偿器、光延迟线、光缓存。
光子晶体波导(PCW)能应用于实现传感,因为它具有尺寸小、易于集成、工作于室温下、带宽宽、在任意波长实现慢光的优势。
<3D-PWE(plane wave expansion)>(The properties and structure optimization of slot photonic crystal waveguide------Xuan Zhang, Huiping Tian, Daquan Yang, Yuefeng Ji)2011年英国St.Andrews大学的M. G. Scullion等人研究了狭缝光子晶体波导的高效耦合接口。
研究组采用基于设计模式色散理论和共振理论提高耦合效率。
通过优化结构,设计了耦合谐振腔式的接口,计算出每个接口在100nm带宽损耗为0.3dB,证明了每个接口在78带宽相应的实验值为 1.5dB。
光子晶体波导谐振腔的设计和应用

光子晶体波导谐振腔的设计和应用光子晶体波导谐振腔是现代光学领域中的一个热门话题。
它利用光子晶体结构的周期性,形成具有独特光学性质的器件。
在纳米电子学、光电子学和量子信息处理等领域,光子晶体波导谐振腔的应用前景非常广阔。
本文将介绍光子晶体波导谐振腔的设计方法和常见的应用领域。
一、光子晶体波导谐振腔的设计方法一般来说,光子晶体波导谐振腔的设计是基于光子晶体的周期性。
在光子晶体中,周期性阵列的折射率异常会形成光子带隙,这种禁带结构可以被用来控制光的传播和捕获特定波长的光子,从而实现谐振腔的效果。
设计光子晶体波导谐振腔首先需要确定光子晶体的材料和结构,一般采用等间距布局的周期性结构。
随后,需要计算光子带隙的位置和宽度,从而确定合适的谐振腔模式。
最后,在确定谐振腔模式后,可以将晶体结构做微调,以提高谐振腔的 Q 值和光谱纯度。
在设计光子晶体波导谐振腔的过程中,有效性和可优化性都是需要考虑的因素。
有效性可以保证谐振腔在制备后可以正常工作,可优化性则可以帮助我们在实验条件下提高谐振腔的性能。
二、光子晶体波导谐振腔的应用目前,光子晶体波导谐振腔已经在多个领域得到应用。
1. 显示技术在显示技术中,光子晶体波导谐振腔可以实现快速的光开关,为光学计算和量子信息处理提供了必要的基础。
光开关可以通过利用谐振腔来控制光子的传播与捕获。
2. 生物医学诊断在生物医学诊断中,光子晶体波导谐振腔可以被用来测量生物分子的互作和生化反应,从而提高医学诊断的准确性。
利用谐振腔纳秒级别的响应时间可以实现高精度的分子检测和分析。
3. 纳米电子学与光电子学在纳米电子学和光电子学领域,光子晶体波导谐振腔可以被用来制备高度集成的耦合器和光发射器,具有较高的速度和稳定性。
此外,在微腔共振中,还可以利用谐振腔增强电子的相互作用,并建立光子和自旋之间的耦合。
总之,光子晶体波导谐振腔作为一种新型的纳米光子学结构,具有广阔的应用前景。
不仅可以应用于显示技术和生物医学诊断,还可以为纳米电子学和光电子学等领域的研究提供新的思路。
光子晶体玻璃材料开发及其光波导特性解析

光子晶体玻璃材料开发及其光波导特性解析光子晶体是一种由周期性介质构成的光学材料,结构上类似于晶体。
光子晶体材料在光子学领域具有广泛的应用潜力,特别是在光波导领域。
本文将对光子晶体玻璃材料的开发以及其光波导特性进行解析。
1. 光子晶体玻璃材料的开发光子晶体玻璃是一种具有周期性结构的光学材料,它的孔隙具有类似于晶体的周期性排列,可以通过调整孔隙的大小和形状来调控光的传播和波导特性。
光子晶体玻璃材料的开发需要以下步骤:1.1 设计结构:根据所需的特性,设计合适的光子晶体玻璃结构。
结构的周期性和孔隙的大小直接影响材料的光学性能。
1.2 材料选择:选择合适的玻璃材料作为基底,通常选择导热性较好且折射率适中的材料。
1.3 制备方法:选择适合的制备方法,如溶胶-凝胶法、干胶共挤出法等。
制备过程需要严密控制温度、时间和溶液浓度等参数,以获得高质量的光子晶体玻璃材料。
1.4 表征和测试:通过光学测试和结构表征,评估光子晶体玻璃材料的性能。
对材料的透过率、折射率、色散等进行测量,以确定其光学特性是否满足需求。
2. 光子晶体玻璃材料的光波导特性光子晶体玻璃材料的最大特点之一是其优异的光波导特性。
光波导是指光在材料中的传播过程,光子晶体玻璃材料由于其孔隙结构的特殊性,具有以下光波导特性:2.1 禁带和频带隙:光子晶体玻璃材料的周期孔隙结构可以形成禁带和频带隙,不同波长的光在禁带内受到阻挡,只有特定波长的光能在材料中传播。
2.2 引导模式:光子晶体玻璃材料可以通过调整孔隙的结构和尺寸来实现对不同模式的光波的选择性传输,从而实现光的定向传输和控制。
2.3 波导损耗:光子晶体玻璃材料具有低损耗的特性,在光波导传输中能够保持较高的传输效率。
2.4 色散特性:光子晶体玻璃材料的光波导特性可以通过调节孔隙结构和材料的折射率来实现对色散的控制,从而应用于光纤通信等领域。
3. 光子晶体玻璃材料的应用前景光子晶体玻璃材料由于其独特的结构和优异的光波导特性具有广阔的应用前景,具体应用包括但不限于以下几个领域:3.1 光纤通信:光子晶体玻璃材料的低损耗和色散特性使其成为光纤通信领域中的理想材料,可以实现高速、大容量的光信号传输。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( r ) e iK r u( r )
满足周期算符本征方程的本征函数,必由一个平面波因子和 一个周期函数组成,即Bloch 波。 K Bloch 波矢
(r ) 是一个周期性调幅的平面波
11
第11章 光子晶体波导
11.1 光子晶体理论
11.1.2 平面波展开法 本征值方程
2 ˆ FH H 2
8
第11章 光子晶体波导
11.1 光子晶体理论
11.1.2 平面波展开法
光子晶体研究方法 : 平面波展开法、传输矩阵法、时域有限 差分法、多重散射法、有限元法等 平面波展开法:将电磁波按平面波形式展开,把求解麦氏方 程问题转化为求解本征方程本征值问题 光子晶体中电磁波的色散关系或能带结构。 E E(r )e it H H (r )e it 单色波
不完全光子带隙
完全光子带隙:一定频率范围内的光子无论其偏振方向或传 播方向如何都被禁止传播,是全方位的光子带隙。 不完全光子带隙:只对特定的偏振态或在特定方向上才存在 的光子带隙。
16
第11章 光子晶体波导
11.1 光子晶体理论
11.1.3 二维光子晶体带隙结构
归一化频率a/
(a) 本底折射率n=3.6
布拉维格子 一种基元构成 复式格子 两种及以上基元构成
图11.2 原胞与基矢 周期:基元沿空间三个方向等效平移的最小距离 a1 (a2 a3 )
原胞:以格点为顶点、周期为边长的平行六面体,最小单元 基矢:原胞三边的矢量。原胞选取不唯一,但体积相同 晶格矢: 任一格点 R la1 ma2 na3 l、m、n为整数
ˆ ( r )和T 对易,二者有共同的本征函数 算符F
T ( r Rl ) T n ( r nRl ) n
方程的本征值:
1
ei K R
l
10
第11章 光子晶体波导
11.1 光子晶体理论
11.1.2 平面波展开法
l
方程的本征值: ei K R
对一维和二维问题,矢量方程可分离成两个独立的TE和 TM模方程,每种 模 式 场 只有三个分量不为零 。 三维问题 的 解为混合模,但结构如果具有镜像对称性,则波矢一定在反 射面内,这时模式分为奇模和偶模,分别类似于TM模和TE 模。因此为简单起见只需要分析偏振模式就可以了。 设磁场沿z方向,将 H K 在倒格子空间按分立的傅里叶级数展开 H K z0 hm e iG r H iK 1 iK H c
图 11.6 正 方 格 子 光 子 晶 体 的 TE 模与 TM 模带隙结构 ( 介质 柱折射率3.34,柱半径r=0.2a)
归一化频率a/
15
第11章 光子晶体波导
11.1 光子晶体理论
11.1.3 二维光子晶体带隙结构
图11.7 三角格子光子晶体的TE模与TM模带隙结构 (本底介质折射率n=3.60,孔半径r=0.46a)
G R 2n
6
第11章 光子晶体波导
11.1 光子晶体理论
11.1.1 光子晶体结构与两种晶格
二维正、倒格子基矢 正方晶格
晶格常数a
a2 ay0 b2 2 y0 a
a2 a x0 3 y0 2 b2 4 y0 3a
a1 ax0 b1 2 x0 a
三角晶格
2
第11章 光子晶体波导
11.1 光子晶体理论
11.1.1 光子晶体结构与两种晶格
(a) 一维
(b) 二维
(c) 三维
图11.1 光子晶体结构示意图
3
第11章 光子晶体波导
11.1 光子晶体理论
11.1.1 光子晶体结构与两种晶格
光子晶体和普通晶体在结构和研究方法上有一定的类比性, 借用了许多固体物理中的概念,如晶格(lattice)、布拉维格 子(bravais lattice)、原胞(primitive cell)、倒格子(reciprocal lattice)、布里渊区(Brillouin zone)、布洛赫(Bloch)函数等。 位置空间的晶格 (正格子) 晶体:基元,周期性空间点阵 格点,晶格
可以在平行六面体顶角上,也可以在面心或体心处。 基矢沿空间对称轴方向,一般用 a 、b 、 c 表示。如立方晶体 的晶胞有简立方(SCC)、体心立方(BCC)、面心立方(FCC)等。 超晶胞:大体积晶胞。
5
第11章 光子晶体波导
11.1 光子晶体理论
11.1.1 光子晶体结构与两种晶格
倒易空间的晶格(倒格子)
1 E 2 E r c2
2 1 H 2 H r c
非均匀介质
ˆ 1 F
H 0
0
磁场始终连续,求解关于磁场的方程较为方便 算符
r
2 ˆ FH H 本征值方程 2c9来自第11章 光子晶体波导
11.1 光子晶体理论
11.1.2 平面波展开法 本征值方程
倒格子基矢: 一组与三维位置空间基矢正交的矢量 定义
b1 2π a2 a3 Ω b2 2π a3 a1 Ω b3 2π a1 a2 Ω 由 b1 b2 b3
ai b j 2 ij
图11.4基矢与倒格子基矢
倒格子:
构成的新点阵
h1、h2、h3为整数
倒格矢: 任一倒格点 G h1b1 h2b2 h3b3 倒格矢与晶格矢满足
14
第11章 光子晶体波导
11.1 光子晶体理论
11.1.3 二维光子晶体带隙结构
光子晶体最大的特征:存在光子带隙 • 影响光子带隙的主要因素: 光子晶体的晶格结构 K 介电常数比 填充率等 • 二维:正方、六角和三角晶格等 • 孔/柱形状:圆形、六角形、方形等
y
Kx
二维情况 TE模: 磁场平行于介质分界面,Hz、Ex、Ey TM模:电场平行于介质分界面,Ez、Hx、Hy。
4
第11章 光子晶体波导
11.1 光子晶体理论
11.1.1 光子晶体结构与两种晶格
维格纳-塞茨原胞 (W-S原胞) 以一个格点为原点,作原点与其 邻近格点连线的中垂面或中垂线, 由这些中垂面或中垂线围成的最 图11.3 W-S原胞、晶胞与晶胞基矢 小体积或面积。 结晶学原胞(晶胞)或布拉维原胞 按对称性选取的单元,格点
令 rn r nRl
K
n
待定波矢
( rn ) e iK r r ( r )
( rn ) e iK r ( r ) e iK r
n
令 ( r ) e iK r u( r )
坐标表象中 u(r ) 是周期函数
u( r ) u( r nRl )
布里渊区
任选一倒格点为原点 (波矢 为0),作出它最近邻点的倒 格点矢量,并作出每个矢量 的垂直平分面或线,这些面 或线所围成区域就是倒格子 W-S原胞,称作第一布里渊 区(1BZ)。次邻近点倒格矢 的垂直平分面或线,与第一 布里渊区边界所围的区域为 2BZ,依次类推。
图11.5 二维倒格子与布里渊区
a1 ax0
b1 2 ( x0 3 y0 ) a 3
倒格子基矢量纲是米-1,倒格子空间实际是一波矢空间,它 的引入简化了坐标空间周期函数的数学表示。 波矢是描述光波传输的重要物理量,倒格子基矢在光子晶体 分析中起着重要作用。
7
第11章 光子晶体波导
11.1 光子晶体理论
11.1.1 光子晶体结构与两种晶格
第11章 光子晶体波导
11.1 光子晶体理论
11.2 光子晶体波导
1
第11章 光子晶体波导
普通晶体 原子、分子、离子等周期排布,形成周期势场。 薛定谔方程电子能带结构,带与带之间有带隙(禁带)。 光子晶体(photonic crystal,PC) 不同介电常数的介质在空间按一定的周期结构排布,排布 周期与光波长相当。 电磁场方程电磁波的传输特性具有和半导体电子能带类 似的电磁波能带结构,这种能带结构称为光子能带 (photonic energy band)。能带间的区域称为光子禁带或光 子带隙 (PBG:photonic band gap) 电磁波频率在带隙内时,则不能在光子晶体中传播。
r r
2 ˆ FH H 2
c
ˆ 1 F
r
1 (r ) 1 (r R ) l
( Rl l1a1 l2a2 l3a3 )
ˆ (r ) F ˆ (r R ) F l
位移算符 T ( Rl )表示移位r 至r Rl
ˆ (r ) H F ˆ (r R ) H (r R ) F ˆ (r )TH TF l l
归一化频率a/
(b) 孔半径r=0.45a
图11.8 三角格光子晶体带隙宽度与位置 随孔径和本底折射率的变化
17
第11章 光子晶体波导
11.2 光子晶体波导
11.2.1 二维光子晶体波导
线缺陷
• 频率落在带隙内的光子态密度为零,光波无法在介质传播。 • 引入线缺陷,光波就被限制在这个线通道内传导。 介电常数缺陷 结构缺陷 • 光子晶体波导(PCW)是依靠光子带隙约束光波,与中心填 充材料的性质无关。可极大程度减小光与物质的相互作用, 如电介质材料对光的吸收、色散和非线性特性等。
y/a
线缺陷
x/a
•线缺陷模的场分布(Ez) (K=X,m=8,a/=0.3067)
(b) 一般本征模场的Ez分布 (K=X,m=6,a/=0.2279)
