最新线段、射线、直线知识点总结及习题

合集下载

七年级数学上册第四章知识点及练习题

七年级数学上册第四章知识点及练习题第四章：平面图形及其位置关系知识梳理一、线段、射线、直线1、线段、射线、直线的定义线段是有两个端点的崩直线，可以量出长度。

将线段向一个方向无限延伸就形成了射线，射线有一个端点，无法量出长度。

将线段向两个方向无限延伸就形成了直线，直线没有端点，也无法量出长度。

结论：射线是直线的一部分，线段是射线和直线的一部分。

2、线段、射线、直线的表示方法线段的表示方法有两种：一是用两个端点来表示，二是用一个小写的英文字母来表示。

射线的表示方法只有一种：用端点和射线上的另一个点来表示，端点要写在前面。

直线的表示方法有两种：一是用直线上的两个点来表示，二是用一个小写的英文字母来表示。

3、直线公理过两点有且只有一条直线，简称两点确定一条直线。

4、线段的比较线段的比较有叠合比较法和度量比较法。

5、线段公理连接两点的线段是最短的，叫做这两点的距离。

6、线段的中点如果线段上有一点，把线段分成相等的两条线段，这个点叫这条线段的中点。

若C是线段AB的中点，则AC=BC=1/2 AB或AB=2AC=2BC。

例题：1、如果线段AB=5cm，BC=3cm，那么A、C两点间的距离是（）解：无法确定A、B、C三点位置是否共线，无法确定答案，选D。

2、已知线段AB=20㎝，C为AB中点，D为CB上一点，E为DB的中点，且EB=3㎝，则CD= ________cm．解：BC=0.5AB=10cm，DB=2EB=6cm，CD=BC－DB=10－6=4cm。

3、平面上有三个点，可以确定直线的条数是（）解：由直线公理，过两点有且只有一条直线，所以三个点可以确定三条直线，选C。

二、角1、角的概念角是由两条有共同端点的射线组成的图形，两条射线叫角的边，共同的端点叫角的顶点。

角还可以看成是一条射线绕着他的端点旋转所成的图形。

2、角的表示方法角用“∠”符号表示，分别用两条边上的两个点和顶点来表示（顶点必须在中间），或在角的内部写上阿拉伯数字或小写的希腊字母来表示。

直线、射线、线段(知识点总结、例题解析)

第四章几何图形初步4.2 直线、射线、线段一、知识考点知识点1【直线】1、直线：把线段向两端无限延伸形成的图形叫做直线。

2、特点：是直的；无粗细之分；无端点；不可以度量；不可以比较长短，无限长。

3、基本性质：经过两点有且只有一条直线（两点确定一条直线）；4、直线有两种表示方法:（1）用直线上任意两点的大写字母,如:表示为直线AB 或直线BA 。

（2）也可以用一个小写字母表示,如:直线l5、直线和点的位置关系：（1）在直线上:点O 在直线l 上,或者说说直线l 经过点O（2）点在直线外:点P 在直线l 外,或者说说直线l 不经过点P6、交点：当两条不同的直线有一个公共点时，我们就称这两条直线相交，这个公共点叫做他们的交点。

O Pl知识点2【射线】1、射线：将线段向一个方向无限延长，就形成了射线，射线有一个端点。

2、特点：是直的,有一个端点,不可以度量,不可以比较长短,无限长。

3、射线有两种表示方法：（1）可以用两个大写英文字母表示，其中一个是射线的端点,另一个是射线上除端点外的任意的一点,端点写在前面。

(如图：可以记作射线OM,但不能记作射线MO) （2）可以用一个小写英文字母表示,比如:射线OM也可以记为射线l。

4、射线的画法：画射线一要画出射线端点，二要画出射线经过一点,并向一旁延伸的情况。

知识点3【线段】1、线段：直线上两个点和它们之间的部分叫做线段，这两个点叫做线段的端点。

2、特点：线段是直的,它有两个端点,他的长度是有限的,可以度量的,可以比较长短。

3、基本性质：(1) 线段公理：两点之间的所有连线中,线段最短（两点之间，线段最短）(2) 两点之间的距离：两点之间线段的长度，叫做这两点之间的距离。

注意：两点间的距离是指线段的长度,是一个数值,而不是指线段本身。

(3) 线段的中点到两端点的距离相等。

(4) 线段的大小关系和它们的长度的大小关系是一致的4、线段有两种表示方法：（1）可以用它的两个端点的大写英文字母来表示，如线段AB（或线段BA）（2）可以用一个小写字母来表示,如线段a5、线段的画法：用直尺和尺规作图（尺规作图）已知：线段a(如图所示),用直尺和圆规画一条线段,使它等于已知线段a第一步：任意画一条射线AC第二步：用圆规量取已知线段a的长度。

直线射线线段试题及答案

直线射线线段试题及答案1. 直线、射线和线段的定义是什么？答案：直线是无限延伸的，没有端点；射线有一个端点，无限延伸；线段有两个端点，长度有限。

2. 如何用字母表示一条直线？答案：直线可以用两个大写字母表示，如直线AB。

3. 线段的中点如何确定？答案：线段的中点可以通过将线段的两个端点的坐标相加后除以2得到。

4. 射线的端点如何表示？答案：射线的端点可以用一个字母表示，如射线OA。

5. 直线和线段的主要区别是什么？答案：直线是无限长的，没有端点；线段是有限的，有两个端点。

6. 线段的延长线是什么？答案：线段的延长线是将线段的一端无限延伸出去的直线。

7. 线段的对称轴是什么？答案：线段的对称轴是一条通过线段中点且垂直于线段的直线。

8. 如何用几何语言描述一个线段？答案：线段可以用两个端点的坐标表示，如线段AB，其中A(x1,y1)，B(x2, y2)。

9. 射线可以被延长吗？答案：射线本身是无限延伸的，但可以延长其定义，使其成为一条新的射线。

10. 直线和射线的共同点是什么？答案：直线和射线都是无限延伸的，但直线没有端点，而射线有一个端点。

11. 线段的垂直平分线是什么？答案：线段的垂直平分线是一条通过线段中点且垂直于线段的直线。

12. 如何用几何画图工具画出一条射线？答案：首先确定射线的端点，然后从端点开始沿着射线的方向无限延伸。

13. 线段可以被分割成几个部分吗？答案：是的，线段可以被分割成几个长度不同的部分。

14. 直线上的点可以无限多吗？答案：是的，直线上的点可以无限多，因为直线是无限延伸的。

15. 线段的延长线和射线有什么区别？答案：线段的延长线是线段的延伸，而射线是从一个端点开始无限延伸的。

直线、射线、线段知识点总结(含例题)

直线、射线、线段知识点1．直线（1）定义：一点在空间沿着一个方向及它的相反方向运动，所形成的图形就是直线．（2）直线公理：经过两点___________直线，并且___________直线．简单说成：___________．（3）表示方法：直线AB或直线a．（4）当两条不同的直线有一个公共点时，我们就称这两条直线___________，这个公共点叫做它们的___________．2．射线（1）定义：直线上的一点和它一旁的部分叫做射线．（2）特征：是直的，有一个端点，不可以度量，不可以比较长短，无限长．（3）表示方法：射线AB或射线a．3．线段（1）定义：直线上两个点和它们之间的部分叫做线段．（2）特征：线段是直的，它有两个端点，它的长度是有限的，可以度量，可以比较长短．（3）表示方法：线段AB或线段a．（4）两点的所有连线中，___________最短．简单说成：两点之间，___________．（5）连接两点间的___________，叫做这两点的距离．4．方法归纳：（1）过一点的直线有___________；直线是是向___________方向无限延伸的，无端点，不可度量，不能比较大小；（2）要注意区别直线公理与线段的性质：直线公理是指___________，线段的性质是指两点之间线段最短；在线段的计算过程中，经常涉及线段的性质、线段的中点以及方程思想．（3）延伸与延长是不同的，线段不能___________，但可以___________，直线和射线能___________，但是不能___________；（4）直线和线段用两个大写字母表示时，与字母的前后顺序___________，但射线必须是表示端点的字母写在前面，不能互换；（5）直线中“有且只有”中的“有”的含义是___________，“只有”的含义是，“有且只有”与“确定”的意义相同；（6）射线：一要确定___________，二要确定___________，二者缺一不可．K知识参考答案：1．（2）有一条，只有一条，两点确定一条直线；（4）相交，交点3．（4）线段，线段最短；（5）线段的长度4．（1）无数条，两个（2）两点确定一条直线（3）延伸，延长，延伸，延长（4）无关（5）存在性，唯一性（6）端点，延伸方向K—重点（1）直线公理；（2）线段的性质K—难点直线、射线、线段的概念K—易错直线、射线、线段的联系和区别一、直线、射线、线段【例1】下列说法中正确的个数为①射线OP和射线PO是同一条射线；②连接两点的线段叫两点间的距离；③两点确定一条直线；④若AC=BC，则C是线段AB的中点．A．1个B．2个C．3个D．4个【答案】A【解析】①射线OP端点是O，从O向P无限延伸，射线PO端点是P，从P向O无限延伸，所以不是同一条射线，故①错误；【名师点睛】（1）直线、射线、线段的表示方法①直线：用一个小写字母表示，如：直线l，或用两个大写字母（直线上的）表示，如直线AB．②射线：是直线的一部分，用一个小写字母表示，如：射线l；用两个大写字母表示，端点在前，如：射线OA．注意：用两个字母表示时，端点的字母放在前边．③线段：线段是直线的一部分，用一个小写字母表示，如线段a；用两个表示端点的字母表示，如：线段AB（或线段BA）．（2）点与直线的位置关系：①点经过直线，说明点在直线上；②点不经过直线，说明点在直线外．二、直线的性质（1）直线公理：经过两点有且只有一条直线．简称：两点确定一条直线．（2）经过一点的直线有无数条，过两点就唯一确定，过三点就不一定了．【例2】平面上有四点，过其中每两点画出一条直线，可以画直线的条数为A．1或4 B．1或6C．4或6 D．1或4或6【答案】D【解析】如图所示：分别根据四点在同一直线上、三点在同一条直线上、任意三点均不在同一条直线上描出各点，再根据两点确定一条直线画出各直线可知：平面上有四点，过其中每两点画出一条直线，可以画直线的条数为1或4或6．故选D．三、线段的性质线段公理：两点的所有连线中，可以有无数种连法，如折线、曲线、线段等，这些所有的线中，线段最短．简单说成：两点之间，线段最短．【例3】把一条弯曲的公路改为直路，可以缩短路程，其理由是A．两点之间，线段最短B．两点确定一条直线C．线段有两个端点D．线段可以比较大小【答案】A【解析】把一条弯曲的公路改为直路，其理由是：两点之间，线段最短．故选A．四、两点之间的距离（1）两点间的距离连接两点间的线段的长度叫两点间的距离．（2）平面上任意两点间都有一定距离，它指的是连接这两点的线段的长度，学习此概念时，注意强调最后的两个字“长度”，也就是说，它是一个量，有大小，区别于线段，线段是图形．线段的长度才是两点的距离．可以说画线段，但不能说画距离．【例4】已知线段AB=8cm，在线段AB的延长线上取一点C，使线段AC=12cm，那么线段AB和AC中点的距离为A．2cm B．3cm C．4cm D．5cm【答案】A五、比较线段的长短（1）比较两条线段长短的方法有两种：度量比较法、重合比较法．就结果而言有三种结果：AB>CD、AB=CD、AB<CD．（2）线段的中点：把一条线段分成两条相等的线段的点．（3）线段的和、差、倍、分及计算做一条线段等于已知线段，可以通过度量的方法，先量出已知线段的长度，再利用刻度尺画条等于这个长度的线段，也可以利用圆规在射线上截取一条线段等于已知线段．【例5】如图，四条线段中，最短和最长的一条分别是A．ac B．bdC．ad D．bc【答案】B【解析】通过观察测量比较可得：d线段长度最长，b线段最短．故选B．。

线段、射线、直线讲义知识点经典例题练习

线段、射线、直线【知识要点梳理】1.填表：2. 关于线段的等分点3．两点间的距离4. 点和直线的位置关系【典型例题探究】例1 （1）下列说法正确的有①一条线段上只有两个点②线段AB与线段BA是同一条线段③经过两点的直线只有一条④射线AB与射线BA是同一条射线⑤线段AB是直线AB的一部分⑥ 两点之间，线段最短⑦ 端点不同的射线一定不是同一条射线 ⑧ 端点相同的射线一定是同一条射线（2）下列说法正确的是( )A.过A 、B 两点直线的长度是A 、B 两点间的距离B.线段AB 就是A 、B 两点间的距离C.在连结A 、B 两点的所有线中,其中最短线的长度是A 、B 两点间的距离D.乘火车从上海到北京要走1462千米,所以上海站与北京站之间的距离是1462千米（3）已知点M 在线段AB 上,在①AB=2AM;②BM=21AB;③AM=BM;④AM+BM=AB 四个式子中，能说明M 是线段AB 的中点的式子有（）A ．1个 B. 2个 C. 3个 D. 4个（4）在直线上顺次取A 、B 、C 三点，使得AB=9cm ，BC=4cm ，如果点O 是线段AC 的中点，则线段OB 为（）cmA ．2.5 B. 3.5 C. 1.5 D. 5(5) 如果线段AB=13 cm ，MA+MB=17 cm ，那么下面说法正确的是（） A ．M 点在线段AB 上 B ．M 点在直线AB 上 C ．M 点在直线AB 外D ．M 点在直线AB 上，也可能在AB 直线外（6）如图，3个机器人，A 、B 、C 排成一直线做流水作业，它们都要不断地从一个固定的零件箱中拿零件，则零件箱放在处最好．（使得各机器人所走的路程总和最小）例2. 往返于A 、B 两地的火车，中途经过三个站点，(假设该车只有硬座,且各站距离不等)问：（1）有多少种不同的票价和车票？（2）如果中途有n 个站点呢？例3. 已知线段MN,在MN 的延长线上取一点P,使MP=2NP ，再在MN 的反延长线上取一点Q,· · ·A B C使MQ=2MN,那么MP 是PQ 的( )A. 3B. 32 C. 21 D. 23例4. 如图，A 、B 、C 、D 是直线l 上顺次四点，M 、N 分别是AB 、CD 的中点，若MN=a ，BC=b ，求AD 的长.例5. 如图，已知B 、C 两点把线段AD 分成2:4:3三部分，M 是AD 的中点，CD=6，求线段MC 的长.* 例6. 已知线段AB=6cm,在直线AB 上画线段BC=4cm,若M 、N 分别是AB 、BC 中点 (1)求M 、N 间的距离.(2)若AB=acm,BC=bcm,其它条件不变,此时M 、N 间的距离是多少?* 例7.（五羊杯邀请赛试题）如图所示，已知B 是线段AC 上的一点，M 是线段AB 的中点，N 为线段AC 的中点，P 为NA 的中点，Q 为MA 的中点．求MN:PQ 的值．E E E E E EA M N lA DBC M【基础达标演练】1. 下列写法中正确的是（） A ．直线AB 、CD 相交于点n B. 直线ab 、cd 相交于点N C ．直线ab 、cd 相交于点nD. 直线AB 、CD 相交于点N2. 下列叙述正确的是（）①线段AB 可表示为线段BA ②射线AB 可表示为射线BA ③直线AB 可表示为直线BA A ．①② B. ①③ C. ②③ D. ①②③3.用一个钉子把一根细木条钉在木板上，用手拨木条，木条能转动，这说明；用两个钉子把细木条钉在木板上，就能固定细木条，这明 .4. 连结两点的____________________________________,叫做两点间的距离.5. (咸宁中考)如图,A 、B 、C 、D 是直线l 上顺次四点, 且线段AC=5,BD=4,则线段AB-CD 等于______.6. 如图,AB=CD,则AC 与BD 的大小关系是( ) A.AC>BD B.AC<BD C.AC=BD D.不能确定7.（云南中考）若线段a AB ,C 是线段AB 上任意一点,M,N 分别是AC 和BC 的中点, 则MN=__________.8. 已知线段AB=10cm,直线AB 上有一点C,且BC=4cm,M 是线段AC 的中点,则AM =____.9．有21条15厘米长的纸条首尾粘贴成一条长纸条，每个粘贴部分的长度为1.5厘米，求粘贴后的长纸条的总长度.第5题图B 第6题图10．若A ，B 两点间的距离是20cm ，现有一点C ，若AC ﹢BC=20cm ，则点C 与线段AB 的关系是什么？若AC ﹢BC=30cm ，则点C 与线段AB 的关系是什么？若 AC ﹢BC=10cm ，则这样的点C 存在吗？【能力提升训练】1.（无锡中考）根据题意填空:在同一平面内的两条相交直线,它们有1个交点,如果在这个平面内再画第三条直线,那么这三条直线最多可有___________个交点;如果在这个平面内再画第四条直线,那么这四条直线最多可有__________个交点,由此我们可以猜想,在同一平面内,六条直线最多可有__________个交点,n (n 为大于1的整数)条直线最多可有_____________个交点.(用含n 的代数式表示)2. 北宋末南宋初,中国象棋基本定型,象棋开始风行全国,中国象棋规定:马走字,现定义:在中国象棋盘上,如图,从点A 到点B,马走的最小步数称为A 与B 的马步距离,记作│AB │m,在图中画出了中国象棋的一部分,上面标有A 、B 、C 、D 、E 五个点,则在│AB │m,│AC │m,│AD │m,│AE │m 中最大的是_______,最小的是______.3. 如图，“回”字形的道路宽为1米，整个“回”字形的长为8米，宽为7米，一个人从入口点A 沿着道路中央走到中点B ，他共走了（）米A ．55米B ．55.5米C ．56米D ．56.5米4. 过平面上四点中任意两点作直线,甲说有一条,乙说有四条,丙说有六条, 丁说他们说的都不对,应该是一条、四条或六条,谁说的对?请画图来说明你的看法.EC AD B 第2题第3题5.已知数轴的原点为O,如图,点A 表示2,点B 表示21 (1) 数轴是什么图形?(2) 数轴在原点O 左边的部分(包括原点)是什么图形,怎样表示? (3) 数轴上不小于-12,且不大于2的部分是什么图形,怎样表示?6. 如图,P 为直线l 外一点,A 、B 为直线l 上两点,把P 和A 、B 连起来, 一共可以得到多少个三角形?若在直线l 上增加一个点C,一共可以得到多少个三角形?若直线l 上有n 个点时,一共可以得到多少个三角形?7．A 、B 、C 是一条公路上三个村庄，C 在AB 之间，A 、B 间路程为100千米，A 、C 间路程为40千米，现在A 、B 之间设一车站P ，设P 、C 之间路程为x 千米. （1）用含x 的代数式表示车站到三个村庄的路程之和.（2）若车站到三个村庄路程之和为102千米，车站应设在何处. （3）若要使车站到三个村庄路程总和最小，则车站应设在何处.321A B O l CAl。

线段、射线、直线知识点总结及习题

线段、射线、直线知识点总结及习题线段、射线、直线是几何学中的基本概念，它们在解决几何问题中起到了核心的作用。

本文将对线段、射线、直线的定义、特性以及常见习题进行总结，帮助读者更好地理解和掌握相关知识。

一、线段的定义与特性线段是由两个端点所确定的一段直线，具有以下特性：1. 线段的长度是有限的，可以通过两个端点的距离来计算。

2. 线段是有方向的，从一个端点指向另一个端点。

3. 线段可以任意延长，但是延长后的部分不再属于原来的线段。

二、射线的定义与特性射线是由一个起点和一个方向确定的一段直线，具有以下特性：1. 射线只有一个起点，但是没有终点。

2. 射线是无限延伸的，可以一直延伸出去。

3. 射线只有一个确定的方向，无法逆转。

三、直线的定义与特性直线是由无数个点连成的轨迹，具有以下特性：1. 直线是无限延伸的，没有起点和终点。

2. 直线上的任意两点可以确定一条直线，直线上的所有点都在同一直线上。

3. 直线没有宽度，是一维的。

四、习题示例1. 以下图形中，哪些是线段、哪些是射线、哪些是直线？（插入图示：线段AB、射线CD、直线EF）解答：线段AB是一段有限长度的直线，射线CD是由一个起点C 和一个方向确定的直线，直线EF是一条无数个点连成的轨迹，没有起点和终点。

2. 两个线段的长度分别是5cm和8cm，它们的和是多少？（插入图示：线段AB=5cm，线段CD=8cm）解答：线段AB和CD的长度分别是5cm和8cm，它们的和是5cm+8cm=13cm。

3. 从一个点出发，向两个不同的方向延伸的直线叫做什么？（插入图示：起点O，向左延伸的直线AB，向右延伸的直线CD）解答：从一个点出发，向两个不同的方向延伸的直线称为射线。

在图中，直线AB是一条由起点O向左延伸的射线，直线CD是一条由起点O向右延伸的射线。

通过以上习题，我们可以加深对线段、射线、直线的理解，并能够熟练运用相关知识解决几何问题。

总结：线段、射线、直线是几何学中的重要概念，它们的定义和特性对于解决几何问题至关重要。

线段、射线、直线知识点总结及习题(精编文档).doc

MO a 【最新整理，下载后即可编辑】线段、射线、直线【知识要点】知识点1、线段、直线、射线的概念：线段：一段拉直的棉线可近似地看作线段，线段有两个端点。

线段的画法：（1）画线段时，要画出两个端点之间的部分，不要画出向任何一方延伸的情况．（2）以后我们说“连结 ”就是指画以A 、B 为端点的线段．射线：将线段向一个方向无限延长，就形成了射线，射线有一个端点。

如手电筒、探照灯射出的光线等。

射线的画法：画射线一要画出射线端点；二要画出射线经过一点，并向一旁延伸的情况．直线：将线段向两个方向无限延长就形成了直线，直线没有端点。

如笔直的铁轨等。

直线的画法：用直尺画直线，但只能画出一部分，不能画端点。

知识点2、线段、直线、射线的表示方法：（1）点的记法：用一个大写英文字母（2）线段的记法：①用两个端点的字母来表示 ②用一个小写英文字母表示如图：记作线段AB 或线段BA ，记作线段a ，与字母顺序无关此时要在图中标出此小写字母（3）射线的记法：用端点及射线上一点来表示，注意端点的字母写在前面如图： B A记作射线OM,但不能记作射线MO（4）直线的记法：①用直线上两个点来表示 ②用一个小写字母来表示如图：记作直线AB 或直线BA ，记作直线l与字母顺序无关。

此时要在图中标出此小写字母知识点3、线段、射线、直线的区别与联系：联系：三者都是直的，线段向一个方向延长可得到射线，线段向两个方向延长可得到直线，故射线、线段都是直线的一部分，线段是射线的一部分。

区别：直线可以向两方延伸，射线可以向一方无限延伸，线段不能延伸，三者的区别见下表：BAl知识点4、直线的基本性质（重点）（1）经过一点可以画无数条直线（2）经过两点只可以画一条直线直线的基本性质：经过两点有且只有一条直线（也就是说：两点确定一条直线）注：“确定”体现了“有”，又体现了“只有”。

经过点K可以画无数条直线经过点A、B只可以画一条直线【典型例题】【例1】如图，下列几何语句不正确的是（）A、直线AB与直线BA是同一条直线B、射线OA与射线OB是同一条射线C、射线OA与射线AB是同一条射线D、线段AB与线段BA是同一条线段【例2】指出右图中的射线（以O为端点）和线段。

七年级数学第11讲直线、射线和线段(解析版)

第11讲直线、射线和线段1.了解方直线、射线与线段的概念；2.理解两点确定一条直线与两点之间线段最短的事实；3.掌握直线、射线、线段的表示方法和画法，以及它们的联系与区别；4.知道两点间的距离和线段中点的含义，并能进行线段的计算.知识点1：直线、射线与线段的概念注意：直线是可以向两边无限延伸的，射线受端点的限制，只能向一边无限延伸；线段不能延伸，所以直线与射线不可测量长度，只有线段可以测量。

知识点2：基本事实1.经过两点有一条直线，并且仅有一条直线，即两点确定一条直线2.两点之间的线段中，线段最短，简称两点间线段最短知识点3：线段的性质两点之间的线段中，线段最短，简称：两点间线段最短。

知识点4：基本概念1.两点间的距离：两个端点之间的长度叫做两点间的距离。

2.线段的等分点：把一条线段平均分成两份的点，叫做这个线段的中点知识点5：双中点模型：C 为AB 上任意一点，M 、N 分别为AC 、BC 中点，则AB MN 21考点1：直线、射线和线段的定义例1.（2023春•广饶县期中）如图，已知三点A 、B 、C ，画射线AB ，画直线BC ，连接AC ．画图正确的是（）A ．B ．C ．D ．【答案】B 【解答】解：画射线AB ，画直线BC ，连接AC ，如图所示：故选：B ．【变式1-1】（2023•邯山区校级开学）下列各图中所给的线段、射线、直线能相交的是（）A ．B ．C ．D ．【答案】B 【解答】解：A 、直线AB 与射线EF 无交点，故此选项不符合题意；B 、直线AB 与射线EF 有交点，故此选项符合题意；C 、直线AB 与射线EF 无交点，故此选项不符合题意；D、直线AB与射线EF无交点，故此选项不符合题意．故选：B．【变式1-2】（2023春•泰山区期中）如图，下列说法正确的是（）A．点O在射线AB上B．点B是直线AB的一个端点C．点A在线段OB上D．射线OB和射线AB是同一条射线【答案】C【解答】解：A、点O在射线AB的反向延长线上，故此选项不符合题意；B、直线没有端点，故此选项不符合题意；C、点A在线段OB上，原说法正确，故此选项符合题意；D、射线OB和射线AB的端点不同，不是同一条射线，故此选项不符合题意．故选：C．【变式1-3】（2022秋•运城期末）下列说法不正确的是（）A．直线MN与直线NM是同一条直线B．射线PM与射线MP是同一条射线C．射线PM与射线PN是同一条射线D．线段MN与线段NM是同一条线段【答案】B【解答】解：A、直线MN与直线NM是同一条直线，选项正确，不符合题意；B、射线PM与射线MP不是同一条射线，选项错误，符合题意；C、射线PM与射线PN是同一条射线，选项正确，不符合题意；D、线段MN与线段NM是同一条线段，选项正确，不符合题意．故选：B．考点2：直线的性质和运用例2.（2022秋•黄陂区校级期末）在下列现象中，体现了基本事实“两点确定一条直线”的有（）A．1个B．2个C．3个D．4个【答案】C【解答】解：第一、二、三幅图中的生活、生产现象可以用基本事实“两点确定一条直线”来解释，第四幅图中利用的是“两点之间，线段最短”的知识．故选：C．【变式2-1】（2022秋•永年区期末）在开会前，工作人员进行会场布置，如图为工作人员在主席台上由两人拉着一条绳子，然后以“准绳”摆放整齐的茶杯，这样做的理由是（）A．两点之间线段最短B．两点确定一条直线C．垂线段最短D．过一点可以作无数条直线【答案】B【解答】解：由两人拉着一条绳子，然后以“准绳”摆放整齐的茶杯，这样做的理由是两点确定一条直线，故选：B．【变式2-2】（2022秋•渭滨区期末）如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）A．两点之间线段最短B．两点确定一条直线C．垂线段最短D．以上都不是【答案】B【解答】解：经过刨平的木板上的两个点，能弹出一条笔直的墨线，此操作的依据是两点确定一条直线．故选：B．例3.（2023春•高青县期中）如图，AB是一段高铁行驶路线图，图中字母表示的5个点表示5个车站，在这段路线上往返行车，需印制多少种车票？（）A．10B．11C．18D．20【答案】D【解答】解：图中线段有AB，AC，AD，AE，BC，BD，BE，CD，CE，DE，共10条，单程要10种车票，往返就是20种，即5×（5﹣1）＝20，故选：D．【变式3-1】（2023春•东平县期中）如图所示，由泰山始发终点至青岛的某一次列车，运行途中停靠的车站依次是：泰山——济南——淄博——潍坊——青岛，那么要为这次列车制作的单程火车票（）种．A．5B．10C．15D．20【答案】B【解答】解：＝10（种），∴要为这次列车制作的单程火车票10种．故选：B．【变式3-2】（2022秋•海门市期末）往返A，B两地的客车，中途停靠两个站，客运站根据两站之间的距离确定票价（距离不相等，票价就不同）．若任意两站之间的距离都不相等，则不同的票价共有（）A．4种B．5种C．6种D．7种【答案】C【解答】解：由题意可知，不同的票价有1+2+3＝6（种），故选：C．【变式3-3】（2022秋•宛城区期末）济青高铁北线，共设有5个不同站点，要保证每两个站点之间都有高铁可乘，需要印制不同的火车票（）A．20种B．42种C．10种D．84种【答案】A【解答】解：如图，图中有5个站点．经分析，往同一个方向（从1站点往5站点的方向），需要印制不同的火车票种类的数量有4+3+2+1＝10（种）．∴保证任意两个站点双向都有车票，需要印制车票种类的数量为2×10＝20（种）．故选：A．考点3：尺规作图-直线、射线和线段例4.（2022秋•忠县期末）已知A、B、C三点如图所示．（1）画直线AB，射线AC，线段BC；（2）在线段BC上任取一点E（不同于B，C），连接AE，并延长AE至D，使DE＝AE；（用尺规作图，不写作法，保留作图痕迹）（3）在完成（1）（2）后，图中的线段共有多少条？并写出以点A为端点的所有线段．【答案】（1）（2）见图，（3）图中共8条线段，以点A为端点的线段：线段AB、线段AC、线段AE、线段AD．【解答】解：（1）画直线AB，线段BC，射线AC，如图；（2）连接AE，并延长AE，在AE的延长线上用圆规截取DE＝AE，如图；（3）图中共8条线段，以点A为端点的线段：线段AB、线段AC、线段AE、线段AD．【变式4-1】（2022秋•惠州期末）如图，平面上有四个点A、B、C、D，根据下列语句画图：（1）射线BA；（2）直线BD与线段AC相交于点E；【答案】（1）见解析；（2）见解析．【解答】解：（1）如图所示：（2）如图所示：【变式4-2】（2022秋•黄陂区期末）如图，平面上有A，B，C，D四个点，根据下列语句画图．（1）画射线AD、BC交于点F．（2）连接AC，并将其反向延长；（3）取一点P，使点P既在直线AB上又在直线CD上；（4）取一点Q，使点Q到A，B，C，D四点的距离之和最小．【答案】作图见解答过程．【解答】解：（1）如图，射线AD、BC交于点F，点F即为所求；（2）如图，连接AC，并将其反向延长，CA即为所求；（3）如图，直线AB和直线CD相交于点P，点P即为所求；（4）如图，连接AC、BD，交点为点Q，点Q即为所求．【变式4-3】（2022秋•济南期末）如图，平面上有A、B、C、D四个点，请根据下列语句作图．（1）画直线AC；（2）线段AD与线段BC相交于点O；（3）射线AB与射线CD相交于点P．【答案】答案见解析．【解答】解：（1）直线AC如图所示．（2）线段AD与线段BC相交于点O，如图所示．（3）射线AB与射线CD相交于点P，如图所示．考点4：线段的性质例5.（2022秋•越秀区期末）如图，把原来弯曲的河道改直，A，B两地间的河道长度变短，这样做的道理是（）A．两点确定一条直线B．两点之间线段最短C．两点之间直线最短D．线段是直线的一部分【答案】B【解答】解：把原来弯曲的河道改直，A，B两地间的河道长度变短，这样做的道理是两点之间线段最短．故选：B．【变式5-1】（2022秋•泉港区期末）小华从家里去学校有4条不同路线，路线a、b、c、d的路程分别为：5.2km、3.6km、2.9km、6.5km．若有一条路线是线段，则属于线段的路线是（）A．路线a B．路线b C．路线c D．路线d【答案】C【解答】解：∵两点之间线段最短，∴路线a、b、c、d的路程分别为：5.2km、3.6km、2.9km、6.5km，若有一条路线是线段，则属于线段的路线是路线c．故选：C．【变式5-2】（2022秋•叙州区期末）如图，某同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长小，能正确解释这一现象的数学知识是（）A．两点之间，直线最短B．两点确定一条直线C．经过一点有无数条直线D．两点之间，线段最短【答案】D【解答】解：由于两点之间线段最短，∴剩下树叶的周长比原树叶的周长小，故选：D．【变式5-3】（2022秋•枣阳市期末）下列四个有关生活、生产中的现象：①用两个钉子就可以把一根木条固定在墙上；②把弯曲的公路改直，就能缩短路程；③植树时，只要定出两棵树的位置，就能确定同一行树所在的直线．其中可以用“两点之间，线段最短”来解释的现象有（）A．①B．②C．③D．以上现象都可以【答案】B【解答】解：①属于“两点确定一条直线”，不可用“两点之间，线段最短”来解释，不符合题意；②可用“两点之间，线段最短”来解释，两点之间，线段最短，减少了距离，符合题意；③属于“两点确定一条直线”，不可用“两点之间，线段最短”来解释，不符合题意，∴可以用“两点之间，线段最短”来解释的现象有②，故选：B．考点5：线段的简单运算例6.（2022秋•东港区校级期末）已知点B在线段AC上，点D在线段AB上．（1）如图1，若AB＝10cm，BC＝6cm，D为线段AC的中点，求线段DB的长度；（2）如图2，若，E为线段AB的中点，EC＝16cm，求线段AC的长度．【答案】（1）线段DB的长度为2cm；（2）线段AC的长度为24cm．【解答】解：（1）如图1所示：∵AB＝10cm，BC＝6cm，∴AC＝AB+BC＝10+6＝16（cm），又∵D为线段AC的中点，∴，∴DB＝DC﹣BC＝8﹣6＝2（cm）；（2）如图2所示，设BD＝xcm，∵，∴AB＝4BD＝4xcm，CD＝3BD＝3xcm，∴BC＝DC﹣DB＝3x﹣x＝2x，∴AC＝AB+BC＝4x+2x＝6x，∵E为线段AB的中点，∴，∴EC＝BE+BC＝2x+2x＝4x，又∵EC＝16cm，∴4x＝16，解得：x＝4，∴AC＝6x＝6×4＝24（cm）．【变式6-1】（2022秋•临县期末）如图，C、D是线段AB上的两点，且D是线段AC的中点，若AB＝10cm，BD＝7cm，则BC的长为（）A．2cm B．3cm C．4cm D．5cm【答案】C【解答】解：∵AB＝10cm，BD＝7cm，∴AD＝3cm，∵D是线段AC的中点，∴AC＝6cm．∴BC＝4cm．故选：C．【变式6-2】（2022秋•交口县期末）直线上有A，B，C三点，已知AB＝8cm，BC＝2cm，则AC的长是（）A．10cm B．6cm C．10cm或6cm D．不能确定【答案】C【解答】解：根据题意可得，如图1，，AC＝AB+BC＝8+2＝10（cm）；如图2，，AC﹣AB﹣BC＝8﹣2＝6（cm）．所以AC的长是10cm或6cm．故答案为：C．【变式6-3】（2022秋•君山区期末）如图，线段AB＝30，AC＝10，点M是线段AC的中点．（1）则线段BC的长度为20；（2）在线段CB上取一点N，满足NB＝3CN．求线段MN的长．【答案】（1）20；（2）10．【解答】解：（1）∵AB＝30，AC＝10，∴BC＝AB﹣AC＝30﹣10＝20，故答案为：20．（2）∵BC＝20，NB＝3CN，∴，又∵点M是AC的中点，AC＝10，∴，∴MN＝MC+NC＝5+5＝10．考点6：线段的中双中点模型例7.（2022秋•秦淮区期末）如图，线段AB＝12cm，C是线段AB上一点，AC＝8cm，D、E分别是AB、BC的中点．（1）求线段CD的长；（2）求线段DE的长．【答案】（1）2cm；（2）4cm．【解答】解：（1）∵D是AB的中点，∴AD＝AB＝×12＝6（cm），∵CD＝AC﹣AD，∴CD＝8﹣6＝2（cm）；（2）∵BC＝AB﹣AC，∴BC＝12﹣8＝4（cm），∵E是BC的中点，∴CE＝BC＝×4＝2（cm），∵DE＝DC+CE，∴DE＝2+2＝4（cm）．【变式7-1】（2022秋•朝阳区期末）如图，点C在线段AB上，AB＝16，点E、F分别是线段AB、AC的中点，且EF＝5．求线段AC的长．【答案】6．【解答】解：∵点E是AB的中点，∴．∵AB＝16，∴．∵AF＝AE﹣EF，EF＝5，∴AF＝8﹣5＝3．∵点F是AC的中点，∴AC＝2AF＝2×3＝6．∴线段AC的长为6．【变式7-2】（2022秋•贵池区期末）如图，C是线段AB上一点，M，N分别是AC，BC的中点．（1）若CN＝CM，BN＝2，求线段AB的长；（2）若AC+BC＝m，求线段MN的长．【答案】（1）12；（2）．【解答】解：（1）∵M，N分别是AC，BC的中点，∴，．∵，∴CM＝4，∴BC＝4，AC＝8，∴AB＝BC+AC＝4+8＝12；（2）∵AC+BC＝m，M，N分别是AC，BC的中点，∴，．∵，∴．【变式7-3】（2022秋•成都期末）如图所示，点C是线段AB上一点，AC＝2BC＝8，点D是线段AB的中点．（1）求线段DC的长；（2）若E是线段BC的中点，F是线段AD的中点，求线段EF的长．【答案】（1）2；（2）7．【解答】解：（1）∵AC＝2BC＝8，∴BC＝4，∴AB＝AC+BC＝12，∵点D是线段AB的中点，∴DB＝AD＝AB＝6，∴DC＝DB﹣BC＝6﹣4＝2；（2）∵E是线段BC的中点，F是线段AD的中点，∴EB＝BC＝2，AF＝AD＝3，∴EF＝AB﹣EB﹣AF＝12﹣2﹣3＝7．1．（2022•柳州）如图，从学校A到书店B有①、②、③、④四条路线，其中最短的路线是（）A．①B．②C．③D．④【答案】B【解答】解：根据题意可得，从学校A到书店B有①、②、③、④四条路线，其中最短的路线是②．故选：B．2．（2021•包头）已知线段AB＝4，在直线AB上作线段BC，使得BC＝2，若D是线段AC的中点，则线段AD的长为（）A．1B．3C．1或3D．2或3【答案】C【解答】解：根据题意分两种情况，①如图1，∵AB＝4，BC＝2，∴AC＝AB﹣BC＝2，∵D是线段AC的中点，∴AD＝＝；②如图2，∵AB＝4，BC＝2，∴AC＝AB+BC＝6，∵D是线段AC的中点，∴AD＝＝×6＝3．∴线段AD的长为1或3．故选：C．3．（2023•广东模拟）在墙壁上固定一根横放的木条，至少需要（）A．1枚钉子B．2枚钉子C．3枚钉子D．随便多少枚钉子【答案】B【解答】解：至少需要2根钉子．故选：B．4．（2022•桂林）如图，点C是线段AB的中点，若AC＝2cm，则AB＝4cm．【答案】4．【解答】解：根据中点的定义可得：AB＝2AC＝2×2＝4cm，故答案为：4．1．（2022秋•宝塔区期末）下列各图中，表示“线段CD”的是（）A．B．C．D．【答案】D【解答】解：A、是直线CD，故此选项不符合题意；B、是射线CD，故此选项不符合题意；C、是射线DC，故此选项符合题意；D、是线段CD，故此选项不符合题意；故选：D．2．（2022秋•淮滨县期末）平面上有A、B、C三点，经过任意两点画一条直线，可以画出直线的数量为（）A．1条B．3条C．1条或3条D．无数条【答案】C【解答】解：①如果三点共线，过其中两点画直线，共可以画1条；②如果任意三点不共线，过其中两点画直线，共可以画3条．故选：C．3．（2022秋•晋中期末）高速公路的建设带动我国经济的快速发展．在高速公路的建设中，通常要从大山中开挖隧道穿过，把道路取直，以缩短路程．这样做蕴含的数学道理是（）A．两点之间，线段最短B．两点之间线段的长度，叫做这两点之间的距离C．两点确定一条直线D．平面内经过一点有无数条直线【答案】A【解答】解：在高速公路的建设中，通常要从大山中开挖隧道穿过，把道路取直，以缩短路程．这样做蕴含的数学道理是两点之间，线段最短．故选：A．4．（2023•铜仁市模拟）已知A、B、C为直线l上的三点，线段AB＝9cm，BC＝1cm，那么A、C两点间的距离是（）A．10cm B．8cmC．10cm或8cm D．以上说法都不对【答案】C【解答】解：分两种情况：①点C在线段AB上，则AC＝AB﹣BC＝9﹣1＝8（cm）；②点C在线段AB的延长线上，AC＝AB+BC＝9+1＝10（cm）．故选：C．5．（2022秋•武侯区期末）已知在同一直线上有A，B，C三个点，且AB＝3，BC＝2，则AC的长为（）A．5B．C．5或1D．或1【答案】C【解答】解：如图1，，AC＝AB﹣BC＝3﹣2＝1；如图2，，AC＝AB+BC＝3+2＝5，所以AC的长为5或1．故选：C．6．（2022秋•大东区期末）如图，BC＝AB，D为AC的中点，DC＝3，则AB的长是（）A．B．5C．D．4【答案】D【解答】解：∵D为AC的中点，DC＝3，∴AC＝2DC＝2×3＝6，∵BC＝AB，∴AB＝AC＝×6＝4．故选：D．7．（2022秋•通道县期末）如图已知线段AB＝14cm，C点在AB上，BC：AC＝3：4，D为BC的中点，则线段AD的长为（）A．10cm B．11cm C．12cm D．13cm【答案】B【解答】解：∵AB＝14cm，BC：AC＝3：4，∴，，∵D为BC的中点，∴，∴AD＝AC+CD＝8+3＝11cm，故选：B．8．（2022秋•婺城区期末）杭衢高铁线上，要保证衢州、金华、义乌、诸暨、杭州每两个城市之间都有高铁可乘，需要印制不同的火车票（）A．20种B．15种C．10种D．5种【答案】A【解答】解：需要印制不同的火车票的种数是：2（1+2+3+4）＝20（种）．故选：A．9．（2022秋•市中区校级期末）如图，在同一平面内有四个点A、B、C、D，请按要求完成下列问题．（注此题作图不要求写出画法和结论）（1）作射线AC；（2）作直线BD与射线AC相交于点O；（3）分别连接AB、AD；（4）我们容易判断出线段AB+AD与BD的数量关系是AB+AD＞BD，理由是两点之间，线段最短．【答案】见试题解答内容【解答】解：（1）（2）（3）如图所示：（4）AB+AD＞BD，理由是：两点之间，线段最短．故答案为：AB+AD＞BD，两点之间线段最短．10．（2022秋•惠山区校级期末）如图，已知点C是线段AB上一点，点D是线段AB的中点，若AB＝10cm，BC＝3cm．（1）求线段CD的长；（2）若点E是直线AB上一点，且BE＝2cm，点F是BE的中点，求线段DF的长．【答案】（1）2cm；（2）6cm或4cm．【解答】解：（1）∵点D是线段AB的中点，AB＝10cm，∴，∵BC＝3cm，∴CD＝BD﹣BC＝2cm；（2）当点E在AB的延长线上时，如图，∵BE＝2cm，点F是BE的中点，∴，∴DF＝BD+BF＝5+1＝6cm；当点E在线段AB上时，如图，∵BE＝2cm，点F是BE的中点，∴，∴DF＝BD﹣BF＝5﹣1＝4cm；综上所述，线段DF的长为6cm或4cm．11．（2022秋•凤山县期末）如图，点C是线段AB上的一点，点M是线段AC的中点，点N是线段BC的中点．（1）如果AB＝12cm，AM＝4cm，求CN的长；（2）如果MN＝8cm，求AB的长．【答案】（1）2；（2）16．【解答】解：（1）∵点M是线段AC的中点，AM＝14cm，∴AC＝2AM，∴AC＝8cm，∵AB＝12cm，∴BC＝AB﹣AC＝4（cm），∵点N是BC的中点，∴CN＝BC＝2（cm），答：CN的长为2cm；（2）∵点M是线段AC的中点，点N是线段BC的中点，∴BC＝2NC，AC＝2MC，∵MN＝NC+MC＝8（cm），∴AB＝BC+AC＝2NC+2MC＝2MN＝16（cm），答：AB的长为16cm．12．（2022秋•忠县期末）如图，长度为42cm的线段AD上有两点B、C，这两点将线段AD分成AB：BC：CD＝2：1：4．（1）求线段AC的长；（2）点M为线段AB的中点，点N为线段CD的中点，求线段MN的长度．【答案】（1）18cm；（2）24cm．【解答】解：（1）AB：BC：CD＝2：1：4．∴AD＝42cm，∴AC＝（cm）；（2）由题意得AB＝（cm），BC＝6（cm），CD＝24（cm），∵M为线段AB的中点，点N为线段CD的中点，∴MB＝（cm），CN＝（cm），∴MN＝MB+BC+CN＝6+6+12＝24（cm）．13．（2022秋•利川市校级期末）如图，已知点B在线段AC上，点D在线段AB上，满足BD：AB＝1：4，且点D，E分别是线段AC，AB的中点，若EC＝24，求线段AB和AC的长度．【答案】24，26．【解答】解：设BD＝x，∵BD：AB＝1：4，∴AB＝4BD＝4x，∵点E是线段AB的中点，∴BE＝AE＝AB＝×4x＝2x，∴DE＝x，∴AD＝3x，∵点D是线段AC的中点，∴AC＝2AD＝6x，∴CE＝AC﹣AE＝6x﹣2x＝24，解得：x＝6，∴AB＝4x＝4×6＝24，AC＝6x＝6×6＝36．。

(完整版)北师版七年级上数学第四章基本平面图形知识点及练习题

4.1 线段、射线、直线1、线段、射线、直线线段：绷紧的琴弦，人行横道线都可以近似的看做线段。

线段有两个端点。

射线：将线段向一个方向无限延长就形成了射线。

射线有一个端点。

直线：将线段向两个方向无限延长就形成了直线。

直线没有端点。

2、名称图形表示方法端点长度直线直线AB (或BA )直线l 无端点无法度量射线射线OM 1个无法度量线段线段AB (或BA ) 线段l2个可度量长度3、直线的性质（1）直线公理：经过两个点有且只有一条直线。

（两点确定一条直线。

）（2）过一点的直线有无数条。

（3）直线是是向两方面无限延伸的，无端点，不可度量，不能比较大小。

4、点和直线的位置关系有两种：①点在直线上，或者说直线经过这个点。

②点在直线外，或者说直线不经过这个点。

※课时达标 1.填写下表:2.如图，共有条线段.3.用两个钉子就可以把木条钉在墙上，其依据是_________ .4.平面上有五条直线，则这五条直线最多有_____交点，最少有_____个交点．5.平面上两条直线的位置关系只有两种，即__________和_________________.6.平面上有四个点，无三点共线，以其中一点为端点，并且经过另一点的射线共有_______条．※课后作业 ★基础巩固1.下列各直线的表示法中，正确的是（）.l BAMOlBA 名称图例端点数延伸方向有无长度线段射线直线 A B C DA.直线AB.直线AB C直线ab D.直线Ab2.下列说法不正确的是( ) .A.直线AB与直线BA是同一条直线B.射线AB与射线BA是同一条射线C.线段AB与线段BA是同一条线段D.线段有两个端点,射线有一个端点,直线没有端点3.下列说法正确的是（）.A.射线比直线短B.两点确定一条直线C.经过三点只能作一条直线D.两条射线的长度的和等于直线的长度4.下列说法正确的是( ).A.过一点P只能作一条直线B.射线AB和射线BA表示同一条射线C.直线AB和直线BA表示同一条直线D.射线a比直线b短5.下列说法正确的是（）.A.延长射线OAB.延长直线lC.延长线段CDD.反向延长直线l6.平面内的三点可确定直线的条数是（）.A.3B.1或3C.0或1D.07.已知C,D在直线AB上，那么直线AB上的射线共有（）.A.6条B.7条C.8条D.9条8.下列说法中，错误的有（）.①射线是直线的一部分；②画一条射线，使它的长度为5厘米；③线段AB和线段BA是同一条线段；④射线AB和射线BA是同一条射线；⑤直线AB和直线BA是同一条直线.A.1个B.2个C.3个D.4个9.在一条笔直的校园大道两旁种树时，先定下两棵树的位置，然后其它树的位置也就确定下来了，这说明了直线的基本性质：________________________. 10.已知平面内的四个点A,B,C,D,过其中的两个点画直线：(1)若A,B,C,D四个点在同一条直线上，可以画出______条直线；(2)若A,B,C,D四个点有三个在同一条直线上，可以画出______条直线；(3)若A,B,C,D四个点中的任意三个都不在同一条直线上，可以画出_______条直线.11.读下列语句，并画出相应图形.(1)经过点M,N画一条直线；(2)直线ba,相交于点P，点A在直线a上，但不在直线b上；(3)三条直线cb,两两相交于点A,B,C.a,☆能力提高12.读句画图:如图所示，已知平面上四个点（1）画直线AB；（2）画线段AC；（3）画射线AD、DC、CB；（4）如图，指出图中有_____条线段，有___ 条射线并写出其中能用图中字母表示的线段和射线 .13.已知直线l上有n个点，试问：（1）此图形上有多少条射线？（2）此图形上有多少条线段？14.如图，线段AB上的点数与线段的总数有如下关系：如果线段AB上有三个点时，线段总共有3条，如果线段AB上有4个点时，线段总数有6条，如果线段AB上有5个点时，线段总数共有10条，……A C B3=2+1A C D B6=3+2+1A C D E B10=4+3+2+1(1)当线段AB上有6个点时，线段总数共有__________条.(2)当线段AB上有100个点时，线段总数共有多少条？●中考在线15.平面上不重合的两点确定一条直线，不同三点最多可确定3条，若平面上不同的n个点最多可确定21条直线，则n的值为（）.A.5B.6C.7D.816.同一平面内互不重合的三条直线的公共点的个数是( ).A.可能是0个，1个，2个B.可能是0个，2个，3个C.可能是0个，1个，2个或3个D.可能是1个或3个4.2 比较线段的长短1、线段的性质（1）线段公理：两点之间的所有连线中，线段最短。

直线射线线段知识点讲解以及例题解析

点的个数
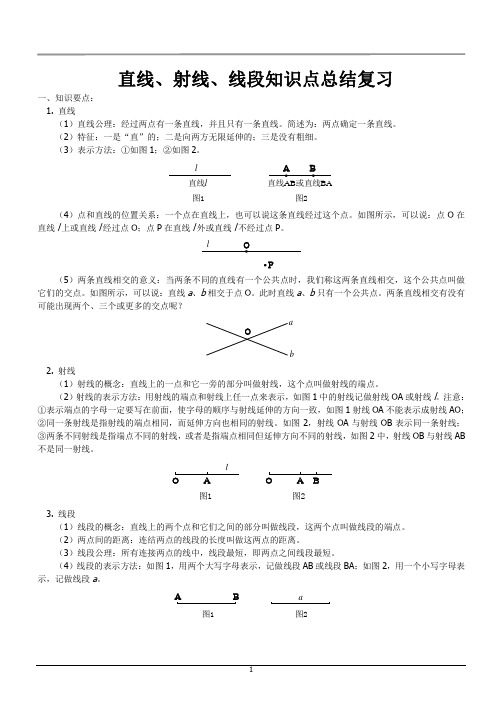
直线条数
2
1＝S2＝
3
3＝S3＝
4
6＝S4＝
5
10＝S5＝
……
……
n
Sn＝
从表中我们可以推断出，平面上有n个点（n≥2），且任意三个点不在同一直线上，这些点一共可作出条直线。
解：平面上有n个点（n≥2），且任意三个点不在同一直线上，这些点一共可作出条直线。
评析：归纳猜想是这类题型的解决思路，多看几种情况，要善于发现规律并正确地进行归纳猜想。
分析：我们可以从简单的入手，当有两个点时，可作出1条直线；当有3个点时，可以作出3条直线；当有4个点时（如图所示）过其中任何一点都有3条直线，共有4×3＝12条，但是因为直线AB与BA、AC与CA、AD与DA……分别是同一条直线，说明每一条直线重复一次，所以实际只能画出直线共×4×3＝6条；考查点的个数n和可作的直线条数Sn，它们之间的关系如下表：
（1）延长直线AB（）
（2）直线AB与直线BA不是同一条直线（）
（3）直线AB上有A点（）
（4）直线AB与直线l不可能是同一条直线（）
分析：（1）直线本身是向两方无限延伸的，因此不用延长。
（2）用两个大写字母表示直线时与字母的顺序无关。
（3）直线AB上一定有点A，即点A在直线AB上。
（4）直线既可用大写字母AB表示又可用小写字母l表示。
例3.如图所示，平原上有A、B、C、D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池，不考虑其他因素，请你画出确定蓄水池H点的位置，使它与四个村庄的距离之和最小。
分析：根据两点之间线段最短，所求点必在线段AD上，也必在线段BC上，即为AD、BC的交点。
解：根据两点之间线段最短，可连结AD、BC且交于一点H，则点H即为所求。

6.2.1直线、射线、线段-(课件)人教版(2024)数学七年级上册

(1)画射线CD；
(2)画直线AD；
(3)连接AB；
(4)画线段BD 与直线AC 相交于点O.
感悟新知
解题秘方：紧扣直线、射线、线段的概念画图. 解：(1)(2)(3)(4)如图6 .2-8 所示.
知3－练
感悟新知
5-1. 如图，在平面内有A，B，C 三点．
知3－练
(1)画直线AC、线段BC、射线AB；
综合应用创新
一条直线把平面分成2 部分，两条直线把平面分成2 ＋2 =4 部分，三条直线把平面分成2 ＋2 ＋3=7 部分，四条直线把平面分成2 ＋2 ＋3＋4 =11 部分，五条直线把平面分成2 ＋2 ＋3＋4 ＋5 =16 部分… 依此可得，n条直线把平面分成2＋2＋3＋4＋5＋… ＋n=
解题秘方：紧扣直线的定义、表示方法以及与点的位置关系进行解答.
知1－练
感悟新知
知1－练
(1)点B 在直线AD___上____，点C 在直线AD ____外___ ； (2)点E 是直线_A__F_(_或__A_E__或__E_F__) __与直线_C_D_(_或__D__E_或__C_E__)
感悟新知
知1－练
例 2 平面内有三个点，过其中任意两点画直线，一共可以画几条直线？画图加以说明. 解题秘方：紧扣“直线的基本事实”，根据三点的位置情况，逐一画出图形.
感悟新知
解：当三点在同一直线上时，可以画一条直线，如图6.2 -3 ①；当三点不在同一直线上时，可以画三条直线，如图 6.2 -3 ② .
知2－讲
图示
感悟新知
特别提醒
知2－讲
1.不论用大写字母还是小写字母表示射线，都必须标明
“射线××”.
2.由于射线可以向一个方向无限延伸，因此射线没有延长

直线、射线、线段复习以及易错题讲解

直线、射线、线段复习以及易错题讲解知识要点： 1. 直线1）直线公理：经过两点有一条直线，并且只有一条直线。

简述为：两点确定一条直线。

2）特征：一是“直”的；二是向两方无限延伸的；三是没有粗细。

3）表示方法：①如图1；②如图2。

4）点和直线的位置关系：一个点在直线上，也可以说这条直线经过这个点。

如图所示，可以说：点O在直线l上或直线l经过点O；点P在直线l外或直线l不经过点P。

5）两条直线相交的意义：当两条不同的直线有一个公共点时，我们称这两条直线相交，这个公共点叫做它们的交点。

如图所示，可以说：直线a、b相交于点O。

此时直线a、b只有一个公共点。

两条直线相交有没有可能出现两个、三个或更多的交点呢？2. 射线1）射线的概念：直线上的一点和它一旁的部分叫做射线，这个点叫做射线的端点。

2）射线的表示方法：用射线的端点和射线上任一点来表示，如图1中的射线记做射线OA 或射线l。

注意：①表示端点的字母一定要写在前面，使字母的顺序与射线延伸的方向一致，如图1射线OA不能表示成射线AO；②同一条射线是指射线的端点相同，而延伸方向也相同的射线。

如图2，射线OA与射线OB表示同一条射线；③两条不同射线是指端点不同的射线，或者是指端点相同但延伸方向不同的射线，如图2中，射线OB与射线AB不是同一射线。

3. 线段（1）线段的概念：直线上的两个点和它们之间的部分叫做线段，这两个点叫做线段的端点。

（2）两点间的距离：连结两点的线段的长度叫做这两点的距离。

（3）线段公理：所有连接两点的线中，线段最短，即两点之间线段最短。

（4）线段的表示方法：如图1，用两个大写字母表示，记做线段AB或线段BA；如图2，用一个小写字母表示，记做线段a。

注意：①线段AB和线段BA是同一条线段；②连结AB就是画以A、B为端点的线段；③延长线段AB是指按从A到B的方向延长，如图所示，也可以说成反向延长BA。

线段的延长线常常画成虚线。

（5）线段大小的比较：①度量法。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B
A
a
M
O
B
A 直线、线段、射线讲义知识点1、线段、直线、射线的概念
线段：一段拉直的棉线可近似地看作线段，线段有两个端点。

射线：将线段向一个方向无限延长，就形成了射线，射线有一个端点。

如手电筒、探照灯射出的光线等。

直线：将线段向两个方向无限延长就形成了直线，直线没有端点。

如笔直的铁轨等。

知识点2、线段、射线、直线的区别与联系名称
图形
表示方法
延伸性端点长度
线段
1、线段AB （或线段BA ）（字母无序）
2、线段a
不能延伸两个有
射线
1、射线OM(字母有序)
2、射线l
向一
方无线延伸
一个无
直线
1、直线AB （或直线BA ）（字
母无序）
2、直线l
两方无限延伸
无
无
联系：三者都是直的，线段向一个方向延长可得到射线，线段向两个方向延长可得到直线，故射线、线段都是直线的一部分，线段是射线的一部分。

【典型例题】
【例1】如图，下列几何语句不正确的是（） A 、直线AB 与直线BA 是同一条直线 B 、射线OA 与射线OB 是同一条射线
C 、射线OA 与射线AB 是同一条射线
D 、线段AB 与线段BA 是同一条线段
【例2】指出右图中的射线（以O 为端点）和线段。

【例3】下列说法错误的是( )
A 、线段A
B 与线段BA 是同一条线段 B 、射线AB 与射线BA 是同一条射线
C 、直线AB 与直线BA 是同一条直线
D 、线段AB 在直线BA 上
l
B
A O C
B
A
O
【例4】下列说法正确的是（）
A 、直线虽然没有端点，但长度可以度量
B 、射线只有一个端点，但长度是可以确定的
C 、线段虽然有两个端点，但长度却可以变化的
D 、只有线段的长度是可以确定的，直线、射线的长度不可以度量【例5】读出下列语句，并画出图形。

（1）直线AB 经过点M ．（2）点A 在直线l 外．（3）经过M 点的三条直线．（4）直线AB 与CD 相交于点O ．
（5）直线l 经过A 、B 、C 三点，点C 在点A 与点B 之间．【例6】读句画图（在右图中画）（1）连结BC 、AD （2）画射线AD
（3）画直线AB 、CD 相交于E
（4）延长线段BC ，反向延长线段DA 相交与F （5）连结AC 、BD 相交于O
知识点4、直线
类型一、点和直线的位置关系：点在直线上或点在直线外。

题型一、过平面上的点画直线
例1已知同一平面内有ABCD 四个点，经过这四个点中的任意两个点共能画多少条直线？
解：1、四个点都在同一直线上只能画一条直线。

2、有三点在同一直线上能画四条直线。

3、任意三点都不在同一直线上画六条直线。

题型二、直线相交问题
D
C
B
A
例2、两条直线相交，有一个交点，三条直线相交最多有3个交点，四条直线相交最多有6个交点，五条直线相交最多有10个交点，N条直线相交最多有N×（n-2）/2个交点。

类型二、直线的基本性质：经过两点有且只有一条直线（也就是说：两点确定一条直线）
例题1要整齐地载一行树，只要确定两端的树坑位置，就能确定这一行树坑所在的直线，这里所用的数学知识是（两点确定一条直线）
练习：1、在正常情况下，射击时要保证瞄准的一只眼睛在准星和缺口确定的直线上，才能射中目标。

（）
2、用两个钉子把细木条钉在木板上，就能固定细木条。

（）
知识点5线段
类型一、找线段
题型一、数线段
数线段，找规律：
（1）下列各图中，线段上的点依次增加，请你填写图中相应的线段数。

（1）条线段；（3）条线段；（6）条线段；（15）条线段（2）请猜想，当线段AB上有10个点时（含A、B两点），有几条线段？
（3）n个点呢（n≥ 2））
由上述规律如果10位同学聚会互相握手，则他们一共握了几次手？
若N个对参加比赛每两个对赛一场，这N个对一共要赛多少长？
题型二、往返于甲乙两地的列车，中途停靠3个站，试求最多有多少中不同的票价？要准备多少种不同的车票？
类型二、
线段的性质：两点的所有连线中，线段最短。

简单说成：两点之间线段最短
两点的距离：连接两点间的线段叫做两点的距离。

题型一：1、如图所示，在我国“西气东输”的过程中，从A城市往B城市架设管道，有三条路可供选择，在不考虑其他因素的情况下，架设管道的最短路线是________，依据是________．
2、如图，从A到B最短的路线是（）
A. A—G—E—B
B. A—C—E—B
C. A—D—G—E—B
D. A—F—E—B
题型二：把弯曲的河道改直，能够缩短航程，这样做的道理（两点之间线段最短）题型三：路径最短
1、如图，平原上有A、B、C、D四个村庄，为解决当地缺水问题，政府准
备投资建一个蓄水池，不考虑其它因素，请画图确定蓄水池H点的位置，
使它与四个村庄的距离之和最小．
答案：连接AD和BC，把蓄水池建在交点上，因为这样H点即在线段AD上，
又在线段BC上，两点之间线段最短．
2、如图，在一块平地上，雨后中间有一条积水沟，沟的两边是平行的，一只蚂蚁在A点，想过水沟来B点取食，几个学生在沟上沿与沟边垂直的方向放了四根小木棍，这只蚂蚁通过第（ 2 ）号木棍，才能使从A到B的路径最短．
答案：根据两点之间线段最短，连接AB，过与木棍相交的一根即可
类型三、线段计算
题型一比例计算题
例1线段AB上有两点P、Q，点P将AB分成两部分，AP：PB=2：3，点Q将AB也分
成两部分，AQ：QB=4：1，PQ=3cm,求AP、QB的长
练习：1、如图，AB：BC：CD=2：3：4，AB的中点M与CD的中点N的距离是3cm，则BC=______．
2、已知：如图，B、C两点把线段AD分成2：4：3三部分，M是AD的中点，
CD=6，求线段MC的长。

题型二：关于中点
例1如图，线段AB＝4.8 cm，C是它的一个三等分点(AC>CB)，D是它的中点，则CB＝（）cm，DC=（）cm.
练习：1、线段AB=8cm，C是AB的中点，D点在CB上，DB=1.5cm，则线段CD=( )cm．
2、如图，AB=40，点C为AB的中点，点D为CB上的一点，点E为BD的中点，且
EB=5，求CD的长．
3、如图，已知线段AB和CD的公共部分BD=1/3AB=1/4CD，线段AB、CD的
中点E、F之间距离是10cm，求AB、CD的长。

4、如图，已知点C为线段AB的中点，点D为线段BC的中点，AB=10cm，求AD的长度.
题型三实际问题中的线段和差问题
例1某班50名同学分别站在公路的A，B两点处，A，B两点相距1000米，A处有30人，B处有20人，要让两处的同学走到一起，并且使所有同学走的路程总和最小，那么集合地点应选在（）
A、点A处
B、线段AB的中点处
C、线段AB上，距点A1000/3米处
D、线段AB上，距点A400米处
例2在同一所学校上学的小明、小伟、小红三位同学分别住在A，B，C三个住宅区．如图，A，B，C三点在一条直线上，且AB＝60 m，BC＝100 m，他们打算合租一辆接送车去上学，由于车位紧张，准备在三个住宅区之间只设一个停靠站，为使三位同学步行到停靠站的路程和最小，你认为停靠站应该设在哪一个小区呢？
题型四分类讨论
例1已知线段AB=4.8cm，Ｃ为ＡＢ中点，Ｄ为ＣＢ中点，点Ｅ在ＡＢ上，且ＣＥ＝１／３ＡＣ，求ＤＥ长。