7年级春季班-第11讲-全等三角形的概念和性质及判定-学生版
《全等三角形》讲义

《全等三角形》讲义一、全等三角形的定义两个能够完全重合的三角形叫做全等三角形。
“完全重合”意味着它们的形状和大小完全相同,对应边相等,对应角也相等。
例如,我们将一个三角形沿着某条直线对折,如果对折后的两部分能够完全重合,那么这就是一个全等三角形。
二、全等三角形的性质1、全等三角形的对应边相等这是全等三角形最基本的性质之一。
如果两个三角形全等,那么它们对应的三条边的长度是相等的。
比如,三角形 ABC 全等于三角形DEF,那么 AB = DE,BC = EF,AC = DF。
2、全等三角形的对应角相等同样,如果两个三角形全等,它们对应的三个角的度数也是相等的。
还是以上面的例子来说,∠A =∠D,∠B =∠E,∠C =∠F。
3、全等三角形的周长相等因为全等三角形的对应边相等,所以它们的周长也必然相等。
4、全等三角形的面积相等由于全等三角形的形状和大小完全相同,所以它们所覆盖的面积也是相等的。
三、全等三角形的判定1、 SSS(边边边)如果两个三角形的三条边分别对应相等,那么这两个三角形全等。
比如说,有三角形 ABC 和三角形 DEF,AB = DE,BC = EF,AC = DF,那么就可以判定三角形 ABC 全等于三角形 DEF。
2、 SAS(边角边)如果两个三角形的两条边及其夹角分别对应相等,那么这两个三角形全等。
假设在三角形 ABC 和三角形 DEF 中,AB = DE,∠A =∠D,AC = DF,那么可以得出这两个三角形全等。
3、 ASA(角边角)当两个三角形的两个角及其夹边分别对应相等时,这两个三角形全等。
例如,在三角形 ABC 和三角形 DEF 中,∠B =∠E,BC = EF,∠C =∠F,那么三角形 ABC 全等于三角形 DEF。
4、 AAS(角角边)如果两个三角形的两个角和其中一个角的对边分别对应相等,那么这两个三角形全等。
比如,在三角形 ABC 和三角形 DEF 中,∠A =∠D,∠B =∠E,BC = EF,那么这两个三角形全等。
全等三角形(知识点讲解)

全等三角形(知识点讲解)全等三角形(知识点讲解)全等三角形是初中数学中的重要概念,也是几何学中的核心内容之一。
在这篇文章中,我们将从定义、判定全等三角形的条件以及全等三角形的性质等方面进行讲解。
一、全等三角形的定义全等三角形指的是具有完全相同的三边和三角的三角形。
简而言之,在几何学中,当两个三角形的对应边长相等、对应角度相等时,我们称这两个三角形是全等的。
二、全等三角形的判定条件为了判断两个三角形是否全等,我们有以下几个常用的判定条件:1. SSS判定法:即边-边-边判定法。
当两个三角形的三条边分别相等时,它们就是全等的。
2. SAS判定法:即边-角-边判定法。
当两个三角形的一对夹角和夹角两边分别相等时,它们就是全等的。
3. ASA判定法:即角-边-角判定法。
当两个三角形的一对夹角和夹角对边分别相等时,它们就是全等的。
4. AAS判定法:即角-角-边判定法。
当两个三角形的两对夹角和一个非夹角边分别相等时,它们就是全等的。
需要注意的是,这些判定条件是相互独立的,即只要满足其中一种条件,就可以判定两个三角形是全等的。
三、全等三角形的性质全等三角形具有以下重要性质:1. 对应边对应角相等性质:全等三角形的对应边对应角相等。
即若∆ABC≌∆DEF,那么 AB = DE, AC = DF, BC = EF,并且∠A = ∠D,∠B = ∠E, ∠C = ∠F。
2. 全等三角形的任意一角都与对应角相等:即若∆ABC≌∆DEF,那么∠A = ∠D, ∠B = ∠E, ∠C = ∠F。
3. 全等三角形的任意一边都与对应边相等:即若∆ABC≌∆DEF,那么 AB = DE, AC = DF, BC = EF。
4. 全等三角形的外角相等:即若∆ABC≌∆DEF,那么∠BAC =∠EDF, ∠ABC = ∠DEF, ∠ACB = ∠DFE。
通过以上性质,我们可以进行全等三角形的各种推理和计算。
四、全等三角形的应用全等三角形在几何学的应用非常广泛。
全等三角形判定ppt课件

若两个三角形全等,则它们的周长也 相等。
对应角相等
在全等三角形中,任意两个对应 的角都相等。
若两个三角形全等,则它们的内 角和也相等,且均为180度。
可以通过测量两个三角形的三个 内角来判断它们是否全等。
面积相等
若两个三角形全等,则它们的面积也相等。 可以通过计算两个三角形的面积来判断它们是否全等。
1 2
定义
两边和它们的夹角分别相等的两个三角形全等。
图形语言
若a=a',∠B=∠B',b=b',则⊿ABC≌⊿A'B'C'。
3
符号语言
∵a=a',∠B=∠B',b=b',∴⊿ABC≌⊿A'B'C'( SAS)。
角边角判定法(ASA)
01
02
03
定义
两角和它们的夹边分别相 等的两个三角形全等。
图形语言
实例1
证明两个三角形全等并求出未知 边长
实例2
利用全等三角形判定方法证明两个 四边形面积相等
实例3
利用全等三角形判定方法解决一个 实际问题,如测量一个不可直接测 量的距离
06
总结与展望
判定全等三角形的方法总结
三边分别相等的两个三角形全等。这是最基本的判定 方法,通过比较三角形的三边长度来确定两个三角形
证明过程
可以通过AAS(角角边)全等条件进行证明,即 如果两个三角形有两个角和其中一个角的对边分 别相等,则这两个三角形全等。这也是一种常用 的全等三角形判定方法。
实际应用举例
在实际应用中,角角边判定法常用于解决与角度 和边长有关的问题。例如,在建筑设计中,如果 需要确保两个建筑结构的角度和边长完全相等, 就可以利用角角边判定法来进行验证。
北师大7年级下册 专题11 全等三角形性质判定(知识点串讲)(学生版)
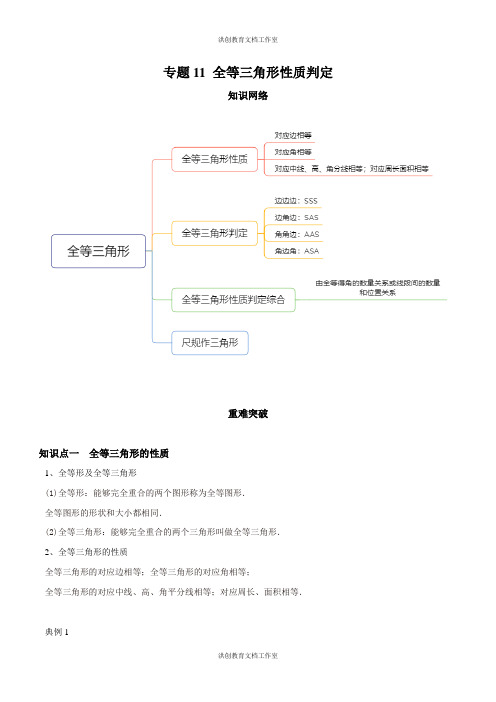
专题11 全等三角形性质判定知识网络重难突破知识点一全等三角形的性质1、全等形及全等三角形(1)全等形:能够完全重合的两个图形称为全等图形.全等图形的形状和大小都相同.(2)全等三角形:能够完全重合的两个三角形叫做全等三角形.2、全等三角形的性质全等三角形的对应边相等;全等三角形的对应角相等;全等三角形的对应中线、高、角平分线相等;对应周长、面积相等.典例1∠=__________ (2017春•大邑县期末)以下图是两个全等的三角形,图中的字母表示三角形的边长,那么1度.典例2(2019秋•龙泉驿区期末)如图为6个边长相等的正方形的组合图形,那么123()∠+∠+∠=A.90︒B.120︒C.135︒D.150︒知识点二全等三角形的判定全等三角形判定①三边分别相等的两个三角形全等,简写成“边边边〞或“SSS〞.②两边及其夹角分别相等的两个三角形全等,简写成“角边角〞或“ASA〞.③两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边〞或“AAS〞.④两边及其夹角分别相等的两个三角形全等,简写成“边角边〞或“SAS〞.注意:证明两个三角形全等,找条件时注意挖掘隐含的等角或等边,如:公共角、公共边、对顶角、平行线中的同位角、内错角等;典例1(2019春•光明区期末)如图,点E,点F在直线AC上,DF=BE,∠AFD=∠CEB,以下条件中不能判断△ADF≌△CBE的是()A .∠B =∠D B .AD =CBC .AE =CFD .∠A =∠C典例2(2019春•商河县期末)如图,ABD BAC ∠=∠,添加以下条件不能判断ABD BAC ∆≅∆的条件是( )A .D C ∠=∠B .AD BC = C .BAD ABC ∠=∠ D .BD AC =知识点三 性质与判定综合典例1(2019春•长清区期末)如下图,ABC ∆是等边三角形,且BD CE =,115∠=︒,那么2∠的度数为()A .15︒B .30︒C .45︒D .60︒典例2如图,点A 、D 、C 、F 在同一条直线上,AD CF =,AB DE =,BC EF =.(1)求证:ABC DEF ∆≅∆;(2)假设55A ∠=︒,88B ∠=︒,求F ∠的度数.典例3(2019春•龙岗区期末)在△ABC与△ABD中,AC=BD,∠C=∠D=90°,AD与BC交于点E.(1)求证:AE=BE;(2)假设AC=3,BC=4,求△ACE的周长.典例4(2019春•龙岗区期末)如图,正方形ABCD(四边相等,四个角都是直角),点E为边AB上异于点A、B的一动点,EF∥AC,交BC于点F,点G为DA延长线上一定点,满足AG=AD,GE的延长线与DF交于点H,连接BH.(1)判断△BEF是三角形.(2)求证:△AGE≌△CDF.(3)探究∠EHB是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.知识点四尺规作三角形典例1(2019春•太原期末):如图,ABC∆,点D是BC延长线上的一点,且CD BC=.求作:ECD∆,使ECD ABC∆≅∆且点E与点A在BC同侧.(要求:尺规作图,保存作图痕迹)稳固训练一、单项选择题(共7小题)1.(2019春•太原期末)如图,ABCA∠=︒,'',点B'在边AB上,线段AB''与AC交于点D,假设40∆≅△A B C∠=︒,那么A CB∠'的度数为()B60A.100︒B.120︒C.135︒D.140︒2.(2019春•金牛区期末)如图,点B、E、C、F在一条直线上,∠A=∠D,∠B=∠DFE,添加以下条件,不能判定△ABC≌△DFE的是()A.BE=CF B.AB=DF C.∠ACB=∠DEF D.AC=DE3.(2019•大邑县模拟)如图,AB=DC,需添加以下()条件后,就一定能判定△ABC≌△DCB.A .AO =BOB .∠ACB =∠DBC C .AC =DBD .BO =CO4.(2019春•龙岗区期末)如图是一个平分角的仪器,其中AB =AD ,BC =DC ,将点A 放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )A .SSSB .SASC .ASAD .AAS5.(2019春•雁塔区校级期末)根据以下条件能画出唯一ABC ∆的是( )A .3AB =,4BC =,8AC =B .4AB =,3BC =,30A ∠=︒ C .30A ∠=︒,70B ∠=︒,80C ∠=︒D .60A ∠=︒,30B ∠=︒,4AB =6.(2019春•雁塔区校级期末)如图,在ABC ∆中,AD BC ⊥,CE AB ⊥,垂足分别为D 、E ,AD 、CE 交于点H ,4EH EB ==,6AE =,那么CH 的长为( )A .1B .2C .3D .47.(2019春•福田区期末)如图,锐角△ABC 中,D 、E 分别是AB 、AC 边上的点,△ADC ≌△ADC ′,△AEB ≌△AEB ′,且C ′D ∥EB ′∥BC ,BE 、CD 交于点F ,假设∠BAC =α,∠BFC =β,那么( )A .2α+β=180°B .2β﹣α=145°C .α+β=135°D .β﹣α=60°二、填空题(共4小题)8.(2019春•锦江区校级期中)如图,ABC DEFAE=,那么DE的长是.BE=,2∆≅∆,39.(2019春•青羊区期末)如下图,AF=DC,BC∥EF,假设要用“SAS〞去证△ABC≌△DEF,那么需添加的条件是.10.(2019春•龙岗区期末)如图,AB=AC,用“SAS〞定理证明△ABD≌△ACE,还需添加条件.11.(2019春•郑州期末)如图,在Rt ABC∠=︒,AB AC=.点D为BC的中点,E为边AB上∆中,90BAC一动点(不与A、B点重合),以点D为直角顶点、以射线DE为一边作90MDN∠=︒,另一条直角边DN与边AC交于点F(不与A、C点重合),分别连接AD、EF,以下结论中正结论是.(把所有正确结论的序号都填在横线上)①BE AF=;②DEF∆是等腰直角三角形;③无论点E、F的位置如何,总有EF DF CF=+成立;④四边形AEDF的面积随着点E、F的位置不同发生变化.三、解答题(共2小题)12.(2019春•金牛区期末):如图,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.13.(2019秋•苍溪县期末):△ABC为等边三角形,点E为射线AC上一点,点D为射线CB上一点,AD=DE.(1)如图1,当E在AC的延长线上且CE=CD时,AD是△ABC的中线吗?请说明理由;(2)如图2,当E在AC的延长线上时,AB+BD等于AE吗?请说明理由;(3)如图3,当D在线段CB的延长线上,E在线段AC上时,请直接写出AB、BD、AE的数量关系.。
《三角形全等的判定》全等三角形PPT课件

画一个△ ′′′,使′′ = ,′’ =
,∠′ = ∠:
(1)画∠′ = ∠;
(2)在射线′上截取′′ = ,在
射线′上截取′′ = ;
(3)连接′′.
【结论】两边和它们的夹角分别相等的三角形全等。也就是说,三角形的两
⫽ .
∠4. 求证:∠5 = ∠6.
∵ ∠1 = ∠2,∠3 = ∠4, = ,
根据易证△ ≌△ ,
∴有 = ,
又∵ ∠3 = ∠4, = ,
则可根据判定△ ≌△ ,
故∠5 = ∠6.
知识梳理
例4:如图,、交于点,、为上两点, = , =
就全等了.如果满足斜边和一条直角边分别相等,这两个直
角三角形全等吗?
教学新知
探索5:任意画出一个△,使∠=90°.再画一个 △ ′’’,使
∠′=90°,′′=,′′=.把画好的△′′′剪下来,放
到△上,它们全等吗?
画 一 个 △ ′′′ , 使 ∠′ = 90° , ′′ =
求证 = .
∵⊥,⊥
∴∠与∠都是直角
在R △ 和Rt △ 中,
=
=
∴ △ ≌ △ ()
∴ = .
知识梳理
知识点1:“边边边”(或“SSS”)
1.三边分别相等的两个三角形全等(可以简写成“边边边”
两个三角形全等吗?上述六个条件中,有些条件是相关的.
能否在上述六个条件中选择部分条件,简捷地判定两个三角
形全等呢?
探索1:先任意画出一个△ ABC.再画一个△ A′B′C′,使△ ABC与
△ A′B′C′满足上述六个条件中的一个(一边或一角分别
相等)或两个(两边、一边一角或两角分别相等).你
全等三角形》讲义(完整版)

全等三角形》讲义(完整版)全等三角形讲义全等三角形定义:若两个三角形形状大小相同,能够完全重合,则它们是全等形三角形。
对应顶点、对应边、对应角均重合。
全等三角形的性质是对应边相等,对应角相等。
全等三角形判定定理:1.边边边定理(SSS):若两个三角形的三条边对应相等,则它们是全等三角形。
2.边角边定理(SAS):若两个三角形的一条边和它们的夹角对应相等,且另一条边对应相等,则它们是全等三角形。
3.角边角定理(ASA):若两个三角形的两个角和它们的夹边对应相等,则它们是全等三角形。
4.角角边定理(AAS):若两个三角形的两个角和其中一个角的对边对应相等,则它们是全等三角形。
5.斜边直角边定理(HL):若两个直角三角形的斜边和一条直角边对应相等,则它们是全等三角形。
角平分线的性质:在角平分线上的点到角的两边的距离相等。
角平分线的判定:到角的两边距离相等的点在角的平分线上。
三角形的角平分线的性质:三角形三个内角的平分线交于一点,并且这一点到三边的距离相等。
典型例题举例:1.已知△ABN≌△ACM,对应角为∠B和∠C,对应边为AB和AC。
2.已知AB=AC,AD是连结点A与BC中点D的支架,求证△ABD≌△ACD。
3.已知点A、F、E、C在同一条直线上,AF=CE,BE∥DF,BE=DF,求证△ABE≌△CDF。
4.在△ABC中,D在AB上,E在AC上,AB=AC,∠B =∠C,求证AD=AE。
5.已知∠1=∠2,∠3=∠4,求证AC=AD,其中D是线段BC上的一点,且BD=DC。
6.在图中,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,AB=DC,BE=CF,判断AB是否平行于CD,说明理由。
7.在图1中,△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连结EG,判断△ABC与△AEG 面积之间的关系,并说明理由。
8.在图中,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF,求证DF=EF。
全等三角形的概念与性质PPT课件

结合2,3两题,说说你是怎样寻找这些对应元素的。 ⑴写出图中相等的线段,相等的角;
相等
全等三角形的对应角有什么关系? 记作: ∆ABC≌∆A1B1C1
相等
全等三角形的性质
全等三角形的对应边相等,对应角相等。
∵△ABC≌ △DFE(已知) ∴ AB=DF, BC=FE, AC=DE ( 全等三角形的对应边相等 ) ∴ ∠ A= ∠ D, ∠ B= ∠ F , ∠ C= ∠ E
(1) △ ABE ≌ △ ACF
(2)△ BCE ≌ △ CBF (3)△ BOF ≌ △ COE
5. △ABC≌△FED
⑴写出图中相等的线段,相等的角;
⑵图中线段除相等外,还有什么关系吗? 请与同伴交流并写出来.
A
D
B
C E
F
感谢观看
O B
③ D
结合2,3两题,说说你是怎样寻找这些对 应元素的。 (1)对应角所对的边是对应边;对应边 所对的角是对应角。
(2)有公共边的,公共边是对应边;有 公共角的,公共角是对应角。
(3)相等的边是
1、如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,则BC=
全等三角形的对应边有什么关系? 图对指结即 A●(∴写对CA中应出合∠重出应=BAB三 角 下 2合 全 角=,EA3D角所列的等所D两F形对全顶三对=,题B∠的的等点角的C,C位边三叫形边=说AF置是角对的是EE说),是对形应符对A你怎应的顶号应C是=样边对点表边D怎变应示..E样化边,并寻的和指找?对出这应它些角们对的应对元应素顶的点。、对应边、对应角。
其它的对应边有:______ A
E
对应角有:__________
∠BAD=∠CAE吗?为什么?
七年级 全等三角形知识点

七年级全等三角形知识点全等三角形,是初中数学中一个非常重要的概念。
在几何图形的学习中,我们经常会涉及到它。
全等三角形指的是两个三角形,它们的三个内角分别相等,同时三条边分别相等,这样的两个三角形就是全等三角形。
在初中数学中,全等三角形的性质极为重要,因为全等三角形对于证明很多几何定理都具有重要作用。
下面就让我们一起来了解全等三角形的知识点。
一、全等三角形的定义及性质两个三角形全等的充要条件为:它们的三个内角相等,三条边分别相等。
全等三角形有以下性质:1. 全等三角形的三个内角相等。
2. 全等三角形的三条边相等。
3. 全等三角形的三个角分别对应着三条边。
4. 全等三角形的任意两边中所夹的角相等。
二、全等三角形的判定方法(一)SAS判定法若两个三角形的两边及其夹角分别相等,则这两个三角形全等。
(二)ASA判定法若两个三角形的两角及它们所夹的边分别相等,则这两个三角形全等。
(三)SSS判定法若两个三角形的三条边分别相等,则这两个三角形全等。
(四)AAS判定法若两个三角形的两角及其对边分别相等,则这两个三角形全等。
三、全等三角形的应用在几何证明中,全等三角形的性质被广泛地应用。
比如我们要证明:垂直线段的中点连线是这两条线段的公共垂线,我们可以利用全等三角形的性质来进行证明。
此外,利用全等三角形还可以证明如下定理:1. 一条平行线把两边分成的两个三角形全等,则这条平行线与这两边所夹的角有关。
2. 一条角平分线把一个角分成的两个小角所对边的线段相等,则这两个小角全等。
3. 点到直线的距离有唯一性。
四、总结全等三角形是初中数学中一个非常重要的概念,而全等三角形的定义、性质和判定方法对应用它们去证明各种几何定理都具有重要作用。
因此初中的同学们,必须掌握全等三角形的知识,才能更好地理解和应用几何定理。
全等三角形及其性质课件

边边边(SSS)证明方法
总结词
三边对应相等的两个三角形全 等
详细描述
如果两个三角形的三组对应边 相等,则这两个三角形全等。 这是全等三角形最直接的证明 方法。
适用情况
当已知三角形的三边长度,并 且需要证明另外两个三角形全 等时,可以考虑使用此方法。
注意事项
在应用此方法时,需要确保所 比较的边确实是对应边。
个三角形全等。
进阶练习题
01
02
03
04Leabharlann 总结词:提升解题技巧1. 利用全等三角形的性 质,证明两个三角形全 等。
2. 通过添加辅助线,证 明两个三角形全等。
3. 在给定条件下,寻找 两个三角形的相等元素 并证明其全等。
综合练习题
总结词:综合运用知识
2. 通过构建全等三角形解决实际问题,如测量、几何作 图等。
全等三角形的判定条件
总结词
SAS、ASA、SSS、AAS、HL是全等三角形的五种判定 条件。
详细描述
SAS(Side-Angle-Side)判定条件指的是两个三角形 如果两边和它们之间的夹角相等,则这两个三角形全等 ;ASA(Angle-Side-Angle)判定条件是指两个三角 形如果两角和它们之间的夹边相等,则这两个三角形全 等;SSS(Side-Side-Side)判定条件是指三个边分别 相等的两个三角形全等;AAS(Angle-Angle-Side) 判定条件是指两个角和其中一个角的对边分别相等的两 个三角形全等;HL(Hypotenuse-Leg)判定条件是 指直角三角形中斜边和一个直角边相等,则这两个直角 三角形全等。这些判定条件是证明两个三角形是否全等 的重要依据,也是解决几何问题的重要工具。
02 三角形的基本性质
七年级全等三角形知识点

七年级全等三角形知识点全等三角形是初中数学中非常重要的一部分,它是平面几何学中基础的一个概念,也是许多复杂性质的前提条件。
在初中学习阶段,深入理解全等三角形的基础知识是非常必要的。
下面,我们来详细地了解一下七年级全等三角形知识点。
一、全等三角形的定义全等三角形是指在平面内,若两个三角形的三边分别对应相等,则这两个三角形完全相同,彼此重合,称之为全等三角形。
二、全等三角形的性质1. 相等必重合:如果两个三角形是全等的,那么它们一定重合在一起。
2. 全等三角形的对应边角相等:在两个全等三角形中,对应的边和对应的角都是相等的。
3. 全等三角形的内角和相等:在一个全等三角形中,三个内角的和等于180度。
三、全等三角形的判定1. SSS判定法:若两个三角形的三边分别相等,则这两个三角形是全等的。
2. SAS判定法:若两个三角形的两边和夹角分别相等,则这两个三角形是全等的。
3. ASA判定法:若两个三角形的一边和两个夹角分别相等,则这两个三角形是全等的。
四、全等三角形的应用1. 利用全等三角形求解三角形的性质:我们可以利用全等三角形的性质来证明之前所学三角形的性质,比如角平分线定理、垂心定理等。
2. 证明两条线段平行:我们可以通过构造全等三角形来证明两条线段平行,这也是初中数学中常用的证明方法之一。
3. 量角度:我们可以利用全等三角形来量角度,比如在一些复杂的图形中,可以通过构造全等三角形来得到某些角度的度数。
五、练习全等三角形在学习了全等三角形的基本知识后,我们需要通过大量的练习来巩固这些知识。
下面,我们提供一些练习题,供大家训练。
1. 若ABC和DEF是两个全等三角形,那么∠B = ?2. 若两个三角形的两个角和一条边分别相等,则这两个三角形是什么关系?3. 通过构造全等三角形,证明AD // BC。
4. 量出下图中的∠ACD的度数。
(插入图片)结语:在初中数学学习阶段,全等三角形的基础知识是非常重要的。
全等三角形知识点总结

全等三角形知识点总结一、全等三角形的概念1. 定义- 能够完全重合的两个三角形叫做全等三角形。
重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
- 例如,△ABC与△DEF全等,记作△ABC≌△DEF,其中A与D、B与E、C与F 是对应顶点,AB与DE、BC与EF、AC与DF是对应边,∠A与∠D、∠B与∠E、∠C 与∠F是对应角。
2. 全等三角形的性质- 对应边相等:若△ABC≌△DEF,则AB = DE,BC = EF,AC = DF。
- 对应角相等:∠A=∠D,∠B = ∠E,∠C=∠F。
- 全等三角形的周长相等,面积相等。
因为全等三角形的对应边相等,所以它们的周长(三边之和)相等;又因为对应边和对应角都相等,根据三角形面积公式(如S=(1)/(2)ahsin B等多种公式都可推出),其面积也相等。
二、全等三角形的判定1. SSS(边边边)判定定理- 内容:三边对应相等的两个三角形全等。
- 例如,在△ABC和△DEF中,如果AB = DE,BC = EF,AC = DF,那么△ABC≌△DEF。
- 作用:可以用来证明两个三角形全等,当已知两个三角形的三边长度分别相等时,就可以直接判定它们全等。
2. SAS(边角边)判定定理- 内容:两边和它们的夹角对应相等的两个三角形全等。
- 例如,在△ABC和△DEF中,如果AB = DE,∠A = ∠D,AC = DF,那么△ABC≌△DEF。
这里要注意必须是两边及其夹角,不能是两边及其中一边的对角。
- 作用:在已知三角形两边长度和它们夹角大小的情况下,用于判定三角形全等。
3. ASA(角边角)判定定理- 内容:两角和它们的夹边对应相等的两个三角形全等。
- 例如,在△ABC和△DEF中,如果∠A = ∠D,AB = DE,∠B = ∠E,那么△ABC≌△DEF。
- 作用:当知道两个三角形两角及其夹边相等时,可判定全等。
4. AAS(角角边)判定定理- 内容:两角和其中一角的对边对应相等的两个三角形全等。
春季班七年级下册教案第11讲:全等三角形的构造法(2)

第11讲 构造全等三角形的方法(2)【学习目标】1. 熟悉并掌握三角形全等的“SSS ”,“ASA ”,“AAS ”,“SAS ”,“HL”条件; 2. 能掌握“倍长中线法”和“截长补短法”。
【学习重点】“倍长中线法”和“截长补短法”的学习。
【学习难点】“倍长中线法”和“截长补短法”的学习,并能对相关题目进行分析方法与技巧的总结与运用。
【知识梳理】1.全等三角形判定方法:(1) “边角边”或“SAS” ;(2) “角边角”或“ASA”;(3) “边边边”或“SSS”;(4) “角角边”或“AAS” ;(5) “斜边、直角边”或“HL” 2.构造全等三角形的方法:(1)通过倍长中线法构造全等三角形;(2)通过截长补短法构造全等三角形。
3.线段的垂直平分线定理:线段垂直平分线上的点,到线段的两端距离相等;4.线段的垂直平分线定理逆定理:到线段两端距离相等的点,在线段垂直平分线上。
5.角平分线定理:角平分线上的点,到角的两边距离相等;6.角平分线定理逆定理:到线段的两端距离相等点,在线段垂直平分线上。
7.等腰三角形三线合一定理:等腰三角形的顶角平分线、底边上的中线和高,三线合一。
【典例剖析】考点一:通过“倍长中线法”构造三角形全等例1:(“希望杯”试题)已知,如图△ABC 中,AB=5,AC=3,则中线AD 的取值范围是 。
例2:(太原中考)△ABC 中, D 为BC 的中点. 过D 点的直线GF 交AC 于F, 交AC 的平行线BG 于点G . DE ⊥GF, 并交AB 于点E. 连结EG ,EF. (1) 求证:BG=CF.(2)请猜想BE+CF 与EF 的大小关系, 并加以证明.例3:(2016黄老培优)以△ABC 的两边AB 、AC 为腰分别向外作等腰Rt △ABD 和等腰Rt △ACE ,∠BAD=∠CAE=90°,连接DE ,M 、N 分别是BC 、DE 的中点.探究:AM 与DE 的位置关系及数量关系. (1)如图① 当△ABC 为直角三角形时,AM 与DE 的位置关系是 , 线段AM 与DE 的数量关系是 ;(2)将图①中的等腰Rt △ABD 绕点A 沿逆时针方向旋转(090)θθ︒<<后,如图②所示,(1)问中得到的两个结论是否发生改变?并说明理由.例4:如图所示,在△ABC中,AD是∠BAC的角平分线,且AE=AF。
初中七年级下册数学讲义第11讲-全等三角形的判定一0XRN2B6DZ0FH

学员姓名:学科教师:年级:辅导科目:授课日期时间主题第11讲-全等三角形的判定一学习目标1.掌握全等形、全等三角形及全等三角形的对应元素;掌握全等三角形的性质,能用符号正确地表示两个三角形全等;能熟练找出两个全等三角形的对应角、对应边;2.会根据已知条件画三角形(已知三边、两边一夹角、两角一夹边);教学内容教师:只给一个条件(一条边或者一个角)画三角形时,大家画出的三角形唯一吗?学生回答教师:如果给定两个条件画三角形,有几种可能情况,画出来的三角形可以确定是唯一的吗?学生思考,动手画教师:那么给出三个条件,有哪几种可能情况呢?他们是否都能确定三角形呢?提示:(三边,三角,两边一角,两角一边)【知识梳理】1.全等三角形的性质:2.全等三角形判定定理1:【例题精讲】题型一:全等三角形的性质例1:若ΔABC≌ΔDEF,且AB = 3,BC = 4,AC = 5,则ΔDEF的周长是例2:如图,ΔABC≌ΔADE,∠B = ∠D,则AC与是对应边,∠CAB = 例3:如图,ΔABF≌ΔCDE,∠B = 30°,∠BAF = 88°,求∠DEC的度数。
试一试:1:如图,ΔABC≌ΔDAE,那么AB = ,∠B =2.如图,ΔABC≌ΔDCB,∠A = ∠D,试写出其余的对应角和对应边对应边:对应角:A BFED CBDA ECDB E CABA DC3. 如图,已知ΔABC ≌ΔADE ,∠CAD = 10°,∠DFB = 90°,∠B = 25°,求∠E 与∠DGB 的度数。
例4:如图,在ΔABC 中,∠A = ∠B ,点D 、E 、F 分别在AC 、BC 、AB 上,AD = BF ,BE = AF ,说明A DFE ∠=∠的理由。
例5: 已知:如图1,B 、C 、E 三点在一条直线上,△ABC 和△DCE 均为等边三角形,连结AE 、DB ,求证:AE =DB例6:如图,于,于,,l . 求证:FAEG DCBC DAFEBDE CD ⊥D DB AB ⊥B BE CD =AE CE ⊥例7:点B F D A ,,,在同一直线上,BF AD =,且BC AE ∥,AE =BC 求证:⑴≌ ⑵例8:如图,已知四边形ABCD 与BEFG 都是正方形。
全等三角形及性质PPT课件

角角边定理
两角和一边对应相等的两个三角 形全等,简称AAS。
若两个三角形有两个角相等,且 其中一个角的对边也相等,则这
两个三角形全等。
举例:若△ABC和△DEF中, ∠A=∠D,∠B=∠E,BC=EF,则
△ABC≌△DEF。
04
全等三角形与相似三角形关系
相似三角形定义及性质
定义:两个三角形如果它们 的对应角相等,则称这两个
行推导。
全等三角形在几何证明中作用
01
02
03
04
证明线段相等
通过全等三角形的对应边相等 来证明两条线段相等。
证明角相等
通过全等三角形的对应角相等 来证明两个角相等。
证明垂直关系
通过全等三角形的性质来证明 两条直线垂直。
证明平行关系
通过全等三角形的性质来证明 两条直线平行。
典型例题解析
例题1
已知△ABC和△DEF全等,且AB=DE,BC=EF,∠B=∠E。 求证:AC=DF。
HL全等(直角三角形)
在直角三角形中,斜边和一条直 角边分别相等的两个三角形全等 。
典型例题解析
解析
根据SAS全等的判定方法,已知两边和夹角分别相等,因 此可以判定△ABC和△DEF全等。
例2
已知△ABC中,∠C = 90°,AC = BC,AD平分∠CAB交BC 于D,DE⊥AB于E,且AB = 6cm,求△DEB的周长。
边角边判定
如果两个多边形的一组对 应边和它们之间的对应角 都相等,则它们是全等的 。
角边角判定
如果两个多边形的一组对 应角和它们之间的夹边都 相等,则它们是全等的。
典型例题解析
1. 例题一
已知两个四边形ABCD和EFGH,其中AB=EF, BC=FG, CD=GH, DA=HE,且∠A=∠E, ∠B=∠F, ∠C=∠G, ∠D=∠H。求证:四边形ABCD与四边形EFGH全等。
三角形全等的判定ppt课件

5.HL(H.L.) 在Rt△ABC与Rt△A1B1C1中,
AB=A1B1(已知)
BC=B1C1(已证) ∴△ABC≌△A1B1C1(HL)
例题精讲
例:已知:如图,点A,C,B,D在同一条直线上,
AC=BD,AM=CN,BM=DN 求证:AM∥CN,BM∥DN.
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
为BC边的中点,那么图中的全等三角形有哪几对?并选
择一对进行证明
△ABD≌△ACD
证明:∵D为BC边的中点
A
∴BD=CD
在△ABD和△ACD中
E
AB=AC
BD=CD
AD=AD
B
D
C
∴ △ABD≌△ACD(SSS)
拓展延伸
8.如图所示,AB=AC,EB=EC,AE的延长线交BC于D,且D
证明:∵AC=BD ∴AC+CB=BD+BC 即AB=CD
M
N
在△AMB和△CND中 AM=CN
BM=DN
A
C
B
D
AB=CD
∴ △AMB≌△CND(SSS)
∴∠A=∠NCD,∠MBA=∠D ∴AM∥CN,BM∥DN
例:如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,
AE=FC
求证:△ABC≌△FDE.
(2)全等三角形对应角相等
PART II 全等三角形的判定 1.SSS(S.S.S.) 在△ABC与△A1B1C1中,
AB=A1B1(已知) BC=B1C1(已知) AC=A1C1(已证)
∴△ABC≌△A1B1C1(SSS)
七年级三角形全等的知识点

七年级三角形全等的知识点在七年级学习数学时,我们接触到了很多与三角形有关的知识,其中一个重要的内容就是三角形的全等问题。
在本文中,我们将详细介绍三角形全等的定义、判定方法以及应用。
一、三角形全等的定义三角形全等的定义可以简单地表述为:两个三角形的各边对应相等,各角对应相等,那么这两个三角形就是全等的。
这里的“对应相等”是指两个三角形中对应的边或角的度量相等。
如果两个三角形的边或角都相等,那么这两个三角形就是全等的。
二、三角形全等的判定方法1. SSS法:即“边-边-边”法。
当两个三角形的三条边分别相等时,这两个三角形就是全等的。
2. SAS法:即“边-角-边”法。
当两个三角形的两边和夹角分别相等时,这两个三角形就是全等的。
3. ASA法:即“角-边-角”法。
当两个三角形的两个角和它们之间的边分别相等时,这两个三角形就是全等的。
4. RHS法:即“直角-斜边-直角”法。
当两个直角三角形的斜边和一个直角边分别相等时,这两个三角形就是全等的。
三、三角形全等的应用1. 几何证明:三角形全等的判定方法可以用于解决很多几何证明题。
比如,证明两条直线平行、四边形各边相等、圆心角的度数等。
2. 测量距离:我们可以利用三角形全等的原理,通过测量三角形的边长,从而计算出不便测量的距离。
3. 组合图形:三角形全等的知识可应用于解决组合图形的面积问题。
通过将一个图形划分出多个全等三角形,可以快速计算出整个图形的面积。
4. 实际应用:在生活中,三角形全等的知识也有很多实际应用。
比如,设计房屋和桥梁时需要考虑全等原理,避免因构造不当导致的结构失稳。
综上所述,三角形全等的知识点对于初中阶段的数学学习至关重要。
通过学习三角形全等的判定方法和应用,我们不仅能够更好地理解数学知识,还能够在日常生活和工作中获得实际应用。
七年级第十一讲全等三角形性质及判定
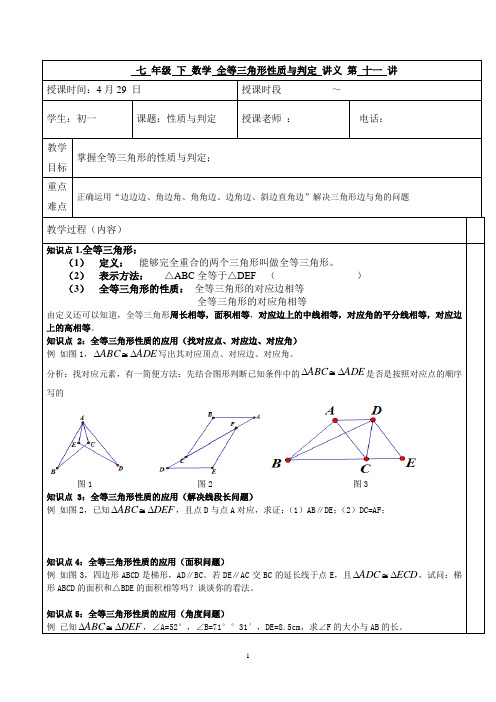
图1 图2 图3 全等三角形性质的应用(解决线段长问题) 知识点 3:全等三角形性质的应用(解决线段长问题) 例 如图 2,已知 ∆ABC ≅ ∆DEF ,且点 D 与点 A 对应,求证: (1)AB∥DE; (2)DC=AF;
全等三角形性质的应用(面积问题) 知识点 4:全等三角形性质的应用(面积问题) 例 如图 3,四边形 ABCD 是梯形,AD∥BC。若 DE∥AC 交 BC 的延长线于点 E,且 ∆ADC ≅ ∆ECD ,试问:梯 形 ABCD 的面积和△BDE 的面积相等吗?谈谈你的看法。
例 4.已知:点 A、C、B、D 在同一条直线,AC=BD,∠M=∠N=90°,AM=CN
求证: MB∥ND
练习:已知:ABC 在同一直线上,BE⊥AC,AB=BE,AD=CE。求证:①∠A=∠E;②AF⊥CE
知识点 7:图形变换中的全等三角形 例 如图:甲所示,A、B、C、D 在同一直线上,AB=CD,DE∥AF,且 DE=AF,求证:△AFC ≅ △DEB。 如果将 BD 沿 AD 边的方向平行移动,B 点在 C 点右侧时,如图乙;B 点与 C 点重合时,如图丙,其余条件 不变,结论是否成立,并说明理由。
例1、 已知:如图:AB=CD , BE=CF , AF=DE.(1)求证:△ABE≌△DCF;(2)AB∥CD
练习:已知如图,B 是 CE 的中点,AD=BC,AB=DC.DE 交 AB 于 F 点。求证: (1)AD∥BC(2)AF=BF.
判定 2、两角和它们的夹边对应相等的两个三角形全等,可以简写成“角边角”或“ASA” ASA” “角边角” 两角和其中一个角的对边对应相等的两个三角形全等,可以简写成“角角边”或“AAS” AAS” “角角边” 注:这一结论很容易由 ASA 推出,将这一结论与 ASA 结合起来,即可推出:两个三角形如果具备两个角 和一条边对应相等,就可判定其全等。 例 2、 求证:三角形的一边的两端点到这边的中线或中线的延长线的距离相等。 分析:这是文字题,必须先根据题意画出图形,再结合题意,写出已知、求证、再证明。 已知:如图 4,AD 为△ABC 的中线,且 CF⊥AD 于点 F,BE⊥AD,交 AD 的延长线于点 E。 求证:BE=CF
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级下学期春季班(学生版)最新讲义本节主要针对全等三角形的相关概念和性质及全等三角形的判定进行讲解,重点是全等三角形的性质的运用和判定两个三角形全等的四个判定定理,要求同学们可以达到灵活运用判定定理进行说明三角形全等的理由.本节课是几何说理的基础,综合性不高,相对简单.全等形、全等三角形及其相关的概念(1)全等形:能够重合的两个图形叫做全等形.(2)能够完全重合的两个三角形叫做全等三角形;两个全等三角形中,互相重合的顶点叫做对应顶点;互相重合的角叫做对应角;互相重合的边叫做对应边.如下图所示:已知:△ABC≌DFE,A与D,B与F是对应顶点,则:(C与E是对应顶点)对应边有:AB与DF,AC与DE,BC与FE.对应角有:A D B F C E∠∠∠∠∠∠与,与,与.全等三角形的概念性质和判定内容分析知识结构模块一:全等三角形的概念和性质知识精讲AB CDE F全等三角形的数学语言:三角形ABC 与三角形A ′B ′C ′全等,记作△ABC ≌△A ′B ′C ′,读作“三角形ABC 全等于三角形A ′B ′C ′”. 全等三角形的性质:(1)全等三角形的对应边相等,对应角相等; (2)全等三角形的面积相等,周长相等;(3)全等三角形的对应线段(高线、中线、角平分线)相等. 全等三角形中应注意的问题:(1)要正确区分“对应边”与“对边”、“对应角”与“对角”的不同含义; (2)符号“≌”表示的双重含义:①“∽”表示形状相同;②“=”表示大小相等; (3)表示两个三角形全等时,表示对应的顶点的字母要写在相对应的位置上; 画三角形:确定三角形形状、大小的条件:六个元素(三条边、三个角)中的如下三个元素:两角及其夹边;两边及其夹角;三边.【例1】 下列说法正确的是( )A .全等三角形是指形状相同的三角形B .全等三角形是指面积相等的三角形C .全等三角形的周长和面积都相等D .所有的等边三角形都全等【例2】 直角三角形斜边上的中线把直角三角形分成的两个三角形的关系是( )A .形状相同B .周长相等C .面积相等D .全等【例3】 如图所示,△ABC ≌△CDA ,且AB =CD ,则下列结论错误的是( ) A .∠1=∠2 B .AC =CA C .∠B =∠D D .AC =BC例题解析21ABCD【例4】 下列各条件中,不能作出唯一的三角形的是 ( )A .已知两边和夹角B .已知两角和夹边C .已知两边和其中一边的对角D .已知三边【例5】 练习画出下列条件的三角形:(1) 画,ABC ∆使40,45,4A B AB cm ∠=︒∠=︒=; (2) 画,ABC ∆使6,8,10AB cm BC cm AC cm ===; (3) 画,ABC ∆使4,3,45AB cm AC cm A ==∠=︒; (4) 画,ABC ∆使8,5,50AB cm AC cm B ==∠=︒.【例6】 下列说法:①形状相同的两个图形是全等形;②面积相等的两个三角形是全等三角形;③全等三角形的周长相等,面积相等;④在△ABC 和△DEF 中,若∠A =∠D ,∠B =∠E ,∠C =∠F ,AB =DE ,BC =EF ,AC =DF ,则两个三角形的关系,可记作△ABC ≌△DEF ,其中说法正确的是( )A .1个B .2个C .3个D .4个【例7】 下列说法中错误的是()A .全等三角形的公共角是对应角,对顶角也是对应角B .全等三角形的公共边也是对应边C .全等三角形的公共顶点是对应顶点D .全等三角形中相等的边所对应的角是对应角,相等的角所对的边是对应边【例8】如图所示,ABE ADC ABC∆∆∆和是分别沿着AB AC、边翻折形成的,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为()A.80° B.100° C.60° D.45°【例9】如图,在矩形ABCD中,AE平分∠DAB交DC于点E,连接BE,过E作EF⊥BE 交AD于F.(1)∠DEF和∠CBE相等吗?请说明理由;(2)请找出图中与ED相等的线段(不另添加辅助线和字母),并说明理由.【例10】如图所示,30255ADF BCE B F BC cm∆≅∆∠=︒∠=︒=,,,,14CD cm DF cm==,.求:(1)1∠的度数;(2)AC的长.α321AB CDEP1A BC DE F【例11】如图,在△ABC中,∠A:∠B :∠ACB=2:5:11,若将△ABC绕点C逆时针旋转,试旋转前后的△A’B’C’中的顶点B’在原三角形的边AC的延长线上,求∠BCA’的度数.【例12】如图,已知△ABC≌△ADE,BC的延长线交AD于点F,交AE的延长线于G,∠ACB=1050,∠CAD=100,∠ADE=250,求∠DFB和∠AGB的度数.模块二:全等三角形的判定ABCA’B’AB CDE FG本模块复习了全等三角形的4个判定定理,主要是已知条件为“两边及夹角对应相等(SAS )”,“两角及夹边对应相等(ASA )”,“两角及其中一角的对边对应相等(AAS )”“三边对应相等(SSS )”的两个三角形全等.【例13】 如图,已知∠B =∠D ,∠1=∠2,AC =AE ,说明△ABC ≌△ADE 的理由.【例14】 如图,已知∠C =∠E ,BE =CD ,说明△ABE 与△ADC 全等的理由,AB 与AD相等吗?为什么?知识精讲例题解析ABC DEF21AB CDE【例15】 如图,已知AD =BC ,AE =BE .说明AC =BD ,∠C =∠D 的理由.【例16】 如图,已知AB =CD ,AD =BC ,说明∠A =∠C 的理由.【例17】 如图,已知BD 是△ABC 的中线,B 、D 、E 、F 在一条直线上,且AE ∥CF ,说明△ADE 与△CDF 全等的理由.A BCDABCD EABCDE F【例18】 如图,已知AC ∥BD ,AC =BD ,(1)说明△AOC 与△BOD 全等的理由;(2)说明EO =FO 的理由.【例19】 如图,CD ⊥AB 于D ,BE ⊥AC 于E ,OD =OE ,说明AB =AC 的理由.【例20】 如图,已知AD ∥BC ,BF ∥DE ,AE =CF .(1) △ADE 与△CBF 全等吗,为什么? (2) 说明AB =CD 的理由; (3) 图中有哪几对全等三角形?ABCD EFO ABCDEOABCDEF【例21】 如图,已知AB =CD ,BM =CM ,AC =BD ,说明AM =DM 的理由.【例22】 如图,∠1=∠2,AC =BD ,E 、A 、B 、F 在同一条直线上,说明:∠CAD =∠DBC 的理由.【例23】 如图所示,AB =AC ,CE =BE ,连结AE 并延长交BC 于D ,说明AD ⊥BC 的理由.21ABC DEFAB CDMABCDE11 / 16【例24】 如图所示,BE 、CD 相交于O ,AB =AC ,AD =AE ,说明OD =OE 的理由.【习题1】 下列命题中正确的是 ( )A .全等三角形的高相等B .全等三角形的中线相等C .全等三角形的角平分线相等D .全等三角形对应角的平分线相等【习题2】 如图,△ABD ≌△CDB ,且AB 、CD 是对应边;下面四个结论中不正确的是( )A .△ABD 和△CDB 的面积相等 B .△ABD 和△CDB 的周长相等C .∠A +∠ABD =∠C +∠CBD D .AD ∥BC ,且AD =BC【习题3】 如图,折叠长方形ABCD ,使顶点D 与BC 边上的N 点重合,如果AD =7厘米,DM =5厘米,∠DAM =390,则AN = 厘米,NM =____________厘米,∠NAB = .【习题4】 尺规作图作AOB 的平分线方法如下:以O 为圆心,任意长为半径画弧交OA 、 随堂检测ABC DEOABCDA B C D MNA12 / 16OB 于C 、D ,再分别以点C 、D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP ,由作法得OCP ODP △≌△的根据是( ) A .SAS B .ASA C .AAS D .SSS【习题5】 如图,CE ⊥AB ,DF ⊥AB ,垂足分别为E 、F ,(1)若AC //DB ,且AC =DB ,则△ACE ≌△BDF ,根据__________; (2)若AC //DB ,且AE =BF ,则△ACE ≌△BDF ,根据__________; (3)若AE =BF ,且CE =DF ,则△ACE ≌△BDF ,根据__________; (4)若AC =BD ,AE =BF ,CE =DF .则△ACE ≌△BDF ,根据__________.【习题6】 如图,已知△ABC ≌△ADE , ∠CAD =150,∠DFB =900,∠B =250.求∠E 和∠DGB 的度数.【习题7】 如图:A 、E 、F 、C 四点在同一条直线上,AE =CF ,过E 、F 分别作BE ⊥AC 、DF ⊥AC ,且AB ∥CD ,AB =CD .试说明:BD 平分EF .A BCEDF ABC DE FGABCDEFG13 / 16【习题8】 已知:如图,△ABC 是等边三角形,过AB 边上的点D 作DG ∥BC ,交AC于点G ,•在GD 的延长线上取点E ,使DE =DB ,连结AE 、CD . 试说明:△AGE ≌△DAC .ABCDEFG14 / 16【作业1】 如图,△ABC ≌△ABD ,C 和D 是对应顶点,若AB =6cm ,AC =5cm ,BC =4cm ,则AD 的长为_________cm . 【难度】★ 【答案】 【解析】【作业2】 如图,给出下列四组条件:①AB DE BC EF AC DF ===,,; ②AB DE B E BC EF ===∠∠,,; ③B E BC EF C F ===∠∠∠∠,,; ④AB DE AC DF B E ===∠∠,,.其中,能使ABC DEF △≌△的条件共有 ( ) A .1组 B .2组 C .3组 D .4组【难度】★ 【答案】 【解析】【作业3】 下列各条件中,不能作出唯一三角形的是( )A .已知两边和夹角B .已知两角和夹边C .已知两边和其中一边的对角D .已知三边【难度】★ 【答案】 【解析】【作业4】 已知△ABC ≌△DEF ,若△ABC 的周长为32,AB =8,BC =12,则DE =_______,DF =_______,EF = _______. 【难度】★★【答案】 【解析】课后作业A B C DEFABCD15 / 16【作业5】 如图△ACE ≌△DBF ,AE =DF ,CE =BF ,AD =8,BC =2.(1)求AC 的长度;(2)说明CE ∥BF 的理由. 【难度】★★ 【答案】 【解析】【作业6】 如图,已知△ABC ≌△AED ,AE =AB ,AD =AC , ∠D -∠E =200,∠BAC =600,求∠C 的度数. 【难度】★★ 【答案】 【解析】【作业7】 如图,△DAC 和△EBC 均是等边三角形,点C 在线段AB 上,AE 、BD 分别与CD 、 CE 交于点M 、 N ,有如下结论①△ACE ≌△DCB ;② CM =CN ;③ AC =DN .其中正确的结论是_______________,证明正确的结论. 【难度】★★ 【答案】 【解析】【作业8】 如图,AD ⊥AB ,AC ⊥AE ,且AD =AB ,AC =AE . 试说明:DC =BE ,DC ⊥BE . 【难度】★★ 【答案】 【解析】ABCDEABCD EM NA BCDEGABCDEF16 / 161EF DCA 【作业9】 如图,已知AE =CF ,∠DAF =∠BCE ,AD =CB . (1)问△ADF 与△CBE 全等吗?请说明理由;(2)如果将△BEC 沿CA 边方向平行移动,可有图中3幅图,如上面的条件不变, 结论仍成立吗?请选择一幅图说明理由. 【难度】★★ 【答案】 【解析】【作业10】 如图,以△ABC 的边AB 、AC 为边向外作等边△ABD 和等边△ACE ,BE与CD 相交于点F .(1)请说明△ABE ≌△ADC 的理由; (2)求∠1的度数. 【难度】★★★ 【答案】 【解析】ABCD EF A BC D E FABC DEFC (A )BD。
