福建省春季高考高职单招数学模拟试题及答案
福建省福州市高职单招数学模拟试卷(三) (2)

福建省福州市高职单招数学模拟试卷(三)班级___________ 座号_______ 姓名__________ 成绩_______一、单项选择题(将正确答案的序号填入括号内。
本大题12小题,每小题4分,共48分)1、 设全集I={小于6的自然数},A={1,2,3},B={2,3,5},则()I C A B ⋂=( ).A {0,1,4}B {1,4,5}C {0,1,4,5}D {1,5}2、下列各组函数中,哪一组的两个函数为同一函数( ).A cos()cos y x y x =-=与B 221,y n y n n Z ==+∈与C y y x ==D 2111x y x y x -=+=-与 3、过点A (2,3)且平行于直线250x y +-=的直线方程为( ).A 250x y ++=B 270x y +-=C 230x y ++=D 220x y ++=4、在等比数列{}n a 中4810a a =,则369a a a =( ).A 15B -15C ±5、在空间,下列命题正确的是( )A 若直线a M ⊥平面 ,直线b M ⊥平面,则a bB 若直线a M 平面 ,直线l M ⊆,则a lC 若M N ⊥平面平面 , l M ⊆,则l ND 若直线a M 平面,若直线a 平面N ,则M N6、某厂第一年产值是a ,从第二年开始进行改革,改革后每年可增产20%,那么这个工厂第五年的产值为 ( ). A 565a ⎛⎫ ⎪⎝⎭ B 465a ⎛⎫ ⎪⎝⎭C 56515a ⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦D 46515a ⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ 7、不等式1023x x -≥-的解集是( ). A 31,2⎛⎫ ⎪⎝⎭ B (]3,1,2⎛⎫-∞⋃+∞ ⎪⎝⎭ C 31,2⎡⎫⎪⎢⎣⎭D ()3,1,2⎡⎫-∞⋃+∞⎪⎢⎣⎭ 8、将一颗骰子连掷3次,其中恰有2次出现奇数点的概率( ).A 18B 14C 12D 389、函数sin cos y x x =•的最小正周期( ). A 3π B π C 2π D 6π 10、如果向量a = (-2,3),b =(5,y),且a b ⊥,那么y 的值是( ). A 152- B 103 C 152 D 103- 11、6个人站成一排照相,其中甲、乙两人一定要相邻,共有多少种不同的排法( ). A 120 B 480,C 240D 60 12、已知12F F 和为双曲线2214x y -=的两个焦点,p在双曲线上,满足122,3F PF π∠=则12F PF 的面积( ).A 1B 23C 43D 3 二、填空题(把答案写在横线上,本大题8小题,每小题5分,共40分)1、函数)5(log 3-=x y 的定义域是 .2、已知5sin ,13αα=-是第四象限角,那么()6Cos πα+= .3、两曲线2216x y +=与1xy =的交点的个数是 .4、求921x x ⎛⎫- ⎪⎝⎭展开式中含3x 项的系数 . 5、已知A(3,-2),B (5,1),把AB 的起点移到(-1,3)后,那么B 点的新坐标是 .6、腰长为2的等腰直角三角形ABC 中,0B 90AC ∠=,PC ABC ⊥平面,且PC =则点p到AB 边的距离是 .7、若双曲线22215x y a -=与椭圆2212516x y +=有共同的焦点,且0a ,则a = . 8、过点A(4,-2)作圆2220x y +=的切线,则此切线方程是 .三、解答题(本大题7小题,共62分。
福建省春季高考高职单招数学模拟试题(十二)及答案.pdf

20.(本小题满分 8 分) 已知函数 f (x) = sin( − x) − cos x,(x R) .
(1) 求函数 f (x) 的最小正周期; (2) 求函数 f (x) 的最大值和最小值;
(3) 若 f ( ) = 1 , (0, ) ,求 sin + cos 的值.
学海无涯
福建省春季高考高职单招数学模拟试题(十二)
班级:
姓名:
座号:
一.选择题:本大题共14小题,每小题5分,满分70分.
成绩:
1.已知集合 A ={−1,0,1},则( )
A.1+ i A
B.1+ i2 A
C.1+ i3 A D.1+ i4 A
2.已知命题 P:“ x R, x2 + 2x + 3 0 ”,则命题 P 的否定为( )
0 0.065 0.070 0.075 0.0800.0850.0900.0950.1000.105
于等于 2.5 微米的颗粒物).右图是某市某月(按 30 天计)根据对“pm2.5” 24 小时平均浓度值测试
的结果画成的频率分布直方图,若规定空气中“pm2.5”24 小时平均浓度值不超过 0.075 毫克/立方米
学海无涯
22. (本小题满分 10 分) 如图①边长为 1 的正方形 ABCD 中,点 E、F 分别为 AB、BC 的中点,将△BEF 剪去,将△AED、△DCF
分别沿 DE、DF 折起,使 A、C 两点重合于点 P 得一三棱锥如图②示.
A. 3
B. 4
C. 6
D. 10
9.已知向量 a = (x − z,1),b = (2, y + z) ,且 a ⊥ b ,若变量 x,y
福建省福州市高职单招数学模拟试卷(一)

福建省福州市高职单招数学模拟试卷(一)(考试时间120分钟,满分150分)班级__________座号____________姓名__________成绩___________一、 单项选择题(42分)1、由平方为1的数所组成的集合为( )A .﹛1﹜B .﹛-1﹜C .﹛1,-1﹜D . 1 2、不等式2x 2+5x-3<0的解( ) A .全体实数 B .空集 C .-3<x <21 D .x <-3或x >213、不等式|X-2|>5的解集为( )A .{x|x >5或 x <-5 ﹜B .{x|-5<x <5﹜C .{x|x >7或 x <-3 ﹜D .{x|-3<x <5﹜ 4、抛物线2112y x =-+的开口方向和顶点坐标为( ) A .开口向上,顶点(0,-1) B .开口向上,顶点(0,1) C .开口向下,顶点(0,-1) D .开口向下,顶点(0,1) 5、下列各函数是偶函数的是( )A .y=3sin3xB . y=2sinx+1C .y=3tanxD . y=2cosx-16、若l 是平面α的斜线,直线m ⊂平面α,且l 在平面α上的射影与直线m 平行,则( ) A .m ⊥l B .m//l C .m 与l 是相交直线 D . m 与l 是异面直线7、等差数列{an }中,a 3+a 5+a 10+a 12=36,则S 14=( ) A . 126 B. 63 C.36 D.188、已知a =(-1,3),b =(x,-1),且a//b ,则x=( ) A . 3 B .31-C .31D .-3 9、直线01=+-y x 的斜率和倾斜角分别是( ) A .045,1 B.0135,1- C.0135,1 D.045,1-10、以()2,3-为圆心,2为半径的圆的方程是( )A .()()22322=+++y x B.()()22322=++-y xC.()()22322=-++y x D. ()()22322=++-y x11、长轴长为10,短轴长为6的椭圆方程为( )A .192522=+y x B.192522=+x yC.192519252222=+=+x y y x 或 D.192522=-y x 12、用0,1,2,3,4,5组成没有重复数字的二位数,共有( )个 A .15 B .20 C. 25 D. 3013.函数22cos sin y x x =-的周期T= ( )A .πB .2πC .2π D .14π 14、一枚硬币连续抛掷3次,至少两次正面向上的概率是( ) A .21 B . 32 C . 83 D .43二、填空题(40分)15、函数 y=()4log 24-x π的定义域为16、y=54+-x x ()5-≠x 的反函数为 17、不等式x 2+5x+m >0的解集为R ,实数m 的取值范围18、和式818414212+++……+64164= 19、设1e ,2e 是两个单位向量,它们的夹角是60°,则(1e -2e )(-31e +22e)= ___20、在(xx 2-)6展开式中,常数项为21、若ABCD 为矩形,DE 垂直于平面ABCD, 点E 到顶点A,B,C 的距离分别为3,4,10, 则DE 的长为____________22、若双曲线线上一点到两个焦点),(),,(050521F F -的距离的差的绝对值为8,则双曲线的虚轴长为_________ 23、焦点到准线的距离为23,且焦点在x 轴正半轴上的抛物线的方程为 . 24、直线082=-+y x 和012=+-y x 的交点为 . 三、解答题(68分,写出详细的解答过程)1、 已知集合A={x|x 2-3x+2>0},B={x|x-a <0}若A ⊃B ,求实数a 取值范围(8分)2、已知:二次函数f(x)=ax 2+bx+c 的图象对称轴为直线x=-3,且过点p(-2,-4)和Q (0,4) ①求a,b,c 的值 ②若f(x)不小于11,求对应x 的取值范围(9分)3、求证:(tan cot )sin cos 1θθθθ+=(8分)4、设{n a }为等差数列,且公差d 为正数,已知 432432115a a a a a a ,,,又-=++ 成等比数列,求1a 和d (8分)5、求椭圆141622=+y x 中,过点M (2,1)且平分于这点的的弦所在的直线方程(11分)6、从圆11122=-+-)()(y x 外一点P (2,3)向该圆引切线,求切线的方程。
福建省春季高考高职单招数学模拟试题(三)及答案
福建省春季高考高职单招数学模拟试题(三)班级: 姓名: 座号:一. 填空题(本大题满分36分)1. 函数2log (2)y x =+的定义域是2. 方程28x =的解是3. 抛物线28y x =的准线方程是 4. 函数2sin y x =的最小正周期是 5. 已知向量(1 )a k = ,,(9 6)b k =- ,。
若//a b ,则实数 k = 6. 函数4sin 3cos y x x =+的最大值是7. 复数23i +(i 是虚数单位)的模是 8. 在ABC ∆中,角 A B C 、、所对边长分别为 a b c 、、,若5 8 60a b B === ,,,则b= 9.在如图所示的正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为10. 从4名男同学和6名女同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为 。
11. 若等差数列的前6项和为23,前9项和为57,则数列的前n 项和n =S 12. 36的所有正约数之和可按如下方法得到:因为2236=23⨯,所以36的所有正约数之和为22222222(133)(22323)(22323)(122)133)91++++⨯+⨯++⨯+⨯=++++=(参照上述方法,可求得2000的所有正约数之和为二.选择题(本大题满分36分) 13.展开式为ad-bc 的行列式是( )(A )a bd c (B)acb d(C)a d bc(D)b a dc14.设-1()f x为函数()f x = )(A) 1(2)2f-= (B) 1(2)4f -=(C) 1(4)2f-= (D) 1(4)4f -=15.直线2310x y -+=的一个方向向量是( ) (A) (2 3)-, (B) (2 3), (C) (3 2)-, (D) (3 2),16函数12()f x x -=的大致图像是( )17.如果0a b <<,那么下列不等式成立的是( ) (A)11a b < (B) 2ab b < (C) 2ab a -<- (D) 11a b-<- 18.若复数12 z z 、满足21z z =,则12 z z 、在复数平面上对应的点12 Z Z 、( ) (A) 关于x 轴对称 (B)关于y 轴对称 (C) 关于原点对称 (D)关于直线y x =对称19. 10(1)x +的二项展开式中的一项是( )(A )45x (B )290x (C ) 3120x (D )4252x 20.既是偶函数又在区间(0 )π,上单调递减的函数是( )(A )sin y x = (B )cos y x = (C )sin 2y x = (D )cos 2y x = 21.若两个球的表面积之比为1:4,则这两个球的体积之比为( ) (A )1:2 (B )1:4 (C )1:8 (D )1:16 22.设全集U R =,下列集合运算结果为R 的是( )D 1 C 1 B 1A 1D CA B(A )N C Z U (B )N C Z U (C )}{φU C (D ){0}U C23.已知 a b c R ∈、、,“240b ac -<”是“函数2()f x ax bx c =++的图像恒在x 轴上方”的( ) (A )充分非必要条件 (B )必要非充分条件 (C )充要条件 (D )既非充分又非必要条件24.已知 A B 、为平面内两定点,过该平面内动点M 作直线AB 的垂线,垂足为N .若2MN AN NB λ=⋅,其中λ为常数,则动点M 的轨迹不可能是( )(A )圆 (B ) 椭圆 (C ) 抛物线 (D )双曲线三、解答题(本大题满分78分)本大题共有7题,解答下列各题必须写出必要的步骤。
福建省春季高考高职单招数学模拟试题(七)及答案

福建省春季高考高职单招数学模拟试题(七)班级: 姓名: 座号:一、选择题(本题有26小题,1-20每小题2分,21-26每小题3分,共58分) 1.设全集U ={1,2,3,4},则集合A ={1, 3},则C U A = (A){1, 4} (B){2, 4} (C){3, 4} (D){2, 3} 2.sin4π= (A)21(B)22 (C)23(D)1 3.函数11)(-=x x f 的定义域为 (A) {x |x <1} (B){x |x >1|} (C){x ∈R |x ≠0} (D){x ∈R |x ≠1}4.若直线y =kx +2的斜率为2,则k =(A)-2(B)2(C)21- (D)215.若函数f (x )为,则f [f (1)]=(A)0 (B)1 (C)2 (D)36.以矩形的一边所在的直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体是 (A)球 (B)圆台 (C)圆锥 (D)圆柱 7.圆x 2+y 2-4x +6y +3=0的圆心坐标是 (A)(2, 3) (B)(-2, 3) (C)(2,-3) (D)( -2,-3)8.等比数列{a n }中,a 3=16,a 4=8,则a 1=( ) (A)64 (B)32 (C)4 (D)2 9.函数xx x f 2)(+=(A)是奇函数,但不是偶函数 (B)既是奇函数,又是偶函数(C)是偶函数,但不是奇函数(D)既不是奇函数,又不是偶函数10.函数)6cos(2)(π+=x x f ,x ∈R 的最小正周期为(A)4π (B)2π (C)π (D)2π11.右图是某职业篮球运动员在连续11场比赛中得分的茎叶统计图,则该组数据的中位数是 (A)31 (B)32 (C)35 (D)36 12.设a , b , c 是两两不共线的平面向量,则下列结论中错误..的是 (A)a +b =b +a(B)a ⋅b =b ⋅a(C)a +(b +c )=(a +b )+c(D) a (b ⋅c )=(a ⋅b )c13.若tan α=21,tan β=31,则tan(α+β)= (A)75 (B)65 (C)1 (D)2 14.若非零实数a , b 满足a >b ,则(A)ba11<(B)2211ba>(C)a 2>b 2 (D)a 3>b 315.在空间中,下列命题正确的是 (A)与一平面成等角的两直线平行 (B)垂直于同一平面的两平面平行 (C)与一平面平行的两直线平行 (D)垂直于同一直线的两平面平行16.甲,乙两位同学考入某大学的同一专业,已知该专业设有3个班级,则他们被随机分到同一个班级的概率为(A)91 (B) 61 (C) 31 (D) 211 2 3 4 52 5 5 46 5 1 97 7 1 (第11题)17.某几何体的三视图如图所示,则该几何体的体积是 (A)π34 (B)2π (C)π38 (D)π310 18.将函数)3sin(π-=x y 的图象上所有点的横坐标缩短到原来的21倍(纵坐标不变),得到的图象所对应的函数是 (A))32sin(π-=x y(B))322sin(π-=x y (C))321sin(π-=x y(D))621sin(π-=x y19.函数f (x )=log 2(1-x )的图象为20.如图,在三棱锥S -ABC 中,SA =SC =AB =BC ,则直线所成角的大小是 (A)30º (B)45º (C)60º (D)90º 21.若{a n }无穷等比数列,则下列数列可能不是.... (A){a 2n } (B){a 2n -1} (C){a n ⋅a n +1} (D){a n +a n +1} 22.若log 2x +log 2y =3,则2x +y 的最小值是(A)24 (B)8 (C)10 (D)12 23.右图是某同学用于计算S =sin1+sin2+sin3+…+sin2012值的程序框图,则在判断框中填写 (A)k >2011? (B)k >2012? (C)k <2011? (D)k <2012? 24.M 是空间直角坐标系Oxyz 中任一点(异于O ),若直线OM 与xOy平面,yoz 平面,zox 平面所成的角的余弦值分别为p , q , r ,则p 2+q 2+r 2=(A) 41(B) 1 (C) 2 (D) 4925.设圆C :(x -5)2+(y -3)2=5,过圆心C 作直线l 与圆交于A ,B 两点,与x 轴交于P 点,若A 恰为线段BP 的中点,则直线l 的方程为 (A)x -2y +1=0,x +2y -11=0 (B)2x -y -7=0,2x +y -13=0 (C)x -3y +4=0,x +3y -14=0(D)3x -y -12=0,3x +y -18=0 26.在平面直角坐标系xOy 中,设不等式组⎪⎪⎩⎪⎪⎨⎧≤+-≥+-≤+≤-002020b y ax y x y x y x ,所表示的平面区域为D ,若D的边界是菱形,则ab =(A)102-(B)102(C)52(D)52-二、选择题(本题分A 、B 两组,任选一组完成)A 组(A)正视图俯视图侧视图(第17题)(第23题)(第20题)27.i 是虚数单位,i12+=(A)1+i(B)1-i (C)2+2i (D)2-2i28.对于集合A ,B ,“A ∩B =A ∪B ”是“A =B ”的(A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分又不必要条件29.在椭圆)0(12222>>=-b a by a x 中,F ,A ,B 分别为其左焦点,右顶点,上顶点,O 为坐标原点,M 为线段OB 的中点,若∆FMA 为直角三角形,则该椭圆的离心率为(A)25- (B)215- (C)552 (D)5530.设函数y =f (x ),x ∈R 的导函数为)(x f ',且f (-x )=f (x ),)()(x f x f <',则不等式成立的是(A)f (0)<e -1f (1)<e 2f (2) (B) e 2f (2)< f (0)<e -1f (1) (C) e 2f (2)<e -1f (1)<f (0) (D)e -1f (1)<f (0)<e 2f (2)B 组31.双曲线192522=-y x 的渐近线方程为(A)3x ±4y =0 (B) 4x ±3y =0 (C) 3x ±5y =0 (D)5x ±3y =0 32.若随机变量X ~B (100, p ),X 的数学期望EX =24,则p 的值是(A)52(B)53(C)256 (D)2519 33.将a , b , c , d , e 五个字母填入右图的五个方格中,每个方格恰好填一个字母,则a , b 不填在相邻两个格子(即它们有一条公共边)中的填法数为 (A)72 (B)96 (C)116 (D)12034.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 是BC 的中点,P , Q 是正方体内部及面上的两个动点,则PQ AM ⋅的最大值是(A)21(B) 1 (C)23(D)45三、填空题(本题有5小题,每小题2分,共10分) 35.不等式x 2-2x <0的解集是 .36.设S n 是等差数列{a n }的前n 项和,若a 1=-2,S 4=10,则公差d = .37.某校对学生在一周中参加社会实践活动时间进行调查,现从中抽取一个容量为n 的样本加以分析,其频率分布直方图如图所示,已知时间不超过2小时的人数为12人,则n = . 38.设点A (x 1,f (x 1)),B (x 2,f (x 2)),T (x 0,f (x 0))在函数f (x )=x 3-ax (a >0)的图象上,其中x 1,x 2是f (x )的两个极值点,x 0(x 0≠0)是f (x )的一个零点,若函数f (x )的图象在T 处的切线与直线AB 垂直,则a = . 39.在数列{a n }中,设S 0=0,S n =a 1+a 2+a 3+…+a n ,其中,,,,11k S k S k k a k k k ≥<⎩⎨⎧-=--1≤k ≤n ,k ,n ∈N *,当n ≤14时,使S n =0的n 的最大值为 . 四、解答题(本题有3小题,共20分)40.(本题6分)在锐角∆ABC 中,角A , B , C 所对的边分别为a , b , c . 已知b =2,c =3,sin A =322. 求∆ABC 的面积及a 的值.(第13题)41.(本题6分)设抛物线C:y=x2,F为焦点,l为准线,准线与Array y轴的交点为H. (I)求|FH|;(II)设M是抛物线C上一点,E(0, 4),延长ME,MF分别交C于点A,B.若A, B, H三点共线,求点M的坐标.42.(本题8分)设函数f(x)=(x-a)e x+(a-1)x+a,a∈R.(I)当a=1时,求f(x)的单调区间;(II)(i)设g(x)是f(x)的导函数,证明:当a>2时,在(0,+∞)上恰有一个x0使得g(x0)=0;(ii)求实数a的取值范围,使得对任意的x∈[0, 2],恒有f(x)≤0成立.注:e为自然对数的底数.福建省春季高考高职单招数学模拟试题(七)参考答案35、{}02x x << ; 36、3 ; 37、150 ; 38 ; 39、12 四、解答题 40、解:ks5u41、解:(Ⅰ)由抛物线方程2y x =知抛物线的焦点坐标为1(0,)4F ,准线方程为14y =-。
福建省春季高考高职单招数学模拟试题(十二)及答案

FCB AED 福建省春季高考高职单招数学模拟试题(十二)班级: 姓名: 座号: 成绩:一.选择题:本大题共14小题,每小题5分,满分70分.1.已知集合{1,0,1}A =-,则( )A .1i A +∈B .21i A +∈C .31i A +∈D .41i A +∈2.已知命题P :“2,230x R x x ∀∈++≥”,则命题P 的否定为( )A.2,230x R x x ∀∈++<B. 2,230x R x x ∃∈++≥C. 2,230x R x x ∃∈++<D. 2,230x R x x ∃∈++≤3.已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是( )A .,,αγβγαβ⊥⊥若则‖B .,,m n m n αα⊥⊥若则‖C .,,m n m n αα若则‖‖‖D .,,m m αβαβ若则‖‖‖4.已知()f x 是定义在R 上的奇函数,当0x ≥时()3x f x m =+(m 为常数),则函数()f x 的大致图象为( )5.已知倾斜角为α的直线l 与直线220x y -+=平行,则tan 2α的值为( )22A.45B.34 C. 43D.236.已知双曲线2221x y a-=的一个焦点为(2,0),则它的离心率为( )327.如图,已知ABCDEF 是边长为1的正六边形,则()BA BC AF ⋅+的值为(A.1-8.某几何体的三视图及尺寸如图示,则该几何体的表面积为( )A. 3πB. 4πC. 6πD. 10π 9.已知向量(,1),(2,)a x z b y z =-=+,且a b ⊥,若变量x,y满足约束条件1325x y x x y ≥-⎧⎪≥⎨⎪+≤⎩,则z 的最大值为 ( ).2 C10.若复数2(1)(1)z x x i =-+-为纯虚数,则实数x 的值为( )A.1-B.0C.1D.1-或1 11. 函数)1ln()(2+=x x f 的图象大致是 ( )160/3120/3100/360/340/380/320/3频率/组距pm2.5(毫克/立方米)0.1050.1000.0950.0900.0850.0800.0750.0700.0650A .B .C .D .12. 已知2()22x f x x =-,则在下列区间中,()0f x =有实数解的是( )A. (-3,-2)B. (-1,0)C. (2,3)D. (4,5)13. 已知11tan ,tan()43ααβ=-=则tan β=( )A.711 B. 117- C. 113- D. 11314. 我国潜艇外出执行任务,在向正东方向航行,测得某国的雷达站在潜艇的东偏北030方向的100海里处,已知该国的雷达扫描半径为70海里,若我国潜艇不改变航向,则行驶多少路程后会暴露目标 ( ) A 、50海里 B 、)225(310-海里 C 、620海里 D 、350海里二.填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. 15.函数1()lg(1)f x x =-的定义域为 .16.近年来,随着以煤炭为主的能源消耗大幅攀升、机动车保有量急 剧增加,我国许多大城市灰霾现象频发,造成灰霾天气的“元凶” 之一是空气中的(直径小于等于微米的颗粒物).右图是某市某月(按30天计)根据对“pm2.5” 24小时平均浓度值测试的结果画成的频率分布直方图,若规定空气中“pm2.5”24小时平均浓度值不超过毫克/立方米为达标,那么该市当月有 天“pm2.5”含量不达标. 17.在△ABC 中,已知60,4,5,A b c ===则sin B = .18. 某程序框图如下图所示,该程序运行后输出的S三.解答题:本大题共6小题,满分60分.19.(本小题满分8分)已知数列{}n a 是公比1q >的等比数列,且1240a a +=,又 2log n n b a =.求数列{n b }的通项公式;20.(本小题满分8分)24小时平均浓度结束开始已知函数()sin()cos ,()f x x x x R π=--∈. (1) 求函数()f x 的最小正周期; (2) 求函数()f x 的最大值和最小值;(3) 若1(),(0,)42f παα=∈,求sin cos αα+的值.21. (本小题满分10分)某产品按行业生产标准分成8个等级,等级系数ξ依次为1,2,,8…,其中5ξ≥为标准A ,3ξ≥为标准B ,产品的等级系数越大表明产品的质量越好,已知某厂执行标准B 生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:3 5 3 3 8 5 5 6 34 6 3 4 75 3 4 8 5 38 3 4 3 4 4 7 5 6 7该行业规定产品的等级系数7ξ≥的为一等品,等级系数57ξ≤<的为二等品,等级系数35ξ≤<的为三等品.FED P(1)试分别估计该厂生产的产品的一等品率、二等品率和三等品率; (2)从样本的一等品中随机抽取2件,求所抽得2件产品等级系数都是8的概率.22. (本小题满分10分)如图①边长为1的正方形ABCD 中,点E 、F 分别为AB 、BC 的中点,将△BEF剪去,将△AED、△DCF 分别沿DE 、DF 折起,使A 、C 两点重合于点P 得一三棱锥如图②示.(1)求证:PD EF ⊥;(2)求三棱锥P DEF -的体积;①②23.(本小题满分12分)已知直线:l y x m=+,m R∈.(1)若以点()2,1M-为圆心的圆与直线l相切与点P,且点P在x轴上,求该圆的方程;(2)若直线l关于x轴对称的直线l'与抛物线21:C x ym=相切,求直线l的方程和抛物线C的方程.24.(本小题满分12分)已知函数32()2f x x ax x=--+.(a R∈). (1)当1=a时,求函数)(xf的极值;(2)若对x R∀∈,有4'()||3f x x≥-成立,求实数a的取值范围.x福建省春季高考高职单招数学模拟试题(十二) 参考答案及评分说明一.选择题:B C B B C A D B C A ABCB 解析:1.∵{1,0,1}A =-,210i A +=∈,故选B.4.由该函数的图象过原点且关于原点对称可排除A 、C ,由()f x 在[0,)+∞为增函数,可排除D ,故选B.5.依题意知:1tan 2α=,从而22tan 4tan 21tan 3ααα==-,选C. 6.由22,13c b a ==⇒=3c e a⇒===,选A. 7.()BA BC AF ⋅+=()BA BC CD BA BD ⋅+=⋅=0,选D.8. 由三视图知,该几何体为圆锥,其底面的半径为1,r =高h =母线3l ==, 故24S rl r πππ=+=表,故选B.9.∵a b ⊥ ∴2()02x z y z z x y -++=⇒=+,点(,)x y 的可行域如图示,当直线2z x y =+过点(1,1)时,Z 取得最大值,max 213z =+=,选C.13.tan tan[()]βααβ=--11tan tan()14311tan tan()13112ααβααβ---===-+-+,选C.二.填空题:15. {|12}x x x >≠且(或{|122}x x x <<>或;16. 27; 17.772. 15.由101211x x x x ->⎧⇒>≠⎨-≠⎩且.16.该市当月“pm2.5”含量不达标有801001601206020()0.0053027333333+++++⨯⨯=(天);17.====⋅⋅-+=72sin sin ,2160cos 54254022ac A bc B a 772三.解题题:19.解:(1)解法1:∵1240a a +=,12256,a a =且1q >解得12832a a =⎧⎨=⎩---------------4分∴214a q a == ∴11211842n n n n a a q --+==⨯=---------------------------------6分∴2log n n b a ==212log 221n n +=+-------------------------------------------8分【解法2:由1240a a +=,12256,a a =且1q >得12832a a =⎧⎨=⎩ ∴214a q a ==---------------------------------------------------4分∴1121222log log log log 42,n n n n n na b b a a a +++-=-===----------------------------5分 又1212log log 83,b a ===-------------------------------------------------------6分∴{}n b 是以3为首项,2为公差的等差数列,----------------------------------------7分 ∴3(1)221n b n n =+-⨯=+;----------------------------------------------------8分 20.解:(1)∵()sin cos ),4f x x x x x R π=-=-∈------------------------------2分∴函数()f x 的最小正周期2T π=--------------------------------------3分 (2)函数()f x 的最大值和最小值分别为.----------------------------------5分(3)由1()4f α=得1sin cos 4αα-=∴21(sin cos )16αα-=,------------------------------------------------------6分1151sin 2,sin 21616αα-==----------------------------------------------------7分∴21531(sin cos )1sin 211616ααα+=+=+=---------------------------------------9分∵(0,)2πα∈,∴sin cos 0αα+>∴sin cos 4αα+=.------------------------------------------------------12分21.解:(1)由样本数据知,30件产品中等级系数7ξ≥有6件,即一等品有6件,二等品有9件,三等品有15件-----------------------------------------------------------3分 ∴样本中一等品的频率为60.230=,故估计该厂生产的产品的一等品率为0.2;-------4分二等品的频率为90.330=,故估计该厂生产的产品的二等品率为0.3;---------------5分三等品的频率为150.530=,故估计该厂生产的产品的三等品的频率为0.5.-----------6分(2)样本中一等品有6件,其中等级系数为7的有3件,等级系数为8的也有3件,--7分记等级系数为7的3件产品分别为1C 、2C 、3C ,等级系数为8的3件产品分别FEDP为1P 、2P 、3P .则从样本的一等品中随机抽取2件的所有可能为:121323(,),(,),(,),C C C C C C 12(,),P P 1323(,),(,)PP P P ,11121321(,),(,),(,),(,),C P C P C P C P 2223(,),(,)C P C P ,3132(,),(,),C P C P 33(,)C P .共15种,-------------------------------10分记从“一等品中随机抽取2件,2件等级系数都是8”为事件A , 则A包含的基本事件有 12(,),P P 1323(,),(,)P P P P 共3种,-------------------------11分故所求的概率31()155P A ==.-------------------------------------------------12分 22.(1)证明:依题意知图①折前,AD AE CD CF ⊥⊥,-------------------------------1分∴,PD PE PF PD⊥⊥,-------------------------------------------------------2分∵PEPF P= ∴PD ⊥平面PEF -----------------------------------4分 又∵EF ⊂平面PEF∴PD EF ⊥----------------------------------------5分(2)解法1:依题意知图①中AE=CF=12 ∴PE= PF=12,在△BEF中2EF ==,-----6分PDEFM 在PEF ∆中,222PE PF EF PE PF +=∴⊥∴8121212121=⋅⋅=⋅⋅=∆PF PE S PEF -------------------8分 ∴13P DEF D PEF PEF V V S PD --∆==⋅11113824=⨯⨯=.-----10分 【(2)解法2:依题意知图①中AE=CF=12∴PE= PF=12,在△BEF中2EF ==,-----------------------6分 取EF 的中点M ,连结PM 则PM EF ⊥,∴PM =-------------7分∴111228PEF S EF PM ∆=⋅==---------------8分 ∴13P DEF D PEF PEF V V S PD --∆==⋅11113824=⨯⨯=.------------------------------10分】 23.解(1)解法1.依题意得点P 的坐标为(,0)m - ∵以点()2,1M -为圆心的圆与直线l 相切与点P ∴MP l ⊥.0(1)112MP l k k m --⋅=⋅=---,解得1m =-.∴点P 的坐标为()1,0. 设所求圆的半径r,则22||112r PM ==+=,------------------------------------5分∴所求圆的方程为()222(1)2x y -++=.--------------------------------------6分【解法2.设所求圆的方程为()2222(1)x y r -++=,--------------------------------1分依题意知点P的坐标为(,0)m -.----------------------------------------------2分∵以点()2,1M -为圆心的圆与直线l 相切于点(),0P m -,∴222(2)1,.m r r ⎧++=⎪⎨=⎪⎩解得1,m r =-⎧⎪⎨=⎪⎩-------------------------------------------5分 ∴所求的圆的方程为()222(1)2x y -++=.------------------------------------6分】(2)解法1.将直线方程y x m =+中的y 换成y -,可得直线l '的方程为y x m =--.--------------------------------------------7分由21,.x y m y x m ⎧=⎪⎨⎪=--⎩得20mx x m ++=,(0)m ≠-----------------------------------9分2Δ14m =-,--------------------------------------------------------------10分∵直线l '与抛物线21:C x y m=相切 ∴∆=,解得12m =±.----------------------------------------------------12分当12m =时,直线l 的方程为12y x =+,抛物线C 的方程为22x y =,-------------13分当12m =-时,直线l 的方程为12y x =-,抛物线C 的方程为22x y =-.----------14分【解法2.将直线方程y x m =+中的y 换成y -,可得直线l '的方程为y x m =--.-----7分设直线l '与抛物线21:C x y m=相切的切点为()00,x y ,---------------------------8分由2y mx =得2y mx'=,则021mx =----①-----------------------------------10分00y x m =--------②200y mx =.---------③①②③联立得1142m m m=-21142m m ⇒=⇒=±,----------------------------12分当12m =时,直线l 的方程为12y x =+,抛物线C 的方程为22x y =,-------------13分当12m =-时,直线l 的方程为12y x =-,抛物线C 的方程为22x y =-.----------14分】24.解:(1)当1=a 时,32()2f x x x x =--+ 2'()321f x x x =--=(1)(31)x x -+,------------------------------------------2分 令'()0f x =,解得121,13x x =-=. 当'()0f x >时,得1x >或13x <-; 当'()0f x <时,得113x -<<.当x 变化时,'()f x ,()f x 的变化情况如下表:-------------------------------------------------------------------------------4分 ∴当13x =-时,函数()f x 有极大值,15()=()2,327f x f -=极大-----------------------5分当1x =时函数()f x 有极小值,()(1)1f x f ==极小---------------------------------6分(2)∵2'()321f x x ax =--,∴对x R ∀∈,4'()||3f x x ≥-成立,即24321||3x ax x --≥-对x R∀∈成立,--------------------------------------7分①当0x >时,有213(21)03x a x -++≥, 即12133a x x+≤+,对(0,)x ∀∈+∞恒成立,----------------------------------9分∵1323x x +≥=,当且仅当13x =时等号成立, ∴212a +≤12a ⇒≤------------------------------------------------------11分②当0x <时,有213(12)03x a x +-+≥,即1123||3||a x x -≤+,对(,0)x ∀∈-∞恒成立,∵13||23||x x +≥=,当且仅当13x =-时等号成立,∴11222a a -≤⇒≥-----------------------------------------------------13分③当0∈x=时,a R综上得实数a的取值范围为11-.-------------------------------------------14分[,]22。
福建省春季高考数学高职单招模拟试题(12)-人教版高三全册数学试题

某某省高考高职单招数学模拟试题单项选择题(本大题共14小题,每小题5分,共70分)1.设全集U ,集合A 和B ,如图所示的阴影部分所表示的集合为( ) A .()u A C B ⋃ B .()u C A B ⋂ C .()u C A B ⋂ D .()u A C B ⋂2.已知命题p:2,10,x R x x p ∃∈+-<⌝则为( ) A .2,10x R x x ∃∈+-> B .2,10x R x x ∀∈+-≥ C .2,10x R x x ∃∉+-≥ D .2,10x R x x ∀∈+-> 3. 统计某产品的广告费用x 与销售额y 的一组数据如下表:广告费用 2356 销售额79 12若根据上表提供的数据用最小二乘法可求得对的回归直线方程是,则数据中的的值应该是( )A .7.9 B .8 C .8.1 D .94.一个几何体的三视图都是边长为2的正方形,则该几何体的表面积是( ) A .4 B .8 C .16 D .245.在ABC ∆中,角A ,B ,C 所对的边分别为a,b,c 且2220a b c +-<,则ABC ∆是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .等腰三角形6.已知函数f(x)的图象是一条连续不断的,x,f(x)的对应值如下表:则在下列区间内,函数f(x)一定有零点的是( ) A .(-2,-1) B .(-1,1) C .(1,2) D .(2,3)7.在直角坐标系中,直线l 的倾斜角30β=,且过(0,1),则直线l 的方程是( )A .313y x =- B .313y x =+ C .31y x =- D .31y x =+ 8.已知定义在R 的函数y=f(x)是奇函数,且在[0,)+∞上的增函数,则y=f(x)的图象可以是( )xyOxyOxyOy Ox9. 双曲线22145x y -=的渐近线方程为( )A.y x =B. y x =C. y x =D. y = 10. 已知(,)2a ππ∈,4sin 5α=,则cos()πα+=( )A. 32B. 32-C. 23 D . 23-11.已知圆221:1O x y +=,圆222:(1)(2)16O x y -+-=,则圆1O 和圆2O 的位置关系是( )A. 内含B. 内切C. 相交D. 外离12. 等于已知向量(1,2),(3,2),a b =-=且,n xa yb =+则x=1,y=1是m //n 的( ) A. 充要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件13.函数2,(1)(),(1)x x f x x x ≤⎧=⎨>⎩且1()2f x =,则x=( )A.12B. 2C. 2-D. 2或2- 14. 某公司生产一种产品,每生产1千件需投入成本81万元,每千件的销售收入R (x )(单位:万元)与年产量x(单位:千件)满足关系:2()324(010)R x x x =-+<≤该公司为了在生产中获得最大利润(年利润=年销售收入—年总成本),则年产量应为( ) A. 5千件B. C.9千件 D. 10千件二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置上) 15.已知i 是虚数单位,则21ii+-= . 16.已知对数函数()log a f x x =的图象如图所示,|(2)|1f =,则a= .ABC D17.设,x y 满足约束条件0,0,2,x y x y ≥⎧⎪≥⎨⎪+≤⎩所表示的平面区域内任取一点P (x,y ),则点P 满足2y x≥的概率是 .18.已知正方形ABCD 中,AB=2,若将ABD ∆沿正方形的对角线BD 所在的直线进行翻折,则在翻折的过程中,四面体A —BCD 的体积最大值是 .三、解答题(本大题共6小题,共60分.解答应写出文字说明,证明过程或演算步骤) 19.(本小题满分共8分)在数列{}n a 中,32n a n =-,(Ⅰ)求数列{}n a 是等差数列; (Ⅱ)求数列{}n a 的前n 项和.n S20.(本小题满分共8分)如图,在四棱锥P —ABCD 中,底面ABCD 是边长为2的正方形,PA=PB=PC=PD =3,点E ,F 分别是PA ,PC 的中点。
福建省春季高考高职单招数学模拟试题及答案word版 2

福建省春季高考高职单招数学模拟试题班级: 姓名: 座号:一、选择题。
1.已知集合{}0,1,2M =,{}1,4B =,那么集合AB 等于()(A ){}1 (B ){}4 (C ){}2,3 (D ){}1,2,3,42.在等比数列{}n a 中,已知122,4a a ==,那么5a 等于(A)6 (B)8 (C)10 (D)16 3.已知向量(3,1),(2,5)==-a b ,那么2+a b 等于( )A.(-1,11)B. (4,7)C.(1,6) D (5,-4)4.函数2log (+1)y x =的定义域是( )(A) ()0,+∞ (B) (1,+)-∞ (C) 1,+∞()(D)[)1,-+∞5.如果直线30x y -=与直线10mx y +-=平行,那么m 的值为( )(A)3-(B)13-(C)13(D) 36.函数=sin y x ω的图象可以看做是把函数=sin y x 的图象上所有点的纵坐标保持不变,横坐标缩短到原来的12倍而得到,那么ω的值为( )(A) 4 (B) 2 (C)12 (D) 37.在函数3y x =,2x y =,2log y x =,y )(A) 3y x = (B) 2x y = (C) 2log y x = (D)y =8.11sin6π的值为( ) (A)2-(B)12-(C)12(D)9.不等式23+20x x -<的解集是( )A. {}2x x >B. {}>1x xC. {}12x x <<D. {}1,2x x x <>或10.实数lg 4+2lg5的值为( ) (A) 2 (B) 5 (C) 10 (D) 2011.某城市有大型、中型与小型超市共1500个,它们的个数之比为1:5:9.为调查超市每日的零售额情况,需通过分层抽样抽取30个超市进行调查,那么抽取的小型超市个数为( )(A) 5 (B) 9 (C) 18 (D) 2012.已知平面α∥平面β,直线m ⊂平面α,那么直线m 与平面β 的关系是( )A.直线m 在平面β内 B.直线m 与平面β相交但不垂直C.直线m 与平面β垂直D.直线m 与平面β平行13.在ABC ∆中,a =2b =,1c =,那么A 的值是( )A .2πB .3πC .4πD .6π 14.一个几何体的三视图如右图所示,该几何体的表面积是( )A .3πB .8πC .12πD .14π15.当>0x 时,122x x+的最小值是( ) A . 1 B . 2C. D . 416.从数字1,2,3,4,5中随机抽取两个数字(不允许重复),那么这两个数字的和是奇数的概率为( )A .45B .35C .25D .1517.当,x y 满足条件1260y x y x y ≥⎧⎪-≤⎨⎪+-≤⎩时,目标函数z x y =+的最小值是( )(A) 2 (B) 2.5(C) 3.5(D)418.已知函数2,0,(),0.x x f x x x ⎧=⎨-<⎩≥如果0()2f x =,那么实数0x 的值为( )(A) 4 (B) 0 (C) 1或 4 (D) 1或-219.为改善环境,某城市对污水处理系统进行改造。
福建省春季高考高职单招数学模拟试题(一)及答案

福建省春季高考高职单招数学模拟试题(一)班级: 姓名: 座号:一、选择题(本大题有15小题,每小题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{}{}0,1,2,0,1M N ==,则M N =A .{}2B .{}0,1C .{}0,2D .{}0,1,2 2.某几何体的三视图如下图所示,则该几何体是A .圆柱B .圆锥C .三棱柱D .三棱锥 3.当输入a 的值为1,b 的值为3-时,右边程序运行的结果是A .1B .2-C .3-D .2 4.函数2sin(2)6y x π=-的最小正周期是A .4πB .2πC .πD .2π 5.下列函数中,在()0,+∞上是减函数的是A .1y x =B .21y x =+C .2xy = D .()()00x x y x x >⎧⎪=⎨-≤⎪⎩6.不等式组101x y x -+≥⎧⎨≤⎩表示的平面区域是7.函数x y sin 1+=的部分图像如图所示,则该函数在[]π2,0的单调递减区间是A .[]0,πB .3,22ππ⎡⎤⎢⎥⎣⎦C .30,2π⎡⎤⎢⎥⎣⎦D .,22ππ⎡⎤⎢⎥⎣⎦2ππ 32π 2π8.方程320x -=的根所在的区间是A .()2,0-B .()0,1C .()1,2D .()2,3DC B A 俯视图侧视图正视图9.已知向量a (2,1)=,b (3,)λ=,且a ⊥b ,则λ= A .6- B .6 C .32 D .32- 10.函数()2log 1y x =-的图像大致是11.不等式230x x ->的解集是A .{}03x x ≤≤B .{}0,3x x x ≤≥或C .{}03x x <<D .{}0,3x x x <>或 12.下列几何体的下底面面积相等,高也相等,则体积最大的是DC BA13.如图,边长为2的正方形内有一内切圆.在图形上随机撒一粒黄豆,则黄豆落到圆内的概率是A .4πB .4πC .44π-D .π14.已知()3cos 5πα-=-,则cos 2a =A .1625B .1625-C .725D .725-15.在某五场篮球比赛中,甲、乙两名运动员得分的茎叶图如下.下列说法正确的是A .在这五场比赛中,甲的平均得分比乙好,且甲比乙稳定B .在这五场比赛中,甲的平均得分比乙好,但乙比甲稳定C .在这五场比赛中,乙的平均得分比甲好,且乙比甲稳定D .在这五场比赛中,乙的平均得分比甲好,但甲比乙稳定二、填空题(本大题有5小题,每小题3分,共15分。
福建省春季高考高职单招数学模拟试题(六)及答案
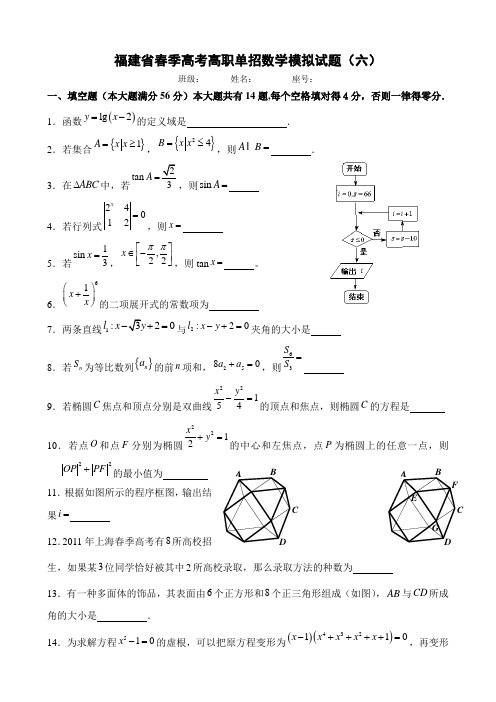
福建省春季高考高职单招数学模拟试题(六)班级: 姓名: 座号:一、填空题(本大题满分56分)本大题共有14题,每个空格填对得4分,否则一律得零分. 1.函数()lg 2y x =-的定义域是 . 2.若集合{}1A x x =≥,{}24B x x =≤,则A B = .3.在ABC ∆中,若tan A =,则sin A =4.若行列式24012x=,则x =5.若1sin 3x =,,22x ππ⎡⎤∈-⎢⎥⎣⎦,则tan x = 。
6.61x x ⎛⎫+ ⎪⎝⎭的二项展开式的常数项为 7.两条直线1:20l x +=与2:20l x y -+=夹角的大小是8.若n S 为等比数列{}n a 的前n 项和,2580a a +=,则63S S =9.若椭圆C 焦点和顶点分别是双曲线22154x y -=的顶点和焦点,则椭圆C 的方程是 10.若点O 和点F 分别为椭圆2212x y +=的中心和左焦点,点P 为椭圆上的任意一点,则22OP PF +的最小值为11.根据如图所示的程序框图,输出结果i =12.2011年上海春季高考有8所高校招生,如果某3位同学恰好被其中2所高校录取,那么录取方法的种数为13.有一种多面体的饰品,其表面由6个正方形和8个正三角形组成(如图),AB 与CD 所成角的大小是 . 14.为求解方程510x-=的虚根,可以把原方程变形为()()432110x x x x x -++++=,再变形DCBAG F EDC BA为()()()221110x x ax x bx -++++=,由此可得原方程的一个虚根为二、选择题(本大题满分20分)本大题共有4题,每题只有一个正确答案,考生应在答题纸相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.15.若向量()2,0a =,()1,1b = ,则下列结论正确的是 ( )A.1a b ⋅= B.a b = C.()a b b -⊥D.//a b16.函数()412x xf x -=的图象关于 ( ) A.原点对称 B.直线y x =对称 C.直线y x =-对称 D.y 轴对称17.直线1:2l y k x ⎛⎫=+ ⎪⎝⎭与圆22:1C x y +=的位置关系为 ( ) A.相交或相切 B.相交或相离 C.相切 D.相交18.若123,,a a a 均为单位向量,则1a =⎝⎭ 是123a a a ++= 的 ( )A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件 三、解答题(本大题74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.19.(本题满分12分)向量()sin 21,cos a x x =- ,()1,2cos b x = .设函数()f x a b =⋅.求函数()f x 的最小正周期及0,2x π⎡⎤∈⎢⎥⎣⎦时的最大值.20.(14分)某甜品店制作一种蛋筒冰激凌,其上部分是半球形,下半部分呈圆锥形(如图),现把半径为10cm 的圆形蛋皮等分成5个扇形,用一个蛋皮围成圆锥的侧面(蛋皮的厚度忽略不计),求该蛋筒冰激凌的表面积和体积(精确到0.01)21.(本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分.已知抛物线2:4F x y =.(1) ABC ∆的三个顶点在抛物线F 上,记ABC ∆的三边,,AB BC CA 所在直线的斜率分别为,,AB BC CA k k k ,若点A 在坐标原点,求AB BC CA k k k -+的值;(2) 请你给出一个以()2,1P 为顶点,且其余各顶点均为抛物线F 上的动点的多边形,写出多边形各边所在直线的斜率之间的关系式,并说明理由.说明:第(2)题将根据结论的一般性程度给与不同的评分.22.(本题满分16分)定义域为R ,且对任意实数12,x x 都满足不等式()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭的所有函数()f x 组成的集合记为M .例如()f x kx b M =+∈.(1) 已知函数(),0,1,02x x f x x x ≥⎧⎪=⎨<⎪⎩证明:()f x M ∈;(2) 写出一个函数()f x ,使得()f x M ∉,并说明理由;23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分, 第3小题满分6分.对于给定首项)00x a >>,由递推式112n n x x +⎛=+⎝()n +∈N 得到数列{}n x ,且对于任意的n +∈N ,都有n x >{}n x(1) 取05x =,100a =,计算123,,x x x 的值(精确到0.01),归纳出n x ,1n x +的大小关系;(2) 当1n ≥时,证明()1112n n n n x x x x +--<-;(3) 当[]05,10x ∈时,用数列{}n x4110n n x x -+-<,请你估计n ,并说明理由.福建省春季高考高职单招数学模拟试题(六)参考答案1、【解】()2,+∞.函数()lg 2y x =-的定义域满足20x ->,即2x >,所以函数()lg 2y x =-的定义域为()2,+∞.2、【解】{}12x x ≤≤.{}{}2422B x x x =≤=-≤≤,所以A B = {}12x x ≤≤.3、【解】11.因为tan 03A =>,则A ∠是锐角,于是2221111tan 199cos A A+=+==, 则29cos 11A =,cos A =,sin tan cos A A A =⋅==. (或由29cos 11A =得22sin 11A =,因为sin 0A >,则sin 11A =.)4、【解】1.242214012x x =⨯-⨯=,则22x =,1x =.5、【解】1arcsin3.因为1sin 3x =,,22x ππ⎡⎤∈-⎢⎥⎣⎦,则1arcsin 3x =. 6、【解】20.61x x ⎛⎫+ ⎪⎝⎭的二项展开式的通项为662166C C r r r r rr T x x x---+==. 令620r -=得3r =.所以61x x ⎛⎫+ ⎪⎝⎭的二项展开式的常数项为36C 20=.7、【解】12π.直线1l 的倾斜角为6π,直线2l 的倾斜角为4π,夹角为4612πππ-=. 8、【解】7-.设公比为q ,则4118a q a q =-,所以38q =-.63633118171S q q S q -==+=-+=--. 9、【解】22194x y +=.双曲线22154x y -=的顶点和焦点坐标分别是()和()3,0±.设椭圆C 的方程为22221x y a b +=,则由题设,3a ==2b =,所以椭圆C 的方程为22194x y +=.10、【解】2设(),P x y ,由()1,0F -得()2222221OP PF x y x y +=++++①因为点P 为椭圆上的任意一点,则2212x y =-,于是①式化为2222221212x OP PF x x ⎛⎫+=+++- ⎪⎝⎭223x x =++()212x =++.因为x ≤≤,而()212x ++图象的对称轴1x ⎡=-∈⎣,所以当1x =-时,22OP PF +有最小值为2.11、【解】7.根据如图所示的程序框图,所得的数据如下表所以输出的7i =.12、【解】168.第一步:从8所高校取2所高校的方法有28C 28=种,第二步:3位同学分配到2所高校的方法有2位同学被分配到同一所高校,所以有2132C C 6=种,所以录取方法的种数为286168⨯=种.13、【解】3π.AB 与CD 是正方形的边,则//AB EF ,//CD FG , 因为EF 和FG 是正三角形EFG 的两边,则AB 与CD 所成的角为3π. 14、【解中的一个.由题设,有()()43222111x x x x x ax x bx ++++=++++,即()()()432432121x x x x x a b x ab x a b x ++++=+++++++,对应相应项的系数得1,21a b ab +=⎧⎨+=⎩解得1,2a b ⎧=⎪⎪⎨⎪=⎪⎩或12a b ⎧=⎪⎪⎨⎪=⎪⎩解210x x +=,因为1004--∆=<,所以5i x =,同理,解21102x x ++=得中的一个.15、【解】2a b ⋅= ,A不正确;2a =,b = ,则a b ≠ ,B不正确;()1,1a b -=-,()()()1,11,10a b b -⋅=-⋅= ,所以()a b b -⊥,C正确;不存在实数λ,使a b λ= ,D不正确.故选C.16、【解】()41222x x x xf x --==-,则()()f x f x -=-,其图象关于原点对称.故选A. 17、【解】解法1.因为直线l 过点1,02⎛⎫-⎪⎝⎭,而点1,02⎛⎫- ⎪⎝⎭在圆22:1C x y +=的内部,所以直线与圆相交.故选D.解法2.圆心为()0,0,半径为1,圆心到直线的距离为11212kd k =≤=<,所以直线与圆相交.故选D.18、【解】若123a a a ++=,当123a a a ==时,得1a =⎝⎭,若133a ⎛⎫= ⎪⎪⎝⎭,当()231,0a a ==,则123a a a ++≠,所以133a ⎛= ⎝⎭是123a a a ++=的必要不充分条件.故选B.19、【解】()2sin 212cos f x a b x x =⋅=-+ sin 2cos2x x =+24x π⎛⎫=+ ⎪⎝⎭.所以,函数()f x 的最小正周期22T ππ==.因为0,2x π⎡⎤∈⎢⎥⎣⎦,所以52,444x πππ⎡⎤+∈⎢⎥⎣⎦,当242x ππ+=,即8x π=时,函数有最大值max y =.20、【解】设圆锥的底面半径为r ,高为h .由题意,圆锥的侧面扇形的周长为121045ππ⋅⋅=()cm ,圆锥底面周长为2r π()cm ,则24r ππ=,2r =()cm .圆锥的=()cm ,圆锥的侧面扇形的面积为11410202S ππ=⨯⨯=()2cm ,半球的面积为 2214282S ππ=⨯⨯=.该蛋筒冰激凌的表面积122887.96S S S π=+=≈()2cm ;圆锥的体积为21123V π=⨯⨯=()3cm ,半球的体积为3214162233V ππ=⨯⨯=()3cm ,所以该蛋筒冰激凌的体积为)1216157.803V V V π=+=≈()3cm .因此该蛋筒冰激凌的表面积约为287.96cm , 体积约为357.80cm . 21、【解】(1) 设(),B B B x y ,(),C C C x y .则B C CB AB BC CA B B C Cy y y y k k k x x x x --+=-+- ()2222444B C C B B B C C x x x x x x x x -=-+-()104B B C C x x x x =-++=⎡⎤⎣⎦.(2) ① 研究PBC ∆.B C C PB P PB BC CP B P B C C Py y y y y y k k k x x x x x x ----+=-+--- ()()()222222444B C C P B PB P BC C P x x x x x x x x x x x x ---=-+---()()()14B P BC C P x x x x x x =+-+++⎡⎤⎣⎦12P x ==. ② 研究四边形PBCD .4444B C C D B P D PPB BC CD DP x x x x x x x x k k k k ++++-+-=-+-0= ③ 研究五边形PBCDE .PB BC CD DE EP k k k k k -+-+ 44444B C C D B P D E E P x x x x x x x x x x +++++=-+-+12Px ==. ④ 研究2n k =边形122k PP P (),2k k +∈≥N ,其中1P P =.()12233421211k k P P P P P P P P k k k k --+-+- ()233421122114444k k P P P P P P P P x x x x x x x x -++++=-+-+- ()1211104k P x -⎡⎤=+-=⎣⎦.⑤研究21n k =-边形1221k PP P - (),2k k +∈≥N ,其1P P =.()1223342112111k k P P P P P P P P k k k k ----+-+- ()23342111221114444k k P P P P P P P P x x x x x x x x ---++++=-+-+- ()12111114k P x --⎡⎤=+-=⎣⎦.⑥研究n 边形12n PP P (),3k n +∈≥N ,其中1P P =.()122334111n n P P P P P P P P k k k k --+-+-()2334121114444n P P P P P P Pn P x x x x x x x x -++++=-+-+- ()()111111142n n P x --+-⎡⎤=+-=⎣⎦.22、【解】(1) 当120x x ≤≤时,()()1212121202244f x f x x x x x x x f ++++⎛⎫-=-=⎪⎝⎭,则不等式()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭成立;当120x x ≤≤时,()()1212121202222f x f x x x x x x x f ++++⎛⎫-=-= ⎪⎝⎭,则不等式()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭成立; 当120x x ≤≤,且1202x x +<时,()()1212121221120222224x xf x f x x x x x x f ++++⎛⎫-=-⋅=≥ ⎪⎝⎭,则 不等式()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭成立; 当120x x ≤≤,且1202x x +≥时,()()12121212112022224x x f x f x x x x x x f ++++⎛⎫-=-=-≥ ⎪⎝⎭,则 不等式()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭成立. 综合以上,不等式()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭成立.所以()f x M ∈ (2) 例如函数()2f x x =-,取11x =-,21x =,则()()121222f x f x x x f ++⎛⎫- ⎪⎝⎭()()()110102f f f -+=-=-<. 所以()fx M ∉.也可以从()2f x x =-的图象看出,()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭,不满足()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭.所以()2f x x M =-∉.(3) 例如函数()2,1,, 1.x x f x x x ⎧≥⎪=⎨<⎪⎩满足()f x M ∈,()222limlim 1n n f n n n n →∞→∞==,()lim lim 1n n f nn nn →∞→∞--==--. 23、【解】(1) 1234.74, 4.67, 4.65x x x ===,猜想1n n x x +<; (2) ()1112n n n n x x x x +----1111222n n n n x x x x -⎛=--+ ⎝112n n x x -=-111122n n x x --⎛=+- ⎝==①因为n x >11110222n n n n n x x x x x +⎛⎛-=-== ⎝⎝,所以1n n x x +>. 由①式,()11102n n n n x x x x +----=<,所以()1112n n n n x x x x +--<-.(3) 由(2)()()()()1121120121111102222n n n n n n n n x x x x x x x x x x +----<-<-<-<<-<- , 所以只要()4011102nx x --<即可,于是()401210n x x >-,因为01012x x x ⎛⎫-= ⎝,所以42log 1015.1n ⎛>≈ ⎝⎭.所以16n =.。
福建省春季高考高职单招数学模拟试题及答案

过椭圆的焦点作直线交椭圆于、两点,是椭圆另一焦x y F A B F 221236251+=福建省春季高考高职单招数学模拟试题班级: 姓名: 座号:一、选择题(本大题共14个小题。
每小题5分,共70分) 1, 下列各函数中,与x y =表示同一函数的是( )(A)xx y 2= (B)2x y = (C)2)(x y = (D)33x y =2,抛物线241x y -=的焦点坐标是( )(A) ()1,0- (B)()1,0 (C)()0,1 ( D)()0,1-3,设函数216x y -=的定义域为A,关于X的不等式a x <+12log 2的解集为B,且A B A = ,则a 的取值范围是( )(A)()3,∞- (B)(]3,0 (C)()+∞,5 (D)[)+∞,54,已知x x ,1312sin =是第二象限角,则=x tan ( ) (A)125 (B) 125- (C) 512 (D)512-5,等比数列{}n a 中,30321=++a a a ,120654=++a a a ,则=++987a a a ( ) (A)240 (B)240± (C) 480 (D)480± 6, tan330︒= ( )(A(B(C) (D)7,设b >a >0,且a +b =1,则此四个数21,2ab ,a 2+b 2,b 中最大的是( ) (A )b (B )a 2+b 2 (C)2ab (D )218,数列1,n +++++++ 3211,,3211,211的前100项和是:( ) (A)201200 (B)201100 (C)101200 (D1011009, 点,则△ABF 2的周长是 ( )(A ).12 (B ).24 (C ).22 (D ).1010, 函数sin 26y x π⎛⎫=+ ⎪⎝⎭图像的一个对称中心是( )(A )(,0)12π-(B )(,0)6π- (C )(,0)6π(D )(,0)3π11.已知0a >且1a ≠,且23a a >,那么函数()x f x a =的图像可能是 ( )12.已知()1f x x x=+,那么下列各式中,对任意不为零的实数x 都成立的是 ( )(A )()()f x f x =- (B )()1f x f x ⎛⎫=⎪⎝⎭(C )()f x x > (D )()2f x >13.如图,D 是△ABC 的边AB 的三等分点,则向量CD 等于 ( )(A )23CA AB + (B )13CA AB +(C )23CB AB +(D )13CB AB +14.如果执行右面的程序框图,那么输出的S 等于( )(A )45 (B )55 (C )90 (D )110 二,填空题(本大题共4个小题,每小题5分,共20分) 15. 函数()ln 21y x =-的定义域是 . 16. 把函数s i n 2y x =的图象向左平移6π个单位,得到的函数解析式为________________.17. 某公司生产A 、B 、C 三种不同型号的轿车,产量之比依次为2:3:4,为了检验该公司的产品质量,用分层抽样的方法抽取一个容量为n 的样本,样本中A 种型号的轿车比B 种型号的轿车少8辆,那么n = .18. 已知函数1(0x y a a -=>且1)a ≠的图象恒过点A . 若点A 在直线 上, 则12m n+的最小值为 .三,解答题(共六个大题,共60分)(A ) (B ) (C ) (D )ADB ()100mx ny mn +-=>19.(10分)已知等差数列{}n a 的前n 项和为n S ,且1310a a +=, 424S =. (1)求数列{}n a 的通项公式;(2)令12111n n T S S S =+++,求证:34n T <.20. (本小题满分10分)编号分别为12312,,,,A A A A 的12名篮球运动员在某次篮球比赛中的得分记录如下:(1) 完成如下的频率分布表:(2)从得分在区间[)10,20内的运动员中随机抽取2人 , 求这2人得分之和大于25的概率.21.如图所示,F 1、F 2分别为椭圆C :)0(12222>>=+b a by a x 的左、右两个焦点,A 、BABO ∆(Ⅰ)求椭圆C 的方程和焦点坐标;(Ⅱ)作与AB 平行的直线l 交椭圆于P 、Q两点,PQ =,求直线l 的方程.22.(10分)已知函数.cos sin sin )(2x x x x f += (1) 求其最小正周期; (2) 当20π≤≤x 时,求其最值及相应的x 值。
福建省春季高考高职单招数学模拟试题(十三)及答案
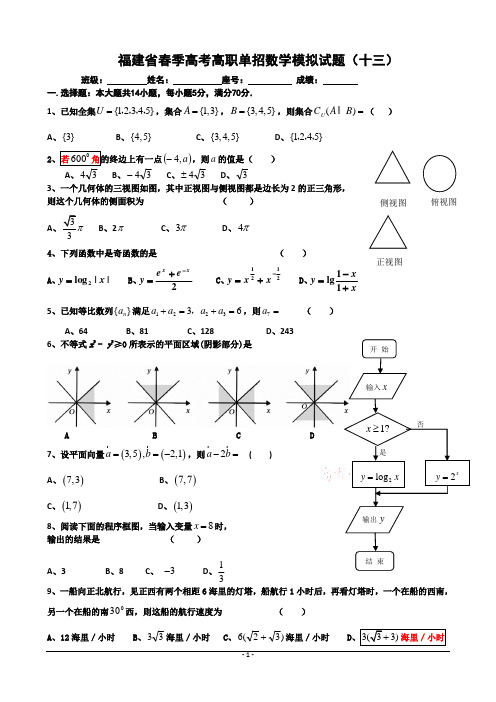
福建省春季高考高职单招数学模拟试题(十三)班级: 姓名: 座号: 成绩:一.选择题:本大题共14小题,每小题5分,满分70分.1、已知全集{12345}U =,,,,,集合{1,3}A =,{3,4,5}B =,则集合()U C A B = ( ) A 、{3} B 、{4,5}C 、{3,4,5}D 、{1245},,,2()a ,4-,则a 的值是( )A 、34B 、34-C 、34±D 、33、一个几何体的三视图如图,其中正视图与侧视图都是边长为2的正三角形, 则这个几何体的侧面积为( ) A B 、2π C 、3π D 、4π4、下列函数中是奇函数的是 ( )A 、||log 2x y =B 、2xx ee y -+=C 、2121-+=xx y D 、xxy +-=11lg5、已知等比数列{}n a 满足122336a a a a +=+=,,则7a = ( ) A 、64 B 、81C 、128D 、2436、不等式x 2 - y 2≥0所表示的平面区域(阴影部分)是A B C D7、设平面向量()()3,5,2,1a b ==- ,则2a b -=( )A 、()7,3B 、()7,7C 、()1,7D 、()1,38、阅读下面的程序框图,当输入变量8x =时, 输出的结果是 ( )A 、3B 、8C 、 3-D 、139、一船向正北航行,见正西有两个相距6海里的灯塔,船航行1小时后,再看灯塔时,一个在船的西南,另一个在船的南030西,则这船的航行速度为 ( )A 、12海里/小时B 、33海里/小时C 、)32(6+海里/小时 D10、不等式()()224540x x x--+>的解集为 ( )A 、{}|05x x <<B 、{}|15x x -<<C 、 {}|10x x -<<D 、{}|15x x x <->或 11、若直线1l :()323y a x =++与直线2l :32y x =+垂直,则实数a 的值为 ( ) A 、79-B 、79C 、13D 、13-13、已知,cos 2sin x x =则=+-xx xx cos sin cos sin ( )A 、21B 、31C 、41D 、5114、将函数sin (0)y x ωω=>的图象向左平移6π个单位,平移后的图象如图所示,则平移后的图象所对应函数的解析式是 ( ) A 、sin()6y x π=+B 、sin()6y x π=- C 、sin(2)3y x π=+D 、sin(2)3y x π=- 二.填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.15、若函数()3f x x =在区间[]43,a a -上是奇函数,则()f x 在区间[]43,a a -上的最小值是 (用具体数字作答) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
过椭圆的焦点作直线交椭圆于、两点,是椭圆另一焦x y F A B F 221236251+=福建省春季高考高职单招数学模拟试题班级: 姓名: 座号:一、选择题(本大题共14个小题。
每小题5分,共70分) 1, 下列各函数中,及x y =表示同一函数的是( ) (A) (B)2x y = (C)2)(x y = (D)33x y = 2,抛物线的焦点坐标是( )(A) ()1,0- (B)()1,0 (C)()0,1 ( D)()0,1-3,设函数216x y -=的定义域为A,关于X的不等式a x <+12log 2的解集为B,且A B A = ,则a 的取值范围是( )(A)()3,∞- (B)(]3,0 (C)()+∞,5 (D)[)+∞,5 4,已知是第二象限角,则=x tan ( ) (A)125 (B) 125- (C) 512 (D)512- 5,等比数列{}n a 中,30321=++a a a ,120654=++a a a ,则=++987a a a ( ) (A)240 (B)240± (C) 480 (D)480± 6, tan330︒= ( )(A(B(C) (D)7,设b >a >0,且a +b =1,则此四个数21,2ab ,a 2+b 2,b 中最大的是( ) (A )b (B )a 2+b 2 (C)2ab (D )218,数列1,n +++++++ 3211,,3211,211的前100项和是:( ) (A)201200 (B)201100 (C)101200 (D1011009, 点,则△ABF 2的周长是 ( )(A ).12 (B ).24 (C ).22 (D ).10 10, 函数图像的一个对称中心是( )(A )(,0)12π- (B )(,0)6π- (C )(,0)6π (D )(,0)3π11.已知0a >且1a ≠,且23a a >,那么函数()x f x a =的图像可能是 ( )12.已知()1f x x x=+,那么下列各式中,对任意不为零的实数x 都成立的是 ( )(A )()()f x f x =- (B ) (C )()f x x > (D )()2f x > 13.如图,D 是△ABC 的边AB 的三等分点,则向量CD 等于 ( )(A )23CA AB + (B )13CA AB +(C )23CB AB +(D )13CB AB +14.如果执行右面的程序框图,那么输出的S 等于( )(A )45 (B )55 (C )90 (D )110 二,填空题(本大题共4个小题,每小题5分,共20分) 15. 函数()ln 21y x =-的定义域是 . 16. 把函数sin 2y x=的图象向左平移6π个单位,得到的函数解析式为________________.17. 某公司生产A 、B 、C 三种不同型号的轿车,产量之比依次为2:3:4,为了检验该公司的产品质量,用分层抽样的方法抽取一个容量为n 的样本,样本中A 种型号的轿车比B 种型号的轿车少8辆,那么n = .18. 已知函数1(0x y a a -=>且1)a ≠的图象恒过点A . 若点A 在直线 上, 则的最小值为 .三,解答题(共六个大题,共60分)19.(10分)已知等差数列{}n a 的前n 项和为n S ,且1310a a +=, 424S =.(A ) (B ) (C ) (D )ADB ()100mx ny mn +-=>(1)求数列{}n a 的通项公式;(2)令,求证:.20. (本小题满分10分)编号分别为12312,,,,A A A A 的12名篮球运动员在某次篮球比赛中的得分记录如下:(1) 完成如下的频率分布表:(2)从得分在区间[)10,20内的运动员中随机抽取2人 , 求这2人得分之和大于25的概率.21.如图所示,F 1、F 2分别为椭圆C :)0(12222>>=+b a by a x 的左、右两个焦点,A 、B 为两个顶点,该椭圆的离心率为55,ABO ∆5 (Ⅰ)求椭圆C 的方程和焦点坐标;(Ⅱ)作及AB 平行的直线l 交椭圆于P 、Q 两点,,求直线l 的方程.22.(10分)已知函数.cos sin sin )(2x x x x f += (1) 求其最小正周期;(2) 当时,求其最值及相应的x 值。
(3) 试求不等式1)(≥x f 的解集23. (10分) 如图2,在三棱锥P ABC -中,5,4,3AB BC AC ===,点D 是线段PB 的中点,平面PAC ⊥平面ABC .(1)在线段AB 上是否存在点E , 使得//DE 平面PAC置, 并加以证明;若不存在, 请说明理由; (2)求证:PA BC ⊥.24、设()()256ln f x a x x =-+,其中a R ∈,曲线()y f x =在点()()1,1f 处的切线及y 轴相交于点()0,6。
(1)确定a 的值;(2)求函数()f x 的单调区间及极值。
福建省春季高考高职单招数学模拟试题(九)参考答案一,选择题(本大题共14个小题,每小题5分,共70分。
)二,填空题(本大题共5个小题,每小题4分,共20分。
)15. 16. 17. 72 18. 3+ 三,解答题(共六个大题,共60分)19.(10分)本小题主要考查等差数列、数列求和、不等式等基础知识,考查运算求解能力和推理论证能力.满分10分.(1)解:设等差数列{}n a 的公差为d , ∵ 1310a a +=, 424S =, ∴ ………2分解得13a =,2d =. ………3分∴ ()32121n a n n =+⨯-=+. ………5分(2)证明:由(1)得()()()1321222n n n a a n n S n n +++===+, ………7分 ∴ ()11111324352n n =++++⨯⨯⨯+=11111111111232435112n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+-+-++-+- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦………8分111112212n n ⎛⎫=+-- ⎪++⎝⎭= ………9分34<. ………10分20.(10分)本小题主要考查统计及概率等基础知识,考查数据处理能力.满分10分.(1) 解:频率分布表:………3分(2)解: 得分在区间[)10,20内的运动员的编号为2A ,3A ,4A ,8A ,11A .从中随机抽取2人,所有可能的抽取结果有:{}23,A A , {}24,A A ,{}28,A A ,{}211,A A ,{}34,A A ,{}38,A A ,{}311,A A ,{}48,A A ,{}411,A A ,{}811,A A ,共10种. (6)分“从得分在区间[)10,20内的运动员中随机抽取2人,这2人得分之和大于25”(记为事件B )的所有可能结果有:{}24,A A ,{}211,A A ,{}34,A A ,{}38,A A ,{}311,A A ,{}48,A A ,{}411,A A ,{}811,A A ,共8种. ………8分 所以.答: 从得分在区间[)10,20内的运动员中随机抽取2人, 这2人得分之和大于25的概率为0.8. ………10分 21. 解:(1) 由题设知:,又222a b c =+,将代入, 得到:,即425a =,所以25a =,24b =,故椭圆方程为,。
3分焦点F 1、F 2的坐标分别为(-1,0)和(1,0),。
4分(2)由(1)知((0,2)A B ,,∴设直线l 的方程为,。
5分 由得 2285200x b ++-=, 。
7分 设P (x 1,y 1),Q (x 2,y 2),则212125208b x x x x -+=⋅=,。
8分1212121)1))y y x x x x ∴-=--=-,。
9分221221)()(||y y x x PQ -+-=∴====解之,(验证判别式为正),所以直线l 的方程为 。
10分 22.(1)T=π;(2)0,0;83,221min max ===+=x y x y π;(3)[]Z k k k ∈++,,24ππππ 23. 本小题主要考查直线及平面的位置关系的基础知识,考查空间想象能力、推理论证能力和运算求解能力.满分10分.(1)解:在线段AB 上存在点E , 使得//DE 平面PAC , 点E 是线段AB 的中点. …1分下面证明//DE 平面PAC :取线段AB 的中点E , 连接DE ,∵点D 是线段PB 的中点,∴DE 是△PAB 的中位线. ∴//DE PA . ∵PA ⊂平面PAC ,DE ⊄平面PAC ,∴//DE 平面PAC . ………6分 (2)证明:∵5,4,3AB BC AC ===,∴222AB BC AC =+.∴AC BC ⊥. ………8分∵平面PAC ⊥平面ABC ,且平面PAC平面ABC AC =,BC ⊂平面ABC ,∴BC⊥平面PAC. ………9分∵PA⊂平面PAC,∴PA BC⊥. ………10分24.。
