2003年黑龙江中考数学试题

合集下载

2003年哈尔滨中考数学试题(含答案)

哈尔滨市2003年初中升学考试数学本试卷满分为120分，考试时间为120分钟．第1卷选择题（30分）一、选择题（每小题分，共30分） 1. 下列式子结果为负数的是（）（A ）（B ）－（C ）（D ）()03-3-()23-()23--2．点P （3，－4）关于原点对称的点的坐标是（）（A ）（3，－4）（B ）（－3，－4）（C ）（3，4）（D ）（－3，4） 3．下列运算正确的是（）（A ）（B ）（C ）（D ） 532a a a =⋅532)(a a =326a a a =÷426a a a =-4．如图1，四边形ABCD 内接于⊙O ，若∠BOD ＝140°，则∠BCD ＝()（A ）140° （B ） 110° （C ）70° （D ）20°5．正方形具有而菱形不一定具有的性质是（）（A ）四条边相等（B ）对角线互相垂直平分（C ）对角线平分一组对角（D ）对角线相等6．若正比例函数y ＝（1－2m ）x 的图像经过点A （，）和点B （，），当＜1x 1y 2x 2y 1x 2x 时＞，则m 的取值范围是（）1y 2y （A ）m ＜0（B ）m ＞0（C ）m ＜（D ）m ＞ 21217．如图2，△ABC 中，AB ＝AC ，点D 在AC 边上，且BD ＝BC ＝AD ，则∠A 的度数为．（）（A ）30° （B ）36° （C ）45° （D ）70°8．现有下列命题：①的平方根是－5；②近似数3.14有3个有效数字； ③单项式与单项()25-310⨯y x 23式是同类项；④正方形既是轴对称图形，又是中心对称图形其中真命题的个数23xy -是（）（A ）1（B ）2（C ）3（D ）49．若一个圆锥的母线长是它底面圆半径的3倍，则它的侧面展开图的圆心角是（）（A ）180° （B ）90° （C ）120° （D ）135°10．下列各图是在同一直角坐标系内，二次函数与一次函数y ＝ax ＋c x c a ax y +++=)(2c 的大致图像，有且只有一个是正确的，正确的是（）（A ）（B ）（C ）（D ）第2卷非选择题（90分）二填空题（每小题3分，共30分）11．据国家统计局公布，去年我国增加就业人数7510000人，将这个数用科学记数法表示为人．12．若分式的值为零，则x ＝．392+-x x 13．分解因式：＝．ab a bx x +--2214．函数中自变量x 的取值范围是．12-+=x x y 15．如果长度分别为5，3，x 的三条线段能组成一个三角形，那么x 的范围是． 16．若在△ABC 中，AB ＝5cm ，BC ＝6cm ，BC 边上的中线AD ＝4cm ，则∠ADC 的度数是度。

黑龙江省2003年中考试卷

黑龙江省2003年中考试卷一、填空题（每小题3分，满分33分）1．生物学家发现一种病毒的直径约为0.000043米，用科学记数法表示为________米． 2．写出满足方程x ＋2y ＝9的一对整数值________．3．如图，△ABC 中，AD ⊥BC ，CE ⊥AB ，垂足分别为D 、E ，AD 、CE 交于点H ，请你添加一个适当的条件：________，使△AEH ≌△CEB ．4．函数43－－＝x x y 中，自变量x 的取值范围是________． 5．矩形一个角的平分线分矩形一边为 1 cm 和 3 cm 两部分，则这个矩形的面积为________2cm ．6．已知一次函数y ＝kx ＋2，请你补充一个条件：________，使y 随x 的增大而减小． 7．如图，在⊙O 中，AB 、AC 为互相垂直且相等的两条弦，OD ⊥AB ，OE ⊥AC ，垂足分别为D 、E ．若AC ＝2 cm ，则⊙O 的半径为________ cm ．8．已知抛物线c x ax y ＋＋＝2与x 轴交点的横坐标为－1，则a ＋c ＝________． 9．五个正整数从小到大排列，若这组数据的中位数是4，惟一众数是5，则这五个正整数的和为________．10．如图，某同学用一个有60°角的直角三角板估测学校旗杆AB 的高度．他将60°角的直角边水平放在1.5米高的支架CD 上，三角板的斜边与旗杆的顶点在同一直线上，他又量得D 、B 的距离为5米，则旗杆AB 的高度约为________米（精确到1米，3取1.73）．11．张大伯从报社以每份0.4元的价格购进了a 份报纸，以每份0.5元的价格售出了b 份报纸，剩余的以每份0.2元的价格退回报社，则张大伯卖报收入________元．二、单项选择题（将正确答案的代号填在题后括号内，每小题3分，满分27分）12．下列计算正确的是（）． A ．5322x x x ＝＋ B ．632x x x＝⋅C ．623)(x x ＝－－ D ．336x x x ＝÷13．将一长方形纸片按下图的方式折叠，BC 、BD 为折痕，则∠CBD 的度数为（）． A ．60° B ．75° C ．90° D ．95°14．某服装原价为200元，连续两次涨价a ％后，售价为242元，则a 的值为（）． A ．5 B ．10 C ．15 D ．20 15．若|a －3|－3＋a ＝0，则a 的取值范围是（）．A ．a ≤3B ．a ＜3C ．a ≥3D ．a ＞316．如图，用8块相同的长方形地砖拼成一个矩形，则每个长方形地砖的面积是（）．A ．200 2cm B ．300 2cm C ．600 2cm D ．2400 2cm 17．从哈尔滨开往A 市的特快列车，途中要停靠两个站点．如果任意两站间的票价都不同，那么有（）种不同的票价．A ．4B ．6C ．10D ．1218．如图，在等边△ABC 中，P 为BC 上一点，D 为AC 上一点，且∠APD ＝60°，BP ＝1，32＝CD ，则△ABC 的边长为（）．A ．3B ．4C ．5D ．619．平面直角坐标系内，点A （n ，1－n ）一定不在（）．A ．第一象限B ．第二象限C ．第三象限D ．第四象限20．如图，⊙O 的直径为10 cm ，弦AB 为8 cm ，P 是弦AB 上一点．若OP 的长为整数，则满足条件的点P 有（）．A ．2个B ．3个C ．4个D ．5个三、解答题（满分60分） 21．（本题5分）先化简，再求值： 13)181(＋＋＋－－x x x x其中23－＝x ．22．（本题6分）关于x 的方程04)1(2＝＋＋＋k x k kx 有两个不相等的实数根．（1）求k 的取值范围；（2）是否存在实数k ，使方程的两个实数根的倒数和等于0?若存在，求出k 的值；若不存在，说明理由．23．（本题6分）某中学在一次健康知识测试中，抽取部分学生成绩（分数为整数，满分100分）为样本，绘制成绩统计图如下，请结合统计图回答下列问题：（1）本次测试中抽样的学生有多少人?（2）分数在90.5～100.5这一组的频率是多少? （3）这次测试成绩的众数落在哪个小组内?（4）若这次测试成绩80分以上（含80分）为优秀，则优秀率不低于多少?24．（本题8分）为美化环境，计划在某小区内用30平方米的草皮铺设一块边长为10米的等腰三角形绿地，请你求出这个等腰三角形绿地的另两边长．25．（本题8分）某空军加油飞机接到命令，立即给另一架正在飞行的运输飞机进行空中加油．在加油过程中，设运输飞机的油箱余油量为1Q 吨，加油飞机的加油油箱余油量为2Q 吨，加油时间为t 分钟，1Q 、2Q 与t 之间的函数图象如图所示，结合图象回答下列问题：（1）加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟? （2）求加油过程中，运输飞机的余油量1Q （吨）与时间t （分钟）的函数关系式；（3）运输飞机加完油后，以原速继续飞行，需10小时到达目的地，油料是否够用?说明理由．26．（本题9分）已知：如图1，BD 、CE 分别是△ABC 的外角平分线，过点A 作AF ⊥BD ，AG ⊥CE ，垂足分别为F 、G ，连结FG ，延长AF 、AG ，与直线BC 相交，易证)(21AC BC AB FG ＋＋＝．图1若（1）BD 、CE 分别是△ABC 的内角平分线（图2）；（2）BD 为△ABC 的内角平分线，CE 为△ABC 的外角平分线（图3），则在图2、图3两种情况下，线段FG 与△ABC 三边又有怎样的数量关系?请写出你的猜想，并对其中的一种情况给予证明．图2图327．（本题9分）为了保护环境，某企业决定购买10台污水处理设备．现有A 、B 两种型号的设备，其经预算，该企业购买设备的资金不高于105万元．（1）请你设计该企业有几种购买方案；（2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；（3）在第（2）问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元?（注：企业处理污水的费用包括购买设备的资金和消耗费）28．（本题9分）已知：如图，直角坐标系内的梯形AOBC ，AC ∥OB ，AC 、OB 的长分别是关于x 的方程04m mx 6x 22＝＋－+的两根，并且5:1:＝BOC AOC S S ∆∆．（1）求AC 、OB 的长；（2）当BC ⊥OC 时，求OC 的长及OC 所在直线的解析式；（3）在第（2）问的条件下，线段OC 上是否存在一点M ，过M 点作x 轴的平行线，交y 轴于F ，交BC 于D ，过D 点作y 轴的平行线，交x 轴于E ，使A O B C F O E D S S 梯形矩形＝21？若存在，请直接写出M 点的坐标；若不存在，说明理由．参考答案一、填空题（每小题3分，满分33分） 1．5103.4－⨯ 2．x ＝1，y ＝4等（只要符合要求即可） 3．AH ＝CB 等（只要符合要求即可） 4．x ≥3且x ≠4 5．4或12 6．K ＝－3等（写不等式或其他条件，符合要求即可） 7．2 8．1 9．17或18或19 10．10 11．（0.3b －0.2a ）二、单项选择题（每小题3分，满分27分）12．D 13．C 14．B 15．A 16．B 17．B 18．A 19．C 20．D 三、解答题（满分60分）21．（本题5分）解：原式13)1811(2＋＋＋－＋－＝x x x x x ÷……………………………………………………1分 31192＋＋＋－＝x x x x ⋅………………………………………………………………1分＝x －3．………………………………………………………………………2分当23－＝x 时，原式2323＝－－－＝．…………………………………………1分 22．（本题6分）解：（1）由题意知，K ≠0，且044)1(2＞－＋＝kk k ⋅∆．……………………………………………………2分∴ 21＞－k 且K ≠0．………………………………………………………………… 1分（2）不存在．……………………………………………………………………………1分设方程的两个根是1x ，2x ． ∵ 04121≠＝x x ，∴ 011212121＝＋＝＋x x x x x x ．∴ 021＝＋x x ．∵ kk x x 121＋＝－＋，…………………………………………………………………1分 ∴ k ＋1＝0，211＜－＝－k ．…………………………………………………………1分∴ 满足条件的实数K 不存在． 23．（本题6分）解：（1）2＋3＋4＋41＝50（人）．…………………………………………………… 1分（2）08.0504＝＝总数频数频率＝．……………………………………………………1分（3）众数落在80.5～90.5这一小组内．………………………………………………2分（4）这次测试成绩的优秀率不低于90%．……………………………………………2分 24．（本题8分）解：分三种情况计算．不妨设AB ＝10米，过点C 作CD ⊥AB ，垂足为D ．CD AB S ABC ⋅∆21＝，CD ＝6（米）．……………………………………………………1分（1）当AB 为底边时，AD ＝DB ＝5（米）（如图1），615622＝＋＝＝BC AC （米）．……………………………………………………2分图1（2）当AB 为腰且三角形为锐角三角形时（如图2）， AB ＝AC ＝10（米），………………………………………………………………………1分 822＝－＝CD AC AD （米），BD ＝29（米），………………………………………1分1022622＝＋＝BC （米）．…………………………………………………………1分图2（3）当AB 为腰且三角形为钝角三角形时（如图3）， AB ＝BC ＝10（米），………………………………………………………………………1分 10618622=+=AC （米）．………………………………………………………1分图325．（本题8分）解：（1）由图象知，加油飞机的加油油箱中装载了30吨油，………………………1分全部加给运输飞机需10分钟．…………………………………………………………1分（2）设b kt Q ＋＝1，把（0，40）和（10，69）代入，得 ⎩⎨⎧.1069,40b k b ＋＝＝…………………………………………………………………………… 1分解方程组得⎩⎨⎧.40,9.2＝＝b k ……………………………………………………………………1分∴ 409.21＋＝t Q （0≤t ≤10）．……………………………………………………2分（3）根据图象可知运输飞机的耗油量为每分钟0.1吨．……………………………1分 ∴ 10小时耗油量为：10×60×0.1＝60（吨）＜69（吨）．∴ 油料够用．…………………………………………………………………………1分26．（本题9分）猜想结果：图中结论)(21BC AC AB FG －＋=．……………………………………2分证明：分别延长AG 、AF 交BC 于H 、K ，……………………………………………1分易证△BAF ≌△BKF ，AF ＝KF ，AB ＝KB ．…………………………………………2分同理可证，AG ＝HG ，AC ＝HC ，∴ HK FG 21＝．………………………………………………………………………1分又∵ HK ＝BK －BH ＝AB ＋AC －BC ，…………………………………………………1分 ∴ )(21BC AC AB FG －＋＝．结论为)(21AB AC BC FG －＋＝………………………………………………………2分如果证明图中结论，可参考上面评分标准给分．27．（本题9分）解：（1）设购买污水处理设备A 型x 台，则B 型（10－x ）台．由题意知，12x ＋10（10－x ）≤105．…………………………………………………1分 x ≤2.5．……………………………………………………………………………………1分 ∵ x 取非负整数，∴ x 可取0，1，2．∴ 有三种购买方案：购A 型0台，B 型10台；购A 型1台，B 型9台；购A 型2台，B 型8台．………………………………………………………………………………………1分（2）由题意得 240x ＋200（10－x ）≥2040．………………………………………1分 x ≥1，∴ x 为1或2．…………………………………………………………………1分当x ＝1时，购买资金为： 12×1＋10×9＝102（万元）；当x ＝2时，购买资金为： 12×2＋10×8＝104（万元）．∴ 为了节约资金，应选购A 型1台，B 型9台．……………………………………1分（3）10年企业自己处理污水的总资金为： 102＋10×10＝202（万元）．……………………………………………………………1分若将污水排到污水厂处理，10年所需费用为：2040×12×10×10＝2448000（元）＝244.8（万元）．………………………………1分 244.8－202＝42.8（万元），∴ 能节约资金42.8万元．……………………………………………………………1分 28．（本题9分）解：（1）∵ 5:1:＝B O C A O C S S ∆∆，∴ 5:1:＝OB AC ．不妨设AC ＝k ，OB ＝5k ．……………………………………………………………1分由题意得⎩⎨⎧⋅.45,652＋＝＝＋m k k m k k ……………………………………………………………1分解得⎩⎨⎧1,1＝＝k m 或⎩⎨⎧--.1,1＝＝k m （不合题意，舍去）∴ AC ＝1，OB ＝5．………………………………………………………………1分（2）∵ ∠OAC ＝∠BCO ＝90°，∠ACO ＝∠BOC ， ∴ △OBC ∽△COA ． ∴ACOC OC OB ＝，AC OB OC ⋅＝2．……………………………………………1分 ∴ 5＝OC 或5＝－OC （舍去）．……………………………………………1分∵ AC ＝1，∴ AO ＝2．∴ C （1，2）．……………………………………… 1分 ∴ 直线OC 的解析式为y ＝2x ．……………………………………………………1分（3）存在，1M （21，1），2M （43，23）．……………………………………… 2分说明：如果学生有不同于本参考答案的解题方法，只要正确，可参照本评分标准，酌情给分．。

关于哈市2003年中考数学命题的反思

关于哈市2003年中考数学命题的反思一、考题背景2003年是哈尔滨市中考改革的第一年，考试由原来的两天改为三天，考试科目和往年相比有所变化。

数学是所有学生必考科目之一，而2003年哈市中考的数学考题备受争议。

本文通过对2003年哈市中考数学考题的分析和反思，希望能够找出问题并提出改进建议。

二、考题分析1. 题型设置不合理2003年哈市中考数学试题中，部分题目所占分数过大，而且题型设置不够平衡。

如选择题过多，填空题和解答题的数量相对较少，容易导致时间不够分配，影响考生发挥。

2. 难度不合适试题难度设置不合理，题目涉及的知识点跨度较大，有些题目过于复杂，导致部分学生难以完成，影响了他们的考试成绩。

3. 题目出错有部分试题存在错误，如选项不对称，或者是题目本身存在歧义，导致部分答题人产生困扰，影响了他们的答题心情和答题效果。

三、影响和启示1. 对学生的影响2003年哈市中考数学试题的不合理性直接影响到了学生的心理和发挥，阻碍了他们正常发挥的机会，容易造成学习压力过大、自信心受挫等问题。

2. 对教学改革的启示试题的出题者需要更加贴近教材和教学实际，增强题目的经典性和稳定性，保证考题能够客观公正地考察学生的能力和水平。

四、改进建议1. 试题设置上，应该合理控制题型数量和难度，保持题目平衡，保证学生在考试时间内能够有序完成试卷。

2. 出题者应该更加注重题目的准确性和清晰度，避免错误和歧义的存在，保证试题的客观性和公正性。

五、结语2003年哈市中考数学试题虽然存在一些问题，但正是这些问题的存在，促使我们思考和反思出题的原则和方法，为今后出题提供了宝贵的经验和启示。

希望通过对过去的反思，能够为未来的中考数学命题提供一些建设性的建议。

以上就是对于哈市2003年中考数学命题的反思，希望能够对未来的中考数学出题提供一些借鉴和启示。

2003年哈市中考数学试题的争议引起了社会各界的广泛关注和深入思考。

在教育改革的大背景下，中考数学试题的合理性和公平性成为了备受关注的焦点。

2003年中考数学试卷

2003年中考数学试卷
2003年中考数学试卷指的是在2003年中考中使用的数学科目的试卷。

这份试卷将由当地教育部门或考试机构组织专家进行命题，并按照中考数学科目的要求进行设计。

以下是 2003年中考数学试卷具体的题目示例：
选择题1：若关于 x 的一元二次方程 x^2 + 4x + k - 1 = 0 有两个不相等的实数根，则 k 的取值范围是 ()
A. k < 5
B. k > 5
C. k < -5
D. k > -5
选择题2：下列图形中，是轴对称图形但不是中心对称图形的是 ()
A. 正三角形
B. 正方形
C. 正五边形
D. 正六边形
填空题1：计算：√4 + | -2| - (1/2)^(-1) = ___．
填空题2：若反比例函数 y = (m - 1)/x 的图象在每一个象限中，y随着x 的增大而减小，则m的取值范围是 ___．
计算题1：计算：(π - 3)^0 - 4sin 45° + | -2| + (1/3)^(-1)．
计算题2：解方程组：{ 3x + y = 2, 4x - 3y = 15 }．
总结：2003年中考数学试卷指的是在2003年中考中使用的数学科目的试卷。

这份试卷旨在测试学生对数学基础知识的掌握程度和问题解决能力，通过选择题、填空题和计算题等多种题型进行考查。

考生需要通过系统的数学学习和复习，掌握基础知识和应试技巧，以提高自己的数学水平，应对这份试卷的挑战。

2003年全国中考数学压轴题精选及解答-

2003年全国中考数学压轴题精选11、（2003年安徽省）（本题满分14分）如图，这些等腰三角形与正三角形的形状有差异，我们把这与正三角形的接近程度称为“正度”。

在研究“正度”时，应保证相似三角形的“正度”相等。

设等腰三角形的底和腰分别为a 、b ，底角和顶角分别为α、β。

要求“正度”的值是非负数。

同学甲认为：可用式子|a －b |来表示“正度”，|a －b |的值越小，表示等腰三角形越接近正三角形；同学乙认为：可用式子|α－β|来表示“正度”，|α－β|的值越小，表示等腰三角形越接近正三角形。

探究：（1）他们的方案哪个较合理，为什么？（2）对你认为不够合理的方案，请加以改进（给出式子即可）；（3）请再给出一种衡量“正度”的表达式β ααb b第24题图（2003年安徽省）附加题:（共两小题，每小题10分，共20分）报考理科实验班的学生必做，不考理科实验班的学生不做）1、要将29个数学竞赛的名额分配给10所学校，每所学校至少要分到一个名额。

（1）试提出一种分配方案，使得分到相同名额的学校少于4所；（2）证明：不管怎样分配，至少有3所学校得到的名额相同；（3）证明：如果分到相同名额的学校少于4所，则29名选手至少有5名来自同一学校。

如图12所示，已知A、B两点的坐标分别为（28，0）和（0，28），动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动。

动直线EF从x轴开始以每秒1个长度单位的速度向上平行移动（即EF∥x轴），并且分别与y轴、线段AB交于E、F点。

连结EP，设动点P与动直线EF同时出发，运动时间为t秒。

（1）当t＝1秒时，求梯形OPFE的面积。

t为何值时，梯形OPFE的面积最大，最大面积是多少？（2）当梯形OPFE的面积等于三角形APF的面积时．求线段PF的长；（3）设t的值分别取1t、2t时（1t≠2t），所对应的三角形分别为△AF1P1和△AF2P2。

试判断这两个三角形是否相似，请证明你的判断。

2003黑龙江中考数学试卷及答案

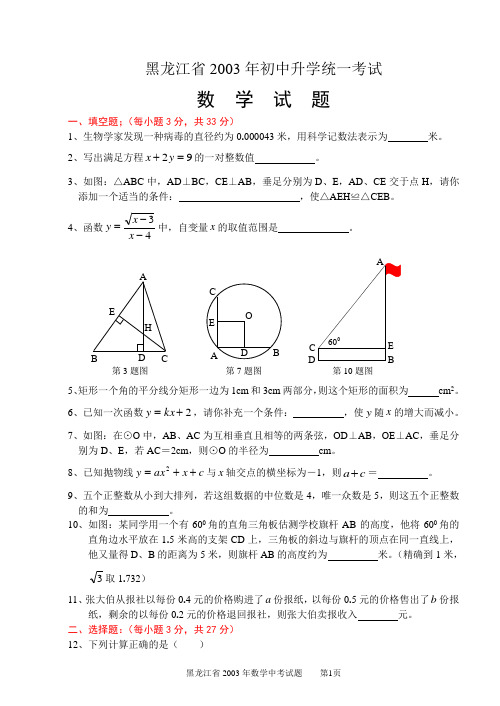
黑龙江省2003年初中升学统一考试数学试题一、填空题；（每小题3分，共33分）1、生物学家发现一种病毒的直径约为0.000043米，用科学记数法表示为米。

2、写出满足方程92=+y x 的一对整数值。

3、如图：△ABC 中，AD ⊥BC ，CE ⊥AB ，垂足分别为D 、E ，AD 、CE 交于点H ，请你添加一个适当的条件：，使△AEH ≌△CEB 。

4、函数43--=x x y 中，自变量x 的取值范围是。

第3题图 HEDCBA第7题图OE DCBA第10题图D5、矩形一个角的平分线分矩形一边为1cm 和3cm 两部分，则这个矩形的面积为 cm 2。

6、已知一次函数2+=kx y ，请你补充一个条件：，使y 随x 的增大而减小。

7、如图：在⊙O 中，AB 、AC 为互相垂直且相等的两条弦，OD ⊥AB ，OE ⊥AC ，垂足分别为D 、E ，若AC ＝2cm ，则⊙O 的半径为 cm 。

8、已知抛物线c x ax y ++=2与x 轴交点的横坐标为－1，则c a +＝。

9、五个正整数从小到大排列，若这组数据的中位数是4，唯一众数是5，则这五个正整数的和为。

10、如图：某同学用一个有600角的直角三角板估测学校旗杆AB 的高度，他将600角的直角边水平放在1.5米高的支架CD 上，三角板的斜边与旗杆的顶点在同一直线上，他又量得D 、B 的距离为5米，则旗杆AB 的高度约为米。

（精确到1米，3取1.732）11、张大伯从报社以每份0.4元的价格购进了a 份报纸，以每份0.5元的价格售出了b 份报纸，剩余的以每份0.2元的价格退回报社，则张大伯卖报收入元。

二、选择题：（每小题3分，共27分） 12、下列计算正确的是（）A 、5322x x x =+B 、632x x x =⋅C 、623)(x x -=-D 、336x x x =÷13、将一张长方形纸片按如图所示的方式折叠，BC 、BD 为折痕，则∠CBD 的度数为（）A 、600B 、750C 、900D 、95014、某服装原价为200元，连续两次涨价a ％后，售价为242元，则a 的值为（）A 、5B 、10C 、15D 、20第13题图C E第16题图15、若033=+--a a ，则a 的取值范围是（）A 、a ≤3B 、a ＜3C 、a ≥3D 、a ＞316、如图：用8块相同的长方形地砖拼成一个矩形，则每个长方形地砖的面积是（） A 、200cm 2 B 、300cm 2 C 、600cm 2 D 、2400cm 2 17、从哈尔滨开往A 市的特快列车，途中要停靠两个站点，如果任意两站间的票价都不同，那么有（）种不同的票价。

2003年龙江初中数学中考试题

2003年龙江初中数学中考试题（模拟题）一．填空题：（本题共10小题，每个小题2分，共20分） 1．计算：∣－5∣－3＝＿＿＿＿＿＿＿。

2．我国陆地面积约为9600000平方千米，用科学记数法可表示为＿＿＿＿＿平方千米。

3．函数y ＝41-x 中自变量x 的取值范围是＿＿＿＿＿。

4．分解因式：a 2－2ab+b 2－1=__________。

5．计算：._______)11(1=-÷-xx x 6．已知：如图，∠ACB ＝∠DBC ，要使△ABC ≌△DCB ，只需增加的一个条件是＿＿＿＿＿（只需填写一个你认为适合的条件）7．如图中，阴影部分表示的四边形是＿＿＿＿＿＿＿。

8．已知梯形的上底长为3cm ，下底长为7cm ，则此梯形中位线长为＿＿＿＿cm. 9．在半径为9cm 的圆中，60°的圆心角所对的弧长为＿＿＿＿＿＿cm.10．下表为杨辉三角系数表，它的作用是指导读者按规律写出形如（a+b ）n（n 为正整数）展开式的系数，请你仔细观察下表中的规律，填出（a+b ）4展开式中所缺的系数。

(a+b)=a+b(a+b)2=a 2+2ab+b 2(a+b)3=a 3+3a 2b+3ab 2+b 3则（a+b ）4=a 4+_______a 3b+6a 2b 2+4ab 3+b 4二．选择题：（本题共10个小题，每个小题3分，满分30分） 11．下列运算正确的是（） A 、 2a+a=3a 2B 、94)9)(4(-⋅-=--C 、(3a 2)3=9a 6 D 、a 2•a 3=a 512．下列二次根式中，最简二次根式是（）A 、22x B 、12+b C 、a 4 D 、x113．下列说法正确的是（）A 、负数和零没有平方根B 、20021的倒数是2002 C 、22是分数 D 、0和1的相反数是它本身 14．二元一次方程组⎩⎨⎧=+-=-1012y x y x 的解是（）A 、 ⎩⎨⎧==37x y B 、 ⎪⎩⎪⎨⎧==311319x y C 、⎩⎨⎧==28x y D 、⎩⎨⎧==73x y15．一元二次方程2x 2－4x+1=0根的情况是（） A 、有两个不相等的实数根 B 、有两个相等的实数根 C 、没有实数根 D 、无法确定 16．下列命题正确的是（）A 、对角线相等的四边形是矩形B 、相邻的两个角都互补的四边形是平行四边形C 、平分弦的直径垂直于弦，并且平分弦所对的两条弧D 、三点确定一个圆 17．在同一直角坐标系中，函数y=3x 与y=x1-图象大致是18．两圆的半径分别为3cm 和4cm ，且两圆的圆心距为7cm ，则这两圆听位置关系是（） A 、相交 B 、外切 C 、内切 D 、相离19．我省为了解决药品价格过高的问题，决定大幅度降低药品价格，其中将原价为a 元的某种常用药降价40%，则降价后此格为（） A 、元4.0a B 、元6.0a C 、60%a 元 D 、40%a 元则餐厅所有员工工资的众数、中位数是（） A 、340 520 B 、520 340 C 、340 560 D 、560 340三、（本题共4个小题，每小题5分，满分20分） 21．计算：0045sin 2)12(121--++22．解不等式组⎩⎨⎧<-<+-0520)1(2x x x 并解集在数轴上表示出来。

【中考专题】黑龙江省大庆市中考数学历年真题汇总卷(Ⅲ)(含答案详解)

黑龙江省大庆市中考数学历年真题汇总卷（Ⅲ）考试时间：90分钟；命题人：数学教研组考生注意： 1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、下列方程变形不正确的是（）A ．4332x x -=+变形得：4323x x -=+B ．方程110.20.5x x --=变形得：1010212x x --=C ．()()23231x x -=+变形得：6433x x -=+D ．211332x x -=+变形得：41318x x -=+ 2、一副三角板按如图所示的方式摆放，则∠1补角的度数为（）A ．45︒B ．135︒C ．75︒D ．165︒ 3、如图，等腰三角形ABC 的底边BC 长为4，面积是20，腰AC 的垂直平分线EF 分别交AC ，AB 边于E ，F 点，若点D 为BC 边的中点，点M 为线段EF 上一动点，则CDM ∆周长的最小值为（） ·线○封○密○外A ．8B ．10C ．12D ．144、如图，已知点B ，F ，C ，E 在一条直线上，AB DE =，AB DE ∥，那么添加下列一个条件后，仍无法判定ABC DEF ≌△△的是（）A ．BF CE =B ．A D ∠=∠C ．AC DF ∥D ．AC DF =5、如图，AB CD ∥，45A ∠=︒，30C ∠=︒，则E ∠的度数是（）A ．10°B ．15°C ．20°D ．25°6、如图，有三块菜地△ACD 、△ABD 、△BDE 分别种植三种蔬菜，点D 为AE 与BC 的交点，AD 平分∠BAC ，AD =DE ，AB =3AC ，菜地△BDE 的面积为96，则菜地△ACD 的面积是（）A ．24B ．27C ．32D ．367、生活中常见的探照灯、汽车大灯等灯具都与抛物线有关．如图，从光源P 点照射到抛物线上的光线,PA PB 等反射以后沿着与直线PF 平行的方向射出，若CAP α∠=︒，DBP β∠=︒，则APB ∠的度数为（）°A ．2αB ．2βC ．αβ+D ．5()4αβ+ 8、如图，一个几何体是由六个大小相同且棱长为1的立方块组成，则这个几何体的表面积是（）A ．16B ．19C ．24D ．36 9、如图，在ABC 中，D 是BC 延长线上一点，50B ∠=︒，80A ∠=︒，则ACD ∠的度数为（） A ．140︒ B ．130︒ C ．120︒ D ．110︒ 10、如图，在矩形ABCD 中，6AB =，8AD =，点O 在对角线BD 上，以OB 为半径作O 交BC 于点E ，连接DE ；若DE 是O 的切线，此时O 的半径为（）·线○封○密○外A ．716B ．2110C ．2116D ．3516第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在平面直角坐标系xOy 中，P 为函数)(0m y x x=>图象上一点，过点P 分别作x 轴、y 轴的垂线，垂足分别为M ，N ．若矩形PMON 的面积为3，则m 的值为______．2、已知点P 是线段AB 的黄金分割点，AP ＞PB ．若AB ＝2，则AP ＝_____．3、如图是正方体的一种展开图，表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来！”，那么在正方体的表面与“！”相对的汉字是________．4、如图，将一个边长为3的正方形纸片进行分割，部分①的面积是边长为3的正方形纸片的一半，部分②的面积是部分①的一半，部分③的面积是部分②的一半，以此类推，n 部分的面积是______．（用含n 的式子表示）5、写出n 的一个有理化因式：_______．三、解答题（5小题，每小题10分，共计50分） 1、先把下列各数在数轴上表示出来，再按照从小到大的顺序用“＜”连接起来． ﹣212，-(﹣4)，0，+(﹣1)，1，﹣|﹣312|2、将两块完全相同的且含60︒角的直角三角板ABC 和AFE 按如图所示位置放置，现将Rt AEF 绕A 点按逆时针方向旋转()090αα︒<<︒．如图，AE 与BC 交于点M ，AC 与EF 交于点N ，BC 与EF 交于点P ． ·线○封○密·○外(1)在旋转过程中，连接,AP CE，求证：AP所在的直线是线段CE的垂直平分线．(2)在旋转过程中，CPN是否能成为直角三角形？若能，直接写出旋转角的度数；若不能，说明理由．3、已知：如图，锐角∠AOB．求作：射线OP，使OP平分∠AOB．作法：①在射线OB上任取一点M；②以点M为圆心，MO的长为半径画圆，分别交射线OA，OB于C，D两点；③分别以点C，D为圆心，大于12CD的长为半径画弧，在∠AOB内部两弧交于点H；④作射线MH，交⊙M于点P；⑤作射线OP．射线OP即为所求．(1)使用直尺和圆规，依作法补全图形（保留作图痕迹）；(2)完成下面的证明．证明：连接CD ．由作法可知MH 垂直平分弦CD ． ∴CP DP =（）（填推理依据）． ∴∠COP ＝．即射线OP 平分∠AOB ． 4、解方程： (1)()8436x x --=； (2)232126x x +--=． 5、完成下面推理填空：如图，已知：AD BC ⊥于D ，EG BC ⊥于G ，1E ∠=∠．求证：AD 平分BAC ∠．解：∵AD BC ⊥于D ，EG BC ⊥（已知）， ∴90ADC EGC ∠=∠=︒（____①_____）， ∴EG AD ∥（同位角相等，两直线平行）， ∴_____②___（两直线平行，同位角相等） ∠1＝∠2（____③_____），又∵1E ∠=∠（已知）， ∴∠2＝∠3（_____④______）， ∴AD 平分BAC ∠（角平分线的定义）． ·线○封○密·○外-参考答案-一、单选题1、D【解析】【分析】根据等式的性质解答．【详解】解：A . 4332x x -=+变形得：4323x x -=+，故该项不符合题意；B . 方程110.20.5x x --=变形得：1010212x x --=，故该项不符合题意； C . ()()23231x x -=+变形得：6433x x -=+，故该项不符合题意；D . 211332x x -=+变形得：46318x x -=+，故该项符合题意；故选：D ．【点睛】此题考查了解方程的依据：等式的性质，熟记等式的性质是解题的关键．2、D【解析】【分析】根据题意得出∠1=15°，再求∠1补角即可．【详解】由图形可得1453015∠=︒-︒=︒∴∠1补角的度数为18015165︒-︒=︒故选：D ．【点睛】本题考查利用三角板求度数和补角的定义，熟记各个三角板的角的度数是解题的关键． 3、C 【解析】【分析】连接AD ，由于△ABC 是等腰三角形，点D 是BC 边的中点，故AD ⊥BC ，再根据三角形的面积公式求出AD 的长，再根据EF 是线段AC 的垂直平分线可知，点C 关于直线EF 的对称点为点A ，故AD 的长为CM +MD 的最小值，由此即可得出结论．【详解】解：连接AD ，∵△ABC 是等腰三角形，点D 是BC 边的中点， ∴AD ⊥BC ， ·线○封○密○外∴11•42022ABC S BC AD AD ==⨯⨯=，解得AD =10， ∵EF 是线段AC 的垂直平分线，∴点C 关于直线EF 的对称点为点A ，∴AD 的长为CM +MD 的最小值，∴△CDM 的周长最短=CM +MD +CD =AD +110410222211BC =+⨯=+=．故选：C ．【点睛】本题考查的是轴对称-最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．4、D【解析】【分析】结合选项中的条件，是否能够构成,,AAS ASA SAS 的形式，若不满足全等条件即为所求；【详解】解：由AB DE 可得B E ∠=∠，判定两三角形全等已有一边和一角；A 中由BF CE =可得BC EF =，进而可由SAS 证明三角形全等，不符合要求；B 中A D ∠=∠，可由ASA 证明三角形全等，不符合要求；C 中由AC DF 可得ACB DFC ∠=∠，进而可由AAS 证明三角形全等，不符合要求；D 中无法判定，符合要求；故选D ．【点睛】本题考查了三角形全等．解题的关键在于找出能判定三角形全等的条件．5、B【解析】【分析】根据平行线的性质求出关于∠DOE ，然后根据外角的性质求解．【详解】解：∵AB ∥CD ，∠A ＝45°， ∴∠A ＝∠DOE ＝45°， ∵∠DOE ＝∠C +∠E ，又∵30C ∠=︒， ∴∠E ＝∠DOE -∠C ＝15°．故选：B 【点睛】本题比较简单，考查的是平行线的性质及三角形内角与外角的关系．掌握两直线平行，内错角相等；三角形的一个外角等于和它不相邻的两个内角的和是解题关键． 6、C 【解析】【分析】利用三角形的中线平分三角形的面积求得S △ABD =S △BDE =96，利用角平分线的性质得到△ACD 与△ABD 的高相等，进一步求解即可．【详解】解：∵AD =DE ，S △BDE =96， ∴S △ABD =S △BDE =96，过点D 作DG ⊥AC 于点G ，过点D 作DF ⊥AB 于点F ， ·线○封○密○外∵AD 平分∠BAC ，∴DG=DF ，∴△ACD 与△ABD 的高相等，又∵AB =3AC ，∴S △ACD =13S △ABD =196323⨯=．故选：C ．【点睛】本题考查了角平分线的性质，三角形中线的性质，解题的关键是灵活运用所学知识解决问题．7、C【解析】【分析】根据平行线的性质可得,EPA PAC EPB PBD ∠=∠∠=∠，进而根据APB APE BPE ∠=∠+∠即可求解【详解】解：,PF AC PF BD ∥∥ ∴,EPA PAC EPB PBD ∠=∠∠=∠∴APB APE BPE ∠=∠+∠αβ=+故选C【点睛】本题考查了平行线的性质，掌握平行线的性质是解题的关键．8、C【解析】【分析】分别求出各视图的面积，故可求出表面积．【详解】由图可得图形的正视图面积为4，左视图面积为 3，俯视图的面积为5 故表面积为2×（4+3+5）=24 故选C ．【点睛】此题主要考查三视图的求解与表面积。

2023年黑龙江省龙东地区中考数学真题试卷(解析版)

2023年黑龙江省龙东地区中考数学真题试卷及答案考生注意：1．考试时间120分钟2．全卷共三道大题，总分120分一、选择题（每小题3分，共30分）1. 下列运算正确的是（）A. B.C. D.【答案】C【解析】分别根据积的乘方，完全平方公式，平方差公式和幂的乘方法则进行判断即可．解：A.，原式计算错误；B. ，原式计算错误；C. ，计算正确；D. ，原式计算错误．故选：C．【点拨】本题考查了积的乘方，完全平方公式，平方差公式和幂的乘方，熟练掌握运算法则，牢记乘法公式是解题的关键．2. 下列新能源汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）A. B. C. D.【答案】A【解析】根据轴对称图形和中心对称图形的定义进行逐一判断即可：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；把一个图形绕着某一个点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．解：A.既是轴对称图形，也是中心对称图形，符合题意；B.是轴对称图形，不是中心对称图形，不符合题意；C.既不是轴对称图形，也不是中心对称图形，不符合题意；D.是轴对称图形，不是中心对称图形，不符合题意；故选A．【点拨】本题主要考查了轴对称图形和中心对称图形的识别，熟知二者的定义是解题的关键．3. 一个几何体由若干大小相同的小正方体组成，它的俯视图和左视图如图所示，那么组成该几何体所需小正方体的个数最少为（）A. 4B. 5C. 6D. 7【答案】B【解析】在“俯视打地基”的前提下，结合左视图知俯视图上一行三个小正方体的上方（第2层）至少还有1个正方体，据此可得答案.解：由俯视图与左视图知，该几何体所需小正方体个数最少分布情况如下图所示：所以组成该几何体所需小正方体的个数最少为5，故选：B．【点拨】本题主要考查由三视图判断几何体，解题的关键是掌握口诀“俯视打地基，主视疯狂盖，左视拆违章”．4. 已知一组数据的平均数是1，则这组数据的众数是（）A. B. 5 C. 和5 D. 1和3【答案】C【解析】先根据平均数的定义列出关于的方程，求出的值，从而还原这组数据，再利用众数的概念求解即可．解：∵数据的平均数是1，∴，解得，则，∴这组数据的众数是和5，故选：C．【点拨】此题主要考查了众数和平均数，解题关键是掌握众数和平均数的概念．5. 如图，在长为，宽为的矩形空地上修筑四条宽度相等的小路，若余下的部分全部种上花卉，且花圃的面积是，则小路的宽是（）A. B. C. 或 D.【答案】A【解析】设小路宽为，则种植花草部分的面积等于长为，宽为的矩形的面积，根据花草的种植面积为，即可得出关于x的一元二次方程，解之取其符合题意的值即可得出结论．解：设小路宽为，则种植花草部分的面积等于长为，宽为的矩形的面积，依题意得：解得：，（不合题意，舍去），∴小路宽为．故选A．【点拨】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．6. 已知关于x的分式方程的解是非负数，则的取值范围是（）A. B. C. 且 D. 且【答案】C【解析】解分式方程求出，然后根据解是非负数以及解不是增根得出关于m的不等式组，求解即可．解：分式方程去分母得：，解得：，∵分式方程的解是非负数，∴，且，∴且，故选：C．【点拨】本题考查了解分式方程，解一元一次不等式组，正确得出关于m的不等式组是解题的关键．7. 某社区为了打造“书香社区”，丰富小区居民的业余文化生活，计划出资500元全部用于采购A，B，C三种图书，A种每本30元，B种每本25元，C种每本20元，其中A种图书至少买5本，最多买6本（三种图书都要买），此次采购的方案有（）A. 5种B. 6种C. 7种D. 8种【答案】B【解析】设采购A种图书x本，B种图书y本，C种图书z本，根据采购三种图书需500元列出方程，再依据x的数量分两种情况讨论求解即可．解：设采购A种图书x本，B种图书y本，C种图书z本，其中且均为整数，根据题意得，，整理得，，①当时，，∴∵且均为整数，∴当时，，∴；当时，，∴；当时，，∴；②当时，，∴∵且均为整数，∴当时，，∴；当时，，∴；当时，，∴；综上，此次共有6种采购方案，故选：B．【点拨】本题主要考查了二元一次方程的应用，正确理解题意、进行分类讨论是解答本题的关键．8. 如图，是等腰三角形，过原点，底边轴，双曲线过两点，过点作轴交双曲线于点，若，则的值是（）A. B. C. D.【答案】C【解析】设，根据反比例函数的中心对称性可得，然后过点A作于E，求出，点D的横坐标为，再根据列式求出，进而可得点D的纵坐标，将点D坐标代入反比例函数解析式即可求出的值．解：由题意，设，∵过原点，∴，过点A作于E，∵是等腰三角形，∴，∴，点D的横坐标为，∵底边轴，轴，∴，∴，∴点D的纵坐标为，∴，∴，解得：，故选：C．【点拨】本题考查了反比例函数的图象和性质，中心对称的性质，等腰三角形的性质等知识，设出点B坐标，正确表示出点D的坐标是解题的关键．9. 如图，在平面直角坐标中，矩形的边，将矩形沿直线折叠到如图所示的位置，线段恰好经过点，点落在轴的点位置，点的坐标是（）A. B. C. D.【答案】D【解析】首先证明，求出，连结，设与交于点F，然后求出，可得，再用含的式子表示出，最后在中，利用勾股定理构建方程求出即可解决问题．解：∵矩形的边，，∴，，，由题意知，∴，又∵，∴，∴，由折叠知，，∴，∴，即，连接，设与交于点F，∴，∵，∴四边形是矩形，∴，，，∴，由折叠知，，∴，∵在中，，∴，解得：，∴点的坐标是，故选：D．【点拨】本题考查了矩形的判定和性质，相似三角形的判定和性质，折叠的性质以及勾股定理的应用等知识，通过证明三角形相似，利用相似三角形的性质求出的长是解题的关键．10. 如图，在正方形中，点分别是上的动点，且，垂足为，将沿翻折，得到交于点，对角线交于点，连接，下列结论正确的是：①；②；③若，则四边形是菱形；④当点运动到的中点，；⑤．（）A. ①②③④⑤B. ①②③⑤C. ①②③D. ①②⑤【答案】B【解析】利用正方形的性质和翻折的性质，逐一判断，即可解答．解：四边形是正方形，，，，，，，，，故①正确，将沿翻折，得到，，∵，，故②正确，当时，，，，即在同一直线上，，，通过翻折的性质可得，，∴，，，四边形是平行四边形，，平行四边形是菱形，故③正确，当点运动到的中点，如图，设正方形的边长为，则，在中，，，，，，，，，，，，，，在中，，故④错误，，，，，，根据翻折的性质可得，，，，故⑤正确；综上分析可知，正确的是①②③⑤．故选：B．【点拨】本题考查了正方形的性质，翻折的性质，相似三角形的判定和性质，正切的概念，熟练按照要求做出图形，利用寻找相似三角形是解题的关键．二、填空题（每小题3分，共30分）11. 据交通运输部信息显示：2023年“五一”假期第一天，全国营运性客运量约5699万人次，将5699万用科学记数法表示为__________．【答案】【解析】科学记数法的表示形式为的形式，其中，n为整数，确定n的值时，要看把原数变成a 时，小数点移动了多少位，n的绝对值与小数点移动的位数相同当原数绝对值时，n是正数；当原数的绝对值时，n是负数．5699万，故答案为：．【点拨】此题考查科学记数法的表示方法科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值．12. 函数y=中，自变量x的取值范围是____________．【答案】【解析】解：由题意得，，解得．13. 如图，在矩形中对角线，交于点，请添加一个条件______________，使矩形是正方形（填一个即可）【答案】或【解析】根据正方形的判定定理可知：邻边相等的矩形是正方形，对角线互相垂直的矩形是正方形.∵邻边相等的矩形是正方形，∴可添加条件或者∵对角线互相垂直的矩形是正方形∴还可以添加条件【点拨】本题考查正方形的判定，找出正方形与矩形的性质差异，即为可添加的条件.14. 一个不透明的袋子中装有3个红球和2个白球，这些小球除标号外完全相同，随机摸出两个小球，恰好是一红一白的概率是__________．【答案】##0.6【解析】首先根据题意列出表格，然后由表格求得所有等可能的结果与随机摸出一红一白的情况，再利用概率公式即可求得答案．解：列表得：红1红2红3白1白2红1（红1，红2）（红1，红3）（红1，白1）（红1，白2）红2（红2，红1）（红2，红3）（红2，白1）（红2，白2）红3（红3，红1）（红3，红2）（红3，白1）（红3，白2）白1（白1，红1）（白1，红2）（白1，红3）（白1，白2）白2（白2，红1）（白2，红2）（白2，红3）（白2，白1）由列表可知：共有20种等可能的结果，其中随机摸出两个小球，恰好是一红一白的情况有12种，∴恰好是一红一白的概率是，故答案为：．【点拨】本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率＝所求情况数与总情况数之比．15. 关于的不等式组有3个整数解，则实数的取值范围是__________．【答案】##【解析】解不等式组，根据不等式组有3个整数解得出关于m的不等式组，进而可求得的取值范围．解：解不等式组得：，∵关于的不等式组有3个整数解，∴这3个整数解为，，，∴，解得：，故答案为：．【点拨】本题考查了解一元一次不等式组，一元一次不等式组的整数解，正确得出关于m的不等式组是解题的关键．16. 如图，是的直径，切于点A，交于点，连接，若，则__________．【答案】34【解析】首先根据等边对等角得到，然后利用外角的性质得到，利用切线的性质得到，最后利用三角形内角和定理求解即可．解：∵，，∴，∴，∵切于点A，∴，∴．故答案为：34．【点拨】此题考查了切线的性质和三角形的外角的性质，三角形内角和定理等知识，解题的关键是熟练掌握以上知识点．17. 已知圆锥的母线长，侧面积，则这个圆锥的高是__________．【答案】12【解析】利用圆锥的侧面积公式可得到底面半径，再利用勾股定理即可得到高．解：根据圆锥侧面积公式变形可得，根据圆锥母线公式，可得，故答案为：12．【点拨】本题考查了圆锥的侧面积公式和母线公式，熟知上述公式是解题的关键．18. 在中，，点是斜边的中点，把绕点顺时针旋转，得，点，点旋转后的对应点分别是点，点，连接，，在旋转的过程中，面积的最大值是__________．【答案】##【解析】过点A作交的延长线于点G，求出，然后由旋转的性质可知点F在以A为圆心的长为半径的圆上运动，则可得如图中G、A.F三点共线时点F到直线的距离最大，求出距离的最大值，然后计算即可．解：如图，在中，，，点是斜边的中点，∴，，，∴，过点A作交的延长线于点G，∴，又∵在旋转的过程中，点F在以A为圆心的长为半径的圆上运动，，∴点F到直线的距离的最大值为，（如图，G、A.F三点共线时）∴面积最大值，故答案为：．【点拨】本题考查了含直角三角形的性质，直角三角形斜边中线的性质，旋转的性质，圆的基本性质等知识，根据旋转的性质求出点F到直线距离的最大值是解答本题的关键．19. 矩形中，，将矩形沿过点的直线折叠，使点落在点处，若是直角三角形，则点到直线的距离是__________．【答案】6或或【解析】由折叠的性质可得点E在以点A为圆心，长为半径的圆上运动，延长交的另一侧于点E，则此时是直角三角形，易得点到直线的距离；当过点D的直线与圆相切于点E时，是直角三角形，分两种情况讨论即可求解．解：由题意矩形沿过点的直线折叠，使点落在点处，可知点E在以点A为圆心，长为半径的圆上运动，如图，延长交的另一侧于点E，则此时是直角三角形，点到直线的距离为的长度，即，当过点D的直线与圆相切与点E时，是直角三角形，分两种情况，①如图，过点E作交于点H，交于点G，∵四边形是矩形，∴，∴四边形是矩形，∵，，，由勾股定理可得，∵，∴，∴到直线的距离，②如图，过点E作交于点N，交于点M，∵四边形是矩形，∴，∴四边形是矩形，∵，，，由勾股定理可得，∵，∴，∴到直线的距离，综上，6或或，故答案为：6或或．【点拨】本题考查了矩形折叠问题切线的应用，以及勾股定理，找到点E 的运动轨迹是解题的关键．20. 如图，在平面直角坐标系中，的顶点A 在直线上，顶点B 在x 轴上，垂直轴，且，顶点在直线上，；过点作直线的垂线，垂足为，交x 轴于，过点作垂直x 轴，交于点，连接，得到第一个；过点作直线的垂线，垂足为，交x 轴于，过点作垂直x 轴，交于点，连接，得到第二个；如此下去，……，则的面积是__________．【答案】【解析】解直角三角形得出，，求出，证明，，得出，，总结得出，从而得出．解：∵，∴，∵轴，∴点A的横坐标为，∵，∴点A的纵坐标为，∴，∴，∵，∴设，则，∴，∴，∴，，∵，∴，∴平分，∵，，∴，∵，，∴，∴，∴，∴，∵，∴，∴，∵，，，∴，∴，∴，∴，，∵轴，轴，∴，，∵轴，轴，轴，∴，∴，，∵，∴，，∴，∵，∴，同理，∴，，∴，∴．故答案为：．【点拨】本题主要考查了三角形相似的判定和性质，解直角三角形，三角形面积的计算，平行线的判定和性质，一次函数规律探究，角平分线的性质，三角形全等的判定和性质，解题的关键是得出一般规律．三、解答题（满分60分）21. 先化简，再求值：，其中．【答案】，原式【解析】先根据分式的混合运算法则化简，然后求出，最后代值计算即可．解：，∵，∴原式．【点拨】本题主要考查了分式的化简求值，求特殊角三角函数值，正确计算是解题的关键．22. 如图，在平面直角坐标系中，已知的三个顶点坐标分别是，．（1）将向上平移4个单位，再向右平移1个单位，得到，请画出．（2）请画出关于轴对称的．（3）将着原点顺时针旋转，得到，求线段在旋转过程中扫过的面积（结果保留）．【答案】（1）见解析（2）见解析（3）【解析】（1）根据平移的性质得出对应点的位置进而画出图形；（2）利用轴对称的性质得出对应点的位置进而画出图形；（3）画出旋转后的图形，根据即可得出答案．（1）解：如图所示，即为所求；（2）如图所示，即为所求；（3）将着原点顺时针旋转，得到，，，，，，，，，，，故线段在旋转过程中扫过的面积为．【点拨】本题考查平移、轴对称变换作图和旋转的性质以及扇形的面积，熟练掌握网格结构准确找出对应点的位置是解题的关键．23. 如图，抛物线与轴交于两点，交轴于点．（1）求抛物线的解析式．（2）拋物线上是否存在一点，使得，若存在，请直接写出点的坐标；若不存在，请说明理由．【答案】（1）（2）存在，点的坐标为或【解析】（1）采用待定系数法，将点和点坐标直接代入抛物线，即可求得抛物线的解析式．（2）过线段的中点，且与平行的直线上的点与点，点连线组成的三角形的面积都等于，则此直线与抛物线的交点即为所求；求出此直线的解析式，与抛物线解析式联立，即可求得答案．（1）解：因为抛物线经过点和点两点，所以，解得，所以抛物线解析式为：．（2）解：如图，设线段的中点为，可知点的坐标为，过点作与平行的直线，假设与抛物线交于点，（在的左边），（在图中未能显示）．设直线的函数解析式为．因为直线经过点和，所以，解得，所以，直线的函数解析式为：．又，可设直线的函数解析式为，因为直线经过点，所以．解得．所以，直线的函数解析式为．根据题意可知，．又，所以，直线上任意一点与点，点连线组成的的面积都满足．所以，直线与抛物线的交点，即为所求，可得，化简，得，解得，所以，点的坐标为，点的坐标为．故答案为：存在，点的坐标为或．【点拨】本题主要考查二次函数的图象和性质、一次函数的图象和性质、一元二次方程、一元一次方程等，灵活结合二次函数和一次函数图象特点是解题的关键．24. 某中学开展主题为“垃圾分类，绿色生活”的宜传活动、为了解学生对垃圾分类知识的掌握情况，该校团委在校园内随机抽取了部分学生进行问卷调在，将他们的得分按A：优秀，B：良好，C：合格，D：不合格四个等级进行统计，并绘制了如下不完整的条形统计图和扇形统计图．（1）这次学校抽查的学生人数是__________人；（2）将条形图补充完整；（3）扇形统计图中C组对应的扇形圆心角度数是__________；（4）如果该校共有2200人，请估计该校不合格的人数．【答案】（1）40 （2）见解析（3）（4）220人【解析】（1）用A：优秀的人数除以其人数占比即可求出参与调查的学生人数；（2）先求出C：合格的人数，再补全统计图即可；（3）用360度乘以C组对应人数占比即可得到答案；（4）用2200乘以样本中D组对应的人数占比即可得到答案．（1）解：人，∴这次学校抽查的学生人数是人，故答案为：40；（2）解：由（1）得C：合格的人数为人，补全统计图如下所示：（3）解：，∴扇形统计图中C组对应的扇形圆心角度数是，故答案为：；（4）解：人，∴估计该校不合格的人数为220人．【点拨】本题主要考查了条形统计图与扇形统计图信息相关联，用样本估计总体，正确读懂统计图是解题的关键．25. 已知甲，乙两地相距，一辆出租车从甲地出发往返于甲乙两地，一辆货车沿同一条公路从乙地前往甲地，两车同时出发，货车途经服务区时，停下来装完货物后，发现此时与出租车相距，货车继续出发后与出租车相遇．出租车到达乙地后立即按原路返回，结果比货车早15分钟到达甲地．如图是两车距各自出发地的距离与货车行驶时间之间的函数图象，结合图象回答下列问题：（1）图中的值是__________；（2）求货车装完货物后驶往甲地的过程中，距其出发地的距离与行驶时间之间的函数关系式；（3）直接写出在出租车返回的行驶过程中，货车出发多长时间与出租车相距．【答案】（1）120 （2）（3）或【解析】（1）利用待定系数法求得的解析式，将代入解析式，解方程即可解答；（2）根据题意可得的值，即为货车装货时距离乙地的长度，结合货车停下来装完货物后，发现此时与出租车相距，可求出装货时间，即点的坐标，再根据货车继续出发后与出租车相遇，求出装完货后货车的速度，即直线的解析式中的值，最后将点B坐标代入直线的解析式，利用待定系数法即可解答；（3）根据（2）中直线的解析式求得点的坐标，结合题意，可得点的坐标，从而可得到出租车返回时的速度，然后进行分类讨论：①出租车和货车第二次相遇前，相距时；②出租车和货车第二次相遇后，距离时，分别进行解答即可．（1）解：结合图象，可得，设直线的解析式为，将代入解析式，可得，解得，直线的解析式为，把代入，得，故答案为：120；（2）解：根据货车停下来装完货物后，发现此时与出租车相距，可得此时出租车距离乙地为，出租车距离甲地为，把代入，可得，解得，货车装完货时，，可得，根据货车继续出发后与出租车相遇，可得（出租车的速度货车的速度），根据直线的解析式为，可得出租车的速度为，相遇时，货车的速度为，故可设直线的解析式为，将代入，可得，解得，直线的解析式为，故货车装完货物后驶往甲地的过程中，距其出发地的距离与行驶时间之间的函数关系式为；（3）解：把代入，可得，解得，，，根据出租车到达乙地后立即按原路返回，结果比货车早15分钟到达甲地，可得,，出租车返回时的速度为，设在出租车返回的行驶过程中，货车出发t小时，与出租车相距，此时货车距离乙地为，出租车距离乙地为，①出租车和货车第二次相遇前，相距时；可得，解得，②出租车和货车第二次相遇后，相距时；可得，解得，故在出租车返回的行驶过程中，货车出发或与出租车相距．【点拨】本题考查了从函数图象获取信息，用待定系数法求一次函数，一次函数的实际应用，能准确地理解题意，根据题中信息求得所需数据是解题的关键．26. 如图①，和是等边三角形，连接，点F，G，H分别是和的中点，连接．易证：．若和都是等腰直角三角形，且，如图②：若和都是等腰三角形，且，如图③：其他条件不变，判断和之间的数量关系，写出你的猜想，并利用图②或图③进行证明．【答案】图②中，图③中，证明见解析【解析】图②：如图②所示，连接，先由三角形中位线定理得到，，再证明得到，则，进一步证明，即可证明是等腰直角三角形，则；图③：仿照图②证明是等边三角形，则．解：图②中，图③中，图②证明如下：如图②所示，连接，∵点F，G分别是的中点，∴是的中位线，∴，同理可得，∵和都是等腰直角三角形，且，∴，∴，∴，∴，∵，∴，∴是等腰直角三角形，∴；图③证明如下：如图③所示，连接，∵点F，G分别是的中点，∴是的中位线，∴，同理可得，∵和都是等腰三角形，且，∴，∴，∴，∴，∵，∴，∴是等边三角形，∴．【点拨】本题主要考查了全等三角形的性质与判定，三角形中位线定理，等边三角形的性质与判定，勾股定理等等，正确作出辅助线构造全等三角形是解题的关键．27. 2023年5月30日上午9点31分，神舟十六号载人飞船在酒泉发射中心发射升空，某中学组织毕业班的同学到当地电视台演播大厅观看现场直播，学校准备为同学们购进A，B两款文化衫，每件A款文化衫比每件B款文化衫多10元，用500元购进A款和用400元购进B款的文化衫的数量相同．（1）求A款文化衫和B款文化衫每件各多少元？（2）已知毕业班的同学一共有300人，学校计划用不多于14800元，不少于14750元购买文化衫，求有几种购买方案？（3）在实际购买时，由于数量较多，商家让利销售，A款七折优惠，B款每件让利m元，采购人员发现（2）中的所有购买方案所需资金恰好相同，试求m值．【答案】（1）A款文化衫每件50元，则B款文化衫每件40元，（2）一共有六种购买方案（3）【解析】（1）设A款文化衫每件x元，则B款文化衫每件元，然后根据用500元购进A款和用400元购进B款的文化衫的数量相同列出方程求解即可；（2）设购买A款文化衫a件，则购买B款文化衫件，然后根据，学校计划用不多于14800元，不少于14750元购买文化衫列出不等式组求解即可；（3）设购买资金为W元，购买A款文化衫a件，则购买B款文化衫件，求出，根据（2）中的所有购买方案所需资金恰好相同，可得W的取值与a的值无关，由此即可求出．（1）解：设A款文化衫每件x元，则B款文化衫每件元，由题意得，，解得，检验，当时，，∴是原方程的解，∴，∴A款文化衫每件50元，则B款文化衫每件40元，答：A款文化衫每件50元，则B款文化衫每件40元；（2）解：设购买A款文化衫a件，则购买B款文化衫件，由题意得，，解得，∵a是正整数，∴a的取值可以为275，276，277，278，279，280，∴一共有六种购买方案；（3）解：设购买资金为W元，购买A款文化衫a件，则购买B款文化衫件，由题意得，，∵（2）中的所有购买方案所需资金恰好相同，∴W的取值与a的值无关，∴，∴．【点拨】本题主要考查了一元一次不等式组的实际应用，分式方程的实际应用，整式的加减的实际应用，正确理解题意列出方程和不等式组是解题的关键．28. 如图，在平面直角坐标系中，菱形的边在x轴上，，的长是一元二次方程的根，过点C作x轴的垂线，交对角线于点D，直线分别交x轴和y轴于点F 和点E，动点M从点O以每秒1个单位长度的速度沿向终点D运动，动点N从点F以每秒2个单位长度的速度沿向终点E运动．两点同时出发，设运动时间为t秒．（1）求直线的解析式．（2）连接，求的面积S与运动时间t的函数关系式．（3）点N在运动的过程中，在坐标平面内是否存在一点Q．使得以A，C，N，Q为项点的四边形是矩形．若存在，直接写出点Q的坐标，若不存在，说明理由．【答案】（1）；（2）；（3）存在，点Q的坐标是或．。

2003年数学中考试题分类汇编

2003年数学中考试题分类汇编方程与不等式：一、选择题：1. （甘肃毕）方程1242=+-x x 的根是 ( ) A 、x 1=－2，x 2=3 B 、 x 1=2，x 2=－3 C 、 x=3 D 、 x=－32.（荆门市）已知实数x 满足x 2＋21x＋ x ＋x 1 =0,那么x ＋x 1的值为（） A 、1或－2 B 、－1或2 C 、1 D 、－23.（大连市）一元二次方程x 2－4＝0的解是 ( )A 、x = 2B 、x =－2C 、x 1 = 2 ，x 2 = －2D 、x 1= 2，x 2 =－2，4．（龙江市）二元一次方程组⎩⎨⎧=+-=-1012y x y x 的解是（）A 、 ⎩⎨⎧==37x y B 、 ⎪⎩⎪⎨⎧==311319x y C 、⎩⎨⎧==28x y D 、⎩⎨⎧==73x y5.（娄底市）二元二次方程组⎩⎨⎧=-=+1522y x y x 的一个解是（）A 、⎩⎨⎧-=-=21y xB 、⎩⎨⎧=-=21y xC 、⎩⎨⎧-==21y xD 、⎩⎨⎧==21y x 6.（郴州市）一元二次方程x 2－2x ＝x 的根是（）A 、x 1＝0 x 2＝2B 、x 1＝0 x 2＝1C 、x 1＝0 x 2＝3D 、x 1＝0 x 2＝47．（金华市）方程x 3－4x=0的解是（）A 、－2，2B 、0，－2C 、0，2D 、0，－2，28.（大连市）一元二次方程x 2＋2x －1＝0的根的情况是( )A 、有两个不相等的实数根B 、有两个相等的实数根C 、没有实数根D 、不能确定9.（常州市）一元二次方程0422=-+y y 的根的情况是（）A 、有两个相等的实数根B 、有两个不相等的实数根，且两根同号C 、有两个不相等的实数根，且两根异号D 、没有实数根10.（龙江市）一元二次方程2x 2－4x ＋1=0根的情况是（）A 、有两个不相等的实数根B 、有两个相等的实数根C 、没有实数根D 、无法确定11．（常德市）对于一元二次方程3y 2 ＋5y —1=0，下列说法正确的是（）A 、方程无实数根B 、方程有两个相等的实数根C 、方程有两个不相等的实数根D 、方程的根无法确定12．（广西省）关于x 的方程02)13(22=-+-+m m x m x 的根的情况是（）A 、有两个相等的实数根B 、有两个不相等的实数根C 、没有实数根D 、有两个实数根13．（烟台市）对于方程022=-+bx x ，下面观点正确的是（）A 、方程有无实数根，要根据b 的取值而定B 、无论b 取何值，方程必有一正根、一负根C 、当b ＞0时．方程两根为正：b ＜0时．方程两根为负D 、∵ －2＜0，∴ 方程两根肯定为负14.（黄石市）方程2x 2＋4x －a 2=0的根的情况是A 、有两个相等的实根B 、无实根C 、有两个不相等的实根D 、只有正根15. （岳阳市）已知a 、b 、c 是△ABC 三边长的长，则方程04)(2=+++a x c b ax 的根的情况是（）A 、没有实数根B 、有两个不相等的正实数根C 、有两个不相等的负实数根D 、有两个异号的实数根16. （海淀区）方程x x 220-+=根的情况是（）A 、只有一个实数根B 、有两个相等的实数根C 、有两个不相等的实数根D 、没有实数根17．（四川省）一元二次方程04322=-+x x 的根的情况是（）A 、有两个相等的实数根 A 、有两个不相等的实数根C 、无实数根D 、不能确定18. （青岛市）方程12+-x x ＝0 的根的情况是（）．A 、有两个相等的实数根B 、有两个不相等的实数根C 、两个实数根的和与积都等于1D 、无实数根19．（武汉市）不解方程，判别方程05752=+-x x 的根的情况是（）A 、有两个相等的实数根B 、有两个不相等的实数根C 、只有一个实数根D 、没有实数根20. （黄冈市）关于x 的方程()011222=+-+x k x k 有实数根，则下列结论正确的是（）．A 、当k ＝21时方程两根互为相反数 A 、当k ＝0时方程的根是x ＝－1 C 、当k ＝士1时方程两根互为倒数 D 、当k ≤41时方程有实数根 21. （甘肃）方程3x 2＋4x ＝0 ( ) A 、只有一个根x 2＝－34 B 、只有一个根x 2＝0 C 、有两个根x 1＝0，x ＝34 D 、有两个根x 1=0，x ＝－342003年数学中考试题分类汇编方程与不等式第 3 页共 18 页整理刘立武22. （河南B ）如果关于x 的方程mx 2－2（m －1）x ＋m ＝0只有一个实数根，那么方程mx 2－（m＋2）x ＋（4－m ）＝0的根的情况是（）A 、没有实数根B 、有两个不相等的实数根C 、有两个相等的实数根D 、只有一个实数根23.（武汉市）一元二次方程012=-x 的根为（）A 、x ＝1 A 、x ＝－1 C 、x 1＝1，x 2＝－1 D 、x 1＝0，x 2＝124．（随州市）下列一元二次方程中无实数解的方程是（）A 、0232=-+x xB 、0322=+-x xC 、1)1(2=-xD 、02=-x x25.（重庆市）下列一元二次方程中，没有实数根的是（）A 、0122=-+x xB 、02222=++x xC 、0122=++x xD 、022=++-x x26. （甘肃省）下列方程中，关于x 的一元二次方程是（）A 、 ()()12132+=+x x ； B 、 02112=-+x x ； C 、 02=++c bx ax ； D 、 1222-=+x x x ；27．（绍兴市）一元二次方程0132=--x x 的两根为1x ,2x ,则1x ＋2x 的值是（）A 、3B 、－3C 、－1D 、128.（舟山市）若x 1，x 2是一元二次方程3x 2＋x ―1＝0的两个根，则2111x x +的值是（） A 、2 B 、1 C 、―1 D 、329. （泉州市）一元二次方程x 2－5x ＋2=0的两个根为x 1 , x 2 ，则x 1＋x 2等于（）A 、 –2B 、 2C 、 –5D 、 530. （太原市）设方程x 2＋x －1＝0的两个实数根分别为x 1、x 2，则2111x x +的值为（） A 、1 B 、－1 C 、5 D 、55 31. （青海省）设1x 、2x 是方程03622=+-x x 的两个根，那么2221x x +的值为（） A 、3 B 、－3 C 、6 D 、－632．（宁夏）一元二次方程032=--x x 的两个根的倒数和等于（） A 、31-B 、－3C 、31 D 、3 33. （南京市）如果一元二次方程0232=-x x 的两个根是x 1，x 2，那么x 1·x 2等于（） A 、2 B 、0 C 、32 D 、－32 34. （甘肃）如果关于x 的方程2x 2＋6kx ＋5k 2＋2=0有两个相等的实数根,那么k 为 ( ) A 、2 B 、－3 C 、4 D 、－535. （海南省）已知x ＝－1是一元二次方程012=++mx x 的一个根，那么 m 的值是（）．A 、0B 、1C 、2D 、一236．（仙桃市）如果方程x 2＋2x ＋m ＝0有两个同号的实数根，则m 的取值范围是（）A 、 m ＜1B 、0＜m ≤1C 、0≤m ＜1D 、m ＞037.（黄埔区）已知关于x 的方程022=++a x x 的两个根的差的平方等于16，那么a 的值为（）A 、－3B 、－6C 、3D 、638．（泰州市）一元二次方程012)1(2=---x x k 有两个不相等的实数根，则k 的取值范围是（）A 、2>kB 、12≠<k k 且C 、2<kD 、12≠>k k 且39. （岳阳市）设方程2x 2－（k ＋1）x ＋k ＋3＝0的两根之差为1，则k 的值是（）A 、9和－3B 、9和3C 、－9和3D 、－9和－340．（湖州市）已知关于x 的方程022=+-m x x 有实数根，则m 的取值范围是（）A 、m ≤－1B 、m ≥－1C 、m ≤1D 、m ≥141. （北京市）如果关于x 的一元二次方程kx 2－6x ＋9=0有两个不相等的实数根，那么k 的取值范围是A 、 k ＜1B 、 k ≠0C 、 k k <≠10且D 、 k ＞142．（辽宁省）已知2是关于x 的方程02232=-a x 的一个根，则2a －1的值是（） A 、3 B 、4 C 、5 D 、643．（辽宁省）关于x 的方程x 2＋2k x ＋1＝0有两个不相等的实数根，则k 的取值范围是（）A ．k ＞－1B ．k ≥－1C ．k ＞1D ．k ≥044. （吉林省）关于x 的一元二次方程()02222=+--m x m x 有两个不相等的实数根，则m的取值范围是（）．A 、m ＞1B 、m ＜1C 、m ＞lD 、m ＜－l45. （陕西省）方程()912=+x 的解是（）． A 、x ＝2 B 、x ＝一4 C 、x 1＝2，x 2＝－4 D 、x 1＝－2，x 2＝－446. （甘肃省）已知3是关于x 的方程012342=+-a x 的一个解，则2a 的值是（） A 、11 B 、12 C 、13 D 、1447. （青岛市）已知012=-+αα，012=-+ββ，且α≠β，则βααβ++的值为（）．A 、2B 、一2C 、一1D 、048.（福州市）已知α、β满足α＋β＝5且αβ＝6，以α、β为两根的一元二次方程是（）A 、0652=++x x A 、0652=+-x xC 、0652=--x xD 、0652=-+x x49. （杭州市）设1x ，2x 是关于x 的方程02=++q px x 的两根，11+x ，12+x 是关于x 的方程02=++p qx x 的两根，则p ，q 的值分别等于（） A 、1，－3 A 、1，3 C 、－1，－3 D 、－1，32003年数学中考试题分类汇编方程与不等式第 5 页共 18 页整理刘立武50. （桂林市）如果关于x 的一元二次方程02=++q px x 的两根分别为1x ＝3、2x ＝1，那么这个一元二次方程是（）．A 、0432=++x x A 、0342=+-x xC 、0342=-+x xD 、0432=-+x x51．（南宁市）已知一元二次方程0232=+-a x x 有实数根，则a 的取值范围是（）A 、a ≤31 A 、a ＜31 C 、a ≤31- D 、 a ≥31 52.（深圳市）已知一元二次方程2x 2－3x －6=0有两个实数根x 1、x 2，直线l 经过点A （x 1＋x 2，0）、B （0，x 1·x 2），则直线l 的解析式为A 、y=2x －3B 、y=2x ＋3C 、y=－2x －3D 、y=－2x ＋3 53．（南宁市）二元一次方程组⎩⎨⎧=+-=+522y x y x 的解是（） A 、⎩⎨⎧==61y x A 、⎩⎨⎧=-=41y x C 、⎩⎨⎧=-=23y x D 、⎩⎨⎧==23y x 54．（宁波市）已知x －y=4，| x|＋| y|=7，那么x ＋y 的值是( )A 、±23B 、±211 C 、±7 D 、±11 55．（盐城市）如果分式方程1x m 1x x +=+无解，则m=（） A 、1 B 、0 C 、－1 D 、－256．（杨州市）已知a －b ＝3，b ＋c ＝5，则代数式ac －bc ＋a 2－ab 的值是（）A 、－15B 、－２C 、－６D 、６57、（黄埔区）若代数式7322++y y 的值为8，那么9642-+y y 的值是（）A 、2B 、－17C 、－7D 、758. （烟台市）若3x －2y ＝0，则yx 等于（） A 、32 B 、23 C 、32- D 、32或无意义 59．（烟台市）已知x 为实数，且()033322=+-+x x x x ，那么x x 32+的值为（） A 、1 B 、－3或1 C 、3 D 、－1或360．（温州市）方程2x ＋1=5的根是( )A 、4B 、3C 、2D 、161．（金华市）下列各个方程中，无解的方程是（）A 、12-=+xB 、3（x －2）＋1=0C 、x 2－1=0D 、21=-x x 62. （南京市）已知⎩⎨⎧==12y x 是方程kx －y=3的解，那么k 的值是（） A 、2 B 、－2 C 、1 D 、－163. （南京市）如果2)2(-x ＝x －2，那么x 的取值范围是（）A 、x ≤2B 、x ＜2C 、x ≥2D 、x ＞264．（广东省）关于x 的方程2（x －1）－a ＝0的根是3，则a 的值为（）A 、4B 、－4C 、5D 、－565．（广州市）将方程132142+-=+-x x x 去分母并化简后得到的方程是（） A 、0322=--x x B 、0522=--x xC 、032=-xD 、052=-x 66、（黄埔区）用换元法解方程用换元法解方程31221122=++-++x x x x 时，下列换元方法中最适宜的是（） A 、 y x =+12B 、 y x =+112C 、 y x =+11D 、 y x x =++112 67. （郴州市）解方程526222=+-+x x x x 时，令x x y 22+=，原方程可化为（） A 、y 2－5y －6＝0 B 、y 2－6y －5＝0 C 、y 2＋5y －6＝0 D 、y 2＋6y －5＝068. （三明市）如果将方程32)2(22222=+++++x x x x 变形为32=+y y ，下列换元正确的是（）A 、y x =+212B 、y x x =+222C 、y x x =+22D 、y x x =++222 69.（海淀区）用换元法解方程()()x x x x +-+=2212，设y x x =+2，则原方程可化为（） A 、 y y 210--=B 、 y y 210++=C 、 y y 210+-=D 、 y y 210-+= 70. （南京市）用换元法解方程x 2＋x ＋1＝xx +22，如果设x 2＋x ＝y ，那么原方程可变形为（） A 、y 2＋y ＋2＝0 B 、y 2－y －2＝0C 、 y 2－y ＋2＝0D 、y 2＋y －2＝071．（武汉市）用换元法解方程061512=+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-x x x x 时，设y x x =-1，则原方程化为关于y 的方程是（）A 、0652=++y y A 、0652=+-y yC 、0652=-+y yD 、0652=--y y2003年数学中考试题分类汇编方程与不等式第 7 页共 18 页整理刘立武72．（昆明市）解分式方程032222=+---x x x x 时，设y x x =-22，则原方程变形为（） A 、0132=++y y A 、0132=+-y y C 、0132=--y y D 、0132=-+y y73．（淮安市）用换元法解方程：0132322=++-+xx x x .若设y x x =+32，则原方程可变形为（）A 、y 2－2y ＋1=0B 、y 2＋2y －1=0C 、y 2－y ＋2=0D 、y 2＋y －2=074．（龙江市）我省为了解决药品价格过高的问题，决定大幅度降低药品价格，其中将原价为a元的某种常用药降价40%，则降价后此格为（）A 、元4.0aB 、元6.0a C 、60%a 元 D 、40%a 元 75．（淮安市）某学校用420元钱到商场去购买“84”消毒液，经过还价，每瓶便宜0.5元，结果比用原价多买了20瓶，求原价每瓶多少元？若设原价每瓶x 元，则可列出方程为（）A 、205.0420420=--x x B 、204205.0420=--xx C 、5.020420420=--x x D 、5.042020420=--x x 76．（泰安市）一种商品每件进价为a 元，按进价增加25%定出售价，后因库存积压降价，按售价的九折出售，每件还能盈利（）A 、0.125a 元B 、0.15a 元C 、0.25a 元D 、1.25a 元77.（河北省）赵强同学借了一本书，共280页，要在两周借期内读完，当他读了一半时，发现平均每天要多读21页才能在借期内读完，他读前一半时，平均每天读多少页？如果设读前一半时，平均每天读x 页，则下面所列方程中，正确的是（）A 、1421140140=-+x xB 、1421280280=++x xC 、1421140140=++x xD 、1211010=++x x78. （江西省）张老师和李老师同时从学校出发，步行15千米去县城购买书籍，张老师比李老师每小时多走1千米、结果比李老师早到半小时，两位老师每小时各走多少千米？设李老师每小时走x 千米，依题意，得到的方程是（）．A 、2115115=-+x x A 、2111515=+-x x C 、 2115115=--x x D 、2111515=--x x 79. （杭州市）某种型号的空调器经过3次降价，价格比原来下降了30%，则其平均每次下降的百分比（精确到1%）应该是（）（A ）26.0% （B ）33.1% （C ）8.5% （D ）11.2%80.（福州市）不等式组⎩⎨⎧>+≥0342x x 的解集是（）A 、x ＞－3 A 、x ≥2 C 、－3＜x ≤2 D 、x ＜－381. （长沙市）不等式组⎩⎨⎧<->+01042x x 的解集为（）．A 、 x ＞1 或x ＜－2 A 、 x ＞1 C 、－2＜x ＜1 D 、 x ＜－282. （盐城市）若0＜a ＜1,则下列四个不等式中正确的是A 、a 11a << B 、 1a 1a << C 、 1a a 1<< D 、 a a 11<<83.（闵行区）下列不等式组无解的是（）A 、⎩⎨⎧<+<-0201x x B 、⎩⎨⎧>+<-0201x x C 、⎩⎨⎧<+>-o x x 201 D 、⎩⎨⎧>+>-0201x x 84. （太原市）不等式组的解集是（）A 、无解B 、x ≤2C 、x ≥－3D 、－3≤x ≤285．（随州市）若a ＜0，关于x 的不等式1+ax ＞0的解集是（）A 、a x 1-< B 、a x 1-> C 、a x 1< D 、a x 1>86. （岳阳市）若代数式52-x的值大于－5且小于1，则x 的取值范围是（）A 、x ＜0B 、0＜x ＜12C 、x ＞12D 、x ＜0或x ＞1287．（金华市）不等式3x －2≥0的解是（）A 、x ≥32B 、x ＞32C 、x ＜32D 、x ≤3288．（泰安市）关于x 的不等式组⎪⎩⎪⎨⎧+〉++-〈ax x x x 4231)3(32，有四个整数解，则a 的取值范围是（）A 、411-＜a ≤25-B 、411-≤a ＜25-C 、411-≤a ≤25-D 、411-＜a ＜25-89．（青海省）如图2，不等式组⎩⎨⎧〉+≤0212x x 的解集在数轴上可表示为（）A 、B 、C 、D 、90．（宁夏）不等式2－x ＜1的解集是（）A 、x ＞－1B 、x ＞1C 、x ＜1D 、x ＜－191．（四川省）不等式组⎩⎨⎧〈-≤-321x x 的解集是（）A 、x ≥－1 A 、x ＜5 C 、－1≤x ＜5 D 、x ≤－1或x ＞592. （厦门市）不等式32-x ≥0的解集是（）．A 、x ≥23B 、x ＞23C 、x ＜32D 、x ≤232003年数学中考试题分类汇编方程与不等式第 9 页共 18 页整理刘立武93. （海淀区）不等式组⎩⎨⎧->+<-35062x x 的解集是（） A 、 23<<xB 、 -<<-83xC 、 -<<83xD 、 x <-8或x >394. （陕西省）把不等式组⎩⎨⎧<-≥+0101x x 的解集表示在数轴上，正确的是（）．95．（桂林市）不等式组⎩⎨⎧><35x x 的解集在数轴上表示，正确的是（）．96、（常州市）已知关于x 的不等式32->-m x 的解集如图所示，则m 的值为（） A 、2 B 、1 C 、0 D 、－197．（烟台市）不等式ax ＞b 的解集是x ＜ab ，那么a 的取值范围是（） A 、a ≤0 B 、a＜0 C 、a ≥0 D 、a ＞0二、填空题：1.（荆州市）方程组⎩⎨⎧=+=++224)2(2y x y x x 的解是2.（常州市）已知一元二次方程0132=--x x 的两个根是1x ，2x ，则=+21x x ，=21x x ，=+2111x x . 3. （杨州市）x=－2是方程2x ＋k －1＝0的根，则k .4. （甘肃省）方程031322=--x x 的根是＿＿＿＿＿＿＿＿＿＿. 5.（常州市）请写出一个根为1=x ，另一根满足11<<-x 的一元二次方程 .6. （无锡市）若⎩⎨⎧==12y x 是关于x 、y 的方程2x －y ＋3k ＝0的解，则k ＝ . 7．（宁波市）若方程2x 2－3x －4＝0的两根为x l ，x 2，则x 1·x 2＝．8．（泰州市）以3 和－2为根的一元二次方程是______________________. A 、B 、C 、D 、 A 、 B 、 C 、D 、9. （徐州市）如果方程032=+-m x x 有实数根，则m 的取值范围是；若方程有一个根为2，则另一个根为，m ＝； 10.（泉州市）在方程01314312=+⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛+-x x x x 中，如果设31+-=x x y ，那么原方程可以化为关于y 的整式方程是 .11. （海南省）已知x 1、x 2是关于x 的一元二次方程()013222=+--x a x a 的两个实数根，如果21122-=+xx ，那么a 的值是 . 12.（闵行区）如果x 1、x 2是方程x 2－5x ＋6＝0的两个根，那么x 1·x 2＝ .13．（广西省）如果方程02=++q px x 的两根分别为12-，12+，那么p ＝，q＝ .14.（南通市）若关于x 的方程()0471222=-+-+k x k x 有两个相等的实数根，则k ＝ . 15. （太原市）方程xx -=7143的解为＿＿＿＿＿＿＿＿＿. 16．（温州市）已知x l 和x 2是一元二次方程x 2－3x －l ＝0的两根，那么x 1x 2＝．17. （温州市）已知x ＋y ＋z ＝0，则222222222111yx z x z y z y x -++-++-+＝＿＿. 18. （龙岩市）已知方程04422=--+-xx x x ，令x 2－x ＝t ，则原方程可化为关于t 的一元二次方程是＿＿＿＿＿＿＿＿＿＿＿＿＿＿.19. （三明市）方程x 2＋2x ＋k ＝0有两个不相等的实数根，则k 的取值范围是＿＿＿＿＿.20．（贵阳市）若x ＝1是方程2x ＋a ＝0的根，则a ＝．21. （贵阳市）若关于x 的一元二次方程()()0112122=++-+x m x m 有实数根，则m 的取值范围是 .22. （湖州市）已知1x ，2x 是方程0172=--x x 的两个实数根，则1x ＋2x ＝．23．（荔湾区）当=a ＿＿＿＿＿时，方程02=++a x x 必有两个相等实数根.24．（随州市）已知1x ，2x 是方程0132=--x x 的两根，则)1)(1(21++x x 的值等于 .25. （泰安市）已知实数x 、y 满足0624422=-++++y x y xy x ，则x ＋2y 的值为 .27.（泰安市）已知关于x 的方程022222=+-+-a a ax x 的两个实数根1x 、2x 满足22221=+x x ，则a 的值为 . 28．（常德市）方程X ２－3X ＝0的根为________.29.（重庆市）已知1x 、2x 是关于x 的方程01)1(22=-++-a x x a 的两个实数根，且1x ＋2x2003年数学中考试题分类汇编方程与不等式第 11 页共 18 页整理刘立武＝31，则21x x ⋅＝ . 30．（辽宁省）若方程x 2＋x －1＝0的两根分别为x 1、x 2，则2221x x +2212x x +＝＿＿＿＿．31.（上海市）方程x x -=++22的根是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.32.（闵行区）方程3-x ＝2的解是＿＿＿＿＿＿＿＿＿＿＿＿＿＿. 33．（辽宁省）用换元法解方程8320322=+-+xx x x ，若设x 2＋3x ＝y ，则原方程可化成关于y的整式方程为．34. （吉林省）已知一元二次方程0652=--x x 的两个根分别为x 1，x 2，则2221x x +＝；35. （黑龙江）写出满足方程92=+y x 的一对整数值 .36.（河北省）在解方程322122-=+-x x x x 时，如果设x x y 22-=，那么原方程可化为关于y 的一元二次方程的一般形式是 .37．（郑州市）若关于x 的一元二次方程02=++n mx x 有两个实数根，则符合条件的一组m 、n 的实数值可以是m=______,n=________. 38．（郑州市）若0)1(32=+-+-y x x ，计算4322y xy y x ++=_______________. 39．（郑州市）一元二次方程032=--a ax x 的两根之和为2a －1，则两根之积为_________. 40. （河南B ）若二元一次方程组⎩⎨⎧=-=+7233y x y x 的解是某个一元二次方程的两个根，则这个一元二次方程是＿＿＿＿＿＿＿＿＿＿＿＿＿ .41. （甘肃省）关于x 的一元二次方程0122=++kx x 有两个相等的实根，则k＝；42. （甘肃省）已知抛物线c bx ax y ++=2的图象与x 轴有两个交点，那么一元二次方程02=++c bx ax 的根的情况是；43.（四川省）已知关于x 的一元二次方程8x 2＋（m ＋1）x ＋m －7＝0有两个负数根，那么实数m 的取值范围是_________________________；44．（建设兵团）不解方程，判别方程5（2x －1）－x ＝0的根的情况是 . 45. （建设兵团）已知方程022=+-k x x 的两根的倒数和是38，则k ＝ .46. （呼和浩特）解方程06)2(5)2(2=++-+x x x x ，其解为＿＿＿＿＿＿＿＿＿.47. （呼和浩特）若m 是实数，则关于x 的方程x 2－mx ＋22m ＋m ＋23＝0的根的情况是＿＿＿＿＿＿＿＿＿.48．（昆明市）如果一元二次方程022=+-k x x 有两个不相等的实数根，那么大的取值范围是 .49. （长沙市）关于x 的方程042=+-k x x 有两个相等的实数根，则实数a 的值为；50. （肇庆市）某种货物的零售价为每件110元，若按八折（零售价的80%）出售，仍可获利10%，则该货物每件和进价为_____________元.51. （龙岩市）某项工程，甲乙两队合做6天可以完成，若甲独做需x 天完成，乙独做比甲多作4天，要求出x 的值，可列出只含x 的方程求解，则列出的方程是＿＿＿＿＿＿＿.52.（山东省）某工厂2002年的年产值为＿26＿948万元，比＿2001年增长8.2％，若年增长率保持不变，预计2005年该厂的年产值为＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿万元（结果精确到万元），53.（烟台市）某工厂2002年的年产值为26948万元，比2001年增长8.2%，若年增长率保持不变，预计2005年该厂的年产值为_________万元(结果精确到万元)．54.（黄石市）抗击“SARS ”期间，某“SARS ”高发在区平均每天投入资金1800万元，用科学记数法表示这一地区60天投入资金总额约为＿＿＿＿＿＿＿＿＿＿＿＿万元. 55.（大连市）某房屋开发公司经过几年的不懈努力，开发建设住宅面积由2000年4万平方米，到2002年的7万平方米.设这两年该房屋开发公司开发建设住宅面积的年平均增长率为x ＿，则可列方程为______________；56.（泉州市）一种商品每件成本100元，按成本增加20%定出价格，则每件商品的价格是＿＿＿＿＿元.57.（娄底市）某种商品的标价为220元，为了吸引顾客，按9折出售，这时仍可盈利10%，则这种商品的进价是＿＿＿＿＿元. 58．（青海省）一年定期的存款，年息为1.98％，到期取款时需扣除利息的20％作为利息税上缴国库，假如某人存入一年的定期储蓄2000元，到期后可得本息和是＿＿＿元.59.（吉林省）某商品的标价是1100元，打八折（按标价的80％）出售，仍可获利10％，则此商品的进价是＿＿＿＿＿＿＿＿＿＿＿＿元．60.（荆门市）不等式1≤3x －7<5的整数解是 . 61.（郴州市）不等式：2x ＞x ＋3的解集是＿＿＿＿＿＿＿＿＿.62. （杨州市）不等式组⎪⎩⎪⎨⎧-><xx x 3214的解集是＿＿＿＿＿＿＿＿＿.63.（徐州市）不等式组⎩⎨⎧<->-0102x x 的解集是；64.（娄底市）不等式⎩⎨⎧<->+0102x x 的解集是＿＿＿＿＿＿＿＿＿ .65．（广西省）不等式组⎩⎨⎧≥->-0301x x 的整数解是 .2003年数学中考试题分类汇编方程与不等式第 13 页共 18 页整理刘立武66. （天津市）不等式组⎩⎨⎧-≤-->+2334)1(223x x x x ，的解集是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.67、（重庆市）已知关于x 的不等式组⎩⎨⎧>--≥-0125a x x 无解，则a 的取值范围是 .68.（河北省）不等式组⎩⎨⎧-<+>-148012x x x 的解集为 .69. （吉林省）不等式组⎩⎨⎧<-<-0120x x 的解集是；70．（贵阳市）不等式组：⎩⎨⎧-><-43x x 的解集为．71.（嘉兴市）不等式组⎩⎨⎧>+<0342x x 的解是_________.72．（河南C ）不等式组⎪⎪⎩⎪⎪⎨⎧+<->--21312,221x x x x 的整数解是___________________________. 73．（广东省）不等式组⎩⎨⎧≥++〈x x xx 1443的解集为 .三、解答题：1. （盐城市）解方程：xx 21x x 22-=--.2. （杨州市）解方程：113162=---x x 3．（宁波市）解方程：x+4-x =4． 4．（泰州市）用换元法解方程 xx x x +=++2221.5. （徐州市）解方程：0314122=--+⎪⎭⎫⎝⎛-x x x x 6.（闵行区）解方程：412)2(3212=-+++-x x x x 7. （仙桃市）解方程 0312)1(22=----x xx x8. （南通市）解方程：2121222=-+-x xx x ； 9．（湖州市）解方程：128822=+++x x x x10、（嘉兴市）解方程22=+-x x11．（荔湾区）解分式方程：153142-+=-+x x x 12. （肇庆市）解方程：223011x x x x ⎛⎫⎛⎫--= ⎪ ⎪--⎝⎭⎝⎭13. （北京市）用换元法解方程x 2-3x+5+2603x x=-14. （天津市）解方程1622++=+x x xx15．（郑州市）解方程1622-+-=x xx x 16．（河南C ）解方程31234222=----x x x x . 17．（河南C ）解方程：1622++=+x x xx 18. （陕西省）用换元法解方程081212=-⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+x x x x ；19. （甘肃省）用换元法解方程：()()7136312=-+++-x x x x ； 20.（安徽省）解方程：312122=+++x x x x21．（建设兵团）用配方法解方程 0762=++x x22．（哈尔滨）用换元法解方程：253322=-+-x x x x23. （黄冈市）解方程：()()122216=---+x x x 24. （昆明市）解方程：2223--=-x xx 25、（舟山市）解方程组：⎩⎨⎧=+=+11322y x y x26. （甘肃省）解方程组⎩⎨⎧=----=0123122x y x x y 27、（黄埔区）解方程组：⎩⎨⎧-=+=+38131322xy x x y28．（温州市）解方程组⎪⎩⎪⎨⎧==x -41-y 1y 1-x2003年数学中考试题分类汇编方程与不等式第 15 页共 18 页整理刘立武29. （岳阳市）解方程组⎩⎨⎧=+=+17522y x y x 30．（金华市）解方程组：⎩⎨⎧=-=-21622y x y x31．（随州市）解方程组：⎩⎨⎧=-++=0162322y xy x xy 32. （青岛市）解方程组：⎩⎨⎧==+127xy y x33. （南京市）解方程组⎪⎩⎪⎨⎧=+=-12202xy x y x .34. （杭州市）解方程组：⎪⎩⎪⎨⎧=+=-++12512y x y x35．（广州市）解方程组⎩⎨⎧=++=--03201222y xy x y x 36. （长沙市）解方程：12212=++-x x 37. （上海市）解方程组：⎪⎩⎪⎨⎧=+-=-.04,04222xy x y x38.（大连市）解方程组.⎩⎨⎧-=-=+124y x y x39.（常州市）解方程组：⎩⎨⎧=---=-01023122y x x y x40. （龙岩市）已知，x 1，x 2是关于x 的方各x 2－kx ＋k －1＝0的两个实根，求：y ＝（x 1－2x 2）（2x 1－x 2）25. （盐城市）已知关于x 的方程x 2+2(2-m )x +3-6m =0⑴求证:无论m 取什么实数，方程总有实数根；⑵如果方程的两个实数根x 1、x 2满足x 1=3x 2，求实数m 的值.41.（荔湾区）已知关于未知数x 的方程01322=-+-m x x ，⑴求使原方程有实数根的m 的取值范围.⑵试写出一个m 值，使原方程两根中一个大于2，一个小于2，并解这个方程. 42. （黑龙江）关于x 的方程()0412=+++kx k kx 有两个不相等的实数根． ⑴求 k 的取值范围；⑵是否存在实数k ，使方程的两个实数根的倒数和等于0？若存在，求出 k 的值；若不存在，说明理由．43．（河南C ）已知关于x 的方程012)14(2=-+++k x k x .⑴求证：该方程一定有两个不相等的实数根；⑵若x 1、x 2是两个实数根，且32)2)(2(21-=--k x x ，求k 的值. 44、（福州市）已知关于x 的方程()0141122=+++-k x k x .⑴k 取什么值时，方程有两个实数根； ⑵如果方程的两个实数根1x 、2x 满足21x x =，求k 的值.45．（杨州市）已知关于x 的方程x 2－（2k －3）x ＋k 2＋1＝0， ⑴ 当k 为何值时，此方程有实数根；⑵ 若此方程的两实数根x 1，x 2满足：｜x 1｜＋｜x 2｜＝3，求k 的值.46. （绍兴市）已知关于x 的方程0122=-+-k x x 有两个不相等的实数根，求k 的取值范围.47. （南通市）设方程组⎩⎨⎧-==--1202x y y x x 的解是⎩⎨⎧==11y y x x ；⎩⎨⎧==22y y x x .求2111x x +和21y y ⋅的值.48.（太原市）正数m 为何值时，方程组⎩⎨⎧+-==+2222mx y y x 只有一个实数解？并求出这时方程组的解.49.（龙岩市）已知：关于x ，y 的方程组⎩⎨⎧-=+=-133k y x k y x 的解满足⎩⎨⎧<>0y x 求k 的取值范围.50. （济南市）已知方程组⎩⎨⎧=+-=++-01022y x a y x 的两个解为⎩⎨⎧==11y y x x 和⎩⎨⎧==22y y x x 且1x 、2x 是两个不相等的实数，若116832212221--=-+a a x x x x ， ⑴ 求a 的值；⑵ 不解方程组判断方程组的两个解能否都是正数，为什么？ 51. （呼和浩特）已知关于x 、y 的方程组⎩⎨⎧=++=-ay x a y x 523的解满足x ＞y ＞0，化简｜a ｜＋｜3－a ｜52.已知方程组⎩⎨⎧+==mx y x y 22有两个实数解⎩⎨⎧==11y y x x 和⎩⎨⎧==22y y x x ，且231121=+x x ，求m 的值53. （肇庆市）已知关于x 的方程22(2)(23)10k x k x ++-+=，其中k 为常数，试分析此方程的根的情况.2003年数学中考试题分类汇编方程与不等式第 17 页共 18 页整理刘立武54.（重庆市）已知x ＝3是方程1210=++xkx 的一个根，求k 的值和方程其余的根.55. （陕西省）设x 1，x 2是关于x 的方程()012=---m x m x （m ≠0）的两个根，且满足0321121=++x x ，求m 的值． 56. （北京市）已知：关于x 的方程x 2-2mx+3m=的两个实数根是x 1,x 2，且(x 1-x 2)2=16.如果关于x 的另一个方程x 2-2mx+6m-9=0的两个实数根都在x 1和x 2之间，求m 的值. 57. （江西省）已知关于x 的方程x m x 22=-有两个不相等的实数根，求m 的取值范围． 58. （南昌市）已知关于x 方程m x mx =--11有实数根，求m 的取值范围.59．（广东省）已知1x ，2x 为方程02=++q px x 的两根，且1x +2x ＝6，202221=+x x ，求p 和q 的值．60.．（广东省）在公式h b a S )(21+=中，已知h 、s 、b ．求a ． 61.（无锡市）解不等式：35123->--x x 62．（镇江市）解不等式：12123x x ++≥ 63.（常州市）解不等式组：⎪⎩⎪⎨⎧>-+<+02)8(21042x x64. （盐城市）解不等式组⎪⎩⎪⎨⎧+<-≥--21x 51x 24)2x (3x ，并把解集在数轴上表示出来.65．（龙江市）解不等式组⎩⎨⎧<-<+-0520)1(2x x x 并解集在数轴上表示出来.66．（常德市）解不等式组：⎪⎩⎪⎨⎧-≤--->+ ⑵ ⑴1)3(2531222x x x x 并把它的解集在数轴上表示出来.67．（泉州市）解不等式组：⎪⎩⎪⎨⎧<+>-3)4(21012x x68．（淮安市）解不等式组：⎪⎩⎪⎨⎧>->+321052x x x69. （三明市）解不等式组⎪⎩⎪⎨⎧-<+≤+ ② ①3128)2(3x x x x70.（十堰市）解不等式组⎪⎩⎪⎨⎧-≤-+xx x x 9963449323 并把它的解集在数轴上表示出来.71.（安徽省）解不等式组：()⎪⎩⎪⎨⎧<--<-3221121x x72. （三明市）已知两个和等于2，积等于－1，求这两个数.73. （太原市）我市某购物中心今年三月份的营业额为500万元，四月份的营业额比三月份减少10%，从五月份起逐月上升，六月份达到648万元，求五、六月份营业额的月平均增长率.74.（大连市）某工厂贮存240吨煤，由于改进炉灶木结构和烧煤技术，每天能节约2吨煤，使贮存的煤比原计划多用4天.问原计划每天烧煤多少吨？75.（荆州市）一自行车队进行训练，训练的路程是55千米，出发后所有队员都保持相同的速度前进，行进一段路程后，1号队员将速度提高10千米超出队伍，当其余队员又前进20千米后，2号队员的速度也提高了10千米，结果2号队员比1号队员晚101小时到达终点，问车队从出发至最后的队员到达终点所花的时间是多少？76.（舟山市）如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a 为10米），围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB 为x 米，面积为S 米2， ⑴求S 与x 的函数关系式⑵如果要围成面积为45米2的花圃，AB 的长是多少米？⑶能围成面积比45米2更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由77．（常德市）学校存煤50吨，由于改进炉灶结构和烧煤技术后，每天能节约煤100千克，已知所存的煤比原计划多烧25天，问原计划每天烧煤多少千克？78.（大连市）某地区现在有果树12000棵，计划今后每年栽果树2000棵. ⑴求果树总数y(棵)与年数x(年)的函数关系式； ⑵预计到第5年该地区有多少棵果树？。

2023年黑龙江省哈尔滨市中考数学真题试卷(解析版)

2023年黑龙江省哈尔滨市中考数学真题试卷及答案一、选择题（每小题3分，共计30分）1. 的绝对值是( )A. B. 10 C. D.【答案】A【解析】根据“正数的绝对值是它本身，0的绝对值为0，负数的绝对值是它的相反数”求解即可．解：因为为负数，所以的绝对值为，故选A．【点拨】本题主要考查求绝对值，掌握“正数的绝对值是它本身，0的绝对值为0，负数的绝对值是它的相反数”是解题的关键．2. 下列运算一定正确的是（）A. B. C. D.【答案】D【解析】根据积的乘方、同类项的定义、幂的乘方和平方差公式逐一判断即可．A．，故本选项原说法错误；B．，故本选项原说法错误；C．，故本选项原说法错误；D．，故本选项正确．故选D．【点拨】此题考查的是幂的运算性质和整式的运算，掌握积的乘方、合并同类项和幂的乘方是解决此题的关键．3. 下列图形中，既是轴对称图形，又是中心对称图形的是（）A. B. C. D.【答案】A【解析】如果一个图形沿着某条直线对折后，直线两旁的部分能够重合，则称这个图形是轴对称图形，这条直线叫做对称轴；中心对称是旋转后与原图重合的图形，根据轴对称图形和中心对称图形的定义进行判断．解：A．既是轴对称图形，又是中心对称图形，故本选项符合题意；B．是轴对称图形，不是中心对称图形，故本选项不符合题意；C．不是轴对称图形，也不是中心对称图形，故本选项不符合题意；D．不是轴对称图形，是中心对称图形，故本选项不符合题意．故选：A．【点拨】本题考查了判断轴对称图形和中心对称图形，熟记定义是解题的关键．4. 七个大小相同的正方体搭成的几间体如图所示，其俯视图是（）A. B. C. D.【答案】C【解析】根据从上边看得到的图形是俯视图，可得答案．解：这个组合体的俯视图如下：故选：C．【点拨】本题考查了画小立方块堆砌图形的三视图，掌握从上边看得到的图形是俯视图是解题的关键．5. 如图，是的切线，A为切点，连接﹐点C在上，，连接并延长，交于点D，连接．若，则的度数为（）A. B. C. D.【答案】B【解析】利用垂线的性质及切线的性质得到和，再利用四边形的内角和为进而可求得，再利用等边对等角及三角形的内角和即可求解．解：，，又是的切线，，，又，，，又，，，故选B．【点拨】本题考查了圆的切线的性质，四边形内角和是，等腰三角形的性质及三角形的内角和，熟练掌握其基本知识是解题的关键．6. 方程的解为（）A. B. C. D.【答案】C【解析】方程两边同时乘以，化为整式方程即可求解．解：程两边同时乘以得，解得：经检验，是原方程的解，故选：C．【点拨】本题考查了解分式方程，熟练掌握解分式方程的步骤是解题的关键．7. 为了改善居民生活环境，云中小区对一块矩形空地进行绿化，这块空地的长比宽多6米，面积为720平方米，设矩形空地的长为x米，根据题意，所列方程正确的是（）A. B. C. D.【答案】A【解析】根据矩形面积公式，可得，即可解答．解：根据题意可得矩形空地的宽为米，可列方程，故选：A．【点拨】本题考查了一元二次方程的应用，根据题意得到等量关系，列出方程是解题的关键．8. 将枚黑棋子5枚白棋子装入一个不透明的空盒子里，这些棋子除颜色外无其他差别，从盒子中随机取出一枚棋子，则取出的棋子是黑棋子的概率是（）A. B. C. D.【答案】D【解析】取出的棋子是黑棋子的概率：，据此即可求解．解：由题意得：取出的棋子是黑棋子的概率为：故选：D【点拨】本题考查概率的计算．熟记概率公式是解题关键．9. 如图，，相交于点，，是的中点，，交于点．若，则的长为（）A. 2B. 4C. 6D. 8【答案】B【解析】根据可得，从而得到，再根据得到，从而得到，最后得到即可求解．解：，，，，，，，，是的中点，，，，，故选：B．【点拨】本题考查相似三角形的性质及判定，掌握相似三角形的性质及判定方法是解决本题的关键．10. 一条小船沿直线从A码头向B码头匀速前进，到达B码头后，停留一段时间，然后原路匀速返回A码头．在整个过程中，这条小船与B码头的距离（单位：）与所用时间（单位：）之间的关系如图所示，则这条小船从A码头到B码头的速度和从B码头返回A码头的速度分别为（）A. B. C. D.【答案】D【解析】根据路程除以时间结合函数图象即可求解．解：依题意，小船从A码头到B码头的速度为，从B码头返回A码头的速度为，故选：D．【点拨】本题考查了函数图象，从函数图象获取信息是解题的关键．二、填空题（每小题3分，共计30分）11. 船闸是我国劳动人民智慧的结晶，三峡船闸的“人”字闸门是目前世界上最大的巨型闸门，重867000千克，用科学记数法表示为_______千克．【答案】【解析】把一个数写成的形式，是正整数，这种形式的记数方法叫做科学记数法．根据科学记数法的定义写出答案．科学记数法就是把一个数写成的形式，是整数，，故答案为：．【点拨】本题考查科学记数法，掌握科学记数法的记数方法是解题的关键．12. 在函数中，自变量x的取值范围是_________．【答案】【解析】根据分母不能为求出自变量x的取值范围．分式中分母不能为，，，故答案为：．【点拨】本题考查求函数自变量的取值范围，熟练掌握分式有意义的条件是解题的关键．13. 已知反比例函数的图像经过点，则a的值为_________．【答案】2【解析】将点的坐标代入函数解析式即可．解：将代入得：，解得：，故答案为：2．【点拨】本题考查了反比例函数的定义，根据反比例函数值求自变量是解题的关键．14. 计算的结果是___________．【答案】【解析】利用二次根式的混合运算法则及分母有理数的方法即可求解．解：，故答案：．【点拨】本题考查了二次根式的混合运算及分母有理数，熟练掌握其运算法则是解题的关键．15. 把多项式分解因式的结果是_____．【答案】【解析】先提取公因式m，然后发现还能利用平方差公式继续分解，即可得到结果．解：故答案为：．【点拨】本题考查因式分解，熟练掌握提公因式法及公式法是解题的关键，注意要分解彻底．16. 抛物线与y轴交点坐标是_________．【答案】【解析】与轴的交点的特点为，令，求出的值，即可求出抛物线与轴的交点坐标．令抛物线中，即，解得，故与轴的交点坐标为，故答案为：．【点拨】本题主要考查了抛物线与y轴的交点坐标，解题的关键是令，求出的值．17. 不等式组的解集是_________________．【答案】【解析】根据解一元一次不等式组的步骤即可求解．解：解①得：解②得：故该不等式组的解集为：故答案为：【点拨】本题考查求解一元一次不等式组，掌握求解一元一次不等式组一般步骤是解题的关键．注意计算的准确性．18. 一个扇形的圆心角是，弧长是，则扇形的半径是_________cm．【答案】3【解析】根据弧长公式即可得到关于扇形半径的方程即可求解．解：设扇形的半径是，则解得：．故答案为3．【点拨】题主要考查了扇形的弧长，正确理解公式是解题的关键．19. 矩形的对角线，相交于点，点在矩形边上，连接．若，，则_________．【答案】或【解析】根据题意画出图形，分点在上和上两种情况讨论即可求解．解：∵四边形是矩形，∴，∴，∵，∴∴，如图所示，当点在上时，∵，∴如图所示，当点在上时，∵，∴，故答案为：或．【点拨】本题考查了矩形的性质，等边对等角，三角形的外角的性质，分类讨论是解题的关键．20. 如图在正方形中，点E在上，连接，，F为的中点连接．若，则的长为_________．【答案】【解析】根据正方形的性质得到，，设，根据勾股定理求出的值，再根据勾股定理即可求出的长．解：正方形，F为的中点，设，在中，即解得故，在中解得（负值舍去）故答案为：．【点拨】本题主要考查了正方形的性质，勾股定理，直角三角形斜边上的中线的性质，熟练掌握勾股定理是解题的关键．三、解答题（共60分）21. 先化简，再求代数式的值，其中．【答案】，【解析】先根据分式混合运算法则代简，再将代入代简式计算即可．解：，当时，原式．【点拨】本题考查分式化简求值，特殊角的三角函数值，分母有理化，熟练掌握分式混合运算法则是解题的关键．22. 如图，方格纸中每个小正方形的边长均为1个单位长度，线段和线段的端点均在小正方形的顶点上．（1）在方格纸中画出，且为钝角（点在小正方形的顶点上）；（2）在方格纸中将线段向下平移2个单位长度，再向右平移1个单位长度后得到线段（点的对应点是点，点的对应点是点），连接，请直接写出线段的长．【答案】（1）画图见解析（2）画图见解析，【解析】（1）找到的格点的，使得，且，连接，则即为所求；（2）根据平移画出，连接，勾股定理即可求解．(1)解：如图所示，即为所求；(2)解：如图所示，，即为所求；．【点拨】本题考查了平移作图，勾股定理与网格，熟练掌握勾股定理是解题的关键．23. 军乐中学开展以“我最喜欢的劳动实践课”为主题的调查活动，围绕“在园艺课，泥塑课，编织课、烹饪课四门劳动实践课中，你最喜欢哪一门课？（必选且只选一门）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的条形统计图，其中最喜欢泥塑课的学生人数占所调查人数的．请你根据图中提供的信息解答下列问题：（1）在这次调查中，一共抽取了多少名学生？（2）请通过计算补全条形统计图；（3）若军乐中学共有1200名学生，请你估计该中学最喜欢烹饪课的学生共有多少名．【答案】（1）（2）见解析（3）【解析】根据最喜欢泥塑课的学生人数为人，占所调查人数的，用即可求解；（2）根据总人数减去其他类型的人数，即可得出最喜欢编织课的学生人数进而补全统计图；（3）根据最喜欢烹饪课的学生的占比乘以，即可求解．(1)解：最喜欢泥塑课的学生人数为人，占所调查人数的，∴这次调查中，一共抽取了名学生（2）解：最喜欢编织课的学生人数为人，补全统计图如图所示，（3）解：估计该中学最喜欢烹饪课的学生共有名【点拨】本题考查了条形统计图，样本估计总体，从统计图中获取信息是解题的关键．24. 已知四边形是平行四边形，点在对角线上，点在边上，连接，，．（1）如图①，求证；（2）如图②，若，过点作交于点，在不添加任何轴助线的情况下，请直接写出图②中四个角（除外），使写出的每个角都与相等．【答案】（1）见解析；（2），理由见解析．【解析】（1）由平行四边形的性质得，，进而有，从而利用即可证明结论成立；（2）先证四边形是菱形，得，又证，得，由（）得得，根据等角的补角相等即可证明．（1）证明：∵四边形是平行四边形，∴，，∴，∵，∴；（2）解：，理由如下：∵四边形是平行四边形，∴四边形是菱形，，∴，，，∴，∵，∴，∴，∴，由（）得，∴，∵，∴．【点拨】本题考查了平行四边形的性质、菱形的判定及性质、等边对等角、全等三角形的判定及性质以及等角的补角相等．熟练掌握全等三角形的判定及性质是解题的关键．25. 佳衣服装厂给某中学用同样的布料生产，两种不同款式的服装，每套款服装所用布料的米数相同，每套款服装所用布料的米数相同，若套款服装和套款服装需用布料米，套款服装和套款服装需用布料米．（1）求每套款服装和每套款服装需用布料各多少米；（2）该中学需要，两款服装共套，所用布料不超过米，那么该服装厂最少需要生产多少套款服装？【答案】（1）每套款服装用布料米，每套款服装需用布料米（2）服装厂需要生产套款服装【解析】（1）每套款服装用布料米，每套款服装需用布料米，根据题意列出二元一次方程组，解方程组即可求解；（2）设服装厂需要生产套款服装，则生产套款服装，根据题意列出一元一次不等式，解不等式即可求解．（1）解：每套款服装用布料米，每套款服装需用布料米，根据题意得，，解得：，答：每套款服装用布料米，每套款服装需用布料米；（2）设服装厂需要生产套款服装，则生产套款服装，根据题意得，，解得：，∵为正整数，∴的最小值为，答：服装厂需要生产套款服装．【点拨】本题考查了二元一次方程组的应用，一元一次不等式的应用，根据题意列出不等式以及方程组是解题的关键．26. 已知内接于，为的直径，N为的中点，连接交于点H．（1）如图①，求证；（2）如图②，点D在上，连接，，，交于点E，若，求证；（3）如图③，在（2）的条件下，点F在上，过点F作，交于点G．，过点F作，垂足为R，连接，，，点T在的延长线上，连接，过点T作，交的延长线于点M，若，求的长．【答案】（1）见解析（2）见解析（3）【解析】（1）连接，根据N为的中点，易证，再根据中位线定理得出结论；（2）连接，先证得，再根据得，根据即可得出结论；（3）连接，先证，再证四边形是矩形，过A作垂足为S，先证出，再能够证出从而，得到等腰直角，利用三角函数求出，再根据求出，最后用勾股定理求出答案即可．（1）证明：如图，连接，为的中点，，，，，，是中位线，；（2）证明：如图，连接，设，，，，，，，，，，；（3）解：连接，，，，，，，，，，，，，，，，四边形是平行四边形，是的直径，，四边形矩形，，，过点A作垂足为S，，，，，，，，是的直径，，，，，，，，，，，，，，，，，，，，，，．【点拨】本题是圆的综合题，考查圆的有关知识、全等三角形的判定与性质、垂径定理、三角函数、勾股定理、圆周角定理等知识，构造辅助线解决问题是解题关键．27. 在平面直角坐标系中，为坐标原点，抛物线与轴交于点，，与轴交于点．（1）求，的值；（2）如图①，是第二象限抛物线上的一个动点，连接，，设点的横坐标为，的面积为，求关于的函数解析式（不要求写出自变量的取值范围）；（3）如图②，在（2）的条件下，当时，连接交轴于点，点在轴负半轴上，连接，点在上，连接，点在线段上（点不与点重合），过点作的垂线与过点且平行于的直线交于点，为的延长线上一点，连接，，使，是轴上一点，且在点的右侧，，过点作，交的延长线于点，点在上，连接，使，若，求直线的解析式．【答案】（1），（2）（3）【解析】（1）把点，代入抛物线解析式，得方程组，求出，的值即可；（2）过点作轴，垂足为，由（1）知，抛物线的解析式是，得，根据“是第二象限抛物线上的一个动点，点的横坐标为”，得，根据，代入整理即可得到关于的函数解析式；（3）以为一边作，的另一边交的延长线于点；作，垂足为；作，垂足为；作轴，垂足为；根据和，求出，根据“，，，”推理出，，得到，结合，推理出，用证，用证，推理出，根据“，”，得出，，，代入，求出，勾股定理算出，根据“，”，设，则，，代入，算出，运用勾股定理计算，计算，结合点在轴负半轴上，得，设直线的解析式为，把，代入求出完整解析式即可．（1）点，在抛物线上，，解得：，，（2）由（1）知，抛物线的解析式是，是抛物线与轴的交点，时，，，，如下图，过点作轴，垂足为，是第二象限抛物线上一点，点的横坐标为，，（3）如下图，以为一边作，的另一边交的延长线于点；作，垂足为；作，垂足为；作轴，垂足为，，由（2）知，，，，，，，，即，，，，，，，，，又，，，，，，，，，在和中，，，，，，，，，，，，，，，轴，，，，，，，，，，，，，设，则，，，，，，，又点在轴负半轴上，，设直线的解析式为，把，代入，得：，解得：，直线的解析式为【点拨】本题是二次函数综合题，难度大，结合全等三角形、勾股定理、三角函数解直角三角形知识点，综合运用知识、画出辅助线、数形结合、分析与计算是解题的关键．。

【历年真题】黑龙江省大庆市中考数学三年高频真题汇总卷(Ⅰ)(含答案详解)

黑龙江省大庆市中考数学三年高频真题汇总卷（Ⅰ）考试时间：90分钟；命题人：数学教研组考生注意： 1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图所示，一座抛物线形的拱桥在正常水位时，水而AB 宽为20米，拱桥的最高点O 到水面AB 的距离为4米．如果此时水位上升3米就达到警戒水位CD ，那么CD 宽为（） A． B ．10米 C． D ．12米2、Rt ABC △和Rt CDE △按如图所示的位置摆放，顶点B 、C 、D 在同一直线上，AC CE =，90B D ∠=∠=︒，AB BC >．将Rt ABC △沿着AC 翻折，得到Rt AB C '△，将Rt CDE △沿着CE 翻折，得Rt CD E '△，点B 、D 的对应点B '、D 与点C 恰好在同一直线上，若13AC =，17BD =，则B D ''的长度为（）．·线○封○密○外A ．7B ．6C ．5D ．43、有理数 m 、n 在数轴上的位置如图，则（m +n ）（m +2n ）（m ﹣n ）的结果的为（）A ．大于 0B ．小于 0C ．等于 0D ．不确定4、如图，E 、F 分别是正方形ABCD 的边CD 、BC 上的点，且CE BF =，AF 、BE 相交于点G ，下列结论中正确的是（）①AF BE =；②AF BE ⊥；③AG GE =；④ABG CEGF S S =四边形△．A ．①②③B ．①②④C ．①③④D ．②③④5、下列单项式中，32a b 的同类项是（）A ．323a b -B ．232a bC ．3a bD ．2ab6、利用如图①所示的长为a 、宽为b 的长方形卡片4张，拼成了如图②所示的图形，则根据图②的面积关系能验证的等式为（）A ．22()4()a b ab a b -+=+B ．22()()a b a b a b -+=-C ．222()2a b a ab b +=++D ．222()2a b a ab b ---+7、点()4,9-关于x 轴的对称点是（） A ．()4,9-- B ．()4,9- C ．()4,9- D ．()4,98、如图，O 是直线AB 上一点，则图中互为补角的角共有（） A ．1对 B ．2对 C ．3对 D ．4对 9、已知单项式5xayb +2的次数是3次，则a +b 的值是（） A ．1 B ．3 C ．4 D ．010、一元二次方程240x -=的根为（） A ．2x =-B ．2x =C ．2x =± D．x =第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分） ·线○封○密○外1、如图，在ABC 中，3cm AB =，6cm BC ，5cm AC =，蚂蚁甲从点A 出发，以1.5cm/s 的速度沿着三角形的边按A B C A →→→的方向行走，甲出发1s 后蚂蚁乙从点A 出发，以2cm/s 的速度沿着三角形的边按A C B A →→→的方向行走，那么甲出发________s 后，甲乙第一次相距2cm ．2、如图，所有三角形都是直角三角形，所有四边形都是正方形，已知14S =，28S =，39S =，425S =，则S =_______．3、比较大小：2351x x ++______2251x x +-（用“>、=或<”填空）．4、如图，E 是正方形ABCD 的对角线BD 上一点，连接CE ，过点E 作EF AD ⊥，垂足为点F ．若3AF =，5EC =，则正方形ABCD 的面积为______．5、若最简二次根式2a -2a ﹣b ＝___．三、解答题（5小题，每小题10分，共计50分）1、如图，在同一剖面内，小明在点A 处用测角仪测得居民楼的顶端F 的仰角为27°，他水平向右前进了30米来到斜坡的坡脚B 处，沿着斜坡BC 上行25米到达C 点，用测角仪测得点F 的仰角为54°，然后，水平向右前进一段路程来到了居民楼的楼底E 处，若斜坡BC 的坡度为3:4，请你求出居民楼EF 的高度．（测角仪的高度忽略不计，计算结果精确到0.1米．参考数据：sin 270.45︒≈，tan 270.51︒≈，sin540.81︒≈，tan54 1.38︒≈） 2、已知：如图，在△ABC 中，AB =AC ，以AC 为直径的⊙O 与BC 交于点D ，DE ⊥AB ，垂足为 E ，ED 的延长线与AC 的延长线交于点F ，(1)求证：DE 是⊙O 的切线； (2)若⊙O 的半径为4，∠F =30°，求DE 的长． 3、已知关于x 的一元二次方程x 2−(2m −2)x +(m 2−2m )=0． (1)请说明该方程实数根的个数情况； (2)如果方程的两个实数根为x 1，x 2，且(x 1+1)⋅(x 2+1)=8，求m 的值． 4、请根据学习“一次函数”时积累的经验和方研究函数2y x =-+的图象和性质，并解决问题． ·线○封○密·○外（1）填空：①当x ＝0时，2y x =-+= ；②当x ＞0时，2y x =-+= ；③当x ＜0时，2y x =-+= ；（2）在平面直角坐标系中作出函数2y x =-+的图象；（3）观察函数图象，写出关于这个函数的两条结论；（4）进一步探究函数图象发现：①函数图象与x 轴有个交点，方程20x -+=有个解； ②方程22x -+=有个解；③若关于x 的方程2x a -+=无解，则a 的取值范围是．5、如图，直线3y x =-+与反比例函数()20=>y x x 的图象交于A ，B 两点． (1)求点A ，B 的坐标； (2)如图1，点E 是线段AC 上一点，连接OE ，OA ，若45AOE ∠=︒，求AE EC的值； (3)如图2，将直线AB 沿x 轴向右平移m 个单位长度后，交反比例函数()20=>y x x 的图象于点P ，Q ，连接AP ，BQ ，若四边形ABQP 的面积恰好等于2m ，求m 的值．-参考答案-一、单选题 1、B 【解析】【分析】·线○封○密·○外以O 点为坐标原点，AB 的垂直平分线为y 轴，过O 点作y 轴的垂线，建立直角坐标系，设抛物线的解析式为y =ax 2，由此可得A （-10，-4），B （10，-4），即可求函数解析式，再将y =-1代入解析式，求出C 、D 点的横坐标即可求CD 的长．【详解】以O 点为坐标原点，AB 的垂直平分线为y 轴，过O 点作y 轴的垂线，建立直角坐标系，设抛物线的解析式为y =ax 2，∵O 点到水面AB 的距离为4米，∴A 、B 点的纵坐标为-4，∵水面AB 宽为20米，∴A （-10，-4），B （10，-4），将A 代入y =ax 2，-4=100a ， ∴125a =-， ∴2125y x =-， ∵水位上升3米就达到警戒水位CD ，∴C 点的纵坐标为-1， ∴21125x -=- ∴x =±5， ∴CD =10，故选：B ．【点睛】本题考查二次函数的应用，根据题意建立合适的直角坐标系，在该坐标系下求二次函数的解析式是解题的关键． 2、A 【解析】【分析】由折叠的性质得ABC AB C '≅，CDE CD E '≅，故ACB ACB '∠=∠，DCE D CE '∠=∠，推出90ACB DCE ∠+∠=︒，由90B D ∠=∠=︒，推出BAC DCE ∠=∠，根据AAS 证明ABC CDE ≅，即可得AB CD CD '==，BC ED CB '==，设BC x =，则17AB x =-，由勾股定理即可求出BC 、AB ，由B D CD CB AB BC ''''=-=-计算即可得出答案．【详解】由折叠的性质得ABC AB C '≅，CDE CD E '≅， ∴ACB ACB '∠=∠，DCE D CE '∠=∠， ∴90ACB DCE ∠+∠=︒， ∵90B D ∠=∠=︒， ∴90BAC ACB ∠+∠=︒， ∴BAC DCE ∠=∠，在ABC 与CDE △中， ·线○封○密○外B D BAC DCE AC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()ABC CDE AAS ≅，∴AB CD CD '==，BC ED CB '==，设BC x =，则17AB x =-，∴222(17)13x x +-=，解得：5x =，∴5BC =，12AB =，∴1257B D CD CB AB BC ''''=-=-=-=．故选：A ．【点睛】本题考查折叠的性质以及全等三角形的判定与性质，掌握全等三角形的判定定理和性质是解题的关键．3、A【解析】【分析】从数轴上看出0n m <<，判断出()()()0200m n m n m n +<+-，，，进而判断()()()2m n m n m n ++-的正负．【详解】解：由题意知：0n m <<∴()()()0200m n m n m n +<+-，，∴()()()20m n m n m n ++->故选A ．【点睛】本题考查了有理数加减的代数式正负的判断．解题的关键在于正确判断各代数式的正负． 4、B 【解析】【分析】根据正方形的性质及全等三角形的判定定理和性质、垂直的判定依次进行判断即可得．【详解】解：∵四边形ABCD 是正方形， ∴AB BC CD AD ===，90ABC BCD ∠=∠=︒，在ABF 与BCE 中，AB BC ABC BCD BF CE =⎧⎪∠=∠⎨⎪=⎩， ∴ABF BCE ≅， ∴AF BE =，①正确； ∵90BAF BFA ∠+∠=︒， BAF EBC ∠=∠， ∴90EBC BFA ∠+∠=︒， ∴90BGF ∠=︒， ∴AF BE ⊥，②正确； ·线○封○密○外∵GF 与BG 的数量关系不清楚，∴无法得AG 与GE 的数量关系，③错误；∵ABF BCE ≅，∴ABF BCE S S =，∴ABF BGF BCE BGF S S S S -=-，即ABG CEGF S S =四边形，④正确；综上可得：①②④正确，故选：B ．【点睛】题目主要考查全等三角形的判定和性质，正方形的性质，垂直的判定等，理解题意，综合运用全等三角形全等的判定和性质是解题关键．5、A【解析】【分析】依据同类项的定义：所含字母相同，相同字母的次数相同，据此判断即可．【详解】解：A.32a b 与323a b -是同类项，选项符合题意；B.32a b 与232a b 所含的字母相同，相同字母的次数不相同，不是同类项，故选项不符合题意；C.32a b 与3a b 所含的字母相同，相同字母的次数不相同，不是同类项，故选项不符合题意；D.32a b 与2ab 所含的字母相同，相同字母的次数不相同，不是同类项，故选项不符合题意；故选：A ．【点睛】本题主要考查的是同类项的定义，掌握同类项的定义是解题的关键．6、A【解析】【分析】整个图形为一个正方形，找到边长，表示出面积；也可用1个小正方形的面积加上4个矩形的面积表示，然后让这两个面积相等即可．【详解】 ∵大正方形边长为：()a b +，面积为：()2a b +； 1个小正方形的面积加上4个矩形的面积和为：()24a b ab -+； ∴()()2222424a b ab a ab b ab a b -+=-++=+．故选：A ．【点睛】此题考查了完全平方公式的几何意义，用不同的方法表示相应的面积是解题的关键． 7、A 【解析】【分析】直接利用关于x 轴对称点的性质得出答案．【详解】解：点P （−4，9）关于x 轴对称点P ′的坐标是：（−4，−9）．故选：A ． ·线○·封○密○外【点睛】此题主要考查了关于x轴对称点的性质，正确得出横纵坐标的关系是解题关键．8、B【解析】【分析】根据补角定义解答．【详解】解：互为补角的角有：∠AOC与∠BOC，∠AOD与∠BO D，共2对，故选：B．【点睛】此题考查了补角的定义：和为180度的两个角互为补角，熟记定义是解题的关键．9、A【解析】【分析】根据单项式的次数的概念求解．【详解】解：由题意得：a+b+2=3，∴a+b=1．故选：A．【点睛】本题考查了单项式的有关概念，解答本题的关键是掌握单项式的次数：所有字母的指数和．10、C【解析】【分析】先移项，把方程化为24,x = 再利用直接开平方的方法解方程即可.【详解】解：240x -=， 24,x ∴= 2,x ∴=± 即122,2,x x故选C 【点睛】本题考查的是一元二次方程的解法，掌握“利用直接开平方的方法解一元二次方程”是解本题的关键. 二、填空题 1、4 【解析】【分析】根据题意，找出题目的等量关系，列出方程，解方程即可得到答案．【详解】解：根据题意， ∵3cm AB =，6cm BC ，5cm AC =， ∴周长为：35614++=（cm ）， ∵甲乙第一次相距2cm ，则甲乙没有相遇，设甲行走的时间为t ，则乙行走的时间为(1)t -， ·线○封○密○外∴1.52(1)214t t +-+=，解得：4t =；∴甲出发4秒后，甲乙第一次相距2cm ．故答案为：4．【点睛】本题考查了一元一次方程的应用，解题的关键是熟练掌握题意，正确的列出方程．2、46【解析】【分析】利用勾股定理分别求出AB 2，AC 2，继而再用勾股定理解题．【详解】解：由图可知，AB 2=32412++=9+25=344+8=12=S S AC S S =，222123446AB AC BC +=+==∴246BC S ==∴故答案为：46．【点睛】本题考查正方形的性质、勾股定理等知识，是基础考点，掌握相关知识是解题关键．3、>【解析】【分析】先求两个多项式的差，再根据结果比较大小即可．【详解】解：∵22351(251)x x x x ++-+-，=22351251x x x x ++--+， =220x +> ∴22351251x x x x ++>+-，故答案为：>．【点睛】本题考查了整式的加减，解题关键是熟练运用整式加减法则进行计算，根据结果判断大小． 4、49 【解析】【分析】延长FE 交AB 于点M ，则EM BC ⊥，3AF BM ==，由正方形的性质得45CDB ∠=︒，推出BME 是等腰直角三角形，得出3EM BM ==，由勾股定理求出CM ，故得出BC ，由正方形的面积公式即可得出答案．【详解】如图，延长FE 交AB 于点M ，则EM BC ⊥，3AF BM ==， ∵四边形ABCD 是正方形， ∴45CDB ∠=︒， ∴BME 是等腰直角三角形， ∴3EM BM ==，·线○封○密○外在Rt EMC 中，4CM =，∴347BC BM CM =+=+=，∴22749ABCD S BC ===正方形．故答案为：49．【点睛】本题考查正方形的性质以及勾股定理，掌握正方形的性质是解题的关键．5、9【解析】【分析】结合同类二次根式的定义：一般地，把几个二次根式化为最简二次根式后，如果它们的被开方数相同，就把这几个二次根式叫做同类二次根式．进行求解即可．【详解】解：∵最简二次根式2a -∴2a ﹣4＝2，3a +b ＝a ﹣b ，解得：a ＝3，b ＝﹣3．∴2a ﹣b ＝2×3﹣（﹣3）＝9．故答案为：9．【点睛】此题考查了同类二次根式的定义，熟记定义是解题的关键．三、解答题1、居民楼EF 的高度约为16.7米【解析】【分析】根据题意如图过C 作CC ⊥CC 于P ，延长FE 交BD 于R ，利用勾股定理得出CP 、BP ，进而结合两个正切值进行分析计算并依据CC =CC +CC 建立方程求解即可得出答案.【详解】解：如图过C 作CC ⊥CC 于P ，延长FE 交BD 于R ， ∵斜坡BC 的坡度为3:4，即CC :CC =3:4, CC =25（米），设CC =3C ,CC =4C ，勾股定理可得：(3C )2+(4C )2=252，解得：m =5或-5（舍去）， ∴CC =15（米），CC =20（米）， ∵CC ⊥CC ，CC //CC ,CC //CC , ∴四边形CERP 是矩形，∴CE =PR ,CC =CC =15（米），设CC =C （米），可得tan 54°=CC CC =CC C ≈1.38，则CC =1.38C （米），又可得tan 27°=CC CC =CC CC +CC +CC =CC50+C ≈0.51，则CC =0.51(50+C )=0.51C +25.5（米）， ·线○封○密·○外∵CC=CC+CC,，∴0.51C+25.5=1.38C+15，解得：C=35029≈16.7（米）.∴CC=1.38×35029答：居民楼EF的高度约为16.7米.【点睛】本题考查仰角与俯角、坡度、解直角三角形等知识知识．注意能借助仰角与俯角构造直角三角形并解直角三角形是解此题的关键，注意掌握数形结合思想与方程思想的应用．2、 (1)见解析(2)【解析】【分析】（1）连接AD、OD，根据等腰三角形的性质和圆周角定理可证得∠EAD=∠ODA，根据平行线在判定与性质可证得OD⊥DE，然后根据切线的判定即可证得结论；（2）根据含30°角的直角三角形的性质求得OF、DF，再根据平行线分线段成比例求解即可．(1)证明：连接AD、OD，∵OA=OD，∴∠OAD=∠ODA，∵AC是⊙O的直径，∴∠ADC=90°即AD⊥BC，又AB=AC，∴∠BAD=∠OAD，∴∠EAD=∠ODA，∴OD ∥AB ，∵DE ⊥AB ，∴OD ⊥DE ，又OD 是半径，∴DE 是⊙O 的切线； (2) 解：在Rt△ODF 中，OD =4，∠F =30°， ∴OF =2OD =8，DF= ∵OD ∥AB ， ∴=OF DF OA DE即84=∴DE = 【点睛】本题考查等腰三角形的性质、圆周角定理、平行线的判定与性质、切线的判定、含30°角的直角三角形性质、平行线分线段成比例，综合性强，难度适中，熟练掌握相关知识的联系与运用是解答的关键． 3、 (1)方程有两个不相等的实数根 (2)m =3或-3 【解析】【分析】·线○封○密○外（1）根据根的判别式先求出Δ的值，再判断即可；（2）根据根与系数的关系得出x 1+x 2=2m -2，x 1•x 2=m 2-2m ，代入计算即可求出答案．(1)解：∵a =1，b =−(2m −2)，c = m 2−2m ，∴24b ac =- =()22m ⎡⎤--⎣⎦2-4(m 2-2m )=4m 2-8m +4-4m 2+8m =4＞0，∴方程有两个不相等的实数根；(2)解：∵(x 1+1)⋅(x 2+1)=8，整理得x 1x 2+(x 1+x 2)+1=8，∵x 1+x 2=2m -2，x 1x 2=m 2-2m ，∴m 2-2m +2m -2+1=8，∴m 2=9，∴m =3或m =-3．【点睛】本题考查了根的判别式以及根与系数的关系，解题的关键是熟练运用根与系数的关系以及一元二次方程的解法．4、（1）2；-x +2，x +2；（2）见解析；（3）函数图象关于y 轴对称；当x =0时，y 有最大值2；（4）①2 2；②1；③2a >．【解析】【分析】（1）利用绝对值的意义，分别代入计算，即可得到答案；（2）结合（1）的结论，画出分段函数的图像即可；（3）结合函数图像，归纳出函数的性质即可；·线（4）结合函数图像，分别进行计算，即可得到答案；【详解】解：（1）①当x ＝0时，22y x =-+=；②当x ＞0时，22y x x =-+=-+；③当x ＜0时，22y x x =-+=+；故答案为：2；-x +2；x +2；（2）函数y ＝-|x |+2的图象，如图所示：（3）函数图象关于y 轴对称；当x =0时，y 有最大值2．（答案不唯一）（4）①函数图象与x 轴有2个交点，方程20x -+=有2个解； ②方程22x -+=有1个解；③若关于x 的方程2x a -+=无解，则a 的取值范围是2a >．故答案为：2；2；1；2a ．【点睛】本题考查了一次函数的图像和性质，绝对值的意义，解题的关键是熟练掌握题意，正确的画出图像．5、 (1)C (1,2)，C (2,1)(2)53(3)103【解析】【分析】（1）联立得{C =−C +3C =2C ，再解方程组即可；（2）先求出C (3,0)，再证△CCC ∽△CCC ，求出CC =√22+22=√8=2√2，再得出CC =CC 2CC =5√24，CC =3√24，即可得到答案；（3）设平移后C CC =−C +3+C ，由四边形ABQP 的面积恰好等于m 2，得到PQ=2√2C{C =−C +3+C C =C 2，得到CC =√2√C 2+6C +1，列方程C 2+6C +1=4C 2−4C +1求解即可.(1)解：有题意得，{C =−C +3C =2C∴−C +3=2C解得C 1=1，C 2=2 C 1=2，C 2=1， ∴C (1,2)，C (2,1)·线(2)解：∵3y x =-+交x 轴于点C∴C (3,0)，∵∠CCC =∠CCC =45°， ∠CCC =∠CCC∴△CCC ∽△CCC ，∴CC CC =CC CC∴CC 2=CC ⋅CC∵C (1,2)，C (3,0)，∴CC =√22+12=√5，CC =√22+22=√8=2√2，∴CC =CC 2CC =5√24，CC =3√24，∴CC CC =53(3)解：设平移后C CC =−C +3+C ，如图，过点D作DF⊥PQ于点F,则ED=m,DF=√2C2C CCCC=(CC+CC)⋅√2C22=√2C(√2+CC)4=C2∴√2+CC=2√2C，∴PQ=2√2C有题意得，{C=−C+3+CC=C2解得，C1=C+3+√C2+6C+12，C2=C+3−√C2+6C+12，∴QH=x1-x2=√C2+6C+1,∴CC=√2√C2+6C+1,∴√2√C2+6C+1=2√2C∴C2+6C+1=4C2−4C+1，∴解得C1=0（舍），C2=103，即C=103【点睛】本题主要考查了反比例函数，一次函数，三角形的相似，列方程组求解等知识，解题的关键是证明三角形相似和列出方程组求解. ·线○封○密○外。

黑龙江省2003中考题

黑龙江省2003中考题一、选择题（每题2分，1～5小题每小题各有一个正确选项，6～10小题每小题各有1～2正确选项的。

）1．下列变化，属于化学变化的是（）A．碘的升华B．铜绿受热分解C．胆矾研碎D．水受热变成水蒸气2．生活中的下列物质，属于纯净物的是（）A．矿泉水B．白酒C．米醋D．干冰3．下列实验操作，叙述正确的是（）A．把烧杯放在铁圈上直接加热B．用燃着的酒精灯去引燃另一只酒精灯C．用氢气还原氧化铜，实验完毕，先停止通入氢气，再停止加热D．实验室制氧气，用排水法收集完毕后，先把导管移出水面，然后再熄灭酒精灯4．2003年3月，美英联军在伊拉克遭遇沙尘暴。

沙尘暴已成为世界环境问题中的一个重点问题，下列措施可以防止沙尘暴的是（）A．植树造林，加强绿化B．合理使用化肥和农药C．工业“三废”经处理后再排放D．矿物产品的综合开发和利用5．生活中处处充满化学，下列生活中的化学知识叙述正确的是（）A．铁制品在干燥的空气中易生锈B．用纯碱溶液除去水壶中的水垢C．硫酸铜可用于游泳池水消毒，亦可用于自来水消毒D．通常用含单质碳的墨水书写档案，以便于保存6．“非典”是一种新发现的传染病，威胁着人们的健康。

防范“非典”的措施是科学洗手、勤通风、定期消毒，常用的消毒液是过氧乙酸（化学式为C2H4O3）的稀溶液。

关于过氧乙酸的说法正确的是（）A．它是由C2H4O3分子构成的B．它是一种氧化物C．它是由2个碳元素、4个氢元素、3个氧元素组成的D．过氧乙酸中碳、氢、氧三种元素的质量比是2：4：37．以下说法违背科学事实的是（）A．医疗上常用体积分数为70%～75%的酒精溶液作消毒剂B．煤、石油、天然气是当今世界上最主要的三大化石燃料，它们都是化合物C．晒盐时，日晒、风吹都有利于氯化钠晶体的析出D．点燃不纯的氢气可能会发生爆炸8．合乎实际并用于工业生产的是（）A．工业上用分离液态空气的方法制取氧气B．用工业酒精勾兑白酒C．高温下用还原剂CO把Fe从它的氧化物中还原出来D．用Zn和HNO3制取H2 9．下列说法错误的是（）A．一定温度下，NaCl饱和溶液比它的不饱和溶液要浓B．铜和氯化银反应生成银和氯化铜C．浓硫酸不慎沾到皮肤上，立即用大量水冲洗D．酸跟碱作用而生成盐和水的反应叫中和反应10．用氢气还原8g氧化铜，将反应后的气体全部通入足量浓硫酸中，浓硫酸的质量增加了0.9g，则剩余的固体是（）A．CuO和Cu B．CuO C．Cu D．无法确定二、填空题（本题共14分）11．用化学用语表示：石灰水中的溶质是；人体内含量最多的元素是；3个氮原子；2个镁离子。

2003年中考题-中考数学试题、初中数学中考试卷、模拟题-初中数学试卷

2003年中考题-中考数学试题、初中数学中考试卷、模拟题、复习资料-初中数学试卷-试卷下载深圳市2003年高中阶段学校招生考试数学试卷（第一卷）一、选择题（本题共有10分题，每题5分，共50分）1．实数695600保留2位有效数字的近似数是：A．690000B．700000C． 6.9×105 D．7.0×1052．实数，sin30°，，，，－3中，有理数的个数是A．2个B．3个C．4个D．5个3．已知三角形的两边a=3，b=7，第三边为c，且a＜b＜c，则c的取值范围是A．4＜c＜7B．7＜c＜10C．4＜c＜10D．7＜c＜134．某班5位同学的身高分别是155，160,160，161，169（单位：厘米），这组数据中，下列说法错误的是：A．众数是160B．中位数是160C．平均数是161D．标准差是5．下列命题正确的是A．的解集为B．关于的方程的解是C．9的平方根是3D．与互为倒数6．计算的结果为A．1B．C．D．7．一个等腰梯形的高恰好等于这个梯形的中位线，若分别以这个梯形的上底和下底为直径作圆，则这两个圆的位置关系是：A．相离B．相交C．外切D．内切8．已知一元二次方程有两个实数根、，直线经过点A，B，则直线的解析式为A．B．C．D．9．如图1，已知四边形ABCD是⊙O的内接四边形，且AB=CD=5，AC=7，BE=3，下列命题错误的是A．⊙AED⊙⊙BEC B．⊙AEB=90°C．⊙BDA=45°D．图中全等的三角形有2对10．如图2，直线，AF：FB=2：3，BC：CD=2：1，则AE：EC是A．5：2B．4：1C．2：1D．3：2第二卷二、非选择题（本部分共4题，其中第11题10分，第12题10分，第13题12分，第14题18分，共50分）11．先化简，再求值：，其中，12．某工人要制造180个同种零件，在制造完40个零件后，他改进技术，每天多制造15个零件，恰好共用6天全部完成。

黑龙江省2003年中考试题

黑龙江省2003年中考试题黑龙江省2003年中考试题（考试时间120分分钟，总分120分）一，知识积累及运用（共19分）1．语文考试，排在第一；答题方法，因人而异；冷静思考，切莫着急。

请你写出平时喜欢的考试答题顺序，以便阅卷老师了解你。

（10字左右）（1分）_______________________________________________________________________________________ 2．读下面的《六月寄语》，回答问题。

（2分）六月，为我们的心灵提供了能享受的一切，轻松地解除了精神的迷惘和束缚，感受到了闲适与欢愉。

田野已是一片新绿，散发着另人沉醉的馨香，整个大地是一副欢乐的景象。

清凉的六月，优雅的六月，希望的六月。

①你能给加点字选择正确的读音吗？享受:__________(A.xiáng B.xiǎng)束缚:__________(A.sù B.shù)②文中还有两个字书写有误,找出来,改正它!___________改为__________ ___________改为__________3.随着时代的发展,一些新生的词汇进入了我们的生活,例如:在网上常见的“美眉”(漂亮女孩)、“菜鸟”（新手）；由外来语演变的“酷”（cool）、“秀”(show)等等。

你怎么看？随便说说。

（30字左右）（2分）________________________________________________________5.古代诗文默写.(9分)①___________________,似曾相识燕归来.(《浣溪沙》一曲新词酒一杯)②长风万里送秋雁,_________________(《宣州谢眺楼饯别校书叔云》③_______________________,梦回吹角连营.(《破阵子•为陈同甫赋壮词以寄之》)④《送杜少府之任蜀州》一诗摒弃了赠别诗常有的哀伤和悱恻,写得乐观开朗.其中劝慰友人,最能表现诗人宽阔胸襟的两句是:___________________,_______________________.⑤孔子提倡“见不贤而内自省也”.在《论语》中,孔子还有过类似的表述,这两句是:_________________,______________.⑥“月亮”是文人笔下常见的景物,曾经勾起许多诗人、词人的创作情思,写出很多名篇佳作.请你写出古代诗词中含一个“月”字的上、下句:_________________,_________________.6.读下面两句诗,任选一句,用“•”标出你想读重音的地方,并请说说理由.(2分)忽如一夜春风来,千树万树梨化开.( 4)岑参《白雪歌送武判官归京》)________________________________________________________二.阅读理解及分析(共41分)(一)阅读下面的文言文语段,回答第7-12题.(12分)臣本布衣躬耕于南阳,苟全性命于乱世,不求闻达于诸侯.先帝不以臣卑鄙,猥自枉屈,三顾臣于草庐之中,咨臣以当世之事,由是感激,遂许先帝以驱驰.后值倾覆,受任于败军之际,奉命于危难之间,尔来二十有一年矣.7.请翻译选文中的两个加点词.(2分)咨:________________ 驱驰:__________________8.请翻译下面这句话.(2分)先帝不以臣卑鄙,猥自枉屈,三顾臣于草庐之中.___________________________________________________9.“遵义会议”之后,毛泽东同志确立了在中国共产党的领导地位.请摘录选文中的句子形容他当时的处境.(2分)______________________________________________________10..诸葛亮自叙了,“三顾茅庐”这一情节,请分析他的用意.(2分)______________________________________________________11.请结合《三国演义》,说出诸葛亮与周瑜联手指挥一场著名的以少胜多的战例,是________________;再说出诸葛亮挥泪斩马谡是因为____________________一事.(2分)12.在《水浒传》中,绰号为“智多星”的人是_______________,也被称为“塞诸葛”.他与一伙儿好汉在“黄泥冈上巧施功”,干的一件大事是__________________.(2分)(二)阅读下面的说明文语段,回答第13-15题.(7分)沙漠地区空气干燥,日光的照射特别强烈.那里日照时间又特别长,一年达到3000小时,而长江流域只有1500小时,华北地区不过2500小时.日光可以用来发电,取暖,煮水,做饭.沙漠湖水含盐,日光使水蒸发,可以取得蒸馏水和盐.把日光变为热能和电能的最良好的工具是半导体,估计将来有可能在沙漠里用便宜的半导体做屋顶,人住在里边冬天不冷,夏天不热.13.选文中的画线句子使用了哪两种说明方法?说说它们的作用.(2分)____________________________________________________14.如果把选文中加点的“估计”、“有可能”去掉，与原文相比，有什么区别？（２分）＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿１５．请结合物理学知识，解说选文中的“日光使水蒸发,可以取得蒸馏水和盐”这一现象．再发挥你的聪明才智，构想并描绘人类未来利用日光资源的美好前景．（３分）(三)阅读下面的文章,回答第16-20题.(13题)珍珠与蚌莫洛①一颗珍珠!②它原来就是一粒砂,----你是知道的.一粒砂,只不过由于一个偶然的机缘,它掉入蚌壳里;它不知道自己的棱角,自己的坚硬,可是却给蚌带来了痛苦,----你可以想象;一片灰屑飞进你的眼睛,你会有着一种如何的感觉.----于是蚌要挤出它,或者消灭它;然而它没有被挤出,也不会消灭,它钉住在蚌壳里面,永远给蚌痛苦.于是在无可奈何之中,蚌以它的唇,以它的肌肉,磨它,舐它,卷动拭擦它,而且也以蜒沫洗它,浸它,润滑它.大海的时间在浪涛的呼啸中过去……悠长的时间过去了,砂没有离开蚌,却改变了.它变成圆润,光滑,坚硬,半透明,泛着淡淡的暗光,一种永恒不变的光泽.③哦,一颗珍珠完成了.④一颗珍珠吗?不,它本质上是一粒砂;但它却已成为一颗不变色泽的珍珠了.⑤是永恒的光泽,不变的光泽;但它却一样保有它自己的砂的土色,只不过它会闪柔和美丽的光,闪朴素而真实的光.⑥但它已有永久的价值了!⑦请你记取,从一粒砂到一颗珍珠的过程.的映照,一个个时代有了波澜壮阔底象征.⑤坐看黄河,我们无法无动于衷.⑥这是一条曾让风云任务敬畏得不能泅渡的英雄河,这是一条当同名乐章响起就会冲湿海外游子眼眶的母亲河,这是一条淹没过许多家园和梦想也滋润了许多沃野和希望的岁月河,这是一条负载厚重的泥沙也负载粗犷的船工号子的生活河.⑦我们已静坐不得徘徊不得,只能与她同行.⑧我们在岸边看河,河在历史里看我们.⑨21.选文的第②段写道:“上一辈尚在感叹那些小去的孤帆远影,排天的浪花已溅湿我们的青春衣衫.”你如何理解这句话?(2分)________________________________________________22.本文主要写“黄河”,为什么又提到了“山”和“云”?(2分)23.试从修辞的角度分析,选文第⑥段蕴含了怎样的感情?(2分)______________________________________________________24.本文以“坐看黄河”为题；文章中又写“我们已静坐不得徘徊不得，只能与她同行”，二者是否矛盾？为什么？（3分）________________________________________________________三.作文(共60分)25.从下面的三个文题中任选一个,写一篇作文.(60分)作文要求 1)不少于600字.(2)除诗歌,戏剧外,文体不限.(3)作文中不要出现真实姓名、校名以及附近的地名。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2003年黑龙江省初中升学统一考试数学试题一、填空题；（每小题3分，共33分）1、生物学家发现一种病毒的直径约为0.000043米，用科学记数法表示为米。

2、写出满足方程92=+y x 的一对整数值。

3、如图：△ABC 中，AD ⊥BC ，CE ⊥AB ，垂足分别为D 、E ，AD 、CE 交于点H ，请你添加一个适当的条件：，使△AEH ≌△CEB 。

4、函数43--=x x y 中，自变量x 的取值范围是。

第3题图 HEDCBA第7题图 OE D CBA第10题图DC 5、矩形一个角的平分线分矩形一边为1cm 和3cm 两部分，则这个矩形的面积为 cm 2。

6、已知一次函数2+=kx y ，请你补充一个条件：，使y 随x 的增大而减小。

7、如图：在⊙O 中，AB 、AC 为互相垂直且相等的两条弦，OD ⊥AB ，OE ⊥AC ，垂足分别为D 、E ，若AC ＝2cm ，则⊙O 的半径为 cm 。

8、已知抛物线c bx ax y ++=2与x 轴交点的横坐标为－1，则c a +＝。

9、五个正整数从小到大排列，若这组数据的中位数是4，唯一众数是5，则这五个正整数的和为。

二、选择题：（每小题3分，共27分） 12、下列计算正确的是（）A 、5322x x x =+B 、632x x x =⋅C 、623)(x x -=- D 、336x x x =÷13、将一张长方形纸片按如图所示的方式折叠，BC 、BD 为折痕，则∠CBD 的度数为（）A 、600B 、750C 、900D 、95014、某服装原价为200元，连续两次涨价a ％后，售价为242元，则a 的值为（）A 、5B 、10C 、15D 、20第13题图EC BA第16题图15、若033=+--a a ，则a 的取值范围是（）A 、a ≤3B 、a ＜3C 、a ≥3D 、a ＞316、如图：用8块相同的长方形地砖拼成一个矩形，则每个长方形地砖的面积是（） A 、200cm 2 B 、300cm 2 C 、600cm 2 D 、2400cm 217、从哈尔滨开往A 市的特快列车，途中要停靠两个站点，如果任意两站间的票价都不同，那么有（）种不同的票价。

A 、4B 、6C 、10D 、1218、如图：在等边△ABC 中，P 为BC 上一点，D 为AC 上一点，且∠APD ＝600，BP ＝1，CD ＝32，则△ABC 的边长为（） A 、3 B 、4 C 、5 D 、6600第18题图DP CB A第20题图 19、平面直角坐标系内，点A （n ，n -1）一定不在（）A 、第一象限B 、第二象限C 、第三象限D 、第四象限20、如图：⊙O 的直径为10cm ，弦AB 为8cm ，P 是弦AB 上一点，若OP 的长为整数，则满足条件的点P 有（）A 、2个B 、3个C 、4个D 、5个三、解答题；（共60分）21、先化简，再求值：13181++÷⎪⎭⎫ ⎝⎛+--x x x x ，其中23-=x22、关于x 的方程04)1(2=+++kx k kx 有两个不相等的实数根。

（1）求k 的取值范围；（2）是否存在实数k ，使方程的两个实数根的倒数和等于0 ？若存在，求出k 的值；若不存在，请说明理由。

23、某中学在一次健康知识竞赛活动中，抽取了一部分同学测试的成绩为样本，绘制的成绩统计图如下，请结合统计图回答下列问题：（1）本次测试中，抽样的学生有多少人？（2）分数在90.5～100.5这一组的频率是多少？（3）这次测试成绩的众数落在哪个小组内？（4）若这次测试成绩80分以上（含80分）为优秀，则优秀率不低于多少？第23题图分数24、为美化环境，计划在某小区内用30平方米的草皮铺设一个边长为10米的等腰三角形绿地，请你求出这块等腰三角形绿地另两边的长。

25、某空军加油飞机接到命令，立即给另一架正在飞行的运输飞机进行空中加油，在加油过程中，设运输飞机的油箱余油量为1Q 吨，加油飞机的加油油箱．．．．余油量为2Q 吨，加油时间为t 分钟，1Q 、2Q 与t 之间的函数图像如图所示，结合图像回答下列问题：（1）加油飞机的加油油箱中装载了多少吨油？将这些油全部加给运输飞机需多少分钟？（2）求加油过程中，运输飞机的余油量1Q （吨）与时间t （分钟）的函数关系式；（3）运输飞机加完油后，以原速继续飞行，需10小时到达目的地，油料是否够用？说明理由。

分钟）26、（9分）已知：如图，BD 、CE 分别是△ABC 的外角平分线，过点A 作AF ⊥BD ，AG ⊥CE ，垂足分别为F 、G ，连结FG ，延长AF 、AG 与直线BC 相交，易证：)(21AC BC AB FG ++=，若：（1）BD 、CE 分别是△ABC 的内角平分线（如图2）；（2）BD 为△ABC 的内角平分线，CE 为△ABC 的外角平分线（如图3），则在图2、图3两种情况下，线段FG 与△ABC 三边又有怎样的数量关系？请写出你的猜测，并对其中的一种情况进行证明。

第26题图1G FEDCBA第26题图2GFE DCBA第26题图3GFE D CBA27、（9分）为了保护环境，某企业决定购买10台污水处理设备，现有A 、B 两种型号（1）请你设计该企业有几种购买方案；（2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；（3）在第（2）问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）28、（9分）已知，如图，直角坐标系中的梯形AOBC 中，AC ∥OB ，AC 、OB 的长分别是关于x 的方程04622=++-m mx x 的两根，并且AOC S ∆∶BOC S ∆＝1∶5（1）求AC 、OB 的长；（2）当BC ⊥OC 时，求OC 的长及OC 所在直线的解析式；（3）在第（2）问的条件下，线段OC 上是否存在一点M ，过M 点作x 轴的平行线交y 轴于F ，交BC 于D ，过D 点作y 轴的平行线交x 轴于E ，使F OE D S 矩形＝AOBC S 梯形21，若存在，请直接写出M 点的坐标；若不存在，请说明理由。

参考答案一、填空题1、4.3×10－5；2、x ＝1，y ＝4等；3、AH ＝CB 等；4、x ≥3且x ≠4；5、4或12； 6、k ＝－3等；7、2；8、1；9、17或18或19；10、10；11、)2.03.0(a b - 二、DCBAB ，BACD 三、解答题：21、原式＝3-x ；当23-=x 时，原式＝2-22、解：（1）由题意知k ≠0，且△＝44)1(2k k k ⋅-+＞0 ∴k ＞21-且k ≠0 （2）不存在。

设方程的两个根是1x 、2x∵21x x ⋅＝41≠0 ∴2111x x +＝2121x x x x ⋅+＝0∴1x ＋2x ＝0 ∵1x ＋2x ＝kk 1+-∴01=+k ，k ＝－1＜21-∴满足条件的实数k 不存在。

23、解：（1）2＋3＋4＋41＝50（人）（2）总数频数频率＝＝504＝0.08 （3）众数落在80.5～90.5这一小组内（4）这次测试成绩的优秀率不低于90％。

24、解：分三种情况计算，不妨设AB ＝10米，过点C 作CD ⊥AB 于D ，则： ABC S ∆＝CD AB ⋅21，∴CD ＝6米（1）当AB 为底边时，AD ＝DB ＝5（米）（如图1）AC ＝BC ＝2256+＝61（米）第24题图1 DCB A第24题图2D CB A 第24题图3DCBA（2）当AB 为腰且三角形为锐角三角形时（如图2） AB ＝AC ＝10（米）AD ＝22CD AC -＝8（米），BD ＝2（米） BC ＝2226+＝102（米）（3）当AB 为腰且三角形为钝角三角形时（如图3）AB ＝BC ＝10（米）AC ＝22186+＝106（米）25、解：（1）由图象知，加油飞机的加油油箱中装载了30吨油，全部加给运输飞机需10分钟（2）设1Q ＝b kt +，把（0，40）和（10，69）代入得：⎩⎨⎧+==b k b 106940 解这个方程组得⎩⎨⎧==409.2b k∴1Q ＝409.2+t （0≤t ≤10）（3）根据图象可知运输飞机的耗油量为每分钟0.1吨∴10小时耗油量为：10×60×0.1＝60（吨）＜69（吨） ∴油料够用26、解：猜测结果：图2结论为)(21BC AC AB FG -+=证明：分别延长AG 、AF 交BC 于H 、K ，易证△BAF ≌△BKF 得AF ＝KF ，AB ＝KB同理可证AG ＝HG ，AC ＝HC∴FG ＝21HK 又∵HK ＝BK －BH ＝AB ＋AC －BC∴)(21BC AC AB FG -+=图3结论为：)(21AB AC BC FG -+=27、解：（1）设购买污水处理设备A 型x 台，则B 型)10(x -台，由题意知：)10(1012x x -+≤105 ∴x ≤2.5又∵x 是非负整数 ∴x 可取0、1、2∴有三种购买方案：①购A 型0台，B 型10台；②购A 型1台，B 型9台；③购A 型2台，B 型8台；（2）由题意得)10(200240x x -+≥2040，解得x ≥1∴x 为1或2当x ＝1时，购买资金为：12×1＋10×9＝102（万元）当x ＝2时，购买资金为：12×2＋10×8＝104（万元） ∴为了节约资金，应选购A 型1台，B 型9台。

（3）10年企业自己处理污水的总资金为：102＋10×10＝202（万元）若将污水排到污水厂处理，10年所需费用为：2040×12×10×10＝2448000（元）＝244.8（万元） ∵244.8－202＝42.8（万元） ∴能节约资金42.8万元。

28、解：（1）∵AOC S ∆∶BOC S ∆＝1∶5第26题图2K H GFED CB A∴AC ∶OB ＝1∶5不妨设AC ＝k ，则OB ＝k 5 由题意得⎩⎨⎧+=⋅=+45652m k k mk k解得⎩⎨⎧==11k m 或⎩⎨⎧-=-=11k m （不符题意；舍去）∴AC ＝1，OB ＝5（2）∵∠OAC ＝∠BCO ＝900，∠ACO ＝∠BOC∴△OBC ∽△COA∴ACOCOC OB =，即AC OB OC ⋅=2 ∴OC ＝5或OC ＝－5（舍去）∵AC ＝1，AO ＝2 ∴C （1，2）∴直线OC 的解析式为y ＝x 2 （3）存在点M ，)1,21(1M ，)23,43(2M。