大学物理学(下册)答案第11章
大学-物理学-第五版-马文蔚-答案上下册第十一章

第十一章光学1、在双缝干涉实验中,两缝间距为mm 30.0,用单色光垂直照射双缝,在离缝m 20.1的屏上测得中央明纹一侧第5条暗纹与另一侧第5条暗纹间的距离为mm 78.22,问所用光的波长为多少?解:双缝干涉暗纹条件'(21)2d x k d λ=±+ (0,1,2,)k =⋅⋅⋅中央明纹一侧第5条暗纹对应于4=k ,由于条纹对称,该暗纹到中央明纹中心的距离为mm 39.11278.22==x 那么由暗纹公式即可求得 337'2211.39100.3010 6.32810m 632.8nm (21) 1.20(241)xd d k λ---⨯⨯⨯⨯===⨯=+⨯⨯+2、用白光垂直入射到间距为mm 25.0=d的双缝上,距离缝m 0.1处放置屏幕,求零级明纹同侧第二级干涉条纹中紫光和红光中心的间距(白光的波长范围是nm 760~400)。
解:第k 级明纹位置应满足'd x k dλ= ),2,1,0(⋅⋅⋅±±=k 对紫光和红光分别取nm 4001=λ,nm 7602=λ;则同侧第二级条纹的间距'3621 1.010()2(760400)10 2.88mm 0.25d x k d λλ-⨯∆=-=⨯⨯-⨯=3、用58.1=n 的透明云母片覆盖杨氏双缝干涉装置的一条缝,若此时屏中心为第五级亮条纹中心,设光源波长为μm 55.0,(1)求云母片厚度。
(2)若双缝相距mm 60.0,屏与狭缝的距离为m 5.2,求0级亮纹中心所在的位置。
解:(1)由于云母片覆盖一缝,使得屏中心处的光程差变为λ5=∆,一条光路中插入厚度为e 的透明介质片光程变化e n )1(-。
所以λ5)1(=-=∆e n解得云母片厚度μm 74.4158.155.0515=-⨯=-=n e λ(2)因为mm 29.260.055.05.2=⨯==∆d D x λ, 又由于中心位置为5级明纹中心,故级条纹距中心为5倍条纹宽度,所以m m 45.1129.2555=⨯=∆=x x4、如图所示,在折射率为50.1的平板玻璃表面有一层厚度为nm 300,折射率为22.1的厚度均匀透明油膜,用白光垂直射向油膜,问:(1)哪些波长的可见光在反射光中干涉加强?(2)若要使透射光中nm 550=λ的光干涉加强,油膜的最小厚度为多少?由上式可得:k dn 22=λ , 1=k 时: nm 732130022.121=⨯⨯=λ 红光 2=k 时: nm 366230022.122=⨯⨯=λ 紫外, 故反射中波长为nm 732的红光产生干涉加强。
第11章思考题解

《大学物理学》(下册)思考题解第11章11-1 在真空中两个点电荷之间的相互作用力是否会因为其他一些电荷被移近而改变答:不会。
两个点电荷之间的相互作用只与它们自己的电荷呈正比与它们之间的距离平方成反比,与其它物质无关。
11-2 有四个点电荷,电量均为q +,分别放在正方形的四个顶点。
问在正方形的中心应该放一个怎样的点电荷'q ,才能使每个电荷处于平衡解:设边长为1,取一个顶点为坐标原点。
如果其他三个顶点的电荷在原点产生的电场,与'q 在原点产生的电场的矢量和为零,则由对称性知,每个电荷都可处于平衡。
如图。
123q q q q ===,'q 待定。
10()4q E i πε=-, 20()4q E i j πε=--, 30()4q E j πε=-, 0'11'()422q E i j πε=-- 平衡时要求 123'0E E E E +++=,其X 分量和Y 分量都要求1'02q q q ---=,于是得:'4q q =-。
11-3 关于电场强度,请回答下列问题: (1)电场中某一点电场强度的定义为0FE q =,若该点未放试验电荷0q ,则该点是否有场强,为什么(2)电荷在电场中某点受到的电场力很大,该点的场强是否也一定很大 (3)有一带正电荷的金属球,其附近某点的场强为1E ,今在该点放一个•OX3E 2E 1E 'E带正电的点电荷1q ,测得1q 所受的力为1F ,若考虑到电量1q 不是足够小,则11F q 是大于,等于还是小该点的场强1E答:(1)电场中某一点的电场强度是电场的固有性质,与该点是否存在其它物质没有关系。
试验电荷0q 仅仅是为了测试该点的电场而放置的,如果试验电荷0q 足够小,它不会影响该点的电场强度的大小和方向。
(2)电荷在电场中某点受到的电场力的大小既与该点的电场性质有关,也与该电荷的大小有关。
如果该点电场数值很小,但放置的电荷数值很大,该电荷在该点受到的电场力也会很大。
大学物理(机械工业出版社)下册-课后练习标准答案

第11章 热力学基础11-1 在水面下50.0 m 深的湖底处(温度为4.0℃),有一个体积为1.0×10-5 m 3的空气泡升到湖面上来,若湖面的温度为17.0℃,求气泡到达湖面的体积。
(大气压P 0 = 1.013×105 Pa ) 分析:将气泡看成是一定量的理想气体,它位于湖底和上升至湖面代表两个不同的平衡状态。
利用理想气体物态方程即可求解本题。
位于湖底时,气泡内的压强可用公式gh p p ρ+=0求出,其中ρ为水的密度(常取ρ = 1.0⨯103 kg·m -3)。
解:设气泡在湖底和湖面的状态参量分别为(p 1,V 1,T 1)和(p 2,V 2,T 2)。
由分析知湖底处压强为gh p gh p p ρρ+=+=021。
利用理想气体的物态方程可得空气泡到达湖面的体积()3510120121212m 1011.6-⨯=+==T p V T gh p T p V T p V ρ11-2 氧气瓶的容积为3.2×10-2 m 3,其中氧气的压强为1.30×107 Pa ,氧气厂规定压强降到1.00×106 Pa 时,就应重新充气,以免经常洗瓶。
某小型吹玻璃车间,平均每天用去0.40 m 3 压强为1.01×105 Pa 的氧气,问一瓶氧气能用多少天?(设使用过程中温度不变) 分析:由于使用条件的限制,瓶中氧气不可能完全被使用。
从氧气质量的角度来分析。
利用理想气体物态方程pV = mRT /M 可以分别计算出每天使用氧气的质量m 3和可供使用的氧气总质量(即原瓶中氧气的总质量m 1和需充气时瓶中剩余氧气的质量m 2之差),从而可求得使用天数321/)(m m m n -=。
解:根据分析有RT V Mp m RT V Mp m RT V Mp m 333122111===;;则一瓶氧气可用天数()()5.933121321=-=-=V p V p p m m m n11-3 一抽气机转速ω=400rּmin -1,抽气机每分钟能抽出气体20升。
大学物理(下)十一章十二章作业与解答

大学物理(下)十一章十二章作业与解答————————————————————————————————作者:————————————————————————————————日期:第十一章恒定磁场一. 选择题1.在一平面内,有两条垂直交叉但相互绝缘的导线,流经两条导线的电流大小相等,方向如图,在哪些区域中有可能存在磁感应强度为零的点?(A) 在Ⅰ、Ⅲ象限(B) 在Ⅰ、Ⅳ象限(C) 在Ⅱ、Ⅲ象限(D) 在Ⅱ、Ⅳ象限[ ]2. 载流导线在同一平面内,形状如图,在圆心O处产生的磁感应强度大小为(A)(B)(C)(D) [ ]注意见第11章课件最后的总结的那个图,半圆载流回路在圆心处的磁感强度是多少?3. 一圆形回路1及一正方形回路2,圆的直径与正方形边长相等,二者中通有大小相同电流,则它们在各自中心处产生的磁感应强度大小之比为(A) 0.90(B) 1.00(C) 1.11(D) 1.22 [ ]注意教材page304,及课件最后总结的那个图4. 在磁感应强度为的均匀磁场中做一半径为r的半球面S,S边线所在平面的法线方向单位矢量与的夹角为θ,则通过半球面S的磁通量(取半球面向外为正)为(A)(B)(C)(D)[ ]5. 如图,无限长载流直导线附近有一正方形闭合曲面S,当S向导线靠近时,穿过S的磁通量和S上各点的磁感应强度的大小B将(A) 增大,B增强(B) 不变,B不变(C) 增大,B不变(D) 不变,B增强[ ]6. 取一闭合积分回路L,使若干根载流导线穿过它所围成的面,若改变这些导线之间的相互间隔,但不越出积分回路,则(A) 回路L内的电流的代数和不变,L上各点的不变(B) 回路L内的电流的代数和不变,L上各点的改变(C) 回路L内的电流的代数和改变,L上各点的不变(D) 回路L内的电流的代数和改变,L上各点的改变[ ]7. 如图,两根导线ab和cd沿半径方向被接到一个截面处处相等的铁环上,恒定电流I 从a端流入而从d端流出,则磁感应强度沿闭合路径L的积分等于(A)(B)(C)(D)[ ]8. 一电荷为q的粒子在均匀磁场中运动,下列说法正确的是(A) 只要速度大小相同,粒子所受的洛仑兹力就相同(B) 在速度不变的前提下,若电荷q变为 -q,则粒子受力反向,数值不变(C) 粒子进入磁场后,其动能和动量都不变(D) 洛仑兹力与速度方向垂直,所以带电粒子运动的轨迹必定是圆[ ]9. 质量为m、电量为q的粒子,以速度v垂直射入均匀磁场中,则粒子运动轨道包围范围的磁通量与磁感应强度的大小之间的关系曲线为[ b ]注意见P317,(11.30)10. 如图,长直载流导线与一圆形电流共面,并与其一直径相重合(两者间绝缘),设长直电流不动,则圆形电流将(A) 向上运动(B) 绕旋转(C) 向左运动(D) 向右运动(E) 不动[ ]11. 磁场中有一载流圆线圈,其既不受力也不受力矩作用,这说明(A) 该磁场一定均匀,且线圈的磁矩方向一定与磁场方向平行(B) 该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向平行(C) 该磁场一定均匀,且线圈的磁矩方向一定与磁场方向垂直(D) 该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向垂直[ ]注意见P325 第二段表述,11.36式12. 用细导线均匀密绕成长为l、半径为a(l >>a)、总匝数为N的螺线管,管内充满相对磁导率为的均匀磁介质,线圈中载有电流I,则管中任一点(A) 磁感应强度大小为(B) 磁感应强度大小为(C) 磁场强度大小为(D) 磁场强度大小为[ ]二. 填空题13.如图,电流元在P点产生的磁感应强度的大小为___________________.14. 真空中有一载有电流I的细圆线圈,则通过包围该线圈的闭合曲面S的磁通量Φ=________________. 若通过S面上某面元的磁通为,而线圈中电流增加为2I时,通过该面元的磁通为,则_______________.0 ; 1︰215. 如图,两平行无限长载流直导线中电流均为I,两导线间距为a,则两导线连线中点P的磁感应强度大小,磁感应强度沿图中环路L的线积分_______________________.0 ;16. 恒定磁场中,磁感应强度对任意闭合曲面的积分等于零,其数学表示式是____________,这表明磁感应线的特征是_________________________. ;闭合曲线17. 一长直螺线管是由直径的导线密绕而成,通以的电流,其内部的磁感应强度大小B =_____________________.(忽略绝缘层厚度)18. 带电粒子垂直磁感应线射入匀强磁场,它做______________运动;带电粒子与磁感应线成300角射入匀强磁场,则它做__________________运动;若空间分布有方向一致的电场和磁场,带电粒子垂直于场方向入射,则它做__________________运动.圆周;螺旋线;变螺距的螺旋线19. 在霍尔效应实验中,通过导电体的电流和的方向垂直(如图).如果上表面的电势较高,则导电体中的载流子带___________电荷;如果下表面的电势较高,则导电体中的载流子带___________电荷.正;负20. 如图,一载流导线弯成半径为R的四分之一圆弧,置于磁感应强度为的均匀磁场中,导线所受磁场力大小为______________,方向为_____________.; y轴正向注意:积分IRBdθ,θ的积分上下限?21. 如图,半径为R的半圆形线圈通有电流I,线圈处在与线圈平面平行指向右的均匀磁场中,该载流线圈磁矩大小为___________,方向____________;线圈所受磁力矩的大小为_________________,方向_____________.;垂直纸面向外;;向上22. 磁场中某点,有一半径为R、载有电流I的圆形实验线圈,其所受的最大磁力矩为M,则该点磁感应强度的大小为_________________.注意见教材324页三. 计算题23. 如图,两长直导线互相垂直放置,相距为d,其中一根导线与z轴重合,另一与x轴平行且在Oxy平面内,设导线中皆通有电流I,求y轴上与两导线等距的P点处的磁感应强度.解:长直载流导线在距其r处的磁感应强度为两长直载流导线在P点产生的磁感应强度方向一沿z轴方向,一沿x轴负方向且方向平行于Oxz平面与Oxy面成45o,如图示。
大学物理学第三版修订版下册第11章答案

习题 11选择题(1 )一圆形线圈在磁场中作以下运动时,那些状况会产生感觉电流()(A)沿垂直磁场方向平移;( B)以直径为轴转动,轴跟磁场垂直;(C)沿平行磁场方向平移;( D)以直径为轴转动,轴跟磁场平行。
[ 答案: B](2)以下哪些矢量场为守旧力场()(A)静电场;( B)稳恒磁场;( C)感生电场;(D)变化的磁场。
[ 答案: A](3)用线圈的自感系数L 来表示载流线圈磁场能量的公式W m 1LI2()2( A )只合用于无穷长密绕线管;( B )只合用于一个匝数好多,且密绕的螺线环;( C )只合用于单匝圆线圈;( D ) 合用于自感系数 L必定的随意线圈。
[ 答案: D](4) 关于涡旋电场,以下说法不正确的选项是():( A)涡旋电场对电荷有作使劲;(B)涡旋电场由变化的磁场产生;( C)涡旋场由电荷激发;( D)涡旋电场的电力线闭合的。
[ 答案: C]11.2填空题(1) 将金属圆环从磁极间沿与磁感觉强度垂直的方向抽出时,圆环将遇到。
[答案:磁力 ](2) 产生动生电动势的非静电场力是,产生感生电动势的非静电场力是,激发感生电场的场源是。
[答案:洛伦兹力,涡旋电场力,变化的磁场](3)长为 l的金属直导线在垂直于平均的平面内以角速度ω 转动,假如转轴的地点在,这个导线上的电动势最大,数值为;假如转轴的地点在,整个导线上的电动势最小,数值为。
[ 答案:端点,1 B l 2;中点,0]2一半径 r =10cm的圆形回路放在 B =的平均磁场中.回路平面与 B 垂直.当回路半径以恒定速率dr=80cm·s-1缩短时,求回路中感觉电动势的大小.dt解 :回路磁通m BS Bπr 2感觉电动势大小d m d(B πr 2)B2πrdr0.40 Vdtdt dt一对相互垂直的相等的半圆形导线组成回路,半径R =5cm ,如题图所示.平均磁场-3T , B 的方向与两半圆的公共直径( 在 Oz 轴上 ) 垂直,且与两个半圆组成相等的B =80× 10 角 当磁场在 5ms 内平均降为零时,求回路中的感觉电动势的大小及方向.解 :取半圆形 cba 法向为 i ,题图πR 2则mB cos12同理,半圆形adc 法向为 j ,则πR 2m 2B cos2∵B 与 i 夹角和 B 与 j 夹角相等,∴ 45则π 2 cosm B Rd m πR 2 cosdB 8 .8910 2Vd td t方向与 cbadc 相反,即顺时针方向.题图如题图所示,载有电流I 的长直导线邻近,放一导体半圆环MeN 与长直导线共面,且端点 MN 的连线与长直导线垂直.半圆环的半径为 b ,环心 O 与导线相距 a .设半圆环以速 度 v 平行导线平移.求半圆环内感觉电动势的大小和方向及 MN 两头的电压U MU N .解 : 作协助线 MN ,则在 MeNM 回路中,沿 v 方向运动时 dm∴MeNM即MeNMNa b dl0 Iv ln a b又∵MNvBcosa b2a b因此 MeN 沿 NeM 方向,大小为Ivlnab2a bM 点电势高于 N 点电势,即U M0 Iva bU Nlnb2 a 题图如题所示,在两平行载流的无穷长直导线的平面内有一矩形线圈. 两导线中的电流方向相反、大小相等,且电流以dI的变化率增大,求:dt(1) 任一时辰线圈内所经过的磁通量;(2) 线圈中的感觉电动势. 解 : 以向外磁通为正则 (1)(2)mb a 0 Il drd a 0 Ildr0Il[ln b a lnd a]b2πrd2πr2πbdd 0l[lndalnba ] dIt πdbdtd2如题图所示, 用一根硬导线弯成半径为r 的一个半圆. 令这半圆形导线在磁场中以频次 f绕图中半圆的直径旋转.整个电路的电阻为R .求:感觉电流的最大值.题图解 :B S Bπr2t 0 )m2 cos(dmπ 2iB rsin( t 0 )dt2∴π2 π 22πf π2 r 2 BfmB rB r 2222 Bf∴ImπrRR如题图所示,长直导线通以电流 I =5A ,在其右方放一长方形线圈,二者共面.线圈长-1垂直于直线平移远离.求:d =0.05mb =0.06m ,宽 a =0.04m ,线圈以速度 v =0.03m ·s 时线圈中感觉电动势的大小和方向.题图解 : AB 、 CD 运动速度 v 方向与磁力线平行,不产生感觉电动势.DA 产生电动势A B) dlvBb vb0 I1(vD2 dBC 产生电动势C B) dlvb0 I2(v 2π(a d )B∴回路中总感觉电动势120Ibv( 1 1 ) 1.6 10 8V π d d a2方向沿顺时针.长度为 l 的金属杆 ab 以速率 v 在导电轨道 abcd 上平行挪动.已知导轨处于平均磁场B 中,B 的方向与回路的法线成60°角 (如题图所示 ), B 的大小为B = kt (k 为正常 ).设时杆t =0位于 cd 处,求:任一时辰 t 导线回路中感觉电动势的大小和方向.解 :mB dS Blvt cos60kt 2lv11klvt 22 2∴dmklvtdt即沿 abcd 方向顺时针方向.题图一矩形导线框以恒定的加快度向右穿过一平均磁场区, B 的方向如题图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系( 设导线框刚进入磁场区时 t =0) .解 : 如图逆时针为矩形导线框正向,则进入时d0, 0 ;dt题图 (a) 题图 (b)在磁场中时d0 , 0;dt出场时d0 , 0,故 I t 曲线如题 10-9 图(b) 所示 .dt题图导线 ab 长为 l ,绕过 O 点的垂直轴以匀角速转动, aO = l磁感觉强度 B 平行于转轴,3如下图.试求:( 1) ab 两头的电势差;( 2) a,b 两头哪一点电势高 ?解: (1)在 Ob 上取 rr dr 一小段2l2B则Ob3 rB drl 29l1 B 同理Oa3rB drl 20 18∴abaO Ob(12)B l 21 B l 21896(2) ∵ab0 即 U a U b∴ b 点电势高.题图如题图所示,长度为 2b 的金属杆位于两无穷长直导线所在平面的正中间,并以速度 v 平行于两直导线运动.两直导线通以大小相等、方向相反的电流 I ,两导线相距 2 a .试求:金属杆两头的电势差及其方向.解:在金属杆上取dr 距左侧直导线为r ,则B dla b 0 Iv 11)dr0 Iv a bAB(v B)a b(lnA2r2a r a b∵AB∴实质上感觉电动势方向从 BA ,即从图中从右向左,∴U ABIvlnaba b题图磁感觉强度为B 的平均磁场充满一半径为 R 的圆柱形空间, 一金属杆放在题图中地点,杆长为2 R ,此中一半位于磁场内、另一半在磁场外.当dB>0时,求:杆两头的感觉电动势的大小dt和方向.解:∵acabbcdabdtdabdt ∴∵1d [3R2 B]3R dBdt44dtd [π2B]π2dB 2R Rdt1212dt[ 3R2π2ac R ] dB412dtdBdt∴ac0 即从a c半径为 R的直螺线管中,有dB>0的磁场,一随意闭合导线abca ,一部分在螺线管内绷直dt成 ab 弦, a , b 两点与螺线管绝缘,如题10-13 图所示.设ab= R,试求:闭合导线中的感觉电动势.解:如图,闭合导线 abca 内磁通量B S π 23R2m B(R)64(π23 R2) dB∴i R64dt∵dB0 dt∴i 0 ,即感觉电动势沿acba ,逆时针方向.题图题图如题图所示,在垂直于直螺线管管轴的平面上搁置导体 ab 于直径地点,另一导体 cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬时管内磁场如题图示方向.试求:(1)ab两头的电势差;(2)cd两点电势高低的状况.解:由E旋 dl dBdS 知,此时 E旋以 O 为中心沿逆时针方向.l dt(1)∵ ab 是直径,在 ab 上到处 E旋与 ab 垂直∴旋 dl 0l∴ ab 0, 有 U a U b(2) 同理,cE dldcd旋∴U d U c 0 即 U c U d题图一无穷长的直导线和一正方形的线圈如题图所示搁置 ( 导线与线圈接触处绝缘 ) .求:线圈与导线间的互感系数. 解: 设长直电流为I ,其磁场经过正方形线圈的互感磁通为2a 0 Ia0 Ia3dr12ln 23a2πr2π∴M12aln 2I 2π两线圈顺串连后总自感为, 在它们的形状和地点都不变的状况下,反串连后总自感为. 试求:它们之间的互感.解: ∵顺串时 LL 1 L 2 2M反串连时 L L 1 L 22M∴L L 4MM L L4 0.15 H题图一矩形截面的螺绕环如题图所示,共有 N 匝.试求:(1) 此螺线环的自感系数;(2) 若导线内通有电流 I ,环内磁能为多少 ? 解:如题图示(1) 经过横截面的磁通为0 NI hdrNIhlnbba2r π2πa磁链N0 N 2Ihb2πlna∴L0 N2hb2πlnIa(2) ∵W m 1LI 22∴0 N 2 I 2hln bW m4πa一无穷长圆柱形直导线,其截面各处的电流密度相等,总电流为 I .求:导线内部单位长度上所储藏的磁能.解:在 rR 时B0 Ir2πR2B 20 I2r 2∴w m2 428 π R取dV 2πrdr ( ∵导线长 l 1 )0 I 2 3 0I2RRr dr则Ww m 2 r dr4πR4 16π。
大学物理学第三版修订版下册第11章答案

习题1111.1选择题(1)一圆形线圈在磁场中作下列运动时,那些情况会产生感应电流() (A )沿垂直磁场方向平移;(B )以直径为轴转动,轴跟磁场垂直; (C )沿平行磁场方向平移;(D )以直径为轴转动,轴跟磁场平行。
[答案:B](2)下列哪些矢量场为保守力场() (A ) 静电场;(B )稳恒磁场;(C )感生电场;(D )变化的磁场。
[答案:A](3) 用线圈的自感系数 L 来表示载流线圈磁场能量的公式221LI W m=()( A )只适用于无限长密绕线管; ( B ) 只适用于一个匝数很多,且密绕的螺线环; ( C ) 只适用于单匝圆线圈; ( D )适用于自感系数L 一定的任意线圈。
[答案:D](4)对于涡旋电场,下列说法不正确的是():(A )涡旋电场对电荷有作用力; (B )涡旋电场由变化的磁场产生; (C )涡旋场由电荷激发; (D )涡旋电场的电力线闭合的。
[答案:C]11.2 填空题(1)将金属圆环从磁极间沿与磁感应强度垂直的方向抽出时,圆环将受到 。
[答案:磁力](2)产生动生电动势的非静电场力是 ,产生感生电动势的非静电场力是 ,激发感生电场的场源是 。
[答案:洛伦兹力,涡旋电场力,变化的磁场](3)长为l 的金属直导线在垂直于均匀的平面内以角速度ω转动,如果转轴的位置在 ,这个导线上的电动势最大,数值为 ;如果转轴的位置在 ,整个导线上的电动势最小,数值为 。
[答案:端点,221l B ω;中点,0]11.3一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中.回路平面与B ϖ垂直.当回路半径以恒定速率tr d d =80cm ·s -1收缩时,求回路中感应电动势的大小. 解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V11.4 一对互相垂直的相等的半圆形导线构成回路,半径R =5cm ,如题11.4图所示.均匀磁场B =80×10-3T ,B 的方向与两半圆的公共直径(在Oz 轴上)垂直,且与两个半圆构成相等的角α当磁场在5ms 内均匀降为零时,求回路中的感应电动势的大小及方向.解: 取半圆形cba 法向为i ϖ, 题11.4图则 αΦcos 2π21B R m =同理,半圆形adc 法向为j ϖ,则αΦcos 2π22B R m=∵ B ϖ与i ϖ夹角和B ϖ与j ϖ夹角相等,∴ ︒=45α 则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV 方向与cbadc 相反,即顺时针方向.题11.5图 11.5 如题11.5图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压N M U U -.解: 作辅助线MN ,则在MeNM 回路中,沿v ϖ方向运动时0d =m Φ∴ 0=MeNM ε 即 MN MeN εε= 又∵ ⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2d cos 0πμπε 所以MeN ε沿NeM 方向,大小为ba ba Iv -+ln 20πμ M 点电势高于N 点电势,即b a ba Iv U U N M -+=-ln 20πμ题11.6图11.6如题11.6所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以tId d 的变化率增大,求: (1)任一时刻线圈内所通过的磁通量; (2)线圈中的感应电动势. 解: 以向外磁通为正则 (1) ]ln [lnπ2d π2d π2000dad b a b Ilr l rIr l rIab bad dm +-+=-=⎰⎰++μμμΦ (2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε11.7 如题11.7图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题11.7图解: )cos(2π02ϕωΦ+=⋅=t r B S B m ϖϖ ∴ Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε ∴ RBfr R I m22π==ε11.8 如题11.8图所示,长直导线通以电流I =5A ,在其右方放一长方形线圈,两者共面.线圈长b =0.06m ,宽a =0.04m ,线圈以速度v =0.03m ·s -1垂直于直线平移远离.求:d =0.05m 时线圈中感应电动势的大小和方向.题11.8图解: AB 、CD 运动速度v ϖ方向与磁力线平行,不产生感应电动势. DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεϖϖϖBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰μεϖϖϖ∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针.11.9 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动.已知导轨处于均匀磁场Bϖ中,B ϖ的方向与回路的法线成60°角(如题11.9图所示),B ϖ的大小为B =kt (k 为正常).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向. 解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m ϖϖΦ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向.题11.9图11.10 一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B ϖ的方向如题11.10图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0). 解: 如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε; 题11.10图(a)题11.10图(b)在磁场中时0d d =tΦ,0=ε; 出场时0d d >tΦ,0<ε,故t I -曲线如题10-9图(b)所示. 题11.11图11.11 导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动,aO =3l磁感应强度B 平行于转轴,如图11.11所示.试求: (1)ab 两端的电势差;(2)b a ,两端哪一点电势高? 解: (1)在Ob 上取dr r r +→一小段 则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高.题11.12图11.12 如题11.12图所示,长度为b 2的金属杆位于两无限长直导线所在平面的正中间,并以速度v ϖ平行于两直导线运动.两直导线通以大小相等、方向相反的电流I ,两导线相距2a .试求:金属杆两端的电势差及其方向.解:在金属杆上取r d 距左边直导线为r ,则 ba b a Iv r r a r Iv l B v b a b a BA AB-+-=-+-=⋅⨯=⎰⎰+-ln d )211(2d )(00πμπμεϖϖϖ ∵ 0<AB ε ∴实际上感应电动势方向从A B →,即从图中从右向左, ∴ ba ba Iv U AB -+=ln 0πμ题11.13图11.13 磁感应强度为B ϖ的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在题11.13图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tBd d >0时,求:杆两端的感应电动势的大小和方向.解: ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε =-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=-- ∴ tB R R acd d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a →11.14 半径为R 的直螺线管中,有dtdB>0的磁场,一任意闭合导线abca ,一部分在螺线管内绷直成ab 弦,a ,b 两点与螺线管绝缘,如题10-13图所示.设ab =R ,试求:闭合导线中的感应电动势.解:如图,闭合导线abca 内磁通量)436π(22R R B S B m -=⋅=ϖϖΦ∴ tB R R i d d )436π(22--=ε ∵0d d >tB∴0<i ε,即感应电动势沿acba ,逆时针方向.题11.14图题11.15图11.15 如题11.15图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题11.15图示方向.试求:(1)ab 两端的电势差;(2)cd 两点电势高低的情况.解: 由⎰⎰⋅-=⋅l S t B l E ϖϖϖϖd d d d 旋知,此时旋E ϖ以O 为中心沿逆时针方向. (1)∵ab 是直径,在ab 上处处旋E ϖ与ab 垂直∴ ⎰=⋅ll 0d ϖ旋∴0=ab ε,有b a U U =(2)同理, 0d >⋅=⎰l E cddc ϖϖ旋ε∴ 0<-c d U U 即d c U U >题11.16图11.16 一无限长的直导线和一正方形的线圈如题11.16图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解: 设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2a a Iar rIaμμΦ∴ 2ln π2012aIM μΦ==11.17两线圈顺串联后总自感为1.0H ,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H .试求:它们之间的互感. 解: ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H题11.18图11.18 一矩形截面的螺绕环如题11.18图所示,共有N 匝.试求: (1)此螺线环的自感系数;(2)若导线内通有电流I ,环内磁能为多少? 解:如题11.18图示 (1)通过横截面的磁通为 ⎰==baab NIhr h r NIlnπ2d π200μμΦ 磁链 ab IhN N lnπ220μΦψ== ∴ ab hN IL lnπ220μψ==(2)∵ 221LI W m =∴ ab hI N W m ln π4220μ=11.19 一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能. 解:在R r <时 20π2RI B rμ=∴ 4222002π82Rr I B w m μμ== 取 r r V d π2d =(∵导线长1=l ) 则 ⎰⎰===RRm I Rrr I r r w W 0204320π16π4d d 2μμπ(资料素材和资料部分来自网络,供参考。
大学物理答案解析第11章

第十一章 恒定磁场11-1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管,两个螺线管的长度相同,R =2r ,螺线管通过的电流相同为I ,螺线管中的磁感强度大小r R B B 、满足( )(A ) r R B B 2= (B ) r R B B = (C ) r R B B =2 (D )r R B B 4=分析与解 在两根通过电流相同的螺线管中,磁感强度大小与螺线管线圈单位长度的匝数成正比.根据题意,用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为(C ).11-2 一个半径为r 的半球面如图放在均匀磁场中,通过半球面的磁通量 为( )(A )B r 2π2 (B ) B r 2π(C )αB r cos π22(D ) αB r cos π2题 11-2 图分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面,根据磁场的高斯定理,磁感线是闭合曲线,闭合曲面的磁通量为零,即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量;S B ⋅=m Φ.因而正确答案为(D ).11-3 下列说法正确的是( )(A ) 闭合回路上各点磁感强度都为零时,回路内一定没有电流穿过 (B ) 闭合回路上各点磁感强度都为零时,回路内穿过电流的代数和必定为零 (C ) 磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度必定为零(D ) 磁感强度沿闭合回路的积分不为零时,回路上任意一点的磁感强度都不可能为零 分析与解 由磁场中的安培环路定律,磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度不一定为零;闭合回路上各点磁感强度为零时,穿过回路的电流代数和必定为零.因而正确答案为(B ).11-4 在图(a)和(b)中各有一半径相同的圆形回路L1 、L2 ,圆周内有电流I1 、I2 ,其分布相同,且均在真空中,但在(b)图中L2 回路外有电流I3 ,P 1 、P 2 为两圆形回路上的对应点,则( ) (A ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B= (B ) ⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B= (C ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B≠ (D )⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B≠题 11-4 图分析与解 由磁场中的安培环路定律,积分回路外的电流不会影响磁感强度沿回路的积分;但同样会改变回路上各点的磁场分布.因而正确答案为(C ).11-5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中,若导体中流过的恒定电流为I ,磁介质的相对磁导率为μr (μr<1),则磁介质内的磁化强度为( ) (A )()r I μr π2/1-- (B ) ()r I μr π2/1- (C ) r I μr π2/- (D ) r μI r π2/分析与解 利用安培环路定理可先求出磁介质中的磁场强度,再由M =(μr-1)H 求得磁介质内的磁化强度,因而正确答案为(B ).11-6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道,当环中电子流强度为8 mA 时,在整个环中有多少电子在运行? 已知电子的速率接近光速. 分析 一个电子绕存储环近似以光速运动时,对电流的贡献为c I e I /Δ=,因而由lNecI =,可解出环中的电子数.解 通过分析结果可得环中的电子数10104⨯==ecIlN 11-7 已知铜的摩尔质量M =63.75 g·mol -1 ,密度ρ =8.9 g · cm -3 ,在铜导线里,假设每一个铜原子贡献出一个自由电子,(1)为了技术上的安全,铜线内最大电流密度26.0A mm m j -=⋅ ,求此时铜线内电子的漂移速率v d ;(2) 在室温下电子热运动的平均速率是电子漂移速率v d 的多少倍?分析 一个铜原子的质量A N M m /=,其中N A 为阿伏伽德罗常数,由铜的密度ρ 可以推算出铜的原子数密度m ρn /=根据假设,每个铜原子贡献出一个自由电子,其电荷为e ,电流密度d m ne j v = .从而可解得电子的漂移速率v d .将电子气视为理想气体,根据气体动理论,电子热运动的平均速率em kTπ8=v 其中k 为玻耳兹曼常量,m e 为电子质量.从而可解得电子的平均速率与漂移速率的关系.解 (1) 铜导线单位体积的原子数为M ρN n A /=电流密度为j m 时铜线内电子的漂移速率14A s m 1046.4--⋅⨯===eN Mj ne j m m d ρv(2) 室温下(T =300 K)电子热运动的平均速率与电子漂移速率之比为81042.2π81⨯≈=ed d m kTv v v 室温下电子热运动的平均速率远大于电子在恒定电场中的定向漂移速率.电子实际的运动是无规热运动和沿电场相反方向的漂移运动的叠加.考虑到电子的漂移速率很小,电信号的信息载体显然不会是定向漂移的电子.实验证明电信号是通过电磁波以光速传递的. 11-8 有两个同轴导体圆柱面,它们的长度均为20 m ,内圆柱面的半径为3.0 mm ,外圆柱面的半径为9.0 mm.若两圆柱面之间有10 μA 电流沿径向流过,求通过半径为6.0 mm 的圆柱面上的电流密度.题 11-8 图分析 如图所示是同轴柱面的横截面,电流密度j对中心轴对称分布.根据恒定电流的连续性,在两个同轴导体之间的任意一个半径为r 的同轴圆柱面上流过的电流I 都相等,因此可得rlI j π2=解 由分析可知,在半径r =6.0 mm 的圆柱面上的电流密度2m A μ3.13π2-⋅==rlIj 11-9 如图所示,已知地球北极地磁场磁感强度B 的大小为6.0×10-5T .如设想此地磁场是由地球赤道上一圆电流所激发的,此电流有多大? 流向如何?解 设赤道电流为I ,则由教材第11-4节例2 知,圆电流轴线上北极点的磁感强度()RIRR IR B 24202/32220μμ=+=因此赤道上的等效圆电流为A 1073.12490⨯==μRBI 由于在地球地磁场的N 极在地理南极,根据右手螺旋法则可判断赤道圆电流应该是由东向西流,与地球自转方向相反.题 11-9 图11-10 如图所示,有两根导线沿半径方向接触铁环的a 、b 两点,并与很远处的电源相接.求环心O 的磁感强度.题 11-10 图分析 根据叠加原理,点O 的磁感强度可视作由ef 、be 、fa 三段直线以及acb 、a d b 两段圆弧电流共同激发.由于电源距环较远,0=ef B .而be 、fa 两段直线的延长线通过点O ,由于0Idl r ⨯=,由毕奥-萨伐尔定律知0be fa ==B B .流过圆弧的电流I 1 、I 2的方向如图所示,两圆弧在点O 激发的磁场分别为21101π4r l I μB =,22202π4r l I μB = 其中l 1 、l 2 分别是圆弧acb 、a d b 的弧长,由于导线电阻R 与弧长l 成正比,而圆弧acb 、a d b 又构成并联电路,故有2211l I l I =将21B B 、叠加可得点O 的磁感强度B . 解 由上述分析可知,点O 的合磁感强度0π4π42220211021=-=-=r l I μr l I μB B B 11-11 如图所示,几种载流导线在平面内分布,电流均为I ,它们在点O 的磁感强度各为多少?题 11-11 图分析 应用磁场叠加原理求解.将不同形状的载流导线分解成长直部分和圆弧部分,它们各自在点O 处所激发的磁感强度较容易求得,则总的磁感强度∑=iB B 0.解 (a) 长直电流对点O 而言,有0d =⨯rl I ,因此它在点O 产生的磁场为零,则点O 处总的磁感强度为1/4 圆弧电流所激发,故有RIμB 800=B 0 的方向垂直纸面向外.(b) 将载流导线看作圆电流和长直电流,由叠加原理可得RIμR I μB π22000-=B 0 的方向垂直纸面向里.(c ) 将载流导线看作1/2 圆电流和两段半无限长直电流,由叠加原理可得RIμR I μR I μR I μR I μB 4π24π4π4000000+=++=B 0 的方向垂直纸面向外.11-12 载流导线形状如图所示(图中直线部分导线延伸到无穷远),求 点O 的磁感强度B .题 11-12 图分析 由教材11-4 节例题2的结果不难导出,圆弧载流导线在圆心激发的磁感强度RαI μB π40=,其中α为圆弧载流导线所张的圆心角,磁感强度的方向依照右手定则确定;半无限长载流导线在圆心点O 激发的磁感强度RIμB π40=,磁感强度的方向依照右手定则确定. 点O 的磁感强度O B 可以视为由圆弧载流导线、半无限长载流导线等激发的磁场在空间点O 的叠加. 解 根据磁场的叠加 在图(a)中,k i k k i B RI μR I μR I μR I μR I μπ24π4π44000000--=---= 在图(b)中,k i k i i B RI μR I μR I μR I μR I μπ41π14π44π4000000-⎪⎭⎫ ⎝⎛+-=---= 在图(c )中,k j i B RIμR I μR I μπ4π4830000---= 11-13 如图(a)所示,载流长直导线的电流为I ,试求通过矩形面积的磁通量.题 11-13 图分析 由于矩形平面上各点的磁感强度不同,故磁通量Φ≠BS .为此,可在矩形平面上取一矩形面元d S =l d x ,如图(b)所示,载流长直导线的磁场穿过该面元的磁通量为x l xId π2d d 0μ=⋅=ΦS B矩形平面的总磁通量ΦΦ⎰=d解 由上述分析可得矩形平面的总磁通量⎰==Φ211200lnπ2d π2d dd d Ilx l xIμμ 11-14 已知10 mm 2 裸铜线允许通过50 A 电流而不会使导线过热.电流在导线横截面上均匀分布.求导线内、外磁感强度的分布.题 11-14 图分析 可将导线视作长直圆柱体,电流沿轴向均匀流过导体,故其磁场必然呈轴对称分布,即在与导线同轴的圆柱面上的各点,B 大小相等、方向与电流成右手螺旋关系.为此,可利用安培环路定理,求出导线表面的磁感强度.解 围绕轴线取同心圆为环路L ,取其绕向与电流成右手螺旋关系,根据安培环路定理,有∑⎰=⋅=⋅I μB 0πr 2d l B在导线内r <R , 2222ππRIr r R I I ==∑,因而 202πRIrμB =在导线外r >R ,I I =∑,因而rIμB 2π0=磁感强度分布曲线如图所示.11-15有一同轴电缆,其尺寸如图(a)所示.两导体中的电流均为I,但电流的流向相反,导体的磁性可不考虑.试计算以下各处的磁感强度:(1)r<R1;(2)R1<r<R2;(3)R2<r<R3;(4)r>R3.画出B-r图线.题11-15 图分析同轴电缆导体内的电流均匀分布,其磁场呈轴对称,取半径为r的同心圆为积分路径,πr2d⋅=⋅⎰BlB,利用安培环路定理∑⎰=⋅Iμd lB,可解得各区域的磁感强度.解由上述分析得r<R12211ππ12πrRμrB=⋅2112πRIrμB=R1<r<R2IμrB22π=⋅rIμB2π2=R2<r<R3()()⎥⎦⎤⎢⎣⎡---=⋅IRRRrIμrB2223223ππ2π222322332πRRrRrIμB--=r >R 3()02π04=-=⋅I I μr B04=B磁感强度B (r )的分布曲线如图(b).11-16 如图所示,N 匝线圈均匀密绕在截面为长方形的中空骨架上.求通入电流I 后,环内外磁场的分布.题 11-16 图分析 根据右手螺旋法则,螺线管内磁感强度的方向与螺线管中心轴线构成同心圆,若取半径为r 的圆周为积分环路,由于磁感强度在每一环路上为常量,因而πr 2d ⋅=⋅⎰B l B依照安培环路定理∑⎰=⋅I μ0d l B ,可以解得螺线管内磁感强度的分布.解 依照上述分析,有∑=⋅I μr B 02πr <R 102π1=⋅r B 01=BR 2 >r >R 1NI μr B 022π=⋅rNIμB 2π02=r >R 202π3=⋅r B 03=B在螺线管内磁感强度B 沿圆周,与电流成右手螺旋.若112R R R <<- 和R 2 ,则环内的磁场可以近似视作均匀分布,设螺线环的平均半径()1221R R R +=,则环内的磁感强度近似为RNIμB 2π0≈11-17 电流I 均匀地流过半径为R 的圆形长直导线,试计算单位长度导线内的磁场通过图中所示剖面的磁通量.题 11-17 图分析 由题11-14 可得导线内部距轴线为r 处的磁感强度()202πR Irμr B =在剖面上磁感强度分布不均匀,因此,需从磁通量的定义()S B d ⎰=r Φ来求解.沿轴线方向在剖面上取面元dS =l dr ,考虑到面元上各点B 相同,故穿过面元的磁通量dΦ=B dS ,通过积分,可得单位长度导线内的磁通量⎰=Sr B Φd解 由分析可得单位长度导线内的磁通量4πd 2π0020Iμr R Ir μΦR==⎰11-18 已知地面上空某处地磁场的磁感强度40.410T B -=⨯,方向向北.若宇宙射线中有一速率715.010m s -=⨯g v 的质子,垂直地通过该处.求:(1)洛伦兹力的方向;(2) 洛伦兹力的大小,并与该质子受到的万有引力相比较.题 11-18 图解 (1) 依照B F ⋅=v q L 可知洛伦兹力L F 的方向为B ⊥v 的方向,如图所示. (2) 因B ⊥v ,质子所受的洛伦兹力N 102.316-⨯==B F v q L在地球表面质子所受的万有引力N 1064.126p -⨯==g m G因而,有101095.1/⨯=G F L ,即质子所受的洛伦兹力远大于重力.11-19 霍尔效应可用来测量血流的速度,其原理如图所示.在动脉血管两侧分别安装电极并加以磁场.设血管直径为d =2.0 mm ,磁场为B =0.080 T ,毫伏表测出血管上下两端的电压为U H =0.10 mV ,血流的流速为多大?题 11-19 图分析 血流稳定时,有H qE B q =v由上式可以解得血流的速度. 解 依照分析m/s 63.0===dBU B E HH v 11-20 带电粒子在过饱和液体中运动,会留下一串气泡显示出粒子运动的径迹.设在气泡室有一质子垂直于磁场飞过,留下一个半径为3.5 cm 的圆弧径迹,测得磁感强度为0.20 T,求此质子的动量和动能.解 根据带电粒子回转半径与粒子运动速率的关系有m /s kg 1012.121⋅⨯===-ReB m p vkeV 35.222==mp E k11-21 从太阳射来的速度为0.80×108 m/s 的电子进入地球赤道上空高层范艾伦辐射带中,该处磁场为4.0 ×10-7T,此电子回转轨道半径为多大? 若电子沿地球磁场的磁感线旋进到地磁北极附近,地磁北极附近磁场为2.0 ×10-5T,其轨道半径又为多少? 解 由带电粒子在磁场中运动的回转半径高层范艾伦辐射带中的回转半径m 101.1311⨯==eB m R v地磁北极附近的回转半径m 2322==eB m R v11-22 如图(a)所示,一根长直导线载有电流I 1 =30 A ,矩形回路载有电流I 2 =20 A .试计算作用在回路上的合力.已知d =1.0 cm ,b =8.0 cm ,l =0.12 m .题 11-22图分析 矩形上、下两段导线受安培力F 1 和F 2 的大小相等,方向相反,对不变形的矩形回路来说,两力的矢量和为零.而矩形的左右两段导线,由于载流导线所在处磁感强度不等,所受安培力F 3 和F 4 大小不同,且方向相反,因此线框所受的力为这两个力的合力.解 由分析可知,线框所受总的安培力F 为左、右两边安培力F 3 和F 4 之矢量和,如图(b)所示,它们的大小分别为dlI I μF π22103=()b d lI I μF +=π22104故合力的大小为()N 1028.1π2π2321021043-⨯=+-=-=b d lI I μd l I I μF F F 合力的方向朝左,指向直导线.11-23 一直流变电站将电压为500kV 的直流电,通过两条截面不计的平行输电线输向远方.已知两输电导线间单位长度的电容为3.0×10-11F ·m -1 ,若导线间的静电力与安培力正好抵消.求:(1) 通过输电线的电流;(2) 输送的功率.分析 当平行输电线中的电流相反时,它们之间存在相互排斥的安培力,其大小可由安培定律确定.若两导线间距离为d ,一导线在另一导线位置激发的磁感强度dIμB π20=,导线单位长度所受安培力的大小BI F B =.将这两条导线看作带等量异号电荷的导体,因两导线间单位长度电容C 和电压U 已知,则单位长度导线所带电荷λ=CU ,一导线在另一导线位置所激发的电场强度dελE 0π2=,两导线间单位长度所受的静电吸引力λE F E =.依照题意,导线间的静电力和安培力正好抵消,即0=+E B F F从中可解得输电线中的电流.解 (1) 由分析知单位长度导线所受的安培力和静电力分别为dI μBI F B π220==dεU C λE F E 022π2== 由0=+E BF F 可得dεU C d I μ02220π2π2=解得A 105.4300⨯==μεCUI (2) 输出功率W 1025.29⨯==IU N11-24 在氢原子中,设电子以轨道角动量π2/h L =绕质子作圆周运动,其半径为m 1029.5110-⨯=a .求质子所在处的磁感强度.h 为普朗克常量,其值为s J 1063.634⋅⨯-分析 根据电子绕核运动的角动量π20h a m L ==v 可求得电子绕核运动的速率v .如认为电子绕核作圆周运动,其等效圆电流v/π20a e T e i ==在圆心处,即质子所在处的磁感强度为02a i μB =解 由分析可得,电子绕核运动的速率π2ma h=v其等效圆电流2020π4/π2ma hev a e i ==该圆电流在圆心处产生的磁感强度T 5.12π82202000===ma heμa i μB 11-25 如图[a]所示,一根长直同轴电缆,内、外导体之间充满磁介质,磁介质的相对磁导率为μr (μr <1),导体的磁化可以忽略不计.沿轴向有恒定电流I 通过电缆,内、外导体上电流的方向相反.求:(1) 空间各区域内的磁感强度和磁化强度;*(2) 磁介质表面的磁化电流.题 11-25 图分析 电流分布呈轴对称,依照右手定则,磁感线是以电缆对称轴线为中心的一组同心圆.选取任一同心圆为积分路径,应有⎰⋅=⋅r H d π2l H ,利用安培环路定理⎰∑=⋅fId l H求出环路内的传导电流,并由H μB =,()H μM r 1-=,可求出磁感强度和磁化强度.再由磁化电流的电流面密度与磁化强度的关系求出磁化电流.解 (1) 取与电缆轴同心的圆为积分路径,根据磁介质中的安培环路定理,有∑=fπ2I r H对r <R 1221f ππr R I I =∑ 得2112πR IrH =忽略导体的磁化(即导体相对磁导率μr =1),有01=M ,21012πR IrμB =对R 2 >r >R 1I I=∑f得rI H 2π2=填充的磁介质相对磁导率为μr ,有()r I μM r 2π12-=,rI μμB r 2π02= 对R 3 >r >R 2()()2223223ππR r R R I I I f -⋅--=∑ 得()()222322332πR R r r R I H --= 同样忽略导体的磁化,有03=M ,()()2223223032πR R r r R I μB --= 对r >R 30=-=∑I I If得04=H ,04=M ,04=B(2) 由r M I s 2π⋅=,磁介质内、外表面磁化电流的大小为()()I μR R M I r si 12π112-=⋅= ()()I μR R M I r se 12π222-=⋅=对抗磁质(1r μ<),在磁介质内表面(r =R 1 ),磁化电流与内导体传导电流方向相反;在磁介质外表面(r =R 2 ),磁化电流与外导体传导电流方向相反.顺磁质的情况与抗磁质相反.H (r )和B (r )分布曲线分别如图(b)和(c )所示.。
大学物理第11章习题答案解析

第11章 电磁感应11.1 基本要求 12别感应电动势的方向。
34567一些简单情况下的磁场能量。
811.2 基本概念 1W qε=23k E :变化的磁场在其周围所激发的电场。
与静电场不同,感生电场的电场线是闭合的,所以感生电场也称有旋电场。
4变化而产生的感应电动势。
5:有使回路保持原有电流不变的性质,是回路本身的“电磁惯性”的量度。
自感系数L ://m L I N I =ψ=Φ 6L ε:当通过回路的电流发生变化时,在自身回路中所产生的感应电动势。
7M :211212M I I ψψ== 812ε:当线圈2的电流2I 发生变化时,在线圈1中所产生的感应电动势。
9m W :贮存在磁场中的能量。
自感贮存磁能:212m W LI =磁能密度m w :单位体积中贮存的磁场能量22111222m B w μH HB μ===10D d d I dt Φ=s d t∂=∂⎰DS ,位移电流并不表示有真实的电荷在空 间移动。
但是,位移电流的量纲和在激发磁场方面的作用与传导电流是一致的。
11d t∂=∂D j 11.3 基本规律 1(1)楞次定律:感生电流的磁场所产生的磁通量总是反抗回路中原磁通量的改变。
楞 次定律是判断感应电流方向的普适定则。
(2)法拉第电磁感应定律:不论什么原因使通过回路的磁通量(或磁链)发生变化,回路 中均有感应电动势产生,其大小与通过该回路的磁通量(或磁链)随时间的变化成正比,即mi d dtεΦ=-2()BBK AAi εd d ==⨯⎰⎰E l v B l ,若0i ε>,则表示电动势方向由A B →;若0i ε<,则表示电动势方向B A →3m K ls i d Φd εd d dtdt =⋅=-=-⎰⎰BE l S (对于导体回路)BK Ai εd =⎰E l (对于一段导体)4L dIεL dt=- 512212d ΨdIεM dt dt=-=- 6sd ⋅⎰D S =0VdV q ρ=⎰l d ⋅⎰E l = - s d t∂⋅∂⎰BS =0sd ⋅⎰B Sc l sd d t ∂⎛⎫⋅=+⋅ ⎪∂⎝⎭⎰⎰D H l j S11.4 学习指导学习法拉第电磁感应定律要注意,公式中的电动势是整个回路的电动势,式中负号是楞 次定律的要求,用以判断电动势的方向。
大学物理下册-毛峰版的习题答案

大学物理下册-毛峰版的习题答案第11章热力学基础习题及答案1、内能和热量的概念有何不同?下面两种说法是否正确?(1)物体的温度越高,则热量越多;(2)物体的温度越高,则内能越大。
答:内能是组成物体的所有分子的动能与势能的总和。
热量是热传递过程中所传递的能量的量度。
内能是状态量,只与状态有关而与过程无关,热量是过程量,与一定过程相对应。
(1)错。
热量是过程量,单一状态的热量无意义。
(2)对。
物体的内能与温度有关。
2、pV图上封闭曲线所包围的面积表示什么如果该面积越大,是否效率越高答:封闭曲线所包围的面积表示循环过程中所做的净功.由于定高,因为还与吸热Q1有关.3、评论下述说法正确与否(1)功可以完全变成热,但热不能完全变成功;(2)热量只能从高温物体传到低温物体,不能从低温物体传到高温物体.(3)可逆过程就是能沿反方向进行的过程,不可逆过程就是不能沿反方向进行的过程.答:(1)不正确.有外界的帮助热能够完全变成功;功可以完全变成热,但热不能自动地完全变成功;(2)不正确.热量能自动从高温物体传到低温物体,不能自动地由低温物体传到高温物体.但在外界的帮助下,热量能从低温物体传到高温物体.(3)不正确.一个系统由某一状态出发,经历某一过程达另一状态,如果存在另一过程,它能消除原过程对外界的一切影响而使系统和外界同时都能回到原来的状态,这样的过程就是可逆过程.用任何方法都不能使系统和外界同时恢复原状态的过程是不可逆过程.有些过程虽能沿反方向进行,系统能回到原来的状态,但外界没有同时恢复原状态,还是不可逆过程.4、用热力学第一定律和第二定律分别证明,在pV图上一绝热线与一等温线不能有两个交点.A净Q1,A净面积越大,效率不一题4图解:(1)由热力学第一定律有QEA若有两个交点a和b,则经等温ab过程有E1Q1A10经绝热ab过程E2A10E2A10从上得出E1E2,这与a,b两点的内能变化应该相同矛盾.(2)若两条曲线有两个交点,则组成闭合曲线而构成了一循环过程,这循环过程只有吸热,无放热,且对外做正功,热机效率为100%,违背了热力学第二定律.5、一循环过程如图所示,试指出:(1)ab,bc,ca各是什么过程;(2)画出对应的pV图;(3)该循环是否是正循环(4)该循环作的功是否等于直角三角形面积(5)用图中的热量Qab,Qbc,Qac表述其热机效率或致冷系数.题5图题6图解:(1)ab是等体过程bc过程:从图知有VKT,K为斜率vR由pVvRT得pK故bc过程为等压过程ca是等温过程(2)pV图如图(3)该循环是逆循环2(4)该循环作的功不等于直角三角形面积,因为直角三角形不是pV图中的图形.(5)eQabQbcQcaQab6、两个卡诺循环如图所示,它们的循环面积相等,试问:(1)它们吸热和放热的差值是否相同;(2)对外作的净功是否相等;(3)效率是否相同答:由于卡诺循环曲线所包围的面积相等,系统对外所作的净功相等,也就是吸热和放热的差值相等.但吸热和放热的多少不一定相等,效率也就不相同.7、4.8kg的氧气在27.0℃时占有1000m3的体积,分别求在等温、等压情况下,将其体积压缩到原来的1/2所需做的功、所吸收的热量以及内能的变化。
大学物理第十一章课后答案

第十一章 电流与磁场11-1 电源中的非静电力与静电力有什么不同?答:在电路中,电源中非静电力的作用是,迫使正电荷经过电源内部由低电位的电源负极移动到高电位的电源正极,使两极间维持一电位差。
而静电场的作用是在外电路中把正电荷由高电位的地方移动到低电位的地方,起到推动电流的作用;在电源内部正好相反,静电场起的是抵制电流的作用。
电源中存在的电场有两种:1、非静电起源的场;2、稳恒场。
把这两种场与静电场比较,静电场由静止电荷所激发,它不随时间的变化而变化。
非静电场不由静止电荷产生,它的大小决定于单位正电荷所受的非静电力,q非F E =。
当然电源种类不同,非F 的起因也不同。
11-2静电场与恒定电场相同处和不同处?为什么恒定电场中仍可应用电势概念? 答:稳恒电场与静电场有相同之处,即是它们都不随时间的变化而变化,基本规律相同,并且都是位场。
但稳恒电场由分布不随时间变化的电荷产生,电荷本身却在移动。
正因为建立稳恒电场的电荷分布不随时间变化,因此静电场的两条基本定理,即高斯定理和环路定理仍然适用,所以仍可引入电势的概念。
11-3一根铜导线表面涂以银层,当两端加上电压后,在铜线和银层中,电场强度是否相同?电流密度是否相同?电流强度是否相同?为什么?答:此题涉及知识点:电流强度d sI =⋅⎰j s ,电流密度概念,电场强度概念,欧姆定律的微分形式j E σ=。
设铜线材料横截面均匀,银层的材料和厚度也均匀。
由于加在两者上的电压相同,两者的长度又相等,故铜线和银层的场强E相同。
由于铜线和银层的电导率σ不同,根据j E σ=知,它们中的电流密度j 不相同。
电流强度d sI =⋅⎰j s ,铜线和银层的j 不同但相差不太大,而它们的横截面积一般相差较大,所以通过两者的电流强度,一般说来是不相同的。
11-4一束质子发生侧向偏转,造成这个偏转的原因可否是:(1)电场?(2)磁场?(3)若是电场和磁场在起作用,如何判断是哪一种场?答:造成这个偏转的原因可以是电场或磁场。
大学物理下册11-15章答案(修改过,红色为修正地方还有以下解释)
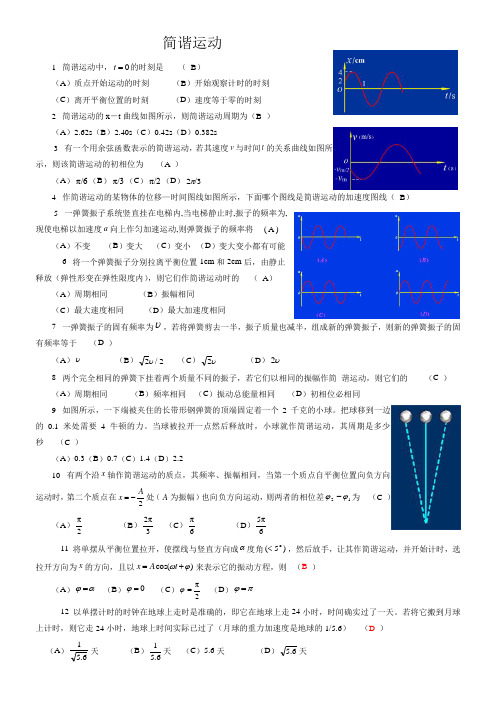
简谐运动1 简谐运动中,0=t 的时刻是 ( B )(A )质点开始运动的时刻 (B )开始观察计时的时刻(C )离开平衡位置的时刻 (D )速度等于零的时刻2 简谐运动的x -t 曲线如图所示,则简谐运动周期为(B )(A )2.62s (B )2.40s (C )0.42s (D )0.382s3 有一个用余弦函数表示的简谐运动,若其速度v 与时间t 的关系曲线如图所示,则该简谐运动的初相位为 (A )(A )π/6(B )π/3(C )π/2(D )/32π4 作简谐运动的某物体的位移—时间图线如图所示,下面哪个图线是简谐运动的加速度图线( B )5 一弹簧振子系统竖直挂在电梯内,当电梯静止时,振子的频率为,现使电梯以加速度a 向上作匀加速运动,则弹簧振子的频率将 ( A )(A )不变 (B )变大 (C )变小 (D )变大变小都有可能6 将一个弹簧振子分别拉离平衡位置1cm 和2cm 后,由静止释放(弹性形变在弹性限度内),则它们作简谐运动时的 ( A )(A )周期相同 (B )振幅相同(C )最大速度相同 (D )最大加速度相同7 一弹簧振子的固有频率为υ,若将弹簧剪去一半,振子质量也减半,组成新的弹簧振子,则新的弹簧振子的固有频率等于 (D )(A )υ (B )2/2υ (C )υ2 (D )υ28 两个完全相同的弹簧下挂着两个质量不同的振子,若它们以相同的振幅作简 谐运动,则它们的 (C ) (A )周期相同 (B )频率相同 (C )振动总能量相同 (D )初相位必相同9 如图所示,一下端被夹住的长带形钢弹簧的顶端固定着一个2千克的小球。
把球移到一边的0.1米处需要4牛顿的力。
当球被拉开一点然后释放时,小球就作简谐运动,其周期是多少秒 (C )(A )0.3(B )0.7(C )1.4(D )2.210 有两个沿x 轴作简谐运动的质点,其频率、振幅相同,当第一个质点自平衡位置向负方向运动时,第二个质点在2A x -=处(A 为振幅)也向负方向运动,则两者的相位差12ϕϕ-为 (C ) (A )2π (B )3π2 (C )6π (D )6π5 11 将单摆从平衡位置拉开,使摆线与竖直方向成α度角)5(o <,然后放手,让其作简谐运动,并开始计时,选拉开方向为x 的方向,且以)cos(ϕω+=t A x 来表示它的振动方程,则 (B )(A )αϕ= (B )0=ϕ (C )2π=ϕ (D )πϕ= 12 以单摆计时的时钟在地球上走时是准确的,即它在地球上走24小时,时间确实过了一天。
大学物理课后答案第十一章

第十一章 机械振动一、基本要求1.掌握简谐振动的基本特征,学会由牛顿定律建立一维简谐振动的微分方程,并判断其是否谐振动。
2. 掌握描述简谐运动的运动方程,理解振动位移,振)cos(0ϕω+=t A x 幅,初位相,位相,圆频率,频率,周期的物理意义。
能根据给出的初始条件求振幅和初位相。
3. 掌握旋转矢量法。
4. 理解同方向、同频率两个简谐振动的合成规律,以及合振动振幅极大和极小的条件。
二、基本内容1. 振动 物体在某一平衡位置附近的往复运动叫做机械振动。
如果物体振动的位置满足,则该物体的运动称为周期性运动。
否则称为非周)()(T t x t x +=期运动。
但是一切复杂的非周期性的运动,都可以分解成许多不同频率的简谐振动(周期性运动)的叠加。
振动不仅限于机械运动中的振动过程,分子热运动,电磁运动,晶体中原子的运动等虽属不同运动形式,各自遵循不同的运动规律,但是就其中的振动过程讲,都具有共同的物理特征。
一个物理量,例如电量、电流、电压等围绕平衡值随时间作周期性(或准周期性)的变化,也是一种振动。
2. 简谐振动 简谐振动是一种周期性的振动过程。
它可以是机械振动中的位移、速度、加速度,也可以是电流、电量、电压等其它物理量。
简谐振动是最简单,最基本的周期性运动,它是组成复杂运动的基本要素,所以简谐运动的研究是本章一个重点。
(1)简谐振动表达式反映了作简谐振动的物体位移随时间)cos(0ϕω+=t A x 的变化遵循余弦规律,这也是简谐振动的定义,即判断一个物体是否作简谐振动的运动学根据。
但是简谐振动表达式更多地用来揭示描述一个简谐运动必须涉及到的物理量、、(或称描述简谐运动的三个参量),显然三个参量A ω0ϕ确定后,任一时刻作简谐振动的物体的位移、速度、加速度都可以由对应地t 得到。
2cos()sin(00πϕωωϕωω++=+-=t A t A v )cos()cos(0202πϕωωϕωω±+=+-=t A t A a (2)简谐运动的动力学特征为:物体受到的力的大小总是与物体对其平衡位置的位移成正比、而方向相反,即,它是判定一个系统的运动过程kx F -=是否作简谐运动的动力学根据,只要受力分析满足动力学特征的,毫无疑问地系统的运动是简谐运动。
大学物理答案第11章

第十一章 恒定磁场11-1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管,两个螺线管的长度相同,R =2r ,螺线管通过的电流相同为I ,螺线管中的磁感强度大小r R B B 、满足( )(A ) r R B B 2= (B ) r R B B = (C ) r R B B =2 (D )r R B B 4=分析与解 在两根通过电流相同的螺线管中,磁感强度大小与螺线管线圈单位长度的匝数成正比.根据题意,用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为(C ).11-2 一个半径为r 的半球面如图放在均匀磁场中,通过半球面的磁通量 为( )(A )B r 2π2 (B ) B r 2π(C )αB r cos π22(D ) αB r cos π2题 11-2 图分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面,根据磁场的高斯定理,磁感线是闭合曲线,闭合曲面的磁通量为零,即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量;S B ⋅=m Φ.因而正确答案为(D ).11-3 下列说法正确的是( )(A ) 闭合回路上各点磁感强度都为零时,回路内一定没有电流穿过 (B ) 闭合回路上各点磁感强度都为零时,回路内穿过电流的代数和必定为零 (C ) 磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度必定为零(D ) 磁感强度沿闭合回路的积分不为零时,回路上任意一点的磁感强度都不可能为零 分析与解 由磁场中的安培环路定律,磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度不一定为零;闭合回路上各点磁感强度为零时,穿过回路的电流代数和必定为零.因而正确答案为(B ).11-4 在图(a)和(b)中各有一半径相同的圆形回路L1 、L2 ,圆周内有电流I1 、I2 ,其分布相同,且均在真空中,但在(b)图中L2 回路外有电流I3 ,P 1 、P 2 为两圆形回路上的对应点,则( )(A ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B =(B ) ⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B = (C ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B ≠ (D ) ⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B≠题 11-4 图分析与解 由磁场中的安培环路定律,积分回路外的电流不会影响磁感强度沿回路的积分;但同样会改变回路上各点的磁场分布.因而正确答案为(C ).11-5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中,若导体中流过的恒定电流为I ,磁介质的相对磁导率为μr (μr<1),则磁介质内的磁化强度为( ) (A )()r I μr π2/1-- (B ) ()r I μr π2/1- (C ) r I μr π2/- (D ) r μI r π2/分析与解 利用安培环路定理可先求出磁介质中的磁场强度,再由M =(μr-1)H 求得磁介质内的磁化强度,因而正确答案为(B ).11-6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道,当环中电子流强度为8 mA 时,在整个环中有多少电子在运行? 已知电子的速率接近光速. 分析 一个电子绕存储环近似以光速运动时,对电流的贡献为c I e I /Δ=,因而由lNec I =,可解出环中的电子数.解 通过分析结果可得环中的电子数10104⨯==ecIlN 11-7 已知铜的摩尔质量M =63.75 g·mol -1,密度ρ =8.9 g · cm -3,在铜导线里,假设每一个铜原子贡献出一个自由电子,(1)为了技术上的安全,铜线内最大电流密度26.0A mm m j -=⋅ ,求此时铜线内电子的漂移速率v d ;(2) 在室温下电子热运动的平均速率是电子漂移速率v d 的多少倍?分析 一个铜原子的质量A N M m /=,其中N A 为阿伏伽德罗常数,由铜的密度ρ 可以推算出铜的原子数密度m ρn /=根据假设,每个铜原子贡献出一个自由电子,其电荷为e ,电流密度d m ne j v = .从而可解得电子的漂移速率v d .将电子气视为理想气体,根据气体动理论,电子热运动的平均速率em kTπ8=v 其中k 为玻耳兹曼常量,m e 为电子质量.从而可解得电子的平均速率与漂移速率的关系.解 (1) 铜导线单位体积的原子数为M ρN n A /=电流密度为j m 时铜线内电子的漂移速率14A s m 1046.4--⋅⨯===eN M j ne j m m d ρv (2) 室温下(T =300 K)电子热运动的平均速率与电子漂移速率之比为81042.2π81⨯≈=edd m kTv v v 室温下电子热运动的平均速率远大于电子在恒定电场中的定向漂移速率.电子实际的运动是无规热运动和沿电场相反方向的漂移运动的叠加.考虑到电子的漂移速率很小,电信号的信息载体显然不会是定向漂移的电子.实验证明电信号是通过电磁波以光速传递的. 11-8 有两个同轴导体圆柱面,它们的长度均为20 m ,内圆柱面的半径为3.0 mm ,外圆柱面的半径为9.0 mm.若两圆柱面之间有10 μA 电流沿径向流过,求通过半径为6.0 mm 的圆柱面上的电流密度.题 11-8 图分析 如图所示是同轴柱面的横截面,电流密度j 对中心轴对称分布.根据恒定电流的连续性,在两个同轴导体之间的任意一个半径为r 的同轴圆柱面上流过的电流I都相等,因此可得rlI j π2=解 由分析可知,在半径r =6.0 mm 的圆柱面上的电流密度2m A μ3.13π2-⋅==rlIj 11-9 如图所示,已知地球北极地磁场磁感强度B 的大小为6.0×10-5T .如设想此地磁场是由地球赤道上一圆电流所激发的,此电流有多大? 流向如何?解 设赤道电流为I ,则由教材第11-4节例2 知,圆电流轴线上北极点的磁感强度()RIRR IR B 24202/32220μμ=+=因此赤道上的等效圆电流为A 1073.12490⨯==μRBI 由于在地球地磁场的N 极在地理南极,根据右手螺旋法则可判断赤道圆电流应该是由东向西流,与地球自转方向相反.题 11-9 图11-10 如图所示,有两根导线沿半径方向接触铁环的a 、b 两点,并与很远处的电源相接.求环心O 的磁感强度.题 11-10 图分析 根据叠加原理,点O 的磁感强度可视作由ef 、be 、fa 三段直线以及acb 、a d b 两段圆弧电流共同激发.由于电源距环较远,0=ef B .而be 、fa 两段直线的延长线通过点O ,由于0Idl r ⨯=,由毕奥-萨伐尔定律知0be fa ==B B .流过圆弧的电流I 1 、I 2的方向如图所示,两圆弧在点O 激发的磁场分别为21101π4r l I μB =,22202π4r l I μB = 其中l 1 、l 2 分别是圆弧acb 、a d b 的弧长,由于导线电阻R 与弧长l 成正比,而圆弧acb 、a d b又构成并联电路,故有2211l I l I =将21B B 、叠加可得点O 的磁感强度B . 解 由上述分析可知,点O 的合磁感强度0π4π42220211021=-=-=r l I μr l I μB B B 11-11 如图所示,几种载流导线在平面内分布,电流均为I ,它们在点O 的磁感强度各为多少?题 11-11 图分析 应用磁场叠加原理求解.将不同形状的载流导线分解成长直部分和圆弧部分,它们各自在点O 处所激发的磁感强度较容易求得,则总的磁感强度∑=iB B 0.解 (a) 长直电流对点O 而言,有0d =⨯rl I ,因此它在点O 产生的磁场为零,则点O 处总的磁感强度为1/4 圆弧电流所激发,故有RIμB 800=B 0 的方向垂直纸面向外.(b) 将载流导线看作圆电流和长直电流,由叠加原理可得RIμR I μB π22000-=B 0 的方向垂直纸面向里.(c ) 将载流导线看作1/2 圆电流和两段半无限长直电流,由叠加原理可得RIμR I μR I μR I μR I μB 4π24π4π4000000+=++=B 0 的方向垂直纸面向外.11-12 载流导线形状如图所示(图中直线部分导线延伸到无穷远),求 点O 的磁感强度B .题 11-12 图分析 由教材11-4 节例题2的结果不难导出,圆弧载流导线在圆心激发的磁感强度RαI μB π40=,其中α为圆弧载流导线所张的圆心角,磁感强度的方向依照右手定则确定;半无限长载流导线在圆心点O 激发的磁感强度R IμB π40=,磁感强度的方向依照右手定则确定.点O 的磁感强度O B 可以视为由圆弧载流导线、半无限长载流导线等激发的磁场在空间点O 的叠加. 解 根据磁场的叠加 在图(a)中,k i k k i B RI μR I μR I μR I μR I μπ24π4π44000000--=---= 在图(b)中,k i k i i B RI μR I μR I μR I μR I μπ41π14π44π4000000-⎪⎭⎫ ⎝⎛+-=---= 在图(c )中,k j i B RIμR I μR I μπ4π4830000---= 11-13 如图(a)所示,载流长直导线的电流为I ,试求通过矩形面积的磁通量.题 11-13 图分析 由于矩形平面上各点的磁感强度不同,故磁通量Φ≠BS .为此,可在矩形平面上取一矩形面元d S =l d x ,如图(b)所示,载流长直导线的磁场穿过该面元的磁通量为x l xId π2d d 0μ=⋅=ΦS B矩形平面的总磁通量ΦΦ⎰=d解 由上述分析可得矩形平面的总磁通量⎰==Φ211200lnπ2d π2d dd d Ilx l xIμμ 11-14 已知10 mm 2裸铜线允许通过50 A 电流而不会使导线过热.电流在导线横截面上均匀分布.求导线内、外磁感强度的分布.题 11-14 图分析 可将导线视作长直圆柱体,电流沿轴向均匀流过导体,故其磁场必然呈轴对称分布,即在与导线同轴的圆柱面上的各点,B 大小相等、方向与电流成右手螺旋关系.为此,可利用安培环路定理,求出导线表面的磁感强度.解 围绕轴线取同心圆为环路L ,取其绕向与电流成右手螺旋关系,根据安培环路定理,有∑⎰=⋅=⋅I μB 0πr 2d l B在导线内r <R , 2222ππRIr r R I I ==∑,因而 202πR IrμB =在导线外r >R ,I I =∑,因而rIμB 2π0=磁感强度分布曲线如图所示.11-15 有一同轴电缆,其尺寸如图(a)所示.两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑.试计算以下各处的磁感强度:(1) r <R 1 ;(2) R 1 <r <R 2 ;(3) R 2 <r <R 3 ;(4) r >R 3 .画出B -r 图线.题 11-15 图分析 同轴电缆导体内的电流均匀分布,其磁场呈轴对称,取半径为r 的同心圆为积分路径,πr 2d ⋅=⋅⎰B l B ,利用安培环路定理∑⎰=⋅I μ0d l B ,可解得各区域的磁感强度.解 由上述分析得r <R 122101ππ12πr R μr B =⋅ 21012πR Ir μB =R 1 <r <R 2I μr B 022π=⋅rI μB 2π02=R 2 <r <R 3()()⎥⎦⎤⎢⎣⎡---=⋅I R R R r I μr B 22232203ππ2π 2223223032πR R r R r I μB --= r >R 3()02π04=-=⋅I I μr B04=B磁感强度B (r )的分布曲线如图(b).11-16 如图所示,N 匝线圈均匀密绕在截面为长方形的中空骨架上.求通入电流I 后,环内外磁场的分布.题 11-16 图分析 根据右手螺旋法则,螺线管内磁感强度的方向与螺线管中心轴线构成同心圆,若取半径为r 的圆周为积分环路,由于磁感强度在每一环路上为常量,因而πr 2d ⋅=⋅⎰B l B依照安培环路定理∑⎰=⋅I μ0d l B ,可以解得螺线管内磁感强度的分布.解 依照上述分析,有∑=⋅I μr B 02πr <R 102π1=⋅r B01=BR 2 >r >R 1NI μr B 022π=⋅rNI μB 2π02=r >R 202π3=⋅r B 03=B在螺线管内磁感强度B 沿圆周,与电流成右手螺旋.若112R R R <<- 和R 2 ,则环内的磁场可以近似视作均匀分布,设螺线环的平均半径()1221R R R +=,则环内的磁感强度近似为 RNIμB 2π0≈11-17 电流I 均匀地流过半径为R 的圆形长直导线,试计算单位长度导线内的磁场通过图中所示剖面的磁通量.题 11-17 图分析 由题11-14 可得导线内部距轴线为r 处的磁感强度()202πR Irμr B =在剖面上磁感强度分布不均匀,因此,需从磁通量的定义()S B d ⎰=r Φ来求解.沿轴线方向在剖面上取面元dS =l dr ,考虑到面元上各点B 相同,故穿过面元的磁通量dΦ=B dS ,通过积分,可得单位长度导线内的磁通量⎰=Sr B Φd解 由分析可得单位长度导线内的磁通量4πd 2π0020Iμr R Ir μΦR==⎰11-18 已知地面上空某处地磁场的磁感强度40.410T B -=⨯,方向向北.若宇宙射线中有一速率715.010m s -=⨯v 的质子,垂直地通过该处.求:(1)洛伦兹力的方向;(2) 洛伦兹力的大小,并与该质子受到的万有引力相比较.题 11-18 图解 (1) 依照B F ⋅=v q L 可知洛伦兹力L F 的方向为B ⊥v 的方向,如图所示. (2) 因B ⊥v ,质子所受的洛伦兹力N 102.316-⨯==B F v q L在地球表面质子所受的万有引力N 1064.126p -⨯==g m G因而,有101095.1/⨯=G F L ,即质子所受的洛伦兹力远大于重力.11-19 霍尔效应可用来测量血流的速度,其原理如图所示.在动脉血管两侧分别安装电极并加以磁场.设血管直径为d =2.0 mm ,磁场为B =0.080 T ,毫伏表测出血管上下两端的电压为U H =0.10 mV ,血流的流速为多大?题 11-19 图分析 血流稳定时,有H qE B q =v由上式可以解得血流的速度. 解 依照分析m/s 63.0===dBU B E HH v 11-20 带电粒子在过饱和液体中运动,会留下一串气泡显示出粒子运动的径迹.设在气泡室有一质子垂直于磁场飞过,留下一个半径为3.5 cm 的圆弧径迹,测得磁感强度为0.20 T,求此质子的动量和动能.解 根据带电粒子回转半径与粒子运动速率的关系有m /s kg 1012.121⋅⨯===-ReB m p vkeV 35.222==mp E k11-21 从太阳射来的速度为0.80×108m/s 的电子进入地球赤道上空高层范艾伦辐射带中,该处磁场为4.0 ×10-7T,此电子回转轨道半径为多大? 若电子沿地球磁场的磁感线旋进到地磁北极附近,地磁北极附近磁场为2.0 ×10-5T,其轨道半径又为多少? 解 由带电粒子在磁场中运动的回转半径高层范艾伦辐射带中的回转半径m 101.1311⨯==eB m R v地磁北极附近的回转半径m 2322==eB m R v11-22 如图(a)所示,一根长直导线载有电流I 1 =30 A ,矩形回路载有电流I 2 =20 A .试计算作用在回路上的合力.已知d =1.0 cm ,b =8.0 cm ,l =0.12 m .题 11-22图分析 矩形上、下两段导线受安培力F 1 和F 2 的大小相等,方向相反,对不变形的矩形回路来说,两力的矢量和为零.而矩形的左右两段导线,由于载流导线所在处磁感强度不等,所受安培力F 3 和F 4 大小不同,且方向相反,因此线框所受的力为这两个力的合力.解 由分析可知,线框所受总的安培力F 为左、右两边安培力F 3 和F 4 之矢量和,如图(b)所示,它们的大小分别为d lI I μF π22103=()b d l I I μF +=π22104故合力的大小为()N 1028.1π2π2321021043-⨯=+-=-=b d lI I μd l I I μF F F 合力的方向朝左,指向直导线.11-23 一直流变电站将电压为500kV 的直流电,通过两条截面不计的平行输电线输向远方.已知两输电导线间单位长度的电容为3.0×10-11F ·m -1,若导线间的静电力与安培力正好抵消.求:(1) 通过输电线的电流;(2) 输送的功率.分析 当平行输电线中的电流相反时,它们之间存在相互排斥的安培力,其大小可由安培定律确定.若两导线间距离为d ,一导线在另一导线位置激发的磁感强度dIμB π20=,导线单位长度所受安培力的大小BI F B =.将这两条导线看作带等量异号电荷的导体,因两导线间单位长度电容C 和电压U 已知,则单位长度导线所带电荷λ=CU ,一导线在另一导线位置所激发的电场强度dελE 0π2=,两导线间单位长度所受的静电吸引力λE F E =.依照题意,导线间的静电力和安培力正好抵消,即0=+E B F F从中可解得输电线中的电流.解 (1) 由分析知单位长度导线所受的安培力和静电力分别为d I μBI F B π220==dεU C λE F E 022π2== 由0=+E BF F 可得dεU C d I μ02220π2π2=解得A 105.4300⨯==μεCUI (2) 输出功率W 1025.29⨯==IU N11-24 在氢原子中,设电子以轨道角动量π2/h L =绕质子作圆周运动,其半径为m 1029.5110-⨯=a .求质子所在处的磁感强度.h 为普朗克常量,其值为s J 1063.634⋅⨯-分析 根据电子绕核运动的角动量π20h a m L ==v 可求得电子绕核运动的速率v .如认为电子绕核作圆周运动,其等效圆电流v/π20a e T e i ==在圆心处,即质子所在处的磁感强度为02a i μB =解 由分析可得,电子绕核运动的速率π2ma h=v其等效圆电流2020π4/π2ma he v a e i ==该圆电流在圆心处产生的磁感强度T 5.12π82202000===ma heμa i μB 11-25 如图[a]所示,一根长直同轴电缆,内、外导体之间充满磁介质,磁介质的相对磁导率为μr (μr <1),导体的磁化可以忽略不计.沿轴向有恒定电流I 通过电缆,内、外导体上电流的方向相反.求:(1) 空间各区域内的磁感强度和磁化强度;*(2) 磁介质表面的磁化电流.题 11-25 图分析 电流分布呈轴对称,依照右手定则,磁感线是以电缆对称轴线为中心的一组同心圆.选取任一同心圆为积分路径,应有⎰⋅=⋅r H d π2l H ,利用安培环路定理⎰∑=⋅fI d l H求出环路内的传导电流,并由H μB =,()H μM r 1-=,可求出磁感强度和磁化强度.再由磁化电流的电流面密度与磁化强度的关系求出磁化电流.解 (1) 取与电缆轴同心的圆为积分路径,根据磁介质中的安培环路定理,有∑=fπ2I r H对r <R 1221f ππrR I I =∑ 得2112πR IrH =忽略导体的磁化(即导体相对磁导率μr =1),有01=M ,21012πR IrμB =对R 2 >r >R 1I I=∑f得rI H 2π2=填充的磁介质相对磁导率为μr ,有()r I μM r 2π12-=,rI μμB r 2π02= 对R 3 >r >R 2()()2223223ππR r R R I I I f -⋅--=∑ 得()()222322332πR R r r R I H --= 同样忽略导体的磁化,有03=M ,()()2223223032πR R r r R I μB --= 对r >R 30=-=∑I I If得04=H ,04=M ,04=B(2) 由r M I s 2π⋅=,磁介质内、外表面磁化电流的大小为()()I μR R M I r si 12π112-=⋅= ()()I μR R M I r se 12π222-=⋅=对抗磁质(1r μ<),在磁介质内表面(r =R 1 ),磁化电流与内导体传导电流方向相反;在磁介质外表面(r =R 2 ),磁化电流与外导体传导电流方向相反.顺磁质的情况与抗磁质相反.H (r )和B (r )分布曲线分别如图(b)和(c )所示.。
大学普通物理学习题答案-第十一章-恒定电流与恒定磁场

第十一章恒定电流与恒定磁场一、选择题1.如图11-1所示,有两根载有相同电流的无限长直导线,分别通过x1=1m、x2=3m的点,且平行于y轴,则磁感应强度B等于零的地方是()。
A.x=2m的直线上B.在x>2m的区域C.在x<1m的区域D.不在x、y平面上图11-11.【答案】A。
解析:根据对称性可得,两条载流导线在x=2m的直线上产生的磁感应强度大小相等;用右手螺旋定则可判断两磁感应强度的方向相反,相互抵消,合磁感应强度为零,故选A。
2.图11-2中6根无限长导线互相绝缘,通过电流均为I,区域Ⅰ、Ⅰ、Ⅰ、Ⅰ均为全等的正方形,哪一个区域指向纸内的磁通量最大()。
A. Ⅰ区域B. Ⅰ区域C. Ⅰ区域D. Ⅰ区域2.【答案】B。
解析:通过Ⅰ区域的磁通量为0,通过Ⅰ区城的磁通量最大且指向纸内,通过Ⅰ区域的磁通量最大但指向纸外,通过IV区域的磁通量为0。
故选B。
3.如图11-3所示,在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路定理可知()。
A.d 0LB l ⋅=⎰,且环路上任意一点B =0 B.d 0LB l ⋅=⎰,且环路上任意一点B ≠0 C.d 0LB l ⋅≠⎰,且环路上任意一点B ≠0 D.d 0LB l ⋅≠⎰,且环路上任意一点B =常量3.【答案】B 。
解析:根据安培环路定理,闭合回路内没有电流穿过,所以环路积分等于0.但是由于圆形电流的存在,环路上任意一点的磁感应强度都不等于0。
故选B 。
4.无限长直圆柱体,半径为R ,沿轴向均匀流有电流,设圆柱体内(r <R )的磁感应强度为B i ,圆柱体外(r>R )的磁感应强度为B e ,则有:()。
A.B i 、B e 均与r 成正比B.B i 、B e 均与r 成反比C.B i 与r 成反比,B e 与r 成正比D.B i 与r 成正比,B e 与r 成反比4.【答案】B 。
解析:导体横截面上的电流密度2πR I J =,以圆柱体轴线为圆心,半径为r 的同心圆作为安培环路,当r <R ,20ππ2r J r B i ⋅=⋅μ,20π2R IrB i μ=;当r <R ,I r B e ⋅=⋅0π2μ,rIB e π20μ=;所以选D 。
大学物理_第五版_下册_第九章到第十一章课后答案

第九章 振动9-1 一个质点作简谐运动,振幅为A ,在起始时刻质点的位移为2A -,且向x 轴正方向运动,代表此简谐运动的旋转矢量为( )题9-1 图分析与解(b )图中旋转矢量的矢端在x 轴上投影点的位移为-A /2,且投影点的运动方向指向O x 轴正向,即其速度的x 分量大于零,故满足题意.因而正确答案为(b ). 9-2 已知某简谐运动的振动曲线如图(a )所示,则此简谐运动的运动方程为( )()()()()()()()()cm π32π34cos 2D cm π32π34cos 2B cm π32π32cos 2C cm π32π32cos 2A ⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡-=t x t x t x t x题9-2 图分析与解 由振动曲线可知,初始时刻质点的位移为 –A /2,且向x 轴负方向运动.图(b)是其相应的旋转矢量图,由旋转矢量法可知初相位为3/π2.振动曲线上给出质点从–A /2 处运动到+A 处所需时间为 1 s ,由对应旋转矢量图可知相应的相位差3/π4Δ=,则角频率()1s 3/π4Δ/Δ-==t ω,故选(D ).本题也可根据振动曲线所给信息,逐一代入方程来找出正确答案.9-3 两个同周期简谐运动曲线如图(a ) 所示, x 1 的相位比x 2 的相位( )(A ) 落后2π (B )超前2π (C )落后π (D )超前π 分析与解 由振动曲线图作出相应的旋转矢量图(b ) 即可得到答案为(b ).题9-3 图9-4 当质点以频率ν 作简谐运动时,它的动能的变化频率为( )(A ) 2v (B )v (C )v 2 (D )v 4 分析与解 质点作简谐运动的动能表式为()ϕωω+=t A m E k 222sin 21,可见其周期为简谐运动周期的一半,则频率为简谐运动频率ν的两倍.因而正确答案为(C ). 9-5 图(a )中所画的是两个简谐运动的曲线,若这两个简谐运动可叠加,则合成的余弦振动的初相位为( )(A ) π23 (B )π21 (C )π (D )0 分析与解 由振动曲线可以知道,这是两个同振动方向、同频率简谐运动,它们的相位差是π(即反相位).运动方程分别为t A x ωcos 1=和()πcos 22+=t ωA x .它们的振幅不同.对于这样两个简谐运动,可用旋转矢量法,如图(b )很方便求得合运动方程为t A x ωcos 21=.因而正确答案为(D ).题9-5 图9-6 有一个弹簧振子,振幅m 10022-⨯=.A ,周期s 01.=T ,初相4/π3=.试写出它的运动方程,并作出t x -图、t -v 图和t a -图.题9-6 图分析 弹簧振子的振动是简谐运动.振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量.求运动方程就要设法确定这三个物理量.题中除A 、ϕ已知外,ω可通过关系式T ω/π2=确定.振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同.解 因T ω/π2=,则运动方程()⎪⎭⎫ ⎝⎛+=+=t π2cos cos T A t ωA x 根据题中给出的数据得 ()()m 75.0π2cos 100.22πt x +⨯=-振子的速度和加速度分别为()()-12s m π75.0π2sin 10π4d /d ⋅+⨯-==-t y x v()()-1222s m π75.0π2cos 10π8d /d ⋅+⨯-==-t y x a t x -、t -v 及t a -图如图所示.9-7 若简谐运动方程为()()m π25.0π20cos 10.0+=t x ,求:(1) 振幅、频率、角频率、周期和初相;(2)s 2=t 时的位移、速度和加速度.分析 可采用比较法求解.将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x c o s作比较,即可求得各特征量.运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t 值后,即可求得结果.解 (1) 将()()m π25.0π20cos 10.0+=t x 与()ϕω+=t A x cos 比较后可得:振幅A =0.10m ,角频率1s π20-=ω,初相ϕ=0.25π,则周期s 1.0/π2==ωT ,频率Hz /1T =v .(2)s 2=t 时的位移、速度、加速度分别为()m 1007.7π25.0π40cos 10.02-⨯=+=t x()-1s m 44.4π25.0π40sin π2d /d ⋅-=+-==t x v()-22222s m 1079.2π25.0π40cos π40d /d ⋅⨯-=+-==t x a9-8 一远洋货轮,质量为m ,浮在水面时其水平截面积为S .设在水面附近货轮的水平截面积近似相等,水的密度为ρ,且不计水的粘滞阻力,证明货轮在水中作振幅较小的竖直自由运动是简谐运动,并求振动周期.分析 要证明货轮作简谐运动,需要分析货轮在平衡位置附近上下运动时,它所受的合外力F 与位移x 间的关系,如果满足kx F -=,则货轮作简谐运动.通过kx F -=即可求得振动周期k m ωT /π2/π2==.证 货轮处于平衡状态时[图(a )],浮力大小为F =mg .当船上下作微小振动时,取货轮处于力平衡时的质心位置为坐标原点O ,竖直向下为x 轴正向,如图(b )所示.则当货轮向下偏移x 位移时,受合外力为∑'+=F P F其中F '为此时货轮所受浮力,其方向向上,大小为gSx mg gSx F F ρρ+=+='题9-8 图则货轮所受合外力为kx gSx F P F -=-='-=∑ρ式中gS k ρ=是一常数.这表明货轮在其平衡位置上下所作的微小振动是简谐运动.由∑=t x m F 22d d /可得货轮运动的微分方程为 0d d 22=+m gSx t x //ρ令m gS /ρω=2,可得其振动周期为gS ρm πωT /2/π2==9-9 设地球是一个半径为R 的均匀球体,密度33m kg 1055-⋅⨯=.ρ.现假定沿直径凿通一条隧道,若有一质量为m 的质点在此隧道内作无摩擦运动.(1) 证明此质点的运动是简谐运动;(2) 计算其周期.题9-9 图分析 证明方法与上题相似.分析质点在隧道内运动时的受力特征即可.证 (1) 取图所示坐标.当质量为m 的质点位于x 处时,它受地球的引力为2x m m G F x -= 式中G 为引力常量,x m 是以x 为半径的球体质量,即3/π43x ρm x =.令3/π4Gm ρk =,则质点受力kx Gmx ρF -==3/π4因此,质点作简谐运动.(2) 质点振动的周期为s 1007.5/π3/π23⨯===ρG k m T9-10 如图(a )所示,两个轻弹簧的劲度系数分别为1k 、2k .当物体在光滑斜面上振动时.(1) 证明其运动仍是简谐运动;(2) 求系统的振动频率.题9-10 图分析 从上两题的求解知道,要证明一个系统作简谐运动,首先要分析受力情况,然后看是否满足简谐运动的受力特征(或简谐运动微分方程).为此,建立如图(b )所示的坐标.设系统平衡时物体所在位置为坐标原点O ,Ox 轴正向沿斜面向下,由受力分析可知,沿Ox 轴,物体受弹性力及重力分力的作用,其中弹性力是变力.利用串联时各弹簧受力相等,分析物体在任一位置时受力与位移的关系,即可证得物体作简谐运动,并可求出频率υ.证 设物体平衡时两弹簧伸长分别为1x 、2x ,则由物体受力平衡,有2211sin x k x k mg ==θ (1)按图(b )所取坐标,物体沿x 轴移动位移x 时,两弹簧又分别被拉伸1x '和2x ',即21x x x '+'=.则物体受力为()()111222sin sin x x k mg x x k mg F '+-='+-=θθ (2) 将式(1)代入式(2)得1122x k x k F '-='-= (3) 由式(3)得11k F x /-='、22k F x /-=',而21x x x '+'=,则得到 ()[]kx x k k k k F -=+-=2121/式中()2121k k k k k +=/为常数,则物体作简谐运动,振动频率 ()m k k k k πm k ωv 2121/21/π21π2/+=== 讨论 (1) 由本题的求证可知,斜面倾角θ 对弹簧是否作简谐运动以及振动的频率均不产生影响.事实上,无论弹簧水平放置、斜置还是竖直悬挂,物体均作简谐运动.而且可以证明它们的频率相同,均由弹簧振子的固有性质决定,这就是称为固有频率的原因.(2) 如果振动系统如图(c )(弹簧并联)或如图(d )所示,也可通过物体在某一位置的受力分析得出其作简谐运动,且振动频率均为()m k k v /π2121+=,读者可以一试.通过这些例子可以知道,证明物体是否作简谐运动的思路是相同的.*9 -11 在如图(a )所示装置中,一劲度系数为k 的轻弹簧,一端固定在墙上,另一端连接一质量为1m 的物体A ,置于光滑水平桌面上.现通过一质量m 、半径为R 的定滑轮B (可视为匀质圆盘)用细绳连接另一质量为2m 的物体C .设细绳不可伸长,且与滑轮间无相对滑动,求系统的振动角频率.题9-11 图分析 这是一个由弹簧、物体A 、C 和滑轮B 组成的简谐运动系统.求解系统的振动频率可采用两种方法.(1) 从受力分析着手.如图(b )所示,设系统处于平衡状态时,与物体A 相连的弹簧一端所在位置为坐标原点O ,此时弹簧已伸长0x ,且g m kx 20=.当弹簧沿x O 轴正向从原点O 伸长x 时,分析物体A 、C 及滑轮B 的受力情况,并分别列出它们的动力学方程,可解得系统作简谐运动的微分方程.(2)从系统机械能守恒着手.列出系统机械能守恒方程,然后求得系统作简谐运动的微分方程.解1 在图(b )的状态下,各物体受力如图(c )所示.其中()i F 0x x k +-=.考虑到绳子不可伸长,对物体A 、B 、C 分别列方程,有()22101d d tx m x x k F T =+-= (1) 22222d d tx m F g m T =- (2) ()2212d d 21tx mR J R F F T T ==-α (3) g m kx 20= (4)方程(3)中用到了22T T F F '=、11T T F F '=、22/mR J =及R a /=α.联立式(1) ~式(4)可得02d d 2122=+++x m m m k t x / (5) 则系统振动的角频率为 ()221//m m m k ++=ω解2 取整个振动装置和地球为研究系统,因没有外力和非保守内力作功,系统机械能守恒.设物体平衡时为初始状态,物体向右偏移距离x (此时速度为v 、加速度为a )为末状态,则由机械能守恒定律,有()20222212021212121x x k ωJ m m gx m E +++++-=v v 在列出上述方程时应注意势能(重力势能和弹性势能)零点的选取.为运算方便,选初始状态下物体C 所在位置为重力势能零点;弹簧原长时为弹性势能的零点.将上述方程对时间求导得()tx x x k t ωωJ t m t m g m d d d d d d d d 00212+++++-=v v v vv 将22/mR J =,v =R ω,22d /d d /d t x t =v 和02kx g m = 代入上式,可得 02d d 2122=+++x m m m k t x / (6) 式(6)与式(5)相同,表明两种解法结果一致.9-12 一放置在水平桌面上的弹簧振子,振幅A =2.0 ×10-2 m ,周期T =0.50s.当t =0 时,(1) 物体在正方向端点;(2) 物体在平衡位置、向负方向运动;(3) 物体在x =-1.0×10-2m 处, 向负方向运动; (4) 物体在x =-1.0×10-2 m 处,向正方向运动.求以上各种情况的运动方程.分析 在振幅A 和周期T 已知的条件下,确定初相φ是求解简谐运动方程的关键.初相的确定通常有两种方法.(1) 解析法:由振动方程出发,根据初始条件,即t =0 时,x =x 0 和v =v 0 来确定φ值.(2) 旋转矢量法:如图(a )所示,将质点P 在Ox 轴上振动的初始位置x 0 和速度v 0 的方向与旋转矢量图相对应来确定φ.旋转矢量法比较直观、方便,在分析中常采用.题9-12 图解 由题给条件知A =2.0 ×10-2 m ,1s π4/2-==T ω,而初相φ可采用分析中的两种不同方法来求.解析法:根据简谐运动方程()ϕω+=t A x cos ,当0t =时有()ϕω+=t A x c o s 0,sin 0ωA -=v .当(1)A x =0时,1cos 1=ϕ,则01=ϕ;(2)00=x 时,0cos 2=ϕ,2π2±=,因00<v ,取2π2=; (3)m 100120-⨯=.x 时,50cos 3.=ϕ,3π3±= ,由00<v ,取3π3=; (4)m 100120-⨯-=.x 时,50cos 4.-=ϕ,3ππ4±= ,由00>v ,取3π44=. 旋转矢量法:分别画出四个不同初始状态的旋转矢量图,如图(b )所示,它们所对应的初相分别为01=ϕ,2π2=,3π3=,3π44=. 振幅A 、角频率ω、初相φ均确定后,则各相应状态下的运动方程为(1)()m t πcos4100.22-⨯=x(2)()()m /2πt π4cos 100.22+⨯=-x(3)()()m /3πt π4cos 100.22+⨯=-x(4)()()m /3π4t π4cos 100.22+⨯=-x 9-13 有一弹簧, 当其下端挂一质量为m 的物体时, 伸长量为9.8 ×10-2 m .若使物体上、下振动,且规定向下为正方向.(1) 当t =0 时,物体在平衡位置上方8.0 ×10-2 m 处,由静止开始向下运动,求运动方程.(2) 当t =0 时,物体在平衡位置并以0.6m·s -1的速度向上运动,求运动方程.分析 求运动方程,也就是要确定振动的三个特征物理量A 、ω和φ.其中振动的角频率是由弹簧振子系统的固有性质(振子质量m 及弹簧劲度系数k )决定的,即ω=k 可根据物体受力平衡时弹簧的伸长来计算;振幅A 和初相φ需要根据初始条件确定.题9-13 图解 物体受力平衡时,弹性力F 与重力P 的大小相等,即F =mg .而此时弹簧的伸长量Δl =9.8 ×10-2m .则弹簧的劲度系数k =F /Δl =mg /Δl .系统作简谐运动的角频率为1s 10-=∆==l g m k //ω(1) 设系统平衡时,物体所在处为坐标原点,向下为x 轴正向.由初始条件t =0 时,x 10 =8.0 ×10-2 m 、v 10 =0 可得振幅()m 10082210210-⨯=+=./ωv x A ;应用旋转矢量法可确定初相π1=[图(a )].则运动方程为()()m π10t cos 100.821+⨯=-x(2)t =0 时,x 20 =0、v 20 =0.6 m·s -1 ,同理可得()m 100622202202-⨯=+=./ωv x A ;2/π2=[图(b )].则运动方程为()()m π5.010t cos 100.622+⨯=-x9-14 某振动质点的x -t 曲线如图(a )所示,试求:(1) 运动方程;(2) 点P 对应的相位;(3) 到达点P 相应位置所需的时间.分析 由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题.本题就是要通过x -t 图线确定振动的三个特征量A 、ω和0ϕ,从而写出运动方程.曲线最大幅值即为振幅A ;而ω、0ϕ通常可通过旋转矢量法或解析法解出,一般采用旋转矢量法比较方便. 解 (1) 质点振动振幅A =0.10 m.而由振动曲线可画出t 0 =0 和t 1 =4 s时旋转矢量,如图(b ) 所示.由图可见初相3/π=0(或3/π50=),而由()3201//ππω+=-t t 得1s 24/π5-=ω,则运动方程为 ()m 3/π24π5cos 10.0⎪⎭⎫ ⎝⎛-=t x题9-14 图(2) 图(a )中点P 的位置是质点从A /2 处运动到正向的端点处.对应的旋转矢量图如图(c ) 所示.当初相取3/π0-=时,点P 的相位为()000=-+=p p t ωϕϕ(如果初相取成3/π50=,则点P 相应的相位应表示为()π2=0t ω+=p 0p . (3) 由旋转矢量图可得()3/π0=-p t ω,则s 61.=p t .9-15 作简谐运动的物体,由平衡位置向x 轴正方向运动,试问经过下列路程所需的最短时间各为周期的几分之几? (1) 由平衡位置到最大位移处;(2) 由平衡位置到x =A /2 处;(3) 由x =A /2处到最大位移处.解 采用旋转矢量法求解较为方便.按题意作如图所示的旋转矢量图,平衡位置在点O .(1) 平衡位置x 1 到最大位移x 3 处,图中的旋转矢量从位置1 转到位置3,故△φ1=2/π,则所需时间 411//T t =∆=∆ωϕ(2) 从平衡位置x 1 到x 2 =A /2 处,图中旋转矢量从位置1转到位置2,故有△φ2=6/π,则所需时间1222//T t =∆=∆ωϕ(3) 从x 2 =A /2 运动到最大位移x 3 处,图中旋转矢量从位置2 转到位置3,有△φ3=3/π,则所需时间633//T t =∆=∆ωϕ题9-15 图9-16 在一块平板下装有弹簧,平板上放一质量为1.0 kg 的重物.现使平板沿竖直方向作上下简谐运动,周期为0.50s,振幅为2.0×10-2 m .求:(1) 平板到最低点时,重物对平板的作用力;(2) 若频率不变,则平板以多大的振幅振动时,重物会跳离平板? (3) 若振幅不变,则平板以多大的频率振动时, 重物会跳离平板?题9-16 图分析 按题意作示意图如图所示.物体在平衡位置附近随板作简谐运动,其间受重力P 和板支持力F N 作用,F N 是一个变力.按牛顿定律,有22d d ty m F mg F N =-= (1) 由于物体是随板一起作简谐运动,因而有()ϕωω+-==t A ty a cos d d 222,则式(1)可改写为()ϕωω++=t mA mg F N cos 2 (2)(1) 根据板运动的位置,确定此刻振动的相位ϕω+t ,由式(2)可求板与物体之间的作用力.(2) 由式(2)可知支持力N F 的值与振幅A 、角频率ω和相位(ϕω+t )有关.在振动过程中,当π=+t ω时N F 最小.而重物恰好跳离平板的条件为N F =0,因此由式(2)可分别求出重物跳离平板所需的频率或振幅.解 (1) 由分析可知,重物在最低点时,相位ϕω+t =0,物体受板的支持力为()N 9612222./=+=+=t mAmg mA mg F N πω 重物对木块的作用力N F ' 与N F 大小相等,方向相反. (2) 当频率不变时,设振幅变为A ′.根据分析中所述,将N F =0及π=+t ω代入分析中式(2),可得m 102.6π4//2222-⨯==='gT ωm mg A(3) 当振幅不变时,设频率变为v '.同样将N F =0及π=+t ω代入分析中式(2),可得Hz 52.3/π21π22==='mA mg ωv 9-17 两质点作同频率、同振幅的简谐运动.第一个质点的运动方程为()ϕω+=t A x cos 1,当第一个质点自振动正方向回到平衡位置时,第二个质点恰在振动正方向的端点,试用旋转矢量图表示它们,并求第二个质点的运动方程及它们的相位差.题9-17 图解 图示为两质点在时刻t 的旋转矢量图,可见第一个质点M 的相位比第二个质点N 的相位超前2/π,即它们的相位差Δφ=π/2.故第二个质点的运动方程应为()2cos 2/πϕω-+=t A x9-18 图(a )为一简谐运动质点的速度与时间的关系曲线,且振幅为2cm ,求(1) 振动周期;(2) 加速度的最大值;(3) 运动方程.分析 根据v -t 图可知速度的最大值v max ,由v max =Aω可求出角频率ω,进而可求出周期T 和加速度的最大值a max =Aω2 .在要求的简谐运动方程x =A cos (ωt +φ)中,因为A 和ω已得出,故只要求初相位φ即可.由v -t 曲线图可以知道,当t =0 时,质点运动速度v 0 =v max /2 =Aω/2,之后速度越来越大,因此可以判断出质点沿x 轴正向向着平衡点运动.利用v 0 =-Aωsinφ就可求出φ.解 (1) 由ωA v =max 得1s 51-=.ω,则 s 2.4/π2==ωT(2)222max s m 1054--⋅⨯==.ωA a(3) 从分析中已知2/sin 0ωA ωA =-=v ,即21sin /-=ϕ6/π5,6/π--=因为质点沿x 轴正向向平衡位置运动,则取6/π5-=,其旋转矢量图如图(b )所示.则运动方程为 ()()cm 6/π55.1cos 2-=t x题9-18 图9-19 有一单摆,长为1.0m ,最大摆角为5°,如图所示.(1) 求摆的角频率和周期;(2) 设开始时摆角最大,试写出此单摆的运动方程;(3) 摆角为3°时的角速度和摆球的线速度各为多少?题9-19 图分析 单摆在摆角较小时(θ<5°)的摆动,其角量θ与时间的关系可表示为简谐运动方程()ϕωθθ+=t cos max ,其中角频率ω仍由该系统的性质(重力加速度g 和绳长l )决定,即l g /=ω.初相φ与摆角θ,质点的角速度与旋转矢量的角速度(角频率)均是不同的物理概念,必须注意区分.解 (1) 单摆角频率及周期分别为s 01.2/π2;s 13.3/1====-ωT l g ω(2) 由0=t 时o max 5==θθ可得振动初相0=ϕ,则以角量表示的简谐运动方程为t θ13.3cos 36π=(3) 摆角为3°时,有()60cos max ./==+θθϕωt ,则这时质点的角速度为()()1max 2max max s2180800cos 1sin /d d --=-=+--=+-=..ωθϕωωθϕωωθθt t t线速度的大小为 1s 2180/d d --==.t l v θ讨论 质点的线速度和角速度也可通过机械能守恒定律求解,但结果会有极微小的差别.这是因为在导出简谐运动方程时曾取θθ≈sin ,所以,单摆的简谐运动方程仅在θ 较小时成立.9-20 为了测月球表面的重力加速度,宇航员将地球上的“秒摆”(周期为2.00s),拿到月球上去,如测得周期为4.90s,则月球表面的重力加速度约为多少? (取地球表面的重力加速度2E s m 809-⋅=.g )解 由单摆的周期公式g l T /π2=可知21T g /∝,故有2M 2E E M T T g g //=,则月球的重力加速度为()2E 2M E M s m 631-⋅==./g T T g9-21 一飞轮质量为12kg ,内缘半径r =0.6m,如图所示.为了测定其对质心轴的转动惯量,现让其绕内缘刃口摆动,在摆角较小时,测得周期为2.0s ,试求其绕质心轴的转动惯量.9-21 题图分析 飞轮的运动相当于一个以刃口为转轴的复摆运动,复摆振动周期为c /π2mgl J T =,因此,只要知道复摆振动的周期和转轴到质心的距离c l ,其以刃口为转轴的转动惯量即可求得.再根据平行轴定理,可求出其绕质心轴的转动惯量.解 由复摆振动周期c /π2mgl J T =,可得22π4/mgrT J =.则由平行轴定理得222220m kg 8324⋅=-=-=./mr mgrT mr J J π9-22 如图(a )所示,质量为1.0 ×10-2kg 的子弹,以500m·s -1的速度射入木块,并嵌在木块中,同时使弹簧压缩从而作简谐运动,设木块的质量为4.99 kg ,弹簧的劲度系数为8.0 ×103 N·m-1 ,若以弹簧原长时物体所在处为坐标原点,向左为x 轴正向,求简谐运动方程.题9-22 图分析 可分为两个过程讨论.首先是子弹射入木块的过程,在此过程中,子弹和木块组成的系统满足动量守恒,因而可以确定它们共同运动的初速度v 0 ,即振动的初速度.随后的过程是以子弹和木块为弹簧振子作简谐运动.它的角频率由振子质量m 1 +m 2 和弹簧的劲度系数k 确定,振幅和初相可根据初始条件(初速度v 0 和初位移x 0 )求得.初相位仍可用旋转矢量法求.解 振动系统的角频率为 ()121s 40-=+=m m k /ω由动量守恒定律得振动的初始速度即子弹和木块的共同运动初速度v 0 为()12110s m 01-⋅=+=.m m v m v又因初始位移x 0 =0,则振动系统的振幅为 ()m 105.2//202020-⨯==+=ωωx A v v 图(b )给出了弹簧振子的旋转矢量图,从图中可知初相位2/π0=,则简谐运动方程为()()m π0.540cos 105.22+⨯=-t x9-23 如图(a )所示,一劲度系数为k 的轻弹簧,其下挂有一质量为m 1 的空盘.现有一质量为m 2 的物体从盘上方高为h 处自由落入盘中,并和盘粘在一起振动.问:(1) 此时的振动周期与空盘作振动的周期有何不同? (2) 此时的振幅为多大?题9-23 图分析 原有空盘振动系统由于下落物体的加入,振子质量由m 1 变为m 1 + m 2,因此新系统的角频率(或周期)要改变.由于()2020/ωx A v +=,因此,确定初始速度v 0 和初始位移x 0 是求解振幅A 的关键.物体落到盘中,与盘作完全非弹性碰撞,由动量守恒定律可确定盘与物体的共同初速度v 0 ,这也是该振动系统的初始速度.在确定初始时刻的位移x 0 时,应注意新振动系统的平衡位置应是盘和物体悬挂在弹簧上的平衡位置.因此,本题中初始位移x 0 ,也就是空盘时的平衡位置相对新系统的平衡位置的位移.解 (1) 空盘时和物体落入盘中后的振动周期分别为k m ωT /π2/π21== ()k m m ωT /π2/π221+='='可见T ′>T ,即振动周期变大了.(2) 如图(b )所示,取新系统的平衡位置为坐标原点O .则根据分析中所述,初始位移为空盘时的平衡位置相对粘上物体后新系统平衡位置的位移,即g km g k m m k g m l l x 2211210-=+-=-= 式中l 1 =m 1/k 为空盘静止时弹簧的伸长量,l 2 =(m 1 +m 2)/k 为物体粘在盘上后,静止时弹簧的伸长量.由动量守恒定律可得振动系统的初始速度,即盘与物体相碰后的速度gh m m m m m m 22122120+=+=v v 式中gh 2=v 是物体由h 高下落至盘时的速度.故系统振动的振幅为()212202021/m m kh k g m ωx A ++='+=v 本题也可用机械能守恒定律求振幅A .9-24 如图所示,劲度系数为k 的轻弹簧,系一质量为m 1 的物体,在水平面上作振幅为A 的简谐运动.有一质量为m 2 的粘土,从高度h 自由下落,正好在(a )物体通过平衡位置时,(b )物体在最大位移处时,落在物体上.分别求:(1)振动周期有何变化? (2)振幅有何变化?题9-24图分析 谐振子系统的周期只与弹簧的劲度系数和振子的质量有关.由于粘土落下前后,振子的质量发生了改变,因此,振动周期也将变化.至于粘土如何落下是不影响振动周期的.但是,粘土落下时将改变振动系统的初始状态,因此,对振幅是有影响的.在粘土落到物体上的两种不同情况中,系统在水平方向的动量都是守恒的.利用动量守恒定律可求出两种情况下系统的初始速度,从而利用机械能守恒定律(或公式()2020/ωx A v +=)求得两种情况下的振幅.解 (1) 由分析可知,在(a )、(b )两种情况中,粘土落下前后的周期均为 k m ωT /π2/π21== ()k m m ωT /π2/π221+='='物体粘上粘土后的周期T ′比原周期T 大.(2) (a ) 设粘土落至物体前后,系统振动的振幅和物体经过平衡位置时的速度分别为A 、v 和A ′、v ′.由动量守恒定律和机械能守恒定律可列出如下各式2/2/212v m A k =' (1)()2/2/2212v '+='m m A k (2)()v v '+=211m m m (3)联立解上述三式,可得 ()A m m m A 211+='/即A ′<A ,表明增加粘土后,物体的振幅变小了.(b ) 物体正好在最大位移处时,粘土落在物体上.则由动量守恒定律知它们水平方向的共同速度v ′=m 1v /(m 1 +m 2 ) =0,因而振幅不变,即A ′=A9-25 质量为0.10kg 的物体,以振幅1.0×10-2 m 作简谐运动,其最大加速度为4.0 m·s -1 求:(1) 振动的周期;(2) 物体通过平衡位置时的总能量与动能;(3) 物体在何处其动能和势能相等? (4) 当物体的位移大小为振幅的一半时,动能、势能各占总能量的多少?分析 在简谐运动过程中,物体的最大加速度2max ωA a =,由此可确定振动的周期T .另外,在简谐运动过程中机械能是守恒的,其中动能和势能互相交替转化,其总能量E =kA 2/2.当动能与势能相等时,E k =E P =kA 2/4.因而可求解本题.解 (1) 由分析可得振动周期s 314.0/π2/π2max ===a A ωT(2) 当物体处于平衡位置时,系统的势能为零,由机械能守恒可得系统的动能等于总能量,即J 100221213max 22k -⨯====.m Aa m A E E ω(3) 设振子在位移x 0 处动能与势能相等,则有42220//kA kx =得 m 100772230-⨯±=±=./A x(4) 物体位移的大小为振幅的一半(即2x A =/)时的势能为 4221212P /E A k kx E =⎪⎭⎫ ⎝⎛==则动能为 43P K /E E E E =-= 9-26 一氢原子在分子中的振动可视为简谐运动.已知氢原子质量m =1.68 ×10-27 Kg ,振动频率υ=1.0 ×1014 Hz ,振幅A =1.0 ×10-11m.试计算:(1) 此氢原子的最大速度;(2) 与此振动相联系的能量.解 (1) 简谐运动系统中振子运动的速度v =-A ωsin (ωt +φ),故氢原子振动的最大速度为12max s m 1028.62-⋅⨯===A πA ωv v(2) 氢原子的振动能量J 1031.32/202max -⨯==v m E9-27 质量m =10g 的小球与轻弹簧组成一振动系统, 按()()cm 3/ππ85.0+=t x 的规律作自由振动,求(1) 振动的角频率、周期、振幅和初相;(2) 振动的能量E ;(3) 一个周期内的平均动能和平均势能.解 (1) 将()()cm 3/ππ85.0+=t x 与()ϕω+=t A x cos 比较后可得:角频率1s π8-=ω,振幅A =0.5cm ,初相φ=π/3,则周期T =2π/ω=0.25 s(2) 简谐运动的能量 J 1090721522-⨯==.ωmA E (3) 简谐运动的动能和势能分别为()ϕωω+=t mA E K 222sin 21 ()ϕωω+=t mA E P 222cos 21 则在一个周期中,动能与势能对时间的平均值分别为()J 109534d sin 2115220222-⨯==+=⎰.ωϕωωmA t t mA T E T K ()J 109534d cos 2115220222-⨯==+=⎰.ωϕωωmA t t mA T E T P 9-28 已知两同方向、同频率的简谐运动的运动方程分别为()()m π75.010cos 05.01+=t x ;()()m π25.010cos 06.02+=t x .求:(1) 合振动的振幅及初相;(2) 若有另一同方向、同频率的简谐运动()()m 10cos 07033ϕ+=t x .,则3ϕ为多少时,x 1 +x 3 的振幅最大? 又3ϕ 为多少时,x 2 +x 3 的振幅最小?题9-28 图分析 可采用解析法或旋转矢量法求解.由旋转矢量合成可知,两个同方向、同频率简谐运动 的合成仍为一简谐运动,其角频率不变;合振动的振幅()12212221cos 2ϕϕ-++=A A A A A ,其大小与两个分振动的初相差12ϕϕ-相关.而合振动的初相位()()[]22112211cos cos sin sin arctanϕϕϕϕϕA A A A ++=/ 解 (1) 作两个简谐运动合成的旋转矢量图(如图).因为2/πΔ12-=-=,故合振动振幅为 ()m 1087cos 2212212221-⨯=-++=.ϕϕA A A A A 合振动初相位 ()()[]rad1.48arctan11cos cos sin sin arctan22112211==++=ϕϕϕϕϕA A A A / (2) 要使x 1 +x 3 振幅最大,即两振动同相,则由π2Δk =得,...2,1,0,π75.0π2π213±±=+=+=k k k要使x 1 +x 3 的振幅最小,即两振动反相,则由()π12Δ+=k 得(),...2,1,0,π25.1π2π1223±±=+=++=k k k9-29 手电筒和屏幕质量均为m ,且均被劲度系数为k 的轻弹簧悬挂于同一水平面上,如图所示.平衡时,手电筒的光恰好照在屏幕中心.设手电筒和屏幕相对于地面上下振动的表达式分别为()11cos ϕω+=t A x 和()22cos ϕω+=t A x .试求在下述两种情况下,初相位φ1 、φ2 应满足的条件:(1) 光点在屏幕上相对于屏静止不动;(2) 光点在屏幕上相对于屏作振幅A ′=2A 的振动.并说明用何种方式起动,才能得到上述结果.题9-29 图分析 落在屏幕上的光点相对地面的运动和屏幕相对于地面的运动都已知道,且是两个简谐运动.因此由运动的合成不难写出光点相对屏的运动(实际上是两个同方向、同频率简谐运动的合成).根据相对运动公式,有屏对地光对屏光对地x x x +=依题意()()2211ϕωϕω+==+==t A x x t A x x cos cos 屏对地光对地所以 ()()212121cos cos ϕπωϕω++++='+=-=t A t A x x x x x 光对屏 可见光点对屏的运动就是两个同方向、同频率简谐运动()11c o sϕω+=t A x 和()22cos ϕπω++='t A x 的合成.用与上题相同的方法即可求解本题.其中合运动振幅()12222πcos 2-+++='A A A A .解 (1) 根据分析和参考上题求解,当要求任一时刻光点相对于屏不动,即0=光对屏x ,就是当()π12π12+=-+k 时,即π212k +=时(,...,,210±±=k ),A ′=0.当光点相对于屏作振幅为2A 的运动时,要求π2π12k =-+,即()π1212-+=k . (2) 由以上求解可知,要使光点相对于屏不动,就要求手电筒和屏的振动始终要同步,即同相位,为此,把它们往下拉A 位移后,同时释放即可;同理,要使光点对屏作振幅为2A 的谐振动,两者必须相位相反,为此,让手电筒位于平衡点0 上方的-A 处,而屏则位于+A 处同。
《大学物理学》习题解答(第11章 静电场)

1
Q L
L
2 0 r 1 4r 2 L2
2 0 r
2
【11.5】一半径为 R 的半圆细环上均匀的分布电荷 Q,求环心处的电场强度。 解取坐标 Oxy ,电荷元 d q d l R d ,由点电荷场强公式
y
d
dl
dq dE eR 4 0 R 2
由于电荷对称分布,场强也对称,则: Ex dEx 0
13
以 1.0 10 C s 的变化率失去电荷,求两球彼此趋近的瞬时相对速率(即
9
1
T q F mg x
l q
dx )是多少? dt
解 (1)如图所示,小球平衡时,
T sin F , T cos mg , F
q
2
4 0 x 2
13
q 2l x , 很小时, tan sin ,因此 x 则 mg tan 2 mg 2l 4 0 x 2 0
E d S E d S ER 2 cos ER 2
S S
z
A F C E O D B
【11.11】边长为 a 的立方体如图所示,其表面分别平行于 xy , yz 和 zx 平 面,立方体的一个顶点为坐标原点。现将立方体置于电场强度
E ( E1 kx)i E2 j 的非均匀电场中, 求立方体各表面及整个立方体表面的
Q d x ,则 L
EP
Qdx Q 1 1 1 Q [ ] 2 2 L 2 4 L ( r x ) 4 0 L r L 2 r L 2 0 4r L2 0
L2
1
(2)若点 P 在棒的垂直平分线上,因对称性, E 沿 x 轴方向的分量叠加为零,因此, E 的方向沿 y 轴, 大小为
大学物理(肖剑荣主编)-习题答案-第11章

个劈尖空气膜,用波长为 564 纳米的单色光垂直照射板面,板上显示出完整的
明暗条纹各 74 条。求金属丝的直径。
解 金属丝与两板之间形成一个劈尖空气膜,其上下表面的反射光相遇而发生干 涉。光程差为 Δ = 2e + λ / 2
由于板上显示出完整的明暗条纹各 74 条,所以该处应为第 74 条明条纹。 由明条纹的条件 2d + λ / 2 = kλ k=74,则 N = d / Δe
能看到第几级明条纹?
解: a + b = 1 mm = 2.0 ´10-3 mm = 2.0 ´10-4 Å 500
由 (a
+
b) sinj
=
kl
知,最多见到的条纹级数 kmax 对应的 j
=
p 2
,
所以有 kmax
=
a+b l
=
2.0 ´104 5900
» 3.39 ,即实际见到的最高级次为 kmax
解得
a = a + b k′ = 1.5 × 10−6 k′ 4
取 k′ = 1 得光栅上狭缝的的最小宽度为1.5 × 10−6 m
(3)由
(a + b)sinϕ = kλ
得
k
=
(
a
+
b) sinϕ λ
当 ϕ=π 2
时,对应 k = k max
k max
=
a+b λ
=
6.0 × 10−6 6000 × 10−10
解 在杨氏双缝干涉实验中,条纹间距 Δx = D λ d
屏幕上 20 条明条纹之间的距离 ΔX = 19Δx = D λ d
ΔX
= 19
大学物理课后习题11第十一章答案

1 1) ,
1
v2 c2
再由题意知
所以有
Ek nm0c2 。
最后得到
( 1 1) n
1
v2 c2
v n2 2n c 。
n 1
*11.11 一个电子的运动速度 v 0.99c ,它的动能是多少?(电子的静
止能量为0.51Mev.)
解:由相对论动能公式
Ek mc2 m0c2 m0c2 ( 1) m0c2 (
间隔为 5s.求:
(1) S 相对于 S 的运动速度.
(2) 乙测得这两个事件发生的地点间的距离.
解: 甲测得 t 4 s, x 0 ,乙测得 t 5 s ,坐标差为 x x2 x1 ′
(1)∴
t
(t
v c2
x)
t
1 t 1 (v)2
c
习题 11
11.1 选择题
(1)在一惯性系中观测,两个事件同时不同地,则在其他惯性系中
观测,他们[
]。
(A)一定同时
(B)可能同时
(C)不可能同时,但可能同地 (D)不可能同时,也
不可能同地
[答案:D ]
(2)在一惯性系中观测,两个事件同地不同时,则在其他惯性系中
观测,他们[
]。
(A)一定同地
(B)可能同地
负号表示
x
2
x1
0
.
11.6 6000m 的高空大气层中产生了一个 介子以速度 v =0.998c 飞向
地球.假定该 介子在其自身静止系中的寿命等于其平均寿命 2×
10-6s.试分别从下面两个角度,即地球上的观测者和 介子静止系中
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第11章 稳恒磁场习 题一 选择题11-1 边长为l 的正方形线圈,分别用图11-1中所示的两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为:[ ](A )10B =,20B = (B )10B =,02IB lπ= (C)01IB lπ=,20B = (D)01I B l π=,02IB lπ=答案:C解析:有限长直导线在空间激发的磁感应强度大小为012(cos cos )4IB dμθθπ=-,并结合右手螺旋定则判断磁感应强度方向,按照磁场的叠加原理,可计算01IB lπ=,20B =。
故正确答案为(C )。
11-2 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,如图11-2所示,则在圆心O 处的磁感应强度大小为多少? [ ](A )0 (B )R I 2/0μ (C )R I 2/20μ (D )R I /0μ 答案:C解析:圆线圈在圆心处的磁感应强度大小为120/2B B I R μ==,按照右手螺旋定习题11-1图习题11-2图则判断知1B 和2B 的方向相互垂直,依照磁场的矢量叠加原理,计算可得圆心O处的磁感应强度大小为0/2B I R =。
11-3 如图11-3所示,在均匀磁场B 中,有一个半径为R 的半球面S ,S 边线所在平面的单位法线矢量n 与磁感应强度B 的夹角为α,则通过该半球面的磁通量的大小为[ ](A )B R 2π (B )B R 22π (C )2cos R B πα (D )2sin R B πα 答案:C解析:通过半球面的磁感应线线必通过底面,因此2cos m B S R B παΦ=⋅=。
故正确答案为(C )。
11-4 如图11-4所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量ΦB 将如何变化?[](A)Φ增大,B 也增大 (B )Φ不变,B 也不变 (C )Φ增大,B 不变 (D )Φ不变,B 增大 答案:D解析:根据磁场的高斯定理0SBdS Φ==⎰,通过闭合曲面S 的磁感应强度始终为0,保持不变。
无限长载流直导线在空间中激发的磁感应强度大小为02IB dμπ=,曲面S 靠近长直导线时,距离d 减小,从而B 增大。
故正确答案为(D )。
11-5下列说确的是[ ](A) 闭合回路上各点磁感应强度都为零时,回路一定没有电流穿过 (B) 闭合回路上各点磁感应强度都为零时,回路穿过电流的代数和必定为零 (C) 磁感应强度沿闭合回路的积分为零时,回路上各点的磁感应强度必定为零(D) 磁感应强度沿闭合回路的积分不为零时,回路上任意一点的磁感应强度都不可能为零I习题11-4图习题11-3图答案:B解析:根据安培环路定理0d i liB lI μ=∑⎰,闭合回路上各点磁感应强度都为零表示回路电流的代数和为零。
回路上各点的磁感应强度由所有电流有关,并非由磁感应强度沿闭合回路的积分所决定。
故正确答案为(B )。
11-6 如图11-6所示,I 1和I 2为真空中的稳恒电流,L ⎰⋅d l的值为[ ](A )012()I I μ+(B )012()I I μ-+ (C )012()I I μ-- (D )012()I I μ-答案:C解析:根据安培环路定理0d i liB lI μ=∑⎰,并按照右手螺旋定则可判断I 1取负值,I 2为正,因此012d ()LB l I I μ⋅=--⎰。
11-7 如图11-7所示,一根很长的电缆线由两个同轴的圆柱面导体组成,若这两个圆柱面的半径分别为R 1和R 2(R 1<R 2),通有等值反向电流,那么下列哪幅图正确反映了电流产生的磁感应强度随径向距离的变化关系?[ ](A ) (B ) (C ) (D )答案:C解析:根据安培环路定理0d i liB lI μ=∑⎰,可得同轴的圆柱面导体的磁感应强度分布为1012220,0,,0r R B I R r R B r r R B μπ<<=⎧⎪⎪<<=⎨⎪>=⎪⎩,作B-r 图可得答案(C )。
11-8一运动电荷q ,质量为m ,垂直于磁场方向进入均匀磁场中,则[ ]习题11-6图12R 112R 12R 习题11-7图(A )其动能改变,动量不变 (B )其动能不变,动量可以改变 (C )其动能和动量都改变 (D )其动能和动量都不变 答案:B解析:垂直于磁场方向进入均匀磁场的电荷受到洛伦兹力的作用,仅提供向心力,改变电荷速度的方向,而不改变速度的大小,从而其动能不变,而动量改变。
故正确答案为(B )。
11-9 如图11-9所示,一根载流导线被弯成半径为R 的1/4圆弧,放在磁感应强度为B 的均匀磁场中,则载流导线所受的安培力为[ ](A )2BIR ,竖直向下 (B )BIR ,竖直向上 (C )2BIR ,竖直向上 (D )BIR ,竖直向下 答案:C解析:连接ab 形成一闭合回路,由于此回路所在平面垂直于磁感应强度方向,因此,回路受力为零,则弧线受力与直线ab 受力大小相等,方向相反。
直导线ab 受力为2ab F BIl BIR ==,方向竖直向下,因此载流弧线所受的安培力2BIR ,方向为竖直向上。
11-10 用细导线均匀密绕成长为l 、半径为a (l >>a )、总匝数为N 的螺线管,通以稳恒电流I ,当管充满相对磁导率为r μ的均匀介质后,管中任意一点磁感应强度大小为[ ](A )0/r NI l μμ (B )l NI r /μ (C )l NI /0μ (D )l NI / 答案:A解析:根据由磁介质时的安培环路定理d iliH l I=∑⎰,得螺线管磁场强度大小为NIH l=,因此管中任意一点磁感应强度大小为00/r r B H NI l μμμμ==。
故正确答案为(A )。
习题11-9图二 填空题11-11 一无限长载流直导线,沿空间直角坐标的Oy 轴放置,电流沿y 正向。
在原点O 处取一电流元I d l ,则该电流元在(a ,0,0)点处的磁感应强度大小为_______________,方向为_____________。
答案:02d 4I la μπ;沿z 轴负方向 解析:根据毕奥-萨伐尔定律03d 4Idl rB rμπ⨯=,Idl 与r 的方向相互垂直,夹角为90°电流元激发的磁感应强度大小为0032d sin d d 44I l a I lB a a μθμππ⋅⋅==,按照右手螺旋定则可判断方向沿z 轴负方向。
11-12 无限长的导线弯成如图11-12所示形状,通电流为I ,BC 为半径R 的半圆,则O 点的磁感应强度大小 ,方向为 。
答案:0044IIRRμμπ+;垂直纸面向里 解析:根据磁感应强度的叠加原理,O 点的磁 感应强度由三部分组成。
0AB B =,0,4BC IB Rμ=方向垂直纸面向里,0,4CDB Rπ=方向垂直纸面向里。
因此,O 点的磁感应强度大小0044AB BC CD IIB B B B RRμμπ=++=+,方向为垂直纸面向里。
11-13 两根长度相同的细导线分别密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管,两个螺线管的长度相同,R =2r ,螺线管通过的电流相同为I ,则螺线管中的磁感应强度大小:R r B B = 。
答案:1:2解析:螺线管中的磁感应强度大小0NB I lμ=,其中长度l 与电流I 相同,因此B 与总匝数N 成正比。
两根导线的长度L 相同,绕在半径不同的长直圆筒上,可得:::1:222R r L L N N r R R rππ===,因此:1:2R rB B 。
11-14 如图11-14所示,均匀磁场的磁感应强度为B =0.2 T ,方向沿x 轴正方向,则通过abod 面的磁通量为_________,通过befo 面的磁通量为__________,通过aefd 面的磁通量为_______。
答案:-0.024Wb ;0Wb ;0.024Wb解析:根据磁通量的定义式cos m B S BS θΦ=⋅=, 磁感应强度与abod 面面积矢量的夹角为1180θ=, 与befo 面面积矢量的夹角290θ=,与aefd 面 面积矢量的夹角为34cos 5θ=。
因此,1cos 0.024Wb abod abod BS θΦ==-,2cos 0Wb befo befo BS θΦ==,3cos 0.024Wb aefd aefd BS θΦ==。
11-15如图11-15所示,一长直导线通以电流I ,在离导线a 处有一电子,电量为e ,以速度v 平行于导线向上运动,则作用在电子上的洛伦兹力的大小为 ,方向为 。
答案:02e Ivaμπ;水平向右 解析:无限长直导线在离导线a 处激发的磁感应强度大小 为02IB aμπ=,方向垂直纸面向里;作用在电子上的洛伦兹力 的大小0sin 2e IvF qvB aμθπ==,按照右手螺旋定则判断电子受力方向为水平向右。
11-16 如图11-16所示,A 和B 是两根固定的直导线,通以同方向的电流1I 和2I ,且1I >2I ,C 是一根放置在它们中间可以左右移动的直导线(三者在同一平面),若它通以反方向的电流I 时,导线C 将____________(填向A 移动、向B 移动、保持静止)。
答案:向B 移动解析:根据右手螺旋定则判断导线A 施加给C 的力AC F 的方向为指向B ,同理导线B 施加给C 的力BC F 的方向为指向A 。
安培力02iI F BIL IL dμπ==,因为1I >2I ,因ab o d efx yz B 30 cm40 cm 30 cm 50 cm习题11-14图vIa此AC BC F F >,从而导线C 所受合力与AC F 相同,因此,导线C 向B 移动。
11-17 一带电粒子以速度v 垂直于均匀磁场B 射入,在磁场中的运动轨迹是半径为R 的圆,若要使运动半径变为2R ,则磁场B 的大小应变为原来的 倍。
答案:2解析:垂直于均匀磁场射入的带电粒子将在磁场中作匀速率圆周运动,圆周的半径为mvr qB=,与B 成反比。
现运动半径变为原来的1/2,则磁场B 的大小应变为原来的2倍。
11-18 一1/4圆周回路abca ,通有电流I ,圆弧部分的半径为R ,置于磁感应强度为B 的均匀磁场中,磁感线与回路平面平行,如图11-18所示,则圆弧ab 段导线所受的安培力大小为 ,回路所受的磁力矩大小为 ,方向为 。
答案:BIR ;214BIR π;竖直向下解析:ab ca bc F F F =+,由于0bc F =,因此ab ca F F BIR == 根据磁力矩定义式M m B =⨯,m 的方向垂直纸面向里,与B 方向的夹角为90°,回路所受的磁力矩大小21sin 4M BIS BIR ϕπ==,按照右手螺旋定则,方向为竖直向下。
