太阳位置计算
日出日落的方位角度计算公式

计算日出日落的方位角度公式要计算任意一个地方在任意一天日出日落的方位角度,可以用下面的公式:方位角=90 - 0.5arccos[2(sinM/cosN)^2- 1]公式中,M表示的是某天太阳直射的纬度,N表示的是某地的纬度,^2表示平方。
例如,北京在北纬40度,则N=40,夏至这一天太阳在北纬23.5度(太阳直射北纬23.5度),即M=23.5,把N和M的值代入上式,可求得方位角=31度意思是,夏至这一天,在北京的人看来,太阳是从东偏北31度的方位升起的,是在西偏北31度的方位落下的。
说明:1本公式是在理想条件下推导出来的,即假设地球是个标准球体。
而实际上地球两极略扁,而且各地也有高山、洼地等,所以计算结果可能与实测结果有一点误差。
2 太阳围绕地球旋转的轨迹实际上是螺旋线(好象在地球外面套一根弹簧),所以实际上每天日出和日落的方位角稍微有点差别。
例如,在春分到夏至这段时间,日出方位角要略小于日落方位角。
昼夜长短的计算公式:Cost=-tgδ*tgφ太阳视位置太阳视位置指从地面上看到的太阳的位置,用太阳高度角和太阳方位角两个角度作为坐标表示。
太阳高度角指从太阳中心直射到当地的光线与当地水平面的夹角,其值在0°到90°之间变化,日出日落时为零,太阳在正天顶上为90°(本万年历中显示的高度角均已进行了蒙气差的订正,蒙气差值取自天文年历)。
太阳方位角即太阳所在的方位,指太阳光线在地平面上的投影与当地子午线的夹角,可近似地看作是竖立在地面上的直线在阳光下的阴影与正南方的夹角。
方位角以正南方向为零,由南向东向北为负,由南向西向北为正,如太阳在正东方,方位角为-90°,在正东北方时,方位为-135°,在正西方时方位角为90°,在正北方时为±180°。
实际上太阳并不总是东升西落,只有在春秋分两天,太阳是从正东方升,正西方落。
在北半球,从春分到秋分的夏半年中,太阳从东偏北的方向升(方位角为-90°到-180°之间),在西偏北的方向落(方位角为90°到180°之间);而从秋分到下一年春分的冬半年中,太阳从东偏南的方向升(方位角为-90°到0°之间),在西偏南的方向落(方位角为0°到90°之间)。
一种计算太阳的位置

一种太阳位置计算摘要一种新的太阳位置的准定算法。
在考虑高浓度热力系统情况下,准确的太阳位置跟踪是非常重要的。
在许多文献中发现简单的太阳位置的算法精确度在0.01度,而复杂的天文算法精度能0.0003度,但需要大量的计算。
在本文中提出的算法是一个精密度在两者之间的情况(最大误差0.0027度),可以应用在所有的太阳能工程应用方面的计算当中,在太阳能工程计算中比较方便的快速算法。
1.引言这项太阳的位置算法的精度高(在2003-2023年这一段时间内,最大的误差0.0027度)和不复杂的算法。
这种准确度应该够所有生活中太阳能工程的需要。
在文献中找到的许多快速计算太阳位置的算法,用于工程应用。
才发现他们需要的计算量较小,但他们最大的不足是通常误差大0.01度。
Spencer公式(Spencer,1971年)达到最大误差超过0.25度;Pitman和Vant-Hull算(Pitman和Vant-Hull,1978年)减小误差到0.02度;Walraven算法(Walraven,1978年),Walraven随后的修正,改进(Walraven,1979年,Archer,1980年;Wilkinson,1981年,1983年;Muir,1983年),误差在0.013度。
Michalsky算法(Michalsky,1988年),用于比较准确的工作,最大误差0.011度;最后一个算法,SPA算法(Blanco-Muriel et al,2001年)最大误差0.008度。
所有这些算法正确的计算时间为有限周期时间。
例:1950-2050用Michalsky算法, 1995-2015用SPA算法。
也有一些高精度天文算法,如Meeus(1988年)提出的数值计算方法, Reda和Andreas (2004年)有一种适合太阳能应用算法,众所周知的SPA(太阳的位置算法)。
在很长一段时见(2000b.C.- 6000a.C)该算法最大误差小于0.0003度,但需要大量的计算。
第24章太阳位置计算

第24章太阳位置计算[许剑伟于家里2008-3-30下午]一、低精度计算:当计算精度要求为0.01度,计算太阳位置时可假设地球运动是一个纯椭圆,也就说忽略月球及行星摄动,计算表达如下。
设JD是儒略日数,可以用第7章表述的方法计算。
T为J2000起算的儒略世纪数:T = (JD-2451545.0)/36525计算时要保留足够的小数位数,5位小数是不够的(除非所需的太阳黄经的精度要求不高),注意,T表达为儒略世纪数,所以T误差0.00001相当于0.37日。
接下来,太阳几何平黄经:Lo = 280°.46645 + 36000°.76983*T + 0°.0003032*T^2 (Date平分点起算)太阳平近点角: M = 357°.52910 + 35999°.05030*T - 0°.0001559*T^2 -0°.00000048*T^3 地球轨道离心率:e = 0.016708617 - 0.000042037*T - 0.0000001236*T^2太阳中间方程:C = +(1°.914600 - 0°.004817*T -0°.000014*T*T) * sin(M)+(0°.019993 - 0°.000101*T) * sin(2M)+ 0°.000290*sin(3M)那么,太阳的真黄经是:Θ= Lo + C真近点角是:v = M + C日地距离的单位是"天文单位",距离表达为:R = 1.000001018 (1-e^2) / (1+e*cos(v)) ……24.5式式中的分子部分的值变化十分缓慢。
它的值是:0.9997190 1800年0.9997204 1900年0.9997218 2000年0.9997232 2100年太阳黄经Θ可由上述的方法算出,它是Date黄道分点坐标中的真几何黄经,需通过计算地心坐标星体位置也可算出。
日出日落的方位角度计算公式

计算日出日落的方位角度公式要计算任意一个地方在任意一天日出日落的方位角度,可以用下面的公式:方位角=90 - 0.5arccos[2(sinM/cosN)^2- 1]公式中,M表示的是某天太阳直射的纬度,N表示的是某地的纬度,^2表示平方。
例如,北京在北纬40度,则N=40,夏至这一天太阳在北纬23.5度(太阳直射北纬23.5度),即M=23.5,把N和M的值代入上式,可求得方位角=31度意思是,夏至这一天,在北京的人看来,太阳是从东偏北31度的方位升起的,是在西偏北31度的方位落下的。
说明:1本公式是在理想条件下推导出来的,即假设地球是个标准球体。
而实际上地球两极略扁,而且各地也有高山、洼地等,所以计算结果可能与实测结果有一点误差。
2 太阳围绕地球旋转的轨迹实际上是螺旋线(好象在地球外面套一根弹簧),所以实际上每天日出和日落的方位角稍微有点差别。
例如,在春分到夏至这段时间,日出方位角要略小于日落方位角。
昼夜长短的计算公式:Cost=-tgδ*tgφ太阳视位置太阳视位置指从地面上看到的太阳的位置,用太阳高度角和太阳方位角两个角度作为坐标表示。
太阳高度角指从太阳中心直射到当地的光线与当地水平面的夹角,其值在0°到90°之间变化,日出日落时为零,太阳在正天顶上为90°(本万年历中显示的高度角均已进行了蒙气差的订正,蒙气差值取自天文年历)。
太阳方位角即太阳所在的方位,指太阳光线在地平面上的投影与当地子午线的夹角,可近似地看作是竖立在地面上的直线在阳光下的阴影与正南方的夹角。
方位角以正南方向为零,由南向东向北为负,由南向西向北为正,如太阳在正东方,方位角为-90°,在正东北方时,方位为-135°,在正西方时方位角为90°,在正北方时为±180°。
实际上太阳并不总是东升西落,只有在春秋分两天,太阳是从正东方升,正西方落。
在北半球,从春分到秋分的夏半年中,太阳从东偏北的方向升(方位角为-90°到-180°之间),在西偏北的方向落(方位角为90°到180°之间);而从秋分到下一年春分的冬半年中,太阳从东偏南的方向升(方位角为-90°到0°之间),在西偏南的方向落(方位角为0°到90°之间)。
太阳位置计算

第24章太阳位置计算[许剑伟于家里 2008-3-30下午]一、低精度计算:当计算精度要求为0.01度,计算太阳位置时可假设地球运动是一个纯椭圆,也就说忽略月球及行星摄动,计算表达如下。
设JD是儒略日数,可以用第7章表述的方法计算。
T为J2000起算的儒略世纪数:T = (JD-2451545.0)/36525计算时要保留足够的小数位数,5位小数是不够的(除非所需的太阳黄经的精度要求不高),注意,T表达为儒略世纪数,所以T误差0.00001相当于0.37日。
接下来,太阳几何平黄经:Lo = 280°.46645 + 36000°.76983*T + 0°.0003032*T^2 (Date平分点起算)太阳平近点角: M = 357°.52910 + 35999°.05030*T - 0°.0001559*T^2 -0°.00000048*T^3地球轨道离心率: e = 0.0 - 0.000042037*T - 0.0000001236*T^2太阳中间方程:C = +(1°.914600 - 0°.004817*T -0°.000014*T*T) * sin(M)+(0°.019993 - 0°.000101*T) * sin(2M)+ 0°.000290*sin(3M)那么,太阳的真黄经是:Θ = Lo + C真近点角是: v = M + C日地距离的单位是"天文单位",距离表达为:R = 1.000001018 (1-e^2) / (1+e*cos(v)) ……24.5式式中的分子部分的值变化十分缓慢。
它的值是:0.9997190 1800年0.9997204 1900年0.9997218 2000年0.9997232 2100年太阳黄经Θ可由上述的方法算出,它是Date黄道分点坐标中的真几何黄经,需通过计算地心坐标星体位置也可算出。
用天文测量简历精确计算太阳位置的方法

用天文测量简历精确计算太阳位置的方法天文测量是一种精确测量天体位置和运动的科学技术,是太空探索和星际旅行的重要基础。
太阳作为地球最为重要的天体之一,它的位置对于日常生活、导航、气象预测以及科学研究都具有重要意义。
本文将介绍几种通过天文测量精确计算太阳位置的方法。
方法一:日晷法日晷是一种将太阳高度角与时间联系起来的仪器,经过精确测量,可以用来计算太阳在天空中的位置。
日晷的基本原理是利用太阳的影子来测量时间。
根据太阳影子在地面上的轨迹以及影子长度的变化,可以确定太阳的高度角和方位角。
通过对太阳高度角和方位角的测量和计算,可以确定太阳在天空中的位置。
方法二:天文学三角测量法天文学三角测量法是利用三角形中的角度和边长来计算未知角度和边长的一种方法。
在天文学中,通过观测天体的位置和运动轨迹,可以使用天文学三角测量法来测量它们的距离、速度和位置等信息。
其中,使用天文学三角测量法测量太阳的位置,是通过观测太阳在两个不同地点的高度角和方位角,以及两个地点的距离来计算太阳在天空中的位置。
方法三:望远镜观测法望远镜观测法是利用望远镜来观察太阳,通过测量太阳的大小和位置,来计算太阳在天空中的位置。
望远镜可以提供更加精确和详细的太阳图像,同时也可以通过望远镜的调节和校正来消除大气的影响,进一步提高观测精度。
方法四:地球磁场观测法地球磁场观测法是利用地球磁场的变化来精确测量太阳位置的一种方法。
太阳活动会影响地球磁场,因此,通过观测地球磁场的变化,可以获得太阳活动的信息。
通过计算地球磁场的变化,以及太阳、地球和观测点的位置,可以计算出太阳在天空中的位置。
以上四种方法是通过天文测量精确计算太阳位置的常用方法。
不同的方法适用于不同的场景和精度要求。
无论使用哪种方法,天文测量的基础仍然是精确测量和计算。
因此,天文学家和测量技术人员需要具备精确测量和计算的技能,以及对天文学的深刻理解和热爱。
相关数据是指对研究对象进行的各种观测、测量、实验等数据,是进行科学研究和分析的基础。
太阳直射点经纬度计算公式

太阳直射点经纬度计算公式1太阳直射点的经纬度计算大家都知道,地球运行时它会不断地运动。
而太阳又永远保持在绝对静止的位置,而绕地球行转一圈等于一天时间。
这就意味着,在一天之内,太阳在地球上有一个“直射点”,它就是日光为期一天的移动所画出的圈上有许多直线,有一个处于东南方的经纬度永远处于太阳直射点。
因此,计算太阳最终直射点的经纬度就成为一个有趣的问题。
无论多么复杂,只要理解了一些基本的原理,就可以计算出结果。
1计算地球的轨道倾角由于太阳的轨道是非平行的,运动的方向也有所变化,所以想要计算出太阳最终直射点的经纬度,首先应该确定出地球轨道的倾角。
具体来说,通过观察太阳最终直射点位置,可以得出它的轨道倾角。
而地球轨道的正确倾角大约是23.4°,这也是太阳在每一天经过的最大角度。
2计算太阳在不同经度下的高度当我们确定了地球轨道的倾角后,就可以计算出太阳在不同的经度下的高度了。
具体来说,只要根据坐标系中的单位弧度确定都经度,确定每一经度对应的太阳升高角,每个日出时刻经度就可以绘制出一条太阳高度曲线。
不难看出,太阳在一天中心经度的最高点就是太阳直射点,其太阳升高角也比其他经度稍高一些。
3计算太阳直射点的经纬度当我们确定了太阳在不同经度下的高度,就可以计算出太阳最终直射点的经纬度了。
具体来说,要首先确定整个斜率的参数,然后将太阳最终直射点放在斜率上,以此来确定太阳最终直射点的经纬度。
到这里,就可以计算出太阳最终直射点的经纬度,有的的这两个经度坐标就可以根据自己的情况,将太阳最终直射点的位置移动过去了。
总之,要计算太阳最终直射点的经纬度,首先要确定地球轨道的倾角,然后计算太阳在不同经度下的高度,最后将太阳最终直射点放在斜率上,以此来计算其经纬度的坐标。
计算方法虽然不难,但一定要理解核心原理,才能准确地计算出最终的结果。
太阳方位计算原理
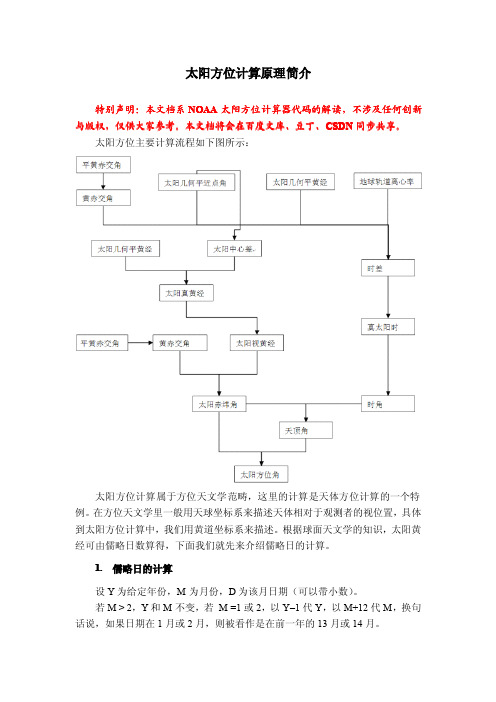
由于在两组坐标系中的矢量 s 相同,我们可以得到: cosz=(sinδ)(sin λ)+(cosδ)(cosλ)cosω 6. 太阳方位角的计算 “定位三角形”并如下图所示,球面三角形 ABC 以弧 AB,BC 和 AC 为边。假设球的半 径为 r,则弧 AB 的弧长为 rc,其中 c 为弧 AB 所对圆心角。这个角称为弧 AB 的中心角。因为边长与中心角是一一对应的在同一个球面三角形中,因此习惯上 用中心角来表示球面三角形的边。这样做的优点是与球的半径无关。球面三角形 的角定义为由包含球面三角形两条边的大圆所在的平面组成的二面角。 球面三角形的角由大写字母(A,B,C)来表示,其对应的边有小写字母(a, b,c)来表示。
对儒略历,取 B = 0
要求的儒略日即为:
JD = INT(365.25(Y+4716))+INT(30.6001(M+1))+D+B-1524.5
(7.1)
使用数值 30.6 取代 30.6001 才是正确的,但我们仍使用 30.6001,以确保总
能取得恰当的整数。事实上可用 30.601 甚至 30.61 来取代 30.6001。例如,5 乘
上面是讲一些预备知识,下面开始正式的计算。 当计算精度要求为 0.01 度,计算太阳位置时可假设地球运动是一个纯椭圆, 也就说忽略月球及行星摄动,计算表达如下。 设 JD 是儒略日数,可以用上面的方法计算。T 为 J2000 起算的儒略世纪数: T = (JD-2451545.0)/36525 计算时要保留足够的小数位数,5 位小数是不够的(除非所需的太阳黄经的精 度要求不高),注意,T 表达为儒略世纪数,所以 T 误差 0.00001 相当于 0.37 日。 接下来,太阳几何平黄经: L0 = 280°.46645 + 36000°.76983*T + 0°.0003032*T2 (当日平分点黄经起算) 太阳平近点角: M = 357°.52910 + 35999°.05030*T - 0°.0001559*T2 -0°.00000048*T3 地球轨道离心率:
Micheal-Yang太阳位置计算公式

太阳方位角/高度角计算公式2014/4/14Micheal-Yang1. 太阳高度角sinHs sin sin cos cos cost ϕδϕδ=⋅+⋅⋅式中,表示太阳高度角,表示地理纬度,表示太阳赤纬,表示时角。
(太阳赤纬和时角的概念请自行百度。
)由式中可见,地理纬度,还需要求太阳赤纬和时角。
太阳赤纬和时角的求法见下。
2. 太阳方位角()()/cosAs sinHs sin sin cosHs cos ϕδϕ=⋅−⋅式中,表示太阳高度角,表示地理纬度,表示太阳赤纬。
3. 太阳赤纬设太阳赤纬为delta ,有:delta(deg)=[0.006918-0.399912cos(b)+0.070257sin(b)-0.006758cos(2b)+0.000907sin(2b)-0.002697cos(3b)+0.00148sin(3b)](180/pi)其中delta 的单位为度(deg);pi=3.1415926为圆周率;b(deg)=360N/365,单位为度(deg); N 为日数,自每年1月1日开始计算。
4. 时角时角由太阳时求得。
太阳时角在正午时约为零,上午为负,下午为正,日出时约为-90°,日没时约为90°。
平均每小时时角变化15°。
太阳时角t = ( 真太阳时(called True Time) - 12 ) * 15°我们知道,一般情况下,我们的时钟显示12:00时,太阳并没有位于正中间,这是因为我们的时钟时间(也叫“平太阳时”)与真太阳时有一定的偏差,而真太阳时的12:00正是太阳位于正中,即方位角为0的时间。
真太阳时=平太阳时+真太阳时时差。
还有一点我们要注意,由于我国全国使用的都是“北京时间”,因此在计算真太阳时时,还要计算由于经度不同带来的时差。
虽然是“北京时间”,但“北京时间”是根据东经120°测得的,因此计算时差时,要以东经120°为标准。
太阳位置求算公式与计算举例

太阳位置求算公式与计算举例默认分类2022-11-14 21:04:44阅读393评论2 字号:大中小订阅太阳位置求算公式与计算举例杨齐聪在新农村建设和城市高楼群落的规划设计中,为了解决土地采用率与满意采光通风最低要求的冲突,常会遇到各幢楼房各部位的采光时间和日墙方位角的计算。
太阳位置可由太阳高度角hs和方位角as打算,依据球面三角基本公式可得:一、太阳高度角hs求算公式Sinhs=sinδsinφ+cosδcosφcosω (1)式中δ为太阳赤纬,表示太阳光线与地球赤道面的夹角,一年四季每天都在变动着,冬至B δ=-23o27,,春分日和秋分日δ=0°,夏至日5二23。
27';φ为测点纬度,如北京φ=39°48'∖西安φ=34°18;上海φ=31o10∖杭州φ=30°19;临海φ=28°51'∖福州φ=26°05'∖台北φ=25°20'∖广州φ=23°08∖3为太阳时角,以当地正午为0。
,上午为负,每小时一15。
,下午为正,每小时+15。
,ω在赤道面上每小时变化为=15°, 3所表示的是真太阳时;与时钟不同。
现举例计算于下:1.求北纬30。
地方冬至日正午时刻和下午1时、2时(均指地方时)的太阳高度角。
①正午时刻太阳时角为0。
,即3=0°将5=—23°27'、φ=30∖ 3=0。
代入(1)式得Sinh !E^=sin(-23027,)sin300+cos(-23027,)cos300cos00=-0.3979×0.5+0.9175×0.8660×1=-0.19895+0.79456=0.5956h正午=36°33'(查正弦数学用表所得,下同)则北纬30。
地方冬至日正午时刻的太阳高度角为36。
33:②下午1时(上午11时与此高度角同),太阳时角为15°,即ω=15o得Sinh 下午 1 0'J =sin(-23o27,)si∩3O o+cos(-23o27,)cos3O o cos15°=-0.19895+0.79456×0.9659=-0.19895+0.7675=0.5685h下午1时二34°39'则北纬30。
太阳方位角计算公式

太阳方位角计算公式太阳方位角是指太阳光线照射地球表面的方向角度,用于描述太阳的位置。
在地理学、气象学、太阳能利用等领域中,太阳方位角的计算十分重要。
本文将介绍常用的太阳方位角计算公式。
1. 太阳方位角的定义太阳方位角是从南方向起算的,以正南为0度,正西为90度,正北为180度,正东为270度。
太阳方位角的范围一般为0到360度。
2. 基于地理位置的太阳方位角计算在计算太阳方位角时,首先需要确定地理位置的经度和纬度。
根据经度和纬度的不同,太阳方位角的计算公式也有所不同。
2.1. 根据地球倾斜角的太阳方位角计算公式当地球自转轴倾斜角为23.5度时,太阳的赤纬(太阳光线与地球赤道平面的夹角)可以通过以下公式来计算:sin(太阳赤纬) = sin(地球倾斜角) * sin(太阳天顶角)其中,太阳天顶角为太阳光线与地球竖直向上的夹角。
太阳方位角可根据以下公式计算:cos(太阳方位角) = cos(90°-太阳赤纬) * sin(方位角) / cos(太阳赤纬)2.2. 根据时角的太阳方位角计算公式时角是太阳位于当地子午线上的角度,可通过以下公式计算:时角 = 当地真太阳时 - 当地标准中午时其中,当地真太阳时是指太阳在当地的真实时刻,而当地标准中午时是指太阳经过当地子午线的时刻。
太阳方位角可以根据以下公式计算:tan(太阳方位角) = sin(时角) / (sin(纬度) * cos (时角) - cos(纬度) * tan(太阳赤纬))3. 示例假设我们要计算纬度为30度,经度为120度的地点的太阳方位角。
首先,我们需要计算太阳赤纬,可以使用第2.1节中的公式:sin(太阳赤纬) = sin(23.5°) * sin(太阳天顶角)然后,根据第2.1节中的公式计算太阳方位角:cos(太阳方位角) = cos(90°-太阳赤纬) * sin(方位角) / cos(太阳赤纬)在有了太阳赤纬的数值之后,我们也可以使用第2.2节中的公式计算太阳方位角:tan(太阳方位角) = sin(时角) / (sin(30°) * cos(时角) - cos(30°) * tan(太阳赤纬))4. 结论本文介绍了通过地理位置的经度和纬度来计算太阳方位角的常用公式。
天文学家如何计算太阳的位置

天文学家如何计算太阳的位置
历书时:历书时是指通过测量太阳在天空中的位置,并将其与地球的自转和公转相结合,计算出的太阳在天空中的角度。
历书时的精度可以达到几秒甚至几毫秒的量级。
太阳视运动:太阳的视运动是指太阳在天空中的运动方式,包括周期性的升起和落下、在天空中的移动轨迹等。
通过观察太阳的视运动,天文学家可以推算出太阳在天空中的位置和时间。
恒星际位置:恒星际位置是指太阳在宇宙中的位置,包括太阳与其他恒星之间的距离和方向。
通过测量太阳与其他恒星之间的距离和方向,天文学家可以计算出太阳在宇宙中的位置和运动轨迹。
太阳辐射量:太阳辐射量是指太阳每秒向外发出的能量总量。
通过测量太阳辐射量,天文学家可以了解太阳的能量输出情况,进而推算出太阳在天空中的位置和时间。
通过结合这些信息,天文学家可以计算出太阳在天空中的位置,从而进行各种观测和研究。
例如,天文学家可以使用太阳视运动测量太阳的周期性变化,使用历书时和恒星际位置确定太阳在宇宙中的距离和方向,使用太阳辐射量测量太阳的能量输出情况。
这些观测和研究有助于我们更好地了解宇宙的形成和演化、探索时间的本质、改进现有技术以及帮助解决其他相关问题。
日出方位角计算公式

日出方位角计算公式日出方位角计算公式:日出方位角=90 - 0.5arccos[2(sinM/cosN)^2- 1];公式中,M-某天太阳直射的纬度,N-某地的纬度,^2-平方。
太阳方位角计算公式:太阳高度角hs:sinhs=sinφ·sinδ+cosψ·cosδ·cosΩ;式中 hs-太阳高度角、φ-地理纬度、δ-赤纬、Ω-时角。
太阳方位角As:COSAs= sinhs·sinψ-sinδ/(coshs·cosψ);式中As-太阳方位角。
太阳高角度:太阳高度角是从观测者所在地和太阳中心的联线与地平面所夹的角度。
天顶角是是高度角的余角,也就是(90°–gS )。
当太阳的高度角为90°,即太阳位于天顶,因此太阳的天顶角为0。
日地距离计算公式:ER=1.000423+0.032359sinθ+0.000086sin2θ-0.008349cosθ+0.000115cos2θ;式中θ称日角,即θ=2πt/365.2422。
太阳方位角的测定方法:对于中国区域,早上太阳光从东边射来,中午太阳光从南边射来,傍晚太阳光从西边边射来,早上的太阳方位角在90°左右(但一年当中,有一定的角度范围变化),正中午的太阳方位角在180°(正南方),傍晚的太阳方位角在270°左右(但一年当中,有一定的角度范围变化)。
例如北京处在北纬约40°,一年中,早上的太阳方位角变化量约为90°±31°;对于陆地卫星系统而言,如美国的Landsat TM/ETM+,该卫星的过境(中国)时间大概是早上到中午之间,因此其太阳方位角一般在0°和90°之间;对于地球上任何位置,当太阳处于春分点或秋分点,即太阳赤纬是0°的时候,初升的太阳方位角是90°整,正午太阳方位角是180°,落日的时候太阳方位角是270°;对北半球而言,当太阳赤纬大于0°的时候太阳从东偏北方向升起,此时太阳方位角小于90°,中午180°,落日时太阳方位角大于270°。
当地平太阳计算规则

当地平太阳计算规则
当地平太阳计算规则是指在一天中,太阳在天空中的位置与地平线的关系。
根据地球自转的原理,太阳在天空中的位置会随着时间的变化而不断变化。
当地平太阳高度角为0度时,太阳正好在地平线上,此时的时间称为当地的日出时间或日落时间。
当地平太阳高度角为90度时,太阳正好在正上方,此时的时间称为当地的正午时间。
当地平太阳计算规则的具体计算方法如下:
1.确定当地的地理位置和时区。
2.根据当地的经纬度和时区,计算出当地的太阳时角。
太阳时角是指太阳在天空中的位置与正南方向的夹角。
3.根据太阳时角和当地的地理位置,计算出当地的太阳高度角。
太阳高度角是指太阳在天空中的位置与地平面的夹角。
4.根据太阳高度角和当地的时间,计算出当地的日出时间、正午时间和日落时间。
需要注意的是,当地平太阳计算规则的具体计算方法可能因地区、时区和时间等因素而有所不同。
在实际应用中,应根据具体情况进行综合考虑,并严格遵循相关的标准和规范。
地理太阳高度计算

地理太阳高度计算太阳高度是指太阳光线与地球表面的夹角,它对于气候、季节和生态系统的变化具有重要影响。
通过计算太阳高度,我们可以了解太阳的位置和光线的强度,从而更好地理解地球的气候和环境。
太阳高度的计算涉及到地理位置、日期和时间等因素。
在不同的地理位置上,太阳高度的变化也会有所不同。
下面将介绍一些常用的方法来计算地理太阳高度。
1. 太阳高度角太阳高度角是指太阳光线与地平线的夹角,它可以用来表示太阳的位置。
太阳高度角的范围通常在-90°到+90°之间,其中正值表示太阳在地平线上方,负值表示太阳在地平线下方。
太阳高度角的计算公式如下:sin(θ) = sin(δ)sin(φ) + cos(δ)cos(φ)cos(H)其中,θ表示太阳高度角,δ表示太阳赤纬,φ表示地理纬度,H 表示太阳时角。
2. 太阳赤纬太阳赤纬是指太阳在黄道上的纬度,它是一个与地球倾斜角度有关的参数。
太阳赤纬的变化与地球公转和自转的周期有关,因此在不同日期和时间,太阳赤纬的数值也会有所不同。
太阳赤纬的计算可以使用以下公式:δ = arcsin(sin(ε)sin(λ))其中,δ表示太阳赤纬,ε表示地球轴倾斜角,λ表示黄经。
3. 地理纬度和经度地理纬度和经度是指地球表面上某一点的位置坐标。
地理纬度是指地点距离地球赤道的角度,通常用度来表示;地理经度是指地点距离本初子午线的角度,也通常用度来表示。
地理纬度和经度的数值可以通过地理坐标系统来确定。
常用的地理坐标系统有经纬度坐标系统和UTM坐标系统。
4. 太阳时角太阳时角是指太阳在地方子午线上的角度,它是一个与时间有关的参数。
太阳时角的范围通常在-180°到+180°之间,其中正值表示太阳在地方子午线东侧,负值表示太阳在地方子午线西侧。
太阳时角的计算可以使用以下公式:H = 15(LST - 12)其中,H表示太阳时角,LST表示当地标准时间。
通过以上的计算方法,我们可以得到太阳高度角的数值。
极昼地点时太阳高度的计算

极昼地点时太阳高度的计算公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]极昼地点0时太阳高度的计算一、正午太阳高度(H)的计算在北半球极昼区的正午太阳高度为当地地方时12时太阳光线与当地地平线的倾角,此时太阳位于正南天空。
其计算方法与非极昼区一致:公式一:正午太阳高度H=90-两地间的纬度差即正午太阳高度H=90-(当地地理纬度±太阳直射点纬度)(“±” 的用法:当地地理纬度与太阳直射点纬度在同一半球时用“-”,不同半球则用“+” )二、最小太阳高度(h)的计算在北半球极昼区的最小太阳高度为当地地方时0时或24时太阳光线与当地地平线的倾角,即子夜时太阳高度,此时太阳位于正北天空(极点除外)。
可分极点、出现极昼的最低纬度和两者之间的地区三种情况。
1、 极点 在地球自转运动中,北极点不动,故太阳始终在正南天空且太阳高度 只有年变化而无日变化,即一日内最小太阳高度和最大太阳高度一样。
假设当日太阳直射点的地理纬度为x,则用公式一可得出:h=H=90-(90-x)=x推论一:如某地在一日内太阳高度保持不变,则该地一定位于极点,且太阳高度的大小与当日太阳直射点的地理纬度数值相等。
2、出现极昼的最低纬度 如图1:N 为北极,O 为地心,M (纬度为x )为太阳直射点,则A 点为晨昏线与某纬线圈的切点,其所在的纬线就是当日出现极昼的最低纬度。
根据几何知识可知∠MOC+∠AOB=90,即A 点的地理纬度为北纬(90°-x )。
读图可知A 点此时的地方时为0时或24时,太阳位于正北方的地平线上,故其最小太阳高度h=0;其正午太阳高度H=90-〔(90-x )-x 〕=2x 。
O A l 1 l 2 MC B N 图1推论二:出现极昼的最低纬度的最小太阳高度h=0;其正午太阳高度H=直射点纬度的2倍。
3、极点和出现极昼的最低纬度之间的地区如图2:N 为北极,O 为地心,M (纬度为x )为太阳直射点,A (纬度为90-x )为切点,P (纬度为y )点为北半球出现极昼现象的某地与0时经线的交点, 1l 、2l 、3l 分别是过M 、P 、A 三点的太阳水平光线,它们相互平行。
计算太阳高度角和太阳方位角确定太阳在天空中的位置

计算太阳⾼度⾓和太阳⽅位⾓确定太阳在天空中的位置地球绕太阳公转,由于地轴的倾斜,地轴与公转轨道平⾯始终保持着⼤概66°34′的夹⾓,这样,才引起太阳直射点在南北纬23°26′之间往返移动,并决定了太阳可能直射的范围:春分、秋分⽇,太阳直射⾚道,即直射点的纬度为0°。
冬⾄⽇,太阳直射南回归线,即直射点的纬度为23°26′S,夏⾄⽇,太阳直射北回归线,即直射点的纬度为23°26′N。
春分⽇左右,太阳位于黄经0°(春分点)时。
春分,每年公历⼤约为3⽉20⽇左右公历6⽉21⽇左右⽇左右。
夏⾄这天,太阳运⾏⾄黄经90夏⾄是⼆⼗四节⽓之⼀,在每年公历夏⾄度(夏⾄点,⽬前处在双⼦座),太阳直射地⾯的位置到达⼀年的最北端,⼏乎直射北回归线,此时,北半球各地的⽩昼时间达到全年最长。
公历9⽉22~24⽇。
太阳在这⼀天到达黄经180度,直射地球⾚道,因秋分秋分,每年的公历此全球⼤部分地区这⼀天的24⼩时昼夜均分,各12⼩时。
秋分过后,太阳直射点开始由⾚道进⼊南半球,北半球开始昼短夜长,⼀天中⽩昼短于⿊夜;北极附近也即将迎来⼀年中连续6个⽉的漫漫长夜与连续6个⽉不灭的星空。
公历12⽉21~23⽇。
冬⾄,时间在每年的公历冬⾄同时,由于地球⾃转,各个时刻太阳的轨迹是不同的。
⼀般来说,同⼀纬度地区在相同的⽇期,正午的太阳⾼度⾓相对于其它时刻来说是最⼤的。
所以影响太阳⾼度⾓的因素有3个,⼀是纬度,⼆是⽇期、三是时刻。
如在冬⾄、夏⾄⽇,太阳直射北回归线,北回归线地区相同时刻的⾼度⾓要⾼于该地区相同时刻不同⽇期的⾼度⾓。
⾃然,在相同⽇期,相同纬度地区中午时刻的⾼度⾓最⾼。
太阳在天空中的位置可以由太阳⾼度⾓和太阳⽅位⾓来确定。
太阳⾼度⾓⼜称太阳⾼度、太阳俯仰⾓,是指太阳光线与地表⽔平⾯得之间的夹⾓。
太阳⽅位⾓即太阳所在的⽅位,是指太阳光线在地平⾯上的投影与当地⼦午线的夹⾓,可以近似看作是树⽴在地⾯上的直线在阳光下的阴影与正南⽅向的夹⾓。
求太阳位置计算公式

求太阳位置计算公式太阳位置计算公式。
太阳是我们太阳系中最重要的星体之一,它对地球的生态系统和气候产生了深远的影响。
因此,了解太阳的位置对于很多领域都是至关重要的,比如农业、建筑、航海和天文学等。
在这篇文章中,我们将探讨太阳位置的计算公式,以便更好地理解太阳的运动规律。
首先,我们需要了解一些基本的天文学概念。
地球围绕太阳运转,因此太阳的位置是随着时间和地点的变化而变化的。
太阳的位置可以用两个参数来描述,太阳的高度角和方位角。
太阳的高度角是指太阳在天空中的高度,通常是以地平线为基准的角度。
而太阳的方位角则是指太阳在地平面上的方向,通常是以正北方向为基准的角度。
为了计算太阳的位置,我们需要使用一些基本的天文学公式。
首先,我们需要知道地球的自转轴与公转轨道之间的倾角,这个倾角约为23.5度。
其次,我们需要知道地球的自转周期,也就是一天的长度,约为24小时。
最后,我们需要知道地球围绕太阳公转的周期,也就是一年的长度,约为365.25天。
有了这些基本的参数,我们就可以开始计算太阳的位置了。
首先,我们需要计算太阳的赤纬和赤经。
赤纬是指太阳在赤道平面上的投影角度,而赤经则是指太阳在黄道平面上的投影角度。
这两个角度可以通过以下公式来计算:sin(δ) = sin(ε) sin(θ)。
cos(α) = cos(θ) cos(δ) / cos(φ)。
其中,δ表示太阳的赤纬,ε表示地球的自转轴与公转轨道的倾角,θ表示太阳的赤纬角,α表示太阳的赤经,φ表示观测点的纬度。
通过这两个公式,我们就可以得到太阳的赤纬和赤经了。
接下来,我们可以计算太阳的高度角和方位角了。
太阳的高度角可以通过以下公式来计算:sin(α) = sin(δ) sin(φ) + cos(δ) cos(φ) cos(H)。
其中,H表示太阳时角,可以通过以下公式来计算:H = 15 (t 12) + λ。
其中,t表示当地的时间,λ表示当地的经度。
通过这两个公式,我们就可以得到太阳的高度角了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
假如给出当前位置的经度、纬度和准确的天文时间,用什么方式计算出太阳当前的位置呢?例如算出类似于方位角和高度角的数据?实际中使用希腊字符表示经纬度,不过为了输入方便,我改用XYZ表示.X是地方纬度,Y是太阳赤纬,t是时角,z=90度-h高度h,方位角A,则sinh=sinXsinY+cosXcosYcostsinA=cosYsint/coshcosA=(sinXsinh-sinY)/(cosXcosh)具体的可以在网上搜示意图或这本书《天文学新概论》苏宜编著华中理工大学出版社 2000年8月第一版 P52的章节第24章太阳位置计算[许剑伟于家里 2008-3-30下午]一、低精度计算:当计算精度要求为0.01度,计算太阳位置时可假设地球运动是一个纯椭圆,也就说忽略月球及行星摄动,计算表达如下。
设JD是儒略日数,可以用第7章表述的方法计算。
T为J2000起算的儒略世纪数:T = (JD-2451545.0)/36525计算时要保留足够的小数位数,5位小数是不够的(除非所需的太阳黄经的精度要求不高),注意,T表达为儒略世纪数,所以T误差0.00001相当于0.37日。
接下来,太阳几何平黄经:Lo = 280°.46645 + 36000°.76983*T + 0°.0003032*T^2 (Date平分点起算)太阳平近点角: M = 357°.52910 + 35999°.05030*T - 0°.0001559*T^2 -0°.00000048*T^3地球轨道离心率: e = 0.016708617 - 0.000042037*T - 0.0000001236*T^2太阳中间方程:C = +(1°.914600 - 0°.004817*T -0°.000014*T*T) * sin(M)+(0°.019993 - 0°.000101*T) * sin(2M)+ 0°.000290*sin(3M)那么,太阳的真黄经是:Θ = Lo + C真近点角是: v = M + C日地距离的单位是"天文单位",距离表达为:R = 1.000001018 (1-e^2) / (1+e*cos(v)) ……24.5式式中的分子部分的值变化十分缓慢。
它的值是:0.9997190 1800年0.9997204 1900年0.9997218 2000年0.9997232 2100年太阳黄经Θ可由上述的方法算出,它是Date黄道分点坐标中的真几何黄经,需通过计算地心坐标星体位置也可算出。
要取得Date黄道坐标中太阳的视黄经λ,还应对Θ进行章动修正及光行差修正。
如果精度要求不高,可用下式修正:Ω = 125°.04 - 1934°.136*Tλ = Θ - 0°.00569 -0°.00478*sin(Ω)某此时候,我们需要把太阳黄经转到J2000坐标中,在1900-2100年范围内可利用下式进行: Θ2000 = Θ - 0°.01397*(year-2000)如果还想取得更高的转换精度(优于0.01度),那么你可以使用第25章的方法进行坐标旋转。
Date黄道坐标中的太阳黄纬不超过1".2,如果对精度要求不是很高,可以置0。
因此,太阳的地心赤经α及赤纬δ可以用下式(24.6式,24.7式)计算,式中ε是黄赤交角(由21章的21.2式计算)。
tanα = cosεsinΘ / cosΘ ……24.6式sinδ = sinεsinΘ ……24.7式如果要想得到太阳的视赤经及赤纬,以上二式中的Θ应换为λ,ε应加上修正量:+0.00256*cos(Ω)[译者注]:实际上就是对Θ补上黄经章动及光行差,ε补上交角章动后再转到赤道坐标中。
也可在赤道坐标中补章动及光行差,但公式不同。
公式24.6当然可以转为:tan(α) = cos(ε)*tan(Θ),接下来,我们要注意α与Θ应在同一象限。
然而,如果你使用计算机语中有ATN2函数(C语言是atan2),那最好保持24.6式不变,这样就可直接利用ATN2函数算出α,即:α = ATN2( cos(ε)*sin(Θ),cos(Θ) )例24.a——计算1992-10-13,0点,即力学时TD=JDE 2448908.5时刻的太阳位置。
我们算得:T = -0.072183436Lo= -2318°.19281 = 201°.80719M = -2241°.00604 = 278°.99396e = 0.016711651C = -1°.89732Θ= 199°.90987 = 199°54' 36"R = 0.99766Ω= 264°.65λ= 199°.90897 = 199°54' 32"εo= 23°26'24".83 = 23°.44023 (由21章的21.2式算得)ε= 23°.43999α视= -161°.61918 = +198°.38082 = 13h.225388 = 13h 13m 31s.4δ视= -7°.78507 = -7°47' 06"使用VSOP87行星理论计算出的的正确值是:(请与上面的结果做一下比较)Θ= 199°54' 26".18λ= 199°54' 21".56β= +0".72R = 0.99760853α视= 13h 13m 30s.749δ视= -7°47' 01".74基于单片机EM78247的光伏发电系统太阳自动跟踪器摘要:由于太阳位置随时间而变化,使光伏发电系统的太阳能电池阵列受光照强度不稳定,从而降低了光伏电池的效率,因此,设计太阳自动跟踪器是提高光伏发电系统工作效率的有效措施。
本文采用单片机EM78247为控制核心,设计了一个双轴太阳自动跟踪器,配合两台交流伺服电机实现光伏电池阵列与阳光照射之间的同步跟踪。
该控制器在硬件和软件各方面采取了多项抗干扰措施,使其具有较好的跟踪效果和较强的抗干扰能力,且运行可靠稳定,具有较高的实际应用价值。
关键词:光伏发电系统;EM78247;太阳自动跟踪器当今社会人们的环保意识越来越强,光伏发电系统的应用普遍受到各国政府重视。
因为它不仅能为我们提供用之不竭的可持续再生电能,并更好地保护人类赖以生存的环境。
但其发电效率较低,发电成本相对较高仍然足制约其大规模应用的重要因素。
在没有出现高效的光伏电池材料之前,研制具有实用价值的阳光随动系统以降低成本,是促进太阳能广泛应用的主要途径之一。
据研究,双轴系统可提高发电量35%左右,单轴系统也可提高20%左右。
国外在20世纪80年代就对太阳跟踪系统进行了研究,如美国、德国在单双轴自动跟踪、西班牙在2倍聚光反射跟踪等方面开发出了相应的商品化自动阳光跟踪器[1]。
我国于20世纪9 0年代左右也对其进行了大量的研究,但一直没有稳定可靠的商品化产品出现,主要原因在于:首先,系统的运行可靠性不高,无法满足使用要求。
由于大部分光伏电站都安装在偏远地区,环境非常恶劣,维护困难,跟踪系统增加了旋转机构与相应的机械机构,可靠性明显下降,如果不能保证整个系统的在各种环境下都能可靠稳定运行,对整个光伏系统反而是灾难性的打击;其次,跟踪器的控制误差偏大。
尤其对反射聚光的跟踪器,如果跟踪误差偏大,不但不能提高发电效率,反而会使太阳能电池组件的受光面积变小,产生热斑等不利影响,从而降低太阳能电池组件的使用寿命;第三是采用进口技术和器件使成本过高。
全部购买国外成熟的技术,大大提高系统的硬件成本与维护成本,使推广更加困难。
本文以EM78247微处理器为核心,针对光伏发电系统的电池组件,设计开发了一种双轴阳光随动控制器,它具有运行稳定可靠、跟踪误差小、成本低等优点,具有很高的推广应用价值。
1 阳光随动控制的基本原理阳光随动控制器,顾名思义其基本功能就是使光伏阵列随着阳光而转动,基本原理框图如图1所示。
图1 光伏阵列阳光随动系统原理框图该系统时刻检测太阳与光伏阵列的位置并将其输入到控制单元,控制单元对这两个信号进行比较并产生相应的输出信号来驱动旋转机构,使阳光时刻垂直入射到光伏阵列的表面上,使光伏阵列始终处于最佳光照条件下,发挥最大光伏转换效率。
虽然太阳在天空中的位置时刻都在变化,但其运行却具有严格的规律性,在地平坐标系中,太阳的位置可由高度角α与方位角ψ来确定,公式如下:(1)式中:δ为太阳赤纬角;φ为当地的纬度角;α为时角。
太阳赤纬角与时角可以由本地时间确定,而对确定的地点,本地的纬度角也是确定,因此只要输入当地相关地理位置与时间信息就可以确定此时此刻的太阳位置。
2 系统的整体设计方案EM78247是一款具有RISC结构的高性能中档单片机,仅有35条单字指令,8 k×14个字节FLASH程序存储器,368×8个字节RAM数据存储器,256×8个字节E2PROM数据存储器,14个中断源,8级深度的硬件堆栈,内部看门狗定时器,低功耗休眠模式,高达25 mA的吸入/拉出电流,外部具有3个定时器模块,2个16位捕捉器/16位比较器/10位PWM模块,10位多通道A/D转换器,通用同步异步接收/发送器等功能模块。
自动阳光跟踪器的控制方式主要有微处理器控制、PLC控制、DSP控制与模拟电路控制4种形式,根据以上原理,本文选择性价比较高的EM78247单片机为控制核心,系统实现的具体原理框图如图2所示。
整个控制器主要由控制单元与驱动执行机构两部分组成。
控制单元由角度计算及反馈控制、启动信号产生、电机驱动信号产生、保护信号处理与人机通讯5个部分组成。
系统功能说明如下:单片机循环检测光伏阵列的位置,并将其与计算出的此时本地太阳的高度角与方位角进行比较来确定光伏阵列是否跟踪上太阳的位置,如果没有启动信号满足启动条件,单片机就发出指令驱动电机转动;保护信号是保证系统在外界以及其他非人为因素情况下所执行的一种操作指令,以确保系统不受损坏,从而提高了整个系统的可靠性。
驱动执行单元主要功能是用来实现电机驱动与旋转,并通过机械传动机构带动光伏电池阵列转动。
2.1 控制单元的硬件设计由于采用了单片机作为主控制单元,大部分工作都由单片机在软件中实现,从而简化了控制电路的硬件设计,简要说明主要控制部分的实现过程。
