专题复习_中考数学归纳与猜想(含答案)-
中考数学专题知识点45 规律猜想型问题2021

一、选择题16.(2021•怀化)观察等式:2+22=23﹣2,2+22+23=24﹣2,2+22+23+24=25﹣2,…,已知按一定规律排列的一组数:2100,2101,2102,…,2199,若2100=m,用含m的代数式表示这组数的和是.m2﹣m【解析】由题意得2100+2101+2102+…+2199=(2+22+23+…+2199)﹣(2+22+23+…+299)=(2200﹣2)﹣(2100﹣2),=(2100)2﹣2100=m2﹣m.10.(2021·济宁) 按规律排列的一组数据:,,□,,,,…,其中□内应填的数是()A.B.C.D.{答案}D{解析}观察这排数据发现:分子为连续的奇数,分母为序号的平方+1,∴第n个数据为:.当n=3时,□的分子为5,分母=32+1=10,∴这个数为=.11.(2021·玉林)观察下列树枝分杈的规律图,若第n个图树枝数用Y n表示,则Y9﹣Y4=()A.15×24B.31×24C.33×24D.63×24B {解析}由第1个图可知是Y1=1,第2个图可知Y2=1+2=3,第3个图Y3=1+2+22=7,第4个图Y4=1+2+22+23=15,可知Y n=2n-1.即Y9=29-1.因此Y9﹣Y4=29-1-(24-1)=29-24=24(25-1)=31×24.10.(2021•绍兴)数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是()A.用3个相同的菱形放置,最多能得到6个菱形B.用4个相同的菱形放置,最多能得到16个菱形C.用5个相同的菱形放置,最多能得到27个菱形D.用6个相同的菱形放置,最多能得到41个菱形B【解析】如图所示,用2个相同的菱形放置,最多能得到3个菱形;用3个相同的菱形放置,最多能得到8个菱形,用4个相同的菱形放置,最多能得到16个菱形.16.(2021•常德)如图中的三个图形都是边长为1的小正方形组成的网格,其中第一个图形有1×1个小正方形,所有线段的和为4,第二个图形有2×2个小正方形,所有线段的和为12,第三个图形有3×3个小正方形,所有线段的和为24,按此规律,则第n个网格中所有线段的和为.(用含n的代数式表示)2n(n+1)【解析】∵第一个图形有1×1个小正方形,所有线段的和为4=2×1×2,第二个图形有2×2个小正方形,所有线段的和为12=2×2×3,第三个图形有3×3个小正方形,所有线段的和为24=2×3×4,•,按此规律,则第n个网格中所有线段的和为2n(n+1).6.(2021•云南)按一定规律排列的单项式:a2,4a3,9a4,16a5,25a6,…,第n个单项式是()A.n2a n+l B.n2a n﹣1C.n n a n+1D.(n+1)2a nA【解析】∵第1个单项式a2=12•a1+1,第2个单项式4a3=22•a2+1,第3个单项式9a4=32•a3+1,第4个单项式16a5=42•a4+1,……∴第n(n为正整数)个单项式为n2a n+1.14.(2021•临沂)实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.如图为表示镭的放射规律的函数图象,据此可计算32mg镭缩减为1mg所用的时间大约是()A.4860年B.6480年C.8100年D.9720年C【解析】由图可知:1620年时,镭质量缩减为原来的12,再经过1620年,即当3240年时,镭质量缩减为原来的14=122,再经过1620×2=3240年,即当4860年时,镭质量缩减为原来的18=123,...,∴再经过1620×4=6480年,即当8100年时,镭质量缩减为原来的125=132,此时32×132=1mg.12.(2021•烟台)由12个有公共顶点O 的直角三角形拼成的图形如图所示,∠AOB =∠BOC =…=∠LOM =30°.若OA =16,则OG 的长为( )A .274B .14C .9√32D .27√3812.A . 解析:由图可知,∠ABO =∠BCO =…=∠LMO =90°,∵AOB =∠BOC =…=∠LOM =30°,∴∠A =∠OBA =∠BCD =…=∠OLM =60°,∴AB =12OA ,OB =√3AB =√32OA ,同理可得,OC =√32OB =(√32)2OA ,OD =√32OC =(√32)3OA ,…OG =√32OF =(√32)6OA =(√32)6×16=274.故选:A .9.(2021•达州)在平面直角坐标系中,等边△AOB 如图放置,点A 的坐标为(1,0),每一次将△AOB 绕着点O 逆时针方向旋转60°,同时每边扩大为原来的2倍,第一次旋转后得到△A 1OB 1,第二次旋转后得到△A 2OB 2,…,依次类推,则点A 2021的坐标为( )A .(﹣22020,−√3×22020)B .(22021,−√3×22021)C .(22020,−√3×22020)D .(﹣22021,−√3×22021)C 【解析】由已知可得:第一次旋转后,A 1在第一象限,OA 1=2, 第二次旋转后,A 2在第二象限,OA 2=22, 第三次旋转后,A 3在x 轴负半轴,OA 3=23, 第四次旋转后,A 4在第三象限,OA 4=24, 第五次旋转后,A 5在第四象限,OA 5=25,第六次旋转后,A6在x轴正半轴,OA6=26,......如此循环,每旋转6次,A的对应点又回到x轴正半轴,而2021=6×336+5,∴A2021在第四象限,且OA2021=22021,示意图如下:OH=12OA2021=22020,A2021H=√3OH=√3×22020,∴A2021((22020,−√3×22020).9.(2021•十堰)将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是()A.2025 B.2023 C.2021 D.2019B【解析】由题意可知:行数为1的方阵内包含“1”,共1个数;行数为2的方阵内包含“1、3、5、7”,共22个数;行数为3的方阵内包含“1、3、5、7、9、11、13、15、17”,共32个数;∴行数为32的方阵内包含“1、3、5、7、......”共322个数,即共1024个数,∴位于第32行第13列的数是连续奇数的第(1024﹣12)═1012个数,∴位于第32行第13列的数是:2×1012﹣1═2023.故选B.9.(2021•随州)根据图中数字的规律,若第n个图中的q=143,则p的值为()A.100 B.121 C.144 D.169B 【解析】通过观察可得规律:p =n 2,q =(n +1)2﹣1,∵q =143,∴(n +1)2﹣1=143,解得:n =11, ∴p =n 2=112=121.6.(2021·鄂州) 已知1a 为实数﹐规定运算:2111a a =-,3211a a =-,4311a a =-,5411a a =-,……,111n n a a -=-.按上述方法计算:当13a =时,2021a 的值等于( ) A .23- B .13 C .12- D .23D{解析}把13a =代入211121133a a =-=-=,把223a =代入321112a a =-=-,把312a =-代入43113a a =-=,把43a =代入得523a =,……,由此发现这几个结果是4个一循环,2021÷4=505……1, 2021a 的值与2a 的值相同,为23.二、填空题 22.(2021·绥化)下面各图形是由大小相同的三角形摆放而成的,图①中有1个三角形,图②中有5个三角形,图③中有11个三角形,图④中有19个三角形…依此规律,则第n 个图形中三角形个数是 .22. n 2+n -1解析:观察图中三角形的个数与图形的序号的关系,有如下规律: 第①个图形: 12+0, 第②个图形: 22+1, 第③个图形: 32+2, 第④个图形: 42+3, . ……第n 个图形: n 2+n -1. 故答案为: n 2+n -1.16.(2021·仙桃)如图,在平面直角坐标系中,动点P 从原点O 出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得点P 1(﹣1,﹣1);接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点P 2;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点P 3;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点P 4,…,按此作法进行下去,则点P 2021的坐标为 .①第n个图形(-1011,-1011)【解析】先根据点坐标的平移变换规律求出点P 2(1,1),P 3(-2,-2),P 4(2,2),P 5(-3,-3),归纳类推得:点P 2n -1(-n ,-n ),其中n 为正整数, ∵2021=2×1011-1,∴点P 2021的(-1011,-1011).13.(2021•嘉兴)观察下列等式:1=12﹣02,3=22﹣12,5=32﹣22,…按此规律,则第n 个等式为2n ﹣1= . n 2﹣(n ﹣1)218.(2021•泰安)如图,点B 1在直线l :y =12x 上,点B 1的横坐标为2,过点B 1作B 1A 1⊥l ,交x 轴于点A 1,以A 1B 1为边,向右作正方形A 1B 1B 2C 1,延长B 2C 1交x 轴于点A 2;以A 2B 2为边,向右作正方形A 2B 2B 3C 2,延长B 3C 2交x 轴于点A 3;以A 3B 3为边,向右作正方形A 3B 3B 4C 3,延长B 4C 3交x 轴于点A 4;…;照这个规律进行下去,则第n 个正方形A n B n B n +1∁n 的边长为 (结果用含正整数n 的代数式表示).√52×(32)n ﹣1【解析】设直线y =12x 与x 轴夹角为α,过B 1作B 1H ⊥x 轴于H ,如图:∵点B 1的横坐标为2,点B 1在直线l :y =12x 上,令x =2得y =1,∴OH =2,B 1H =1,OB 1=√OH 2+B 1H 2=√5,∴tanα=B 1H OH=12,Rt △A 1B 1O 中,A 1B 1=OB 1•tanα=√52,即第1个正方形边长是√52,∴OB 2=OB 1+B 1B 2=√5+√52=√52×3,Rt △A 2B 2O 中,A 2B 2=OB 2•tanα=√52×3×12=√52×32, 即第2个正方形边长是√52×32, ∴OB 3=OB 2+B 2B 3=√52×3+√52×32=√52×92, Rt △A 3B 3O 中,A 3B 3=OB 3•tanα=√52×92×12=√52×94,P 1 P 3P 2P 4即第3个正方形边长是√52×94=√52×(32)2, ∴OB 4=OB 3+B 3B 4=√52×92+√52×94=√52×274,Rt △A 4B 4O 中,A 4B 4=OB 4•tanα==√52×274×12=√52×278, 即第4个正方形边长是√52×278=√52×(32)3,...... 观察规律可知:第n 个正方形边长是√52×(32)n ﹣1. 18.(2021•扬州)将黑色圆点按如图所示的规律进行排列:图中黑色圆点的个数依次为:1,3,6,10,…,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为 .1275【解析】第①个图形中的黑色圆点的个数为:1, 第②个图形中的黑色圆点的个数为:(1+2)×22=3, 第③个图形中的黑色圆点的个数为:(1+3)×32=6, 第④个图形中的黑色圆点的个数为:(1+4)×42=10,…第n 个图形中的黑色圆点的个数为n(n+1)2,则这列数为1,3,6,10,15,21,28,36,45,55,66,78,91,…, 其中每3个数中,都有2个能被3整除, 33÷2=16…1,16×3+2=50, 则第33个被3整除的数为原数列中第50个数,即50×512=1275.16.(2021·铜仁)观察下列各项:112,124,138,1416,…,则第n 项是______________. 12nn +{解析}此题属于数字类规律问题。
2019中考数学专题复习之归纳类比思想专项训练题一(附答案详解)

____________________________________________________________________________________________
(1)根据规律填空:(x﹣1)(xn+xn﹣1+…+x+1)=;
(2)试求26+25+24+23+22+2+1的值;
(3)试确定22017+22016+…+2+1的个位数字.
7.阅读与探究:
在第六章《实数》中,我们学习了平方根和立方根.下表是平方根和立方根的部分内容.
平方根
立方根
定义
一般地,如果一个数的平方等于 ,那么这个数叫做 的平方根或二次方根.这就是说,如果 ,那么 叫做 的平方根.
解决问题:
(1)若x>0时,x+ 有最小值为,此时x=;
(2)如上图,已知点A在反比例函数y (x>0)的图像上,点B在反比例函数y (x>0)的图像上,AB∥y轴,过点A作AD⊥y轴于点D,过点B作BC⊥y轴于点C.求四边形ABCD周长的最小值
(3)学校准备在图书馆后面的场地上建一个面积为100平方米的长方形自行车棚.图书馆的后墙只有5米长可以利用,其余部分由铁围栏建成,如下图是小尧同学设计的图纸,设所需铁围栏L米,自行车棚长为x米.L是否存在最小值,如果存在,那么当x为何值时,L最小,最小为多少米?如果不存在,请说明理由.
正数的立方根是正数;0的立方根是0;负数的立方根是负数.
2024年中考数学复习猜想归纳题经典考题讲练

猜想归纳题经典考题讲练解题要点剖析归纳猜想题是指给出一定条件(可以是有规律的算式、图形或图表),通过学生认真阅读、仔细观察、综合分析、顺势归纳和大胆猜想,得出结论,进而加以验证的数学探索题.解答归纳猜想题,要善于从问题中提供的数字或图形信息出发,通过计算、验证、类比、比较、测量、绘图等方式寻找其共同之处,这个存在于个例中的共性,就是规律.这一过程体现了总结归纳的数学思想,是人们认识新生事物的一般过程,也是人们探索发现新知的重要手段,有利于培养创造性思维能力.正是由于这类问题有利于培养学生思维的深刻性和创造性,所以备受命题专家的青睐,成为中考的热点.经典考题解析例1 观察图1-1中的“品”字形中各数之间的规律,根据观察到的规律得出a的值为( ).A. 23B. 75C. 77D. 139分析因为每个“品”字形的上边的数为连续的奇数1,3,5,7,9,11(有 6个数),左下边的数为2¹,2²,2³,….所以,b=2⁶=64.因为每个“品”字形的上边的数与左下边的数的和正好等于右下边的数,所以,a=11+64=75.解答选 B.小结寻找一列数中呈现的规律,可以先观察其中一个数和前一个数(或前几个数)之间的关系,本例中,如观察上边的数,不难发现后一个数与前一个数的差是2;然后根据发现的规律,写出能体现这一规律的相关式子,本例中上边的数依次为1,3,5,7,9,11,可改写为1,1+2,1+2×2,1+2×3,1+2×4,1+2×5,考虑到这些数与第n个数中n的关系,不难得出第n个数为1+2×(n-1)=2n-1.在探寻数的规律时,有时还需要将数进行适当的拆分(体现和差关系)或分解(体现积商关系),如本例中每个“品”字形的右下边的数为上边的数与左下边数的和.例2某广场用同一种如图1-2(a)所示的地砖拼图案,第1次拼成形如图(b)所示的图案,第2次拼成形如图(c)所示的图案,第3次拼成形如图(d)所示的图案,第4次拼成形如图(e)所示的图案……按照这样的规律进行下去,第 n次拼成的图案共有地砖块.分析首先求出图1-2(b)(c)(d)(e)图案中的地砖的数量,探究规律后即可解决问题.第1次拼成形如图1-2(b)所示的图案共有4块地砖,4=2×(1×2);第2次拼成形如图1-2(c)所示的图案共有 12块地砖,12=2×(2×3);第3次拼成形如图1-2(d)所示的图案共有 24块地砖,24=2×(3×4);第4次拼成形如图1-2(e)所示的图案共有 40块地砖,40=2×(4×5);………按照这样的规律进行下去,第 n次拼成的图案中地砖数为2×n(n+1)=2n²+2n,故答案为2n²+2n.解答2n²+2n.小结本题考查规律探究,解题的关键是从特殊情况出发,了解特殊情况下[图1-2(b)一(e)]地砖数量与图序数(第几次拼的图)间的关系,从而发现问题的数值特征,根据数值特征去猜想第n次情况下的结论.例3 观察下列运算过程,并计算.计算:1+2+22+⋯+210.解设S=1+2+22+⋯+210.①①×2得:2 2S=2+22+23+⋯+211.②②—①得: S=2¹¹−1.所以,1+2+22+⋯+210=211−1.。
中考数学复习攻略 专题1 规律探索与归纳推理(含答案)

重点专题突破专题一 规律探索与归纳推理中考重难点突破数式规律数式规律类问题通常是先给出一组数或式子,要求通过观察、归纳这组数或式子的共性规律,写出一个一般性的结论.解决这类题目的关键是找出题目中的规律,即不变的和变化的,变化部分与序号的关系.常见数列 规律❶2,4,6,8,10,12,… 2n (从2开始的连续偶数) ❷1,3,5,7,9,11,… 2n -1(从1开始的连续奇数)❸1,4,9,16,25,36,… n 2(正整数平方) ❹2,4,8,16,32,64,… 2n (2的整数次幂) ❺-1,1,-1,1,-1,1,…(-1)n (奇负偶正)❻1,-1, 1,-1, 1,-1,… (-1)n +1或(-1)n -1(奇正偶负)【例1】(2021·铜仁中考)观察下列各项:112 ,214 ,318 ,4116 ,…,则第n 项是__n +12n __.【解析】根据已知可得出规律:第一项:112 =1+121 ,第二项:214 =2+122 ,第三项:318 =3+123 ,…,从而可以得出第n 项.本题属于数字类规律问题,根据已知各项的规律得出结论是解决此类题目的关键. 【例2】(2020·百色一模)观察下列等式:1-12 =12 ,2-25 =85 ,3-310 =2710 ,4-417 =6417,…,根据你发现的规律,则第20个等式为 __20-20401 =8 000401__ .【解析】根据题意可知,这列等式的左边的被减数是从1开始的连续整数,减数是一个分数,并且分子和被减数相同,分母是被减数的平方加1;右边也是一个分数,分子是被减数的立方,分母和减数的分母相同,由此可写出第20个等式为:20-20202+1 =203202+1 ,最后化简即可.1.按一定规律排列的单项式:a ,-2a ,4a ,-8a ,16a ,-32a ,…,则第n 个单项式是( A )A .(-2)n -1a B .(-2)n aC .2n -1a D .2n a 2.(2020·百色二模)小说《达·芬奇密码》中的一个故事里出现了一串神秘排列的数:1,1,2,3,5,8,…,则这列数的第8个数是__21__.3.观察下面由※组成的图案和算式,解答问题:1+3=4=22,1+3+5=9=32, 1+3+5+7=16=42, 1+3+5+7+9=25=52, ……猜想:1+3+5+7+9+…+(2n -1)+(2n +1)+(2n +3)=__(n +2)2__.图形规律图形规律类问题主要涉及图形的组成、分拆等过程,解答此类问题时,要将后一个图形与前一个图形进行比较,明确哪部分发生了变化,哪部分没有发生变化,分析其联系和区别,有时需要多画出几个图形进行观察,有时规律是循环性的,在归纳时要运用对应思想和数形结合思想.【例3】观察下列砌钢管的横截面图:则第n 个图的钢管数是__32 n 2+32 n __(用含n 的式子表示).【解析】本题可先依次列出n =1,2,3,…时的钢管数,再根据规律依次类推,可得出第n 个图的钢管数.第1个图的钢管数为1+2=3=3×1; 第2个图的钢管数为2+3+4=9=3×(1+2); 第3个图的钢管数为3+4+5+6=18=3×(1+2+3);第4个图的钢管数为4+5+6+7+8=30=3×(1+2+3+4);……依次类推,第n 个图的钢管数为3×(1+2+3+4+…+n )=32 n 2+32n .4.(源于沪科七上P83)在公园内,牡丹按正方形种植,在它的周围种植芍药,如图反映了牡丹的列数(n )和芍药的数量规律,那么当n =11时,芍药的数量为( B )A .84株B .88株C .92株D .121株 5.(2021·遂宁中考)下面图形都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第__20__个图形共有210个小球.6.下图是一组有规律的图案,它们是由边长相同的小正方形组成的,其中部分小正方形涂有阴影,依此规律,第n 个图案中有m 个涂有阴影的小正方形,那么m 与n 的函数关系式为__m =4n +1__.与坐标有关的规律与坐标有关的规律类问题要求探索图形在运动过程中的规律,通常以平面直角坐标系为载体探索点的坐标的变化规律.解答时,应先写出前几次的变化过程,并将相邻两次的变化过程进行比照,明确哪些地方发生了变化,哪些地方没有发生变化,逐步发现规律,从而使问题得以解决.【例4】如图,直线l 为y =3 x ,过点A 1(1,0)作A 1B 1⊥x 轴,与直线l 交于点B 1,以原点O 为圆心,OB 1长为半径画圆弧交x 轴于点A 2;再作A 2B 2⊥x 轴,交直线l 于点B 2,以原点O 为圆心,OB 2长为半径画圆弧交x轴于点A 3……按此作法进行下去,则点A n 的坐标为(__2n -1,0__).【解析】∵直线l 为y =3 x ,点A 1(1,0),A 1B 1⊥x 轴,∴当x =1时,y =3 ,即B 1(1,3 ).∴tan ∠A 1OB 1=3 .∴∠A 1OB 1=60°,∠A 1B 1O =30°.∴OB 1=2OA 1=2.∵以原点O 为圆心,OB 1长为半径画圆弧交x 轴于点A 2,∴A 2(2,0).同理可得A 3(4,0),A 4(8,0),…,∴A n (2n -1,0).7.如图,在平面直角坐标系中,A (-1,1),B (-1,-2),C (3,-2),D (3,1),一只瓢虫从点A 出发以2个单位长度/秒的速度沿A →B →C →D →A 循环爬行,问第2 021 s 瓢虫所在点的坐标是( A )A .(3,1)B .(-1,-2)C .(1,-2)D .(3,-2)8.如图,在平面直角坐标系中,△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3,…都是等腰直角三角形,其直角顶点P 1(3,3),P 2,P 3,…均在直线y =-13 x +4上,设△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3,…的面积分别为S 1,S 2,S 3,…,依据图形所反映的规律,S 2 022=__942 021 __.中考数学专题过关1.如图,第1个图形中有1个正方形,按照如图所示的方式连接对边中点得到第2个图形,图中共有5个正方形;连接第2个图形中右下角正方形的对边中点得到第3个图形,图中共有9个正方形;按照同样的规律得到第4个图形、第5个图形……,则第7个图形中共有正方形( B )A .21个B .25个C .29个D .32个2.如图,在平面直角坐标系中,将△ABO 沿x 轴向右滚动到△AB 1C 1的位置,再到△A 1B 1C 2的位置……依次进行下去,若已知点A (4,0),B (0,3),则点C 100的坐标为( B )A .⎝⎛⎭⎫1 200,125 B .(600,0)C .⎝⎛⎭⎫600,125 D .(1 200,0)3.(2021·百色一模)有一列有序数对:(1,2),(4,5),(9,10),(16,17),…,按此规律,第11对有序数对为 __(121,122)____.4.观察下列一组数:-23 ,69 ,-1227 ,2081 ,-30243,…,它们是按一定规律排列的,那么这一组数的第n 个数是__(-1)n ·n (n +1)3n__.5. (2021·眉山中考)观察下列等式:x 1=1+112+122 =32 =1+11×2 ;x 2=1+122+132 =76 =1+12×3 ;x 3=1+132+142 =1312 =1+13×4;……根据以上规律,计算x 1+x 2+x 3+…+x 2 020-2 021=__-12 021__.6.如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第1个图案有4个三角形,第2个图案有7个三角形,第3个图案有10个三角形……按此规律摆下去,第n 个图案有__(3n +1)__个三角形(用含n 的代数式表示).7.(2021·扬州中考)将黑色圆点按如图所示的规律进行排列:图中黑色圆点的个数依次为:1,3,6,10,…,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为__1__275__.。
中考数学复习专题——找规律(含答案)

中考数学试复习专题——找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有__________个小圆圈.(1) (2) (3)2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 个菱形,第n 幅图中有 个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为______________.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个33⨯的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个44⨯的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1010⨯的正方形图案, 则其中完整的圆共有 个.1 2 3n … … 第1个图 2个图 3个图 …6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n 个图案需要用白色棋子 枚(用含有n 的代数式表示,并写成最简形式).○ ○ ○ ○ ○ ○ ○ ○ ○○ ○ ○ ○ ● ● ○ ○ ● ● ● ○○ ● ○ ○ ● ● ○ ○ ● ● ● ○○ ○ ○ ○ ○ ○ ○ ○ ● ● ● ○○ ○ ○ ○ ○7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需 根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对(n ,m )表示第n 排,从左到右第m 个数,如(4,2)表示实数9,则表示实数17的有序实数对是 .9、如图 2 ,用n 表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n 的关系是10、观察图4的三角形数阵,则第50行的最后一个数是 ( )1-2 3-4 5 -67 -8 9 -10。
中考数学思想方法 【猜想归纳】数式规律中的猜想归纳思想(学生版+解析版)

数式规律中的猜想归纳思想知识方法精讲1.规律型:数字的变化类探究题是近几年中考命题的亮点,尤其是与数列有关的命题更是层出不穷,形式多样,它要求在已有知识的基础上去探究,观察思考发现规律.(1)探寻数列规律:认真观察、仔细思考,善用联想是解决这类问题的方法,通常将数字与序号建立数量关系或者与前后数字进行简单运算,从而得出通项公式.(2)利用方程解决问题.当问题中有多个未知数时,可先设出其中一个为x,再利用它们之间的关系,设出其他未知数,然后列方程.2. 猜想归纳思想归纳猜想类问题也是探索规律型问题,这类问题一般给出一组具有某种有规律的数、式、图形,或是给出与图形有关的操作变化过程,或某一具体的问题情境,通过认真观察、分析推理,探究其中蕴含的规律,进而归纳或猜想出一般性的结论。
考查学生的归纳、概括、类比能力。
有利于培养学生思维的深刻性和创造性。
解决归纳猜想类问题的基本思路是“观察→归纳→猜想→证明(验证)”,具体做法:(1)认真观察所给的一组数、式、图等,发现它们之间的关系;(2)根据它们之间的关系分析、概括,归纳它们的共性和蕴含的变化规律,猜想得出一个一般性的结论;(3)结合题目所给的材料情景证明或验证结论的正确性。
归纳猜想类问题可以分成四大类:(1)数式归纳猜想题这类题通常是先给出一组数或式子,通过观察、归纳这组数或式子的共性规律,写出一个一般性的结论。
找出题目中规律,即不变的和变化的,变化的部分与序号的关系是解这类题的关键。
(2)图形归纳猜想题此类题通常给出一组图形的排列(或操作得到一系列的图形)探求图形的变化规律,以图形为载体考查图形所蕴含的数量关系。
其解题关键是找出相邻两个图形之间的位置关系和数量关系。
(3)结论归纳猜想题结论归纳猜想题常考数值结果、数量关系及变化情况。
发现或归纳出周期性或规律性变化,是解题的关键。
(4)类比归纳猜想题类比归纳猜想题通常是指由两类对象的具有某些相同或相似的性质,和其中一类对象的某些已知的性质,推断出另一类对象也具有这些性质的一种题型,有时也指两个对象在研究方法、学习过程上类比,考查类比归纳推理能力。
中考数学总复习热点专题突破训练专题四归纳与猜想新人教版1204335-数学备课大师【全免费】

专题四归纳与猜想专题提升演练1.观察下面的几个算式:1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,……,根据你所发现的规律,请直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1的值为( )A.100B.1 000C.10 000D.100 0002.将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示9,则表示58的有序数对是( )A.(11,3)B.(3,11)C.(11,9)D.(9,11)3.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是.4.下图是用长度相等的小棒按一定规律摆成的一组图案,第(1)个图案中有6根小棒,第(2)个图案中有11根小棒……则第(n)个图案中有根小棒.5.【问题情境】如图①,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.【探究展示】(1)证明AM=AD+MC.(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.【拓展延伸】(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图②,探究展示(1)(2)中的结论是否成立?请分别作出判断.证明延长AE,BC并交于点N,如图①(甲),图①(甲)∵四边形ABCD是正方形,∴AD∥BC.∴∠DAE=∠ENC.∵AE平分∠DAM,∴∠DAE=∠MAE.∴∠ENC=∠MAE.∴MA=MN.在△ADE和△NCE中,错误!未找到引用源。
∴△ADE≌△NCE(AAS).∴AD=NC.∴MA=MN=NC+MC=AD+MC.(2)AM=DE+BM成立.证明:过点A作AF⊥AE,交CB的延长线于点F,如图①(乙)所示.图①(乙)∵四边形ABCD是正方形,∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC.∵AF⊥AE,∴∠FAE=90°.∴∠FAB=90°-∠BAE=∠DAE.在△ABF和△ADE中,错误!未找到引用源。
2022年中考数学专题复习:猜想与证明解答题训练

2022年中考数学专题复习:猜想与证明解答题训练1.在学习完“图形的旋转”后,某数学兴趣小组做了如下探究ABC和DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,DEF的顶点E与ABC的斜边BC的中点重合.将DEF绕点E作逆时针旋转,该过程中,线段DE与线段AB相交于点P,线段EF与射线CM相交于点Q.(1)问题提出:如图∠,当点Q在线段AC上,且AP=AQ时,BPE和CQE是否全等.如果全等,写出证明过程;若不赞同,请说明理由.(2)问题解决:如图∠,当点Q在线段CA的延长线上时,BPE和CQE是否有存在与第(1)问相同的关系,如果相同写出证明过程;如果不同,请说明它们的关系.当BP=a,CQ92a时,求P,Q两点间的距离(用含a的代数式表示).2.如图,在等腰直角三角形ABC和ADE中,AC=AB,AD=AE,连接BD,点M、N 分别是BD,BC的中点,连接MN.(1)如图1,当顶点D在边AC上时,请直接写出线段BE与线段MN的数量关系是,位置关系是.(2)当ADE ∆绕点A 旋转时,连接BE ,上述结论是否依然成立,若成立请就图2情况给出证明:若不成立,请说明理由.(3)当AC =5时,在ADE ∆绕点A 旋转过程中,以D ,E ,M ,N 为顶点可以组成平行四边形,请直接写出AD 的长.3.问题背景:如图1,在ABC 中,90ACB ∠=︒,AC BC =,AD 是BC 边上的中线,E 是AD 上一点,将CAE 绕点C 逆时针旋转90︒得到CBF ,AD 的延长线交边BF 于点P .问题探究:(1)探究EP ,FP 之和与BP 之间的数量关系.∠先将问题特殊化,如图2,当CE AD ⊥时,直接写出EP ,FP 之和与BP 之间的数量关系;∠再探究一般情形,如图1,当CE 不垂直AD 时,证明∠中的结论仍然成立; (2)拓展探究:如图3,若AD 的延长线交BF 的延长线于点P 时,直接写出一个等式,表示EP ,FP ,BP 之间的数量关系.4.如图,已知CD 是线段AB 的垂直平分线,垂足为D ,C 点在D 点上方,∠BAC =30°,P 是直线CD 上一动点,E 是射线AC 上除A 点外的一点,PB =PE ,连接BE .(1)如图1,若点P 与点C 重合,求∠ABE 的度数;(2)如图2,若P 在C 点上方,试猜想线段PD ,AC ,CE 的数量关系并说明理由; (3)若AC =6,CE =2,则PD 的值为 .(直接写出结果)5.【问题背景】如图1:在四边形ABCD 中,AB AD =,120BAD ∠=︒,E 、F 分别是BC 、CD 上的点,且60EAF ∠=︒,小王同学探究此问题的方法是:延长FD 到点G ,使DG BE =,连接AG ,再证明AEF AGF ≅△△,可得出结论 .【探索延伸】如图2,若在四边形ABCD 中,AB AD =,E 、F 分别是BC ,CD 上的点12BAD ∠,上述结论是否仍然成立 【学以致用】如图3,四边形ABCD 是边长为5的正方形,45EBF ∠=︒,求DEF 的周长.6.如图1,在平面直角坐标系中,()0,4A ,()2,2C --,且∠ACB =90°,AC =BC .(1)求点B 的坐标;(2)如图2,若BC 交y 轴于点M ,AB 交x 轴与点N ,过点B 作BE y ⊥轴于点E ,作BF x⊥轴于点F,请探究线段MN,ME,NF的数量关系,并说明理由;(3)如图3,若在点B处有一个等腰Rt∠BDG,且BD=DG,∠BDG=90°,连接AG,点H为AG的中点,试猜想线段DH与线段CH的数量关系与位置关系,并证明你的结论.7.在Rt∠ABC中,∠BCA=90°,BC=AC,点E是∠ABC外一动点(点B,点E位于AC 异侧),连接CE,AE.(1)如图1,点D是AB的中点,连接DC,DE,当∠ADE为等边三角形时,求∠AEC的度数;(2)当∠AEC=135°时,∠如图2,连接BE,用等式表示线段BE,CE,EA之间的数量关系,并证明;∠如图3,点F为线段AB上一点,AF=1,BF=7,连接CF,EF,直接写出∠CEF面积的最大值.8.在数学活动课上,老师出示了以下两个问题,请你解答老师提出的问题:(1)如图∠,在ABCD中,BE AD⊥,垂足为E,F是CD边上一点,连接EF,BF,若EF BF=,试判断DF与CF的数量关系,并加以证明.(2)如图∠,若F是ABCD边CD上一点,连接BF,将CBF沿着边BF所在的直线折=,试判断DF与叠,点C的对应点为C',连接DC'并延长交AB于点G,若AG BGCF的数量关系,并加以证明.9.在∠ABC中,CD∠AB于点D.(1)如图1,当点D是线段AB中点时,延长AC至点E,使得CE=CB,连接EB.∠按要求补全图1;∠若AB=AC EB的长.(2)如图2,当点D不是线段AB的中点时,作∠BCE(点E与点D在直线BC的异侧),使∠BCE=2∠CAB,CE=CB,连接AE,用等式表示线段AB,CD,AE的数量关系,并说明理由.10.如图,在∠ABC中,AB=6,AC=BC=5,CD∠AB于点D,点P从点A出发,以每秒5个单位长度的速度沿折线AC—CB向终点B运动,当点P不与A,B,C重合时,过点P作PQ∠AB交AB于点Q,过点P作PM∠PQ,使得PM=2PQ,点M、点D在PQ的同侧,连结MQ,设点P的运动时间为t(s)(1)线段CD=.(2)当点P在线段BC上时,PC=.(用含t的代数式表示)(3)当点M落在∠BCD的内部时,求t的取值范围;(4)连结CM,当∠CPM为锐角三角形时,直接写出t的取值范围.11.△ABC为等边三角形,AB=4,AD∠BC于点D,E为线段AD上一点,AE=AE为边在直线AD右侧构造等边△AEF.连结CE,N为CE的中点.(1)如图1,EF与AC交于点G,∠连结NG,求线段NG的长;∠连结ND,求∠DNG的大小.(2)如图2,将△AEF绕点A逆时针旋转,旋转角为α.M为线段EF的中点.连结DN、MN.当30°<α<120°时,猜想∠DNM的大小是否为定值,并证明你的结论.12.如图,在△ABC中,AB=AC,D为直线BC上一动点(不与点B,C重合),在AD的右侧作△ADE,使得AE=AD,△DAE=△BAC,连接CE.(1)当D在线段BC上时,∠求证:△BAD∠△CAE;∠若AC∠DE,求证:BD=DC;(2)当CE∠AB时,若△ABD中最小角为20°,试探究△ADB的度数(直接写出结果)13.在ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC.如图∠,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.(2)如果AB>AC,如图∠,且点D在线段BC上运动.(1)中结论是否成立,为什么?(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=BC=3,CD=x,求线段CP的长.(用含x的式子表示).14.如图,以四边形ABCD的边AB,AD为边分别向外侧作等边三角形ABF和等边三角形ADE,连接EB,FD相交于点G.(1)当四边形ABCD为正方形时(如图∠),EB和FD的数量关系是______.(不用证明)(2)当四边形ABCD为矩形时(如图∠),EB和FD具有怎样的数量关系?并加以证明.∠是否(3)四边形ABCD由正方形到矩形再到一般平行四边形的变化过程中,EGD∠的度数.发生变化?如果改变,请说明理由;如果不变,请在图∠中求出EGD15.如图,在平面直角坐标系中已知A(2,2),B(6,2),点C是x轴正半轴上一点,连接OA,AB,BC,得到梯形OABC.点P是x轴正半轴上一动点(与点O不重合),AD,AE分别平分∠OAP和∠P AB,且交x轴于点D,E.(1)若梯形OABC的面积为12,直接写出C点的坐标;(2)当点P运动时,∠OP A与∠OEA之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律;(3)若∠AOC=44°,当点P运动到使∠ODA=∠OAE时,∠OAD的度数是多少?=,点D为BC边所在直线上的一个动点(不与点B、16.如图,在ABC中,AB ACC 重合),在AD 的右侧作ADE ,使得,AE AD DAE BAC =∠=∠,连接CE .(1)求证:ABD ACE ∠=∠;(2)当点D 为线段BC 的中点时,判断DE 与AC 的位置关系,并说明理由; (3)探究DAE ∠与DCE ∠的数量关系,直接写出其结果_______.17.如图1,∠ABC 中,∠BAC =90°,AB =AC ,D ,E 在BC 上,∠DAE =45°,为了探究BD ,DE ,CE 之间的等量关系,现将∠AEC 绕A 顺时针旋转90°后成∠AFB 连接DF ,(1)填空:AFD ∆≅ (填一个三角形); (2)试判断BD ,DE ,CE 之间的等量关系式;(3)如图2,在∠ABC 中,∠BAC =120°,AB =AC ,D ,E 在BC 上,∠DAE =60°,∠ADE =45°,试仿照上面的方法,利用图形的旋转变换,探究BD ,DE ,CE 之间的等量关系,并说明理由18.自主探究:在ABC 中,AB AC =,90BAC ∠=︒,点D 在射线BC 上(与B 、C 两点不重合),以AD 为边作正方形ADEF ,使点E 与点B 在直线AD 的异侧,射线BA 与直线CF 相交于点G .(1)当点D在线段BC上时,如图(1),判断:线段BC与线段CG的数量关系和位置关系,并说明理由;(2)当点D在线段BC的延长线上时,如图(2),写出线段BC与线段CG的数量关系与位置关系,不必证明;(3)在(2)的基础上,随着点D位置的变化,当G为CF中点,AB正方形ADEF的边长.19.如图,正方形ABCD的顶点C处有一等腰直角三角形CEP,∠PEC=90°,连接AP,BE.(1)若点E在BC上时,如图1,线段AP和BE之间的数量关系是;(2)若将图1中的∠CEP顺时针旋转使P点落在CD上,如图2,则(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)在(2)的基础上延长AP,BE交于F点,若DP=PC=2,求BF的长.20.如图,在矩形ABCD中,AB=6,BC=8,点E是AD边上的动点,将矩形ABCD 沿BE折叠,点A落在点A′处,连接A′C、A′D.(1)如图1,当AE=时,A′D∠BE;(2)如图2,若AE=3,求S△A′CB.(3)点E在AD边上运动的过程中,∠A′CB的度数是否存在最大值,若存在,求出此时线段AE的长;若不存在,请说明理由.参考答案:1.(1)见详解.(2)见详解.2.(1)12MN BE =;MN BE ⊥ (2)成立;见解析3.(1)∠2EP FP BP +=(2)2EP FP PB -=4.(1)90°(2)PD 12+AC =CE , (3)1或55.【问题背景】EF BE DF =+;【探索延伸】结论EF BE DF =+仍然成立;理由见解析;【学以致用】106.(1)()4,4-(2)MN ME NF =+(3)CH DH ⊥且CH DH =7.(1)∠AEC =135°;(2)∠BE +EA ,∠48.(1)DF CF =(2)DF CF =9.(1)∠见解析;∠(2)4CD 2+AB 2=AE 2,10.(1)4;(2)()55t -;(3)33<<117t 或19<<211t ;(4)325<<1149t 或7319<<4911t .11.(1)∠NG =∠120DNG ∠=︒;(2)DNM ∠的大小是定值 12.(2)100°或40°或20°13.(1)CF 与BD 位置关系是垂直(2)AB >AC 时,CF ∠BD 的结论成立,(3)24x x CP =-+或24x CP x =+ 14.(1)BE DF =;(2)BE DF =,;(3)(3)不变,60°15.(1)C (8,0);(2)不变,∠OP A =2∠OEA ,(3)34°. 16.(1)见解析;(2)DE ∠AC ;(3)∠DAE +∠DCE =180°或∠DAE =∠DCE 17.(1)∠AED ;(2)BD 2+CE 2=DE 2,(3)CE 2=BD 2+DE 2,18.(1)BC CG =,BC CG ⊥;(2)BC CG =,BC CG ⊥;(319.(1)AP ;(2)成立;(320.(1)4;(2)725;(3)8-。
专题复习-中考数学归纳与猜想(含答案)-

专题复习-中考数学归纳与猜想(含答案)-- 2 -专题复习 归纳与猜想归纳与猜想问题指的是给出一定条件(可以是有规律的算式、图形或图表),让学生认真分析,仔细观察,综合归纳,大胆猜想,得出结论,进而加以验证的数学探索题。
其解题思维过程是:从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论,这类问题有利于培养学生思维的深刻性和创造性。
一、知识网络图二、基础知识整理猜想规律型的问题难度相对较小,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。
其中蕴含着“特猜想性猜想猜想猜想数猜想图猜想数猜想数猜想变- 3 -- 4 -⑴写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示:⑵猜想并写出与第n 个图形相对应的等式。
解:⑴5×56=5-56⑵11+-=+⨯n nn n n n 。
例2〖归纳猜想型〗将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一片又按同样的方法剪成四小片,再将其中的一小片正方形纸片剪成四片,如此循环进行下去,将结果填在下表中,并解答所提出的问题:所剪次1 2 3 4 5 …数正方形4 7 10 13 16 …个数⑴如果能剪100次,共有多少个正方形?据上表分析,你能发现什么规律?⑵如果剪n次共有A n个正方形,试用含n、A n的等式表示这个规律;⑶利用上面得到的规律,要剪得22个正方形,共需剪几次?⑷能否将正方形剪成2004个小正方形?为什么?⑸若原正方形的边长为1,设a n表示第n次所剪的正方形的边长,试用含n的式子表示a n;- 5 -- 6 -⑹试猜想a 1+a 2+a 3+…+a n 与原正方形边长的关系,并画图示意这种关系.解:⑴100×3+1=301,规律是:本次剪完后得到的小正方形的个数比上次剪完后得到的小正方形的个数多3个; ⑵A n =3n +1;⑶若A n =22,则3n +1=22,∴n =7,故需剪7次; ⑷若A n =2004,则3n +1=2004,此方程无自然数解,∴不能将原正方形剪成2004个小正方形; ⑸a n =12n ;⑹a 1=12<1,a 1+a 2=12+14=34<1,a 1+a 2+a 3=12+14+18=78<1,……从而猜想到:a 1+a 2+a 3+…+a n <1.直观的几何意义1 a a a- 7 -如图所示。
专题复习 归纳与猜想(含答案)-

①1×12=1-12 ②2×23=2-23 ③3×34=3-34④4×45=4-45 ……专题复习 归纳与猜想归纳与猜想问题指的是给出一定条件(可以是有规律的算式、图形或图表),让学生认真分析,仔细观察,综合归纳,大胆猜想,得出结论,进而加以验证的数学探索题。
其解题思维过程是:从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论,这类问题有利于培养学生思维的深刻性和创造性。
一、知识网络图二、基础知识整理猜想规律型的问题难度相对较小,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。
其中蕴含着“特殊——一般——特殊”的常用模式,体现了总结归纳的数学思想,这也正是人类认识新生事物的一般过程。
相对而言,猜想结论型问题的难度较大些,具体题目往往是直观猜想与科学论证、具体应用的结合,解题的方法也更为灵活多样:计算、验证、类比、比较、测量、绘图、移动等等,都能用到。
由于猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养创造性思维能力,所以备受命题专家的青睐,逐步成为中考的又一热点。
★ 范例精讲【归纳与猜想】例1【河北实验区05】观察右面的图形(每个正方形的边长均为1)和相应等式,探究其中的规律:⑴写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示:⑵猜想并写出与第n 个图形相对应的等式。
解:⑴5×56=5-56⑵11+-=+⨯n nn n n n 。
例2〖归纳猜想型〗将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一片又按同样的方法剪成四小片,再将其中的一小片正方形纸片剪成四片,⑵如果剪n 次共有A n 个正方形,试用含n 、A n 的等式表示这个规律; ⑶利用上面得到的规律,要剪得22个正方形,共需剪几次? ⑷能否将正方形剪成2004个小正方形?为什么? ⑸若原正方形的边长为1,设a n 表示第n 次所剪的正方形的边长,试用含n 的式子表示a n ;⑹试猜想a 1+a 2+a 3+…+a n 与原正方形边长的关系,并画图示意这种关系.解:⑴100×3+1=301,规律是:本次剪完后得到的小正方形的个数比上次剪完后得到的小正方形的个数多3个;⑵A n =3n +1;⑶若A n =22,则3n +1=22,∴n =7,故需剪7次; ⑷若A n =2004,则3n +1=2004,此方程无自然数解, ∴不能将原正方形剪成2004个小正方形;⑸a n =12n ;⑹a 1=12<1,a 1+a 2=12+14=34<1,a 1+a 2+a 3=12+14+18=78<1,……从而猜想到:a 1+a 2+a 3+…+a n <1.直观的几何意义如图所示。
备战中考数学(北京课改版)巩固复习第七章观察、猜想与证明(含解析)

备战中考数学(北京课改版)巩固复习第七章观察、猜想与证明(含解析)2019备战中考数学(北京课改版)巩固复习-第七章观察、猜想与证明(含解析)一、单选题1.警方抓获一个由甲、乙、丙、丁四人组成的盗窃团伙,其中有一人是主谋,经过审讯,A、B、C三名警察各自得出结论,A:主谋只有可能是甲或乙;B:甲不可能是主谋;C:乙和丙都不可能是主谋.已知三名警察中只有一人推测正确,则主谋是()A. 甲B. 乙C. 丙D. 丁2.(思维拓展)如图所示,①代表0,②代表9,③代表6,则④代表()A. 1B. 3个队至少要积()A. 6分B. 7分C. 8分D. 9分5.警方抓获一个由甲、乙、丙、丁四人组成的盗窃团伙,其中有一人是主谋,经过审讯,A、B、C三名警察各自得出结论,A:主谋只有可能是甲或乙;B:甲不可能是主谋;C:乙和丙都不可能是主谋.已知三名警察中只有一人推测正确,则主谋是()A. 甲B. 乙C. 丙D. 丁6.有4张牌,每张牌的一面都写上一个英文字母,另一面都写上一个数字.规定:当牌的一面为字母R时,它的另一面必须写数字2.你的任务是:为了检验如图的4张牌是否有违反规定的写法,你翻看哪几张牌就够了?你的选择是()A. (a)B. (a)、(c)C. (a)、(d)D. 非以上答案7.10月30日到11月1日,在诏安一中举办了全县中小学生运动会.运动前夕,七年级决定开展校园环境保护的实践活动,1班与3班均想报名参加.老师有个想法:1班有50名同学,3班有53名同学,让两班分别进行一个举手表决:想参加的同学举手,当举手的人数和没有举手的人数之差是一个奇数时,该班就不参加;如果是偶数,该班就参加活动.老师的想法是()A. 1班参加B. 3班参加C. 两班都参加D. 两班都不参加8.小柔要榨果汁,她有苹果、芭乐、柳丁三种水果,且其颗数比为9:7:6,小柔榨完果汁后,苹果、芭乐、柳丁的颗数比变为6:3:4,已知小柔榨果汁时没有使用柳丁,关于她榨果汁时另外两种水果的使用情形,下列叙述何者正确?()A. 只使用苹果B. 只使用芭乐C. 使用苹果及芭乐,且使用的苹果颗数比使用的芭乐颗数多 D. 使用苹果及芭乐,且使用的芭乐颗数比使用的苹果颗数多9.A,B,C,D四人参加某一期的体育彩票兑奖活动,现已知:如果A中奖,那么B也中奖:如果B中奖,那么C中奖或A不中奖:如果D不中奖,那么A中奖,C不中奖:如果D中奖,那么A也中奖则这四个人中,中奖的人数是()A. 1B. 2C. 3D. 410.甲、乙、丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲、乙各比赛了4局,丙当了3次裁判.问第2局的输者是()A. 甲B. 乙C. 丙D. 不能确定11.在取石头游戏中,总共有18颗在一起,现有两人在一起做游戏,确定每人一次只能取1﹣4颗,谁先取到最后一颗为胜.问先手先取()颗必胜.A. 1B. 2C. 3D.412.气象爱好者孔宗明同学在x(x为正整数)天中观察到:①有7个是雨天;②有5个下午是晴天;③有6个上午是晴天;④当下午下雨时上午是晴天.则x等于()B. 8C. 9D.10二、填空题13.如果甲的身高数或体重数至少有一项比乙大,则称甲不亚于乙,在200个小伙子中,如果某人不亚于其他199人,就称他为棒小伙子,那么,200个小伙子中的棒小伙子最多可能有________ .14.有编号为A、B、C三个盒子,分别装有水果糖、奶糖、巧克力糖中的一种,将它们分给甲、乙、丙三位小客人.己知甲没有得到A盒;乙没有得到B盒,也没有得到奶糖;A盒中没有装水果糖,B盒中装着巧克力糖.则丙得到的盒子编号是________,得到的糖是________ 15.在一次数学游戏中,老师在A、B、C三个盘,子里分别放了一些糖果,糖果数依次为ab0, c,记为G=(a, b, c).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束.n次操作后的糖果数记为G0=(a, b,c).(1)若G=(4,7,10),则第________ 次操作后游戏结束;(2)小明发现:若G=(4,8,18),则游戏永远无法结束,那么G2019=________16.一个黑暗的房间里有3盏关着的电灯,每次都按下其中的2个开关,最后________将3盏电灯都开亮.(填“能”或“不能”)17.甲、乙、丙、丁四个人一起到餐馆大吃海喝了一顿,因为甲的钱包落在宿舍,所以钱就由乙、丙、丁三个人出.回到宿舍以后,甲找到了钱包,想要把钱还给其他三个人,结果乙摆摆手说:“不用了,我反正还欠你40元钱,正好抵了.”丙说:“你把补我的那份给丁吧,我正好欠他90块钱.”于是甲只付钱给丁,一共给了310元.那么,在餐馆付饭钱时丁付了________元.18.(1)A、B、C、D、E、F六个足球队进行单循环赛,当比赛进行到某一天时,统计出A、B、C、D、E五个队分别比赛了5、4、3、2、1场球,由此可知还没有与B队比赛的球队是________(2)有红黄蓝黑四种颜色的小球若干个,每个人可以从中任意先取两个,需要________人才能保证至少有2人选的小球颜色彼此相同.19.黑板上写有1,,,…共有100个数字,每次操作,先从黑板上的数选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+ab,则经过99次操作后,黑板上剩下的数是________20.小明同学每天早上6:00钟开始起床,起床穿衣的时间需要5分钟,起床穿衣后他立即用煤气灶煮面条吃,有下面几道工序:①洗锅盛水2分钟;②洗菜3分钟;③准备面条和佐料2分钟;④用锅把水烧开7分钟;⑤用烧开的水煮面条和菜要3分钟.若小明要将面条煮好,最少需要________分钟.三、解答题21.有12名游客要赶往离住地40千米的一个火车站去乘火车,离开车时间只有3小时了,他们步行的速度为每小时6千米,靠走路是来不及了,唯一可以利用的交通工具只有一辆小汽车,但这辆小汽车连司机在内最多能乘5人,汽车的速度为每小时60千米.(1)甲游客说:我们肯定赶不上火车;(2)乙游客说:只要我们肯吃苦,一定能赶上火车;(3)丙游客说:赶上或赶不上火车,关键取决于我们自己.亲爱的同学,当你身处其境,一定也有自己的想法,请你就某位游客的说法,用数学知识以理其人,由于难度不同,请你慎重选择.选择(1)答对只能给3分,选择(2)答对可以给4分,选择(3)答对我们奖赏你满分6分.22.小红、小强、小华三名同学中有一个把教室打扫得干干净净,事后,老师问他们三人是谁做的好事.小红说:“是小强做的”;小强说:“不是我做的”;小华说:“不是我做的”如果他们三人中有两个说了假话,一人说了真话,那么老师能判定教室是哪个打扫的吗?(要有分析)23.有人认为数学没有多少使用价值,我们只要能数得清钞票,到菜场算得出价钱这点数学知识就够了.根据你学习数学的体会,谈谈你对数学这门学科的看法.四、综合题24.一组对边平行,另一组对边相等且不平行的四边形叫做等腰梯形.(1)类比研究我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对四边形进行研究,完成表.四边形对称性边角对角线平行四边形________.两组对边分别平行,两组对边分别相等.两组对角分别相等.对角线互相平分.等腰梯形轴对称图形,过平行的一组对边中点的直一组对边平行,另一组对边相等.________.________.线是它的对称轴.(2)演绎论证证明等腰梯形有关角和对角线的性质.已知:在等腰梯形ABCD中,AD∥BC,AB=DC,AC、BD是对角线.求证:证明:揭示关系我们可以用图来揭示三角形和一些特殊三角形之间的关系.(3)请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系.答案解析部分一、单选题1.【答案】C【考点】推理与论证【解析】【解答】解:假设A判断正确:主谋只有可能是甲或乙正确,则B错误:甲不可能是主谋,故甲有可能是主谋,C错误:乙和丙都不可能是主谋,这样乙和丙可能是主谋,这样无法确定主谋;假设B判断正确,则甲不可能是主谋;故A错误:主谋只有可能是甲或乙,则甲、乙不是主谋,C也错误,乙和丙都不可能是主谋,故乙和丙可能是主谋,则丙是主谋;假设C判断正确,则乙和丙都不可能是主谋;故A错误:主谋只有可能是甲或乙,则甲、乙不是主谋,而B错误的话,即甲是主谋,故出现矛盾;故选:C.【分析】分别假设A,B,C的推理正确,进而根据三名警察中只有一人推测正确,进而分析得出符合题意的答案.2.【答案】B【考点】推理与论证【解析】【解答】解:∵如图所示,①代表0,②代表9,③代表6,,∴图①可以代表0点,图②可以代表9点,图③可以代表6点,∴则④代表3点.故选:B.【分析】根据图形得出图①可以代表0点,图②可以代表9点,图③可以代表6点,进而得出答案.3.【答案】D【考点】推理与论证【解析】【解答】解:小明应先洗开水壶用1分钟,再烧开水用15分钟,在烧水期间,洗茶壶用1分钟,洗茶杯用1分钟,放茶叶用2分钟,给同学打电话用1分钟,一共用5分钟,不用算入总时间,故为使客人早点喝上茶,小明最快可在16分钟内完成这些工作.故选:D.【分析】利用已知得出烧水时间里完成洗茶壶、洗茶杯、再放茶叶、给同学打电话最节省时间进而得出答案.4.【答案】B【考点】推理与论证【解析】【解答】解:4个队单循环比赛共比赛4×3÷2=6场,每场比赛后两队得分之和或为2分(即打平),或为3分(有胜负),所以6场后各队的得分之和不超过18分,①若一个队得7分,剩下的3个队得分之和不超过11分,不可能有两个队得分之和大于或等于7分,所以这个队必定出线,②如果一个队得6分,则有可能还有两个队均得6分,而净胜球比该队多,该队仍不能出线.应选B.【分析】易得小组赛的总场数为小组数×(小组数﹣1)÷2,可得4个队的总积分,进而分类讨论小组得6分或7分能否出线即可.5.【答案】C【考点】推理与论证【解析】【解答】解:假设A判断正确:主谋只有可能是甲或乙正确,则B错误:甲不可能是主谋,故甲有可能是主谋,C错误:乙和丙都不可能是主谋,这样乙和丙可能是主谋,这样无法确定主谋;假设B判断正确,则甲不可能是主谋;故A错误:主谋只有可能是甲或乙,则甲、乙不是主谋,C也错误,乙和丙都不可能是主谋,故乙和丙可能是主谋,则丙是主谋;假设C判断正确,则乙和丙都不可能是主谋;故A错误:主谋只有可能是甲或乙,则甲、乙不是主谋,而B错误的话,即甲是主谋,故出现矛盾;故选:C.【分析】分别假设A,B,C的推理正确,进而根据三名警察中只有一人推测正确,进而分析得出符合题意的答案.6.【答案】C【考点】推理与论证【解析】【解答】解:由于当牌的一面为字母R 时,它的另一面必须写数字2,则必须翻看a是否正确,这样c就不用翻看了,7后面不能是R,要查d.故为了检验如图的4张牌是否有违反规定的写法,翻看a,b两张牌就够了.故选:C.【分析】由于题意知,一定要翻看a,而7后面不能是R,要查d.7.【答案】A【考点】推理与论证【解析】【解答】解:∵1班有50名同学,∴1班举手的人数和没有举手的人数是同奇或同偶,∴1班举手的人数和没有举手的人数之差是一个偶数;∵3班有53名同学,∴3班举手的人数和没有举手的人数是一奇一偶,∴3班举手的人数和没有举手的人数之差是一个奇数;∵当举手的人数和没有举手的人数之差是一个奇数时,该班就不参加;如果是偶数,该班就参加活动,∴3班就不参加,1班就参加活动.故选:A.【分析】根据1班有50名同学,可得1班举手的人数和没有举手的人数是同奇或同偶,依此可得1班举手的人数和没有举手的人数之差是一个偶数;根据3班有53名同学,可得3班举手的人数和没有举手的人数是一奇一偶,依此可得3班举手的人数和没有举手的人数之差是一个奇数;再根据约定即可得到老师的想法.8.【答案】B【考点】推理与论证【解析】【解答】解:∵苹果、芭乐、柳丁三种水果,且其颗数比为9:7:6,∴设苹果为9x颗,芭乐7x颗,铆钉6x颗(x 是正整数),∵小柔榨果汁时没有使用柳丁,∴设小柔榨完果汁后,苹果a颗,芭乐b颗,∵小柔榨完果汁后,苹果、芭乐、柳丁的颗数比变为6:3:4,∴ ,,∴a=9x,b= x,∴苹果的用量为9x﹣a=9x﹣9x=0,芭乐的用量为7x﹣b=7x﹣x= x>0,∴她榨果汁时,只用了芭乐,故答案为:B.【分析】根据榨果汁前的三种水果的棵数比可将三种水果的棵数用含x的代数是表示,再根据榨果汁后的比值表示出各种水果的用量即可判断榨果汁时另外两种水果的使用情形。
最新九年级中考数学复习:猜想与证明压轴题

2023年九年级中考数学复习:猜想与证明压轴题1.在等边ABC 中,D 是边AC 上一动点,连接BD ,将BD 绕点D 顺时针旋转120︒,得到DE ,连接CE .(1)如图1,连接AE ,当B 、A 、E 三点共线时,若4AB =,求AE 的长;(2)如图2,取CE 的中点F ,连接DF ,猜想AD 与DF 的数量关系,并证明你的猜想; (3)如图3,在(2)的条件下,连接BE AF 、交于G 点,若GF DF =,请直接写出CDBE的值.2.如图,在等边ABC 中,5AB =,点D 为边AB 上一点,点E 为边AC 上一点,连接DE .(1)如图1,过点E 作EF BC ∥交AB 于点F ,延长ED 交CB 延长线于点G ,若1AE BG ==,求DB 的长;(2)如图2,将DE 绕点D 逆时针旋转60︒得到DH ,连接AH ,请猜想CE 、AH 、BD 的数量关系并证明;(3)如图3,点K 为边BC 上一点,连接DK 、EK ,在第(2)问的条件下,当DEK 周长最小时,请直接写出DEH △的面积.3.在正方形ABCD中,M是BC边上一点,且点M不与B、C重合,点P在射线AM上,将线段AP绕点A顺时针旋转90︒得到线段AQ,连接BP,DQ.(1)如图1,当点P在线段AM上时,依题意补全图1;(2)在图1的条件下,延长BP,QD交于点H,求证:90H∠=︒.(3)在图2中,当点P在线段AM的延长线上时,连接DP,若点P,Q,D恰好在同一条直线时,猜想DP,DQ,AB之间的数量关系,并证明.4.在ABC中,90=,点D为线段AC上一点,将线段BD绕点B ∠=︒,BA BCABC顺时针旋转90︒,得到线段BE,连接DE.(1)①请补全图形:CD AD ED之间的数量关系____________;①直接写出,,(2)取AD中点F,连接BF、CE,猜想CE与BF的位置关系与数量关系,并证明.5.ABC与△DCE均为等边三角形,D在边AC上,连接BE.(1)如图1,若4AB =,2CE =,求BE 的长;(2)如图2,若AB DC >,在平面内将图1中DCE △绕点C 顺时针旋转(0120)αα︒<<︒,连接BD 、AE ,交于点O ,连接OC ,在CDE △运动过程中,猜想线段AO ,OC ,BO 之间存在的数量关系,并证明你的猜想.6.(1)正方形ABCD 中,对角线AC 与BD 相交于点O ,如图1,请直接猜想并写出AO 与CD 之间的数量关系: ;(2)如图2,将(1)中的BOC 绕点B 逆时针旋转得到11BO C △,连接11AO DC ,,请猜想线段1AO 与1DC 的数量关系,并证明你的猜想;(3)如图3,矩形ABCD 和Rt BEF △有公共顶点,且9030BEF EBF ABD ∠=︒∠=∠=︒,,则AEDF= .7.如图所示,在ABC 中,AB BC =,90ABC ∠=︒,点D 为直线BC 上的一个动点(不与B 、C 重合),连接AD ,将线段AD 绕点D 按顺时针方向旋转90︒,使点A 旋转到点E ,连接EC .操作感知:如果点D 在线段BC 上运动,过点E 作EF BC ⊥交直线BC 于F ,如图所示,从而求得DCE ∠=___________︒.猜想论证:如果点D 在线段CB 的延长线上运动,如图所示,以上结论是否依然成立,并说明理由.拓展应用:连接BE ,当点D 在直线BC 上运动时,若2AB =,则BE 的最小值为 ___________.8.如图1,在等腰三角形ABC 中,120A ∠=︒,AB AC =,AD AE =,连接BE ,点M 、N 、P 分别为DE 、BE 、BC 的中点.(1)观察猜想:图1中,点D 、E 分别在边AB 、AC 上,线段NM 、NP 的数量关系是______,MNP ∠的大小为______;(2)探究证明:把ADE 绕点A 顺时针方向旋转到如图2所示的位置,连接MP 、BD 、CE ,图1中的结论还成立吗?若成立,请证明;若不成立,请说明理由.9.综合与实践 问题情境:如图①,点E 为正方形ABCD 内一点,①AEB =90°,将Rt ①ABE 绕点B 按顺时针方向旋转90°,得到①CBE '(点A 的对应点为点C ).延长AE 交CE '于点F ,连接DE . 猜想证明:(1)试判断四边形BE FE '的形状,并说明理由;(2)如图①,若DA =DE ,请猜想线段CF 与FE '的数量关系并加以证明; 解决问题:(3)如图①,若AB =5,CF =1,请直接写出DE 的长.10.如图1,四边形ABCD 和四边形DEFG 都是正方形,点A 在DG 上,连接AE ,CG .(1)求证:AE CG =;(2)猜想:AE 与CG 之间的位置关系,并证明你的猜想;(3)在其它条件不变的前提下,如果将正方形ABCD 绕着点D 按逆时针旋转任意角度(如图2).那么(2)中结论是否还成立?若成立,请给出证明;若不成立,请说明理由; (4)如图3,将正方形ABCD 绕着点D 旋转到某一位置时恰好使得AD EG ∥,AE GE =.当正方形DEFG ABCD 的边长.11.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中①C=90°,①B =①E=30°.(1)操作发现如图2,固定①ABC,使①DEC绕点C顺时针旋转.当点D恰好落在AB边上时.①线段DE与AC的位置关系是.(不需证明)①设①BDC的面积为S1,①AEC的面积为S2,则S1与S2的数量关系是,证明你的结论;(2)猜想论证当①DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了①BDC和①AEC中BC,CE边上的高,请你证明小明的猜想.12.如图,点A(a,0),B(0,b),且a、b满足(a﹣2)2+|4b﹣8|=0.(1)如图1,求a,b的值;(2)如图2,点C在线段AB上(不与A、B重合)移动,AB①BD,且①COD=45°,猜想线段AC、BD、CD之间的数量关系并证明你的结论;(3)如图3,若P为x轴正半轴上异于原点O和点A的一个动点,连接PB,将线段PB绕点P 顺时针旋转90°至PE ,直线AE 交y 轴于点Q ,当P 点在x 轴上移动时,线段BE 和线段BQ 中哪一条线段长为定值,并求出该定值.13.【问题情境】如图1,点E 为正方形ABCD 内一点,①AEB =90°,将Rt ①ABE 绕点B 按顺时针方向旋转90°,得到CBE '△.延长AE 交CE '于点F ,连接DE .(1)【猜想证明】试判断四边形BE FE '的形状,并说明理由;(2)如图2,若DA =DE ,猜想线段CF 与FE '的数量关系并加以证明; (3)【解决问题】如图1,若AB =13,CF =7,请直接写出DE 的长度.14.如图1,在Rt ABC △中,90A ∠=︒,AB AC =,点D ,E 分别在边AB ,AC 上,AD AE =,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是______,位置关系是______; (2)探究证明:把ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断PMN 的形状,并说明理由;(3)拓展延伸:把ADE 绕点A 在平面内自由旋转,若3AD =,5AB =,请直接写出PMN 面积的最大值______.15.如图1,已知正方形BEFG,点C在BE的延长线上,点A在GB的延长线上,且AB=BC,过点C作AB的平行线,过点A作BC的平行线,两条平行线相交于点D.(1)证明:四边形ABCD是正方形;(2)当正方形BEFG绕点B顺时针(或逆时针)旋转一定角度,得到图2,使得点G在射线DB上,连接BD和DF,点Q是线段DF的中点,连接CQ和QE,猜想线段CQ和线段QE的关系,并说明理由;(3)将正方形BEFG绕点B旋转一周时,当①CGB等于45°时,直线AE交CG于点H,探究线段CH、EG、AH的长度关系.16.如图,在Rt△ABC中,①BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE.连接CE、DE,点F是DE的中点.(1)求证:BD=CE;(2)如图1所示,在点D运动的过程中,连接CF,CF的延长线与AB交于点P,连接DP ,试猜想DP 与CE 的位置关系和数量关系,并证明你猜想的结论.(3)如图2所示,在点D 运动的过程中,当BD =2CD 时,连接CF ,CF 的延长线与BA 的延长线交于点G ,求AGCE的值.17.如图1,已知△ABC 为等边三角形,点D ,E 分别在边AB 、AC 上, AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想在图1中,线段PM 与PN 的数量关系是______,①MPN 的度数是______; (2)探究证明若△ABC 为直角三角形, ①BAC =90° , AB =AC ,点DE 分别在边AB ,AC 上, AD =AE ,把△ADE 绕点A 在平面内自由旋转,如图2.连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.判断△PMN 的形状,并说明理由; (3)拓展延伸若△ABC 中①BAC =120°, AB =AC =13,点D ,E 分别在边AB ,AC 上, AD =AE =5 ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.把△ADE 绕点A 在平面内自由旋转,如图3.①△PMN 的是______三角形.①若△PMN 面积为S ,直接利用①中的结论,求S 的取值取值范围.18.阅读材料:如图①,ABC 与DEF 都是等腰直角三角形,90ACB EDF ∠=∠=︒,且点D 在AB 边上,AB 、EF 的中点均为O ,连接BF 、CD 、CO ,显然,点C 、F 、O 在同一条直线上,可以证明BOF COD ≌,所以BF CD =. 解决问题:△绕点O旋转到图①的位置,猜想此时线段BF与CD的数量关(1)将图①中的Rt DEF系,并证明你的结论.(2)如图①,若ABC与DEF都是等边三角形,AB、EF的中点均为O,上述(1)中结论仍然成立吗?如果成立,请说明理由;如果不成立,请求出BF与CD之间的数量关系.(3)如图①,若ABC与DEF都是等腰三角形,AB、EF的中点均为O,且顶角∠=∠=,请直接写出BF与CD之间的数量关系(用含有α的式子表示出来).ACB EDFα参考答案:1.(1)2AE =; (2)12DF AD =,(3)CD BE =2.(1)2(2)CE AH BD =+,3. (3)2222DP DQ AB +=,4.(1) 222AD CD DE +=(2)2CE BF =,CE BF ⊥,5.(1)BE =(2)BO AO CO =+,6.(1)AO =;(2)11AO ;(37.操作感知:135;猜想论证:结论不成立,;拓展应用:BE 8.(1)MN NP =,60︒(2)成立,9.(1)四边形B E 'FE 是正方形,(2)线段CF 与FE '的数量关系是CF =FE ',10. (2)AE ①CG .(3)(2)中结论仍然成立.111.(1)①DE AC ∥,①12S S =12.(1)a =2,b =2(2)CD =BD +AC .(3)BQ 是定值,4BQ =13.(1)正方形,(2)CF E F '=,14.(1)PM PN =,PM PN ⊥(2)等腰直角三角形,(3)815.(2)CQ ①QE ,CQ =QE .(3)如图3-1中,当①CGB =45°时,结论:CH +EG =AH .如图3-2中,当①CGB =45°时,结论:CH =EG +AH .16. (2)PD =CE ,PD ①CE ,(3)AG CE =17.(1)PM =PN ,120°(2)①PMN 是等腰直角三角形,(3)①等边S18.(1)BF CD =;(2)不成立,BF CD =(3)tan 2BF CD α=。
中考数学第二轮复习专题讲解归纳与猜想

三.归纳与猜想一、 知识综述归纳是一种重要的推理方法,是根据具体事实和特殊现象,通过实验、观察、比较、概括出一般的原理和结论。
猜想是一种直觉思维,它是通过对研究对象的实验、观察和归纳、猜想它的规律和结论的一种思维方法。
猜想往往依据直觉来获得,而恰当的归纳可以使猜想更准确。
我们在进行归纳和猜想时,要善于从变化的特殊性中寻找出不变的本质和规律。
二、理解掌握例1、用等号或不等号填空:(1)比较2x 与x 2+1的大小①当x =2时,2x x 2+1;②当x =1时,2x x 2+1;③当x =-1时,2x x 2+1.(2)可以推测:当x 取任意实数时,2x x 2+1.分析:本题是通过计算发现和猜想一般规律题,正确计算和发现规律是关键。
解:(1)<,=,<; (2)≤。
例2、观察下列分母有理化的计算:12121-=+,23231-=+,34341-=+,45451-=+…从计算结果中找出规律,并利用这一规律计算:1)2002)(200120021341231121(+++++++++ =____。
分析:解本题时,要抓住分每有理化后的结果都是两数之差,且可以错位相消。
还要注意相消后所剩下的是什么。
解:1)2002)(200120021341231121(+++++++++=)12002)(20012002342312(+-++-+-+-=)12002)(12002(+-=2002—1 =2001。
例3、 观察下列数表:1 2 3 4 … 第一行 2 3 4 5 … 第二行 3 4 5 6 … 第三行 4 5 6 7 … 第四行 … … … … 第一列 第二列 第三列 第四列 根据数表所反映的规律,猜想第6行与第6列的交叉点上的数应为____,第n 行与第n 列交叉点上的数应为____。
(用含正整数n 的式子表示)分析:本题要求的是同行同列交叉点上的数,因此,必须先研究同行同列交叉点上的数有什么规律,然后利用此规律解题。
【优选】2020届数学中考复习讲解课件:专题复习(二) 规律与猜想

20
14.(2019·玉林)如图,在矩形 ABCD 中,AB=8,BC=4,一发光电 子开始置于 AB 边的点 P 处,并设定此时为发光电子第一次与矩形的边碰 撞,将发光电子沿着 PR 方向发射,碰撞到矩形的边时均反射,每次反射的 反射角和入射角都等于 45°.若发光电子与矩形的边碰撞次数经过 2 019 次 后,则它与 AB 边的碰撞次数是 673 .
12
按照以上规律,解决下列问题:
(1)写出第 6 个等式: 121=61+616 (2)写出你猜想的第 n 个等式:
; 2n2-1=n1+n(2n1-1)
(用含
n
的等
式表示),并证明. 证明:∵n1+n(2n1-1)=n(22nn--11)+n(2n1-1)=n2(n2-n1-+11)=
2n2-1,
22
(2019·鄂州)如图,在平面直角坐标系中,点 A1,A2,A3,…,
An 在
x
轴上,点
B1,B2,B3,…,Bn 在直线
y=
3 3x
上.若
A1(1,0),且
△ A1B1A2,△ A2B2A3,…,△ AnBnAn+1 都是等边三角形,从左到右的小三
角形(阴影部分)的面积分别记为 S1,S2,S3,…,Sn,则 Sn 可表示为( D ) A.22n 3
A.(
22,-
2 2)
B.(1,0)
C.(-
22,-
2 2)
D.(0,-1)
26
17.(2019·广元)如图,过点
A0(0,1)作
y
轴的垂线交直线
l:y=
3 3x
于
点 A1,过点 A1 作直线 l 的垂线,交 y 轴于点 A2,过点 A2 作 y 轴的垂线交
2021年浙江省中考数学三轮复习冲刺压轴题最后猜想:四边形(Word版含答案)

2021年浙江省中考数学三轮复习冲刺压轴题最后猜想:四边形1.(1)问题呈现:如图①,在一次数学折纸活动中,有一张矩形纸片ABCD ,点E在AD上,点F在BC上,小华同学将这张矩形纸片沿EF翻折得到四边形C′D′EF,C′F交AD于点H ,小华认为△EFH是等腰三角形,你认为小华的判断符合题意吗?请说明理由.(2)问题拓展:如图②,在“问题呈现”的条件下,当点C的对应点C′落在AD上时,已知DE=a ,CD=b ,CF=c ,写出a、b、c满足的数量关系,并证明你的结论.(3)问题应用:如图③,在平行四边形ABCD中,AB=3,AD=4.将平行四边形ABCD沿对角线AC 翻折得到△ACE ,AE交BC于点F .若点F为BC的中点,则平行四边形ABCD的面积为________.2.(1)(探究证明)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:如图①,在矩形ABCD中,EF⊥GH ,EF分别交AD、BC于点E、F ,GH分别交AB、DC于点G、H ,求证:EFGH =ABAD;(2)(结论应用)如图②,将矩形ABCD沿EF折叠,使得点B和点D重合,若AB=2,BC=3.求折痕EF的长;(3)(拓展运用)如图③,将矩形ABCD沿EF折叠.使得点D落在AB边上的点G处,点C落在点P处,得到四边形EFPG ,若AB=2,BC=3,EF=2√103,请求BP的长.3.如图,矩形ABCD中,AB=4,BC=5,M为AB的中点,点P是BC边上一点(不与B ,C重合),连接MP ,PF⊥MP交CD于点F .点B ,B'关于MP对称,点C ,C′关于PF对称,连接B'C .(1)求证:△PFC∽△MPB .(2)①当BP=2时,B'C'=________;②求B'C的最小值.(3)是否存在点P ,使点B',C′重合?若存在,请求出此时M ,F的距离;若不存在,请说明理由.4.如图,在△ABC中,∠C=90°,且BC,AC,AB是三个连续的偶数,在边AB上取点M,N(点M 在BN之间),使BM=3AN.点D,E分别是边AC,BC的中点,当点P从点D出发沿DE方向匀速运动到点E时,点Q恰好从点M出发沿BA方向匀速运动到点N.记QN=x,PD=y,当Q为AB中点时,y=2.(1)求BC,AC,AB的长.(2)求y关于x的函数表达式.(3)①连结PQ,当PQ所在直线与△ABC的某一边所在的直线垂直时,求所有满足条件的x的值.②过点P作PH⊥AB于点H,当△PQH为等腰三角形时,求x的值.5.如图1,在△ABC中,BD为∠ABC的平分线,点D在AC上.(1)求证:ADCD =ABBC(2)如图2,已知AE为BC边的中线,且AE=BE.在射线BD上取一点A'使AE=A'E,A'E交AC于点F,过点A'作AB的垂线,交BA的延长线于点G,连接EG交BD于点H,连接CH.①求证:四边形AGA′F为矩形;②若tanC=34,△BGH的面积为S,请求出△CEH的面积(用含S的代数式表示).6.△ABC为等边三角形,AB=8,AD⊥BC于点D,点E为线段AD上一点,AE=2√3.以AE为边作等边三角形AEF,连接CE,N为CE的中点.(1)如图1,当点E和点F在直线AC两侧时,EF与AC交于点M,连接MN,①求证:ME=MF;②求线段MN的长;(2)将图1中的△AEF绕点A逆时针旋转,旋转角为α,点M为线段EF的中点,连接BE,MN,DM,①如图2,当α=90°时,请直接写出DMBE的值;②连接BN,在△AEF绕点A逆时针旋转过程中,当线段BN最大时,请直接写出tan∠DAN的值.7.如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在边CD延长线上,且满足∠MAN=90°,联结MN ,AC ,MN与边AD交于点E .(1)求证:AM=AN(2)如果∠CAD=2∠NAD,求证:AM2=√2AB⋅AE;(3)MN交AC点O ,若CMBM =k,则OMON=________(直接写答案、用含k的代数式表示).8.综合与探究问题情境在Rt△ABC中,∠BAC=90°,AB=AC ,点D是射线BC上一动点,连接AD ,将线段AD绕点A逆时针旋转90°至AE ,连接DE ,CE .(1)探究发现如图1,BD=CE ,BD⊥CE ,请证明;探究猜想;(2)如图2,当BD=2DC时,猜想AD与BC之间的数量关系,并说明理由;(3)探究拓广当点D在BC的延长线上时,探究并直接写出线段BD ,DC ,AD之间的数量关系.9.综合与实践.问题情境:综合与实践课上,同学们开展了以“图形的旋转”为主题的数学活动.实践操作:如图1,将等腰Rt△AEF绕正方形ABCD的顶点A逆时针方向旋转,其中∠AEF=90,EA=EF ,连接CF ,点H为CF的中点,连接HD ,HE ,DE ,得到△DHE .(1)应用探究:勤奋组:如图2,当点E恰好落在正方形ABCD的对角线AC上时,判断△DHE的形状,并说明理由;(2)善思组:如图3,当点E恰好落在正方形ABCD的边AB上时,(1)中的结论还成立吗?请说明理由;深入探究:(3)创新小组:为定值,请你直接写出其值________.发现若连接BE ,在旋转Rt△AEF的过程中,BECF10.如图,在平行四边形ABCD中,过点D作DE⊥AC于点E,DE的延长线交AB于点F,过点B作BG//DF交DC于点G,交AC于点M.过点G作GN⊥DF于点N.(1)求证:四边形NEMG为矩形;(2)若AB=26,GN=8,sin∠CAB=513,求线段AC的长.11.已知:正方形ABCD的边长为4,E是边CB上的一个动点,过点D作DF⊥DE,交BA的延长线于点F,EF交对角线AC于点M,DE交AC于点N.(1)求证:CE=AF;(2)求证:FM=EM;(3)随着点E在边CB上的运动,NA⋅MC的值是否变化?若不变,请求出NA⋅MC的值;若变化,请说明理由.12.如图,在折纸游戏中,正方形ABCD沿着BE,BF将BC,AB翻折,使A,C两点恰好落在点P .(1)求证:∠EBF=45° .(2)如图,过点P作MN//BC,交BF于点Q .①若BM=5,且MP⋅PN=10,求正方形折纸的面积.②若QP=12BC,求AMBM的值.13.如图(1)证明推断:如图(1),在正方形ABCD中,点E,Q分别在边BC,AB上,DQ⊥AE于点O,点G,F分别在边CD,AB上,GF⊥AE .求证:AE=FG;(2)类比探究:如图(2),在矩形ABCD中,BCAB=k(k为常数).将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形FEPG,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;(3)拓展应用:在(2)的条件下,连接CP,当时k=34,若tan∠CGP=43,GF=2√5,求CP的长.14.点E是矩形ABCD边AB延长线上的一动点,在矩形ABCD外作Rt△ECF,其中∠ECF=90°,过点F作FG⊥BC,交BC的延长线于点G,连接DF,交CG于点H.(1)发现:如图1,若AB=AD,CE=CF,猜想线段DH与HF的数量关系是________;(2)探究:如图2,若AB=nAD,CF=nCE,则(1)中的猜想是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)拓展:在(2)的基础上,若射线FC过AD的三等分点,AD=3,AB=4,则直接写出线段EF的长.15.如图,过正方形ABCD的顶点A作AP⊥AQ,将∠PAQ绕点A旋转,AP交射线CB交于点E,AQ交射线CD交于点F,连接EF,M为EF的中点,连接BM.(1)求证:AE=AF;(2)写出CF与BM的数量关系,并说明理由;(3)若BC=4,BE=2,直接写出BM的长.16.在矩形ABCD中,AB=2BC,点E是直线AB上的一点,点F是直线BC上的一点,且满足AE= 2CF,连接EF交AC于点G.(1)tan∠CAB=________;(2)如图1,当点E在AB上,点F在线段BC的延长线上时,①求证:EG=FG;②求证:CG=√5BE;4(3)如图2,当点E在BA的延长线上,点F在线段BC上时,AC与DF相交于点H,①EG=FG这个结论是否仍然成立?请直接写出你的结论:②当CF=1,BF=2时,请直接写出GH的长.17.(1)证明推断:如图(1),在正方形ABCD中,点E,Q分别在边BC,AB上,DQ⊥AE于点O,点G,F分别在边CD,AB上,GF⊥AE.求证:FG=AE;(2)类比探究:如图(2),在矩形ABCD中,BCAB =23将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形EFGP,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;(3)拓展应用:在(2)的条件下,连接CP,若BEBF =34,GF=2√10,求CP的长.18.教材呈现:如图是华师版九年级上册数学教材第103页的部分内容.已知:如图①,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.求证:CD=12AB.(1)请写出完整的证明过程.(2)结论应用:如图②,BE、CF是锐角△ABC的两条高,M、N分别是BC、EF的中点,判断EF与MN的位置关系,并证明你的结论.(3)在(2)的条件下,若EF=6,BC=24,则MN的长为________.19.如图,四边形ABCD为矩形,G是对角线BD的中点.连接GC并延长至F,使CF=GC,以DC、CF为邻边作▱DCFE,连接CE.(1)若四边形DCFE是菱形,判断四边形CEDG的形状,并证明你的结论.(2)在(1)条件下,连接DF,若BC=√3,求DF的长.20.如图,在平面直角坐标系xOy中,四边形OABC是矩形,点B的坐标是(8,6),点M为OA边上的一动点(不与点O、A重合),连接CM,过点M作直线l⊥CM,交AB于点D,在直线l上取一点E(点E在点M右侧),使得CMME =43,过点E作EF//AO,交BO于点F,连接BE,设OM=m(0<m<8).(1)填空:点E的坐标为________(用含m的代数式表示);(2)判断线段EF的长度是否随点M的位置的变化而变化?并说明理由;(3)①当m为何值时,四边形BCME的面积最小,请求出最小值;②在x轴正半轴上存在点G,使得△GEF是等腰三角形,请直接写出3个符合条件的点G的坐标(用含m的代数式表示).21.已知等腰Rt△ABC和等腰Rt△AEF中,∠ACB=∠AFE=90°,AC=BC ,AF=EF ,连接BE ,点Q为线段BE的中点.(1)如图1,当点E在线段AC上,点F在线段AB上时,连接CQ ,若AC=8,EF=2 √2,求线段CQ的长度.(2)如图2,B、A、E三点不在同一条直线上,连接CE ,且点F正好落在线段CE上时,连接CQ、FQ ,求证:CQ=FQ .(3)如图3,AC=8,AE=4 √2,以BE为斜边,在BE的右侧作等腰Rt△BEP ,在边CB上取一点M ,使得MB=2,连接PM、PQ ,当PM的长最大时,请直接写出此时PQ2的值.22.请完成下面的几何探究过程:(1)观察填空:如图1,在Rt△ABC中,∠C=90°,AC=BC=4,点D为斜边AB上一动点(不与点A,B重合),把线段CD绕点C顺时针旋转90°得到线段CE,连DE,BE,则①∠CBE的度数为________;②当BE=________时,四边形CDBE为正方形.(2)探究证明:如图2,在Rt△ABC中,∠C=90°,BC=2AC=4,点D为斜边AB上一动点(不与点A,B重合),把线段CD绕点C顺时针旋转90°后并延长为原来的两倍得到线段CE,连DE,BE则:①在点D的运动过程中,请判断∠CBE与∠A的大小关系,并证明;②当CD⊥AB时,求证:四边形CDBE为矩形(3)拓展延伸:如图2,在点D的运动过程中,若△BCD恰好为等腰三角形,请直接写出此时AD的长.23.探索与应用:如图(1)问题解决:如图1.在平行四边形纸片ABCD(AD>AB)中,将纸片沿过点A的直线折叠,使点B落在AD上的点B′处,折线AE交BC于点E,连接B'E.求证:四边形ABEB′是菱形.(2)规律探索:如图2,在平行四边形纸片ABCD(AD>AB)中,将纸片沿过点P的直线折叠,点B 恰好落在AD上的点Q处,点A落在点A′处,得到折痕FP,那么△PFQ是等腰三角形吗?请说明理由. (3)拓展应用:如图3,在矩形纸片ABCD(AD>AB)中,将纸片沿过点P的直线折叠,得到折痕FP,点B落在纸片ABCD内部点B′处,点A落在纸片ABCD外部点A′处,A′B′与AD交于点M,且A′M=B′M.已知:AB=4,AF=2,求BP的长.24.定义:若一个三角形存在两个内角之差是第三个内角的两倍,则称这个三角形为关于第三个内角的“差倍角三角形”.例如,在ΔABC中,∠A=100°,∠B=60°,∠C=20°,满足∠A−∠B=2∠C,所以ΔABC是关于∠C的“差倍角三角形”.(1)若等腰ΔABC是“差倍角三角形”,求等腰三角形的顶角∠A的度数;(2)如图1,ΔABC中,AB=3,AC=8,BC=9,小明发现这个ΔABC是关于∠C的“差倍角三角形”.他的证明方法如下:证明:在BC上取点D,使得BD=1,连结AD,(请你完成接下去的证明)(3)如图2,五边形ABCDE内接于圆,连结AC,AD与BE相交于点F,G,AB=BC=DE,ΔABE是关于∠AEB的“差倍角三角形”.①求证:四边形CDEF是平行四边形;②若BF=1,设AB=x,y=S四边形CDEFSΔAEG,求y关于x的函数关系式.25.如图,以矩形OABC的顶点O为坐标原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系,已知OA=8,OC=10,将矩形OABC绕点O逆时针方向旋转α(0<α<180°)得到矩形ODEF.(1)当点E恰好落在y轴上时,如图1,求点E的坐标.(2)连接AC,当点D恰好落在对角线AC上时,如图2,连接EC,EO,①求证:△ECD≌△ODC;②求点E的坐标.(3)在旋转过程中,点M是直线OD与直线BC的交点,点N是直线EF与直线BC的交点,若BM=1BN,请直接写出点N的坐标.226.如图1,在Rt△ABC中,∠ABC=90°,D,E分别为边BC,AC上的点,连接DE,过D作DF ⊥DE交AC边于点F(F不与点C重合),点G为射线DF上一点,连接EG,使∠BAC=∠DEG=α.(1)连接CG,求证:△DEF∽△CGF;(2)当α=45°时,请探究AE,BD与CG三者满足的数量关系,并证明;CD,AC=10,请直(3)如图2,点M,N分别为EG和AC的中点,连接MN.若tanα=2,BD=13接写出MN的最小值.27.如图(1)问题发现如图1,Rt△ABC中,∠ACB=90°,AC=3,BC=4.CD⊥AB于点D,则CD的长为________;(2)问题探究如图2,矩形ABCD中,AB=3,BC=4,点M、N分别在BD,BC上,求CM+MN的最小值;(3)问题解决有一度假山庄,它的平面图为矩形ABCD,现在山庄管理人员想在山庄内找到一点G(点G不在AB、BC、AD上)与CD共同构成一个三角形的绿化区,并且度假山庄大门E到点G的距离与到拐角B的距离相等,如图3,经过测量得知AB=30m,BC=40m,BE=10m,请问绿化区△GCD的面积是否存在最小值,若存在,请求出最小值;若不存在,请说明理由.28.如图,平面直角坐标系中,四边形ABCO为矩形,C点在x轴上,A点在y轴上,B点坐标是(3,3√3).点E从点A出发,沿AO向点O运动,速度为每秒√3个单位长度,同时点F从点A出发,沿AB向点B运动,速度为每秒1个单位长度,当一点到达终点时,另一点也随之停止运动.将△AEF沿直线EF折叠,点A的对应点为G点,设运动时间为t秒.(1)当点G落在线段OB上时,t=________;当点G落在线段CB上时,t=________;(2)在整个运动过程中,求△EFG与△ABO重叠部分的面积S与t的函数表达式,并写出t的取值范围;(3)当点G落在线段BC上时,是否在x轴上存在点N,直线EF上存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.29.正方形ABCD的边长是5,点M是直线AD上一点,连接BM,将线段BM绕点M逆时针旋转90°得到线段ME,在直线AB上取点F,使AF=AM,且点F与点E在AD同侧,连接EF,DF.(1)如图1,当点M在DA延长线上时,求证:△ADF≌△ABM;(2)如图2,当点M在线段AD上时,四边形DFEM是否还是平行四边形,说明理由;(3)在(2)的条件下,线段AM与线段AD有什么数量关系时,四边形DFEM的面积最大?并求出这个面积的最大值.30.如图1,正方形ABCD的边长为5,点E为正方形CD边上一动点,过点B作BP⊥AE于点P ,将△APB绕点A逆时针旋转90°得△AP′D,延长BP交P′D于点F ,连结CP.(1)判断四边形的AP′FP的形状,并说明理由;(2)若DF=1,求S△CPB;(3)如图2,若点E恰好为CD的中点时,请判断CP与DF的数量关系,请说明理由.31.已知矩形OABC在平面直角坐标系中,点A(1,0),点C(0,2),点O(0,0),把矩形OABC绕点O 顺时针旋转135°,得到矩形ODEF,点A ,B ,C的对应点分别为D ,E ,F .DE交y轴于点M .(1)如图①,求∠FOM的大小及OM的长;(2)将矩形ODEF沿y轴向上平移,得到矩形O′D′E′F′,点O ,D ,E ,F的对应点分别为O′,D′,E′,F′,设OO′=t(0<t≤2).①如图②,直线D′E′与x轴交于点N ,若CN//BO,求t的值;②若矩形O′D′E′F′与矩形OABC重叠部分面积为S,当重叠部分为五边形时,试用含有t的式子表示S,并写出t的取值范围(直接写出答案即可).32.在平面直角坐标系中,矩形OABC的顶点A ,C分别在x轴、y轴上,点B的坐标为(2,2√3),将矩形OABC绕点A顺时针旋转α,得到矩形O1AB1C1,点O ,B ,C的对应点分别为O1,B1,C1.(1)如图①,当α=45°时,O1C1与AB相交于点E ,求点E的坐标;(2)如图②,当点O1落在对角线OB上时,连接BC1,四边形OAC1B是何特殊的四边形?并说明理由;(3)连接BC1,当BC1取得最小值和最大值时,分别求出点B1的坐标(直接写出结果即可).33.如图,在平面直角坐标系xOy中,已知A(9,0)、B(9,12),点M、N分别是线段OB、AB上的个单位、2个单位,作MH⊥OA于H.现点M、N分别从点O、A同时出发,动点,速度分别是每秒53当其中一点到达端点时,另一个点也随之停止运动,设运动时间为t秒(t≥0).(1)是否存在t的值,使四边形BMHN为平行四边形?若存在,求出t的值;若不存在,说明理由;(2)是否存在t的值,使△OMH与以点A、N、H为顶点的三角形相似?若存在,求出t的值;若不存在,说明理由;(3)是否存在t的值,使四边形BMHN为菱形?若存在,求出t的值;若不存在,请探究将点N的速度改变为何值时(匀速运动),能使四边形BMHN在某一时刻为菱形.34.如图所示,BA⊥x轴于点A ,点B的坐标为(﹣1,2),将△OAB沿x轴负方向平移3个单位,平移后的图形为△EDC .(1)直接写出点C和点E的坐标;(2)在四边形ABCD中,点P从点A出发,沿“AB→BC→CD”移动,移动到点D停止.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:①当t为何值时,点P的横坐标与纵坐标互为相反数;②用含t的式子表示点P在运动过程中的坐标(写出过程);③当5秒<t<7秒时,四边形ABCP的面积为4,求点P的坐标.35.如图(1),在平面直角坐标系中,点A ,B的坐标分别为(﹣1,0),(3,0),将线段AB先向上平移2个单位长度,再向右平移1个单位长度,得到线段CD ,连接AC ,BD ,构成平行四边形ABDC .(1)请写出点C的坐标为________,点D的坐标为________,S四边形ABDC________;(2)点Q在y轴上,且S△QAB=S四边形ABDC ,求出点Q的坐标;(3)如图(2),点P是线段BD上任意一个点(不与B、D重合),连接PC、PO ,试探索∠DCP、∠CPO、∠BOP之间的关系,并证明你的结论.答案1. (1)解:小华的判断是正确的.在矩形ABCD中,AD∥BC,∴∠HEF=∠EFC.由折叠,得∠HFE=∠EFC,∴∠HFE=∠HEF∴HE=HF∴△EFH是等腰三角形(2)解:a2+b2=c2.在矩形ABCD中,∠D=90°,由折叠,得∠D′=∠D=90°,D′E=DE=a,C′D′=CD=b,C′F=CF=c,由问题呈现,得C′E=C′F=c.在Rt△C′D′E中,D′E2+C′D′2=C′E2,∴a2+b2=c2.(3)3√72. (1)证明:如图①,过点A作AP∥EF,交BC于P,过点B作BQ∥GH,交CD于Q,BQ交AP 于T.∵四边形ABCD是矩形,∴AB∥DC,AD∥BC.∴四边形AEFP、四边形BGHQ都是平行四边形,∴AP=EF,GH=BQ.又∵GH⊥EF,∴AP⊥BQ,∴∠BAT+∠ABT=90°.∵四边形ABCD是矩形,∴∠ABP=∠C=90°,AD=BC,∴∠ABT+∠CBQ=90°,∴∠BAP=∠CBQ,∴△ABP∽△BCQ,∴APBQ =ABBC,∴EFGH =ABAD.(2)解:如图②中,连接BD.∵四边形ABCD是矩形,∴∠C=90°,AB=CD=2,∴BD=√BC2+CD2=√32+22=√13, ∵D,B关于EF对称,∴BD⊥EF,∴EFBD =ABAD,∴√13=23,∴EF=2√133.(3)解:如图③中,过点F作FH⊥EG于H,过点P作PJ⊥BF于J.∵四边形ABCD是矩形,∴AB=CD=2,AD=BC=3,∠A=90°,∴2√103DG = 23,∴DG=√10,∴AG=√DG2−AD2=√10−9=1,由翻折可知:ED=EG,设ED=EG=x,在Rt△AEG中,∵EG2=AE2+AG2,∴x2=AG2+AE2,∴x2=(3﹣x)2+1,∴x = 53,∴DE =EG = 53 , ∵FH ⊥EG ,∴∠FHG =∠HGP =∠GPF =90°, ∴四边形HGPF 是矩形, ∴FH =PG =CD =2,∴EH = √FF 2−FH 2=(2√103)=23,∴GH =FP =CF =EG ﹣EH = 53﹣ 23 =1,∵PF ∥EG ,EA ∥FB , ∴∠AEG =∠JPF , ∵∠A =∠FJP =90°, ∴△AEG ∽△JFP , ∴ AE FJ=AG PJ =EG FP,∴43FJ=1PJ =531 ,∴FJ = 45 ,PJ = 35 ,∴BJ =BC ﹣FJ ﹣CF =3﹣ 45 ﹣1= 65 ,在Rt △BJP 中,BP = √BJ 2+PJ 2=√(35)2+(65)2=3√55 .3. (1)证明:∵PF ⊥MP , ∴∠FPC+∠MPB =90°, ∵∠PMB+∠MPB =90°, ∴∠FPC =∠PMB , ∵∠FCP =∠B , ∴△PFC ∽△MPB ;(2)解:①1 ②如图2,连接MB',CM , ∵M 为AB 的中点, ∴MB =MB'=2, ∴MB'+ CB'≥CM , ∴当点B'在线段CM 上时,CB'有最小值, ∵CM = √BC 2+BM 2=√25+4=√29 , ∴CB'的最小值= √29 ﹣2;(3)解:存在,理由如下:如图4,设B',C'重合点为N ,连接PN ,MN ,NF ,∵点B ,N 关于MP 对称,点C ,N 关于PF 对称,∴BP =PN ,PC =PN ,MN =BM =2,FN =CF ,∠B =∠MNP =90°,∠C =∠PNF =90°, ∴点M ,点N ,点F 三点共线,PB =PC =PN = 52 , ∵∠MPF =90°,∴∠MPB+∠FPC =90°=∠MPB+∠BMP , ∴∠BMP =∠FPC , 又∵∠B =∠C =90°, ∴△BMP ∽△CPF , ∴ BPCF =BM CP, ∴CF = 52×522=258,∴MF =MN+NF =2+ 258 =418.4. (1)解:设AC=x ,则BC=x-2,AB=x+2,由勾股定理,得 (x −2)2+x 2=(x +2)2 ,解得 x =8 ,或 x =0 (舍去), ∴BC=6,AC=8,AB=10.(2)解:设AN=a ,则BM=3a , y =kx +b ,∵ED 为△ABC 的中位线,∴ED= AB 2=5由题意,得 {x =0y =5,{x =10−4a y =0,{x =5−ay =2 , 把 {x =0y =5,{x =10−4a y =0,{x =5−ay =2 代入 y =kx +b , 得 {b =5k(10−4a)+b k(5−a)+b =2=0 ,解得 {a =57b =5k =−710 ,∴ y =−710x +5(3)解:① 1)当PQ ⊥BC 时,四边形ADPQ 为平行四边形,则DP=AQ , y =a +x ,即 −710x +5=57+x , 解得 x =300119 ;2)当PQ⊥AC时,四边形PQBE为平行四边形,则PE=BQ,5−y=10−a−x,即5−(−710x+5)=10−57−x,解得x=650119;3)当PQ⊥AB时(如图1),作DH⊥AB于H,则AH=a+x−y=165,即57+x−(−710x+5)=165,解得x=524119.∴当x=300119,650119,524119时,PQ所在直线与△ABC的某一边所在的直线垂直.(3)②如图2,作PH⊥AB于点H,则QH=PH=EBsinB= 3×45=125,AH= 57+x−125=y+ADcosA=y+4×45,把y=−710x+5,代入,得5 7+x−125=−710x+5+4×45,解得x=692119.(3)②如图3,作PH⊥AB于点H,则QH=PH=EBsinB= 3×45=125,AH= 57+x+125=y+ADcosA=y+4×45,把y=−710x+5,代入,得5 7+x+125=−710x+5+4×45,解得x=3561195. (1)证明:方法1.过点D作DM∥AB交BC于点M.则△ABC∽△DMC,∠1=∠2,ADCD =BMCM∴DMCM=ABBC∵BD为∠ABC的平分线∴∠1=∠3 ∴∠2=∠3∴DM=BM∴ADCD =BMCM=DMCM=ABBC即ADCD=ABBC方法2.过点C作CM∥AB交BD的延长线于点M,通过相似可证. 方法3.过点D作BA,BC的垂线,通过两个等高三角形面积比可证.(2)解:①证明:由题意知,AE=BE=CE∴∠3=∠4,∠BAC=90°即AC⊥AB又∠1=∠3,A′G=AB∴∠1=∠4,AG∥AC∴A′E∥AB∴四边形AGA′F为平行四边形∵A′G⊥AB∴▱AGA′F为矩形②解:由题意,在Rt△ABC中,可设AB=3t,AC=4t,则BC=5t∴EF=32t,A′E=52t,∴AG=A′F=52t−32t=t在△BEG中由(1)可得: EHGH =BEBG=52t3t+t=58∵AE为BC边的中线,∴S△CEH=S△BEH∴S△CEHS△BEH=S△BEHS△BGH=EHGH=58∴S△CEH=5S△BGH=5S6. (1)解:①如图1中,∵△ABC是等边三角形,AD⊥BC,∴∠CAD= 12CAB=30°,∵△AEF是等边三角形,∴AE=AF,∠EAF=60°,∴∠EAM=∠FAM=30°,∴ME=MF.②∵AE=AF,EM=MF,∴AM⊥EF,∵AM=AE•cos30°=2 √3×√32=3,∵等边三角形中AC=AB=8,∴CM=AC-AM=5,∵EM=MF= √3,∴CE= √CM2+ME2=√52+(√3)2=2√7,∵CN=NE,∴MN= 12EC= √7.(2)①√32;②7√397. (1)证明:∵四边形ABCD是正方形,∴AB=AD,∠CAD=45°=∠ACB,∠BAD=90°=∠CDA=∠B,∴∠BAM+∠MAD=90°,∵∠MAN=90°,∴∠MAD+∠DAN=90°,∴∠BAM=∠DAN,∵AD=AB,∠ABC=∠ADN=90°,∴△ABM≅△ADN(ASA)∴AM=AN;(2)证明:∵AM=AN,∠MAN=90°∴∠MNA=45°,∵∠CAD=2∠NAD=45°,∴∠NAD=22.5°,∴∠CAM=∠MAN−∠CAD−∠NAD=22.5°,∴∠CAM=∠NAD,∠ACB=∠MNA=45°,∴△AMC~△AEN,∴AMAE =ACAN,∴AM⋅AN=AC⋅AE,∵AN=AM,AC=√2AB,∴AM2=√2AB⋅AE;(3)kk+28. (1)解:由题意得,∠BAC=∠DAE=90°∵∠BAD+∠CAD =∠CAE+∠CAD∴∠BAD=∠CAE∵线段AD绕点A逆时针旋转90°至AE∴AD=AE又∵AB=AC,∴△BAD≌△CAE∴BD=CE,∠B=∠ACE=45°∴∠ECD=90°,BD⊥CE.(2)解:由(1)得:△BAD≌△CAE∴BD=CE,∠B=∠ACE=45°∵CD=13BC,BD=2DC,即BD=23BC,∴BD=CE=23BC,∵AD=AE∴DE=√AD2+AE2=√2AD∴∠B=∠ACB=45°∴∠BCE=∠ACB+∠ACE =90°∴CD2+CE2=DE2,即(13BC)2+(23BC)2=2AD2,∴AD=√106BC;(3)解:如图,过点A作AM⊥BC交BC于点M∵∠BAC=90°,AB=AC∴BM=CM=12BC∴AM=BM=CM=12BC∴AM=12BC=12(BD−CD),DM=CM+CD=12BC+CD=12(BD+CD)∵AM2+DM2=AD2∴[12(BD−CD)]2+[12(BD+CD)]2=AD2∴BD2+CD2=2AD2.9. (1)解:结论:△DHE是等腰直角三角形.理由:如图2中,∵四边形ABCD是正方形,∴∠CDF=90°,∠DCA=45°,∵点H是CF的中点,∴DH=DH=HF=12CF,∵∠CEF=90°,CH=HF,∴EH=CH=HF=12CF,∴DH=HE,∵DH=CH=HE,∴∠HCD=∠HDC,∠HCE=∠HEC,∵∠DHF=∠HDC+∠HCD,∠FHE=∠HCE+∠HEC,∴∠DHE=2∠DCH+2∠HCE=2∠DCA=90°,∴△DHE是等腰直角三角形.(2)解:如图3中,结论成立.理由:连接BH,过点H作HG⊥AB于G.∵四边形ABCD是正方形,∠EAF=45°∴A,F,A共线,∵CB=CD,∠BCH=∠DCH=45°,CH=CH,∴△BCH≌△DCH(SAS),∴DH=BH,∠CDH=∠CBH,∵∠FEA=∠HGA=∠CBA=90°,∴EF∥GH∥BC,∴BGEG =CHHF,∵CH=HF,∴GB=GE,∵HG⊥BE,∴HB=HE,∴∠HBE=∠HEB,HE=HD,∵∠CDA=∠CBA=90°,∠CDH=∠ABH,∴∠ADH=∠ABH=∠HEB,∵∠HEB+∠AEH=180°,∴∠ADH+∠AEH=180°,∴∠DHE+∠DAE=180°,∵∠DAE=90°,∴∠DHE=90°,∴△DHE是等腰直角三角形.(3)√2210. (1)解:∵DE⊥AC,GN⊥DF,∴∠GNE=∠MEN=90°,∵BG//DF,∴∠MGN+∠GNE=180°,∴∠MGN=90°,∴四边形NEMG是矩形.(2)解:∵四边形NEMG是矩形,GN=8,∴∠AMB=∠AMG=90°,ME=GN=8,∵sin∠CAB= 513,AB=26,∴MB= AB⋅sin∠CAB=10,∴AM=√AB2−MB2=24,∵四边形ABCD是平行四边形,∴AB//CD ,AB=CD ,∴∠CAB=∠ACD ,在△ABM 和△CDE 中, {∠BMA =∠DEC∠CAB =∠ACD AB =CD,∴△ABM ≌△CDE ,∴CE=AM=24,∴AC=AM+CE-ME=24+24-8=40.11. (1)解:∵四边形 ABCD 是正方形, ∴ DC =DA,∠DCE =∠DAF =90° ,又∵ ∠CDE +∠ADE =90°,∠ADF +∠ADE =90° , ∴ ∠CDE =∠ADF ,∴ △ECD ≅△FAD (ASA)∴ CE =AF .(2)解:作 EI//AB ,交 AC 于点I ,连接 DM ,∵ △ECD ≅△FAD ,DF ⊥DE ,∴DF=DE ,∠FDE=90°,则 △FDE 为等腰直角三角形.∵AC 为正方形对角线,∠IEC=∠B=90°, ∴ ∠EIC =∠ECI =45° ,∴ CE =IE ,又∵ FA =CE ,∴ FA =EI ,∵ EI//FA ,∴ ∠IEM =∠AFM , ∠EIM =∠FAM , ∴ △FAM ≌△EM(ASA) ,∴ FM =ME .(3)解:不变由(1),(2)可知△FDE为等腰直角三角形,FM=EM,∴DM⊥FE,∠MDE=∠MDF=45°,∵∠DNA=45°+∠CDN=∠MDE+∠CDN=∠MDC,又∵∠DAN=∠DCM=45°,∴△AND∽△CDM.∴ANCD =ADCM.∴NA⋅MC=AD⋅CD=4×4=16.12. (1)证明:∵正方形ABCD沿着BE,BF将BC,AB翻折,使A,C两点恰好落在点P . ∴△ABF≌△PBF,△BPE≌△BCE,∴AE=A′E,BE=B′E,∠PBF =12∠ABP,∠PBE =12∠PBC,∴∠EBF=∠PBF+∠PBE= 12(∠ABP+∠CBP)=12∠CBA=45∘(2)解:①由折叠的性质可得∠BPE=∠C=90°,∴∠MPB+∠NPE=90°,∵MN//BC,正方形ABCD∴四边形MBCN为矩形,∴∠PMB=∠ENP=90°,BM=CN=5;∴∠MPB+∠MBP=90°,∴∠NPE=∠MBP,∴△MBP∽△NPE,∴PMNE =BMPN,∴PM·PN=BM·NE∵BM=5,且MP⋅PN=10,∴NE=2,∴CE=PE=3,∴PN=√PE2−NE2=√32−22=√5,∴PM=2√5∴MN=AD=3√5正方形折纸的面积= AD2=45;②由折叠可知∠AFB=∠BPE,AF=PF,∵AD//MN∴∠AFB=∠FQP,∴∠BPE=∠FQP,∴PF=QP=12BC=AF,∴AF=FD=12BC,设EC=x,则DE= DC-x =BC-x;PE=x,∵在直角三角形DEF中,EF2=DF2+DE2∴(12BC+x)2=(12BC)2+(BC−x)2,∴x=13BC,∴PE=CE=13BC,∴EF=56BC,∵AD//MN∴△MBP∽△NPE,∴PNDF =PEEF=25,∵AF=FD=12BC,∴PN=15BC,∴MQ=MN-PQ-PN=BC-12BC-15BC=310BC,∵AD//MN∴△MBQ∽△ABF,∴BMAB =MQAF=310BC12BC=35,∴AMBM =2313. (1)证明:∵四边形ABCD是正方形,∴AB=DA,∠ABE=90°=∠DAQ,∴∠QAO+∠OAD=90°,∵AE⊥DQ,∴∠ADO+∠OAD=90°,∴∠QAO=∠ADO,∴△ABE≅△DAQ(ASA),∴AE=DQ,∵DQ⊥AE,GF⊥AE,∴DQ∥GF,∵FQ∥DG,∴四边形DQFG是平行四边形,∴GF=DQ,∵AE=DQ,∴AE=FG;(2)解:结论:GFAE=k .理由如下:如图2中,过G作GM⊥AB于M,∵AE⊥GF,∴∠AOF=∠GMF=∠ABE=90°,∴∠BAE+∠AFO=90°,∠AFO+∠FGM=90°,∴∠BAE=∠FGM,∴△ABE∼△GMF,∴GFAE =GMAB,∵∠AMG=∠D=∠DAM=90°,∴四边形AMGD是矩形,∴GM=AD,∴GFAE =ADAB=BCAB=k(3)解:如图3中,过点P作PM⊥BC交BC的延长线于M.∵ FB//GC , FE//GP ,∴∠CGP =∠BFE ,∴ tan ∠CGP =tan ∠BFE =43=BE BF ,∴设 BE =4k , BF =3k ,则 EF =AF =5k , AB =BF +AF =3k +5k =8k ,∵ FG AE=34 , FG =2√5 , ∴ AE =8√53 ,∴ (4k)2+(8k)2=(8√53)2 , ∴ k =23 或 k =−23 (不合题意,舍去),∴ BE =83 , BF =2 , EF =AF =103 , AB =163 ,∵ BC AB =k =34 , ∴BC =4,∴ CE =BC −BE =4−83=43 , AD =PE =BC =4 ,∵∠EBF =∠FEP =∠PME =90°,∴∠FEB =∠EPM ,∴ △FEB ∼△EPM ,∴EF PE =BF ME =BE MP , ∴ 1034=2ME =83MP ,∴解之得: ME =125, MP =165 , ∴ CM =EM −CE =125−43=1615 , ∴ CP =√CM 2+PM 2=√(1615)2+(165)2=16√101514. (1)DH=HF(2)解: DH =HF 仍然成立,理由如下:∵四边形ABCD 是矩形, FG ⊥BC , ∠ECF =90° ,∴ ∠CGF =∠ECF =∠EBC =90°∴ ∠FCG +∠BCE =90° ,∵ ∠BCE +∠CEB =90° ,∴ ∠FCG =∠CEB ,∴ ΔFCG ∼ΔCEB ,∴ GF BC =FC CE =n ,∴四边形ABCD 是矩形, AB =nAD ,∴CD BC =n , ∴ GF BC=CD BC , ∴ GF =CD ,∵四边形ABCD 是矩形,∴ CD ⊥BC ,∵ FG ⊥BC ,∴ CD//FG ,∴ ∠HDC =∠HFG , ∠HCD =∠HGF ,在 ΔHCD 和 ΔHGF 中,{∠HDC =∠HFGCD =GF∠HCD =∠HGF, ∴ ΔHCD ≌ΔHGF(ASA) ,∴ DH =HF(3)解:如图所示,延长FC 交AD 于R ,∵四边形ABCD是矩形,∴AB=CD=4,AD=BC=3,∠RDC=90°,RD//CH,∵AB=nAD,CF=nCE,∴n=ABAD =43,∴CE=43CF,分两种情况:①当AR=13AD时,∵AD=3,∴AR=1,DR=2,在RtΔCDR中,由勾股定理得:CR=√DR2+CD2=√22+42=2√5,∵RD//CH,DH=DF,∴RC=CF=2√5,∴CE=34×2√5=32√5,②当DR=13AD时,同理可得:DR=1,DC=√17,CF=RC=√17,CE=3√174,由勾股定理得:EF=√CF2+CE2=(√4)=5√174,综上所说,若射线FC过AD的三等分点,AD=3,AB=4,则线段EF的长为5√52或5√17415. (1)解:∵四边形ABCD是正方形∴AB=AD,∠BAD=∠ABC=∠ACB=∠ADF=90°,BC=DC 又AP⊥AQ∴∠EAF=90°∴∠EAB=∠FAD=90°−∠BAF,∠ABE=180°−90°=90°∴∠ABE=∠ADF∴△ABE≌△ADF(ASA)∴AE=AF(2)解:CF=√2BM,理由如下;过点F作FG//BM交BC于G,如图则EBBG =EMMF∵M为EF中点∴EM=MF∴EB=BG∵△ABE≌△ADF∴EB=DF∴BG=DF又BC=DC∴CG=CF∴FG=√CG2+CF2=√2CF ∵EM=MF,EB=BG∴BM=12FG=√22CF∴CF=√2BM(3)解:①当点E在线段CB的延长线上时由(2)知,BG=BE=2∴CG=CF=2∴√2BM=CF=2∴BM=√2②当点E在线段CB上时过点F作FG//BM交BC于G,如下图所示同理可得BG=BE=2∴CG=CF=BC+BG=6∴√2BM=CF=6∴BM=3√2综上所述,BM的长为√2或3√216. (1)12(2)解:①证明:过点E作EH⊥AB,交AC于点H,则∠AEH=90°.∵四边形ABCD是矩形,∴∠B=∠AEH=90°.∴EH∥BF,∴∠EHG=∠FCG,∠HEG=∠CFG,在Rt△ABC和Rt△AEH中,∵AB=2BC,∴tan∠CAB=BCAB =EHAE=12,∴AE=2EH,∵AE=2CF,∴EH=CF,∴△EHG≌△FCG(ASA),∴EG=FG.②证明:设EH=x,则AE=2x,Rt△AEH中,根据勾股定理得,AH=√AE2+EH2=√5x,∵EH∥BF,∴ AH HC = AE EB ,∴ √5x HC = 2x EB , ∴CH = √52BE , ∵△EHG ≌△FCG ,∴HG =CG ,∴CG = √54BE .(3)解:①成立;过点E 作EI ∥BC 交AC 于点I ,如图2所示:∵四边形ABCD 是矩形,∴∠AEI =∠ABC =90°,AB ∥CD ,AB =CD ,在Rt △AEI 和Rt △ABC 中,∠ABC =∠AEI =90°,AB =2BC , ∴tan ∠IAE =IE AE =BC AB =12 , ∴AE =2IE ,∵AE =2CF ,∴IE =CF ,∵EI ∥BC ,∴∠EIG =∠FCG ,∠IEG =∠CFG ,在△EIG 和△FCG 中,{∠EIG =∠FCGEI =CF∠IEG =∠CFG, ∴△EIG ≌△FCG (ASA ),∴EG =FG ;②解:过点F 作FP ∥AB 交AC 于P ,如图3所示:则FP ∥CD ,∠CFP =∠ABC =90°,在Rt△CFP和Rt△ABC中,AB=2BC,∴tan∠CPF=CFPF =tan∠CAB=BCAB=12,∴PF=2CF,∵AE=2CF,∴AE=PF=2,同(2)得:△AEG≌△PFG(AAS),∴AG=PG,∵BF=2,CF=1,∴BC=3,CD=AB=2BC=6,∴AC=√AB2+BC2=√62+32=3 √5,∵FP∥AB,∴△CPF∽△CAB,∴PCAC =CFBC=13,∴PC=13AC=√5,PA=AC﹣PC=2 √5,∴AG=PG=12PA=√5,∵FP∥CD,∴△PFH∽△CDH,∴PHCH =PFCD=26=13,∴PH=14PC=√54,∴GH=PG+PH=√5+√54=5√54.17. (1)解:如图(1),∵四边形ABCD是正方形,∴AB=DA,∠ABE=90°=∠DAQ.∴∠QAO+∠OAD=90°.∵AE⊥DQ,∴∠ADO+∠OAD=90°.∴△ABE≌△DAQ(ASA),∴AE=DQ.∵四边形ABCD是正方形,AE⊥DQ,AE⊥GF,∴DG∥QF,DQ∥GF,∴四边形DQFG是平行四边形,∴DQ=GF,∴FG=AE;(2)GFAE =23.理由:如图(2)中,作GM⊥AB于M.∵AE⊥GF,∴∠AOF=∠GMF=∠ABE=90°,∴∠BAE+∠AFO=90°,∠AFO+∠FGM=90°,∴∠BAE=∠FGM,∴△ABE∽△GMF,∴GF:AE=GM:AB,∵∠AMG=∠D=∠DAM=90°,∴四边形AMGD是矩形,∴GM=AD,∴GF:AE=AD:AB,∵四边形ABCD是矩形,∴BC=AD,∴GF:AE=BC:AB,∵BCAB =23,∴GFAE =23.(3)解:如图(3)中,作PM⊥BC交BC的延长线于M.由BE :BF =3:4 ,设BE =3k ,BF =4k ,则EF =AF =5k , ∵ GF AE =23 , GF =2√10 , ∴AE = 3√10 ,在直角三角形ABE 中,根据勾股定理,得 BE 2+AB 2=AE 2 , ∴ (3k)2+(9k)2=(3√10)2∴k =1或﹣1(舍去),∴BE =3,AB =9,∵BC :AB =2:3,∴BC =6,∴BE =CE =3,AD =PE =BC =6,∵∠EBF =∠FEP =∠PME =90°,∴∠FEB+∠PEM =90°,∠PEM+∠EPM =90°, ∴∠FEB =∠EPM ,∴△FBE ∽△EMP ,∴ FB EM=FE EP =BE PM , ∴ 4EM =56=3PM ,∴EM = 245 ,PM = 185 ,∴CM =EM ﹣EC = 245 ﹣3= 95 ,∴PC = √CM 2+PM 2=√(95)2+(185)2 = 95√5 . 18. (1)证明:取 BC 中点为E ,连接 DE .∵CD是斜边AB上的中线∴BD=12AB,又∵BE=12BC∴DE为Rt△ABC中位线∴DE//AC,DE=12AC∵∠ACB=90°,∴DE⊥BC∴DE垂直平分BC∴CD=BD∴CD=12AB(2)MN垂直平分EF证明:连接MF,ME∵BE、CF是锐角△ABC两条高∴BE⊥AC,CF⊥AB∴∠BEC=90°,∠CFB=90°∴在Rt△BEC中,M为BC中点,EM=12BC在Rt△CFB中,FM=12BC,∴MF=ME,又∵N为EF中点,∴MN为EF中垂线.(3)3√1519. (1)解:四边形CEDG是菱形,理由如下:∵四边形ABCD为矩形,G是对角线BD的中点,∴GB=GC=GD,∵CF=GC,∴GB=GC=GD=CF,∵四边形DCFE是菱形,∴CD=CF=DE,DE//CG,∴DE=GC,∴四边形CEDG是平行四边形,∵GD=GC,∴四边形CEDG是菱形(2)解:∵CD=CF,GB=GD=GC=CF,∴△CDG是等边三角形,∴CD=BG,GCD=∠DGC=60°,∴∠DCF=∠BGC=120°,∴△BGC≌△DCF(SAS),∴DF=BC=√3.20.(1)(m+ 92,34m)(2)解:设直线BO的解析式为:y=kx,把点B的坐标是(8,6),代入上式可得:6=8k,解得:k= 34,∴直线BO的解析式为:y= 34x,∵点E的坐标为(m+ 92,34m),EF//AO,∴点F的坐标为(m,34m),∴EF= m+ 92-m= 92,即:线段EF的长度不会随点M的位置的变化而变化(3)解:①连接CE,过点E作EQ⊥BC于点Q,∵点E的坐标为(m+ 92,34m),∴EQ=6- 34m,∵OC=6,OM=m,∴CM= √36+m2,∵OCMN =OMNE=CMME=43,∴ME= 34CM= 34√36+m2,∴四边形BCME的面积= 12CM⋅ME+12BC⋅QE= 38m2−3m+752= 38(m−4)2+632,即:当m=4时,四边形BCME的面积最小值为:632;②(a)当点G为顶角顶点时,如图,则G(m+92+m2,0),即:G(m+94,0),(b)当点E为顶角顶点时,如图,则EG=EF= 92,EH= 34m,GH= √(92)2−(34m)2=34√36−m2,∴G(m+92+34√36−m2,0)或G(m+92−34√36−m2,0),综上所述:G的坐标可以是:G(m+94,0)或G(m+92+34√36−m2,0)或G(m+92−34√36−m2,0).21. (1)解:∵等腰Rt△ABC和等腰Rt△AEF ,∠ACB=∠AFE=90°,∴AC=BC=8,AF=EF=2√2,∴AB=√AC2+BC2=√2AC=8√2,AE=√2EF=4,∴CE=AC-AE=8-4=4,∴BE=√CE2+BC2=4√5,∵Q是线段BE的中点,∴CQ=12BE=2√5;(2)证明:如图,延长FQ至K,使KQ= FQ,连接KB,延长FC至G点,∵Q为BE的中点,∴FQ=KQ,在△EFQ与△BKQ中,{FQ= KQ∠FQE=∠KQBEQ=BQ),∴△EFQ≌△BKQ (SAS),∴EF= BK,∠FEQ =∠KBQ,∴AF= BK, EF ∥BK,∴∠KBC=∠BCG,∴∠ACB=90°,∴∠FCA+∠BCG = 180°-∠ACB=90°,∵∠FAC+∠FCA=∠AFE=90°,∴∠BCG =∠FAC,又∠KBC =∠BCG,∴∠FAC=∠KBC,在△AFC与△BKC中,{AF= BK∠FAC=∠KBCAC= BC),∴△AFC≌△BKC(SAS),∴CF= CK,∠FCA=∠KCB,∴∠FCK =∠FCA+∠ACK =∠KCB+∠ACK = 90°,∴△FCK为等腰直角三角形,又Q为FK中点,∴CQ=FQ;(3)680+128√171722. (1)45°;2√2(2)证明:①∠CBE=∠A,理由如下:由旋转的性质得:∠BCE=∠ACD,∵BC=2AC,CE=2CD,∴BCAC =CECD=2,∴ΔBCE∽ΔACD,∴∠CBE=∠A;②∵CD⊥AB,∴∠ADC=∠BDC=90°,由①得:ΔBCE∽ΔACD,∴∠BEC=∠ADC=90°,又∵∠DCE=90°,∴四边形CDBE是矩形;(3)解:在点D的运动过程中,若ΔBCD恰好为等腰三角形,存在两种情况:①当CD=BD时,则∠DCB=∠DBC,∵∠DBC+∠A=90°,∠ACD+∠DCB=90°,∴∠A=∠ACD,∴CD=AD,∴CD=BD=AD,AB,∴AD=12∵AB=√AC2+BC2=√22+42=2√5,∴AD=√5;②当BD=BC=4时,AD=AB−BD=2√5−4;综上所述:若ΔBCD恰好为等腰三角形,此时AD的长为√5或2√5−4 23. (1)解:由平行四边形的性质可知AD//BC,∴∠AB′E=∠CEB′,由翻折可知∠AB′E=∠ABE,∴∠CEB′=∠ABE,。
中考数学复习专题讲座教案:归纳猜想型问题

中考数学复习专题讲座七:归纳猜想型问题(一)一、中考专题诠释归纳猜想型问题在中考中越来越被命题者所注重。
这类题要求根据题目中的图形或者数字,分析归纳,直观地发现共同特征,或者发展变化的趋势,据此去预测估计它的规律或者其他相关结论,使带有猜想性质的推断尽可能与现实情况相吻合,必要时可以进行验证或者证明,依此体现出猜想的实际意义。
二、解题策略和解法精讲归纳猜想型问题对考生的观察分析能力要求较高,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。
其中蕴含着“特殊——一般——特殊”的常用模式,体现了总结归纳的数学思想,这也正是人类认识新生事物的一般过程。
相对而言,猜想结论型问题的难度较大些,具体题目往往是直观猜想与科学论证、具体应用的结合,解题的方法也更为灵活多样:计算、验证、类比、比较、测量、绘图、移动等等,都能用到。
由于猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养创造性思维能力,所以备受命题专家的青睐,逐步成为中考的持续热点。
三、中考考点精讲考点一:猜想数式规律通常给定一些数字、代数式、等式或者不等式,然后猜想其中蕴含的规律。
一般解法是先写出数式的基本结构,然后通过横比(比较同一等式中不同部分的数量关系)或纵比(比较不同等式间相同位置的数量关系)找出各部分的特征,改写成要求的格式。
例1(沈阳)有一组多项式:a+b2,a2﹣b4,a3+b6,a4﹣b8,…,请观察它们的构成规律,用你发现的规律写出第10个多项式为.考点:多项式。
810360专题:规律型。
分析:首先观察归纳,可得规律:第n个多项式为:a n+(﹣1)n+1b2n,然后将n=10代入,即可求得答案.解答:解:∵第1个多项式为:a1+b2×1,第2个多项式为:a2﹣b2×2,第3个多项式为:a3+b2×3,第4个多项式为:a4﹣b2×4,…∴第n个多项式为:a n+(﹣1)n+1b2n,∴第10个多项式为:a10﹣b20.故答案为:a10﹣b20.点评:此题考查的知识点是多项式,此题难度不大,注意找到规律第n个多项式为:a n+(﹣1)n+1b2n是解此题的关键.例2(珠海)观察下列等式:12×231=132×21,13×341=143×31,23×352=253×32,34×473=374×43,62×286=682×26,…以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:①52×=×25;②×396=693×.(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a、b),并证明.考点:规律型:数字的变化类。
猜想与证明-2021届中考数学压轴大题专项训练(解析版)
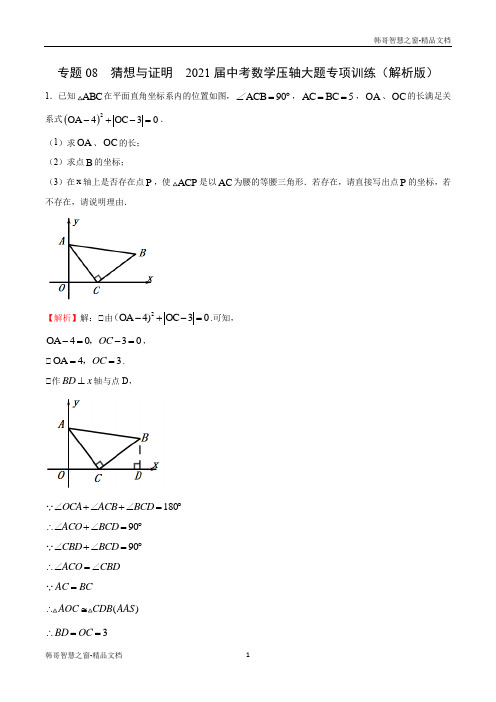
专题08 猜想与证明 2021届中考数学压轴大题专项训练(解析版)1.已知ABC 在平面直角坐标系内的位置如图,ACB 90∠=︒,AC BC 5==,OA 、OC 的长满足关系式()2OA 4OC 30-+-=. (1)求OA 、OC 的长; (2)求点B 的坐标;(3)在x 轴上是否存在点P ,使ACP 是以AC 为腰的等腰三角形.若存在,请直接写出点P 的坐标,若不存在,请说明理由.【解析】解:⑴由2OA 4)OC 30-+-=(.可知, OA 4030OC -=-=,,⑴OA 43OC ==,. ⑴作BD x ⊥轴与点D ,180OCA ACB BCD ∠+∠+∠=︒ 90ACO BCD ∴∠+∠=︒ 90CBD BCD ∠+∠=︒ ACO CBD ∴∠=∠AC BC =()AOC CDB AAS ∴≅3BD OC ∴==4CD OA ==347OD OC CD ∴=+=+=(73)B ∴,⑴存在.当点P 在x 轴的负半轴时,使AP=AC ,则ACP △为等腰三角形,P 的坐标为(30)-,; 当点P 在x 轴的负半轴时,使CP=AC ,由勾股定理得,CP=AC=5,则ACP △为等腰三角形,P 的坐标为(20)-,; 当点P 在x 轴的正半轴时,使AC=CP ,则ACP △为等腰三角形,5CP AC ==358OP OC CP ∴=+=+=,(80)P ∴,; 所以存在,点P (30)-,或(20)-,或(8)0,. 2.在平面坐标系xoy 中,已知线段AB ,且A B 、的坐标分别为(1,2),(4,2)A B ,点C 为线段AB 的中点. (1)线段AB 与x 轴的位置关系是 (2)求点C 的坐标。
(3)在y 轴上是否存在点P ,使得三角形PAC 面积为3.若存在,求出点P 的坐标;若不存在,请说明理由.【解析】解:(1)因为A 、B 点的纵坐标相同,所以线段AB 与x 轴平行; (2)1242A B (,),(,),C 是线段AB 的中点,⑴C 点坐标为:5,22⎛⎫⎪⎝⎭(3)在y 轴上存在点P ,使得三角形PAC 的面积为3.其理由如下: 由(2)知:5(1,2),C ,22A ⎛⎫⎪⎝⎭, 53122AC ∴=-= 1•32PACP A S AC y y ∆=-=即:13322P A y y ⨯⨯-= 24P y ∴-=6P y ∴= 或2P y =- ,⑴P 点坐标为:06(,)或02-(,)时,三角形PAC 的面积为3. 3.探索与证明:(1)如图⑴,直线m 经过正三角形ABC 的顶点A ,在直线m 上取点D ,E ,使得60ADB ∠=︒,60AEC ∠=︒.通过观察或测量,猜想线段BD ,CE 与DE 之间满足的数量关系,并予以证明;(2)将(1)中的直线m 绕着点A 逆时针方向旋转一个角度到如图⑴的位置,120ADB ∠=︒,120AEC ∠=︒.通过观察或测量,猜想线段BD ,CE 与DE 之间满足的数量关系,并予以证明.【解析】解:(1)DE=BD +CE ,证明如下 ⑴⑴ABC 为等边三角形 ⑴AB=CA ,⑴BAC=60° ⑴60ADB ∠=︒,60AEC ∠=︒ ⑴ADB CEA ∠=∠⑴⑴ABD +⑴BAD=180°-⑴ADB=120° ⑴CAE +⑴BAD=180°-⑴BAC=120° ⑴⑴ABD=⑴CAE 在⑴ABD 和⑴CAE 中ADB CEA ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩⑴⑴ABD⑴⑴CAE⑴BD=AE ,AD= CE ⑴DE=AE +AD= BD +CE ; (2)CE =BD +DE ,证明如下 ⑴⑴ABC 为等边三角形 ⑴AB=CA ,⑴BAC=60°⑴120ADB ∠=︒,120AEC ∠=︒ ⑴ADB CEA ∠=∠⑴⑴ABD +⑴BAD=180°-⑴ADB=60° ⑴CAE +⑴BAD=⑴BAC=60° ⑴⑴ABD=⑴CAE 在⑴ABD 和⑴CAE 中ADB CEA ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩⑴⑴ABD⑴⑴CAE ⑴BD=AE ,AD= CE ⑴AD= AE +DE ⑴CE= BD +DE .4.如图,钝角ABC 中,AB AC =,D 为上AC 一点,60ADB ∠=︒,E 为BD 上一点,30BCE ∠=︒.(1)作AF BC ⊥于F ,BG CE ⊥交CE 的延长线于G . ⑴判断BF 与BG 的大小关系,并说明理由. ⑴求证BFA BGE ≌△△;(2)若7BE =,1DE =,求CE 的长. 【解析】解:(1)⑴BF BG =,理由是: ⑴AB AC =,AF BC ⊥于F ,⑴12BF BC =, ⑴作BG CE ⊥于G ,30BCE ∠=︒, ⑴12BG BC =, ⑴BF BG =. ⑴⑴AB AC =, ⑴A ABC CB =∠∠,⑴()19029030603ABC ACB ∠=︒-∠=︒-∠+︒=︒-∠=∠, ⑴1434∠+∠=∠+∠,即ABF EBG ∠=∠, 由⑴知,BF BG =,⑴ABF EBG ≌△△(ASA ).(2)作BH DA ⊥交射线DA 于H ,CM BD ⊥交BD 的延长线于M⑴7BE =,1DE =,⑴8BD =,由(1)ABF EBG ≌△△可知,7AC AB BE ===, ⑴60ADB ∠=︒, ⑴30DBH ∠=︒, ⑴142DH BD ==, 由勾股定理,得22248BH BD DH =-=,⑴1AH ==,⑴413AD DH AH =-=-=,734CD AC AD =-=-=,⑴122DM CD ==,CM =,3EM =,⑴CE =⑴CE5.如图,在ABC 中,45ABC ∠=︒,点P 为边BC 上的一点,3BC BP =,且15PAB ∠=︒,点C 关于直线PA 的对称点为D ,连接BD ,又APC △的PC 边上的高为AH .(1)求BPD ∠的大小;(2)判断直线BD ,AH 是否平行?并说明理由; (3)证明:BAP CAH ∠=∠.【解析】(1)⑴15PAB ∠=︒,45ABC ∠=︒, ⑴154560APC ∠=︒+︒=︒, ⑴点C 关于直线PA 的对称点为D , ⑴PD PC =,AD AC =,⑴ADP ACP ≌△△, ⑴60APC APD ∠=∠=︒, ⑴18012060BPD ∠=︒-︒=︒; (2)直线BD ,AH 平行.理由:⑴3BC BP =, ⑴1122BP PC PD ==, 如图,取PD 中点E ,连接BE ,则BEP △为等边三角形,BDE 为等腰三角形, ⑴60BEP ∠=︒, ⑴1302BDE BEP ∠=∠=︒, ⑴90DBP ∠=︒,即BD BC ⊥. 又⑴APC △的PC 边上的高为AH , ⑴AH BC ⊥,⑴//BD AH ;(3)如图,过点A 作BD 、DP 的垂线,垂足分别为G 、F .⑴∠=∠APC APD ,即点A 在DPC ∠的平分线上, ⑴A НAF =.⑴90CBD ∠=︒,45ABC ∠=︒, ⑴45GBA CBA ∠=∠=︒, 即点A 在GBC ∠的平分线上, ⑴AG AH =,⑴AG AF =, ⑴点A 在GDP ∠的平分线上. 又⑴30BDP ∠=︒,⑴150GDP ∠=︒, ⑴1150752ADP ∠=⨯︒=︒, ⑴75C ADP ∠=∠=︒,⑴Rt ACH 中,15CAH ∠=︒,⑴BAP CAH ∠=∠.6.如图,边长为ABCD 中,P 是对角线AC 上的一个动点(点P 与A 、C 不重合),连接BP ,将BP 绕点B 顺时针旋转90°到BQ ,连接QP ,QP 与BC 交于点E ,QP 延长线与AD (或AD 延长线)交于点F .(1)连接CQ ,证明:CQ AP =;(2)设,AP x CE y ==,试写出y 关于x 的函数关系式,并求当x 为何值时,38CE BC =; (3)猜想PF 与EQ 的数量关系,并证明你的结论. 【解析】(1)证明:⑴线段BP 绕点B 顺时针旋转90︒得到线段BQ , ⑴BP=BQ ,90PBQ ∠=︒, ⑴四边形ABCD 是正方形, ⑴BA=BC ,90ABC ∠=︒, ⑴=ABC PBQ ∠∠,⑴ABC PBC PBQ PBC ∠-∠=∠-∠,即ABP CBQ ∠=∠, 在⑴BAP 和⑴BCQ 中,⑴BA BC ABP CBQ BP BQ =⎧⎪∠=∠⎨⎪=⎩,⑴△BAP △BCQ ≅(SAS ), ⑴CQ=AP . (2)如图,⑴四边形ABCD 是正方形, ⑴1452BAC BAD ∠=∠=︒,1452BCA BCD ∠=∠=︒, ⑴+=180-45=135APB ABP ∠∠︒︒︒,⑴DC=AD= 由勾股定理可得:AC =,⑴AP=x , ⑴PC=4-x ,⑴⑴PBQ 是等腰直角三角形, ⑴45BPQ ∠=︒,⑴18045135APB CPQ ∠+∠=︒-︒=︒, ⑴CPQ ABP ∠=∠, ⑴45BAC ACB ∠=∠=︒, ⑴△△APB CEP ,⑴AP AB CE CP=,⑴4x y x=-,⑴()()2140<<44y x x x x =-=-+,由3388CE BC ==⨯=⑴244y x =-+=,得到2430x x -+=,()()310x x --=,得x=3或x=1. 当x=3或1时,38CE BC =. (3)结论:PF=EQ ,理由是:如图,当F 在边AD 上时,过P 作PG FQ ⊥,交AB 于G ,则90GPF ∠=︒,⑴45BPQ ∠=︒, ⑴45GPB ∠=︒,⑴45GPB PQB ∠=∠=︒, ⑴PB=BQ ,ABP CBQ ∠=∠, ⑴△△PGB QEB ≅(SAS ), ⑴EQ=PG , ⑴90BAD ∠=︒,⑴F 、A 、G 、P 四点共圆, 连接FG ,⑴45FGP FAP ∠=∠=︒, ⑴⑴FPG 是等腰直角三角形,⑴PF=PG , ⑴PF=EQ .当F 在AD 的延长线上时,如图所示,同理可得:PF=PG=EQ .7.问题提出:(1)同一平面内的两条线段AB 和BC ,已知3AB =,2BC =,则线段AC 最大值是______;最小值是______. 问题探究:(2)如图,四边形ABCD 中,4AB =,2AD =,CB CD =,且60BCD ∠=︒,问AC 是否存在最大值?若存在,求出最大值;若不存在,请说明理由.问题解决:(自行作图并解决)(3)在ABE △中,AE =BE =AB 为一边作正方形ABCD ,连接CE ,问CE 是否存在最大值或者最小值?若存在,求出相应最值;若不存在,请说明理由. 【解析】(1)由题意,分以下两种情况: ⑴当点,,A B C 不在同一条直线上时,由三角形的三边关系定理得:AB BC AC AB BC -<<+,3232AC ∴-<<+,即15AC <<;⑴当点,,A B C 在同一直线上时,点B 在点,A C 的中间时,则325AC AB BC =+=+=, 点C 在点,A B 的中间时,则321AC AB BC =-=-=, 综上,线段AC 的取值范围为15AC ≤≤, 则线段AC 最大值是5,最小值是1, 故答案为:5,1;(2)存在,求解过程如下:如图,连接AC ,将ACD △绕点C 逆时针旋转60︒,点A 的对应点为点E ,连接AE 、BE 、CE ,,60CB CD BCD ∠=︒=, ∴旋转后点D 的对应点为点B ,由旋转的性质得:2,,60BE AD AC EC ACE ===∠=︒,ACE ∴是等边三角形, AE AC ∴=,⑴当点,,A B E 不在同一条直线上时,AB BE AE AB BE -<<+,即4242AE -<<+,26AC ∴<<;⑴当点,,A B E 在同一条直线上时,426AE AB BE =+=+=,6AC ∴=,综上,当点,,A B E 在同一条直线上时,AC 有最大值,最大值为6;(3)如图,将ABE △绕点B 逆时针旋转90︒,点E 的对应点为点F ,连接EF 、BF 、CF , 四边形ABCD 是正方形,,90AB BC ABC ∴=∠=︒,∴旋转后点A 的对应点为点C ,由旋转的性质得:90BF BE CF AE EBF ====∠=︒,在Rt BEF △中,EF ==,⑴当点,,C F E 不在同一条直线上时,EF CF CE EF CF -<<+,CE ∴<<CE <<⑴当点,,C F E 在同一条直线上时,CE EF CF =+==综上,当点,,C F E 在同一条直线上时,CE 有最大值,最大值为8.如图,在直角ABC ∆中,90ACB ∠=,4AC =,60BAC ∠=,CD 是边AB 上的中线,直线//BM AC ,E 是边CA 延长线上一点,连接ED 并延长交直线BM 于点F ,将EDC ∆沿CD 翻折得E DC '∆,射线DE '交直线BM 于点G .(1)如图1,当CD EF ⊥时,求BF 的长.(2)如图2,当点G 在点F 的上方时,求证:~BDF BGD ∆∆.(3)如果DFG ∆的面积为AE 的长.【解析】解:(1)90ACB ∠=︒,60BAC ∠=90906030ABC BAC ∴∠=︒-∠=︒-︒=︒, ∴在Rt ACB ∆中:28AB AC ==,CD 是边AB 上的中线,142CD BD AD AB ∴====, ADC ∴∆是等边三角形,4AC AD CD ∴===,60ECD ∠=︒CD EF ⊥, 90906030CED ECD ∴∠=︒-∠=︒-︒=︒,∴在Rt EDC ∆中:28CE CD ==,844AE CE AC ∴=-=-=,//BM AC ,FBD EAD ∴∠=∠,∴在FBD ∆和EAD ∆中,FBD EAD BD AD BDF ADE ∠=∠⎧⎪=⎨⎪∠=∠⎩,,4BF AE ∴==,故答案为:4.(2)由(1)可知:ADC ∆为等边三角形,60ACD ADC ∴∠=∠=︒180120BDC ADC ∴∠=︒-∠=︒, EDC ∆沿CD 翻折得EDC '∆,60E CD ECD ACD '∴∠=∠=∠=︒,AED CE D '∠=∠, 60120180E CD BDC '∴∠+∠=︒+︒=︒,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
①1×12=1-12 ②2×23=2-23 ③3×34=3-34④4×45=4-45 ……专题复习 归纳与猜想归纳与猜想问题指的是给出一定条件(可以是有规律的算式、图形或图表),让学生认真分析,仔细观察,综合归纳,大胆猜想,得出结论,进而加以验证的数学探索题。
其解题思维过程是:从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论,这类问题有利于培养学生思维的深刻性和创造性。
一、知识网络图二、基础知识整理猜想规律型的问题难度相对较小,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。
其中蕴含着“特殊——一般——特殊”的常用模式,体现了总结归纳的数学思想,这也正是人类认识新生事物的一般过程。
相对而言,猜想结论型问题的难度较大些,具体题目往往是直观猜想与科学论证、具体应用的结合,解题的方法也更为灵活多样:计算、验证、类比、比较、测量、绘图、移动等等,都能用到。
由于猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养创造性思维能力,所以备受命题专家的青睐,逐步成为中考的又一热点。
★ 范例精讲【归纳与猜想】例1观察右面的图形(每个正方形的边长均为1)和相应等式,探究其中的规律:⑴写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示:⑵猜想并写出与第n 个图形相对应的等式。
解:⑴5×56=5-56⑵11+-=+⨯n nn n n n 。
例2〖归纳猜想型〗将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一片又按同样的方法剪成四小片,再将其中的一小片正方形纸片剪成四片,如此循环进行下去,将结果填在下表中,并解答所提出的问题:⑴如果能剪100次,共有多少个正方形?据上表分析,你能发现什么规律? ⑵如果剪n 次共有A n 个正方形,试用含n 、A n 的等式表示这个规律; ⑶利用上面得到的规律,要剪得22个正方形,共需剪几次? ⑷能否将正方形剪成2004个小正方形?为什么?⑸若原正方形的边长为1,设a n 表示第n 次所剪的正方形的边长,试用含n 的式子表示a n ;⑹试猜想a 1+a 2+a 3+…+a n 与原正方形边长的关系,并画图示意这种关系.解:⑴100×3+1=301,规律是:本次剪完后得到的小正方形的个数比上次剪完后得到的小正方形的个数多3个;⑵A n =3n +1;⑶若A n =22,则3n +1=22,∴n =7,故需剪7次; ⑷若A n =2004,则3n +1=2004,此方程无自然数解, ∴不能将原正方形剪成2004个小正方形;⑸a n =12n ;⑹a 1=12<1,a 1+a 2=12+14=34<1,a 1+a 2+a 3=12+14+18=78<1,……从而猜想到:a 1+a 2+a 3+…+a n <1.直观的几何意义如图所示。
例3下图中,图⑴是一个扇形AOB ,将其作如下划分:第一次划分:如图⑵所示,以OA 的一半OA 1为半径画弧,再作∠AOB 的平分线,得到扇形的总数为6个,分别为:扇形AOB 、扇形AOC 、扇形COB 、扇形A 1OB 1、扇形A 1OC 1、扇形C 1OB 1;1a 1 a 2 a 3第二次划分:如图⑶所示,在扇形C 1OB 1中,按上述划分方式继续划分,可以得到扇形的总数为11个;第三次划分:如图⑷所示;……依次划分下去.2005个?为什么? 解:由5n +1=2005,得n =20045,∵n 不是整数,∴不可能。
优化训练1. 如图,细心观察图形,认真分析各式,然后解答问题:(1)2+1=2 S 1=12 (2)2+1=3 S 2=22 (3)2+1=4 S 3=32⑴请用含有n (n 是正整数)的等式表示上述变化规律; ⑵推算出OA 10的长;⑶求出S 12+S 22+S 32+…+S 102的值. 解:⑴(n )2+1=n +1,S n =n2;⑵∵OA 1=1,OA 2=2,OA 3=3,…,∴OA 10=10;A 6 … A 5 1 1A 4 1 A 3 A 2 1 A 111 O S 1 S2 S3 S4 S 5图⑷第三次划分 图⑴ A B O 图⑵第一次划分 A B O A 1 C B 1 C 1 图⑶第二次划分 A B OA 1 CB 1C 1⑶S 12+S 22+S 32+…+S 102=14(1+2+3+…+10)=554.2. 观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放,记第n 个图中的小黑点的个数为y .解答下列问题:= 57 ;⑶你能猜想y 与n 之间的关系式吗?你是怎么得到的,请与同伴交流;⑷下边给出一种研究方法。
请你根据上表中的数据,把n 作为横坐标,把y 作为纵坐标,在平面直角坐标系中描出相应的各点(n ,y ).猜一猜上述各点是否在某一函数的图象上?如果在某一函数的图象上,请你求出该函数的关系式。
解:⑴观察y 这一行,后面的数比前一个数依次增大2,4,6,…,2(n -1),所以当n =5时,y =13+2(5-1)=21;⑵由⑴知,当n =8时,y =21+10+12+14=57; ⑶略;⑷根据点的排列情况,在一条曲线上,猜想是抛物线,图象略。
设二次函数的解析式为y =ax 2+bx +c ,由(1,1)、(2,3)、(3,7)三点可得,⎩⎪⎨⎪⎧a +b +c =14a +2b +c =39a +3b +c =7,解得⎩⎪⎨⎪⎧a =1b =-1c =1,故所求的函数关系式为y =x 2-x +1. 反思:问题通过从“特殊”到“一般”的归纳过程来探究规律结果,先在坐标系中描出各点的位置,再依据点的位置特征判断变量之间可能的关系,最后根据猜想求解,这正是“课标”倡导的思想。
3. 一个自然数a 恰等于另一个自然数b 的平方,则称自然数a 为完全平方数,如64=82,64就是一个完全平方数.若a =20022+20022×20032+20032,求证:a 是一个完全平方数,并写出a 的平方根. 解:先从较小的数字探索:a 1=12+12×22+22=32=(1×2+1)2,a 2=22+22×32+32=72=(2×3+1)2,a 3=32+32×42+42=132=(3×4+1)2,a 4=42+42×52+52=212=(4×5+1)2,…图1 图2 图3 图4 图5⑴ ⑵⑶⑷于是猜想:a =20022+20022×20032+20032=(2002×2003+1)2=(4010007)2, 证明采用配方法(略).推广到一般,若n 是正整数,则a =n 2+n 2(n +1)2+(n +1)2是一个完全平方数[n (n +1)+1]2.解题策略:猜想是数学中重要的思想和方法之一。
较大的数字问题可仿较小数字问题来处理,实现了以简驭繁的策略。
在解题时,如果你不能解决所提出的问题,可先解决“一个与此有关的问题”。
你能不能想出一个更容易着手的问题?一个更普遍的问题?一个更特殊的问题?你能否解决这个问题的一部分?这就是数学家解题时的“绝招”。
4. 下列是由同型号黑白两种颜色的正三角形瓷砖按一定规律铺设的图形.仔细观察图形可知:图①有1块黑色的瓷砖,可表示为;21)11(1⨯+=图②有3块黑色的瓷砖,可表示为;22)21(21⨯+=+ 图③有6块黑色的瓷砖,可表示为23)31(321⨯+=++ 实践与探索:⑴请在图④的虚线框内画出第4个图形;(只须画出草图) ⑵第10个图形有 块黑色的瓷砖;(直接填写结果) ⑶第n 个图形有 块黑色的瓷砖.(用含n 的代数式表示)解:⑴如右图;⑵55,12n (n +1)(n 为正整数);5. 【归纳猜想】观察下列图形,如图所示,若第1个图形中的空白面积为1,第2个图形中非阴影部分的面积为34,第3个图形中非阴影部分的面积为916,第4个图形中非阴影部分的面积为2764,……探究:第n 个图形中非阴影部分的面积为多少(用字母n表示)?图① 图② 图③ 图④解:当n =1时,S =1;当n =2时,S =34=(34)2-1;当n =3时,S =916=(34)3-1;当n =4时,S =2764=(34)4-1;所以,第n 个图形中非阴影部分的面积为(34)n -1;点拨:认真分析n 、S 与34三者之间存在的内在关系探求其规律。
6. 随着信息技术的高速发展,电话进入了千家万户,据调查某校初三⑴班的同学家都装上了电话,暑假期间全班每两个同学都通过一次电话,如果该班有56名同学,那么同学们之间共通了多少次电话?为解决该问题,我们可把该班人数n 与通电话次数s 间的关系用下列模型来表示:⑴若把n 作为点的横坐标,s 作为纵坐标,根据上述模型中的数据,在给出的平面直角坐标系中,描出相应各点,并用平滑的曲线连接起来; ⑵根据图中各点的排列规律,猜一猜上述各点会不会在某一函数的图象上?如果在,求出该函数的解析式; ⑶根据⑵中得出的函数关系式,求该班56名同学间共通了多少次电话. 解:⑴略;⑵根据图中各点的排列规律,猜想各点可能在一个二次函数的图象上,用待定系数法可求得s =21n 2-21n ; ⑶当n =56时,s =1540; 7. 在数学活动中,小明为了求2341111122222n ++++⋅⋅⋅+的值(结果用n 表示),设计如图1所示的几何图形。
⑴请你利用这个几何图形, 求2341111122222n ++++⋅⋅⋅+的值为 ; ⑵请你利用图2,再设计一个能求图1 图2122123124122341111122222n ++++⋅⋅⋅+的值的几何图形。
解:(1)112n -;(2)如图1或如图2或如图3或如图4等,图形正确。
8. 如图,正方形表示一张纸片,根据要求需多次分割,把它分割成若干个直角三角形.操作过程如下:第一次分割,将正方形纸片分成4个全等的直角三角形,第二次分割将上次得到的直角三角形中一个再分成4个全等的直角三角形;以后按第二次分割的作法进行下去. ⑴请你设计出两种符合题意的分割方案图;⑵设正方形的边长为a ,请你就其中一种方案通过操作和观察将第二、⑶在条件⑵下,请你猜想:分割所得的最小直角三角形面积S 与分割次数n 有什么关系?用数学表达式表示出来. 解:⑴现提供如下三种分割方案:⑵每次分割后得到的最小直角三角形的面积都是上一次最小直角三角形面积的41,所以当n =2时,S 2=41×41a 2=161a 2;当n =3时,S 3=41S 2=641a 2;⑶当分割次数为n 时,S n =n 41a 2(n ≥1,且n 为正整数).9. 下面的图形是由边长为1的正方形按照某种规律排列而组成的.12121212212212212212312312312312412412⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⑴观察图形,填写下表:图形①②③正方形的个数8 13 18图形的周长18 28 38个图形中,正方形的个数为 5n+3 ,周长为 10n+8 (都用含n的代数式表示);⑶这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系式为y=2x+2 .10.定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形。
