MATLAB超松弛迭代法求解接地金属槽内电位分布

合集下载

matlab逐次超松弛迭代法

matlab逐次超松弛迭代法
逐次超松弛迭代法（Gauss-Seidel迭代法）是一种用于解线性方程组的迭代方法，通常用于求解大型稀疏线性方程组。

在MATLAB 中，可以使用该方法来解决线性方程组的数值解。

首先，让我们来了解一下逐次超松弛迭代法的基本原理。

该方法是基于迭代的思想，通过不断迭代更新解向量的各个分量，直到满足一定的收敛条件为止。

具体步骤如下：
1. 首先，需要将线性方程组表示为矩阵形式 Ax = b，其中A 是系数矩阵，x是未知向量，b是常数向量。

2. 然后，将系数矩阵A分解为下三角矩阵L、对角矩阵D和上三角矩阵U，即A = L + D + U。

3. 接下来，可以根据逐次超松弛迭代法的迭代公式来更新解向量x的各个分量，直到满足一定的精度要求或者迭代次数达到指定的值为止。

在MATLAB中，可以通过编写相应的代码来实现逐次超松弛迭代
法。

具体步骤如下：
1. 首先，需要编写一个函数来实现逐次超松弛迭代法的迭代过程，可以使用for循环来进行迭代更新解向量的各个分量。

2. 其次，需要编写主程序来调用该函数，并传入系数矩阵A、常数向量b以及迭代的初始解向量作为输入参数。

3. 最后，可以设置迭代的终止条件，例如迭代次数的最大值或者解的精度要求，以及初始解向量的初值。

需要注意的是，在实际应用中，逐次超松弛迭代法的收敛性和稳定性需要进行分析和验证，以确保得到正确的数值解。

此外，还需要注意选择合适的松弛因子来加速收敛速度。

总的来说，逐次超松弛迭代法是一种常用的求解线性方程组的数值方法，在MATLAB中可以通过编写相应的代码来实现该方法，并得到线性方程组的数值解。

典型静电场场图的解析解(含Matlab程序)

么 z 平面上的复位函数就可以写成
w( z ) F [ ( z )]
U 0 ( z )

(18)
遗憾的是， ( z ) 不能用初等函数表示。幸好，由z
d

(1 e ) 可以得到 x d
(a)
平面上的带状区域变换到 z 平面上的平行板边缘

d
(1 u eu cos v) (19) (v e sin v)
w( z ) ( z ,0)
(2) 从 w 分离出虚部，即得到通量函数。然后可借助 Matlab 或 Mathematica 等软件分别画出和的等值线，即得到等位线和电场线。以下通过几个例子来详细说明。
1. 二维问题
复变函数法是分析二维电磁场的有力工具[5]。以复变量 z x jy 表示平面上的点 ( x, y ) ，设以 z 为变量的复函数
典型静电场场图的解析解
陈德智（dzhchen@）强电磁工程与新技术国家重点实验室（华中科技大学），湖北武汉 430074
摘要：场图是帮助理解电磁场概念、观察场的分布特点和寻求电磁场问题解决方案的有力工具，在电磁场教学与科研中都有重要作用。本文讨论典型静电场问题的场图绘制方法，包括平行平面场（二维场）和可以归结为点电荷相互作用的三维静电场两种类型。对于二维静电场，使用复位函数，其实部与虚部分别对应电位函数和通量函数，两个函数的等值线相互正交，分别表示等位线和电场线。文中介绍了由电位求取复位函数并利用复位函数作图的方法，给出了使用 Matlab 语言的绘图程序。对于由一组共线的点电荷产生的电场，根据其电场线方程，利用电场线起始角可以方便地控制电场线的空间分布， Matlab 实现也非常容易。本文给出的方法能够方便地精确绘制几乎所有常见的典型静电场问题场图，对于电磁场的教学与科研有一定参考价值。因为简单，这些方法也显得别有趣，笔者在课堂上介绍这些内容时，很大地激发了学生的学习热情。关键词：电磁场；场图；复位函数；点电荷；Matlab

重金属地空间分布地matlab程序

27.232 14.482 58.06
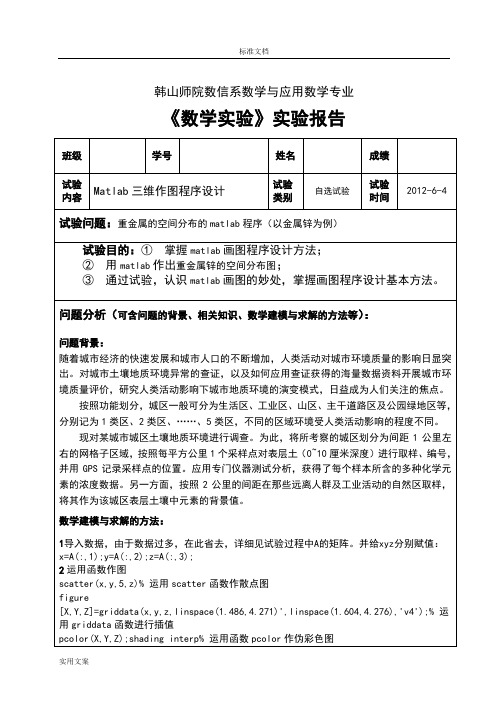
24.58 13.319 69.90
24.153 12.45 87.65
22.965 13.535 99.49
23.198 13.523 142.86
24.685 14.278 61.43
28.654 8.755 53.06
24.003 15.286 51.53
21.684 13.101 47.55
22.193 12.185 229.80
17.079 5.894 34.39
15.255 5.11 54.29
15.007 5.535 76.53
3.518 2.571 133.98
3.469 2.308 76.12
3.762 2.17 127.35
3.927 2.11 154.49
16.032 3.061 94.08
15.801 3.966 104.18
15.087 3.512 37.14
16.872 2.798 101.73
17.734 3.629 91.02
16.823 4.207 115.20
17.008 4.775 59.49
17.203 6.218 81.73
17.005 7.212 70.51
3.573 6.213 429.29
4.741 6.434 186.22
5.375 8.643 46.84
5.635 7.965 311.02
5.394 8.631 182.65
5.291 7.349 253.16
4.742 7.293 175.71
4.948 7.293 1626.02
5.567 6.782 615.10
16.947 7.487 104.90

超松弛迭代法求解接地金属槽内电位分布

实验一用超松弛迭代法求解接地金属槽内电位分布1、实验内容：试用超松弛迭代法求解接地金属槽内电位的分布。

已知：，给定边值如图所示。

给定初值：误差范围：计算迭代次数，分布。

一.实验思路由边界条件用泊松方程的五点差分格式求得中央点的点位。

再以所得点及边界再次利用泊松方程的五点差分格式求出另四个点，依照此方法求出其余点的电位分布。

用最佳收敛因子的经验公式计算收敛因子。

利用超松弛迭代法进行差分方程的求解，当遇到边界是采用边界值或者边界差分格式。

直到所有节点电位满足误差条件。

二．实验设计原理：有限差分法有限差分法（Finite Differential Method）是基于差分原理的一种数值计算法。

其基本思想：将场域离散为许多小网格，应用差分原理，将求解连续函数?的泊松方程的问题换为求解网格节点上?的差分方程组的问题。

编程时将边值编入到程序中，这样可以省略输入，从而直接输入迭代因子进行求解，可以减少编程的难度。

迭代时所用公式是和书上一样，为a[i][j]=b[i][j]+w/4*(b[i+1][j]+b[i][j+1]+a[i][j-1]+a[i-1][j]-4*b[i][j]);其中a代表k+1，而b代表k。

三、程序运行界面及结果四．源程序代码#include<iostream>#include<math.h>#include<iomanip>using namespace std;classoverrei //over-relaxation iterative method {private:intm,n;doublex,e;double **p,**q;public:int k;overrei(int m0,int n0,double e0) {inti;e=e0;k=0;m=m0;n=n0;p=new double *[m];for(i=0;i<m;i++)p[i]=new double[n];q=new double *[m];//迭代因子求解for(i=0;i<m;i++)q[i]=new double[n];if(m==n)x=2/(1+sin(3.141592654/(m-1)));elsex=2-3.141592654*sqrt(2)*sqrt(1/((m-1)*(m-1))+1/((n-1)*(n-1))); cout<<"最佳收敛因子:"<<x<<endl;}void Initialization(); //赋边界条件void Cal(); //计算void Diedai(); //迭代函数void Show(); //输出部分};void overrei::Initialization() //赋边界条件{inti,j;for(i=0;i<m;i++) //边界条件for(j=0;j<n;j++){if(i==0){p[i][j]=100;q[i][j]=100;}else{p[i][j]=0;q[i][j]=0;}}cout<<"初始点位:"<<endl;Show();}void overrei::Cal() //计算{inti,j;int c=1;while(1){c=1;for(i=0;i<m;i++){for(j=0;j<n;j++){if((p[i][j]-q[i][j])>e||(q[i][j]-p[i][j])>e) //相邻两次迭代误差是否小于1e-5{c=0;break;}}if(c==0) break;}if(c==1 && k!=0) break;Diedai();}}void overrei::Diedai() //迭代函数{inti,j;double y=x/4;if(k%2){for(i=1;i<m-1;i++)for(j=1;j<n-1;j++){q[i][j]=p[i][j]+y*(q[i-1][j]+q[i][j-1]+p[i+1][j]+p[i][j+1]-4*p[i][j]);}}else{for(i=1;i<m-1;i++)for(j=1;j<n-1;j++){p[i][j]=q[i][j]+y*(p[i-1][j]+p[i][j-1]+q[i+1][j]+q[i][j+1]-4*q[i][j]);}}k++;}void overrei::Show() //输出部分{inti,j;for(i=0;i<m;i++){for(j=0;j<n;j++){cout<<setw(12)<<setprecision(6)<<fixed<<q[i][j]<<ends;}cout<<endl;}}int main(){cout<<" **************************************"<<endl; cout<<" 超松弛迭代法求解接地金属槽内电位的分布"<<endl; cout<<" **************************************"<<endl; overrei A(5,5,1e-5);A.Initialization();A.Cal();cout<<"电位分布:"<<endl;A.Show();cout<<"迭代次数:"<<A.k<<endl;return 0;}实验二按对称场差分格式求解电位的分布一.实验思路只计算一半的区域，对另一半进行对称性计算，减小计算量。

逐次超松弛迭代法 matlab -回复

逐次超松弛迭代法matlab -回复什么是逐次超松弛迭代法（Gauss-Seidel）？为什么需要这种迭代方法？如何在MATLAB中实现逐次超松弛迭代法？有哪些注意事项和应用场景？我们将逐一解答这些问题。

逐次超松弛迭代法，也被称为Gauss-Seidel迭代法，是一种数值计算方法，用于解决线性方程组。

它采用逐步逼近的方式求解，相较于直接求解的方法，计算上更加简化。

为什么需要逐次超松弛迭代法呢？当涉及到解决大型线性方程组时，直接解法可能会面临计算量大、迭代时间长的问题。

而逐次超松弛迭代法通过逼近的方式，可以将线性方程组划分为多个小规模问题，分步进行迭代，有效降低了计算时间。

在MATLAB中，我们可以使用以下步骤实现逐次超松弛迭代法：1. 构建线性方程组表达式：首先，将线性方程组转换为矩阵形式Ax=b，其中A为系数矩阵，x为未知数向量，b为常数向量。

2. 初始化参数：设定初始值x0，并指定迭代的最大次数N和误差控制值epsilon。

3. 迭代计算：循环进行迭代计算直到满足结束条件，具体步骤如下：a. 根据逐次超松弛迭代法公式，更新x的值：x(i+1) = (1 - w) * x(i) + (w / A(i,i)) * (b(i) - A(i,:)*x(i) + A(i,i)*x(i))其中，w(w > 0)是松弛因子，可以理解成迭代的步长。

通常情况下，根据实际问题的特点和经验选择合适的w值。

b. 判断迭代是否终止：计算当前迭代的相对误差，如果小于设定的误差控制值epsilon，则停止迭代。

c. 更新迭代次数，并检查是否达到最大迭代次数N，如果达到则停止迭代。

4. 输出结果：返回迭代最终结果x，作为线性方程组的解。

在使用逐次超松弛迭代法时，需要注意以下几点：1. 松弛因子w的选择：选择合适的松弛因子w对收敛速度和精度有较大影响。

如果选择不当，可能会导致迭代结果不收敛或者收敛速度很慢。

通常情况下，可以通过试验和调整，选择使得迭代过程尽快收敛的合适值。

Matlab-求解金属槽槽内电位分布---副本培训讲学

M a t l a b-求解金属槽槽内电位分布---副本Matlab 求解金属槽槽内电位分布摘要运用有限差分法将场域离散为许多小网格，将求解连续函数ϕ的泊松方程的问题换为求解网格节点上ϕ的差分方程组的问题。

用matlab程序计算出槽内电位分布的结果。

通过数值解和精确解的比较来验证有限差分法的可行性。

关键词:有限差分法; Matlab；金属槽槽内电位Solving the metal slots potential with MatlabAbstract:U sing the finite difference method (FDM)field is discreted into many small grid, transform ing the problem solving poisson equation with continuous function ϕ for solving the differential equations of grid node ϕ. We use Matlab program to calculate the potential distribution in slot results. The values got from these two methods are compared, which would be a validation of the feasibility of the Finite Difference Method.1 引言如图1所示，尺寸为a×a的正方形金属导体槽三面接地，上方是一块密实的但与之绝缘的金属盖板，其电位100Vϕ=，求槽内电位的分布情况。

这是二维静态场域的边值问题，在直角坐标系中，接地导体矩形槽中的电位函数p满足拉普拉斯方程2222x yϕϕ∂∂+=∂∂。

Xaa图1 正方形金属槽其边界条件满足第一类边界条件问题0(x,y)0x ϕ== (x,y)0x aϕ==(x,y)0y ϕ== (x,y)100y aϕ==我们由此可求出矩形导体槽内电位的分布数值解．将金属槽内场域D 用正方形网格进行粗略划分，其网格节点分布如图2所示网格间距为h=a/4,各边的节点数为L+1=5.234512345图2 网格划分2 求解2.1数值解求解过程由于本文采用的是超松弛迭代法的差分方程形式，现给出公式(n 1)(n)(n)(n)(n 1)(n 1)2(n),,1,,11,,1,,(4)4i ji ji ji j i ji j i j i jw h f ϕϕϕϕϕϕϕ+++++--=++++--（2.1）进行迭代，因为满足拉普拉斯方程故 f=0。

有限差分法计算金属槽内电位分布

班级：物理08-2B 姓名：胡艳学号：08070201010有限差分法计算金属槽内电位分布一、选题依据求解电位分布问题是物理学中最常见的问题之一，采用有限差分法解决此类问题是十分有效的。

差分方程确定之后，一般选用迭代法求解，这是由于方程组系数矩阵中有大量元素为零，并且系数矩阵形成比较简单，有规律和重复。

在迭代过程中常常可以一边形成系数矩阵一边计算，以节省内存，因而迭代法比直接法更常用。

迭代法中又以超松弛迭代法最常用，以下给出超松弛迭代方法的公式。

对于二维场泊松方程等距剖分差分格式公式为()()()()()()()⎪⎪⎭⎫ ⎝⎛Φ--+Φ+-+Φ++Φ++Φ+Φ=+Φj i n j i n j i n j i n j i n ji n ji n ,41,1,111,,14,,1α（2.67）式中α称为加速收敛因子或超松弛因子，它的数值决定超松弛程度，影响迭代解收敛的速度。

α取值范围是1 ≤ α <2 （2.68）加速收敛因子α取值因问题而异，对于第一类边值问题，若一方形场域由正方形网格划分，每边的节点数为（n+1），则加速收敛因子α可按下式计算：nπαs i n12+=（2.69）若一矩形场域由边长为h 的正方形网格划分为mh 和nh ，且m 和n 都很大（一般都要大于15），那么加速收敛因子α为n m 221122+-=πα （2.70）一般情况下，α的最佳值只能是凭经验选取。

对于其他形状的场域，也可用等效矩形面积的处理方法，即得出等效矩形面积后，再用式（2.70）求出最佳的α。

下面我们来看一个计算电位分布的实例。

二、处理过程实例：有一长接地金属槽，横截面积如图2.15所示，其侧壁与底面电位均为零，顶盖电位为100V ，求槽内电位分布。

分析：对于此槽中间区段电位分布，可理想化为二维问题。

选定直角坐标系，槽内电位函数Φ满足拉普拉斯方程，构成一类边值问题。

2222=∂Φ∂+∂Φ∂yxVay a x 1006.0,0=Φ=<<Vay a x y a x ay x 06.00,0,06.00,0=Φ=Φ=Φ≤==≤≤≤=<<按有限差分法计算步骤，解题过程如下。

工程电磁场C++编程作业-一、用超松弛迭代法求解接地金属槽内电位的分布二、按对称场差分格式求解电位的分布

工程电磁场实验报告——C++编程课题一、用超松弛迭代法求解接地金属槽内电位的分布二、按对称场差分格式求解电位的分布一、用超松弛迭代法求解接地金属槽内电位的分布一、实验原理二、程序框图：三、实验内容：1、用超松弛迭代法求解接地金属槽内点位分布1）内容及要求：2）实验思路：由超松弛迭代法，将网格分成5*5列，边界点正好都是网格的节点，对所有的节点进行编号，并记录节点的坐标位置，并用一个二维数组进行表示u1[5][5],此数组表示的是迭代后的值。

考虑到迭代前后的数值不一样，再用一个二维数组表示迭代之前的数值u2[5][5]。

运用C++的知识在计算机上将边界值和内节点进行赋值，即将节点离散化。

然后开始迭代。

迭代开始之前将另一个数组b赋值，用数组a给其赋值，表示迭代之前的值，好用于后面精度的比较。

开始进行迭代时，根据超松弛公式将迭代方程编写输入。

每次迭代结束后将数组a和数组b对应的值进行比较，即是精度的计算。

如果误差大于所规定的误差0.00001，将a的值赋给b，然后继续进行迭代。

直到当迭代前后数值误差小于所规定的误差时停止迭代。

并比较迭代因子的大小对收敛次数的影响，选取最烧收敛次数的迭代因子作为实验最后的输出结果。

最后输出最适合迭代因子、迭代的次数和迭代后各点的电位值。

3）程序如下：//********用超松弛迭代法求解接地金属槽内电位的分布********#include<iostream.h>#include<math.h>#include<iomanip.h>Void main(){double u1[5][5],u2[5][5];int flag=1000,i,j,e,n;double a,d;//a最佳加速收敛因子for(i=0;i<5;i++)for(j=0;j<5;j++){if(i==0)u1[i][j]=100;else u1[i][j]=0;}cout<<"迭代前各电位点上的初始值:"<<endl;for(i=0;i<5;i++){for(j=0;j<5;j++){cout<<u1[i][j]<<" ";//输出迭代初值}cout<<endl;}cout<<"\n";for(d=1;d<2;d+=0.01)//找取迭代次数最少的加速收敛因子{n=0;for(j=0;j<5;j++){u1[0][j]=100;}for(i=1;i<5;i++)for(j=0;j<5;j++){u1[i][j]=0;}do//迭代x次{for(i=0;i<5;i++){for(j=0;j<5;j++){u2[i][j]=u1[i][j];}}for(i=1;i<4;i++)for(j=1;j<4;j++){u1[i][j]=u2[i][j]+(d/4)*(u2[i+1][j]+u2[i][j+1]+u1[i-1][j]+u1[i][j-1]-4*u2[i][j]);}for(i=1;i<4;i++)//判断精度{{for(j=1;j<4;j++){if(fabs(u1[i][j]-u2[i][j])>1e-5){e=1; break; }else e=0; }if(e==1) break; }}n++;//迭代次数}while(e);if(n<flag) {flag=n; a=d; }}cout<<"收敛因子:"<<a<<endl;cout<<endl;cout<<"迭代次数:"<<flag<<endl;cout<<endl;cout<<"各节点上最终电位近似值:"<<endl;for(i=0;i<5;i++){for(j=0;j<5;j++){cout<<setiosflags(ios::fixed)<<setprecision(5)<<setw(8)<<u1[i][j]<<" ";//对齐输出}cout<<endl; }cout<<endl; }4）输出结果：5）总结：最佳收敛因子：1.18此时的最少迭代次数：102、按对称场差分格式求解电位的分布1）内容及要求：2）实验思路：类似与第一题的思路，但只计算一半的区域，对另一半进行对称性计算，减小计算量。

电磁场仿真实验-用超松弛法求二维静电场域的电位分布

姓名：梁鸿宇学号：19 班级：10通信实验目的:通过用MATLAB等软件编程计算电磁场问题，掌握有限差分法的基本思想，掌握电磁场数值计算的基本思想和方法，掌握MATLAB等软件编程技巧，学会用MATLAB等软件应用于有限差分法的数值解。

实验内容：用MATLAB等软件编程计算电磁场问题，给出有关波形和图表。

分析数值解和解析解的优缺点。

题目如下：实验程序与结果分析：程序（MATLAB）%电位函数为φ(x,y) ,边界条件φ(x,y)=0(x=0);φ(x,y)=50(y=0);% φ(x,y)=100(x=a);φ(x,y)=100(y=a);hx=11;hy=11; %设置网格节点数v1=ones(hy,hx); %设置行列二维数组m=10;n=10; %横纵向网格数%上下两行的Dirichlet条件边界值:v1(1,:)=ones(1,hx)*50;v1(hy,:)=ones(1,hx)*100;%左右两列的Dirichlet条件边界值:for i=1:hyv1(i,1)=0;v1(i,hx)=100;end%计算松弛因子t1=(cos(pi/m)+cos(pi/n))/2;w=2/(1+sqrt(1-t1^2));v2=v1;maxt=1;t=0; %初始化k=0while(maxt>1e-6) %由V1迭代V2.迭代精度为k=k+1 %计算迭代次数maxt=0;for i=2:hy-1 %从2到hy-1行循环for j=2:hx-1 %从2到hx-1列循环v2(i,j)=v1(i,j)+(v1(i,j+1)+v1(i+1,j)+v2(i-1,j)+v2(i,j-1)-4*v1(i,j))*w/4;% 拉普拉斯方程差分式t=abs(v2(i,j)-v1(i,j));if(t>maxt) maxt=t;endendendv1=v2endcontour(v2,20) %画等电位线图hold onx=1:1:hx;y=1:1:hy[xx,yy]=meshgrid(x,y); %形成栅格[Ex,Ey]=gradient(v2,,; %计算梯度AE=sqrt(Ex.^2+Ey.^2);Ex=Ex./AE;Ey=Ey./AE; % 场强归一化，使箭头等长quiver(xx,yy,Ex,Ey, %根据梯度数据画箭头axis([,hx+,-2,13]) %设置坐标边框plot([1,1,hx,hx,1],[1,hy,hy,1,1],'k') %画导体边框text(hx/,hy+,'100V','fontsize',11); %上标注text(hx/2,,'50V','fontsize',11); %下标注text,hy/2,'0V','fontsize',11); %左标注text(hx+,hy/2,'100V','fontsize',11); %右标注hold offhx=11;hy=11;输出图形（MATLAB）总结和体会：这次仿真实验，是自己学习NATLAB的基本操作的，在了解这个全英版的软件之前，觉得很茫然。

逐次超松弛迭代法 matlab

逐次超松弛迭代法matlab什么是逐次超松弛迭代法？逐次超松弛迭代法（简称SOR）是一种用于数值解线性代数方程组的迭代方法。

它是对高斯-赛德尔迭代法的一种改进方法，能够加快迭代速度并增加收敛稳定性。

SOR迭代法的基本原理是在每一步迭代中引入一个超松弛因子，在更新解向量的同时，利用当前和先前的解向量信息，进行更快的收敛。

在MATLAB中，可以使用SOR迭代法来求解线性代数方程组。

在具体应用时，需要提供方程组的系数矩阵以及右侧的常数向量。

而在SOR迭代法中，还需要指定迭代的初始解向量、超松弛因子以及迭代的最大次数等参数。

首先，我们需要定义一个方程组的系数矩阵A和常数向量b。

在MATLAB 中，可以使用矩阵表示法来定义A和b。

例如，假设我们有一个3x3的方程组，可以使用以下代码来定义A和b：A = [2, -1, 0; -1, 2, -1; 0, -1, 2];b = [1; 2; 3];接下来，我们需要初始化一些迭代的参数，包括初始解向量x0、超松弛因子omega和迭代的最大次数max_iter。

其中，初始解向量x0可以选择一个任意的值，omega一般取值在0和2之间，max_iter可以根据需要设定一个足够大的值。

x0 = [0; 0; 0];omega = 1.2;max_iter = 100;然后，我们可以开始使用SOR迭代法来求解方程组。

在每一步迭代中，我们需要根据上一步的解向量计算当前的解向量，直到达到指定的迭代次数或者满足收敛条件为止。

x = x0;for k = 1:max_iterfor i = 1:length(b)x(i) = (1 - omega) * x(i) + (omega / A(i, i)) * (b(i) - A(i, [1:i-1, i+1:end]) * x([1:i-1, i+1:end]));end判断迭代是否收敛if norm(A * x - b) < 1e-6break;endend在迭代过程中，我们可以添加一些判断条件来判断迭代是否收敛，例如当方程的残差（两侧误差）小于某个指定的阈值时，可以认为方程组已经解出。

matlab逐次超松弛迭代法

matlab逐次超松弛迭代法
逐次超松弛迭代法（Gauss-Seidel Overrelaxation Method）
是一种用于求解线性方程组的数值方法，常用于解决大型稀疏矩阵
的方程组。

在MATLAB中，可以通过编写逐次超松弛迭代法的代码来
实现该算法。

首先，让我们回顾一下逐次超松弛迭代法的基本原理。

该方法
是基于迭代的思想，通过不断迭代计算得到线性方程组的近似解。

在每一次迭代中，通过更新当前解向量的各个分量来逐步逼近方程
组的精确解。

逐次超松弛迭代法引入了松弛因子，可以加速收敛速度。

在MATLAB中，可以使用以下步骤来实现逐次超松弛迭代法：
1. 首先，编写一个函数来表示线性方程组的系数矩阵和右侧向量。

这个函数可以接受系数矩阵、右侧向量和当前解向量作为输入，并返回更新后的解向量。

2. 接下来，编写主程序来调用这个函数，并设置迭代的终止条件。

可以选择设置最大迭代次数或者设定一个收敛精度作为终止条
件。

3. 在主程序中，使用一个循环来进行迭代计算，直到满足设定的终止条件为止。

在每一次迭代中，调用上述编写的函数来更新解向量。

4. 最后，输出得到的近似解向量作为结果。

需要注意的是，逐次超松弛迭代法的收敛性与松弛因子的选择有关，通常需要根据具体的线性方程组进行调整。

总之，在MATLAB中实现逐次超松弛迭代法需要编写系数矩阵和右侧向量的函数以及主程序来进行迭代计算，并且需要注意收敛性和松弛因子的选择。

希望这个回答能够帮助你更好地理解和实现逐次超松弛迭代法。

利用超松弛迭代法求解问题

利用超松弛迭代法求解问题在电场中，利用有限差分法求解场域中各个节点的点位。

其中求解差分方程组的解运用到了超松弛方法。

超松弛方法是高斯—塞德尔迭代法的变形。

它在迭代过程中，为了加速收敛，再把所得结果依次带入进行计算的同时，还使用把每一次迭代的变化量加权后再代入的方法。

运用超松弛迭代法求解下述问题：试用超松弛迭代法求解接地金属槽内的电位的分布。

已知：A=4CM,H=A\4=10CM给定边值：如图示；给定初值：Φ=0误差范围：E=10^-5计算：迭代次数N=？，Φ的分布。

分析：（1）、节点按从下到上，从左到右的顺序排列。

（2）、按高斯—塞德尔迭代公式进行迭代。

（3）、选择加速因子Α，且A在1到2之间。

以下为该题程序段：#INCLUDE <IOSTREAM.H>#INCLUDE<MATH.H>#INCLUDE<IOMANIP.H>BOOL SUCCESS(DOUBLE A[5][5][2], DOUBLE B) 构建函数其中DOUBLE A 代表记录数据前后两次的值。

{INT I,J;FOR (I=1;I<5;I++)FOR (J=1;J<5;J++) 依次对定义数组赋值{IF ( FABS(A[I][J][1]-A[I][J][0]) > B ) 误差在题设范围内则返回值TRUERETURN TRUE;} 否则返回FALSE RETURN FALSE;}INT MAIN(){INT N,I,J;DOUBLE A[5][5][2];DOUBLE B;B=0.00005;DOUBLE S=1.21;WHILE (1){N=0;COUT<<"输入加速因子数值(1<= A < 2 ) "<<ENDL; 输入题设CIN>>S;FOR(I=0;I<5;I++)FOR(J=0;J<5;J++){A[I][J][0]=0;A[I][J][1]=0;}FOR (I=0;I<5;I++){A[I][4][0]=100;A[I][4][1]=100;}WHILE ( N==0 || SUCCESS(A,B)){FOR(I=1;I<4;I++)FOR(J=1;J<4;J++){A[I][J][0]=A[I][J][1];A[I][J][1]=A[I][J][1]+(A[I-1][J][1]+A[I+1][J][1]+A[I][J+1][1]+A[I][J-1][1] [I][J][1]*4)*S/4; 由高斯—塞德尔迭代公式写出相应公式。

项目训练二求二维金属槽内的点位分布

班级：通信13-2 姓名：闫振宇学号：1306030222 指导教师：徐维老师成绩：电子与信息工程学院信息与通信工程系项目训练二计算金属槽电位分布1. 实验目的和任务1) 利用有限差分法计算金属槽电位分布。

2) 学会并掌握利用MATLAB 软件计算求解电位分布问题。

3) 学会简单利用MATLAB 软件解决数学物理问题。

2. 实验容1) 利用MATLAB 编写一个计算机程序； 2) 以步距为40α的正方形网格离散化场域，然后应用有限差分法求电位ϕ的数值解；3) 求相邻两次迭代值得指定的最大允许误差小于105-的迭代收解。

4) 根据场分布的对称性，试以半场域为计算对象，并以步距40α将给半场域以正方形网格予以分割，然后应用有限差分法求电位ϕ的数值解；5) 分别取∂为n 个不同的值和最佳解∂o ，求电位ϕ的数值解，以此分析加速收敛因子的作用，从迭代收敛时的迭代次数和最终数值解这两方向总结自己的看法；6) 用计算机描绘等位线的分布；7) 取中心点)2,2(ba p 处的电位的精确值与数值解进行比较，说明误差围。

3. 实验原理有限差分法原理：有限差分法的基本思想是把连续的定解区域用有限个离散点构成的网格来代替，这些离散点称作网格的节点；把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似；把原方程和定解条件中的微商用差商来近似，积分用积分和来近似。

于是原微分方程和定解条件就近似地代之以代数方程组，即有限差分方程组，解此方程组就可以得到原问题在离散点上的近似解。

差分表达式：（有限差分方程）在x0y 平面把所求解的区域划分成若干的小正方形格子，每个格子的边长都为h ，假设某顶点的0上的电位是ϕ0，周围四个顶点的电位分别为ϕ1，ϕ2，ϕ3和ϕ4。

将这几点的电位用泰勒级数展开，化简，近似可得：)(414321ϕϕϕϕϕ+++=上式表明，任一点的电位等于它周围四个点电位的平均值。

图3-1 差分网格差分方程的数值解法:平面有多少个节点，就能得到多少个差分方程，当这些节点数目较大时，使用迭代法求解差分方程组比较方便。

基于matlab的电磁场分析

1.基于matlab－PDE Toolbox的泊松（拉普拉斯）方程求解在二维电磁场的有限元法计算中，用矩阵方程编制的计算程序长、大，而又复杂，且输入数据要化费很大的劳动。

而MATLAB是一种以矩阵运算为基础的交互式语言，它是采用有限元法来求解偏微分方程的。

因此在计算中，我们选用MATLAB提供的一个用户图形界面（GUI）的偏微分方程工具箱（PDE Toolbox）进行数值求解，采用的是三角形网格自动剖分。

下面举例说明。

【例1－1】横截面为矩形的无限长槽由3块接地导体板构成，如图3－3所示，槽的盖板接直流电压100V，求矩形槽的电位分布。

解：这是二维平面场问题。

由于电位函数和电场强度之间关系为利用麦克斯韦方程和关系式，得到泊松方程式中，为介电常数，为体电荷密度。

由于所求区域内体电荷密度，得到拉普拉斯方程：其边界满足狄里赫利（Didchlet）条件：，，本题运用MATLAB的偏微分方程工具箱（PDE Toolbox）进行数值求解。

在命令窗口中输入命令pdetool，打开PDE图形用户界面，计算步骤为：（1）网格设置：选择菜单Options下的Grid和Grid Spacing…，将X-axis linear Spacings设置为［-1.5：0.2：1.5］，Y-axis linear Spacings取Auto。

（2）区域设置：选择菜单Draw下的Rectangle／Square或按，画矩形。

（3）应用模式设置：在工具条中单击Generic Scalar下拉列表框，选Electrostatics（静电学）应用模式。

（4）输入边界条件：进入Boundary Mode或按，输入：1、左边界：狄里赫利（Diriehlet）条件：h＝1，r＝0。

2、右边界：狄里赫利（Dirichlet）条件：h＝1，r＝0。

3、上边界：狄里赫利（Dirichlet）条件：h＝1，r＝100。

4、下边界：狄里赫利（Dirichlet）条件：h＝1，r＝0。

项目训练二求二维金属槽内的点位分布

0 1 2 3 4
将这几点的电位用泰勒级数展开，化简，近似可得：
1

0

1 ( ) 2 3 4 4 1
上式表明，任一点的电位等于它周围四个点电位的平均值。
图 3-1 差分网格
差分方程的数值解法: 平面内有多少个节点，就能得到多少个差分方程，当这些节点数目较大时，使用迭代法求解差分方程组比较方便。 a. 简单迭代法：用迭代法解二维电位分布时，将包含边界在内的节点均以下标（i，j）表示，i，j 分别表示沿 x，y 方向的标点。次序是 x 方向从左到右，y 方向从上到下，我们用上标 n 表示某点电位的第 n 次的迭代值。下式得出点（i，j）的第 n+1 次电位的计算公式：
n n 1 n 1 1 n ( ) i , j 1 i 1, j i , j 1 4 i 1, j

c. 超松弛迭代法：
n 1 i, j

此式也称为异步迭代法，异步迭代法比简单迭代法收敛速度加快一倍左右。
为了加快收敛速度，常采用超松弛迭代法。计算时，将某点的新老电位值之差乘以一
图 4-3 三维电位分布图等位线分布图
4.6 中心点电位的数值解和精确解的比较
4.6.1 中心点 p ( , ) 的数值解：
因为电位是从上至下逐渐呈递减状，中间点的所在等位线的 a b 为 50V。
, 2 2
a b 2 2 a b 2 2
4.6.2 中心点 p ( , ) 的精确解：
在不同的 m 取值下， a b 的取值会不同。
, 2 2
m=1.2， a b =49.5133V
, 2 2 , 2 2
m=1.4， a b =49.5149V M=1.6， a b =49.5161V

MATLAB超松弛迭代法求解接地金属槽内电位分布

用超松弛迭代法求解接地金属槽内电位分布一、实验内容：试用超松弛迭代法求解接地金属槽内电位的分布。

已知：cm a 4=，mm a h 104/== 给定边值如图所示。

给定初值：0)0(,=j i ϕ 误差范围：510-=ε 计算迭代次数，j i ,ϕ分布。

二．实验设计原理：有限差分法有限差分法（Finite Differential Method ）是基于差分原理的一种数值计算法。

其基本思想：将场域离散为许多小网格，应用差分原理，将求解连续函数ϕ的泊松方程的问题换为求解网格节点上ϕ的差分方程组的问题。

编程时已经考虑到题目要求，所以直接将边值编入到程序中，编写成function 的M 文件，这样只要调用此M 文件，输入变量为迭代因子，即可输出电位矩阵和迭代次数。

迭代时所用公式为U2(i,j)=U1(i,j)+a*(U1(i,j+1)+U1(i+1,j)+U2(i-1,j)+U2(i,j-1)-4*U1(i,j))/4 其中U2代表k+1，而U1代表k 。

以上分析了迭代程序的实现，但是迭代循环如何终止并未说明。

题目中的误差范围ε=0.00001，即当两次迭代结果相差不超过ε时停止，这里必须是九点都满足不超过ε，而并不是其中某一点达到即可。

当迭代次数过多时，程序会运行很长时间，（本题要求电位点数较少，不会出现迭代次数过多的情况。

当然点数越多结果越精确。

）当迭代因子a2时，迭代不收敛，程序会陷入死循环，因此需要限制循环次数，迭代100000次无结果则退出循环，防止程序崩溃。

这样可以画出流程图如下所示：否是三、程序运行界面及结果=ϕ= V100 ϕ 0=ϕ0=ϕ启动输入迭代因子迭代次数k=0 k=k+1 开始循环迭代函数判断相邻二次差值是否小于给定值输出k,电位U1适当改变迭代因子a的值是否能够减少迭代次数？我做了如下试验:迭代因子a 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9迭代次数k 17 11 14 51 不收敛可见，这样的更改在a取合适的值的时候能带来迭代次数十分显著的减少，但什么样的a才是“合适的”值，因为当a太小时，每次迭代U不能获得足够的增量。

用超松弛迭代法求解接地金属槽内电位分布

实验一用超松弛迭代法求解接地金属槽内电位分布一、实验原理（有限差分法介绍）有限差分法（Finite Differential Method）是基于差分原理的一种数值计算法。

其基本思想：将场域离散为许多小网格，应用差分原理，将求解连续函数ϕ的泊松方程的问题转换为求解网格节点上ϕ的差分方程组的问题。

二．实验内容与要求1. 试用超松弛迭代法求解接地金属槽内电位的分布。

已知：，cma4=mmah104/==给定边值如图所示。

给定初值：0)0(,=jiϕ误差范围：510−=ε计算迭代次数，ji,ϕ分布。

2、按对称场差分格式求解电位的分布（即求出D域的场分布，由对称性可得全域的场分布）已知，cma4=mmh14040==给定边值：如图1示给定初值)()(.1j401001jp12ji−=−−=ϕϕϕ误差范围: 510−=ε图1 接地金属槽内半场域的网格剖分计算：1）迭代次数，Nji,ϕ；2）按电位差10=Δϕ画出槽中等位线分布图。

图1.7 接地金属槽内网格0=ϕ=V 100 ϕ0=ϕ0=ϕ电磁场数值计算与仿真实验指导书63、分片场域的静电场分析（选做）用有限差分法计算区域内的电位、电场强度，绘制等位线。

并计算区域的电容，分析单元的大小对电容计算结果的影响，给出曲线。

100伏0伏εr1=2 εr2=4εr3=1εr4=3电磁场数值计算与仿真实验指导书7三、实验程序内容程序一：#include<iostream.h>#include<math.h>void main(){double m[5][5],n[5][5];int N=0,b=1;int i,j;double e=0.00001;double a=2/(1+sin(3.1415926/4));for(i=0;i<=4;i++)for(j=0;j<=4;j++){m[i][j]=0;n[i][j]=0;}m[1][4]=100;m[2][4]=100;m[3][4]=100;n[1][4]= m[1][4];n[2][4]= m[1][4];n[3][4]= m[1][4];for(j=4;j>=0;j--){for(i=0;i<=4;i++)cout<<"m["<<i<<"]["<<j<<"]"<<"="<<m[i][j]<<'\t';cout<<endl;}while(b==1){b=0;N=N+1;for(i=1;i<=3;i++)for(j=1;j<=3;j++)m[i][j]=m[i][j]+a*(m[i-1][j]+m[i][j-1]+m[i+1][j]+m[i][j+1]-4*m[i][j])/4; for(i=1;i<=3;i++)for(j=1;j<=3;j++){ if(fabs(m[i][j]-n[i][j])>=e)b=1;n[i][j]=m[i][j];}for(j=4;j>=0;j--){for(i=0;i<=4;i++)cout<<"m["<<i<<"]["<<j<<"]"<<"="<<m[i][j]<<'\t'; cout<<endl;}cout<<"N="<<N<<endl;}实验结果：N＝13程序二：#include<iostream.h>#include<math.h>void main(){static double m[41][41],n[41][41];int N=0,b=1;int i,j;double e=0.00001;double a=2/(1+sin(3.1415926/4));for(i=2;i<=40;i++)for(j=2;j<=41;j++){m[i][j]=100*(j-1);m[i][j]=m[i][j]/40;n[i][j]=m[i][j];for(j=41;j>=1;j--){ for(i=1;i<=41;i++)cout<<m[i][j]<<'\t';cout<<endl;}while(b==1){b=0;N=N+1;for(i=2;i<=21;i++)for(j=2;j<=40;j++){m[i][j]=m[i][j]+a*(m[i-1][j]+m[i][j-1]+m[i+1][j]+m[i][j+1]-4*m[i][j])/4; }for(i=2;i<=21;i++)for(j=2;j<=40;j++){ if(abs(m[i][j]-n[i][j])>=e)b=1;n[i][j]=m[i][j];}}for(i=2;i<=21;i++)for(j=2;j<=40;j++)m[42-i][j]=m[i][j];cout<<endl;for(j=41;j>=1;j--){ for(i=1;i<=41;i++)cout<<m[i][j]<<'\t';cout<<endl;}cout<<"N="<<N<<endl;}实验结果：N＝17等位线分布程序及图：（mathematic）。

工程电磁场实验报告用超松弛迭代法求解接地金属槽内的电位分布

南京理工大学工程电磁场实验报告班级：1m 班姓名：mmmm学号：mmm2013.06.16实验一用超松弛迭代法求解接地金属槽内的电位分布一、实验目的1、掌握如何使用超松弛法来近似求解金属槽内的电位值。

2、掌握利用C++来实现超松弛迭代法。

二、实验原理有限差分法是基于差分原理的一种计算方法。

对于下面的的一个二维泊松方程的差分格式，利用差分就可以得到每一个点的电位。

图1 有限法网格分割其电位值是： 2012341()4Fh ϕϕϕϕϕ=+++-其中F ρε=-， h 为网格间距。

若令F=0，则电位情况则变成了拉普拉斯的差分格式：012341()4ϕϕϕϕϕ=+++图2 迭代法求电位值1、高斯-赛德尔计算法：(1)112,1,,11,,11[]4k k k k k i j i j i j i j i j Fh ϕϕϕϕϕ+++--++=+++-直到(1)(),,k k i j i j ϕϕε+-<为止。

2、对于超松弛法，我们引入一个加速收敛因子α并且得到下面的计算公式：(1)()112(),,1,,11,,1,[4]4k k k k k k k i j i j i j i j i j i j i j Fh αϕϕϕϕϕϕϕ+++--++=++++--直到(1)(),,k k i j i j ϕϕε+-<为止。

借助计算机来求解的时候，其流程图如下：图3 迭代法求电位值的流程图三、实验内容（1）、题目要求利用超松弛迭代法求解接地金属槽内的电位分布，给定图如下。

已知a=4cm,h=a/4=10mm 。

给定初值(0),j 0i ϕ=,误差范围为510ε-=。

求迭代次数N=？以及电位分布,i j ϕ。

图4 超松弛法求接地金属槽内的电位值（2）、利用C++来编写计算机的求解程序，其程序如下：程序（3）、求解结果运行程序后，就能得到求解的结果。

图5 运行程序后的初始界面图6 求解结果（4）结果分析1、从实验结果可以看到，当加速收敛因子的大小不同的时候，两者的迭代次数是有差异，所以选取合适的最佳的收敛因子可以大大加速求解的速度，节省存储空间，提高效率。

MATLAB超松弛迭代法求解接地金属槽内电位分布

matlab逐次超松弛迭代法

典型静电场场图的解析解(含Matlab程序)

重金属地空间分布地matlab程序

超松弛迭代法求解接地金属槽内电位分布

逐次超松弛迭代法 matlab -回复

Matlab-求解金属槽槽内电位分布---副本培训讲学

有限差分法计算金属槽内电位分布

工程电磁场C++编程作业-一、用超松弛迭代法求解接地金属槽内电位的分布二、按对称场差分格式求解电位的分布

电磁场仿真实验-用超松弛法求二维静电场域的电位分布

逐次超松弛迭代法 matlab

matlab逐次超松弛迭代法

利用超松弛迭代法求解问题

项目训练二 求二维金属槽内的点位分布

基于matlab的电磁场分析

项目训练二 求二维金属槽内的点位分布

MATLAB超松弛迭代法求解接地金属槽内电位分布

用超松弛迭代法求解接地金属槽内电位分布

工程电磁场实验报告用超松弛迭代法求解接地金属槽内的电位分布

项目训练二求二维金属槽内的点位分布

项目训练二求二维金属槽内的点位分布