2018年(35届)全国高中物理竞赛复赛理论考试试题及解答与评分标准
高中物理全国物理竞赛复赛试题解答2018年09月

2GMRh R v Rh 将物体的运动用极坐标 t 、 r t 描写,角动量守恒和能量守恒可分别表为
2 2 0
arccos
v arccos v
R h v0
⑩
r2
和
d R h v0 dt
2 2
⑪
1 dr 1 2 d Mm 1 2 Mm m r mv0 G G 2 dt 2 dt r 2 Rh
守恒定律
mv0min R h mv R ,即 v v0min
Rh R
②
由能量守恒定律有
1 2 Mm 1 2 Mm mv0min G mv G 2 Rh 2 R
将②式代入③式得
③
v0min
2GMR R h 2 R h
1 2GM 1 1 2GM 2 2 2 2 v12 2 r2 r1 v1 r2 r1 v1 r1
将 r1 和 v1 视为已知,上式是
0
1 1 满足的一个一元二次方程。 r2 r1 显然满足方程①②,因而 r2 r1 是一元二次方程的解。利用韦达定理,另一解是 1 1 2GM 1 ③ 2 r2 r1 r1 v1
④
当物体初速度 v0 低于 v0min 时,其轨道都将与地球表面相交,因此会坠落到地面上。所 以物体绕地球作椭圆或圆形轨道运动,但不会坠落到地球表面的条件是
‐ 1 ‐
第 35 届全国中学生物理竞赛复赛理论考试试题解答
2018 年 9 月 22 日 一、 (40 分) 假设地球是一个质量分布各向同性的球体, 地球自转及地球大气的影响可忽略。 从地球上空离地面高度为 h 的空间站发射一个小物体,该物体相对于地球以某一初速度运 动,初速度方向与其到地心的连线垂直。已知地球半径为 R ,质量为 M ,引力常量为 G 。 (1)若该物体能绕地球做周期运动,其初速度的大小应满足什么条件? (2)若该物体的初速度大小为 v0 ,且能落到地面,求其落地时速度的大小和方向(即 速度与其水平分量之间的夹角) 、以及它从开始发射直至落地所需的时间。 已知:对于 c 0 , b 2 4ac 0 ,有
2018年第35届全国物理竞赛复赛试题与解答

a bx cx2 c
b
2 c 3/ 2
arcsin 2cx b C
式中 C 为积分常数。
参考解答: (1)解法(一)
假设小物体初始速度大小为 v0 ,在地球引力场中其能量为
E
1 2
mv02
G
Mm Rh
式中 m 是小物体的质量。小物体相对于地球中心的角动量为
L mv0 R h
该物体能绕地球做周期运动,其能量应
内球和球壳内表面之间为真空。内球半径为 r 0.200 m ,温度保持恒定,
R1 R2
比辐射率为 e 0.800 ;球壳的导热系数为 =1.00 102J m1 s1 K1 ,内、
r
外半径分别为 R1 0.900m 、 R2 1.00 m ,外表面可视为黑体;该实验装
置已处于热稳定状态,此时球壳内表面比辐射率为 E 0.800 。斯特藩常
位置,和此种情形下 A0 应满足的条件; (3)如果小球只能完成 n 次往返运动(向右经过原点,然后向左经过原点,算 1 次往返),
求小球最终静止的位置,和此种情形下 A0 应满足的条件; (4)如果小球只能完成 n 次往返运动,求小球从开始运动直至最终静止的过程中运动的总
路程。
三、(40 分)如图,一质量为 M 、长为 l 的匀质细杆 AB 自由悬挂于 y 通过坐标原点 O 点的水平光滑转轴上(此时,杆的上端 A 未在图中标 出,可视为与 O 点重合),杆可绕通过 O 点的轴在竖直平面(即 x-y 平
①
1 2
mv12
G
Mm r1
1 2
mv22
G
Mm r2
②
式中 m 是小物体的质量。消去 v2 得
1 r22
2018年第35届全国中学生物理竞赛复赛试题与答案

第35届全国中学生物理竞赛复赛理论考试试题2018年9月22日说明:所有解答必须写在答题纸上,写在试题纸上的无效(35届复赛)一、(40分)假设地球是一个质量分布各向同性的球体。
地球自转及地球大气的影响可忽略。
从地球上空离地面高度为h 的空间站发射一个小物体,该物体相对于地球以某一初速度运动,初速度方向与其到地心的连线垂直。
已知地球半径为R,质量为M,引力常量为G 。
(1)、若该物体能绕地球做周期运动,其初速度的大小应满足什么条件?(2)、若该物体的初速度大小为0v ,且能落到地面,求其落地时速度的大小和方向(速度与其水平分量之间的夹角)、以及它从开始发射直至落地所需的时间。
已知:对于0c <,240b ac ∆=->,有23/222arcsin 2()xdxa bx cxb cx b Cc c a bx cx +++=-+-∆++⎰式中C 为积分常数。
解:(1)、E 0=时对应的0V 大 201G 02mMmV R h-=+大 解得 02GMV R h=+大 小球做椭圆运动,最近点和地球相切20(R h)mvR mV +=小22011G G 22RmM mMmV mV R h -=-+小 解得 02R()(2R h)GM V R h =++小(2)、如图,角动量守恒 0(R h)mRvcos mV α+=机械能守恒 22011G G22RmM mMmV mV R h -=-+解2:22011G G22mM mM mV mV R h r-=-+ 得 22022GM GMv v R h r=-++ 0(R h)r cos v v α+=得 22222222220sin 1cos cos ()rv rv r v r v r v R h v ααα=-=-=-+则有2222002()r 2(R h)rdr GM v GMr v dt R h=--+-++ 略(35届复赛)二、(40分)如图,一劲度系数为k 的轻弹簧左端固定,右端连一质量为m 的小球;弹簧水平,它处于自然状态时小球位于坐标原点O;小球可在水平地面上滑动,它与地面之间的动摩擦因数为μ。
第35届全国中学生物理竞赛决赛试题
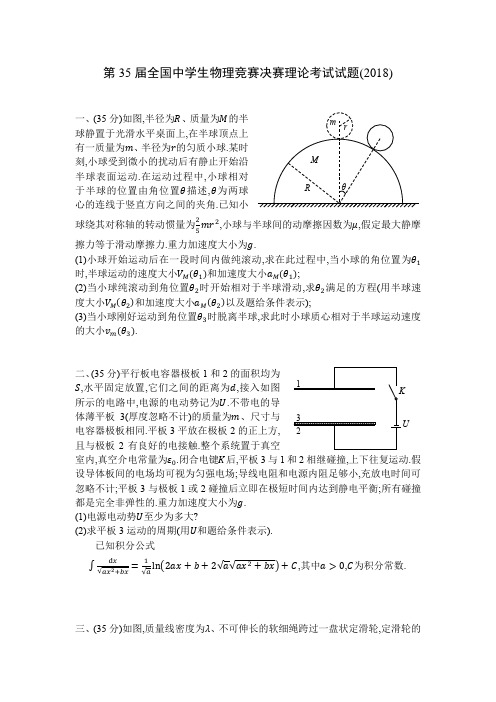
第35届全国中学生物理竞赛决赛理论考试试题(2018)一、(35分)如图,半径为R 、质量为M 的半球静置于光滑水平桌面上,在半球顶点上有一质量为m 、半径为r 的匀质小球.某时刻,小球受到微小的扰动后有静止开始沿半球表面运动.在运动过程中,小球相对于半球的位置由角位置θ描述,θ为两球心的连线于竖直方向之间的夹角.已知小球绕其对称轴的转动惯量为25mr 2,小球与半球间的动摩擦因数为μ,假定最大静摩擦力等于滑动摩擦力.重力加速度大小为g .(1)小球开始运动后在一段时间内做纯滚动,求在此过程中,当小球的角位置为θ1时,半球运动的速度大小V M (θ1)和加速度大小a M (θ1);(2)当小球纯滚动到角位置θ2时开始相对于半球滑动,求θ2满足的方程(用半球速度大小V M (θ2)和加速度大小a M (θ2)以及题给条件表示);(3)当小球刚好运动到角位置θ3时脱离半球,求此时小球质心相对于半球运动速度的大小v m (θ3).二、(35分)平行板电容器极板1和2的面积均为S ,水平固定放置,它们之间的距离为d ,接入如图所示的电路中,电源的电动势记为U ,.不带电的导体薄平板3(厚度忽略不计)的质量为m 、尺寸与电容器极板相同.平板3平放在极板2的正上方,且与极板2有良好的电接触.整个系统置于真空室内,真空介电常量为ε0.闭合电键K 后,平板3与1和2相继碰撞,上下往复运动.假设导体板间的电场均可视为匀强电场;导线电阻和电源内阻足够小,充放电时间可忽略不计;平板3与极板1或2碰撞后立即在极短时间内达到静电平衡;所有碰撞都是完全非弹性的.重力加速度大小为g .(1)电源电动势U 至少为多大?(2)求平板3运动的周期(用U 和题给条件表示).已知积分公式∫dx √ax 2+bx =1√a ln(2ax +b +2√a√ax 2+bx)+C ,其中a >0,C 为积分常数.三、(35分)如图,质量线密度为λ、不可伸长的软细绳跨过一盘状定滑轮,定滑轮的θ m r M R 1 3 2 KU半径为R ,轴离地面高度为l ,.系统原处于静止状态.在t =0时,滑轮开始以恒定角速度ω逆时针转动,绳子在滑轮带动下开始运动,绳子与滑轮间的动摩擦因数为μ,.滑轮两侧的绳子在运动过程中始终可视为沿竖直方向,绳的两端在运动过程中均没有离开地面,地面上的绳子可视为集中在一点.已知重力加速度为g ,.绳子在与滑轮左、右侧相切处的张力分别记为T 1、T 2(均非已知量).(1)分别列出在绳子速度达到最大值之前,滑轮两侧绳子的竖直部分及滑轮上任意一小段绳子的运动所满足的动力学方程;(2)求绳子可达到的最大速度的大小.(可以参考的数学关系式:dy dx +αy =e −αx d (ye αx )dx , ∫e αx cos x dx =e αx 1+α2(αcos x +sin x )+C 1, ∫e αx sin x dx =e αx 1+α2(αsin x −cos x )+C 2,C 1与C 2为积分常数)四、(35分)如图,一张紧的弦沿x 轴水平放置,长度为L ,.弦的左端位于坐标原点.弦可通过其左、右与振源连接,使弦产生沿y 方向的横向受迫振动,振动传播的速度为u . (1)固定弦的右端P 2,将其左端与P 1与振源连接,稳定时,左端P 1的振动表达式为y (x =0,t )=A 0cos ωt ,其中A 0为振幅,ω为圆频率.(i)已知弦上横波的振幅在传播方向上有衰减,衰减常量为γ(γ>0),求弦上各处振动的振幅;(已知:在无限长弦上沿x 轴正方向传播的振幅逐渐衰减的横波表达式为y (x,t )=Ae −γx cos (ωt −ωxu +φ),其中A 和φ分别为x =0处振动的振幅和初相位)(ii)忽略波的振幅在传播方向上的衰减,求弦上驻波的表达式,并确定波腹和波节处的x 坐标.(2)将P 1、P 2都与振源连接,P 1、P 2处的振动表达式分别为y (x =0,t )=A 0cos ωt 、y (x =L,t )=A 0cos (ωt +φ0),其中φ0为常量.忽略波的振幅在传播方向上的衰减,分别计算φ0=0和φ0=π情形下线上各处振动的表达式以及共振时的圆频率ω应满足的条件.R ω L 地面 O O P 1 P 2 xy五、(35分)质量为M 的绝热薄壁容器处于远离其他星体的太空(可视为真空)中.在某惯性系中观察,该容器的初始速度为零.容器的容积为V ,容器中充有某种单原子分子理想气体,气体的初始分子数、分子质量分别为N 0、m ,气体的初始温度为T 0.t =0时容器壁上出现面积为S 的一个小孔,由于小孔漏气导致容器开始运动.假设小孔较小,容器中的气体在泄露过程中始终处于平衡态.已知气体分子速度沿x 方向的分量v x 的麦克斯韦分布函数为f (v x )=√m 2πkT e mv x 22kT ,(k 为玻尔兹曼常量).在泄露过程中,求:(1)当气体的分子数密度为n 、温度为T 时在单位时间内从小孔单位面积泄出的气体分子数; (2)当容器中气体温度为T 时,从小孔泄出的气体分子相对于容器的平均动能;(3)t 时刻容器中气体的温度;(4)t 时刻容器运动速度的大小(假设M ≫N 0m ).已知积分公式:∫xe −Ax 2dx ∞0=12A ,∫x 2e −Ax 2dx ∞0=14√πA 3,∫x 3e −Ax 2dx ∞0=12A 2.六、(35分)介质的折射率n 可以大于0,也可以小于0.n 小于0的介质称为负折射介质.光在负折射介质内传播,其光程为负值(相位随传播距离的变化规律于在折射率为正的介质中的相反).如果定义折射角于入射角在界面法线同侧时折射角为负,可以证明折射定律在界面两边有负折射介质时仍然成立,即n 1sin θ1=n 2sin θ2,其中的n 1和n 2均可以大于0或小于0,θ2为折射角. (1)设想一束平行光入射到界面上,根据惠更斯原理,画出图a 和图b 所示情况下进入介质2的光线及对应的子波的示意图,并依此证明折射定律成立; (2)如图c 所示,半径为R 的球面将空间隔开为两个区域,其折射率分别记为n 1(n 1>0)、n 2(n 2<0),C 点是球面的球心,取某一光轴与球面的交点O 为原点.图中已画出此情形下一段入射光线和折射光线,x 和y 分别为入射光线、折射光线与光轴的交点坐标.记物距为s 1,像距为s 2.在傍轴近似下导出球面的成像公式和横向放大率公式.请明确指出最后结果中各个量的正负号约定;(3)介质1为空气,即n 1=1,n 2可大于0也可小于0.在球面(参考图c )前放置一普通薄凸透镜,透镜的光轴通过球心C ,焦点位于负折射介质区域内,透镜的焦距f =1.5R ,透镜中心O ′点与O 点的距离为d ,.一束沿光轴传播的平行光入射到薄透镜.分n 1>0 n 2>0 n 1>0 n 2<0 图a 图b x y C α1 α2 θ2 θ1 β n 1 n 2 M RO 序号 n2 d 1 1.5 0.35R 2 1.5 0.85R 3 -1.5 0.35R 4 -1.5 0.85R别就表中四组参数计算入射光在光轴上会聚点离O 点的距离,并画出序号4情形的光路示意图.七、(35分)在固体材料中,考虑相互作用后,可以利用“准粒子”的概念研究材料的物理性质.准粒子的动量与能量之间的关系可能与真实粒子的不同.当外加电场或磁场时,准粒子的运动往往可以用经典力学的方法来处理.在某种二维界面结构中,存在电量为q 、有效质量为m 的准粒子,它只能在x −y 平面内运动,其动能K 与动量大小p 之间的关系可表示为K =p 22m +αp ,其中α为正的常量.(1)对于真实的自由粒子,动能K =p 22m ,其中m 为该粒子质量,试从动能定理出发,推导该粒子速度v 与动量p 之间的关系式;(2)仿照(1)的方法,推导准粒子运动的速度v 与动量p 之间的关系式;(3)用动能表示准粒子运动速度的大小(4)将该二维界面结构置于匀强磁场中,磁场沿z 轴正方向,磁感应强度大小为B ,求动能为K 的准粒子做匀速率圆周运动的半径、周期和角动量的大小;(5)将该二维界面结构放置在匀强电场中,准粒子可能在垂直于电场的方向上产生加速度.如果电场沿x 轴正方向,电场强度大小为E ,.当准粒子的速度大小为v (v ≠α)、方向与x 轴正方向成θ角时,求其运动的加速度分量a x 和a y .八、(35分)热辐射入射到反射镜,反射镜可利用热辐射的辐射压力对外做功,这一过程可以用动力学或热学来研究.为简化起见,将热辐射视为一维黑体辐射,正入射到平面理想反射(完全反射)镜上.反射镜所受辐射压力与外界阻力相互平衡,以速度v 做匀速运动,运动方向与入射辐射的方向相同.已知在实验室参考系中温度为T 的一维黑体辐射谱(单位时间内在频率ν附近单位频率间隔内辐射出的辐射能)为φ(ν,T )=2ℎνe ℎνkT ⁄−1,式中ℎ为普朗克常量,k 为玻尔兹曼常量.真空中的光速为c .(1)从一维黑体辐射光子与运动理想反射镜碰撞的动力学观点出发,计算在实验室参考系中镜子利用光子克服阻力做功的功率η.(2)从热学角度看,辐射的入射过程与相继发生的反射过程可视为作为工作物质的反射镜经历一微小的理想热机循环:入射过程可视为镜子从高温热源吸热,反射过程可视为镜子向低温热源放热,最后镜子恢复原状.基于这一观点,证明在反射镜参照系中入射辐射与反射辐射均为一维黑体辐射,并在反射镜参照系中计算该热机的效率.(3)在实验室参考系中计算该热机的效率.。
寻根问底 探寻问题本源——另解2018年第35届全国中学生竞赛复赛理

• 38 •
理科考试研究•综合版
2020年2月1日
由此得九=血-如严
将A”视为初始压缩量血,利用(1)(2)小问的结
果以及血的表达式可知,小球最终静止于
“如晋_九<0,当也譽 <丸少+ 1)叫.
K
K
k
x = A _ (% +2)“ng <Q
k
~
当⑷ + 1 »mg
k
<凡
壬⑷ +2)/zjng
-
k
久二人
-A。
:0
A
O] 02
图3
小球在向右运动过程中,以O为平衡点,第一次 时振幅为4。-讐,第二次时振幅为血-警,第三
次时振幅为^0 -笔坐,…,第n次时振幅为Ao
2020年2月1日
理科考试研究・综合版
・39・
k 小球在向左运动过程中,以02为平衡点,第一次 时振幅为人0 -半严,第二次时振幅为人0 - "学",第三
-警 >0 K
记小球第一次返回到原点左边速度为零的位置 为-4,(/1, >0),则
①"1 k 由此类推,第n次向右运动至速度为零的位置为 B”(B” >0),第n次返回至速度为零的位置为-4” (九>0).则有: 九胡=警
B「A严警
=察 "k
"" k
பைடு நூலகம்
作者简介:费新良(1984 -),男,浙江湖州人,硕士研究生,中学一级教师,研究方向:中学物理教学.
现,总有一种意犹未尽的感觉.原因就是没有从根本
上去寻找这个题目的运动特征.
2从振动回归本源
其实初看小球的运动感觉是一种振动,但是不是 简谐运动呢?从长时间而言,整个系统中小球的振幅 将越来越小,显然不能把长时间的运动(指能产生多 个来回往复运动)称为简谐运动.因此很多学生可能 就放弃从简谐运动入手的想法.
