北太平洋SST(1980-1992)的EOF分解及初步分析
EOF分解程序

fid=fopen('','r');Num=360;data=zeros(360,180,Num);for i=1:Numaaa=fscanf(fid,'%s',7);data(:,:,i)=fscanf(fid,'%f',[360,180]);endsst1=data(1:90,11:70,1:Num); % 选取所需要区域的数据sst2=data(311:360,11:70,1:Num);sst3=zeros(140,60,Num);sst3(90:-1:1,1:60,1:Num)=sst1;sst3(140:-1:91,1:60,1:Num)=sst2;sst=sst3;for i=1:140for j=1:60for k=1:Numif(sst(i,j,k)==-1000)||((sst(i,j,k)==-32768))sst(i,j,k)=NaN;endendendendsst_area1=zeros(Num,8400); % zeros全零数组for i=1:Num;squ=squeeze(sst(:,:,i)); % 执行该指令后sst数据转换为二维数组sst_area1(i,:)=reshape(squ,1,8400); % 将数据转变为二维endsst_nan=isnan(sst_area1);i=0;for j=1:8400if sum(sst_nan(:,j))==0;i=i+1;sst_region(:,i)=sst_area1(:,j);endend% 求距平~注意季节的变换X=zeros(size(sst_region)); % 学者给的程序for i=1:12X(i:12:Num-12+i,:)=sst_region(i:12:end,:) - repmat( mean(sst_region(i:12:end,:),1) , size(sst_region(i:12:end,:),1), 1);endR=X*X'; % 协方差矩阵R=X*X'是8400*8400的方阵~现定义矩阵R=X'*X是156*156的矩阵[v,d]=eig(R); % 进行EOF分解~因为X'*X 与X*X'的秩相同所以特征值相同~d为x的特征值组成的对角阵~v为X*X'的特征向量~[diagonal,I]=sort(diag(d),'descend');v=v(:,I);G=diagonal/sum(diagonal);Gs=0;for i=1:length(G)Gs(i)=sum(G(1:i));if Gs(i)> break;endendN=length(Gs)%v=fliplr(v); % 矩阵作左右翻转%d=rot90(d,2); % 矩阵上下翻转后再左右翻转(查看生成的对角阵是由小到大排列的~此指令可使其由大到小排列~fliplr(flipud(d))=rot90(d,2))%diagonal=diag(d);spacef=X'*v;for i=1:Num;spacef(:,i)=spacef(:,i)/sqrt(diagonal(i)); % 空间本征函数endtimef=X*spacef; % 时间本征函数sum_d=sum(diagonal);count=0;for i=1:Num;count=count+diagonal(i);G1(i)=count/sum_d; % G1(i)是累积方差贡献率endfor i=1:Num;G2(i)=diagonal(i)/sum_d; % G2(i)是方差贡献率end%**************************************************************************% 将删去的陆地与冰点的填充值补回sst_area2=zeros(Num,8400);sst_area2(:,:)=NaN;i=1;spacef2=spacef';for j=1:8400if sum(sst_nan(:,j))==0;sst_area2(:,j)=spacef2(:,i);i=i+1;endendsst_area3=sst_area2';%************************************************************************** % 画图% subplot(2,1,2) % 将绘图窗口划分为2*1个子窗口,并在第2个子窗口中绘图figure(1)x=1:Num;plot(x,timef(:,1),'g');%ylim([ -80 80 ]);% xlabel('1980-1992年156个月','fontsize',15,'fontname','隶书')ylabel('INDEX','fontsize',12,'fontname','黑体')set(gca,'xtick',(1:6:Num))set(gca,'xticklabel',{'1980','','1981','','1982','','1983','','1984','','1985','','1986','','1987','','1988','','1989','','1990','','1991','','1992','','1993'})title('北太平洋第1模态1980至1992年SST时间序列', 'color','k','fontsize',15,'fontname','幼圆')grid onhold off% %subplot(2,1,1)% lon=[:];% lat=[:];% m_proj('Equidistant Cylindrical','lat',[ ],'lon',[ ]);%m_contourf(lon,lat,rot90(reshape(sst_area3(:,6),140,60)',2),30,'linestyle','none');% colorbar% m_coast('patch',[.95 .95 .95]);% m_coast('color','k');% m_grid('linestyle','none','tickdir','out','linewidth',;% % xlabel('longitude','fontsize',15,'fontname','comic sans ms');% % ylabel('latitude','fontsize',15,'fontname','comic sans ms');% title(['北太平洋第6模态填色图'],'fontsize',15,'fontname','幼圆');lon=[:];lat=[:];figure(2)m_proj('lambert','lat',[ ],'lon',[ ]);m_contourf(lon,lat,rot90(reshape(sst_area3(:,1),140,60)',2));% colorbar;m_coast('patch',[1 .85 .7]);%m_elev('contourf',[500:500:6000]);m_grid('box','fancy','tickdir','in');%colormap(flipud(copper));% xlabel('longitude','fontsize',15,'fontname','幼圆');% ylabel('latitude','fontsize',15,'fontname','幼圆');title(['北太平洋第1模态填色图'],'fontsize',15,'fontname','幼圆'); colorbar。
20世纪80年代中期以来东亚大槽和东中国海海温关系的年代际减弱和成因分析

20世纪80年代中期以来东亚大槽和东中国海海温关系的年代际减弱和成因分析王国松;侯敏;李琰;牟林;尚建设;宋军;高佳;李程;李欢【摘要】基于HadlSST (Hadley Centre Sea-ice and Sea surface Temperature Data Set)的月平均海温(SST)资料,对1960-2012年中国近海冬季SST的长期变化趋势进行了详细分析.结果显示冬季SST经历了一个显著的升温过程,增幅达0.018℃/年,在80年代末期发生了显著的气候增暖过程.对东亚冬季风子系统与冬季东中国海SST关系的年代际变化进行了分析.结果发现在1960-2012年间,东亚冬季风5个关键子系统中,东亚大槽与东中国海冬季SST年际变率上关系最为密切.进一步研究发现,自20世纪80年代中期以来,东亚大槽和东中国海冬季SST都发生了明显的年代际变化,其中东亚大槽为年代际减弱,而东中国海冬季SST发生了年代际增暖.尽管1960-2012年间东亚大槽与东中国海冬季SST有显著的负相关关系,但这种统计相关在1989-2012年期间显著减弱.这种相关减弱的原因很可能是由于NPO (North Pacific Oscillation)的年代际变化背景下的东亚大槽的强度减弱有关.【期刊名称】《海洋通报》【年(卷),期】2016(035)006【总页数】8页(P649-656)【关键词】海温;东亚冬季风;东亚大槽;中国近海;年季变化【作者】王国松;侯敏;李琰;牟林;尚建设;宋军;高佳;李程;李欢【作者单位】国家海洋信息中心,天津300171;国家海洋局海洋-大气化学与全球变化重点实验室,福建厦门361005;天津市滨海新区气象局,天津300457;国家海洋信息中心,天津300171;国家海洋局海洋-大气化学与全球变化重点实验室,福建厦门361005;国家海洋信息中心,天津300171;山东省商河县气象局,山东济南251600;国家海洋信息中心,天津300171;国家海洋信息中心,天津300171;国家海洋信息中心,天津300171;国家海洋信息中心,天津300171【正文语种】中文【中图分类】P732.5从地理位置上看,渤、黄、东海紧密相连,海水交换频繁,因此东中国海SST长期变化有比较一致的趋势。
eof分解海温的意义

eof分解海温的意义
EOF分解是一种信号分解的方法,也称为经验正交函数分解法(Empirical Orthogonal Function, EOF)。
它是一种用于分析气候和海洋数据的方法,用来分解多个变量之间的相关性和变化。
EOF分解的意义在于,它可以将一个复杂的变量(例如海温)分解成多个简单的变量,即EOF模态。
这些EOF模态可以用来解释不同时间尺度和空间尺度上的变化,从而提高我们对海洋和气候变化现象的理解。
通过分析和研究这些EOF模态,我们可以揭示海洋和气候变化的机理和规律,并对未来的变化进行预测和评估。
对于海洋温度数据,EOF分解可以提取出不同时间尺度上的变化,比如年际、年代际和多年际的变化。
这些变化可以对应不同的海洋现象,如厄尔尼诺南方涛动(ENSO)和北极涛动(AO)。
通过对这些现象的研究,我们可以更好地理解全球气候系统的运作,并预测未来的变化。
同时,EOF分解也可以帮助我们了解海洋温度在空间尺度上的变化。
例如,它可以识别出海温异常发生的区域,如东太平洋暖池和西北太平洋冷涡,从而提高我们对区域海洋环境变化的认识,有助于制定相关的保护和管理措施。
总之,EOF分解是一种强大的工具,能够帮助我们更好地了解海洋和气候变化现象的本质和规律。
通过对不同时间尺度和空间尺度上海洋温度的分解和分析,我们可以为海洋环境的保护和管理作出更加全面准确的预测和决策。
太平洋次表层海温距平的立体EOF分析及其与ENSO的关系

太平洋次表层海温距平的立体EOF分析及其与ENSO的关系张立峰;许建平;何金海【期刊名称】《海洋预报》【年(卷),期】2005(22)4【摘要】应用太平洋次表层海温距平资料构造了一个立体的西低东高的四级阶梯模型,使用EOF方法对此模型进行时空分解,并讨论与ENSO循环的关系.结果表明,EOF分解的前两个主分量方差贡献达到42.58%,其中第一主分量代表了暖池-厄尔尼诺(拉尼娜)模态;第二主分量代表了次表层温度距平的东西运移模态.后者存在着突变和渐变两个过程,在赤道及其附近,由冷位相变暖位相为渐变过程,暖位相变冷位相是突变过程,在赤道外南北纬10°附近则反之,厄尔尼诺正是东西运移模态突变的结果.时滞相关分析估算,一次ENSO循环的平均周期约为41个月,即3.42a,厄尔尼诺、拉尼娜模态与温度距平的东西运移模态的位相差平均约为9.7个月.运用逐步回归法求得一个对nino3指数预报效果比较理想的预报方程,其中EOF分解的第一时间系数对nino3距平指数有重要的预报价值,第二时间系数对nino3距平指数预报意义虽然不如第一时间系数明显,但仍具有一定的参考价值.【总页数】9页(P27-35)【作者】张立峰;许建平;何金海【作者单位】南京气象学院大气科学系,江苏,南京,210044;国家海洋局海洋动力过程与卫星海洋学重点实验室,浙江,杭州,310012;国家海洋局第二海洋研究所,浙江,杭州,310012;国家海洋局海洋动力过程与卫星海洋学重点实验室,浙江,杭州,310012;南京气象学院大气科学系,江苏,南京,210044【正文语种】中文【中图分类】P731【相关文献】1.热带太平洋次表层三维海温距平场的EOF分析 [J], 张立峰;许建平;何金海2.赤道太平洋次表层海温距平的EEOF分析及与厄尔尼诺的关系 [J], 杜华栋;李婧;叶志敏;兰伟仁3.西太平洋暖池次表层海温异常与ENSO关系的CGCM模拟结果 [J], 周广庆;李崇银4.ENSO事件中次表层海温距平在10°N附近向西传播的机理 [J], 巢纪平;蔡怡5.ENSO—7赤道西太平洋异常纬向风所驱动的热带太平洋次表层海温距平的循环[J], 李崇银;穆明权因版权原因,仅展示原文概要,查看原文内容请购买。
北太平洋SST(1980-1992)的EOF分解及初步分析

北太平洋SST(1980-1992)的EOF分解及初步分析北太平洋SST(1980-1992)的EOF分解及初步分析数据来源:本⽂利⽤来⾃英国⽓象局Hadley⽓候预测和研究中⼼的HadISST海温资料,对北太平洋(20N-80N 130E-90W)1980⾄1992年156个⽉的SST进⾏研究,。
本⽂选取下载了1870年1⽉⾄2011年3⽉的全球SST数据,数据格式为*.netcdf,分辨率为1°。
以下给出了数据下载的途径和链接:①/doc/8249cd8783d049649b66585f.html /hadobs/hadisst/index.html点击页⾯中⼼处蓝⾊“main data page”:图1②/doc/8249cd8783d049649b66585f.html /hadobs/hadisst/data/download.html选择SST数据下载:图2数据处理:本⽂选取下载了1870年1⽉⾄2011年3⽉的全球SST数据,数据格式为*.netcdf,数据名为HadISST_sst.nc,截取北太平洋(20N-80N 130E-90W)1980年1⽉⾄1992年12⽉156个⽉份的SST数据进⾏经验正交函数(Empirical Othorgnal Function)分解,简记为EOF分解,得到该区域该时段的海温时空特征。
在编写Matlab程序过程中,应特别注意:⑴剔除与其它站点相关系数⼩的站点的数据~简单的认为剔除陆地和冬季结冰点的数据;⑵求距平值的协⽅差矩阵时,要进⾏逐⽉平均求距平,⽽不能是156个⽉的平均值,否则会导致第1模态的⽅差贡献率很⼤;⑶当变量数m远⼤于观测样本数n时,导致协⽅差矩阵mRm=(nXm’)*(nXm)的阶数较⼤,可先求(nXm)*(nXm’)矩阵的特征值和特征向量,再求(nXm’)*(nXm)的特征值和特征向量,这叫做时空转换;⑷M⽂件编写时要尽量减少循环量,提⾼运算速度;⑸EOF分析能够有效地体现物理场主要信息,保留次要信息,并排除外来的随机⼲扰。
热带太平洋上层洋流异常的复EOF分析

热带太平洋上层洋流异常的复EOF分析卢姁;包赟;吕庆平【摘要】采用复EOF分析方法,对全年热带太平洋海域的上层洋流异常做了统计动力诊断,主要结论有:热带太平洋上层洋流异常复EOF分解第一、二模态的空间场均为赤道所俘获,并在赤道南北方向均呈迅速衰减的态势,其表现为赤道陷波的形式.第一、二模态时间系数为复数,其辐角均集中在两个状态,其模则表示了流场异常的大小.该时间系数均有年际变化和年代际变化,其年际变化的周期均与ENSO相同;在冬季,其年代际变化周期分别与北太平洋主要气候模态PDO和NPGO,以及热带外北太平洋流场异常复EOF分解前两模态的周期相同或相近,这反映了热带与中纬度各大气、海洋系统之间的相互耦合.由各模态流场异常可得相应的垂直运动异常,从而可估计SSTA的动力变化;第一模态在赤道东、西太平洋处呈现东西向的跷跷板变化;第二模态则在西太平洋赤道上以及其北侧的西太平洋暖池处,呈现南北向的跷跷板变化.第一模态的性质为海洋赤道Kelvin波的异常,可称之为ENSO的主要模态;第二模态的性质为海洋混合Rossby-重力惯性波的异常,可称之为ENSO的次要模态.【期刊名称】《海洋预报》【年(卷),期】2014(031)002【总页数】11页(P56-66)【关键词】复EOF分析;热带太平洋;大洋环流异常【作者】卢姁;包赟;吕庆平【作者单位】中国人民解放军61741部队,北京100094;中国人民解放军61741部队,北京100094;中国人民解放军东海舰队海洋水文气象中心,浙江宁波315122【正文语种】中文【中图分类】P732.61 引言海洋,尤其是热带海洋,是大气运动的重要能源,对气候变化有着不可忽视的影响。
大洋环流既影响海洋热含量的分布,也影响到海洋向大气的热量输送过程。
低纬度海洋获得了较多的太阳辐射能,通过大洋环流可将其中一部分输送到中高纬度海洋,然后再提供给大气。
前人对热带太平洋海洋状态的异常多集中在表层温度异常(SSTA)上,并探讨了其与东亚冬、夏季风异常和长江中下游及华北降水、温度异常之间的关系[1]。
EOF

最近做了一些数据分析,用到EOF分解,但是并没有发现网上有中文的相关资源,个人认为这个东西的理解对搞物理海洋和大气科学的人还是非常重要的,这里谈点自己的理解,也请大家多批评指正。
EOF Decomposition 即正交经验函数分解,英文也常用PCA(Pri ncipal Components Analysis)即主成分分析。
撒一把芝麻在地上,让你用个尽可能小的椭圆把它们圈起来。
这个椭圆的长轴,就是这堆芝麻的第一主成分,所谓first leading EOF,也叫Mode-1,短轴呢,就是第二主成分了。
如果这群芝麻撒得特听话,基本排成一条线,你的椭圆就会特别扁,这时候长轴就特别能描述这群芝麻的特点。
理想化一下,芝麻们就排成一直线,椭圆就理想成Ax+B了。
长轴和短轴差别越大,即长轴的“方差贡献”越大,描述地越好。
这是最简单的对EOF的理解。
说起将EOF用在大气海洋,不可不提的一个人就是John Kutzbach,U niv. Wisconsin-Madison 的senior scientist。
以前的EOF是一个纯数学概念,和海洋大气并不搭界,而Kutzbach 第一个把EOF引入海洋大气界,开始彻底改变人们对数据分析和物理现象的认识。
Kutzbach 是个很有传奇色彩的人物,有很多开创性的工作。
比如虽然大家公认Wallace 是Arctic Oscillation 的提出者,其实Kutzbach 很早就发现了AO的存在。
再比如Earth's Climate System 概念的提出及学科系统的完善,他也是功不可没。
Ruddiman 著Earth's Climate: Past and Future 的时候,第一句话就是献给Kutzbach,极高地评价他headedthe effort to make the study of Earth's climate a science. 还有很多鲜为人知的故事,在此不表。
北太平洋SST的EOF分解及初步分析

北太平洋SST的EOF分解及初步分析北太平洋SST (Sea Surface Temperature) 是指北太平洋地区水面温度的分布情况。
EOF (Empirical Orthogonal Function) 分解是一种统计方法,用于分析数据中的空间变异性。
在北太平洋SST的EOF分解中,通常会得到一组空间模态(EOF模态),以及对应的时间系数(PC)。
首先,需要确定北太平洋SST的观测数据集。
可以使用卫星遥感数据或从海洋观测站获取的实测数据。
这些数据需要具有时间和空间信息。
接下来,对北太平洋SST数据进行预处理。
通常会进行平滑、去趋势、去季节性等处理,以减少噪音和随机变异。
然后,进行EOF分解。
EOF分解是一种通过计算协方差矩阵的特征值和特征向量,来确定主要变化模式的方法。
特征向量描述了空间分布模态,特征值表示相应变量的能量。
得到EOF模态后,可以通过分析每个EOF模态所解释的方差百分比,来确定每个模态的重要性。
通常选择方差百分比较高的模态,作为主要的空间变化模式。
在得到主要模态后,可以计算每个模态的时间系数(PC)。
时间系数表示每个模态在不同时间点上的变化幅度。
通过分析时间系数,可以了解每个模态在不同时间尺度上的重要性。
接下来,对每个主要模态进行初步分析。
可以对每个模态进行时空分析,找出与其他变量(如气候因子)的关联性,以及对气候事件(如厄尔尼诺事件)的响应等。
需要注意的是,北太平洋SST的EOF分解及初步分析是基于统计方法,因此结果可能受到数据质量、预处理方法和分解参数等因素的影响。
对结果进行稳健性检验是非常重要的。
综上所述,北太平洋SST的EOF分解及初步分析是一种用于揭示海洋表面温度场的主要变化模式及其与其他因素的关联性的方法。
通过分析EOF模态和时间系数,可以了解北太平洋SST在不同时间和空间尺度上的特征和变化规律。
这对于理解北太平洋海洋环境的变化,并预测气候事件的发生具有重要意义。
太平洋海温与我国大陆降水的EOF分析

设海温场为 y ) 降水场为 z )其 中 t ( , ( , . 为样
本 容量 , 海 温 格 点 数 , 我 国大 陆 降 水 场 格 点 为 P为 数 , 本 文 中 , =142P =110 s=126 在 t 3 , 6 , 8 。利 用
收稿 日期 :0 1 0一l 2 1 一l O
7月降水呈负相关 , 而与华北小部分地区降水呈正 相关 , 而西 太平 洋赤 道 3月 海温 是 同 中太平 洋 北 部
图4 7月降水与 3月海温相关 区域
3 5 冬季 太 平洋海 温与夏 季 降水 .
人称 该地 区为 “ 北方 活动 中心 ” 水 区 ; 有一 个 就 冷 还 是 加里福 尼亚 海 流 区 ( 。我 国 6 E) 月 降 水 与 上
2 1 第 1期 0 2年 第3 卷 6
贵 .州 气 象
Ju o m ̄ O mzo t wl y f G huMe o o e g Vo 3 N0. L 6 1
文章编 号 :0 3— 5 8 2 1 ) 1 0 1 0 10 6 9 ( 0 2 0 — 0 8— 3
太 平洋海温 与我 国大陆降水的 E F分析 O
洋 、 太 平 洋 及 西 太 平 洋 中 部 海 温 的 关 系 , 嘉 北 黄 佑 曾用 东 亚 雨 日与 赤 道 太 平 洋 海 温 作 了相 关 分
(
( 一 () ・ ((p - () )丁 £ p ) )£ ) yp ) ) ) ,,
p
求得 相关 系数 阵 R, E F方 法对 R阵展 开有 用 O
由 公式R = √ 一 + 。£ 2 t / 确定,为样本容量长度, n
本 文取 a= .5 由 t 布 表查 得 t 00 , 分 的值 。
东海黑潮流量的年际和年代际变化

东海黑潮流量的年际和年代际变化齐继峰;尹宝树;杨德周;徐振华【摘要】本文基于日本气象厅1956-2005年间在东海PN断面获得的观测资料,结合NCEP风场资料,研究了东海黑潮流量的年际和年代际变化特征,并探讨了西北太平洋风场和太平洋年代际振荡(PDO)对黑潮流量年际和年代际变化的影响.结果表明,东海黑潮流量基本服从正态分布,主要集中在19-33Sv范围内,其多年平均值为24.30 Sv(1 Sv=106m3/s);季平均、冬、夏季黑潮流量都存在着显著的年际和年代际变化.东海黑潮流量输送具有长期的线性增强趋势,在1956-2005年间它们分别增加了8.73Sv、9.86Sv和9.38Sv.相关与合成分析结果表明,黑潮源区和东海黑潮流域上空的经向风异常是黑潮流量年际变化的重要影响因素,而PDO则对黑潮流量的年代际变化有重要作用.【期刊名称】《海洋与湖沼》【年(卷),期】2014(045)006【总页数】7页(P1141-1147)【关键词】东海;黑潮;经向风;年际变化;年代际变化【作者】齐继峰;尹宝树;杨德周;徐振华【作者单位】中国科学院海洋研究所青岛266071;中国科学院海洋环流与波动重点实验室青岛266071;中国科学院大学北京100049;中国科学院海洋研究所青岛266071;中国科学院海洋环流与波动重点实验室青岛266071;中国科学院海洋研究所青岛266071;中国科学院海洋环流与波动重点实验室青岛266071;中国科学院海洋研究所青岛266071;中国科学院海洋环流与波动重点实验室青岛266071【正文语种】中文【中图分类】P731黑潮是北太平洋的西边界流, 也是世界著名的洋流之一。
它起源于菲律宾以东海域, 沿台湾以东流向东北进入东海, 然后穿越吐噶喇海峡流出东海, 最终经日本以南海域汇入北太平洋。
黑潮具有流速强、流量大、高温、高盐等特性, 将低纬度海域的高温、高盐水输送到中纬度区域, 从而成为影响北太平洋海洋环境和气候变化的重要因素。
中国海洋大学论文模板

中 国 海 洋 大 学RERIODICAL OF OCEAN UNIVERSITY OF CHINA第34卷 第5期 2004年9月34(5):689~696 Sept., 2004综 述北太平洋副热带海洋环流气候变化研究*刘秦玉(中国海洋大学 物理海洋实验室,海洋-大气相互作用与气候实验室,山东 青岛 266003)摘 要: 北太平洋副热带环流的变化在全球气候变化和热量的经向输送中占重要地位。
本文对近10年有关北太平洋副热带海洋环流气候变化的研究进行了综述。
主要研究成果有:用卫星高度计首次观测到全球海洋Rossby 波的传播特征;确定了气候意义下北太平洋副热带逆流为2支,揭示了其中一支与北太平洋模态水的存在有关,另一支是夏威夷群岛附近海洋-大气-陆地相互作用的结果;首次发现了台湾以东黑潮流量有显著的准100天振荡等。
本文还提出了在北太平洋副热带环流研究中目前存在的新科学问题。
关键词: 北太平洋; 副热带环流; 海洋-大气相互作用; 温跃层中图法分类号: P732.6 文献标识码: A 文章编号: 1672-5174(2004)05-689-08北太平洋副热带环流(Subtropical Gyre in North Pacific )是指由北赤道流、黑潮、黑潮延伸体、北太平洋流及加里福尼亚流组成的位于北太平洋副热带海域的环流圈。
在该环流圈中还存在北太平洋副热带逆流和黑潮延伸体以南的再循环流。
该环流圈在北太平洋海洋的经向热输送和气候变化中起着重要作用。
自从太平洋年代际振荡(PDO )提出以来,鉴于副热带环流北部(40°N , 170°W )是PDO 的振荡中心之一,该海域的海气相互作用引起科学家的关注。
有关太平洋气候年际、年代际变化研究指出,在整个太平洋海表面温度(SST )、海平面气压和风应力场低频变化中存在着一个年际变化的El Nino -南方涛动(ENSO )和太平洋年代际振荡,这2个明显的振荡在空间分布上有一定的相似性。
北大西洋涛动(NAO)指数的比较及其年代际变率
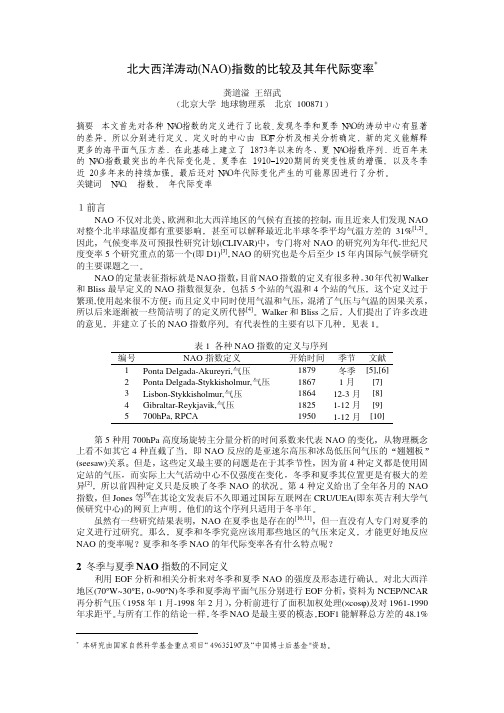
而且 这种增强从 1960 年代中期就开始了 一直持续了近 20 多年 这在近百年的记录中 是前所未有的 对于夏季 则是以 1910 到 1920 年代的突变性质的增强最为显著 1912 年
虽然有一些研究结果表明 NAO 在夏季也是存在的[10,11] 但一直没有人专门对夏季的 定义进行过研究 那么 夏季和冬季究竟应该用那些地区的气压来定义 才能更好地反应
NAO 的变率呢 夏季和冬季 NAO 的年代际变率各有什么特点呢
2 冬季与夏季 NAO 指数的不同定义
利用 EOF 分析和相关分析来对冬季和夏季 NAO 的强度及形态进行确认 对北大西洋 地区(70°W~30°E 0~90°N)冬季和夏季海平面气压分别进行 EOF 分析 资料为 NCEP/NCAR 再分析气压 1958 年 1 月-1998 年 2 月 分析前进行了面积加权处理(×cosϕ)及对 1961-1990 年求距平 与所有工作的结论一样 冬季 NAO 是最主要的模态 EOF1 能解释总方差的 48.1%
80
70
60
50
40
30
20
10
0
-80
-60
-40
-20
0
20
40
图 1 夏季北大西洋地区海平面气压 EOF 分析第 2 特征向量分布
a
b
70
70
50
50
30
30
10
10
-80 -60 -40 -20 0 20 40
EOF分析用于β中尺度暴雨系统的探索

EOF分析用于β中尺度暴雨系统的探索于杰;张继权;张铭【摘要】本文将2008年上海“8.25”暴雨过程的WRF中尺度数值模式模拟结果作为实况资料集,应用EOF(Empirical Orthogonal Function)方法对该资料集进行诊断,以探讨将该方法应用于暴雨p中尺度系统的可行性.主要结论有:当数值模式输出足够稠密、精细的样本,能够较好反映实况时,利用EOF方法对天气尺度和α、β中尺度系统的天气过程进行诊断是可行的.对本文的暴雨过程,EOF分解位势偏差场的前三个模态分别反映了α中尺度中端、低端和β中尺度天气系统的演变特征,分别对应于波长和振荡频率不同的驻波波列.其可分别称之为暴雨背景模态、暴雨系统模态和暴雨雨团模态.各波列物理性质不同,分别属于准地转的Rossby波、准平衡的涡旋波和非平衡的重力惯性波.天气系统EOF分解的物理本质为:可将一个变形和移动的天气系统分解为若干个具有不同物理性质且时空尺度不同相互独立的模态(驻波波列).这有助于明确和深化对天气系统的认识.EOF分解能够进行天气系统的尺度分离,且分离后得到的各种尺度的天气系统是独立和有特定物理意义的,这更体现了该尺度分离方法的优点.本文中当EOF分解后各波列(模态)在某地时空指数发生三波锁相,且该地的位势表现为低空为负、高空为正,同时低层位势急剧降低时,则有可能在此处发生暴雨.【期刊名称】《大气科学》【年(卷),期】2014(038)004【总页数】9页(P795-803)【关键词】EOF分析;β中尺度;暴雨;位势高度【作者】于杰;张继权;张铭【作者单位】解放军理工大学气象海洋学院全军危险性天气监测预警研究中心,南京211101;东北师范大学环境科学学院,长春130024;东北师范大学环境科学学院,长春130024;解放军理工大学气象海洋学院全军危险性天气监测预警研究中心,南京211101【正文语种】中文【中图分类】P443EOF(Empirical Orthogonal Function)分解技术在气候诊断中已得到充分发展,成为气候科学研究分析变量场特征的重要工具,并取得丰硕的研究成果(Mendonça and Bonatti,2009;Athanasiadis et al.,2010;Tao and Chen,2012;Chang et al.,2013;Xu et al.,2013;李崇银等,2013;支星和徐海明,2013;张世轩等,2013)。
太平洋次表层三维海温距平的EOF分析及其对ENSO的试预报

太平洋次表层三维海温距平的EOF分析及其对ENSO的试预报张立峰 1 何金海 2 许建平 3(1.杭州市气象局, 浙江 杭州 310008; 2.南京信息工程大学 大气科学系, 江苏 南京 210044; 3.国家海洋局 海洋动力过程与卫星海洋学重点实验室, 浙江 杭州 310012)摘 要应用太平洋次表层海温距平资料构造了一个立体的西低东高的四级阶梯模型,使用EOF方法对此模型进行时空分解,重点讨论分解结果与ENSO循环的关系,并对nino3距平指数进行试预报。
结果表明, EOF 分解的前两个主分量方差贡献达到42.58%,其中第一主分量代表了暖池-厄尔尼诺(拉尼娜)模态;第二主分量代表了次表层温度距平的东西运移模态。
后者存在着突变和渐变两个过程,在赤道及其附近,由冷位相变暖位相为渐变过程,暖位相变冷位相是突变过程,在赤道外南北纬10度附近则反之,厄尔尼诺正是东西运移模态突变的结果。
时滞相关分析估算,一次ENSO循环的平均周期约为41个月,即3.42年,厄尔尼诺、拉尼娜模态与温度距平的东西运移模态的位相差平均约为9.7个月。
应用逐步回归方法得到超前nino3距平指数3、6、12个月的三个预报方程。
预报结果表明,第一、二时间系数对nino3距平指数均具有一定的预报价值,预报时效可达到一年。
关键词: 次表层海温距平,阶梯模型,ENSO循环,nino3距平指数,预报1 引言已有大量研究从各种角度对ENSO进行分析,特别是对热带风场和海表温度场的研究,取得很多研究结果。
最近发现赤道西太平洋暖池与厄尔尼诺的关系[1-6],使我们对ENSO的认识从海洋表面深入到海洋内部。
蒲书箴等[7]利用实测资料研究表明,赤道太平洋次表层水温在厄尔尼诺期间早于表层水温的变化,在跃层深度以Kelven波速向东传播。
Yves- M,Warren .B .W[8]等用TOGA(热带海洋和全球大气计划)等观测资料,分析了全球上层400米热容量距平的变化,发现赤道太平洋上层400m热容量EOF的第一、二模态与赤道中东太平洋和赤道中西太平洋的厄尔尼诺信号有关。
EOF分析及其应用(教学课件)

第1 模态——降水量的突然增加。 第2 模态——从南向北的快速推进过程。 第3模态——东西分布型态,及在季风爆发
后印度半岛降水快速增加的过程。 第4模态——印度次大陆东海岸降水的准双
周振荡型态。
EOF分析及其应用
中国气象科学研究院
1
一、引 言 经验正交函数(EOF)方法:最早由统计学家
pearson(1902)提出,由Lorenz(1956)引入 气象问题分析中。该方法以场的时间序列为分析对 象,由于对计算条件要求甚高,直到20世纪60年代 后期才在实际工作中得到广泛应用。 近30年来,出现了适合于各种分析目的的EOF分析 方法,如扩展EOF(EEOF)方法,旋转EOF (REOF)方法,风场EOF(EOFW)方法,复变量 EOF(CEOF)方法。
z11 z12 z1n
V
v21
vm1
v22 vm2
v2m
vmm
Z
z 21
zm1
z 22 zm2
z2n
zmn
v j (v1j ,v2 j ,,vmj )T
是第j个典型场,只是空间的函数。
6
第t个空间场可表示为
x1t v11
v12
v1m
x2t
19
第1 模态——降水量的突然增加
20
降水量的第2 模态 -从南向北的快速推进过程
21
降水量的第3 模态
东西分布型态,及在季风爆发后印度半岛降水快速增加 的过程
22
降水量的第4 模态 印度次大陆东海岸降水的准双周振荡型态
23
我国盛夏500 hPa 风场的EOF 分析及 其与大尺度气候异常的关系
赤道外北太平洋冬夏海温场的EOF分析

赤道外北太平洋冬夏海温场的EOF分析路凯程;廖前锋;张铭【期刊名称】《海洋预报》【年(卷),期】2011(028)005【摘要】利用较高分辨率的SODA资料,对赤道外北太平洋海洋上层各层的海温,特别是对中纬度北太平洋海温明显异常的海域(其被定义为关键区)做了海温的EOF 分析,得到以下结论:北太平洋第一模态空间场上,冬、夏在中纬度北太平洋中西部均有较强正值带出现.在关键区第一模态空间场上,冬、夏两季近表层在日本本州岛的东、西面海域均分别有较强正值区,而次表层则仅存前者;这表明近表层海温(前者)受辐射、蒸发等影响明显,而次表层海温(后者)则其主要受流场垂直运动的影响,前者属海温的热力变化而后者则属海温的动力变化,两者性质不同.北太平洋和关键区的第一模态冬、夏海温变化的趋势均相近,两者在年尺度上均有持续性;两者的年际变化冬、夏均不明显,但均有明显的约20年的年代际变化;两者时间系数的演变均与太平洋年代际振荡(PDO)中的冷、暖位相期有较好的对应;这两个模态均可称为PDO模态.%Based on the higher resolution SODA data, EOF diagnosis on temperature of upper seawater is made in extratropical North Pacific, especially in mid-latitude where SST anomalies obvious seas (which is called key area). The results show that for the first mode of space field, there is positive high value zone at 40 °N Midwest of North Pacific in winter and summer. The anomalous trends of SST in winter and summer are same, which is sustained in year-scale. There are no obvious interannual variations between the two seasons, but 20-year inter-decadalvariations are significant, suggesting the impacts of North Pacific Decadal Oscillation (PDO) on the SST change. In the east and west sea region of the Honshu, there are strong positive anomalies in winter and summer near sea surface, while only the east region remains at sub-surface. It indicates that the ocean temperature of near-surface is significantly affected by solar radiation and evaporation, but the sub-surface temperature is mainly controlled by the vertical motion of flow field.【总页数】11页(P50-60)【作者】路凯程;廖前锋;张铭【作者单位】中国人民解放军39506部队82分队,北京100076;中国人民解放军理工大学气象学院大气环流与短期气候预测实验室,江苏南京211101;中国人民解放军理工大学训练部,江苏南京210000;中国人民解放军理工大学气象学院大气环流与短期气候预测实验室,江苏南京211101【正文语种】中文【中图分类】P732【相关文献】1.赤道东太平洋和印度洋-南海暖池海温场的协同作用对西太平洋副热带高压的影响 [J], 陈迪;高山红;陈锦年;高山2.西太平洋副热带高压变化与赤道太平洋海温场的联系 [J], 陈迪;陈锦年;左涛3.西太平洋暖池变异及其对西太平洋次表层海温场的影响 [J], 陈锦年;何宜军;孙树远;许兰英;宋贵霆;张艳慧4.中国冬夏季气温和降水异常耦合关系的SVD与MEOF分析对比 [J], 李丽平;马晨誉;倪语蔓;袁爱军;王盘兴5.用CEOF分析中蒙地温场的空间分布及时变特征 [J], 王钟睿;汤懋苍因版权原因,仅展示原文概要,查看原文内容请购买。
EOF 分解方法反演海浪参数的有效性研究

EOF 分解方法反演海浪参数的有效性研究陈忠彪;何宜军;丘仲锋;张彪【摘要】【目的】进一步确认经验正交函数(EOF)分解处理导航 X 波段雷达图像序列方法的有效性。
【方法】基于两套导航 X 波段雷达同步观测的实验数据,利用经验正交函数分解算法反演海浪的有效波高(SWH)、峰值周期、主波波向和主波波长。
【结果】4种参数均方根误差分别为0.1~0.2 m,0.6~0.9 s,5.01º和7.09 m。
【结论】经验正交函数分解反演不同海浪参数的方法适用于处理近岸海区的非均匀波浪场。
%Objective]A new proposed algorithm based on empirical orthogonal function (EOF) to process X-band marine radar image sequences was validated.[Methods]By using the experi﹣mental data measured simultaneously by two X-band marine radar systems,different wave pa﹣rameters were retrieved and compared.[Results]The root-mean-square errors of the significant wave height,peak wave period,main wave direction and main wavelength between the two ra﹣dar systems were0.1~0.2 m,0.6~0.9 s,5.01ºand 7.09 m,respectively.[Conclusion]This algorithm is suitable to be used in the heterogeneous wave filed at nearshore region.【期刊名称】《广西科学》【年(卷),期】2015(000)003【总页数】5页(P337-340,345)【关键词】导航X波段;EOF;反演;近岸;海浪【作者】陈忠彪;何宜军;丘仲锋;张彪【作者单位】南京信息工程大学海洋科学学院,江苏省海洋环境探测工程技术研究中心,江苏南京 210044;南京信息工程大学海洋科学学院,江苏省海洋环境探测工程技术研究中心,江苏南京 210044;南京信息工程大学海洋科学学院,江苏省海洋环境探测工程技术研究中心,江苏南京 210044;南京信息工程大学海洋科学学院,江苏省海洋环境探测工程技术研究中心,江苏南京 210044【正文语种】中文【中图分类】P731.22【研究意义】海浪对人们的生产和生活有重要影响,如海洋工程、渔业生产、水产养殖和航行运输等都要考虑海浪的作用。
EOF分解与GA优化的热带太平洋海温场动力预报模型反演'

EOF分解与GA优化的热带太平洋海温场动力预报模型反演'洪梅;张韧;万齐林;刘科峰;余丹丹【期刊名称】《气象学报》【年(卷),期】2010(068)005【摘要】基于NCEP/NCAR提供的1950-2000年月平均海温场资料,首先用EOF 方法对海温场序列进行时、空分解,在考虑相邻时段位势场空间模态基本稳定的前提下,引入动力系统重构思想,以EOF分解的空间模态时间系数序列作为动力模型变量,用遗传算法全局搜索和并行计算优势,进行了模型参数的优化反演,建立了EOF 分解时间系数的非线性预报模型.通过模型积分和EOF时、空重构,实现了海温场的中长期预报.试验结果表明,在1-6月时效预报上,模型预报海温场与实际海温场非常吻合;对于7-15月时效的预报.尽管模型预报的海温场与实际海温场存在一些出入,但基本构型大致相符,特别是对12月以七的海温场形态和范围仍然能较为准确地描述.所有时效的预报结果均能对1997年的El Nino事件特征有不同程度的描述.该研究方法为海温场以及El Nino/La Nina事件的预报提供了一种新的思路,文中提出的反演热带太平洋海温场与El Nino/La Nina的动力统计模型的研究思想和技术途径,在热带太平洋海温场的预测试验中(特别是中、长期预报)表现出良好的预报效果,为热带太平洋海温场及其异常的El Nino/La Nina事件的中、长期预报提供了有益的研究和参考方法.【总页数】9页(P731-739)【作者】洪梅;张韧;万齐林;刘科峰;余丹丹【作者单位】解放军理工大学气象学院海洋与空间环境系,南京,211101;中国气象局广州热带海洋气象研究所,广州,510080;解放军理工大学气象学院海洋与空间环境系,南京,211101;中国气象局广州热带海洋气象研究所,广州,510080;中国气象局广州热带海洋气象研究所,广州,510080;解放军理工大学气象学院海洋与空间环境系,南京,211101;解放军理工大学气象学院海洋与空间环境系,南京,211101【正文语种】中文【中图分类】P423;P433【相关文献】1.EOF分解与Kalman滤波相结合的副高位势场数值预报优化 [J], 刘科峰;张韧;姚跃;张吉荣;徐海斌;王辉瓒2.EOF迭代模型的月动力延伸预报产品释用方法 [J], 池俊成;史印山3.基于遗传算法优化的ENSO指数的动力预报模型反演 [J], 张韧;洪梅;王辉赞;陈奕德;王彦磊4.基于EOF分解的中期平均气温距平客观预报方法 [J], 黄威;张恒德;鲍媛媛;康志明5.EOF 分解方法反演海浪参数的有效性研究 [J], 陈忠彪;何宜军;丘仲锋;张彪因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北太平洋SST(1980-1992)的EOF分解及初步分析数据来源:本文利用来自英国气象局Hadley气候预测和研究中心的HadISST海温资料,对北太平洋(20N-80N 130E-90W)1980至1992年156个月的SST进行研究,。
本文选取下载了1870年1月至2011年3月的全球SST数据,数据格式为*cdf,分辨率为1°。
以下给出了数据下载的途径和链接:①点击页面中心处蓝色“main data page”:图1②选择SST数据下载:图2数据处理:本文选取下载了1870年1月至2011年3月的全球SST数据,数据格式为*cdf,数据名为,截取北太平洋(20N-80N 130E-90W)1980年1月至1992年12月156个月份的SST数据进行经验正交函数(Empirical Othorgnal Function)分解,简记为EOF分解,得到该区域该时段的海温时空特征。
在编写Matlab程序过程中,应特别注意:⑴剔除与其它站点相关系数小的站点的数据~简单的认为剔除陆地和冬季结冰点的数据;⑵求距平值的协方差矩阵时,要进行逐月平均求距平,而不能是156个月的平均值,否则会导致第1模态的方差贡献率很大;⑶当变量数m远大于观测样本数n时,导致协方差矩阵mRm=(nXm’)*(nXm)的阶数较大,可先求(nXm)*(nXm’)矩阵的特征值和特征向量,再求(nXm’)*(nXm)的特征值和特征向量,这叫做时空转换;⑷M文件编写时要尽量减少循环量,提高运算速度;⑸EOF分析能够有效地体现物理场主要信息,保留次要信息,并排除外来的随机干扰。
数据分析:用主成分分析(Principal Component Analysis)的方法,即PCA对结果进行分析:主成分分析是多元统计分析中一个非常重要的内容,它是一种从多个变量化为少数变量的统计方法。
由于多个变量之间是相互影响的,它们之间的关系是非常复杂的,为简化分析又不损失信息,并提取它们之间相互关系的主要特征,主成分分析利用多个变量之间的相互关系构造一些新变量,这些新变量不仅能综合反映原来多个变量的信息,而且彼此之间是相互独立的,同时是按方差贡献大小排列的。
方差贡献率小的变量通常规律性很差,其实际物理意义也不清晰,因此在实际分析过程中常常视为误差量或噪声而忽略,只取方差贡献率大的变量来研究,从而达到降维分析的目的。
通过对相应数据处理分析,前13个主成分的累积方差贡献率占总方差的,对前13个主模态的方差贡献率和累积方差贡献率列表格:图3现仅列出北太平洋前5个主模态的空间分布填色图及时间序列,并对第1和第3模态进行分析:北太平洋第1模态填色图及时间序列图4北太平洋第2模态填色图及时间序列图5北太平洋第3模态填色图及时间序列图6北太平洋第4模态填色图及时间序列图7北太平洋第5模态填色图及时间序列图8对第1主模态进行分析:北太平洋洋流图9图10(a)图10(b)图10(a)是第1模态空间分布型,它解释海温场总方差的%,此型在北太平洋西、中部被一片强负值控制,负中心约在170°E,40°N和150°W,40°N附近,而北太平洋东部和北美沿岸为较弱的正值区,说明北太平洋西、中部海温与东部海温是反相关关系,负区与北太平洋西风漂流区(如图9)吻合。
由美国海洋学家斯蒂文•黑尔于1996年发现的太平洋年代际振荡(PDO)被科学研究的初步结果表明其与厄尔尼诺(El Niño)和拉尼娜(La Nina)现象有着极其密切的关系。
该型可以反映和PDO有关的大尺度分布特征,因此这种分布型是全球海洋与大气相互作用的一个重要组成部分,它是北太平洋海温非季节变化的最重要的型式。
Monthly values for the PDO index: 1900—January2008 图11图10(c)观察发现图11(Monthly values for the PDO index: 1900—January2008)1980年至1992年时间段的指数和第1模态的时间序列图10(c)有很好的对应关系,可以验证北太平洋海表面温度第1模态空间分布型确实与PDO有很强的相关性。
资料显示,近100多年来,PDO已出现了两个完整的周期:第一周期的“冷位相”发生于1890年至1924年,而1925年至1946年为“暖位相”;第二周期的“冷位相”出现于1947年至1976年,1977年至90年代后期为“暖位相”。
当PDO现象以“暖位相”形式出现时,北美大陆附近海面的水温就会异常升高,而北太平洋洋面温度却异常下降。
并且,在20-30年的冷、暖位相中,会存在短期的反向指数。
由时间序列可知:1980年至1988年底,时间序列指数基本为正值,说明图10(a)中蓝色区域海表面温度低于红色区域海表面温度,即北太平洋西、中部海温低于东部海温;1989年初至1992年初,时间序列指数为负值,说明10(a)中蓝色区域海表面温度高于红色区域海表面温度,即北太平洋西、中部海温高于东部海温。
此分析和历史资料相吻合。
对第3主模态进行分析:图12(a)图11(a)是第3模态空间分布型,它解释海温场总方差的%,此型在北太平洋阿留申群岛南部被一片强正值控制,正值中心约在150°W,40°N附近,而其西南部和日本海海域为一片较强的负区与之相互补偿,其东南部北美洲沿岸为较弱的负值区,说明北太平洋中部海表面温度与东、西两侧海表面温度呈反相关。
正、负中心基本上与北太平洋大气活动中心(阿留申低压与西太平洋高压)对应。
表明正、负区域是海气相互作用最活跃的区域。
查阅资料可知,这种模态的变化,对我国的天气与气候有明显的影响。
图12(b)结合第3模态的时间序列可知:1980年至1983年6月、1987年6月至1988年底及1990年,时间序列指数基本为负值,说明图10(a)中蓝色区域海表面温度高于红色区域海表面温度,即北太平洋西、中部海温高于东部海温;1983年7月至1987年初、1989年及1991年初至1992年底,时间序列指数为正值,说明10(a)中蓝色区域海表面温度低于红色区域海表面温度,即北太平洋西、中部海温高于东部海温。
总结:本文通过对北太平洋1980年至1992年SST数据处理、EOF分解和初步分析,掌握了主成分分析、时空转换的原理和方法,提高了Matlab的编程和绘图技巧并对主模态和时间序列的分析进行了联系。
在此过程中克服了很多困难,受益匪浅。
但和很多同学相比,仍然有很大差距,将会更加虚心请教,刻苦钻研,以取得不断进步。
参考文献:[1]左军成.海洋水文环境要素的分析方法和预报[2]胡基福.气象统计原理与方法[3]黄嘉佑.气象统计分析与预报方法[4]杜凌.海洋要素计算(2011)PPT[5]姜霞.气象统计原理与方法(2011)PPTM文件:clear;clc;close alladdress='E:\oceanelement\';fid=(address,'NC_NOWRITE');sstid = (fid,'sst');sst=(fid,sstid); % 读取nc格式数据%**************************************************************************sst1=sst(1:90,11:70,1320:1475); % 选取所需要区域的数据sst2=sst(311:360,11:70,1320:1475);sst3=zeros(140,60,156);sst3(90:-1:1,1:60,1:156)=sst1;sst3(140:-1:91,1:60,1:156)=sst2;sst=sst3;%**************************************************************************sst_area1=zeros(156,8400); % zeros全零数组for i=1:156;squ=squeeze(sst(:,:,i)); % 执行该指令后sst数据转换为二维数组sst_area1(i,:)=reshape(squ,1,8400); % 将数据转变为二维end%**************************************************************************% 剔除与其它站点相关系数小的站点的数据~简单的认为剔除陆地和冬季结冰点的数据sst_area1(sst_area1<-10000)=NaN; % 陆地和冰点的填充值为+30~将此值定义为NaN% i=1;% for j=1:8400% if sst_area1(i,j)==% sst_area1(i,j)=NaN; % 冰点的填充值为% i=i+1;% end% endsst_nan=isnan(sst_area1);i=0;for j=1:8400if sum(sst_nan(:,j))==0;i=i+1;sst_region(:,i)=sst_area1(:,j);endend%**************************************************************************% 求距平~注意季节的变换X=zeros(size(sst_region)); % 学者给的程序for i=1:12X(i:12:144+i,:)=sst_region(i:12:end,:) - repmat( mean(sst_region(i:12:end,:),1) , size(sst_region(i:12:end,:),1), 1);end% s=0; % 自己的~很多循环计算慢% for k=1:12;% for j=1:4344;% for i=k:12:144+k% s=s+sst_region(i,j);% end% s_ave=s/13;% for i=k:12:144+k% ave_region(i,j)=s_ave;% end% s=0;% end% end% X=sst_region-ave_region; % X1是156*8400的矩阵%**************************************************************************% 由于变量数(8400)>观测样本数~协方差矩阵的阶数较大~因此可用时空转换的方法提高计算速度R=X*X'; % 协方差矩阵R=X*X'是8400*8400的方阵~现定义矩阵R=X'*X是156*156的矩阵[v,d]=eig(R); % 进行EOF分解~因为X'*X与X*X'的秩相同所以特征值相同~d为x的特征值组成的对角阵~v为X*X'的特征向量~v=fliplr(v); % 矩阵作左右翻转d=rot90(d,2); % 矩阵上下翻转后再左右翻转(查看生成的对角阵是由小到大排列的~此指令可使其由大到小排列~fliplr(flipud(d))=rot90(d,2))diagonal=diag(d);spacef=X'*v;for i=1:156;spacef(:,i)=spacef(:,i)/sqrt(diagonal(i)); % 空间本征函数endtimef=X*spacef; % 时间本征函数sum_d=sum(diagonal);count=0;for i=1:156;count=count+diagonal(i);G1(i)=count/sum_d; % G1(i)是累积方差贡献率endfor i=1:156;G2(i)=diagonal(i)/sum_d; % G2(i)是方差贡献率end%**************************************************************************% 将删去的陆地与冰点的填充值补回sst_area2=zeros(156,8400);sst_area2(:,:)=NaN;i=1;spacef2=spacef';for j=1:8400if sum(sst_nan(:,j))==0;sst_area2(:,j)=spacef2(:,i);i=i+1;endendsst_area3=sst_area2';%**************************************************************************% 画图% subplot(2,1,2) % 将绘图窗口划分为2*1个子窗口,并在第2个子窗口中绘图x=1:156;plot(x,timef(:,6),'g');ylim([ -80 80 ]);% xlabel('1980-1992年156个月','fontsize',15,'fontname','隶书')ylabel('INDEX','fontsize',12,'fontname','黑体')set(gca,'xtick',(1:6:162))set(gca,'xticklabel',{'1980','','1981','','1982','','1983','','1984','','1985','','1986','','1987','','1988','','1 989','','1990','','1991','','1992','','1993'})title('北太平洋第6模态1980至1992年SST时间序列', 'color', 'k','fontsize',15,'fontname','幼圆')grid onhold off% %subplot(2,1,1)% lon=[:];% lat=[:];% m_proj('Equidistant Cylindrical','lat',[ ],'lon',[ ]);% m_contourf(lon,lat,rot90(reshape(sst_area3(:,6),140,60)',2),30,'linestyle','none'); % colorbar% m_coast('patch',[.95 .95 .95]);% m_coast('color','k');% m_grid('linestyle','none','tickdir','out','linewidth',;% % xlabel('longitude','fontsize',15,'fontname','comic sans ms');% % ylabel('latitude','fontsize',15,'fontname','comic sans ms');% title(['北太平洋第6模态填色图'],'fontsize',15,'fontname','幼圆');lon=[:];lat=[:];m_proj('lambert','long',[ ],'lat',[ ]);m_contourf(lon,lat,rot90(reshape(sst_area3(:,1),140,60)',2));% colorbar;m_coast('patch',[1 .85 .7]);m_elev('contourf',[500:500:6000]);m_grid('box','fancy','tickdir','in');colormap(flipud(copper));% xlabel('longitude','fontsize',15,'fontname','幼圆');% ylabel('latitude','fontsize',15,'fontname','幼圆');title(['北太平洋第1模态填色图'],'fontsize',15,'fontname','幼圆');。
