64位乘法器实验报告
一种64位Booth乘法器的设计与优化

关 爵 :B o 编码;并行乘法器 ; 4 ot h 6 位乘法器 ;设计优化 ;功耗
De i n a tm i a i n o 4- i Bo t u tp i r sg nd Op i z to f6 - t o h M li le b
H E Jun. ZH U Yi ng
化, 通过 多种 方法验证设计 优化 的正确性 ,采用标准单元库进行逻辑综合评估 。结果表 明,工作频率可达 1 H 以上 , .G z 0 面积减少 9 4 . %, 6 动态 功耗和漏 电功耗分别减少 6 4 . %和 l. %,能有效减少乘法器 的面积和功耗 ,达 到预期 目 。 3 18 9 标
.பைடு நூலகம்
C e r aeteae dp we o u t no n a d ce s aa o rc ns mpi fmulpire etv l se p ce h r n o t l f cieya x e td i e
.
[ e od IB o c d g p a e m l lr 6一i l lrd s t i t n p w r o sm t n K y r s o t e o i ;a ll u i i ; b t i ;ei o i z i ; o e cn u p o w h n n r l t e 4 t i e p mu p n g p m ao i
DOI 03 6 /i n10 .4 82 1.60 6 :1.9 9 .s.0 03 2 .0 21.6 js
1 概述
乘法器是微处理器和数字信号处理器( S )h D P q最基本
面 积具 有重要 意义 。
本文针对 国产多核处理器的整数乘法器,对其 B oh ot 编码方式进行优化 ,提出一种新的 B o ot h编码方式。
计算机组成原理实验_乘法器

数学与计算机学院计算机组成原理实验报告年级08信计学号2008431066 姓名刘泽隶实验地点主楼528 指导教师陈昊实验项目运算器部件实验乘法器实验日期2010-11-10一、实验目的理解并掌握乘法器的原理。
二、实验原理(1)从右到左用乘数的每一位乘以被乘数,每一次乘得的中间结果比上一次的结果往左移一位。
(2)积的位数比被乘数和乘数的位数要多得多。
如果忽略符号位,n位的被乘数和m位的乘数相乘的结果的位数有(m+n)位。
每一位的乘法:(1)如果乘数位是1,则简单的复制被乘数到合适的位置(1*被乘数);(2)如果乘数位是0,则在合适的位置置0。
三、实验步骤(1) 打开QuartusⅡ,参照3.4节,安装ByteBlasterⅡ。
(2) 将子板上的JTAG端口和PC机的并行口用下载电缆连接。
打开实验台电源。
(3) 执行Tool->Progmmer命令,将Hamming.sof下载到FPGA中。
SOF(SRAMobject file)类型的文件是一种课下载到FPGA中的目标文件。
注意在执行Programmer命令中,英在program/configure下的方框中打钩,然后下载。
(4) 在实验台上通过模式开关选择FPGA-CPU独立调试模式010。
(5)将开关CLKSEL拨到0,将短路子DZ3短接且短路子DZ4断开,使FPGA-CPU所需要的时钟使用正单脉冲时钟。
四、实验现象本实验实现4位数的Booth乘法(有符号数乘法)输入输出规则对应如下:(1)输入的4位被乘数md3~md0对应开关SD11~SD8。
(2)输入的4位乘数mr3~mr0对应开关SD3~SD0。
(3)按单脉冲按钮,输入脉冲,也即节拍。
(4)乘积productp8-p0,对应灯A8-A0。
(5)当计算结束时,final信号为1,对应灯A7。
如表所示的booth算法运算过程,4位乘法一共需要0-8共9个小步骤计算出结果,本实验也是通过9个小步骤实现的,通过按单脉冲按钮输入脉冲,观察积寄存器的变化,掌握booth乘法器的原理。
抄作业_verilog_实现64bits乘法器-3.9

抄作业_verilog_实现64bits乘法器-3.9抄⼀个Verilog⼤作业。
题⽬描述:⽤VerilogHDL设计实现64bit⼆进制整数乘法器基本功能:1.底层乘法器使⽤16*16\8*8\8*32\8*16⼩位宽乘法器来实现,底层乘法器可以使⽤FPGA内部IP实现;2.基于modelsim仿真软件对电路进⾏功能验证;3.基于Quartus平台对代码进⾏综合及综合后仿真,芯⽚型号不限;4.电路综合后的⼯作频率不低于50MHz。
第 1 章电路的设计思想1.1 不作优化的乘法器结构对于⼀个乘法来说,它的计算步骤是⽤乘数的每⼀位以从低到⾼的顺序与被乘数相乘再错位相加。
那么,如果把64位因数与64位因数相乘的结果展开以后会发现,错位相加的那些加数是可以⽤16×16位乘法器或者8×64位乘法器的错位相加的加数来凑⼀起的。
我可以通过把四个3×3位乘法器的运算结果进⾏移位和相加以后,可以实现⼀个6×6位乘法器的运算结果。
在上图中,因为乘法器是要调⽤3×3位乘法器,所以需要把两个因数分别切割成两个3位来调⽤乘法器。
所以需要2×2=4个乘法器。
根据题⽬所给出的允许调⽤的乘法器⾥,为了使调⽤的乘法器个数最⼩,我的⼦乘法器选择的范围将聚焦在16×16位乘法器和8×32位乘法器。
不论调⽤这⾥⾯那个乘法器,最终都是需要16个乘法器的。
16个乘法器并⾏运算同时送出数据。
若调⽤16位乘法器设计电路,⽆优化的情况下需要调⽤16个乘法器,8×32位乘法器同理。
此外,64位电路的设计的移位设计有着极强的规律,在电路的设计中,这种规律性会体现在电路结构的相似性。
调⽤8×32位乘法器的设计的分析思路与⽅法与上⽂类似。
1.2 乘法器结构的折叠优化不论采⽤8×32位还是16位的⼦乘法器来设计64位乘法器,如果⽤⼗六个乘法器并⾏运算,然后再对结果进⾏移位和相加。
乘法器——精选推荐

乘法器⽬录⼀、实验⽬的 (1)⼆、实验原理 (1)三、实验内容 (1)四、实验条件 (3)五、实验步骤及仿真 (3)编码如下; (3)仿真如下: (5)六、收获与总结 (5)乘法器⼀、实验⽬的设计⼀个能进⾏两个⼗进制数相乘的乘法器,乘数和被乘数均⼩于100,通过按键输⼊,并⽤数码管显⽰,显⽰器显⽰数字时从低位向⾼位前移,最低位为当前显⽰位。
当按下相乘键后,乘法器进⾏两个数的相乘运算,数码管将乘积显⽰出来。
⼆、实验原理1、了解乘法器的⼯作原理。
2、了解复杂时序电路的设计流程。
三、实验内容1、乘数和被乘数的输⼊仍⽤数据开关K1-K10分别代表数字1、2、…、9、0,⽤编码器对数据开关K1~K10的电平信号进⾏编码,编码器真值表:数据开关电平信号编码器输出K1 K2 K3 K4 K5 K6 K7 K8 K9 K10 Q3 Q2 Q1 Q0↑0 0 0 0 0 0 0 0 0 0 ↑ 0 0 0 0 0 0 0 0 0 0 ↑ 0 0 0 0 0 0 0 0 0 0 ↑ 0 0 0 0 0 0 0 0 0 0 ↑ 0 0 0 0 0 0 0 0 0 0 ↑ 0 0 0 0 0 0 0 0 0 0↑ 0 0 0 0 0 0 0 0 0 0 ↑ 0 0 0 0 0 0 0 0 0 0 ↑ 0 0 0 0 0 0 0 0 0 0 ↑ 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 00 1 1 11 0 0 0 1 0 0 1 0 0 0 0⽤两个数码管显⽰乘数,两个数码管显⽰被乘数。
设置“相乘”信号mul,当乘数输⼊完毕后,mul有效使输⼊的乘数送寄存器模块寄存。
再输⼊被乘数,显⽰在另两个数码管上。
设置“等于”信号equal,当乘数和被乘数输⼊后,equal有效,使被乘数送寄存模块寄存,同时启动乘法摸块。
两数相乘的⽅法很多,可以⽤移位相加的⽅法,也可以将乘法器看成计数器,乘积的初始值为零,每⼀个时钟周期将被乘数的值加到积上,同时乘数减⼀,这样反复执⾏,直到乘数为零。
一种64位Booth乘法器的设计与优化

一种64位Booth乘法器的设计与优化何军;朱英【摘要】In order to solve the issue of large area and power dissipation overhead of the 64-bit integer multiplier of the homebred multr-core processor, the Booth encoding algorithm is optimized and a new Booth encoding is put forward. The correction of the optimized design is verified through multiple methods, and the design is logic synthesized based on standard cell library. As is turned out that the design can work at 1.0 GHz at least, its area is reduced by 9.64% and its dynamic and leakage power dissipation is decreased by 6.34% and 11.98%, which means the optimization can decrease the area and power consumption of multiplier effectively as expected.%针对国产多核处理器的64位整数乘法器面积和功耗开销大的问题,提出一种新的Booth编码方式,对其Booth编码方式进行优化,通过多种方法验证设计优化的正确性,采用标准单元库进行逻辑综合评估.结果表明,工作频率可达1.0 GHz以上,面积减少9.64%,动态功耗和漏电功耗分别减少6.34%和l 1.98%,能有效减少乘法器的面积和功耗,达到预期目标.【期刊名称】《计算机工程》【年(卷),期】2012(038)016【总页数】2页(P253-254)【关键词】Booth编码;并行乘法器;64位乘法器;设计优化;功耗【作者】何军;朱英【作者单位】上海高性能集成电路设计中心,上海201204;上海高性能集成电路设计中心,上海201204【正文语种】中文【中图分类】TP3681 概述乘法器是微处理器和数字信号处理器(DSP)中最基本的运算单元,其速度与处理器的性能密切相关[1]。
相乘器实验报告

一、实验目的1. 理解相乘器的基本原理和工作方式。
2. 掌握相乘器的构造方法和测试方法。
3. 分析相乘器的性能指标,如精度、速度和功耗。
4. 培养动手能力和实验操作技能。
二、实验原理相乘器是一种实现两个数相乘的电子电路。
根据乘法运算的原理,可以将乘法分解为一系列加法和移位操作。
相乘器通常采用补码形式进行运算,以保证运算的符号位正确。
三、实验器材1. 74LS181 4位并行乘法器2. 74LS86 4位全加器3. 74LS123 4位同步移位寄存器4. 74LS00 2输入与非门5. 74LS02 2输入或非门6. 74LS20 4位D触发器7. 74LS244 8位三态缓冲器8. 74LS08 2输入与门9. 74LS139 2-4线译码器10. 74LS74 4位D触发器11. 74LS32 4位优先编码器12. 74LS175 8位锁存器13. 74LS04 6反相器14. 74LS573 8位三态锁存器15. 74LS112 4位双向移位寄存器16. 电源17. 测试仪18. 负载电阻19. 接线板四、实验步骤1. 根据实验原理图,搭建相乘器电路。
2. 检查电路连接是否正确,确保电路无短路和开路现象。
3. 在测试仪上设置测试数据,如A=3,B=5。
4. 逐个检查相乘器的各个模块,观察输出结果。
5. 记录相乘器的输出结果,与测试仪显示结果进行对比。
6. 逐步改变输入数据,观察相乘器的性能表现。
7. 分析相乘器的精度、速度和功耗等性能指标。
五、实验结果与分析1. 实验结果(1)当A=3,B=5时,相乘器输出结果为15。
(2)改变输入数据,观察相乘器的输出结果,结果符合预期。
2. 分析(1)相乘器的精度:在实验过程中,相乘器的输出结果与测试仪显示结果基本一致,说明相乘器的精度较高。
(2)相乘器的速度:相乘器的运算速度较快,可以满足实际应用需求。
(3)相乘器的功耗:相乘器的功耗相对较低,有利于降低系统功耗。
实验三 模拟乘法器应用实验报告
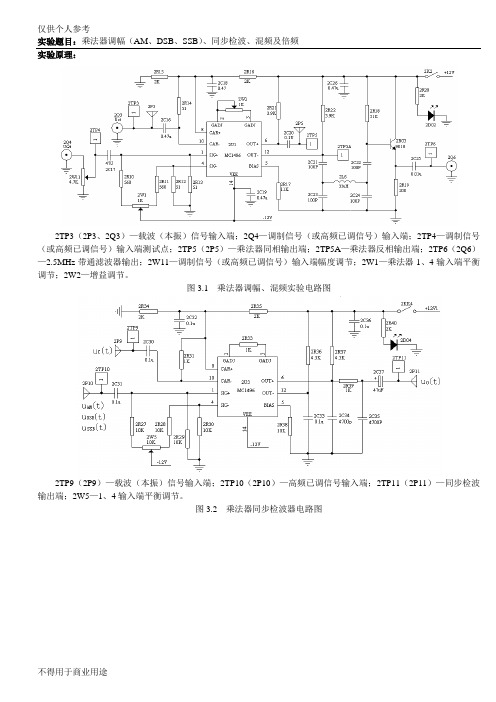
实验题目:乘法器调幅(AM、DSB、SSB)、同步检波、混频及倍频实验原理:2TP3(2P3、2Q3)—载波(本振)信号输入端;2Q4—调制信号(或高频已调信号)输入端;2TP4—调制信号(或高频已调信号)输入端测试点;2TP5(2P5)—乘法器同相输出端;2TP5A—乘法器反相输出端;2TP6(2Q6)—2.5MHz带通滤波器输出;2W11—调制信号(或高频已调信号)输入端幅度调节;2W1—乘法器1、4输入端平衡调节;2W2—增益调节。
图3.1 乘法器调幅、混频实验电路图2TP9(2P9)—载波(本振)信号输入端;2TP10(2P10)—高频已调信号输入端;2TP11(2P11)—同步检波输出端;2W5—1、4输入端平衡调节。
图3.2 乘法器同步检波器电路图2TP7(2P7)—信号输入端;2TP8(2P8)—信号输出端;2W3—调节中心频率;2W4—调节输出幅度。
实验内容及步骤:一. 普通波调幅(AM )1. 电路连接《调幅与调频接收模块》接±12V 电源电压;打开“乘法器调幅 混频”电路的电源开关(电源指示灯点亮);2TP3接载波信号C u (20KHz ,100mV PP );2TP4接调制信号u Ω(1kHz 、300mVpp );用示波器同时观测C u 、u Ω和同相输出端(2TP5)。
注:C u 由示波器(Wave Gen )提供;u Ω由信号源(F20A A 路)提供,并以u Ω所接示波器通道做触发源。
2. 电路调整调节2W11,使2TP4端幅度最大;调节示波器使波形清晰稳定;调节2W1,使2TP5输出信号为AM 已调波AM u (如图3.4);调节2W2,使AM u 的波峰、波谷无压缩失真(2W1、2W2往往配合调节)。
3. 时域测量记录或存储C u 、u Ω和AM u 的时域波形,按图3.4计算调制度m :图3.4 AM 波时域波形%100⨯+-=BA BA m4.频域测量①频谱仪射频输入(RF IN)接反相输出端2TP5A。
64位乘法器实验报告

64位乘法器实验报告64位乘法器设计实验是我在科大的第一个课程设计,verilog程序的熟练掌握对于微电子专业的学生来讲是非常必要的,对于此次设计我也花费了很长时间。
本设计分为3个部分,即控制和(1)状态选择部分,(2)乘法器部分,(3)加法器部分。
以下我将按此顺序进行说明。
需要指出的是,在实际设计中的顺序恰好是颠倒的,这与设计思路有关,在刚开始的时候由于对整体没有一个很好的把握就先选择最简单的一部分几加法器开始入手,然后就是乘法器,最后作乐一个状态控制电路将两部分联系起来。
状态选择部分设计:本电路状态选择部分设计比较简单,只有一个控制信号sel来控制电路的工作状态,我选定的状态是:sel为00的时候做加法,sel为01时做减法,sel为10时做乘法。
从节省功耗的角度出发,当电路处于加法状态的时候,乘法器最好是能够不工作,反之也一样在乘法器工作时要求加法器也处于不工作状态。
我在设计中在两个电路块的输入上都加了一个二选一开关,使不处于工作状态的电路块的输入始终为0,可是使电路减少由动态翻转产生的功耗。
加法器的设计:为了能更好地掌握加法器的设计过程,本部分采用门级描述语言,本加法器采用流水线的设计方案。
实际上该部分是不需要流水,因为乘法器是本电路的关键路径,即使乘法器采用流水线的设计方案延迟也肯定比加法器要大。
为了能够掌握流水线设计,加法器也采用了流水线来实现。
加法器的整体结构见附图(1),有超前进位产生电路,和超前进位电路来实现。
超前进位产生电路是对两个64位输入按位进行异或和与从而产生超前进位电路的输入信号P,Q。
教材上在此处也产生了部分和结果S,但我认为在此处产生结果不妥,因为要产生部分和结果必须有上一级的进位信号,对于本加法器进位信号将在下一步才产生。
所以我将作后结果的产生放在了最后一拍来完成将P与产生的进位信号按位异或即可得到最后结果。
但要注意P与进位信号CP产生的时间是不一致的,所以P信号要送到寄存器中等待一拍。
64位乘法运算实验报告

64位乘法运算实验报告一、实验任务实现两个64位无符号数的乘法,程序主体部分用汇编语言实现。
二、程序算法我们用两个16位数组x[4]和y[4]来保存64位无符号数,而相乘所得的积用一个16位数组r[11]的r[4]-r[11]8个16位数来存储,使用r[4]-r[11]这几个位置来存储只是为了编程时表示方便,举例如下:将64位数1234123412341234和1234567812345678表示成x[4]={1234 1234 1234 1234} 和y[4]={1234 5678 1234 5678}。
我们发现用mul语句实现乘法运算时,高16位在dx中,低16位在ax中,而每次x[4]中的某一位和y[4]中的某一位相乘时,比如说x[3]和y[3]相乘时,积的低16位可以存储在r[10]中,而积的高16位可以存储在r[9]中,依次类推,x[3]和y[2]相乘时,高低16位分别加到r[9]和r[8]中,然后将进位值加到相应位,这样一直推算到r[5]和r[4],便完成了所有的位相乘,最后得出结果。
三、源程序及注释//64位乘法程序#include <iostream.h>int main(int argc, char* argv[]){//x[4]和y[4]分别保存被乘数和乘数的各个位,r[11]保存积的各个位unsigned short int x[4],y[4],r[11];unsigned short int a,b,c,d,e,f,g,h;//提示输入两个64位无符号数cout<<"Please input two 64-bit Numbers:\n";cout<<"Number1:";cin>>a>>b>>c>>d; //输入被乘数cout<<"Number2:";cin>>e>>f>>g>>h; //输入乘数x[0] = a; //64位被乘数和乘数分四个16位存放x[1] = b;x[2] = c;x[3] = d;y[0] = e;y[1] = f;y[2] = g;y[3] = h;for(int k=0;k<11;k++) //积的各位赋初值0{r[k] = 0x0000;} //以i=0且j=0举例说明for(int i=0;i<4;i++) //i=0{for(int j=0;j<4;j++) //j=0{a = r[10-i-j]; //a=r[10]b = r[9-i-j]; //b=r[9]c = r[8-i-j]; //c=r[8]d = r[7-i-j]; //d=r[7]e = r[6-i-j]; //e=r[6]f = x[3-i]; //f=x[3],被乘数的最低位g = y[3-j]; //g=y[3],乘数的最低位_asm{mov ax,fmul g //两数的最低位相乘,积的低位保留在ax,高位保留在dxadd a,ax //积的低位存储在aadc b,dx //积的高位再加上进位存储在badc c,0 //若高位相加有进位,加上进位adc d,0 //若高位相加有进位,加上进位adc e,0 //若高位相加有进位,加上进位}r[10-i-j] = a; //保存运算结果r[9-i-j] = b;r[8-i-j] = c;r[7-i-j] = d;r[6-i-j] = e;}}cout<<"Theresultis:"<<x[0]<<x[1]<<x[2]<<x[3]<<"*"<<y[0]<<y[1]<<y[2]<<y[3]<<"="< <r[3]<<r[4]<<r[5]<<r[6]<<r[7]<<r[8]<<r[9]<<r[10]<<'\n';return 0;}四、实验结果。
2023年计算机应用实验报告

实验一乘法运算实验一、实验目的:1、了解调试程序DEBUG的常用命令和功能。
2、掌握多字节乘法运算程序的编写方法。
3、学会程序调试方法。
二、实验原理一、实验目的:1、掌握宏汇编语言源程序的编辑方法。
2、学会用MASM 及LINK 程序将源程序文献转换成可执行文献的方法。
3、学会调用DOS 软中断功能来显示字符串的方法。
二、实验环节:1、运用全屏幕编辑程序来编辑源程序,文献扩展名为ASM,操作如下:A>NE 盘号:文献名.ASM2、运用MASM 程序将源程序文献汇编成目的文献,目的文献扩展名为OBJ,操作如下:A>MASM 盘号:文献名.ASM 盘号:文献名.OBJ在编辑中发生错误,要用NE 程序来修改源程序文献。
3、用L I NK 程序将目的文献转换成可执行文献,可执行文献扩展名为EXE,操作如下:A>L I NK 盘号:文献名.OBJ 盘号:文献名.EXE 4、在DOS 环境下执行可执行文献。
三、实验内容:按照宏汇编语言源程序格式的规定,编写一个文献,显示如下字符串:I like mi c r oc o mputer v ery much.四、实验报告内容:1、 实验用源程序STACKS SEGMENT STACK 滩栈段实验四显示字符串实验 DWI 2 8 DU P(?);只有128个字节STACKS ENDS DATAS SEGM ENT;数据段MSG1 D B'I lik e m i crocomputer very much.?$'DATA S ENDSCODES SEGMENT;代码段ASSUME CS: CODE S,DS:DATASSTART: MOV AX,DATAS ;初始化MOV DS,AXMOV DX,OFFSET MSGIMOV AH,9INT 2 1 HMOV AX, 4 COO H ;退出程序I NT 21HC ODES END SEND START2、实验结果分析实验显示出了“I 1 ike mic r o c o mputer ver y much.实验五显示字符串实验一、实验目的:1、进一步掌握字符串的显示方法。
64位乘法器—verilog

一.设计思想输入两组64位数,a,b。
对其中一个数a,低位扩充一位0,高位扩充两位符号位,然后采用基4波兹编码进行编码。
编码一共有5种情况,分别为:0,+1,+2,-1,-2。
则相对应的部分积为0,b,2b,-b,-2b。
一共会有三十二个部分积。
分别将这三十二个部分积都扩充到128位,高位补充符号位,低位补充为0。
第一个部分积低位不补0,第二个部分积地位补两个0,第三个部分积最低位补四个0,以此类推……会得到32个128位数,将这32个数全部相加,高位溢出不管,得出一个128位数,即为最终结果。
二.电路模块1.电路用一个子模块,即基4波兹编码模块。
输入一个64位数x以及要编码的三位数,则根据输入的三位数,输出一个66位数,这个66位数为0,x,2x,-x,-x。
模块如下所示:2.将输入的64位数in2,低位补0,高位扩两位符号位,再对其从低位到高位进行基4波兹编码,得到3位部分积,再将部分积扩充为128位,再将这些部分积相加,溢出丢弃,得到最终值。
电路框架如下所示:三.仿真波形如下所示:四.代码见附件:decode.v,mul_64.v。
测试代码为tb.v五.综合结果见附件:report_area2.txt,report_time2.txt,report_power2.txt,代码:module decode(in,x,y);input[2:0]in;input[63:0]x;output reg[65:0]y;always@(in)begincase(in)3'b000:y<=66'd0;3'b111:y<=0;3'b001:y<={{2{x[63]}},x};3'b010:y<={x[63],x[63],x};3'b011:y<={x[63],x,1'b0};3'b101:y<=~{x[63],x[63],x}+1;3'b110:y<=~{x[63],x[63],x}+1;3'b100:y<=~{x[63],x,1'b0}+1;endcaseendendmodulemodule mul_64(in1,in2,out);input[63:0]in1,in2;output[127:0]out;wire[66:0]r_in2;wire[65:0]code_1,code_2,code_3,code_4,code_5,code_6,code_7,code_8,code_9,code_10,code_11,code_12, code_13,code_14,code_15,code_16,code_17,code_18,code_19,code_20,code_21,code_22,code_2 3,code_24,code_25,code_26,code_27,code_28,code_29,code_30,code_31,code_32;wire[127:0]k_code_1,k_code_2,k_code_3,k_code_4,k_code_5,k_code_6,k_code_7,k_code_8,k_code_9,k_co de_10,k_code_11,k_code_12,k_code_13,k_code_14,k_code_15,k_code_16,k_code_17,k_code_18, k_code_19,k_code_20,k_code_21,k_code_22,k_code_23,k_code_24,k_code_25,k_code_26,k_cod e_27,k_code_28,k_code_29,k_code_30,k_code_31,k_code_32;assign r_in2={{2{in2[63]}},in2,1'b0};decode m_1(.in(r_in2[2:0]),.x(in1),.y(code_1));assign k_code_1={{62{code_1[65]}},code_1};decode m_2(.in(r_in2[4:2]),.x(in1),.y(code_2));assign k_code_2={{60{code_2[65]}},code_2,2'b00};decode m_3(.in(r_in2[6:4]),.x(in1),.y(code_3));assign k_code_3={{58{code_3[65]}},code_3,4'b0000};decode m_4(.in(r_in2[8:6]),.x(in1),.y(code_4));assign k_code_4={{56{code_4[65]}},code_4,6'b000000};decode m_5(.in(r_in2[10:8]),.x(in1),.y(code_5));assign k_code_5={{54{code_5[65]}},code_5,8'b00000000};decode m_6(.in(r_in2[12:10]),.x(in1),.y(code_6));assign k_code_6={{52{code_6[65]}},code_6,10'b0000000000};decode m_7(.in(r_in2[14:12]),.x(in1),.y(code_7));assign k_code_7={{50{code_7[65]}},code_7,12'b000000000000};decode m_8(.in(r_in2[16:14]),.x(in1),.y(code_8));assign k_code_8={{48{code_8[65]}},code_8,14'b00000000000000};decode m_9(.in(r_in2[18:16]),.x(in1),.y(code_9));assign k_code_9={{46{code_9[65]}},code_9,16'b0000000000000000};decode m_10(.in(r_in2[20:18]),.x(in1),.y(code_10));assign k_code_10={{44{code_10[65]}},code_10,18'b000000000000000000};decode m_11(.in(r_in2[22:20]),.x(in1),.y(code_11)); assign k_code_11={{42{code_11[65]}},code_11,20'd0};decode m_12(.in(r_in2[24:22]),.x(in1),.y(code_12)); assign k_code_12={{40{code_12[65]}},code_12,22'd0};decode m_13(.in(r_in2[26:24]),.x(in1),.y(code_13)); assign k_code_13={{38{code_13[65]}},code_13,24'd0};decode m_14(.in(r_in2[28:26]),.x(in1),.y(code_14)); assign k_code_14={{36{code_14[65]}},code_14,26'd0};decode m_15(.in(r_in2[30:28]),.x(in1),.y(code_15)); assign k_code_15={{34{code_15[65]}},code_15,28'd0};decode m_16(.in(r_in2[32:30]),.x(in1),.y(code_16)); assign k_code_16={{32{code_16[65]}},code_16,30'd0};decode m_17(.in(r_in2[34:32]),.x(in1),.y(code_17)); assign k_code_17={{30{code_17[65]}},code_17,32'd0};decode m_18(.in(r_in2[36:34]),.x(in1),.y(code_18)); assign k_code_18={{28{code_18[65]}},code_18,34'd0};decode m_19(.in(r_in2[38:36]),.x(in1),.y(code_19)); assign k_code_19={{26{code_19[65]}},code_19,36'd0};decode m_20(.in(r_in2[40:38]),.x(in1),.y(code_20)); assign k_code_20={{24{code_20[65]}},code_20,38'd0};decode m_21(.in(r_in2[42:40]),.x(in1),.y(code_21)); assign k_code_21={{22{code_21[65]}},code_21,40'd0};decode m_22(.in(r_in2[44:42]),.x(in1),.y(code_22)); assign k_code_22={{20{code_22[65]}},code_22,42'd0};decode m_23(.in(r_in2[46:44]),.x(in1),.y(code_23)); assign k_code_23={{18{code_23[65]}},code_23,44'd0};decode m_24(.in(r_in2[48:46]),.x(in1),.y(code_24)); assign k_code_24={{16{code_24[65]}},code_24,46'd0};decode m_25(.in(r_in2[50:48]),.x(in1),.y(code_25));assign k_code_25={{14{code_17[65]}},code_25,48'd0};decode m_26(.in(r_in2[52:50]),.x(in1),.y(code_26));assign k_code_26={{12{code_26[65]}},code_26,50'd0};decode m_27(.in(r_in2[54:52]),.x(in1),.y(code_27));assign k_code_27={{10{code_27[65]}},code_27,52'd0};decode m_28(.in(r_in2[56:54]),.x(in1),.y(code_28));assign k_code_28={{8{code_28[65]}},code_28,54'd0};decode m_29(.in(r_in2[58:56]),.x(in1),.y(code_29));assign k_code_29={{6{code_29[65]}},code_29,56'd0};decode m_30(.in(r_in2[60:58]),.x(in1),.y(code_30));assign k_code_30={{4{code_30[65]}},code_30,58'd0};decode m_31(.in(r_in2[62:60]),.x(in1),.y(code_31));assign k_code_31={{2{code_31[65]}},code_31,60'd0};decode m_32(.in(r_in2[64:62]),.x(in1),.y(code_32));assign k_code_32={code_32,62'd0};assignout=k_code_1+k_code_2+k_code_3+k_code_4+k_code_5+k_code_6+k_code_7+k_code_8+k_co de_9+k_code_10+k_code_11+k_code_12+k_code_13+k_code_14+k_code_15+k_code_16+k_co de_17+k_code_18+k_code_19+k_code_20+k_code_21+k_code_22+k_code_23+k_code_24+k_c ode_25+k_code_26+k_code_27+k_code_28+k_code_29+k_code_30+k_code_31+k_code_32;endmodule。
乘法器实验报告

实验报告实验题目:乘法器姓名:闫盼蛟学号:2009432017一.实验目的理解并掌握乘法器的原理二.实验原理1.有符号数乘法——Booth乘法器Booth算法是一个更有效的计算有符号数乘法的算法,算法的新颖之处在于减法也可以用于计算乘积。
假定2(10)×6(10),或者说0010B×0110B:Booth发现加法和减法可以得到同样的结果。
Booth算法的关键在于把1分类为开始、中间、结束3种。
如图:1的结束1的中间1的开始当然一串0的时候加法减法都不做。
因此,总结1的分类情况有4种。
如下表:Booth算法是根据乘数的相邻2位来决定操作,第一步根据相邻2为的4中情况来进行加或减操作,第二步仍然是将积寄存器右移。
算法描述如下:(1)根据当前位和其右边的位,做如下操作。
00:0的中间,无任何操作01:1的结束,将被乘数加到积的左半部分10:1的开始,积的左半部分减去被乘数11:1的中间,无任何操作(2)将积寄存器右移一位。
需要注意的是,因为Booth乘法器实有符号数的乘法,因此积寄存器移位的时候,为了保留符号位,进行算术右移,不像前面的算法逻辑右移就可以了。
三.实验代码LIBRARY IEEE;USE IEEE.Std_logic_1164.ALL;ENTITY booth_multiplier ISGENERIC(k : POSITIVE := 3); --input number word length less onePORT( multiplicand : IN BIT_VECTOR(k DOWNTO 0);multiplier : IN BIT_VECTOR(k DOWNTO 0);clock : IN BIT;product : INOUT BIT_VECTOR((2*k + 2) DOWNTO 0);final : OUT BIT);END booth_multiplier;ARCHITECTURE structural OF booth_multiplier ISSIGNAL mdreg : BIT_VECTOR(k DOWNTO 0);SIGNAL adderout : BIT_VECTOR(k DOWNTO 0);SIGNAL carries : BIT_VECTOR(k DOWNTO 0);SIGNAL augend : BIT_VECTOR(k DOWNTO 0);SIGNAL tcbuffout : BIT_VECTOR(k DOWNTO 0);SIGNAL adder_ovfl : BIT;SIGNAL comp : BIT;SIGNAL clr_md : BIT;SIGNAL load_md : BIT;SIGNAL clr_pp : BIT;SIGNAL load_pp : BIT;SIGNAL shift_pp : BIT;SIGNAL boostate : NATURAL RANGE 0 TO 2*(k + 1) :=0;BEGINPROCESS --main clocked process containing all sequential elementsBEGINW AIT UNTIL (clock'EVENT AND clock = '1');--register to hold multiplicand during multiplicationIF clr_md = '1' THENmdreg <= (OTHERS => '0');ELSIF load_md = '1' THENmdreg <= multiplicand;ELSEmdreg <= mdreg;END IF;--register/shifter accumulates partial product valuesIF clr_pp = '1' THENproduct <= (OTHERS => '0');product((k+1) downto 1) <= multiplier;ELSIF load_pp = '1' THENproduct((2*k + 2) DOWNTO (k + 2)) <= adderout; --add to top halfproduct((k+1) DOWNTO 0) <= product((k+1) DOWNTO 0); --refresh bootm halfELSIF shift_pp = '1' THENproduct <= product SRA 1; --shift right with sign extendELSEproduct <= product;END IF;END PROCESS;--adder adds/subtracts partial product to multiplicandaugend <= product((2*k+2) DOWNTO (k+2));addgen : FOR i IN adderout'RANGEGENERATElsadder : IF i = 0 GENERATEadderout(i) <= tcbuffout(i) XOR augend(i) XOR product(1);carries(i) <= (tcbuffout(i) AND augend(i)) OR(tcbuffout(i) AND product(1)) OR(product(1) AND augend(i));END GENERATE;otheradder : IF i /= 0 GENERATEadderout(i) <= tcbuffout(i) XOR augend(i) XOR carries(i-1);carries(i) <= (tcbuffout(i) AND augend(i)) OR(tcbuffout(i) AND carries(i-1)) OR(carries(i-1) AND augend(i));END GENERATE;END GENERA TE;--twos comp overflow bitadder_ovfl <= carries(k-1) XOR carries(k);--true/complement buffer to generate two's comp of mdregtcbuffout <= NOT mdreg WHEN (product(1)='1') ELSE mdreg;--booth multiplier state counterPROCESS BEGINW AIT UNTIL (clock'EVENT AND clock = '1');IF boostate < 2*(k + 1) THENboostate <= boostate + 1;final <='0';ELSEfinal <='1';boostate <= 0;END IF;END PROCESS;--assign control signal values based on statePROCESS(boostate)BEGIN--assign defaults, all registers refreshclr_md <= '0';load_md <= '0';clr_pp <= '0';load_pp <= '0';shift_pp <= '0';--boostate <=0;IF boostate = 0 THENload_md <= '1';clr_pp <= '1';ELSIF boostate MOD 2 = 0 THEN --boostate = 2,4,6,8 ....shift_pp <= '1';ELSE --boostate = 1,3,5,7......IF product(1) = product(0) THENNULL; --refresh ppELSEload_pp <= '1'; --update productEND IF;END IF;END PROCESS;END structural;四.实验步骤(1)打开Quartus Ⅱ。
64位高性能嵌入式CPU中乘法器单元的设计与实现

学论作签: 、 位文者名 赵忠 民
Z 7 月1 ‘ 0 年3 日 0
经指导教师同意, 本学位论文属于保密, 在
本授 权书 。 指 导教师签名 : 年 月 日
年解密后适用
学 位论文作者签名:
年 月 日
同济大学学位论文原创性声明
本人郑重声明:所呈交的学位论文,是本人在导师指导下,进 行研究工作所取得的成果。除文中己经注明引用的内 容外,本学位 论文的研究成果不包含任何他人创作的、已公开发表或者没有公开 发表的作品的内容。 对本论文所涉及的研究工作做出贡献的其他个 人和集体,均己 在文中以明 确方式标明。本学位论文原创性声明的 法律责任由本人承担。
进行 了设计与实现 。
关键词 :定点乘法器,树型结构,Boh编码,进位保留加法器,42 ot - 压缩器, 混合电路结构
Ab t 以 sr a
AB T C S RA T
Muii s o h e ui f r rcs . a ei pi p ioe t ky to mc poesr h m ids n ni e lpe t lr n f e ns io o T e n g r c l
9 等, 步减少了Waa 树所需的 : 2 进一 lc le 计数器 个数[ [ 3 1
在乘法器拓 扑结构方面,进 入上世纪九十年代之后,进位保留加法被广泛
Booth算法_乘法器实验报告

Booth 乘法器实验报告一、实验目的1、理解并掌握乘法器的原理。
2、理解并掌握Booth 算法,及其实现方式。
二、实验原理1、乘法规律假定是十进制数的各位要么为0要么为1,例如1000*1001从上面可以得出乘法的基本规律:(1)从右到左用乘数的每一位乘以被乘数,每一次乘得的中间结果比上一次的结果往左移一位。
(2)积的位数比被乘数和乘数的位数要多得多。
(3)若十进制各位限制为0或1,则乘法变成①若乘数位为1,则简单的复制被乘数到合适的位置; ②若乘数位是0,则在合适的位置置0。
2、有符号数乘法—Booth 乘法器 (1)1的分类Booth 算法的关键在于把1分类为开始、中间、结束3种,如下图Booth 算法1的分类示意图 (2)算法描述以前乘法器的第一步是根据乘数的最低位来决定是否将被乘数加到中间结果积,而Booth 算法则是根据乘数的相邻两位来决定操作,第一步根据相邻2位的4种情况来进行加或减操作,第二步仍然是将积寄存器右移。
算法描述如下: ①根据当前位和其右边的位,作如下操作 00:0的中间,无任何操作;01:1的结束,将被乘数加到积的左半部分;1的结束被乘数 1 0 0 010 乘数 × 1 0 0 110 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0积 1 0 0 1 0 0 0101的中间 1的开始10:1的开始,积的左半部分减去被乘数; 11:1的中间,无任何操作。
②将积寄存器算术右移一位。
对于Booth算法,举例如下:210*-310=-610,或者说是00102*11012=1111 10102。
运算过程见下表。
Booth算法运算过程1 1:10->积=积-被乘数2:积右移一位 0010 1110 1101 01111 0110 12 1:01->积=积+被乘数2:积右移一位 0010 0001 0110 10000 1011 03 1:10->积=积-被乘数2:积右移一位 0010 1110 1011 01111 0101 14 1:11->nop2:积右移一位 0010 1111 0101 11111 1010 1三、实验步骤1、在PC机上完成ISE的安装。
64位高性能CPU中乘法器单元的设计与实现毕业论文

64位高性能CPU中乘法器单元的设计与实现摘要随着工艺水平的发展,集成电路设计向着速度更快,面积更小的方向稳步发展着。
处理器作为集成电路设计产品的代表,更是需要体现出这种发展趋势。
乘法器是现代微处理器芯片中的关键部件,其主要设计思想,就是在结构复杂度和电路类型,以及速度和面积之间进行均衡。
本文以此为基本出发点,首先对基4的改进Booth算法给出详细的推导,产生的部分积数目较传统的Booth算法减半,为后续的设计减小了压力。
然后,本文研究乘法器的核心部分——部分积压缩器的树型结构,并对用于压缩部分积的各种加法阵列结构进行分析和比较,提出一种以CSA 和4-2压缩器共同作为基本加法单元的混合电路结构,构建了一种独创的改进Wallace树型结构的乘法器,它在部分积求和过程中的硬件利用率达到了最高,有效地改进了传统Wallace树和其他结构的缺陷。
本论文编码采用硬件编程语言V erilog HDL来描述TOP-DOWN的设计全过程。
使用ModelSim软件对64位定点Wallace树型乘法器进行功能验证,得出此Wallace树型乘法器能正确实现乘法功能,并在一定程度上提高运行速度。
关键词定点乘法器;树型结构;Booth编码;混合电路结构The design and implementation of the multiplier module in CPU with 64-bit high-performanceAbstractAs technical level develops,IC design progresses in both the ways of higher speed and smaller area steadily.CPU is more likely to represent this trend for itis a typical product of IC design.Multiplier is one of the key units of microprocessor. The main design principle for a multiplier is a trade off balance among structure,implementation complexity,speed and area. Multiplication is based on partial product additions.In this thesis,first of all,the modified radix-4 Booth algorithm in conditions of signedmultiplication is figured out.The number of partial product can be reduced to half of the number by original Booth algorithm,which deco mpresses the follow steps.After that,tree structures of the compressors considering are presented,this thesis then proposes a novel architecture for 64-bit fixed-point tree multiplier, employing both carry-save adder and 4-2 compressor as its basic adder units under the frame work of a particular instruction set architecture. It offers the best efficiency in obtaining the sum of the partial products and improves the shortcomings of the original Wallace tree and other prior arts.In this paper, hardware encoding Verilog HDL programming language is described the design of TOP DOWN the entire process.This thesis reports the implementation of a 64-bit fixed-point pipe tree multiplier in V erilog HDL, processing functional verification with the ModelSim software and arithmetic logic unit to increase the operating speed.Keywords fixed-point multiplier; tree structure; Booth encoder;hybrid circuit structure目录摘要 (I)Abstract (II)第1章绪论 (1)1.1 课题背景 (1)1.2国内外研究现状 (1)1.2.1 国外研究情况 (2)1.2.2 国内研究情况 (2)1.3 课题的研究内容及论文安排 (3)1.3.1 主要工作 (3)1.3.2 论文安排 (3)第2章乘法器相关知识简介 (5)2.1 全定制设计方法流程 (5)2.2 乘法运算的基本原理 (7)2.2.1 乘法器的一种硬件实现方法 (7)2.2.2 移位相加乘法器的分析 (10)2.3 本章小结 (10)第3章改进Wallace树型乘法器结构分析与设计 (11)3.1 Booth算法 (11)3.1.1 Booth算法基本原理 (11)3.1.2 基4的Booth算法 (13)3.2 补位逻辑 (15)3.3 阵列乘法器 (17)3.3.1 乘法器中加法阵列结构 (17)3.3.2 乘法器结构的选择 (20)3.4 改进的乘法器结构设计 (25)3.4.1 基于4-2压缩器的乘法器结构设计 (25)3.4.2 采用混和电路结构的Wallace树型乘法器设计 (28)3.5阵列乘法器分析比较 (30)3.6 本章小结 (32)第4章改进Wallace树型乘法器实现与功能验证 (34)4.1 加法器模块生成 (35)4.1.1 一位全加器 (35)4.1.2 CSA模块 (37)4.1.3 4-2压缩器模块 (37)4.2 乘法器模块 (38)4.3 波形仿真和验证 (39)4.3.1 波形仿真 (40)4.3.2 结果分析 (41)4.4 本章小结 (41)结论 (42)致谢 (44)参考文献 (45)附录 (47)第1章绪论1.1课题背景随着微电子技术的不断进步、计算机技术的不断发展,集成电路经历了小规模、中规模、大规模的发展过程,目前已经进入超大规模(VLSI)和甚大规模集成电路(ULSI)阶段。
最新乘法器实验报告

最新乘法器实验报告实验目的:本实验旨在验证乘法器的工作原理,并通过实际操作加深对数字电路中乘法运算实现的理解。
通过构建和测试不同的乘法器电路,我们将分析其性能和适用场景,以及可能的改进方向。
实验设备和材料:1. FPGA开发板2. 集成电路芯片(包括乘法器芯片)3. 示波器4. 电源5. 连接线和面包板6. 计算机辅助设计(CAD)软件7. 数字逻辑分析仪实验步骤:1. 设计一个基本的乘法器电路图,使用CAD软件进行电路模拟。
2. 根据电路图在FPGA开发板上搭建实际电路。
3. 准备测试向量,包括一系列的二进制数值,用于乘法器的输入。
4. 连接电源,使用示波器观察乘法器的输出结果。
5. 对输出结果进行分析,验证其正确性,并记录在实验报告中。
6. 改变输入值,重复步骤4和5,以测试乘法器对不同输入的处理能力。
7. 使用数字逻辑分析仪进一步分析乘法器的性能,包括运算速度和资源消耗。
8. 根据实验结果,提出可能的改进措施和乘法器的应用前景。
实验结果:在本次实验中,我们成功搭建并测试了一个基本的乘法器电路。
通过对不同输入值的测试,我们发现乘法器能够准确地计算出两个二进制数的乘积。
实验数据显示,乘法器的运算速度和资源消耗符合预期,但在处理大数值乘法时存在一定的局限性。
讨论与改进:实验结果表明,所构建的乘法器在处理小数值乘法时表现良好,但在处理大数值时,由于资源限制和运算速度的约束,性能有所下降。
为了改进这一点,可以考虑使用更高效的算法,如Booth算法或Wallace 树算法,来优化乘法器的设计。
此外,通过优化电路布局和使用更高性能的集成电路,也可以提高乘法器的整体性能。
结论:通过本次实验,我们验证了乘法器的基本原理和工作性能,并通过实际操作加深了对其设计和应用的理解。
未来的研究可以集中在提高乘法器的运算速度和减少资源消耗上,以适应更广泛的应用需求。
乘法器实验报告

乘法器实验报告乘法器实验报告引言:乘法器是计算机中常用的一种算术逻辑单元,用于实现多位数的乘法运算。
在计算机的运算过程中,乘法运算是十分常见的,因此乘法器的设计和性能对计算机的整体性能具有重要影响。
本实验旨在通过设计和实现一个乘法器电路,探究其工作原理和性能。
一、乘法器的原理乘法器是一种复杂的电路,其主要功能是将两个输入数相乘,并输出乘积。
乘法器的实现方式有很多种,其中常用的有布斯乘法器和Wallace树乘法器等。
布斯乘法器是一种逐位相乘并累加的方法,而Wallace树乘法器则采用了并行计算的思想,能够提高计算速度。
二、乘法器的设计与实现本实验中,我们采用了布斯乘法器的设计方法。
首先,我们需要将输入的两个乘数进行分解,将每个乘数分解为若干个位数和权重的乘积。
然后,通过逐位相乘并累加的方法,得到最终的乘积。
乘法器的设计需要考虑到位数的扩展和进位的处理,以确保计算的准确性和稳定性。
三、乘法器的性能评估在设计乘法器的过程中,我们需要考虑到其性能指标,如计算速度和资源占用等。
计算速度是指乘法器完成一次乘法运算所需的时间,而资源占用则是指乘法器所需要的硬件资源数量。
在实验中,我们通过测试乘法器在不同位数和输入数据下的计算速度和资源占用情况,来评估其性能。
四、乘法器的应用领域乘法器在计算机科学和工程领域有着广泛的应用。
在计算机芯片设计中,乘法器是必不可少的组件之一。
乘法器的性能和效率直接影响到计算机的整体性能。
此外,在信号处理、图像处理和通信系统中,乘法器也扮演着重要的角色。
因此,对乘法器的研究和优化具有重要的意义。
结论:通过本次实验,我们了解了乘法器的原理、设计和性能评估方法。
乘法器作为一种常见的算术逻辑单元,对计算机的性能具有重要影响。
在今后的学习和研究中,我们将进一步探索乘法器的优化和应用,以提高计算机的整体性能。
注:本实验报告仅为虚拟写作,实际内容仅供参考,不涉及实际实验操作。
乘法器实验报告

乘法器实验报告篇一:计组-4位乘法器实验报告实验4位乘法器实验报告XXX 姓名:课程名称:计算机组成实验时间:XXX 学号:同组学生姓名:无实验地点:指导老师: XXX 专业:计算机科学与技术一、实验目的和要求1. 熟练掌握乘法器的工作原理和逻辑功能二、实验内容和原理实验内容:根据课本上例3-7的原理,来实现4位移位乘法器的设计。
具体要求:1. 乘数和被乘数都是4位2. 生成的乘积是8位的3. 计算中涉及的所有数都是无符号数4.需要设计重置功能5.需要分步计算出结果(4位乘数的运算,需要四步算出结果)实验原理:1. 乘法器原理图2. 本实验的要求:1. 需要设计按钮和相应开关,来增加乘数和被乘数2. 每按一下M13,给一个时钟,数码管的左边两位显示每一步的乘积3. 4步计算出最终结果后,LED灯亮,按RESET重新开始计算三、主要仪器设备1. Spartan-III开发板2. 装有ISE的PC机1套 1台四、操作方法与实验步骤实验步骤:1. 创建新的工程和新的源文件2. 编写verilog代码(top模块、display模块、乘法运算模块、去抖动模块以及UCF引脚)3. 进行编译4. 进行Debug 工作,通过编译。
5.. 生成FPGA代码,下载到实验板上并调试,看是否与实现了预期功能操作方法: TOP:module alu_top(clk, switch, o_seg, o_sel);input wire clk;input wire[4:0] switch;output wire [7:0] o_seg; // 只需七段显示数字,不用小数点 output wire [3:0] o_sel; // 4个数码管的位选wire[15:0] disp_num;reg [15:0] i_r, i_s;wire [15:0] disp_code;wire o_zf; //zero detectorinitialbegini_r i_s endalu M1(i_r, i_s, switch[4:2], o_zf, disp_code);display M3(clk, disp_num, o_seg, o_sel);assign disp_num = switch[0]?disp_code:(switch[1] ? i_s : i_r);endmoduleDISPLAY:module display(clk, disp_num, o_seg, o_sel); input wire clk;input wire [15:0] disp_num; //显示的数据output reg [ 7:0] o_seg; //七段,不需要小数点output reg [ 3:0] o_sel; //4个数码管的位选reg [3:0] code = 4'b0;reg [15:0] count = 15'b0;always @(posedge clk)begincase (count[15:14])2'b00 :begino_sel 2'b01 :begino_sel code 2'b10 :begino_sel 2'b11 :begino_sel code endcasecase (code)4'b0000: o_seg 4'b0011: o_seg 乘法器实验报告)0000000; 4'b1001: o_seg count end endmoduleUCF:Net “clk” loc=”T9”;Net “o_seg[0]” loc=”E14”;Net “o_seg[1]” loc=”G13”; Net “o_seg[2]” loc=”N15”; Net “o_seg[3]” loc=”P15”; Net “o_seg[4]” loc=”R16”; Net “o_seg[5]” loc=”F13”; Net “o_seg[6]” loc=”N16”; Net “o_seg[7]” loc=”P16”; Net “o_sel[0]” loc=”D14”; Net “o_sel[1]” loc=”G14”; Net “o_sel[2]” loc=”F14”; Net “o_sel[3]” loc=”E13”; Net “switch[0]” loc=”M10”; Net “switch[1]” loc=”F3”; Net “switch[2]” loc=”G4”; Net “switch[3]” loc=”E3”; Net “switch[4]” loc=”F4”;2. ALU控制器的实现:? 输入用 2 + 6 = 8 个拨动开关篇二:1496模拟乘法器实验报告实验课程名称:_高频电子线路- 1 -- 2 -- 3 -- 4 -- 5 -篇三:EDA 8位乘法器实验报告南华大学船山学院实验报告( XX ~XX 学年度第二学期)课程名称实验名称EDA8位乘法器姓名学号专业计算机科学与技术班级 01地点 8-212教师一、实验目的:学习和了解八位乘法的原理和过程二、设计思路:纯组合逻辑构成的乘法器虽然工作速度比较快,但过于占用硬件资源,难以实现宽位乘法器,基于PLD器件外接ROM 九九表的乘法器则无法构成单片系统,也不实用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
64位乘法器实验报告64位乘法器设计实验是我在科大的第一个课程设计,verilog程序的熟练掌握对于微电子专业的学生来讲是非常必要的,对于此次设计我也花费了很长时间。
本设计分为3个部分,即控制和(1)状态选择部分,(2)乘法器部分,(3)加法器部分。
以下我将按此顺序进行说明。
需要指出的是,在实际设计中的顺序恰好是颠倒的,这与设计思路有关,在刚开始的时候由于对整体没有一个很好的把握就先选择最简单的一部分几加法器开始入手,然后就是乘法器,最后作乐一个状态控制电路将两部分联系起来。
状态选择部分设计:本电路状态选择部分设计比较简单,只有一个控制信号sel来控制电路的工作状态,我选定的状态是:sel为00的时候做加法,sel为01时做减法,sel为10时做乘法。
从节省功耗的角度出发,当电路处于加法状态的时候,乘法器最好是能够不工作,反之也一样在乘法器工作时要求加法器也处于不工作状态。
我在设计中在两个电路块的输入上都加了一个二选一开关,使不处于工作状态的电路块的输入始终为0,可是使电路减少由动态翻转产生的功耗。
加法器的设计:为了能更好地掌握加法器的设计过程,本部分采用门级描述语言,本加法器采用流水线的设计方案。
实际上该部分是不需要流水,因为乘法器是本电路的关键路径,即使乘法器采用流水线的设计方案延迟也肯定比加法器要大。
为了能够掌握流水线设计,加法器也采用了流水线来实现。
加法器的整体结构见附图(1),有超前进位产生电路,和超前进位电路来实现。
超前进位产生电路是对两个64位输入按位进行异或和与从而产生超前进位电路的输入信号P,Q。
教材上在此处也产生了部分和结果S,但我认为在此处产生结果不妥,因为要产生部分和结果必须有上一级的进位信号,对于本加法器进位信号将在下一步才产生。
所以我将作后结果的产生放在了最后一拍来完成将P与产生的进位信号按位异或即可得到最后结果。
但要注意P与进位信号CP产生的时间是不一致的,所以P信号要送到寄存器中等待一拍。
以与CP信号保持时序上的一致。
毋庸置疑64位加法器的设计肯定要采用超前进位电路来实现。
考虑到一般的与门或或门的扇入不大于4的原则,我对超前进位电路采取每4组一个超前进位块,同时分层超前进位来实现。
这样做的好处是能降低每个超前进位块的设计复杂程度,实现电路在性能和复杂性之间的一个优化。
电路超前进位部分的总体结构见附图(2)。
超前进位按设计要求是产生除最高进位之外的所有进位信号。
同时最高位的进位信号是由一个额外的组合电路来实现。
CP[63]=G[63]|(P[63] & G[62])|(P[63] & P[62] & G[61])|(P[63]&P[62]&P[61]&G[60])|(P[63]&P[62]&P[61]&P[60]&G[59]);在所有进位信号产生之后加法器的输出就是:sum[64:0]<={CP[63],(P_sec[63:0]^{CP[62:0],sel[0]})};sel[0]下面将对此做出解释。
我设定sel信号为01时做减法,sel为00时做加法。
减法电路设计比较简单只要在sel为0是将输入信号Y取反再加1即可。
为了减法不增加额外的开销,我将sel[0]作为加法器的最低位进位信号,这样就可以解决加1的问题。
需要注意的是减法器的最高位不是进位信号,而是借位信号。
为1表明输入X小于Y。
乘法器电路设计:该部分是本电路设计的重点,我采用的方法是将乘数Y分为4段,每段16位分别与乘数X相乘,该部分采用booth编码算法,在得到结果后再将4个部分积移位相加即得到乘法结果。
结构图见图(3)。
Booth算法采用相加和相减的操作计算补码数据的乘积。
Booth算法对乘数从低位开始判断,根据两个数据位的情况决定进行加法、减法还是仅仅移位操作。
判断的两个数据位为当前位及其右边的位(初始时需要增加一个辅助位0),移位操作是向右移动。
在上例中,第一次判断被乘数0110中的最低位0以及右边的位(辅助位0),得00;所以只进行移位操作;第二次判断0110中的低两位,得10,所以作减法操作并移位,这个减法操作相当于减去2a 的值;第三次判断被乘数的中间两位,得11,于是只作移位操作;第四次判断0110中的最高两位,得01,于是作加法操作和移位,这个加法相当于加上8a的值,因为a的值已经左移了三次。
一般而言,设y=y0,y l y2…y n为被乘数,x为乘数,y i是a中的第i位(当前位)。
根据y j 与y i+1的值,Booth算法表示如下表所示,其操作流程如下图所示。
在Booth算法中,操作的方式取决于表达式(y i+1-y i)的值,这个表达式的值所代表的操作为:0 无操作+1 加x-1 减xBooth算法操作表示y i y i+1操作说明0 0 无处于0串中,不需要操作0 1 加x 1串的结尾1 0 减x 1串的开始1 1 无处于1串中,不需要操作乘法器的设计要真正实现比较复杂,我的设计也只能是大概地实现其功能,所以对移位相加,就没有在详细地编写程序。
不管怎么样这次设计我还是收获颇丰,由于本科不是这个专业,所以在变成方面相当有欠缺。
在设计过程中漏洞百出,经过长时间调试终于解决所有问题。
下面是我总结的一些修改谬误的经验,总结的相当不全面,请多见谅:在编程中的错误小结:always @ (posedge sclk or negedge rst) // Bring the clock scl by way of sclkbegin //And the frequency of scl is half of sclk'sif (!rst)scl<=1;elsescl<=~sclk; !!!!!正确应该为scl<=~scl;end该错误的后果是导致scl的输出波形一直为1,不能实现对sclk的2分频在模拟波形的时候将会出现错误!!!注意在写分频程序的时候应该避免此类错误。
2)在line_data_singdate.v 中单词singdate 被写成sigdate,该错误导致在top文件中的singdata mo(.sclk(sclk),.data(data),.d_ena(d_ena));语句中将出现未定义的错误。
3)为语法错误,在循环或条件语句中,应该让这些语句的头尾对应出现,是个好习惯否则在程序较长的时候可能会漏掉end语句。
** Error: E:/verilog/16_adder/main_programme.v(72): Undefined variable: b0.错误之处always@(P[0]or G[0] or P[1] or G[1] or P[2] or G[2] or P[3] or 1‘b0) always敏感变量中不应该有常数值beginCP[0]<=G[0]|(P[0]&1’b0); 此处1’b0 不多余不应该存在下同CP[1]<=G[1]|(P[1]&G[0])|(P[1]&P[0]&1’b0);CP[2]<=G[2]|(P[2]&G[1])|(P[2]&P[1]&G[0])|(P[2]&P[1]&P[0]&1’b0);** Error: E:/verilog/16_adder/main_programme.v(73): near ")": syntax error在上述错误修正之后该错误消失,说明该错误为有其他错误所引起的。
// bring result,always@(P_sec or G_sec or CP)beginif(!rst)sum[64:0]<=65'b0;elsesum[64:0]<={CP[63],(P[63:0]^{1'b0,CP[62:0]})}; 此处的错误要尽量避免位数上对应不上P的最底位应与1‘b0相异或。
应注意在高低位安排上要保持一致。
endendmodule在编写程序的过程中添加新的输入或输出时要注意以下几点:以我在设计中加入输入信号sel信号为例1)在主程序中需要加入sel的程序块中加入sel,切记以下是容易遗漏的地方,若always块中出现sel,则always的敏感信号中也必须有sel。
2)在testbench中也要有该信号的输出,并且要记住在sixty_adder m0(.X(X),.Y(Y),.sum(sum),.clk(clk),.rst(rst),.sel(sel)); 语句中也要把sel添加进去。
在检查输出一直为0错误时的一些办法,对于这类错误系统在编译的时候没有报错,说明不是语法问题。
检查起来比较困难,经我的分析,输出一直为0可能由以下几点原因造成的。
1)可能乘法器的输入一直为0,在本程序中乘法器的输入是由sel选通实现的,由于sel信号还同时控制加法器的输入信号,而加法器工作正常,说明sel选通输入的程序没有问题。
2)还有一个原因就是乘法器一直处于复位状态,但检查之后发现复位信号一切正常。
3)能让乘法器一直为0扎还有一种可能。
就是在case语句的最后default语句中乘法器的输入被一直置0,若问题出在此处,说明case语句的条件一直不成立,也就是说问题可能发生在case上。
经检查发现case({Y_tmp1[0], aid}) 出现了问题,由于aid信号为4位信号,而定义的状态信号为两位,因此case的状态就一直是defaule,问题找到正确语句应改为 case({Y_tmp1[0], aid[1]}),次错误比较不显眼,需要对程序进行仔细分析才能找到。
