无机材料科学基础 第5章 热力学应用
材料科学基础 第5章 相 图剖析

由于 所以
dni dni
dG (i i )dni
在 相和 相处于平衡时,dG=0 ,故:
i i
即两相平衡的条件是两相中同一组元的化学 位相等。此时,在两相之间转移趋于平衡。 若多元系中有C个组元,P个相,则它们的相 平衡条件可以写成:
由热力学原理可知,当组元在不同相间转 移时,将引起体系自由能的变化。对于一个多 元系,这种自由能变化可用下式表示:
dG Vdp SdT
dn
i
i
在等温等压条件下,可简化为:
dG
dn
i
i
如果体系中只有 和 两相,当极少量(d n i)的 i 组元从 相转移到 相中,则B
Pb
10
20
30
40
50
60
70
80
90
500 400 tA 300 327.5℃ 231.9℃ M α +L 183℃ 19 α +β F Pb 10 20 30 40 50 60 70 80 90 G Sn E 61.9 L+β N β 97.5 L
200 α 100
tB
W W1 W2
2的质量 Wx W1 x1 体系中相 W21 x 体系中相 的质量 体系中物质的总质量 2
t1 t2 M R P Q
L1
L2 L E x x2 20 40 K S N B 100
由上两式可得:
体系中 相1 相 中 B2 组元的含量 B 中 组元的含量 B组元的含量
W1 (x x1 ) W2 (x 2 x)
1083
时间
Cu 0
30
材料科学基础第5章 材料的相结构与相图 ppt课件[1]
![材料科学基础第5章 材料的相结构与相图 ppt课件[1]](https://img.taocdn.com/s3/m/534d1746700abb68a882fb0c.png)
一、纯金属特点
1、优良的导电、导热性能; 2、高的化学稳定性; 3、美观的金属光泽; 4、但强度、硬度较低; 5、制取困难;价格高;资源有限
2020/10/28
4
二、合金的基本概念
1、定义
是由两种或两种以上金属元素, 或金属元素与非金属元素,经熔 炼、烧结等方法组合而成并具有 金属特性的物质。
2020/10/28
5
钢:Fe-C合金;
黄铜:Cu-Zn合金; 黄铜 防锈铝:Al-Mg合金。
2、合金的特点 Al-Cu两相合金 强度高、硬度高;性能可大幅 度调节;价格较低、应用广。
2020/10/28
6
3、相
是合金中具有晶体结构相同、 成分相同和性能相同,并以界 面相互分开的组成部分。
2020/10/28
7
纯铁:由α-Fe(铁素体相) 单相构成,为单相合金;
3、作用:为合金的强化相。
2020/10/28
28
(二)金属间化合物
1、定义
合金结晶时,当其溶质浓度大 于溶解度时,将析出结构不同于任 何组元的新相,该相具有一定的金 属特征,称为金属间化合物。
2020/10/28
29
3、分类:
正常价化合物、电子化合物 、 间隙相和间隙化合物 。
1)正常价化合物
P(珠光体)= F + Fe3C Fe3C形状:片状和球状。
2020/10/28
12
❖ 当Fe3C为片状 时,构成P片状
❖ HB≈200 ❖ δ=15% ❖ Ψ=30%
2020/10/28
珠光体
13
当Fe3C为球状 时,构成P球状
HBS≈163 δ=20% Ψ=40%
2020/10/28
热力学应用课件

热力学数据的获得: 1. 查相关手册: 叶大伦,《实用无机物热力学数据手册》 矿物及有关化合物的热力学数据手册 CRC handbook of chemistry and physics Thermochemical properties of inorganic substance supplement Handbook of thermodynamic tables and chart 2.实验测量或计算 量热法 原电池电动势测量法 测化学反应平衡常数K,而平衡时 根据二元相图 半经验公式计算:
T(K)
(kJ/mol)
G
R,T
T(K)
(kJ/mol)
G
R,T
T(K)
(kJ/mol)
GR ,T
298 400 500 600 700
35.17 35.92 36.95 38.19 40.21
800 900 1000 1100 1200
42.2 43.34 45.37 47.85 51.19
1.定义:(1955年由Margrave提出)
热力学势函数Φ
T
GT HT 0
一般T0取298K, GT H 298 ' T 由于热力学基本函数G和H 都是状态函数, Φ函数在相变点具有 T 连续性,所以也是一连续的状态函数,故而对于每一种物质有 形成热力学势:
对于纯固相反应,分子间的碰撞只能在固体表面进行,固体的物 质的量浓度对反应速率和平衡没有影响,因此,固体的“浓度” 作为常数,即纯固相不计入平衡常数计算。 根据Van’t Hoff化学反应等温式:
反应吉布斯函数Δ GT,p ,将完全由与反应相关的物质的生成吉布
无机材料科学基础第五章热力学应用

确定CaCO3的分解温度 作 ΔGT0 ~ T 图 , 当 ΔGT0=0 时 , 求 得 CaCO3 分 解 温 度 为 : 1123K 由以上例题可以看出经典计算方法很复杂,尤其是复杂的固 相反应。
近似法 假设 ΔCP 不随温度而变(即 ΔCP=0 ),或把热容看作常数 (即ΔCP=常数)。 近似方程(1): 条件ΔCP=0 ΔG0T =ΔH0298 - TΔS0298
§5-1 热力学在凝聚态体系中应用的特点
凝聚态系统---没有气相或可以忽略气相的系统。 硅酸盐系统属于凝聚态系统 热力学在凝聚态体系中应用的特点: 一﹑化学反应过程的方向性 物理化学过程通常都发生在凝聚态系统中;一般都是多相 体系,因为相组成复杂﹑质点扩散速度慢,凝聚系统很难达
到热力学意义上平衡,产物常处于亚稳态(玻璃体或胶体状
0 ' G 0 H T T.R R .298 R .T
'R .T ('R ) 生成物 ( 'R ) 反应物
i i
热力学势函数(Φ函数)是热力学基本函数的一种组 合,没有什麽实际物理意义。Φ函数是个状态函数。
2. 热力学势函数法计算ΔGR0 Φ 函数法计算反应的Δ GR.TO的具体方法: ① 查出各物质的标准生成热Δ H0298、各温度下物质的ΔΦ T′ ② 计算反应的Δ H0298、R和ΔΦ T′ ③ 求出反应的Δ G0R、T,Δ GTO=Δ H0298-TΔΦ T′
求ΔGR.T
ΔG0R.T =ΔH0-Δa T lnT-1/2ΔbT2-1/2Δc T-1+y T
2﹑已知反应物和生成物的标准生成热ΔH0R.298﹑标准熵S0298 和
热容CP=f(T),求ΔG0R,T (1)列出反应物、生成物的ΔH0R.298、S0298和CP中的 a、b、c (2) 计算反应的ΔH0R.298、ΔS0298 和ΔCP 中的Δa、Δb、Δc ΔH0R.298=∑(niΔH0i.R.298)产物 -∑(niΔH0i.R.298)反应物
大二化学课件无机材科科学基础-热力学应用

T≡-
GT0
H0 T0
T
(5-13)
GT0为物质于T 下的标准自由能;HT00为物质在某一参
考温度T0下的热焓。若取T0=298K,上式可写成:
T = -
GT0
H
0 298
T
(5-14)
热力学基本函数G和H都是状态函数,G函数在相
变点具有连续性,故T也是一连续的状态函数。
每一种物质的形成热力学势T :
G
0 R
=
H0 –aTlnT
–
1 2
bT2 –
1 cT-1 + yT 2
(5-9a)
从 基 本 热 力 学 函 数 关 系 式 出 发 计 算 G0R
的过程繁琐。当体系内存在相变(如多晶转
变)时G0R 的计算要在由相变温度点所分割的 不同温度区间内用不同反应热容系数(a、 b、c)来分段计算,其工作量巨大。
假设一固相反应体系在一定热力学条件
下,可能生成一系列反应产物Ai (Gi<0)。 按 反 应 自 由 能 Gi 从 小 到 大 排 列 : G1 ,
G2 … Gn,可得到一反应产物序列A1,A2 … An。
根据能量最低原理:反应产物的热力学稳
定性取决于其Gi在序列中的位置。
反应自由能越低的反应,生成物热力学稳 定性越高。
c T2
H 0R= H0+ aT +
12bT2 -
c T
H0 积分常数依反应于标况下可确定:
H0
= H 0R298- 298 a -
2982 b +
2
c 298
(5-5) (5-6) (5-7) (5-8a)
(5-8b)
[(
材料科学基础-第五章 材料的相结构及相图

相律在相图中的应用
C
2 二元系
P 1 2
3 1
f 2 1 0
3 2 1 0
含义
单相合金,成分和温度都可变 两相平衡,成分、相对量和温度 等因素中只有一个独立变量 三相平衡,三相的成分、相对 量及温度都确定 单相合金其中两个组元的含量 及温度三个因素均可变 两相平衡,两相的成分、数量 及温度中有两个独立变量 三相平衡,所有变量中只有 一个是独立变量 四相平衡所有因素都确定不变
结构简单的具有极高的硬度及熔点,是合金工具钢和硬 质合金的重要组成相。
I. 间隙化合物
间隙化合物和间隙固溶体的异同点
相同点: 非金属原子以间隙的方式进入晶格。
不同点: 间隙化合物:间隙化合物中的金属组元大多与自 身原来的结构类型不同 间隙固溶体:间隙固溶体中的金属组元仍保持自 身的晶格结构
I. 尺寸因素
II. 晶体结构因素 组元间晶体结构相同时,固溶度一般都较大,而且有可 能形成无限固溶体。若不同只能形成有限固溶体。
III. 电负性差因素
两元素间电负性差越小,越易形成固溶体,且形成的 固溶体的溶解度越大;随两元素间电负性差增大,固 溶度减小。
1)电负性差值ΔX<0.4~0.5时,有利于形成固溶体 2)ΔX>0.4~0.5,倾向于形成稳定的化合物
Mg2Si
Mg—Si相图
(2)电子化合物
由ⅠB族或过渡金属元素与ⅡB,ⅢB,ⅣB族元素 形成的金属化合物。 不遵守化合价规律,晶格类型随化合物电子浓度 而变化。 电子浓度为3/2时: 呈体心立方结构(b相); 电子浓度为21/13时:呈复杂立方结构(g相); 电子浓度为21/12时。呈密排六方结构(e相);
NaCl型 CaF2型 闪锌矿型 硫锌矿型 (面心立方) (面心立方) (立方ZnS) (六方ZnS)
材料科学基础(讲稿5章)

Cu-Ni合金的铸态组织 ×50 树枝状
39
3)特点 (ⅰ) 冷却速度较快. (ⅱ) 开始结晶温度低于液相线. (ⅲ) 结晶中,剩余液相特别是晶粒内部成分不 均匀,先结晶的部分含高熔点组元较多,后 结晶的部分含低熔点组元较多;固相平均成 分偏离固相线,液相平均成分是否偏离液相 线随冷却速度而异. (ⅳ) 结晶终了温度低于固相线. (ⅴ) 通常不能应用杠杆定律. (ⅵ) 室温铸态有晶内偏析,形成树枝状组织.
Zn 2+、Ga 3+、Ge 4+、As 5+在Cu+中的最大固溶度(摩尔分数) 分别为38%、20%、12%、7%
6
Zn 2+、Ga 3+、Ge 4+、As 5+在Cu+中达最大 固溶度时所对应的e/a≈1.4→极限电子浓度
超过极限电子浓度,固溶体就不稳定,会 形成新相。 计算电子浓度时,元素的原子价指的是: 原子平均贡献出的共有电子数,与该元素 在化学反应时的价数不完全一致。
不平衡共晶形成原因分析
56
3)离异共晶——合金中 先共晶相的量很多,共晶 体的量很少时,共晶体中 与先共晶相相同的相依附 于先共晶相生长,将共晶 体中的另一相孤立在先共 晶相的晶界处.这种共晶 体两相分离的组织称为离 异共晶.
57ቤተ መጻሕፍቲ ባይዱ
Pb-Sb共晶离异组织(铸态)×400 α 相依附初生晶α 析出,形成离异的 白色网状β
58
3、包晶相图及其结晶
(1)相图分析 液相线 单相区 两相区 固相线 三相区 固溶度曲线 (2)包晶反应 在一定温度下,由一固定成分的液相与一个固定成 分的固相作用,生成另一个成分固定的固相的反应, 称为包晶反应。
材料科学基础 第五章 5.1-5.4相图

5.2.3 杠杆定律
设成份为 X的合金的总重量为1,液相的相对重量为 QL,其 成份为 X1,固相相对重量为Qα,其成份为X2,则 :
5.2.4 相图的类型和结构 根据组元的多少,可分为单元系、二元系、三元 系 …. 相图。
二元系相图的类型有:
① 液态无限溶解,固态无限溶解 -匀晶相图; ②液态无限溶解,固态有限溶解 -共晶相图和包晶
共晶组织:共晶转变产物。(是两相混合物)
共晶合金的特殊性质: ①比纯组元熔点低,简化了熔化和铸造的操作; ②共晶合金比纯金属有更好的流动性,其在凝固之 中防止了阻碍液体流动的枝晶形成,从而改善铸造 性能; ③恒温转变(无凝固温度范围)减少了铸造缺陷, 例如偏聚和缩孔; ④共晶凝固可获得多种形态的显微组织,尤其是规 则排列的层状或杆状共晶组织可能成为优异性能的 原位复合材料(in-situ composite )。
5.2.2 相律
相律(phase rule)是表示在平衡条件下,系统的自 由度数、组元数和相数之间的关系,是系统的平 衡条件的数学表达式。 相律数学表达式:f = C – P + 2 式中 P—平衡相数 C—体系的组元数 f—体系自由度(degrees of freedom) 数 2-温度和压力 自由度数 f:是指不影响体系平衡状态的独立可 变参数(温度、压力、浓度等)的数目。 在恒压下,相律表达式: f = C – P + 1
相律的应用
① 利用它可以确定系统中可能存在的最多平衡相数 单元系,因f ≥0,故 P≤1-0+1=2,平衡相最大为二个。 注意:这并不是说,单元系中能够出现的相数不能超过二 个,而是说,某一固定 T下,单元系中不同的相只能有两 个同时存在,而其它相则在别的条件下存在。
材料科学基础第五章
晶体的滑移过程不仅没有降低位错数量,反而大 大增加,这意味着,在变形过程中位错以某种机制 增殖了。 (1)Frank-Read 位错源 (Frank-Read Source)
由弗兰克-瑞德源提出的一种位错增殖机制
F-R源动作过程 材料科学基础第五章
刃位错AB的两端A和B被位错用结点钉扎住
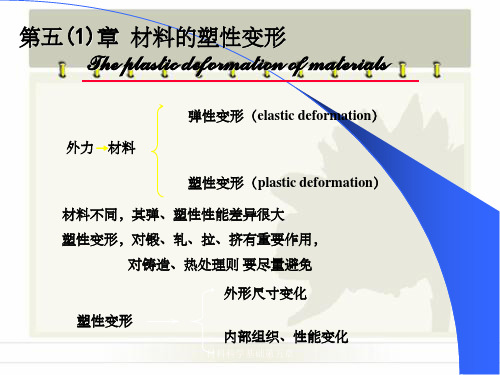
塑性变形
外形尺寸变化
内部组织、性能变化
材料科学基础第五章
※ 1. 弹性和粘弹性(Elasticity and Viscoelasticity)
一. 弹性变形(Elastic Deformation)
二. 低碳钢的拉伸试验
三. 弹性变形: 可逆性
四.
外力去处后可完全恢复
五.
材料科学基础第五章
本质:可从原子间结合力的 角度来了解之
材料科学基础第五章
转动的原因 两对力偶:
s1 -s2
为上下两滑移面的法向分应力
在该力偶作用下,使滑移面转至轴 向平行
t1-t2 垂直于滑移方向的分切应力
在该力偶作用下,使滑移方向转到最大 分切应力方向
t1 -t2 是//滑移方向的真正引起滑
移的有效分切应力
材料科学基础第五章
晶体滑移晶体转动位向变化取向因子变化 分切应力值变化
几何 硬 化现象 软
5. 多系滑移 Multiple slip
外力下,滑移首先发生在分切应力最大,且te tc的滑 移系-原始滑移系(primary slip system)上。但由于伴 随晶体转动空间位向变化另一组原取向不利(硬取向) 滑移系逐渐转向比较有利的取向(软取向),从而开始滑 移,形成两组(或多组)滑移系同时进行或交替进行,称 为多系滑移。
材料科学基础-第5章

当前你正在浏览到的事第十五页PPTT,共三十七页。
第二节 形核
一、自发形核
2. 临界大小
在一定过冷度下,ΔGV为负值,而σ恒 为正值。可见晶体总是希望有最大的体
五、结晶的一般过程
温度变化规律: 材料的熔体在熔点以上不断
散热,温度不断下降,到理论结 晶温度并不是马上变成固态的晶 体,继续降温而出现过冷。过冷 到某一程度开始结晶,放出结晶 潜热,可能会使其温度回升。到 略低于熔点的温度时,放出的热 量和散热可达到平衡,这时处于 固定温度,在冷却曲线上出现平 台。结晶过程完成,没有潜热的 补充,温度将重新不断下降,直 到室温。
第五章 晶体生长与晶体缺陷
• 概述 • §5.1 液体的性质和结构 • §5.2 凝固的热力学条件 • §5.3 形核过程 • §5.4 晶体的长大 • §5.5 铸锭的组织 • §5.6 单晶体的凝固
当前你正在浏览到的事第一页PPTT,共三十七页。
第五章 晶体生长与晶体缺陷
• §5.7 玻璃态与金属玻璃 • §5.8 点缺陷 • §5.9 线缺陷 • §5.10 面缺陷
示为n为n单i 位n 体=积ex原p(子-数△小G/,knT)i为在n个原于中(含5.有1)i个原子的原子团 数 知目,当,△△GG增为加原时子,团n 与i 减数小目。相△同的G的单来个源原有子两的个自,一由个能与差固。、由液式相(5.1)
的自由能差有关,另一个是把固相与液相分开的界面能:前者在平 衡温度时为零,低于熔点时为负值,高于熔点时为正值;后者永 远为正值。
晶核而长大,所以金属凝固时,晶核必须要求等
无机材料科学基础第五章固溶体

将外来组元引入晶体结构,占据主晶相质点位置一部分或间隙位置一部分,仍保持一个晶相,这种晶体称为固溶体(即溶质溶解在溶剂中形成固溶体),也称为固体溶液。
固溶体的分类
置换型固溶体
间隙型固溶体
形成固溶体后对晶体性质的影响
固溶体的研究方法
第五章 固溶体
A
根据外来组元在主晶相中所处位置 ,可分为置换固溶体和间隙固溶体。
在金属氧化物中,主要发生在金属离子位置上的置换,如:MgO-CaO,MgO-CoO,PbZrO3-PbTiO3,Al2O3-Cr2O3等。
C3S的固溶体C54S16MA2.相当于18个Si中有两个被置换。
间隙式固溶体,亦称填隙式固溶体,其溶质原子位于点阵的间隙中。
01
金属和非金属元素H、B、C、N等形成的固溶体都是间隙式的。如:在Fe-C系的α固溶体中,碳原子就位于铁原子的BCC点阵的八面体间隙中。
3、固溶强化
实际应用:铂、铑单独做热电偶材料使用,熔点为1450℃,而将铂铑合金做其中的一根热电偶,铂做另一根热电偶,熔点为1700℃,若两根热电偶都用铂铑合金而只是铂铑比例不同,熔点达2000℃以上。
4、形成固溶体后对材料物理性质的影响 固溶体的电学、热学、磁学等物理性质也随成分而连续变化,但一般都不是线性关系。固溶体的强度与硬度往往高于各组元,而塑性则较低。
主要是氧化镁杂质的存在,阻碍了晶界的移动速度,使气体容易消除,从而得到透明氧化铝陶瓷。
另外,氧化铝掺杂其他一些氧化物可制的相应颜色的各类宝石制品。
详见P79页。
透明Al2O3 陶瓷
”
A
B
C
固溶体类型的大略估计
固溶体类型的实验判别
固溶体组成的确定
五、固溶体的研究方法
无机材料科学基础相图热力学基本原理及相平衡PPT教案

γ-鳞石英
但 由 于 转 变 速度慢 ,实际 可长期 存在。
第2页/共124页
二、相 律
根据吉布斯相律 f = c-p+2
f - 自由度数 c - 独立组分数 p - 相数 2 - 温度和压力外界因素
硅酸盐系统的相律为 : f = c-p+1
凝聚系统:不含气象或气象可以忽略的系统。
第3页/共124页
即 热 力学非 平衡态 ,经常 出现于 硅酸盐 系统中 。
α-石英
870 ℃
573℃
α-鳞石英 163℃
1470℃ α-方石英 180~270℃
β-石英
β-鳞石英 117℃
β-方石英
说 明 : 介 稳 态的出 现不一 定都是 不利的 。由于 某些介 稳态具 有 所 需 要 的 性 质,因 而创造 条件(快 速冷却 或掺加 杂质) 有 意 把 它 保 存下来 。 如 : 水 泥 中 的β - C2S,陶 瓷中介 稳的四 方氧化 锆 ; 耐 火 材 料 硅砖 中的鳞 石英以 及所有 的玻璃 材料。
熔体(1600℃) 熔体 (1670℃)
α-石英
870 ℃
573℃
α-鳞石英 163℃
1470℃α-方石英
1723 ℃
180~270℃
熔融石英 急 冷
β-石英
β-鳞石英
β-方石英
石英玻璃
117℃ γ-鳞石英 重 建 型 转 变(慢)
位 移 型 (快) 转 变
第11页/共124页
SiO2相图
1、平衡加热:以使材料任意两个微区的温差区域无限小的速度加热。
第4页/共124页
2、 组 分 、 独 立组分 (组 元 )组 分 : 组 成系统 的物质 。 独 立 组 分 :足 以表示 形成平 衡系统 中各相 所需要 的最少 数目的 组分: c = 组 分 数 - 独立 化学反 应数目 -限制 条件 例如:
材料科学基础-第五章-材料的相结构及相图-PPT

Mg2Si
Mg—Si相图
(2)电子化合物
由ⅠB族或过渡金属元素与ⅡB,ⅢB,ⅣB族元素
形成的金属化合物。
不遵守化合价规律,晶格类型随化合物电子浓度而
变化。
电子浓度为3/2时: 呈体心立方结构(b相);
电子浓度为21/13时:呈复杂立方结构(g相);
电子浓度为21/12时。呈密排六方结构(e相);
体。
III. 电负性差因素
IV. 两元素间电负性差越小,越易形成固溶体,且形
成的固溶体的溶解度越大;随两元素间电负性差
增大,固溶度减小。
1)电负性差值ΔX<0.4~0.5时,有利于形成固溶体
2)ΔX>0.4~0.5,倾向于形成稳定的化合物
IV. 电子浓度因素
V. 电子浓度的定义是合金中各组成元素的价电子数总
子的价电子数恰好使负离子具有稳定的电子层
结构。
金属元素与周期表中的ⅣA,ⅤA,ⅥA元素
形成正常价化合物。
有较高的硬度,脆性很大。
例如:Mg2Si、Mg2Sn、Mg2Pb、MgS、MnS等
(1)正常价化合物
正常价化合物的分子式只有AB,A2B或AB2两种。
常见类型:
NaCl型
CaF2型
Cu原子形成四面体(16个)。
每个镁原子有4个近邻镁原子和12个近邻铜原子;
每个铜原子有6个近邻的铜原子和6个近邻的镁原子
。
Cu
Mg
II. 拉弗斯(Laves)相
②MgZn2型:六方晶系。
Mg原子形成硫锌矿结构;Zn原子形成四面体。
每个Mg原子有4个近邻Mg原子和12个近邻Zn原
子。
每个Zn原子有6个近邻Zn原子和6个近邻Mg原子
材料科学基础第五章3-2界面偏聚

T↑ → C↓↓,成指数下降。原因:组态熵的影响增大。
但是,如果温度过低,虽然平衡时的C应该更高,但是受扩散限制, 反而无法达到较高的平衡值。
5
(3) 畸变能差(E)和最大固溶度(Cm)
E↑ → C↑↑ ,二者成指数关系。
溶质原子在晶内和晶界的畸变能E大小,与溶质和溶剂原子的差
25
不同角下的第二相分布:
Θ=180o
图中绿色为第二相
120°
β相在晶界铺展开来
晶界与晶棱上第二相的形状
第二相存在于界角:
cos(x/2) = 1/[2sin(/2)] cos(180-y) = 1/[(3)tg(/2)]
180° 120° 60°
0°
xy 120° 90°
109°28’ 0° 180°
形状 球形 曲面四面体 网络状骨骼 片状
存在于界角上的第二相
G = Vmp = 2 /RVm 即:G/Vm = 2 /R = p (驱动力)
通过以上分析可见,晶界曲率是晶界迁移的驱动力,界面曲率越大, 曲率半径越小,则驱动力越大,界面迁移速度越大。
界面总是向凹侧推进,界面迁移减小界面曲率,降低压力差和自由 能差,以趋向于热力学稳定状态。
13
三、影响界面迁移率的因素
界面能的变化与Fy力作功相等
Fy
y
l
d d
其中 y l
Fy
d d
结论:当界面处于低界面能位向,界面不发生转动,否 则Fy驱动界面转动,dγ/dθ为扭矩项
界面平衡的热力学条件 (A)0 1 OR 2 OS 3 OT
单相多晶体平衡时,在与晶棱垂直 面上的晶界交成3线节点,线与线之 间夹角接近120o。
热力学数据在无机化学中的应用01

热力学数据在无机化学中的应用引言化学热力学数据在化学领域里有着广泛的应用。
在无机化学范围内,主要讨论能量平衡和一定条件下,化学反应进行的方向及限度和反应发生条件,还有就是判断一些无机物的溶解性。
1、在化学反应中的应用1.1 判断化学反应进行的方向及发生条件综合焓变(△H)和熵变(△S)这两个能量项, 热力学用自由能(G)这个状态函数的变化量(△G)来判断反应进行的方向, 即吉布斯一亥姆霍兹提出的[1]:△G = △H - T△S (1)或△Gθ298 = △Hθ298 - T△Sθ298(2)当△G < 0 过程自发△G = 0 过程处于平衡态△G > O 过程非自发(或逆过程自发)因此, 在恒温恒压下进行的化学反应:(1 ) 体系焓减或熵增, △G < 0 , 反应自发进行。
(2 ) 当反应热很小, 熵效应对反应进行的方向起决定性作用。
(3 ) 反应熵变很小,特别在低温时, T△S此项影响不大,△H决定反应进行的方向。
(4 ) 反应熵变较大, 特别当温度变化较大时, 有可能导致△G符号的改变, 从而改变反应进行的方向。
例1 石灰窑中烧制石灰的反应为CaCO3(s)→ CO2(g) + CaO(s)试计算欲使石灰石以一定速度分解所需的最低温度是多少?解: 查得有关物质的△Gθ、△Hθ和SθCaCO3(s) →CO2(g) + CaO(s) △Gθ(KJ•mol-1) -1128.8 -604.2 -394.0△Hθ(KJ•mol-1) -1207.0 -635.1 -393.0Sθ (J•mol-1•K-1) 92.9 39.7 214.0计算得该反应的△Gθ298= 130.6 KJ•mol-1 , 则该反应在室温下不能自发进行。
再计算得该反应的△Hθ298=178.9 J•mol-1;△Sθ298=160.8J•mol-1•K-1,1根据△G θ = △H θ - T △S θ 欲使反应自发进行,必需△G θ < 0,即T △S θ > △H θ。
热力学研究在无机化学中的应用

这样, Si - O 单键 ( 实际上是 + p - d) 的键能比 C - O 单键 (纯)大就不难理解了。
再如碱金属元素的性质递变规律。随着原子序数增加,半径 增大,金属变得活泼,但Li常表现出反常性,如电极电位是: θ(Li+/Li) < θ(Na+/Na) > θ(Cs+/Cs ) 这在无机化学中是以Li+离子半径最小, 具有较大的水合焓来 解释的。 M(s)-e -e M+(aq)
同学们也许会问,Si的半径大于C,它同氧之间的键能应 比C同O的键能小,为什么Si-O单键键能比C-O单键键能大。 这个深层的原因得联系两个原子的结构: C为第二周期元素,由于内层只有1s电子,半径较小,当 与第二个原子即O键合时除了形成键外, 还可以生成p-p键。 因而在两个原子之间存在多重键: 如氧与碳生成CO2和CO。 C O C
上述第二步复述形式,不是唯一的(盖斯定律),还可设计出好 多种,如 ΔfHmθ(NX3) 1 3 N (g) + X (g) NX3 2 2 2 2
ΔfHmθ(N3+,g) 3ΔfHmθ(X-,g)
N3+(g)+ 3X- ΔfHmθ(NX3)=ΔfHmθ(N3+,g)+3ΔfHmθ(X-,g)-ΔlatHmθ(NX3) z1 z2 θ 这里使用了标准生成焓和晶格焓的定义。 ΔlatHm =f r +r + - ΔfHmθ(NCl3)-ΔfHmθ(NF3)=3[ΔfHmθ(Cl-,g)-ΔfHmθ(F-,g)] +[ΔlatHmθ(NF3) –ΔlatHmθ(NCl3)] =[(-246)-(-270.7)]+[(F-半径小, NF3晶格能大)-(Cl-半 径大, NCl3晶格能小)] = [ >0 ] +[ >0 ] > 0 因此,由此得到第三步,热力学结论:NF3有很高的稳定性是 因为 F- 离子的生成焓负值大和小的 F- 与 N3 + 结合形成的 NF3 的晶 格有较多的能量放出之故。
潘金生《材料科学基础》(修订版)(名校考研真题 材料热力学)【圣才出品】

第5章 材料热力学一、填空题相平衡时,系统内的相数可以通过系统自由度、______和对系统平衡状态能够产生影响的外界因素数目的关系式来进行计算。
[北京工业大学2009研]【答案】组元数【解析】相平衡时,可以根据吉布斯相律来计算相数,其通式为:f=C-P+2,式子中C为系统组元数,P为平衡共存的相的数目,f为自由度。
二、判断题玻璃在常温下能长期稳定存在,因而它是热力学稳定态。
()[南京工业大学2008研]【答案】×【解析】玻璃在常温下长期保持介稳态,是稳定的。
三、名词解释1.相平衡[北京工业大学2009研]答:相平衡是指系统中各相的化学势相等且各个组元在各相中的化学势相等的状态。
2.热力学势函数( 函数)[中南大学2004研]答:热力学势函数是热力学基本函数的一种组合,热力学势函数也是一种连续的状态函数。
四、简答题1.固体中原子的扩散必须具备哪些基本条件?[西安交通大学2003研]答:固体中原子的扩散必须存在化学位梯度。
2.Al合金时效处理时往往先析出亚稳相,在热力学和动力学理论基础上讨论未析出平衡相的原因。
不少沉淀相与母相基体之间存在特定的位向关系,试分析这种位向关系的产生原因。
[清华大学2005研]答:(1)未析出平衡相的原因先析出亚稳相是由于平衡相与母相之间的界面能高,而亚稳相与母相间的界面能低,界面能是固态相变形核时的主要能垒,要克服这个平衡相形核能垒往往需要很大的过冷度,系统才能发生明显的形核。
以动力学看,在一定过冷度下,如果亚稳相更快形成,而平衡相要慢很多,那么在时效处理时,合金中就会先形成亚稳相。
(2)沉淀相与母相基体之间特定位向关系产生原因要实现低的界面能,母相与新相之问的主要界面上的原子必须要有很好的匹配关系,这只能在一定的位向关系条件下才能实现,因此沉淀相与母相间存在特定的位向关系。
3.参照所示的Cu-Zn相图(图5-1),有一铜棒较长时间置于400℃的Zn液中,请画出从铜棒表面到内部沿深度方向的:Zn的浓度分布、相分布、化学位分布。
无机材料科学基础答案

1、熔体的概念:不同聚合程度的各种聚合物的混合物硅酸盐熔体的粘度与组成的关系(决定硅酸盐熔体粘度大小的主要因素是硅氧四面体网络连接程度)在熔体中加入LiO2、Na2O 、K2O 和BaO 、PbO 等,随加入量增加,粘度显着下降。
在含碱金属的硅酸盐熔体中,当Al2O3/Na2O ≤1时,用Al2O3代替SiO2可以起“补网”作用,从而提高粘度。
一般加入Al2O3、SiO2和ZrO2有类似的效果。
流动度为粘度的倒数,Φ=粘度的理论解释:绝对速度理论η=η0exp(ΔE/kT)自由体积理论=B exp [ ]=Aexp( )过剩熵理论 = Cexp [ ] = Cexp ( )2、非晶态物质的特点 :近程有序,远程无序3、玻璃的通性(1)各向同性(若有应力,为各向异性) (2)介稳性(3)熔融态向玻璃态转化的可逆与渐变性(4)、熔融态向玻璃态转化时其物化性质随温度变化的连续性4、 Tg 、Tf , 相对应的粘度和特点钠钙硅酸盐熔体粘度与温度关系表明:熔融温度范围内,粘度为50~500dPa·s 。
工作温度范围粘度较高,约103~107dPa·s 。
退火温度范围粘度更高,约~ dPa·s 。
Tg-脆性温度、退火温度,Tf-软化温度、可拉丝的最低温度 5、单键强度 > 335 kJ/mol(或80 kcal/mol)的氧化物——网络形成体。
单键强度 < 250 kJ/mol(或60 kcal/mol)的氧化物——网络变性体。
在250~335 kJ/mol 为——中间体,其作用介于玻璃的网络形成体和网络变性体之间。
6、玻璃形成的热力学观点:熔体是物质在TM 以上存在的一种高能状态。
据随温度降低,熔体释放能量大小不同,冷却途径分为结晶化,玻璃化,分相ΔGv 越大析晶动力越大,越不容易形成玻璃。
ΔGv 越小析晶动力越小,越容易形成玻璃。
玻璃形成的动力学观点:)(00T T KV -α0T T B-)(0T T C D P -∆0T T B-η1过冷度增大,熔体质点动能降低,有利于质点相互吸引而聚结和吸附在晶核表面,有利于成核。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章热力学应用
§5-1 热力学应用计算方法
一、经典法
已知在标准条件下反应物与生成物从元素出发的生成热△H0298。
生成自由能△G0298及反应物与产物的热容温度关系式Cp=a+bT+cT-2中各系数时,计算任何温度下反应自由能变化可据吉布斯—赤赤姆霍兹关系式进行
[α(△G0R/T)/Αt]P=-△H0R/T2(5-5)
据基尔霍夫公式:
△H0R=△H012298+∫T298△cpo/T (5-6)
和考虑反应热容变化关系:
△cp=△a+△bT+△c/T2(5-7)
可积分求得:
△H0R=△H0+△aT+½△bT2+△c/T (5-8a)
△H0为积分常数:
△H0=△H012298+298△a-2982△b/2+△c/298 (5-8b)
将(5-6)式代入(5-5)式并积分,便得任何温度下反应自由能变化△G0298的一般公式:△G0298=△H0-△aTLnT-½△Bt2-½△cT-1-Yt (5-9a)
y=(△G0R·298-△H0)/298+△aLn(298)+298△b/2+△c/2×2982
(5-9b)
经典法计算反应△G0298一般步骤:
1、由有关数据手册,索取原始热力学基本数据:反应物和生成物的△H0298、△G0298(S0298)以及热容关系式中的各项温度系数:a、b、c。
2、计算标况下(298K)反应热△H0R·298,反应自由能变化△G0R·298, G0R·298或反应熵变△S0R·298以及反应热容变化△Cp中各温度系数△a、△b、△c。
3、将△H0R`298、△a、△b以及△c分别代入式(5-8b)各项,计算积分常数△H0。
4、△G0R`298、△a、△b以及△c分别代入式(5-9b)各项,计算积分常数y。
5、将△H0、y、△a、△b以及△c代入(5-9a)式得△G0R~T函数关系式。
二、Ф函数法:
热力学势函数是热力学基本函数的一种组合,其定义为:
ФT=-(G0T—H0T0)/T
若T0=298K,则Ф'T=-(G0T—H0298)/T
对于某一种物质有形成热力学势△Ф'T
△Ф'T=-△G0T-△H0298/T (5-15)
对于任一反应过程有:
△Ф'RT=-△G0RT—△H0298/T (5-16)
∴△G0RT=△H0R 298—T△Ф'RT(5-17)
△Ф'RT=∑1(△ФR)生成物—∑2(△Ф'R)反应物(5-18)
Ф函数计算反应△G0R的步骤:
1、查出与反应有关物质(从元素出发的)标准生成热H0298,不同温度下物质的△Ф'R、△Ф'T;
2、计算标况下反应△H0R 298和依(5-18)式计算反应△Ф'RT;
3、依式(5-17)计算不同温度下反应△G0RT。
三、△G计算法举例
根据已知的热化学数据分别用经典法和Ф'函数法就水泥生产工艺过程中重要分解反应:CaCO3⇒CaO(S)+CO2(g)
作反应自由能△G0实例计算并分析热分解温度和分解压力间关系。
1、经典计算法;
2、Ф函数法计算。
(P146~148)
§5-2 热力学应用实例
一、纯固相参与的固相反应
SiO2—CaO系统:
(一)CaO+Si02=CaO·SiO2
(二)3CaO+2Si02=3CaO·2SiO2
(三)2CaO+3Si02=2CaO·SiO2
(四)3CaO+Si02=3CaO·SiO2
查手册,按前述方法计算结果如表5-4 如图5-3(A)
如CaO/SiO2=1,1.5,2,3等数值,各反应自由能变化与温度的关系由表5-5和图5-3给出。
分析图5-3,随CaO/SiO2增加C2S、C3S形成势的变化。
二、伴有气相参与的固相反应
CaCO3—SiO2系统
(一)CaCO3+Si02=CaO·SiO2+CO2
(二)3 CaCO3+2Si02=3CaO·2SiO2+3CO2
(三)2 CaCO3+Si02=2CaO·SiO2+2CO2
(四)3 CaCO3+Si02=3CaO·SiO2+3CO2
采用前述方法计算△G0RT如表5-9
可知在标准状态下CS、C2S3、Cb分别于858K、885K、868K开始自发生成。
C3S在950K开始自发生成,与纯方解石分解温度(1123K)比较,可推知各种硅酸钙的生成反应均在CaCO3分解反应剧烈开始之前就已开始。
如考虑CO2分压对反应的影响,根据(5-4)式得以下四个反应△G R(T)随温度及CO2分压变化关系式:
(一)△G R1=140.1—(0.163+8.314×10-3Lnplo2)T
(二)△G R2=437-(0.4947-0.025Ln Lnplo2)T
(三)△G R3=282.2-(0.325-0.017 Lnplo2)T
(四)△G R4=471.7-(0.497-0.025 Lnplo2)T
可见CO2分压的改变,可显著地影响△G R—T直线的斜率,P CO2越小,△G R—T直线斜率越大,致使同一温度下反应自由能越小,同时△G R=0,所对应的温度越低。
三、伴有熔体参与的固相反应
用热力学方法分析用刚玉坩埚熔制纯镍熔体的可能性。
设高温(1800K)镍熔体与刚玉存在如下反应:
1/3AI2O3(S)+Ni(l)=NiO(S)+2/3AI(l)(18800K)
由前述方法计算反应△G0RT得:
△G01800K=219.67(KJ/mol)
由式(5-4)得:
△G01800K=△G01800+RTLnα2/3AI/αNi
把熔体当作理想溶液处理
△G01800K=△G01800+2/3LnXAI=219.67+5.54×10-3TLnXAI
当铝被镍还原并熔于镍熔体中达最大程度时△G01800K=0
∴(XAI)max=exp{-219.67/5.54×10-3×1800}=2.71×10-10
可见,刚玉坩埚可用于熔融高纯度镍的容器。
四、反应热平衡计算
设反应物100%按化学计量发生,且反应在绝热的条件下进行,此时温度为T的反应物之Ai混合反应生成温度为T'的生成物之Bi,则整个反应体系的热量变化△H可构制如下途径计算:
∑T Ai△H→∑298K Ai△H→∑298K Bi△H3 →∑T`Bi
△H
即△H=△H1+△H2+△H3
=∫298T∑CpAidT+△H0R`298+∫T'298∑Cp·BidT
=-∑(△H0T-△H0298)Ai+△H0R·298+∑(△H0T'-△H0298)Bi
若反应系统压力保持恒定,则反应过程总放热量为系统总负焓变:
Q放=-△H=∑(△H0T-△H0298)Ai-∑(△H0T'-△H0298)Bi-△H0R·298
五、金属氧化物的高温稳定性
将各种氧化物标准生成自由能与温度的函数关系用图线方式汇集成△G0R~T图
1、利用氧化物标准生成△G0R~T图,可方便地比较各种金属氧化物的热力学稳定性。
△G0负值越大,钙金属氧化物稳定性越高;
2、利用△G0R~T图,可获得任一温度下纯金属与其氧化物呈平衡时有关气相的知识;
3、利用气态氧化物的生成自由能可计算高温下与固态氧化物达到平衡的气相中有关氧化物的蒸气压。
