人教版八年级上册期末考试
人教版八年级上册数学期末考试试题带答案

人教版八年级上册数学期末考试试卷一、选择题。
(每小题只有一个正确答案)1.下列四个图案中,是轴对称图形的是()A .B .C .D .2.如果线段a ,b ,c 能组成三角形,那么它们的长度比可能是()A .1∶2∶4B .2∶3∶4C .3∶4∶7D .1∶3∶43.石墨烯是现在世界上最薄的纳米材料,其理论厚度仅是0.00000000034m ,这个数用科学记数法表示正确的是()A .3.4×10-9m B .0.34×10-9mC .3.4×10-10mD .3.4×10-11m 4.下列运算中,正确的是()A .22a a a ⋅=B .224()a a =C .236a a a ⋅=D .2323()a b a b =⋅5.如图,点P 是∠AOB 的平分线OC 上一点,PD ⊥OA ,垂足为D ,若PD =2,则点P 到边OB 的距离是()A .4B C .2D .16.若分式13x +有意义,则x 的取值范围是()A .x >3B .x <3C .x ≠-3D .x =37.如图,在△ABC 中,∠A =80°,∠C =60°,则外角∠ABD 的度数是()A .100°B .120°C .140°D .160°8.下列各式是完全平方式的是()A .214x x -+B .21x +C .22x xy y -+D .221a a +-9.已知一个多边形的内角和是1080°,则这个多边形是()A.五边形B.六边形C.七边形D.八边形10.如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①△ACD≌△BCE;②AD=BE;③∠AOB=60°;④△CPQ是等边三角形.其中正确的是()A.①②③④B.②③④C.①③④D.①②③二、填空题11.点()2,1M-关于y轴的对称点的坐标为______.12.如果多边形的每个内角都等于150︒,则它的边数为______.13.如图,△ABC≌△DCB,A、B的对应顶点分别为点D、C,如果AB=6cm,BC=12cm,AC=10cm,DO=3cm,那么OC的长是_____cm.14.在△ABC中,AB=AC,AB的垂直平分线交AC于D,交AB于E,连接BD,若∠ADE =40°,则∠DBC=_____.15.已知13aa+=,则221+=aa_____________________;16.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β=_____.三、解答题17.解方程:21133xx x-=---.18.先化简,再求值:(3x+2)(3x﹣2)﹣10x(x﹣1)+(x﹣1)2,其中x=﹣1.19.如图:已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.20.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠EAB=110°,∠C=60°,点D在GH上,求∠BDC的度数.21.甲、乙两工程队共同完成一项工程,乙队先单独做1天后,再由甲、乙两队合作2天就完成了全部工程,已知甲队单独完成这项工程所需的天数是乙队单独完成工程所需天数的2倍,则甲、乙两工程队单独完成工程各需多少天?22.如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.23.如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.求证:(1)AE=CD.(2)若AC=12cm,求BD的长.24.某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)该商场两次共购进这种运动服多少套?(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?25.如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.(1)若点Q与点P的运动速度相等,经过3秒后,△BPD与△CQP是否全等?请说明理由;(2)若点Q与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP 全等?参考答案1.C【解析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,对各项进行判断找出不是轴对称图形即可.【详解】A.不是轴对称图形;B.不是轴对称图形;C.是轴对称图形;D.不是轴对称图形;故选:C .【点睛】考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.2.B【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析求解.【详解】A 、1+2<4,不能组成三角形;B 、2+3>4,能组成三角形;C 、3+4=7,不能够组成三角形;D 、1+3=4,不能组成三角形.故选B .【点睛】考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.3.C【详解】试题分析:根据科学记数法的概念可知:用科学记数法可将一个数表示10n a ⨯的形式,所以将0.00000000034用科学记数法表示103.410-⨯,故选C .考点:科学记数法4.B【解析】【分析】根据同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘,对各选项分析判断后利用排除法求解.【详解】A 选项:23a a a ⋅=,故是错误的;B选项:()224a a=,故是正确的;C选项:235a a a⋅=,故是错误的;D选项:()3243=⋅,故是错误的;a b a b故选:B.【点睛】考查了同底数幂乘法和幂的乘方,解题关键是运用了同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘.5.C【分析】根据角平分线的性质解答.【详解】解:如图,作PE⊥OB于E,∵点P是∠AOB的角平分线OC上一点,PD⊥OA,PE⊥OB,∴PE=PD=2,故选C.【点睛】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.6.C【解析】【分析】考查分式有意义的条件:分母≠0,即x+3≠0,解得x的取值范围.【详解】∵x+3≠0,∴x≠-3.故选:C.考查的是分式有意义的条件:当分母不为0时,分式有意义.7.C【解析】【分析】根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【详解】由三角形的外角性质得,∠ABD=∠A+∠C=80°+60°=140°.故选C.【点睛】考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.8.A【解析】【分析】根据完全平方式(a2+2ab+b2和a2-2ab+b2)进行判断.【详解】A、是完全平方式,故本选项正确;B、不是完全平方式,故本选项错误;C、不是完全平方式,故本选项错误;D、不是完全平方式,故本选项错误;故选:A.【点睛】考查了对完全平方式的应用,主要考查学生的判断能力.9.D【分析】根据多边形的内角和=(n﹣2)•180°,列方程可求解.【详解】设所求多边形边数为n,∴(n﹣2)•180°=1080°,解得n=8.【点睛】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.10.A【分析】由已知条件运用等边三角形的性质得到三角形全等,进而得到更多结论,然后运用排除法,对各个结论进行验证从而确定最后的答案.【详解】∵△ABC和△CDE是正三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD,∴∠ACD=∠BCE,∴△ADC≌△BEC(SAS),故①正确,∴AD=BE,故②正确;∵△ADC≌△BEC,∴∠ADC=∠BEC,∴∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,故③正确;∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC,∴△CDP≌△CEQ(ASA).∴CP=CQ,∴∠CPQ=∠CQP=60°,∴△CPQ是等边三角形,故④正确;故选A.【点睛】考查等边三角形的性质及全等三角形的判定等知识点;得到三角形全等是正确解答本题的关键.11.()2,1【分析】关于y 轴对称的点,纵坐标相同,横坐标互为相反数.【详解】∵关于y 轴对称的点,纵坐标相同,横坐标互为相反数∴点()2,1M -关于y 轴的对称点的坐标为()2,1.故答案为:()2,1【点睛】考核知识点:轴对称与点的坐标.理解轴对称和点的坐标关系是关键.12.12【分析】先求出这个多边形的每一个外角的度数,再用360°除以外角的度数即可得到边数.【详解】∵多边形的每一个内角都等于150°,∴多边形的每一个外角都等于180°﹣150°=30°,∴边数n =360°÷30°=12.故答案为12.【点睛】本题考查了多边形的内角与外角的关系,求出每一个外角的度数是解答本题的关键.13.7【解析】【分析】根据△ABC ≌△DCB 可证明△AOB ≌△DOC ,从而根据已知线段即可求出OC 的长.【详解】∵△ABC ≌△DCB ,∴AB=DC ,∠A=∠D ,又∵∠AOB=∠DOC (对顶角相等),∴△AOB ≌△DOC ,∴OC=BO=BD-DO=AC-DO=7.故答案是:7.【点睛】考查了全等三角形的性质解题的关键是注意掌握全等三角形的对应边相等,注意对应关系.14.15°.【分析】先根据线段垂直平分线的性质得出DA=DB ,∠AED=∠BED=90︒,即可得出∠A=∠ABD ,∠BDE =∠ADE ,然后根据直角三角形的两锐角互余和等腰三角形的性质分别求出∠ABD ,∠ABC 的度数,即可求出∠DBC 的度数.【详解】∵AB 的垂直平分线交AC 于D ,交AB 于E ,∴DA=DB ,∠AED=∠BED=90︒,∴∠A=∠ABD ,∠BDE =∠ADE ,∵∠ADE =40︒,∴∠A=∠ABD=9040︒-︒=50︒,∵AB =AC ,∴∠ABC=150652︒-︒=︒,∴∠DBC =∠ABC-∠ABD=15︒.故答案为15︒.【点睛】本题考查线段垂直平分线的性质,等腰三角形的性质.15.7【分析】把已知条件平方,然后求出所要求式子的值.【详解】∵13a a +=,∴219a a ⎛⎫+= ⎪⎝⎭,∴2212+a a +=9,∴221+=a a =7.故答案为7.【点睛】此题考查分式的加减法,解题关键在于先平方.16.240°【详解】已知等边三角形的顶角为60°,根据三角形的内角和定理可得两底角和=180°-60°=120°;再由四边形的内角和为360°可得∠α+∠β=360°-120°=240°.故答案是:240°.17.无解【解析】【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】21133x x x -=---2-x=x-3-1-2x=-3-1-2x=3当x=3时,x-3=0,所以原分式方程无解.【点睛】考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.18.8x -3,-11【解析】【分析】原式利用平方差公式,完全平方公式,以及单项式乘以多项式法则计算,去括号合并即可得到结果.【详解】原式=9x 2-4-10x 2+10x+x 2+1-2x=8x-3当x=-1时,原式=-8-3=-11.【点睛】考查了整式的混合运算,平方差公式,以及完全平方公式,熟练掌握运算法则是解本题的关键.19.见解析【分析】先作CD的垂直平分线和∠AOB的平分线,它们的交点为P点,则根据线段垂直平分线的性质和角平分线的性质得到PC=PD,且P到∠AOB两边的距离相等.【详解】解:如图,点P为所作.【点睛】本复考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.20.50°【分析】先利用平行线求出∠CBG,再用邻补角的定义求出∠CBD,最后用三角形的内角和定理即可得出结论.【详解】解:∵EF∥GH,∴∠CBG=∠EAB,∵∠EAB=110°,∴∠CBG=110°,∴∠CBD=180°﹣∠CBG=70°,在△BCD中,∵∠C=60°,∴∠BDC=180°﹣∠C﹣∠CBD=180°﹣60°﹣70°=50°,即:∠BDC的度数为50°.【点睛】此题主要考查了平行线的性质,邻补角的定义,三角形内角和定理,求出∠CBD=70°是解本题的关键.21.甲需8天,乙需4天【解析】【分析】根据乙队先单独做1天后,再由两队合作2天就完成了全部工程则等量关系为:乙一天的工作量+甲乙合作2天的工作量=1,再设未知数列方程,解方程即可.【详解】设乙队单独完成所需天数x天,则甲队单独完成需2x天,1112(1++=2x x x解得:x=4,当x=4时,分式方程有意义,所以x=4是分式方程的解,所以甲、乙两队单独完成工程各需8天和4天.答:甲、乙两队单独完成工程各需8天和4天.【点睛】考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.22.证明见解析【详解】试题分析:首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.试题解析:∵AB=AC=AD,∴∠C=∠ABC,∠D=∠ABD.∴∠ABC=∠CBD+∠D.∵AD∥BC,∴∠CBD=∠D.∴∠ABC=2∠D.又∵∠C=∠ABC,∴∠C=2∠D.23.(1)见解析;(2)6【分析】(1)根据DB ⊥BC ,CF ⊥AE ,得出∠D =∠AEC ,再结合∠DBC =∠ECA =90°,且BC =CA ,证明△DBC ≌△ECA ,即可得证;(2)由(1)可得△DBC ≌△ECA ,可得CE=BD ,根据BC=AC=12cm AE 是BC 的中线,即可得出12CE BC =,即可得出答案.【详解】证明:(1)证明:∵DB ⊥BC ,CF ⊥AE ,∴∠DCB +∠D =∠DCB +∠AEC =90°.∴∠D =∠AEC .又∵∠DBC =∠ECA =90°,且BC =CA ,在△DBC 和△ECA 中90D AEC DBC ECA BC AC ∠∠∠∠⎪⎩︒⎧⎪⎨====,∴△DBC ≌△ECA (AAS ).∴AE =CD ;(2)由(1)可得△DBC ≌△ECA∴CE=BD ,∵BC=AC=12cm AE 是BC 的中线,∴162CE BC cm ==,∴BD=6cm .【点睛】本题考查了全等三角形的判定和性质,直角三角形斜边上的中线,证明△DBC ≌△ECA 解题关键.24.(1)商场两次共购进这种运动服600套;(2)每套运动服的售价至少是200元【分析】(1)设该商场第一次购进这种运动服x 套,第二次购进2x 套,然后根据题意列分式解答即可;(2)设每套售价是y 元,然后根据“售价-两次总进价≥成本×利润率”列不等式并求解即可.【详解】解:(1)设商场第一次购进x 套运动服,由题意得6800032000102x x-=解这个方程,得200x =经检验,200x =是所列方程的根22200200600x x +=⨯+=;答:商场两次共购进这种运动服600套;(2)设每套运动服的售价为y 元,由题意得600320006800020%3200068000y --+ ,解这个不等式,得200y ≥.答:每套运动服的售价至少是200元.【点睛】本题主要考查了分式方程和一元一次不等式的应用,弄清题意、确定量之间的关系、列出分式方程和不等式是解答本题的关键.25.(1)全等;(2)当点Q 的运动速度为54厘米/秒时,能够使△BPD 与△CQP 全等.【分析】(1)根据时间和速度分别求得两个三角形中的边的长,根据SAS 判定两个三角形全等;(2)根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P 运动的时间,再求得点Q 的运动速度.【详解】(1)因为t =3秒,所以BP =CQ =1×3=3(厘米),因为AB =10厘米,点D 为AB 的中点,所以BD =5厘米.又因为PC =BC BP -,BC =8厘米,所以PC =835-=(厘米),所以PC =BD .因为AB =AC ,所以∠B=∠C,所以△BPD≌△CQP(SAS).(2)因为P v≠Q v,所以BP≠CQ,当△BPD≌△CPQ时,因为∠B=∠C,AB=10厘米,BC=8厘米,所以BP=PC=4厘米,CQ=BD=5厘米,所以点P,点Q运动的时间为4秒,所以54Qv 厘米/秒,即当点Q的运动速度为54厘米/秒时,能够使△BPD与△CQP全等.【点睛】考查了全等三角形的判定,等腰三角形的性质.解题时,主要是运用了路程=速度×时间的公式.熟练运用全等三角形的判定和性质,能够分析出追及相遇的问题中的路程关系.。
人教版数学八年级上册期末考试试卷有答案
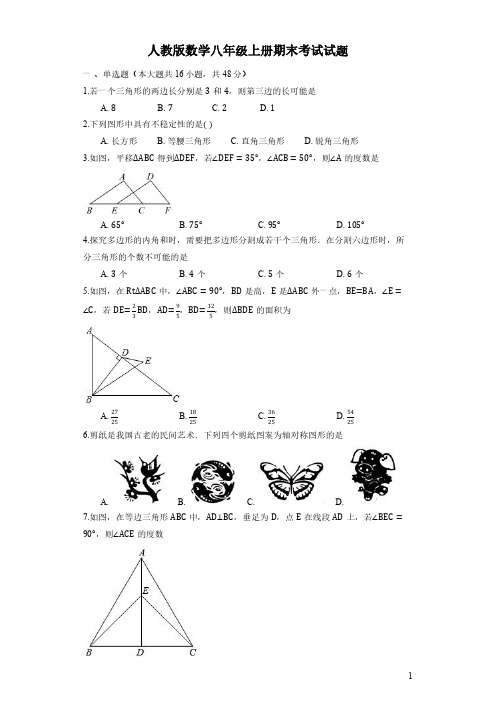
人教版数学八年级上册期末考试试题一、单选题(本大题共16小题,共48分)1.若一个三角形的两边长分别是3和4,则第三边的长可能是A.8B.7C.2D.12.下列图形中具有不稳定性的是( )A.长方形B.等腰三角形C.直角三角形D.锐角三角形3.如图,平移ΔABC得到ΔDEF,若∠DEF=35°,∠ACB=50°,则∠A的度数是A.65°B.75°C.95°D.105°4.探究多边形的内角和时,需要把多边形分割成若干个三角形.在分割六边形时,所分三角形的个数不可能的是A.3个B.4个C.5个D.6个5.如图,在RtΔABC中,∠ABC=90°,BD是高,E是ΔABC外一点,BE=BA,∠E=∠C,若DE=23BD,AD=95,BD=125,则ΔBDE的面积为A.2725B.1825C.3625D.54256.剪纸是我国古老的民间艺术.下列四个剪纸图案为轴对称图形的是A. B. C. D.7.如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,若∠BEC= 90°,则∠ACE的度数A.60°B.45°C.30°D.15°8.下列式子不能用“两数和乘以这两数差的公式”计算的是A.(3b−a)(3b+a)B.(3b−a)(−3b−a)C.(3b−a)(6b+2a)D.(3b−a)(a−3b)9.下列多项式相乘,能用平方差公式计算的是A.(5x+2y)(3x−2y)B.(2x−y)(2x+y)C.(−m+n)(m−n)D.(a−2b)(2a+b)10.如图是小明的作业,那么小明做对的题数为A.2B.3C.4D.511.下列从左边到右边的变形中,是因式分解的是A.a2−9=(a−3)(a+3)B.(x−y)2=x2−y2C.x2−4+4x=(x+2)(x−2)+4xD.x2+3x+1=x(x+3+1x)12.如果多项式x2−5x+c可以用十字相乘法因式分解,那么下列c的取值正确的是A.2B.3C.4D.513.下列分式中属于最简分式的是( )A.x+2y+2B.1−x2x−2C.2x+2y6x−6yD.x2−9x+314.如果把分式2x2−3y2x−y中的x和y的值都变为原来的2倍,那么分式的值A.不变B.缩小为原来的12C.变为原来的2倍D.变为原来的4倍15.假期正是读书的好时候,小颖同学到重庆图书馆借了一本书,共280页,要在两周借期内读完,当她读了一半时,发现平均每天要多读21页才能在借期内读完,她读前一半时,平均每天读多少页?如果设读前一半时,平均每天读x页,则下面所列方程中,正确的是A.140x+140x−21=14B.280x+280x+21=14C.140140101016.体育测试中,小进和小俊进行800米跑测试,小进的速度是小俊的1.25倍,小进比小俊少用了40秒,设小俊的速度是x米/秒,则所列方程正确的是A.40×1.25x−40x=800 B.800x−8002.25x=40C.800x−8001.25x=40D.8001.25x−800x=40二、填空题(本大题共6小题,共18分)17.一个正多边形的每个内角都等于120°,那么它的内角和是______.18.如图,BD是ΔABC的角平分线,DE⊥AB于点E.ΔABC的面积为20,AB=12,BC=8,则DE的长为______.19.两位同学将同一个二次三项式进行因式分解时,一位同学因看错了一次项系数而分解成(x−1)(x−9);另一位同学因看错了常数项而分解成(x−2)(x−4),则原多项式因式分解的正确结果是:______.20.如图,在ΔABC中,BC边的垂直平分线交BC于D,交AB于E.若CE平分∠ACB,∠B=42°,则∠A=______.21.某校九年级学生去距学校6千米的地铁站参观,一部分同学们步行先走,过了40分钟后,其余学生乘坐公共汽车出发,结果他们同时到达,已知公共汽车的速度的步行学生速度的3倍,求步行学生的速度.若设步行学生的速度为x km/h,则可列方程______.22.化简:(1x−4−8x2−16)⋅(x+4)=______.三、计算、画图、解答题(本大题共6小题,共48分)23.如图,∠B=∠E,BF=EC,AB=DE.求证:AC//DF.24.在如图所示的网格(每个小正方形的边长为1)中,ΔABC的顶点A的坐标为(−2,1),顶点B的坐标为(−1,2). (1)在网格图中画出两条坐标轴,并标出坐标原点; (2)作ΔA'B'C'关于x轴对称的图形ΔA''B''C''; (3)求ΔABB''的面积.25.因式分解(1)3a2−6ab+3b2. (2)m2(m−2)+4(2−m).26.先化简再求值: (1)y(x+y)+(x+y)(x−y)−x2,其中x=−2,y=12. 27.(2)2(a−3)(a+2)−(3+a)(3−a),其中a=−2.27.已知分式y−a y+b,当y=−3时无意义,当y=2时分式的值为0,求当y=−7时分式的值.28.为庆祝建党100周年,学校组织初二学生乘车前往距学校132千米的某革命根据地参观学习.二班因事耽搁,比一班晚半小时出发,为了赶上一班,平均车速是一班平均车速的1.2倍,结果和一班同时到达.求一班的平均车速是多少千米/时?答案和解析1.【答案】C;【解析】解:设第三边长x. 根据三角形的三边关系,得1<x<7. 故选:C. 根据三角形的三边关系求得第三边的取值范围解答即可. 此题主要考查三角形三边关系的知识点,此题比较简单,注意三角形的三边关系.2.【答案】A;【解析】解:等腰三角形,直角三角形,锐角三角形都具有稳定性, 长方形不具有稳定性. 故选:A. 根据三角形具有稳定性解答. 此题主要考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用.3.【答案】C;【解析】解:∵平移ΔABC得到ΔDEF,∠DEF=35°, ∴∠B=∠DEF=35°, ∵∠ACB=50°, ∴∠A=180°−∠B−∠ACB=95°. 故选:C. 由平移的性质可得∠B=∠DEF=35°,从而利用三角形的内角和定理即可求∠A的度数. 此题主要考查三角形的内角和定理,平移的性质,解答的关键是由平移的性质得到∠B=∠DEF.4.【答案】A;【解析】解:分割六边形,可以从一顶点连接对角线,分割成四个三角形,如图1; 可以在某条边上任取一点,连接这点和各顶点,分割成五个三角形,如图2; 可以在六边形内取任取一点,连接这点和各顶点,分割成六个三角形,如图3. 故选:A. 分割六边形,可以从一顶点连接对角线,分割成四个三角形;可以在某条边上任取一点,连接这点和各顶点,分割成五个三角形;可以在六边形内取任取一点,连接这点和各顶点,分割成六个三角形. 此题主要考查了多边形内角和问题,解题关键是把多边形分割成若干三角形来研究.5.【答案】C;【解析】解:∵∠ABD=∠C=∠E,,AB=BE, 在BD上截取BF=DE, 在ΔABF与ΔBED中, AB=BE∠ABD=∠EBF=DE, ∴ΔABF≌ΔBED(SAS), ∴SΔBDE=SΔABF. ∴SΔABD=12BD⋅AD=12⋅125⋅95=5425. ∵DE=23BD, ∴BF=23BD, ∴SΔABF=23SΔABD=3625, ∴SΔBDE=3625. 故选:C. 根据SAS证明ΔABF与ΔBED全等,进而利用全等三角形的性质解答即可. 此题主要考查全等三角形的判定和性质,关键是根据SAS证明ΔABF与ΔBED全等.6.【答案】C;【解析】解:A、不是轴对称图形,本选项不符合题意; B、不是轴对称图形,本选项不符合题意; C、是轴对称图形,本选项符合题意; D、不是轴对称图形,本选项不符合题意. 故选:C. 根据轴对称图形的概念求解即可. 此题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,7.【答案】D;【解析】解:∵等边三角形ABC中,AD⊥BC, ∴BD=CD,即:AD是BC的垂直平分线, ∴BE=CE, ∴∠EBC=∠ECB, ∵∠BEC=90°, ∴∠EBC=∠ECB=45°, ∵ΔABC是等边三角形, ∴∠ACB=60°, ∴∠ACE=∠ACB−∠ECB=15°, 故选:D. 先判断出AD是BC的垂直平分线,进而求出∠ECB=45°,即可得出结论. 此题主要考查了等边三角形的性质,垂直平分线的判定和性质,等腰三角形的性质,求出∠ECB是解本题的关键.8.【答案】D;【解析】解:A、(3b−a)(3b+a)=(3b)2−a2,故A不符合题意; B、(3b−a)(−3b−a)=−(3b−a)(3b+a)=−[(3b)2−a2],故B不符合题意; C、(3b−a)(6b+2a)=2(3b−a)(3b+a)=2[(3b)2−a2],故C不符合题意; D、(3b−a)(a−3b)=−(a−3b)(a−3b)=−(a−3b)2,故D符合题意; 故选:D. 根据平方差公式进行分析求解即可. 此题主要考查整式的混合运算,解答的关键是对平方差公式的掌握与应用.9.【答案】B;【解析】解:A、原式=15x2−10xy+6xy−4y2=15x2−4xy−4y2,不符合题意; B、原式=4x2−y2,符合题意; C、原式=−(m−n)2=−(m2−2mn+n2)=−m2+2mn−n2,不符合题意; D、原式=2a2+ab−4ab−2b2=2a2−3ab−2b2,不符合题意. 故选:B. 利用平方差公式的结构特征判断即可. 此题主要考查了平方差公式,熟练掌握平方差公式的结构特征是解本题的关键.10.【答案】A;【解析】解:(1)∵a m=3,a n=7, ∴a m+n=a m⋅a n=3×7=21,本小题正确; (2)原式=(−0.125)2020×82020×8 =(−0.125×8)2020×8 =(−1)2020×8 =1×8 =8,本小题正确; (3)原式=2a2b÷ab−ab÷ab (4)原式=(−2)3⋅a3 =−8a3,本小题错误; (5)原式=2x2+x−6x−3 =2x2−5x−3,本小题错误, 则小明做对的题数为2. 故选:A. (1)利用同底数幂的乘法法则计算得到结果,即可作出判断; (2)原式变形后,逆用积的乘方运算法则计算得到结果,即可作出判断; (3)原式利用多项式除以单项式法则计算得到结果,即可作出判断; (4)原式利用积的乘方运算法则计算得到结果,即可作出判断; (5)原式利用多项式乘多项式法则计算,合并得到结果,即可作出判断. 此题主要考查了整式的混合运算,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.11.【答案】A;【解析】解:A、符合因式分解的定义,故本选项符合题意; B、右边不是整式的积的形式,不符合因式分解的定义,故本选项不符合题意; C、右边不是整式的积的形式,不符合因式分解的定义,故本选项不符合题意; D、右边不是整式的积的形式(含有分式),不符合因式分解的定义,故本选项不符合题意. 故选:A. 多项式的因式分解是将多项式变形为几个整式的乘积形式,由此解答即可. 此题主要考查因式分解的定义.解答该题的关键是掌握因式分解的定义,属于基础题型.12.【答案】C;【解析】解:当c=4时, x2−5x+c =x2−5x+4 =(x−1)(x−4). 故选:C. ∵4=−1×(−4),−1+(−4)=−5,∴可以用十字相乘法因式分解. 此题主要考查了因式分解−十字相乘法,熟练掌握十字相乘法分解因式的方法是解题关键.13.【答案】A;【解析】解:A、x+2y+2是最简分式,故本选项符合题意; B、原式=−12,不是最简分式,故本选项不符合题意; C、原式=x+y3x−3y,不是最简分式,故本选项不符合题意; D、原式=x−3,该式子不是最简分式,故本选项不符合题意; 故选:A. 最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分. 此题主要考查了分式的基本性质和最简分式,能熟记分式的化简过程是解此题的关键,首先要把分子分母分解因式,然后进行约分.14.【答案】C;【解析】解:∵2.(2x)2−3.(2y)22x−2y=8x2−12y22x−2y=4(2x2−3y2)2(x−y)=2(2x2−3y2)x−y, ∴把分式2x2−3y2x−y中的x和y的值都变为原来的2倍,则分式的值变为原来的2倍. 故选:C. 根据分式的基本性质解决此题. 此题主要考查分式的基本性质,熟练掌握分式的基本性质是解决本题的关键.15.【答案】C;【解析】解:读前一半用的时间为:140x, 读后一半用的时间为:140x+21. 由题意得,140x+140x+21=14, 故选:C. 设读前一半时,平均每天读x页,关键描述语为:“在两周借期内读完”;等量关系为:读前一半用的时间+读后一半用的时间=14,据此列方程即可. 此题主要考查了由实际问题列分式方程,解答本题的关键是读懂题意,设出未知数,找出等量关系,列出分式方程.16.【答案】C;【解析】解:小进跑800米用的时间为8001.25x秒,小俊跑800米用的时间为800x秒, ∵小进比小俊少用了40秒, 方程是800x−8001.25x=40, 故选:C. 先分别表示出小进和小俊跑800米的时间,再根据小进比小俊少用了40秒列出方程即可. 该题考查了列分式方程解应用题,能找出题目中的相等关系式是解此题的关键.17.【答案】720°;【解析】解:设所求正多边形边数为n, ∵正n边形的每个内角都等于120°, ∴正n边形的每个外角都等于180°−120°=60°. 又因为多边形的外角和为360°, 即60°⋅n=360°, ∴n=6. 所以这个正多边形是正六边形. 所以内角和是120°×6=720°. 故答案为:720°. 设所求正多边形边数为n,根据内角与外角互为邻补角,可以求出外角的度数.根据任何多边形的外角和都是360度,由60°⋅n=360°,求解即可. 此题主要考查了多边形内角和外角的知识,解答本题的关键在于熟练掌握任何多边形的外角和都是360°并根据外角和求出正多边形的边数.18.【答案】2;【解析】解:作DF⊥BC于F, ∵BD是ΔABC的角平分线,DE⊥AB,DF⊥BC, ∴DF=DE, ∴12×AB×DE+12×BC×DF=20,即12×12×DE+12×8×DF=20, ∴DF=DE=2. 故答案为:2. 作DF⊥BC于F,根据角平分线的性质得到DF=DE,根据三角形面积公式计算即可. 此题主要考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解答该题的关键.19.【答案】(x-3)2;【解析】解:根据题意得:(x−1)(x−9)=x2−10x+9,(x−2)(x−4)=x2−6x+ 8, 原多项式为x2−6x+9=(x−3)2. 故答案为:(x−3)2. 根据两位同学的结果确定出原多项式,分解即可. 此题主要考查了因式分解−十字相乘法,熟练掌握因式分解的方法是解本题的关键.20.【答案】54°;【解析】解:∵E在线段BC的垂直平分线上, ∴BE=CE, ∵CE平分∠ACB, ∴∠ACD=2∠ECB=84°, 又∵∠A+∠B+∠ACB=180°, ∴∠A=180°−∠B−∠ACB=54°, 故答案为:54°. 由线段垂直平分线和角平分线的定义可得∠B=∠ECB=∠ACE=40°,在ΔABC中由三角形内角和定理可求得∠A. 此题主要考查线段垂直平分线的性质,掌握垂直平分线上的点到线段两端点的距离相等是解答该题的关键.21.【答案】6x−63x=23;【解析】解:设步行学生的速度为x km/h,则汽车的速度为3x km/h, 由题意得,6x−63x=23, 故答案为:6x−63x=23. 表示出汽车的速度,然后根据汽车行驶的时间等于步行行驶的时间减去时间差列方程即可. 此题主要考查了实际问题抽象出分式方程,读懂题目信息,理解两种行驶方式的时间的关系是解答该题的关键.22.【答案】1;【解析】解:(1x−4−8x2−16)⋅(x+4) =x+4−8(x+4)(x−4)⋅(x+4) =x−4(x+4)(x−4)⋅(x+4) =1, 故答案为:1. 先根据分式的减法法则算减法,再算乘法即可. 此题主要考查了分式的混合运算,能正确根据分式的运算法则进行化简是解此题的关键,注意运算顺序.23.【答案】证明:∵BF=EC, ∴BF+CF=EC+CF, ∴BC=EF, 在△ABC和△DEF中, BC=EF∠B=∠EAB=DE, ∴△ABC≌△DEF(SAS), ∴∠ACB=∠DFE, ∴AC∥DF.;【解析】 证明ΔABC≌ΔDEF(SAS),由全等三角形的性质得出∠ACB=∠DFE,由平行线的判定可得出结论. 此题主要考查了全等三角形的判定与性质、平行线的判定.解答该题的关键是证明ΔABC≌ΔDEF.24.【答案】解:(1)如图,平面直角坐标系如图所示: (2)如图,△A″B″C″即为所求; =3×4-12×1×1-12×3×3-12×2×4=3. (3)S△ABB″;【解析】 (1)根据A,B两点坐标确定平面直角坐标系即可; (2)利用轴对称的性质分别作出A',B',C'的对应点A'',B'',C''即可; (3)把三角形面积看成矩形面积减去周围三个三角形面积即可. 此题主要考查作图−轴对称变换,三角形的面积等知识,解答该题的关键是掌握轴对称变换的性质,学会用分割法求三角形面积.25.【答案】解:(1)原式=3(a2-2ab+b2) =3(a-b)2; (2)原式=m2(m-2)-4(m-2) =(m-2)(m2-4) =(m-2)(m-2)(m+2) =(m-2)2(m+2).;【解析】 (1)先提公因式3,再利用完全平方公式即可进行因式分解; (2)先提公因式(m−2),再利用平方差公式进行因式分解即可. 此题主要考查提公因式法、公式法分解因式,掌握平方差公式、完全平方公式的结构特征是解决问题的关键.26.【答案】解:(1)原式=xy+y2+x2-y2-x2 =xy, 当x=-2,y=12时, 原式=-2×12=-1; (2)原式=2(a2+2a-3a-6)-(9-a2) =2a2-2a-12-9+a2 =a2-2a-21, 当a=-2时,原式=(-2)2-2×(-2)-21 =4+4-21 =-13.;【解析】 (1)直接利用单项式乘多项式以及平方差公式化简,再合并同类项,最后把已知数据代入得出答案; (2)直接利用多项式乘多项式以及平方差公式化简,再合并同类项,最后把已知数据代入得出答案. 此题主要考查了整式的混合运算−化简求值,正确运用乘法公式计算是解题关键.27.【答案】解:∵当y=-3时无意义, ∴-3+b=0, ∴b=3. ∵当y=2时分式的值为0, ∴2-a=0,2+3≠0, ∴a=2. ∴该分式为y−2y+3, 当x=-7时, y−2y+3 =−7−2−7+3 =−9−4 =94. 答:当x=-7时分式的值为94.;【解析】 分式无意义的条件是分母等于0,分式等于0的条件是分子等于0,且分母不等于0. 此题主要考查分式无意义的条件和分式值为0的条件,解题时注意分式为0的条件是分子等于0,且分母不等于0.28.【答案】解:设一班的平均车速是x千米/时,则二班的平均车速是1.2x千米/时, 依题意得:132x-1321.2x=12, 解得:x=44, 经检验,x=44是原方程的解,且符合题意. 答:一班的平均车速是44千米/时.;【解析】 设一班的平均车速是x千米/时,则二班的平均车速是1.2x千米/时,利用时间=路程÷速度,结合二班比一班少用半小时,即可得出关于x的分式方程,解之经检验后即可得出一班的平均车速. 此题主要考查了分式方程的应用,找准等量关系,正确列出分式方程是解答该题的关键.。
人教版八年级上册数学期末考试试卷及答案

人教版八年级上册数学期末考试试题一、单选题1.下列文字中,是轴对称图形的是()A .我B .爱C .中D .国2.用科学记数法表示0.0000003是()A .60.310-⨯B .70.310-⨯C .6310-⨯D .7310-⨯3.等腰三角形的两边长为2cm ,5cm ,则该等腰三角形的周长为()A .9cmB .12cmC .9cm 或12cmD .6cm 或12cm4.下列各式运算正确的是()A .326a a a ⨯=B .()428=a aC .()220a a -+=D .()23622a a =5.点A (-2,3)向右平移3个单位后得到点B ,那么点B 关于x 轴对称的点的坐标是A .(1,-3)B .(1,3)C .(-1,3)D .(-1,-3)6.如图,在△ABC 与△ADC 中,若BAC DAC ∠=∠,则下列条件不能判定△ABC 与△ADC 全等的是()A .B D∠=∠B .BCA DCA ∠=∠C .BC DC =D .AB AD =7.已知()()222x m x x x +-=--,那么m 的值是()A .1B .-1C .2D .-28.如图,在Rt △ABC 中,90C = ∠,AD 平分∠BAC ,交BC 于点D ,若20AB =,△ABD 的面积为60,则CD 长()A .12B .10C .6D .49.如图,在△ABC 中,AB AC =,BD CD =,边AB 的垂直平分线交AC 于点E ,连接BE ,交AD 于点F ,若66C ∠=︒,则∠AFE 的度数为()A .60B .62°C .66D .7210.如图,数轴上点A 、B 、C 、D 分别表示数0、1、2、3,若x 为整数(0x ≠),则分式21x x -表示的点落在哪条线段上?()A .ACB .BC C .BD D .CD11.如图,把一块等腰直角三角尺放在直角坐标系中,直角顶点A 落在第二象限,锐角顶点B 、C 分别落在x 轴、y 轴上,已知点A (-2,2)、C (0,-3),则点B 的坐标为()A .(-4,0)B .(-5,0)C .(-7,0)D .(-8,0)12.如图,有10个形状大小一样的小长方形①,将其中的3个小长方形①放入正方形②中,剩余的7个小长方形①放入长方形③中,其中正方形②中的阴影部分面积为21,长方形③中的阴影部分面积为93,那么一个小长方形①的面积为()A .5B .6C .9D .10二、填空题13.分解因式26m m +=_________.14.计算:3242a b ab ÷=______.15.已知:26910a a b -+++=,那么22a b +=______.16.当=a ___________时,关于x 的方程12325x a x a +-=-+的解为零.17.如图,点D 、A 、B 、C 是正十边形依次相邻的顶点,分别连接AC 、BD 相交于点P ,则∠DPC =______度.18.等腰直角三角形ABC 中,AB AC =,90BAC ∠= ,且△ABC 的面积为16,过点B 作直线EF AC ∥,点G 是直线EF 上的一个动点,连接AG ,将AG 绕点A 顺时针旋转90 ,得到线段AH ,连接BH ,则线段BH 的最小值为______.19.如图,已知AE =BE ,DE 是AB 的垂线,F 为DE 上一点,BF =11cm ,CF =3cm ,则AC =_______.20.如图,在等腰△ABC 中,AB=AC=13,BC=10,D 是BC 边上的中点,M 、N 分别是AD 和AB 上的动点.则BM+MN 的最小值是_________________.三、解答题21.计算:(1)02312020222--++⨯(2)()()()22a b a b a b +--+22.化简求值:2222m n mn n m m m ⎛⎫--÷- ⎪⎝⎭,其中3,1m n ==-.23.解分式方程:2231022x x x x-=+-24.如图,四边形ABED 中,90B E ACD ∠=∠=∠= ,BC DE =.(1)求证:ABC CED ∆=∆.(2)发现:若AB a =,BC b =,AC c =,请用两种方法计算四边形ABCD 的面积,并探究a 、b 、c 之间有什么数量关系?(3)应用:①根据(2)中的发现,当8AB =,6BC =时,AC 的长为___;②如图,若30P ∠= ,4PM =,7PN =,点F 在PN 上,点G 在射线PM 上连接FM 、FG 、NG ,求MF FG GN ++的最小值.25.为了进一步丰富校园文体活动,学校准备购进一批篮球和足球,已知每个篮球的进价比每个足球的进价多20元,用1800元购进篮球的数量是用700元购进足球的数量的2倍,求每个篮球和足球的进价各是多少元?26.如图,90ACB ∠=︒,AC BC =,AD CE ⊥,BE CE ⊥,垂足分别为D ,E .(1)求证:ACD CBE △△≌;(2)试探究线段AD ,DE ,BE 之间有什么样的数量关系,请说明理由.27.如图,Rt △ABC 与Rt △DEF 中,点B 、E 、C 、F 在一条直线上,AC 与DE 相交于点O ,90BAC EDF ∠=∠=︒,AB DE =,BE CF =,则:(1)求证:AC DE ⊥;(2)连接AD 、AE 、DC ,若12,5AC AB ==,求四边形AECD 的面积.28.如图是33⨯的网格,网格中每个小正方形的顶点叫做格点,当三角形的三个顶点是格点时,这个三角形叫做格点三角形,图中阴影部分的三角形就是格点三角形.(1)请在图一、图二中分别作出与阴影部分成轴对称的格点三角形,要求所作格点三角形在33⨯的网格内且位置不同;(2)思考:在33⨯的网格内一共可以作___个符合(1)中要求的格点三角形.参考答案1.C2.D3.B4.B5.A6.C7.A8.C9.D10.C11.C12.Am m+13.(6)14.22a b15.1016.1517.144【详解】解:∵DAB ∠和ABC ∠是正十边形的两个内角,∴(102)18014410DAB ABC -⨯︒∠=∠==︒,DA AB BC ==,∴180********,22DAB ABD ︒-∠︒-︒∠===︒1801801441822ABC BCA ︒-∠︒-︒∠===︒,∴14418126PBC ABC ABD ∠=∠-∠=︒-︒=︒,∴12618144DPC PBC PCB ∠=∠+∠=︒+︒=︒,故答案为:144【点睛】可不是主要考查了正多边形内角和问题,解题的关键是熟练掌握基本知识.18.【分析】如图所示:连接CG .由旋转的性质可知AG AH =,90GAH ∠=︒,再由90BAC ∠=︒,可知HAB CAG ∠=∠.可证ABH ACG ≅ .可得BH CG =.BH 最小转化成求CG 最小.只需CG BG ⊥就可以了.由此可得四边形ABGC 是正方形.由ABC 的面积是16,可求BH 的值为【详解】如图所示:连接CG .由旋转的性质可知:AG AH =,90GAH ∠=︒.∵90BAC ∠=︒∴BAC BAG GAH BAG ∠-∠=∠-∠,即HAB CAH ∠=∠.在ABH 和ACG 中,AB AC HAB CAH AH AG =⎧⎪∠=∠⎨⎪=⎩ABH ACG≅ ∴BH CG=要让BH 最小,也就是要CG 最小,∴CG BG ⊥时,CG 最小.∵EF AC ∥,90BAC ∠=︒,∴90ABG BAC ∠=∠=︒∵CG BG⊥∴四边形ABGC 时矩形,∵AB AC=∴矩形ABGC 是正方形.∴AB BG CG AC ===.∵△ABC 的面积为16,∴•162AB AC =,解得:AB AC ==.∴AB AC CG BH ====故答案为:【点睛】本题考查了全等三角形的性质和判定定理、矩形的性质和判定定理、正方形的性质和判定定理、等腰直角三角形的性质等知识.证得三角形全等,由求BH 转化成求CG ,和让CG BG ⊥时,CG 最短是解决本题的关键.19.14cm【分析】由AE =BE ,DE 是AB 的垂线得出DE 是AB 的中线,进而可得DE 是AB 的垂直平分线,由此即可得到AF =BF ,再根据线段的和差即可得解.【详解】解:∵AE =BE ,DE 是AB 的垂线,∴DE 是AB 的中线,∴DE是AB的垂直平分线,∵F为DE上一点,∴AF=BF,∴AC=AF+CF=BF+CF,∵BF=11cm,CF=3cm,∴AC=14cm,故答案为:14cm.【点睛】此题考查了等腰三角形的三线合一以及垂直平分线的性质,熟练掌握等腰三角形的三线合一以及垂直平分线的性质是解此题的关键.20.120 13【分析】作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,然后根据轴对称的性质可知BM′+M′N′为所求的最小值.【详解】解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.∵AB=AC,D是BC边上的中点,∴AD是∠BAC的平分线,∴M′H=M′N′,∴BH是点B到直线AC的最短距离(垂线段最短),∵AB=AC=13,BC=10,D是BC边上的中点,∴AD⊥BC,∴AD=12,∵S△ABC=12AC×BH=12BC×AD,∴13×BH=10×12,解得:BH=120 13;故答案为12013.21.(1)2(2)233ab b --【分析】(1)根据零次幂、负指数幂可进行求解;(2)根据完全平方公式及多项式乘以多项式可进行求解.(1)解:原式=111428++⨯11122=++=2;(2)解:原式=()222222a ab b a ab b ---++=222222a ab b a ab b -----=233ab b --.22.2m n -;12【分析】先根据分式混合运算法则进行化简,然后再代入求值即可.【详解】解:原式22222m n m mn n m m m ⎛⎫--=÷- ⎝⎭22222m n m mn n m m--+=÷()()22m n mm m n -=⋅-2m n=-把m=3,n=−1代入得:原式()231=--231=+24=12=23.4x =【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】2231022x x x x-=+-解:方程可变为:()()31022x x x x -=+-,方程两边同乘以x (x+2)(x ﹣2)得:3(x ﹣2)﹣(x+2)=0,解得,x =4,检验:当x =4时,x (x+2)(x ﹣2)≠0,所以,原分式方程的解为x =4.24.(1)见解析;(2)第一种方法:S 四边形ABCD=2ab +22c ,第二种方法:22222a b ab ++;a 、b 、c 之间的数量关系是222+=a b c ;(3)①10【分析】(1)根据BAC ECD ∠=∠,B E ∠=∠,BC ED =即可证明两个三角形全等;(2)第一种面积求法直接是S △ABC+S △ACD ,代入表示即可;第二种面积表示用S 梯形ABED-S △CED 来表示,就可以得到a 、b 、c 之间的数量关系;(3)①根据(2)中的结论,代入数值即可计算;②作点M 关于PN 的对称点1M ,作点N 关于PM 的对称点1N ,连接11M N ,线段11M N 与PN 的交点即为F ,与PM 的交点即为点G ,连接P 1M ,P 1N ,此时MF FG GN ++的值最小,代入(2)中的结论,即可算出这个最小值;【详解】(1)∵∠B=∠E=∠ACD=90°,∴∠DCE+∠ACB=90°,∠ACB+∠BAC=90°,∴∠BAC=∠DCE ,在△ABC 和△CED 中,BAC ECD B E BC ED ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△CED ;(2)第一种方法:S 四边形ABCD=S △ABC+S △ACD=2ab +22c ,第二种方法:由(1)可知,△ABC ≌△CED ,∴CD=c ,DE=b ,CE=a ,S 四边形ABCD =S 梯形ABED-S △CED=22a b a b ab ++-()(),=22222a b ab ++,∴2ab +22c =22222a b ab ++,∴222+=a b c ,即a 、b 、c 之间的数量关系是222+=a b c ;(3)①∵AB=8,BC=6,∴22268AC =+=100,∴AC=10,②作点M 关于PN 的对称点1M ,作点N 关于PM 的对称点1N ,连接11M N ,线段11M N 与PN 的交点即为F ,与PM 的交点即为点G ,连接P 1M ,P 1N ,此时MF FG GN ++的值最小;如图所示:∵点M 与1M 关于PN 对称,点N 与1N 关于PM 对称,∴1M F=MF ,PM=P 1M =4,∴GN=G 1N ,PN=P 1N =7,∠1M PF=∠FPM=∠MP 1N =30°,∴∠11M PN =3×30°=90°∴MF+FG+GN=M 1F+FG+N 1G≥M 1N 1,当点M 1、F 、G 、N 1四点共线时最短,在△11M PN 中,∠11M PN =90°,PM=4,P 1N =7,∴由(2)可知,211M N =2247+=65,∴11M N∴MF FG GN ++25.每个足球的进价是70元,每个篮球的进价是90元【详解】解:设每个足球的进价是x 元,则每个篮球的进价是()20x +元.由题意得:1800700220x x=⨯+.解得:70x =.检验:当70x =时,()200x x +≠,所以,原方程的解为70x =.∴2090x +=.答:每个足球的进价是70元,每个篮球的进价是90元.【点睛】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.26.(1)见解析(2)BE DE AD +=,见解析【分析】(1)由“AAS”可证ACD CBE △△≌;(2)由全等三角形的性质可得CD BE =,AD CE =,即可求解.【详解】(1)证明:∵AD CE ⊥,BE CE ⊥,∴90E ADC ∠=∠=︒,∴1290∠+∠=︒,∵90ACB ∠=︒,∴3290∠+∠=︒,∴13∠=∠,在ACD 和CBE △中,13ADC E AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ACD CBE △△≌(AAS ).(2)解:BE DE AD +=,理由如下:∵ACD CBE △△≌,∴CD BE =,AD CE =.∵CD DE CE +=,∴BE DE AD +=.27.(1)见详解(2)四边形AECD 的面积为30【分析】(1)由题意易得BC EF =,然后根据“HL”可证ABC DEF ≌△△,则有//AB DE ,进而问题可求证;(2)由(1)可知△DEF 是由△ABC 向右平移所得到,则根据平移的性质可得AD=BE ,然后根据勾股定理可得BC=13,进而问题可求解.(1)证明:∵BE CF =,∴BE EC CF EC +=+,即BC EF =,∵90BAC EDF ∠=∠=︒,AB DE =,∴ABC DEF ≌△△(HL ),∴B DEF ∠=∠,∴//AB DE ,∴90EOC A ∠=∠=︒,∴AC DE ⊥;(2)解:由(1)可知△DEF 是由△ABC 向右平移所得到,则根据平移的性质可得AD=BE ,//AD EC ,∴四边形AECD 是梯形,∵12,5AC AB ==,90BAC ∠=︒,∴13BC ==,设△ABC 边BC 上的高为h ,∴6013AB AC h BC ⋅==,∴()()1111601330222213AECD S AD EC h BE EC h BC h =+=+=⋅=⨯⨯=四边形.【点睛】本题主要考查勾股定理、平移的性质及全等三角形的性质与判定,勾股定理、平移的性质及全等三角形的性质与判定是解题的关键.28.(1)见解析(2)3【分析】(1)根据轴对称图形的性质作出轴对称图形即可;(2)作出所有轴对称图形即可得到答案.(1)如图一、二,即为所作图形,(虚线为对称轴)(2)可以作出3个符合(1)中要求的格点三角形.第3个如图所示,故答案为:3。
人教版八年级上册数学期末考试试卷含答案

人教版八年级上册数学期末考试试题一、单选题1.点M (﹣2,1)关于x 轴的对称点N 的坐标是()A .(2,1)B .(﹣2,1)C .(﹣2,﹣1)D .(2,﹣1)2.使分式321x x --有意义的x 的取值范围是()A .x >12B .x <12C .x≠3D .x≠123.一个三角形的两边长分别为3cm 和8cm ,则此三角形第三边长可能是()A .3cmB .5cmC .7cmD .11cm4.如图,已知ABC DCB ∠=∠,添加以下条件,不能判定ABC DCB ∆≅∆的是()A .AB DC =B .BE CE =C .AC DB=D .A D∠=∠5.如果2(2)9x m x +-+是个完全平方式,那么m 的值是()A .8B .-4C .±8D .8或-46.若分式211x x -+的值为0,则x 的值为().A .0B .1C .﹣1D .±17.下列运算正确的是()A .x 2+x 2=2x 4B .a 2•a 3=a 5C .(﹣2x 2)4=16x 6D .(x+3y )(x ﹣3y )=x 2﹣3y 28.如图,已知D 为△ABC 边AB 的中点,E 在AC 上,将△ABC 沿着DE 折叠,使A 点落在BC 上的F 处.若∠B=65°,则∠BDF 等于()A .65°B .50°C .60°D .57.5°9.若(x+a )(x 2﹣x ﹣b )的乘积中不含x 的二次项和一次项,则常数a 、b 的值为()A.a=1,b=﹣1B.a=﹣1,b=1C.a=1,b=1D.a=﹣1,b=﹣1 10.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于12MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,有下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.其中说法正确的个数是()A.1B.2C.3D.4二、填空题11.当x≠__时,分式11xx-+有意义.12.分解因式:3x2﹣12xy+12y2=_____.13.数据0.0000000001,用科学记数法表示为____.14.关于x的分式方程3111mx x+=--的解为正数,则m的取值范围是________.15.若一个正多边形的每一个外角都是30°,则这个正多边形的内角和等于____度.16.已知m+2n+2=0,则2m•4n的值为_____.17.如图,△ABC的两条高BD、CE相交于点O且OB=OC.则下列结论:①△BEC≌△CDB;②△ABC是等腰三角形;③AE=AD;④点O在∠BAC的平分线上,其中正确的有_____.(填序号)18.如图,已知每个小方格的边长为1,A、B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是等腰三角形,这样的格点C有________个。
人教版八年级上册数学期末考试试卷带答案

人教版八年级上册数学期末考试试题一、单选题1.下列图形中是轴对称图形的是()A .B .C .D .2.用以下长度的三条线段,不能围成三角形的是()A .1,2π,2B .1,2,1.5C 312,,D .0.4,2+13.在△ABC 和△DEF 中,若AB =DE ,∠A =∠D ,BC =EF ,若AC≠DF ,则一定有A .AC >DFB .∠C =∠FC .∠F+∠C=180°D .∠F >90°4.下列等式恒成立的个数有()①339a a a ⋅=②()()3223a a =③()444a b a b =÷÷④()()212a a a a +-+=A .1个B .2个C .3个D .4个5.若分式2321x x x +++的值为0,则x =()A .﹣1B .﹣2C .0D .﹣1或﹣26.若A (﹣3,a+3)和A '(a ﹣2,b )关于x=()A .﹣3B .13C .3D .17.晨曦因少算了一个内角得出一多边形的内角和为980°,则该多边形的边数为()A .6B .8C .10D .98.由图,可得代数恒等式()A .()2222a b a ab b +=++B .()()22232a b a b a ab b++=++C .()()2224a b a b a ab b++=++D .()222232a b a ab b +++=9.在△ABC 中,CD 平分∠BCA ,与AB 交于点D .若BD =3,AD =4,∠A =30°,△ABC中BC边上的高为()A.103B.73C.157D.14310.如图,在Rt△ABC中,∠B=60°,D是线段BC上一动点,将A绕点D顺时针旋转90°至点E,连接CE.当CE取最小值时,∠ACE=()A.45°B.65°C.75°D.105°二、填空题11.分解因式:a4﹣4a2=_______.12.坐标平面上有点A(0,3),B(6,0),坐标轴上存在_____个点C,使△ABC为等腰三角形.13.当a=_____时,方程11(2)(3)23ax a xx x x x-+=-----无解.14.若等腰三角形一条腰上的高与另一腰的夹角为50°,则等腰三角形的底角为_____°.15.如图,∠B=50°,∠C=70°,∠BAD平分线与∠ADC外角平分线交于点F,则∠F=_____.16.如图,将一副直角三角板,按如图所示的方式摆放,则∠α的度数是__________.17.等腰三角形ABC顶角∠C=120°,已知C(0,1),A0),B在x轴上.M(1,0)和点N 关于y 轴对称,P 、Q 分别为边AC 、BC 上的一个动点.四边形PQNM 的周长最小为_____.18.如图,AB=AD ,∠1=∠2,如果增加一个条件_____,那么△ABC ≌△ADE .三、解答题19.化简:2()()()2x y x y x y x ⎡⎤-++-÷⎣⎦.20.在Rt △ABC 中,∠B =90°.(1)尺规作图:在AC 上取一点D ,使DB =DC ;(2)若BD =6,求AC 的长.21.记a <x≤b 为(a ,b].化简:2231()(1)(1)242k k k k k k+⋅-+-+,并在[﹣1,3)中选择合适的整数k 代入求值.22.如图,△ABC 中,AB=AC ,作AD ⊥BC ,CE ⊥AB ,垂足分别为D ,E ,AD 和CE 相交于点F ,若已知AE=CE.(1)求证:△AEF ≌△CEB ;(2)求证:AF=2CD23.阅读材料,回答问题:数学归纳法是一种证明整数范围内的代数式的常用方法.为证明整数范围内有2222123n +++⋯⋯+=(1)(21)6n n n ++可以按照这种思路:(1)当n =1时,显然等式成立.(2)假设当n =k (k 为任意正整数)时等式成立,那就可以得到关系式2222123k +++⋯⋯+=(1)(21)6k k k ++①然后,把关系式①作为已知条件,证明当n =k+1时等式成立,也就是证明()222221231k k +++⋯⋯+++=[](1)(11)2(1)16k k k +++++(3)这样,由(1)可得,n=k =1时,等式成立;由(2)可得,因为当n =k =1时等式成立,所以当n =k+1=2时等式就成立;因为n =k =2时等式成立,所以当n =k+1=3时等式就成立……如此像多米诺骨牌一样,就可以得出等式成立.(1)根据材料,补全等式2222123n +++⋯⋯+=(1)(21)6n n n ++(n 为正整数)的证明:证明:当n =1时,等式右边=1(11)(21)6⨯+⨯+=1=12=等式左边,等式成立;假设当n =k 时等式成立,那么就有2222123k +++⋯⋯+=(1)(21)6k k k ++①;当n =k+1时,等式左边=()222221231k k +++⋯⋯+++;把①代入得,等式左边=_____∴当n 为任意正整数时,都有2222123n +++⋯⋯+=(1)(21)6n n n ++.(2)运用数学归纳法,仿照(1),求证:()111122311n n n n +++=⨯⨯++L L (n 为正整数)24.在平面直角坐标系中,O 为原点,点A (b ,a ),点D (b ,a+2),满足()2284a b a b +≤--.分别作AB ⊥x 轴于点B ,AC ⊥y 轴于点C ,连接BC .(1)求∠OBC ;(2)动点P 以1个单位长度每秒的速度按路径D→B→O 运动,点Q 以3个单位长度每秒的速度按路径A→B→O 运动,当点Q 到达点O 时,两点停止运动.是否存在时刻t ,使以P ,C ,O 为顶点的三角形和以Q ,C ,A 为顶点的三角形全等?若存在,求t 值;若不存在,说明理由;(3)存在M (﹣4,m )和N (n ,0),使∠MCN =∠OBC ,若MN =t ,直接写出m ,n ,t 的关系式.25.如图,△ABC、△AFD、△BEG均为等腰直角三角形,BD⊥AD,CE⊥BD,FG交BD于点H.若12ADBD ,S△EHG=3,求S△FDH.26.甲、乙两人做某种机械零件(1)已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个(2)已知甲计划做零件60个,乙计划做零件100个,甲、乙的速度比为3:4,结果甲比乙提前20分钟完成任务,则甲每小时做零件个,乙每小时做零件个27.晓芳利用两张正三角形纸片,进行了如下探究:初步发现:如图1,△ABC和△DCE均为等边三角形,连接AE交BD延长线于点F,求证:∠AFB=60°;深入探究:如图2,在正三角形纸片△ABC的BC边上取一点D,作∠ADE=60°交∠ACB 外角平分线于点E,探究CE,DC和AC的数量关系,并证明;拓展创新:如图3,△ABC和△DCE均为正三角形,连接AE交BD于P,当B,C,E三点共线时,连接PC,若BC=3CE,直接写出下列两式分别是否为定值,并任选其中一个进行证明:(1)3AP PD PC-;(2)2AP PC PD BD PC PE++-+.参考答案1.B2.D3.C4.B5.B6.C7.B8.B9.D10.C11.a2(a+2)(a-2)12.813.1-14.70或20 15.80︒16.75︒17.318.AC=AE【详解】∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC ,∴∠BAC=∠DAE ,而AB=AD ,∴当AC=AE 时,△ABC ≌△ADE .故答案为:AC=AE .19.x-y【分析】先利用平方差公式和完全平方公式计算括号内的,再计算除法可得结果.【详解】解:原式=(x 2-2xy+y 2+x 2-y 2)÷2x=(2x 2-2xy )÷2x =x-y .故答案为:x-y .20.(1)见解析(2)12【分析】(1)如图,作BC 的垂直平分线交AC 于点D ,连接BD ,则点D 即为所求;(2)设BC 的垂直平分线交BC 于E ,∵DE 是BC 的垂直平分线,∴DE BC ⊥,则90DEC ∠=︒,BD CD =,BDE CDE ∠=∠,∵90ABC ∠=︒,∴90ABC DEC ∠=∠=︒,∴DE AB ∥,∴,ABD BDE A CDE ∠=∠∠=∠,∴ABD A ∠=∠,∴BD AD =,∵6BD =,∴212AC AD DC BD =+==,21.11k +,当2k =时,原式=13【分析】先根据分式的混合计算法则化简分式,再根据题目所给的定义结合分式有意义的条件选择满足题意的k 值代值计算即可.【详解】解:()()223111242k k k k k k +⎛⎫⋅- ⎪+-+⎝⎭()()()()()311222222k k k k k k k k k k ⎛⎫=- ⎪ ⎪++⎝+-⎭++()()()()2211222k k k k k k k +-=+-+()()()()()2111222k k k k k k k +-=+-+11k =+,∵分式要有意义,∴1010020k k k k +≠⎧⎪-≠⎪⎨≠⎪⎪+≠⎩,∵13k -≤<,∴符合题意的整数k 只能是2,∴当2k =时,原式11213==+.22.(1)证明见解析;(2)证明见解析.【详解】试题分析:(1)要证明△AEF ≌△CEB ,已知条件有AE=EC ,∠AEF=∠BEC=90°,还差一个条件,由AD ⊥BC ,CE ⊥AB 可得∠B+∠BAD=90°,∠B+∠BCE=90°,所以得出∠EAF=∠ECB ,因此可证明出△AEF ≌△CEB ;(2)由(1)结论可得:AF=BC ,即要证明BC=2CD ,由等腰三角形三线合一性质不难证明.试题解析:(1)证明:∵AD ⊥BC ,∴∠B+∠BAD=90°,∵CE ⊥AB ,∴∠B+∠BCE=90°,∴∠EAF=∠ECB ,在△AEF 和△CEB 中,AEF BEC AE CEEAF BCE ∠∠⎧⎪⎨⎪∠∠⎩===,∴△AEF ≌△CEB ;(2)∵△AEF ≌△CEB ,∴AF=BC ,∵AB=AC ,AD ⊥BC ,∴CD=BD ,BC=2CD ,∴AF=2CD .点睛:掌握全等三角形的性质以及判定、等腰三角形三线合一性质.23.(1)()()()23216k k k +++⋅(2)证明见解析【分析】(1)只需要证明()()()()()()2111211121166k k k k k k k +++++⎡⎤++⎣⎦++=即可;(2)仿照题意进行证明即可.(1)证明:当n =1时,等式右边=1(11)(21)6⨯+⨯+=1=12=等式左边,等式成立;假设当n =k 时等式成立,那么就有2222123k +++⋯⋯+=(1)(21)6k k k ++①;当n =k+1时,等式左边=()222221231k k +++⋯⋯+++;把①代入得,等式左边=()()()212116k k k k ++++()()()21116k k k k +⎡⎤=+++⎢⎥⎣⎦()266216k k k k +++=+⋅()227616k k k ++=+⋅()()()23216k k k ++=+⋅∴当n 为任意正整数时,都有2222123n +++⋯⋯+=(1)(21)6n n n ++,故答案为:()()()23216k k k +++⋅;(2)解:当n =1时,等式右边=1111122==+=等式左边,等式成立;假设当n =k 时等式成立,那么就有()111122311k k k k +++=⨯⨯++L L ①;当n =k+1时,等式左边=()()()111112231111k k k k ++++⨯⨯++++L L ;把①代入得,等式左边=()()1112k k k k ++++1112k k k ⎛⎫=+ ⎪++⎝⎭212112k k k k ++=⋅++()21112k k k +=⋅++12k k +=+等式右边12k k +=+,∴左边=右边,∴当n 为任意正整数时,都有()111122311n n n n +++=⨯⨯++L L (n 为正整数);24.(1)45°(2)存在,52t =(3)4m n t ++=【分析】(1)∵()2284a b a b +≤--即228168160a ab b -++++≤()()22440a b -++≤∵()()22440a b -++≥∴40,40a b -=+=解得4,4a b ==-∵点A (b ,a ),点D (b ,a+2),∴()()4,4,4,6A B --∵AB ⊥x 轴于点B ,AC ⊥y 轴于点C ,∴4OB OC ==,∵90BOC ∠=°,∴45OBC ∠=︒,(2)依题意,6,4DB OB ==,4AB =∴8AB OB +=∵点Q 以3个单位长度每秒的速度按路径A→B→O 运动,∴83t =时,两点停止运动,当Q 在B 点时,43t =,①当403t <<时,P 点在AD 上运动,Q 在AB 上运动,AQC 是直角三角形PCO △是钝角三角形,两三角形不可能全等,②当4833t ≤<时,如图,若AQC CPO≌则PC AQ =,又4AC AB ==∴Rt Rt APC BQA≌∴AP BQ=此时2,334AP PD AD t BQ t AB t =-=-=-=-即234t t -=-解得1t =(舍去)若AQC OPC ≌,此时383OQ AB OB t t =+-=-,2AP PD AD t =-=-则832t t -=-解得52t =综上所述,52t =符合题意,(3)解:如图,在x 轴上取点M ',使得OM AM'=∵90,4,CAM COM AC CO AM OM ''∠=∠=︒===∴AMC OM C' ≌∴CM CM '=,ACM OCM '∠=∠∵45MCN OBC ∠=∠=︒,∴45ACM OCN ∠+∠=︒∴45NCO OCM MON'∠+∠=︒=∠即MCN M CN'∠=又,MC M C CN CN'==∴OM AM '=,M (﹣4,m )和N (n ,0),MN =t ,∴4,OM AM m ON n'==-=-∴4ON OM n m t'+=-+-=整理得4m n t ++=25.9【分析】连接CD ,EF ,证明ABD BCE △≌△,结合已知条件,得出E 为DB 的中点,,证明FHE BHG ≌,可证明H 为BE 的中点,进而根据3FHEGHB HFG S S S === △,即可求解.【详解】解:如图,连接CD ,EF ,∵12AD BD =设,2AD a BD a==∵△ABC 、△AFD 、△BEG 均为等腰直角三角形,BD ⊥AD ,CE ⊥BD ,∴,90AB BC ADB BEC =∠=∠=︒,90BAD ABD EBC ∠=︒-∠=∠,∴ABD BCE△≌△∴AD BE ==a ,∴CE 垂直平分BD∴EB ED a==∵,,AD BD CE BD AF AD ⊥⊥⊥,∴AF DE∥∴45AFD EDF ∠=∠=︒∵45ADF ∠=︒∴ADF EDF∠=∠在ADF 与EDF 中AD DE ADF EDF FD FD =⎧⎪∠=∠⎨⎪=⎩∴ADF ≌EDF ,∴EF AF a ==,∵BE BG a ==,∴EF BG =,又90FEB GBE ∠=∠=︒,FHE GHB ∠=∠,∴FHE GHB ≌,∴HE HB =,FHEBHG S S = ,12HE a ∴=,13222DH a a a =-=,则HE 13DH =,∴13FHEFHD S S = ,又3FHE GHB HFG S S S === △∴FHD S =926.(1)设甲每小时做零件18个,乙每小时做零件12个;(2)甲每小时做零件45个,乙每小时做零件60个.【分析】(1)设乙每小时做x 个,则甲每小时做(x+6)个,甲做90个所用的时间为906x +,乙做60个所用的时间为60x;(2)设甲每小时做3x 个零件,表示出乙每小时做的零件个数,然后根据“结果甲比乙提前20分钟完成任务”列出方程即可.【详解】(1)设乙每小时做零件x 个,则甲每小时做零件(x+6)个,依题意得906x +=60x解得x=12经检验:x=12是原方程的解,符合题意∴x+6=12+6=18答:设甲每小时做零件18个,乙每小时做零件12个(2)设甲每小时做3x 个零件,则乙每小时做4x 个零件,根据题意得,603x +2060=1004x,解得:x=15,经检验:x=15是原分式方程的解,且符合题意,则3×15=45,4×15=60.答:甲每小时做45个,乙每小时做60个,故答案为45;60.27.初步发现:证明见解析;深入探究:CE+DC=AC ,证明见解析;拓展创新:(1)2,证明见解析;(2)1,证明见解析【分析】初步发现:只需要利用SAS 证明△BCD ≌△ACE 得到∠CBD=∠CAE ,由∠BOC=∠AOF ,推出∠AFO=∠BCO=60°,由此即可证明结论;深入探究:在AB 上取一点G 使得BG=BD ,连接DG ,先证明△BDG 是等边三角形,得到BG=BD=DG ,∠BGD=60°,再利用ASA 证明△AGD ≌△DCE 得到CE=GD=BD ,即可证明CE+DC=AC ;拓展创新:(1)如图所示,在AE 上取一点F ,使得EF=PD ,先证明△ACE ≌△BCD 得到AE=BD ,∠AEC=∠BDC ,再证明△CPD ≌△CFE 得到PD=FE ,∠PCD=∠FCE ,PC=CF ,进而证明△PCF 是等边三角形,得到PC=PF ;过点C 作CG ⊥BD 于G ,CH ⊥AE 于H ,利用面积法证明CG=CH ,得到3BP PE =,得到34AE BD PC PD ==+23AP PC PD =+,由此即可得到结论;(2)根据(1)所求分别用PC 和PD 表示出分子和分母的线段的和差即可得到答案.【详解】解:初步发现:如图所示,设AC 与BF 交于O ,∵△ABC 和△CDE 都是等边三角形,∴CB=CA ,CD=CE ,∠ACB=∠DCE=60°,∴∠ACB-∠ACD=∠DCE-∠ACD ,即∠BCD=∠ACE ,∴△BCD ≌△ACE (SAS ),∴∠CBD=∠CAE ,∵∠BOC=∠AOF ,∠AOF+∠AFO+∠OAF=180°,∠CBO+∠BOC+∠BCO=180°,∴∠AFO=∠BCO=60°,即∠AFB=60°;深入探究:CE+DC=AC ,证明如下:如图所示,在AB 上取一点G 使得BG=BD ,连接DG ,∵△ABC 是等边三角形,∴AC=BC=AB ,∠ACB=∠B=60°,∴∠ACF=120°,△BDG 是等边三角形,∴BG=BD=DG ,∠BGD=60°,∴∠AGD=120°,AG=DC ,∵CE 平分∠ACF ,∴1602ECF ACE ACF ∠=∠=∠=︒,∴∠DCE=120°,∵∠ADC=∠ADE+∠CDE=∠B+∠BAD ,∠B=∠ADE=60°,∴∠CDE=∠BAD ,在△AGD 和△DCE 中,DAG EDCAG DC AGD DCE∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AGD ≌△DCE (ASA ),∴CE=GD=BD ,∴CE+DC=BD+DC=BC ,∴CE+DC=AC;拓展创新:(1)32AP PDPC -=,证明如下:如图所示,在AE 上取一点F ,使得EF=PD ,∵△ABC 和△CDE 都是等边三角形,∴AC=BC ,CD=CE ,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD ,∴∠BCD=∠ACE ,在△ACE 和△BCD 中,AC BCACE BCD CE CD=⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD (SAS ),∴AE=BD ,∠AEC=∠BDC ,在△CPD 和△CFE 中,CD CECDP CEF DP EF=⎧⎪∠=∠⎨⎪=⎩,∴△CPD ≌△CFE (SAS ),∴PD=FE ,∠PCD=∠FCE ,PC=CF ,∴∠PCD+∠DCF=∠FCE+∠DCF ,∴∠PCF=∠DCE=60°,∴△PCF 是等边三角形,∴PC=PF ;过点C 作CG ⊥BD 于G ,CH ⊥AE 于H ,∵△ACE ≌△BCD ,∴ACE BCD S S =△△,∴1122BD CG AE CH ⋅=⋅,∴CG=CH ,∵BC=3CE ,∴3BCP PCE S S =△△,∴11322BP CG PE CH ⋅=⨯⋅,∴3BP PE =,∴33334AE BD BP PD PE PD PF EF PD PC PD ==+=+=++=+,∴3423AP AE PE PC PD PF EF PC PD =-=+--=+,∴32322AP PD PC PD PDPC PC -+-==;(2)21AP PC PDBD PC PE ++=-+,证明如下:由(1)可得223235AP PC PD PC PD PC PD PC PD ++=+++=+,343435BD PC PE PC PD PC PF EF PC PD PC PC PD PC PD -+=+-++=+-++=+,∴21AP PC PDBD PC PE ++=-+;。
人教版八年级上册数学期末考试试卷含答案

人教版八年级上册数学期末考试试题一、单选题1.计算23x x ⋅的结果为()A .6x B .5x C .4x D .3x 2的值在()A .1和2之间B .2和3之间C .3和4之间D .4和5之间3.如图,A D ∠=∠,ACB DBC ∠=∠,那么ABC DCB △≌△的依据是()A .SASB .ASAC .AASD .SSS 4.如图,△ABC ≌△ADE ,下列说法错误的...是()A .BC=DEB .AB ⊥DEC .∠CAE=∠BAD D .∠B=∠D5.用直尺和圆规作一个角等于已知角,如图,能得出∠A O B '''=∠AOB 的依据是()A .(SAS )B .(SSS )C .(ASA )D .(AAS )6.在综合实践活动课上,小明用三根木棒首尾顺次相接摆三角形.下列每组数分别是三根木棒的长度(单位:cm ),其中能摆出直角三角形的一组是()A .4,4,7B .32,42,52C .9,12,15D .6,7,87.如图,ABC 的三边AB ,BC ,CA 长分别是20,30,40,其三条角平分线将ABC 分为三个三角形,则ABO S :BCO S △:CAO S △等于()A .1:1:1B .1:2:3C .2:3:4D .3:4:58.如图所示的2×4的正方形网格中,△ABC 的顶点都在小正方形的格点上,这样的三角形称为格点三角形,则点A 到BC 的距离等于()A B .CD9.若实数m ,n 满足30m -=,且m ,n 恰好是Rt ABC 的两条边长,则第三条边长为()A .3或4B .5C .5D10.如图,AD 是△ABC 的角平分线,DE ⊥AC ,垂足为E ,BF AC ∥交ED 的延长线于点F ,若BC 恰好平分∠ABF ,AE=2BF ,给出下列四个结论:①DE=DF ;②DB=DC ;③AD ⊥BC ;④AC=3BF ,其中正确的结论共有()A .4个B .3个C .2个D .1个二、填空题11.已知一个等腰三角形的两边分别为4和10,则它的周长为_____.12.计算:23(66)32ab ab a b --+=______.13.分解因式26m m +=_________.14.如图, ABE ≌ DCE ,AE =2cm ,BE =1.2cm ,∠A =25°,∠B =48°,那么DE =_____cm ,∠C =_________°.15.如图,在Rt △ABC 中,∠ACB=90°,∠B=15°,AB 的垂直平分线与BC 交于点D ,交AB 于点E ,连接AD .则∠CAD 的度数为_________.16.在△ABC 中,AB =AC ,AB 的垂直平分线分别交AB 和直线AC 于D 、E 两点,且∠EBC =30°,则∠A 的度数为___________.17.等腰ABC 一腰上的高与另一腰的夹角为50°,则ABC 顶角的度数为________.18.如图,Rt ABC ∆中,90C ∠=︒,8AC =,6BC =,利用尺规在AC ,AB 上分别截取AD ,AE .使AD AE =,分别以D ,E 为圆心,以大于12DE 为长的半径作弧,两弧在BAC ∠内交于点F ,作射线AF 交边BC 于点G ,点P 为边AB 上的一动点,则GP 的最小值为________.19.已知关于x 的分式方程233x k x x -=--有一个正数解,则k 的取值范围为________.20.如图所示,在ABC ∆中,90,C DE AB ∠=︒⊥于点,E AC AE =,且55CDA ∠=︒,则B ∠=___度.三、解答题21.化简:(1)223x y x y -++;(2)22224(3)3(4)x y xy xy x y ---+.22.如果a 的算术平方根是4,b ﹣1是8的立方根,求a ﹣b ﹣4的平方根.23.分解因式:(1)22363x xy y -+(2)328x x-24.如图,AB =AD ,BC =DC ,求证:∠ABC =∠ADC .25.已知MAN ∠.(1)用尺规完成下列作图:(保留作图痕迹,不写作法)①作MAN ∠的平分线AE ;②在AE 上任取一点F ,作AF 的垂直平分线分别与AM 、AN 交于P 、Q ;(2)在(1)的条件下线段AP 与AQ 有什么数量关系,请直接写出结论.26.如图,在△ABC 中,点D 是AB 的中点,点F 是BC 延长线上一点,连接DF ,交AC 于点E ,连接BE ,∠A =∠ABE .(1)求证:ED 平分∠AEB ;(2)若AB =AC ,∠A =40°,求∠F 的度数.27.如图,长方形纸片ABCD ,AD ∥BC ,将长方形纸片折叠,使点D 与点B 重合,点C 落在点C'处,折痕为EF .(1)求证:BE =BF .(2)若AB =4,AD =8,求AE 的长.28.如图,在等边三角形ABC 中,D 是AB 上的一点,E 是CB 延长线上一点,连接,CD DE 、已知,6EDB ACD BC ∠=∠=,(1)求证:DEC ∆是等腰三角形(2)当5,8,2BDC EDB EC AD ∠=∠==时,求EDC ∆的面积.参考答案1.B2.C3.C4.B5.B6.C7.C8.C9.B10.A11.2412.222244a b a b ab -+-【分析】根据单项式乘以多项式计算即可;【详解】原式222244a b a b ab =-+-;故答案是:222244a b a b ab -+-.13.(6)m m +【分析】直接提取公因式m ,进而分解因式得出答案.【详解】解:26m m+=m (m+6).故答案为:m (m+6).【点睛】此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.14.248【分析】根据全等三角形的性质即可求得结果.【详解】∵ ABE ≌ DCE∴DE=AE=2cm ,∠C=∠B=48°故答案为:2,48【点睛】本题考查了全等三角形的性质,掌握全等三角形的性质是关键.15.60°##60度【分析】由垂直平分线的性质可求得BD=DA,且可求得∠ADC=2∠B=30°,在Rt△ACD中可求得∠CAD的度数.【详解】解:∵DE为线段AB的垂直平分线,∴BD=DA,∴∠DAB=∠B=15°,∴∠ADC=2∠B=30°,∵∠ACD=90°,∴∠CAD=90°-∠ADC=90°-30°=60°,故答案为:60°.【点睛】本题主要考查线段垂直平分线的性质及等腰三角形的性质,利用线段垂直平分线上的点到线段两端点的距离相等得到BD=DA是解题的关键.16.40°或160°或80°【分析】结合题意,分E在线段AC上、AC延长线上、CA延长线上,三种情况分析;根据等腰三角形的性质得到∠ABC=∠ACB,根据线段垂直平分线的性质得到EA=EB,得到∠ABE=∠EAB,结合三角形的内角和的性质,列一元一次方程并求解,即可得到答案.【详解】解:根据题意,分E在线段AC上、AC延长线上、CA延长线上,三种情况分析;当E在线段AC上,如图:∵AB=AC,∴∠ABC=∠ACB,∠ABC+∠ACB+∠A=180°,∵DE垂直且平分AB,∴EA=EB,∴∠ABE=∠A,∴∠ABC=∠ACB=∠ABE+∠EBC=∠A+30°,∴∠A+2(∠A+30°)=180°,解得∠A =40°;当E 在CA 延长线上,如图∵AB =AC ,∴∠ABC =∠ACB ,∵DE 垂直且平分AB ,∴EA =EB ,∴∠ABE =∠BAE ,∴∠ABC =∠ACB =∠EBC ﹣∠ABE =∠EBC ﹣∠BAE =30°﹣∠BAE ,∵∠ABC+∠ACB =∠BAE ,∴2(30°﹣∠BAE )=∠BAE ,解得∠BAE =20°,∴∠A =180°﹣20°=160°.当E 在AC 延长线上,如下图:∵AB =AC ,∴∠ABC =∠ACB ,∠ABC+∠ACB+∠A =180°,∴∠ABC =1802A︒-∠∵DE 垂直且平分AB ,∴EA =EB ,∴∠ABE =∠A ,∴∠ABE=∠ABC+∠EBC=1802A︒-∠+30°,∴∠A=1802A︒-∠+30°,解得∠A=80°;故答案为:40°或160°或80°.17.40°或140°【分析】由于等腰三角形分为锐角、直角、钝角等腰三角形,当为等腰直角三角形时不符合题意,分两种情况讨论:①若∠A<90°;②若∠A>90°;求出顶角∠BAC的度数.【详解】解:分两种情况讨论:①若∠A<90°,如图1所示:∵BD⊥AC,AB=AC,∴∠A+∠ABD=90°,∵∠ABD=50°,∴∠A=90°−50°=40°;②若∠A>90°,如图2所示:同①可得:∠DAB=90°−50°=40°,∴∠BAC=180°−40°=140°;综上所述,ABC顶角的度数为40°或140°,故答案为:40°或140°.18.83【分析】利用角平分线的性质设出GC=GP=x ,根据等积法得到方程168452x x ⨯⨯=+,得出结果.【详解】解:如图,当GP ⊥AB 时,GP 最小,根据作图知AG 平分∠BAC ,∠C=90°,∴GC=GP ,设GC=GP=x ,在直角△ABC 中,∠C=90°,10==,又∵ABCACG ABG S S S =+△△△,即11168=45222AC x AB x x x ⨯⨯⋅+⋅=+,解得x=83,故答案为83.【点睛】本题考查角平分线的性质,注意掌握利用等积法求三角形的高或点的线的距离的方法.19.k<6且k≠3【分析】根据解分式方程的步骤,可得分式方程的解,根据分式方程的解是正数,可得不等式,解不等式,可得答案,并注意分母不分零.【详解】解:233x k x x -=--,方程两边都乘以(x-3),得x=2(x-3)+k ,解得x=6-k≠3,关于x 的方程程233x k x x -=--有一个正数解,∴x=6-k >0,k <6,且k≠3,∴k 的取值范围是k <6且k≠3.故答案为k <6且k≠3.【点睛】本题主要考查了解分式方程、分式方程的解、一元一次不等式等知识,能根据已知和方程的解得出k 的范围是解此题的关键.20.20【分析】利用HL 得到△ACD ≌△AED ,由此可得到∠CDA=∠ADE ,再通过三角形内角和及角的和与差求出∠CAE ,可得到最终结果.【详解】解:∵DE ⊥AB ,∠C=90°,AC=AE ,AD=AD ,∴△ACD ≌△AED (HL ),∴∠CDA=∠ADE=55°,∠CAD=∠DAE ,∵∠CAD=180°-90°-55°=35°,∴∠CAE=70°,∴∠B=180°-90°-70°=20°.故答案为:20.【点睛】本题考查了全等三角形的判定与性质,属于基础题,熟练掌握全等三角形的判定与性质是解决本题的关键.21.(1)4x(2)2xy -【分析】(1)合并同类项即可.(2)去括号后,合并同类项,即可.(1)解:223x y x y -++=2(31)(11)x y ++-=4x .(2)解:22224(3)3(4)x y xy xy x y ---+=2222124312x y xy xy x y-+-=22(1212)(43)x y xy -+-+=2xy -.【点睛】本题考查了整式的加减、去括号、合并同类项,熟练掌握去括号法则,准确进行合并同类项是解题的关键.22.3±【分析】首先根据算术平方根的性质求出a 的值,然后根据立方根的性质求出b 的值,最后代入a ﹣b ﹣4即可求出平方根.【详解】解:由题意2416a ==,12b -==,3b ∴=,49a b ∴--=4a b ∴--的平方根为3±.【点睛】此题考查了平方根,算术平方根和立方根的性质,解题的关键是熟练掌握平方根,算术平方根和立方根的性质.23.(1)23()x y -;(2)2(2)(2)x x x +-【分析】(1)原式提取公因式,再利用完全平方公式分解即可;(2)原式提公因式后,利用平方差公式分解即可.【详解】解:(1)22363x xy y -+()2232x xy y =-+23()x y =-;(2)328x x-()224x x =-2(2)(2)x x x =+-【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.24.见解析.【分析】连接AC ,根据SSS 证明△ACD ≌△ACB 即可得到结论.【详解】证明:连接AC在△ACD 与△ACB 中,AD AB AC AC CD CB =⎧⎪=⎨⎪=⎩,∴△ACD ≌△ACB ,∴ABC ADC ∠=∠.25.(1)①作图见解析;②作图见解析;(2)AP=AQ ,理由见解析【分析】(1)①根据角平分线的作图方法求解即可;②根据线段垂直平分线的作图方法求解即可;(2)只需要证明△ATP ≌△ATQ 即可得到AP=AQ .【详解】解:(1)①如图所示,以A 为圆心,以任意长为半径画弧,分别与AM ,AN 交于点H 、G ,再分别以H 、G 为圆心,以大于HG 长的一半为半径画弧,二者交于点O ,过点O 作射线AE即为所求;②如图所示,分别以A 、F 为圆心,以大于AF 长的一半为半画弧,二者分别交于J 、K ,连接JK 分别交AM 于P ,AN 于Q ,AE 于T ;(2)AP=AQ,理由如下:∵JK是线段AF的垂线平分线,∴∠PTA=∠QTA=90°,∵AE是∠MAN的角平分线,∴∠MAE=∠NAE,又∵AT=AT,∴△ATP≌△ATQ(ASA),∴AP=AQ.【点睛】本题主要考查了角平分线和线段垂直平分线的尺规作图,角平分线的定义,线段垂直平分线的性质,全等三角形的性质与判定等等,解题的关键在于能够熟练掌握相关知识进行求解.26.(1)证明见解析;(2)∠F=20°.【分析】(1)先证EA=EB,再利用等腰三角形的三线合一性质即可得出结论.(2)根据等腰三角形的性质求出∠ABE,再由等腰三角形的性质证明∠BDF=90°,然后由直角三角形的性质即可得出答案.【详解】(1)证明:∵∠A=∠ABE,∴EA=EB,∵AD=DB,∴ED平分∠AEB;(2)解:∵∠A=40°,∴∠ABE=∠A=40°,∵AB=AC,∴∠ABC=∠ACB=70°,∵EA =EB ,AD =DB ,∴ED ⊥AB ,∴∠FDB =90°,∴∠F =90°﹣∠ABC =20°.【点睛】本题考查的是线段垂直平分线的判定与性质、等腰三角形的判定与性质以及三角形内角和定理等知识,熟练掌握等腰三角形的判定与性质是解题的关键.27.(1)证明见解析;(2)3.【分析】(1)先根据折叠的性质可得BEF DEF ∠=∠,再根据平行线的性质可得BFE DEF ∠=∠,从而可得BEF BFE ∠=∠,然后根据等腰三角形的判定即可得证;(2)先根据长方形的性质可得90A ∠=︒,再根据折叠的性质可得BE DE =,设BE DE x ==,从而可得8AE x =-,然后在Rt ABE △中,利用勾股定理可求出x 的值,由此即可得出答案.【详解】证明:(1)由折叠的性质得:BEF DEF ∠=∠,AD BC ,BFE DEF ∴∠=∠,BEF BFE ∴∠=∠,BE BF ∴=;(2) 四边形ABCD 是长方形,90A ∴∠=︒,由折叠的性质得:BE DE =,设BE DE x ==,则8AE AD DE x =-=-,在Rt ABE △中,4AB =,90A ∠=︒,222AB AE BE ∴+=,即2224(8)x x +-=,解得5x =,8853AE x ∴=-=-=.【点睛】本题考查了折叠问题、勾股定理、等腰三角形的判定等知识点,熟练掌握折叠的性质是解题关键.28.(1)证明见解析;(2)16【分析】(1)证明:根据等边三角形的性质得到60ABC ACB ∠=∠=︒,推出∠E=∠BCD ,得到DE=DC ,由此得到结论;(2)设EDB ACD x ∠=∠=,则5BDC x ∠=,求出15x =o ,得到690EDC x ∠==︒,推出△DEC 是等腰直角三角形,过点D 作DF EC ⊥于点F ,证得△DFE 、△DFC 都是等腰直角三角形,求出DF=4,即可根据三角形的面积公式求出答案.【详解】(1)证明:ABC ∆ 是等边三角形60ABC ACB ∴∠=∠= ,E EDB ACD BCD ∠+∠=∠+∠∴,EDB ACD ∠=∠ ,E BCD ∴∠=∠,DE DC ∴=,DEC ∴∆是等腰三角形;(2)设EDB ACD x ∠=∠=,则5BDC x ∠=,60ACB ∠=60BCD x ∠=∴- ,60E x ∠=∴- ,在DEC ∆中,180E EDC DCE ∠+∠+∠=︒,60560180x x x x ∴+ ,解得15x =o ,690EDC x ∴∠== ,DEC ∴∆是等腰直角三角形,过点D 作DF EC ⊥于点F ,如图所示,DF EC ⊥ ,,DFE DFC ∆∆∴都是等腰直角三角形,12DF EC∴=8EC = ,∴DF=4,EDC ∴∆的面积为:11841622EC DF ⋅⋅=⨯⨯=。
人教版八年级上册数学期末考试试卷带答案

人教版八年级上册数学期末考试试题一、单选题1.下列图形中,不是轴对称图形的是()A .B .C .D .2.当1x =时,下列分式没有意义的是()A .1x x +B .1xx -C .1x x-D .1x x +3.下列各组数可能是一个三角形的边长的是()A .4,4,9B .4,5,6C .2,6,8D .1,2,34.某病毒的直径约为80~120纳米,1纳米=91.010-=⨯米,若用科学记数法表示110纳米,则正确的结果是()A .91.110-⨯米B .81.110-⨯米C .71.110-⨯米D .61.110-⨯米5.六边形的外角和是()A .360°B .540°C .720°D .900°6.下列计算正确的是()A .224x x x +=B .()222x y x y -=-C .()326=x yx y D .235()x x x -⋅=7.计算11x x x +-的结果为()A .1B .x C .1x D .2x x +8.已知7a b +=,8a b -=则22a b -的值是()A .11B .15C .56D .609.如图,已知∠ABC=∠DCB ,下列所给条件不能证明△ABC ≌△DCB 的是()A .∠A=∠DB .AB=DC C .∠ACB=∠DBCD .AC=BD10.如图,在△ABC 中,∠C=90°,AD 平分∠BAC 交BC 于点D ,DE ⊥AB 于点E ,则下列结论:①AD 平分∠CDE ;②∠BAC=∠BDE ;③DE 平分∠ADB ;④若AC=4BE ,则S △ABC =8S △BDE 其中正确的有()A .1个B .2个C .3个D .4个二、填空题11.因式分解:4x 2﹣9=_____.12.点M (-5,3)关于x 轴对称的点N 的坐标是________.13.如果实数a ,b 满足a+b =6,ab =8,那么a 2+b 2=_____.14.如图,小明把一块三角形的玻璃片打碎成三块,现要到玻璃店去配一块完全相同的玻璃片,那么最省事的办法是带_________去.15.如图,在△ABC 中,∠C =90°,AD 平分∠BAC ,若CD =8,点E 是AB 上一动点,DE 的最小值为_________.16.分式3232a b c 与246a b a b c-的最简公分母是_____.17.把一副三角板按如图所示的方式放置,则图中钝角α是______o .三、解答题18.计算:2202001()(1)(4)2π----+-.19.解分式方程:3211x x x +=--20.先化简,再求值:1x x +÷(x -1x ),其中x=3.21.如图,在△ABC 中,∠A >∠B .(1)作边AB 的垂直平分线DE ,与AB ,BC 分别相交于点D ,E (用尺规作图,保留作图痕迹,不要求写作法).(2)在(1)的条件下,连接AE ,若∠B =45°,求∠AEC 的度数.22.如图,点C ,E ,F ,B 在同一直线上,点A ,D 在BC 异侧,AB ∥CD ,AE=DF ,∠A=∠D ,(1)求证:AB=CD ;(2)若AB=CF ,∠B=30°,求∠D 的度数.23.如图1所示,边长为a 的正方形中有一个边长为b 的小正方形,如图2中阴影部分剪裁后拼成的一个长方形.(1)设如图1中阴影部分面积为S 1,如图2中阴影部分面积为S 2,请直接用含a ,b 的代数式表示S 1,S 2;(2)请写出上述过程所揭示的乘法公式;(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+124.如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A 沿AB向B点运动,点Q同时从顶点B沿BC向C点运动,它们的速度都为1cm/s,当到达终点时停止运动,设它们的运动时间为t秒,连接AQ、CP交于点M.(1)求证:△ABQ≌△CAP.(2)求证:点P、Q在运动的过程中,∠CMQ的度数不变化,并求出∠CMQ的度数.(3)当t为何值时△PBQ是直角三角形?25.某体育用品商场用32000元购进了一批运动服,上市后很快销售一空.商场又用68000元紧急购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)该商场两次共购进这种运动服多少套?(2)若两批运动服每套的售价相同,第二批售完后获利比第一批售完后获利多12000元,则每套运动服的售价是元.26.如图,∠DAB=∠CAE,AD=AB,AC=AE.(1)求证△ABE≌△ADC;(2)设BE与CD交于点O,∠DAB=30°,求∠BOC的度数.27.已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.参考答案1.D【分析】根据轴对称图形的定义(如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形)逐项判断即可得.【详解】解:A、是轴对称图形,故本选项不符合题意;B 、是轴对称图形,故本选项不符合题意;C 、是轴对称图形,故本选项不符合题意;D 、不是轴对称图形,故本选项符合题意;故选:D .【点睛】本题考查了轴对称图形,熟记轴对称图形的定义是解题关键.2.B【分析】由分式有意义的条件分母不能为零判断即可.【详解】1x x ,当x=1时,分母为零,分式无意义.故选B.【点睛】本题考查分式有意义的条件,关键在于牢记有意义条件.3.B【分析】根据三角形的三边关系:三角形两边之和大于第三边,计算两个较小的边的和,看看是否大于第三边即可.【详解】解:A 、4+4<9,不能组成三角形,故此选项不符合题意;B 、5+4>6,能组成三角形,故此选项符合题意;C 、2+6=8,不能组成三角形,故此选项不符合题意;D 、1+2=3,不能组成三角形,故此选项不符合题意.故选:B.【点睛】此题主要考查了三角形的三边关系,关键是掌握三角形的三边关系定理.4.C【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n 由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:110纳米=110×10-9米=1.1×10-7米.故选:C .【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.5.A【分析】根据多边形外角和都是360°即可得出答案.【详解】∵多边形的外角和都是360°,∴六边形的外角和是360°.故选:A.【点睛】本题主要考查多边形外角和,掌握多边形外角和都是360°是解题的关键.6.D【分析】根据合并同类项法则、完全平方公式、积的乘方法则、同底数幂的乘方法则计算,判断即可.【详解】x2+x2=2x2,A错误;(x-y)2=x2-2xy+y2,B错误;(x2y)3=x6y3,C错误;(-x)2•x3=x2•x3=x5,D正确;故选:D.【点睛】本题考查的是合并同类项、完全平方公式、积的乘方、同底数幂的乘法,掌握它们的运算法则是解题的关键.7.A【分析】根据同分母分式相加减,分母不变,分子相加减计算即可得解.【详解】解:原式=11111 x x xx x x x++--===.故选:A.考点:分式的加减法【点睛】本题主要考查分式的加减运算,掌握运算法则是解题关键.8.C【分析】直接利用平方差公式将a2-b2分解为(a+b)(a-b),代入数据后即可得出结论.【详解】解:∵a+b=7,a-b=8,∴a2-b2=(a+b)(a-b)=7×8=56.故选:C.【点睛】本题考查了平方差公式的应用,公式法因式分解.解题的关键是利用平方差公式将a2-b2分解为(a+b)(a-b).9.D【详解】A.添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;B.添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;C.添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;D.添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意.故选D.10.B【分析】根据题中条件,结合图形及角平分线的性质得到结论,与各选项进行比对,排除错误答案,选出正确的结果.【详解】解:∵AD平分∠BAC,∴∠DAC=∠DAE,∵∠C=90°,DE⊥AB,∴∠C=∠E=90°,∵AD=AD,∴△DAC≌△DAE(AAS),∴∠CDA=∠EDA,∴①AD平分∠CDE正确;无法证明∠BDE=60°,∴③DE平分∠ADB错误;∵BE+AE=AB,AE=AC,∵AC=4BE,∴AB=5BE,AE=4BE,∴S△ADB=5S△BDE,S△ADC=4S△BDE,∴S△ABC=9S△BDE,∴④错误;∵∠BDE=90°-∠B,∠BAC=90°-∠B,∴∠BDE=∠BAC,∴②∠BAC=∠BDE正确.故选B.11.(2x+3)(2x﹣3).【分析】根据平方差公式进行分解即可.【详解】原式=22(2)3x -=(2x+3)(2x ﹣3),故答案为(2x+3)(2x ﹣3).12.(-5,-3).【详解】根据平面直角坐标系内关于x 轴对称,纵坐标互为相反数,横坐标不变,点M (-5,3)关于y 轴的对称点为(-5,-3).13.20【详解】∵6,a b +=∴222()236,a b a ab b +=++=∵ab=8,∴22a b +=36-2ab=36-2×8=20.14.③【分析】根据全等三角形的判定可即可求解.【详解】解:第①块和第②块都没有保留完整的边,而全等三角形的判定定理中,至少存在一条边,第③块保留了一边边和两个角,则利用ASA 判定定理可得到一个全等三角形,进而可带③去,故答案为:③.【点睛】本题考查了全等三角形的条件,解题的关键是需要注意的是只靠一个角或两条边不能等得到全等.15.8【分析】过点D 作DE ⊥AB 于E ,根据点与直线垂线段最短,则当DE ⊥AB 时有最小值,再根据角平分线的性质即可求解.【详解】解:过点D 作DE ⊥AB 于E ,如图所示:根据点与直线垂线段最短,则当DE ⊥AB 时有最小值,∵∠C =90°,AD 平分∠BAC ,CD =8,∴DE=CD=8,故答案为:8.16.6a 3b 4c【分析】取各分式分母中系数的最小公倍数与各字母因式最高次幂的乘积作公分母,叫最简公分母.【详解】解:先分离出两个分式的分母2a 3b 2c,6a 2b 4c ,其中a 、b 、c 的最高次幂分别为3、4、1故分式3232a b c ,246a b a b c-的最简公分母是6a 3b 4c .故答案为6a 3b 4c.17.105【分析】利用三角形内角和定理计算即可.【详解】解:由三角形的内角和定理可知:α=180°-30°-45°=105°,故答案为105.18.4【分析】原式分别化简21()2=4--,2020(1)=1-,0(=14)π-,然后再进行加减运算即可得到答案.【详解】解:2202001()(1)(4)2π----+-=4﹣1+1=419.1x =-【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】解:3211x x x +=--去分母得,()321x x +-=,解得,1x =-,经检验,1x =-是原方程的解.所以,原方程的解为:1x =-.20.11x -;12【分析】先计算括号内分式的减法,再将除法转化为乘法,最后约分即可化简原式,继而将x 的值代入计算可得答案.【详解】解:1x x+÷(x -1x )=211x x x x +-÷=()()111x x x x x +⨯+-=11x -当x=3时,原式=131-=12.21.(1)作图见解析(2)90°【分析】(1)依据垂直平分线的作图方法,即可得到边AB 的垂直平分线DE ;(2)依据垂直平分线的性质,即可得到∠BAE=∠B ,再根据三角形外角性质,即可得到∠AEC 的度数.(1)如图所示DE 为所求;(2)∵DE 是AB 的垂直平分线,∴AE =BE ,∴∠EAB =∠B =45°,∵AEC ∠是ABE ∆的外角,∴∠AEC =∠EAB ﹢∠B =90°.【点睛】本题主要考查了线段垂直平分线的的性质以及基本作图,解决问题的关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.22.(1)证明见解析;(2)∠D=75°【分析】(1)易证得ABE DCF△≌△,即可得AB CD=;(2)易证得ABE DCF△≌△,即可得AB CD=,又由AB=CF,∠B=30°,即可证得△ABE 是等腰三角形,解答即可.【详解】证明:(1)∵AB∥CD,∴∠B=∠C.在△ABE和△DCF中,∠A=∠D∠C=∠B AE=DF,∴ABE DCF AAS≌().∴AB=.(2)解:∵ABE DCF△≌△,∴AB=CD,∵AB=CF,∴CD=CF.∴△CDF是等腰三角形,∵∠C=∠B=30°,∴∠D=12×(180°−30°)=75°.【点睛】本题考查全等三角形问题和等腰三角形的性质,关键是根据AAS证明三角形全等,再利用全等三角形的性质解答.23.(1)S1=a2-b2,S2=(a+b)(a﹣b);(2)(a+b)(a﹣b)=a2﹣b2;(3)216.【分析】(1)直接计算两个图形的面积即可;(2)根据两个图形面积相等可得(a+b)(a-b)=a2-b2;(3)从左到右依次利用平方差公式即可求解.【详解】解:(1)S1=a2-b2,S2=(a+b)(a﹣b);(2)(a+b)(a﹣b)=a2﹣b2;(3)原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)+1=(22﹣1)(22+1)(24+1)(28+1)+1=(24﹣1)(24+1)(28+1)+1=(28﹣1)(28+1)+1=(216﹣1)+1=216.24.(1)证明见解析(2)证明见解析;∠CMQ=60°(3)当第43秒或第83秒时,△PBQ为直角三形【分析】(1)利用等边三角形的性质可知AB=AC,∠B=∠CAP=60°,结合AP=BQ即可得证;(2)由△APC≌△BQA知∠BAQ=∠ACP,再利用三角形外角的性质可证得∠CMQ=60°;(3)可用t分别表示出BP和BQ,分∠PQB=90°和∠BPQ=90°两种情况,分别利用直角三角形的性质可得到关于t的方程,则可求得t的值.(1)∵△ABC是等边三角形,∴AB=AC,∠B=∠CAP=60°,又AP=BQ,∴△ABQ≌△CAP(SAS).(2)∵△ABQ≌△CAP,∴∠BAQ=∠ACP,又∠CMQ=∠ACP﹢∠CAM∴∠CMQ=∠BAQ﹢∠CAM=∠BAC=60°.(3)由题意知AP=BQ=t,PB=4﹣t,①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,即4﹣t=2t,解得t=4 3;②当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP,即t=2(4﹣t),解得t=8 3;综上所述,当第43秒或第83秒时,△PBQ为直角三形.25.(1)商场两次共购进这种运动服600套;(2)240【分析】(1)设商场第一次购进x套运动服,则第二次购进2x套运动服,抓住每套进价多了10元列分式方程求解即可.(2)求出两次购进运动服的进价,根据“第二批售完后获利比第一批售完后获利多12000元”可列出一元一次方程得解.【详解】(1)设商场第一次购进x套运动服,由题意得:680003200010 2x x-=.解这个方程,得x=200.经检验,x=200是所列方程的根.2x+x=2×200+200=600.答:商场两次共购进这种运动服600套.(2)第一批运动服的进价为32000200=160(元),第二批运动服的进价为68000400=170(元),设每套运动服的售价是x元,由题意得:400(x﹣170)﹣200(x﹣160)=12000,解得:x=240故答案为240.26.(1)见解析;(2)150°.【分析】(1)先利用角的和差证出∠DAC=∠BAE,再利用SAS证△ABE≌△ADC即可;(2)设AB与OD交于点F,根据(1)中全等可得:∠ABE=∠D,根据三角形的内角和定理可证∠BOF=∠DAB=30°,从而求出∠BOC的度数.【详解】解:(1)∵∠DAB=∠CAE∴∠DAB+∠BAC=∠CAE+∠BAC∴∠DAC=∠BAE在△ABE和△ADC中AB AD BAE DAC AE AC ⎧⎪∠=∠⎨⎪⎩==∴△ABE ≌△ADC ;(2)设AB 与OD 交于点F∵△ABE ≌△ADC∴∠ABE=∠D∵∠BFO=∠DFA∴∠BOF=180°-∠ABE -∠BFO=180°-∠D -∠DFA=∠DAB=30°∴∠BOC=180°-∠BOF=150°27.(1)证明见解析;(2)BE=AF ,证明见解析.【分析】(1)连接AD ,根据等腰三角形的性质可得出AD=BD 、∠EBD=∠FAD ,根据同角的余角相等可得出∠BDE=∠ADF ,由此即可证出△BDE ≌△ADF (ASA ),再根据全等三角形的性质即可证出BE=AF ;(2)连接AD ,根据等腰三角形的性质及等角的补角相等可得出∠EBD=∠FAD 、BD=AD ,根据同角的余角相等可得出∠BDE=∠ADF ,由此即可证出△EDB ≌△FDA (ASA ),再根据全等三角形的性质即可得出BE=AF .【详解】(1)证明:连接AD,如图①所示.∵∠A=90°,AB=AC ,∴△ABC 为等腰直角三角形,∠EBD=45°.∵点D 为BC 的中点,∴AD=12BC=BD ,∠FAD=45°.∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,∴∠BDE=∠ADF .在△BDE 和△ADF 中,EBD FADBD AD BDE ADF∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BDE ≌△ADF (ASA ),∴BE=AF ;(2)BE=AF ,证明如下:连接AD,如图②所示.∵∠ABD=∠BAD=45°,∴∠EBD=∠FAD=135°.∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°,∴∠EDB=∠FDA .在△EDB 和△FDA 中,EBD FADBD AD EDB FDA∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△EDB ≌△FDA (ASA ),∴BE=AF .。
人教版八年级上册数学期末试卷及答案

人教版八年级上册数学期末试题一、单选题1.下列图形中,是轴对称图形的是()A .B .C .D .2.以下列数值为长度的各组线段中,不能围成三角形的是()A .2,3,4B .3,5,6C .2,2,5D .4,4,63.下列计算正确的是()A .22a a a ⋅=B .330a a ÷=C .()3253ab a b =D .221a a -=4.下列分式是最简分式的()A .223ac a bB .23aba a -C .22ab a b ++D .222a aba b --5.若224x mx ++是完全平方式,则m 的值是()A .16±B .4±C .2±D .1±6.已知图中的两个三角形全等,则∠1的度数为()A .43B .55C .82D .677.等腰三角形的周长为10cm ,其中一边长为4cm ,则该等腰三角形的底边长为()A .5cmB .4cmC .3cm 或4cmD .2cm 或4cm 8.一个多边形的内角和比四边形内角和多360 ,则这个多边形是()A .五边形B .六边形C .七边形D .八边形9.若2x y +=,15xy =,则()()22x y --的值是()A .11B .14C .15D .1810.如图,已知△ABC 中,D 、E 分别为BC 、AC 上的点,且满足AB AD CD CE ===,若∠36BAD = ,则∠ADE 的度数为()A .36°B .35°C .26°D .72°二、填空题11.因式分解:224a b -=_____.12.点()2,3P -关于x 轴对称的点的坐标为_________.13.数据0.0000001米,用科学记数法表示为_______米.14.甲完成一项工作需t 小时,乙完成同样工作比甲少用1小时,设工作总量为1,则乙的工作效率为__________.15.如图,在△ABC 中,∠C=90°,AD 平分∠BAC ,AB=5,CD=2,则△ABD 的面积是________.16.如图,已知AD ∥BC ,∠BAD=90°,∠C=60°,CB=CD ,若AD=1,则BC=____.三、解答题17.计算:(1)()()3421x x +-(2)2(2)(2)()m n m n m n +---18.解分式方程:(1)15122x x x +=++(2)2351311x x x x +=---19.先化简,再求值:()22212•21121a a a a a a a -+-÷++--,其中12a =.20.如图,点A 、E 、B 、D 在同一直线上,AC 、DF 相交于点G ,FE AD ⊥,垂足为E ,CB AD ⊥垂足为B ,且FE CB =,AE BD =.求证:△ABC ≌△DEF .21.如图,在平面直角坐标系中,已知A (3,3),B (1,1),C (4,-1).(1)画出△ABC 关于y 轴的轴对称图形△A 1B 1C 1,并写出A 1、B 1、C 1坐标;(2)在(1)的条件下,连接AA 1、AB 1,直接写出△AA 1B 1的面积.22.如图,D 、E 分别是AB 、AC 的中点,CD ⊥AB 于D ,BE ⊥AC 于E ,求证:AC=AB .23.某学校为美化校园,安排甲、乙两工程队对面积为990m 2的区域进行绿化.已知甲队每天能完成的绿化面积是乙队每天能完成绿化面积的2倍,若先由乙队完成面积的13,再由甲、乙共同完成,时间共用11天.问甲、乙两工程队每天能完成绿化的面积分别是多少平方米?24.如图,正方形ABCD 的边长为4,动点P 从点A 开始沿A→D→C 的方向,以每秒2个单位的长度运动,动点Q 从点B 出发,沿B→C→D 以每秒1个单位的长度运动.当点P 到达C 点后,P 、Q 两点同时停止运动.设运动时间为t ,△BPQ 的面积为S .(1)填空:当动点P 到达D 点时,t=;(2)请用含t 的式子表示面积S .25.轴对称变换是几何证明中重要的图形变换之一,即寻找对称轴,将对称轴的一侧图形进行翻折,来构造满足条件的几何辅助线.例:在△ABC 中,过点A 作AD ⊥BC 于点D ,若AC+CD=BD ,则∠B 与∠C 满足什么关系?分析:将△ADC 沿直线AD 翻折,得到△ADE ,通过相关定理即可得到结论.(1)请猜想∠B 与∠C 的关系,并说明理由;(2)如图3,A 、D 为线段BC 同侧两点,∠BAC=∠BDC=60°,∠ACB+12∠ACD=90°,求证:AB=AC+CD .26.如图,在平面直角坐标系中,点(0)A m ,、点(,0)B n 分别在y 轴、x 轴的正半轴上,若m 、n 满足()()2240m n n -+-=.(1)填空:m =,n =;(2)如图,点P 是第一象限内一点,连接AP 、OP ,使∠APO=45°.过点B 作BC ⊥OP 于点D ,交y 轴于点C ,证明:DP=DB .(3)若在线段OA 上有一点M (0t ,),连接BM ,将BM 绕点B 逆时针旋转90°得到BN ,连接AN 交x 轴于点E ,请直接写出点E 的坐标(用含有t 的代数式表示).参考答案1.A2.C3.D4.C5.C6.C7.D8.B9.C10.A11.()()22a b a b +-【详解】解:原式=(a+2b)(a-2b).故答案为:(a+2b )(a-2b )12.()2,3--【详解】解:点()2,3P -关于x 轴对称点的坐标为:()2,3--,故答案为()2,3--.13.7110-⨯【详解】解:70.0000001110-=⨯故答案为:7110-⨯14.1t-1【详解】解:∵乙的工作时间为(t-1),工作总量为1,∴乙的工作效率为11t -.故答案为:11t -.15.5【详解】解:如图,过D 作DE ⊥AB 于E ,△DAE 和△DAC 中,AD 平分∠BAC ,则∠DAE=∠DAC ,∠DEA=∠DCA=90°,DA=DA ,∴△DAE ≌△DAC (AAS ),∴DE=DC=2,∴△ABD 的面积=12×AB×DE=12×5×2=5,故答案为:5;16.2【分析】连接BD ,证明△BCD 是等边三角形,可得BD =BC ,∠DBC =60°,求出∠ABD =30°,然后根据含30°角的直角三角形的性质求出BD 即可.【详解】解:连接BD ,∵∠C=60°,CB=CD ,∴△BCD 是等边三角形,∴BD =BC ,∠DBC =60°,∵AD ∥BC ,∠BAD=90°,∴∠ABC =90°,∴∠ABD =30°,∵∠BAD=90°,AD=1,∴BD =2AD =2,∴BC =BD =2,故答案为:2.17.(1)2654x x +-(2)22322m mn n +-【分析】(1)根据多项式乘多项式进行计算即可;(2)运用平方差与完全平方公式进行计算即可.(1)解:()()3421x x +-=26834x x x +--=2654x x +-(2)2(2)(2)()m n m n m n +---=()222242m n m mn n ---+=222242m n m mn n --+-=22322m mn n +-18.(1)-3x =(2)12x =-【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.(1)解:15122x x x +=++,方程两边同时乘以21x +()得:25x =+,解得-3x =,把-3x =代入2123140x +=-+=-≠()(),所以-3x =是原方程的解;(2)解:2351311x x x x +=---,方程两边同时乘以(1)(1)x x -+得:()()()3151311x x x x x -+=+-+-,化简得:84x -=,解得12x =-,把12x =-代入()()1131111224x x ⎛⎫⎛⎫-+=---+=- ⎪⎪⎝⎭⎝⎭≠0,所以原方程的解为12x =-.19.()211a a -+,23-【分析】根据分式的乘除法可以化简题目中的式子,再把a 值代入化简式子中求解即可.【详解】解:()22212•21121a a a a a a a -+-÷++--=()()222121••121a a a a a a --+--+=()211a a -+,把12a =代入原式得原式=121122133122⎛⎫⨯- ⎪-⎝⎭==-+.20.见解析【详解】证明:∵EF ⊥AD ,CB ⊥AD ,∴∠ABC=∠DEF=90°,又∵AE=BD ,∴AE+EB=BD+EB ,∴AB=DE ,在△ABC 与△DEF 中FE CB ABC DEF AB DE =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ).21.(1)图见解析,A 1(-3,3),B 1(-1,1),C 1(-4,-1)(2)△AA 1B 1的面积为6【分析】(1)直接利用关于y 轴对称点的性质得出对应点位置进而得出答案;(2)利用三角形面积公式进而得出答案.(1)解:如图所示:△A 1B 1C 1,即为所求;A 1(-3,3),B 1(-1,1),C 1(-4,-1);(2)解:△AA 1B 1的面积为:12×6×2=6.22.证明见解析【分析】连接BC ,由CD 垂直于AB ,且D 为AB 中点,即CD 所在直线为AB 的垂直平分线,根据线段垂直平分线上的点到线段两端点的距离相等,得到AC=BC ,又E 为AC 中点,且BE 垂直于AC ,即BE 所在的直线为AC 的垂直平分线,同理可得BC=AB ,等量代换即可得证.【详解】证明:如图,连接BC∵CD ⊥AB 于D ,D 是AB 的中点,即CD 垂直平分AB ,∴AC=BC (中垂线的性质),∵E 为AC 中点,BE ⊥AC ,∴BC=AB (中垂线的性质),∴AC=AB .23.甲工程队每天能完成绿化的面积为100平方米,乙工程队每天能完成绿化的面积为50平方米【分析】设乙工程队每天能完成绿化的面积为x 平方米,根据“由甲、乙共同完成,时间共用11天”列分式方程求解即可.【详解】解:设乙工程队每天能完成绿化的面积为x 平方米,则甲工程队每天能完成绿化的面积为2x 平方米,由题意得:1299099033112x x x⨯⨯+=+,整理得:33022011x x +=,即55011x =,方程两边同时乘以x ,得,11550x =,解得50x =,验根:当50x =时分母不为0,所以50x =是原方程的解,答:甲工程队每天能完成绿化的面积为100平方米,乙工程队每天能完成绿化的面积为50平方米.24.(1)2(2)22(02)4(24)t x S t t x <≤⎧=⎨-+<≤⎩【分析】(1)用AD 的长除以动点P 的速度可求出t ;(2)分0<t≤2时和2<t≤4时两种情况,分别利用三角形的面积公式列式计算即可.(1)解:∵正方形ABCD 的边长为4,动点P 的速度为每秒2个单位的长度,∴t =4÷2=2,故答案为:2;(2)当0<t≤2时,点P 在线段AD 上,如图:∵BQ =t ,∴114222S BQ CD t t =⋅=⨯=;当2<t≤4时,点P 在线段CD 上,如图:∵BQ =t ,CP =8-2t ,∴()21182422S BQ CP t t t t =⋅=⨯-=-+;综上所述:()()2202424t t S t t t ⎧<≤⎪=⎨-+<≤⎪⎩.25.(1)∠C=2∠B ,证明见解析(2)见解析【分析】(1)在DB 上截取一点E ,使DE=DC ,利用SAS 证明△ADE ≌△ADC ,推出AE=AC ,∠AED=∠C ,再证明BE=AE ,利用三角形的外角性质即可得到∠C=2∠B ;(2)延长AC 至E ,使AE=AB ,设∠ACD=2α,得到∠BCE=90°+α,∠BCD=90°-α+2α=90°+α,再推出△ABE 是等边三角形,利用AAS 证明△BCD ≌△BCE ,据此即可证明AB=AC+CD .(1)解:结论:∠C=2∠B ,证明:在DB 上截取一点E ,使DE=DC ,连接AE ,∵AD⊥BC,∴∠ADC=∠ADE=90°,在△ADE与△ADC中,AD AD ADE ADCDE DC=⎧⎪∠=∠⎨⎪=⎩,∴△ADE≌△ADC(SAS),∴AE=AC,∠AED=∠C,∴BD=BE+ED,又∵BD=AC+CD,∴AC=BE,∴BE=AE,∴∠B=∠BAE,∴∠AED=2∠B,∴∠C=2∠B;(2)证明:延长AC至E,使AE=AB,连接BE,设∠ACD=2α,∵∠ACB+12∠ACD=90°,则∠ACB=90°-α,∴∠BCE=90°+α,∴∠BCD=90°-α+2α=90°+α,∵∠BAC=60°,BA=BE ,∴△ABE 是等边三角形,∴∠E=60°,AB=AE ,在△BCD 与△BCE 中,D E BCD BCE BC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCD ≌△BCE(AAS),∴CD=CE ,∵AE=AC+CE=AC+CD ,∴AB=AC+CD .26.(1)4,4m n ==(2)见解析(3)E (2-12t ,0)【分析】(1)根据()()2240m n n -+-=得到040m n n -=⎧⎨-=⎩即可求解;(2)过点A 向OP 作垂线交于点E ,证明△AOE ≌△BOD ,进而可得到结论;(3)过点N 作NC ⊥x 轴交于点C ,可证△BOM ≌△BCN ,之后再证明△AOE ≌△ECN ,即可得到结论;(1)解:()()2240m n n -+-= ,040m n n -=⎧∴⎨-=⎩,4m n ∴==,故答案为:4,4m n ==;(2)证明:过点A 向OP 作垂线交于点E ,则∠AEP=90°,∵∠AOP+∠POB=90°,∠AOP+∠OAE=90°,∴∠POB=∠OAE ,又OA=OB ,∠AEO=∠BDO=90°,∴△AOE ≌△BOD ()AAS ,∴DB=OE ,AE=OD ,又∵∠APO=45°,∠AEP=90°,∴AE=EP,∴EP=OD ,∵OE=OD+DE ,DP=DE+EP ,∴OE=DP ,∴DP=DB ,(3)解:如图,过点N 作NC ⊥x 轴交于点C ,由题可知BM BN =,90MBN MOB ∠=∠=︒,90MBO OBN ∠+∠=︒ ,90OBN CNB ∠+∠=︒,MBO CNB ∴∠=∠,∴△BOM ≌△BCN ()AAS ,OM BC t ∴==,OB NC =,OA OB = ,OA NC ∴=,90AOC NCE ∠=∠=︒ ,OEA CEN ∠=∠,∴△AOE ≌△ECN ()AAS ,12OE EC OC ∴==,4OC OB CB t =-=- ,∴OC=4-t ,∴OE=12OC=2-12t ,∴E (2-12t ,0).。
人教版八年级上册数学期末考试试卷及答案

人教版八年级上册数学期末考试试题一、单选题1.下列图形中,不具有稳定性的是()A.等腰三角形B.平行四边形C.锐角三角形D.等边三角形2.下面的轴对称图形中,对称轴数量最多的是()A.B.C.D.3.下面的计算正确的是()A.(ab)2=ab2B.(ab)2=2ab C.a3•a4=a12D.(a3)4=a12 4.当x=﹣2时,下列分式没有意义的是()A.22xx-+B.2xx-C.22xx+D.22xx--5.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是()A.115°B.65°C.40°D.25°6.计算(2x﹣1)(x+2)的结果是()A.2x2+x﹣2B.2x2﹣2C.2x2﹣3x﹣2D.2x2+3x﹣2 7.等腰三角形的一边长是5,另一边长是10,则周长为()A.15B.20C.20或25D.258.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=6,AB=12,则△ABD的面积是()A.18B.24C.36D.729.若正整数m 使关于x 的分式方程2(2)(1)21m x x x x x x -=-+-+-的解为正数,则符合条件的m 的个数是()A .2B .3C .4D .510.如图,将△ABC 沿着DE 减去一个角后得到四边形BCED ,若∠BDE 和∠DEC 的平分线交于点F ,∠DFE =α,则∠A 的度数是()A .180°﹣αB .180°﹣2αC .360°﹣αD .360°﹣2α二、填空题11.在一场足球比赛中,运动员甲、乙两人与足球的距离分别是8m ,17m ,那么甲、乙两人的距离d 的范围是______.12.化简:23222y xyx y x xy+--的计算结果是______.13.把多项式x 2﹣6x +m 分解因式得(x +3)(x ﹣n ),则m +n 的值是______.14.若|2x ﹣4|+(y +3)2=0,点A (x ,y )关于x 轴对称的点为B ,点B 关于y 轴对称的点为C ,则点C 的坐标是______.15.如图,在四边形中ABCD 中,BD 平分∠ABC ,∠DAB +∠DCB =180°,DE ⊥AB 于点E ,AB =8,BC =4,则BE 的长度是______.16.如图,已知:,D E 分别是ABC 的边BC 和边AC 的中点,连接,DE AD .若224,ABC S cm = 则DEC 的面积是____________________.三、解答题17.计算:(结果用幂的形式表示)3x2•x4﹣(﹣x3)218.如图,已知∠A=∠C,AE、CF分别与BD交于点E、F.请你从下面三项中再选出两个作为条件,另一个作为结论,写出一个真命题,并加以证明.①AB∥DC;②AE∥CF;③DE=BF.19.如图,在△ABC中,(1)尺规作图:作边AC的垂直平分线,交AB于点D,交AC于点E,连结CD.(2)若△BCD的周长等于18,AE=4,求△ABC的周长.20.已知T=244()2m mmm m++⋅+.(1)化简T.(2)若m2+2m﹣3=0,求此时T的值.21.为了响应打赢“蓝天保卫战”的号召,黄老师上下班的交通方式由驾车改为骑自行车,黄老师家距离学校的路程是9千米,在相同的路线上,驾车的平均速度是骑自行车的平均速度的3倍,所以黄老师每天上班要比开车早出发20分钟,才能按原驾车的时间到达学校.(1)求黄老师驾车的平均速度;(2)据测算,黄老师的汽车在上下班行驶过程中平均每小时碳排放量约为2.4千克,按这样计算,求黄老师一天(按一个往返计算)可以减少的碳排放量.22.常见的分解因式的方法有提公因式法、公式法及十字相乘法,而有的多项式既没有公因式,也不能直接运用公式分解因式,但是某些项通过适当的调整能构成可分解的一组,用分组来分解一个多项式的因式,这种方法叫分组分解法.如x 2+2xy +y 2﹣16,我们细心观察这个式子就会发现,前三项符合完全平方公式,分解后与后面的部分结合起来又符合平方差公式,可以继续分解,过程为:x 2+2xy +y 2﹣16=(x +y )2﹣42=(x +y +4)(x+y ﹣4).它并不是一种独立的因式分解的方法,而是为提公因式或运用公式分解因式创造条件.阅读材料并解答下列问题:(1)分解因式:2a 2﹣8a +8;(2)请尝试用上面的方法分解因式:x 2﹣y 2+3x ﹣3y ;(3)若△ABC 的三边a ,b ,c 满足a 2﹣ab ﹣ac +bc =0,请判断△ABC 的形状并加以说明.23.如图,在ABC 中,AB AC =,点D 在BC 边上,点E 在AC 边上,连接AD ,DE .已知12∠=∠,AD DE =.(1)求证:ABD DCE △△≌;(2)若2BD =,5CD =,求AE 的长.24.如图①,在△ABC 中,∠ABC 和∠ACB 的平分线交于点O ,∠A =α.(1)如图①,若∠A =50°,求∠BOC 的度数.(2)如图②,连接OA,求证:OA平分∠BAC.(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.25.在长方形ABCD中,AB=4,BC=8,点P、Q为BC边上的两个动点(点P位于点Q 的左侧,P、Q均不与顶点重合),PQ=2(1)如图①,若点E为CD边上的中点,当Q移动到BC边上的中点时,求证:AP=QE;(2)如图②,若点E为CD边上的中点,在PQ的移动过程中,若四边形APQE的周长最小时,求BP的长;(3)如图③,若M、N分别为AD边和CD边上的两个动点(M、N均不与顶点重合),当BP =3,且四边形PQNM的周长最小时,求此时四边形PQNM的面积.参考答案1.B【分析】根据三角形具有稳定性,四边形不具有稳定性即可作出选择.【详解】解:平行四边形属于四边形,不具有稳定性,而三角形具有稳定性,故A符合题意;故选:B.【点睛】本题考查了多边形和三角形的性质,解题的关键是记住三角形具有稳定性,四边形不具有稳定性.2.C【分析】根据轴对称图形的概念分别得出对称轴的条数进而求解.【详解】解:A、有2条对称轴,B、有2条对称轴,C 、有3条对称轴,D 、有1条对称轴,故对称轴最多的是选项C .故选:C .【点睛】此题主要考查了轴对称的概念.轴对称的关键是寻找对称轴,两边图象折叠后可重合.3.D【分析】根据幂的乘方与积的乘方,同底数幂的乘法运算法则进行计算即可.【详解】解:A .(ab )2=a 2b 2,故A 不符合题意;B .(ab )2=a 2b 2,故B 不符合题意;C .a3•a4=a7,故C 不符合题意;D .(a 3)4=a 12,故D 符合题意;故选:D .【点睛】本题考查了幂的乘方与积的乘方,同底数幂的乘法,熟练掌握它们的运算法则是解题的关键.4.A【分析】根据分式的分母为0时,分式无意义即可解答.【详解】解:A .分式22x x -+没有意义时,x=-2,故A 符合题意;B .分式2xx -没有意义时,x=2,故B 不符合题意;C .分式22x x+没有意义时,x=0,故C 不符合题意;D .分式22x x--没有意义时,x=0,故D 不符合题意;故选:A .5.C【分析】根据三角形内角和定理求出∠2,根据全等三角形的性质解答即可.【详解】解:由三角形内角和定理得,∠2=180°-115°-25°=40°,∵两个三角形全等,∴∠1=∠2=40°,故选:C .【点睛】本题考查的是全等三角形的性质、三角形内角和定理,掌握全等三角形的对应角相等是解本题的关键.6.D【分析】原式利用多项式乘多项式法则计算即可得到结果.【详解】解:原式=2x2+4x-x-2=2x2+3x-2.故选:D.【点睛】此题考查了多项式乘多项式,熟练掌握法则是解本题的关键.7.D【分析】由于没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【详解】解:分两种情况:当腰为5时,5+5=10,所以不能构成三角形;当腰为10时,5+10>10,所以能构成三角形,周长是:10+10+5=25.故选D.【点睛】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答.8.C【分析】作DH⊥AB于D,如图,根据角平分线的性质得到DH=DC=6,然后根据三角形面积公式计算.【详解】解:作DH⊥AB于D,如图,∵AD平分∠BAC,DH⊥AB,DC⊥AC,∴DH=DC=6,∴S△ABD=12×12×6=36.故选:C.【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了三角形面积公式.9.A【分析】先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求m的取值范围,进而可求解.【详解】解:去分母得:m=x(x-1)-(x-2)(x+2),即m=4-x,解得x=4-m,由x为正数且(x-1)(x+2)≠0可得:4-m>0且m≠6或3,,解得:m<4且m≠3,.∵m为正整数,∴m的值为1,2共2个数.故选:A.【点睛】本题考查了分式方程的解,由于我们的目的是求m的取值范围,求得x=4-m,即可列出关于m的不等式了,另外,解答本题时,易漏掉(x-1)(x+2)≠0,这个隐含的条件而造成的,这应引起同学们的足够重视.10.B【分析】根据∠DFE=α得到∠FDE+∠FED,再根据角平分线的性质求出∠BDE+∠CED=360°-2α,利用外角的性质得到∠ADE+∠AED=2α,最后根据三角形内角和求出结果.【详解】解:∵∠DFE=α,∴∠FDE+∠FED=180°-α,由角平分线的定义可知:∠BDF=∠FDE,∠CEF=∠FED,∴∠BDE+∠CED=2∠FDE+2∠FED=360°-2α,∴∠ADE+∠AED=180°-∠BDE+180°-∠CED=2α,∴∠A=180°-(∠ADE+∠AED )=180°-2α,故选B .【点睛】本题考查了角平分线的定义,三角形内角和,三角形外角的性质,解题的关键是利用角平分线得到相等的角,根据内角和进行计算.11.925cm dcm#【分析】分别画图表示出距离最短和最长时的情况,从而得到取值范围.【详解】解:如图,足球、甲、乙在一条直线上时,此时甲、乙两人的距离d 最短,且为17-8=9cm ;如图,甲、足球、乙在一条直线上时,此时甲、乙两人的距离d 最长,且为17+8=25cm ;综上:甲、乙两人的距离d 的范围是925cm d cm #,故答案为:925cm dcm #.【点睛】本题考查了两点之间的距离,理解最长和最短的位置,解题的关键是注意分情况画出图形.12.722y x y【分析】通分并利用同分母分式的加法法则进行计算即可求出答案.【详解】解:23222y xyx y x xy+--=()()3422xy xyx x y x x y +--=()72xy x x y -=722y x y-故答案为:722yx y-.【点睛】本题考查了分式的加法,题目比较简单,在进行计算时要注意把最后结果进行化简是本题的关键.13.-18【分析】根据题意列出等式,利用多项式相等的条件求出m 与n 的值,代入原式计算即可求出值.【详解】解:根据题意得:x 2-6x+m=(x+3)(x-n )=x 2+(3-n )x-3n ,∴3-n=-6,m=-3n ,解得:m=-27,n=9,则原式=-27+9=-18,故答案为:-18.【点睛】此题考查了因式分解-十字相乘法,熟练掌握因式分解的方法是解本题的关键.14.(-2,3)【分析】依据非负数的性质,即可得到x ,y 值,依据关于x 轴、y 轴对称的点的坐标特征,即可得出点C 的坐标.【详解】解:∵|2x ﹣4|+(y +3)2=0,∴2x-4=0,y+3=0,∴x=2,y=-3,∴A (2,-3),∵点A (x ,y )关于x 轴对称的点为B ,∴B (2,3),∵点B 关于y 轴对称的点为C ,∴C (-2,3),故答案为:(-2,3).【点睛】本题主要考查了非负数的性质以及关于x 轴、y 轴对称的点的坐标特征,解决本题的关键是掌握好对称点的坐标规律:关于x 轴对称的点,横坐标相同,纵坐标互为相反数;关于y 轴对称的点,纵坐标相同,横坐标互为相反数.15.6【分析】过D 作DF ⊥BC ,垂足为F ,首先证明∠DAE=∠FCD ,再证明△AED ≌△CFD ,可得AE=FC ,然后证明Rt △BFD ≌Rt △BED 可得FB=BE ,再根据线段的和差关系可得AB=2BE-BC ,则可得出答案.【详解】解:如图,过D 作DF ⊥BC ,垂足为F,∵∠BCD+∠FCD=180°,∠BAD+∠BCD=180°,∴∠DAE=∠FCD ,∵BD 为∠ABC 的平分线,DE ⊥BA ,DF ⊥BC ,∴DF=DE ,在△AED 和△CFD 中,DEA DFCDAE FCD DE DF∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AED ≌△CFD (AAS ),∴AE=FC ,在Rt △BFD 和Rt △BED 中,DB DBDF DE =⎧⎨=⎩,∴Rt △BFD ≌Rt △BED (HL ),∴FB=BE ,∴AB=AE+BE=BE-BC+BE=2BE-BC ,∵AB=8,BC=4,∴BE=6.故答案为:6.【点睛】本题考查了全等三角形的判定与性质,角平分线的性质等知识,解决本题的关键是作出辅助线.16.6cm 2【分析】由D 是BC 的中点,得中线AD 平分ABC ∆的面积,同理DE 平分ADC ∆的面积,从而可得答案.【详解】解:D Q 为BC 的中点,224,ABC S cm = 2112,2ABD ACD ABC S S S cm ∆∆∆∴===E 为AC 的中点,216.2DEC ADC S S cm ∆∆∴==故答案为6cm 2.17.2x 6【分析】根据同底数幂的乘法和幂的乘方计算即可.【详解】解:3x 2•x 4-(-x 3)2=3x 6-x 6=2x 6.18.见解析【分析】由已知设AB ∥DC ,DE =BF ,得到∠B=∠D ,BE=DF ,再根据∠A=∠C ,利用AAS 证明△ABE ≌△CDF ,得到∠AEB=∠CFD ,再根据平行线的判定即可证明.【详解】解:命题为:若AB ∥DC ,DE =BF ,则AE ∥CF ;证明:∵AB ∥CD ,∴∠B=∠D ,∵DE=BF ,∴DE+EF=BF+EF ,即BE=DF ,又∵∠A=∠C ,∴△ABE ≌△CDF (AAS ),∴∠AEB=∠CFD ,∴AE ∥CF .19.(1)见解析(2)26【分析】(1)根据要求作出图形即可.(2)求出BC+AB=18,AC=8,可得结论.(1)解:如图,直线DE 即为所求.(2)∵DE 垂直平分线段AC ,∴DA=DC ,AE=CE=4,∴AC=8,∵△BDC 的周长=BC+BD+DC=BC+BD+DA=BC+AB=18.∴△ABC 的周长=BC+AB+AC=18+8=26.20.(1)22m m+(2)3【分析】(1)原式通分并利用同分母分式的减法法则计算,约分即可得到结果;(2)已知等式变形得到m 2+2m=3,代入计算即可求出T 的值.【小题1】解:T =2442m m m m m +⎛⎫+⋅ ⎪+⎝⎭=22442m m m m m m ⎛⎫++⋅ ⎪+⎝⎭=22442m m m m m ++⋅+=()2222m m m m +⋅+=22m m +;【小题2】∵m 2+2m ﹣3=0,∴m 2+2m =3,∴T =m 2+2m =3.21.(1)54千米/小时(2)0.8千克【分析】(1)可设黄老师骑自行车的平均速度为x 千米/小时,根据时间的等量关系列出方程即可求解;(2)由(1)可得黄老师开车的平均速度,再计算黄老师一天(按一个往返计算)可以减少碳排放量多少千克.(1)解:设黄老师骑自行车的平均速度为x 千米/小时,依题意有,99133x x -=,解得x=18,经检验,x=18是原方程的解.则354,x =故黄老师驾车的平均速度为54千米/小时;(2)解:由(1)可得黄老师开车的平均速度为18×3=54(千米/小时),954×2×2.4=0.8(千克).故可以减少碳排放量0.8千克.22.(1)()222a -(2)()()3x y x y ++-(3)等腰三角形【分析】(1)先提公因式2,再利用完全平方公式分解;(2)先分组,再利用分组分解法求解;(3)把等式左边利用分组分解法因式分解得到()()0a c a b --=,利用三角形三边的关系得到a=c 或a=b ,从而可判断△ABC 的形状.解:2288a a -+=()2244a a -+=()222a -;(2)2233x y x y--+=()()()3x y x y x y -++-=()()3x y x y ++-;(3)2a ab ac bc--+=2a ab bc ac--+=()()a abc b a -+-=()()a abc a b ---=()()a c ab --=0∴a=c 或a=b∴△ABC 为等腰三角形.23.(1)见解析(2)3【分析】(1)根据AAS 可证明ABD DCE ≌△△.(2)根据ABD DCE ≌△△,得出AB =DC =5,CE =BD =3,求出AC =5,则AE 可求出.(1)证明:∵AB AC =,∴B C ∠=∠.又∵12∠=∠,AD DE =,∴ABD DCE ≌△△(AAS ).解:∵ABD DCE ≌△△,∴5AB DC ==,2CE BD ==.∵AC AB =,∴5AC =.∴523AE AB EC =-=-=.24.(1)115°(2)见解析(3)见解析【分析】(1)利用三角形的内角和先求出∠ABC 与∠ACB 的和,再根据角平分的定义求出∠OBC 与∠OCB 的和即可解答;(2)根据角平分线的性质定理,想到过点O 作OD ⊥BC ,OE ⊥AB ,OF ⊥AC ,垂足分别为D ,E ,F ,证出OE=OF 即可解答;(3)根据角平分的定义求出∠OCP=90°即可解答.(1)解:(1)∵∠A=50°,∴∠ABC+∠ACB=180°-∠A=130°,∵∠ABC 和∠ACB 的平分线交于点O ,∴∠OBC=12∠ABC ,∠OCB=12∠ACB ,∴∠OBC+∠OCB=12∠ABC+12∠ACB=65°,∴∠BOC=180°-(∠OBC+∠OCB )=115°;(2)证明:过点O 作OD ⊥BC ,OE ⊥AB ,OF ⊥AC ,垂足分别为D ,E ,F ,∵∠ABC和∠ACB的平分线交于点O,OD⊥BC,OE⊥AB,OF⊥AC,∴OD=OE,OD=OF,∴OE=OF,∴OA平分∠BAC;(3)证明:∵OC平分∠ACB,OP平分∠ACD,∴∠ACO=12∠ACB,∠ACP=12∠ACD,∴∠OCP=∠ACO+∠ACP=12∠ACB+12∠ACD=12∠BCD=12×180°=90°,∴OC⊥CP.25.(1)见解析(2)4(3)4【分析】(1)由“SAS”可证△ABP≌△QCE,可得AP=QE;(2)要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,则此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H点,那么先证明∠GEH=45°,再由CQ=EC即可求出BP的长度;(3)要使四边形PQNM的周长最小,由于PQ是定值,只需PM+MN+QN的值最小即可,作点P关于AD的对称点F,作点Q关于CD的对称点H,连接FH,交AD于M,交CD 于N,连接PM,QN,此时四边形PQNM的周长最小,由面积和差关系可求解.(1)解:证明:∵四边形ABCD是矩形,∴CD=AB=4,BC=AD=8,∵点E是CD的中点,点Q是BC的中点,∴BQ=CQ=4,CE=2,∴AB=CQ,∵PQ=2,∴BP=2,∴BP=CE,又∵∠B=∠C=90°,∴△ABP≌△QCE(SAS),∴AP=QE;(2)如图②,在AD上截取线段AF=PQ=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC的延长线于H点.∵GH=DF=6,EH=2+4=6,∠H=90°,∴∠GEH=45°,∴∠CEQ=45°,设BP=x,则CQ=BC-BP-PQ=8-x-2=6-x,在△CQE中,∵∠QCE=90°,∠CEQ=45°,∴CQ=EC,∴6-x=2,解得x=4,∴BP=4;(3)如图③,作点P关于AD的对称点F,作点Q关于CD的对称点H,连接FH,交AD于M,交CD于N,连接PM,QN,此时四边形PQNM的周长最小,连接FP交AD于T,∴PT=FT=4,QC=BC-BP-PQ=8-3-2=3=CH,∴PF=8,PH=8,∴PF=PH,又∵∠FPH=90°,∴∠F=∠H=45°,∵PF⊥AD,CD⊥QH,∴∠F=∠TMF=45°,∠H=∠CNH=45°,∴FT=TM=4,CN=CH=3,∴四边形PQNM的面积=12×PF×PH-12×PF×TM-12×QH×CN=12×8×8-12×8×4-12×6×3=7.。
人教版八年级上册数学期末考试试题及答案

人教版八年级上册数学期末考试试卷一、单选题1.以下是北京2022年冬奥会会徽参选的一部分图形,其中是轴对称图形的是()A .B .C .D .2.一颗瓜籽质量约为0.000021千克,数0.000021用科学记数法表示为()A .40.2110-⨯B .52.110-⨯C .42.110-⨯D .50.2110-⨯3.将一副三角板按如图所示的方式放置,图中∠CAF 的大小等于()A .50°B .60°C .75°D .85°4.下列计算正确的是()A .2222()a b a b =B .623a a a ÷=C .2224(3)6xy x y =D .725()()m m m -÷-=-5.如图,在ABC 中,90C ∠=︒,以点A 为圆心,适当长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以点M ,N 为圆心,大于MN 的长为半径画弧,两弧交于点P ,射线AP 交BC 于点D ,若1CD =,4AB =,则ABD △的面积是()A .2B .4C .6D .86.如图,要测量河两岸相对的两点A ,B 的距离,先在AB 的垂线BF 上取两点C ,D ,使CD BC =,再作出BF 的垂线DE ,使A ,C ,E 在一条直线上,可以说明EDC ABC V V ≌,得ED AB =,因此测得ED 的长就是AB 的长,判定EDC ABC V V ≌最恰当的理由是()A .边角边B .角角边C .边边边D .角边角7.在平面坐标系中,点2(31)P x --,所在的象限是()A .第一象限B .第二象限C .第三象限D .第四象限8.如图,若ABC 是等边三角形,6AB =,BD 是AC 边上的高,延长BC 到E ,使CE CD =,则BE =()A .7B .8C .9D .109.对于两个非零的实数a ,b ,定义运算*如下:11a b b a *=-.例如:113443*=-.若2x y *=,则xy x y-的值为()A .12B .2C .12-D .2-10.如图,在ABC 中,90BAC ∠=︒,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于G ,交BE 于H .下列结论:①BE BCE S S =△A △;②2BAG ACF ∠=∠;③AFG AGF ∠=∠;④BH CH =.其中所有正确结论的序号是()A .①③B .①②③C .②③④D .①②③④二、填空题11.若分式3a a+的值为0,则a =___________.12.一个多边形的内角和是它的外角和的4倍,则这个多边形的边数是________.13.如图,AB=AC=4cm ,DB =DC ,若∠ABC 为60°,则BE 为________.14.如图,D 是AB 边上的中点,将ABC ∆沿过D 的直线折叠,使点A 落在BC 上F 处,若50B ∠=︒,则BDF ∠=__________度.15.如图,在Rt ABC 中,90C ∠=︒,60A ∠=︒,5cm AC =,若点M 从点B 出发以2cm/s 的速度向点A 运动,点N 从点A 出发以lcm/s 的速度向点C 运动,设M ,N 分别从点B ,A 同时出发,运动的时间为s t ,当t =_______s 时,AMN 是MN 为底边的等腰三角形.三、解答题16.计算(1)022021(3)3(1)π---+-;(2)2()(2)(2)a b a b a b --+-.17.解分式方程:14233x x x-=+--.18.先化简22321(1)24a a a a -+-÷+-,再从33a -<<中选取一个你喜欢的整数a 的值代入求值.19.ABC 在平面直角坐标系中的位置如图所示.(1)请作出ABC 关于y 轴对称的111A B C △,并写出111,,A B C 三点的坐标:1A _______,1B ________,1C _________;(2)将ABC 向右平移6个单位长度,作出作出平移后的222A B C △;(3)观察111A B C △与222A B C △,它们是否关于某直线对称?若是,请在图上画出这条对称轴.20.已知ABC 的两边长a 和b 2(4)0b -=.(1)若第三边长为c ,求c 的取值范围.(2)若ABC 是等腰三角形,求ABC 的周长.21.如图,已知CA =CD ,∠1=∠2.(1)请你添加一个条件,使得△ABC ≌△DEC .你添加的条件是;(2)添加条件后证明:△ABC ≌△DEC .22.在我市“绿水青山”行动中,某社区计划对某区域进行绿化,经投标由甲、乙两个工程队来完成甲工程队平均每个月比乙工程队少绿化250m ,甲工程队单独绿化2450m 和乙工程队单独绿化2600m 所用时间相同,甲工程队每月绿化多少平方米?23.在平面直角坐标系中,点A 的坐标是()5,0-,点B 的坐标是()0,5,点C 是x 轴上一点,AD BC ⊥于D 交y 轴于点E ,(1)如图1,图中与BOC 全等的三角形是__________;(2)如图1,小明过点O 作OM AE ⊥于M ,ON BC ⊥于N ,证明了OD 平分ADC ∠,请写出证明过程;(3)如图2,若点C 在线段AO 上,过点B 作BF BC ⊥,使BF BC =,连接AF 交y 轴于点G ,若点G 的坐标为70,4⎛⎫ ⎪⎝⎭,请直接写出OC 的长.参考答案1.B【分析】根据轴对称图形的概念可直接进行排除选项.【详解】解:A 、不是轴对称图形,故不符合题意;B 、是轴对称图形,符合题意;C 、不是轴对称图形,故不符合题意;D 、不是轴对称图形,故不符合题意;故选B .【点睛】本题主要考查轴对称图形的概念,熟练掌握轴对称图形的概念是解题的关键.2.B【分析】根据负指数幂的科学记数法可直接进行排除选项.【详解】解:由数0.000021用科学记数法表示为52.110-⨯,故选B .【点睛】本题主要考查科学记数法,熟练掌握负指数幂的科学记数法是解题的关键.3.C【分析】利用三角形内角和定理和三角形的外角的性质计算即可.【详解】∵∠DAC =∠DFE+∠C =60°+45°=105°,∴∠CAF =180°﹣∠DAC =75°,故选C .【点睛】考查了三角形外角的性质,解题关键是利用了三角形的外角的性质.4.D【详解】试题分析:A .积的乘方等于乘方的积,故A 错误;B .同底数幂的除法底数不变指数相减,故B 错误;C .积的乘方等于乘方的积,故C 错误;D .同底数幂的除法底数不变指数相减,故D 正确;故选D .考点:同底数幂的除法;幂的乘方与积的乘方.5.A【分析】由作图可知AD 平分∠CAB ,点D 到AB 的距离就等于DC=1,根据公式可求面积.【详解】解:由作图可知AD 平分∠CAB ,点D 到AB 的距离就等于DC ,1CD =,4AB =,所以,ABD △的面积为:141=22⨯⨯,故选:A .【点睛】本题考查了角平分线的画法和性质,解题关键是知道AD 是角平分线,并根据角平分线的性质求出高.6.D【分析】根据全等三角形的判定定理判断即可.【详解】证明:∵AB BF ⊥,DE BF ⊥,∴∠ABC=∠EDC=90°,在EDC △和ABC 中,EDC ABC CD CB DCE BCA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴EDC ABC V V ≌(角边角),故选:D .【点睛】本题考查了全等三角形的判定,解题关键是根据已知条件判断用了哪个判定定理,两角一边时注意边的位置.7.D【详解】试题分析:根据实数的意义可知21x --<0,可知其在第四象限.故选D.点睛:此题主要考查了平面直角坐标系的象限,解题关键是明确各象限的点的特点,然后可判断.第一象限的点的特点为(+,+),第二象限的点的特点为(-,+),第三象限的点的特点为(-,-),第四象限的点的特点为(+,-).8.C【分析】因为△ABC 是等边三角形,所以∠ABC =∠ACB =60°,BD 是AC 边上的高,则∠DBC =30°,AD =CD =12AC ,再由题中条件CE =CD ,即可求得BE .【详解】解:∵△ABC 是等边三角形,∴∠ABC =∠ACB =60°,AB =BC =6,∵BD 是AC 边上的高,∴AD =CD =12AC =3,∠DBC =12∠ABC =30°,∵CE =CD ,∴CE =12AC =3,∴BE =BC +CE =6+3=9.故选:C .【点睛】本题考查了等腰三角形的性质及等边三角形的性质,考查了学生综合运用数学知识的能力,得到AD =CD =12AC 是正确解答本题的关键.9.A【分析】根据新定义,把2x y *=转化为分式的运算即可.【详解】解:根据定义运算*,2x y *=,112y x-=,去分母得,2x y xy -=,代入xy x y-得,122xy xy =,故选:A.【点睛】本题考查了新定义运算以及分式运算,解题关键是根据新定义运算找到x、y之间的关系,再整体代入.10.B【分析】根据中线的性质即可判断①;根据三角形内角和定理求出∠BAD=∠ACB,再用角平分线的定义推出②;根据三角形内角和定理求出∠ABC=∠DAC,再用外角的性质可判断③;根据等腰三角形的判定判断④.【详解】解:∵BE是中线,∴AE=CE,∴△ABE的面积=△BCE的面积,故①正确;∵AD为高,∴∠ADB=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,∴∠ACB=∠BAD,∵CF是∠ACB的平分线,∴∠ACB=2∠ACF,∴∠BAD=2∠ACF,即∠BAG=2∠ACF,故②正确;∵CF是角平分线,∴∠ACF=∠BCF,∵AD为高,∴∠ADC=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,∴∠ABC=∠CAD,∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,∴∠AFG =∠AGF ,故③正确;根据已知条件不能推出∠HBC =∠HCB ,即不能推出BH =CH ,故④错误;故选:B .【点睛】本题考查了三角形内角和定理,三角形的外角性质,三角形的角平分线、中线、高,等腰三角形的判定等知识点,能综合运用定理进行推理是解此题的关键.11.3-【分析】根据分式的值为0可得:30,0a a +=≠,进而可求解.【详解】解:由题意得:30,0a a +=≠,∴3a =-;故答案为3-.【点睛】本题主要考查分式的值为0,熟练掌握分式的值为0满足的条件是解题的关键.12.十【分析】设这个多边形有n 条边,则其内角和为()2180,n -︒ 外角和为360︒,再根据题意列方程可得答案.【详解】解:设这个多边形有n 条边,则其内角和为()2180,n -︒ 外角和为360︒,()21804360n ∴-︒=⨯︒28,n ∴-=10,n ∴=故答案为:十.【点睛】本题考查的是多边形的内角和与外角和,掌握利用多边形的内角和与外角和定理列一元一次方程解决问题是解题的关键.13.2cm【分析】由题意可得AE为中垂线,进而可得BE的长.【详解】解:因为AB=AC,∠ABC=60°,所以△ABC为等边三角形,又DB=DC,所以可得AE为△ABC的中垂线,所以BE=12BC=2cm故答案为:2cm.14.80【分析】先根据折叠的性质可得AD DF=,根据等边对等角的性质可得B BFD∠=∠,再根据三角形的内角和定理列式计算即可求解.【详解】解:DEF是DEA△沿直线DE翻折变换而来,AD DF∴=,DQ是AB边的中点,AD BD∴=,BD DF∴=,B BFD∴∠=∠,50B∠=︒,180180505080BDF B BFD∴∠=︒-∠-∠=︒-︒-︒=︒.故答案为:80.【点睛】本题考查的是折叠的性质,以及等边对等角、三角形内角和定理,熟知折叠的性质是解答此题的关键.15.10 3【分析】由题意易得BM=2tcm ,AN=tcm ,则有AB=2AC=10cm ,()102AM t cm =-,进而可得AM=AN ,然后可得102t t -=,最后求解即可.【详解】解:由题意得:BM=2tcm ,AN=tcm ,∵∠C=90°,∠A=60°,∴∠B=30°,∵5cm AC =,∴AB=2AC=10cm ,∴()102AM t cm =-,∵AMN 是MN 为底边的等腰三角形,∴AM=AN ,即102t t -=,解得:103t =,∴当103t =s 时,AMN 是MN 为底边的等腰三角形;故答案为103.【点睛】本题主要考查含30°角的直角三角形的性质及等腰三角形的性质,熟练掌握含30°角的直角三角形的性质及等腰三角形的性质是解题的关键.16.(1)19-;(2)22322a ab b --+【分析】(1)根据零次幂及负指数幂可直接进行求解;(2)根据乘法公式进行整式的乘法运算即可.【详解】解:(1)原式=111991--=-;(2)原式=22222224322a ab b a b a ab b -+-+=--+.【点睛】本题主要考查零次幂、负指数幂及乘法公式,熟练掌握零次幂、负指数幂及乘法公式是解题的关键.17.方程无解【分析】先去分母,然后再进行方程的求解.【详解】解:14233x x x-=+--去分母得:()1423x x =-+-,去括号、移项得:2461x x -=--,解得:3x =,经检验:当3x =时,分母为零,∴原方程无解.【点睛】本题主要考查分式方程的解法,熟练掌握分式方程的解法是解题的关键.18.见解析【详解】分析:根据分式的运算法则先化简,然后取一个使分式有意义的值,代入计算即可求出答案.详解:原式=232a a +-+×2221a a a ()()()+--=21a a --∵a ≠﹣2,2,1,∴a =0.当a =0时,原式=2.点睛:本题考查了分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.19.(1)画图见解析,1A (1,4),1B (2,3),1C (0,1);(2)画图见解析,(3)是,画图见解析.【分析】(1)根据轴对称的性质画图并写出坐标即可;(2)根据平移的性质画图即可;(3)对称,根据对称轴的性质画出图形即可.【详解】(1)如图,111A B C △是所求作三角形,1A (1,4),1B (2,3),1C (0,1);(2)如图,222A B C △是所求作三角形;(3)111A B C △与222A B C △关于某直线对称,对称轴如图所示.【点睛】本题考查了坐标平面内的图形变换,解题关键是熟练掌握轴对称和平移的特征及坐标变化规律,如何根据点的位置确定对称轴.20.(1)513c <<,(2)22.【分析】(1)根据非负数的性质求出a 、b ,再根据三角形三边关系确定c 的取值范围;(2)对腰进行分类讨论求周长,注意能否构成三角形.【详解】解:(12(4)0b +-=,∴90a -=,40b -=,∴9a =,4b =,第三边长为c ,求c 的取值范围是:949+4c -<<,即513c <<.(2)由(1)得,9a =,4b =,ABC 是等腰三角形,当a 为腰时,ABC 的周长为:9+9+4=22,当b 为腰时,4+4<9,不能构成三角形,舍去.【点睛】本题考查了三角形三边关系和不等式,以及非负数的性质,解题关键是熟知三角形的三边关系和非负数的性质,灵活运用它们解题.21.(1)CB=CE (或∠B=∠E ,∠A=∠D 有一个即可);(2)证明见解析【分析】(1)根据SAS 即可得到答案;(2)根据等式的性质求出∠ACB=∠ECD ,根据全等三角形的判定SAS 证明即可.【详解】(1)解:添加的条件为:CB=CE ;(2)证明:∵∠1=∠2,∴∠1+∠ACE=∠2+∠ACE ,∴∠ACB=∠ECD ,在△ABC 和△DEC 中CB CE ACB DCE CA CD =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEC .【点睛】本题主要考查对全等三角形的判定,等式的性质等知识点的理解和掌握,能熟练地根据全等三角形的判定定理进行证明是解此题的关键.22.甲工程队每月绿化150平方米.【分析】设甲工程队每天完成绿化面积xm 2,则乙工程队每天完成绿化面积为(x +50)m 2,由“甲工程队完成绿化450m 2的面积与乙工程队完成绿化600m 2的面积所用时间相同”列出方程可求解.【详解】解:设甲工程队每天完成绿化面积xm 2,则乙工程队每天完成绿化面积为(x +50)m 2,根据题意列方程得,45060050x x =+,解得,x=150,经检验,x=150是分式方程的解,答:甲工程队每月绿化150平方米.【点睛】本题考查了分式方程的应用,解题关键是找准等量关系,恰当的设未知数列出方程,注意:分式方程要检验.23.(1)△AOE ,(2)证明见解析,(3)32.【分析】(1)根据“角边角”判定BOC AOE ≅ ;(2)根据角平分线的判定证OM=ON 即可;(3)过点F 作FH ⊥y 轴,垂足为H ,证△FBH ≌△CBO ,△FHG ≌△AOG ,可求出OC .【详解】解:(1)∵点A 的坐标是()5,0-,点B 的坐标是()0,5,∴OA=OB ,∵AD BC ⊥,∴∠ADB=∠AOB=90°,∵∠DEB=∠AEO ,∴∠OBC=∠OAE ,在△BOC 和△AOE 中,BO AO OBC OAE COB EOA =⎧⎪∠=∠⎨⎪∠=∠⎩,∴BOC AOE ≅ ,故答案为:△AOE .(2)由(1)可知,∠OBC=∠OAE ,OA=OB ,∵OM AE ⊥,ON BC ⊥,∴∠OMA=∠ONB=90°,在△BON 和△AOM 中,BO AO OBC OAE ONB OMA =⎧⎪∠=∠⎨⎪∠=∠⎩,∴BON AOM ≅ ,∴ON=OM,∴DO 平分∠ADC.(3)过点F 作FH ⊥y 轴,垂足为H ,可得,∠FHB=90°,∵BF BC ⊥,∴∠CBF=90°,∠CBO+∠FBG=90°,∠HFB+∠FBG=90°,∴∠CBO=∠HFB ,在△BOC 和△FHB 中,BC BFOBC HFB COB BHF=⎧⎪∠=∠⎨⎪∠=∠⎩,∴BOC FHB ≅ ,∴FH=OB=OA ,HB=OC ,在△AOG 和△FHG 中,OA HFAOG FHG AGO FGH=⎧⎪∠=∠⎨⎪∠=∠⎩,∴AOG FHG ≅ ,∴OG=GH=74,OH=72,OC=BH=OB-OH=5-72=32.【点睛】本题考查了全等三角形的判定与性质,角平分线的判定,坐标与图形,解题关键是把握已知条件,适当的作辅助线,构建全等三角形.。
人教版八年级上册数学期末考试试卷及答案

人教版八年级上册数学期末考试试题一、单选题1.下列图形中,不是轴对称图形的是()A .B .C .D .2.下列长度的三条线段,能组成三角形的是()A .3,4,8B .5,6,10C .5,5,11D .5,6,113.代数式1x x +,52x ,33x x ,x π,14x -中,分式的个数是()A .4B .3C .2D .14.如图,小明书上的三角形被墨迹遮挡了一部分,但他很快想办法在作业本画了一样的三角形,那么这两个三角形完全一样的依据是()A .AASB .ASAC .SSSD .SAS 5.要使分式32x -有意义,则x 的取值范围是()A .2x >B .2x <C .2x ≠-D .2x ≠6.如图,△ABC 中,90ACB ∠=︒,沿CD 折叠△CBD ,使点B 恰好落在AC 边上的点E 处.若22A ∠=︒,则EDA ∠等于()A .46°B .56°C .36°D .77°7.下列计算正确的是()A .5510a a a +=B .6424a a a ⋅=C .01a =D .5525()a a =8.如图,在△AED 和△CFB 中,已知BE =DF ,添加下列一组条件后,不能判定△AED ≌△CFB 的是()A .BC =AD ,CF =AEB .∠B =∠D ,CF =AEC .BC =AD ,∠B =∠D D .∠B =∠D ,∠C =∠A9.一个多边形的每个内角都等于135°,则这个多边形的边数为()A .8B .9C .10D .1110.如图所示,在△ABC 中,∠A=60°,AB=AC ,BD 是△ABC 的角平分线,延长BC 至E ,使CE=CD ,若△ABC 的周长为20,BD=a ,则△DBE 的周长是()(用含a 的式子表示)A .10+2aB .15+2aC .20+aD .10+a二、填空题11.因式分解:2m 3﹣2m =______________.12.已知点M(﹣6,2),则M 点关于x 轴对称点的坐标是_________.13.新冠病毒平均直径为0.0001毫米,但它以飞沫传播为主,而飞沫的直径是大于5微米的,所以N95或医用口罩能起到防护作用,用科学记数法表示0.0001是____________.14.若分式22x x --的值为0,则x =_________.15.若关于x 的二次三项式236x kx ++是一个完全平方式,则k =______.16.如图,在△ABC 中,CD ,BE 分别是AB ,AC 边上的高,且CD ,BE 相交于点P ,若∠A =70°,则∠BPC =___°.17.如图,△AEB≌△DFC,AE⊥CB,DF⊥BC,垂足分别为E、F,且AE=DF,若∠C=28°,则∠A=__________.三、解答题18.计算:(2x+5y)(3x-2y)-2x(x-3y)19.先化简,再求值:222111211x x xx x x x+-÷---+-,其中x=-2.20.如图,点C、E、F、B在同一直线上,AB∥CD,CE=BF,∠A=∠D.求证:AB=CD.21.如图,△ABC中,∠C=90°,∠A=30°.(1)用尺规作图作∠CBA的角平分线BD,交AC于点D(保留作图痕迹,不要求写作法和证明);(2)在上图中,若BD=10cm ,求DC 的长22.一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.(1)甲,乙两公司单独完成此项工程,各需多少天?(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?23.如图,在△ABC 中,已知AB=AC ,AB 的垂直平分线交AB 于点N ,交AC 于点M ,连接MB(1)若∠ABC=65°,则∠NMA 的度数为(2)若AB=10cm ,△MBC 的周长是18cm①求BC 的长度②若点P 为直线MN 上一点,则△PBC 周长的最小值为cm24.如图,已知ABC 中,90C ∠=︒,AD 是BAC ∠的平分线,DE AB ⊥于点E ,点F 在边AC 上,BD FD =.求证:(1)DC DE =;(2)CF EB =;(3)2AB AF EB -=.25.如图,在等腰Rt △ABC 中,角ACB =90°,P 是线段BC 上一动点(与点B ,C 不重合)连接AP ,延长BC 至点Q ,使CQ =CP ,过点Q 作QH ⊥AP 于点H ,交AB 于点M .(1)∠APC =α,求∠AMQ 的大小(用含α的式子表示);(2)在(1)的条件下,过点M 作ME ⊥QB 于点E ,试证明PC 与ME 之间的数量关系,并证明.26.已知,如图1,在平面直角坐标系中,点A 、B 分别在x 轴、y 轴的正半轴上,点C 在第一象限,90ACB ∠=︒,AC=BC ,点A 的坐标为(m,0),点C 的横坐标为n ,且2228170m n m n +--+=.(1)直接写出m ,n 的值;(2)如图2,D 为边AB 的中点,以点D 为顶点的直角∠EDF 的两边分别交边BC 于E ,交边AC 于F①求证:DE=DF ;②求证:12ABC DECF S S =△四边形;(3)在平面坐标内有点G(点G 不与点A 重合),使得△BCG 是以BC 为直角边的等腰直角三角形,请直接写出满足条件的点G 的坐标.参考答案1.D2.B3.B4.B5.D6.A7.D8.B9.A10.A11.2(1)(1)m m m +-12.(-6,-2)13.4110-⨯14.-215.12±16.110°17.62°【详解】∵△AEB ≌△DFC ,∴∠C=∠B=28°,∵AE ⊥CB ,∴∠AEB=90°,∴∠A=62°.故答案为62°.点睛:本题主要利用全等的两个三角形对应角相等解题.18.2241710x xy y +-【分析】根据整式的混合运算法则和运算顺序,进行计算即可.【详解】解:原式=22264151026x xy xy y x xy-+--+=2241710x xy y +-【点睛】本题主要考查了整式的混合运算,熟练掌握整式的混合运算法则和运算顺序是解题的关键.19.21--x x ;16-【分析】先根据分式的混合计算法则化简,然后代值计算即可.【详解】解:222111211x x x x x x x +-÷---+-()()()()21111111x x x x x x x -+=÷--+--()()()()21111111x x x x x x x -+=⋅--+--111x x =--()11x xx x --=-21x x=--当x=-2时,原式()211622=-=--+.20.见解析【分析】由“AAS”可证△AEB ≌△DFC ,可得AB =CD .【详解】证明:∵AB //CD ,∴∠B =∠C ,∵CE =BF ,∴CE+EF =BF+EF ,∴CF =BE ,在△AEB 和△DFC 中,A DBC BE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AEB ≌△DFC (AAS ),∴AB =CD .21.(1)见解析(2)5cm【分析】(1)用尺规作∠ABC 的平分线交AC 于点D 即可;(2)在(1)的前提下,根据角平分线的性质和30度角所对直角边等于斜边一半,AD =10,即可求CD 的长度.(1)如图所示:(2)∵△ABC 中,∠C=90°,∠A=30°∴∠ABC=90°-∠A=90°-30°=60°∵BD 平分∠ABC∴∠DBC=160302⨯= ∵△DBC 中,∠C=90°,∠CBD=30°∴1110522CD BD ==⨯=cm 答:CD 长5cm22.(1)甲,乙两公司单独完成此项工程,各需20天,30天;(2)让一个公司单独完成这项工程,甲公司的施工费较少.【分析】(1)设甲公司单独完成此项工程需x 天,则乙公司单独完成此项工程需1.5x 天,根据“甲、乙两公司合做,12天可以完成这项工程”,即可得出关于x 的分式方程,解之经检验后即可得出结论;(2)设乙公司每天的施工费为y元,则甲公司每天的施工费为(y+1500)元,根据“甲、乙两公司合做,12天的施工费为102000元”,即可得出关于y的一元一次方程,解之即可得出y值,再利用施工费=每天需付的施工费×施工天数,可分别求出甲、乙两队单独完成这项工程所需的施工费,比较后即可得出结论.【详解】解:(1)设甲公司单独完成此项工程需x天,则乙公司单独完成此项工程需1.5x 天.根据题意,得111x 1.5x12 +=,解得x=20.经检验,x=20是方程的解且符合题意.1.5x=30.∴甲,乙两公司单独完成此项工程,各需20天,30天.(2)设乙公司每天的施工费为y元,则甲公司每天的施工费为(y+1500)元,依题意得:12y+12(y+1500)=102000,解得:y=3500.∴甲公司单独完成这项工程所需施工费为(3500+1500)×20=100000(元),乙公司单独完成这项工程所需施工费为3500×30=105000(元).∵100000<105000,∴若让一个公司单独完成这项工程,甲公司的施工费较少.23.(1)40°;(2)①8cm;②18【分析】(1)先根据等腰三角形的性质求出∠A=50°,根据垂直平分线的定义得到∠ANM=90°,然后根据直角三角形两锐角互余求解即可;(2)①根据垂直平分线的性质得AM=BM,△MBC的周长是18cm,AC=AB=10cm,即可求BC的长度;②当点P与点M重合时,△PBC周长的最小,即为△MBC的周长.【详解】解:(1)∵AB=AC,∴∠ABC=∠C∵∠ABC=65°,∴∠C=65°,∴∠A=50°,∵MN是AB的垂直平分线,∴∠ANM=90°,∴∠NMA=90°-50°=40°;(2)①∵MN 是线段AB 的垂直平分线,∴AM=MB .∵△MBC 的周长是18cm ,AB=10cm ,∴BM+MC+BC=AM+MC+BC=AC+BC=AB+BC=18cm ,∴BC=18-AB=18-10=8cm ;②∵MN 是线段AB 的垂直平分线,∴点A 和点B 关于直线MN 对称,∴当点P 与点M 重合时,△PBC 周长的值最小,∴△PBC 的周长的最小值为18cm .24.(1)详见解析;(2)详见解析;(3)详见解析【分析】(1)根据三角形内角和求得∠CDA =∠EDA ,根据全等三角形的判定证得△ACD ≌△AED (ASA )继而根据全等三角形的性质即可求证;(2)根据全等三角形的判定和性质即可求证;(3)根据全等三角形的性质可得AC =AE ,CF =BE ,继而根据线段和差即可求解.【详解】证明:(1)∵AD 是BAC ∠的平分线∴∠CAD =∠EAD∵90C ∠=︒,DE AB ⊥于点E∴∠C =∠AED =90°∴180°-∠C -∠CAD =180°-∠AED -∠EDA即∠CDA =∠EDA在△ACD 和△AED 中AD CDA EDACAD EADAD ∠=∠∠∠⎧⎪=⎨⎪⎩=∴△ACD ≌△AED (ASA )∴DC =DE(2)在Rt △CDF 和Rt △EDB 中CD EDFD BD=⎧⎨=⎩∴Rt△CDF≌Rt△EDB(HL)=∴CF EB(3)由(1)知△ACD≌△AED(ASA)∴AC=AE∴AB=AE+BE=AC+BE=AF+CF+BE由(2)知,CF=BE∴AB=AF+2BE即2-=AB AF EB25.(1)∠AMQ=45°+α;(2)PC=ME;【分析】(1)由等腰直角三角形的性质得出∠BAC=∠B=45°,∠PAB=45°-α,由直角三角形的性质即可得出结论;(2)由AAS证明△APC≌△QME,得出PC=ME,【详解】(1)∠AMQ=45°+α;理由如下:∵∠PAC=α,△ACB是等腰直角三角形,∴∠BAC=∠B=45°,∠PAB=45°-α,∵QH⊥AP,∴∠AHM=90°,∴∠AMQ=180°-∠AHM-∠PAB=45°+α;(2)结论:PC=ME.理由:连接AQ,作ME⊥QB,如图所示:∵AC⊥QP,CQ=CP,∴∠QAC=∠PAC=α,∴∠QAM=45°+α=∠AMQ,∴AP=AQ=QM ,在△APC 和△QME 中,MQE PAC ACP QEM AP QM ∠∠⎧⎪∠∠⎨⎪⎩===,∴△APC ≌△QME (AAS ),∴PC=ME ,26.(1)m =1,n =4(2)①见解析;②见解析(3)G 的坐标为(3,11),(7,8),(-3,3)【分析】(1)根据2228170m n m n +--+=,得出m=1,n=4;(2)①连接CD ,则CD ⊥AB ,CD 平分∠ACB ,△BCD 和△ACD 都为等腰直角三角形,再证BDE CDF ≌△△,得出DE=DF ;②由①知BDE CDF ≌△△,可得BDE CDF S S = ,可证得DBC DECF S S = 四边形,再由12DBC ABC S S = ,即可证得结论;(3)作出以BC 为直角边的等腰直角三角形1BCG 、2BCG 、3BCG ,可证得312Rt G CP Rt BG Q Rt BG R Rt CAM ≌≌≌,可得34G P BQ BR CM ====,123CP G Q G R AM ====,即可得出点G 的坐标.(1)解:2228170m n m n +--+= ,()()22140m n ∴-+-=,10m ∴-=,n-4=0,解得m=1,n=4;(2)证明:①如图:连接CD ,∵在△ABC 中,AC=BC ,D 为边AB 的中点,∴CD ⊥AB ,45DCB B DCA ∠=∠=∠=︒,∴△DBC 和△DAC 都是等腰直角三角形,∴DB =DC ,∵90BDE EDC EDC CDF ∠+∠=∠+∠=︒,∴∠BDE=∠CDF ,在△DBE 和△DCF 中B DCFBD CD BDE CDF∠=∠⎧⎪=⎨⎪∠=∠⎩∴()DBE DCF ASA ≌,∴DE=DF ;②∵BDE CDF ≌△△,∴BDE CDFS S = ∴ΔΔΔΔΔDCF DEC DEC DBE DBC DECF S S S S S S =+=+=四边形∵ΔΔ12DBC ABCS S =∴S 四边形DECF=12S △ABC(3)解:∵m=1,n=4,∴点A 的坐标为(1,0),点C 的横坐标为4,如图:过点C 向x 轴和y 轴分别作垂线,垂足为点M 、N ,∵90BCN NCA NCA ACM ∠+∠=∠+∠=︒,∴∠BCN=∠ACM ,在△CMA 和△CNB 中CMA CNBACM BCN AC BC∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CMA CNB AAS ≌,∴CM=CN=4,BN=AM=4-1=3,OB=3+4=7,()0,7B ∴,()4,4C ,如图:作出以BC 为直角边的等腰直角三角形1BCG 、2BCG 、3BCG,作1G Q y ⊥轴于点Q ,2G R y ⊥于点R ,由题意可知:123=BG BG CG BC AC ===,在1BG Q 与2BG R 中,121212===BQG BRG QBG RBG BG BG ∠∠⎧⎪∠∠⎨⎪⎩()12Rt BG Q Rt BG R AAS ∴ ≌,=BQ BR ∴,12=G Q G R ,作CM x ⊥轴于点M ,作CP x ∥轴,3G P CP ⊥于点P ,CM y ∴ 轴,=180RBC ACB MCA ∴∠+∠+∠︒,=90RBC MCA ∴∠+∠︒,2=90RBC RBG ∴∠+∠︒,2=RBG MCA ∴∠∠,在CAM V 与2BG R 中,222===CMA BRG MCA RBG CA BG ∠∠⎧⎪∠∠⎨⎪⎩()2Rt CAM Rt BG R AAS ∴ ≌,==4CM BR ∴,2==3AM G R ,同理可证得()3Rt G CP Rt CAM AAS ≌,312Rt G CP Rt BG Q Rt BG R Rt CAM ∴ ≌≌≌,34G P BQ BR CM ∴====,123CP G Q G R AM ====,∴G 的坐标为(3,11),(7,8),(-3,3).。
人教版八年级上册数学期末考试试卷有答案

人教版八年级上册数学期末考试试题一、单选题1.下列长度的三根木条首尾相连,能组成三角形的是()A .3,4,8B .8,7,15C .2,2,3D .5,5,112.下列运算中正确的是()A .2510xx x⋅=B .()428x x -=-C .()224xy xy -=D .532x x x ÷=3.若分式x 1x 2-+的值为零,则x 的值是()A .0B .1C .1-D .2-4.如图将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠3=30°,则∠2=()A .50°B .60°C .30°D .20°5.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是()A .六边形B .八边形C .十二边形D .十六边形6.等腰三角形的顶角为80°,则其底角的度数是()A .100°B .80°C .50°D .40°7.把代数式x 2﹣4x+4分解因式,下列结果中正确的是()A .(x ﹣2)2B .(x+2)2C .x (x ﹣4)+4D .(x ﹣2)(x+2)8.已知实数a 、b 满足a+b =0,且ab≠0,则b aa b+的值为()A .﹣2B .﹣1C .1D .29.如图,把一张长方形纸片沿EF 折叠后,点D 、C 分别落在点D′、C′的位置.若65EFB ∠=︒,则∠AED′的大小是()A .70︒B .65︒C .50︒D .25︒10.如图,△ABC 中AB 边上的高是()A .线段ADB .线段AC C .线段CD D .线段BC二、填空题11.计算:111a a a +=++____________.12.点()3,2A -关于y 轴对称的点的坐标是______.13.若代数式4xx -有意义,则实数x 的取值范围是_____.14.已知x+y =10,xy =1,则代数式x 2y+xy 2的值为_____.15.已知a+b=4,a-b=3,则a 2-b 2=____________.16.如图,在△ABC 和△DEF 中,点B 、F 、C 、E 在同一直线上,BF =CE ,AC ∥DF ,请添加一个条件,使△ABC ≌△DEF ,这个添加的条件可以是________.(只需写一个,不添加辅助线)17.如图,在ABC 中,AB AC =,36A ∠=︒,AB 的中垂线DE 交AC 于点D ,交AB 于点E ,在下列结论中:①BD 平分ABC ∠;②点D 是线段AC 的中点:③AD BD BC ==;④BDC 的周长等于AB BC +.正确结论的序号是____________.18.如图,已知AE =BE ,DE 是AB 的垂线,F 为DE 上一点,BF =11cm ,CF =3cm ,则AC =_______.19.如图,在△ABC 中,∠A=50°,∠ABC=70°,BD 平分∠ABC ,则∠BDC 的度数是_____.20.如图,点B 、E 、C 、F 在一条直线上,AB ∥DE ,AB=DE ,BE=CF ,AC=6,则DF=________三、解答题21.分解因式:(1)x 2﹣4;(2)2a (b+c )﹣3(b+c ).22.计算:(1)(﹣5y 2)3;(2)43x y •32yx ;(3)4(x+1)2﹣(2x+3)(2x ﹣3).23.(1)解方程:233x x=-;(2)已知23a b =≠0,求代数式22524a b a b --•(a ﹣2b )的值.24.如图,在△ABC 中,AB =AC ,点D 在AB 上,点E 在AC 上,AD =AE .求证:CD =BE .25.如图,在Rt △ABC 中,∠C =90°,∠CAB 的平分线交BC 于点D ,又DE 是AB 的垂直平分线,垂足为E .(1)求∠CAD 的大小;(2)若BC =3,求DE 的长.26.如图所示,△ABC 是等边三角形,D 点是AC 的中点,延长BC 到E ,使CE=CD .(1)用尺规作图的方法,过D 点作DM ⊥BE ,垂足是M (不写作法,保留作图痕迹);(2)求证:BM=EM .27.星期天,小明和小军在同一小区门口同时出发,沿相同路线去离该小区1800米的青少年宫参加羽毛球训练,为响应“节能环保,绿色出行”的号召,两人都步行前往.已知小明的速度是小军的速度的1.2倍,小明比小军提前6分钟到达,求两人的速度.28.如图①,在△ABC中,∠B=45°,∠C=30°,过点A作直线AC的垂线交BC于点D.(1)求∠BAD的度数;(2)若AC=,求AB的长;(3)如图②,过点A作∠DAC的角平分线交BC于点P,点D关于直线AP的对称点为E,试探究线段CE与BD之间的数量关系,并对结论给予证明.参考答案1.C2.D3.B4.A5.B6.C7.A8.A9.C10.C11.1【分析】根据同分母分式相加,分母不变,分子相加,即可求解.【详解】解:111111a a a a a ++==+++.故答案为:1【点睛】本题主要考查了同分母分式的加减运算,熟练掌握同分母分式相加减,分母不变,分子相加减是解题的关键.12.()3,2--【分析】根据点坐标关于y 轴对称的变换规律即可得.【详解】点坐标关于y 轴对称的变换规律:横坐标互为相反数,纵坐标不变,则点()3,2A -关于y 轴对称的点的坐标是()3,2--,故答案为:()3,2--.【点睛】本题考查了点坐标规律探索,熟练掌握点坐标关于y 轴对称的变换规律是解题关键.13.x≠4【分析】分式有意义,分母不能为0,即x-4≠0,x≠4.【详解】解:∵x-4≠0,∴x≠4.故答案为:x≠4.【点睛】本题考查了分式有意义的条件,分式有意义的条件是分母不为0,代入求解即可.14.10【分析】将所求代数式适当变形后整体代入x+y=10,xy=1即可求解.【详解】解:∵x+y=10,xy=1,∴x 2y+xy 2=xy (x+y )=1×10=10,故答案为:10.【点睛】此题考查了代数式求值,因式分解-提公因式法.注意整体思想在解题中的应用.15.12.【详解】a 2-b 2=(a+b )(a-b )=4×3=12.故答案为:12.考点:平方差公式.16.AC=DF (答案不唯一)【详解】∵BF =CE ,∴BF +FC =CE +FC ,即BC=EF ;∵AC ∥DF ,∴∠ACB=∠DFE ,△ABC 和△DEF 中有一角一边对应相等,∴根据全等三角形的判定,添加AC=DF ,可由SAS 得△ABC ≌△DEF ;添加∠B=∠E ,可由ASA 得△ABC ≌△DEF ;添加∠A=∠D ,可由AAS 得△ABC ≌△DEF .故答案为:AC=DF .(答案不唯一)17.①③④【分析】根据AB AC =,36A ∠=︒,可知ABC 为等腰三角形,进而可知72ABC ∠=︒,由DE 为AB 的中垂线,可知36DBC ∠=︒,根据角度可知BD 平分ABC ∠,故①正确,根据36DBC ∠=︒,72C ∠=︒,72BDC ∠=︒,根据等角对等边可知BD BC AD ==,故③正确,则BDC 周长为:BD BC DC AD DC BC AC BC ++=++=+,故④正确;根据角之间的关系,72BDC C ∠=∠=︒,36DBC ∠=︒,可知BD DC ≠,故AD DC ≠,故②错误.【详解】解:∵AB AC =,∴ABC 为等腰三角形,∵36A ∠=︒,∴()18036272ABC C ∠=∠=︒-︒÷=︒,∵DE 为AB 的中垂线,∴AD=BD ,∴36ABD A ∠=∠=︒,∴723636DBC ∠=︒-︒=︒,∴BD 平分ABC ∠,故①正确;∵36DBC ∠=︒,72C ∠=︒,∴180367272BDC ∠=︒-︒-︒=︒,∴BD BC AD ==,故③正确;∴BDC 周长为:BD BC DC AD DC BC AC BC ++=++=+,故④正确;∵72BDC C ∠=∠=︒,36DBC ∠=︒,∴BD DC ≠,故AD DC ≠,故②错误;故答案为:①③④.18.14cm【分析】由AE =BE ,DE 是AB 的垂线得出DE 是AB 的中线,进而可得DE 是AB 的垂直平分线,由此即可得到AF =BF ,再根据线段的和差即可得解.【详解】解:∵AE =BE ,DE 是AB 的垂线,∴DE 是AB 的中线,∴DE 是AB 的垂直平分线,∵F 为DE 上一点,∴AF =BF ,∴AC =AF+CF =BF+CF ,∵BF =11cm ,CF =3cm ,∴AC =14cm ,故答案为:14cm .【点睛】此题考查了等腰三角形的三线合一以及垂直平分线的性质,熟练掌握等腰三角形的三线合一以及垂直平分线的性质是解此题的关键.19.85°【分析】根据三角形内角和得出∠C=60°,再利用角平分线得出∠DBC=35°,进而利用三角形内角和得出∠BDC 的度数.【详解】∵在△ABC 中,∠A=50°,∠ABC=70°,∴∠C=60°,∵BD 平分∠ABC ,∴∠DBC=35°,∴∠BDC=180°﹣60°﹣35°=85°.故答案为:85°20.6.【分析】根据题中条件由SAS 可得△ABC ≌△DEF ,根据全等三角形的性质可得AC=DF=6.【详解】∵AB ∥DE ,∴∠B=∠DEF ∵BE=CF ,∴BC=EF ,在△ABC 和△DEF 中,AB DE B DEF BC EF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ),∴AC=DF=6.考点:全等三角形的判定与性质.21.(1)(x+2)(x-2)(2)(b+c )(2a-3)【分析】(1)原式利用平方差公式分解即可;(2)原式提取公因式即可得到结果.【小题1】解:原式=x 2-22=(x+2)(x-2);【小题2】原式=(b+c )(2a-3).【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.22.(1)-125y 6(2)223x (3)8x+13【分析】(1)利用积的乘方与幂的乘方运算法则进行计算;(2)利用分式乘法运算法则进行计算;(3)利用完全平方公式,平方差公式计算乘方和乘法,然后去括号,合并同类项进行化简.【小题1】解:原式=(-5)3•(y 2)3=-125y 6;【小题2】原式=346xy x y=223x ;【小题3】原式=4(x 2+2x+1)-(4x 2-9)=4x 2+8x+4-4x 2+9=8x+1323.(1)x=9;(2)58-【分析】(1)根据分式方程的解法即可求出答案.(2)先根据分式的乘法运算进行化简,然后将a=2x ,b=3x 代入原式即可求出答案.【详解】解:(1)∵233x x=-,∴2x=3x-9,∴x=9,经检验,x=9是原方程的解.(2)∵23a b=≠0,设a=2x ,b=3x ,原式=()()()()5222a b a b a b a b -⋅-+-=()52a b a b-+=()52326x x x x-+=58-24.见解析【分析】根据AB=AC 得出∠DBC=∠ECB ,利用SAS 证明△BDC ≌△CEB ,进而利用全等三角形的性质解答即可.【详解】解:证明:∵AB=AC ,∴∠DBC=∠ECB ,∵AD=AE ,∴AB-AD=AC-AE ,即DB=EC ,在△DBC 和△ECB 中,DB ECDBC ECB BC CB=⎧⎪∠=∠⎨⎪=⎩,∴△BDC ≌△CEB (SAS ),∴CD=BE .25.(1)30°(2)1【分析】(1)先说明△ABD 是等腰三角形,再根据三角形的内角和即可得出答案;(2)设DC 的长为y ,根据直角三角形的性质列出关于y 方程,解出y 即可.(1)解:∵DE 是AB 的垂直平分线,∴AD=BD ,∴∠B=∠EAD ,又∵AD 是∠CAB 的平分线,∴∠CAD=∠EAD ,设∠CAD=x ,则3x=90°,∴x=30°,∴∠CAD=30°;(2)∵AD 是∠CAB 的平分线,DC ⊥AC ,DE ⊥AB ,∴DC=DE ,设DC=y ,则DE=y ,BD=3-y ,又∵∠B=30°,∴y=32y-,解得y=1,∴DE=1.26.(1)见解析;(2)见解析.【分析】(1)根据角平分线的作法作图即可;(2)要证BM=EM 可证BD=DE ,根据三线合一得出BM=EM .【详解】(1)解:作图如下;(2)证明:∵△ABC是等边三角形,D是AC的中点∴BD平分∠ABC(三线合一)∴∠ABC=2∠DBE∵CE=CD∴∠CED=∠CDE又∵∠ACB=∠CED+∠CDE∴∠ACB=2∠E又∵∠ABC=∠ACB∴2∠DBC=2∠E∴∠DBC=∠E∴BD=DE又∵DM⊥BE∴BM=EM.27.小军的速度是50米/分,小明的速度是60米/分【分析】设小军的速度是x米/分,则小明速度是1.2x米/分,由题意:沿相同路线去离该小区1800米的青少年宫参加羽毛球训练,小明比小军提前6分钟到达,列出分式方程,解方程即可.【详解】解:设小军的速度是x米/分,则小明速度是1.2x米/分,依题意得:1800180061.2x x-=,解得:x=50,经检验,x=50是原方程的解,且符合题意,则1.2×50=60,答:小军的速度是50米/分,小明的速度是60米/分.28.(1)15°(2)2(3)CE=2BD【分析】(1)利用三角形内角和定理求出∠BAC=105°,再由∠DAC=90°,即可得出答案;(2)作AF ⊥BC 于F ,由含30°角的直角三角形的性质得AF=12角形的性质得AF=BF ,从而求出AB 的长;(3)作AF ⊥BC 于F ,设DF=x ,则AD=2x ,,AC=,则,由点D 关于直线AP 的对称点为E ,得AE=AD=2x ,可表示出CE 的长,从而得出结论.(1)解:∵∠B=45°,∠C=30°,∴∠BAC=180°-∠B-∠C=180°-45°-30°=105°,∵AD ⊥AC ,∴∠DAC=90°,∴∠BAD=∠BAC-∠DAC=105°-90°=15°;(2)作AF ⊥BC 于F ,∵∠C=30°,∴AF=12,∵∠ABF=45°,∴∴=2;(3)CE=2BD ,理由如下:作AF ⊥BC 于F ,∵∠DAF+∠CAF=90°,∠CAF+∠C=90°,∴∠DAF=∠C=30°,设DF=x,则AD=2x,3,AC=23,∵3,∴3,∵点D关于直线AP的对称点为E,∴AE=AD=2x,∴CE=AC-AE=23,∴CE=2BD.。
人教版八年级上册数学期末考试试卷及答案

人教版八年级上册数学期末考试试题一、单选题1.当分式22x -有意义时,x 的取值范围是()A .2x >B .2x <C .2x ≠D .2x =2.在211133122x xy a x x y m π+++,,,,,中,分式的个数是()A .2B .3C .4D .53.下列图形中,不是..轴对称图形的是()A .B .C .D .4.已知三角形的三边长分别为2、x 、10,若x 为正整数,则这样的三角形个数为()A .1B .2C .3D .45.下列计算正确的是()A .2323a a a +=B .326a a a ⋅=C .()236a a =D .()2224a a -=-6.下列各式由左边到右边的变形中,是分解因式的为()A .()a x y ax ay+=+B .()24444x x x x -+=-+C .()2105521x x x x -=-D .()()2163443x x x x x -+=-++7.如果把分式xy x y +中的x 和y 都扩大2倍,则分式的值()A .扩大4倍B .扩大2倍C .不变D .缩小2倍8.若关于x 的方程2222x m x x ++=--有增根,则m 的取值是()A .0B .2C .-2D .19.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中αβ∠+∠的度数是A .180°B .220°C .240°D .260°10.张老师和李老师同时从学校出发,步行15千米去书店购买书籍,张老师比李老师每小时多走1千米,结果比李老师早到半小时,两位老师每小时各走多少千米?设李老师每小时走x 千米,根据题意,所列的方程是()A .1515112x x -=+B .1515112x x -=+C .1515112x x -=-D .1515112x x -=-二、填空题11.分解因式:x 2-9=______.12.将0.000000823用科学记数法表示为___________13.四边形的外角度数之比为1:2:3:4,则它最大的内角度数为_____.14.比较大小:4442333315.如图,Rt △ABC 中,∠BCA=90°,∠A=30°,BC=2cm ,DE 是AC 边的垂直平分线,连接CD ,则△BCD 的周长是__________________.16.已知12a b =,则分式252a b a b+-的值为______.17.对于实数a ,b ,c ,d ,规定一种运算a b c d =ad-bc ,如102(2)-=1×(-2)-0×2=-2,那么当(1)(2)(3)(1)x x x x ++--=27时,则x=_____.18.如图,在ABC 中,AB AC =,40A ∠=︒,E 为BC 延长线上一点,ABC ∠与ACE ∠的平分线相交于点D ,则∠D 的度数为______.三、解答题19.计算:(1)()201201742π-⎛⎫-+--- ⎪⎝⎭;(2)()()2323x y x y +--+.20.分解因式:(1)316m m -;(2)()228a b ab -+.21.解分式方程:(1)233x x =-;(2)28124x x x -=--.22.先化简,再求值:21211x x x x x x x --⎛⎫-÷ ⎪-+⎝⎭,其中3x =.23.如图:△ABC 和△ADE 是等边三角形,证明:BD=CE .24.在争创文明城市的活动中,某市一“少年突击队”决定清运一堆重达100吨的垃圾,开工后附近居民主动参加到义务劳动中,使清运垃圾的速度比原计划提高了一倍,结果提前4小时完成,“少年突击队”原计划每小时清运垃圾多少吨?25.已知,如图,点B 、F 、C 、E 在同一直线上,AC 、DF 相交于点G ,AB ⊥BE ,垂足为B ,DE ⊥BE ,垂足为E ,且AB =DE ,BF =CE .求证:(1)△ABC ≌△DEF ;(2)GF =GC .26.观察下列等式:111122=-⨯,1112323=-⨯,1113434=-⨯,将以上三个等式两边分别相加得:1111111113111223342233444++=-+-+-=-=⨯⨯⨯.解答下面的问题:(1)猜想并写()11n n =+.(2)求111112233420202021+++⋅⋅⋅⋅⋅⋅+⨯⨯⨯⨯的值.(3)探究并解方程:()()()()()211133366918x x x x x x x ++=++++++.27.已知:如图,点E ,A ,C 在同一条直线上,AB ∥CD ,AB=CE ,AC=CD .求证:BC=ED .28.如图,在ABC 中,D 是BC 的中点,过点D 的直线GF 交AC 于点F ,交AC 的平行线BG 于点G ,交AB 于点E ,连接EG 、EF .(1)求证:BG CF =.(2)请你判断:BE CF +与EF 的大小关系,并加以证明.参考答案1.C2.B3.C4.C5.C6.C7.B8.A9.C10.B11.(x +3)(x -3)12.8.23×10-713.144°14.<15.6cm.16.417.2218.20°【分析】根据角平分线的性质得到1,122DBC ABC DCE ACE ∠=∠∠=∠,再利用三角形外角的性质计算.【详解】解:∵ABC ∠与ACE ∠的平分线相交于点D ,∴1,122DBC ABC DCE ACE ∠=∠∠=∠,∵∠ACE=∠A+∠ABC ,∠DCE=∠D+∠DBC ,∴∠D=∠DCE-∠DBC=11()2022ACE ABC A ∠-∠=∠=︒,故答案为:20°.【点睛】此题考查了三角形的外角性质及角平分线的性质,熟记三角形外角的性质定理是解题的关键.19.(1)1;(2)224129x y y -+-【分析】(1)先计算负指数幂,零指数幂,绝对值,再计算加法即可;(2)先调整符号,利用平分差公式计算,再利用完全平方公式展开计算去括号即可.【详解】解:(1)()201201742π-⎛⎫-+--- ⎪⎝⎭,=414+-,=1;(2)()()2323x y x y +--+,=()()2323x y x y +---⎡⎤⎡⎤⎣⎦⎣⎦,=()2223x y --,=()224129x y y --+,=224129x y y -+-.20.(1)()()44m m m +-;(2)()22a b +【分析】(1)先提取公因式,然后再根据平方差公式进行因式分解即可;(2)先利用完全平方公式展开,然后合并同类项,进而再因式分解即可.【详解】解:(1)原式=()()()21644m m m m m -=+-;(2)原式=()22222448442a ab b ab a ab b a b -++=++=+.【点睛】本题主要考查因式分解,熟练掌握因式分解的方法是解题的关键.21.(1)9x =;(2)无解【分析】先将分式方程化为整式方程,解出整式方程,再将所求的解代入最简公分母中检验,即可求解.【详解】解:(1)233x x =-方程两边同时乘以()3x x -,得:()233x x =-,解得:9x =,检验:当9x =时,()()39930x x -=⨯-≠,所以原方程的解为9x =;(2)28124x x x -=--方程两边同时乘以()24x -,得:()()2248x x x +--=,解得:2x =,检验:当2x =时,224240x -=-=,所以2x =是增根,原方程无解.【点睛】本题主要考查了解分式方程,熟练掌握解分式方程的一般步骤,并记住要检验是解题的关键.22.11x x +-,2【分析】根据分式的运算法则进行化简,再代入求值即可.解:原式()()()()()()()2221121212121111111211x x x x x x x x x x x x x x x x x x x x x x x ⎡⎤-+----+=-÷=÷=⨯=⎢⎥--+-+---⎢⎥⎣⎦.当x=3时,原式1312131x x ++===--.【点睛】本题考查分式化简求值,熟练掌握该知识点是解题关键.23.见解析【分析】根据等边三角形的性质可得到两组边对应相等,一组角相等,从而利用SAS 判定两三角形全等,根据全等三角形的对应边相等即可得到BD=CE .【详解】证明:∵△ABC 和△ADE 是等边三角形,∴AB=AC ,AD=AE ,∠BAC=∠DAE=60°.∴∠BAD=∠CAE .在△BAD 与△CAE 中,,,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE (SAS ).∴BD=CE【点睛】此题考查了等边三角形的性质及全等三角形的判定与性质;证明线段相等常常通过三角形全等进行解决,全等的证明是正确解答本题的关键.24.12.5吨【分析】设原计划每小时清运x 吨,根据“使清运垃圾的速度比原计划提高了一倍,结果提前4小时完成,”列出方程,即可求解.【详解】解:设原计划每小时清运x 吨,根据题意得:10010042x x-=,解得:12.5x=,经检验,12.5x=是原方程的解,且符合题意,答:“少年突击队”原计划每小时清运垃圾12.5吨.【点睛】本题主要考查了分式方程的应用,明确题意,准确得到等量关系是解题的关键.25.(1)证明见解析,(2)证明见解析.【分析】(1)先根据BF=CE证明BC=EF,然后利用“边角边”即可证明△ABC和△DEF 全等;(2)根据全等三角形对应角相等可得∠ACB=∠DFE,再根据等角对等边证明即可.【详解】证明:(1)∵BF=CE,∴BF+FC=CE+FC,即BC=EF,∵AB⊥BE,DE⊥BE,∴∠B=∠E=90°,在△ABC和△DEF中,∵AB DEB E BC EF=⎧⎪∠=∠⎨⎪=⎩,∴△ABC≌△DEF(SAS);(2)∵△ABC≌△DEF∴∠ACB=∠DFE∴GF=GC.【点睛】本题考查了全等三角形的判定与性质和等腰三角形的判定,比较简单,证明出BC =EF是解题的关键.26.(1)111n n⎛⎫-⎪+⎝⎭;(2)20202021;(3)2x=【分析】(1)根据材料可直接得出答案;(2)根据(1)的规律,将算式写出差的形式,计算即可;(3)先按照(1)的结论进行化简,再解分式方程,即可得到答案.【详解】解:(1)根据题意,可知:()111n n 1n n 1=-++;故答案为:111n n ⎛⎫- ⎪+⎝⎭;(2)由(1)可知,111112233420202021+++⋅⋅⋅⋅⋅⋅+⨯⨯⨯⨯=1111111(1()()(2233420202021-+-+-+⋅⋅⋅⋅⋅⋅+-=111111112233420202021-+-+-+⋅⋅⋅⋅⋅⋅+-=112021-=20202021;(3)由(1)可知,()()()()()211133366918x x x x x x x ++=++++++,∴211111113()33366918x x x x x x x -+-+-=++++++,∴21113()3918x x x -=++,∴2119918x x x -=++,∴299(9)18x x x =++,∴22918x x x +=+,∴2x =;经检验,2x =是原分式方程的解.∴2x =.【点睛】本题考查了解分式方程以及有理数的混合运算,掌握分式方程的解法是解题的关键.27.见解析【分析】首先由AB ∥CD ,根据平行线的性质可得∠BAC=∠ECD ,再由条件AB=CE ,AC=CD 可证出△BAC 和△ECD 全等,再根据全等三角形对应边相等证出CB=ED .【详解】证明:∵AB ∥CD ,∴∠BAC=∠ECD ,∵在△BAC 和△ECD 中,AB=EC ,∠BAC=∠ECD ,AC=CD ,∴△BAC ≌△ECD (SAS ).∴CB=ED .【点睛】本题考查了平行线的性质,全等三角形的判定和性质.28.(1)见解析;(2)BE CF EF +>,见解析【分析】(1)证BDG CDF ≌可得BG CF =;(2)根据全等得到DG DF =,再根据三角形三边关系即可得到结果.【详解】(1)∵BG ∥AC ,∴C GBD ∠=∠,∵D 是BC 的中点,∴BD=DC ,在△BDG 和△CDF 中,C GBDBD CD BDG CDF∠=∠⎧⎪=⎨⎪∠=∠⎩,∴BDG CDF ≌,∴BG CF =;(2)BE CF EF +>,由BDG CDF ≌得DG DF =,∵ED GF ⊥,∴EG EF =,∵CF BG =,∴+>BG BE EG ,∴BE CF EF +>.。
人教版八年级上册数学期末考试试卷含答案

人教版八年级上册数学期末考试试题一、单选题1.七巧板是我国的一种传统智力玩具,下列用七巧板拼成的图形是轴对称图形的是()A .B .C .D .2.已知△ABC 中,∠A =20°,∠B =70°,那么△ABC 是()A .直角三角形B .锐角三角形C .钝角三角形D .正三角形3.已知△ABC ≌△DEF ,∠A =80°,∠E =50°,则∠F 的度数为()A .30°B .50°C .80°D .100°4.已知三角形两边长分别为7、11,那么第三边的长可以是()A .2B .3C .4D .55.下列计算正确的是()A .2323a a a +=B .326a a a ⋅=C .()236a a =D .()2224a a -=-6.若分式12x -有意义,则x 的取值范围是()A .x =2B .x >2C .x <2D .x≠27.若24a a k ++表示一个完全平方式,则k 的值为()A .4±B .4C .8±D .88.如图,等腰三角形ABC 的周长为21,底边BC=5,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则△BEC 的周长为()A .13B .14C .15D .169.如图,在△ABC 中,∠ABC 和∠ACB 的平分线交于点E ,过点E 作MN BC 交AB 于M ,交AC 于N ,若BM+CN=9,则线段MN 的长为()A .6B .7C .8D .910.如图,△DAC 和△EBC 均是等边三角形,AE 、BD 分别与CD 、CE 交于点M 、N ,且A 、C 、B 在同一直线上,有如下结论:①△ACE ≌△DCB ;②CM =CN ;③AC =DN ;④PC 平分∠APB ;⑤∠APD =60°,其中正确结论有()A .①②③④⑤B .①②④⑤C .①②③⑤D .①②⑤二、填空题11.分解因式:2x 2x -=___.12.计算:()23262x y x y -= ______.13.如图,将一副直角三角板,按如图所示的方式摆放,则∠α的度数是__________.14.如图,∠DAE =∠ADE =15°,AD 平分∠BAC ,DF ⊥AB ,若AE =8,则DF =_____.15.数据0.000000102m ,用科学记数法表示这个数为______.16.若一个多边形的每一个内角都是150︒,则它是______边形.17.如图,在△ABC 中,AB =AC =10,BC =12,AD =8,AD 是∠BAC 的平分线.若P ,Q 分别是AD 和AC 上的动点,则PC+PQ 的最小值是_____.三、解答题18|﹣4|+(﹣1)0﹣(12)﹣1.19.先化简再求值:21111x x x ⎛⎫÷- ⎪-+⎝⎭其中3x =.20.如图,已知CD ⊥AB ,BE ⊥AC ,垂足分别为点D ,E ,且AB =AC ,BE 交CD 于点O .(1)求证:DB =EC .(2)求证:AO 平分∠BAC .21.如图,在边长为1的正方形网格中有一个 ABC,完成下列各图(用无刻度的直尺画图,保留作图痕迹).(1)作 ABC关于直线MN对称的 A1B1C1;(2)求 ABC的面积;(3)在直线MN上找一点P,使得PA+PB最小.22.如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,请你添加一个条件,使△ABC≌△DEF,并加以证明.23.某文化用品商店用1000元购进了一批圆规,很快销售一空;商店又用1000元购进了第二批该种圆规,但进价比原来上涨了25%,结果第二次所购进圆规的数量比第一次少40件.(1)求两批圆规购进的进价分别是多少;(2)若商店将第一批圆规以每件7元,第二批圆规以每件8元的价格全部售出,则共可盈利多少元?24.如图,ABC 中,EF 垂直平分AC ,交AC 于点F ,交BC 于点E ,AD BC ⊥,垂足为D ,且BD DE =,连接AE .(1)求证:AB CE =;(2)若ABC 的周长为14cm ,6cm AC =,则DC 的长为________cm .25.配方法是数学中非常重要的一种思想方法,它是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法.定义:若一个整数能表示成22a b +(a ,b 是整数)的形式,则称这个数为“完美数”.例如,5是“完美数”.理由:因为22512=+,所以5是“完美数”.解决问题:(1)已知29是“完美数”,请将它写成22a b +(a ,b 是整数)的形式:;(2)若245x x -+可配成()2x m n -+(m ,n 为常数),则mn 的值为;探究问题:(3)已知222450x y x y +-++=,求x y +的值.26.在△ABC 中,AB =AC ,∠BAC =100°,点D 在BC 边上,△ABD 和△AFD 关于直线AD 对称,∠FAC 的平分线交BC 于点G ,连接FG .(1)求∠DFG 的度数;(2)设∠BAD =θ,①当θ为何值时,△DFG 为等腰三角形;②△DFG 有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.参考答案1.D 2.A 3.B 4.D 5.C 6.D 7.B 8.A 9.D 10.B 11.()x x 2-12.4412x y -13.75︒14.415.71.0210-⨯16.十二17.48518.619.11x -,12【详解】解:原式21111x x x x +-÷=-+()()111xx x x x+=⋅+-11x =-,当3x =时,原式12=.20.(1)见解析;(2)见解析【分析】(1)根据垂直的定义得到∠ADC =∠AEB =90°,根据AAS 判定△ADC ≌△AEB (AAS ),得出AD =AE 可得到结论;(2)根据垂直的定义得到∠BDO =∠CEO =90°,根据AAS 判定△BDO ≌△CEO (AAS ),得出OD =OE ,根据角平分线的判定即可得到结论.【详解】(1)证明:∵CD ⊥AB ,BE ⊥AC ,∴∠ADC =∠AEB =90°,在△ADC 和△AEB 中,DAC EAB ADC AEB AC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△AEB (AAS ),∴AD =AE ,∴AB ﹣AD =AC ﹣AE ,即DB =EC ;(2)证明:∵CD ⊥AB ,BE ⊥AC ,∴∠BDO =∠CEO =90°,在△BDO 和△CEO 中,BDO CEO DOB EOC BD CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BDO ≌△CEO (AAS ),∴OD =OE ,∵CD ⊥AB ,BE ⊥AC ,∴AO 平分∠BAC .21.(1)作图见解析;(2)52;(3)作图见解析【分析】(1)分别作出三个顶点关于直线MN 的对称点,再首尾顺次连接即可;(2)用长为2、宽为3的矩形面积减去四周三个直角三角形的面积即可得出答案;(3)连接AB 1,与直线MN 的交点即为所求.【详解】解:(1)如图所示,△A 1B 1C 1即为所求.(2)S △ABC =2×3﹣2×12×1×2﹣12×1×3=52;(3)如图所示,点P 即为所求.22.CE =BF (答案不唯一),证明见解析.【分析】根据全等三角形的判定定理进行分析,即可.【详解】添加:CE =BF ,证明:∵AC ∥DF ,∴∠C =∠F ,∵CE =BF ,CE BE BF BE +=+,∴BC =EF ,ACB DFE 在和中AC DF C F CB FE =⎧⎪∠=∠⎨⎪=⎩∴△ACB ≌△DFE (SAS ).23.(1)第一批购进圆规的单价为5元/件,第二批进价为6.25元/件;(2)680元【分析】(1)设第一批购进圆规的单价为x 元/件,则第二批购进圆规的单价为(1+25%)x 元/件,根据数量=总价÷单价结合第二次所购进圆规的数量比第一次少40件,即可得出关于x 的分式方程,解之经检验后即可得出结论;(2)利用数量=总价÷单价及第二次所购进圆规的数量比第一次少40件,可分别求出第一批及第二批购进圆规的数量,再利用利润=销售单价×销售数量−进货总价,即可求出结论.【详解】解:(1)设第一批购进圆规的单价为x 元/件,则第二批购进圆规的单价为(1+25%)x 元/件,依题意得:10001000401.25x x-=,解得:x =5,经检验,x =5是原方程的解,且符合题意.则第二批进价为:1.25 6.25x =元/件答:第一批购进圆规的单价为5元/件,第二批进价为6.25元/件;(2)第一批购进圆规的数量为1000÷5=200(件),第二批购进圆规的数量为200−40=160(件),共盈利(200×7−1000)+(160×8−1000)=400+280=680(元).答:一共盈利680元.24.(1)见解析;(2)4【分析】(1)根据线段垂直平分线性质可得AB=AE ,AE=CE ,再利用等式性质即可得解;(2)根据三角形周长求出AB+BC=14-AC=8cm ,然后再证AB+BD=DE+EC=DC ,把AB+BC 转化为AB+BC=AB+BD+DC=2DC=8cm 即可.【详解】(1)证明:∵AD ⊥BC ,BD=DE ,即AD 是BE 的垂直平分线,∴AB=AE ,又∵EF 垂直平分AC ,∴AE=CE ,∴AB=CE ;(2)解:∵6cm AC =,ABC 的周长为14cm ,∴AB+BC+AC=14cm ,∴AB+BC=14-AC=14-6=8cm,∵BD DE,AB=CE,∴AB+BD=DE+EC=DC,∵AB+BC=AB+BD+DC=2DC=8cm,∴DC=4cm.故答案为:4.25.(1)29=52+22;(2)2;(3)-1【分析】(1)根据“完美数”的定义判断即可;(2)利用配方法进行转化,然后求得对应系数的值;(3)配方后根据非负数的性质可得x和y的值,进行计算即可;【详解】解:(1)∵29=52+22,∴29是“完美数”,故答案为:29=52+22;(2)∵x2-4x+5=(x2-4x+4)+1=(x-2)2+1,又x2-4x+5=(x-m)2+n,∴m=2,n=1,∴mn=2×1=2,故答案为:2;(3)x2+y2-2x+4y+5=0,x2-2x+1+(y2+4y+4)=0,(x-1)2+(y+2)2=0,∴x-1=0,y+2=0,∴x=1,y=-2,∴x+y=1-2=-1.26.(1)80°;(2)①10°,25°或40°;②5°或45°.【详解】试题分析:(1)由轴对称可以得出△ADB≌△ADF,就可以得出∠B=∠AFD,AB=AF,在证明△AGF≌△AGC就可以得出∠AFG=∠C,就可以求出∠DFG的值;(2)①当GD=GF时,就可以得出∠GDF═80°,根据∠ADG=40+θ,就有40°+80°+40°+θ+θ=180°就可以求出结论;当DF=GF时,就可以得出∠GDF=50°,就有40°+50°+40°+2θ=180°,当DF=DG时,∠GDF=20°,就有40°+20°+40°+2θ=180°,从而求出结论;②由已知条件可以得出∠DFG=80°,当∠GDF=90°时,就有40°+90°+40°+2θ=180°就可以求出结论,当∠DGF=90°时,就有∠GDF=10°,得出40°+10°+40°+2θ=180°求出结论.试题解析:(1)∵AB=AC,∠BAC=100°,∴∠B=∠C=40°.∵△ABD和△AFD关于直线AD对称,∴△ADB≌△ADF,∴∠B=∠AFD=40°,AB=AF∠BAD=∠FAD=θ,∴AF=AC.∵AG平分∠FAC,∴∠FAG=∠CAG.在△AGF和△AGC中,AF=AC,∠FAG=∠CAG,AG=AG,∴△AGF≌△AGC(SAS),∴∠AFG=∠C.∵∠DFG=∠AFD+∠AFG,∴∠DFG=∠B+∠C=40°+40°=80°.答:∠DFG的度数为80°;(2)①当GD=GF时,∴∠GDF=∠GFD=80°.∵∠ADG=40°+θ,∴40°+80°+40°+θ+θ=180°,∴θ=10°.当DF=GF时,∴∠FDG=∠FGD.∵∠DFG=80°,∴∠FDG=∠FGD=50°.∴40°+50°+40°+2θ=180°,∴θ=25°.当DF=DG时,∴∠DFG=∠DGF=80°,∴∠GDF=20°,∴40°+20°+40°+2θ=180°,∴θ=40°.∴当θ=10°,25°或40°时,△DFG为等腰三角形;②当∠GDF=90°时,∵∠DFG=80°,∴40°+90°+40°+2θ=180°,∴θ=5°.当∠DGF=90°时,∵∠DFG=80°,∴∠GDF=10°,∴40°+10°+40°+2θ=180°,∴θ=45°∴当θ=5°或45°时,△DFG为直角三角形.。
2024-2025学年人教版八年级数学上册期末检测模拟试卷(一)(解析版)

2024—2025年度第一学期人教版八年级数学期末检测考试数学模拟试题(一)(考试时间:120分钟试卷满分:150分)1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.一、选择题(本大题共12小题,每小题3分,满分36分.在每个小题给出的四个选项中,只有一项符合题目要求的)1. 下列图形中,不是轴对称图形的是()A. B.C. D.【答案】D【解析】【分析】本题考查了轴对称图形的识别,熟练掌握轴对称图形的概念是解题的关键:如果一个平面图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴.根据轴对称图形的概念逐项分析判断即可得出答案.【详解】解:A. 是轴对称图形,故选项A不符合题意;B. 是轴对称图形,故选项B不符合题意;C. 是轴对称图形,故选项C不符合题意;D. 不是轴对称图形,故选项D 符合题意;故选:D .2. ABC 中,作AC 边上的高,以下作法正确的是( )A. B.C. D.【答案】C【解析】【分析】本题主要考查了三角形高线的作法,正确把握相关定义是解题关键,经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高.根据三角形高的定义,即可求解.【详解】解:在ABC 中,画出边AC 上的高,即是过点B 作AC 边的垂线段,正确的是C . 故选:C .3. 如图,ABC 中40,30B C ∠=°∠=°,延长BA 到点D ,则CAD ∠的度数是( )A. 50°B. 70°C. 80°D. 110°【答案】B【解析】 【分析】本题考查三角形的外角,根据三角形的外角等于与它不相邻的两个内角的和,进行求解即可.【详解】解:∵CAD ∠是ABC 的一个外角,∴403070CAD B C ∠=∠+∠=°+°=°,故选B .4. 如图,BD 平分ABC ∠交AC 于点D ,DE BC ⊥于点E ,若4AB =,5BC =,9ABC S = ,则DE 的长为( )A. 2B. 3C. 4D. 5【答案】A【解析】 【分析】本题考查了角平分线的性质定理,掌握角平分线的性质得到DE DF =是解题的关键. 过点D 作DF AB ⊥于点F ,由角平分线的性质可得DE DF =,根据三角形的面积计算方法()1·92ABC S DE AB BC =+= ,由此即可求解. 【详解】解:如图所示,过点D 作DF AB ⊥于点F ,∵BBBB 是ABC ∠的角平分线,,DE BC DF AB ⊥⊥,∴DE DF =, ∵()111 (9222)ABC ABD BCD S S S AB DF BC DE DE AB BC =+=+=+= , ∴1818245DE AB BC ===++, 故选:A .5. 在边长为a 的正方形中挖掉一个边长为b 的小正方形(a b >),把余下的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个因式分解的等式,则这个等式是( )A. 222()2a b a ab b −=−+B. 22()()a b a b a b +−=−C. 22()()a b a b a b −=+−D. 2()a ab a a b −=−【答案】C【解析】 【分析】本题考查了平方差公式与几何图形.解题的关键在于正确表示两个图形中阴影部分的面积.根据阴影部分面积相等列等式即可.【详解】解:由面积相等可知22()()a b a b a b −=+−,故选:C .6. 下列运算中结果正确的是 ( ).A. 6³²a a a ⋅=B. 623623÷=a a aC. ()6²³a a −=− D. ()222422ab a b −=【答案】C【解析】 【分析】本题考查同底数幂的乘法运算、单项式除以单项式、同底数幂的除法运算、积的乘方运算及幂的乘方运算,熟练掌握相关运算法则是解决问题的关键.根据同底数幂的乘法运算、单项式除以单项式、同底数幂的除法运算、积的乘方运算及幂的乘方运算分别求解即可得到结论.详解】解:A 、323256a a a a a +⋅==≠,该选项不符合题意;B 、62624362333a a a a a −÷==≠,该选项不符合题意;C 、()326a a −=−,该选项符合题意;D 、()222424242ab a b a b −=≠,该选项不符合题意; 故选:C .7. 化简211m m m m −−÷ 的结果是( ) A. m B. 1m C. 1m − D. 11m − 【答案】A【解析】 【分析】本题主要考查了分式的除法运算等知识点,根据分式的除法运算法则即可求出答案,解题的关键是熟练运用分式的除法运算法则.【【详解】211m m m m−−÷ 211m m m m −×−= m =,故选:A .8. 如图,已知点D 在AC 上,点B 在AE 上,ABC DBE ≌,5DB =,12AE =,则BC 的长为( )A. 7B. 5C. 12D. 6【答案】A【解析】 【分析】本题考查了全等三角形的性质,由全等三角形的性质得出5AB DB ==,BC BE =,结合BC BE AE AB ==−计算即可得解.【详解】解:∵点D 在AC 上,点B 在AE 上,ABC DBE ≌,∴5AB DB ==,BC BE =,∴1257BC BE AE AB ==−=−=,故选:A .9. 如图,在ABC 中,点E 是边AD 的中点,2BD CD =,若6BDE S = ,则阴影部分的面积为( )A. 6B. 3C. 4D. 2【答案】B【解析】 【分析】本题考查了三角形的中线与面积关系,解题的关键是掌握三角形的中线将三角形分成面积相等的两部分.根据E 是边AD 的中点,得ACE DCE S S =△△,ABE DBE S S = ,再根据CDE 和BDE 同高,根据两底的关系,得出面积关系,即可得出结论.【详解】解: 点E 是边AD 的中点,6BDE S = ,6ABE DBE S S ∴==△△,AE DE =,ACE DCE S S =△△,以BD 边为底的BDE 和以DC 边为底的CDE 的高相等,2BD CD =, ∴132DCE BDE S S ==△△, ∴3ACE DCES S ==△△, 故选:B .10. 关于x 的方程233x k x x =−−−无解,则k 的值为( ) A. 3±B. 3C. 3−D. 无法确定 【答案】B【解析】【分析】本题考查了分式方程无解问题,先将分式方程移项,去分母,合并同类项得6x k =−,再由原方程无解得30x −=,联立方程组,求解即可.23k x =−, 去分母得:()23x k x −=−,合并同类项得:6x k =−,原方程无解,∴630x k x =− −=, 解得3k =,故选:B .11. 如图,将正五边形一角沿直线MN 折叠,折叠后得到点D ,则12∠+∠=( )A. 108°B. 72°C. 216°D. 144°【答案】C【解析】 【分析】本题考查折叠的性质,正多边形的内角和,先确定108D ∠=°,再根据折叠的性质得108D D ′∠=∠=°,再根据四边形内角和及邻补角的定义可得结论.解题的关键是掌握:.正多边形每个内角和:()2180n −×°,每个内角度数:()2180n n−×°. 【详解】解:∵五边形ABCDE 是正五边形, ∴()521801085D −×°∠==°,∵将正五边形一角沿直线MN 折叠,折叠后得到点D ,∴108D D ′∠=∠=°, ∴36023602108144DND DMD D ′′∠+∠=°−∠=°−×°=°,∵1180DND ′∠=°−∠,2180DMD ′∠=°−∠,∴()12360360144216DND DMD ∠+∠=°−∠+∠=°−°=′′°. 故选:C .12. 某同学在计算()()234141++时,把3写成41−后,发现可以连续运用两数和乘以这两数差公式计算:()()()()()()()22222341414141414141161255++=−++=−+=−=.请借鉴该同学的经验,计算:2481511111111122222 +++++= ( ) A. 15122− B. 16122+ C. 1 D. 2【答案】D【解析】【分析】本题考查平方差公式,将原式乘以1212×−之后,连续使用平方差公式进而得出答案. 【详解】解:2481521111111112222 +++++ 24815111111211111222222 =×−+++++ 1615112122=×−+ 151511222=−+ 2=,故选:D .二、填空题(本大题共4小题,每小题4分,满分16分)13. 若221a a +=,那么多项式()()2(1)222a a a −−+−的值是______. 【答案】8【解析】【分析】本题考查的是整式的混合运算,化简求值,先计算整式的乘法运算,再合并同类项得到化简的结果,再把221a a +=代入计算即可.【详解】解:221a a += ,()()2(1)222a a a ∴−−+−()222124a a a =−+−−222128a a a =−+−+229a a =−−+ ()229a a =−++ 19=−+8=.故答案为:8.14. 当m =_________时,方程233x m x x =−−−无解. 【答案】3−【解析】 【分析】本题考查了分式方程无解的情况,熟悉掌握分式方程无解的含义是解题的关键. 去分母后,根据无解时x 的取值情况运算求解即可. 【详解】解:对233x m x x =−−−进行去分母可得:()23x x m =−−, 整理可得:6x m ,∵当30x −=时,此分式方程无解,∴3x =,∴36m =+,解得:3m =−,故答案为:3−.15. 如图,在ABC (AB AC >)中,AD 、AE 分别为三角形的角平分线、中线,若713AB AC =,ED kDC =,则k 的值为_____.【答案】37【解析】【分析】本题考查了角平分线的性质,三角形中线的性质,掌握角平分线的性质是解题的关键.过点D 作DM AB ⊥于点M ,DN AC ⊥于点N ,根据三角形角平分线的性质得出DM DN =,设BC 边上的高为h ,根据等面积法得出AB BD AC DC =,则可得出720CD BC =,根据AE 为ABC 中,BC 边的中线,得出320DE =,据此求解即可. 【详解】解:如图,过点D 作DM AB ⊥于点M ,DN AC ⊥于点N ,∵AD 为BAC ∠角平分线,∴DM DN =,设BC 边上的高为h , ∴11221122ABD ADC AB DM BD h S S AC DN DC h ⋅⋅==⋅⋅ , ∴AB BD AC DC=, ∵713AB AC =, ∴137AB AC = ∴137BD DC =,即137BD CD =, ∴720CD BC =, ∵AE 为ABC 中,BC 边的中线, ∴12BE EC BC ==, ∴320DE EC CD BC =−=, ∵ED kDC =, ∴37DE k DC == 故答案为:37. 【点睛】本题考查了角平分线的性质,三角形中线的性质,掌握角平分线的性质是解题的关键. 16. 如图,在等边三角形ABC 中,E 是AC 边的中点,P 是ABC 的中线AD 上的动点,且9AD =,则EP CP +的最小值是_______.的【答案】9【解析】【分析】本题主要考查了轴对称-最短路线问题以及等边三角形的性质,熟练掌握等边三角形和轴对称的性质是解题的关键.要求EP CP +的最小值,需考虑通过作辅助线转化,EP CP 的值为,BP EP ,从而找出其最小值求解即可.【详解】连接BE ,交AD 于点F ,连接BP ,如图所示.ABC 是等边三角形,AD 是BC 边上的中线,AD BC ∴⊥,AD ∴是BC 的垂直平分线,PB PC ∴=,PC PE PB PE ∴+=+.当,,B P E 三点共线时,BP PE +最小,EP CP +有最小值,∴当点P 在点F 处时,EP CP +BE 的长.E 是AC 边的中点,BE ∴是ABC 的中线,BE AC ∴⊥,11,22ABC AC BC S AC BE BC AD ==×=× △, 9BE AD ∴==,即EP CP +的最小值为9.三、解答题(本大题共9小题,满分98分.解答应写出文字说明,证明过程或演算步骤) 17. 解方程(1)1111a a a+=−−(2)12132163x x −=−− 【答案】(1)无解 (2)4x =【解析】【分析】本题考查了分式方程的解法,熟悉掌握分式方程的运算法则是解题的关键.(1)根据分式方程的运算法则进行运算即可;(2)根据分式方程运算法则进行运算即可;【小问1详解】 解:1111a a a+=−− 解:整理可得:1111a a a −=−−, 所有项同乘1a −可得:11a a −=−,移项可得:11a a −−=−−,合并可得:22a −=−,系数化为1可得:1a =,检验:把1a =代入1a −可得:110−=,∴此方程无解;【小问2详解】12132163x x −=−− 解:整理可得: ()121321321x x −=−−, 所有项同乘()321x −可得:2161x −−= ,移项可得:2116x =++ ,合并可得:28x =,系数化为1可得:4x =,检验:把4x =代入()321x −可得:()3241210×−≠,∴4x =是原方程的解. 18. 先化简,再求值:()32342236334xy x y x y xy x y −+÷−,其中,21x y ==,. 的【答案】223124x xy y −+−,2. 【解析】 【分析】此题考查了整式混合运算-化简求值,原式利用单项式乘多项式,多项式除以单项式法则计算得到最简结果,把x 与y 的值代入计算即可求出值,熟练掌握运算法则是解本题的关键. 【详解】解:原式()4234252236334x y x y x y x y −+÷− ()()()4222342225223363334x y x y x y x y x y x y ÷−−÷−+÷− 223124x xy y =−+−, 当2x =,1y =时,原式2312221114124=−×+××−=−+−=. 19. 如图,在ABC 中,90BAC ∠=°,1C ∠=∠,(1)求证:AD BC ⊥(2)如果3AB =,4AC =,5BC =,求AD 的长.【答案】(1)详见解析(2) 2.4AD =【解析】【分析】本题考查三角形的内角和定理、垂直定义、三角形的面积:(1)利用三角形的内角和定理求得90ADC ∠=°即可;(2)利用三角形的等面积求解即可.【小问1详解】证明:∵90BAC ∠=°,1C ∠=∠,∴190C CAD CAD BAC ∠+∠=∠+∠=∠=°,在ADC △中,()1801809090ADCC CAD ∠=°−∠+∠=°−°=°, ∴AD BC ⊥;【小问2详解】解:∵90BAC ∠=°,AD BC ⊥,的∴1122ABC S AB AC BC AD =⋅=⋅ , ∵3AB =,4AC =,5BC =, ∴34 2.45AB AC AD BC ⋅×===. 20. 如图,在四边形ABCD 中,CA 平分BCD ∠,AB BC ⊥,AD CD ⊥,垂足分别为B ,D ,E 为AC 上一点,连接EB ,ED .求证:(1)BC CD =;(2)EB ED =.【答案】(1)见解析 (2)见解析【解析】【分析】本题主要考查了全等三角形的判定和性质,角平分线的性质,垂直的定义,熟练掌握全等三角形的判断方法是解题的关键.(1)根据题意推出ABC ADC △≌△,即可得到答案BC CD =;(2)证明出EBC EDC △≌△EB ED =.【小问1详解】证明:∵CCCC 平分BCD ∠,∴ACB ACD ∠=∠,∵,AB BC AD CD ⊥⊥,∴90ABC ADC ∠=∠=°,∵AC AC =,∴ABC ADC △≌△()AAS ,∴BC CD =;【小问2详解】证明:由(1)知ACB ACD ∠=∠,BC CD =,∵EC EC =,∴()SAS ECB ECD △≌△∴EB ED = .21. 如图,ABC 中,点D 在BC 边上,100BAD ∠=°,ABC ∠的平分线交AC 于点E ,过点E 作EF AB ⊥,垂足为F ,且55AEF ∠=°,连接DE .(1)求证:DE 平分ADC ∠(2)若8,6,10AB AD CD ===,三角形ACD 的面积是16,求ABE 的面积. 【答案】(1)见解析 (2)8【解析】【分析】本题考查了角平分线的判定和性质,三角形的内角和定理,三角形面积公式,熟练掌握角平分线上的点到角的两边的距离相等是解题关键.(1)过点E 作EG AD ⊥,EH BC ⊥,根据角平分线的性质得到EF EG =,EF EH =,进而得到EG EH =,再根据角平分线的判定定理即可证明结论;(2)根据三角形的面积公式求出2EH =,再根据三角形的面积公式计算,即可求出ABE 的面积.【小问1详解】证明:过点E 作EG AD ⊥交AD 于点G ,EH BC ⊥交BC 于点H ,∵90F ∠=°,55AEF ∠=°,∴905535EAF ∠=°−°=°,∴180145BAC EAF ∠=°−∠=°,∴35CAD BAC BAD ∠=∠−∠=°,AE ∴平分FAD ∠,EF AF ⊥ ,EG AD ⊥,EF EG ∴=,BE 平分ABC ∠,EF BF ⊥,EH BC ⊥,EF EH ∴=,EG EH ∴=,EG AD ⊥ ,EH BC ⊥,DE ∴平分ADC ∠;【小问2详解】解:16ACD S = ,16ADE CDE S S ∴+= ,111622AD EG CD EH ∴⋅+⋅=, 6AD = ,10CD =,EG EH =, ∴()1162AD CD EG +⋅=, ∴2EG EH ==,∴2EF EG ==,8AB = ,1182822ABE S AB EF ∴=⋅=××= . 22. 如图,ABC 在平面直角坐标系中,顶点()20A ,.(1)画出ABC 关于x 轴对称的图形A B C ′′′ ,其中、、A B C 分别和A B C ′′′、、对应;并写出B ′点的坐标;(2)若y 轴上有一点P ,且满足APC ABC S S = ,直接写出点P 坐标.【答案】(1)见解析,()3,3B ′−(2)90,2P 或50,2 −【解析】【分析】本题考查了轴对称作图及坐标系中求面积,熟知关于x 轴对称的点的坐标特点是解题关键. (1)根据关于x 轴对称的点的坐标特点画出A B C ′′′ ,根据点在坐标系的位置写出B ′点的坐标即可; (2)先用割补法求出ABC S ,进而利用12APC PC OA S ⋅⋅= 求出PC 长,即可求出结论.【小问1详解】解:根据关于x 轴对称的点的坐标特征,分别找出点、、A B C 关于x 轴的对称点,顺次连接A B C ′′′、、,如图:A B C ′′′ 即为所求;()3,3B ′−,;【小问2详解】 解:1117331312232222ABC S =⨯-⨯⨯-⨯⨯-⨯⨯= , APC ABC S S = ,72APC S ∴= , ()20A ,,即2OA =,17222PC ∴⨯⋅=, 72PC ∴=, ()0,1C ,90,2P ∴ 或50,2 −. 23. (1)班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:大巴与小车的平均速度各是多少?(2)某一工程,在工程招标时,接到甲乙两个工程队的投标书.施工一天需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元.工程领导们根据甲乙两队的投标书测算,可有三种施工方案:方案A :甲队单独完成这项工程刚好如期完成;方案B :乙队单独完成这项工程比规定日期多用5天;方案C :若甲乙两队合作4天后,余下的工程由乙队单独做也正好如期完成.在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?【答案】(1)40,60(2)方案C【解析】【分析】本题考查分式方程的应用.(1)根据“大巴车行驶全程所需时间=小车行驶全程所需时间+小车晚出发的时间+小车早到的时间”列分式方程求解可得;(2)设甲单独完成这一工程需x 天,则乙单独完成这一工程需(5)x +天.根据方案C ,可列方程得444155x x x x −++=++,解方程即可解决问题. 【详解】解:(1)设大巴的平均速度为x 公里/小时,则小车的平均速度为1.5x 公里/小时, 根据题意,得:9090111.524x x =++, 解得:40x =,经检验:40x =是原方程的解, 1.540 1.560x =×=,答:大巴平均速度为40公里/小时,小车的平均速度为60公里/小时;(2)设甲单独完成这一工程需x 天,则乙单独完成这一工程需(5)x +天.根据方案C ,可列方程得444155x x x x −++=++, 解这个方程得20x ,经检验:20x 是所列方程的根.即甲单独完成这一工程需20天,乙单独完成这项工程需25天.所以A 方案的工程款为1.52030×=(万元), B 方案的工程款为1.12527.5×=(万元),但乙单独做超过了日期,因此不能选, C 方案的工程款为1.54 1.14 1.11628×+×+×=(万元), ∵2830<,的∴在不耽误工期的前提下,选择C 方案最节省工程款.24. 现有长与宽分别为a 、b 的小长方形若干个,用两个这样的小长方形拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:(1)根据图1,教材已给出关于a 、b 的关系式:222()2a b a ab b +=++;根据图2,关于a 、b 的关系式可表示为:______;根据上面的思路与方法,解决下列问题:(2)①若22440m n +=,28m n +=,则mn =______; ②若()()456m m −−=,则22(4)(5)m m −+−=______. (3)如图3,点C 是线段AB 上的一点,以AC ,BC 为边向两边作正方形,设7AB =,两正方形的面积和1216S S +=,求图中阴影部分面积. 【答案】(1)22()4()a b ab a b −+=+;(2)①6;②13;(3)16.5 【解析】【分析】本题考查完全平方公式的几何背景,完全平方公式的变形应用,整式化简求值,解题的关键是掌握完全平方公式的应用.(1)两种方法计算大正方形的面积可得答案;(2)①由28m n +=,可得224464m n mn ++=,而22440m n +=,故6mn =; ②由22[(4)(5)](1)1m m −−−=−=,知22(4)(5)2(4)(5)1m m m m −+−−−−=,又(4)(5)6m m −−=,故22(4)(5)13m m −+−=; (3)由7AC BC +=,得22249AC BC AC BC ++⋅=,又2216AC BC +=,故16.5AC BC ⋅=;即图中阴影部分面积为16.5.【详解】解:(1)大正方形的面积用面积公式计算为()2a b +,用小正方形面积加上4个长方形面积为()24a b ab −+,∴关于a 、b 的关系式可表示为:()()224a b ab a b −+=+; 故答案为:22()4()a b ab a b −+=+;(2)①28m n += , 2(2)64m n ∴+=,224464m n mn ∴++=, 22440m n += ,40464mn ∴+=,6mn ∴=;故答案为:6;②22[(4)(5)](1)1m m −−−=−= ,22(4)(5)2(4)(5)1m m m m ∴−+−−−−=,(4)(5)6m m −−= ,22(4)(5)261m m ∴−+−−×=,22(4)(5)13m m ∴−+−=,故答案为:13;(3)根据题意得:7AC BC +=, 22249AC BC AC BC ∴++⋅=, 1216S S += ,2216AC BC ∴+=,16.5AC BC ∴⋅=; 16.5CD BC ∴⋅=; ∴图中阴影部分面积为16.5.25. (1)如图①,在ABC 中,若5AB =,3AC =,求BC 边上的中线AD 的取值范围.解决此问题可以用如下方法:延长AD 到点E 使DEAD =,再连接BE ,这样就把AB ,AC ,2AD 集中在ABE 中,则中线AD 的取值范围是 ;(2)问题解决:如图②,在ABC 中,D 是BC 边的中点,DE DF ⊥于点D ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,判断此时:BE CF +与EF 的大小关系,并说明理由?(3)问题拓展:如图③,在四边形ABCD 中,180B D ∠+∠=°,CB CD =,160BCD ∠=°,以C 为顶点作80ECF ∠=°,边CE ,CF 分别交AB ,AD 于E ,F 两点,连接EF ,判断此时:BE 、DF 与EF 的数量关系, 并说明理由【答案】(1)14AD <<;(2)EF EB CF <+,见解析;(3)BE DF EF +=【解析】【分析】本题考查全等三角形的综合应用,涉及三角形全等的判定及性质,三角形三边关系,线段垂直平分线的性质,添加常用辅助线构造全等三角形是解题的关键.(1)延长AD 到点E 使DE AD =,再连接BE ,证明(SAS)ADC EDB ≌△△,可得AC BE =,再由三角形三角关系可得14AD <<;(2)延长FD 至G ,使FD DG =,连接BG ,证明()SAS CFD BGD ≌,可得BG FC =,连接EG ,可知EFG 是等腰三角形,则EF EG =,在EBG 中,利用三角形的三边关系可求解;(3)延长AB 至H 使BH DF =,连接CH ,证明(SAS)CBH CDF ≌,可推导出80ECH ECF ∠=∠=°,再证明()SAS HCE FCE ≌,则EH EF =,能推导出BE DF EF +=.【详解】解:(1)延长AD 到点E 使DE AD =,再连接BE ,CD BD = ,ADC BDE ∠=∠,AD DE =,()SAS ADC EDB ∴ ≌,3AC BE ∴==,在ABE 中,AB BE AE AB BE −<<+,28AE ∴<<,2AE AD = ,14AD ∴<<,故答案为:14AD <<;(2)EF EB CF <+.理由:延长FD 至G ,使FD DG =,连接BG ,CD BD = ,CDF BDG ∠=∠,FD DG =, ()SAS CFD BGD ∴ ≌, BG FC ∴=,连接EG ,ED FD ⊥ ,FD DG =, ∴EG 是FG 的垂直平分线, EF EG ∴=,在EBG 中,EG EB BG <+,即EF EB CF <+; (3)延长AB 至H 使BH DF =,连接CH ,180ABC D∠+∠=° ,180ABC CBH ∠+∠=°, CBH D ∴∠=∠,CB CD = ,BH DF =, ()SAS CBH CDF ∴ ≌, CH CF ∴=,BCH DCF ∠=∠, 160BCD ∠=° ,80ECF ∠=°,80DCF ECB BCH ECB ∴∠+∠=∠+∠=°, 80ECH ECF ∴∠=∠=°, CH FC = ,EC EC =,()SAS HCE FCE ∴ ≌, EH EF ∴=,BE BH EH ,+=∴+=.BE DF EF。
人教版数学八年级上册期末考试试卷带答案

人教版数学八年级上册期末考试试题一、单项选择题(每小题2分,共12分)1.如果一个三角形的两边长分别为2和5,则第三边长可能是(A)2(B)3(C)5(D)82.下列计算中正确的是(A)a2+a3=a5(B)a2⋅a3=a5(C)(a2)3=a5(D)a6÷a3=a23.京剧是我国的国粹,是介绍、传播中国传统艺术文化的重要媒介.在下面的四个京剧脸谱中,不.是.轴对称图形的是(A)(B)(C)(D)4.六边形的内角和是(A)180°(B)360°(C)540°(D)720°5.一艘轮船在静水中的最大航速为35km/h,它以最大航速沿江顺流航行120km所用时间,与以最大航速逆流航行90km所用时间相等.设江水的流速为vkm/h,则可列方程为(A)120903535=+-v v(B )120903535=-+v v(C)120903535=+-v v(D)120903535=-+v v6.如图,直线l是线段AB的垂直平分线,点C在直线l外,且与A点在直线l的同一侧,点P是直线l上的任意点,连接AP,BC,CP,则BC与AP+PC的大小关系是(A)>(B)<(C)≥(D)≤二、填空题(每小题3分,共24分)7.计算:02(1)3--⨯=.8.某病毒直径约0.00000008米.将0.00000008这个数用科学记数法表示为.9.当a=2020时,分式293--aa的值是.10.点P(-2,-4)关于y轴对称点的坐标是.(第6题)11.若a+b=5,ab=6,则(a-b)2=.12.如图,若△ABC ≌△DEF ,且∠B=60°,∠F-∠D=56°则∠A=°.(第12题)(第14题)13.如果a c =b ,那么我们规定(a ,b)=c ,例如:因为23=8,所以(2,8)=3.若(3,5)=a ,(3,6)=b ,(3,m)=2a-b ,则m=.14.如图,AD 是△ABC 的平分线,DF ⊥AB 于点F ,DE=DG ,AG=16,AE=8,若S △ADG =64,则△DEF 的面积为.三、解答题(每小题5分,共20分)15.计算:(23ab 2-2ab)⋅12ab.16.计算:(36x 4y 3-24x 3y 2+3x 2y 2)÷(-6x 2y 2).17.因式分解:x 3-25x.18.解方程:34122+=--x x x.四、解答题(每小题7分,共28分)19.如图,在四边形ABCD 中,AB ∥CD ,∠1=∠2,DB=DC.(1)求证:AB+BE=CD.(2)若AD=BC ,在不添加任何补助线的条件下,直接写出图中所有的等腰三角形.(第19题)20.在平面直角坐标系中,△ABC 的位置如图所示.(1)画出△ABC 关于x 轴对称的△A 1B 1C 1.(2)在坐标平面内确定点P ,使△PBC 是以BC 为底边的等腰直角三角形,请直接写出P 点坐标.(第20题)21.先化简,再求值:(2x+4)(2x-3)-4(x+2)(x-2),其中x=12.22.某同学化简分式2221()211x x x x x x+÷--+-出现了错误,解答过程如下:原式=22222121121x x x x x x x x x x++÷-÷-+--+(第一步)=332222(1)(1)x x x x x x -+---(第二步)=22(1)2(1)x x x -+-(第三步)(1)该同学解答过程从第步开始错误的.(2)写出此题正确的解答过程,并从-2<x<3的范围内选取一个你喜欢的x 值代入求值.五、解答题(每小题8分,共16分)23.两个工程队共同参与一项筑路工程,甲队单独施工一个月完成总工程的31,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.问哪个队的施工速度快?24.如图,在△ABC中,AC=BC,∠ACB=90°,延长CA至点D,延长CB至点E,使AD=BE,连接AE,BD,交点为O.(1)求证:OB=OA;(2)连接OC,若AC=OC,则∠D的度数是度.(第24题)六、解答题(每小题10分,共20分)25.【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如:图①可以得到恒等式(a+b)2=a2+2ab+b2,基于此,请解答下列问题:(1)根据图②,写出一个代数恒等式:.(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2的值.(3)小明同学用图③中x张边长为a的正方形,y张边长为b的正方形,z张长、宽分别为a,b的长方形纸片拼出一个面积为(2a+b)(a+2b)的长方形,则x+y+z=.【知识迁移】(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图④表示的是一个边长为m的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图④中图形的变化关系,写出一个代数恒等式:.图①图②图③图④(第25题)26.如图,等边△ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.(1)如图①,点E为AB的中点,求证:AE=DB.(2)如图②,点E在边AB上时,AE DB(填:“>”,“<”或“=”).理由如下:过点E 作EF ∥BC ,交AC 于点F(请你完成以下解答过程).图①图②(第26题)(3)在等边△ABC 中,点E 在直线AB 上,点D 在直线BC 上,且ED=EC.若AB=1,AE=2时,直接写出CD 的长.参考答案及评分标准一、单项选择题(每小题2分,共12分)1.C2.B3.A4.D5.A6.D二、填空题(每小题3分,共24分)7.198.8810-⨯9.202310.(2,-4)11.112.3213.25614.16三、解答题(每小题5分,共20分)15.解:原式=23ab 2⋅12ab-2ab ⋅12ab=13a 2b 3-a 2b 2.(5分)16.解:原式=-6x 2y+4x-12.(5分)17.解:原式=x(x 2-25)=x(x+5)(x-5).(5分)18.解:方程两边同时乘(x-2),得3x-4=x-2.解得x=1.(3分)检验:当x=1时,x-2=-1≠0.(4分)所以,原方程的解是x=1.(5分)四、解答题(每小题7分,共28分)19.(1)证明:∵AB ∥CD ,∴∠ABD=∠EDC.∵DB=DC ,∠1=∠2,∴△ABD ≌△EDC.(3分)∴AB=DE ,BD=CD.∴DE+BE=CD ,∴AB+BE=CD.(5分)(2)△BCD ,△BCE.(7分)20.解:(1)如图所示.(3分)(2)所确定的P 点为如图所示.(5分)P(-1,3)或P(2,-2).(7分)21.解:原式=4x 2+2x-12-4(x 2-4)=4x 2+2x-12-4x 2+16=2x+4.(5分)当x=12时,原式=2×12+4=5.(7分)22.解:(1)一(1分)(2)原式=22221(1)(1)21(1)(1)11x x x x x x x x x x x x x x x +++-÷=⋅=-+--+-.(4分)要使原式有意义,x≠1,0,-1,(5分)则当x=2时,原式=2221-=4.(7分)五、解答题(每小题8分,共16分)23.解:设乙队单独完成总工程需要x 个月,根据题意,得(1分)解得:(5分)121)131(31=⨯++x 1=x经检验x=1是原分式方程的解.(6分)∴甲队单独完成总工作需要3个月,乙队单独完成工作需要1个月.∵3>1∴乙队快(7分)答:乙队的施工速度快。
人教版八年级上册数学期末考试试卷含答案

人教版八年级上册数学期末考试试题一、单选题1.下列图案中,属于轴对称图形的有()A .5个B .3个C .2个D .4个2.以下列各组线段为边,能组成三角形的是()A .2cm ,3cm ,5cmB .5cm ,6cm ,10cmC .1cm ,1cm ,3cmD .3cm ,4cm ,9cm3.在1x ,n m π+,25ab ,30.7xy y +﹣,5b c a -+,23x π中,分式有()A .2个B .3个C .4个D .5个4.下列因式分解正确的是()A .a 2+1=a (a+1)B .2(1)(1)1x x x +-=-C .a 2+a ﹣5=(a ﹣2)(a+3)+1D .22()xy y y xy x x =++5.如果把分式2x yxy+中的x 和y 都扩大2倍,那么分式的值()A .不变B .扩大2倍C .扩大4倍D .缩小2倍6.如图,△ABC 中边AB 的垂直平分线分别交BC ,AB 于点D ,E ,AE =3cm ,△ADC 的周长为9cm ,则△ABC 的周长是()A .10cmB .12cmC .15cmD .17cm7.如果249x mx -+是完全平方式,则m 的值为()A .6B .±6C .12D .±128.能使分式2121--+x x x 的值为零的所有x 的值是()A .x =1B .x =﹣1C .x =1或x =﹣1D .x =2或x =19.某林场原计划在一定期限内固沙造林240公顷,实际每天固沙造林的面积比原计划多4公顷,结果提前5天完成任务.设原计划每天固沙造林x 公顷,根据题意列方程正确的是A .24024054x x +=+B .24024054x x -=+C .24024054x x +=-D .24024054x x -=-10.如图,∠ABC 和∠ACB 的平分线相交于点F ,过点F 作DE ∥BC ,交AB 于D ,交AC 于E ,下列结论正确的是()①BD =CE ②△BDF ,△CEF 都是等腰三角形③BD+CE =DE ④△ADE 的周长为AB+AC .A .①②B .③④C .①②③D .②③④二、填空题11.分解因式:228a -=______.12.已知等腰三角形有一个角是50°,则它的另外两个角是_____.13.若关于x 的分式方程322x mx x -=--无解,则m =__________.14.若31x -与4x互为相反数,则x 的值为________________.15.若(x+2y)(2x ﹣ky ﹣1)的结果中不含xy 项,则k 的值为_____.16.已知a+b=﹣3,ab=1,求a2+b2=_____.17.关于x 的分式方程3111m x x+=--的解为正数,则m 的取值范围是___________.18.如图,△ABC 中,AB =6,AC =7,BD 、CD 分别平分∠ABC 、∠ACB ,过点D 作直线平行于BC ,交AB 、AC 于E 、F ,则△AEF 的周长为_______.19.如图,∠AOB =60°,OC 平分∠AOB ,如果射线OA 上的点E 满足△OCE 是等腰三角形,那么∠OEC 的度数为______.三、解答题20.计算:(1)(-1)2016+(π-3.14)0-(12)-2(2)(2a ﹣3b )(﹣3b ﹣2a )21.解分式方程:(1)11222x x x-=---(2)23124x x x -=--22.先化简(1﹣11x -)÷22441x x x -+-,然后从﹣1,0,1这三个数中选取一个合适的数作为x 的值代入求值.23.平面直角坐标系中,△ABC 的三个顶点坐标分别为A (0,4),B (2,4),C (3,-1).(1)试在平面直角坐标系中,标出A 、B 、C 三点;(2)求△ABC 的面积.(3)若△A 1B 1C 1与△ABC 关于x 轴对称,写出A 1、B 1、C 1的坐标,并画出△A 1B 1C 1.24.如图所示,在△ABC 中,AD ⊥BC 于D ,CE ⊥AB 于E ,AD 与CE 交于点F ,且AD=CD ,(1)求证:△ABD ≌△CFD ;(2)已知BC=7,AD=5,求AF 的长.25.列方程解应用题:某商店用2000元购进一批小学生书包,出售后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了2元,结果购买第二批书包用了6600元.(1)请求出第一批每只书包的进价;(2)该商店第一批和第二批分别购进了多少只书包;(3)若商店销售这两批书包时,每个售价都是30元,全部售出后,商店共盈利多少元?26.如图,△ABC是等腰直角三角形,∠BAC=90°,△ACD是等边三角形,E为△ABC内一点,AC=CE,∠BAE=15°,AD与CE相交于点F.(1)求∠DFE的度数;(2)求证:AE=BE.27.将一副三角板按如图所示的方式摆放,AD是等腰直角三角板ABC斜边BC上的高,另一块三角板DMN的直角顶点与点D重合,DM、DN分别交AB、AC于点E、F.(1)请判别△DEF的形状.并证明你的结论;(2)若BC=4,求四边形AEDF的面积.参考答案1.D 2.B 3.B 4.D 5.D 6.C 7.D 8.B 9.B 10.D11.()()222a a +-【分析】先提取公因式,然后再根据平方差公式进行因式分解即可.【详解】解:228a -=()224a -,=()()222a a +-.故答案为:()()222a a +-.【点睛】本题主要考查因式分解,熟练掌握因式分解的方法是解题的关键.12.65°,65°或80°,50°【分析】从当等腰三角形的顶角是50°时,当等腰三角形的底角是50°时两种情况进行分析,然后利用三角形内角和定理即可得出答案.【详解】解:当等腰三角形的顶角是50°时,其底角为:180°﹣50°×2=65°.当等腰三角形的底角是50°时,其顶角为:180°﹣50°×2=80°,故答案为:65°,65°或80°,50°.【点睛】本题考查等腰三角形的性质以及三角形的内角和定理应用,掌握三角形内角和定理以及等腰三角形的性质是解题关键.13.2【分析】去分母,将分式方程转化为整式方程,根据分式方程有增根时无解求m 的值.【详解】去分母,得x-3(x-2)=m,整理,得-2x+6=m,当x=2时,原方程有增根,分式方程无解,此时-2×2+6=m,解得m=2,故答案为2.【点睛】本题考查分式方程无解计算,解题时需注意,分式方程无解要根据方程的特点进行判断,既要考虑分式方程有增根的情况,又要考虑整式方程无解的情况.14.4【分析】根据31x-与4x互为相反数可以得到31x-+4x=0,再根据分式存在有意义的条件可以得到1-x≠0,x≠0,计算解答即可.【详解】∵31x-与4x互为相反数∴31x-+4x=0又∵1-x≠0,x≠0∴原式去分母得3x+4(1-x)=0解得x=4故答案为4【点睛】本题考查的是相反数的意义、分式存在有意义的条件和解分式方程,根据相反数的意义得到31x-+4x=0是解题的关键.15.4【分析】根据多项式乘以多项式法则展开,合并同类项,即可得出﹣k+4=0,求出即可.【详解】解:(x+2y)(2x﹣ky﹣1)=2x2﹣kxy﹣x+4xy﹣2ky2﹣2y=2x2+(﹣k+4)xy﹣2ky2﹣2y﹣x,∵(x+2y)(2x﹣ky﹣1)的结果中不含xy项,∴﹣k+4=0,解得:k=4,故答案为4.【点睛】本题考查了多项式乘以多项式法则,能根据多项式乘以多项式法则展开是解此题的关键.16.7【详解】解:∵a+b=-3,ab=1,∴a 2+b 2=(a+b )2-2ab =(-3)2-2×1=7.故答案为:7.17.2m >且3m ≠【分析】方程两边同乘以x-1,化为整数方程,求得x ,再列不等式得出m 的取值范围.【详解】方程两边同乘以x-1,得,m-3=x-1,解得x=m-2,∵分式方程3111m x x+=--的解为正数,∴x=m-2>0且x-1≠0,即m-2>0且m-2-1≠0,∴m >2且m≠3,故答案为:m >2且m≠3.18.13【分析】根据平行线的性质得到EDB DBC ∠=∠,FDC DCB ∠=∠,根据角平分线的性质得到EBD DBC ∠=∠,FCD DCB ∠=∠,等量代换得到EDB EBD ∠=∠,FDC FCD ∠=∠,于是得到ED EB =,FD FC =,即可得到结果.【详解】解://EF BC ,EDB DBC ∴∠=∠,FDC DCB ∠=∠,ABC ∆ 中,ABC ∠和ACB ∠的平分线相交于点D ,EBD DBC ∴∠=∠,FCD DCB ∠=∠,EDB EBD ∴∠=∠,FDC FCD ∠=∠,ED EB ∴=,FD FC =,6AB = ,7AC =,AEF ∴∆的周长为:AE EF AF AE ED FD AF ++=+++AE EB FC AF=+++6713AB AC =+=+=.故答案为:13.【点睛】本题考查了等腰三角形的判定与性质,角平分线定义,平行线性质,注意证得BED∆与CDF 是等腰三角形是解此题的关键.19.75°或30°或120°【分析】分三种情况:当OC=OE 时,当OC=CE 时,当OE=CE 时,分别求解即可.【详解】解:∵OC 平分∠AOB ,∴∠AOC=12∠AOB=12×60°=30°,分三种情况:①当OC=OE 时,如图,∵OC=OE ,∴∠OEC=∠OCE ,∴∠OEC=12(180°-∠COE )=12(180°-30°)=75°;②当OC=CE 时,如图,∵OC=CE ,∴∠OEC=∠COE=30°;③当OE=CE 时,如图,∵OE=CE ,∴∠OCE=∠COE=30°,∴∠OEC=180°-∠OCE-∠OEC=180°-30°-30°=120°,综上,∠OEC 的度数为75°或30°或120°,故答案为:75°或30°或120°.20.(1)-2(2)﹣4a 2+9b 2【分析】(1)先计算乘方,零指数幂以及负整数指数幂,再进行有理数的加减计算即可;(2)利用平方差公式进行计算即可.(1)解:原式=1+1-4=-2(2)解:原式=﹣6ab ﹣4a 2+9b 2+6ab=﹣4a 2+9b 2【点睛】本题主要考查整式的计算,涉及的知识点有乘方的运算,零指数幂的求解,负整数指数幂,正确地计算能力是解决问题的关键.21.(1)无解(2)12x =-【分析】(1)先把分式方程化为整式方程求解,然后检验即可;(2)先把分式方程化为整式方程求解,然后检验即可.(1)解:11222x x x-=---方程两边同时乘以()2x -得:()1122x x -=---,去括号得:1124x x -=--+,移项得:2141x x -+=-+-,合并得:2x =,经检验2x =时分母为0,∴原方程无解(2)解:23124x x x -=--方程两边同时乘以()()22x x -+得:()()2243x x x +--=,去括号得:22243x x x +-+=,移项得:234x =-,合并得:21x =-,系数化为1得:12x =-,经检验12x =-是原方程的解,∴原方程的解为12x =-.【点睛】本题主要考查了解分式方程,熟知解分式方程的方法是解题的关键,注意分式方程要检验.22.12x x +-;当x=0时,原式=﹣12【分析】首先对括号内的式子通分相减,同时把除法转化为乘法,分子分母能因式分解的进行因式分解,约分后即可化简,再根据分式有意义的条件确定x 的值,最后代入计算即可.【详解】解:原式=()()()2221111121144122x x x x x x x x x x x x +-----+⋅=⋅=--+---;若分式有意义,则﹣1,0,1这三个数中x 只能取0,当x =0时,原式=011022+=--.【点睛】本题考查了分式的化简求值,正确对分式的分子和分母进行因式分解是关键.23.(1)画图见解析;(2)S △ABC=5;(3)A 1(0,-4),B 1(2,-4)C 1(3,1);画图见解析【分析】(1)根据三点的坐标,在直角坐标系中分别标出位置即可.(2)以AB 为底,则点C 到AB 得距离即是底边AB 的高,结合坐标系可得出高为点C 的纵坐标的绝对值加上点B 的纵坐标的绝对值,从而根据三角形的面积公式计算即可.(3)关于x 轴对称的点的坐标,横坐标不变,纵坐标互为相反数,从而可得出A1、B1、C1的坐标;在坐标系中描出这三个点,依次连接这三个点即可得到所画的图形.【详解】(1)如图所示:(2)由图形可得:AB=2,AB边上的高=|-1|+|4|=5,∴△ABC的面积=12AB×5=5.(3)∵A(0,4),B(2,4),C(3,-1),△A1B1C1与△ABC关于x轴对称,∴A1(0,-4)、B1(2,-4)、C1.(3,1).所画△A1B1C1如图所示:【点睛】本题考查了坐标与图形,画已知图形的轴对称图形,求图形的面积等知识,掌握坐标与图形的有关知识是关键.24.(1)证明见解析;(2)3.【分析】(1)利用ASA,可证△ABD≌△CFD;(2)由△ABD≌△CFD,得BD=DF,所以BD=BC﹣CD=2,所以AF=AD﹣DF=5﹣2.【详解】(1)证明:∵AD⊥BC,CE⊥AB,∴∠ADB=∠CDF=∠CEB=90°,∴∠BAD+∠B=∠FCD+∠B=90°,∴∠BAD=∠ECD,在△ABD和CFD中,ADB CDF BAD DCF AD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△CFD (AAS ),(2)∵△ABD ≌△CFD ,∴BD=DF ,∵BC=7,AD=DC=5,∴BD=BC ﹣CD=2,∴AF=AD ﹣DF=5﹣2=3.【点睛】本题考查了全等三角形的判定与性质,解题的关键点证明两个三角形全等.25.(1)20元(2)第一批购进100只,第二批购进300只(3)3400元【分析】(1)设第一批书包的单价为x 元,然后可得到第二批书包的单价,最后依据第二所购书包的数量是第一批购进数量的3倍列方程求解即可;(2)依据书包的数量=总价÷单价求解即可;(3)先求得全部卖出后的总售价,然后用总售价-总进价可求得获得的利润.(1)解:设第一批书包的单价为x 元.根据题意得:6600200032x x=⨯+,解得:x=20.经检验:x=20是分式方程的解.答:第一批每只书包的进价是20元.(2)第一批进货的数量=2000÷20=100个;第二批的进货的数量=3×100=300个.(3)30×(100+300)-2000-6600=3400元.【点睛】本题主要考查的是分式方程的应用,根据第二所购书包的数量是第一批购进数量的3倍列出关于x 的方程是解题的关键.26.(1)∠DFE=90°;(2)见解析【分析】(1)先求得∠BAD=30°,∠BAE=∠EAD=15°,即可求得∠EAC=75°,由AC=CE,可求得∠EAC=∠AEC=75°,即可求得∠DFE=90°;(2)在Rt△AFC中,求得∠FCA=30°,AC=2AF=AB,过点E作EG⊥AB于点G,求得AG=AF,得到BG=AG,即可得到△ABF为等腰三角形,即可证明AE=BE.【详解】解:(1)∵△ACD是等边三角形,∴∠CAD=60°,∵∠BAC=90°,∴∠BAD=90°-60°=30°,∵∠BAE=15°,∴∠BAE=∠EAD=15°,∴∠EAC=90°-15°=75°,∵AC=CE,∴∠EAC=∠AEC=75°,∴∠DFE=∠EAD+∠AEC=15°+75°=90°;(2)由(1)得∠DFE=90°,即∠AFC=∠AFE=90°,∵△ABC是等腰直角三角形,∠BAC=90°,△ACD是等边三角形,∴∠CAD=60°,AB=AC,∴∠FCA=30°,∴AC=2AF,即AB=2AF,过点E作EG⊥AB于点G,∵∠BAE=∠EAD=15°,且∠EFA=90°,EG⊥AB,∴EG=EF,又AE=AE,∴Rt△EAG≌Rt△EAF(HL),∴AG=AF,∴AB=2AG,∴BG=AG,又EG⊥AB,∴△ABF为等腰三角形,∴AE=BE.27.(1)△DEF 是等腰直角三角形,理由见解析;(2)2【分析】(1)可得∠CAD =∠B =45°,根据同角的余角相等求出∠CDF =∠ADE ,然后利用“角边角”证明△ADE 和△CDF 全等,则结论得证;(2)根据全等三角形的面积相等可得S △ADE =S △CDF ,从而求出S 四边形AEDF =S △ABD =218BC ,可求出答案.【详解】(1)解:△DEF 是等腰直角三角形.证明如下:∵AD ⊥BC ,∠BAD =45°,∴∠EAD =∠C ,∵∠MDN 是直角,∴∠ADF+∠ADE =90°,∵∠CDF+∠ADF =∠ADC =90°,∴∠ADE =∠CDF ,在△ADE 和△CDF 中,DAE CDF AD CD ADE CDF ∠∠⎧⎪=⎨⎪∠∠⎩==,∴△ADE ≌△CDF (ASA ),∴DE =DF ,又∵∠MDN =90°,∴∠EDF =90°,∴△DEF 是等腰直角三角形;(2)∵△ADE ≌△CDF ,∴S △ADE =S △CDF ,∵△ABC 是等腰直角三角形,AD ⊥BC∴AD=BD=12BC ,∴S 四边形AEDF =S △ABD =2221111()2228AD BC BC =⨯==2148⨯=2.。
人教版八年级上册数学期末考试试卷附答案

人教版八年级上册数学期末考试试题一、单选题1.下列运算中,结果正确的是()A .824a a a÷=B .()222a b a b +=+C .()2242a ba b =D .()()2122a a a -+=-2.围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是轴对称图形的是()A .B .C .D .3.若分式12x +有意义,则x 的取值范围是()A .2x ≥-B .2x >-C .0x ≠D .2x ≠-4.将数字0.0000023用科学记数法表示为()A .52.310-⨯B .62.310-⨯C .50.2310-⨯D .62.310-⨯5.在平面直角坐标系中.点(1,2)P -关于x 轴对称的点的坐标是()A .(1,2)B .(1,2)-C .(1,2)-D .(1,2)--6.如图,已知∠ABC =∠DEF ,AB =DE ,添加以下条件,不能判定△ABC ≌△DEF 的是()A .∠A =∠DB .∠ACB =∠DFEC .AC =DFD .BE =CF7.已知等腰三角形的其中两边长分别为4,9,则这个等腰三角形的周长是()A .13B .17C .22D .17或228.如图,在ABC 中,AD 、AE 分别是边BC 上的中线与高,4AE =,CD 的长为5,则ABC 的面积为()A .8B .10C .20D .409.如图,在ABC 中,40B ∠=︒,60C ∠=°,AD 平分BAC ∠交BC 于点D ,在AB 上截取AE AC =,则EDB ∠的度数为()A .30°B .20°C .10°D .15°10.如图,由4个全等的小长方形与一个小正方形密铺成一个大的正方形图案,该图案的面积为100,里面的小正方形的面积为16,若小长方形的长为a ,宽为b ,则下列关系式中:①222100a ab b ++=;②22216a ab b -+=;③2256a b +=;④2240a b -=,正确的有()个A .1B .2C .3D .4二、填空题11.因式分解:2363x x -+=______.12.一个n 边形的内角和为1080°,则n=________.13.方程213x x=+的解为______________.14.已知25,23mn ==,则+2m n =__________.15.如图,点F ,A ,D ,C 在同一条直线上,ABC DEF △≌△,3AD =,CF 10=,则AC 等于_____.16.如图,Rt ABC ∆中,90C ∠=︒,30A ∠=︒,D ,E 分别为AC ,AB 边上的点,将ADE 沿DE 翻折,点A 恰好与点B 重合,若3CD =,则AD =______.17.如图,ABC 中,OD 、OE 分别是AB 、BC 边上的垂直平分线,OD 、OE 交于点O ,连接OA 、OC ,已知40B ∠=︒,则OAC ∠=______.三、解答题18.化简:()()()2212x x x +---19.ABC 在如图所示的平面直角坐标系中,A 点坐标为()3,4.(1)画出ABC 关于y 轴对称的111A B C △;(2)求ABC 的面积.20.如图,在ABC 中,AD 是BC 边上的高,CE 平分ACB ∠,若20CAD ∠=︒,50B ∠=︒,求AEC ∠的度数.21.先化简:532224m m m m -⎛⎫++÷⎪--⎝⎭,然后,m 在1,2,3中选择一个合适的数代入求值.22.如图,在ABC 中,AD BC ⊥,E 是AD 上一点,且DE DC =,连接BE 并延长交AC 于点F ,BE AC =.(1)求证:BED ACD ≌;(2)猜想BF 与AC 的位置关系,并证明.23.某施工队对一段2400米的河堤进行加固,在施工800米后,采用新的施工机器,每天工作的效率比原来提高了25%,共用了26天完成全部工程.(1)求原来每天加固河堤多少米?(2)若承包方原来每天支付施工队工资800元,提高工作效率后,每天支付给施工队的工资也增加了25%,那么整个工程完成后承包方需要支付工资多少元?24.如图,90B ∠=︒,90C ∠=︒,E 为BC 中点,DE 平分ADC ∠.(1)求证:AE 平分DAB ∠;(2)求证:AE DE ⊥;(3)求证:DC AB AD +=.25.如图,在等边ABC 中,D 为BC 边上一点,连接AD ,将ACD △沿AD 翻折得到AED ,连接BE 并延长交AD 的延长线于点F ,连接CF .(1)若20CAD ∠=︒,求CBF ∠的度数;(2)若a CAD ∠=,求CBF ∠的大小;(3)猜想CF ,BF ,AF 之间的数量关系,并证明.参考答案1.C 2.D 3.D 4.B 5.A 6.C 7.C 8.C 9.B10.C11.23(1)x -12.813.3x =14.1515.6.516.617.50°18.72x +19.【详解】(1)分别作A 、B 、C 三点关于y 轴的对称点A 1、B 1、C 1,△A 1B 1C 1即为所求;(2)S △ABC=3×3111312123222-⨯⨯-⨯⨯-⨯⨯=72.20.85°【分析】由高的定义可得出∠ADB =∠ADC =90,在△ACD 中利用三角形内角和定理可求出∠ACB 的度数,结合CE 平分∠ACB 可求出∠ECB 的度数.由三角形外角的性质可求出∠AEC 的度数,【详解】解:∵AD 是BC 边上的高,∴∠ADB =∠ADC =90.在△ACD 中,∠ACB =180°﹣∠ADC ﹣∠CAD =180°﹣90°﹣20°=70°.∵CE 平分∠ACB ,∴∠ECB =12∠ACB =35°.∵∠AEC 是△BEC 的外角,50B ∠=︒,∴∠AEC =∠B+∠ECB =50°+35°=85°.答:∠AEC 的度数是85°.【点睛】本题考查了三角形内角和定理、角平分线的定义以及三角形外角的性质,利用三角形内角和定理及角平分线的性质,求出∠ECB 的度数是解题的关键.21.26--m ,-8【分析】先按照分式的混合计算法则进行化简,然后根据分式有意义的条件求出m 的值,最后代值计算即可.【详解】解:532224m m m m ⎛⎫ ⎪⎝-÷⎭++--()24532222m mm m m ⎛⎫--=-÷ ⎪---⎝⎭()222923m m m m--=⋅--()()()332223m m m m m+--=⋅--()23m =-+26m =--,∵分式要有意义且除数不为0,∴3020m m -≠⎧⎨-≠⎩,∴32m m ≠⎧⎨≠⎩,∴当1m =时,原式2168=-⨯-=-.22.(1)见解析;(2)BF ⊥AC ,理由见解析【分析】(1)利用HL 证明Rt △BED ≌Rt △ACD 即可;(2)根据全等三角形的性质可得∠EBD=∠CAD ,再由∠BED+∠EBD=90°,∠AEF=∠BED ,得到∠EBD+∠AEF=90°,则∠CAD+∠AEF=90°,∠AFE=90°,由此即可证明BF ⊥AC .【详解】:(1)∵AD ⊥BC ,∴∠ADC=∠BDE=90°,在RtBED 和Rt △ACD 中,DE DCBE AC=⎧⎨=⎩,∴Rt △BED ≌Rt △ACD (HL );(2)BF ⊥AC ,理由如下:∵Rt △BED ≌Rt △ACD ,∴∠EBD=∠CAD ,∵∠BED+∠EBD=90°,∠AEF=∠BED ,∴∠EBD+∠AEF=90°,∴∠CAD+∠AEF=90°,∴∠AFE=90°,∴BF ⊥AC .23.(1)原来每天加固河堤80米;(2)整个工程完成后承包方需要支付工资24000元.【分析】(1)设原来每天加固河堤a 米,则采用新的加固模式后每天加固5(125%)4a a +=米,然后根据用26天完成了全部加固任务,列方程求解即可;(2)先算出提高工作效率后每天加固的长度,然后进行求解即可.【详解】解:(1)设原来每天加固河堤a 米,则采用新的加固模式后每天加固5(125%)4a a +=米.根据题意得:80024008002654a a -+=,解这个方程得:80a =经检验可知,80a=是原分式方程的根,并符合题意;答:原来每天加固河堤80米;(2)558010044a=⨯=(米)∴承包商支付给工人的工资为:8002400800800800(125%)24000 80100-⨯+⨯+=(元).答:整个工程完成后承包方需要支付工资24000元.【点睛】本题主要考查了分式方程的应用,解题的关键在于能够准确找到等量关系列出方程求解.24.(1)见解析;(2)见解析;(3)见解析【分析】(1)延长DE交AB延长线于F,由∠B=∠C=90°,推出AB∥CD,则∠CDE=∠F,再由DE平分∠ADC,即可推出∠ADF=∠F,得到AD=AF,即△ADF是等腰三角形,然后证明△CDE≌△BFE得到DE=FE,即E是DF的中点,即可证明AE平分∠BAD;(2)由(1)即可用三线合一定理证明;(3)由△CDE≌△BFE,得到CD=BF,则AD=AF=AB+BF=AB+CD.【详解】解:(1)如图所示,延长DE交AB延长线于F,∵∠B=∠C=90°,∴AB∥CD,∴∠CDE=∠F,∵DE平分∠ADC,∴∠CDE=∠ADE,∴∠ADF=∠F,∴AD=AF,∴△ADF是等腰三角形,∵E是BC的中点,∴CE=BE,∴△CDE≌△BFE(AAS),∴DE=FE,∴E是DF的中点,∴AE平分∠BAD;(2)由(1)得△ADF 是等腰三角形,AD=AF ,E 是DF 的中点,∴AE ⊥DE ;(3)∵△CDE ≌△BFE ,∴CD=BF ,∴AD=AF=AB+BF=AB+CD .25.(1)20°;(2)CBF α∠=;(3)AF=CF+BF ,理由见解析【分析】(1)由△ABC 是等边三角形,得到AB=AC ,∠BAC=∠ABC=60°,由折叠的性质可知,∠EAD=∠CAD=20°,AC=AE ,则∠BAE=∠BAC-∠EAD-∠CAD=20°,AB=AE ,()1180=802ABE AEB BAE ==︒-︒∠∠∠,∠CBF=∠ABE-∠ABC=20°;(2)同(1)求解即可;(3)如图所示,将△ABF 绕点A 逆时针旋转60°得到△ACG ,先证明△AEF ≌△ACF 得到∠AFE=∠AFC ,然后证明∠AFE=∠AFC=60°,得到∠BFC=120°,即可证明F 、C 、G 三点共线,得到△AFG 是等边三角形,则AF=GF=CF+CG=CF+BF .【详解】解:(1)∵△ABC 是等边三角形,∴AB=AC ,∠BAC=∠ABC=60°,由折叠的性质可知,∠EAD=∠CAD=20°,AC=AE ,∴∠BAE=∠BAC-∠EAD-∠CAD=20°,AB=AE ,∴()1180=802ABE AEB BAE ==︒-︒∠∠∠,∴∠CBF=∠ABE-∠ABC=20°;(2)∵△ABC 是等边三角形,∴AB=AC,∠BAC=∠ABC=60°,由折叠的性质可知,EAD CAD α∠=∠=,AC=AE ,∴602BAE BAC EAD CAD α∠=∠-∠-∠=︒-,AB=AE ,11∴()1180=602ABE AEB BAE α==︒-︒+∠∠∠,∴CBF ABE ABC α∠=∠-∠=;(3)AF=CF+BF ,理由如下:如图所示,将△ABF 绕点A 逆时针旋转60°得到△ACG ,∴AF=AG ,∠FAG=60°,∠ACG=∠ABF ,BF=CG在△AEF 和△ACF 中,=AE ACEAF CAF AF AF=⎧⎪∠∠⎨⎪=⎩,∴△AEF ≌△ACF (SAS ),∴∠AFE=∠AFC ,∵∠CBF+∠BCF+∠BFD+∠CFD=180°,∠CAF+∠CFA+∠ACD+∠CFD=180°,∴∠BFD=∠ACD=60°,∴∠AFE=∠AFC=60°,∴∠BFC=120°,∴∠BAC+∠BFC=180°,∴∠ABF+∠ACF=180°,∴∠ACG+∠ACF=180°,∴F 、C 、G 三点共线,∴△AFG 是等边三角形,∴AF=GF=CF+CG=CF+BF.。
人教版八年级上册数学期末考试试卷含答案

人教版八年级上册数学期末考试试题一、单选题1.下面的图形是轴对称图形的是()A .B .C .D .2.数据0.00000164用科学记数法可表示为()A .51.6410-⨯B .61.6410-⨯C .716.410-⨯D .50.16410-⨯3.下列多项式中,能运用平方差公式分解因式的是()A .22a b +B .22a b-C .22a b -+D .22a b --4.计算:3223x y ⎛⎫-= ⎪⎝⎭()A .632x y-B .63827x y C .53827x y -D .63827x y -5.将分式222x x y+中的x ,y 同时扩大4倍,则分式的值()A .扩大4倍B .扩大2倍C .缩小到原来的一半D .保持不变6.已知2x =是分式方程113k x x x -+=-的解,那么k 的值为()A .0B .1C .2D .47.在ABC 中,AB AC =,AD BC ⊥于点D ,若8AB =,5CD =,则ABC 的周长为()A .13B .18C .21D .268.如图,点E 在AC 上,则A B C D DEB ∠+∠+∠+∠+∠的度数是()A .90°B .180°C .270°D .360°9.如图,两个正方形的边长分别为a 、b ,若7a b +=,3ab =,则阴影部分的面积是()A .40B .492C .20D .2310.如图,已知直角三角形ABC 中,90ACB ∠=︒,60CAB ∠=︒,在直线BC 或AC 上取一点P ,使得ABP △为等腰三角形,则符合条件的点有()A .4个B .5个C .6个D .7个二、填空题11.正五边形的外角和等于_______◦.12.已知221x x -=-,则代数式()52x x +-的值为______.13.已知30x yx -=,则y x=______.14.分式方程:2211x x x+=--的解是___________.15.在ABC 中,AB AC =,AB 的垂直平分线与AC 所在直线相交所得的锐角为42°,则B ∠=______.16.如图,B C ∠=∠,译添加一个条件______使得ABE ACD △△≌.17.如图,5AB AC ==,110BAC ∠=︒,AD 是∠BAC 内的一条射线,且25BAD ∠=︒,P 为AD 上一动点,则PB PC -的最大值是______.18.如图,在平面直角坐标系中,已知()2,0A ,()0,3B ,若在第一象限中找一点C ,使得AOC OAB ≅△△,则C 点的坐标为_______.三、解答题19.计算:()()()323235a a a a a -+-+÷.20.已知23m n=,求224421n mn n m m m ⎛⎫--+÷ ⎪⎝⎭的值.21.在()()223x x a x b -++的运算结果中,2x 的系数为4-,x 的系数为7-,求a ,b 的值并对式子224ax b +进行因式分解.22.如图,AB ,CD 相交于点E 且互相平分,F 是BD 延长线上一点,若2FAC BAC ∠=∠,求证:AC DF AF +=.23.某商场计划在年前用30000元购进一批彩灯,由于货源紧张,厂商提价销售,实际的进货价格比原来提高了20%,结果比原计划少购进100盏彩灯.该商场实际购进彩灯的单价是多少元?24.如图1,射线BD 交△ABC 的外角平分线CE 于点P ,已知∠A=78°,∠BPC=39°,BC=7,AB=4.(1)求证:BD平分∠ABC;(2)如图2,AC的垂直平分线交BD于点Q,交AC于点G,QM⊥BC于点M,求MC的长度.25.如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N.求证:(1)AD=BE;(2)∠BMC=∠ANC;(3)△CMN是等边三角形.26.如图所示,点M是线段AB上一点,ED是过点M的一条直线,连接AE、BD,过点B 作BF//AE交ED于F,且EM=FM.(1)若AE=5,求BF的长;(2)若∠AEC=90°,∠DBF=∠CAE,求证:CD=FE.参考答案1.C 2.B 3.C 4.D 5.A 6.D 7.D 8.B 9.C 10.C 11.36012.413.1314.0x =15.66°或24°16.AB AC =(答案不唯一)【详解】解: B C ∠=∠,,A A ∠=∠添加:,AB AC =∴(),ABE ACD ASA ≌△△故答案为:,AB AC =(答案不唯一)17.5【分析】作点B 关于射线AD 的对称点B ',连接AB '、CB '、B'P .则AB AB '=,PB PB '=,AB C 'V 是等边三角形,在PB C ' 中,PB PC B C -'≤',当P 、B '、C 在同一直线上时,PB PC '-取最大值B C ',即为5.所以PB PC '-的最大值是5.【详解】解:如图,作点B 关于射线AD 的对称点B ',连接AB '、CB ',B'P .则AB AB '=,PB PB '=,25B AD BAD ∠=∠='︒,110252560B AC BAC BAB ∠=∠-∠=︒-︒-︒=''︒.∵5AB AC ==,∴5AB AC '==,∴AB C 'V 是等边三角形,∴5B C '=,在PB C ' 中,PB PC B C -'≤',当P 、B '、C 在同一直线上时,PB PC '-取最大值B C ',即为5.∴PB PC '-的最大值是5.故答案为:5.18.()2,3【详解】根据题意C 点在第一象限内,且AOC OAB ≅△△,如图,又已知OAB 和AOC △有已知公共边AO ,∴(23)C ,.故答案为(2)3,.【点睛】本题考查全等三角形的性质,由已知公共边结合三角形全等的性质找到点C 的位置是解答本题的关键.19.210a --【分析】先利用平方差公式进行整式的乘法运算,同步计算多项式除以单项式,再合并同类项即可.【详解】解:原式222495110a a a =---=--.【点睛】本题考查的是平方差公式的运用,多项式除以单项式,掌握“整式的混合运算”是解本题的关键.20.2【分析】先计算括号内分式的加法,再把除法转化为乘法,约分后可得结果,再把23m n =化为23,n m =再整体代入即可.【详解】解:原式222442n mn m mm n m-+=⋅-()22222n m m n mm n m m--=⋅=-∵23m n=∴23n m =,代入上式,得:原式322m m mm m-===.【点睛】本题考查的是分式的化简求值,掌握“整体代入法求解分式的值”是解本题的关键.21.1a =-,2b =,()()411x x +-【分析】先计算多项式乘以多项式,再结合题意可得64b -=-,327a b -=-,解方程组求解,a b 的值,再利用平方差公式分解因式即可.【详解】解:∵()()223x x a x b -++3223623x bx x bx ax ab =+--++()()323623x b x b a x ab=+-+-++∴64b -=-,327a b -=-解得:1a =-,2b =∴()()222444411ax b x x x +=-+=+-.22.【详解】证明:∵AB ,CD 互相平分∴AE BE =,CE DE =又∵AEC BED ∠=∠∴AEC BED△△≌∴CAE DBE =∠∠,AC BD =∵2FAC BAC ∠=∠∴CAE FAE ∠=∠∴DBE FAE ∠=∠∴AF BF =∵BF BD DF =+∴AC DF AF +=.23.商场实际购进彩灯的单价是60元【分析】设商场原计划购进彩灯的单价为x 元,则商场实际购进彩灯的单价为(120%)x +元,由题意:某商场计划在年前用30000元购进一批彩灯,由于货源紧张,厂商提价销售,实际的进货价格比原来提高了20%,结果比原计划少购进100盏彩灯.列出分式方程,解方程即可.【详解】解:设商场原计划购进彩灯的单价为x 元,则商场实际购进彩灯的单价为(120%)x +元,根据题意得:3000030000100(120%)x x-=+,解得:50x =,经检验,50x =是原分式方程的解,且符合题意,则(120%)60x +=(元),答:商场实际购进彩灯的单价为60元.24.(1)见解析(2)MC=1.5【分析】(1)由∠ACF=∠A+∠ABF ,∠ECF=∠BPC+∠DBF ,得∠ABF=∠ACF-78°,∠DBF=∠ECF-39°,再根据CE 平分∠ACF ,得∠ACF=2∠ECF ,则∠ABF=2∠ECF-78°=2(∠ECF-39°)=2∠DBF ,从而证明结论;(2)连接AQ ,CQ ,过点Q 作BA 的垂线交BA 的延长线于N ,利用HL 证明Rt△QNA≌Rt△QMC,得NA=MC,再证明Rt△QNB≌Rt△QMB(HL),得NB=MB,则BC=BM+MC=BN+MC=AB+AN+MC,从而得出答案.(1)证明:∵∠ACF=∠A+∠ABF,∠ECF=∠BPC+∠DBF,∴∠ABF=∠ACF-78°,∠DBF=∠ECF-39°,∵CE平分∠ACF,∴∠ACF=2∠ECF,∴∠ABF=2∠ECF-78°=2(∠ECF-39°)=2∠DBF,∴BD平分∠ABC;(2)解:连接AQ,CQ,过点Q作BA的垂线交BA的延长线于N,∵QG垂直平分AC,∴AQ=CQ,∵BD平分∠ABC,QM⊥BC,QN⊥BA,∴QM=QN,∴Rt△QNA≌Rt△QMC(HL),∴NA=MC,∵QM=QN,BQ=BQ,∴Rt△QNB≌Rt△QMB(HL),∴NB=MB,∴BC=BM+MC=BN+MC=AB+AN+MC,∴7=4+2MC,∴MC=1.5.25.(1)见解析;(2)见解析;(3)见解析【分析】(1)根据等边三角形的性质和题意,可以得到△ACD ≌△BCE 的条件,从而可以证明结论成立;(2)由△ACD ≌△BCE 得∠CBE=∠CAD ,由△ABC 和△DEC 都是等边三角形得60ACB ECD ∠=∠=︒,由平角定义得60ACN ∠=︒,再由三角形内角和定理可得结论;(3)根据(1)中的结论和等边三角形的判定可以证明△CMN 是等边三角形.【详解】(1)证明:∵△ABC 和△CDE 都是等边三角形,∴BC=AC ,CE=CD ,∠BCA=∠ECD=60°,∴∠BCA+∠ACE=∠ECD+∠ACE ,∠ACE=60°,∴∠BCE=∠ACD ,在△ACD 和△BCE 中AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△BCE (SAS );∴AD =BE ;(2)由(1)得△ACD ≌△BCE ∴∠CBE=∠CAD ,∵△ABC 和△DEC 都是等边三角形∴60ACB ECD ∠=∠=︒∴60ACN ∠=︒∵180,180CBM BCM BMC CAN ACN ANC ∠+∠+∠=︒∠+∠+∠=︒∴∠BMC =∠ANC ;(3)由(1)知,△ACD ≌△BCE ,则∠ADC=∠BEC ,即∠CDN=∠CEM ,∵∠ACE=60°,∠ECD=60°,∴∠MCE=∠NCD ,在△MCE 和△NCD 中,MCE NCD MEC NDC CE CD ∠∠⎧⎪∠∠⎨⎪⎩===,∴△MCE≌△NCD(AAS),∴CM=CN,∵∠MCN=60°,∴△MCN是等边三角形.26.(1)BF=5;(2)见解析.【分析】(1)证明△AEM≌△BFM即可;(2)证明△AEC≌△BFD,得到EC=FD,利用等式性质,得到CD=FE.【详解】(1)∵BF//AE,∴∠MFB=∠MEA,∠MBF=∠MAE,∵EM=FM,∴△AEM≌△BFM,∴AE=BF,∵AE=5,∴BF=5;(2)∵BF//AE,∴∠MFB=∠MEA,∵∠AEC=90°,∴∠MFB=90°,∴∠BFD=90°,∴∠BFD=∠AEC,∵∠DBF=∠CAE,AE=BF,∴△AEC≌△BFD,∴EC=FD,∴EF+FC=FC+CD,∴CD=FE.。
人教版八年级语文上册期末考试卷(附答案)

人教版八年级语文上册期末考试卷(附答案)(考试时间:120分钟;试卷满分:150分)一.(16分)阅读下面的文段,完成1~3题。
打开课本,我们看到了英勇的人民解放军横渡长江,锐不可当.;目睹.了北宋汴京街上行人摩肩接( zhǒng )的繁华景象;体会到我国科研人员面对封锁(dān )精竭虑搞科研的不易;感受到朱德对慈爱且一生劳(lù)的母亲的殷殷情怀;结识汉文帝口中(kè)尽职守的"真将军"——周亚夫;欣赏苏州园林中的"隔而未隔,界而未界"的镂.空的花墙廊子,像一幅幅的完美图画……还瞻.仰了巍峨、雄伟、庄严的人民英雄纪念碑……可以说,优秀的作品,不仅是知识的结晶,更是人类情感与思想的结晶。
这些优秀作品,激励我们前进的动力。
1.文段中加点字的读音和拼音处应填写的汉字书写不正确的一项是( )(3分)A. dāng 踵B. dǔ弹C. lóu 禄D. zhān 恪2.填入文段中画横线处的成语,最恰当的一项是( )(3分)A.别具一格B.自出心裁C.一丝不苟D.惟妙惟肖3.文中画横线句有语病,请选出修改正确的一项( )(3分)A.这些出色作品,激励我们前进的动力。
B.这些优秀作品,激起我们前进。
C.这些优异作品,鼓励我们前进的动力。
D.这些优秀作品,激发我们前进的动力。
4.互联网时代,数字阅读已经成为一种常见的阅读方式。
在活动中,小鲁从网上搜集到一些关于数字阅读的资料,下面是关于2023年中国数字阅读各年龄段用户阅读时长和阅读频率的统计图。
请阅读统计图,写出你的探究结果。
(3分)5.学校开展"书房文化"活动,作为本次活动的学生志愿者,请你根据要求完成以下任务。
(4分)在读书人的心目中,书房是不可或缺的治学休闲之所,更是读书人放牧思想的田园。
我国文人有给自己的书房命名的雅好。
梁启超变法维新,面对国家的内忧外患,临危受命,遂将自己的书斋取名"饮冰室"。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版八年级上册期末考试语文试卷(一)语言的积累与运用(28分)1.下列词语的字形和加点字的注音完全正确的一项是( )(3分)A. 阻遏.(jié)垂髫.(tiáo)伎俩.(liǎng)频.临(bīn)销声匿.迹(nì)B. 愧怍.(zuó)亵.玩(xiè)伧.俗(chěn)轩.敞(xuān)惟妙惟肖.(xiào)C. 游说.(shuì)嶙.峋(lín)侥.健(jiǎo)雾凇.(sōng)不可名.状(míng)D. 赃.物(zāng)消.魂(xiāo)倏.尔(shū)相与.(yù)鳏.寡孤独(guān)2.对下列句子中加点的词语,理解不完全正确的一项是( )(3分)A.审题失误,是作文的最大失误,因为它会使我们的作文失之毫厘,差之千里.........。
(失之毫厘,差之千里:指开头时错了一点点,结果就造成很大的错误。
)B.2001年3月17日零时,万州市民向国林乘渝出租车,途中一持刀者冲入车内,殴打向国林,该出租车驾驶员李永江对事件的发生视而不见、充耳不闻....,使歹徒更加肆无忌惮,行凶后逃走。
(充耳不闻:塞住耳朵,听不见别人的话。
)C.在第九届国际广告节上,大连星海会展中心变成了异彩纷呈的广告大舞台,作品、媒介、设备、网络等精彩绝伦又各具特色的展厅同时亮相,优秀广告的创意巧妙绝伦....,倾倒了一批又一批前来参观的客人。
(巧妙绝伦:形容精巧美妙到了极点。
)D.回顾刚刚成为历史的一年,我市经济终于在山重水复中渐现柳暗花明....的新境。
(柳暗花明:比喻经过曲折以后出现的新局面。
)3.选择准确的词语,将其序号填在前面句中的横线上。
(3分)⑴他们小声地谈论着,似乎怕惊扰忧郁(A.严肃 B.肃穆)的空气。
(西蒙诺夫《蜡烛》)⑵苏州园林在每一个角落都注意(A.图画B.图案)美。
(叶圣陶《苏州园林》)⑶他的游记里,十分(A.崇尚B.推崇)这座桥,说它“是世界上独一无二的”。
(茅以升《中国石拱桥》)4.指出下列句子主要使用的表达方式。
(3分)A. 有一天,两个强盗闯进了圆明园。
一个强盗洗劫,另一个强盗放火。
雨果所指的这“两个强盗是:。
B. 竺可桢《大自然的语言》是按照实践————再实践——的认识规律作为说明顺序的。
C.根据谈家桢《奇妙的克隆》的内容,给“克隆”这个概念下一个定义:5.下列语句没有语病的一句是(4分)( )A. 从他的发言里,给了我很大的启发。
B. 我们要尽可能地节省不必要的开支和浪费。
C. 团结一致是能否搞好工作的关键。
D. 大家都讲究卫生,我们的健康就有保障了。
6.请把下列短语组成两副对联。
(4分)九州春色民安国富莺歌燕舞春暖风和人寿年丰龙腾虎跃四海征程鸟语花香①,。
②,。
7.中新网酒泉10月15日电本社记者孙自法在酒泉卫星发射中心载人航天发射场现场报道,中国第一艘载人飞船“神舟”五号发射升空十多分钟后,已成功进入预定轨道。
中国首位航天员杨利伟由此踏上中国人期待了千年之久的太空之旅。
北京时间十五日上午九时整,“神舟”五号载人飞船由“神箭”——“长征二号F”运载火箭从此间载人航天发射场发射升空,“神箭”升空十多分钟后,中国载人航天工程指挥部总指挥宣布,“神舟”五号载人飞船已成功进入预定轨道,发射取得成功。
这是中国首次进行载人航天飞行,也是全世界第二百四十一次载人飞行和第九百五十二人次进入太空。
同时,本次发射是长征系列运载火箭第七十一次飞行,也是一九九六年十月以来,中国航天发射连续第二十九次获得成功。
(3分)8.原苏联著名小说《钢铁是怎样炼成的》,题目有什么深刻含义? (2分)(二)古诗文积累(12分)9.古诗文默写。
(8分,每空1分)(1) 《爱莲说》中“,”常被后人用来抒写个人情志,表明自己洁身自好,不受污浊社会的沾染。
(2) 刘禹锡所写陋室的居住环境是:“,”。
(3) 大道之行也,,,讲信修睦。
⑷庭下,,盖竹柏影也。
10.阅读下面古诗,按要求回答问题。
(4分)望岳(杜甫)岱宗夫如何?齐鲁青未了。
造化钟神秀,阴阳割昏晓。
荡胸生层云,决眦入归鸟。
会当凌绝项,一览众山小。
(1)“阴阳割昏晓”一句写出了泰山的特点。
(2分)(2)“会当凌绝项,一览众山小”寓含的人生哲理是什么?(2分)二、文言文阅读(15分)阅读《三峡》,完成ll——15题。
自三峡七百里中,两岸连山,略无阙处。
重岩叠嶂,隐天蔽日,自非亭午夜分,不见曦月。
至于夏水襄陵,沿溯阻绝。
或王命急宣,有时朝发白帝,暮到江陵,其间千二百里,虽乘奔御风不以疾也。
春冬之时,则,回清倒影。
,悬泉瀑布,飞漱其间。
清荣峻茂,良多趣味。
每至晴初霜旦,林寒涧肃,常有高猿长啸,属引凄异,空谷传响,哀转久绝。
故渔者歌曰:“巴东三峡巫峡长,猿鸣三声泪沾裳!”11.将文章中空缺的语句补在横线上。
(2分)12.解释下列句子中的词语。
(2分)(1)沿溯阻绝溯:(2)良多趣味良:(3)或王命急宣或:(4)属引凄异属引:13.翻译句子(6分)①虽乘奔御风不以疾也。
②空谷传响,哀转久绝。
③夏水襄陵,沿溯阻绝。
14.“清荣峻茂”一句所写的对象依次是:(2分)15.如果你到三峡旅游,你会选择哪个季节前往,为什么?请用自己的话说说理由。
(3分)三、现代文阅读(40分)(一)阅读下面的文章,完成16——19题。
(18分)奇妙的对称世界(谈祥柏)许多大哲学家、大思想家和大科学家都相信,宇宙是被一种无比完美的对称规律支配的。
整个动物世界,最明显的特点是躯干部分两侧的对称性。
以一匹马为例,通过鼻子到两腿中间可以作一条中轴线,在其两侧有完全对称的器官:眼睛、耳朵、鼻孔、腿……动物为什么会演变出这种对称性呢?大家知道,任何动物在其所处的环境中,左和右两面的情况是基本相同的,它们为了更好的适应环境,需要在两面都能同样的看、听、嗅、触摸,于是就形成了这种对称性。
艺术家则利用对称创造出美。
铜器、漆器、雕刻、壁画、织锦、刺绣……其中的图案,一概少不了对称。
在被称为“立体的画”、“凝固的音乐”的建筑艺术中,也留下了对称的足迹。
我国的建筑,从古代的宫殿到近代的一般住房,绝大部分是对称的,故宫是其中的典范。
从天安门到端门、午门形成了一条中轴线,各种各样的建筑都围绕这条中轴线铺开。
三大殿更是依据对称的原则而建,整体形成了一种端庄凝重、气势恢宏的美,传达着王权的威严。
为什么对称就美呢?万花筒里杂乱无序的碎玻璃片并不美,奥妙就在于三片反光镜构成了三重反射对称,使得杂乱无序的彩色碎玻璃片经过镜面反射后,形成对称的美丽图案。
可见,对称的美在于:在杂乱中形成规律,在无序中引入秩序。
对称的现象引发了科学家对未知领域的探索。
我们知道原子内有原子核,核外有电子。
电子质量很微小,带有负电;原子核内还有质子,质子的质量要比电子大得多,却带正电。
这种情况是不大相称的。
那么,会不会存在着带正电荷的“电子”,带负电荷的“质子”呢?1932年,人们果然发现了带正电荷的电子——反电子。
后来又发现了反质子、反中子。
总之,粒子和反粒子的对称,已经是千真万确的事实了。
那么,会不会存在反氧、反氢、反水,以至于反行星、反宇宙呢?科学家正是运用对称原理,在进一步提出和探索这些问题呢。
16.文章从哪三个方面说明“宇宙是被一种无比完美的对称规律支配的”?(6分)①②③17.文中画线处所举万花筒的例子的作用是什么?(3分)18.对称可以创造美;同样,不对称也可以创造美。
自由选用下面资料,结合文章内容和自己的理解,说说这两种美的差异。
至少使用两种说明方法。
(6分)资料①:苏州园林可绝不讲究对称,好像故意避免似的。
东边有了一个亭子或者一道回廊,西边决不会来一个同样的亭子或者一道同样的回廊。
……池沼或河道的边沿很少砌齐整的石岸,总是高低屈曲任其自然。
(选自《苏州园林》)资料②:你见过我国古代艺术瑰宝——马踏飞燕吗?飞奔的骏马只有一只蹄踏在飞燕上,四蹄姿态各不相同,打破了对称。
铜马足下的飞燕用来衬托良马之神速。
19.对偶就体现了语言的对称美。
请你从本册“课外背诵古诗词”中默写出三组对偶句。
(3分)①②③(二)阅读下面的文章,完成20——24题(22分)用爱倾听(方冠晴)那段日子,我被楼上楼下的住户折磨得快疯掉了。
我家住二楼。
住我楼下的,是一对下岗夫妇。
为了生活,这对夫妇买了一辆破旧的三轮摩托车,每天出去载客,深更半夜才回来。
那辆摩托车破旧得像严重的哮喘病人,“突突突”的响声像哮喘病人的咳嗽,不但巨大,而且让人揪心般的难受。
每晚,我躺在床上,刚有一点睡意的时候,那辆摩托车就拼命“咳嗽”着回来了,声音攀.上楼来,钻.进窗内,搅.得我睡意全消。
我楼上的那家住户,不知怎么心血来潮,给女儿买了一支箫。
每天天刚麻麻亮,他就逼着女儿练习。
那声音呜呜咽咽,毫不连贯,毫无乐感,听在耳里,像鬼哭狼嚎。
我每晚被楼下摩托车的“咳嗽”搅得没有睡意,早晨又早早地被楼上的箫声“哭”醒,弄得我精神不振,心情烦躁。
我想,应该好好与楼上楼下的住户谈一谈。
但临到他们的门口,我又犹豫了,谈什么呢?让他们不要再发出噪音?可楼下的那个住户,破摩托车就是他们的饭碗;楼上的那个住户,箫声就是家长对孩子的希望。
难道我要他们放弃饭碗放弃希望?我不忍开口,他们也不会答应。
几经考虑,我决定搬家,搬到一个清静的地方去居住,那样有利于我的写作,也有利于我的健康。
我找到一位朋友,诉说了我的苦衷..,叫他帮我物色好的住所。
朋友笑眯眯的听着,然后问我:“你觉得我居住的环境怎么样?”我说:“就是觉得你这里清静,所以叫你帮我找住的地方。
”朋友得意的点点头,说:“好吧,你先在我家里坐一个小时,感受一下。
”一个小时后,隔壁的阳台上传来一种含糊不清的类似于说话的声音,像原始部落的人用特殊的声音在喊叫,声音刺耳而使人不明所以,让人听了格外不舒服。
我问朋友这是什么声音。
朋友说:“一个9岁的男孩,在学说话。
你仔细听听,他说的是什么?”我侧耳倾听,那男孩无疑在重复一句话,但我怎么听都听不明白他在说什么。
我猜测说:“他好像在说,羊刚仆倒在地。
”朋友哈哈大笑,说:“你错了。
他是说阳光普照大地。
”说着话,他拉开了通往阳台的门,以使那孩子的声音更大一些。
这时我听到,有一位妇女,在不断地纠正那个男孩。
妇女说的,正是“阳光普照大地”。
但无论妇女怎么纠正,那男孩说的,仍是“羊刚仆倒在地”。
朋友见我一脸诧异,便解释说:“这孩子是个弃儿,一出生就又聋又哑,所以他的生身父母抛弃了他。
是我的邻居将他捡了回来,不但抚养他,而且到处求医问药为他治疗。
从他4岁开始,我的邻居就开始锲而不舍地坚持每天教他说话,到他5岁的时候,有一天,他居然开口叫妈妈了,虽然声音那么模糊,但我们都听清了。
我的邻居当时就激动得哭了,我们在场的许多人都热泪盈眶。
