山东建筑大学《结构力学》——互等定理

合集下载

专升本【结构力学】试题(卷)答案解析

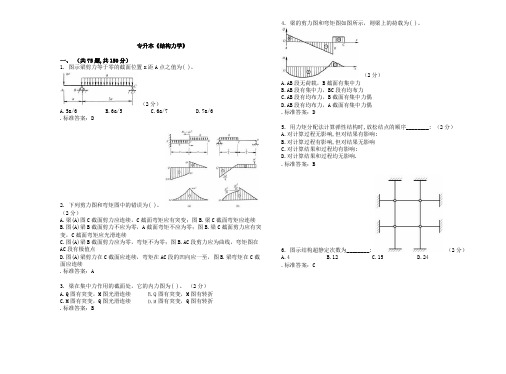
专升本《结构力学》一、（共75题,共150分）1. 图示梁剪力等于零的截面位置x距A点之值为( )。

（2分）A.5a/6B.6a/5C.6a/7D.7a/6.标准答案：D2. 下列剪力图和弯矩图中的错误为( )。

（2分）A.梁(A)图C截面剪力应连续，C截面弯矩应有突变；图B.梁C截面弯矩应连续B.图(A)梁B截面剪力不应为零，A截面弯矩不应为零；图B.梁C截面剪力应有突变，C 截面弯矩应光滑连续C.图(A)梁B截面剪力应为零，弯矩不为零；图B.AC段剪力应为曲线，弯矩图在AC 段有极值点D.图(A)梁剪力在C截面应连续，弯矩在AC段的凹向应一至，图B.梁弯矩在C截面应连续.标准答案：A3. 梁在集中力作用的截面处，它的内力图为( )。

（2分）A.Q图有突变，M 图光滑连续图有突变，M 图有转折C.M图有突变，Q 图光滑连续图有突变，Q 图有转折.标准答案：B 4. 梁的剪力图和弯矩图如图所示，则梁上的荷载为( )。

（2分）A.AB段无荷载，B截面有集中力B.AB段有集中力，BC 段有均布力C.AB段有均布力，B截面有集中力偶D.AB段有均布力，A截面有集中力偶.标准答案：D5. 用力矩分配法计算弹性结构时,放松结点的顺序________: （2分）A.对计算过程无影响,但对结果有影响;B.对计算过程有影响,但对结果无影响C.对计算结果和过程均有影响;D.对计算结果和过程均无影响..标准答案：B6. 图示结构超静定次数为________: （2分）A.4B.12C.15D.24 .标准答案：C7. 图示结构截面K的轴力值Nk为________: （2分）A.B.C.D..标准答案：C8. 用几何组成规则分析图示体系是:________ :（2分）A.无多余约束的几何不变体系；B.有多余约束的几何不变体系；C.可变体系；D.瞬变体系。

.标准答案：A9. 等截面直杆AB的A端的转动刚度SAB________: （2分）A.仅与杆件的线刚度有关;B.仅与杆两端的支承情况有关;C.与杆件的线刚度及荷载情况有关;D.与杆件的线刚度及两端支承情况有关. .标准答案：D10. 悬臂梁受载如图，弯矩图有三种答案:图A.图B.、和图C.。

《结构力学》典型习题与解答

《结构力学》经典习题及详解一、判断题（将判断结果填入括弧，以 √表示正确，以 × 表示错误。

）1．图示桁架结构中有3个杆件轴力为0 。

（×）2．图示悬臂梁截面A 的弯矩值是ql 2。

(×)3．静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。

（√ ） 4．一般来说静定多跨梁的计算是先计算基本部分后计算附属部分。

（× ） 5．用平衡条件能求出全部力的结构是静定结构。

（ √ ）6．求桁架力时截面法所截取的隔离体包含两个或两个以上的结点。

（√ ） 7．超静定结构的力法基本结构不是唯一的。

（√）8．在桁架结构中，杆件力不是只有轴力。

（×） 9．超静定结构由于支座位移可以产生力。

（√ ） 10．超静定结构的力与材料的性质无关。

（× ） 11．力法典型方程的等号右端项不一定为0。

（√ ）12．计算超静定结构的位移时，虚设力状态可以在力法的基本结构上设。

（√）13．用力矩分配法计算结构时，汇交于每一结点各杆端分配系数总和为1，则表明分配系数的计算无错误。

（× ）14．力矩分配法适用于所有超静定结构的计算。

（×）15．当AB 杆件刚度系数i S AB 3 时，杆件的B 端为定向支座。

(×)二、单项选择题（在每小题的四个备选答案中选出一个正确答案，并将其代号填在题干后面的括号。

不选、错选或多选者，该题无分。

）1．图示简支梁中间截面的弯矩为（ A ）A．82qlB．42qlC．22qlD．2 ql2．超静定结构在荷载作用下产生的力与刚度（B）A．无关 B．相对值有关C．绝对值有关 D．相对值绝对值都有关3．超静定结构的超静定次数等于结构中（B ）A．约束的数目 B．多余约束的数目C．结点数 D．杆件数4．力法典型方程是根据以下哪个条件得到的（C）。

A．结构的平衡条件B．结构的物理条件C．多余约束处的位移协调条件D．同时满足A、B两个条件5．图示对称结构作用反对称荷载，杆件EI为常量，利用对称性简化后的一半结构为（A ）。

互等定理

（↓）（单击鼠标左键返回）目录
建筑力学
目录
静定结构的位移\互等定理如图所示为应用位移互等定理的例子。这里，线位移 12 和角位
移 21 在数值上是相等的。
目录
静定结构的位移\互等定理
1.3 反力互等定理
如图所示为同一超静定结构的两个支座分别发生单位位移的两种状态。根据功的互等定理可得
r12= r21
这就是反力互等定理，即：对超静定结构，在第一状态中由支座1的单位位移引起的支座2处的反力r21，等于第二状态中由支座2 的单位位移引起的支座1处的反力r12。这里，反力rij有两个下标，第一个下标表示产生反力的地点，第二个下标表示产生反力的原因。
公式推导：
导出如下平面杆
件结构位移计算的一般公式。这种计算结构位移的方法通常称为单位荷载法。
外力虚功为
内力虚功为
We FKK R1c1 R2c2 FKK Rc
Wi
l FNds
l FSds
Mkds
l
根据式We= Wi有 FKK Rc
得 K K l Fl FNNddss llFFSSds
l FNds
l FSds
Mkds
l
MMkkddss RRcc
ll
（单击鼠标左键返回）
目录
静定结构的位移\结构位移计算的一般公式
13.3.2 虚单位荷载的设置
（单击鼠标左键返回）
目录
静定现结在构考的察位剪移切\静变定形结对构位在移荷的载影作响用。下由的图位b可移得计，算
【例13.1】求图(a)所示简支梁的中点C的竖向位移ΔCV。已知梁
AE段：
M1
2
2x 2
=－x

山东建筑大学工程力学期末试题

20KN
B A a D a a
C
只需分别对 AD 段和 BC 段进行强度计算。
三、作图题（20分） 1、作图示杆的轴力图。（5分）
90kN 20kN 20kN 5kN 15kN 10kN
三、作图题（20分） 1、作图示杆的轴力图。（5分）
90kN 20kN 20kN
40kN 20kN
50kN
5kN
6、力偶对刚体的作用效应与其在作用面内的位置无关。 7、作用在刚体上的一个力，可以从原来的作用位置平行移动到该刚体内任意指定点，但必须附加一个力偶，附加力偶的矩等于原力对指定点的矩。
8、材质相同的压杆，其柔度越大越容易失稳。
9、当切应力超过材料的剪切比例极限时，剪切胡克定律与切应力互等定理都不成立。 10、平行移轴公式表示图形对于任意两个相互平行轴的惯性矩之间的关系。

b a c 0

F
W
9、压杆失稳是指压杆在轴向压力作用下（D ）（A）局部横截面的面积迅速变化（B）危险截面发生屈服或断裂（C）不能维持平衡状态而突然发生运动（D）不能维持直线平衡而突然变弯
10、单元体处于纯剪切应力状态，其主应力特点为（A ）
（A）（B）（C）（D）
1 0, 2 0, 3 0, 1 3 1 0, 2 0, 3 0, 1 3
2014工程力学复习
1、两个力偶的力偶矩矢相等，则此两力偶等效。 2、在任何情况下，摩擦力的大小总是等于摩擦系数与法向反力的乘积。 3、空间任意力系的最后合成结果可能是一个合力，或一个合力偶，或一个力螺旋或力系平衡。 4、当力与轴平行或相交时，力对轴的矩等于零。 5、重心在物体内的位置以及重心坐标都是确定的。 6、力偶对任意点之矩恒等于力偶矩，与矩心的位置无关。 7、因静摩擦力的大小可在一定范围内变化，故物体有一平衡范围。√ 8、空间任意力系向不同点简化，主矢与简化中心的位置无关，主矩一般与简化中心的位置有关。√ 9、力对任意轴的矩等于其所有分力对同一轴之矩的代数和。 √ 10、平面图形的重心一定位于图形内部。×

山东建筑大学结构力学期末考试复习题

《结构力学》一、判断题1、体系组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必须满足的条件。

（正确）2、有多余约束的体系一定是超静定结构。

（错误）4、荷载作用在静定多跨梁的附属部分时，基本部分一般内力不为零。

（正确）4、弯矩图的叠加不是指图形的简单拼合，而是指两图对应的弯矩纵值叠加。

（正确）5、图示弯矩图是正确的。

（错误）6、在温度变化与支座移动因素作用下，静定与超静定结构都有内力。

（错误）7、〃次超静定结构，任意去掉〃个多余约束均可作为力法基本结构。

（错误）8、图示结构，当B支座下沉时，内力与E/绝对值成正比。

（正确）----- 1------ 19、用位移法求解结构内力时如果•图为零，则方程中的自由项R〃一定为零。

（错误）10、图示结构用位移法计算时，其基本未知量的数目为3个。

（正确）二、选择题 1、作为结构的体系应是（A）。

A、儿何不变体系；B、几何可变体系：C、瞬变体系：D、几何不变体系或瞬变体系。

2、图示体系的几何组成性质为。

（B）A、几何不变，无多余联系；B、几何不变，有多余联系；C、瞬变；D、常变。

3、三絞拱在竖向满跨均布荷我作用下合理拱轴线是。

（B）A、圆弧线；B、抛物线；C、悬链线；D、椭圆线。

4、求图示梁饺C左侧截面的转角位移时，其虚拟单位力状态应取。

（C）5、导出单位荷载法的原理是° （B）A、虚位移原理；B、虚力原理；C、叠加原理；D、静力平衡条件。

6、图示对称刚架，不计轴向变形，弯矩图为。

（D）A、两杆件均为内侧受拉；B、两杆件均为外侧受拉；C、两杆件均为部分外侧受拉；D、两杆件弯矩都为零。

7、在力法方程^..X y+A,p=A r.^Q (D)A、 Aj=OB、 Ai>0C、 Ai<0D、 ABC都可能8、超静定结构在荷载作用下的内力和位移计算时，各杆的刚度应为。

（D）A、均用相对值；B、均必须用绝对值：C、内力计算用绝对值，位移计算用相对值；D、内力计算可用相对值，位移计算须用绝对值。

9.5互等定理《结构力学》

9.8 线性变形体系的互等定理
线性变形体系的互等定理
1. 功的互等定理:
第 I 状态
方法一
先加广义力P1后再加广义力P2
W1
1 2
P111
P112
1 2
P222
先加广义力P2后再加广义力P1
W2
1 2
P222
P221
1 2
P111
由W1=W 2
P112 P221
11 11
2 P2
12
22
第 Ⅱ 状态 2 P2
（3） yc 应取自直线图中。
2. 若与 yc 在杆件的同侧，yc取正值；
反之，取负值。
3. 如图形较复杂，可分解为简单图形.
三、应用举例
例 1. 已知 EI 为常数，求A、B两点相对水平位移 ΔAB。
A
B
h
q
1
q
1
l
ql2 / 8
h h
MP
Mi
解：作荷载弯矩图和单位荷载弯矩图
AB
yC
EI
1 EI
C q
1 l ql2 1 l ) 22 8 32
ql2 / 8
17 ql4 ()
384 EI
ql2 / 32
ql2 / 8
例 4. 图示梁 EI 为常数，求C点竖向位移。
ql2 / 2
q ql2 / 8
MP A l/2C l/2 B
l/2
1
Mi
C
q ql / 2
ql2 / 8
ql2 / 8 q
2 3
ql2 8
l
h
qh3l ()
12EI
三、应用举例
例 2. 已知 EI 为常数，求铰C两侧截面相对转角 C 。

结构力学§5-7 互等定理

∴ 由(1)、(2)可得：
FP1 Δ11 1
2 Δ21
(a) 第一状态
Δ12 1
FP2 2 Δ22
(b) 第二状态
FP112 FP221
(a)
功的互等定理：（最基本的定理）第一状态的外力在第二状态的位移上所作的虚功，等于第二状态的外力在第一状态的位移上所作的虚功。
2. 位移互等定理（功的互等定理的一个特例 — 单位力）
1. 功的互等定理
设有两组外力FP1和FP2分别作用于同一线弹性结构上，如图所示，(a)、(b)分别称为结构的第一状态和第二状态。
FP1 Δ11 1
2 Δ21
Δ12 1
FP2 2 Δ22
(a) 第一状态
(b) 第二状态
为证明功的互等定理,这两组力按不同次序先后作用于同一结构上, 所作的总功分别如下：
FP1＝1
1
2
δ21
δ12 1
FP2＝1 2
(a) 第一状态
(b) 第二状态
功的互等定理为若令：FP1 =FP2 =1
FP112 FP221
则有：112 121
即：
12 21
(b)
位移互等定理: 第二个单位力所引起的第一个单位力作用点沿其方向上的位移，等于第一个单位力所引起的第二个单位力作用点沿其方向上的位移。(单位力——广义力，位移——广义位移）
第5章虚功原理与结构位移计算
§5-1 刚体体系的虚功原理与位移计算 §5-2 结构位移计算的一般公式 §5-3 荷载作用下的位移计算 §5-4 荷载作用下的位移计算举例 §5-5 图乘法 §5-6 温度变化时的位移计算 §5-7 互等定理
§5-7 互等定理
本节介绍线性变形体系的四个互等定理，其中最基本的是功的互等定理，其它三个定理均可由此推导出来。

在线网课《结构力学A1(山东联盟-山东建筑大学)》课后章节测试答案

第一章测试1【多选题】(100分)结构力学的主要内容是（）A.讨论结构的稳定性，以及在动力荷载作用下的反应B.结构的组成规律与合理形式计算简图的合理选择C.在外力或其他因素影响下，结构的内力和变形计算第二章测试1【单选题】(20分)作为结构的体系应是：A.几何不变体系或瞬变体系B.几何不变体系C.几何可变体系D.瞬变体系2【单选题】(20分)图示体系虽有3个多余约束，但为保证其几何不变，哪两根链杆是不能同时去掉的。

A.a和eB.a和cC.a和bD.c和e3【单选题】(20分)图示体系为：A.几何不变无多余约束B.几何不变有多余约束C.几何可变D.几何瞬变4【单选题】(20分)图示体系为：A.几何不变有多余约束B.几何可变C.几何不变无多余约束D.几何瞬变5【判断题】(20分)有多余约束的体系一定是几何不变体系。

A.错B.对第三章测试1【判断题】(15分)几何不变体系一定是静定结构。

A.错B.对2【单选题】(15分)静定结构在荷载作用下，其全部反力和内力：A.都可由静力平衡条件求得，而且数值是确定的B.特殊情况下，才可由静力平衡条件唯一地确定C.可由静力平衡条件求得，但数值有时是不确定的D.不能只由平衡条件来确定，还必须考虑变形条件3【判断题】(15分)静定结构在支座移动、变温及荷载分别作用下，均产生位移和内力。

A.错B.对4【判断题】(15分)多跨静定梁仅当基本部分承受荷载时，其它部分的内力和反力均为零。

A.对B.错5【单选题】(15分)A.B.-0.5pC.0.5pD.p6【判断题】(15分)图示为一杆段的M、Q图，若Q图是正确的，则M图一定是的。

A.错B.对7【判断题】(15分)图示梁上的荷载P将使CD杆产生内力。

A.错B.对8【单选题】(15分)图示桁架内力为零的杆有（）A.6根B.7根C.8根D.9根9【单选题】(10分)A.B.C.D.10【判断题】(10分)图示三铰拱左支座的竖向反力为零。

《结构力学习题》(含答案解析)

《结构力学习题》(含答案解析)本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March20 第三章静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.M C.=1=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M kM p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

Aa a9、图示桁架各杆EA =常数，由于荷载P是反对称性质的，故结点B的竖向位移等于零。

2121二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数，a = 2m 。

a a a 10kN/m12、求图示结构E 点的竖向位移。

EI = 常数。

l l l /3 2 /3/3q13、图示结构，EI=常数，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m 3m 3m14、求图示刚架B 端的竖向位移。

q15、求图示刚架结点C 的转角和水平位移，EI = 常数。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝常数。

l ll/217、求图示刚架横梁中Ｄ点的竖向位移。

EI＝常数。

18、求图示刚架中D点的竖向位移。

(整理)《结构力学》.

3：[判断题]1、(本小题2分)在竖向均布荷载作用下，三铰拱的合理轴线为圆弧线。

参考答案：错误4：[判断题]2、(本小题2分)几何可变体系在任何荷载作用下都不能平衡。

考参答案：错误5：[判断题]3、(本小题2分)在温度变化与支座移动因素作用下静定与超静定结构都有内力。

参考答案：错误6：[判断题]4、(本小题2分)静定结构受外界因素影响均产生内力，内力大小与杆件截面尺寸无关。

参考答案：错误7：[判断题]5、(本小题2分) 按虚荷载原理所建立的虚功方程等价于几何方程。

参考答案：正确8：[单选题]1、(本小题3分）力法的基本未知量是A：结点角位移和线位移B：多余约束力C：广义位移D：广义力参考答案：B9：[单选题]2、（本小题3分）静定结构有温度变化时A：无变形，无位移，无内力B：有变形，有位移．无内力C：有变形．有位移，有内力D：无变形．有位移，无内力参考答案：B10：[单选题]3、（本小题3分）变形体虚功原理A：只适用于静定结构B：只适用于线弹性体C：只适用于超静定结构D：适用于任何变形体系参考答案：D11：[单选题]4、（本小题3分）由于静定结构内力仅由平衡条件决定,故在温度改变作用下静定结构将A：产生内力B：不产生内力C：产生内力和位移D：不产生内力和位移参考答案：B12：[单选题]5、（本小题3分）常用的杆件结构类型包括A：梁、拱、排架等B：梁、拱、刚架等C：梁、拱、悬索结构等D：梁、刚架、悬索结构等参考答案：B1：[判断题]1、（本小题2分）有多余约束的体系一定是几何不变体系。

参考答案：错误2：[判断题]2、（本小题2分）静定结构的内力与荷载有关，而与材料的性质、截面的形状及大小无关。

参考答案：正确3：[判断题]3、（本小题2分）三个刚片由三个铰相联的体系一定是静定结构。

参考答案：错误4：[判断题]4、（本小题2分）位移法未知量的数目与结构的超静定次数有关。

参考答案：错误5：[判断题]5、（本小题2分）力矩分配法中的分配系数、传递系数与外来因素（荷载、温度变化等）有关。

结构力学课件第6章温度、支座、互等定理

∑∫F
α td s + ∑ ∫ M
α ∆ td s
∆Kt
M ds = ∑ α t ∫ FN d s + ∑ α ∆ t ∫ h
∆ kt = ∑ α tAω F + ∑
N
α ∆t
h
对等截面直杆
Aω M
F N 图面积
式中
M图面积
α ——材料的线膨胀系数 t1 + t2 t= （杆件的截面对称于形心轴） 2 ∆ t = t2 − t1
(a) 第一状态
r21
由反力互等定理，则有：由反力互等定理，则有： r12 = r21
即反力偶r 等于反力r 即反力偶 12等于反力 21 数值上相等，量纲相同）（数值上相等，量纲相同）
4. 反力位移互等定理这个定理同样是功的互等定理的一种特殊情况。这个定理同样是功的互等定理的一种特殊情况。
∑ α tAω
对桁架： ∆ t = ∑ α tFN l 问题：如何求位移？问题：当桁架有制造误差∆li 时,如何求位移？如何求位移
FN
+
∑
α∆t
h
Aω M
∆ ∆l = ∑ FNi ∆ li
刚架施工时温度为20 例：刚架施工时温度为 0C ，试求冬季外侧温度为 -100C ，内侧温度为 0 0C 时,A点的竖向位移 ∆ Ay 。已知点的竖向位移 l=4 m, α = 10 −5 ,各杆均为矩形截面杆，高度 h=0.4 m 各杆均为矩形截面杆，各杆均为矩形截面杆解：构造虚拟状态
§6.6 静定结构温度变化 6.6 时的位移计算
(1) 一般公式
∆ K = ∑ ∫ FN du + ∑ ∫ M dϕ + ∑ ∫ FS γ ds − ∑ FR c

《结构力学》典型习题与解答

《结构力学》经典习题及详解一、判断题（将判断结果填入括弧内，以 √表示正确，以 × 表示错误。

）1．图示桁架结构中有3个杆件轴力为0 。

（×）2．图示悬臂梁截面A 的弯矩值是ql 2。

(×)ll3．静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。

（√ ） 4．一般来说静定多跨梁的计算是先计算基本部分后计算附属部分。

（× ） 5．用平衡条件能求出全部内力的结构是静定结构。

（ √ ）6．求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。

（√ ） 7．超静定结构的力法基本结构不是唯一的。

（√）8．在桁架结构中，杆件内力不是只有轴力。

（×）9．超静定结构由于支座位移可以产生内力。

（√ ） 10．超静定结构的内力与材料的性质无关。

（× ）11．力法典型方程的等号右端项不一定为0。

（√ ）12．计算超静定结构的位移时，虚设力状态可以在力法的基本结构上设。

（√）13．用力矩分配法计算结构时，汇交于每一结点各杆端分配系数总和为1，则表明分配系数的计算无错误。

（× ）14．力矩分配法适用于所有超静定结构的计算。

（×）15．当AB 杆件刚度系数i S AB 3 时，杆件的B 端为定向支座。

(×)二、单项选择题（在每小题的四个备选答案中选出一个正确答案，并将其代号填在题干后面的括号内。

不选、错选或多选者，该题无分。

）1．图示简支梁中间截面的弯矩为（ A ）qlA．82qlB．42qlC．22qlD．2 ql2．超静定结构在荷载作用下产生的内力与刚度（B）A．无关 B．相对值有关C．绝对值有关 D．相对值绝对值都有关3．超静定结构的超静定次数等于结构中（B ）A．约束的数目 B．多余约束的数目C．结点数 D．杆件数4．力法典型方程是根据以下哪个条件得到的（C）。

《结构力学》参考资料

A.FB.0C.2FD.F/2
25.图中取A支座反力为力法的基本末知量(向上为正)，则为:（C）
A.3P/16；B.4P/16；C.5P/16；D.不定，取决于EI值
26.下列哪个选项不是按照荷载作用性质以及结构的反应特征分类的（D）
A.静力荷载B.动力荷载C.移动荷载D.恒载
27.图示结构，当高度h增加时，杆1的内力（C）
A.增大B.减小C.不变D.不确定
28.图示体系是：（A）
A.几何瞬变有多余约束B.几何不变C.几何常变D.几何瞬变无多余约束
29.力法典型方程的副系数，其依据是（A）。
A.位移互等定理B.反力互等定理C.反力位移互等定理D.虚位移原理
30.设体系上作用的任意平衡力系，又设体系发生符合约束条件的无限小的刚体位移，则外力在位以上所做的虚功总和恒等于零是（A）。
17.荷载作用在静定多跨梁的附属部分时，基本部分一般内力不为零。（对）
18.虚功中的力和位移没有因果关系。（对）
19.力矩分配法中的分配系数、传递系数与荷载无关。（对）
20.影响线仅用于解决活载作用下结构的计算问题，不能用于恒载作用下的计算。（错）
21.任何三铰拱的合理拱轴都是二次抛物线（错）
22.图乘法可以用来计算曲杆。（错）
34.力矩分配法中的分配系数，传递系数与外界因素（荷栽，温度变化等）有关。（错）
35.的互等定理仅适用于线性变形体系。（对）
36.位移法典型方程的右端项一定为零（对）
37.两个弯矩图的叠加不是指图形的简单拼合，而是指两图对应的弯矩纵矩叠加。（对）
38.位移法以结点力为基本未知量。（错）
39.对图中a图所示桁架用力法计算时，取图b作为基本体系(杆AB被去掉),则

《结构力学》期末考试复习题及参考答案

《结构力学》专升本一1、图1 属几何体系。

（） A. 不变，无多余约束 B. 不变，有多余约束 C. 可变，无多余约束 D. 可变，有多余约束图12、两个刚片，用三根链杆联结而成的体系是：（） A ．几何常变 B ．几何瞬变C ．几何不变D ．几何不变或几何常变或几何瞬变 3、三个刚片用( )的三个铰两两相联可以组成几何不变体系。

A ．共线 B ．不共线 C ．虚拟 D ．非虚拟4、静定结构的几何组成特征是( )。

A ．体系几何不变B ．体系几何不变且无多余约束C ．体系几何可变D ．体系几何瞬变 5、计算内力的一般方法是( )。

A ．静力分析B ．节点法C ．截面法D ．综合几何、物理和静力学三方面 6、在温度改变的影响下，静定结构将：（） A. 有内力、有位移 B. 无内力、有位移 C. 有内力、无位移 D. 无内力、无位移7、梁的绝对最大弯矩表示在一定移动荷载作用下（）。

A. 梁某一截面的最大弯矩B. 梁某一截面绝对值最大的弯矩C. 梁所有截面最大弯矩中的最大值D. 当移动荷载处于某一最不利位置时相应的截面弯矩8、欲使支座B 截面出现弯矩最大负值maxB M ,梁上均布荷载的布局应为：（）9、作用于静定多跨梁基本部分上的荷载在附属部分上（）。

A ．绝对不产生内力B ．一般不产生内力C ．一般会产生内力D ．一定会产生内力B A CD(a)(b)2110、在竖向荷载作用下，三铰拱（）A ．有水平推力B ．无水平推力C ．受力与同跨度、同荷载作用下的简支梁完全相同D ．截面弯矩比同跨度、同荷载作用下的简支梁的弯矩要大 11、图3所示结构内力为零的杆件有（）。

A ．BE 杆，B ．AE 、BE 杆，C ．AE 、BE 、CE 杆D ．AE 、CE 杆12、图4所示对称刚架，在反对称荷载作用下，求解时取半刚架为（ D ）A ．图（a ）B ．图（b ）C ．图（c ）D ．图（d ）图4 图（a ）图（b ）图（c ）图（d ）13、图5所示桁架下弦承载，下面画出的杆件内力影响线，此杆件是：（）A.chB.ciC.djD.cj14、图6所示简支梁上有单位力偶移动，其截面C 的剪力影响线应该是第图。

结构力学主要定理

§11-1概述1．变形功与变形能弹性杆受拉力P作用（图11-1），当P从零开始到终值缓慢加载时，力P在其作用方向上的相应位移也由零增至而做功，称为变形功。

（11-1）与此同时弹性杆被拉长而具有做功的能力，表明杆件内储存了变形能。

单位体积储存的应变能称为应变比能（11-2）整个杆件的变形能为（11-3）如果略去拉伸过程中的动能及其它能量的变化与损失，由能量守恒原理，杆件的变形能U在数值上应等于外力做的功W，即有U=W （11-4）这是一个对变形体都适用的普遍原理称为功能原理，弹性固体变形是可逆的，即当外力解除后，弹性体将恢复其原来形状，释放出变形能而做功。

但当超出了弹性范围，具有塑性变形的固体，变形能不能全部转变为功，因为变形体产生塑性变形时要消耗一部分能量，留下残余变形。

2．应变余功与余能变形体受外力作用时的余功定义为其中P1是外力从零增加到的终值，仿照功与变形能相等的关系，将余功相应的能称为余能，用U c表示。

余功与余能相等，即可仿照前面，定义单位体积余应变能（或应变余能），称为余应变比能由此整个结构余应变能可写成应指出：余功、余应变能、余应变比能具有功的量纲，是变形体的另一能量参数，但都没有具体的物理概念，只是常力所做的功减去变力所做功余下的那部分功。

3．能量原理固体力学中运用功与能有关的基本原理统称为能量原理，由此发展出来的方法称为能量法。

能量原理是在总体上从功与能的角度考察变形体系统的受力、应力与变形的原理与方法，是进一步学习固体力学的基础，也是当今应用甚广的有限元法求解力学问题的重要基础。

4．本章内容本章只涉及能量原理在材料力学中常用的部分内容，如：变形能、互等定理、卡氏定理、虚功原理、单位载荷法及图乘法，更为深入的，如最小势能原理，最小余能原理等变分原理，可参考其它专著。

§11-2 杆件变形能计算杆件不同受力情况下的变形能。

1．轴向拉伸或压缩线弹性杆件（图11-3）拉、压杆应变比能则整个杆的变形能或（11-5）（11-6）其中，N是内力（轴力），A是截面面积，l是杆长。