用Excel求解线性规划及线性方程组的方法
线性规划实验-Excel求解

用Excel求解线性规划问题实验(实验题目在最后)一、Excel函数使用Excel求解线性规划问题时,SUMPRODUCT函数可以大大降低资料录入工作量,提高工作效率。
计算数组或向量的乘积时,使用SUMPRODUCT 函数,格式如下:SUMPRODUCT(数组1,数组2,…,数组n)其中2≤n≤30,即最多可以使用30个数组参数,返回值为n个数组对应元素乘积之和。
以图1为例,在单元格D1中输入公式=SUMPRODUCT(A1:B1,A2:B2,A3:B3)得到111(相当于A1*A2*A3 + B1*B2*B3 = 1*2*3 + 3*5*7 = 111)。
在单元格D2中输入公式=SUMPRODUCT(A1:C1,A2:C2)得到53(相当于A1*A2 + B1*B2 + C1*C2 = 1*2 + 3*5 + 4*9 = 53)。
图1. 乘积和(SUMPRODUCT函数)计算结果11二、求解实例1. 问题描述与模型建立某玩具厂生产猫和龟两种玩具,制造一个玩具猫可获利30元,制造一个玩具龟可获利20元。
制造一个猫需要2小时机工和1小时手工;制造一个龟需要1小时机工和1小时手工。
在一周内,机工不能超过100h ,手工不能超过80h ,猫的产量不能超过45个。
求产品的最佳生产量和最大利润。
设1x 为一周内猫的生产量,2x 为一周内龟的生产量。
可建立如下线性规划模型:⎪⎩⎪⎨⎧≤≤+≤++=458010022030max 1212121x x x x x x x g2. 数据录入(1)启动Excel ,建立如图2所示的Excel 工作表,输入系数矩阵A 到区域C2:D4;输入约束常数b 到区域F2:F4;输入目标系数到区域C5:D5。
(2)指定单元格C6和D6存储变量1x 和2x 的值,称之为可变单元格。
在可变单元格中输入数字1表示给定初始值121==x x ,但并非一定这样;若这两个单元格不输入内容,Excel 将按0处理,不影响求解。
用EXCEL求解线性规划

用EXCEL求解线性规划
要用EXCEL求解线性规划问题,需要遵循以下步骤:
1. 给定问题中的约束条件和目标函数。
2. 打开EXCEL,建立一个新的工作表。
3. 在工作表中输入问题的约束条件和目标函数。
在输入目标函数时,需要将所有项移动到等号左侧,使它成为一个线性方程。
需要注意将不等式约束条件转化为等式约束条件,可以通过添加松弛变量来实现。
4. 使用EXCEL的“规划”工具,在工具栏中点击“数据”-“分
析”-“规划器”,打开“规划器”。
5. 在“规划器”中,选择需要优化的目标单元格,在“约束条件”
中输入所有约束条件所在的单元格,设置变量单元格的范围。
6. 可以在“选项”中添加其他约束条件。
例如,可以设定变量的整数或二元特性等。
7. 单击“求解”按钮,EXCEL将自动求解最优解,并输出最优
值和变量值。
需要注意的是,线性规划问题求解的结果是一个数值,而不是图形。
因此,需要谨慎分析问题以确保从数值结果中得到了正确的结论。
怎么利用EXCEL求解线性规划

利用线性回归方法求解生产计划方法一:1、建立数学模型:①设变量:设生产拉盖式书桌x台,普通式书桌y台,可得最大利润②确定目标函数及约束条件目标函数:y=max+115P90x约束条件:200x .....................⑴+y10≤20x .....................⑵4≤+y16128x .....................⑶+y1015≤220yx ..........................⑷,≥2、在Excel中求解线性规划①首先,如图1所示,在Excel工作表格输入目标函数的系数、约束方程的系数和右端常数项:图1②将目标方程和约束条件的对应公式输入各单元格中F2=MMULT(B6:C6,F6:F7);F3=MMULT(B3:C3,F6:F7);F2=MMULT(B4:C4,F6:F7);F2=MMULT(B5:C5,F6:F7);出现图2样式:图2线性规划问题的电子表格模型建好后,即可利用“线性规划”功能进行求解。
选择“工具”→“规划求解”出现“规划求解参数”窗口,如图3所示:图3在该对话框中,目标单元格选择F2,问题类型选择“最大值”,可变单元格选择F6:F7,点击“添加”按钮,弹出“添加约束条件”窗口,如图4所示:图4根据所建模型,共有4个约束条件,针对约束(1):2002010≤+y x ,左端“单元格所引用位置”选择F3,右端“约束值”选择D3,符号类 型选择“<=”,同理继续添加约束(2)(3)(4),完成后选择“确定”,回到“规划求解参数”对话框,如5图所示:图5④点击“选项”按钮,弹出“规划求解选项”对话框,选择“采用线性模型”和“假定非负”两项,如图6所示:图6⑤点击“确定”→“求解”,选择“运算结果报告”“敏感性报告”“极限值报告”三项,最后点击“确定”,输出结果: 运算结果报告:敏感性报告:极限报告:方法二:1、建立数学模型设生产拉盖式书桌x 台,普通式书桌y 台,总利润为Z 元 确定目标函数及约束条件 目标函数:y x Z 90115max += 约束条件:⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0,22010151281642002010..y x y x y x y x t s 2、在Excel 中规划求解在Excel 中建立线性规划模型,如图1所示:图11)在E2中输入“=B2*B6+C2*C6”如图2所示,同理 E3=B3*B6+C3*C6E4=B4*B6+C4*C6B7=B5*B6+C5*C6图22)单击“工具”菜单下的“规划求解”,在弹出的“规划求解参数”对话框输入各项参数:✓目标单元格选择B7✓问题类型选择“最大值”✓可变单元选择B6:C6✓约束条件选择B6:C6≥0;E2:E4≤D2:D4参数设置完毕,如图3:图33)点击“选项”,弹出“规划求解选项”对话框,选择“采用线性模型”、“假定非负”和“显示迭代结果”,说明要求求解的问题是线性模型且所求的变量必须为非负,如图4所示:图44)点击“确定”→“求解”,选择“运算结果报告”“敏感性报告”“极限值报告”三项,最后点击“确定”,输出结果:运算结果报告:敏感性报告:极限值报告:。
巧用Excel解线性方程组(没学matlab先用这个,呵呵)

线性方程组在工程技术、经济等领域有着广泛的应用。
许多实际问题可以归结为一个线性方程组的解,因此线性方程组的解法已成为广大工程技术人员、经济工作者必须掌握的知识。
在线性代数领域,Excel可以通过插入函数来直接求行列式的值,逆矩阵和矩阵的乘积。
但Excel并没有直接求解线性方程组的功能,本人发现Excel的规划求解可用来解线性方程组,现把这种方法介绍给大家。
例如要解线性方程组x1+x2+2x3+3x4=13x1-x2-x3-2x4=-42x1+3x2-x3-x4=-6x1+2x2+3x3-x4=-4可按如下的步骤来解这个方程组:1.打开Excel。
2.由于在本方程组中未知数有4个,所以预留4个可变单元格的位置A1-A4。
3.将活动单元格移至B1处,从键盘键入:=A1+A2+2*A3+3*A4:然后回车(此时B1显示0)。
即在B1处输入方程组中第一个方程等号左边的表达式。
4.在B2处从键盘键入:=3*A1-A2-A3-2*A4;然后回车(此时B2显示0)。
即在B2处输入方程组中第二个方程等号左边的表达式。
5.在B3处从键盘键入:=2*A1+3*A2-A3-A4;然后回车(此时B3显示0)。
即在B3处输入方程组中第三个方程等号左边的表达式。
6.在B4处从键盘键入:=A1+2*A2+3*A3-A4;然后回车(此时B4显示0)。
即在B4处输入方程组中第四个方程等号左边的表达式。
7.点击工具规划求解,出现规划求解参数对话框。
9.对话框中第三栏为:可变单元格;我们预留的可变单元格为A1-A4,所以在可变单元格框内键入 A 1: A 4。
10.对话框中最后一栏为:约束;首先点击添加按钮,屏幕出现添加约束对话框。
11.在添加约束对话框的单元格引用位置键入:B1;在中间的下拉式菜单中选取=;在约束值处键入:1;然后按添加按钮,屏幕出现空白的添加约束对话框。
12.在添加约束对话框的单元格引用位置键入:B2;在中间的下拉式菜单中选取=;在约束值处键入:-4;然后按添加按钮,屏幕出现空白的添加约束对话框。
如何利用Excel2016 软件的规划求解功能求解线性方程组

如何利用Excel2016 软件的规划求解功能求解线性方程组将线性方程组视为线性规划的特殊情形。
以方程组中一个方程作为目标函数;将方程组中各个方程作为约束条件;方程组中各个变量作为决策变量。
按Excel 软件的规划求解方法求解。
以4 元线性方程组为例:操作步骤如下:1.在A2:A7 单元格分别输入“方程1”、“方程2”、“方程3”、“方程4”、“可变单元”、“目标函数”;在B1:E1、G1、I1 单元格分别输入“系数1”、“系数2”、“系数3”、“系数4”、“约束表达式”、“常数”。
2.在B2:E5 区域中输入方程组各方程的系数,在I2:I5 单元格输入方程组各方程的常数。
3.将B6:E6 的4 个单元格设为决策变量单元。
4.在G2:G5 单元格设置约束表达式,在G2 中输入“=B2*B$6+C2*C$6+D2*D$6+E2*E$6”,选定G2 单元格,利用填充句柄向下填充至G5 单元格。
5.在B7:E7 单元格依次输入方程1 的各个系数。
6.在G7 单元格设置目标函数,输入“=B7*B$6+C7*C$6+D7*D$6+E7*E$6”,如下图所示:求解实施步骤如下。
1.对于Excel 2016,点击“开发工具”功能,点击其中的“Excel加载项”功能,找到“规划求解加载项”,在前边打对勾,点击“确定”。
点击后,找到“数据”功能,可以看到新增了“规划求解”功能。
在“设置目标单元格”栏中输入表示目标函数值的单元格地址$G$7(也可直接单击G7单元格),并在“等于”一栏中选择“值为”单选项,并在其右的文本栏中输入8。
在“可变单元格”一栏中输入决策变量的单元格地址“$B$6:$E$6”。
在“约束”中,通过“添加”按钮,在弹出的“添加约束”对话框中添加约束条件:在“单元格引用位置”输入表示“约束表达式”的单元格地址“$G$2:$G$5”,将其右的关系运算符选为“=”,在“约束值”栏中输入表示“常数”单元格地址“$I$2:$I$5”,单击“确定”。
利用Excel中的加载宏新加入的规划求解功能解决线性规划问题

利用Excel中的加载宏新加入的规划求解功能解决线性规划问题(郑来运PPT例1)
具体步骤如下:
1.打开Excel,单击“工具”弹出菜单,然后单击“加载宏”会出现如下画面:
选择“规划求解”点击确定,这样你的Excel就有了能解决线性规划问题的功能。
2.依次输入以下数据作为准备工作,如下图:图中用不同的色块表示约束条件和可变部分
3.在表中选中D2的位置然后点击函数,出现“插入函数”的弹出框后,选择”常用函数”中的”SUMPRODUCT”,
如下图所示。
点击确定后在弹出的对话框中array1选择B2:C2,在Array2中选择B6:C6,同时可以看到公式的生成。
用相同的方法让D3,D4,都相应填上公式
选中E6输入公式SUMPRODUCT(B5:C5,B6:C6)
4.单击“工具”选择“规划求解”设置目标单元格为E6,可变单元格为B6,C6,并添加约束条件,如下图
单击“求解”
选择保存规划求解结果,点击“确定”得到求解结果。
excel线性规划求解

To Calculate Total LHS, 選擇SUMPRODUCT
1 2
選定第一列範圍
選定第二列範圍
SUMPRODUCT(F6:G6,G3:G3)=F6*F3 + G6*G3
Then repeat the same steps for constraint #2 and #3
輸入Slack 公式
求最小值
1.輸入變數x1, x2的值所在的儲存格 2.『新增』限制式
1.輸入限制式左邊及右邊的儲存格 2.選擇適當的符號
左邊
右邊
1.選擇後之結果 2.按『新增』
1.此限制式表示 constraint #1and #2 2.再新增 constraint #3
Constraint #3的左邊,右邊及符號
1.前三項限制式(constraints#1,#2,#3) 2.選擇『選項』
新增 constraint #4: x1 >=0 constraint #5: x2 >=0
按『求解』後的結果
想將此圖轉貼於 EXCEL工作表上 1.選此按鈕 2.回到EXCEL
1.按貼上的按鈕或 『編輯』下的貼上, 即顯示圖案。 2. 將之移至適當位置
完成
线性规划求解
Linear Programming Problem
輸入公式Βιβλιοθήκη 列出EXCEL的求解方式: Min:Minimum Objective Value=F4*F3+G4*G3 LHS: Left Hand Side RHS: Right Hand Side Slack: RHS - LHS for “<=“ LHS- RHS for “>=“
EXCEL求解线性规划问题

约束右端值降低15时,目旳函数值旳变化量。
解:(1)最优解为x1=0, x2=12.4, x3=9.5
(2) x1旳目旳系数降低5,占允许降低旳百分比=5/∞=0%,x2 旳目旳系数增长4,占允许增长旳百分比=4/7.8=51.2%。
变化旳百分比和为51.2%,没有超出100%,所以最优解不变。
(3)第一资源约束右端值增长30,占允许增长旳30 /∞=0%, 第二资源约束右端值增长4 ,占允许增长旳4/15=26.7%,
•初值和终值分别指 单元格在此次求解 前旳数值和求解后 旳数值。
敏感性分析报告(1)
可变单元格中 • “单元格”指决策变量所在单元格旳地址 • “名字”是决策变量旳名称 • “终值”是决策变量旳终值,即最优值 • “递减成本”指最优解中档于0旳变量,相应旳目旳函数中旳系数
增长或降低多少,最优解不再为0 • “目旳式系数”目旳函数中旳系数,为已知条件 • “允许旳增量”与“允许旳减量”表达目旳函数中旳系数在增量
(1)引用旳类型
三种类型 :
相对引用、 绝对引用、混合引用
(2) 相对引用
格式: A3 、B6
使用相对引用后,系统将会记住建立公式旳单元格和被 引用旳单元格旳相对位置,在复制这个公式时,新旳公式单 元和被引用旳单元依然保持这种相对位置。
(3)绝对引用 格式:$a$3 $d$5
绝对引用是指被引用旳单元与引用旳公式单元旳位置 关系是绝正确,不论将这个公式复制到任何单元,公式所 引用旳还是原来单元格旳数据。
2) 在弹出旳对话框中旳“可用加载宏”列表框 中,选定待添加旳加载宏“规划求解”选项旁 旳复选框,然后单击“拟定”.单击“拟定” 后,“工具”菜单下就会出现一项“规划求解”
3. “规划求解”各参数设置
用Excel求解线性规划及线性方程组的方法

第23卷总第44期 西北民族学院学报(自然科学版)Vol.23,No.2 2002年6月 Journal of N orthw est Minorities U niversity(Natural Science)J une,2002用Excel求解线性规划及线性方程组的方法王培麟(番禺职业技术学院,广东番禺511483)[摘 要]对利用美国微软公司开发的Office组件中的电子表格软件Excel求解线性规划的方法给予了介绍,并将该功能给予扩充,给出了用该软件求解线性方程组的方法1[关键词]Excel;线性规划;求解方法[中图分类号]TP271+.7 [文献标识码]A [文章编号]1009-2102(2002)02-0037-03Excel是美国微软公司开发的Office组件中的电子表格软件,它具有强大的电子表格处理功能,使用户能够轻松地制作表格,并具有对数据进行检索、分类、筛选、排序、计算、分析与统计等功能1对大多数用户而言,也许更注重于Excel的表格功能,而对于它的计算功能,特别是数学计算功能可能就不是十分熟悉1本文将介绍用Excel解线性规划及线性方程组的方法与技巧11 用Excel解线性规划 用Excel解线性规划,必须在Excel系统中加载“规划求解”项目1如果没有,可以启动Excel软件,进入Excel用户界面,然后使用“工具”菜单下“加载宏”菜单项之“规划求解”子项,则可完成“规划求解”项的加载1下面通过例1的求解来说明使用Excel解线性规划问题的方法1例1 线性规划模型为:min s=2x1+7x2+4x3+9x4+5x51S.t 3x1+2x2+x3+6x4+18x5≥700x1+0.5x2+0.2x3+2x4+0.5x5≥300.5x1+x2+0.2x3+2x4+0.5x5=200x1≤50;x2≤60;x3≤50;x4≤70;x5≤40; x1,x2,x3,x4,x5≥01求解的具体方法为:首先要建立电子表格模型,输入如图1所示的工作表1工作表的格式不是固定不变的,可根据具体的需要进行调整1建立工作表的步骤为:1)确定一些单元格来代表决策变量,本例中x1,x2,…,x5为决策变量,需要将它们放到一些单元格中,称为可变单元格1一般地,可变单元格使用Excel的某行一块连续的区域,如[收稿日期]2002-04-01[作者简介]王培麟(1963—),男,副教授,硕士,主要从事数学和计算机方面的教学与研究1—73—本例中有5个决策变量,则可用区域B2:F2作为可变单元格(注意:B1:F1放的是说明,其下放的是可变单元格)1求解前,可变单元格放的是决策变量的初值,一般我们使用0作为初始值(此时,这些单元格不做任何输入,表示它们的初值为0)12)输入目标函数系数,本例中将它们输入在B3:F3单元格1图1 规划求解电子表格模型3)确定目标单元格,并在其中输入目标函数表达式1本例中取G3作为目标单元格1在G3中输入公式:=SUMPRODUCT($B$2:$F$2,B3:F3),它的含义是目标函数表达式:s=2x1,+7x2+4x3+9x4+5x51注意公式中决策变量单元格使用的是绝对地址,这样做是为了方便公式的复制14)输入约束条件左右两端的数据,并将目标函数单元格中的公式复制到目标函数下面相应的单元格中,本例中需将公式复制到G4∶G111通过以上步骤就建立好了电子表格模型,然后就可以进入规划的求解阶段1具体步骤为:1)选取菜单栏中“工具”菜单下的“规划求解”菜单项,弹出如图2所示的“规划求解参数”对话框12)在“设置目标单元格”文本框中输入目标单元格地址,本例中为G313)在“等于”项目上选定“最小值”选项14)在“可变单元格”文本框中输入可变单元格区域地址,本例中为B2:F215)单击“添加”按扭,弹出如图3所示的“添加约束”对话框1图2 规划求解对话框 图3 添加约束对话框——83在其中依次输入所有约束条件,每输入一个约束条件后,单击“添加”按扭,进入下一个约束条件的输入1本例中约束条件如下:G4:G5>=H4:H5;G6=H6;G7:G11<=H7:H11;B2:F2>=0然后按“确定”按扭,返回“规划求解参数”对话框16)单击“选项”按扭,弹出“规划求解”选项对话框,在该对话框中,可以输入“最长运算时间”、“迭代次数”、“精度”、“收敛度”等参数1如果无特殊需要,建议使用默认值1选取“采用线性模型”后按“确定”按扭返回,“规划求解”对话框17)单击“求解”按扭,规划求解软件开始运行,运算结束后,弹出“规划求解结果”对话框,通过该对话框可以保存求解结果,并给出运算结果报告,同时可变单元格和目标单元格分别显示最优解和最优值12 用Excel 解线性方程组 将线性方程组看作目标函数永远都为0,而约束条件均为等式的线性规划,则可以利用Excel 的规划求解功能求解线性方程组1下面通过例2的求解来说明使用Excel 解线性方程组的方法1例2 设所要求解的线性方程组为:x1-x 2+x 3-2x 4=22x 1-x 3+4x 4=43x 1+2x 2+x 3=-1-x 1+2x 2-x 3+2x 4=-41求解的具体方法为:首先要建立电子表格模型,输入如图4所示的工作表1图4 线性方程组求解电子表格模型注意到该表格中目标函数系数单元格中的系数全部为01在目标单元格中输入公式:=SUMPRODUCT ($B $2:$E $2,B3:E3),并将该公式复制到目标单元格下面相应的单元格中,本例中为F4:F7区域1然后选取菜单栏中“工具”菜单下的“规划求解”菜单项,弹出如图2所示的“规划求解参数”对话框1在该对话框中,设置目标单元格和可变单元格的方法与解线性规划是一样的,本例中,目标单元格为F3,可变单元格为(转第49页)311 与传统方法相比缺乏整体性 由于计算机屏幕内容的变换,与传统的板书相比,讲完课后回顾总结时,知识的整体性不够1因此,在教学设计过程中不可完全用计算机代替板书,应另外分几幅屏幕进行总结,以保证内容的完整性1312 教学中与学生眼神的交流相对减少 课堂上使用计算机需要教师操纵演示进度,教师被局限于电脑前控制鼠标,过多时间注视显示器,故与学生眼神交流相对减少1这样,一方面不易及时了解学生的反应;另一方面学生的注意力因缺少与教师的交流,降低了学习兴趣1因此,教师应适时离开电脑,适当采用教鞭指示,或穿插使用其他合适媒体,以充分发挥教师这一主要媒体的作用1对教学内容与教学手段的选择要严格把关,要注重教学效果,防止一味追求使用多媒体技术而忽视学生这一学习主体1313 学生长时间地注视容易产生视疲劳 由于放映条件要求室内光线不宜过亮,导致学生记录不便,再则长时间注视屏幕,学生容易疲劳1因此,对教学内容的选择要求针对性强,软件的制作要求精,其设计、编辑既要有知识,又要有趣味性,同时还应将色彩、动画、图片、声音与艺术有机地结合起来,以提高学生的学习兴趣1314 CA I课件的制作最好具有课堂教学与自学的双重性 用于教学要求交互性好,充分运用其超文本(无固定顺序的信息组织结构称为非线性,其中文字信息称超文本,如果还有其他媒体信息则称超媒体)功能,调用内容方便,以减少中间环节造成的信息丢失和失真,最好有学生自学的部分1综上所述,随着计算机的普及和应用1多媒体教学不仅是一种教学手段和方法,而且是一种独特的教学过程,充分体现了现代化的教学思想和教学理论的形成1我们相信开展多媒体教学将是实现药理教学中现代化教学的途径,将有着广阔的前景1当然,随着观念的发展、知识的更新和技术的进步,多媒体药理教学还会有许多问题存在,如教学软件的设计,教具的配套问题,如何恰当使用多媒体等,有待于进一步探索,力求在教学实践中获得最大的教学效果,真正体现教学现代化1(接第39页)B2:E2,但是“等于”项要设置为0,即线性方程组被看作是目标函数为0的线性规划,同时在填入约束条件时,所有的约束条件均是等式,该例中填入的约束条件为F4:F7=G4:G71最后按下“求解”按扭,运行完成后,在可变单元格中放的就是所求线性方程组的解13 结束语 本文给出了用Excel求解线性规划和线性方程组的一般方法及技巧,对于有最优解的线性规划和有解的线性方程组都可以进行求解,方法简捷、精度较高,适合于求解大型线性规划和高阶线性方程组1但是,对于有无穷多最优解的线性规划问题和有无穷多解的线性方程组,该方法只能给出其中的一个解,这一点在使用时应给予注意1参考文献:[1]李铁军.学用Excel2000[M].北京:清华大学出版社,19991[2]谢胜智,陈戈止1运筹学[M].成都:西南财经大学出版社,19991。
用Excel求解LP(线性规划)问题

▪
x1 , x2 ≥ 0
整理ppt
3
2、输入系数:
输入系数
▪ 在单元格A2:D4中分
别输入两个不等式约 束的系数与常数项,在 单元格A5:B5中分别
输入目标函数的两个 系数,在单元格A1:B1
中任意输入两个数分 别作为决策变量x1,x2 的值(如右图,C列暂 空) 。
整理ppt
4
3、LP模型的EXCEL输入(两 种方法)
▪ 在C2单元格中输入“=A2*A$1+B2*B$1”,并复 制到C3、C4、C5中,使它们分别变为 “=A3*A$1+B3*B$1” 、“=A4*A$1+B4*B$1”和 “=A5*A$1+B5*B$1”。
整理ppt
5
利用EXCEL的SUMPRODUCT 函数进行计算
▪ sumproduct是求两个数组(矩阵)相乘的结果 ▪ 数组的输入: ▪ “选中所有的数组元
②在“可变单元格(B)”栏后的空白中 填入$A$1:$B$1;
整理ppt
8
③光标指向“约束”栏,按“添加”, 出现“添加约束”对话框(如下图),
对话框“改变约束”
▪ 依次填入约束关系,每输完一条,按“添加”, 输入所有约束条件后,按“确定”,
整理ppt
9
又退回到下图状态,在下图中可以选 “更改”、“删除”、“全部重设” 来编辑约束条件及其他设置。
3、用Excel求解LP(线 性规划)问题
整理ppt
1
1、检查是否加载了宏“规划求解”? 即查看Excel窗口的“工具”菜单下 是否有“规划求解”菜单条?
▪ 找到与你的微机中已
在机房中,这装的Office版本一致
一步骤已经为的Office安装盘。单
Excel求解线性规划问题实验教程要点

数学与信息科学学院Excel求解线性规划问题实验教程二零一三零八月目录1.关于“规划求解” (1)2.如何加载“规划求解” (2)3.“规划求解”各参数解释和设置 (3)4.“规划求解”的步骤 (6)5.Excel求解线性规划问题 (8)6.Excel求解运输问题 (14)7.Excel求解目标规划问题 (18)8.Excel求解整数规划问题 (22)1.关于“规划求解”“规划求解”是Excel中的一个加载宏,借助“规划求解”,可求得工作表上某个单元格(被称为目标单元格)中公式(公式:单元格中的一系列值、单元格引用、名称或运算符的组合,可生成新的值。
公式总是以等号(=)开始)的最优值。
“规划求解”将对直接或间接目标单元格中公式相关联的一组单元格中的数值进行调整,最终在目标单元格公式中求得期望的结果。
“规划求解”通过调整所指定的可更改的单元格(可变单元格)中的值,从目标单元格公式中求得所需的结果。
在创建模型过程中,可以对“规划求解”中的可变单元格数值应用约束条件(约束条件:“规划求解”中设置的限制条件。
可以将约束条件应用于可变单元格、目标单元格或其它与目标单元格直接或间接相关的单元格。
而且约束条件可以引用其它影响目标单元格公式的单元格。
使用“规划求解”可通过更改其它单元格来确定某个单元格的最大值或最小值。
)Microsoft Excel的“规划求解”工具取自德克萨斯大学奥斯汀分校的Leon Lasdon 和克里夫兰州立大学的Allan Waren共同开发的Generalized Reduced Gradient(GRG2)非线性最优化代码。
线性和整数规划问题取自Frontline Systems公司的John Watson 和Dan Fylstra提供的有界变量单纯形法和分支边界法。
2.如何加载“规划求解”安装office的时候,系统默认的安装方式不会安装宏程序,需要用户根据自己的需求选择安装。
下面是加载“规划求解”宏的步骤:(1)在“工具”菜单上,单击“加载宏”。
【必须收藏】只用60秒就能解决的Excel线性规划,你却熬了整个通宵...

【必须收藏】只用60秒就能解决的Excel线性规划,你却熬
了整个通宵...
箭头处“蓝色字”,
每天学一个表格技能!
领导给小王同志12个金额,让他凑数据,凑成26005元和33459元。
左拼右凑这个金额,凑了一个通宵,还没凑对,十分着急,同事3分钟就给解决了
❶在Excel中调出线性规划我们在Excel选项里面,找到加载项然后勾选规划求解加载项,点击确定
❷我们在C1单元格输入公式:=SUMPRODUCT(A2:A13*B2:B13)
❸前面加载了加载项之后,在数据选项卡下,就有了规划求解进行相关设置后,运行得到最终的结果,操作动图如下所示:
其中的设置是,设置目标是C1单元格,目标值是26005,可变的单元格区域是B2:B13,遵守约束是B2:B13是二进制
最终B2:B13单元格中的数据为1的这些值累加起来,正好就能得到我们需要的26005了
剩下的数据正好就是33459元了。
模糊凑数据
如果给定的一个金额是系统也不可能准确的凑出来,Excel一直在计算的过程中的时候,可以随时按ESC退出
或者我们改变公式,使得进行模糊的凑数据接近这个值,我们现在要把这些数据最接近30000
我们可以在C1输入公式:=ABS(SUMPRODUCT(A2:A13,B2:B13)-30000)
然后在线性规划中的设置是:C1是最小值
然后运行,这个时候,会一直在那里转,这个时候,我们需要按ESC,然后
保留求解
得到了一组结果。
这个例子还是找到了正好等于30000的数据。
如果不等于的话,那么会得出一个最接近的结果。
当然,平时不用这个功能的时候,需要把这个功能给关闭了,否则每次打开Excel的速度会变慢一点。
线性规划的EXCEL求解

关于“规划求解选项”各可选项的说明 (3)
• 装入模型:输入对所要调入模型的引用 • 保存模型:将打开“保存模型”对话框, 输入模型的保存位置,只有当需要在工作 表上保存多个模型时,单击此命令,第一 个模型会自动保存。
一类特殊的线性规划问题:运输问 题
例1 某公司经销甲产品。它下设三个加工厂。 每日的产量分别是:A1为7吨,A2为4吨,A3为9吨。 该公司把这些产品分别运往四个销售点。各销售点 每日销量为:B1为3吨,B2为6吨,B3为5吨,B4为 6吨。已知从各工厂到各销售点的单位产品的运价如 下表所示。问该公司应如何调运产品,在满足各销 点的需要量的前提下,使总运费为最少。
( j 1, 2,3, 4) (i 1, 2,3)
这类问题,我们称之为运输问题。产量正好和销 量相等的运输问题称为产销平衡问题,产销平衡问题 有以下特征:
1. 平衡运输问题必有可行解,也必有最优解. 2. 平衡运输问题的约束方程系数矩阵 A 的所有各阶子 式只取 0,1 或 -1 三个值. 3. 如果平衡运输问题中的所有产量 ai 和销量 bj 4. 都是整数,那么,它的任一基可行解都是整数解.
线性规划问题的EXCEL求解
• 用EXCEL求解线性规 划问题前,需要在工 具菜单上选择加载宏: 弹出对话框
勾选规划工具,点击“确定”即可
• 若已加载过则无需再次加载。若安装不完全,也是无法加 载的,需要重新安装。 • 加载宏之后,工具菜单上即出现“规划求解”按钮,可以 用来求解许多规划问题,当然包含线性规划问题
例:某工厂生产三种产品,各种产品所需的原材料和设备 台时及能供给数量如下表所示,问如何安排生产利润最大?
甲
原材料 工时 单位利润 3 2 4
乙
利用Excel求解线性方程组

利用Excel求解线性方程组{x1+x2=7…① x1-x2=-5…②}实例
一、打开excel,点击菜单栏中的数据选项,如图1:
二、在单元格a1中输入x1,在单元格a2中输入x2,在单元格a3中输入x1+x2,在a4单元格中输入x1-x2,如下图:
三、在单元格b3输入公式”=b1+b2”,回车;在单元格b4输入公式”=b1-b2”,回车,如图:
四、将b3单元格设为活动单元格,再点击命令按钮“规划求解”,如图:
五、在规划求解参数对话框中,设置目标为b3单元格绝对地址,到目标值(选中)为7,通过更改可变单元格,用鼠标选中b1:b2单元格,遵守约束里点击添加按钮,在添加约束对话框中,单元格引用中选择b4单元格,点击下拉按钮选择”=”,在约束栏填-5,再点击确定,如图:
六、再点击求解,即可在b1和b2单元格中求出x1和x2的值,如图:
Δ若点击数据菜单项没有规划求解,怎么办呢?可在文件菜单项中的选项子菜单中点击加载项,选择规划求解加载项,然后点击确定即可,如图:。
利用excel求解线性规划问题讲解学习

利用e x c e l求解线性规划问题利用excel求解线性规划问题“规划求解”示例例1 美佳公司计划制造Ⅰ、Ⅱ两种家电产品。
已知各制造一件时分别占用的设备A,B的台时、调试工序时间及每天可用于这两种家电的能力、各售出一件时的获利情况,如下表所示。
问该公司应制造两种家电各多少件,使获取的利润为最大。
1.建立数学模型2. 打开excel,输入下列数据。
3、如何在工作表中设置问题条件?先设置目标单元格,即最大利润,把它放在E1单元格上,可变单元格放置计划生产Ⅰ和Ⅱ产品的件数,这里把它放在C10:D10区域。
F4:F6是约束单元格,要对它们的值进行约束。
单击E1,在编辑框输入如图所示的公式。
⎪⎪⎩⎪⎪⎨⎧>=<=+<=+<=+=,52426155..2max212121221xxxxxxxt sxxz注意,表示绝对引用的美元符号,可以单击F4功能键添加。
4、单击E4单击格式,在编辑栏上输入公式:=$C$4*$C$10+$D$4*$D$10。
绝对引用单元格有一个好处,显示的单元格位置变化时,引用的数据没改变。
5、单击E5单击格式,在编辑栏上输入公式:=$C$5*$C$10+$D$5*$D$10。
6、单击E6单击格式,在编辑栏上输入公式:=$C$6*$C$10+$D$6*$D$10。
7、如何使用规划求解功能?单击工具菜单,如果看不到规划求解选项不要慌,先选加载宏。
然后勾选规划求解,确定单击数据菜单——点击“模拟分析”——8、单击“规划求解”:指定目标单元格。
一种方法是先选中目标单元格E1,单击工具---规划求解。
另一种先单击工具---规划求解,再输入目标单元格名称。
输入可变单元格区域。
比较快的方法是,单击折叠框,用鼠标选中可变单元格区域:$C$11:$E$11。
注意勾选最大值哦。
设置目标: $E$1;点选“最大值”;设置:可变单元: $C$10:$D$109.设置条件不等式。
单击添加,单击折叠框,选择单元格和不等号,单击关闭窗口,接着添加另一个条件。
excel使用方程

在Excel中,您可以使用各种函数和公式来创建和解决方程。
以下是一些常用的方法:1.使用公式和函数:Excel有大量的内置函数,可以用于数学和逻辑运算。
例如,要计算两个数的和,您可以使用=SUM(A1, B1)。
2. 使用Solver:Solver是Excel中的一个插件,可以帮助您解决线性规划问题。
如果您的方程组是非线性的,Solver可能不适用。
但如果是线性方程组,Solver是一个很好的工具。
3. 使用数组公式:对于更复杂的方程,您可能需要使用数组公式。
数组公式可以处理多个值并返回一个结果。
例如,要计算一组数字的总和,您可以使用=SUM(A1:A10)。
4. 定义名称:如果您有一个非常长的公式或表达式,定义一个名称可以使其更易于阅读和管理。
例如,您可以创建一个名称来代表一个变量或常数,然后在您的公式中使用该名称。
5. 使用宏:如果您正在处理非常复杂的方程或重复的任务,编写VBA宏可能是一个好主意。
VBA是Excel 的编程语言,允许您自动化任务并创建自定义函数。
6. 使用外部工具:对于更高级的数学和统计问题,您可能需要使用其他工具或软件,如Python的NumPy库或R语言。
7. 求解线性方程组:如果您的方程组是线性的,您可以使用Excel的“数据”菜单中的“假设分析”工具来求解。
只需选择“线性方程组”并输入您的系数矩阵和常数向量即可。
8. 使用内建函数:Excel有大量的内建函数,可以帮助您进行各种数学和逻辑运算。
例如,ABS函数返回一个数的绝对值,SQRT函数返回一个数的平方根,等等。
9. 利用图表:对于某些方程(如二次方程),您可以使用Excel的图表功能来找到根。
只需绘制方程的图,然后找到与x轴交点的y值即可找到根。
10. 自定义函数:对于非常复杂的任务,您可能需要编写自己的VBA函数。
通过VBA,您可以创建自己的函数并在Excel中使用它们。
记住,对于复杂的数学问题,可能需要结合多种方法来找到解决方案。
用excel计算线性规划

用Excel 2007求解线性规划(1)
安装Excel规划求解加载项:Office按钮——Excel选项—— 加载项——转到——加载宏——规划求解加载项
用Excel 2007求解线性规划(1)
在“数据”选项卡中出现带有“规划求解”按钮的“分析”组
用Excel 2007求解线性规划(2)
设计电子表格
技巧:也可以在单元格D5中输入公式: =SUMPRODUCT(B5:C5,$B$12:$C$12)
用Excel 2007求解线性规划(3)
应用规划求解工具:数据——分析——规划求解
用Excel 2007求解线性规划(3)
应用规划求解工具:规划求解参数——规划求解选项
用Excel 2007求解线性规划(4)
求解结果
用Excel 2003求解线性规划(2)
设计电子表格
目标函数和约束 条件的系数
用Excel 2003求解线性规划(2)
设计电子表格
输入公式
输入公式
用Excel 2003求解线性规划(3)
应用规划求解工具: B10 -菜单栏-工具-规划求解
目标函数单元格 目标函数类型
变量单元格
添加约束
用Excel 2003求解线性规划(3)
用Excel 2003求解线性规划
求解以下这个线性规划问题
max 600 x 1000 y
10 x 4 y 300 5 x 4 y 200 4 x 9 y 360 x0 y0
用Excel 2003求解线性规划(1)
安装线性规划加载项: 菜单栏——工具——工具——加载宏——规划求解
特殊饲料的营养要求是至少30%的蛋白质和至多5%的 纤维。该农场希望确定每天最小成本的饲料配制。
用EXCLE求解线性规划问题

4.在约束条件左端项系数存放单元格右边的单元格中输入约束 条件左端项的计算公式,计算出约束条件左端项对应于目前决 策变量的函数值。 5.在步骤4的的数据右边输入约束条件中右端项(即常数项)
6.确定目标函数值存放单元格,并在该单元格中输入目标函数 值电容计算公式。
例.求下列线性规划问题
SUMPRODUCT(B3:C3,B10:C10)
例.求解如下的线性规划问题 某企业的产品生产数据如下
分共厂 门 生产时间 窗 0 2小时 2小时 500 4小时 12小时 18小时 每周可利用时间
s.t
第一步:选择决策变量单元格 决策变量的一般初始值赋0。
第二步:目标单元格,用函数公式表示。
用EXCLE求解线性规划问题
1.“线性规划求解”的安装(文件
选项)
加载项 规划求解加载项 选择在数据加载项
转到
加载数据规划求解选项以后,在“数据”菜单中就 会出现“规划求解”
线性规划求解的步骤:
1.确定目标函数系数存放单元格,并在这些单元格中输入目标 函数系数。 2.确定决策变量存放单元格,并任意输入一组数据; 3.确定约束条件中左端项系数存放单元格,并输入约束条件左 端项系数;
G 11 Total Proft 12 =sumproduct(C4:D4,C12:D12)
第三步:约束条件左边项用函数表示
5 6 7 8 9
E Hours Used SUMPRODUCT(C7:D7,$C$12:$D$12) SUMPRODUCT(C8:D8,$C$12:$D$12) SUMPRODUCT(C9:D9,$C$12:$D$12)
第四步:激活规划求解,确定可变单元格和目标 单元格
第五步:增加约束 条件
Excel2010 线性规划求解用法
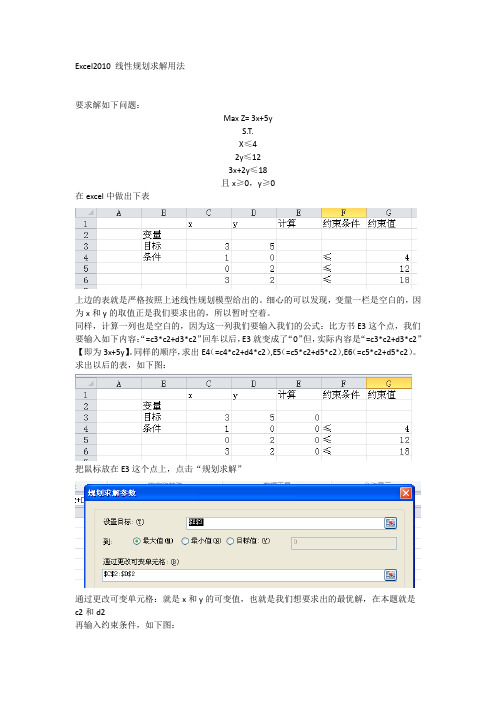
Excel2010 线性规划求解用法
要求解如下问题:
Max Z= 3x+5y
S.T.
X≤4
2y≤12
3x+2y≤18
且x≥0,y≥0
在excel中做出下表
上边的表就是严格按照上述线性规划模型给出的。
细心的可以发现,变量一栏是空白的,因为x和y的取值正是我们要求出的,所以暂时空着。
同样,计算一列也是空白的,因为这一列我们要输入我们的公式:比方书E3这个点,我们要输入如下内容:“=c3*c2+d3*c2”回车以后,E3就变成了“0”但,实际内容是“=c3*c2+d3*c2”【即为3x+5y】。
同样的顺序,求出E4(=c4*c2+d4*c2),E5(=c5*c2+d5*c2),E6(=c5*c2+d5*c2)。
求出以后的表,如下图:
把鼠标放在E3这个点上,点击“规划求解”
通过更改可变单元格:就是x和y的可变值,也就是我们想要求出的最优解,在本题就是
c2和d2
再输入约束条件,如下图:
因为我们把公式都已经算出来了(E4,E5,E6)因此,直接引用,同时别忘记x和y的取值也要进行约束,都是≥0的。
都设定好了,点击求解
再看我们的excel表格
得出最优解为x=2,y=6
计算完毕。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23卷总第44期 西北民族学院学报(自然科学版)Vol.23,No.2 2002年6月 Journal of N orthw est Minorities U niversity(Natural Science)J une,2002
用Excel求解线性规划及线性方程组的方法
王培麟
(番禺职业技术学院,广东番禺511483)
[摘 要]对利用美国微软公司开发的Office组件中的电子表格软件Excel求解线性规划的方法给予了介绍,并将该功能给予扩充,给出了用该软件求解线性方程组的方法1
[关键词]Excel;线性规划;求解方法
[中图分类号]TP271+.7 [文献标识码]A [文章编号]1009-2102(2002)02-0037-03
Excel是美国微软公司开发的Office组件中的电子表格软件,它具有强大的电子表格处理功能,使用户能够轻松地制作表格,并具有对数据进行检索、分类、筛选、排序、计算、分析与统计等功能1对大多数用户而言,也许更注重于Excel的表格功能,而对于它的计算功能,特别是数学计算功能可能就不是十分熟悉1本文将介绍用Excel解线性规划及线性方程组的方法与技巧1
1 用Excel解线性规划
用Excel解线性规划,必须在Excel系统中加载“规划求解”项目1如果没有,可以启动Excel软件,进入Excel用户界面,然后使用“工具”菜单下“加载宏”菜单项之“规划求解”子项,则可完成“规划求解”项的加载1
下面通过例1的求解来说明使用Excel解线性规划问题的方法1
例1 线性规划模型为:
min s=2x1+7x2+4x3+9x4+5x51
S.t 3x1+2x2+x3+6x4+18x5≥700
x1+0.5x2+0.2x3+2x4+0.5x5≥30
0.5x1+x2+0.2x3+2x4+0.5x5=200
x1≤50;x2≤60;x3≤50;x4≤70;x5≤40; x1,x2,x3,x4,x5≥0
1
求解的具体方法为:首先要建立电子表格模型,输入如图1所示的工作表1
工作表的格式不是固定不变的,可根据具体的需要进行调整1建立工作表的步骤为:
1)确定一些单元格来代表决策变量,本例中x1,x2,…,x5为决策变量,需要将它们放到一些单元格中,称为可变单元格1一般地,可变单元格使用Excel的某行一块连续的区域,如
[收稿日期]2002-04-01
[作者简介]王培麟(1963—),男,副教授,硕士,主要从事数学和计算机方面的教学与研究1
—
7
3
—
本例中有5个决策变量,则可用区域B2:F2作为可变单元格(注意:B1:F1放的是说明,其下放的是可变单元格)1求解前,可变单元格放的是决策变量的初值,一般我们使用0作为初始值(此时,这些单元格不做任何输入,表示它们的初值为0)1
2)输入目标函数系数,本例中将它们输入在B3:F3单元格1
图1 规划求解电子表格模型
3)确定目标单元格,并在其中输入目标函数表达式1本例中取G3作为目标单元格1在G3中输入公式:=SUMPRODUCT($B$2:$F$2,B3:F3),它的含义是目标函数表达式:
s=2x1,+7x2+4x3+9x4+5x51
注意公式中决策变量单元格使用的是绝对地址,这样做是为了方便公式的复制1
4)输入约束条件左右两端的数据,并将目标函数单元格中的公式复制到目标函数下面相应的单元格中,本例中需将公式复制到G4∶G111
通过以上步骤就建立好了电子表格模型,然后就可以进入规划的求解阶段1具体步骤为:
1)选取菜单栏中“工具”菜单下的“规划求解”菜单项,弹出如图2所示的“规划求解参数”对话框1
2)在“设置目标单元格”文本框中输入目标单元格地址,本例中为G31
3)在“等于”项目上选定“最小值”选项1
4)在“可变单元格”文本框中输入可变单元格区域地址,本例中为B2:F21
5)单击“添加”按扭,弹出如图3所示的“添加约束”对话框1
图2 规划求解对话框 图3 添加约束对话框
—
—
8
3
在其中依次输入所有约束条件,每输入一个约束条件后,单击“添加”按扭,进入下一个约束条件的输入1本例中约束条件如下:
G4:G5>=H4:H5;G6=H6;G7:G11<=H7:H11;B2:F2>=0
然后按“确定”按扭,返回“规划求解参数”对话框1
6)单击“选项”按扭,弹出“规划求解”选项对话框,在该对话框中,可以输入“最长运算时间”、“迭代次数”、“精度”、“收敛度”等参数1如果无特殊需要,建议使用默认值1选取“采用线性模型”后按“确定”按扭返回,“规划求解”对话框1
7)单击“求解”按扭,规划求解软件开始运行,运算结束后,弹出“规划求解结果”对话框,通过该对话框可以保存求解结果,并给出运算结果报告,同时可变单元格和目标单元格分别显示最优解和最优值1
2 用Excel 解线性方程组
将线性方程组看作目标函数永远都为0,而约束条件均为等式的线性规划,则可以利用Excel 的规划求解功能求解线性方程组1
下面通过例2的求解来说明使用Excel 解线性方程组的方法1
例2 设所要求解的线性方程组为:x
1-x 2+x 3-2x 4=2
2x 1-x 3+4x 4=4
3x 1+2x 2+x 3=-1-x 1+2x 2-x 3+2x 4=-4
1
求解的具体方法为:首先要建立电子表格模型,输入如图4所示的工作表1
图4 线性方程组求解电子表格模型
注意到该表格中目标函数系数单元格中的系数全部为01
在目标单元格中输入公式:=SUMPRODUCT ($B $2:$E $2,B3:E3),并将该公式复制到目标单元格下面相应的单元格中,本例中为F4:F7区域1然后选取菜单栏中“工具”菜单下的“规划求解”菜单项,弹出如图2所示的“规划求解参数”对话框1在该对话框中,设置目标单元格和可变单元格的方法与解线性规划是一样的,本例中,目标单元格为F3,可变单元格为
(转第49页)
311 与传统方法相比缺乏整体性 由于计算机屏幕内容的变换,与传统的板书相比,讲完课后回顾总结时,知识的整体性不够1因此,在教学设计过程中不可完全用计算机代替板书,应另外分几幅屏幕进行总结,以保证内容的完整性1
312 教学中与学生眼神的交流相对减少 课堂上使用计算机需要教师操纵演示进度,教师被局限于电脑前控制鼠标,过多时间注视显示器,故与学生眼神交流相对减少1这样,一方面不易及时了解学生的反应;另一方面学生的注意力因缺少与教师的交流,降低了学习兴趣1因此,教师应适时离开电脑,适当采用教鞭指示,或穿插使用其他合适媒体,以充分发挥教师这一主要媒体的作用1对教学内容与教学手段的选择要严格把关,要注重教学效果,防止一味追求使用多媒体技术而忽视学生这一学习主体1
313 学生长时间地注视容易产生视疲劳 由于放映条件要求室内光线不宜过亮,导致学生记录不便,再则长时间注视屏幕,学生容易疲劳1因此,对教学内容的选择要求针对性强,软件的制作要求精,其设计、编辑既要有知识,又要有趣味性,同时还应将色彩、动画、图片、声音与艺术有机地结合起来,以提高学生的学习兴趣1
314 CA I课件的制作最好具有课堂教学与自学的双重性 用于教学要求交互性好,充分运用其超文本(无固定顺序的信息组织结构称为非线性,其中文字信息称超文本,如果还有其他媒体信息则称超媒体)功能,调用内容方便,以减少中间环节造成的信息丢失和失真,最好有学生自学的部分1
综上所述,随着计算机的普及和应用1多媒体教学不仅是一种教学手段和方法,而且是一种独特的教学过程,充分体现了现代化的教学思想和教学理论的形成1我们相信开展多媒体教学将是实现药理教学中现代化教学的途径,将有着广阔的前景1当然,随着观念的发展、知识的更新和技术的进步,多媒体药理教学还会有许多问题存在,如教学软件的设计,教具的配套问题,如何恰当使用多媒体等,有待于进一步探索,力求在教学实践中获得最大的教学效果,真正体现教学现代化1
(接第39页)
B2:E2,但是“等于”项要设置为0,即线性方程组被看作是目标函数为0的线性规划,同时在填入约束条件时,所有的约束条件均是等式,该例中填入的约束条件为F4:F7=G4:G71最后按下“求解”按扭,运行完成后,在可变单元格中放的就是所求线性方程组的解1
3 结束语
本文给出了用Excel求解线性规划和线性方程组的一般方法及技巧,对于有最优解的线性规划和有解的线性方程组都可以进行求解,方法简捷、精度较高,适合于求解大型线性规划和高阶线性方程组1但是,对于有无穷多最优解的线性规划问题和有无穷多解的线性方程组,该方法只能给出其中的一个解,这一点在使用时应给予注意1
参考文献:
[1]李铁军.学用Excel2000[M].北京:清华大学出版社,19991
[2]谢胜智,陈戈止1运筹学[M].成都:西南财经大学出版社,19991。
