《线性代数》同济大学版课后习题答案详解
《线性代数》同济大学第四版课后答案

《线性代数》同济⼤学第四版课后答案线性代数同济⼤学第四版课后答案习题⼀习题⼀1-5 SslO(3)1 1 1 ab c a2 b2 c2^c^+cc^+ab^-ac^-bc^-cb2 -(a-b)(b-c)(c-a).(4)X v X+ V解v x+ V X■:v+v * V⼆MvH") i+i:论+i ')+(.r+v) VX-1'34-C T+I)3-.T32解逆序数为4: 4h 43, 42. 32,3解逆序数为5: 3 2.3 L 42. 4 1,2 L4L利⽤对⾓线法则计算下列三阶⾏列式:2 0 1-18 3(1) 1(1)1+■XVX1cV-+VT1⽅沪=3.n (.Y+>)-i^3- 3.T2=-2(.?+V^⼯按⾃然数从⼩到⼤为标准次序.求下列各排列的逆序数:(1)1 23 4(2)4 13 2(3)34 2 1(4)24 1 3(5)1 3 …(2沪1) 2 4 …O);(6)1 3 ?… (⼒—1) (2?z) (2n-2)…* ⼯(1)解逆序数为0解逆序数为3: 2 1.4 1.4 3-(5)解逆序数为观驴:32(1 个)5 2,5 4(2 个)7 2, 7 4. 7 6(3 个)(”1)2, 011)4, (”1)6,…为(”1)(”2) (n-1 个)(6)解逆序数为乃(『Li):32(1 个)5 2,5 4(2 ^t) (2n-1)2, (2n-l)4, (”1)6,…、(2/L1)(2/L2)(n-l个)42(1 个)6 2,6 4(2 个)(5)2, (2M)4, (2n)6,…,(2n)(2n-2) (n-1个)3.写出四阶⾏列式中含有因⼦GU723的项.解含因⼦①畑的项的⼀般形式为(-])%的冰X町其中帀是2和4构成的排列,这种排列共有两个,即24和42.所以含因⼦a^a23的项分别是(-1 )衍1似23他刃44⼆(⼀1 )^11^32^44=-^!凶曲的轴(⼀1 )%1攸曲琢也⼫(T )%1⼝滋34偽⼫&1也刃曲42?4. 计算下列各⾏列式:4 12 4(iho 5 2 0; 0 1172 14 1 (2) ? ¥ ? i ;⼀ ab ac ae(3) bd ⼀ cd de cf -ef *94 -1 109 9 10— 1 2 -20 0 —2 =0-[0 3 14 勺+扭3 P 17 143+ 4O 42021Ci0 00 —1 0 0 -i1 c o -1 d-1230411100上q42 07 202112 5 141100解\170200-1-2102 02 4 9-36172023 15119-9-O--00-0 0 4 23 011-12 0「-310—12 3 O 4 1210■1-12 O解\1-ab ac ae-bee 解bd -cd de =acif b -c eif 灯-叮b c -ehl 1 1 / =adfbce 1-11 = Aabcdef |1 1 -1 (4)l+c/b a 00+此2〔1+甸 a0)(—严才打⼀冷55.证明:cP ab b 1(1) 2a c/+b 2b 1 1 1=(?-/>)3, 证明a obb \c 2-c A ⼔2 ab —R ⼣—⼚F2r/ a+b 勿 2z? b-a 2b-2a 1 1 1 | GT 11 0 0 cix+bv av+bz ciz+bx v v zc/y+bz az+bx ax+by-(q 3+b 3)y ⼆ x az+bx ay+bv av+bz z A VA --!A-oo 1<7 o1 c - 1Ty ⼀o d -l oo0 1+ab cioo 1〃15 B-loTooad \+cd 0n 计呼豐严⽫cdTLab-ci 1 b-a l^-a 2 2b-2a⼆@-a)(b-氓件 J(⼚Tp证明ax+bv av+bz az+bx civ+bz az+bx cix+bv■6C +bx ay+by ay+ bzx ciy+bz ciz+bx y ciy+bz az+bx=a v1az+bx ca+bv / ■<+b z az+bx ca+bv⼆ax+by ay+bz x ax+by ay+bz .x ay+bz z v⼆ciz+bx y az+bx x■JV g+by⼆crx+bv v V v av+ bzilr-'x y z y z x=a3y⼆x+b3⼆Y yz x y\x v zX V⼆,v V z-d y ⼆Y +⼣V S Xar ⼆X V ■■<⼆H ⼆x\z x va2(“+1)2 (c+2)2 (n+3¥⑶b2 (〃+l『0+2)2(b+3Y=0;c2 (c+1)2 (c+2)3 (c+3)2 d2 (H+l¥ (d+2)2 (〃+3⼙—1—iu CM⼨*-+scP-£cl J1+冷£r +Krl E + w S +U ;+-+gI+吕C(E+P)令+⼷)N+m"(E ) c (cl+9) 泾⼗ q)+0 N+q)(R £1bz)2i47/2(5)10 0 b(b-ci)0 b 2(b 2-a 2) c 2(c 1 d-a d(d - a) )d 2(d 2-a 2) 1 1 =(b - a)(c - a)(d-a) b _ c b-a1 c-a c(c ⼀ a)2-a 7-(b ⼀ ci)(c ⼀ ci)(ci ⼀ ct)5b 2(b^ra)c 2(c-\-ci)d 2{d-Va\ R 1 1 6 c-b d-b 0 c(c-b)(c+b^d) d(d-b)(d+b+a)-(b - a)(c ⼀ c)(" - a)(c — Z?)(rf- b)1 1 咚+b+a) d(d+b+ci)oo ⼆X“~h(7 [T 丫+ * … ⼗亿科证明⽤数学归纳法证明.当⼼2时"2⼆诊⼗g+%命题成⽴?假设对于(7L1)阶⾏列式命题成⽴.即⼑刑_1=* ?+⼗岛_2⼯+馮_”则及按第⼀列展开更有—1 0 ■…0 2-1 OO2⼆也门乜(-1严上卫⼆1 1 …⼆xQ 起⼀1+。
《线性代数》同济大学版 课后习题答案详解

|2A1|(2)3|A1|8|A|18216
17设矩阵A可逆证明其伴随阵A*也可逆且(A*)1(A1)*
证明由 得A*|A|A1所以当A可逆时有
|A*||A|n|A1||A|n10
从而A*也可逆
因为A*|A|A1所以
(A*)1|A|1A
又 所以
(A*)1|A|1A|A|1|A|(A1)*(A1)*
5设 问
(1)ABBA吗?
解ABBA
因为 所以ABBA
(2)(AB)2A22ABB2吗?
解(AB)2A22ABB2
因为
但
所以(AB)2A22ABB2
(3)(AB)(AB)A2B2吗?
解(AB)(AB)A2B2
因为
而
故(AB)(AB)A2B2
6举反列说明下列命题是错误的
(1)若A20则A0
解取 则A20但A0
解 令
则
故
29设n阶矩阵A及s阶矩阵B都可逆求
(1)
解设 则
由此得
所以
(2)
解设 则
由此得
所以
30求下列矩阵的逆阵
(1)
解设 则
于是
(2)
解设 则
第三章 矩阵的初等变换与线性方程组
1把下列矩阵化为行最简形矩阵
(1)
解 (下一步r2(2)r1r3(3)r1)
~ (下一步r2(1)r3(2))
~ (下一步r3r2)
(3)
解 (下一步r12r4r22r4r33r4)
~ (下一步r23r1r32r1)
~ (下一步r216r4r316r2)
~
~
矩阵的秩为3 是一个最高阶非零子式
10设A、B都是mn矩阵证明A~B的充分必要条件是R(A)R(B)
《线性代数》同济大学版 课后习题答案详解讲解学习

《线性代数》同济大学版 课后习题答案详解第一章 行列式1. 利用对角线法则计算下列三阶行列式:(1)381141102---;解381141102--- =2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4.(2)ba c a cb cb a ;解ba c a cbc b a =acb +bac +cba -bbb -aaa -ccc =3abc -a 3-b 3-c 3.(3)222111c b a cb a ;解222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).(4)yx y x x y x y y x y x +++.解yx y x x y x y y x y x +++ =x (x +y )y +yx (x +y )+(x +y )yx -y 3-(x +y )3-x 3 =3xy (x +y )-y 3-3x 2 y -x 3-y 3-x 3 =-2(x 3+y 3).2. 按自然数从小到大为标准次序, 求下列各排列的逆序数: (1)1 2 3 4; 解 逆序数为0 (2)4 1 3 2;解 逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解 逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解 逆序数为3: 2 1, 4 1, 4 3. (5)1 3 ⋅ ⋅ ⋅ (2n -1) 2 4 ⋅ ⋅ ⋅ (2n ); 解 逆序数为2)1(-n n :3 2 (1个) 5 2, 5 4(2个) 7 2, 7 4, 7 6(3个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n -1)2, (2n -1)4, (2n -1)6, ⋅ ⋅ ⋅, (2n -1)(2n -2) (n -1个)(6)1 3 ⋅ ⋅ ⋅ (2n -1) (2n ) (2n -2) ⋅ ⋅ ⋅ 2. 解 逆序数为n (n -1) : 3 2(1个) 5 2, 5 4 (2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n -1)2, (2n -1)4, (2n -1)6, ⋅ ⋅ ⋅, (2n -1)(2n -2) (n -1个) 4 2(1个) 6 2, 6 4(2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n )2, (2n )4, (2n )6, ⋅ ⋅ ⋅, (2n )(2n -2) (n -1个) 3. 写出四阶行列式中含有因子a 11a 23的项. 解 含因子a 11a 23的项的一般形式为(-1)t a 11a 23a 3r a 4s ,其中rs 是2和4构成的排列, 这种排列共有两个, 即24和42. 所以含因子a 11a 23的项分别是(-1)t a 11a 23a 32a 44=(-1)1a 11a 23a 32a 44=-a 11a 23a 32a 44, (-1)t a 11a 23a 34a 42=(-1)2a 11a 23a 34a 42=a 11a 23a 34a 42. 4. 计算下列各行列式:(1)7110025*******214; 解71100251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-; 解 2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r 000003212213041214=--=====r r . (3)efcf bf decd bd ae ac ab ---;解ef cf bf de cd bd ae ac ab ---ec b e c b e c b adf ---= abcdef adfbce 4111111111=---=.(4)dc b a100110011001---. 解d c b a 100110011001---dc b aab ar r 10011001101021---++===== dc a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ad a ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1.5. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 .(2)yx z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++ bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bx az z y b y by ax z x bx az y z bz ay x a +++++++=22zy x y x z x z y b y x z x z y z y x a 33+=y x z x z y z y x b y x z x z y z y x a 33+=yx z x z y z y x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;证明2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2, c 2-c 1得)5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2得) 022122212221222122222=++++=d d c c b b a a .(4)444422221111d c b a d c b a d c b a=(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d );证明444422221111d c b a d c b a d c b a)()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b ad a c a b ---------=)()()(111))()((222a d d a c c a b b d c b a d a c a b +++---=))(())((00111))()((a b d b d d a b c b c c bd b c a d a c a b ++-++------=)()(11))()()()((a b d d a b c c b d b c a d a c a b ++++-----==(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ).(5)1221 1 000 00 1000 01a x a a a a x x x n n n+⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅---Λ=x n+a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .证明 用数学归纳法证明. 当n =2时,2121221a x a x a x a x D ++=+-=, 命题成立.假设对于(n -1)阶行列式命题成立, 即 D n -1=x n -1+a 1 x n -2+ ⋅ ⋅ ⋅ +a n -2x +a n -1, 则D n 按第一列展开, 有11100 100 01)1(11-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--+=+-x x a xD D n n n n =xD n -1+a n =x n +a1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .因此, 对于n 阶行列式命题成立.6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90︒、或依副对角线翻转, 依次得n nn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nn n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= , 11113 a a a a D n n nn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(--==, D 3=D .证明 因为D =det(a ij ), 所以nnn n n n nnnn a a a a a a a a a a D 2211111111111)1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=- ⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--=-- )1()1(331122111121nnn n nn n n a a a a a a a aD D n n n n 2)1()1()2( 21)1()1(--+-+⋅⋅⋅++-=-=.同理可证nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=- )1(11112)1(2D D n n T n n 2)1(2)1()1()1(---=-=.D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k 为k 阶行列式):(1)aaD n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0;解aa a a a D n 0 0010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开))1()1(10 00000 0000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a aan n n nn a a a +⋅⋅⋅-⋅-=--+)2)(2(1 )1()1(=a n -a n -2=a n -2(a 2-1).(2)xa a a x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得ax x a ax x a a x x a aa a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0 , 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n -1.(3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n n n n n ; 解 根据第6题结果, 有nnn n n n n n n n a a a n a a a n a a aD )( )1()( )1( 1111)1(1112)1(1-⋅⋅⋅--⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=---++此行列式为范德蒙德行列式.∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++---=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+-++-⋅-⋅-=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+-=11)(j i n j i .(4)n nnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112;解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开)nn n n n nd d c d c b a b a a 00011111111----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=Λ0)1(1111111112c d c d c b a b a b nn n n n nn ----+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-+.再按最后一行展开得递推公式D 2n =a n d n D 2n -2-b n c n D 2n -2, 即D 2n =(a n d n -b n c n )D 2n -2. 于是∏=-=ni i i i i n D c b d a D 222)(.而111111112c b d a d c b a D -==,所以∏=-=n i i i i i n c b d a D 12)(.(5) D =det(a ij ), 其中a ij =|i -j |; 解 a ij =|i -j |,4321 4 01233 10122 21011 3210)det(⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅==n n n n n n n n a D ij n0 4321 1 11111 11111 11111 1111 2132⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅--⋅⋅⋅-=====n n n n r r r r152423210 22210 02210 00210 0001 1213-⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅-+⋅⋅⋅+=====n n n n n c c c c =(-1)n -1(n -1)2n -2.(6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n ≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121nn n n a a a a a a a a a c c c c +-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=====--10 0001 000 100 0100 0100 0011332212132 1111312112111011 000 00 11000 01100 001 ------+-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅⋅⋅⋅=nn n a a a a a a a a∑=------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 00010 000 00 10000 01000 001)11)((121∑=+=ni in a a a a Λ.8. 用克莱姆法则解下列方程组:(1)⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解 因为14211213513241211111-=----=D , 142112105132412211151-=------=D ,28411235122412111512-=-----=D , 42611135232422115113-=----=D ,14202132132212151114=-----=D , 所以111==D D x , 222==D D x , 333==D D x , 144-==DDx . (2)⎪⎪⎩⎪⎪⎨⎧=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解 因为665510006510006510065100065==D , 15075100165100065100650000611==D ,11455101065100065000601000152-==D ,70351100650000601000051001653==D , 39551000601000051000651010654-==D ,2121105100065100651100655==D , 所以66515071=x , 66511452-=x , 6657033=x , 6653954-=x , 6652124=x .9. 问λ, μ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 系数行列式为μλμμμλ-==1211111D .令D =0, 得 μ=0或λ=1.于是, 当μ=0或λ=1时该齐次线性方程组有非零解.10. 问λ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解?解 系数行列式为λλλλλλλ--+--=----=101112431111132421D=(1-λ)3+(λ-3)-4(1-λ)-2(1-λ)(-3-λ) =(1-λ)3+2(1-λ)2+λ-3. 令D =0, 得λ=0, λ=2或λ=3.于是, 当λ=0, λ=2或λ=3时, 该齐次线性方程组有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换. 解 由已知:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A TB .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T.4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635.(2)⎪⎪⎭⎫⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫ ⎝⎛---=632142.(4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ;解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x 322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA . 因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B )2=A 2+2AB +B 2吗? 解 (A +B )2≠A 2+2AB +B 2. 因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610,所以(A +B )2≠A 2+2AB +B 2.(3)(A +B )(A -B )=A 2-B 2吗?解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.6. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0; 解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ; 解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E .(3)若AX =AY , 且A ≠0, 则X =Y . 解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k. 解⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k .8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k.解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ,⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA k k kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k kk k k k k k A A A ⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵. 证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA . 证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以(AB )T =(BA )T =A T B T =AB , 即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB )T =AB , 所以 AB =(AB )T =B T A T =BA . 11. 求下列矩阵的逆矩阵: (1)⎪⎭⎫ ⎝⎛5221; 解⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故*||11A A A =-⎪⎭⎫ ⎝⎛--=1225.(2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解 ⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A |=1≠0, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,所以 *||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos . (3)⎪⎪⎭⎫⎝⎛---145243121;解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以*||11A A A =-⎪⎪⎪⎭⎫⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a O 0021(a 1a 2⋅ ⋅ ⋅a n≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A O 0021, 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211O . 12. 解下列矩阵方程: (1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ;解⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232.(2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ;解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ; 解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X .解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012.13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 因为A k =O , 所以E -A k =E . 又因为E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1),所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O ,有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E ⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1,)3(41)2(1A E E A -=+-. 16. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|. 解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A |-1=-8⨯2=-16.17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)-1=(A -1)*. 证明 由*||11A A A =-, 得A *=|A |A -1, 所以当A 可逆时, 有|A *|=|A |n |A -1|=|A |n -1≠0, 从而A *也可逆.因为A *=|A |A -1, 所以 (A *)-1=|A |-1A . 又*)(||)*(||1111---==A A A A A , 所以(A *)-1=|A |-1A =|A |-1|A |(A -1)*=(A -1)*. 18. 设n 阶矩阵A 的伴随矩阵为A *, 证明: (1)若|A |=0, 则|A *|=0; (2)|A *|=|A |n -1. 证明(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)-1=E , 由此得 A =A A *(A *)-1=|A |E (A *)-1=O ,所以A *=O , 这与|A *|≠0矛盾,故当|A |=0时, 有|A *|=0. (2)由于*||11A A A =-, 则AA *=|A |E , 取行列式得到|A ||A *|=|A |n . 若|A |≠0, 则|A *|=|A |n -1;若|A |=0, 由(1)知|A *|=0, 此时命题也成立. 因此|A *|=|A |n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E )B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E AB ⎪⎪⎭⎫⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E )B =A 2-E , 即 (A -E )B =(A -E )(A +E ).因为01001010100||≠-==-E A , 所以(A -E )可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B . 解 由A *BA =2BA -8E 得 (A *-2E )BA =-8E , B =-8(A *-2E )-1A -1 =-8[A (A *-2E )]-1 =-8(AA *-2A )-1 =-8(|A |E -2A )-1 =-8(-2E -2A )-1 =4(E +A )-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B . 解 由|A *|=|A |3=8, 得|A |=2. 由ABA -1=BA -1+3E 得 AB =B +3A , B =3(A -E )-1A =3[A (E -A -1)]-1A11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1. |P |=3,⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-=Λ11111120 012001,故⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731.24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B )B -1=B -1+A -1=A -1+B -1,而A -1(A +B )B -1是三个可逆矩阵的乘积, 所以A -1(A +B )B -1可逆, 即A -1+B -1可逆. (A -1+B -1)-1=[A -1(A +B )B -1]-1=B (A +B )-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛3000320012101301300120010100121. 解设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A ,⎪⎭⎫ ⎝⎛-=12131B ,⎪⎭⎫ ⎝⎛--=30322B ,则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A , 所以⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠. 解4100120021010*********0021010010110100101==--=--=D C B A ,而01111|||||||| ==D C B A , 故|||||||| D C B A D C B A ≠.28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4.解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A , 则 ⎪⎭⎫ ⎝⎛=21A O O A A , 故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ,1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ; 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A . 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得 ⎪⎩⎪⎨⎧=+=+==s nE BD CD O BD CD OAD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫ ⎝⎛4121031200210001.解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A B C O A⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫ ⎝⎛--340313021201;解 ⎪⎪⎭⎫ ⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫ ⎝⎛100001000001.(2)⎪⎪⎭⎫ ⎝⎛----174034301320;解 ⎪⎪⎭⎫ ⎝⎛----174034301320(下一步: r 2⨯2+(-3)r 1, r 3+(-2)r 1. )~⎪⎪⎭⎫⎝⎛---310031001320(下一步: r 3+r 2, r 1+3r 2. ) ~⎪⎪⎭⎫⎝⎛0000310010020(下一步: r 1÷2. )~⎪⎪⎭⎫ ⎝⎛000031005010.(3)⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311;解 ⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫ ⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫ ⎝⎛---00000000002210032011.(4)⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.解 ⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132(下一步: r 1-2r 2, r 3-3r 2, r 4-2r 2. )~⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110(下一步: r 2+2r 1, r 3-8r 1, r 4-7r 1. )~⎪⎪⎪⎭⎫ ⎝⎛--41000410002020111110(下一步: r 1↔r 2, r 2⨯(-1), r 4-r 3. )~⎪⎪⎪⎭⎫ ⎝⎛----00000410001111020201(下一步: r 2+r 3. )~⎪⎪⎪⎭⎫⎝⎛--00000410003011020201.2. 设⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A , 求A .解 ⎪⎪⎭⎫⎝⎛100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身.⎪⎪⎭⎫⎝⎛100010101是初等矩阵E (1, 2(1)), 其逆矩阵是E (1, 2(-1)) ⎪⎪⎭⎫⎝⎛-=100010101.⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=100010101987654321100001010A⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=287221254100010101987321654.3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫ ⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫⎝⎛---101011001200410123 ~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003 ~⎪⎪⎭⎫ ⎝⎛----2/102/11002110102/33/26/7001故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267. (2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫⎝⎛--------20104301100001001200110012102321 ~⎪⎪⎪⎭⎫⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫⎝⎛-------106126311101042111000010000100001故逆矩阵为⎪⎪⎪⎭⎫⎝⎛-------10612631110104211. 4. (1)设⎪⎪⎭⎫ ⎝⎛--=113122214A , ⎪⎪⎭⎫⎝⎛--=132231B , 求X 使AX =B ;解 因为⎪⎪⎭⎫ ⎝⎛----=132231 113122214) ,(B A ⎪⎪⎭⎫⎝⎛--412315210 100010001 ~r ,所以 ⎪⎪⎭⎫ ⎝⎛--==-4123152101B A X .(2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B .解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(TT B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r ,所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1TT T B A X ,从而⎪⎭⎫ ⎝⎛---==-4741121BA X .5. 设⎪⎪⎭⎫⎝⎛---=101110011A , AX =2X +A , 求X .解 原方程化为(A -2E )X =A . 因为⎪⎪⎭⎫⎝⎛---------=-101101110110011011) ,2(A E A⎪⎪⎭⎫⎝⎛---011100101010110001~,所以 ⎪⎪⎭⎫ ⎝⎛---=-=-011101110)2(1A E A X .6. 在秩是r 的矩阵中,有没有等于0的r -1阶子式? 有没有等于0的r 阶子式? 解 在秩是r 的矩阵中, 可能存在等于0的r -1阶子式, 也可能存在等于0的r 阶子式.例如, ⎪⎪⎭⎫⎝⎛=010*********A , R (A )=3.0000是等于0的2阶子式, 010001000是等于0的3阶子式.7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样? 解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式:(1)⎪⎪⎭⎫ ⎝⎛---443112112013;解 ⎪⎪⎭⎫ ⎝⎛---443112112013(下一步: r 1↔r 2. )~⎪⎪⎭⎫ ⎝⎛---443120131211(下一步: r 2-3r 1, r 3-r 1. )~⎪⎪⎭⎫⎝⎛----564056401211(下一步: r 3-r 2. )~⎪⎭⎫ ⎝⎛---000056401211, 矩阵的2秩为, 41113-=-是一个最高阶非零子式.(2)⎪⎪⎭⎫⎝⎛-------815073*********;解 ⎪⎪⎭⎫ ⎝⎛-------815073*********(下一步: r 1-r 2, r 2-2r 1, r 3-7r 1. )~⎪⎭⎫ ⎝⎛------15273321059117014431(下一步: r 3-3r 2. ) ~⎪⎭⎫ ⎝⎛----0000059117014431,矩阵的秩是2, 71223-=-是一个最高阶非零子式.(3)⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812.解 ⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812(下一步: r 1-2r 4, r 2-2r 4, r 3-3r 4. )~⎪⎪⎪⎭⎫ ⎝⎛------02301024205363071210(下一步: r 2+3r 1, r 3+2r 1. )~⎪⎪⎪⎭⎫ ⎝⎛-0230114000016000071210(下一步: r 2÷16r 4, r 3-16r 2. )~⎪⎪⎪⎭⎫ ⎝⎛-02301000001000071210~⎪⎪⎪⎭⎫ ⎝⎛-00000100007121002301,矩阵的秩为3,070023085570≠=-是一个最高阶非零子式. 10. 设A 、B 都是m ⨯n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ). 证明 根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3.12. 求解下列齐次线性方程组:(1)⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛--212211121211~⎪⎪⎭⎫ ⎝⎛---3/410013100101,于是 ⎪⎪⎩⎪⎪⎨⎧==-==4443424134334x x x x x x x x ,故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x (k 为任意常数). (2)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎭⎫⎝⎛-000001001021,于是 ⎪⎩⎪⎨⎧===+-=4432242102x x x x x x x x ,故方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10010012214321k k x x x x (k 1, k 2为任意常数).(3)⎪⎩⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎪⎭⎫⎝⎛-----7421631472135132~⎪⎪⎪⎭⎫ ⎝⎛1000010000100001,于是 ⎪⎩⎪⎨⎧====00004321x x x x ,故方程组的解为。
同济大学线性代数第六版课后答案(全).

第一章 行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102---;解 381141102---=2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4. (2)b a c a c b cb a ;解 ba c a cb cb a=acb +bac +cba -bbb -aaa -ccc =3abc -a 3-b 3-c 3.(3)222111c b a c b a ;解 222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).(4)y x y x x y x y yx y x +++.解 yx y x x y x y yx y x +++=x (x +y )y +yx (x +y )+(x +y )yx -y 3-(x +y )3-x 3 =3xy (x +y )-y 3-3x 2 y -x 3-y 3-x 3 =-2(x 3+y 3).2. 按自然数从小到大为标准次序, 求下列各排列的逆序数:(1)1 2 3 4; 解 逆序数为0 (2)4 1 3 2;解 逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解 逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解 逆序数为3: 2 1, 4 1, 4 3. (5)1 3 ⋅ ⋅ ⋅ (2n -1) 2 4 ⋅ ⋅ ⋅ (2n );解 逆序数为2)1(-n n :3 2 (1个) 5 2, 5 4(2个) 7 2, 7 4, 7 6(3个)⋅⋅⋅⋅⋅⋅(2n-1)2, (2n-1)4, (2n-1)6,⋅⋅⋅, (2n-1)(2n-2) (n-1个)(6)1 3 ⋅⋅⋅(2n-1) (2n) (2n-2) ⋅⋅⋅ 2.解逆序数为n(n-1) :3 2(1个)5 2, 5 4 (2个)⋅⋅⋅⋅⋅⋅(2n-1)2, (2n-1)4, (2n-1)6,⋅⋅⋅, (2n-1)(2n-2) (n-1个)4 2(1个)6 2, 6 4(2个)⋅⋅⋅⋅⋅⋅(2n)2, (2n)4, (2n)6,⋅⋅⋅, (2n)(2n-2) (n-1个)3.写出四阶行列式中含有因子a11a23的项.解含因子a11a23的项的一般形式为(-1)t a11a23a3r a4s,其中rs是2和4构成的排列,这种排列共有两个,即24和42.所以含因子a11a23的项分别是(-1)t a11a23a32a44=(-1)1a11a23a32a44=-a11a23a32a44,(-1)t a11a23a34a42=(-1)2a11a23a34a42=a11a23a34a42.4.计算下列各行列式:(1)71100251020214214; 解 71100251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-; 解 2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r 000003212213041214=--=====r r . (3)efcf bf de cd bd aeac ab ---;解 efcf bf de cd bd ae ac ab ---e c b e c b ec b adf ---=abcdef adfbce 4111111111=---=.(4)dc b a 100110011001---. 解d c b a 100110011001---dc b aab ar r 10011001101021---++===== dc a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ada ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 5. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=y x z x z y zy x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ; 证明 2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2, c 2-c 1得) 5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2得)022122212221222122222=++++=d d c c b b a a . (4)444422221111d c b a d c b a d c b a =(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ); 证明 444422221111d c b a d c b a d c b a )()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b ad a c a b ---------=)()()(111))()((222a d d a c c a b b d c b a d a c a b +++---=))(())((00111))()((a b d b d d a b c b c c b d b c a d a c a b ++-++------=)()(11))()()()((a b d d a b c c b d b c a d a c a b ++++-----==(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ).(5)1221 1 000 00 1000 01a x a a a a x x xn n n+⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--- =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .证明 用数学归纳法证明.当n =2时, 2121221a x a x a x a x D ++=+-=, 命题成立. 假设对于(n -1)阶行列式命题成立, 即 D n -1=x n -1+a 1 x n -2+ ⋅ ⋅ ⋅ +a n -2x +a n -1, 则D n 按第一列展开, 有11100 100 01)1(11-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--+=+-x x a xD D n n n n =xD n -1+a n =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n . 因此, 对于n 阶行列式命题成立.6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90︒、或依副对角线翻转, 依次得nnn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nn n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= , 11113 a a a a D n nnn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(--==, D 3=D .证明 因为D =det(a ij ), 所以 nnn n n n nnnn a a a a a a a a a a D 2211111111111 )1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=-⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--=-- )1()1(331122111121nnn n nn n n a a a a a a a a D D n n n n 2)1()1()2( 21)1()1(--+-+⋅⋅⋅++-=-=.同理可证 nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=- )1(11112)1(2D D n n T n n 2)1(2)1()1()1(---=-=. D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k 为k 阶行列式): (1)aa D n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解 aa a a a D n 010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 0000 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa a a x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得 ax x a ax x a a x x a a a a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n -1. (3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n n nn n ; 解 根据第6题结果, 有nn n n n n n n n n a a a n a a a n a a aD )( )1()( )1( 11 11)1(1112)1(1-⋅⋅⋅--⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=---++此行列式为范德蒙德行列式.∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++---=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+-++-⋅-⋅-=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+-=11)(j i n j i .(4)nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112; 解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开) nn n n n nd d c d c b a b a a 00011111111----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn ----+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-+. 再按最后一行展开得递推公式D 2n =a n d n D 2n -2-b n c n D 2n -2, 即D 2n =(a n d n -b n c n )D 2n -2. 于是 ∏=-=ni i i i i n D c b d a D 222)(.而 111111112c b d a d c b a D -==, 所以 ∏=-=ni i i i i n c b d a D 12)(.(5) D =det(a ij ), 其中a ij =|i -j |; 解 a ij =|i -j |, 043214 01233 10122 21011 3210)det(⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅==n n n n n n n n a D ij n 04321 1 11111 11111 11111 1111 2132⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅--⋅⋅⋅-=====n n n n r r r r15242321 0 22210 02210 00210 0001 1213-⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅-+⋅⋅⋅+=====n n n n n c c c c =(-1)n -1(n -1)2n -2. (6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121 nn n n a a a a a a a a a c c c c +-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=====--10 0001 000 100 0100 0100 0011332212132 1111312112111011 000 00 11000 01100 001 ------+-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅⋅⋅⋅=nn n a a a a a a a a∑=------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 00010 000 00 10000 01000 001)11)((121∑=+=ni i n a a a a .8. 用克莱姆法则解下列方程组:(1)⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解 因为14211213513241211111-=----=D , 142112105132412211151-=------=D , 284112035122412111512-=-----=D , 426110135232422115113-=----=D , 14202132132212151114=-----=D , 所以 111==D D x , 222==D D x , 333==D D x , 144-==DDx .(2)⎪⎪⎩⎪⎪⎨⎧=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解 因为 665510006510006510065100065==D , 150751001651000651000650000611==D , 114551010651000650000601000152-==D , 70351100650000601000051001653==D , 395510601000051000651010654-==D , 2121105100065100651100655==D , 所以66515071=x , 66511452-=x , 6657033=x , 6653954-=x , 6652124=x .9. 问λ, μ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 系数行列式为μλμμμλ-==1211111D .令D =0, 得 μ=0或λ=1.于是, 当μ=0或λ=1时该齐次线性方程组有非零解.10. 问λ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解?解 系数行列式为λλλλλλλ--+--=----=101112431111132421D=(1-λ)3+(λ-3)-4(1-λ)-2(1-λ)(-3-λ) =(1-λ)3+2(1-λ)2+λ-3. 令D =0, 得λ=0, λ=2或λ=3.于是, 当λ=0, λ=2或λ=3时, 该齐次线性方程组有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换. 解 由已知:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y ,⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A T B .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503, ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T . 4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫⎝⎛=49635.(2)⎪⎪⎭⎫⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫⎝⎛---=632142. (4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ; 解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B )2=A 2+2AB +B 2吗? 解 (A +B )2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但 ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610, 所以(A +B )2≠A 2+2AB +B 2. (3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.6. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y , 则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k . 解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k . 8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k .解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫⎝⎛=222002012λλλλλ,⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵.证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA .证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以 (AB )T =(BA )T =A T B T =AB , 即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB )T =AB , 所以 AB =(AB )T =B T A T =BA . 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为 ⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解 ⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A |=1≠0, 故A -1存在. 因为 ⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,所以 *||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos . (3)⎪⎪⎭⎫⎝⎛---145243121;解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以 *||11A A A =-⎪⎪⎪⎭⎫⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程:(1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ;解 ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232. (2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311111012112X ;解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131⎪⎪⎭⎫⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ;解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111.(4)⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X .解 11010100001021102341100001010--⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012.13. 利用逆矩阵解下列线性方程组: (1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x ,从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x ,故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ). 另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或 E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或 E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1, )3(41)2(1A E E A -=+-.16. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|.解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A |-1=-8⨯2=-16. 17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)-1=(A -1)*.证明 由*||11A A A =-, 得A *=|A |A -1, 所以当A 可逆时, 有 |A *|=|A |n |A -1|=|A |n -1≠0, 从而A *也可逆.因为A *=|A |A -1, 所以 (A *)-1=|A |-1A .又*)(||)*(||1111---==A A A A A , 所以(A *)-1=|A |-1A =|A |-1|A |(A -1)*=(A -1)*. 18. 设n 阶矩阵A 的伴随矩阵为A *, 证明: (1)若|A |=0, 则|A *|=0; (2)|A *|=|A |n -1. 证明(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)-1=E , 由此得 A =A A *(A *)-1=|A |E (A *)-1=O ,所以A *=O , 这与|A *|≠0矛盾,故当|A |=0时, 有|A *|=0. (2)由于*||11A A A =-, 则AA *=|A |E , 取行列式得到|A ||A *|=|A |n . 若|A |≠0, 则|A *|=|A |n -1;若|A |=0, 由(1)知|A *|=0, 此时命题也成立. 因此|A *|=|A |n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E )B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E )B =A 2-E , 即 (A -E )B =(A -E )(A +E ).因为01001010100||≠-==-E A , 所以(A -E )可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B . 解 由A *BA =2BA -8E 得 (A *-2E )BA =-8E , B =-8(A *-2E )-1A -1 =-8[A (A *-2E )]-1 =-8(AA *-2A )-1 =-8(|A |E -2A )-1 =-8(-2E -2A )-1 =4(E +A )-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B .解 由|A *|=|A |3=8, 得|A |=2. 由ABA -1=BA -1+3E 得 AB =B +3A ,B =3(A -E )-1A =3[A (E -A -1)]-1A 11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511,求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)]=diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B )B -1=B -1+A -1=A -1+B -1,而A -1(A +B )B -1是三个可逆矩阵的乘积, 所以A -1(A +B )B -1可逆, 即A -1+B -1可逆.(A -1+B -1)-1=[A -1(A +B )B -1]-1=B (A +B )-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解 设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B ,则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫⎝⎛+=222111B A O B B A A ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A , 所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠.解 4100120021010*********0021010010110100101==--=--=D C B A , 而 01111|||||||| ==D C B A ,故 |||||||| D C B A D C B A ≠.28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A ,则 ⎪⎭⎫⎝⎛=21A O O A A ,故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A , 1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求 (1)1-⎪⎭⎫ ⎝⎛O B A O ; 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则 ⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n EBC OBC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C OC A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A . 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得 ⎪⎩⎪⎨⎧=+=+==s nEBD CD O BD CD OAD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001. 解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A B C O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201;解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫⎝⎛100001000001.(2)⎪⎪⎭⎫⎝⎛----174034301320;解 ⎪⎪⎭⎫⎝⎛----174034301320(下一步: r 2⨯2+(-3)r 1, r 3+(-2)r 1. )~⎪⎪⎭⎫⎝⎛---310031001320(下一步: r 3+r 2, r 1+3r 2. )~⎪⎪⎭⎫⎝⎛0000310010020(下一步: r 1÷2. )~⎪⎪⎭⎫⎝⎛000031005010.(3)⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311;解 ⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011.(4)⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.解 ⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132(下一步: r 1-2r 2, r 3-3r 2, r 4-2r 2. )~⎪⎪⎪⎭⎫⎝⎛-----1187701298804202111110(下一步: r 2+2r 1, r 3-8r 1, r 4-7r 1. )~⎪⎪⎪⎭⎫⎝⎛--41000410002020111110(下一步: r 1↔r 2, r 2⨯(-1), r 4-r 3. )~⎪⎪⎪⎭⎫⎝⎛----00000410001111020201(下一步: r 2+r 3. )~⎪⎪⎪⎭⎫⎝⎛--000410*******20201. 2. 设⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A , 求A .解 ⎪⎪⎭⎫⎝⎛100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身.⎪⎪⎭⎫⎝⎛100010101是初等矩阵E (1, 2(1)), 其逆矩阵是E (1, 2(-1)) ⎪⎪⎭⎫⎝⎛-=100010101.⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=100010101987654321100001010A⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=287221254100010101987321654.3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫⎝⎛-------106126311101042111000010000100001故逆矩阵为⎪⎪⎪⎭⎫⎝⎛-------10612631110104211. 4. (1)设⎪⎪⎭⎫ ⎝⎛--=113122214A , ⎪⎪⎭⎫⎝⎛--=132231B , 求X 使AX =B ;解 因为⎪⎪⎭⎫ ⎝⎛----=132231 113122214) ,(B A ⎪⎪⎭⎫⎝⎛--412315210 100010001 ~r ,所以 ⎪⎪⎭⎫⎝⎛--==-4123152101B A X .(2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B . 解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r ,所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X . 5. 设⎪⎪⎭⎫⎝⎛---=101110011A , AX =2X +A , 求X .解 原方程化为(A -2E )X =A . 因为⎪⎪⎭⎫⎝⎛---------=-101101110110011011) ,2(A E A⎪⎪⎭⎫⎝⎛---011100101010110001~,所以 ⎪⎪⎭⎫⎝⎛---=-=-011101110)2(1A E A X .6. 在秩是r 的矩阵中,有没有等于0的r -1阶子式? 有没有等于0的r 阶子式?解 在秩是r 的矩阵中, 可能存在等于0的r -1阶子式, 也可能存在等于0的r 阶子式.例如, ⎪⎪⎭⎫⎝⎛=010*********A , R (A )=3.0000是等于0的2阶子式, 010001000是等于0的3阶子式. 7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样?解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式:(1)⎪⎪⎭⎫⎝⎛---443112112013;解 ⎪⎪⎭⎫⎝⎛---443112112013(下一步: r 1↔r 2. )~⎪⎪⎭⎫⎝⎛---443120131211(下一步: r 2-3r 1, r 3-r 1. )~⎪⎪⎭⎫⎝⎛----564056401211(下一步: r 3-r 2. )~⎪⎭⎫ ⎝⎛---000056401211, 矩阵的2秩为, 41113-=-是一个最高阶非零子式.(2)⎪⎪⎭⎫⎝⎛-------815073*********;解 ⎪⎪⎭⎫⎝⎛-------815073*********(下一步: r 1-r 2, r 2-2r 1, r 3-7r 1. )~⎪⎭⎫ ⎝⎛------15273321059117014431(下一步: r 3-3r 2. ) ~⎪⎭⎫ ⎝⎛----0000059117014431, 矩阵的秩是2, 71223-=-是一个最高阶非零子式.(3)⎪⎪⎪⎭⎫⎝⎛---02301085235703273812. 解 ⎪⎪⎪⎭⎫⎝⎛---02301085235703273812(下一步: r 1-2r 4, r 2-2r 4, r 3-3r 4. )~⎪⎪⎪⎭⎫⎝⎛------023*********63071210(下一步: r 2+3r 1, r 3+2r 1. )~⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210(下一步: r 2÷16r 4, r 3-16r 2. )~⎪⎪⎪⎭⎫⎝⎛-02301000001000071210 ~⎪⎪⎪⎭⎫⎝⎛-00000100007121002301, 矩阵的秩为3, 070023085570≠=-是一个最高阶非零子式.10. 设A 、B 都是m ⨯n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ).证明 根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2;(3)当k ≠1且k ≠-2时, R (A )=3.12. 求解下列齐次线性方程组: (1)⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛--212211121211~⎪⎪⎭⎫ ⎝⎛---3/410013100101,于是 ⎪⎪⎩⎪⎪⎨⎧==-==4443424134334x x x x x x x x ,故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x (k 为任意常数).(2)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎭⎫⎝⎛-000001001021,于是 ⎪⎩⎪⎨⎧===+-=4432242102x x x xx x x x ,故方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10010********1k k x x x x (k 1, k 2为任意常数).(3)⎪⎩⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎪⎭⎫⎝⎛-----7421631472135132~⎪⎪⎪⎭⎫ ⎝⎛1000010000100001,于是 ⎪⎩⎪⎨⎧====0004321x x x x ,故方程组的解为 ⎪⎩⎪⎨⎧====00004321x x x x .(4)⎪⎩⎪⎨⎧=++-=+-+=-+-=+-+03270161311402332075434321432143214321x x x x x x x x x x x x x x x x .解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎪⎭⎫⎝⎛-----3127161311423327543~⎪⎪⎪⎪⎪⎭⎫⎝⎛--000000001720171910171317301,于是 ⎪⎪⎩⎪⎪⎨⎧==-=-=4433432431172017191713173x x x x x x x xx x ,故方程组的解为⎪⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛1017201713011719173214321k k x x x x (k 1, k 2为任意常数).13. 求解下列非齐次线性方程组: (1)⎪⎩⎪⎨⎧=+=+-=-+83111021322421321321x x x x x x x x ;解 对增广矩阵B 进行初等行变换, 有。
线性代数 第五版(同济大学)课后习题答案

−b b b 0 2
c −c c 2 0
e e −e = adf bce
−1 1 1
1 −1 1
1 1 −1
−1 1
r +r r3 +r1
0 0 a −1 0 0
0 2 1 b −1 0
= −adf bce
= 4abcdef.
(4)
0
1 2 = = = = = =
1 + ab b −1 0
a 1 c
= = = =a
裂开
再次
2
y z x
2 (3) 逆序数为 5: 3 2, 3 1, 4 2, 4 1, 2 1. (4) 逆序数为 3: 2 1, 4 1, 4 3. (5) 逆序数为
n(n−1) : 2
第一章 行列式
3 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1 个 5 2, 5 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 个 7 2, 7 4, 7 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 个 .................................................................................. (2n − 1) 2, (2n − 1) 4, (2n − 1) 6, . . . , (2n − 1) (2n − 2). . . . . . . . . . . . . .(n − 1) 个 (6) 逆序数为 n(n − 1): 3 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1 个 5 2, 5 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 个 7 2, 7 4, 7 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 个 .................................................................................. (2n − 1) 2, (2n − 1) 4, (2n − 1) 6, . . . , (2n − 1) (2n − 2). . . . . . . . . . . . . .(n − 1) 个 4 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1 个 6 2, 6 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 个 .................................................................................. (2n) 2, (2n) 4, (2n) 6, . . . , (2n) (2n − 2) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (n − 1) 个 3 . 写出四阶行列式中含有因子 a11 a23 的项.
(同济大学)线性代数第五版课后答案

成都大学诗叶子制作第一章 行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102---;解 381141102---=2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4. (2)ba c a cb cb a ;解 ba c a cb cb a =acb +bac +cba -bbb -aaa -ccc=3abc -a 3-b 3-c 3.(3)222111c b a c b a ;解 222111c b a c b a =bc 2+ca 2+ab 2-ac 2-ba 2-cb 2=(a -b )(b -c )(c -a ).成都大学诗叶子制作(4)y x y x x y x y yx y x +++.解 yx y x x y x y yx y x +++=x (x +y )y +yx (x +y )+(x +y )yx -y 3-(x +y )3-x 3 =3xy (x +y )-y 3-3x 2 y -x 3-y 3-x 3 =-2(x 3+y 3).2. 按自然数从小到大为标准次序, 求下列各排列的逆序数:(1)1 2 3 4; 解 逆序数为0 (2)4 1 3 2;解 逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解 逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解 逆序数为3: 2 1, 4 1, 4 3. (5)1 3 ⋅ ⋅ ⋅ (2n -1) 2 4 ⋅ ⋅ ⋅ (2n );解 逆序数为2)1(-n n :3 2 (1个) 5 2, 5 4(2个)7 2, 7 4, 7 6(3个)⋅⋅⋅⋅⋅⋅(2n-1)2, (2n-1)4, (2n-1)6,⋅⋅⋅, (2n-1)(2n-2) (n-1个)(6)1 3 ⋅⋅⋅(2n-1) (2n) (2n-2) ⋅⋅⋅ 2.解逆序数为n(n-1) :3 2(1个)5 2, 5 4 (2个)⋅⋅⋅⋅⋅⋅(2n-1)2, (2n-1)4, (2n-1)6,⋅⋅⋅, (2n-1)(2n-2) (n-1个)4 2(1个)6 2, 6 4(2个)⋅⋅⋅⋅⋅⋅(2n)2, (2n)4, (2n)6,⋅⋅⋅, (2n)(2n-2) (n-1个)3.写出四阶行列式中含有因子a11a23的项.解含因子a11a23的项的一般形式为(-1)t a11a23a3r a4s,其中rs是2和4构成的排列,这种排列共有两个,即24和42.所以含因子a11a23的项分别是(-1)t a11a23a32a44=(-1)1a11a23a32a44=-a11a23a32a44,(-1)t a11a23a34a42=(-1)2a11a23a34a42=a11a23a34a42.4.计算下列各行列式:成都大学诗叶子制作成都大学诗叶子制作(1)7110025*******214; 解 71100251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-; 解 2605232112131412-26053212213041224--=====c c 041203212213041224--=====r r 0000003212213041214=--=====r r . (3)efcf bf de cd bd aeac ab ---;解 efcf bf de cd bd aeac ab ---e c b e c b e c b adf ---=abcdef adfbce 4111111111=---=.成都大学诗叶子制作(4)dc b a 100110011001---. 解 d c b a 100110011001---dc b aab ar r 10011001101021---++===== d c a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ada ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 5. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++成都大学诗叶子制作bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=y x z x z y zy x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ; 证明2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2, c 2-c 1得) 5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2得)成都大学诗叶子制作022122212221222122222=++++=d d c c b b a a . (4)444422221111d c b a d c b a d c b a =(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ); 证明 444422221111d c b a d c b a d c b a )()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b ad a c a b ---------=)()()(111))()((222a d d a c c a b b d c b a d a c a b +++---=))(())((00111))()((a b d b d d a b c b c c b d b c a d a c a b ++-++------= )()(11))()()()((a b d d a b c c b d b c a d a c a b ++++-----= =(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ).成都大学诗叶子制作(5)12211 000 00 1000 01a x a a a a x x x n n n+⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--- =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .证明 用数学归纳法证明.当n =2时, 2121221a x a x a x a x D ++=+-=, 命题成立. 假设对于(n -1)阶行列式命题成立, 即 D n -1=x n -1+a 1 x n -2+ ⋅ ⋅ ⋅ +a n -2x +a n -1, 则D n 按第一列展开, 有 11100 100 01)1(11-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--+=+-xx a xD D n n n n =xD n -1+a n =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n . 因此, 对于n 阶行列式命题成立.6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90︒、或依副对角线翻转, 依次得n nn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nn n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= , 11113 a a a a D n nnn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(--==, D 3=D .证明 因为D =det(a ij ), 所以成都大学诗叶子制作nnn n n n nnnn a a a a a a a a a a D 2211111111111 )1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=- ⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--=-- )1()1(331122111121nnn n nn n n a a a a a a a a D D n n n n 2)1()1()2( 21)1()1(--+-+⋅⋅⋅++-=-=.同理可证 nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=- )1(11112)1(2D D n n Tn n 2)1(2)1()1()1(---=-=. D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k 为k 阶行列式):(1)aaD n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解成都大学诗叶子制作aa a a a D n 0 0010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 00 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa aa x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得 ax x a ax x a a x x a a a a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 000 00 )1(=[x +(n -1)a ](x -a )n -1.成都大学诗叶子制作(3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n nn n n ; 解 根据第6题结果, 有 nnn n n n n n n n a a a n a a a n a a aD )( )1()( )1( 11 11)1(1112)1(1-⋅⋅⋅--⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=---++此行列式为范德蒙德行列式. ∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++---=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+-++-⋅-⋅-=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+-=11)(j i n j i .(4)nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112; 解成都大学诗叶子制作nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开) nn n n n nd d c d c b a b a a 00011111111----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn ----+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-+. 再按最后一行展开得递推公式D 2n =a n d n D 2n -2-b n c n D 2n -2, 即D 2n =(a n d n -b n c n )D 2n -2. 于是 ∏=-=ni i i i i n D c b d a D 222)(.而 111111112c b d a d c b a D -==, 所以 ∏=-=n i i i i i n c b d a D 12)(. (5) D =det(a ij ), 其中a ij =|i -j |;成都大学诗叶子制作解 a ij =|i -j |, 04321 4 01233 10122 21011 3210)det(⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅==n n n n n n n n a D ij n 043211 11111 11111 11111 1111 2132⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅--⋅⋅⋅-=====n n n n r r r r 15242321 0 22210 02210 00210 0001 1213-⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅-+⋅⋅⋅+=====n n n n n c c c c =(-1)n -1(n -1)2n -2.(6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 111 1121成都大学诗叶子制作nn n n a a a a a a a a a c c c c +-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=====--10001 000 100 0100 0100 0011332212132 11113121121110 00011 000 00 11000 01100 001 ------+-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅⋅⋅⋅=n n n a a a a a a a a∑=------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 000100 10000 01000 001)11)((121∑=+=ni i n a a a a .8. 用克莱姆法则解下列方程组: (1)⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解 因为成都大学诗叶子制作14211213513241211111-=----=D , 142112105132412211151-=------=D , 284112035122412111512-=-----=D , 426110135232422115113-=----=D , 14202132132212151114=-----=D , 所以 111==D D x , 222==D D x , 333==D D x , 144-==D D x .(2)⎪⎪⎩⎪⎪⎨⎧=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解 因为 665510006510006510065100065==D , 150751001651000651000650000611==D , 114551010651000650000601000152-==D ,成都大学诗叶子制作70351100650000601000051001653==D , 39551000601000051000651010654-==D , 2121100005100065100651100655==D , 所以66515071=x , 66511452-=x , 6657033=x , 6653954-=x , 6652124=x .9. 问λ, μ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 系数行列式为μλμμμλ-==1211111D .令D =0, 得 μ=0或λ=1.于是, 当μ=0或λ=1时该齐次线性方程组有非零解.10. 问λ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ成都大学诗叶子制作有非零解?解 系数行列式为λλλλλλλ--+--=----=101112431111132421D=(1-λ)3+(λ-3)-4(1-λ)-2(1-λ)(-3-λ) =(1-λ)3+2(1-λ)2+λ-3. 令D =0, 得λ=0, λ=2或λ=3.于是, 当λ=0, λ=2或λ=3时, 该齐次线性方程组有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换. 解 由已知:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,成都大学诗叶子制作故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y ,⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A T B .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB成都大学诗叶子制作⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T .4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫⎝⎛=49635.(2)⎪⎪⎭⎫⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫⎝⎛---=632142. (4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ;成都大学诗叶子制作解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA . (2)(A +B )2=A 2+2AB +B 2吗? 解 (A +B )2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A ,成都大学诗叶子制作 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148, 但 ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610, 所以(A +B )2≠A 2+2AB +B 2.(3)(A +B )(A -B )=A 2-B 2吗?解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A , 故(A +B )(A -B )≠A 2-B 2. 6. 举反列说明下列命题是错误的:(1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ; 解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解 取成都大学诗叶子制作 ⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y , 则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k . 解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k . 8. 设⎪⎪⎭⎫ ⎝⎛=λλλ001001A , 求A k . 解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ, ⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A , ⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A , ⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A ,成都大学诗叶子制作 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=k A k k k k k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫ . 用数学归纳法证明:当k =2时, 显然成立.假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121. 9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵.证明 因为A T =A , 所以成都大学诗叶子制作 (B T AB )T =B T (B T A )T =B T A T B =B T AB ,从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA .证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以 (AB )T =(BA )T =A T B T =AB ,即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB )T =AB , 所以 AB =(AB )T =B T A T =BA .11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A , 故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解 ⎪⎭⎫ ⎝⎛-=θθθθc o s s i n s i n c o s A . |A |=1≠0, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,成都大学诗叶子制作 所以 *||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos . (3)⎪⎪⎭⎫ ⎝⎛---145243121; 解 ⎪⎪⎭⎫ ⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为 ⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012. (4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程:成都大学诗叶子制作 (1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ; 解 ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232. (2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ; 解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫ ⎝⎛---=32538122.(3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ; 解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X .成都大学诗叶子制作 解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012. 13. 利用逆矩阵解下列线性方程组: (1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,成都大学诗叶子制作 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x . 14. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1),所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E ,由定理2推论知(E -A )可逆, 且(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ),故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ),两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.成都大学诗叶子制作 证明 由A 2-A -2E =O 得A 2-A =2E , 即A (A -E )=2E ,或 E E A A =-⋅)(21, 由定理2推论知A 可逆, 且)(211E A A -=-. 由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E ,或 E A E E A =-⋅+)3(41)2( 由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2,即 |A ||A -E |=2,故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-, 又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1,成都大学诗叶子制作 )3(41)2(1A E E A -=+-. 16. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|. 解 因为*||11A A A =-, 所以 |||521||*5)2(|111----=-A A A A A |2521|11---=A A =|-2A -1|=(-2)3|A -1|=-8|A |-1=-8⨯2=-16. 17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)-1=(A -1)*.证明 由*||11A A A =-, 得A *=|A |A -1, 所以当A 可逆时, 有 |A *|=|A |n |A -1|=|A |n -1≠0,从而A *也可逆.因为A *=|A |A -1, 所以(A *)-1=|A |-1A .又*)(||)*(||1111---==A A A A A , 所以 (A *)-1=|A |-1A =|A |-1|A |(A -1)*=(A -1)*.18. 设n 阶矩阵A 的伴随矩阵为A *, 证明:(1)若|A |=0, 则|A *|=0;(2)|A *|=|A |n -1.证明(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)-1=E , 由此得成都大学诗叶子制作A =A A *(A *)-1=|A |E (A *)-1=O ,所以A *=O , 这与|A *|≠0矛盾,故当|A |=0时, 有|A *|=0. (2)由于*||11A A A =-, 则AA *=|A |E , 取行列式得到|A ||A *|=|A |n . 若|A |≠0, 则|A *|=|A |n -1;若|A |=0, 由(1)知|A *|=0, 此时命题也成立. 因此|A *|=|A |n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E )B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E )B =A 2-E , 即 (A -E )B =(A -E )(A +E ).因为01001010100||≠-==-E A , 所以(A -E )可逆, 从而成都大学诗叶子制作⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B . 解 由A *BA =2BA -8E 得 (A *-2E )BA =-8E , B =-8(A *-2E )-1A -1 =-8[A (A *-2E )]-1 =-8(AA *-2A )-1 =-8(|A |E -2A )-1 =-8(-2E -2A )-1 =4(E +A )-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B . 解 由|A *|=|A |3=8, 得|A |=2. 由ABA -1=BA -1+3E 得 AB =B +3A ,B =3(A -E )-1A =3[A (E -A -1)]-1A成都大学诗叶子制作11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511,求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ成都大学诗叶子制作⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112 ⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B )B -1=B -1+A -1=A -1+B -1,而A -1(A +B )B -1是三个可逆矩阵的乘积, 所以A -1(A +B )B -1可逆, 即A -1+B -1可逆.(A -1+B -1)-1=[A -1(A +B )B -1]-1=B (A +B )-1A . 26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解 设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B ,则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫⎝⎛+=222111B A O B B A A ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A ,成都大学诗叶子制作所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠.解 4100120021100101002000021010010110100101==--=--=D C B A , 而 01111|||||||| ==D C B A ,故 |||||||| D C B A D C B A ≠.28. 设⎪⎪⎪⎭⎫⎝⎛-=22023443O O A , 求|A 8|及A 4. 解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A , 则 ⎪⎭⎫⎝⎛=21A O O A A ,故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ,成都大学诗叶子制作1682818281810||||||||||===A A A A A . ⎪⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求 (1)1-⎪⎭⎫ ⎝⎛O B A O ; 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则 ⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n EBC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C OC O C A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A . 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321.成都大学诗叶子制作由此得 ⎪⎩⎪⎨⎧=+=+==s nE BD CD O BD CD OAD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵: (1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001. 解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则成都大学诗叶子制作⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A B C O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201;解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )成都大学诗叶子制作~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫⎝⎛100001000001.(2)⎪⎪⎭⎫⎝⎛----174034301320;解 ⎪⎪⎭⎫⎝⎛----174034301320(下一步: r 2⨯2+(-3)r 1, r 3+(-2)r 1. )~⎪⎪⎭⎫⎝⎛---310031001320(下一步: r 3+r 2, r 1+3r 2. )~⎪⎪⎭⎫⎝⎛0000310010020(下一步: r 1÷2. )~⎪⎪⎭⎫⎝⎛000031005010.成都大学诗叶子制作(3)⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; 解 ⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011. (4)⎪⎪⎪⎭⎫⎝⎛------34732038234202173132. 解 ⎪⎪⎪⎭⎫⎝⎛------34732038234202173132(下一步: r 1-2r 2, r 3-3r 2, r 4-2r 2. )~⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110(下一步: r 2+2r 1, r 3-8r 1, r 4-7r 1. )成都大学诗叶子制作~⎪⎪⎪⎭⎫⎝⎛--41000410002020111110(下一步: r 1↔r 2, r 2⨯(-1), r 4-r 3. )~⎪⎪⎪⎭⎫⎝⎛----00000410001111020201(下一步: r 2+r 3. )~⎪⎪⎪⎭⎫⎝⎛--00000410003011020201. 2. 设⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A , 求A .解 ⎪⎪⎭⎫⎝⎛100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身.⎪⎪⎭⎫⎝⎛100010101是初等矩阵E (1, 2(1)), 其逆矩阵是E (1, 2(-1)) ⎪⎪⎭⎫⎝⎛-=100010101.⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=100010101987654321100001010A⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=287221254100010101987321654.成都大学诗叶子制作3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023成都大学诗叶子制作~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫⎝⎛-------106126311101042111000010000100001故逆矩阵为⎪⎪⎪⎭⎫⎝⎛-------10612631110104211. 4. (1)设⎪⎪⎭⎫ ⎝⎛--=113122214A , ⎪⎪⎭⎫⎝⎛--=132231B , 求X 使AX =B ;解 因为成都大学诗叶子制作⎪⎪⎭⎫ ⎝⎛----=132231 113122214) ,(B A ⎪⎪⎭⎫⎝⎛--412315210 100010001 ~r ,所以 ⎪⎪⎭⎫⎝⎛--==-4123152101B A X .(2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B . 解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r ,所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X . 5. 设⎪⎪⎭⎫⎝⎛---=101110011A , AX =2X +A , 求X .解 原方程化为(A -2E )X =A . 因为⎪⎪⎭⎫⎝⎛---------=-101101110110011011) ,2(A E A⎪⎪⎭⎫⎝⎛---011100101010110001~,成都大学诗叶子制作所以 ⎪⎪⎭⎫⎝⎛---=-=-011101110)2(1A E A X .6. 在秩是r 的矩阵中,有没有等于0的r -1阶子式? 有没有等于0的r 阶子式?解 在秩是r 的矩阵中, 可能存在等于0的r -1阶子式, 也可能存在等于0的r 阶子式.例如, ⎪⎪⎭⎫⎝⎛=010*********A , R (A )=3.0000是等于0的2阶子式, 010001000是等于0的3阶子式. 7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样?解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:成都大学诗叶子制作⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式:(1)⎪⎪⎭⎫⎝⎛---443112112013;解 ⎪⎪⎭⎫⎝⎛---443112112013(下一步: r 1↔r 2. )~⎪⎪⎭⎫⎝⎛---443120131211(下一步: r 2-3r 1, r 3-r 1. )~⎪⎪⎭⎫⎝⎛----564056401211(下一步: r 3-r 2. )~⎪⎭⎫ ⎝⎛---000056401211, 矩阵的2秩为, 41113-=-是一个最高阶非零子式.(2)⎪⎪⎭⎫⎝⎛-------815073*********;成都大学诗叶子制作解 ⎪⎪⎭⎫⎝⎛-------815073*********(下一步: r 1-r 2, r 2-2r 1, r 3-7r 1. )~⎪⎭⎫ ⎝⎛------15273321059117014431(下一步: r 3-3r 2. ) ~⎪⎭⎫ ⎝⎛----0000059117014431, 矩阵的秩是2, 71223-=-是一个最高阶非零子式.(3)⎪⎪⎪⎭⎫⎝⎛---02301085235703273812. 解 ⎪⎪⎪⎭⎫⎝⎛---02301085235703273812(下一步: r 1-2r 4, r 2-2r 4, r 3-3r 4. )~⎪⎪⎪⎭⎫⎝⎛------023*********63071210(下一步: r 2+3r 1, r 3+2r 1. )~⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210(下一步: r 2÷16r 4, r 3-16r 2. )成都大学诗叶子制作~⎪⎪⎪⎭⎫⎝⎛-02301000001000071210 ~⎪⎪⎪⎭⎫⎝⎛-00000100007121002301, 矩阵的秩为3, 070023085570≠=-是一个最高阶非零子式.10. 设A 、B 都是m ⨯n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ).证明 根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2;成都大学诗叶子制作(3)当k ≠1且k ≠-2时, R (A )=3.12. 求解下列齐次线性方程组:(1)⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛--212211121211~⎪⎪⎭⎫ ⎝⎛---3/410013100101,于是 ⎪⎪⎩⎪⎪⎨⎧==-==4443424134334x x x x x x x x ,故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x (k 为任意常数).(2)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有成都大学诗叶子制作A =⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎭⎫⎝⎛-000001001021,于是 ⎪⎩⎪⎨⎧===+-=4432242102x x x xx x x x ,故方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10010*********k k x x x x (k 1, k 2为任意常数).(3)⎪⎩⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有 A =⎪⎪⎪⎭⎫⎝⎛-----7421631472135132~⎪⎪⎪⎭⎫ ⎝⎛1000010000100001,于是 ⎪⎩⎪⎨⎧====0004321x x x x ,故方程组的解为。
线性代数课后答案解析 第二版 同济大学出版社

线性代数习题解答 同济大学出版社习题11.求下列各排列的逆序数:(1)1 2 3 4; (2)4 1 3 2;(3)4 1 5 3 2; (4)3 7 1 2 4 5 6; (5)1 3 … (21)n - 2 4 … (2)n ; (6)1 3 … (21)n - (2)n (22)n - … 2. 2.利用对角线法则计算下列二阶、三阶行列式:(1)3214---; (2)201141183---;(3)a b c b c a c a b ; (4)x y x y yx y x x yxy+++.3.在六阶行列式中,下列两项各应带什么符号: (1)233142561465a a a a a a ;(2)334214516625a a a a a a . 4.计算下列各行列式:(1)000100020010000000n n -; (2)1234214334124321------;(3)2100121001210012; (4)0451250201720343115023013-------;(5)abac aebdcd de bfcfef---; (6)1111111111111111x x y y+-+-.5.证明:(1)11121314152122232425313241425152000000000a a a a a a a a a a a a a a a a =; (2)2222111a abb aa b b +=3()a b -;(3)111111222222b cc a a bb c c a a b b c c a a b +++++++++=1112222ab ca b c a b c ; (4)222244441111a b c d a b c d a b c d ; ()()()()()a b a c a d b c b d =-----()()-+++c d a b c d ;(5)1221100001000001n n n x x xa a a a x a -----+111n n n n x a x a x a --=++++ .6.计算下列各n 阶行列式:(1)11aa,其中对角线上元素都是a ,未写出的元素都是0;(2)111x a a a x a a a x --- ;(3)123111100100100n a a a a,230≠其中n a a a ; (4)12111111111na a a +++,120n a a a ≠ 其中;(5)111222(1)(2)()(1)(2)()12111n n n n n n a a a n a a a n a a a n ---------------;(6)det(),n ij ij D a a i j ==-其中. 7.利用拉普拉斯定理计算下列各行列式:(1)320000430000002100003200000032000054;(2)3002034040030560; (3)112110000nnn nna b a b D c d c d =.解答习题11.(1)0;(2)4;(3)6;(4)7;(5)(1)2-n n ;(6)(1)-n n . 2.(1)-14;(2)-4;(3)3333---ab a b c ;(4)332()-+x y . 3.(1)正号;(2)负号. 4.(1)(1)(2)2(1)!---n n n ;(2)900;(3)5;(4)-799;(5)4abcdef ;(6)22x y . 5.提示:(1)用行列式定义证明;(2)、(3)、(4)用行列式性质证明;(5)用数学归纳法证明.6.(1)22(1)--n aa ;(2)1[1(1)](1)--+---n x n a x a ;(3)23121()()nn i ia a a a a =-∑ ;(4)1211()(1)=+∑nn i i a a a a ;(5)1()≥>≥-∏n i j i j ;(6)12(1)(1)2----n n n . 7.(1)2;(2)2;(3)1()=-∏niii i i a db c .习题21.有6名选手参加乒乓球比赛,成绩如下:选手1胜选手2,4,5,6负于选手3;选手2胜选手4,5,6负于选手1,3;选手3胜选手1,2,4负于选手5,6;选手4胜选手5,6负于选手1,2,3;选手5胜选手3,6负于选手1,2,4;若胜一场得1分,负一场得零分试用矩阵表示输赢状况,并排序.2.某种物资以3个产地运往4个销地,两次调运方案分别为矩阵A 与矩阵B .且357220430123A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,132021570648B ⎛⎫ ⎪= ⎪ ⎪⎝⎭试用矩阵表示各产地运往各销地两次的物资调运量.3.设111123111124111051A B ⎛⎫⎛⎫⎪ ⎪=-=-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,,求32AB A -与TA B .4.某厂研究三种生产方法,生产甲、乙、丙三种产品,每种生产方法的每种产品数量用如下矩阵表示:234123241A ⎛⎫ ⎪= ⎪ ⎪⎝⎭甲乙丙方法一方法二方法三 若甲、乙、丙各种产品每单位的利润分别为10元,8元,7元,试用矩阵的乘法求出以何种方法获利最多.5.设12101312A B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭,,问(1)AB BA =吗?(2)()2222A B A AB B +=++吗?(3)()()22A B A B A B +-=-吗?6.举反例说明下列命题是错误的: (1)若2A O =,则A O =;(2)若2A A =,则A O =或A E =;(3)若AX AY =,且A O ≠,则X Y =. 7.设101A λ⎛⎫=⎪⎝⎭,求23kA A A ,,,. 8.设AB 、都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB BA =. 9.用伴随矩阵法求下列矩阵的逆阵:(1)1225⎛⎫ ⎪⎝⎭; (2)cos sin sin cos θθθθ-⎛⎫⎪⎝⎭; (3)121342541-⎛⎫ ⎪- ⎪ ⎪-⎝⎭; (4)1234012300120001⎛⎫⎪⎪ ⎪ ⎪⎝⎭. 10.解下列矩阵方程: (1)25465321X -⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭;(2)211113210432111X -⎛⎫-⎛⎫⎪= ⎪ ⎪⎝⎭ ⎪-⎝⎭;(3)010100143100001201001010120X -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭.11.设方阵A 满足225A A E O +-=,证明3A E +可逆,并求其逆矩阵.12.已知对给定方阵A ,存在正整数k ,成立kA O =,试证E A -可逆,并指出()1E A --的表达式.13.设A 为3阶方阵,12A =,求()125A A -*-. 14.设方阵A 可逆,证明其伴随矩阵A *也可逆,且()()11AA -**-=.15.设131020101A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,2AB E A B +=+,求B .16.设三阶矩阵A B ,满足关系:16A BA A BA -=+,且100210041007A ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭, 求B .17.设033110123A ⎛⎫ ⎪= ⎪ ⎪-⎝⎭,2AX A X =+,求X .18已知AP P =Λ,其中100100210000211001P ⎛⎫⎛⎫⎪ ⎪=-Λ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,=,求A 及5A .19.设A B ,和A B +均可逆,证明11A B --+也可逆,并求其逆矩阵.20.将矩阵2131425442622140A -⎛⎫⎪-⎪= ⎪--- ⎪-⎝⎭化为行阶梯形矩阵,并求矩阵A 的一个最高阶非零子式.21.用初等变换法求下列矩阵的逆:(1)111211120⎛⎫ ⎪- ⎪ ⎪⎝⎭; (2)321315323⎛⎫⎪ ⎪ ⎪⎝⎭;(3)3201022112320121--⎛⎫⎪ ⎪ ⎪--- ⎪⎝⎭; (4)1357012300120001-⎛⎫⎪⎪⎪⎪⎝⎭.22.下列矩阵的秩.:(1)1234124511012⎛⎫ ⎪- ⎪ ⎪⎝⎭; (2)321312131370518---⎛⎫ ⎪-- ⎪ ⎪--⎝⎭; (3)1001310312011457⎛⎫⎪-⎪ ⎪-⎪⎝⎭; (4)24131121023636a -⎛⎫ ⎪- ⎪ ⎪⎝⎭.23.设A 为n 阶矩阵,且2A A =,证明()()R A R A E n +-=.24.设34432022O A O ⎛⎫⎪- ⎪= ⎪ ⎪⎝⎭,求84A A ,. 25.设矩阵A 和B 均可逆,求分块矩阵O A B O ⎛⎫⎪⎝⎭的逆矩阵,并利用所得结果求矩阵005200218300520⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭的逆矩阵.解答习题21.123456110111200111311100400011500101600100⎛⎫⎪⎪⎪⎪⎪⎪⎪⎪⎝⎭,选手按胜多负少排序为1 2 3 4 5 6.2.357213202043215701230648 A B⎛⎫⎛⎫⎪ ⎪+=+⎪ ⎪⎪ ⎪⎝⎭⎝⎭48924191007611⎛⎫⎪= ⎪ ⎪⎝⎭.3.111123111 3331111242111111051111 AB A⎛⎫⎛⎫⎛⎫⎪⎪ ⎪-=-----⎪⎪ ⎪⎪⎪ ⎪--⎝⎭⎝⎭⎝⎭21322217204292-⎛⎫⎪=--⎪⎪-⎝⎭058123056124290051TTA B⎛⎫⎛⎫⎪ ⎪=---⎪ ⎪⎪ ⎪⎝⎭⎝⎭002123058559124056860051290⎛⎫⎛⎫⎛⎫⎪⎪ ⎪=---=-⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭.4.1072844759A⎛⎫⎛⎫⎪ ⎪=⎪ ⎪⎪ ⎪⎝⎭⎝⎭,方法一获利最多. (1)AB BA≠,因为34124638AB BA⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭,,所以AB BA≠.(2)()2222A B A AB B +≠++因为 2225A B ⎛⎫+=⎪⎝⎭()2222281425251429A B ⎛⎫⎛⎫⎛⎫+== ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭但 2238681010162411812341527A AB B ⎛⎫⎛⎫⎛⎫⎛⎫++=++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭所以()2222A B A AB B +≠++(3)()()22A B A B A B +-≠- 因为 22022501A B A B ⎛⎫⎛⎫+=-=⎪ ⎪⎝⎭⎝⎭,,()()220206250109A B A B ⎛⎫⎛⎫⎛⎫+-== ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,而 223810284113417A B ⎛⎫⎛⎫⎛⎫-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故()()22A B A B A B +-≠-6.(1)取1111A O ⎛⎫=≠ ⎪--⎝⎭,而2A O =; (2)取1000A ⎛⎫=⎪⎝⎭,有A O A E ≠≠,,而2A A =; (3)取101010000001A X Y ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,有X Y ≠,而AX AY =.7. 21010101121A AA λλλ⎛⎫⎛⎫⎛⎫===⎪⎪ ⎪⎝⎭⎝⎭⎝⎭;3210101021131A A A λλλ⎛⎫⎛⎫⎛⎫=== ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭;由此推出 ()10231kA k k λ⎛⎫==⎪⎝⎭,,下面利用数学归纳法证明这个结论. 当12k k ==,时,结论显然成立. 假设1k -时结论成立,即有 ()11011k Ak λ-⎛⎫=⎪-⎝⎭则对于k 时,有 ()11010101111kk A A A k k λλλ-⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭,故结论成立. 8. 证明 由已知:T A A = TB B =充分性:由AB BA =,得T TAB B A =,所以()TAB AB =即 AB 是对称矩阵. 必要性:由()TAB AB =得,T T B A AB =所以BA AB =.9. (1) 公式法:1225A ⎛⎫= ⎪⎝⎭1A =112112225,2(1),2(1),1A A A A ==⨯-=⨯-=112112225221AA A A A *-⎛⎫⎛⎫== ⎪ ⎪-⎝⎭⎝⎭ 11A A A -*= 故 15221A --⎛⎫= ⎪-⎝⎭初等行变换法:()12102501AE ⎛⎫=⎪⎝⎭21212100121r r -⎛⎫−−−→ ⎪-⎝⎭12210520121r r --⎛⎫−−−→ ⎪-⎝⎭所以 15221A--⎛⎫= ⎪-⎝⎭. (2) 10A =≠ 故1A -存在11211222cos sin sin cos A A A A θθθθ===-=从而 1c o s s i n s i n c o s A θθθθ-⎛⎫=⎪-⎝⎭(3) 公式法;2A =, 故1A -存在 112131420A A A =-== 而 1222321361A A A =-==- 13233332142A A A =-==-故 11A A A -*=2101313221671-⎛⎫⎪ ⎪=-- ⎪⎪--⎝⎭初等行变换法:()121100342010541001AE -⎛⎫⎪=- ⎪ ⎪-⎝⎭ 2131351211000213100146501r r r r ---⎛⎫ ⎪−−−→-- ⎪ ⎪--⎝⎭3271211000213100011671r r --⎛⎫ ⎪−−−→-- ⎪ ⎪--⎝⎭2313120157102013610011671r r r r +---⎛⎫ ⎪−−−→-- ⎪ ⎪--⎝⎭3210021002013610011671r r +-⎛⎫ ⎪−−−→-- ⎪ ⎪--⎝⎭2122101001310103220011671r --⎛⎫ ⎪ ⎪−−−→-- ⎪- ⎪-⎝⎭所以 12101313221671A --⎛⎫⎪ ⎪=-- ⎪ ⎪--⎝⎭.(4)由对角矩阵的性质知 12110101n a a A a -⎛⎫ ⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪⎝⎭. 10. (1) 125461321X --⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭35461221--⎛⎫⎛⎫= ⎪⎪-⎝⎭⎝⎭22308-⎛⎫= ⎪⎝⎭(2) 1211113210432111X --⎛⎫-⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪-⎝⎭10111312324323330⎛⎫-⎛⎫ ⎪=-- ⎪ ⎪⎝⎭ ⎪-⎝⎭22182533-⎛⎫⎪= ⎪-- ⎪⎝⎭ (3) 11143120120111X --⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪---⎝⎭⎝⎭⎝⎭243110111011212-⎛⎫⎛⎫⎛⎫= ⎪⎪⎪-⎝⎭⎝⎭⎝⎭66101301212⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭11104⎛⎫⎪= ⎪⎝⎭11. 由22A A E O --=得22A A E -= 两端同时取行列式: 22A A -=即 2A A E -=,故 0A ≠ 所以A 可逆,而22A E A +=2220A E A A +==≠ 故2A E +也可逆.由22A A E O --=得()2A A E E -=所以 11()2A A A E A E ---=,则11()2AA E -=- 又由22A A E O --=(2)3(2)4A E A A E E +-+=-(2)(3)4A E A E E +-=-所以 11(2)(2)(3)4(2)A E A E A E A E --++-=-+则 11(2)(3)4A E E A -+=-. 12.()11k E A E A A ---=+++ .13. 因为11AA A-*=,所以 ()1111111255522A A A A A A A -*-----=-=- ()31112288216A A A ---=-=-=-=-⨯=-.14. 由11AA A-*=,得1A A A *-=, 所以 当A 可逆时,有110nn A A A A-*-==≠,从而A *也可逆.因为1A A A *-=,所以()11A AA --*=又()()1111A A A A A**---==,所以()()()11111A AA AA A A -**--*--===15. 由2AB E A B +=+得()2A E B A E -=-即()()()A E B A E A E -=-+因为 0011010100A E -==-≠,所以()A E -可逆,则 201030102B A E ⎛⎫ ⎪=+= ⎪ ⎪⎝⎭.16.600020001⎛⎫⎪ ⎪ ⎪⎝⎭.17.033123110⎛⎫ ⎪- ⎪ ⎪⎝⎭18. 因为AP P =Λ,所以1A P P -=Λ;又 1P =-, 1100210411P --⎛⎫ ⎪=- ⎪ ⎪-⎝⎭,55115⎛⎫⎪Λ ⎪ ⎪⎝⎭= 所以 1100110021012102115411A P P ---⎛⎫⎛⎫⎛⎫⎪⎪⎪=Λ=-- ⎪⎪⎪ ⎪⎪⎪-⎝⎭⎝⎭⎝⎭100200611⎛⎫ ⎪= ⎪ ⎪--⎝⎭5100200611A ⎛⎫⎪= ⎪ ⎪--⎝⎭.19. 因为()1111A B A E CA B B B A ----+=+=+,由()()1A B A B E -++=得()()()()111111AB A A B B A B A B B ------++=++=则()()1111A B A A B B B B E ----++==所以11A B --+可逆,其逆为()1A B A B -+.20. 213241221312131425400124262001221400011r r r r r r A -+---⎛⎫⎛⎫ ⎪ ⎪-- ⎪ ⎪=−−−→ ⎪ ⎪---- ⎪ ⎪--⎝⎭⎝⎭ 32344221312131001200120000000100010000r r r r r r B -↔+--⎛⎫⎛⎫⎪⎪-- ⎪ ⎪−−−→−−−→= ⎪⎪⎪ ⎪⎝⎭⎝⎭B 的秩为3,其一个3阶非零子式为13112001--,对应于A 的3阶非零子式为131254262----. 故2131001200010000-⎛⎫⎪- ⎪⎪⎪⎝⎭即为矩阵A 的行阶梯形矩阵,矩阵A 的一个最高阶非零子式为131254262----. 21.(1)111222111444513444⎛⎫- ⎪ ⎪⎪- ⎪ ⎪ ⎪-- ⎪⎝⎭,(2)72363211211022⎛⎫- ⎪ ⎪-- ⎪ ⎪- ⎪⎝⎭,(3)11240101113621610--⎛⎫ ⎪-⎪ ⎪-- ⎪--⎝⎭,(4)131120012100120001--⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. 22.(1)2,(2)3,(3)4,(4)当4a =-时,秩为2;当4a ≠-时,秩为3.24.34432022O A O ⎛⎫⎪- ⎪= ⎪ ⎪⎝⎭,令13443A ⎛⎫= ⎪-⎝⎭ 22022A ⎛⎫= ⎪⎝⎭ 则12A O A OA ⎛⎫=⎪⎝⎭故8182A O A O A ⎛⎫=⎪⎝⎭8182A O OA ⎛⎫= ⎪⎝⎭8888816121210A A A A A ===444414426450052022O A O A OA O ⎛⎫⎪⎛⎫ ⎪==⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭25. nn s ns s A O E O C B OE ⨯⎛⎫⎪⎝⎭ 111n nA r ns ns s EO A O C B OE --⨯⎛⎫−−−→ ⎪⎝⎭()2111r Cr nns n ns EOA O OB C A E ---⨯⎛⎫−−−−−→ ⎪-⎝⎭左乘 ()121111s s B r nns n nsA O EO B C A B O E -----⨯⎛⎫−−−−→ ⎪ ⎪-⎝⎭左乘 11111s s n s n nA O A OBC A B C B -----⨯⎛⎫⎛⎫= ⎪ ⎪ ⎪-⎝⎭⎝⎭利用这个结果取103021121412A B C ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,则由11111ss n s n n A O A O B C A B C B -----⨯⎛⎫⎛⎫= ⎪ ⎪ ⎪-⎝⎭⎝⎭得 112040111113212A B --⎛⎫⎛⎫== ⎪ ⎪--⎝⎭⎝⎭,,114021201241111312113512224B CA ----⎛⎫⎛⎫⎛⎫⎛⎫=-⋅= ⎪⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎝⎭-,则 1124080111212262424A B --⎛⎫⎛⎫== ⎪ ⎪--⎝⎭⎝⎭,故 110002400012001212001213012482412143526-⎛⎫⎛⎫⎪ ⎪-⎪ ⎪=⎪ ⎪--⎪ ⎪--⎝⎭⎝⎭习题31.设α=(1,1,0,-1)T ,β=(-2,1,0,0)T ,γ=(-1,-2,0,1)T ,求35αβγ-+.2.设34αβ+=(2,1,1,2)T 23αβ+=(-1,2,3,1)T求,αβ.3.解向量方程325X αβ-=其中,α=(3,5,7,9)T ,β=(-1,5,2,0)T .4.判断向量β能否由其余向量线性表示?若能,写出表示式.(1)β=(0,10,8,7)T ,1α=(-1,2,3,9)T ,2α=(1,3,1,0)T ,3α=(1,8,5,-2)T .(2)β=(1,2,1,1)T ,1α=(1,1,1,1)T ,2α=(1,1,-1,-1)T ,3α=(1,-1,1,-1)T ,4α=(1,-1,-1,1)T .5.设1α=(1+k ,1,1,1)T ,2α=(1,1+k ,1,1)T ,3α=(1,1,1+k ,1)T ,β=(1,3,2,1)T ,试问k 取何值时,β可由123,,ααα线性表示?并写出表示式.6.设1α=(1,0,2,3)T ,2α=(1,1,3,5)T ,3α=(1,-1,a +2,1)T ,4α=(1,2,4,a +8)T ,β=(1,1,b +3,5)T ,试问当,a b 为何值时.(1)β不能由1234,,,αααα线性表示;(2)β能由1234,,,αααα线性表示,且表示法唯一,并写出该表示式; (3)β能由1234,,,αααα线性表示,且表示法不唯一,并写出两个表示式.7.设向量β可由向量组12,,,m ααα 线性表示,但不能由121,,,m ααα- 线性表示,则向量组12,,,m ααα 与向量组121,,,,m αααβ- 等价.8.判断下列向量组是否线性相关?(1)1α=(2,2,7,-1)T ,2α=(3,-1,2,4)T ,3α=(1,1,3,1)T .(2)1α=(1,4,2,7)T ,2α=(3,2,4,5)T ,3α=(1,-1,2,2)T ,4α=(1,4,2,7)T .9.问k 取何值时下列向量组线性相关?线性无关?1α=(k ,2,1)T ,2α=(2,k ,0)T ,3α=(1,-1,1)T10.设向量组123,,ααα线性无关,112323βααα=--,21232βααα=++,3123βααα=-+,讨论向量组123,,βββ的线性相关性.11.已知向量组12,,,m ααα 线性无关,设112βαα=+,223βαα=+,…,11m m m βαα--=+,1m m βαα=+,讨论向量组12,,,m βββ 的线性相关性.12.设向量组12,,,m ααα 不含零向量,且αk (k =2,3,…,m)不能由121,,,k ααα- 线性表示,则向量组12,,,m ααα 线性无关.13.求下列向量组的秩及一个极大线性无关组,并用极大线性无关组线性表示其余向量.(1)1α=(2,1,3,-1)T ,2α=(3,-1,2,0)T ,3α=(1,3,4,-2)T ,4α=(4,-3,1,1)T .(2)1α=(1,2,3,-1)T ,2α=(3,2,1,-1)T ,3α=(2,3,1,1)T ,4α=(2,2,2,-1)T ,5α=(5,5,2,0)T .(3)1α=(1,2,-1,1)T ,2α=(2,0,k ,0)T ,3α=(0,-4,5,-2)T ,4α=(2,2,2,-1).(4)1α=(1,0,1,2)T ,2α=(0,1,1,2)T ,3α=(-1,1,0,k )T ,4α=(1,2,k ,6)T ,5α=(1,1,2,4)T .14.设12{,,,}m R ααα =12{,,,}t R βββ ,且12,,,m ααα 可由12,,,t βββ 线性表示,则向量组12,,,m ααα 与向量组12,,,t βββ 等价.15.设有两个向量组1α=(1,2,-1,3)T ,2α=(2,5,a ,8)T ,3α=(-1,0,3,1)T ;1β=(1,a ,2a -5,7)T ,2β=(3,3+a ,3,11)T ,3β=(0,1,6,2)T ,若1β可由123,,ααα线性表示,试判断这两个向量组是否等价?16.已知向量组1β=(0,1,-1)T ,2β=(a ,3,1)T ,3β=(b ,1,0)T 与向量组1α=(1,2,-3)T ,2α=(2,1,-1)T ,3α=(3,0,1)T 具有相同的秩,且3β可由123,,ααα线性表示,求,a b .17.判断下列集合是否是向量空间?为什么?若是向量空间,求出其维数及一个基. (1)V 1={(x 1,x 2,…,x n )T ∈R n |a 1x 1+a 2x 2 + … +a n x n =0},其中a i (i = 1,2,…,n )为R 中固定的数.(2)V 2={(x 1,x 2,…,x n )T ∈R n |a 1x 1+a 2x 2 + … +a n x n =1},其中a i (i = 1,2,…,n )为R 中固定的数.18.设123,,n R ααα∈.证明,若1122330k k k ααα++=且k 1k 2 ≠ 0,则L(α1,α3)=L(α2,α3).19.求下列向量生成子空间的维数与一个基.(1)1α=(-1,3,4,7)T ,2α=(2,1,-1,0)T ,3α=(1,2,1,3)T ,4α=(-4,1,5,6)T .(2)1α=(2,1,3,-1)T ,2α=(1,-1,3,-1)T ,3α=(4,5,3,-1)T ,4α=(1,5,3,-1)T .20.设1α=(1,0,-1)T ,2α=(2,1,1)T ,3α=(1,1,1)T ;1β=(3,1,4)T ,2β=(5,2,1)T ,3β=(1,1,-6)T .(1)证明123,,ααα与123,,βββ都是R 3的基; (2)求由基123,,ααα到基123,,βββ的过渡矩阵;(3)求坐标变换公式;(4)求α=(8,3,0)分别在基123,,ααα与基123,,βββ下的坐标.21.设α=(1,0,-1,0,1)T ,β=(0,1,0,2,0)T . (1)求αβ与的内积 [αβ,]; (2)求αβ与的长度||α||,||β||; (3)求αβ与的夹角θ.22.用施密特正交化方法将下列向量组标准正交化.(1)1α=(1,1,1,1)T ,2α=(3,3,-1,-1)T ,3α=(-2,0,6,8)T ; (2)1α=(1,1,1,0)T ,2α=(1,0,1,0)T ,3α=(-1,2,3,0)T . 23.求与向量1α=(1,0,-1,2)T ,2α=(0,1,1,0)T 都正交的向量. 24.判别下列矩阵是否为正交矩阵?并说明理由.(1)1100221100221111222211112222⎛⎫ ⎪⎪⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪-- ⎪⎝⎭,(2)11133311022211666⎛⎫⎪⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭25.设,n R αβ∈,A 是n 阶正交矩阵,证明:(1)[,A A αβ]=[,αβ]; (2)||A α||=||α||;(3)A α与A β的夹角等于α与β的夹角. 26.证明,若12,,,n ααα 是R n 的一组标准正交基,A 是n 阶正交矩阵,则12,,,n A A A ααα 也是R n 的一组标准正交基.解答习题31.(0,-8,0,2)T2.α=(10,-6,-10,2)T ,β=(-7,4,7,-1)T 3.X =12(14,-10,11,27)T 4.(1)能,β=α1+α3.(2)能,β=14(5α1+α 2 - α3 - α4) 5.k =3,β=13(2α2+α3) 6.(1)1,0a b =-≠,(2)12311,(2(1))1a b a b b a βααα≠-=-+++++ (3)2131,0.2a b βαβαα=-===-或8.(1)线性无关.(2)线性相关.9.k =3或k =-2时线性相关;k ≠3且k ≠ -2时线性无关. 10.线性无关.11.m 是奇数时线性无关,m 是偶数时线性相关.13.(1)秩=2;α1,α2是极大线性无关组;α3=2α1-α2,α4=-α1+2α2. (2)秩=3;α1,α2,α3是极大线性无关组;α4=121122αα+,α5=α2+α3. (3)k ≠3时:秩=4.k =3时:秩=3;α1,α2,α4是极大线性无关组;α3=-2α1+α2.(4)k ≠ 0且k ≠ 3时:秩=4;α1,α2,α3,α4是极大线性无关组;α5=α1+α2. k =3时:秩=3;α1,α2,α3是极大线性无关组;α4=α1+2α2,α5=α1+α2. k =0时:秩=3;α1,α2,α4是极大线性无关组;α3=-α1+α2,α5=α1+α2. 15.a =4,β1,β2,β3可由α1,α2,α3线性表示,但β1,β2,β3与α1,α2,α3不等价. 16.a =20,b = 5.17.(1)V 1是向量空间.当a i = 0 (i = 1,2,…,n)时:V 1=R n ;dimV 1 = n ;坐标单位向量ε1,ε2,…,εn 是V 1的基.当a i = 0 (i = 1,2,…,n)不全零时:dimV 1 = n -1;不妨设a 1≠0,则e 1 = (-a 2,a 1,0,…,0)T ,e 2 = (-a 3,0,a 1,…,0),…,e n -1 = (-a n ,0,…,a 1)是V 1的基.(2)V 2不是向量空间.19.(1)dimL(α1,α2,α3,α4) = 2;基是α1,α2. (2)dimL(α1,α2,α3,α4) = 3;基是α1,α2,α4.20.(2)317527408-⎛⎫⎪- ⎪ ⎪-⎝⎭;(3)112233317527408x y x y x y -⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭;(4)3,2,1与11145,,444--. 21.(1)0;(2)3,5;(3)2π.22.(1)123111(1,1,1,1),(2,2,2,2),(11,1,1)242T TT e e e ==--=--,. (2)123111(1,1,1,0),(1,2,1,0),(1,0,1,0)362T T T e e e ==-=-. 23.(-4,-2,2,3).24.(1)是正交矩阵;(2)是正交矩阵.习题41. 用消元法解下列线性方程组:(1)123412341234 2 0,3 630,51050;x x x x x x x x x x x x ++-=⎧⎪+--=⎨⎪++-=⎩ (4)23y z 4,2y 4z 5,38y 2z 13,4 y 9z 6;x x x x ++=⎧⎪-+=-⎪⎨+-=⎪⎪-+=-⎩2.三个工厂分别有3吨、2吨和1吨的产品要送到两个仓库储藏,两个仓库各储藏产品4吨和2吨,用ij x 表示从第i 个工厂送到第j 个仓库的产品数(1,2,3;1,2i j ==),试列出ij x 所满足的关系式,并求解由此得到的线性方程组.3.写出一个以x 1222341001c c -⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭(12,c c ∈ )为全部解的齐次线性方程组.4.确定,a b 的值使下列齐次线性方程组有非零解,并在有非零解时,求其全部解:(1)1231231232 30,3470, 20;x x x x x x x x ax -+=⎧⎪-+=⎨⎪-+=⎩ (2)123123123 0,0, 20.ax x x x bx x x bx x ++=⎧⎪++=⎨⎪++=⎩5.λ取何值时,下列非齐次线性方程组有唯一解、无解或有无限多个解?并在有无限多个解时求解:(1)1231232123 1, , ;x x x x x x x x x λλλλλ⎧++=⎪++=⎨⎪++=⎩ (2)123123123(2) 2 21, 2(5) 42, 2 4(5) 1.x x x x x x x x x λλλλ-+-=⎧⎪+--=⎨⎪--+-=--⎩6.设A 是实矩阵,证明()()T R A A R A =.7.求下列齐次线性方程组的基础解系:(1)123412341234 81020,24 5 0,38 620;x x x x x x x x x x x x -++=⎧⎪++-=⎨⎪++-=⎩ (2)123412341234232 0,35420,87630;x x x x x x x x x x x x --+=⎧⎪++-=⎨⎪++-=⎩8.设12,αα是某个齐次线性方程组的基础解系,证明:1212,2αααα+-也是该线性方程组的基础解系.9.设A 是n 阶方阵,0Ax =只有零解,求证:对任意的正整数k ,0kA x =也只有 零解.10.设A 22139528-⎛⎫=⎪-⎝⎭,求一个42⨯矩阵B ,使AB =0,且R (B )2=.11.求一个齐次线性方程组,使它的基础解系由下列向量组成:1ξ0123⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,2ξ3210⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭. 12.求下列非齐次线性方程组的通解:(1)1212341234 5,2 21,53220;x x x x x x x x x x +=⎧⎪+++=⎨⎪+++=⎩ (2)123412341234 52311,536 1,242 6.x x x x x x x x x x x x -+-=⎧⎪++-=-⎨⎪+++=-⎩13.证明:线性方程组121232343454515,,,,x x a x x a x x a x x a x x a -=-=-=-=-=.有解的充分必要条件是123450a a a a a ++++=.14.设四元非齐次线性方程组Ax b =的系数矩阵A 的秩为2,已知它的三个解向量为1η,2η,3η,其中1η4321⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,2η1351⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,3η2632-⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,求该方程组的通解.15.设矩阵A 121201101t t t ⎛⎫⎪= ⎪ ⎪⎝⎭,齐次线性方程组0Ax =的基础解系含有两个线性无关的解向量,试求方程组0Ax =的全部解.16.设A 21120131,11λμ⎛⎫ ⎪= ⎪ ⎪⎝⎭b 010⎛⎫ ⎪= ⎪ ⎪⎝⎭,η1111⎛⎫ ⎪- ⎪= ⎪ ⎪-⎝⎭,如果η是方程组Ax b =的一个解,试求方程组Ax b =的全部解.17.设η*是非齐次线性方程组Ax b =的一个解,1ξ,2ξ,…,n r ξ-是对应的齐次线性方程组的一个基础解系,证明:(1)η*,1ξ,2ξ,…,n r ξ-线性无关;(2) η*,η*+1ξ,…,η*+n r ξ-线性无关.18.若1η,2η,…,s η为非齐次线性方程组Ax b =的s 个解,12,,,s k k k 为常数,且121s k k k +++= ,证明:1k 1η+2k 2η+…+s k s η也是非齐次线性方程组Ax b =的解. 19.设非齐次线性方程组Ax b =的系数矩阵A 的秩为r ,1η,2η,…,1n r η-+是它的1n r -+个线性无关的解,试证:它的任一解可表示为x =1k 1η+2k 2η+…+1n r k -+1n r η-+,其中1211n r k k k -++++= .20.用克拉默(Cramer )法则解下列方程组:(1)1234123412341234 5, 2 42,23 52,3 2110;x x x x x x x x x x x x x x x x +++=⎧⎪+-+=-⎪⎨---=-⎪⎪+++=⎩ (2)12342345123234345 0,0,23 2, 23 2,23 2.x x x x x x x x x x x x x x x x x +++=⎧⎪+++=⎪⎪++=⎨⎪++=-⎪⎪++=⎩21.判断齐次线性方程组12312312322 0,240,5820;x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩ 是否仅有零解.22.问,λμ取何值时,齐次线性方程组123123123 0,0, 20;x x x x x x x x x λμμ++=⎧⎪++=⎨⎪++=⎩ 有非零解?23.问λ取何值时,齐次线性方程组123123123(1) 2 40,2(3) 0, (1)0;x x x x x x x x x λλλ--+=⎧⎪+-+=⎨⎪++-=⎩有非零解?24.证明:平面上三条不同的直线0,0,0ax by c bx cy a cx ay b ++=++=++=相交于一点的充分必要条件是 0a b c ++=.解答习题41.(1)11221121234222110,(,)00001x c c x c c c c c x x c -+-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==+∈ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ . (2)212121210x c y c c z c ----⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=+=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,(c ∈ ).2.ij x (1,2,3;1,2i j ==)所满足的关系式为:111221223132112131122232 3,2,1,4, x x x x x x x x x x x x +=+=+=++=++=1112212231322,6;x x x x x x ⎧⎪⎪⎪⎪⎨⎪⎪⎪+++++=⎪⎩ 11121212211122213123221111221122100101101001x c c x c c x c c c x c x c x c ++⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪---- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--==++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,(12,c c ∈ ). 3.134234220,340.x x x x x x -+=⎧⎨+-=⎩4.(1)123111x c x c c x c --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,(c ∈ ).(2)当0b =或10a -=时,即0b =或1a =时,齐次线性方程组有非零解.当1a =时,有1231001x c x c x c --⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,(c ∈ ).当0b =时,有1231(1)11x c x a c c a x c --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,(c ∈ ).5.(1)当1,2λ≠-时,非齐次线性方程组有唯一解;当2λ=-时,非齐次线性方程组无解;当1λ=时,非齐次线性方程组有无限多个解,有1122112321111010001x c c x c c c x c ----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪==++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,(12,c c ∈ ). (2)当1λ≠且10λ≠时,非齐次线性方程组有唯一解; 当10λ=时,非齐次线性方程组无解;当1λ=时,非齐次线性方程组有无数多个解,有112211232122122010001x c c x c c c x c -+-⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪==++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,(12,c c ∈ ).7.(1)1ξ43410-⎛⎫ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪⎝⎭,2ξ01401⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭, (2)1ξ11971901⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭,2ξ219141910⎛⎫- ⎪ ⎪ ⎪-= ⎪ ⎪⎪ ⎪⎝⎭.10.115118008B -⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭11.12312420,230.x x x x x x -+=⎧⎨-+=⎩12.(1)x 111161,01702c -⎛⎫-⎛⎫ ⎪ ⎪⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭(c ∈ ).(2)x 1291172211,72001010c c ⎛⎫⎛⎫- ⎪ ⎪⎛⎫⎪ ⎪ ⎪- ⎪ ⎪ ⎪-=++ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭(12,c c ∈ ).14.x 1131221()(),c c ηηηηη=+-+-(12,c c ∈ ).15.x 121011,1001c c ⎛⎫⎛⎫ ⎪ ⎪-- ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭(12,c c ∈ ).16.λμ=,当12λ=,非齐次线性方程组有无限多个解,x 1211122311,100001c c ⎛⎫⎛⎫--⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪- ⎪-=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(12,c c ∈ ). 当12λ≠,非齐次线性方程组有无限多个解,有x 011122,112201c -⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭(c ∈ ).20.(1)12341231x x x x ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭, (2)1234511111x x x x x ⎛⎫⎛⎫⎪ ⎪- ⎪ ⎪ ⎪ ⎪= ⎪ ⎪-⎪ ⎪ ⎪⎪⎝⎭⎝⎭.21.齐次线性方程组仅有零解.22.当0μ=或1λ=时,齐次线性方程组有非零解. 23.当0,23λ=或时,齐次线性方程组有非零解.习题51.求下列矩阵的特征值和特征向量.(1)3151⎛⎫ ⎪-⎝⎭;(2)200202311-⎛⎫ ⎪ ⎪ ⎪⎝⎭;(3)122212221⎛⎫ ⎪ ⎪ ⎪⎝⎭,(4)1111111111111111⎛⎫⎪-- ⎪ ⎪-- ⎪--⎝⎭. 2.证明下列各题:(1)设A 是幂等矩阵(即满足2A A =),则A 的特征值只能0是或1;. (2)设A 是正交矩阵,则A 的实特征值的绝对值为1.3.已知3阶矩阵A 的特征值为1,0,2-,计算行列式2A A E -+.4.已知3阶矩阵A 的特征值为1,2,3-,计算行列式*|32|A A E ++.5.设,A B 都是n 阶方阵,且A 可逆,证明AB 与BA 相似.6.判断矩阵⎪⎪⎪⎭⎫ ⎝⎛----=201335212A 可否对角化,若能的话,将它化为标准形.7.设矩阵20022311A a -⎛⎫ ⎪= ⎪ ⎪⎝⎭与10002000b -⎛⎫ ⎪Λ= ⎪ ⎪⎝⎭相似,求,a b ;并求一个可逆矩阵P ,使1P AP -=Λ.8.设20131405A a ⎛⎫ ⎪= ⎪ ⎪⎝⎭,问a 为何值时,矩阵A 可对角化?9.试求一个正交的相似变换矩阵,将下列实对称矩阵化为对角矩阵:(1)120222023-⎛⎫ ⎪-- ⎪ ⎪-⎝⎭;(2)400031013⎛⎫ ⎪ ⎪ ⎪⎝⎭;(3)222254245-⎛⎫ ⎪- ⎪ ⎪--⎝⎭;(4)0111101111011110-⎛⎫ ⎪- ⎪ ⎪- ⎪-⎝⎭. 10.将矩阵102012220A -⎛⎫⎪= ⎪ ⎪⎝⎭用两种方法对角化:(1)求一个可逆矩阵P ,使1P AP -为对角阵;(2)求一个正交矩阵T ,使1T AT -为对角矩阵.11.设3阶矩阵A 的特征值为1232,1,2λλλ=-==;对应的特征向量依次为1231101,1,1101ξξξ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,求矩阵A .12.设3阶实对称矩阵A 的特征值1231,0,1λλλ=-==;属于12,λλ的特征向量依次为12221,221ξξ⎛⎫⎛⎫⎪ ⎪==- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,求一个正交矩阵T ,使1T AT -为对角矩阵.13.设3阶实对称矩阵A 的特征值1231,1λλλ=-==;属于特征值11λ=-的特征向量为1011ξ⎛⎫⎪= ⎪ ⎪⎝⎭,求矩阵A .14.设120020211⎛⎫ ⎪= ⎪ ⎪---⎝⎭A ,求100A . 15.在某国,每年有比例为p 的农村居民移居城镇,有比例为q 的城镇居民移居农村.假设该国总人数不变,且上述人口迁移的规律也不变.把n 年后农村人口和城镇人口占总人数的比例依次记为n x 和n y (1)n n x y +=.(1)求11n n x y ++⎛⎫⎪⎝⎭与n n x y ⎛⎫⎪⎝⎭的关系式并写成矩阵形式:11++⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭n n n n x x A y y ; (2)设目前农村人口与城镇人口相等,即001212x y ⎛⎫ ⎪⎛⎫= ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭,求n n x y ⎛⎫⎪⎝⎭.解答习题51.(1)1212112,4;,15λλξξ⎛⎫⎛⎫=-=== ⎪ ⎪-⎝⎭⎝⎭;(2)1231230011,2,2;(,,)210111λλλξξξ-⎛⎫ ⎪=-==-=- ⎪ ⎪⎝⎭;(3)1231231011,5;(,,)011111λλλξξξ⎛⎫ ⎪==-== ⎪ ⎪--⎝⎭; (4)12341234111111002,2;(,,,)10101001λλλλξξξξ-⎛⎫ ⎪⎪=-==== ⎪ ⎪⎝⎭. 3.9. 4.-25.6.A 不可对角化.7.100110,2;210,21112---⎛⎫⎛⎫ ⎪ ⎪==-=-= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭a b P P AP .8.3=a .9.(1)12213332122,13335212333-⎛⎫ ⎪⎛⎫ ⎪ ⎪ ⎪=--=- ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪- ⎪⎝⎭T T AT ; (2)10102110,422411022-⎛⎫⎪ ⎪⎛⎫ ⎪ ⎪==⎪ ⎪ ⎪ ⎪⎝⎭ ⎪-⎪⎝⎭T T AT ;(3)12251153511452,115351052033-⎛⎫-- ⎪ ⎪⎛⎫ ⎪ ⎪⎪=-= ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪ ⎪⎝⎭T T AT ;(4)111112261211111122612,1211026123310212-⎛⎫-⎪ ⎪⎛⎫ ⎪-- ⎪⎪ ⎪⎪== ⎪ ⎪- ⎪ ⎪-⎝⎭ ⎪ ⎪ ⎪⎝⎭T T AT . 10.(1)11223221,02123-⎛⎫⎛⎫⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭P P AP ;(2)11223333221,03333212333-⎛⎫ ⎪⎛⎫ ⎪ ⎪⎪=-= ⎪ ⎪ ⎪- ⎪⎝⎭ ⎪- ⎪⎝⎭T T AT . 11.233453442--⎛⎫ ⎪=-- ⎪ ⎪--⎝⎭A .12.12213331122,03331212333-⎛⎫ ⎪-⎛⎫ ⎪ ⎪⎪=-= ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪- ⎪⎝⎭T T AT . 13.100001010⎛⎫ ⎪=- ⎪ ⎪-⎝⎭A .14.101100100100122002050(12)13⎛⎫⎪- ⎪= ⎪ ⎪- ⎪⎝⎭A. 15.(1)1111++-⎛⎫⎛⎫⎛⎫=⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭n n n n x x p q y y p q ;(2)2()(1)12()2()(1)⎛⎫⎛⎫+---= ⎪⎪++---⎝⎭⎝⎭n n n n x q p q p q y p q p q p p q .习题61.证明:123000000a a a ⎛⎫⎪ ⎪ ⎪⎝⎭与23100000a a a ⎛⎫ ⎪⎪ ⎪⎝⎭合同. 2.写出下列二次型的矩阵表示: (1)121323422f x x x x x x =-++;(2)2224424f x xy y xz z yz =+++++;(3)22221234121314232424264f x x x x x x x x x x x x x x =+++-+-+-.3.设A 是一个n 阶对称矩阵.如果对任一个n 维列向量x ,都有0Tx Ax =,试证0A =. 4.用拉格朗日配方法化下列二次型为标准形. (1)123422x x x x -;(2)22121213222x x x x x x ++-.*5.用初等变换法化下列二次型为标准形.(1)12132346x x x x x x -+;(2)222123232334x x x x x +++.6.用正交变换法化下列二次型为标准形.(1)22212312132325228x x x x x x x x x +++++;(2)121314232434 222222x x x x x x x x x x x x +--++. 7.求一个正交变换把二次曲面的方程22234545101x xy y xz z yz ++-+-=化成标准方程.8.化下列二次型为规范形.(1)22212312133524x x x x x x x +++-;(2)22212312232422x x x x x x x +++-.9.证明:秩等于r 的对称矩阵可以表成r 个秩等于1的对称矩阵之和. 10.判别下列二次型是否正定:(1)2221231231223(,,)2342f x x x x x x x x x x =+-++;(2)2222123412341213142434(,,,)3919242612f x x x x x x x x x x x x x x x x x x =+++-++--.11.t 满足什么条件时,下列二次型是正定的:(1)222123123121323(,,)5224f x x x x x x tx x x x x x =+++-+; (2)2221231231223(,,)2322f x x x x x x tx x x x =++-+.12.试证:如果A 是正定矩阵,那么A 的主子式全大于零. 13.试证:如果A 是正定矩阵,那么 (1)(0)kA k >是正定矩阵; (2)1A -是正定矩阵.14.试证:如果,A B 是同阶正定矩阵,那么A B +也是正定矩阵.*15.试证:实二次型12(,,,)n f x x x 是半正定的充分必要条件是12(,,,)n f x x x 的正惯性指数等于它的秩.*16.试证:实二次型12(,,,)T n f x x x x Ax = 是半正定的充分必要条件是A 的特征值全大于或等于零.解答习题62.(1)112323021(,,)201110x f x x x x x -⎛⎫⎛⎫ ⎪⎪=- ⎪⎪ ⎪⎪⎝⎭⎝⎭;(2)121(,,)242121x f x y z y z ⎛⎫⎛⎫ ⎪⎪= ⎪⎪ ⎪⎪⎝⎭⎝⎭;(3)1212343411211132(,,,)23101201x x f x x x x x x --⎛⎫⎛⎫ ⎪⎪-- ⎪⎪= ⎪⎪ ⎪⎪--⎝⎭⎝⎭.4.(1)1132133244242222222222222222x y yx y yx y yx y y⎧=+⎪⎪⎪=-⎪⎪⎨⎪=+⎪⎪⎪=-+⎪⎩,22221234f y y y y=+--;(2)112322323x y y yx yx y y=+-⎧⎪=⎨⎪=-+⎩,222123f y y y=--.5.(1)112321233233626526x y y yx y y yx y y⎧=--⎪⎪⎪=--⎨⎪⎪=+⎪⎩,222123f y y y=+-;(2)1122332311221122x yx y yx y y⎧⎪=⎪⎪=+⎨⎪⎪=-⎪⎩,22212325f y y y=++.6.(1)11232233323x y y yx y yx y=-+⎧⎪=-⎨⎪=⎩,2221235f y y y=+-;(2)1124212431344134111222111222111222111222x y y yx y y yx y y yx y y y⎧=++⎪⎪⎪=-+-⎪⎪⎨⎪=-++⎪⎪⎪=+-⎪⎩,222212343f y y y y=-+++.7.4133212133221213322x u v y u v w z u v w ⎧=+⎪⎪⎪=-++⎨⎪⎪=-+⎪⎩,222111u v +=.8.(1)112322323522122x y y y x y x y y ⎧=-+⎪⎪⎪=⎨⎪⎪=-+⎪⎩,222123f y y y =-+; (2)112322333111222222212x y y y x y y x y ⎧=--⎪⎪⎪=+⎨⎪⎪=⎪⎩222123f y y y =++. 10.(1)负定;(2)正定. 11.(1)0.80t -<<;(2)151533t -<<.。
同济大学线性代数第六版课后答案(全).

第一章 行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102---;解 381141102---=2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4. (2)b a c a c b cb a ;解 ba c a cb cb a=acb +bac +cba -bbb -aaa -ccc =3abc -a 3-b 3-c 3.(3)222111c b a c b a ;解 222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).(4)y x y x x y x y yx y x +++.解 yx y x x y x y yx y x +++=x (x +y )y +yx (x +y )+(x +y )yx -y 3-(x +y )3-x 3 =3xy (x +y )-y 3-3x 2 y -x 3-y 3-x 3 =-2(x 3+y 3).2. 按自然数从小到大为标准次序, 求下列各排列的逆序数:(1)1 2 3 4; 解 逆序数为0 (2)4 1 3 2;解 逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解 逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解 逆序数为3: 2 1, 4 1, 4 3. (5)1 3 ⋅ ⋅ ⋅ (2n -1) 2 4 ⋅ ⋅ ⋅ (2n );解 逆序数为2)1(-n n :3 2 (1个) 5 2, 5 4(2个) 7 2, 7 4, 7 6(3个)⋅⋅⋅⋅⋅⋅(2n-1)2, (2n-1)4, (2n-1)6,⋅⋅⋅, (2n-1)(2n-2) (n-1个)(6)1 3 ⋅⋅⋅(2n-1) (2n) (2n-2) ⋅⋅⋅ 2.解逆序数为n(n-1) :3 2(1个)5 2, 5 4 (2个)⋅⋅⋅⋅⋅⋅(2n-1)2, (2n-1)4, (2n-1)6,⋅⋅⋅, (2n-1)(2n-2) (n-1个)4 2(1个)6 2, 6 4(2个)⋅⋅⋅⋅⋅⋅(2n)2, (2n)4, (2n)6,⋅⋅⋅, (2n)(2n-2) (n-1个)3.写出四阶行列式中含有因子a11a23的项.解含因子a11a23的项的一般形式为(-1)t a11a23a3r a4s,其中rs是2和4构成的排列,这种排列共有两个,即24和42.所以含因子a11a23的项分别是(-1)t a11a23a32a44=(-1)1a11a23a32a44=-a11a23a32a44,(-1)t a11a23a34a42=(-1)2a11a23a34a42=a11a23a34a42.4.计算下列各行列式:(1)71100251020214214; 解 71100251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-; 解 2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r 000003212213041214=--=====r r . (3)efcf bf de cd bd aeac ab ---;解 efcf bf de cd bd ae ac ab ---e c b e c b ec b adf ---=abcdef adfbce 4111111111=---=.(4)dc b a 100110011001---. 解d c b a 100110011001---dc b aab ar r 10011001101021---++===== dc a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ada ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 5. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=y x z x z y zy x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ; 证明 2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2, c 2-c 1得) 5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2得)022122212221222122222=++++=d d c c b b a a . (4)444422221111d c b a d c b a d c b a =(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ); 证明 444422221111d c b a d c b a d c b a )()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b ad a c a b ---------=)()()(111))()((222a d d a c c a b b d c b a d a c a b +++---=))(())((00111))()((a b d b d d a b c b c c b d b c a d a c a b ++-++------=)()(11))()()()((a b d d a b c c b d b c a d a c a b ++++-----==(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ).(5)1221 1 000 00 1000 01a x a a a a x x xn n n+⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--- =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .证明 用数学归纳法证明.当n =2时, 2121221a x a x a x a x D ++=+-=, 命题成立. 假设对于(n -1)阶行列式命题成立, 即 D n -1=x n -1+a 1 x n -2+ ⋅ ⋅ ⋅ +a n -2x +a n -1, 则D n 按第一列展开, 有11100 100 01)1(11-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--+=+-x x a xD D n n n n =xD n -1+a n =x n +a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n . 因此, 对于n 阶行列式命题成立.6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90︒、或依副对角线翻转, 依次得nnn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nn n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= , 11113 a a a a D n nnn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(--==, D 3=D .证明 因为D =det(a ij ), 所以 nnn n n n nnnn a a a a a a a a a a D 2211111111111 )1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=-⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--=-- )1()1(331122111121nnn n nn n n a a a a a a a a D D n n n n 2)1()1()2( 21)1()1(--+-+⋅⋅⋅++-=-=.同理可证 nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=- )1(11112)1(2D D n n T n n 2)1(2)1()1()1(---=-=. D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k 为k 阶行列式): (1)aa D n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解 aa a a a D n 010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 0000 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa a a x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得 ax x a ax x a a x x a a a a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n -1. (3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n n nn n ; 解 根据第6题结果, 有nn n n n n n n n n a a a n a a a n a a aD )( )1()( )1( 11 11)1(1112)1(1-⋅⋅⋅--⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=---++此行列式为范德蒙德行列式.∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++---=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+-++-⋅-⋅-=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+-=11)(j i n j i .(4)nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112; 解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开) nn n n n nd d c d c b a b a a 00011111111----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn ----+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-+. 再按最后一行展开得递推公式D 2n =a n d n D 2n -2-b n c n D 2n -2, 即D 2n =(a n d n -b n c n )D 2n -2. 于是 ∏=-=ni i i i i n D c b d a D 222)(.而 111111112c b d a d c b a D -==, 所以 ∏=-=ni i i i i n c b d a D 12)(.(5) D =det(a ij ), 其中a ij =|i -j |; 解 a ij =|i -j |, 043214 01233 10122 21011 3210)det(⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅==n n n n n n n n a D ij n 04321 1 11111 11111 11111 1111 2132⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅--⋅⋅⋅-=====n n n n r r r r15242321 0 22210 02210 00210 0001 1213-⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅-+⋅⋅⋅+=====n n n n n c c c c =(-1)n -1(n -1)2n -2. (6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121 nn n n a a a a a a a a a c c c c +-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=====--10 0001 000 100 0100 0100 0011332212132 1111312112111011 000 00 11000 01100 001 ------+-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅⋅⋅⋅=nn n a a a a a a a a∑=------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 00010 000 00 10000 01000 001)11)((121∑=+=ni i n a a a a .8. 用克莱姆法则解下列方程组:(1)⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解 因为14211213513241211111-=----=D , 142112105132412211151-=------=D , 284112035122412111512-=-----=D , 426110135232422115113-=----=D , 14202132132212151114=-----=D , 所以 111==D D x , 222==D D x , 333==D D x , 144-==DDx .(2)⎪⎪⎩⎪⎪⎨⎧=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解 因为 665510006510006510065100065==D , 150751001651000651000650000611==D , 114551010651000650000601000152-==D , 70351100650000601000051001653==D , 395510601000051000651010654-==D , 2121105100065100651100655==D , 所以66515071=x , 66511452-=x , 6657033=x , 6653954-=x , 6652124=x .9. 问λ, μ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 系数行列式为μλμμμλ-==1211111D .令D =0, 得 μ=0或λ=1.于是, 当μ=0或λ=1时该齐次线性方程组有非零解.10. 问λ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解?解 系数行列式为λλλλλλλ--+--=----=101112431111132421D=(1-λ)3+(λ-3)-4(1-λ)-2(1-λ)(-3-λ) =(1-λ)3+2(1-λ)2+λ-3. 令D =0, 得λ=0, λ=2或λ=3.于是, 当λ=0, λ=2或λ=3时, 该齐次线性方程组有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换. 解 由已知:⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y ,⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A T B .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503, ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T . 4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫⎝⎛=49635.(2)⎪⎪⎭⎫⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫⎝⎛---=632142. (4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ; 解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B )2=A 2+2AB +B 2吗? 解 (A +B )2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但 ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610, 所以(A +B )2≠A 2+2AB +B 2. (3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.6. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y , 则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k . 解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k . 8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k .解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫⎝⎛=222002012λλλλλ,⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵.证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA .证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以 (AB )T =(BA )T =A T B T =AB , 即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB )T =AB , 所以 AB =(AB )T =B T A T =BA . 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为 ⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解 ⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A |=1≠0, 故A -1存在. 因为 ⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,所以 *||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos . (3)⎪⎪⎭⎫⎝⎛---145243121;解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以 *||11A A A =-⎪⎪⎪⎭⎫⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程:(1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ;解 ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232. (2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311111012112X ;解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131⎪⎪⎭⎫⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ;解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111.(4)⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X .解 11010100001021102341100001010--⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012.13. 利用逆矩阵解下列线性方程组: (1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x ,从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x ,故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ). 另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或 E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或 E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1, )3(41)2(1A E E A -=+-.16. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|.解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A |-1=-8⨯2=-16. 17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)-1=(A -1)*.证明 由*||11A A A =-, 得A *=|A |A -1, 所以当A 可逆时, 有 |A *|=|A |n |A -1|=|A |n -1≠0, 从而A *也可逆.因为A *=|A |A -1, 所以 (A *)-1=|A |-1A .又*)(||)*(||1111---==A A A A A , 所以(A *)-1=|A |-1A =|A |-1|A |(A -1)*=(A -1)*. 18. 设n 阶矩阵A 的伴随矩阵为A *, 证明: (1)若|A |=0, 则|A *|=0; (2)|A *|=|A |n -1. 证明(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)-1=E , 由此得 A =A A *(A *)-1=|A |E (A *)-1=O ,所以A *=O , 这与|A *|≠0矛盾,故当|A |=0时, 有|A *|=0. (2)由于*||11A A A =-, 则AA *=|A |E , 取行列式得到|A ||A *|=|A |n . 若|A |≠0, 则|A *|=|A |n -1;若|A |=0, 由(1)知|A *|=0, 此时命题也成立. 因此|A *|=|A |n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E )B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E )B =A 2-E , 即 (A -E )B =(A -E )(A +E ).因为01001010100||≠-==-E A , 所以(A -E )可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B . 解 由A *BA =2BA -8E 得 (A *-2E )BA =-8E , B =-8(A *-2E )-1A -1 =-8[A (A *-2E )]-1 =-8(AA *-2A )-1 =-8(|A |E -2A )-1 =-8(-2E -2A )-1 =4(E +A )-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B .解 由|A *|=|A |3=8, 得|A |=2. 由ABA -1=BA -1+3E 得 AB =B +3A ,B =3(A -E )-1A =3[A (E -A -1)]-1A 11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511,求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)]=diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B )B -1=B -1+A -1=A -1+B -1,而A -1(A +B )B -1是三个可逆矩阵的乘积, 所以A -1(A +B )B -1可逆, 即A -1+B -1可逆.(A -1+B -1)-1=[A -1(A +B )B -1]-1=B (A +B )-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解 设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B ,则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫⎝⎛+=222111B A O B B A A ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A , 所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠.解 4100120021010*********0021010010110100101==--=--=D C B A , 而 01111|||||||| ==D C B A ,故 |||||||| D C B A D C B A ≠.28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A ,则 ⎪⎭⎫⎝⎛=21A O O A A ,故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A , 1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求 (1)1-⎪⎭⎫ ⎝⎛O B A O ; 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则 ⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n EBC OBC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C OC A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A . 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得 ⎪⎩⎪⎨⎧=+=+==s nEBD CD O BD CD OAD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001. 解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A B C O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201;解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫⎝⎛100001000001.(2)⎪⎪⎭⎫⎝⎛----174034301320;解 ⎪⎪⎭⎫⎝⎛----174034301320(下一步: r 2⨯2+(-3)r 1, r 3+(-2)r 1. )~⎪⎪⎭⎫⎝⎛---310031001320(下一步: r 3+r 2, r 1+3r 2. )~⎪⎪⎭⎫⎝⎛0000310010020(下一步: r 1÷2. )~⎪⎪⎭⎫⎝⎛000031005010.(3)⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311;解 ⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011.(4)⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.解 ⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132(下一步: r 1-2r 2, r 3-3r 2, r 4-2r 2. )~⎪⎪⎪⎭⎫⎝⎛-----1187701298804202111110(下一步: r 2+2r 1, r 3-8r 1, r 4-7r 1. )~⎪⎪⎪⎭⎫⎝⎛--41000410002020111110(下一步: r 1↔r 2, r 2⨯(-1), r 4-r 3. )~⎪⎪⎪⎭⎫⎝⎛----00000410001111020201(下一步: r 2+r 3. )~⎪⎪⎪⎭⎫⎝⎛--000410*******20201. 2. 设⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A , 求A .解 ⎪⎪⎭⎫⎝⎛100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身.⎪⎪⎭⎫⎝⎛100010101是初等矩阵E (1, 2(1)), 其逆矩阵是E (1, 2(-1)) ⎪⎪⎭⎫⎝⎛-=100010101.⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=100010101987654321100001010A⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=287221254100010101987321654.3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫⎝⎛-------106126311101042111000010000100001故逆矩阵为⎪⎪⎪⎭⎫⎝⎛-------10612631110104211. 4. (1)设⎪⎪⎭⎫ ⎝⎛--=113122214A , ⎪⎪⎭⎫⎝⎛--=132231B , 求X 使AX =B ;解 因为⎪⎪⎭⎫ ⎝⎛----=132231 113122214) ,(B A ⎪⎪⎭⎫⎝⎛--412315210 100010001 ~r ,所以 ⎪⎪⎭⎫⎝⎛--==-4123152101B A X .(2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B . 解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r ,所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X . 5. 设⎪⎪⎭⎫⎝⎛---=101110011A , AX =2X +A , 求X .解 原方程化为(A -2E )X =A . 因为⎪⎪⎭⎫⎝⎛---------=-101101110110011011) ,2(A E A⎪⎪⎭⎫⎝⎛---011100101010110001~,所以 ⎪⎪⎭⎫⎝⎛---=-=-011101110)2(1A E A X .6. 在秩是r 的矩阵中,有没有等于0的r -1阶子式? 有没有等于0的r 阶子式?解 在秩是r 的矩阵中, 可能存在等于0的r -1阶子式, 也可能存在等于0的r 阶子式.例如, ⎪⎪⎭⎫⎝⎛=010*********A , R (A )=3.0000是等于0的2阶子式, 010001000是等于0的3阶子式. 7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样?解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式:(1)⎪⎪⎭⎫⎝⎛---443112112013;解 ⎪⎪⎭⎫⎝⎛---443112112013(下一步: r 1↔r 2. )~⎪⎪⎭⎫⎝⎛---443120131211(下一步: r 2-3r 1, r 3-r 1. )~⎪⎪⎭⎫⎝⎛----564056401211(下一步: r 3-r 2. )~⎪⎭⎫ ⎝⎛---000056401211, 矩阵的2秩为, 41113-=-是一个最高阶非零子式.(2)⎪⎪⎭⎫⎝⎛-------815073*********;解 ⎪⎪⎭⎫⎝⎛-------815073*********(下一步: r 1-r 2, r 2-2r 1, r 3-7r 1. )~⎪⎭⎫ ⎝⎛------15273321059117014431(下一步: r 3-3r 2. ) ~⎪⎭⎫ ⎝⎛----0000059117014431, 矩阵的秩是2, 71223-=-是一个最高阶非零子式.(3)⎪⎪⎪⎭⎫⎝⎛---02301085235703273812. 解 ⎪⎪⎪⎭⎫⎝⎛---02301085235703273812(下一步: r 1-2r 4, r 2-2r 4, r 3-3r 4. )~⎪⎪⎪⎭⎫⎝⎛------023*********63071210(下一步: r 2+3r 1, r 3+2r 1. )~⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210(下一步: r 2÷16r 4, r 3-16r 2. )~⎪⎪⎪⎭⎫⎝⎛-02301000001000071210 ~⎪⎪⎪⎭⎫⎝⎛-00000100007121002301, 矩阵的秩为3, 070023085570≠=-是一个最高阶非零子式.10. 设A 、B 都是m ⨯n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ).证明 根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2;(3)当k ≠1且k ≠-2时, R (A )=3.12. 求解下列齐次线性方程组: (1)⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛--212211121211~⎪⎪⎭⎫ ⎝⎛---3/410013100101,于是 ⎪⎪⎩⎪⎪⎨⎧==-==4443424134334x x x x x x x x ,故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x (k 为任意常数).(2)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎭⎫⎝⎛-000001001021,于是 ⎪⎩⎪⎨⎧===+-=4432242102x x x xx x x x ,故方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10010********1k k x x x x (k 1, k 2为任意常数).(3)⎪⎩⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎪⎭⎫⎝⎛-----7421631472135132~⎪⎪⎪⎭⎫ ⎝⎛1000010000100001,于是 ⎪⎩⎪⎨⎧====0004321x x x x ,故方程组的解为 ⎪⎩⎪⎨⎧====00004321x x x x .(4)⎪⎩⎪⎨⎧=++-=+-+=-+-=+-+03270161311402332075434321432143214321x x x x x x x x x x x x x x x x .解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎪⎭⎫⎝⎛-----3127161311423327543~⎪⎪⎪⎪⎪⎭⎫⎝⎛--000000001720171910171317301,于是 ⎪⎪⎩⎪⎪⎨⎧==-=-=4433432431172017191713173x x x x x x x xx x ,故方程组的解为⎪⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛1017201713011719173214321k k x x x x (k 1, k 2为任意常数).13. 求解下列非齐次线性方程组: (1)⎪⎩⎪⎨⎧=+=+-=-+83111021322421321321x x x x x x x x ;解 对增广矩阵B 进行初等行变换, 有。
同济大学-线性代数-习题册+答案
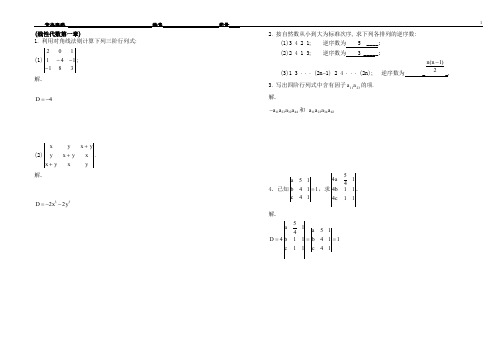
所以 B A E
1
0 0 1 1 0 2 2 0 1 A E 0 1 0 0 3 0 0 3 0 1 0 0 2 0 1 1 0 2
2
13 设方阵 A 满足 A A 2E O 证明 A 及 A 2E 都可逆 并求 A 及 ( A 2 E )
解.
0 0 ; 1 d
a
1 4 D 10 0 2 1 5 1 0 2 2 1 2 1 2 4 0 7 0 0 15 7 0 1 0 2 1 2 2 4 0 1 2 20 0 15 1 7 0 7 0 2 1 2 0 2 1 7 0 1 1 7 0 2 20 0 0 17 85 2 4 0 0 9 45
D 2 x3 2 y3
解.
a D4b c
5 1 a 5 1 4 1 1 b 4 1 1 1 1 c 4 1
专业班级
姓名
学号
2
5 计算下列各行列式
4 1 (1) 10 0
解.
1 2 5 1
2 0 2 1
4 2 ; 0 7
a 1 0 1 b 1 (3) 0 1 c 0 0 1
所以 B AB 也是对称矩阵。
T
10.设 A 为 n 阶方阵,且 A
专业班级
姓名
学号
6
1 4 2 0 3 1 12 解矩阵方程 X . 1 2 1 1 0 1
解.
1 4 2 0
1 0 1 14 设 A 0 2 0 且 AB E A2 B 求 B 1 0 1
1 | B | _______ 9 ______.
* 1 ,则 2A* 2 A 2 11.设矩阵 A 、 B 、C 满足 AB AC ,则 B C 成立的一个充分条件是____C_____. (A) A 为方阵 (B) A 为非零矩阵 (C) A 为可逆方阵 (D) A 为对角阵
线性代数(同济版) 课后习题答案 第一章

c
1
(3 ) a
1 b b2
1 c = bc 2 + ca 2 + ab 2 − ac 2 − ba 2 − cb 2 c2 = ( a − b )(b − c )(c − a ) y x+ y x x+ y x y
a2
x
(4 )
y x+ y
= x( x + y ) y + yx( x + y ) + ( x + y ) yx − y 3 − ( x + y )3 − x 3 = 3 xy( x + y ) − y 3 − 3 x 2 y − 3 y 2 x − x 3 − y 3 − x 3 = −2( x 3 + y 3 )
4 0
10
2
17 17
2 1
3 − 1 2 1 c4 − c2 3 − 1 2 2 ( 2 ) 1 2 3 2 1 2 3 0 5 0 2 1 2 6 2 1 4 0 2 1 3 0 4 0 5 0 2 1 0 6 2 1 4 0 2 0 3 0 0 0
= 0
r4 − r2 3 − 1 2 2
r4 − r1 3 − 1 2 2
x + b3 z
x + b3 y
a2
( 3 ) 左边 =
b2 c2 d2
a 2 + ( 2a + 1) ( a + 2) 2 b 2 + ( 2b + 1) ( b + 2) 2 c 2 + ( 2c + 1) ( c + 2) 2 d 2 + ( 2d + 1) ( d + 2) 2
[同济大学(第四版)] 线性代数习题解答
![[同济大学(第四版)] 线性代数习题解答](https://img.taocdn.com/s3/m/c6228fc4bb4cf7ec4afed014.png)
线性代数答案解答第一章 行列式1.利用对角线法则计算下列三阶行列式:(1)381141102---; (2)ba c a cbc b a (3)222111c b a c b a; (4)yxyx x y x y y x yx +++. 解 (1)=---381141102811)1()1(03)4(2⨯⨯+-⨯-⨯+⨯-⨯)1()4(18)1(2310-⨯-⨯-⨯-⨯-⨯⨯- =416824-++- =4-(2)=ba c a cb cb a ccc aaa bbb cba bac acb ---++3333c b a abc ---=(3)=222111c b a c b a 222222cb ba ac ab ca bc ---++))()((a c c b b a ---=(4)y x y x x y x yyx y x +++ yx y x y x yx y y x x )()()(+++++=333)(x y x y -+-- 33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=2.按自然数从小到大为标准次序,求下列各排列的逆序数:(1)1 2 3 4; (2)4 1 3 2; (3)3 4 2 1; (4)2 4 1 3; (5)1 3 … )12(-n 2 4 … )2(n ;(6)1 3 … )12(-n )2(n )22(-n … 2. 解(1)逆序数为0(2)逆序数为4:4 1,4 3,4 2,3 2(3)逆序数为5:3 2,3 1,4 2,4 1,2 1 (4)逆序数为3:2 1,4 1,4 3(5)逆序数为2)1(-n n :3 2 1个 5 2,54 2个 7 2,7 4,7 6 3个 ……………… … )12(-n 2,)12(-n 4,)12(-n 6,…,)12(-n )22(-n)1(-n 个(6)逆序数为)1(-n n3 2 1个 5 2,54 2个 ……………… … )12(-n 2,)12(-n 4,)12(-n 6,…,)12(-n )22(-n)1(-n 个4 2 1个 6 2,6 4 2个 ……………… … )2(n 2,)2(n 4,)2(n 6,…,)2(n )22(-n )1(-n 个3.写出四阶行列式中含有因子2311a a 的项. 解 由定义知,四阶行列式的一般项为43214321)1(p p p p t a a a a -,其中t 为4321p p p p 的逆序数.由于3,121==p p 已固定,4321p p p p 只能形如13□□,即1324或1342.对应的t 分别为10100=+++或22000=+++∴44322311a a a a -和42342311a a a a 为所求.4.计算下列各行列式:(1)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢71100251020214214; (2)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-2605232112131412;(3)⎥⎥⎥⎦⎥⎢⎢⎢⎣⎢---ef cf bf de cdbd ae ac ab ; (4)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d cb a100110011001 解(1)7110025102021421434327c c c c --0100142310202110214---=34)1(143102211014+-⨯--- =143102211014--321132c c c c ++1417172001099-=0(2)2605232112131412-24c c -260532122130412-24r r -0412032122130412-14r r -000032122130412-=0(3)ef cf bf de cdbd ae ac ab ---=ec b e c b ec b adf --- =111111111---adfbce =abcdef 4(4)d cb a 10110011001---21ar r +d cb a ab 10011011010---+=12)1)(1(+--d c a ab 101101--+ 23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdad ab +-+111=1++++ad cd ab abcd5.证明:(1)1112222b b a a b ab a +=3)(b a -;(2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=yxzx z yz yx b a )(33+; (3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ; (4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅; (5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 . 证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b ab a b a ab 22)1(22213-----=+21))((ab a a b a b +--=右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bzay y x by ax x z bxaz z yb +++ zy x y x z x z y b y x z x z y z y xa 33+分别再分 右边=-+=233)1(yxz x z y zy x b y xzx z yz y x a (3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边 9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 964496449644964422222++++++++d d d d c c c cb b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a 949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+dd d c c c bb b a a a(4) 444444422222220001a d a c ab a ad ac ab aa d a c ab a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b ad a c a b --------- =)()()(111))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =⨯---))()((ad a c a b)()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b)()()()(112222b d a b bd d b c a b bc c ++++++++ =))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立,即 ,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-xx a xD D n n n n右边=+=-n n a xD 1所以,对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依 副对角线翻转,依次得n nnn a a a a D 11111=, 11112n nn n a a a a D = ,11113a a a a D n nnn =,证明D D D D D n n =-==-32)1(21,)1(. 证明 )det(ij a D =nnn n n n nnnn a a a a a a a a a a D 2211111111111)1(--==∴=--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nn n nn n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-=同理可证nn n n n n a a a a D 11112)1(2)1(--=D D n n T n n 2)1(2)1()1()1(---=-=D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式(阶行列式为k D k ):(1)aaD n 11=,其中对角线上元素都是a ,未写出的元素都是0;(2)xa a ax a aa x D n =;(3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n nnnn ------=---+; 提示:利用范德蒙德行列式的结果.(4) nnnnn d c d c b a b a D000011112=;(5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121,021≠n a a a 其中.解(1) aa a a a D n 00010000000000001000 =按最后一行展开)1()1(100000000000010000)1(-⨯-+-n n n a a a)1)(1(2)1(--⋅-+n n n a a a (再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行,得ax xa a x xa a x x a a a a x D n ------=00000再将各列都加到第一列上,得ax a x a x a a a an x D n ----+=0000000)1()(])1([1a x a n x n --+=-(3)从第1+n 行开始,第1+n 行经过n 次相邻对换,换到第1行,第n 行经)1(-n 次对换换到第2行…,经2)1(1)1(+=++-+n n n n 次行 交换,得nn nn n n n n n n a a a n a a a n a a a D )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-∙-∙-=---=1121)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nnnnn d c d c b a b a D 011112=n n n n n nd d c d c b a b a a 00000011111111----展开按第一行00000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222---n n n n n n D c b D d a 都按最后一行展开 由此得递推公式:222)(--=n n n n n n D c b d a D 即 ∏=-=ni i i i i n D c b d a D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=0432140123310122210113210)det( --------==n n n n n n n n a D ij n,3221r r r r --0432111111111111111111111--------------n n n n ,,141312c c c c c c +++15242321022210022*******0001---------------n n n n n =212)1()1(----n n n(6)n n a a a D +++=11111111121,,433221c c c c c c ---nn n n a a a a a a a a a a +-------10000100010000100010001000011433221展开(由下往上)按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------0000000000000000000000022433221n n n a a a a a a a a ----+--000000000000000001133221++nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑+==n i in a a a a8.用克莱姆法则解下列方程组:⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x解 (1)11213513241211111----=D 8120735032101111------=145008130032101111---=14214205410032101111-=---=112105132412211151------=D 11210513290501115----=112123313090509151------=233130905112109151------=1202300461000112109151-----=14238100112109151----=142-=112035122412111512-----=D 811507312032701151-------=31390011230023101151-=28428401910023101151-=----=42611135232422115113-=----=D14202132132212151114=-----=D1,3,2,144332211-========∴DD x DD x DD x DD x (2)5100065100065100065100065=D 展开按最后一行61000510065100655-'D D D ''-'=65 D D D ''-'''-''=6)65(5D D '''-''=3019 D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',)51001651000651000650000611=D 展开按第一列6510065100650006+'D 46+'=D 460319+''''-'''=D 1507= 51010651000650000601000152=D 展开按第二列5100651006500061-6510065000610005-365510651065⨯-=1145108065-=--=51100650000601000051001653=D 展开按第三列51006500061000516500061000510065+6100510656510650061+=703114619=⨯+= 51000601000051000651010654=D 展开按第四列61000510065100655000610005100651-- 51065106565--=395-=11000051000651000651100655=D 展开按最后一列D '+10005100651006512122111=+=665212;665395;665703;6651145;665150744321=-==-==∴x x x x x . 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 μλμμμλ-==12111113D , 齐次线性方程组有非零解,则03=D 即 0=-μλμ得 10==λμ或不难验证,当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解? 解λλλ----=111132421D λλλλ--+--=101112431 )3)(1(2)1(4)3()1(3λλλλλ-------+-= 3)1(2)1(23-+-+-=λλλ齐次线性方程组有非零解,则0=D 得 32,0===λλλ或不难验证,当32,0===λλλ或时,该齐次线性方程组确有非零解.第二章 矩阵及其运算1.已知线性变换: ⎪⎩⎪⎨⎧++=++=++=,323,53,22321332123211y y y x y y y x y y y x 求从变量321,,x x x 到变量321,,y y y 的线性变换.解由已知:⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x故 ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫⎝⎛----=321423736947y y y⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947xx x y x x x y x x x y2.已知两个线性变换 ⎪⎩⎪⎨⎧++=++-=+=,54,232,232133212311y y y x y y y x y y x ⎪⎩⎪⎨⎧+-=+=+-=,3,2,3323312211z z y z z y z z y 求从321,,z z z 到321,,x x x 的线性变换. 解 由已知⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛-=321310102013514232102z z z ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z 所以有 ⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236zz z x z z z x z z z x3.设⎪⎪⎪⎭⎫ ⎝⎛--=111111111A , ,150421321⎪⎪⎪⎭⎫ ⎝⎛--=B求.23B A A AB T 及- 解A AB 23-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=1504213211111111113⎪⎪⎪⎭⎫ ⎝⎛---1111111112⎪⎪⎪⎭⎫ ⎝⎛-=0926508503⎪⎪⎪⎭⎫ ⎝⎛---1111111112⎪⎪⎪⎭⎫ ⎝⎛----=22942017222132 ⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=150421321111111111B A T⎪⎪⎪⎭⎫ ⎝⎛-=0926508504.计算下列乘积:(1)⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-127075321134; (2)()⎪⎪⎪⎭⎫ ⎝⎛1233,2,1; (3)()2,1312-⎪⎪⎪⎭⎫ ⎝⎛; (4)⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛-20413121013143110412; (5)⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321332313232212*********),,(x x x a a a a a a a a a x x x ;(6)⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解 (1)⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎪⎭⎫⎝⎛=49635(2)()⎪⎪⎪⎭⎫ ⎝⎛123321)10()132231(=⨯+⨯+⨯=(3)()21312-⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎪⎭⎫ ⎝⎛---=632142(4)⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎪⎭⎫⎝⎛---=6520876 (5)()⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫⎝⎛321332313232212131211321x x x a a a a a a a a a x x x()333223113323222112313212111x a x a x a x a x a x a x a x a x a ++++++=⎪⎪⎪⎭⎫⎝⎛⨯321x x x 322331132112233322222111222x x a x x a x x a x a x a x a +++++=(6) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎪⎪⎭⎫⎝⎛---=90003400421025215.设⎪⎪⎭⎫ ⎝⎛=3121A , ⎪⎪⎭⎫⎝⎛=2101B ,问:(1)BA AB =吗?(2)2222)(B AB A B A ++=+吗? (3)22))((B A B A B A -=-+吗? 解(1)⎪⎪⎭⎫ ⎝⎛=3121A , ⎪⎪⎭⎫ ⎝⎛=2101B 则⎪⎪⎭⎫ ⎝⎛=6443AB ⎪⎪⎭⎫⎝⎛=8321BA BA AB ≠∴(2) ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎪⎭⎫ ⎝⎛=2914148但=++222B AB A ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛43011288611483⎪⎪⎭⎫ ⎝⎛=27151610故2222)(B AB A B A ++≠+(3) =-+))((B A B A =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛10205222⎪⎪⎭⎫⎝⎛9060而 =-22B A =⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛430111483⎪⎪⎭⎫ ⎝⎛7182故 22))((B A B A B A -≠-+6.举反列说明下列命题是错误的: (1)若02=A ,则0=A ;(2)若A A =2,则0=A 或E A =; (3)若AY AX =,且0≠A ,则Y X =.解 (1) 取⎪⎪⎭⎫ ⎝⎛=0010A 02=A ,但0≠A (2) 取⎪⎪⎭⎫ ⎝⎛=0011A A A =2,但0≠A 且E A ≠ (3) 取⎪⎪⎭⎫ ⎝⎛=0001A ⎪⎪⎭⎫ ⎝⎛-=1111X ⎪⎪⎭⎫⎝⎛=1011YAY AX =且0≠A 但Y X ≠7.设⎪⎪⎭⎫ ⎝⎛=101λA ,求kA A A ,,,32 . 解 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=12011011012λλλA⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==130********23λλλA A A 利用数学归纳法证明: ⎪⎪⎭⎫ ⎝⎛=101λk A k当1=k 时,显然成立,假设k 时成立,则1+k 时⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==1)1(01101101λλλk k A A A kk由数学归纳法原理知:⎪⎪⎭⎫ ⎝⎛=101λk A k8.设⎪⎪⎪⎭⎫ ⎝⎛=λλλ001001A ,求k A .解 首先观察⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎪⎭⎫ ⎝⎛=22202012λλλλλ ⎪⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A由此推测 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121)2(≥k用数学归纳法证明:当2=k 时,显然成立.假设k 时成立,则1+k 时,⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k kkk k k k k A A A⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ由数学归纳法原理知: ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(1219.设B A ,为n 阶矩阵,且A 为对称矩阵,证明AB B T 也是对称矩阵. 证明 已知:A A T =则 AB B B A B A B B AB B T T T T TT T T ===)()( 从而 AB B T 也是对称矩阵.10.设B A ,都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是 BA AB =.证明 由已知:A A T = B B T =充分性:BA AB =⇒A B AB T T =⇒)(AB AB T= 即AB 是对称矩阵.必要性:AB AB T=)(⇒AB A B T T =⇒AB BA =.11.求下列矩阵的逆矩阵:(1)⎪⎪⎭⎫ ⎝⎛5221; (2)⎪⎪⎭⎫⎝⎛-θθθθcos sin sin cos ; (3)⎪⎪⎪⎭⎫ ⎝⎛---145243121; (4)⎪⎪⎪⎪⎪⎭⎫⎝⎛4121031200210001; (5)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2500380000120025;(6)⎪⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021)0(21≠a a a n解(1)⎪⎪⎭⎫⎝⎛=5221A 1=A1),1(2),1(2,522122111=-⨯=-⨯==A A A A⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛=*122522122111A A A A A *-=A A A 11 故 ⎪⎪⎭⎫⎝⎛--=-12251A(2)01≠=A 故1-A 存在θθθθcos sin sin cos 22122111=-===A A A A从而 ⎪⎪⎭⎫ ⎝⎛-=-θθθθcos sin sin cos 1A(3) 2=A , 故1-A 存在024312111==-=A A A 而 1613322212-==-=A A A 21432332313-==-=A A A故 *-=A A A 11⎪⎪⎪⎭⎫⎝⎛-----=1716213213012 (4)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=4121031200210001A 24=A 0434232413121======A A A A A A 68122444332211====A A A A12411032001)1(312-=-=A 12421012021)1(413-=-=A3121312021)1(514=-=A 4421012001)1(523-=-=A5121312001)1(624-=-=A 2121021001)1(734-=-=A*-=A AA 11 故⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=-4112124581031612100212100011A (5)01≠=A 故1-A 存在而002141312111==-==A A A A 005242322212===-=A A A A 320043332313-====A A A A850044342414=-===A A A A从而⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=-85003200005200211A (6)⎪⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 1001121112.解下列矩阵方程:(1) ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛12643152X ; (2) ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛--234311111012112X ;(3) ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-101311022141X ; (4) ⎪⎪⎪⎭⎫⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X .解(1) ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-126431521X ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=12642153⎪⎪⎭⎫⎝⎛-=80232 (2) 1111012112234311-⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-=X ⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫⎝⎛---=32538122 (3) 11110210132141--⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛-=210110131142121 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫⎝⎛=04111 (4) 11010100001021102341100001010--⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎪⎭⎫ ⎝⎛---=20143101213.利用逆矩阵解下列线性方程组:(1) ⎪⎩⎪⎨⎧=++=++=++;353,2522,132321321321x x x x x x x x x (2)⎪⎩⎪⎨⎧=-+=--=--.0523,132,2321321321x x x x x x x x x 解 (1) 方程组可表示为 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛321153522321321x x x故 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x从而有 ⎪⎩⎪⎨⎧===001321x x x(2) 方程组可表示为 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x故 ⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x故有 ⎪⎩⎪⎨⎧===305321x x x14.设O A k =(k 为正整数),证明 121)(--++++=-k A A A E A E .证明 一方面, )()(1A E A E E --=- 另一方面,由O A k =有)()()(1122k k k A A A A A A A E E -+--+-+-=-- ))((12A E A A A E k -++++=-故 )()(1A E A E ---))((12A E A A A E k -++++=- 两端同时右乘1)(--A E就有121)(--++++=-k A A A E A E15.设方阵A 满足O E A A =--22,证明A 及E A 2+都可逆,并求1-A 及 1)2(-+E A .证明 由O E A A =--22得E A A 22=- 两端同时取行列式: 22=-A A 即 2=-E A A ,故 0≠A 所以A 可逆,而22A E A =+0222≠==+A A E A 故E A 2+也可逆. 由O E A A =--22E E A A 2)(=-⇒E A E A A A 112)(--=-⇒)(211E A A -=⇒-又由O E A A =--22E E A A E A 4)2(3)2(-=+-+⇒ E E A E A 4)3)(2(-=-+⇒11)2(4)3)(2()2(--+-=-++∴E A E A E A E A)3(41)2(1A E E A -=+∴-16.设⎪⎪⎪⎭⎫ ⎝⎛-=321011330A ,B A AB 2+=,求B .解 由B A AB 2+=可得A B E A =-)2(故A E A B 1)2(--=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---=-3210113301210113321⎪⎪⎪⎭⎫⎝⎛-=01132133017.设Λ=-AP P 1,其中⎪⎪⎭⎫ ⎝⎛--=1141P ,⎪⎪⎭⎫ ⎝⎛-=Λ2001,求11A . 解 Λ=-AP P 1故1-Λ=P P A 所以11111-Λ=P P A3=P ⎪⎪⎭⎫ ⎝⎛-=*1141P ⎪⎪⎭⎫ ⎝⎛--=-1141311P而 ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=Λ11111120012001故⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎪⎭⎫ ⎝⎛--=6846832732273118.设m 次多项式m m x a x a x a a x f ++++= 2210)(,记m m A a A a A a E a A f ++++= 2210)()(A f 称为方阵A 的m 次多项式.(1)设⎪⎪⎭⎫ ⎝⎛=Λ2100λλ,证明: ⎪⎪⎭⎫ ⎝⎛=Λk kk2100λλ,⎪⎪⎭⎫ ⎝⎛=Λ)(00)()(21λλf f f ; (2)设1-Λ=P P A ,证明: 1-Λ=P P A k k ,1)()(-Λ=P Pf A f .证明(1) i)利用数学归纳法.当2=k 时⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=Λ212120000λλλλ⎪⎪⎭⎫ ⎝⎛=222100λλ命题成立,假设k 时成立,则1+k 时⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=ΛΛ=Λ+212110000λλλλk k kk ⎪⎪⎭⎫⎝⎛=++121100k k λλ 故命题成立.ii)左边m m a a a E a f Λ++Λ+Λ+=Λ= 2210)(⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=m m m a a a 21211000001001λλλλ⎪⎪⎭⎫ ⎝⎛++++++++=m m mm a a a a a a a a 2222210121211000λλλλλλ ⎪⎪⎭⎫ ⎝⎛=)(00)(21λλf f =右边 (2) i) 利用数学归纳法.当2=k 时12112---Λ=ΛΛ=P P P P P P A 成立假设k 时成立,则1+k 时11111-+--+Λ=ΛΛ=⋅=P P P P P P A A A k k k k 成立,故命题成立, 即 1-Λ=P P A k kii) 证明 右边1)(-Λ=P Pf12210)(-Λ++Λ+Λ+=P a a a E a P m m11221110----Λ++Λ+Λ+=P P a P P a P P a PEP a m m m m A a A a A a E a ++++= 2210)(A f ==左边19.设n 阶矩阵A 的伴随矩阵为*A ,证明: (1) 若0=A ,则0=*A ; (2) 1-*=n AA .证明(1) 用反证法证明.假设0≠*A 则有E A A =-**1)( 由此得O A E A A AA A ===-*-**11)()(O A =∴* 这与0≠*A 矛盾,故当0=A 时 有0=*A (2) 由于*-=A AA 11, 则E A AA =* 取行列式得到: nA A A =*若0≠A 则1-*=n A A若0=A 由(1)知0=*A 此时命题也成立故有1-*=n A A20.取⎪⎪⎭⎫⎝⎛==-==1001D C B A ,验证DC B AD C B A ≠检验: =D C BA =--10100101101001011010*********002--410012002==而 01111==D C B A故 DCB A DCB A ≠21.设⎪⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A ,求8A 及4A 解 ⎪⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A ,令⎪⎪⎭⎫ ⎝⎛-=34431A ⎪⎪⎭⎫ ⎝⎛=22022A 则⎪⎪⎭⎫ ⎝⎛=21A O O A A故8218⎪⎪⎭⎫ ⎝⎛=A OO A A ⎪⎪⎭⎫⎝⎛=8281A O O A 1682818281810===A A A A A⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=464444241422025005O O A OO A A22.设n 阶矩阵A 及s 阶矩阵B 都可逆,求1-⎪⎪⎭⎫⎝⎛O B A O .解 将1-⎪⎪⎭⎫⎝⎛O B A O 分块为⎪⎪⎭⎫ ⎝⎛4321C C C C其中 1C 为n s ⨯矩阵, 2C 为s s ⨯矩阵3C 为n n ⨯矩阵, 4C 为s n ⨯矩阵 则⎪⎪⎭⎫ ⎝⎛⨯⨯O B A O s s n n ⎪⎪⎭⎫ ⎝⎛4321C C C C ==E ⎪⎪⎭⎫⎝⎛s n E O O E 由此得到⎪⎪⎩⎪⎪⎨⎧=⇒==⇒==⇒==⇒=----122111144133)()(B C E BC B O C O BC A O C O AC A C E AC s n 存在存在 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛---O A B O O B A O 111.第三章 矩阵的初等变换与线性方程组1.把下列矩阵化为行最简形矩阵:(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2) ⎪⎪⎪⎭⎫ ⎝⎛----174034301320;(3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; (4) ⎪⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--3403130212011312)3()2(~r r r r -+-+⎪⎪⎪⎭⎫⎝⎛---020*********)2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--30003100120133~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----1740343013201312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫ ⎝⎛---310031001320 21233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫⎝⎛000031005010 (3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311141312323~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311 )5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎪⎭⎫⎝⎛-----221002210022100343112423213~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛---00000000002210032011(4) ⎪⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛-----1187701298804202111110 141312782~r r r r r r --+⎪⎪⎪⎪⎪⎭⎫⎝⎛--4100041000202011111034221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎪⎭⎫⎝⎛----0000041000111102021 32~r r +⎪⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.在秩是r 的矩阵中,有没有等于0的1-r 阶子式?有没有等于0的r 阶 子式?解 在秩是r 的矩阵中,可能存在等于0的1-r 阶子式,也可能存在等 于0的r 阶子式.例如,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00000000010000100001α3)(=αR 同时存在等于0的3阶子式和2阶子式.3.从矩阵A 中划去一行得到矩阵B ,问B A ,的秩的关系怎样? 解 )(A R ≥)(B R设r B R =)(,且B 的某个r 阶子式0≠D r .矩阵B 是由矩阵A 划去一行得 到的,所以在A 中能找到与D r 相同的r 阶子式D r ,由于0≠=D D r r , 故而)()(B R A R ≥.4.求作一个秩是4的方阵,它的两个行向量是)0,0,1,0,1(,)0,0,0,1,1(- 解 设54321,,,,ααααα为五维向量,且)0,0,1,0,1(1=α,)0,0,0,1,1(2-=α,则所求方阵可为,54321⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=αααααA 秩为4,不妨设⎪⎩⎪⎨⎧===)0,0,0,0,0(),0,0,0,0()0,,0,0,0(55443αααx x 取154==x x 故满足条件的一个方阵为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-00000100000100000011001015.求下列矩阵的秩,并求一个最高阶非零子式:(1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013; (2) ⎪⎪⎪⎭⎫⎝⎛-------815073131213123; (3) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013r r 21~↔⎪⎪⎪⎭⎫ ⎝⎛---443120131211 ⎪⎪⎪⎭⎫ ⎝⎛------564056401211~12133r r r r 2000056401211~23秩为⎪⎪⎪⎭⎫⎝⎛----r r 二阶子式41113-=-.(2) ⎪⎪⎪⎭⎫ ⎝⎛-------815073131223123⎪⎪⎪⎭⎫⎝⎛---------152733210591********~27122113r r r r r r 200000591170144313~23秩为⎪⎪⎪⎭⎫⎝⎛-----r r .二阶子式71223-=-.(3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---02301085235703273812434241322~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛------02301024205363071210 131223~r r r r ++⎪⎪⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210344314211614~r r r r r r r r -÷÷↔↔⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-0000010*******00231秩为3三阶子式07023855023085570≠=-=-.6.求解下列齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+++=-++=-++;0222,02,02432143214321x x x x x x x x x x x x (2)⎪⎩⎪⎨⎧=-++=--+=-++;05105,0363,02432143214321x x x x x x x x x x x x (3) ⎪⎪⎩⎪⎪⎨⎧=-+-=+-+=-++=+-+;0742,0634,0723,05324321432143214321x x x x x x x x x x x x x x x x (4)⎪⎪⎩⎪⎪⎨⎧=++-=+-+=-+-=+-+.0327,01613114,02332,075434321432143214321x x x x x x x x x x x x x x x x解 (1) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛--212211121211⎪⎪⎪⎪⎭⎫⎝⎛---3410013100101~即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-==4443424134334x x xx x x x x 故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x(2) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛----5110531631121⎪⎪⎪⎭⎫ ⎝⎛-000001001021~ 即得⎪⎪⎩⎪⎪⎨⎧===+-=4432242102x x x x x x x x 故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛10010*********k k x x x x(3) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----7421631472135132⎪⎪⎪⎪⎪⎭⎫⎝⎛1000010000100001~即得⎪⎪⎩⎪⎪⎨⎧====00004321x xx x故方程组的解为⎪⎪⎩⎪⎪⎨⎧====00004321x x x x(4) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----3127161311423327543⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000001720171910171317301~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=-=4433432431172017191713173x x x x x x x x x x故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛1017201713011719173214321k k x xx x7.求解下列非齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+=+-=-+;8311,10213,22421321321x x x x x x x x (2) ⎪⎪⎩⎪⎪⎨⎧-=+-=-+-=+-=++;694,13283,542,432z y x z y x z y x z y x(3) ⎪⎩⎪⎨⎧=--+=+-+=+-+;12,2224,12w z y x w z y x w z y x (4) ⎪⎩⎪⎨⎧-=+-+=-+-=+-+;2534,4323,12w z y x w z y x w z y x解 (1) 对系数的增广矩阵施行行变换,有⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛--60003411100833180311102132124~2)(=A R 而3)(=B R ,故方程组无解.(2) 对系数的增广矩阵施行行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----69141328354214132⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--0000000021101201~ 即得⎪⎩⎪⎨⎧=+=--=zz z y z x 212亦即⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛021112k z y x(3) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫ ⎝⎛----111122122411112⎪⎪⎪⎭⎫ ⎝⎛-000000100011112~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧===++-=0212121w z z y y z y x 即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00021010210012121k k w z y x(4) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛-----000007579751025341253414312311112~⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----000007579751076717101~即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==--=++=w w z z w z y w z x 757975767171 即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00757610797101757121k k w z y x8.λ取何值时,非齐次线性方程组 ⎪⎩⎪⎨⎧=++=++=++2321321321,,1λλλλλx x x x x x x x x (1)有唯一解;(2)无解;(3)有无穷多个解?解 (1) 0111111≠λλλ,即2,1-≠λ时方程组有唯一解.(2) )()(B R A R < ⎪⎪⎪⎭⎫ ⎝⎛=21111111λλλλλB ⎪⎪⎭⎫ ⎝⎛+-+----22)1)(1()2)(1(00)1(11011~λλλλλλλλλλ由0)1)(1(,0)2)(1(2≠+-=+-λλλλ 得2-=λ时,方程组无解.(3) 3)()(<=B R A R ,由0)1)(1()2)(1(2=+-=+-λλλλ, 得1=λ时,方程组有无穷多个解.9.非齐次线性方程组 ⎪⎩⎪⎨⎧=-+=+--=++-23213213212,2,22λλx x x x x x x x x 当λ取何值时有解?并求出它的解.解 ⎪⎪⎪⎪⎭⎫ ⎝⎛+-----⎪⎪⎪⎭⎫ ⎝⎛----=)2)(1(000)1(321101212111212112~2λλλλλλB方程组有解,须0)2)(1(=+-λλ得2,1-==λλ当1=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛001111321k x x x当2-=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛022111321k x x x10.设⎪⎩⎪⎨⎧--=-+--=--+=-+-,1)5(42,24)5(2,122)2(321321321λλλλx x x x x x x x x问λ为何值时,此方程组有唯一解、无解或有无穷多解?并在有无穷多解 时求解.解 ⎪⎪⎪⎭⎫ ⎝⎛---------154224521222λλλλ初等行变换~⎪⎪⎪⎪⎪⎭⎫⎝⎛---------2)4)(1(2)10)(1(00111012251λλλλλλλλ 当0≠A ,即02)10()1(2≠--λλ 1≠∴λ且10≠λ时,有唯一解.当02)10)(1(=--λλ且02)4)(1(≠--λλ,即10=λ时,无解.当02)10)(1(=--λλ且02)4)(1(=--λλ,即1=λ时,有无穷多解.此时,增广矩阵为⎪⎪⎪⎭⎫ ⎝⎛-000000001221原方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛00110201221321k k x x x (R k k ∈21,)11.试利用矩阵的初等变换,求下列方阵的逆矩阵:(1) ⎪⎪⎪⎭⎫⎝⎛323513123; (2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023. 解 (1)⎪⎪⎪⎭⎫ ⎝⎛100010001323513123⎪⎪⎪⎭⎫ ⎝⎛---101011001200410123~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----10121121023200010023~⎪⎪⎪⎪⎪⎭⎫⎝⎛----2102121129227100010003~⎪⎪⎪⎪⎪⎭⎫⎝⎛----21021211233267100010001~故逆矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛----21021211233267(2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《线性代数》同济大学版 课后习题答案详解第一章 行列式1. 利用对角线法则计算下列三阶行列式:(1)381141102---;解381141102--- =2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4.(2)ba c a cb cb a ;解ba c a cbc b a =acb +bac +cba -bbb -aaa -ccc =3abc -a 3-b 3-c 3.(3)222111c b a cb a ;解222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).(4)yx y x x y x y y x y x +++.解yx y x x y x y y x y x +++ =x (x +y )y +yx (x +y )+(x +y )yx -y 3-(x +y )3-x 3 =3xy (x +y )-y 3-3x 2 y -x 3-y 3-x 3 =-2(x 3+y 3).2. 按自然数从小到大为标准次序, 求下列各排列的逆序数: (1)1 2 3 4; 解 逆序数为0 (2)4 1 3 2;解 逆序数为4: 41, 43, 42, 32. (3)3 4 2 1;解 逆序数为5: 3 2, 3 1, 4 2, 4 1, 2 1. (4)2 4 1 3;解 逆序数为3: 2 1, 4 1, 4 3. (5)1 3 ⋅ ⋅ ⋅ (2n -1) 2 4 ⋅ ⋅ ⋅ (2n ); 解 逆序数为2)1(-n n :3 2 (1个) 5 2, 5 4(2个) 7 2, 7 4, 7 6(3个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n -1)2, (2n -1)4, (2n -1)6, ⋅ ⋅ ⋅, (2n -1)(2n -2) (n -1个)(6)1 3 ⋅ ⋅ ⋅ (2n -1) (2n ) (2n -2) ⋅ ⋅ ⋅ 2. 解 逆序数为n (n -1) : 3 2(1个) 5 2, 5 4 (2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n -1)2, (2n -1)4, (2n -1)6, ⋅ ⋅ ⋅, (2n -1)(2n -2) (n -1个) 4 2(1个) 6 2, 6 4(2个) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅(2n )2, (2n )4, (2n )6, ⋅ ⋅ ⋅, (2n )(2n -2) (n -1个) 3. 写出四阶行列式中含有因子a 11a 23的项. 解 含因子a 11a 23的项的一般形式为(-1)t a 11a 23a 3r a 4s ,其中rs 是2和4构成的排列, 这种排列共有两个, 即24和42. 所以含因子a 11a 23的项分别是(-1)t a 11a 23a 32a 44=(-1)1a 11a 23a 32a 44=-a 11a 23a 32a 44, (-1)t a 11a 23a 34a 42=(-1)2a 11a 23a 34a 42=a 11a 23a 34a 42. 4. 计算下列各行列式:(1)71100251020214214; 解71100251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-; 解2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r000003212213041214=--=====r r . (3)efcf bf decd bd ae ac ab ---;解ef cf bf de cd bd ae ac ab ---ec b e c b e c b adf ---= abcdef adfbce 4111111111=---=.(4)dc b a100110011001---. 解d c b a 100110011001---dc b aab ar r 10011001101021---++===== dc a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ad a ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1.5. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 .(2)yx z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++ bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bx az z y b y by ax z x bx az y z bz ay x a +++++++=22zy x y x z x z y b y x z x z y z y x a 33+=y x z x z y z y x b y x z x z y z y x a 33+=yx z x z y z y x b a )(33+=.(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;证明2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2, c 2-c 1得)5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4-c 3, c 3-c 2得) 022122212221222122222=++++=d d c c b b a a .(4)444422221111d c b a d c b a d c b a=(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d );证明444422221111d c b a d c b a d c b a)()()(0)()()(001111222222222a d d a c c a b b a d d a c c a b b ad a c a b ---------=)()()(111))()((222a d d a c c a b b d c b a d a c a b +++---=))(())((00111))()((a b d b d d a b c b c c bd b c a d a c a b ++-++------=)()(11))()()()((a b d d a b c c b d b c a d a c a b ++++-----==(a -b )(a -c )(a -d )(b -c )(b -d )(c -d )(a +b +c +d ).(5)1221 1 000 00 1000 01a x a a a a x x x n n n+⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--- =x n+a 1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .证明 用数学归纳法证明. 当n =2时,2121221a x a x a x a x D ++=+-=, 命题成立.假设对于(n -1)阶行列式命题成立, 即 D n -1=x n -1+a 1 x n -2+ ⋅ ⋅ ⋅ +a n -2x +a n -1, 则D n 按第一列展开, 有11100 100 01)1(11-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅--+=+-x x a xD D n n n n =xD n -1+a n =x n +a1x n -1+ ⋅ ⋅ ⋅ +a n -1x +a n .因此, 对于n 阶行列式命题成立.6. 设n 阶行列式D =det(a ij ), 把D 上下翻转、或逆时针旋转90︒、或依副对角线翻转, 依次得n nn n a a a a D 11111 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=, 11112 n nn n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= , 11113 a a a a D n n nn ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,证明D D D n n 2)1(21)1(--==, D 3=D .证明 因为D =det(a ij ), 所以nnn n n n nnnn a a a a a a a a a a D 2211111111111)1( ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=- ⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--=-- )1()1(331122111121nnn n nn n n a a a a a a a aD D n n n n 2)1()1()2( 21)1()1(--+-+⋅⋅⋅++-=-=.同理可证nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=- )1(11112)1(2D D n n T n n 2)1(2)1()1()1(---=-=.D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(.7. 计算下列各行列式(D k 为k 阶行列式):(1)aaD n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0;解aa a a a D n 0 0010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开))1()1(10 00000 0000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a aan n n nn a a a +⋅⋅⋅-⋅-=--+)2)(2(1 )1()1(=a n -a n -2=a n -2(a 2-1).(2)xa a a x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得ax x a ax x a a x x a aa a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0 , 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n -1.(3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n n n n n ; 解 根据第6题结果, 有nnn n n n n n n n a a a n a a a n a a aD )( )1()( )1( 1111)1(1112)1(1-⋅⋅⋅--⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=---++此行列式为范德蒙德行列式.∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++---=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+-++-⋅-⋅-=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+-=11)(j i n j i .(4)n nnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112;解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开)nn n n n nd d c d c b a b a a 00011111111----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn ----+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-+.再按最后一行展开得递推公式D 2n =a n d n D 2n -2-b n c n D 2n -2, 即D 2n =(a n d n -b n c n )D 2n -2. 于是∏=-=ni i i i i n D c b d a D 222)(.而111111112c b d a d c b a D -==,所以∏=-=n i i i i i n c b d a D 12)(.(5) D =det(a ij ), 其中a ij =|i -j |; 解 a ij =|i -j |,4321 4 01233 10122 21011 3210)det(⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅==n n n n n n n n a D ij n0 4321 1 11111 11111 11111 1111 2132⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅--⋅⋅⋅-=====n n n n r r r r152423210 22210 02210 00210 0001 1213-⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅-+⋅⋅⋅+=====n n n n n c c c c =(-1)n -1(n -1)2n -2.(6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n ≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121nn n n a a a a a a a a a c c c c +-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=====--10 0001 000 100 0100 0100 0011332212132 1111312112111011 000 00 11000 01100 001 ------+-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅⋅⋅⋅=nn n a a a a a a a a∑=------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 00010 000 00 10000 01000 001)11)((121∑=+=ni in a a a a .8. 用克莱姆法则解下列方程组:(1)⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;解 因为14211213513241211111-=----=D , 142112105132412211151-=------=D ,28411235122412111512-=-----=D , 42611135232422115113-=----=D ,14202132132212151114=-----=D , 所以111==D D x , 222==D D x , 333==D D x , 144-==DDx . (2)⎪⎪⎩⎪⎪⎨⎧=+=++=++=++=+150650650651655454343232121x x x x x x x x x x x x x .解 因为665510006510006510065100065==D , 15075100165100065100650000611==D ,11455101065100065000601000152-==D ,70351100650000601000051001653==D , 39551000601000051000651010654-==D ,2121100005100065100651100655==D , 所以66515071=x , 66511452-=x , 6657033=x , 6653954-=x , 6652124=x .9. 问λ, μ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 系数行列式为μλμμμλ-==1211111D .令D =0, 得 μ=0或λ=1.于是, 当μ=0或λ=1时该齐次线性方程组有非零解.10. 问λ取何值时, 齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解?解 系数行列式为λλλλλλλ--+--=----=101112431111132421D=(1-λ)3+(λ-3)-4(1-λ)-2(1-λ)(-3-λ) =(1-λ)3+2(1-λ)2+λ-3. 令D =0, 得λ=0, λ=2或λ=3.于是, 当λ=0, λ=2或λ=3时, 该齐次线性方程组有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换. 解 由已知:⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A TB .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T.4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635.(2)⎪⎪⎭⎫⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫ ⎝⎛---=632142.(4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ;解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x 322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA . 因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B )2=A 2+2AB +B 2吗? 解 (A +B )2≠A 2+2AB +B 2. 因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610,所以(A +B )2≠A 2+2AB +B 2. (3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.6. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解 取⎪⎭⎫⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y . 解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k.解⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k .8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k.解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ,⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k kk k k k k k A A A ⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵. 证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA . 证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以 (AB )T =(BA )T =A T B T =AB , 即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB )T =AB , 所以 AB =(AB )T =B T A T =BA .11. 求下列矩阵的逆矩阵: (1)⎪⎭⎫ ⎝⎛5221; 解⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A , 故*||11A A A =-⎪⎭⎫ ⎝⎛--=1225.(2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解 ⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A |=1≠0, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,所以*||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos .(3)⎪⎪⎭⎫⎝⎛---145243121;解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A AA A A A A A ,所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n≠0) .解⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程: (1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ;解⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232. (2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ;解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫⎝⎛---=32538122.(3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ;解11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X .解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫⎝⎛---=201431012.13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ). 另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有 (E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1. 证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E ⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1,)3(41)2(1A E E A -=+-.16. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|. 解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A |-1=-8⨯2=-16. 17. 设矩阵A 可逆, 证明其伴随阵A *也可逆, 且(A *)-1=(A -1)*. 证明 由*||11A A A =-, 得A *=|A |A -1, 所以当A 可逆时, 有|A *|=|A |n |A -1|=|A |n -1≠0, 从而A *也可逆.因为A *=|A |A -1, 所以 (A *)-1=|A |-1A . 又*)(||)*(||1111---==A A A A A , 所以(A *)-1=|A |-1A =|A |-1|A |(A -1)*=(A -1)*. 18. 设n 阶矩阵A 的伴随矩阵为A *, 证明: (1)若|A |=0, 则|A *|=0; (2)|A *|=|A |n -1. 证明(1)用反证法证明. 假设|A *|≠0, 则有A *(A *)-1=E , 由此得 A =A A *(A *)-1=|A |E (A *)-1=O ,所以A *=O , 这与|A *|≠0矛盾,故当|A |=0时, 有|A *|=0. (2)由于*||11A A A =-, 则AA *=|A |E , 取行列式得到|A ||A *|=|A |n . 若|A |≠0, 则|A *|=|A |n -1;若|A |=0, 由(1)知|A *|=0, 此时命题也成立. 因此|A *|=|A |n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E )B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E AB ⎪⎪⎭⎫⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E )B =A 2-E , 即 (A -E )B =(A -E )(A +E ).因为01001010100||≠-==-E A , 所以(A -E )可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B . 解 由A *BA =2BA -8E 得 (A *-2E )BA =-8E , B =-8(A *-2E )-1A -1 =-8[A (A *-2E )]-1 =-8(AA *-2A )-1 =-8(|A |E -2A )-1 =-8(-2E -2A )-1 =4(E +A )-1=4[diag(2, -1, 2)]-1)21 ,1,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B . 解 由|A *|=|A |3=8, 得|A |=2. 由ABA -1=BA -1+3E得AB =B +3A , B =3(A -E )-1A =3[A (E -A -1)]-1A11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1. |P |=3,⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731.24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B )B -1=B -1+A -1=A -1+B -1,而A -1(A +B )B -1是三个可逆矩阵的乘积, 所以A -1(A +B )B -1可逆, 即A -1+B -1可逆. (A -1+B -1)-1=[A -1(A +B )B -1]-1=B (A +B )-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛3000320012101301300120010100121. 解设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A ,⎪⎭⎫ ⎝⎛-=12131B ,⎪⎭⎫ ⎝⎛--=30322B ,则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A , 所以⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B EA O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠. 解 4101200210100101002000021010010110100101==--=--=D C B A , 而01111|||||||| ==D C B A , 故|||||||| D C B A D C B A ≠. 28. 设⎪⎪⎪⎭⎫⎝⎛-=22023443O O A , 求|A 8|及A 4.解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A , 则 ⎪⎭⎫ ⎝⎛=21A O O A A ,故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A , 1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ; 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C ,所以⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A . 解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得 ⎪⎩⎪⎨⎧=+=+==s nE BD CD O BD CD OAD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫ ⎝⎛4121031200210001.解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A B C O A ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫ ⎝⎛--340313021201;解 ⎪⎪⎭⎫ ⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫ ⎝⎛100001000001.(2)⎪⎪⎭⎫ ⎝⎛----174034301320;解 ⎪⎪⎭⎫ ⎝⎛----174034301320(下一步: r 2⨯2+(-3)r 1, r 3+(-2)r 1. )~⎪⎪⎭⎫ ⎝⎛---310031001320(下一步: r 3+r 2, r 1+3r 2. )~⎪⎪⎭⎫⎝⎛0000310010020(下一步: r 1÷2. )~⎪⎪⎭⎫ ⎝⎛000031005010.(3)⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311;解 ⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫ ⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫ ⎝⎛---00000000002210032011.(4)⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.解 ⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132(下一步: r 1-2r 2, r 3-3r 2, r 4-2r 2. )~⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110(下一步: r 2+2r 1, r 3-8r 1, r 4-7r 1. )~⎪⎪⎪⎭⎫ ⎝⎛--41000410002020111110(下一步: r 1↔r 2, r 2⨯(-1), r 4-r 3. )~⎪⎪⎪⎭⎫ ⎝⎛----00000410001111020201(下一步: r 2+r 3. )~⎪⎪⎪⎭⎫ ⎝⎛--00000410003011020201.2. 设⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A , 求A .解 ⎪⎪⎭⎫⎝⎛100001010是初等矩阵E (1, 2), 其逆矩阵就是其本身.⎪⎪⎭⎫⎝⎛100010101是初等矩阵E (1, 2(1)), 其逆矩阵是E (1, 2(-1)) ⎪⎪⎭⎫⎝⎛-=100010101.⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=100010101987654321100001010A⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=287221254100010101987321654.3. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫ ⎝⎛---101011001200410123 ~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫ ⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫ ⎝⎛----2/102/11002110102/33/26/7001故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267. (2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫⎝⎛----00100301100001001220594012102321 ~⎪⎪⎪⎭⎫⎝⎛--------20104301100001001200110012102321 ~⎪⎪⎪⎭⎫⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021~⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010000100001故逆矩阵为⎪⎪⎪⎭⎫ ⎝⎛-------10612631110104211.4. (1)设⎪⎪⎭⎫ ⎝⎛--=113122214A , ⎪⎪⎭⎫⎝⎛--=132231B , 求X 使AX =B ;解 因为⎪⎪⎭⎫ ⎝⎛----=132231 113122214) ,(B A ⎪⎪⎭⎫⎝⎛--412315210 100010001 ~r ,所以 ⎪⎪⎭⎫⎝⎛--==-4123152101B A X .(2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B .解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(TT B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r ,所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1TT T B A X ,从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X .5. 设⎪⎪⎭⎫⎝⎛---=101110011A , AX =2X +A , 求X .解 原方程化为(A -2E )X =A . 因为⎪⎪⎭⎫⎝⎛---------=-101101110110011011) ,2(A E A⎪⎪⎭⎫⎝⎛---011100101010110001~,所以 ⎪⎪⎭⎫ ⎝⎛---=-=-011101110)2(1A E A X .6. 在秩是r 的矩阵中,有没有等于0的r -1阶子式? 有没有等于0的r 阶子式? 解 在秩是r 的矩阵中, 可能存在等于0的r -1阶子式, 也可能存在等于0的r 阶子式.例如, ⎪⎪⎭⎫⎝⎛=010*********A , R (A )=3.0000是等于0的2阶子式, 010001000是等于0的3阶子式. 7. 从矩阵A 中划去一行得到矩阵B , 问A , B 的秩的关系怎样? 解 R (A )≥R (B ).这是因为B 的非零子式必是A 的非零子式, 故A 的秩不会小于B 的秩.8. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.9. 求下列矩阵的秩, 并求一个最高阶非零子式:(1)⎪⎪⎭⎫⎝⎛---443112112013;解 ⎪⎪⎭⎫ ⎝⎛---443112112013(下一步: r 1↔r 2. )~⎪⎪⎭⎫ ⎝⎛---443120131211(下一步: r 2-3r 1, r 3-r 1. )~⎪⎪⎭⎫⎝⎛----564056401211(下一步: r 3-r 2. )~⎪⎭⎫ ⎝⎛---000056401211, 矩阵的2秩为, 41113-=-是一个最高阶非零子式.(2)⎪⎪⎭⎫ ⎝⎛-------815073*********;解 ⎪⎪⎭⎫ ⎝⎛-------815073*********(下一步: r 1-r 2, r 2-2r 1, r 3-7r 1. )~⎪⎭⎫ ⎝⎛------15273321059117014431(下一步: r 3-3r 2. ) ~⎪⎭⎫ ⎝⎛----0000059117014431,矩阵的秩是2, 71223-=-是一个最高阶非零子式.(3)⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812.解 ⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812(下一步: r 1-2r 4, r 2-2r 4, r 3-3r 4. )~⎪⎪⎪⎭⎫ ⎝⎛------02301024205363071210(下一步: r 2+3r 1, r 3+2r 1. )~⎪⎪⎪⎭⎫ ⎝⎛-0230114000016000071210(下一步: r 2÷16r 4, r 3-16r 2. )~⎪⎪⎪⎭⎫ ⎝⎛-02301000001000071210~⎪⎪⎪⎭⎫ ⎝⎛-00000100007121002301,矩阵的秩为3, 070023085570≠=-是一个最高阶非零子式.10. 设A 、B 都是m ⨯n 矩阵, 证明A ~B 的充分必要条件是R (A )=R (B ). 证明 根据定理3, 必要性是成立的.充分性. 设R (A )=R (B ), 则A 与B 的标准形是相同的. 设A 与B 的标准形为D , 则有A ~D , D ~B .由等价关系的传递性, 有A ~B .11. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3.12. 求解下列齐次线性方程组:(1)⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛--212211121211~⎪⎪⎭⎫ ⎝⎛---3/410013100101,于是 ⎪⎪⎩⎪⎪⎨⎧==-==4443424134334x x x x x x x x ,故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x (k 为任意常数). (2)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎭⎫⎝⎛-000001001021,于是 ⎪⎩⎪⎨⎧===+-=4432242102x x x x x x x x ,故方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10010012214321k k x x x x (k 1, k 2为任意常数).(3)⎪⎩⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x ;解 对系数矩阵A 进行初等行变换, 有A =⎪⎪⎪⎭⎫⎝⎛-----7421631472135132~⎪⎪⎪⎭⎫ ⎝⎛1000010000100001,于是 ⎪⎩⎪⎨⎧====00004321x x x x ,故方程组的解为⎪⎩⎪⎨⎧====00004321x x x x .(4)⎪⎩⎪⎨⎧=++-=+-+=-+-=+-+03270161311402332075434321432143214321x x x x x x x x x x x x x x x x .解 对系数矩阵A 进行初等行变换, 有。
