2017年中考数学复习指导抛物线内接三角形面积的计算通法

合集下载

5抛物线(二次函数)中的三角形面积

抛物线中的三角形面积基本题型：AB 为()0≠+=k d kx y :l 与抛物线()02≠++=a c bx ax y 相交，点P 在抛物线上。

（1）已知ABP S ∆，求点P 的坐标：利用斜弦长公式求出AB ，进而求出AB 边上的高AB h 。

设点P 为()c bt at ,t ++2，利用点到直线的距离公式列出点P 到直线AB 的距离AB l P d -，而AB l P h d AB=-，则可求得点P 的坐标。

（2）如图，若点P 在AB 上方的抛物线上时，求ABP S ∆的最大值：利用斜弦长公式求出AB 。

作/l ∥AB l 且与抛物线相切，则切点为所求。

设/l 为/d kx y +=代入抛物线()02≠++=a c bx ax y ，因为它们只有一个交点。

所（2）弦长公式抛物线与x 轴两交点之间的距离：若抛物线()02≠++=a c bx ax y 与x 轴两交点为()()0021，，，x B x A ，由于1x 、2x 是方程02=++c bx ax 的两个根，故ac x x a b x x =⋅-=+2121,()()a a ac b a c a b x x x x x x x x AB ∆=-=-⎪⎭⎫⎝⎛-=-+=-=-=444222122122121（3）斜弦长公式：一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 两个交点()()2211y x B y x A ，，，，由于1x 、2x 是方程02=-+-+)n c (x )k b (ax 的两个根，()()n c a k b /---=42∆()()()()()()()。

ak x x x x kx xk n kx n kx x x y y x x AB /221221222122212212212211411∆∙+=-++=-+=--++-=-+-=（4）两平行线之间的距离公式：已知两平行线11b kx y :l +=，与()21220b b ,k ,b kx y :l ≠≠+=，1l 与2l 之间的距离记作d ，则有1221+-=k b b d 。

中考数学复习指导抛物线内接三角形面积计算通法.doc

2019-2020 年中考数学复习指导抛物线内接三角形面积的计算通法一、问题的提出(2016年酒泉中考题) 如图 1(1) ，已知抛物线经过A(3,0) ， B(0,3) 两点.(1)求此抛物线的解析式和直线AB 的解析式;(2)如图 1(1) ，动点E，从O点出发，沿着OA的方向以 1 个单位 / 秒的速度向终点 A 匀速运动，同时，动点 F 从点 A出发，沿着 AB 方向以 2 个单位/秒的速度向终点B 匀速运动，当 EF 中任意一点到达终点时另一点也随之停止运动. 连结EF，设运动时间为t 秒，当t 为何值时，V AEF为直角三角形?(3)如图 1(2) ，取一根橡皮筋，两端点分别固定在 A ， B 处，用铅笔拉着这根橡皮筋使笔尖 P 在直线 AB 上方的抛物线上移动，动点P 与 A ， B 两点构成无数个三角形，在这些三角形中是否存在一个面积最大的三角形?如果存在，求出最大面积，并指出此时点P 的坐标; 如果不存在，请简要说明理由.本题第 (3) 问是求抛物线内接不规则三角形的最大面积问题，解这类问题有没有一种通用的方法呢 ?值得我们探究 .二、几种特殊情况1.抛物线内接三角形有一边在 x 轴上:(这里约定A点的横坐标记为 x A，A点的纵坐标记为为 y A)如图 2(1) ，有S ABC 1 AB OC 1x A x B y C.2 2如图 2(2) ，有S ABC1AB DC 1x A x B y C .2 2如图 2(3) ，有SABC1 AB DC 1x A x B y C .22 x 轴平行 : 如图 3(1) ，有2. 抛物线内接三角形有一边与S ABC1AB DC 1x A x B y C y D , 2 1 AB OC 2 1 x B 或 S ABCx A y D y C ; 如图 3(2) 2 2 ，有SABC1AB DC 1x A x B y C y D ,2 1 2 1SABCx A y D y C . 或 2 AB OC 2 x B在以上特殊情况下，只要求出A 、B 、C 、D 的坐标，代入即可以求出抛物线内接三角形的面积 .三、建立模型当抛物线内接三角形的三边均不与坐标轴平行时( 如图 4) ，三角形的面积又该怎么计算呢?解题的基本思路是将任意三角形转化为上述特殊的三角形，然后类比解决 .如图 4，过点 C 作“轴的垂线交 AB 于点 D , 则 ABC 被分成了两个以 CD 为一公共边的三角形 .过点 A 作 AECD 于点 E ，过 B 作 BF CD 于点 F ，则S ABCSCDAS ABC 1 1 CD BF CD ( AE BF ) ，CD AE2 2CD y C y D ，AE BF x C x A x B x C. Q x A x C x B,AE BF x A x B ,SABC 1x A x B y C y D.2ABC 的面积公式:综合上述，已知三角形三个顶点坐标，可得抛物线内接设 a x A x B , h y C y D.a 为两点的横坐标之差，可看成是两点之间的水平距离，可以称为水平宽 ; h表示的是两点的纵坐标之差，可称为铅直高. 在坐标系中，不规则三角形的面积公式可表示为:SABC 1ah .2.此公式适用于坐标系中的任意三角形，它和一般三角形的面积公式形成了完美的一致当三角形的三个顶点都在抛物线上时，点的横坐标不可能州样，不妨设x A x C x B.则 a x A x B ，即是水平宽.过点 C 作x轴的垂线，与直线AB 的交点记为 D ，则 h y C y D，即是铅直高，于是有SABC 1ah1x A x B y C y D.2 2四、问题解决上述问题中，过点P 作 PN // x轴，垂足为 N ，交 AB 于点 M ( 如图 1(2)) ，抛物线解析式为y x2 2x 3 ,直线 AB 的解析式为y x 3 .设 N ( x, x 3) ，则 M ( x, x2 2x 3) .于是有SABC 1 x A x B y P x M21 (3 0) ( x2 2x 3) ( x 3)23 9x2 x2 23 (x 3 )2 27 ,2 2 8即当x 3 时， V ABP 面积最大，最大面积是27，此时 P 点的坐标为( 3 , 27 ).2 8 2 8五、模型应用 ( 动点B在定点A与C之内 )例 1 如图 5，二次函数与x 轴交于点C,与y轴交于点A，B为直线AC下方抛物线上一点，求V ABC 面积的最大值.解易得点 A(0, 4) ，点 C (6,0) ，则水平宽 a x A x C 6 .直线 AC 的解析式为 y 2 x 4 .设点 B 的坐标为 (x, 1x233 x 4) , 3 4则点 D 的坐标为 ( x, 2x 4) .3铅垂高 h y B y D 2 x 4 ( 1 2 4 x 4) 1 x2 2x ,3 2 3 3故 S ABC 1 6 ( 1 x2 2x) x2 6x ( x 3)2 9 .2 3Q 0 x 6 ,当 x 3 时，即当点B(3, 5) 时，ABC 面积最大，最大面积是9.评注题中的ABC 满足公式中的A, C 为定点，B为一动点，但在运动过程中，B的横坐标介于 A, C 的横坐标之间，所以直接套用公式即得. 由此题可看出，在这种动点问题中，水平宽是两个定点间的水平跨度，铅直高即是由动点向x 轴作垂线，垂线与两定点的连线交于一点，动点和这个交点在竖直方向的跨度.六、模型拓展 ( 动点P在定点A与C之外 )例 2 如图 6(1) ，二次函数与x 轴交于点C，与y轴交于点A，直线AB与 x 轴平行，且点 B 在抛物线上，点 P 是直线 AC 上方抛物线上的动点，是否存在点 P ，使S P A C 2S A B,C若存在，求出点P 的坐标，若不存在，说明理由.解析由题意不难得出S ABC 8 ,要使 S PAC 2S ABC，即求 S PAC 16 .因为PAC 为动点三角形，由通用公式S PAC ah ，其中 a 为水平宽， a x C x A 6 , h 为铅直高，应该过动点P 向x轴作垂线;交直线 AC 于点 D ，则h y P y D.问题是此时动点 P 不在两定点A,C之间，而是运动到了两定点A, C 之外，那么通用公式还成立吗 ?由图 6(2) 可知，当动点P 在两定点A, C之外时，SPAC SPDCSPDA1 1PD AF2PD CE1PD (CE1PD2 1ah .AF ) ( x C x A )2 2 2由此可见，当动点运动到两定点之外时，通用公式依然成立. 区别是 : 动点在两定点之间时，动点图形的面积是两个规则图形的面积之和，用的是加法运算; 动点在两定点之外时，动点图形的面积是两个规则图形的面积之差，用的是减法运算.。

抛物线与三角形的面积

抛物线与三角形的面积-CAL-FENGHAI.-(YICAI)-Company One1抛物线与三角形的面积抛物线与三角形面积相结合的问题涉及代数、几何的许多定理、公式，有一定的难度，近年来的中考试题中，经常出现抛物线与三角形面积结合的综合题，以考查学生的综合运用所学知识解决问题的能力。

这节课我们共同来探索一下顶点都在抛物线2y ax bx c =++上的三角形面积的求法。

1、已知抛物线: 224233y x x =--+(1)求抛物线与坐标轴交点坐标及顶点坐标; (2)画出抛物线的草图;(3)设抛物线与x 轴交于A 、B 两点（点A 在点B 的左边），与y 轴交于C 点，顶点为D 。

求：①△DAB 和△CAB 的面积； ②四边形ABCD 的面积； ③ △ACD 的面积(4)求直线AC 的解析式；（5）抛物线上有一动点P 在直线AC 上方，问：是否存在一点P ，使△PAC 的面积最大，若存在，求出△PAC 的最大面积及P 点坐标；若不存在，请说明理由。

2、如图，抛物线c bx x y ++-=2与x 轴交与A(1,0),B(- 3，0)两点，（1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴与C 点，在该抛物线的对称轴上是否存在点Q ，使得△QAC 的周长最小若存在，求出Q 点的坐标；若不存在，请说明理由. （3）在（1）中的抛物线上的第二象限上是否存在一点P ，使△PBC 的面积最大，若存在，求出点P 的坐标及△PBC 的面积最大值.若没有，请说明理由.A BC练习：1、在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AM ＝x ．（1）用含x 的代数式表示△ＭNP 的面积S ；（2）当x 为何值时，⊙O 与直线BC 相切（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM 重合的面积为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少2、如图1，抛物线经过点A (4，0)、B （1，0)、C （0，－2）三点．（1）求此抛物线的解析式；（2）P 是抛物线上的一个动点，过P 作PM ⊥x 轴，垂足为M ，是否存在点P ，使得以A 、P 、M 为顶点的三角形与△OAC 相似若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由；（3）在直线AC 上方的抛物线是有一点D ，使得△DCA 的面积最大，求出点D 的坐标．图1AB M N D 图 2 O A BC M N P 图 1O AB M N 图 3 O3、(2011漳州中考题)如图1，抛物线y=mx2-1lmx+24m(m<0)与x轴交于B、C两点(点B在点C的左侧)，抛物线上另有一点A在第一象限内，且∠BAC=900．(1)填空：OB=________，）OC=________；(2)连结OA，将△OAC沿x轴翻折后得到△ODC，当四边形OACD是菱形时，求此时抛物线的解析式；(3)如图2，设垂直于x轴的直线l：x=n与(2)中所求的抛物线交于点M，与CD交于点N，若直线l沿x轴方向左右平移，且交点M始终位于抛物线上A、C两点之间时，试探究：当n为何值时，四边形AMCN的面积取得最大值，并求出这个最大值。

2017中考数学全国试题汇编------二次函数中三角形面积倍数关系

2017中考数学全国试题汇编------二次函数中三角形面积倍数关系25. ((2017湖北十堰))抛物线y ＝x 2＋bx ＋c 与x 轴交于A (1，0)，B (m ，0)，与y 轴交于C .(1) 若m ＝－3，求抛物线的解析式，并写出抛物线的对称轴；(2) 如图1，在(1)的条件下，设抛物线的对称轴交x 轴于D ，在对称轴左侧的抛物线上有一点E ，使S △ACE ＝ 103S △ACD ，求E 点的坐标；(3) 如图2，设F (－1，－4)，FG ⊥y 轴于G ，在线段OG 上是否存在点P ，使∠OBP ＝∠FPG ? 若存在，求m 的取值范围；若不存在，请说明理由．解：（1）y =x 2+2x -3（2）∵点A （1，0），C （0，-3） ∴直线AC 为y = 3x -3∴过点D （-1，0）且平行于AC 的直线L 1为：y = 3x +3 ∴直线AC 向上平移6个单位得到直线L 1 ∴将直线AC 向上平移106203⨯=个单位得到直线L 2：y =3x +17 联立方程组，xxＬ２Ｌ１ｘｙＯＤＣＢAy =x 2+2x -3 y =3x +17 解得，x 1=-4x 1=5y 1=5y 1=32 (不合题意，舍去) ∴点E 坐标为（-4，5）（3）设点P （0，y ）①当m ＜0时，如图所示，易证△POB ～△FPG ，得OB OPPG FG =∴41m yy --=+ ∴m =y 2+4y =(y +2)2-4 ∵-4＜y ＜0 ∴-4≤m ＜0②当m ＞0时，如图所示，易证△POB ～△FPG ，得OB OPPG FG=∴41m yy -=+ ∴m = -y 2 -4y = -(y +2)2+4 ∵-4＜y ＜0 ∴0＜m ≤4综上所述，m 的取值范围是：-4≤m ≤4，且m24．（2017湖北武汉）已知点A (－1，1)、B (4，6)在抛物线y ＝ax 2＋bx 上 (1) 求抛物线的解析式(2) 如图1，点F的坐标为(0，m)（m＞2），直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为H．设抛物线与x轴的正半轴交于点E，连接FH、AE，求证：FH∥AE(3) 如图2，直线AB分别交x轴、y轴于C、D两点．点P从点C出发，沿射线CD方向匀速运动，速度为每秒2个单位长度；同时点Q从原点O出发，沿x 轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM＝2PM，直接写出t的值【答案】（1）抛物线的解析式为：y=x2－x；（2）证明见解析；（3）；.（3）进行分类讨论即可得解.试题解析：（1）∵点A（－1，1），B（4，6）在抛物线y=ax2+bx上∴a－b=1，16a+4b=6解得：a=，b=－∴抛物线的解析式为：y=x2－x设直线AF的解析式为y=kx+m∵A (－1,1)在直线AF上，∴－k+m=1即：k=m－1∴直线AF 的解析式可化为：y =(m －1)x +m 与y =x 2－x 联立，得（m －1）x +m =x 2－x ∴(x +1)（x －2m ）=0 ∴x =－1或2m ∴点G 的横坐标为2m考点：二次函数综合题. 24.如图，抛物线c bx x y ++=221与x 轴交于B A 、两点，与y 轴交于点C ，其对称轴交抛物线于点D ，交x 轴于点E ，已知6==OC OB .⑴求抛物线的解析式及点D 的坐标；⑵连接F BD ,为抛物线上一动点，当EDB FAB ∠=∠时，求点F 的坐标； ⑶平行于x 轴的直线交抛物线于N M ,两点，以线段MN 为对角线作菱形MPNQ ，当点P 在x 轴上，且MN PQ 21=时，求菱形对角线MN 的长. 【考点】HF ：二次函数综合题．【分析】（1）由条件可求得B 、C 坐标，利用待定系数法可求得抛物线解析式，进一步可求得D 点坐标；（2）过F 作FG ⊥x 轴于点G ，可设出F 点坐标，利用△FAG ∽△BDE ，由相似三角形的性质可得到关于F 点坐标的方程，可求得F 点的坐标；（3）可求得P 点坐标，设T 为菱形对角线的交点，设出PT 的长为n ，从而可表示出M 点的坐标，代入抛物线解析式可得到n 的方程，可求得n 的值，从而可求得MN 的长．【解答】解：（1）∵OB=OC=6，∴B（6，0），C（0，﹣6），∴，解得，∴抛物线解析式为y=x2﹣2x﹣6，∵y=x2﹣2x﹣6=（x﹣2）2﹣8，∴点D的坐标为（2，﹣8）；（2）如图1，过F作FG⊥x轴于点G，设F（x，x2﹣2x﹣6），则FG=|x2﹣2x﹣6|，在y=x2﹣2x﹣6中，令y=0可得x2﹣2x﹣6=0，解得x=﹣2或x=6，∴A（﹣2，0），∴OA=2，则AG=x+2，∵B（6，0），D（2，﹣8），∴BE=6﹣2=4，DE=8，当∠FAB=∠EDB时，且∠FGA=∠BED，∴△FAG∽△BDE，∴=，即==，当点F在x轴上方时，则有=，解得x=﹣2（舍去）或x=7，此进F 点坐标为（7，）；当点F在x轴上方时，则有=﹣，解得x=﹣2（舍去）或x=5，此进F点坐标为（5，﹣）；综上可知F点的坐标为（7，）或（5，﹣）；（3）∵点P在x轴上，∴由菱形的对称性可知P（2，0），如图2，当MN在x轴上方时，设T为菱形对角线的交点，∵PQ=MN，∴MT=2PT，设PT=n，则MT=2n，∴M（2+2n，n），∵M在抛物线上，∴n=（2+2n）2﹣2（2+2n）﹣6，解得n=或n=，∴MN=2MT=4n=+1；当MN在x轴下方时，同理可设PT=n，则M（2+2n，﹣n），∴﹣n=（2+2n）2﹣2（2+2n）﹣6，解得n=或n=（舍去），∴MN=2MT=4n=﹣1；综上可知菱形对角线MN的长为+1或﹣1．24．（2017湖北鄂州）已知，抛物线23=++（a< 0 ）与x轴交于A（3，y ax bx0）、B两点，与y轴交于点C. 抛物线的对称轴是直线x=1，D为抛物线的顶点，点E 在y 轴C 点的上方，且CE =12. （1）求抛物线的解析式及顶点D 的坐标；（2）求证：直线DE 是△ACD 外接圆的切线；（3）在直线AC 上方的抛物线上找一点P ，使12ACP ACD S S ∆∆=，求点P 的坐标；（4）在坐标轴上找一点M ，使以点B 、C 、M 为顶点的三角形与△ACD 相似，直接写出点M 的坐标.【考点】二次函数，相似，圆【解析】（1）利用对称性求出点B 的坐标为（-1,0），再求抛物线的解析式及顶点D 的坐标（2）求证△ACD 和△AED 为直角三角形，就知道直线DE 是△ACD 外接圆的切线（3）找出CD 的中点坐标N ，再过点N 作NP ∥AC ，就能找到P 点（4）多次利用相似寻找点M【解答】（1）∵抛物线的对称轴是直线 abx -= =1，点A （3,0）根据抛物线的对称性知点B 的坐标为（-1,0）将（3,0）（-1,0）带入抛物线解析式中得⎩⎨⎧+-=++=303390b a b a解得⎩⎨⎧=-=21b a∴ 32y 2++-=x x 当 =1时，y=4∴顶点D （1,4）. （2）当 x=0时，y=3∴点C 的坐标为（0,3） ∵A （3,0），D （1,4） ∴23)30()03(52)04()31(2)34()01(222222=-+-==-+-==-+-=CA AD CD∴222AD CD CA =+∴△ACD 为直角三角形，∠ACD =90°. ∴AD 为△ACD 外接圆的直径 ∵点E 在轴C 点的上方，且CE =27. ∴E （0，27） ∵A （3,0），D （1,4）∴285)30()027(52)04()31(25)274()01(222222=-+-==-+-==-+-=EA AD ED∴222AE AD DE =+∴△AED 为直角三角形，∠ADE =90°. ∴AD ⊥DE又∵AD 为△ACD 外接圆的直径∴DE 是△ACD 外接圆的切线（此问中用相似证∠ADE =90°亦可）（3）解：∵A （3,0），D （1,4）,C （0,3） ∴直线AC 的解析式y= - x+3 取CD 的中点坐标N ，则N （21，27）过点N 作NP ∥AC ，交抛物线于点1P ,2P ,设直线NP 表达式为y= - x+b 把N （21，27）带入y= - x+b 得b=4 ∴直线NP 表达式为y= - x+424（2017湖北宜昌）．已知抛物线y=ax2+bx+c，其中2a=b＞0＞c，且a+b+c=0．（1）直接写出关于x的一元二次方程ax2+bx+c=0的一个根；（2）证明：抛物线y=ax2+bx+c的顶点A在第三象限；（3）直线y=x+m与x，y轴分别相交于B，C两点，与抛物线y=ax2+bx+c相交于A，D两点．设抛物线y=ax2+bx+c的对称轴与x轴相交于E．如果在对称轴左侧的抛物线上存在点F，使得△ADF与△BOC相似，并且S△ADF =S△ADE，求此时抛物线的表达式．【考点】HF：二次函数综合题．【分析】（1）根据a+b+c=0，结合方程确定出方程的一个根即可；（2）表示出抛物线的对称轴，将2a=b代入，并结合a+b+c=0，表示出c，判断顶点坐标即可；（3）根据表示出的b与c，求出方程的解确定出抛物线解析式，由直线y=x+m 与x，y轴交于B，C两点，表示出OB=OC=|m|，可得出三角形BOC为等腰直角三角形，确定出三角形三角形ADE面积，根据三角形ADF等于三角形ADE面积的一半求出a的值，即可确定出抛物线解析式．【解答】解：（1）∵抛物线y=ax2+bx+c，a+b+c=0，∴关于x的一元二次方程ax2+bx+c=0的一个根为x=1；（2）证明：∵2a=b，∴对称轴x=﹣=﹣1，把b=2a代入a+b+c=0中得：c=﹣3a，∵a＞0，c＜0，∴△=b2﹣4ac＞0，∴＜0，则顶点A（﹣1，）在第三象限；（3）由b=2a，c=﹣3a，得到x==，解得：x1=﹣3，x2=1，二次函数解析式为y=ax2+2ax﹣3a，∵直线y=x+m与x，y轴分别相交于点B，C两点，则OB=OC=|m|，∴△BOC是以∠BOC为直角的等腰直角三角形，即此时直线y=x+m与对称轴x=﹣1的夹角∠BAE=45°，∵点F在对称轴左侧的抛物线上，则∠DAF＞45°，此时△ADF与△BOC相似，顶点A只可能对应△BOC的直角顶点O，即△ADF是以A为直角顶点的等腰直角三角形，且对称轴为x=﹣1，设对称轴x=﹣1与OF交于点G，∵直线y=x+m过顶点A（﹣1，﹣4a），∴m=1﹣4a，∴直线解析式为y=x+1﹣4a，联立得：，解得：或，这里（﹣1，﹣4a）为顶点A，（﹣1，﹣4a）为点D坐标，点D到对称轴x=﹣1的距离为﹣1﹣（﹣1）=，AE=|﹣4a|=4a，=××4a=2，即它的面积为定值，∴S△ADE这时等腰直角△ADF的面积为1，∴底边DF=2，而x=﹣1是它的对称轴，此时D、C重合且在y轴上，由﹣1=0，解得：a=1，此时抛物线解析式为y=x2+2x﹣3．27（2017江苏盐城）．如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，抛物线y=x2+bx+c经过A、C两点，与x轴的另一交点为点B．（1）求抛物线的函数表达式；（2）点D为直线AC上方抛物线上一动点；①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1，△BCE的面积为S2，求的最大值；②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．【考点】HF：二次函数综合题．【分析】（1）根据题意得到A（﹣4，0），C（0，2）代入y=﹣x2+bx+c，于是得到结论；（2）①如图，令y=0，解方程得到x1=﹣4，x2=1，求得B（1，0），过D作DM ⊥x轴于M，过B作BN⊥x轴交于AC于N，根据相似三角形的性质即可得到结论；②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形，取AB的中点P，求得P（﹣，0），得到PA=PC=PB=，过作x轴的平行线交y轴于R，交AC的延线于G，情况一：如图，∠DCF=2∠BAC=∠DGC+∠CDG，情况二，∠FDC=2∠BAC，解直角三角形即可得到结论．【解答】解：（1）根据题意得A（﹣4，0），C（0，2），∵抛物线y=﹣x2+bx+c经过A、C两点，∴，∴，∴y=﹣x2﹣x+2；（2）①如图，令y=0，∴﹣x2﹣x+2=0，∴x1=﹣4，x2=1，∴B（1，0），过D作DM⊥x轴于M，过B作BN⊥x轴交于AC于N，∴DM∥BN，∴△DME∽△BNE，∴==，设D（a，=﹣a2﹣a+2），∴M（a，a+2），∵B（1.0），∴N（1，），∴==（a+2）2+；∴当a=2时，的最大值是；②∵A（﹣4，0），B（1，0），C（0，2），∴AC=2，BC=，AB=5，∴AC2+BC2=AB2，∴△ABC是以∠ACB为直角的直角三角形，取AB的中点P，∴P（﹣，0），∴PA=PC=PB=，∴∠CPO=2∠BAC，∴tan∠CPO=tan（2∠BAC）=，过作x轴的平行线交y轴于R，交AC的延长线于G，情况一：如图，∴∠DCF=2∠BAC=∠DGC+∠CDG，∴∠CDG=∠BAC，∴tan∠CDG=tan∠BAC=，即，令D（a，﹣a2﹣a+2），∴DR=﹣a，RC=﹣a2﹣a，∴，∴a1=0（舍去），a2=﹣2，∴x D=﹣2，情况二，∴∠FDC=2∠BAC，∴tan∠FDC=，设FC=4k，∴DF=3k，DC=5k，∵tan∠DGC==，∴FG=6k，∴CG=2k，DG=3k，∴∴RC=k，RG=k，DR=3k﹣k=k，∴==，∴a1=0（舍去），a2=，点D的横坐标为﹣2或﹣．22（2017山东日照）．如图所示，在平面直角坐标系中，⊙C 经过坐标原点O ，且与x 轴，y 轴分别相交于M （4，0），N （0，3）两点．已知抛物线开口向上，与⊙C 交于N ，H ，P 三点，P 为抛物线的顶点，抛物线的对称轴经过点C 且垂直x 轴于点D ．（1）求线段CD 的长及顶点P 的坐标；（2）求抛物线的函数表达式；（3）设抛物线交x 轴于A ，B 两点，在抛物线上是否存在点Q ，使得S 四边形OPMN =8S△QAB ，且△QAB ∽△OBN 成立？若存在，请求出Q 点的坐标；若不存在，请说明理由．【考点】HF ：二次函数综合题．【分析】（1）连接OC ，由勾股定理可求得MN 的长，则可求得OC 的长，由垂径定理可求得OD 的长，在Rt △OCD 中，可求得CD 的长，则可求得PD 的长，可求得P 点坐标；（2）可设抛物线的解析式为顶点式，再把N 点坐标代入可求得抛物线解析式；（3）由抛物线解析式可求得A 、B 的坐标，由S 四边形OPMN =8S △QAB 可求得点Q 到x轴的距离，且点Q只能在x轴的下方，则可求得Q点的坐标，再证明△QAB∽△OBN即可．【解答】解：（1）如图，连接OC，∵M（4，0），N（0，3），∴OM=4，ON=3，∴MN=5，∴OC=MN=，∵CD为抛物线对称轴，∴OD=MD=2，在Rt△OCD中，由勾股定理可得CD===，∴PD=PC﹣CD=﹣=1，∴P（2，﹣1）；（2）∵抛物线的顶点为P（2，﹣1），∴设抛物线的函数表达式为y=a（x﹣2）2﹣1，∵抛物线过N（0，3），∴3=a（0﹣2）2﹣1，解得a=1，∴抛物线的函数表达式为y=（x﹣2）2﹣1，即y=x2﹣4x+3；（3）在y=x2﹣4x+3中，令y=0可得0=x2﹣4x+3，解得x=1或x=3，∴A（1，0），B（3，0），∴AB=3﹣1=2，∵ON=3，OM=4，PD=1，∴S 四边形OPMN =S △OMP +S △OMN =OM•PD +OM•ON=×4×1+×4×3=8=8S △QAB ， ∴S △QAB =1，设Q 点纵坐标为y ，则×2×|y |=1，解得y=1或y=﹣1，当y=1时，则△QAB 为钝角三角形，而△OBN 为直角三角形，不合题意，舍去，当y=﹣1时，可知P 点即为所求的Q 点，∵D 为AB 的中点，∴AD=BD=QD ，∴△QAB 为等腰直角三角形，∵ON=OB=3，∴△OBN 为等腰直角三角形，∴△QAB ∽△OBN ，综上可知存在满足条件的点Q ，其坐标为（2，﹣1）．。

第五讲+抛物线中三角形的面积问题

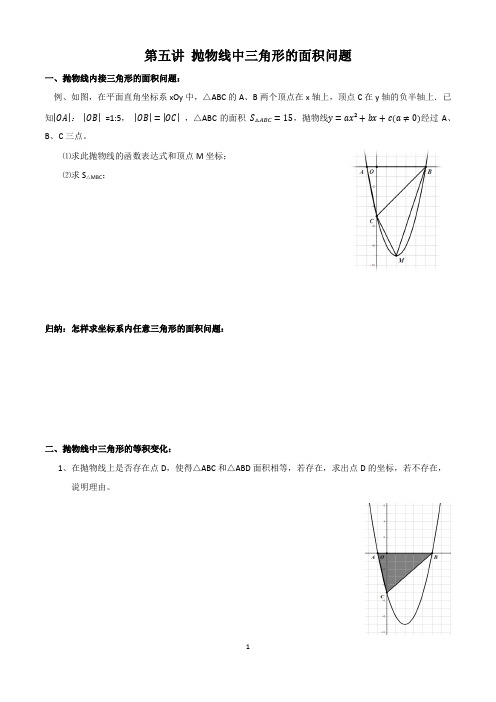
第五讲抛物线中三角形的面积问题一、抛物线内接三角形的面积问题：例、如图，在平面直角坐标系xOy中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知|OA|：|OB|=1:5，|OB|=|OC|，△ABC的面积S△ABC=15，抛物线y=ax²+bx+c(a≠0)经过A、B、C三点。

⑴求此抛物线的函数表达式和顶点M坐标；⑵求S△MBC；归纳：怎样求坐标系内任意三角形的面积问题：二、抛物线中三角形的等积变化：1、在抛物线上是否存在点D，使得△ABC和△ABD面积相等，若存在，求出点D的坐标，若不存在，说明理由。

2、在抛物线上是否存在点E，使得△ABC和△BCE面积相等，若存在，求出点E的坐标，若不存在，说明理由。

S△ABC。

若存在，求出点M的坐标；若不存在，请说明理由3、在抛物线上是否存在点M，使S△MBC= 134、（2011成都）在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为7√？若存在，求出点M的坐标；若不存在，说明理由.5、点P（2，-3）是抛物线对称轴上的一点，在线段OC上有一动点M，以每秒2个单位的速度从O向C 运动，（不与点O，C重合），过点M作MH∥BC，交X轴于点H，设点M的运动时间为t秒，试把△PMH 的面积S表示成t的函数，当t为何值时，S有最大值，并求出最大值；6、在抛物线的对称轴上有一点P的纵坐标为5，在直线上BC求一点M使得S△PBM∶S△ABC=1:5.7、在直线BC下方抛物线上是否存在一个点F，使得△BCF的面积最大，若存在，求出点F的坐标，并求出最大面积，若不存在，说明理由。

练习：1、如图，抛物线与x轴交于A（x1，0）、B（x2，0）两点，且x1＜x2，与y轴交于点C（0，-4），其中x1，x2是方程x2-4x-12=0的两个根．（1）求A、B两点坐标；（2）求抛物线的解析式；（3）点M是线段AB上的一个动点（不与A、B两点重合），过点M作MN∥BC，交AC于点N，连接CM，在M点运动时，△CMN的面积是否存在最大值？若存在，求出△CMN面积最大时点M的坐标；若不存在，请说明理由．2、（2010玉溪）如图，在平面直角坐标系中，点A的坐标为（1，△AOB（1）求点B的坐标；（2）求过点A、O、B的抛物线的解析式；（4）在（2）中x轴下方的抛物线上是否存在一点P，过点P作x轴的垂线，交直线AB于点D，线段OD 把△AOB分成两个三角形．使其中一个三角形面积与四边形BPOD面积比为2：3 ？若存在，求出点P的坐标；若不存在，请说明理由．yAB。

探究抛物线中三角形面积求法

．
2
3
通过这节课的学习,主要探究了抛物线中的三角形面积求法.
B
对于不同形状、不同形式放置在平面直角坐标系的三角形面积求法，要充分挖掘其底边或高的特征而展开问题的分析，要着重抓住水平或竖直的线段长度与点的坐标相互转化为问题解决的切入口。
作业布置:
1.请课后每四人小组找三道你们认为很好的,并渗透抛物线中三角形面积的题目交给我.（要有答案）
探究抛物线中三角形面积求法
交讨流论讨交论流
如图，抛物线的顶点A坐标为（1，4）,且经过点B(-1，0）.根据以上条件你能获得哪些信息？
y
A(1,4) C
3
B
-1 O
D
3
x
x 1
（1）连结BC，BD，CD.则S△BCD= 6 .
（2）在抛物线上是否存在一点P，使S△PBD=S△CBD，若存在，求出P点的坐标；若不存在，请说明理由.
•
由题意，得
• • • • •
① ②
解解EE这这HH个个方方32程23程EE，，PP得得，aa，即即 (32 ．2a(2 或或a4 2a a 4a5 )a 5)( a 5( a5 )（5 5 )（舍3 2舍(2 3a 去(a 去 5 ）5 )）)．．．H
E
•3Biblioteka P•即P点的坐标为P( 3 ,0) 或 P( 2 ,0)
M
（3）P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2∶3的两部分，请求出P点的坐标
• 解：（3）设P点的坐标为（a，0），因为线段BC过B，C两点，所以BC所
在的直线方程为 yx5 ．
那么，PH与直线 BC的交点坐标为 E(a，a5．)

高中抛物线三角形面积公式

高中抛物线三角形面积公式高中数学中，抛物线是一个常见的曲线类型。

而抛物线的一个重要性质是，它可以被用来构造出一个三角形，其面积可以通过一个简单的公式来计算。

我们需要了解抛物线的基本概念。

抛物线是一个平面曲线，其形状类似于一个开口向上或向下的碗。

它可以由一个二次方程来描述，即y=ax^2+bx+c，其中a、b、c是常数，x和y是抛物线上的点的坐标。

接下来，我们来看看如何构造一个抛物线三角形。

首先，在抛物线上任选三个点，将它们连接起来，就可以得到一个三角形。

这个三角形的一个顶点是抛物线的顶点，而另外两个顶点则是我们任选的两个点。

接着，我们来看看如何计算这个三角形的面积。

首先，我们需要求出三角形的底边长和高。

底边长可以通过两个顶点的横坐标之差来计算，而高则是从三角形的顶点到底边的垂直距离。

具体来说，我们可以先求出三角形的底边长b，即b=x2-x1，其中x1和x2分别是任选的两个点的横坐标。

接着，我们需要求出三角形的高h。

由于三角形的顶点在抛物线上，因此我们可以通过求出抛物线在顶点处的切线来得到高的长度。

在这里，我们就需要用到一些微积分的知识。

我们可以先求出抛物线在顶点处的导数，即y'=2ax+b。

由于导数表示的是曲线在某一点处的斜率，因此我们可以用这个导数来求出抛物线在顶点处的切线的斜率。

接着，我们可以得到这条切线的方程，即y=2ax0+b，其中x0是抛物线的顶点的横坐标。

我们可以求出这条切线与底边的交点的纵坐标，即三角形的高h。

具体来说，我们可以将这条切线的方程代入三角形底边的方程中，得到一个二次方程。

通过求解这个二次方程，我们可以得到这条切线与底边的交点的纵坐标y0。

因此，三角形的面积可以通过公式S=1/2bh来计算，其中b是底边长，h是三角形的高。

需要注意的是，由于抛物线的形状类似于一个碗，因此在选取三个点构成三角形时，我们需要保证这个三角形是有意义的。

具体来说，三个点应该按照从左到右或从右到左的顺序排列，这样才能够构成一个有意义的三角形。

初中抛物线求三角形面积乐乐课堂

初中抛物线求三角形面积乐乐课堂导语：今天乐乐课堂为大家带来了一个有趣又实用的数学知识——初中抛物线求三角形面积。

抛物线是一个经典的曲线，在几何学和物理学中有着广泛的应用。

学习如何通过抛物线求三角形面积不仅能加深对抛物线性质的理解，还能拓展数学思维，培养创造解题方法的能力。

让我们一起来探索这个有趣的数学问题吧！一、抛物线的定义和性质抛物线是由平面上的一条直线与一个定点相互关联形成的图形。

这个定点称为焦点，与这条直线上的各点到焦点的距离相等。

抛物线的形状特点是左右对称，上半部分比下半部分开口大或开口小。

二、求抛物线与直线的交点1. 联立方程我们可以通过联立抛物线和直线所对应的方程，求得它们的交点坐标。

假设抛物线的方程为f(x)=ax^2+bx+c，直线的方程为y=mx+n，其中a、b、c、m、n为已知常数。

联立这两个方程，得到二次方程ax^2+bx+c=mx+n，化简为ax^2+(b-m)x+(c-n)=0。

2. 求交点坐标利用求解二次方程的方法，我们可以得到交点的x坐标。

再将x坐标代入抛物线方程中，即可得到交点的y坐标。

这样就求得抛物线与直线的交点坐标。

三、求三角形面积的步骤1. 求焦点坐标通过抛物线方程的形式可以得到焦点的坐标。

如果抛物线的方程为f(x)=ax^2+bx+c，在求交点的过程中已经得到了焦点坐标。

2. 确定三个交点由于抛物线是左右对称的，所以交点可以确定为两个。

将焦点的坐标设为F(a,b)，已知交点的横坐标为x1、x2，则交点的坐标为A(x1,y1)和B(x2,y2)。

3. 求三角形面积利用向量的方法可以求得三角形的面积。

设向量AB=a，向量AF=b，向量BF=c，则三角形的面积可以表示为|a×b|/2，其中×表示叉乘。

四、实例演练为了更好地理解如何利用初中抛物线求三角形面积，我们来看一个实际的例子。

例题：已知抛物线y=x^2与直线y=2x+1相交于A、B两点，求三角形OAB的面积。

抛物线内接三角形面积公式

抛物线内接三角形面积公式
抛物线的标准方程为 y = ax^2 + bx + c，其中a ≠ 0。

如果把抛物线的顶点设为坐标原点 (0,0)，那么抛物线的顶点
坐标为 (h, k)，其中 h = -b/(2a)，k = c - b^2/(4a)。

接下来，我们设抛物线上任意一点的坐标为 (x, ax^2 + bx + c)。

我们知道，任意抛物线上的一点到抛物线顶点的距离可以用欧几里得距离公式计算：
d = √((x-h)^2 + (ax^2 + bx + c - k)^2)
现在我们要求抛物线上的三个点坐标 (x1, y1)，(x2, y2)，(x3,
y3)，使得这个三角形与抛物线相内切。

由于内切三角形的性质，三个点到抛物线顶点的距离都是相同的。

因此我们可以将这个距离简化为：
d = √((x1-h)^2 + (ax1^2 + bx1 + c - k)^2)
根据欧几里得距离公式，这个内切三角形的面积可以通过海伦公式计算：
s = √(p(p-d1)(p-d2)(p-d3))
其中 p = (d1 + d2 + d3)/2 是三个边长的半周长。

我们可以进一步简化这个面积公式，将三个边长用 d 表示：s = √(3d^2(d-p))
其中d = √((x1-h)^2 + (ax1^2 + bx1 + c - k)^2) 是三个边长的距离，p = (3d)/2 是三个边长的半周长。

这就是抛物线内接三角形的面积公式。

抛物线中三角形面积问题

学生通过合作学习，讨论来完成问题
作业布置
如图：抛物线y=-(x^2)+2x+3与x轴交于A、B两点
（点A在点B的左侧）.与y轴交于点C，点M((5/2)，(7/4)),N(-2,-5),
求四边形CMBN的面积。
学生自由选择一个图形进行面积的计算，鼓励用多种方法进行解决。
探究一
如图：抛物线y=-x²+2x+3与x轴交于A、B两点，
点C是抛物线与y轴交点。
2、点E在抛物线上，且CE∥AB，求S△ABE
3、在（2）的条件下，BF∥AE，F在抛物线上，求S△AEF
4、在（2）的条件下，直线AE解析式为y=x+1，G（-2,-5)在抛物线上，求S△AEG
2、感受转化思想在数学学习中的重要作业
3、培养学生合作交流能力，语言表达能力。
教学重点：三角形面积计算和点坐标的计算
教学难点：用平行线进行三角形的转化
解决措施：利用白板，展示图形的变形转化过程，让学生对图形的变化有直观的认识。
教学设计
教学环节
教师活动
学生活动
预习检测
展示四个图形
学生解答后，老师进行方法的归纳。
应用和延伸
如图：抛物线y=-x²+2x+3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点D是抛物线的顶点。
（1）点P(m,n)是抛物线与x轴所围成的封闭区域内一点（包括边界），若以D、C、P、B为顶点的四边形面积是△BCD面积的2倍，求出m的取值范围。
（2）Q是直线BC上方抛物线上的一点，求△CBQ最大面积。
在抛物线上且ceab求sabe3在2的条件下bfae在抛物线上求saef4在2的条件下直线ae解析式为yx1g25在抛物线上求saeg依次提出问题归纳结论变式练习1学生分别解决三个问题归纳出同底等高三角形面积相等2利用结论解决问题探究二如图

抛物线中三角形面积最值问题的七种求解策略

图10的正切函数值，则问题便可逐步解决.解析在上找点£，使= 由外角定理，知•①易知直线S C 解析式为y-6.设 £(m ，m -6)，由 fi (6,0)，D (2, -8)，则 B £2 = (m -6)' + (m -6)2, ED 2 = (m - 2)2 + (m + 2)2.由 B £ = £7)，知（;n -6)2 +(m -6)2 = (m -2)2 +(m + 2)2，解得 m =|，即 £(夺，-爭)•又易知 C £>2 + fiC 2 = fi /)2,则乙BCD = 90。

.qi n由 C (0, -6),£(|■，-$)，Z )(2, -8),知 CD =2^",C £=^,P J lain^CED = j .②由①②和 A C(?B = 2 A CflD ,则 tan Z _ C(?B =当点<?在点B 左侧时,(),（ -8,0).当点<?在点B 右侧时,(?2(8,0).综上，(?（ -8,0)或(8,0).从上面题目的解答可以发现:抛物线中角的存在性问题，一般运用角的特殊性及坐标条件构造基本图形，并运用图形的性质，进行推理得出有关相等线段，并表示出有关点的坐标,代入二次函数或一次函数的解析式，或运用勾股定理计算作答.在解答过程中，既要构造几何图形，根据几何直观和几何性质、定理理性分析、推理，还要运用函数与方程知识进行计算和数据分析.综合运用几何推理、函数与方程思想等多方面技能，有较强的综合性及创新探究意识，可以很好地考查学生的综合素养[2].“问题是数学的心脏”，数学的真正组成部分是问题和解，在学习过程中，在一定学习范围或主题内，围绕一定目标或某一中心问题，按照一定的逻辑结构精心设计一组问题，即为“一题多问”，采用“一题多问” 的方式，用同一道题目将多个知识点表现出来，可以帮助学生梳理旧知，形成网络，将数学技能及方法得以综合运用.“一题多问”引导学生从不同角度、不同方位进行不同层次的思考，提高学生分析问题、解决问题和提出问题的能力，可以让学生跳出“题海”，提高解题效益，提升数学素养.参考文献：[1 ]罗峻，段利芳.一次函数与反比例函数图象相交的性质之证明与运用[J ]•数理化学习（初中版），2018(12) :23 -28.[2]罗峻，段利芳.当完美正方形偶遇美丽的45度角[J ]. 理科考试研究（初中），2019,26(22) :29 -32.(收稿日期：2020 -09 -21 )抛物线中三角形面积最值问题的七种求鮮策略段昆山(易县教育局教研室河北保定074200)摘要：以二次函数为栽体，结合几何图形求面积最值问题具有难度大、综合性强，区分度高的特表.本文以某地初三上学期期末考试试卷最后一题为例，谈一谈此类问题的七种求解策略.关键词：最值问题；转化；面积；求解策略纵观近年各地中考试卷，以二次函数为载体，结合几何图形求面积最值问题的题型是各地中考的高频考点之一.这类试题综合运用多种数学思想方法, 不仅考查了二次函数与三角形面积的相关知识，又为后续学习高中知识奠定了基础.1试题呈现题目如图1,在平面直角坐标系中，抛物线y = <M c 2 +心+2(a #0)与.t 轴交于两点（点4在点B作者简介:段昆山（1976 -),男，河北保定人，本科，中学一级教师，研究方向：数学教育.的左侧），与y 轴交于点C ，抛物线经过点£»(- 2，- 3) 和点£(3，2)，点P 是第一象限抛物线上的一个动点.(1) 求抛物线的表达式；(2) 当A B P C 的面积取最大值时，求A fiP C 面积及点P 的坐标.2试题解析 2. 1第（1)问解析将点A £的坐标代人函数表达式，得丄_ 了，3_r故抛物线的表达式为y +2.2.2第（2)问解析 2. 2. 1分割法三角形面积通常用面积公式（底乘髙的一半）来求,在平面直角坐标系中求斜三角形的面积用这个公式难度大，那如何求呢？那就需要运用转化的方法把斜三角形分割成底与高分别与坐标轴平行的三角形，充分利用定点的横纵坐标来求三角形面积•如图2,过点P 作丄;c 轴于点F ，A fiP C 被分割成两个三角形，即A //P C 和所以SA B P C =S 娜c + SAW ，过点C 作C Z )丄/^于点Z ),过点B 作BE _L PF 于点 E ，S A H P C =夸PH x CD.解法1如图3,连接S C ，过点P 作W ///y 轴交S C 于点//，将点C ，S 代入一次函数表达式，可得直线的表达式为y = -+ 2.设点 P U ，+如 +2),则点+2).所以 S A P C B =-％2 +4%.f 4a -2b +2 =-3, 19a +36+2=2,解得,根据二次函数性质，利用配方法，当* = 2时， S apm 的最大值为4.故当A B P C 的面积取最大值时，点P (2,3),S A P C B 二 4.2.2.2补形法在平面直角坐标系中求斜三角形的面积不仅可以运用分割法，也可以转换思路，用补形的方法把不规则图形转化成规则图形，将斜三角形面积转化成矩形面积减去三角形的面积，再充分利用定点的横纵坐标，就可以求斜三角形面积了 • 图4如图4,过点P 作轴，垂足为点£,过点5作 fiZ )丄/)£，垂足为点£»，贝丨J 四边形为矩形•所以S APCB = S 酿形OBOE - S A P E (：一 S APDB _ S a (X b .解法2如图5,过点P 作轴，垂足为点£，过点B 作丄/)£；,垂足为点/)，所以四边形 OBD £为矩形.所以 s A PC b 二 S 四边形〇B D e : — S A P E (： - S _ s A 0C B 二(-+ ^-x + 2) x 4 - (- -^-x2 + -^-x ) x x x ~y - (4-x) x (- ~^x2 ++ 2) x -^--4=-x ~+ 4x.根据二次函数性质，利用配方法，当x =2时，^ A P C B的最大值为4.故当A B P C的面积取最大值时，点P(2,3),■5而=4_2.2.3铅垂法如图6，过A P S C的顶点分别作出水平线的垂线, 外侧两条垂线间的距离叫做水平宽.中间的垂线与 S C相交于点£，线段就叫做铅垂高.如图7,因为S apcb=S A peb+S&PCE二y PE x EU +j PE x EF =所以铅垂法本质上也是分割法.，铅垂高I图7解法3如图8,过点P作P//丄;c轴交B C于点//，设点，-+ 2)，则点 //(x，+ 2)•所以11,312^apcb =^2^~^2X+Y"x+2+y*-2)x4=-x+4x.在直线B C上.根据平行线间的距离相等，所以ABPC 和A B fiC的高相等，底是BC.所以厶B P C和A B//C的面积相等.求A B P C的面积就转化成求A//£C的面积.解法4如图10,过点Z3作户////沉交7轴于点所以 S&P C B= S A C H B-将点c，B代人一次函数表达式，可得直线C B的表达式为y= - 士;'：+ 2.因为W///S C,所以设直线P//的表达式为y根据二次函数性质，利用配方法，当x= 2时，S apos的最大值为4.故当A S P C的面积取得最大值时，点P(2,3),^ APCB=^*2.2.4平行线法如图9，W///B C，点//，P在直线W/上，点5，CH E P设点户(％，- y i2 + y x+ 2)，所以-2 =-—x +b,b22+ ~z~x + 2 + ~z~x2,//C=-y^2+2x+2-2TT22x.x2 +2x+PJflll S A P C B = ^H C xOB =-x2-t-4x.利用配方法，当x= 2时,S A P(：iB的最大值为4.故当A S P C的面积取得最大值时，点P(2,3)，^ APCB=^*2.2.5相似法如图11，求三角形的面积可以用面积公式足为点D.所以BC= VOC2 + OB2 = 7^5.求三角形的面积只要求出高就可以了.高如何求呢？我们仔细观察图形发现丄SO,所以™//y轴.所以 APHC= AOCB•因为P E±B C，所以 APEH=厶COB.所以ABOC w•所以g = I I所以= PH^~° .这样就可以求出高了.解法5如图12,过点P作丄BC,垂足为点 £，PD丄50交 SC 于点由题意，5C= VOC1+ OB2 = 2/5 ,APEH^ABOC.m i0BPH = BC'因为+ 2x,PE PH x BOBC¥(-士解法6如图13,过点P作P£//fiC,因为将点C,B代入一次函数表达式，同理可得直线C Z?的表达式为;^=-士尤+2.所以设直线的表达式为y=-+ 6.1,j=- y x + b-H i2+3+2y= - ~z~x+ ~zrx+1.1/22整理，得-士尤2 +~|~尤+2=-士a:+ 6 一士丨2 +2% +2-6=0.所以 A =4-4 x(-士）x(2 -6) =8 -26 =0.解得6=4_所以点P(2,3)，A P C fi最大值为4 .2.2.7中点法如图14,设直线S C与抛物线交于B,C两点，直线B C的解析式可设为y= ^+ n，抛物线解析式可设为y= m2 +心+ C，求其交点坐标就是联立两解析式’所以 ax2 + + c = n w c + n_ 整理，得[y= mx+ n.ax2+ (b- m)x+ c- n= 0. fffVJs x, + x2 = ——因为直a%2 +2a〇，所以 S A P C fl =^^(-士尤2 +2幻x2V^x士 =-x2 + 4x.利用配方法，当* =2时，S A P efl的最大值为4.故当A S P C的面积取得最大值时，点P(2,3),^ APCB-4-2.2.6切线法如图13,若使点P在抛物线上，S A P eB最大，则需使P£//BC，且与抛物线有且只有一个交点才能使心^8最大.因为底B C确定，只要高最大.因为点P 在抛物线上与抛物线有且只有一个交点时，SC 边上的高才最大.线B C平移到与抛物线只有一个交点时，七即& = 也就是％所以过点P作*轴的垂线，垂足M是O S的中点.所以当抛物线被直线 B C所截,P为抛物线上一动点（此时点P为线段SC 与抛物线所组成的封闭图形上抛物线上一点）丄%轴于点m,交s c于点yv,当点yv为b c中点时，s APC8 的面积有最大值.解法7如图15,过点尸作P////S C,所以& = X B+X C^所以点P 坐标为（2,3).所以=S 四边形"W /Y ;+ S APMB ""SA O R Cx (2+ 3) x 2+冬 x 2x 3_4-x 2x 4=4.' 2 2此法适用于填空、选择或验证.3感悟解法这一类以二次函数为载体，结合几何图形求面积最值问题的题型涉及的知识面多、难度大、综合性强, 要想顺利解答此类问题，必须抓住以下几点.（1)立足转化，抓住动点（设动为定）.合理构造辅助线，以转化思想为基本出发点，抓住动点，根据不同思路过动点作平行，或作垂直等辅助线，把复杂问题转化为简单问题，把未知问题转换为已知问题.（2)数形结合，设出动点坐标.充分挖掘已知条件与隐含条件，要明确角边在数量关系变化中哪些是保持不变的量，哪些是变化的量.哪些是变化的量.这需要在充分理解的基础上，进行多方位思考、多角度着手、多层次探索m ，利用相似、面积公式、根与系数的关系等知识，表示出相关的数量关系.（3)根据相关的数量关系，把面积表示成一个含有某未知量的二次函数关系式，然后利用公式法或配方法求出最值.参考文献：[1] 段昆山.构造图形求准确数形结合找临界一•一类“儿何”型新定义压轴题解法浅析[J ].中学数学教学，2020(01) ：79 -80.[2]周威.圆锥曲线中几个特殊三角形面积最值问题探究[J ].理科考试研究,2020(09) :25 - 27.(收稿日期：2020 _08-15)指向“深度学习”的教学课壹教学策略李娜沈南山(合肥师范学院数学与统计学院安徽合肥230601)摘要：从认知结构观点来看，“深度学习”是一种理解性的学习，注重学习思维的批利性、学习内容的整合性、知识体系的建构性和知识学习的迁移性.指向深度学习的数学课堂教学需要深入追问学什么、怎么学、学得怎么样三个教学本源问题，其教学策略应当注重数学知识对象的多重表征、数学学习脚手架的适时搭建、数学学习问题的逻辑引领、数学学习方法的积极反思等.关键词：初中数学；深度学习；教学策略1 “深度学习”的基本特征“深度学习”（Deep Learning )最早由美国学者 Marlon 等人于1976年提出的一个比较性学习概念，是相对于孤立记忆和非批判性接受知识的浅层学习 (Surface Learning )而言的.随后国内外学者对“深度学习”开展理论与实践研究，其基本内涵是在教师引领下,学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程，并在这个过程中学生掌握学科的核心知识，理解学习的过程,把握学科的本质及思想方法，形成积极的内在学习动机、高级的社会性感情、积极的态度、正确的价值观等m .“深度学习”的基本特征蕴含理论和实践两个层面.理论上，从知识结构观点来看，深度学习是基于学基金项目：合肥师范学院研究生创新基金项目“深度学习理念下初中数学课堂问题提出的教学实践研究”（项目编号:2020yjs 033).作者简介：李娜（ 1995 -)，女，安徽阜阳人，硕士研究生，研究方向：数学教育；沈南山（1964 -),男，安徽六安人，博士，教授，研究方向：数学课程与教学论研究.。

探究割补法在求解抛物线内接三角形面积问题中的应用

探究割补法在求解抛物线内接三角形面积问题中的应用陈巧【摘要】抛物线与三角形是初中数学的核心内容,它们的有机结合可以构建综合题和探究型的试题,特别是抛物线内接三角形面积问题,更是成为各地数学中考的热点题型,而割补法在解决此类题型时具有明显的优势.文章以一道中考复习题为例,通过灵活运用割补法来深入探究抛物线内接三角形的面积问题.【期刊名称】《中学教研：数学版》【年(卷),期】2017(000)007【总页数】3页(P46-48)【关键词】抛物线;内接三角形;割补法【作者】陈巧【作者单位】开元中学浙江杭州 310016【正文语种】中文【中图分类】O123.1抛物线内接三角形是指3个顶点都在抛物线上的三角形,它在有关二次函数的习题中经常出现,也是初中数学学习的难点之一.内接三角形的面积问题，由于涉及知识面广、综合性强,使得很多学生不知如何下手.笔者在长期的教学中发现，若学生能灵活掌握割补法，则能大大提高解决此类问题的正确率.所谓割补法，就是把不规则的图形通过等面积替换，转换位置，使不规则图形变成规则图形，以便使用公式求解的一种方法.这种数形结合的割补法，可以大大减少计算量，同时对于引导学生透过表象把握问题本质、培养学生举一反三的解题能力具有一定的指导意义[1].下面，笔者通过一道中考复习题来详细说明割补法在求解抛物线内接三角形面积问题中的实际应用.例1 已知二次函数y=x2-2x-3，设函数与x轴交于点A,B(其中点A在点B的左边)，与y轴交于点C，顶点为D.1)求△BCD的面积;2)若点P是抛物线上位于直线BC下方的一个动点，试求△BCP面积的最大值;3)问：抛物线上是否存在点Q，使得S△BCQ=S△BCD?本题具有典型性，整个题目都是围绕抛物线内接三角形面积问题展开的.在第1)小题中，易求得B(3，0)，C(0，-3)，D(1，-4)，从而本题可看作是根据三角形的3个顶点坐标来求三角形的面积.由于此类三角形为非特殊三角形，不便直接使用面积公式求解，但可用割补法来解决.以下提供4种常规的割补方法：方法1 如图1，根据S△BCD=S矩形OBNM-S△OBC-S△BDN-S△CDM即可求解. 方法2 如图2，根据S△BCD=S梯形OCDF+S△BDF-S△OBC即可求解.方法3 如图3，易求得直线BD的方程为y=2x-6，从而，根据S△BCD=S△BCG+S△DCG即可求解.方法4 如图4，易求得直线BC的方程为y=x-3,从而E(1,-2)，根据S△BCD=S△BED+S△CED即可求解.不难看出：方法3和方法4的解题原理是一样的，都是将一个三角形分割成两个三角形，然后利用共有的底求解.这种割补法是比较常规的方法，学生比较容易理解，但若要将其上升到普遍规律的高度，进而得出固定的解题公式，则有点难度. 事实上，如图5，过△ABC的3个顶点分别作出与水平线垂直的3条直线l1,l2,l3,其中直线l2与直线AB相交于点D.记l1与l3之间的距离为△ABC的“水平宽(记作a)”，线段CD的长度为△ABC的“铅垂高(记作h)”.在方法4中，水平宽a即为线段BO的长,铅垂高h即为线段DE的长，从而第2)小题难度有所提高，但依然可以运用割补法，只是将固定的点D变成了动点P.延用上述结论即S△=ah,如图6，可设点P的坐标为(m,m2-2m-3),则点E的坐标为(m,m-3)，此时点B，C间的水平宽BO=3，铅垂高为h，则-m2+m,第3)小题同样可利用结论S△=ah，如图7，这里点Q的坐标不确定，可设点Q的坐标为(n,n2-2n-3),则点F的坐标为(n,n-3)，从而点B，C间的水平宽BO=3，铅垂高h=FQ，此时点F与点Q相对位置不确定，因此在此小题中，点F不一定在线段BC上(即点F不一定在点Q上方)，故FQ=|(n-3)-(n2-2n-3)|=|-n2+3n|.事实上，当点F不在线段BC上时(如图8)，BG·GF-BG·GQ-QF·GO=BG(GF-GQ)-QF·GO=BG·QF-QF·GO=QF·(BG-GO)=QF·BO=ah.因此，点F不在线段BC上时，S△=ah仍然成立.于是在引入水平宽(a)和铅垂高(h)的概念后，求解抛物线内接三角形面积问题的割补法就可以归纳为具有普遍指导意义的公式“S△=ah”解决.通过上述解题论证不难发现，割补法在求解抛物线内接三角形面积问题时都可以适用.例2 如图9，抛物线的顶点坐标为C(1，4)，交x轴于点A(3，0)，交y轴于点B.1)求抛物线的解析式和△CAB的面积.2)问：抛物线上是否存在一点P，使S△PAB=S△CAB?若存在，求出点P的坐标；若不存在，请说明理由.分析1)如图9，易得抛物线的解析式为y=-x2+2x+3，从而点B的坐标为(0，3)，进而可得直线AB的解析式为y=-x+3.过点C作CD∥y轴交AB于点D,得点D的坐标为(1,2).在△CAB中，水平宽a=3，铅垂高h=2，于是2)如图10，因为点P在抛物线上，所以可设P(m,-m2+2m+3).过点P作PG∥y 轴交AB于点G,得点G的坐标为(m,-m+3).在△PAB中，水平宽a=3，铅垂高|-m2+3m|.数学作为一门科学，必然有其规律可循.笔者通过详细讲解割补法在求解抛物线内接三角形面积问题中的应用，目的就是寻找这种规律性.作为一线教师，在平常的教学过程中，不能满足于向学生生硬地灌输课本知识，而是要通过对规律的探究，使学生不仅知其然，还要知其所以然.割补法在实际应用中千变万化，只有对其作进一步地提炼，如文中所探讨的“引入‘水平宽’和‘铅垂高’的概念”，从而将这种割补法以公式的形式固定下来.只有这样才能使学生掌握割补法的要义，也才能使学生以不变应万变，灵活应用，提高解题的效率和正确率.1)求椭圆的标准方程;2)若k1+k2=0，求实数k的值.原解 1)由椭圆C经过点离心率为,知2)①当0<k<+∞时,因为直线AB经过焦点(3，0)，所以可设直线AB的方程为y=k(x-3),联立②当k=0时，k1=,k2=-，从而k1+k2=-≠0.③当k不存在时，此时斜率k1,k2均不存在，不合题意.综上所述，k=.通过研究笔者发现:点P正好是过右焦点作垂直于x轴的直线与曲线的交点(位于x 轴上方)，而所求k正好是离心率，并发现这不是巧合.对于第2)小题可作如下变式推广.变式1 已知椭圆C：+=1(其中a>b>0)经过点过椭圆C的右焦点作斜率为k的直线，交椭圆于点A,B，记PA,PB的斜率为kPA,kPB.若kPA+kPB=m，求实数k的值.解 1)当0<k<+∞时，因为直线AB经过焦点(c，0)，所以可设直线AB的方程为y=k(x-c),联立2k-m=·,·=·=,2)当k=0时，kPA=-,kPB=，从而3)当k不存在时，斜率kPA,kPB均不存在，不合题意.变式2 已知双曲线C：-=1(其中a>0，b>0)经过点过椭圆C的右焦点作斜率为k 的直线，交椭圆于点A,B，记PA,PB的斜率为kPA,kPB.若kPA+kPB=m，求实数k的值.解 1)当0<k<+∞时,因为直线AB经过焦点(c，0)，所以可设直线AB的方程为y=k(x-c)，联立·=·=-,2)当k=0时，kPA=-，kPB=，从而3)当k不存在时，斜率kPA,kPB均不存在，不合题意.变式3 已知抛物线C：y2=2px(其中p>0)经过点过抛物线C的焦点作斜率为k的直线，交抛物线于点A,B，记PA,PB的斜率为kPA,kPB.若kPA+kPB=m，求实数k的值.解 1)当0<k<+∞时，因为直线AB经过焦点所以可设直线AB的方程为y=,联立2)当k=0时，A(0,0)，点B不存在，则kPA=-2，kPB不存在.3)当k不存在时，斜率kPA,kPB均不存在，不合题意.以上就是对这道赛题的一般推广，请读者批评指正.。

设点法在求解抛物线内接三角形面积问题中的应用

的一类问题，较大.有效地解决这一问题.运用设点法解题的基本思路是：1.设点.2.3.4.公式解题.在解题时，线的方程，问题便能迎刃而解.例1.已知抛物线y 2=2px 三点A ,B ,C ，连接A ，B ，C 面积.解：由于A ,B ,C 点的坐标分别为：A æèçöø÷a 22p ,a ,B æèçb 22p ,则AB 两点间的距离为|AB |=直线AB 的方程为2px -(a +则C 点到直线AB 的距离：d 4p +()a +b 蔡彧凯廖小莲思路探寻50()a +b y +ab =0，4x -()a +c y +ac =0.由于直线AB 过抛物线的焦点F ，所以将点F (1,0)代入直线AB 的方程可得ab =-4；由点B 在准线l 上的投影为E ，所以E 点的坐标为(-1,b )，所以k EF ∙k AC =0-b 1-(-1)×4a +c =-1，即c =2b -a ，而AB =C 到AB2则S ΔABC =|a -b |8×|c 2-()a +b c +ab |=|a -b |34，设a =2t ,b =-２t，则S ΔABC =|f ()t |=f ()t =2æèöøt +1t 3≥16，所以三角形ABC 面积的最小值为16.在解答有关抛物线问题的过程中，我们经常使用设线法求解，而在这一题中我们运用设点法，在设出点A 、B 、C 的坐标后，由点的坐标来写出直线的方程，再根据题目条件一一进行计算、化简，便能得到可直接应用基本不等式的式子，进而求得面积的最小值.例3.如图2，已知点A （4，4）在抛物线y 2=2px上，过点B (1,1)的直线交抛物线于点P (x 1,y 1),Q (x 2,y 2),若直线AP 与OQ 交于点I ，记ΔIPQ ，ΔIAO 的面积分别为S 1，S 2.求S 1S 2的最小值.图2解：由题意可设点P (p 24,p ),Q (q24,q )，则直线PQ 的方程为：4x -()p +q y +pq =0，因为B ()1,1∈PQ ，所以4-()p +q +pq =0，化简得q =-4+pp -1，所以直线AP 的方程为:4x -()4+p y +4p =0，直线OQ 的方程为:4x -qy =0，联立两方程可得y I =4p -4p +2，所以S 1S 2=IP ×IQ IA ×IO =-()p -y I ()q -y I ()4-y I y I=()p2-2p +4()12-6p +3p 264()p -12，设p =t +1，对上式进行化简可得S 1S 2=()t 2+3()3t 2+964t2=364éëùût +3t 2≥916，当且仅当t =3，即y I =p =3+1时等号成立.所以S 1S 2的最小值为916.解答本题依旧采用的是设点法，设出P 、Q 两点的坐标，然后分别写出直线PQ 、AP 、OQ 的方程，根据题意得到关于p 与q 的一个关系式，通过联立方程组求得I 点的纵坐标，再利用三角形的面积公式以及两点之间距离公式求得S 1S 2的表达式，最后设p =t +1，化简后便可运用基本不等式求得S 1S 2的最小值.解答抛物线内接三角形面积问题并不一定要用设线法，设点法也是一种很不错的选择.运用设点法来解答抛物线内接三角形面积问题，不仅能简化繁琐的计算，还能优化解题的方案，有利于提高解题的效率.（作者单位:湖南人文科技学院数学与金融学院）思路探寻51。