16位超前进位加法器
基于逻辑结构的超前进位加法器的设计

基于逻辑结构的超前进位加法器的设计白首华;胡天彤【摘要】通过对计算机加法器的研究,从门电路标准延迟模型出发,在对超前进位加法器逻辑公式研究的基础上,在主要考虑速度的前提下,给出了超前进位加法器的逻辑电路的设计方案。
主要对16位、32位加法器的逻辑电路进行分析设计,通过计算加法器的延迟时间来对比超前进位加法器与传统串行进位链加法器,得出超前进位算法在实际电路中使加法器的运算速度达到最优。
%Through the research of computer adder, from the standard delay model of a gate and mainly considering the premise of speed, the paper gives the carry advance adder design scheme of the logic circuit. It mainly makes the analysis of the circuit design to the 16, 32-bit adder, through calculatingthe delay time to compare carry look-ahead adder with the traditional serial binary adder chain, and drawing a conclusion: the advanced carry algorithm makes adder operation speed to achieve the most optimal condition in the practical circuit.【期刊名称】《山西电子技术》【年(卷),期】2012(000)004【总页数】3页(P3-4,6)【关键词】串行进位链;超前进位加法器;时间延迟【作者】白首华;胡天彤【作者单位】郑州航空工业管理学院,河南郑州450015;郑州航空工业管理学院,河南郑州450015【正文语种】中文【中图分类】TP302.2在计算机处理器中,加法器的速度直接决定了整个电路的速度,为了提高整个电路的速度,需要提高加法器的速度。
16位超前进位加法器实验报告
实验名称:十六位超前进位加法器一、实验目的设计、验证并优化16位超前进位加法器的逻辑功能。
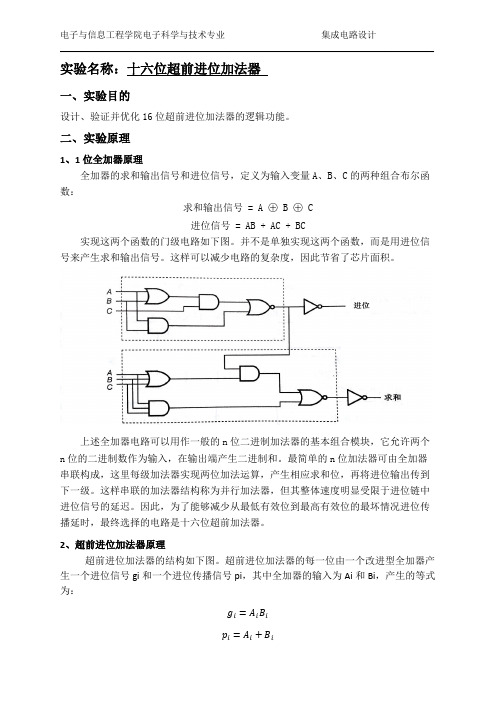
二、实验原理1、1位全加器原理全加器的求和输出信号和进位信号,定义为输入变量A、B、C的两种组合布尔函数:求和输出信号 = A ⊕ B ⊕ C进位信号 = AB + AC + BC实现这两个函数的门级电路如下图。
并不是单独实现这两个函数,而是用进位信号来产生求和输出信号。
这样可以减少电路的复杂度,因此节省了芯片面积。
上述全加器电路可以用作一般的n位二进制加法器的基本组合模块,它允许两个n 位的二进制数作为输入,在输出端产生二进制和。
最简单的n位加法器可由全加器串联构成,这里每级加法器实现两位加法运算,产生相应求和位,再将进位输出传到下一级。
这样串联的加法器结构称为并行加法器,但其整体速度明显受限于进位链中进位信号的延迟。
因此,为了能够减少从最低有效位到最高有效位的最坏情况进位传播延时,最终选择的电路是十六位超前加法器。
2、超前进位加法器原理超前进位加法器的结构如下图。
超前进位加法器的每一位由一个改进型全加器产生一个进位信号gi和一个进位传播信号pi,其中全加器的输入为Ai和Bi,产生的等式为:改进的全加器的进位输出可由一个进位信号和一个进位传输信号计算得出,因此进位信号可改写为:式中可以看出,当gi = 1(Ai = Bi = 1)时,产生进位;当pi = 1(Ai =1或Bi = 1)时,传输进位输入,这两种情况都使得进位输出是1。
近似可以得到i+2和i+3级的进位输出如下:下图为一个四位超前进位加法器的结构图。
信号经过pi和gi产生一级时延,经过计算C产生一级时延,则A,B输入一旦产生,首先经过两级时延算出第1轮进位值C’不过这个值是不正确的。
C’再次送入加法器,进行第2轮2级时延的计算,算出第2轮进位值C,这一次是正确的进位值。
这里的4个4位超前进位加法器仍是串行的,所以一次计算经过4级加法器,一级加法器有2级时延,因此1次计算一共经过8级时延,相比串行加法器里的16级时延,速度提高很多。
16bit加法器进位链拆分

16bit加法器进位链拆分16位加法器是一种用于实现二进制加法运算的电路或设备。
它能够接收两个16位的二进制数并输出它们的和,同时还能输出产生的进位信息。
在16位加法器中,采用了进位链拆分的设计方法。
本文将详细介绍16位加法器和进位链拆分的原理、设计和应用。
首先,让我们来了解一下二进制加法的基本原理。
在二进制加法中,只有两个数位以及一个进位作为输入,然后进行逐位相加,并将结果和进位相应地传递下去。
而每一位的计算都是独立的,不受其他位数的影响。
16位加法器中,需要对16位输入进行逐位相加,并且能够产生进位。
为了实现这一功能,我们可以采用一种称为进位链拆分的技术。
进位链拆分是一种将进位按照不同位数进行拆分的方法,以提高加法器的性能和工作速度。
进位链拆分的基本原理是将进位按照不同的位数进行拆分,然后分别传递到不同位数的加法器中。
这样做的好处是可以减小每个加法器的运算压力,并且并行计算各个位数的和与进位,提高整个加法器的工作速度。
在16位加法器中,进位链拆分可以将进位信号按照每4位进行拆分,即将第1位的进位拆分到第2位,第3位的进位拆分到第4位,以此类推。
这样,每4位之间的进位相互独立,可以同时进行计算。
具体的设计过程如下:首先,将两个16位的输入数分别用寄存器存储起来。
然后,将这两个输入数按照每4位进行拆分,分别得到4个4位的字。
接下来,针对每个4位的字,设计一个4位加法器。
在4位加法器中,需要进行4位的加法运算,并输出结果和产生的进位。
可以使用四个全加器来实现这一功能。
全加器是一种有三个输入和两个输出的逻辑门电路,可以实现三个二进制数的相加运算。
将四个全加器按照进位链的方式相连,即将第一个全加器的进位输出连接到第二个全加器的进位输入上,依次类推。
这样,就可以实现4位加法器的运算。
接着,将4位加法器的输出和进位信号分别传递到下一个4位加法器中。
同时,将每个4位加法器的输出结果进行合并,得到最终的16位输出。
16位超前加法器实验报告

16位超前加法器设计实验一、实验分析:四位超前进位加法器HDL程序:module add4_head ( a, b, ci, s, pp, gg);input[3:0] a;input[3:0] b;input ci;output[3:0] s;output pp;output gg;wire[3:0] p;wire[3:0] g;wire[2:0] c;assign p[0] = a[0] ^ b[0];assign p[1] = a[1] ^ b[1];assign p[2] = a[2] ^ b[2];assign p[3] = a[3] ^ b[3];assign g[0] = a[0] & b[0];assign g[1] = a[1] & b[1];assign g[2] = a[2] & b[2];assign g[3] = a[3] & b[3];assign c[0] = (p[0] & ci) | g[0];assign c[1] = (p[1] & c[0]) | g[1];assign c[2] = (p[2] & c[1]) | g[2];assign pp = p[3] & p[2] & p[1] & p[0];assign gg = g[3] | (p[3] & (g[2] | p[2] & (g[1] | p[1] & g[0])));assign s[0] = p[0] ^ ci;assign s[1] = p[1] ^ c[0];assign s[2] = p[2] ^ c[1];assign s[3] = p[3] ^ c[2];endmodulep表示进位否决信号(pass),如果p为0就否决调前一级的进位输入。
否决的意思就是即使前一级有进位,本级也不会向后一级产生进位输出。
16位加法器电路设计

16位加法器电路设计
加法器电路是计算机中常见的数字电路,用于将两个二进制数相加并得出和。
16位加法器电路设计是指设计一个能处理16位二进制数相加的电路。
在设计16位加法器电路时,需要考虑以下几个关键方面:
1. 选择合适的器件:需要选择适合的逻辑门和触发器等数字电路器件。
常用的器件包括AND门、OR门、XOR门、全加器等。
2. 划分模块:将16位加法器电路划分为若干个小模块,简化设计过程。
常见的模块包括单位加法器和级联器。
3. 单位加法器设计:单位加法器是实现加法运算的基本单元。
在16位加法器电路中,每一位均由一个单位加法器完成。
单位加法器由两个输入(被加数位和加数位)和两个输出(和位和进位位)组成。
4. 级联器设计:级联器用于连接多个单位加法器,将进位位从低位传递到高位。
在16位加法器电路中,需要将每一位的进位位和前一位的进位位相连。
5. 测试和验证:设计完成后,需要进行测试和验证,确保16位加法器电路的正确性和性能。
通过以上步骤设计完成的16位加法器电路能够实现对16位二进制数的相加操作。
在实际应用中,可以将多个16位加法器电路级联以实现更大位数的加法运算。
设计一个高效可靠的16位加法器电路是数字电路设计的重要任务之一,对于计算机的性能和功能具有重要影响。
通过仔细考虑各个方面的设计和实施,可以实现一个满足要求的16位加法器电路。
16位加法器设计

计算机组成原理课程设计报告题目 16位加法器设计B院系信息科学技术学院专业计算机科学与技术班级 11计本(2)教师学生学号内容提要本设计在其他基本加法器的基础上改进为超前进位加法器,它避免了串行进位加法器的进位延迟,提高了速度。
其主要分为四章,第一章为设计概述,主要介绍设计的任务、目标,以及设计环境,第二章为总体设计方案,其主要介绍本设计中系统设计的框架。
第三章为仿真测试,给出了系统在仿真环境下波形测试结果,看是否满足题目要求。
第四章为设计心得总结,主要是介绍在经过本次设计后,自己的一些心得体会。
最后还给出了本设计的一些参考文献。
前言计算机组成原理是一门实践性很强的课程;其课程设计目的在于综合运用所学知识,全面掌握微型计算机及其接口的工作原理、编程和使用方法;在设计中,通过小组协作提出设计方案,进行软件设计、调试,最后获得正确的结果,可以加深和巩固对理论知识的更好掌握,进一步建立计算机应用系统体概念,初步掌握单片机软、硬件开发方法,为以后进行实际的单片机软、硬件应用开发奠定良好的基础。
本设计是利用74181、74182芯片组成了16位加法器的组间组内并行。
目录1设计概述 (5)1.1设计任务 (5)1.2 设计要求 (5)1.3设计环境 (5)2总体设计方案 (6)3仿真测试 (9)4设计个人总结 (10)参考文献: (10)1设计概述1.1设计任务1、掌握MaxPlus2软件的使用方法。
2、熟悉74系列芯片的组成和工作过程。
3、掌握半加器,一位全加器的设计原理,掌握超前进位产生电路的设计方法。
4、正确将电路原理图下载到试验箱中。
5、正确通过实验箱连线实现一位二进制数的相加并得到正确结果。
6、完成设计实验报告。
7、完成课程设计答辩。
1.2 设计要求1、巩固和运用所学课程,理论联系实际,提高分析、解决计算机技术实际问题的独立工作能力。
2、学会使用MAX-PLUSⅡ软件设计电路原理图及功能模拟3、熟悉常用的门电路1.3设计环境MaxPlus22总体设计方案1、半加器的设计原理 半加器逻辑电路半加器逻辑表达式 S=B A ⊕ AB C =半加器真值表A B C S 0 0 0 0 0 1 0 1 1 0 0 1 11 1 02、一位全加器的设计原理 一位全加器逻辑电路CA B S=1&74182一位全加器逻辑表达式进位输出()i i i i i i B A C B A C +⊕=-1相加之和 1-⊕⊕=i i i i C B A F 一位加法器真值表A B 1-i C F i C 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 1 1 0 1 1 0 1 0 1 111113、十六位并行加法器的设计思路1. 先设计一个半加器然后两个半加器合并成一个一位的全加器,最后用16个一位的全加器组合成一个16位的全加器;2. 先设计一个一位全加器,然后16个并联组成一个16位全加器3. 使用4片74181和1片74182芯片采用双重分组跳跃进位组成16位并行加法器这里我们组采用的是第三个方法来实现16位并行加法器的。
16位全加器

四川理工大学课程设计任务书设计题目:采用门电路设计一个16位的全加器电路院系:计算机学院专业:计算机科学与技术班级:2008级6班指导教师:朱文忠学生姓名:赵******************目录:一引言 (1)1.1 设计背景 (1)1.2 设计分工 (1)二设计目的 (2)2.1 设计目的 (2)2.2 设计内容 (2)三设计过程 (2)3.1 硬件方案 (2)3.1.1 一位全加器的原理及设计 (2)3.1.2 四位全加器的原理及设计 (4)3.1.3 十六位全加器的原理及设计 (7)3.2 软件方案 (9)3.3 可行性论证 (13)3.4 结论 (15)四参考文献 (16)引言1. 设计背景随着计算机科学技术的发展,人们获得信息的途径更加多样,获取信息的速度更加快捷。
硬件的发展允许程序员编出很多精彩的使用软件,也使得计算机更加普及。
中央处理器CP U的好坏是影响和制约计算机速度和性能的关键因素。
而加法器是组成C PU的的重要部件,一般运算速度的快慢就取决与每秒执行加法的次数,加法器是算术逻辑单元中的基本逻辑器件。
例如:为了节省资源,减法器和硬件乘法器都可由加法器来构成。
但宽位加法器的设计是很耗费资源的,因此在实际的设计和相关系统的开发中需要注意资源的利用率和进位速度等两方面的问题。
多位加法器的构成有两种方式:并行进位和串行进位方式。
并行进位加法器设有并行进位产生逻辑,运算速度快;串行进位方式是将全加器级联构成多位加法器。
并行进位的并行加法器又可以分为组内并行、组间串行的进位链和组内并行、组间并行的进位链。
通常,并行加法器比串行级联加法器占用更多的资源,并且随着位数的增加,相同位数的并行加法器比串行加法器的资源占用差距也会越来越大。
它们的目的就是要进位信号的产生尽可能的快,因此产生了二重进位链或更高重进位链,显然进位速度的提高是以硬件设计的复杂化为代价来实现的。
2. 设计分工赵**(081010*****):硬件方案、排版吴**(081010*****):可行性论证、结论王**(081010*****):软件方案、找资料设计目的1.设计目的(1)掌握1位全加器的形成;(2)掌握4位片SN74LS181的原理;(3)用4片SN74LS181以并/串形成16位字长的ALU;(4)形成16位运算器数据通路结构;(5)将设计结果下载到实验板上,进行验证。
数字集成电路课程设计16位加法器

数字集成电路课程设计——16位加法器设计参数:*输入两个16位的补码*输出一个17位的补码*允许采用流水线、单元复用等技术实现设计要求:*使用RTL级Verilog描述加法器架构*使用门级验证加法器功能(ModelSim等仿真)*优化方向:加法器等效总门数最少*等效门数计算示例:INV=1, NOR2=NAND2=2, DFF=4最终优化结果:图1.1单个全加器单元的最终优化方案图1.2 第17位结果的运算电路最终总共等效门数= 16 X 17 + 7 = 279仿真结果:1 2 3 4 5图2. ModelSim仿真结果如图2所示,箭头1所指区域为两个16位全0的加数,无进位,输出和为0;箭头2所指区域为0与1000000000000000(-32768)相加,无进位,输出和为11000000000000000(-32768);箭头3所指区域为0与1111111111111111(-1)相加,无进位,输出和为11111111111111111(-1);箭头4所指区域为-1与1000000000000000(-32768)相加,无进位,输出和为10111111111111111(-32769);箭头4所指区域为-1与1000000000000000(-32768)相加,进位为1,输出和为11000000000000000(-32768)。
可见已正确实现了16位补码加法器的功能。
设计思路:首先,我们需要明确加法器的设计。
按照题目的要求,我们的加法器必须满足以下几个原则:1、16位加法器,且可以计算出第17位的进位;2、可以计算补码;3、设计出的结构门数最少.由上面的要求,我们可以有对应的设计:1.我们假定16位数据本身就是以补码形式储存的,那么最高位就是符号位,0代表正数,1代表负数;由此,我们可以根据二进制加法的规则得知,计算补码不需要对储存的补码进行任何形式的修改,利用正常的全加器结构就可以计算出正确的结论,包括位数扩展的要求也能满足;2.要完成17位的补码计算,需要进行符号位扩展,也就是将加数和被加数的最高位重复一次变成17位的数据,如1000000000000000变为11000000000000000;在编码的时候,需要17个加法器,但是最后一个加法器的加数和被加数重复使用16位的数据,而进位则采用16位得到的进位;3.加法器必须是一般意义上的加法器,除非采用流水线结构,否则不应使用时序逻辑,如下图所示的设计就不合理。
16位超前进位加法器

16位超前进位加法器设计目录摘要 (1)1需求分析1.1加法器的发展........................................................................ 错误!未定义书签。
1.2几种串行加法器性能比较 (3)1.2.1串行进位加法器 (3)1.2.1超前进位加法器 (3)2主要内容 (4)2.1设计原理 (6)2.2设计思路 (4)3 设计思想 (5)4 实现方法 (6)4.1顶层方案图的设计与实现 (6).4.1.1顶层方案的整体设计 (6)4.1.2元器件选择和引脚锁定 (7)4.2功能模块的设计与实现 (8)4.2.1设计描述 (8)4.2.2创建RTL代码并得到电路图....................................................... .94.3功能仿真 (11)4.4编程与下载 (12)4.5硬件仿真结果 (12)5小结 (13)参考文献 (13)附录 (14)摘要:加法运算是最重要最基本的运算,所有的其他基本算术运算乘除等都最终可以用加法运算来表示在不同的场合对加法器的要求不同,要的要求速度快有的要求面积小超前进位加法器相比于串行进位加法器是一种快速加法运算器,根据用户的要求追求速度与面积的平衡。
关键词:超前进位加法器串行进位加法器速度面积1需求分析1.1 加法器的发展加法运算是最基本的运算,所有其他基本算术运算都是以加法运算为基础。
但因为加法运算存在进位问题,使得某一位计算结果的得出和所有低于他的位相关,因此,为了减少进位传输所耗的时间提高计算速度人们设计了多种类型的加法器。
如跳跃进位加法器,进位选择加法器,超前进位加法器等他们都是利用各位之间的状态来预先产生高位进位信号从而减少进位从低位到高位的传递时间1.2 几种加法器的性能比较1.2.1串行进位加法器串行进位加法器的每一位加和值都依赖于上一位进位信号,即进位信号是串行的经过加法器的每一位。
性能改进的16位超前进位加法器_李嘉

性能改进的16位超前进位加法器李 嘉,蒋 林(西安邮电学院 陕西西安 710061)摘 要:加法运算是最重要最基本的运算,所有的其他基本算术运算,减、乘、除、模乘运算最终都能归结为加法运算。
在不同的场合使用的加法器对其要求也不同,有的要求速度更快,有的要求面积更小。
基于速度更快的要求,对3种常用加法器从结构与性能上进行比较,给出了综合面积与速度的比较。
进而对超前进位加法器进行了进一步改进,加入了流水线结构设计,大大提高了其速度性能。
关键词:串行进位加法器;超前进位加法器;流水线;逻辑综合中图分类号:T P342+.21 文献标识码:B 文章编号:1004-373X(2007)22-172-03A 16-bit C LA with Improved PerformanceL I Jia,JIA N G L in(Xi an Institute o f P ost and T elecom municat i o ns,Xi an,710061,Chi na)Abstract :T he addition o perat ion is the mo st impo rtant fundamental o per ation,all other o perat ions including subtr action multiplication division and modular mult iplication can be implemented by addition operatio n.A dders using at var ious cases are different since the requirement are different.Some ask for faster,others ask for smaller.T hree co mmon used adder s are com -pared in the st ruct ur al and perfo rmance,based o n the requirement o f faster.T hen so me amelio ratio ns on the CL A are made by adding pipline str ucture to impro ve its perfo rmance fo r w or king faster.Keywords :ripple adder ;car ry loo k -ahead adder;pipeline;log ic sy nthesis收稿日期:2007-04-23加法运算是最重要最基本的运算,所有的其他基本算术运算,减、乘、除、模乘运算最终都能归结为加法运算。
基于方块超前进位的快速进位跳跃加法器

第38卷第6期2006年12月 南 京 航 空 航 天 大 学 学 报Jou rnal of N an jing U n iversity of A eronau tics &A stronau ticsV o l .38N o.6 D ec .2006基于方块超前进位的快速进位跳跃加法器崔晓平 王成华(南京航空航天大学信息科学与技术学院,南京,210016)摘要:提出了一种基于方块超前进位的快速进位跳跃加法器。
该加法器的跳跃方块采用不等尺寸的二级方块超前进位逻辑,其可变的方块尺寸缩小了关键路径的延时,而方块内部的快速超前进位逻辑使得延时进一步减小。
除第一个方块以外,其他每个方块进位仅有两级门延时。
该进位跳跃加法器已用PSp ice 仿真工具进行了功能验证和仿真。
门级延时和PSp ice 仿真分析表明,所提出的进位跳跃加法器的速度优于通用优化方块分配的进位跳跃加法器。
关键词:;进位跳跃加法器;超前进位;门级延时中图分类号:T P 342121 文献标识码:A 文章编号:100522615(2006)0620786205 收稿日期:2006203222;修订日期:2006205222 作者简介:崔晓平,女,讲师,1962年1月生,E 2m ail :cuixp 126@ 。
Fa st Carry -Sk ip Adder Ba sed on Block Carry -L ookaheadCu i X iaop ing ,W ang Cheng hua(Co llege of Info r m ati on Science and T echno logy ,N anjing U niversity of A eronautics &A stronautics ,N anjing ,210016,Ch ina )Abstract :A fast carry 2sk i p adder is p ropo sed based on variab le 2sized tw o 2level b lock carry 2lookahead logic .T he variab le b lock sizes m in i m ize critical path delay .W ith in b lock s ,the fast carry 2lookahead log 2ic is u sed to decrease the delay .W hen the carry of the first b lock is generated ,each of the o ther six b lock s has on ly tw o gate delays .T he adder is functi onally verified and si m u lated u sing PSp ice .T he analysis of the gate delay and the si m u lati on reveal that the p ropo sed adder can p rovide the faster speed than the conven ti onal carry 2sk i p adder w ith the op ti m al b lock distribu ti on .Key words :adder ;carry 2sk i p adder ;carry 2lookahead ;gate delay引 言加法运算是计算机最基本的算术运算,其他运算例如减、乘、除等都可以由加法运算来完成。
16位超前进位加法器实验报告
实验名称:十六位超前进位加法器一、实验目的设计、验证并优化16位超前进位加法器的逻辑功能。
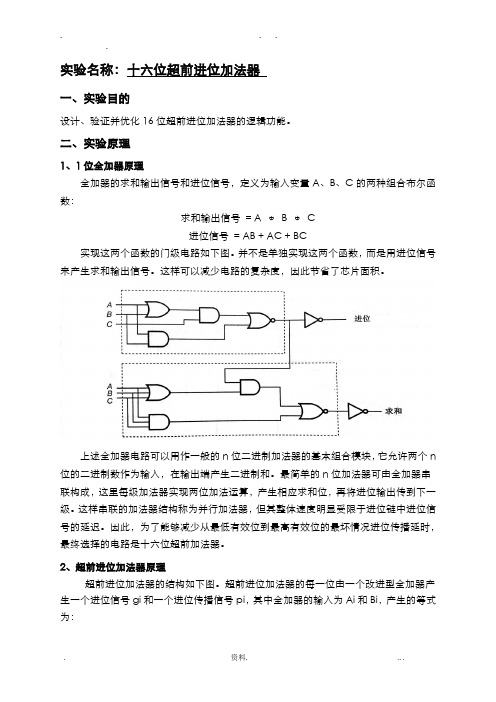
二、实验原理1、1位全加器原理全加器的求和输出信号和进位信号,定义为输入变量A、B、C的两种组合布尔函数:求和输出信号= A ⊕B ⊕C进位信号= AB + AC + BC实现这两个函数的门级电路如下图。
并不是单独实现这两个函数,而是用进位信号来产生求和输出信号。
这样可以减少电路的复杂度,因此节省了芯片面积。
上述全加器电路可以用作一般的n位二进制加法器的基本组合模块,它允许两个n 位的二进制数作为输入,在输出端产生二进制和。
最简单的n位加法器可由全加器串联构成,这里每级加法器实现两位加法运算,产生相应求和位,再将进位输出传到下一级。
这样串联的加法器结构称为并行加法器,但其整体速度明显受限于进位链中进位信号的延迟。
因此,为了能够减少从最低有效位到最高有效位的最坏情况进位传播延时,最终选择的电路是十六位超前加法器。
2、超前进位加法器原理超前进位加法器的结构如下图。
超前进位加法器的每一位由一个改进型全加器产生一个进位信号gi和一个进位传播信号pi,其中全加器的输入为Ai和Bi,产生的等式为:改进的全加器的进位输出可由一个进位信号和一个进位传输信号计算得出,因此进位信号可改写为:式中可以看出,当gi = 1(Ai = Bi = 1)时,产生进位;当pi = 1(Ai =1或Bi = 1)时,传输进位输入,这两种情况都使得进位输出是1。
近似可以得到i+2和i+3级的进位输出如下:下图为一个四位超前进位加法器的结构图。
信号经过pi和gi产生一级时延,经过计算C产生一级时延,则A,B输入一旦产生,首先经过两级时延算出第1轮进位值C’不过这个值是不正确的。
C’再次送入加法器,进行第2轮2级时延的计算,算出第2轮进位值C,这一次是正确的进位值。
这里的4个4位超前进位加法器仍是串行的,所以一次计算经过4级加法器,一级加法器有2级时延,因此1次计算一共经过8级时延,相比串行加法器里的16级时延,速度提高很多。
超前进位加法器

超前进位加法器超前进位加法器是一种在数字电路中常用的电子设备,它具有在加法操作中进位能力更高的特点。
在这篇文章中,我们将探讨超前进位加法器的工作原理、应用场景以及它对现代科技的影响。
首先,让我们了解一下超前进位加法器的工作原理。
超前进位加法器是一种高性能的加法电路,它能够在进行数字加法时更快地产生进位信号。
它通过利用多个位的输入信号和输出信号之间的时序关系来实现进位的超前生成。
通过这种方式,超前进位加法器能够大大提高加法操作的速度和效率。
超前进位加法器的应用场景非常广泛。
它常常被用于高速计算机、图像处理器和通信设备等领域。
在高速计算机中,超前进位加法器可以快速地进行大量的数字运算,从而提高计算机的整体性能。
在图像处理器中,超前进位加法器可以快速地对图像进行处理和分析,提供更高质量的图像处理效果。
在通信设备中,超前进位加法器可以实现高速数据传输和信号处理,提供更快速和可靠的通信服务。
超前进位加法器对现代科技的影响不可忽视。
首先,它极大地提高了数字电路的运算速度和效率。
在过去,传统的进位生成方式虽然能够实现进位的生成,但速度较慢,效率不高。
而超前进位加法器的出现,解决了这个问题,使得数字电路能够更快地进行加法运算。
其次,超前进位加法器的应用为人们的生活带来了便利。
在现代社会中,大量的数字运算都离不开超前进位加法器的支持,例如银行的财务计算、医院的影像处理等。
最后,超前进位加法器的不断创新和发展,也推动了数字电路领域的技术进步。
总结起来,超前进位加法器是一种在数字电路中常用的高性能加法电路。
它通过利用多个位的输入信号和输出信号之间的时序关系,提前生成进位信号,从而大大提高了加法操作的速度和效率。
超前进位加法器的应用场景广泛,它在高速计算机、图像处理器和通信设备等领域发挥着重要作用。
超前进位加法器的出现和应用,不仅极大地提高了数字电路的运算速度和效率,也为人们的生活带来了便利。
随着技术的不断创新和发展,相信超前进位加法器在未来将会有更广泛的应用和更大的影响。
16位超前进位加法器的设计_谢莹

第27卷第4期合肥工业大学学报(自然科学版)Vol.27No.4 2004年4月JO URN AL O F HEFEI UN IV ERSITY O F TECHNO LOGY Apr.2004 16位超前进位加法器的设计谢 莹, 陈 琳(安庆师范学院教育技术系,安徽安庆 246011)摘 要:电子计算机是由具有各种逻辑功能的逻辑部件组成的,加法器就属于其中的组合逻辑电路。
如果对传统的加法器电路进行改进,在超前进位链的基础上,用一种新的超前进位链树的设计方法不仅可以克服串行进位加法器速度低的缺点,也可以解决单纯的超前进位加法器带负载能力不足等问题,从而在实际电路中使加法器的运算速度达到最优。
根据这种理论,可以推导得到最优的任意位加法器。
关键词:半加器;全加器;超前进位加法器;4位超前进位加法器;16位超前进位加法器中图分类号:T P342.21 文献标识码:A 文章编号:1003-5060(2004)04-0450-05Design of16-bit carry look-ahead adderXIE Ying, CHEN Lin(Dept.of Ed ucational Technology,Anqing Teachers College,Anqing246011,China)Abstract:A com puter is com prised of so me logic parts w hich hav e serial lo gic functions,and the adder is one o f the combine logic circuits.In o rder to im prov e the traditio nal adder circuit,based on the carry lo ok-ahead techno logy,a new desig n o f ca rry look-ahead chain is presented so tha t the low speed of serial adders and the less car ry capacity of the pure carry look-ahead adder ca n be ov erco me.Thus the o ptimum com pute speed can be achiev ed in the real circuit.Based on the presented idea,the ex cellent ra ndo m bit adder can be deduced.Key words:half adder;full adder;carry look-ahead adder;4-bit carry look-ahead adder;16-bit carry lo ok-ahead adder0 引 言电子计算机是由具有各种逻辑功能的逻辑部件组成的,这些逻辑部件按其功能结构又可分为组合逻辑电路和时序逻辑电路。
杭电计组实验2-超前进位加法器设计实验

杭州电子科技大学计算机学院
实验报告
实验项目:实验2-超前进位加法器设计实验
课程名称:计算机组成原理与系统结构课程设计
姓名:学号:同组姓名:学号:
实验位置(机号):
实验日期:指导教师:
#100;
A = 1011;
B = 1101;C0 = 0;
#100;
A = 1010;
B = 0010;C0 = 1;
#100;
A = 0111;
B = 1000;C0= 0;
#100;
A = 0011;
B = 0100;C0 = 1;
#100;
A = 1001;
B = 0001;C0 = 0;
#100;
end
Endmodule
RTL图
二、结果
思考题:
(1)综合得到的电路图,它和想要设计的电路在引脚的输入输出方面是完全相同的,但是相比较内部的RTL图,实验实现的结果是相同的,但是我编写的实验代码并没有调用实验一的全加器设计。
(2)尝试编写8位超前进位加法器设计实验
module add_8 ( input [7:0]a, input [7:0]b, input cin, output [7:0] s, output co );
wire [7:0]c_tmp;
wire [7:0]g;
wire [7:0]p;。
16位加法器设计报告

Brent Kung树结构的16位加法器的设计仿真及优化1.利用Hspice软件设计具体电路结构Brent Kung树结构加法器设计简介Brent Kung树结构加法器是一种超前进位加法器,即进位提前被计算出来,送给加和电路,减小了进位顺序传递的延时,实现此加法器减小了设计的复杂度。
提高了设计的效率。
具体电路实现需要4个模块电路设计。
数据A和B通过缓冲器输入进来,然后经过进位生成和进位产生电路模块生成P和G信号。
P与G信号经过点操作模块生成相应的进位值,最后加和生成SUM。
电路结构采用动态逻辑结构,逻辑结构由NMOS下拉网络实现,构成PDN的过程和静态CMOS完全一样,晶体管的数目明显少于静态情况。
动态逻辑同时具有较快的开关速度。
动态逻辑同时在功耗方面有明显的优势。
Brent Kung树结构加法器电路设计进位生成和进位传播模块均采用动态逻辑进行设计,具体实现公式为Pi=ai+bi,Gi=ai&bi;具体电路实现如下:图1 进位传播和进位产生信号的动态实现图中的反相器为对称的,p生成电路的逻辑努力为2/3,g生成电路的逻辑努力为1。
点计算模块具体生成对应的进位传播和进位产生Gi j和Pi j;其对应的具体公式为:Gi j=Gi k+Pi k*Gk-1 j。
采用动态逻辑减小复杂度具体电路结构如下:图2点模块电路产生信号的动态实现求和电路利用多米诺实现求和即利用选择电路实现电路结构,在此电路中求和的两种条件计算为:Si0为ai与bi的同或,Si1为ai 与bi的异或,具体电路结构如下:图5动态逻辑实现和选择电路电路中利用两个时钟,由clk产生clkd是由下面的电路实现的,传输门总是导通,时钟路径的延时可以通过这些器件的尺寸来调整。
因为延时必须有一个严格的界限,即第二个门的所有输入必须在clkd的上升沿之前完成翻转,因此可能需要使clk进过多个以下的延时电路才能满足时序要求。
时钟延时利用反向器的缓冲器和传输门来实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
result = result << 1;
bin = bin << 1;
end
result[0] = bin[B_SIZE-1];
bcd <= result;
end
end
endmodule
/******************************4位二进制超前进位加法模块************************************/
module B_BCD ( binary, bcd );
parameter B_SIZE = 16; //B_SIZE为二进制数所占的位数,可根据需要进行扩展
input binary; //binary为待转换的二进制数,bcd为转换后的BCD码
output bcd;
assign s[0]=a[0]^b[0]^cp0;
assign s[1]=a[1]^b[1]^(g[0]|p[0]&cp0);
assign s[2]=a[2]^b[2]^(g[1]|p[1]&(g[0]|p[0]&cp0));
assign s[3]=a[3]^b[3]^(g[2]|p[2]&(g[1]|p[1]&(g[0]|p[0]&cp0)));
wire[3:0] S0,S1,S2,S3; //每四位的二进制和
assign A3=A[15:12];
assign A2=A[11:8];
assign A1=A[7:4];
assign A0=A[3:0];
assign B3=B[15:12];
assign B2=B[11:8];
assign g=a&b;
assign cp[1]=g[0]|p[0]&cp0;
assign cp[2]=g[1]|p[1]&(g[0]|p[0]&cp0);
assign cp[3]=g[2]|p[2]&(g[1]|p[1]&(g[0]|p[0]&cp0));
assign c_out=g[3]|p[3]&(g[2]|p[2]&(g[1]|p[1]&(g[0]|p[0]&cp0)));
always@( binary )
begin
bin = binary;
result = 0;
begin
repeat ( B_SIZE-1 ) //使用repeat语句进行循环计算
begin
result[0] = bin[B_SIZE-1];
output c_out;
output[3:0] s;
wire [3:0]p,g; //si=ai^bi^ci; ci=g[i-1]|p[i-1]&c[i-1](与&的优先级高于或|)
wire[3:1] cp; //进位产生函数 g[i-1]=a[i-1]&b[i-1],
assign p=a|b; //进位传递函数 p[i-1]=a[i-1]|b[i-1]
module BCD_16(clk,A,B,Y); //A,B--16位输入 ,S—20位的BCD和输出
input[15:0] A,B;
input clk;
output wire[19:0] Y;
wire[3:0] A0,A1,A2,A3,B0,B1,B2,B3;
wire C_1,C_2,C_3,C_4; //16位二进制加法中每四位的一个进位
assign B1=B[7:4];
assign B0=B[3:0];
sum_1 f0(A0,B0,1'b0,C_1,S0); //----------------调用4位二进制加法器模块,实现十六位二进制加法器
sum_1 f1(A1,B1,C_1,C_2,S1);
sum_1 f2(A2,B2,Cቤተ መጻሕፍቲ ባይዱ2,C_3,S2);
if ( result[3:0] > 4 )
result[3:0] = result[3:0]+4'd3;
if ( result[7:4] > 4 )
result[7:4] = result[7:4]+4'd3;
if ( result[11:8] > 4 )
endmodule
result[11:8] = result[11:8]+4'd3;
if ( result[15:12] > 4 )
result[15:12] = result[15:12]+4'd3;
if ( result[19:16] > 4 )
result[19:16] = result[19:16]+4'd3; //扩展时应参照此6条if语句续写
module sum_1(a,b,cp0,c_out,s); //(a[3],a[2],a[1],a[0],b[3],b[2],b[1],b[0],c0,cp,s[3],s[2],s[1],s[0]);
input[3:0]a,b; //!!注意,上述表达方式是错误的
input cp0;
//16位二进制超前进位加法器---BCD码显示
//加法模块采用超前进位法
//B——BCD转换模块采用加三移位法实现
/********************************************\
Filename : BCD_16.v
Description : a 16-bit binary-to-bcd module
Revision : 2012/12/3
\********************************************/
/**************************top模块***********************************************/
sum_1 f3(A3,B3,C_3,C_4,S3);
B_BCD b1(.binary({S3,S2,S1,S0}),.bcd(Y));//------------------------------调用二进制转BCD模块
endmodule
/********************二进制转BCD模块,实现十六位二进制转换成20位的BCD码********************/
wire [B_SIZE-1 : 0] binary;
reg [B_SIZE-1 : 0] bin;
reg [B_SIZE+3 : 0] bcd; // bcd的长度应根据实际情况进行修改
reg [B_SIZE+3 : 0] result; //result的长度=bcd的长度
