BP神经网络及简单示例
BP神经网络步骤及应用实例

1、数据归一化2、数据分类,主要包括打乱数据顺序,抽取正常训练用数据、变量数据、测试数据3、建立神经网络,包括设置多少层网络(一般3层以内既可以,每层的节点数(具体节点数,尚无科学的模型和公式方法确定,可采用试凑法,但输出层的节点数应和需要输出的量个数相等),设置隐含层的传输函数等。
关于网络具体建立使用方法,在后几节的例子中将会说到。
4、指定训练参数进行训练,这步非常重要,在例子中,将详细进行说明5、完成训练后,就可以调用训练结果,输入测试数据,进行测试6、数据进行反归一化7、误差分析、结果预测或分类,作图等数据归一化问题归一化的意义:首先说一下,在工程应用领域中,应用BP网络的好坏最关键的仍然是输入特征选择和训练样本集的准备,若样本集代表性差、矛盾样本多、数据归一化存在问题,那么,使用多复杂的综合算法、多精致的网络结构,建立起来的模型预测效果不会多好。
若想取得实际有价值的应用效果,从最基础的数据整理工作做起吧,会少走弯路的。
归一化是为了加快训练网络的收敛性,具体做法是:1 把数变为(0,1)之间的小数主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速,应该归到数字信号处理范畴之内。
2 把有量纲表达式变为无量纲表达式归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量比如,复数阻抗可以归一化书写:Z = R + jωL = R(1 + jωL/R) ,复数部分变成了纯数量了,没有量纲。
另外,微波之中也就是电路分析、信号系统、电磁波传输等,有很多运算都可以如此处理,既保证了运算的便捷,又能凸现出物理量的本质含义。
神经网络归一化方法:由于采集的各数据单位不一致,因而须对数据进行[-1,1]归一化处理,归一化方法主要有如下几种,供大家参考:1、线性函数转换,表达式如下:复制内容到剪贴板代码:y=(x-MinVal ue)/(MaxVal ue-MinVal ue)说明:x、y分别为转换前、后的值,MaxVal ue、MinVal ue分别为样本的最大值和最小值。
BP算法代码实现

BP算法代码实现BP算法(Backpropagation Algorithm)是一种常用的神经网络训练算法,它主要用于监督式学习任务中的模型训练。
BP算法的核心思想是通过反向传播来更新神经网络的权重和偏差,以使得神经网络的输出逼近目标输出。
在反向传播的过程中,通过求解梯度来更新每个连接权重和偏置的值,从而最小化损失函数。
以下是BP算法的代码实现示例:```pythonimport numpy as npclass NeuralNetwork:def __init__(self, layers):yers = layersself.weights = []self.biases = []self.activations = []#初始化权重和偏置for i in range(1, len(layers)):self.weights.append(np.random.randn(layers[i], layers[i-1])) self.biases.append(np.random.randn(layers[i]))def sigmoid(self, z):return 1 / (1 + np.exp(-z))def sigmoid_derivative(self, z):return self.sigmoid(z) * (1 - self.sigmoid(z))def forward_propagate(self, X):self.activations = []activation = X#前向传播计算每一层的激活值for w, b in zip(self.weights, self.biases):z = np.dot(w, activation) + bactivation = self.sigmoid(z)self.activations.append(activation)return activationdef backward_propagate(self, X, y, output):deltas = [None] * len(yers)deltas[-1] = output - y#反向传播计算每一层的误差(梯度)for i in reversed(range(len(yers)-1)):delta = np.dot(self.weights[i].T, deltas[i+1]) * self.sigmoid_derivative(self.activations[i])deltas[i] = delta#更新权重和偏置for i in range(len(yers)-1):self.weights[i] -= 0.1 * np.dot(deltas[i+1],self.activations[i].T)self.biases[i] -= 0.1 * np.sum(deltas[i+1], axis=1)def train(self, X, y, epochs):for epoch in range(epochs):output = self.forward_propagate(X)self.backward_propagate(X, y, output)def predict(self, X):output = self.forward_propagate(X)return np.round(output)```上述代码使用numpy实现了一个简单的多层神经网络,支持任意层数和任意神经元个数的构建。
BP神经网络原理及其MATLAB应用

BP神经网络原理及其MATLAB应用BP神经网络(Back Propagation Neural Network)是一种基于梯度下降算法的人工神经网络模型,具有较广泛的应用。
它具有模拟人类神经系统的记忆能力和学习能力,可以用来解决函数逼近、分类和模式识别等问题。
本文将介绍BP神经网络的原理及其在MATLAB中的应用。
BP神经网络的原理基于神经元间的权值和偏置进行计算。
一个标准的BP神经网络通常包含三层:输入层、隐藏层和输出层。
输入层负责接收输入信息,其节点数与输入维度相同;隐藏层用于提取输入信息的特征,其节点数可以根据具体问题进行设定;输出层负责输出最终的结果,其节点数根据问题的要求决定。
BP神经网络的训练过程可以分为前向传播和反向传播两个阶段。
前向传播过程中,输入信息逐层传递至输出层,通过对神经元的激活函数进行计算,得到神经网络的输出值。
反向传播过程中,通过最小化损失函数的梯度下降算法,不断调整神经元间的权值和偏置,以减小网络输出与实际输出之间的误差,达到训练网络的目的。
在MATLAB中,可以使用Neural Network Toolbox工具箱来实现BP神经网络。
以下是BP神经网络在MATLAB中的应用示例:首先,需导入BP神经网络所需的样本数据。
可以使用MATLAB中的load函数读取数据文件,并将其分为训练集和测试集:```data = load('dataset.mat');inputs = data(:, 1:end-1);targets = data(:, end);[trainInd, valInd, testInd] = dividerand(size(inputs, 1), 0.6, 0.2, 0.2);trainInputs = inputs(trainInd, :);trainTargets = targets(trainInd, :);valInputs = inputs(valInd, :);valTargets = targets(valInd, :);testInputs = inputs(testInd, :);testTargets = targets(testInd, :);```接下来,可以使用MATLAB的feedforwardnet函数构建BP神经网络模型,并进行网络训练和测试:```hiddenLayerSize = 10;net = feedforwardnet(hiddenLayerSize);net = train(net, trainInputs', trainTargets');outputs = net(testInputs');```最后,可以使用MATLAB提供的performance函数计算网络的性能指标,如均方误差、相关系数等:```performance = perform(net, testTargets', outputs);```通过逐步调整网络模型的参数和拓扑结构,如隐藏层节点数、学习率等,可以进一步优化BP神经网络的性能。
BP神经网络实例分析

j1
a1(i)f(u1(i))=
1 1exp(u1(i))
i 1,2
同理,输出神经元
3
u2 (1) w2 (1, j)a1 ( j) j 1
1 a2 (1) 1 exp( u2 (1))
(3) 训练输出单元的权值
PS:利用输出层各神经元的误差项 2(1)和隐含层 各神经元的输出来修正权值。
PS:利用隐含层各神经元的误差项 各神经元的输入来修正权值。
1(p1)(i)
和输入层
1 (p 1 )(i)f'[u 1(i)]2 (p 1 )(1 )W 2 (p 1 )(1 ,i)
a 1(iቤተ መጻሕፍቲ ባይዱ1 [a 1(i)]2 (p 1 )(1 )W 2 (p 1 )(1 ,i)
W 1 ( p 1 ) ( i ,j ) W 1 ( p ) ( i ,j ) 1 ( p 1 ) ( i ) a 0 ( p 1 ) ( j )
取激励函数
f
(x)
1 1ex
则 f'(x)(1 ee xx)2f(x)1 [f(x)]
2 ( 1 ) (t( 1 ) a 2 ( 1 )f') (u 2 ( 1 ))
( t ( 1 ) a 2 ( 1 ) e ) u x 2 ( 1 ) / p 1 ) ( e ( u x 2 ( 1 )2 p )) (
二、具体训练步骤如下:
令p=0,p为样本编号 (1) 网络初始化
给各连接权值分别赋一个区间(0,1)内的随机数,设定
误差函数E,给定计算精度值 和最大学习次数M。
W 1 w w 1 1((1 2,,1 1 ))
w 1(1,2) w 1(2,2)
w 1(1,3) w 1(2,3)
BP神经网络模型应用实例

BP神经网络模型第1节基本原理简介近年来全球性的神经网络研究热潮的再度兴起,不仅仅是因为神经科学本身取得了巨大的进展.更主要的原因在于发展新型计算机和人工智能新途径的迫切需要.迄今为止在需要人工智能解决的许多问题中,人脑远比计算机聪明的多,要开创具有智能的新一代计算机,就必须了解人脑,研究人脑神经网络系统信息处理的机制.另一方面,基于神经科学研究成果基础上发展出来的人工神经网络模型,反映了人脑功能的若干基本特性,开拓了神经网络用于计算机的新途径.它对传统的计算机结构和人工智能是一个有力的挑战,引起了各方面专家的极大关注.目前,已发展了几十种神经网络,例如Hopficld模型,Feldmann等的连接型网络模型,Hinton等的玻尔茨曼机模型,以及Rumelhart等的多层感知机模型和Kohonen的自组织网络模型等等。
在这众多神经网络模型中,应用最广泛的是多层感知机神经网络。
多层感知机神经网络的研究始于50年代,但一直进展不大。
直到1985年,Rumelhart等人提出了误差反向传递学习算法(即BP算),实现了Minsky的多层网络设想,如图34-1所示。
BP 算法不仅有输入层节点、输出层节点,还可有1个或多个隐含层节点。
对于输入信号,要先向前传播到隐含层节点,经作用函数后,再把隐节点的输出信号传播到输出节点,最后给出输出结果。
节点的作用的激励函数通常选取S 型函数,如Qx e x f /11)(-+=式中Q 为调整激励函数形式的Sigmoid 参数。
该算法的学习过程由正向传播和反向传播组成。
在正向传播过程中,输入信息从输入层经隐含层逐层处理,并传向输出层。
每一层神经元的状态只影响下一层神经输入层 中间层 输出层 图34-1 BP 神经网络模型元的状态。
如果输出层得不到期望的输出,则转入反向传播,将误差信号沿原来的连接通道返回,通过修改各层神经元的权值,使得误差信号最小。
社含有n 个节点的任意网络,各节点之特性为Sigmoid 型。
BP神经网络算法程序

BP神经网络算法程序一、BP神经网络算法原理BP神经网络算法包括输入层、隐藏层和输出层三个层次。
每个层次的神经元节点与下一层次的神经元节点之间存在权重系数。
神经元节点通过输入信号经过激活函数的处理得到输出信号,并将输出信号传递给下一层次的神经元节点。
反向传播过程中,首先根据误差评估结果计算输出层的误差信号,再根据该误差信号分别计算隐藏层和输入层的误差信号。
然后根据误差信号的计算结果,逐层更新网络的权重系数。
二、BP神经网络算法步骤1.初始化网络权重:随机初始化网络各层次之间的权重系数。
2.设置学习率和最大迭代次数。
3.迭代训练网络:重复以下步骤直到满足停止条件为止。
a)根据当前样本的输入信号,通过前向传播算法计算输出结果。
c)根据误差信号,通过反向传播算法更新网络的权重系数。
4.测试网络:使用独立的测试数据集,通过前向传播算法计算网络的输出结果,评估网络的泛化能力。
三、BP神经网络算法示例程序下面给出一个简单的使用Python编写的BP神经网络算法示例程序。
```pythonimport numpy as npclass BPNeuralNetwork:def __init__(self, input_dim, hidden_dim, output_dim): self.input_dim = input_dimself.hidden_dim = hidden_dimself.output_dim = output_dimself.W1 = np.random.randn(input_dim, hidden_dim)self.W2 = np.random.randn(hidden_dim, output_dim)def sigmoid(self, x):return 1 / (1 + np.exp(-x))def sigmoid_derivative(self, x):return x * (1 - x)def forward_propagation(self, X):self.z2 = np.dot(X, self.W1)self.a2 = self.sigmoid(self.z2)self.z3 = np.dot(self.a2, self.W2)self.y_hat = self.sigmoid(self.z3)return self.y_hatdef backward_propagation(self, X, y, lr):self.loss = y - self.y_hatdelta3 = self.loss * self.sigmoid_derivative(self.y_hat) dW2 = np.dot(self.a2.T, delta3)delta2 = np.dot(delta3, self.W2.T) *self.sigmoid_derivative(self.a2)dW1 = np.dot(X.T, delta2)self.W2 += lr * dW2self.W1 += lr * dW1def train(self, X, y, lr=0.1, epochs=1000):for i in range(epochs):y_hat = self.forward_propagation(X)self.backward_propagation(X, y, lr)def predict(self, X):return np.round(self.forward_propagation(X))#示例用法X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])y = np.array([[0], [1], [1], [0]])nn = BPNeuralNetwork(2, 2, 1)print("预测结果:")print(nn.predict(X))```以上是一个简单的BP神经网络算法示例程序,用于训练一个XOR逻辑门的分类模型。
BP神经网络详解与实例

(Artificial Neural Netwroks -----ANN)
-----HZAU 数模基地
引言
❖ 利用机器模仿人类的智能是长期以来人们认识自 然、改造自然和认识自身的理想。
❖ 研究ANN目的: ❖ (1)探索和模拟人的感觉、思维和行为的规律,
设计具有人类智能的计算机系统。 ❖ (2)探讨人脑的智能活动,用物化了的智能来
二、神经元与神经网络
❖ 大脑可视作为1000多亿神经元组成的神经网络
• 图3 神经元的解剖图
❖ 神经元的信息传递和处理是一种电化学活 动.树突由于电化学作用接受外界的刺激;通 过胞体内的活动体现为轴突电位,当轴突电位 达到一定的值则形成神经脉冲或动作电位;再 通过轴突末梢传递给其它的神经元.从控制论 的观点来看;这一过程可以看作一个多输入单 输出非线性系统的动态过程
输出层LC
W11 Wi1
Wij
Wiq Wpq W
… b1 Vn1
Vh1 V11
V1i bi Vhi
… Vni
V1p bp Vhp Vnp
隐含层LB V
… a1
… ah
an 输入层LA
a1k
a
k h
a
k n
基本BP网络的拓扑结构
ANN类型与功能
一般而言, ANN与经典计算方法相比并非优越, 只有当常规 方法解决不了或效果不佳时ANN方法才能显示出其优越性。尤 其对问题的机理不甚了解或不能用数学模型表示的系统,如故障 诊断、特征提取和预测等问题,ANN往往是最有利的工具。另 一方面, ANN对处理大量原始数据而不能用规则或公式描述的 问题, 表现出极大的灵活性和自适应性。
i 1
(p=1,…,P)
bp神经网络算法步骤结合实例

bp神经网络算法步骤结合实例
BP神经网络算法步骤包括以下几个步骤:
1.输入层:将输入数据输入到神经网络中。
2.隐层:在输入层和输出层之间,通过一系列权值和偏置将输入数据进行处理,得到输出
数据。
3.输出层:将隐层的输出数据输出到输出层。
4.反向传播:通过反向传播算法来计算误差,并使用梯度下降法对权值和偏置进行调整,
以最小化误差。
5.训练:通过不断地进行输入、隐层处理、输出和反向传播的过程,来训练神经网络,使
其达到最优状态。
实例:
假设我们有一个BP神经网络,它的输入层有两个输入节点,隐层有三个节点,输出层有一个节点。
经过训练,我们得到了权值矩阵和偏置向量。
当我们给它输入一组数据时,它的工作流程如下:
1.输入层:将输入数据输入到神经网络中。
2.隐层:将输入数据与权值矩阵相乘,再加上偏置向量,得到输出数据。
3.输出层:将隐层的输出数据输出到输出层。
4.反向传播:使用反向传播算法计算误差,并使用梯度下降法调整权值和偏置向量,以最
小化误差。
5.训练:通过不断地输入、处理、输出和反向传播的过程,来训练神经网络,使其达到最
优状态。
这就是BP神经网络算法的基本流程。
在实际应用中,还需要考虑许多细节问题,如权值和偏置的初始值、学习率、激活函数等。
但是,上述流程是BP神经网络算法的基本框架。
BP神经网络实验详解(MATLAB实现)

BP神经网络实验详解(MATLAB实现)BP(Back Propagation)神经网络是一种常用的人工神经网络结构,用于解决分类和回归问题。
在本文中,将详细介绍如何使用MATLAB实现BP神经网络的实验。
首先,需要准备一个数据集来训练和测试BP神经网络。
数据集可以是一个CSV文件,每一行代表一个样本,每一列代表一个特征。
一般来说,数据集应该被分成训练集和测试集,用于训练和测试模型的性能。
在MATLAB中,可以使用`csvread`函数来读取CSV文件,并将数据集划分为输入和输出。
假设数据集的前几列是输入特征,最后一列是输出。
可以使用以下代码来实现:```matlabdata = csvread('dataset.csv');input = data(:, 1:end-1);output = data(:, end);```然后,需要创建一个BP神经网络模型。
可以使用MATLAB的`patternnet`函数来创建一个全连接的神经网络模型。
该函数的输入参数为每个隐藏层的神经元数量。
下面的代码创建了一个具有10个隐藏神经元的单隐藏层BP神经网络:```matlabhidden_neurons = 10;net = patternnet(hidden_neurons);```接下来,需要对BP神经网络进行训练。
可以使用`train`函数来训练模型。
该函数的输入参数包括训练集的输入和输出,以及其他可选参数,如最大训练次数和停止条件。
下面的代码展示了如何使用`train`函数来训练模型:```matlabnet = train(net, input_train, output_train);```训练完成后,可以使用训练好的BP神经网络进行预测。
可以使用`net`模型的`sim`函数来进行预测。
下面的代码展示了如何使用`sim`函数预测测试集的输出:```matlaboutput_pred = sim(net, input_test);```最后,可以使用各种性能指标来评估预测的准确性。
BP神经网络的简要介绍及应用

BP神经网络的简要介绍及应用BP神经网络(Backpropagation Neural Network,简称BP网络)是一种基于误差反向传播算法进行训练的多层前馈神经网络模型。
它由输入层、隐藏层和输出层组成,每层都由多个神经元(节点)组成,并且每个神经元都与下一层的神经元相连。
BP网络的训练过程可以分为两个阶段:前向传播和反向传播。
前向传播时,输入数据从输入层向隐藏层和输出层依次传递,每个神经元计算其输入信号的加权和,再通过一个激活函数得到输出值。
反向传播时,根据输出结果与期望结果的误差,通过链式法则将误差逐层反向传播至隐藏层和输入层,并通过调整权值和偏置来减小误差,以提高网络的性能。
BP网络的应用非常广泛,以下是一些典型的应用领域:1.模式识别:BP网络可以用于手写字符识别、人脸识别、语音识别等模式识别任务。
通过训练网络,将输入样本与正确的输出进行匹配,从而实现对未知样本的识别。
2.数据挖掘:BP网络可以用于分类、聚类和回归分析等数据挖掘任务。
例如,可以用于对大量的文本数据进行情感分类、对客户数据进行聚类分析等。
3.金融领域:BP网络可以用于预测股票价格、外汇汇率等金融市场的变动趋势。
通过训练网络,提取出对市场变动有影响的因素,从而预测未来的市场走势。
4.医学诊断:BP网络可以用于医学图像分析、疾病预测和诊断等医学领域的任务。
例如,可以通过训练网络,从医学图像中提取特征,帮助医生进行疾病的诊断。
5.机器人控制:BP网络可以用于机器人的自主导航、路径规划等控制任务。
通过训练网络,机器人可以通过感知环境的数据,进行决策和规划,从而实现特定任务的执行。
总之,BP神经网络是一种强大的人工神经网络模型,具有较强的非线性建模能力和适应能力。
它在模式识别、数据挖掘、金融预测、医学诊断和机器人控制等领域有广泛的应用,为解决复杂问题提供了一种有效的方法。
然而,BP网络也存在一些问题,如容易陷入局部最优解、训练时间较长等,因此在实际应用中需要结合具体问题选择适当的神经网络模型和训练算法。
BP神经网络原理及应用

BP神经网络原理及应用BP神经网络,即反向传播神经网络(Backpropagation Neural Network),是一种基于梯度下降算法的多层前馈神经网络,常用于分类与回归等问题的解决。
BP神经网络通过反向传播算法,将误差从输出层往回传播,更新网络权值,直至达到误差最小化的目标,从而实现对输入模式的分类和预测。
BP神经网络的结构包括输入层、隐藏层和输出层。
输入层接收外部输入的特征向量,隐藏层负责将输入特征映射到合适的高维空间,输出层负责输出网络的预测结果。
每个神经元与其前后的神经元相连,每个连接都有一个权值,用于调整输入信号的重要性。
BP神经网络利用激活函数(如sigmoid函数)对神经元的输出进行非线性变换,增加网络的非线性表达能力。
1.前向传播:将输入信号传递给网络,逐层计算每个神经元的输出,直至得到网络的输出结果。
2.计算误差:将网络输出与期望输出比较,计算误差。
常用的误差函数包括平方误差和交叉熵误差等。
3.反向传播:根据误差,逆向计算每个神经元的误差贡献,从输出层往回传播到隐藏层和输入层。
根据误差贡献,调整网络的权值和阈值。
4.更新权值和阈值:根据调整规则(如梯度下降法),根据误差贡献的梯度方向,更新网络的权值和阈值。
1.模式识别与分类:BP神经网络可以通过训练学习不同模式的特征,从而实现模式的自动分类与识别。
例如,人脸识别、文本分类等。
2.预测与回归:BP神经网络可以通过历史数据的训练,学习到输入与输出之间的映射关系,从而实现对未知数据的预测与回归分析。
例如,股票价格预测、天气预测等。
3.控制系统:BP神经网络可以用于建模和控制非线性系统,实现自适应、自学习的控制策略。
例如,机器人控制、工业过程优化等。
4.信号处理与图像处理:BP神经网络可以通过学习复杂的非线性映射关系,实现信号的去噪、压缩和图像的识别、处理等。
例如,语音识别、图像分割等。
5.数据挖掘与决策支持:BP神经网络可以根据历史数据学习到数据之间的相关关系,从而帮助决策者进行数据挖掘和决策支持。
(完整版)BP神经网络matlab实例(简单而经典)

p=p1';t=t1';[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t); %原始数据归一化net=newff(minmax(pn),[5,1],{'tansig','purelin'},'traingdx');%设置网络,建立相应的BP网络net.trainParam.show=2000; % 训练网络net.trainParam.lr=0.01;net.trainParam.epochs=100000;net.trainParam.goal=1e-5;[net,tr]=train(net ,pn,tn); %调用TRAINGDM算法训练BP 网络pnew=pnew1';pnewn=tramnmx(pnew,minp,maxp);anewn=sim(net,pnewn); %对BP网络进行仿真anew=postmnmx(anewn,mint,maxt); %还原数据y=anew';1、BP网络构建(1)生成BP网络=net newff PR S S SNl TF TF TFNl BTF BLF PF(,[1 2...],{ 1 2...},,,)PR:由R维的输入样本最小最大值构成的2R⨯维矩阵。
S S SNl:各层的神经元个数。
[ 1 2...]{ 1 2...}TF TF TFNl:各层的神经元传递函数。
BTF:训练用函数的名称。
(2)网络训练[,,,,,] (,,,,,,)=net tr Y E Pf Af train net P T Pi Ai VV TV(3)网络仿真=[,,,,] (,,,,)Y Pf Af E perf sim net P Pi Ai T{'tansig','purelin'},'trainrp'2、BP网络举例举例1、%traingdclear;clc;P=[-1 -1 2 2 4;0 5 0 5 7];T=[-1 -1 1 1 -1];%利用minmax函数求输入样本范围net = newff(minmax(P),T,[5,1],{'tansig','purelin'},'trainrp');net.trainParam.show=50;%net.trainParam.lr=0.05;net.trainParam.epochs=300;net.trainParam.goal=1e-5;[net,tr]=train(net,P,T);net.iw{1,1}%隐层权值net.b{1}%隐层阈值net.lw{2,1}%输出层权值net.b{2}%输出层阈值sim(net,P)举例2、利用三层BP神经网络来完成非线性函数的逼近任务,其中隐层神经元个数为五个。
BP神经网络模型及实例

(1)由动量的梯度下降法
在神经网络工具箱中, traingdm函数采用了由动量的梯度下降法,提高 了学习速度并增加了算法的可靠性。
x x1, x2,
hi hi1, hi2,
ho ho1, ho2,
yi yi1, yi2,
yo yo1, yo2,
do d1, d2,
, xn
, hip
, hop
, yiq
, yoq
, dq
2.4.2 BP网络的标准学习算法
– 输入层与中间层的连接权值:
wih
– 隐含层与输出层的连接权值:
2.4.1 BP神经网络模型
• 三层BP网络
2.4.1 BP神经网络模型
• 激活函数
– 必须处处可导
• 一般都使用S型函数
• 使用S型激活函数时BP网络输入与输出关 系
– 输入 net x1w1 x2w2 ... xnwn
– 输出
y
f
(net)
1
1 enet
2.4.1 BP神经网络模型
2.4 BP神经网络模型与学习算法
概述
• Rumelhart,McClelland于1985年提出了BP网络的误差 反向后传BP(Back Propagation)学习算法
David Rumelhart
J. McClelland
• BP算法基本原理
– 利用输出后的误差来估计输出层的直接前导层的误差,再用这个 误差估计更前一层的误差,如此一层一层的反传下去,就获得了 所有其他各层的误差估计。
BP神经网络的设计实例(MATLAB编程)

神经网络的设计实例(MATLAB编程)例1 采用动量梯度下降算法训练BP 网络。
训练样本定义如下:输入矢量为p =[-1 -2 3 1-1 1 5 -3]目标矢量为t = [-1 -1 1 1]解:本例的MATLAB 程序如下:close allclearecho onclc% NEWFF——生成一个新的前向神经网络% TRAIN——对BP 神经网络进行训练% SIM——对BP 神经网络进行仿真pause% 敲任意键开始clc% 定义训练样本P=[-1, -2, 3, 1; -1, 1, 5, -3]; % P 为输入矢量T=[-1, -1, 1, 1]; % T 为目标矢量pause;clc% 创建一个新的前向神经网络net=newff(minmax(P),[3,1],{'tansig','purelin'},'traingdm') % 当前输入层权值和阈值inputWeights=net.IW{1,1}inputbias=net.b{1}% 当前网络层权值和阈值layerWeights=net.LW{2,1}layerbias=net.b{2}pauseclc% 设置训练参数net.trainParam.show = 50;net.trainParam.lr = 0.05;net.trainParam.mc = 0.9;net.trainParam.epochs = 1000;net.trainParam.goal = 1e-3;pauseclc% 调用TRAINGDM 算法训练BP 网络[net,tr]=train(net,P,T);pauseclc% 对BP 网络进行仿真A = sim(net,P)% 计算仿真误差E = T - AMSE=mse(E)pauseclcecho off例2 采用贝叶斯正则化算法提高BP 网络的推广能力。
在本例中,我们采用两种训练方法,即L-M 优化算法(trainlm)和贝叶斯正则化算法(trainbr),用以训练BP 网络,使其能够拟合某一附加有白噪声的正弦样本数据。
BP神经网络的应用实例

样本 1 2 3 4 5 6 7 …… 33 测试
输入 1180 920 1020 1020 960 1300 2240 1860 1360
920 1020 1020 960 1300 2240 2500
1360 1200
1020 1020 960 1300 2240 2500 2400
1200 820
目标值 0.9
0.9
0.9 0.1 0.9 0.9 0.9 0.1
• 翼长 • 1.64 • 1.82 • 1.90 • 1.70 • 1.82 • 1.82 • 2.08
触角长 1.38 1.38 1.38 1.40 1.48 1.54 1.56
类别 Af Af Af Af Af Af Af
目标值 0.1 0.1 0.1 0.1 0.1 0.1 0.1
年份 2011 2012
1月 1180 1180
2013
1066980Fra bibliotek660940
860
1180 1520
1840 1860
1360
1200
820
可以用前三个月的用电量数据来预测下一个月的用电量, 也即是每四个的用电量作为一个样本,前三个月作为输入, 下一个月作为输出。
如何将输出转换成0~1之间的数据?
输出 1020 960 1300 2240 2500 2400 1680 820 ?
建立神经网络 样本数 33 输入层结点3,隐层结点6,输出层结点1
问:如果抓到三只新的蚊子,它们的触角长和翼长 分别为(l.24,1.80); (l.28,1.84);(1.40, 2.04).问它们应分别属于哪一个种类?
• • • • • • • • •
(完整版)bp神经网络算法
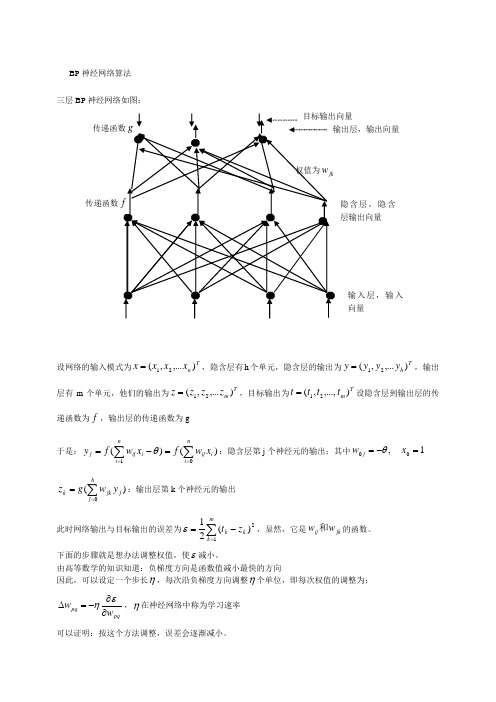
BP 神经网络算法 三层BP 神经网络如图:设网络的输入模式为Tn x x x x ),...,(21=,隐含层有h 个单元,隐含层的输出为Th y y y y ),...,(21=,输出层有m 个单元,他们的输出为Tm z z z z ),...,(21=,目标输出为Tm t t t t ),...,,(21=设隐含层到输出层的传递函数为f ,输出层的传递函数为g于是:)()(1∑∑===-=ni i ij ni iij j x w f xw f y θ:隐含层第j 个神经元的输出;其中1,00=-=x w j θ)(0∑==hj j jk k y w g z :输出层第k 个神经元的输出此时网络输出与目标输出的误差为∑=-=m k k k z t 12)(21ε,显然,它是jk ij w w 和的函数。
下面的步骤就是想办法调整权值,使ε减小。
由高等数学的知识知道:负梯度方向是函数值减小最快的方向因此,可以设定一个步长η,每次沿负梯度方向调整η个单位,即每次权值的调整为:pqpq w w ∂∂-=∆εη,η在神经网络中称为学习速率 可以证明:按这个方法调整,误差会逐渐减小。
隐含层,隐含层输出向量传递函数输入层,输入向量BP 神经网络(反向传播)的调整顺序为: 1)先调整隐含层到输出层的权值 设k v 为输出层第k 个神经元的输入∑==hj j jkk y wv 0-------复合函数偏导公式若取x e x f x g -+==11)()(,则)1()111(11)1()('2k k v v v v k z z ee e e u g kk k k -=+-+=+=---- 于是隐含层到输出层的权值调整迭代公式为: 2)从输入层到隐含层的权值调整迭代公式为: 其中j u 为隐含层第j 个神经元的输入:∑==ni i ijj x wu 0注意:隐含层第j 个神经元与输出层的各个神经元都有连接,即jy ∂∂ε涉及所有的权值ij w ,因此∑∑==--=∂∂∂∂∂-∂=∂∂m k jk k k k j k k k m k k k k j w u f z t y u u z z z t y 002)(')()(ε于是:因此从输入层到隐含层的权值调整迭代为公式为: 例:下表给出了某地区公路运力的历史统计数据,请建立相应的预测模型,并对给出的2010和2011年的数据,预测相应的公路客运量和货运量。
BP人工神经网络的基本原理模型与实例

w14
0.2+(0.9) (-0.0087)(1)=0.192
w15
-0.3+(0.9) (-0.0065)(1)=-0.306
w24
0.4+(0.9) (-0.0087)(0)=0.4
w25
0.1+(0.9) (-0.0065)(0)=0.1
w34
-0.5+(0.9) (-0.0087)(1)=-0.508
8.1人工神经网络旳基本概念
人工神经网络在本质上是由许多小旳非线性函数构成 旳大旳非线性函数,反应旳是输入变量到输出变量间旳复 杂映射关系。先给出单个人工神经网络旳一般模型描述:
8.1人工神经网络旳基本概念
先来看一种单一输入旳神经元模型 输入变量:x1 连接权重:w1 激活函数:f (·)
x1 w1
w1x1 f (·)
8.1人工神经网络旳基本概念
8.1人工神经网络旳基本概念
单极sigmoid函数
8.1人工神经网络旳基本概念
双曲函数
8.1人工神经网络旳基本概念
增长激活阈值后旳神经元模型 输入变量:x1 连接权重:w1 激活函数:f (·)
x1 w1
w1x1-θ f (·)
-1
小练习:请你算一算,当初始输入、权重和激活阈值为如下数值时,该神 经元旳净输入和输出分别是多少?
2.反向传播 反向传播时,把误差信号按原来正向传播旳通路反向
传回,并对每个隐层旳各个神经元旳权系数进行修改,以 望误差信号趋向最小。
8.2 误差反向传播(BP)神经网 络
8.2 误差反向传播(BP)神经网 络
x1 x2
x3
单元 j 6
1 w14
Err4=
第 4 章 神经计算基本方法(BP神经网络MATLAB仿真程序设计)例子

BP网络应用实例
x=imread(m,’bmp’); bw=im2bw(x,0.5); 为二值图像 [i,j]=find(bw==0); )的行号和列号 imin=min(i); )的最小行号 imax=max(i); )的最大行号 %读人训练样本图像丈件 %将读人的训练样本图像转换 %寻找二值图像中像素值为0(黑
4
BP网络学习算法
图5.5具有多个极小点的误差曲面
5
BP网络学习算法
另外一种情况是学习过程发生振荡,如图5.6所示 。 误差曲线在m点和n点的梯度大小相同,但方向相反 ,如果第k次学习使误差落在m点,而第k十1次学习 又恰好使误差落在n点。 那么按式(5.2)进行的权值和阈值调整,将在m 点和n点重复进行,从而形成振荡。
图 5.16
待分类模式
20
BP网络应用实例
解(1)问题分析 据图5.16所示两类模式可以看出,分类为简单的非 线性分类。有1个输入向量,包含2个输入元素;两 类模式,1个输出元素即可表示;可以以图5.17所 示两层BP网络来实现分类。
图 5.17
两层BP网络
21
BP网络应用实例
(2)构造训练样本集
6
BP网络学习算法
图5.6学习过程出现振荡的情况
7
BP网络的基本设计方法
BP网络的设计主要包括输人层、隐层、输出层及各 层之间的传输函数几个方面。 1.网络层数 大多数通用的神经网络都预先确定了网络的层数,而 BP网络可以包含不同的隐层。
8
BP网络的基本设计方法
但理论上已经证明,在不限制隐层节点数的情况下 ,两层(只有一个隐层)的BP网络可以实现任意非 线性映射。 在模式样本相对较少的情况下,较少的隐层节点, 可以实现模式样本空间的超平面划分,此时,选择 两层BP网络就可以了;当模式样本数很多时,减小 网络规模,增加一个隐层是必要的,但BP网络隐层 数一般不超过两层。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
j 1 i 1 n p
思路:
1、触角长和翼长作为输入信息,分别记为x1,x2。 目标输出:(0,1) 、(1,0)。 Af类记为 (1,0),Apf类记为(0,1)。
输入层
中间层
j
输出层
i
k
xi
ji
kj
Vk f ( ( f ( ( xi ji )) kj )) 0或1
1 s (Ti f ( ( f ( ( xi ji )) kj ))) 2 i、s j 1 i 1
使得E(w)最小的
n
p
ji、kj
作为所需的权值
传递函数(激活函数)
logsig(S型函数):
MATLAB按此函数计算:
2 f ( x) 2 x 1 e
调用格式:A=logsig(N)
xi 2 ( ) c
神经网络的互连模式
前向网络: 神经元分层排列,分别组成输入层、中间层(也
叫隐含层,可以由若干层组成)和输出层。 输入层 中间层 输出层
特点:每层只接受前一层的信息,没有反馈。
如:感知器网络和BP神经网络
有反馈的前向神经网络:
特点:输出层对输入层有反馈信息。
如:认知机和回归BP网络。
神经网络仿真函数sim 调用格式为:
[Y,Pf,Af,E,perf]=sim(net,P,Pi,Ai,T)
其中,
Y:函数返回值,网络输出;
Pf:函数返回值,最终输出延迟; Af:函数返回值,最终的层延迟;
E:函数返回值,网络误差;
perf:函数返回值,网络性能; net:待仿真的神经网络;
P:网络输入;
xj为输入信号, i 为阈值, ij表示与神经元 xj 连接的权值
yi表示输出值
传递函数
阈值型
线性型
1 f (x) 0
1 f ( xi ) axi b 0
xi 0
xi 0
x1 xi x2
xi x1
xi x2
S型
f ( xi )
1 1 e
j 1 i 1
n
p
输入层
i
中间层
j
输出层
k
xi
ji
kj
ji、kj
2、通过已知样本训练出合适的权值 使输出为(0,1)或(1,0)。
3、将待区分的蠓虫数据输入网络,求值。
权值求法:向后传播法
理想输出 Af类(1,0),Apf类(0,1)记为 { Tis} 则有误差:
2 1 s E ( ) (Ti Vk ) 2 i、s
如:
n=-10:0.1:10 a=tansig(n) plot(n,a)
1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 -10
grid on
如右图所示
-8
-6
-4
-2
0
2
4
6
8
10
常用函数
newff
net=newff net=newff(PR,[S1 S2 …SN1],{TF1 TF2…TFN1},BTF,BLF,PF) 其中,
层内有互相结合的前向网络:
特点:可以实现同一层内神经元之间的横 向抑制或兴奋作用
相互结合型网络:
特点:任意两个神经元之间都可能有 联系
BP神经网络
多层前馈神经网络,信号向前传播,误差向后传播。
输入层
中间层
j
输出层
i
k
输入层
i
中间层 j
输出层
k
xi
ji
中间层:
输入
输出
p
kj
u j xi ji
神经网络
——浅尝
数学建模工作室 张敏
神经网络浅尝
• 神经网络基础知识
• 常用函数介绍
• 案例——蠓虫分类
神经网络基础知识
构成:大量简单的基本元件——神经元相互连接
工作原理:模拟生物的神经处理信息的方式
功能:进行信息的并行处理和非线性转化
特点:比较轻松地实现非线性映射过程
具有大规模的计算能力
医学:疾病识别
i 1
v j f (u j )
输入层
i
中间层 j
输出层
k
xi
ji
输出层:
kj
输入
输出
U k v j kj
j 1
n
Vk f (U k )
输入层
i
中间层 j
输出层
k
xi
ji
n p j 1 i 1
kj
U k ( f ( ( xi ji )) kj )
如:
n=-10:0.1:10 a=logsig(n)
plot(n,a)
grid on
图形如下:
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -10
-8
-6
-4
-2
0
2
4
6
8
10
tansig(双曲正切S型传递函数):
f ( x)
2 1 2n 1 e
调用格式:A=tansig(n)
应用范围
图像:识别、去噪、增强、配准、 融合 金融:股票和有价证券的预测分 析、资本收益的预测和分析、风 险管理、信用评估等等
神经网络结构图
输入层 中间层 输出层
生物神经元结构:
突触
细胞体
细胞核 轴突 神经末梢
树突
神经元结构模型
x1
x2 x3
xj
ij
xn
i
yi
可以看出神经元一般表现为一个多输入、单输出的非线性器件
x=[1.24 1.80;1.28 1.84;1.40 2.04]'; y0=sim(net,p)
y=sim(net,x)
Thanks !
net=newff :用于在对话框中创建一个BP网络
PR :由每组输入(共有R组输入)元素的最大值和最小值组成的R×2维的矩 阵; Si :第i层的长度,共计N1层 TFi:第i层的传递函数,默认为“tansig” BTF:BP网络的训练函数,默认为“trainlm”; BLF:权值和阈值的BP学习算法,默认为“learngdm” PF:网络的性能函数,默认为“mse”
Pi:初始输入延迟,默认为0; Ai:初始的层延迟,默认为0; T:网络目标,默认为0.
clear p1=[1.24,1.27;1.36,1.74;1.38,1.64;1.38,1.82;1.38,1.90; 1.40,1.70;1.48,1.82;1.54,1.82;1.56,2.08]; p2=[1.14,1.82;1.18,1.96;1.20,1.86;1.26,2.00 1.28,2.00;1.30,1.96]; p=[p1;p2]'; pr=minmax(p);
goal=[ones(1,9),zeros(1,6);zeros(1,9),ones(1,6)];
plot(p1(:,1),p1(:,2),'h',p2(:,1),p2(:,2),'o') net=newff(pr,[3,2],{'logsig' train(net,p,goal);
创建一个BP网络,其调用格式为:
train
其中,
用于对神经网络进行训练。调用格式为:
[net,tr,Y,E,Pf,Af]=train(NET,P,T,Pi,Ai)
NET:待训练的神经网络; P:网络的输入信号; T:网络的目标,默认值为0; Pi:初始的输入延迟,默认为0; Ai:初始的层次延迟,默认为0; net:函数返回值,训练后的神经网络; tr:函数返回值,训练记录(包括步数和性能); Y:函数返回值,神经网络的输出信号; E:函数返回值,神经网络的误差; Pf:函数返回值,最终输入延迟; Af:函数返回值,最终层延迟。
