第5章-对冲击荷载的反应
结构动力学_克拉夫(第二版)课后习题

例题E2-1 如图E2-1所示,一个单层建筑理想化为刚性大梁支承在无重的柱子上。
为了计算此结构的动力特性,对这个体系进行了自由振动试验。
试验中用液压千斤顶在体系的顶部(也即刚性大梁处)使其产生侧向位移,然后突然释放使结构产生振动。
在千斤顶工作时观察到,为了使大梁产生0.20in[0.508cm]位移需要施加20 kips[9 072 kgf]。
在产生初位移后突然释放,第一个往复摆动的最大位移仅为0.16 in[0. 406 cm],而位移循环的周期为1.4 s。
从这些数据可以确定以下一些动力特性:(1)大梁的有效重量;(2)无阻尼振动频率;(3)阻尼特性;(4)六周后的振幅。
2- 1图E2-1所示建筑物的重量W为200 kips,从位移为1.2 in(t=0时)处突然释放,使其产生自由振动。
如果t=0. 64 s时往复摆动的最大位移为0.86 in,试求(a)侧移刚度k;(b)阻尼比ξ;(c)阻尼系数c。
2-2 假设图2- la 所示结构的质量和刚度为:m= kips ·s 2/in ,k=40 kips/in 。
如果体系在初始条件in 7.0)0(=υ、in/s 6.5)0(=υ&时产生自由振动,试求t=1.0s 时的位移及速度。
假设:(a) c=0(无阻尼体系); (b) c=2.8 kips ·s/in 。
2-3 假设图2- 1a 所示结构的质量和刚度为:m=5 kips ·s 2/in ,k= 20 kips/in ,且不考虑阻尼。
如果初始条件in 8.1)0(=υ,而t=1.2 s 时的位移仍然为1.8 in ,试求:(a) t=2.4 s 时的位移; (b)自由振动的振幅ρ。
例题E3-1 一种便携式谐振荷载激振器,为在现场测量结构的动力特性提供了一种有效的手段。
用此激振器对结构施以两种不同频率的荷载,并分别测出每种情况下结构反应的幅值与相位。
由此可以确定单自由度体系的质量、刚度和阻尼比。
特大洪水对桥梁冲击的力学分析

毕业论文题目特大洪水对桥梁冲击的力学分析学院(全称)土木建筑学院专业、年级理论与应用力学学生姓名吴禹学号指导教师李晓红论文评阅人前言桥梁是道路跨越河流的主要形式,它起到保障公路运输畅通和排泄洪水的作用。
至今桥梁水毁仍是世界各国桥梁破坏最主要的原因,而其水毁形式多样,有的冲毁桥墩、桥台导致上部结构破坏,有的冲断桥头路堤和流堤等调治构造物,中断交通,威胁两岸安全。
桥梁墩台是直接修建在河道或海湾之中的,一旦水毁,修复困难,后果也较严重[1]。
位于平昌县白衣镇的白衣大桥,在2007年该区域发生的百年一遇的“7.6”大洪灾中,桥墩在建造过程中因受到该洪水的冲击导致垮塌,该事件对社会产生了极大影响,并导致工程停工9个月。
这只是一个典型的例子,国内外其他地区发生桥梁水毁的事例不在少数。
因而人们对现代桥梁的水毁防治越来越重视,发生水毁的原因与如何避免桥梁结构发生水毁已成为国内外学术界、工程界研究的热点。
桥梁的水毁的防治应着眼于预防,避免水毁的发生。
对于绝大多数的桥梁这也是可以做到的。
要做好对桥梁的水毁防治工作,就先要全面深入的研究水流特别是洪水对桥梁产生的作用影响,这也是本课题的落脚点,通过对洪水冲击桥墩的力学性能分析,充分认识到受冲击的桥墩的受力情况、位移变形、受拉产生的裂缝及进行宽度计算,以此为基础,把握水毁本质,为水毁防治工作提供依据和采取的措施。
本文研究的重点在于以受到洪水冲击的白衣大桥桥墩为背景,建立桥墩的三维空间有限元模型,对其在四种不同荷载工况下的第一主应力、Mises等效应力、墩高方向的位移与全桥变形、前墩墩底的受拉区裂缝进行分析并计算桥墩失去承载能力的临界水流下的裂缝宽度,根据计算分析结果,找出威胁桥墩安全的主要因素,提出关于提高桥墩抵抗洪水冲击的建议与措施。
选定荷载、确定结构计算模式和结构分析计算是本文对洪水冲击作用下的桥墩进行分析计算的三个主要部分。
在这其中,通过相关资料的阅读,本文将桥墩分为施工状态和成桥状态,第三章分别分析了在这两种状态下应考虑的荷载及荷载组合,介绍了不同荷载的计算方法与公式;第四章,主要采用数值方法对桥墩进行了模型建立与计算求解。
结构动力学基础理论

第四章
运动方程的建立
y (t)
单自由度 体系模型
c m k
F (t)
质量块m,用来表示结构的质量和惯性特性 自由度只有一个:水平位移y(t) 无重弹簧,刚度为 k,提供结构的弹性恢复力 无重阻尼器,阻尼系数c,表示结构的能量耗散,提供结构的阻尼力 随时间变化的荷载F(t)
单自由度体系运动方程的建立(直由度数为单元节点可发生的 独立位移未知量的总个数。 综合了集中质量法和广义坐标法的某些特点,是最灵活有效的 离散化方法,它提供了既方便又可靠的理想化模型,并特别适 合于用电子计算机进行分析,是目前最为流行的方法。 已有不少专用的或通用的程序(如SAP,ANSYS等)供结构分 析之用。包括静力、动力 和稳定分析。
代入:
单自由度无阻尼体系运动方程的解:
v(t )
0 v
sint v0 cost
(3-11)
第六章 简谐振动荷载反应
谐振荷载:
p (t )
k 1
则组合系数Ak(t)称为体系的广义坐标。
nπ x ( x ) bn sin l n 1
广义坐标 位移函数
广义坐标表示相应位移函数的幅值,是随时间变化的函数。 广义坐标确定后,可由给定的位移函数确定结构振动的位移曲线。 以广义坐标作为自由度,将无限自由度体系转化为有限个自由度。
1.3 动力荷载类型
概念:动荷载是时间的函数!
分类: 确定性荷载 动荷载 非确定性荷载
周期性荷载 非周期性荷载
确定性荷载:荷载的变化是时间的确定性函数。
FP
例如: 简谐荷载
t
FP
冲击荷载
t
结构动力学

第一章概述1.动力荷载类型:根据何在是否随时间变化,或随时间变化速率的不同,荷载分为静荷载和动荷载根据荷载是否已预先确定,动荷载可以分为两类:确定性(非随机)荷载和非确定性(随机)荷载。
确定性荷载是荷载随时间的变化规律已预先确定,是完全已知的时间过程;非确定性荷载是荷载随时间变化的规律预先不可以确定,是一种随机过程。
根据荷载随时间的变化规律,动荷载可以分为两类:周期荷载和非周期荷载。
根据结构对不同荷载的反应特点或采用的动力分析方法不同,周期荷载分为简谐荷载(机器转动引起的不平衡力)和非简谐周期荷载(螺旋桨产生的推力);非周期荷载分为冲击荷载(爆炸引起的冲击波)和一般任意荷载(地震引起的地震动)。
2.结构动力学与静力学的主要区别:惯性力的出现或者说考虑惯性力的影响3.结构动力学计算的特点:①动力反应要计算全部时间点上的一系列解,比静力问题复杂且要消耗更多的计算时间②于静力问题相比,由于动力反应中结构的位置随时间迅速变化,从而产生惯性力,惯性力对结构的反应又产生重要的影响4.结构离散化方法:将无限自由度问题转化为有限自由度问题集中质量法:是结构分析中最常用的处理方法,把连续分布的质量集中到质点,采用真实的物理量,具有直接直观的优点。
广义坐标法:广义坐标是形函数的幅值,有时没有明确的物理意义,但是比较方便快捷。
有限元法:综合了集中质量法与广义坐标法的特点,是广义坐标的一种特殊应用,形函数是针对整个结构定义的;有限元采用具有明确物理意义的参数作为广义坐标,形函数是定义在分片区域的。
①与广义坐标法相似,有限元法采用了形函数的概念,但不同于广义坐标法在全部体系(结构)上插值(即定义形函数),而是采用了分片的插值(即定义分片形函数),因此形函数的公式(形状)可以相对简单。
②与集中质量法相比,有限元法中的广义坐标也采用了真实的物理量,具有直接直观的优点。
5.结构的动力特性:自振频率、振型、阻尼第二章分析动力学基础及运动方程的建立1.广义坐标:能决定质点系几何位置的彼此独立的量;必须是相互独立的参数2.约束:对非自由系各质点的位置和速度所加的几何或运动学的限制;(从几何或运动学方面限制质点运动的设施)3.结构动力自由度,与静力自由度的区别:结构中质量位置、运动的描述动力自由度:结构体系在任意瞬间的一切可能的变形中,决定全部质量位置所需要的独立参数的数目静力自由度:是指确定体系在空间中的位置所需要的独立参数的数目为了数学处理上的简单,人为在建立体系的简化模型时忽略了一些对惯性影响不大的因素确定结构动力自由度的方法:外加约束固定各质点,使体系所有质点均被固定所必需的最少外加约束的数目就等于其自由度4.有势力的概念与性质:有势力(保守力):每一个力的大小和方向只决定于体系所有各质点的位置,体系从某一位置到另一位置所做的功只决定于质点的始末位置,而与各质点的运动路径无关。
第5章 对冲击荷载的反应

t1
(5-18)
荷载引起的速度的改变。t1值小时,在荷载 v
作用期间所引起的位移 (t1 ) 是属于 (t1 ) 2量级的,而速 是属于t1量级的.因此,既然冲量也是t1量 度改变 v 级的,故当t1趋近于零时弹性力项 kv(t ) 自表达式消失, 而对持续时间短的荷载,它的值很小,可以忽略.
§5.3
矩形脉冲
高等结构动力学
阶段I 在阶段I期间突然施加的恒荷载,称为单阶荷载。单阶荷载的特解即 为它所引起的静挠度 (5-10)
从这个结果,一般解中的自由振动常数可由满足静止的初始条件来确定,从 而很容易得到一般解:
当0≤t≤t1时: (5-7*) 阶段Ⅱ 在此阶段内,自由振动再次由方程(5-2*)给出: 当t=t-t1≥0时: (5-8*)
高等结构动力学
高等结构动力学
第五章
对冲击荷载的反应
高等结构动力学
第五章 对冲击荷载的反应
§5.1 冲击荷载的一般性质 §5.2 正弦波脉冲 §5.3 矩形脉冲 §5.4 三角形脉冲 §5.5 震动谱或反应谱 §5.6 冲击荷载反应的近似分析
§5.1 冲击荷载的一般性质
高等结构动力学
§5.1 冲击荷载的一般性质
§5.5
震动或反应谱
高等结构动力学
§5.5
震动或反应谱(2)
根据表5-1所示数据可作出图5-6中的一条曲线,其它曲线亦 可用相同的方法画出,分别对应于其它冲击荷载形式。这些曲 线称为冲击荷裁的位移反应谱或简称反应谱。 利用这些曲线可以在工程所需精度内,估计作用在简单结 构上的给定冲击荷载所产生的最大效应。
§5.6 冲击荷载反应的近似分析 应用如下的近似关系: 或
高等结构动力学
17 单自由度体系在冲击荷载作用下的反应
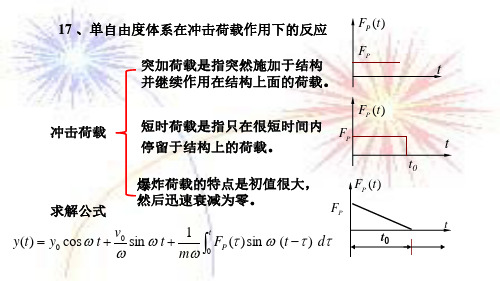
F t P ()F tt 0F t P ()F Pt突加荷载是指突然施加于结构并继续作用在结构上面的荷载。
短时荷载是指只在很短时间内停留于结构上的荷载。
爆炸荷载的特点是初值很大,然后迅速衰减为零。
()cos sin 1()sin ()000=++−⎰P ty t y t v t m F t d ωωωωτωττF t P ()F Ptt 017 、单自由度体系在冲击荷载作用下的反应冲击荷载求解公式17.1 、突加荷载P PF t t F t ()000=≤≥⎧⎨⎩F t P ()F Pt图1如果结构的初始位移和初始速度都等于零,则受迫振动可按下式计算:m m t t y t F F m m y t F t d F t d P PtP P t⎰⎰=−=−=−=−=−ωωωτωωωωτωττωττcos ()(1cos )(1cos )()()sin ()sin ()11022st 00t ω2=F m y Pst =max (())2y t y st动力放大系数μ=217.2 、短时荷载t t F t F t t P P⎩≥⎨=⎧≤0()00F t P ()F Ptt 0图2如果结构的初始位移和初始速度都等于零,则受迫振动可按下式计算:当t ≤ t 0时m y t t y t F P=−=−ωωω()(1cos )(1cos )2st =max (())2y t y st动力放大系数μ=2当t ≥ t 0时m y t t t t y t F t t P=−−=−ωωωωω22()(cos ()cos )2sin sin ()20st 00Ty t y y t t ==ωπ2(())2sin2sinmax st st 0Tt 数系大放力动=μπ2sin17.3 、爆炸荷载P P F t F t t t t t t ()(1)00=−≤≥⎧⎨⎪⎩⎪F t P ()F Ptt 0如果结构的初始位移和初始速度都等于零,则受迫振动可按下式计算:图3当t ≤ t 0时t t y t y t t t st =−−+ωωω()(1cos )sin 00t Ty t y y t T ==−πμπ2/(())2(1)arctan(2/)0max st st 0当t ≥ t 0时t y t y t t t t =−+−−ωωωω()(cos (sin sin ()))10st 0y t y =μ(())max stt t T t TTTT t t 数系大放力动=+−−πππμππ221cos sin2200022220022。
《土木工程材料》课后题 参考答案

《土木工程材料》复习思考题参考答案第1章 复习思考题一、填空题1. 宏观,细观,微观2. 51.53. 小,大4. 最大冻融循环次数5. 软化系数,0.85二、选择题1. B ;2. A ;3. D ;4. C ;5. B ;6. D三、简答题1.答:当某种材料的孔隙率增大时,下表内其他性质如何变化?(用符号表示:↑增大、↓下降、─不变、?不定)2. 答:脆性材料——在外力作用下达到破坏荷载时的变形值很小,破坏时有突发性;抗压强度远大于抗拉强度,可高达数倍甚至数十倍;承受冲击或震动荷载的能力很差,适宜承受静压力,用于受压部位。
韧性材料——在冲击或震动荷载作用下,能吸收较大能量,同时产生较大变形,特别是塑性变形大,破坏前有明显预兆;抗拉强度接近或高于抗压强度。
适合承受拉力或动载,对于承受冲击荷载和有抗震要求的结构,应具有较高的韧性。
3. 答:提高材料的耐久性,对保证工程结构长期处于正常使用的状态,减少维护费用,延长使用年限、节约材料,具有十分重要的意义。
材料的耐久性与其抗渗性有直接关系,改善抗渗性的措施均有利于提高材料的耐久性。
如生产制备材料时,尽量增大其密实度,提高强度;改善内部孔隙结构,减少连通性孔隙;做好防水措施,对于亲水性材料,表面用憎水材料覆盖或涂层等。
四、计算题1.解:填充1m 3卵石需用砂子的体积大小等于卵石的孔隙体积。
//001550(1)100%(1)100%41.5%2650g P ρρ=-⨯=-⨯= /31.0*0.415s g V P m ==2.一块烧结普通砖的外形尺寸为240mm ⨯115mm ⨯53mm ,吸水饱和后重2940g ,烘干至恒重为2580g 。
将该砖磨细并烘干后取50g ,用李氏瓶测得其体积为18.58 cm 3。
试求该砖的密度、表观密度、孔隙率、质量吸水率、开口孔隙率及闭口孔隙率。
解:砖的密度:350 2.69/18.58m g cm V ρ=== 砖的表观密度:3002580 1.76/2411.5 5.3m g cm V ρ===⨯⨯ 砖的孔隙率:0 1.76(1)100%(1)100%34.6%2.69P ρρ=-⨯=-⨯= 砖的质量吸水率:129402580100%100%14.0%2580m m m w m --=⨯=⨯= 砖的开口孔隙率:360100%24.6%2411.5 5.3k v P w ==⨯=⨯⨯ 砖的闭口孔隙率:34.6%24.6%10.0%b k P P P =-=-=3. 解:① 甲材料的孔隙率:0 1.4(1)100%(1)100%48.1%2.7P ρρ=-⨯=-⨯= 体积吸水率: 0140017%23.8%1000V m w W W ρρ==⨯=② 设乙材料的总体积为1m 3,则吸收水的体积为0.462m 3。
第五章 动载试验 2

第五章动载试验1、结构中遇到的动载有两类:振动荷载与移动荷载。
结构动力荷载的类型分为以下5种:(1)地震荷载(2)机械设备振动和冲击荷载(3)高层建筑和高耸构筑物的风振(4)环境振动5)爆炸引起的振动2、动力试验对于在实际工作中主要承受动力作用的结构或构件,为了研究结构在施加动力荷载作用下的工作性能,一般要进行动力试验。
动力试验的特点:由于荷载特性不同,动力试验的加载设备和测试手段与静力试验有很大的差别,而且要比静力试验复杂得多。
3、动力试验总结:荷载是动力形式出现,它的速度以一定频率对结构产生动力响应,由于加速度作用引起惯性力,以致荷载大小又直接与结构本身的质量有关,动力加载对结构产生共振使应变及挠度增大,其次动力荷载作用于结构还有应变速率,应变速率的大小又直接影响结构的材料的强度。
加载速度越高,引起结构或构件的应变速率愈高,则试件强度和弹性模量也就相应提高,在冲击荷载作用下强度与弹性模量变化尤为显著。
第五章动载试验4、振动试验的目的是测定结构的特性、结构的响应及结构的破坏特性等。
结构振动试验通常有以下几项内容:1)结构动力特性测定;测定结构自振特性(2)结构的振动反应测量;测定结构在外界动力荷载作用下的振动反应参数。
如何正确模拟结构所受的动力加载,是结构动载试验首先要解决的问题。
1、惯性力加载:惯性力加载是利用运动物体质量的惯性力,对结构施加动荷载。
按产生惯性力的方法可分为冲击力、离心力及直线位移惯性力加载。
(1)冲击荷载这种荷载作用于试件上的时间较短,属于突然加载,一般用于测定试件在冲击荷载作用下的承载力、抗裂等性能,也用于测定结构本身的各种动力特性,如固有频率等。
一般落重的高度为2.5米以下,重量不大于试验跨内结构自重的0.1%。
突卸的方法可以用绞索张拉结构使其产生一个初始位移,当荷载突然卸去,结构便作自由振动。
该法适用于动力特性测定试验,结构自振时没有附加质量的影响,其他还有离心力加载和曲柄连杆系统的水平振动。
第5章土木工程荷载教材

• 考虑建筑物横向刚度相对较小,一般以横向为地震荷载演算方向。
F =
a
2.3.1 地震作用
地震区域分布
• 全球主要地震活动带有三个: • 环太平洋地震带,是地震活动最强烈的地带,发生全球约80%的地震; • 欧亚地震带,占全球地震的15%。 • 海岭地震带:分布在太平洋、大西洋、印度洋中的海岭。
• 乙类:重要建筑物,如重点抗震城市的生命线工程与抗震救灾需 要的建筑;按基本烈度提高一度进行设防与相关构造。
• 丙类:甲、乙、丁类以外的一般建筑物;按基本烈度设防与进行 相关构造。
• 丁类:次要建筑物,地震破坏后果不会造成重大伤亡与较大经济 损失。按基本烈度降低一度进行设防与相关构造。
• 六度区内百万以上人口城市的高层建筑,按七度设防。
损坏,但加以修缮后可继续使用,材料受力处于塑性阶段,但被控制在 一定限度内,残余变形不大。 3. 大震不倒: • 在较基本烈度高 1 度的第三水准烈度作用下,结构出现严重破坏,但材 料的变形仍在控制范围内,不至于迅速倒塌,赢得撤离时间。
2.3.2 风荷载
风的形成与危害
• 风是由于大气层的温度差、气压差等大气现象导致的空气流动现象。建筑 物会对风形成阻挡,因此风会对于建筑物形成反作用。
风力作用。
风玫瑰图
如图所表示的某一地区的冬季、夏季主导风向的图形。
2.3.2 风荷载
建筑形体与风的作用
• 迎风面风力为压力,侧风面随着与风的夹角的变化,风力逐渐有压力转变 为吸力;
• 矩形、圆形、三角形等不同的平面形状的建筑物,各个侧面所受的风力作 用差异很大。
• 建筑物表面粗糙会加大风力的作用。
工程结构荷载与可靠度设计原理-完整版

2021/5/9
§2.3 雪荷载
漂积作用的影响: • 使敞风较好的平屋面或小坡度屋面上的雪压小于
邻近地面上的雪压; • 在高低跨屋面的情况下,在低屋面形成局部较大
其他几种水压力在结构物上的分布模式
§3.2 水压力及流水压力
二、动水压力
➢ 当水流过结构物表面时,会对结构物产生切应力 和正应力。
➢ 切应力只有在水高速流动时,才表现出来。
➢ 正应力=静水压力+动水压力。
即:
p p静 p动
p p静 p动 p'
p动 时段平均动压力(Pa);
p'
2021/5/9
大汽车荷载的概率大小,对荷载效应进行折减。 车道数越多,折减率越大。
2021/5/9
§2.4 车辆荷载 车辆荷载布置图
2021/5/9
单位(m)
§2.4 车辆荷载 ➢ 列车荷载 • 列车荷载应采用中华人民共和国铁路标准活载, 及“中-活载”。
我国城市桥梁设计荷载标准规定的城-A级车道荷载
2021/5/9
hi
i
2021/5/9
第i层土的厚度(m)
第i层土的天然重度,若土层位
于地下水位以下,计算土的自
重应力时应取土的有效重度
' i
§2.1 结构自重
土的有效重度
' i
若土层位于地下水位以下,由于受到水的 浮力作用,单位体积中,土颗粒所受的重 力扣除浮力后的重度称为土的有效重度, 是土的有效密度与重力加速度的乘积
2021/5/9
定第五章__土的击实试验

第五章击实试验第一节击实试验的基本原理一、基本概念1. 土的压实性工程中,用于填筑路堤等的填料均处于松散的三相状态,在以机械方法施加击实功能的条件下,可以压实增加密度,使其具有足够的强度、较小的压缩性和很小的透水性。
土的这种通过碾压施以一定压实功能,密度增加的特性称为土的压实性。
在用粘性土作为填筑材 表示填土的密实性。
料时,常用干密度d2。
击实试验为了获得最理想的压实效果,需要充分了解土的压实特性,其中,影响压实特性的主要因素是含水率和施加的压实功能。
为此,在工程实践中常常在模拟现场施工条件(包括施工机械和施工方法)下,找出压实密度与填土含水率之间的关系,从而获得压实填土的最佳密度(既最大干密度)和相应的最优含水率。
击实试验就是为了这种目而利用标准化的击实仪具,得到土的最大干密度与击实方法(包括土的含水率和击实功能等)的关系,据以在现场控制施工质量,保证在一定的施工条件下压实填土达到设计的密实度标准。
所以击实试验是填土工程如路堤、土坝、机场跑道及房屋填土地基设计施工中不可缺少的重要试验项目.工程经验表明,欲将填土压实,必须使其含水率降低在饱和状态以下,即要求土体处于三相介质的非饱和状态。
土在瞬时冲击荷载重复作用下,颗粒重新排列,其固相密度增加,气相体积减少;当锤击力作用于土样时,首先产生压缩变形,当锤击力消失后,土又出现了回弹现象。
因此,土的击实过程,即不是固结过程,也不同于一般压缩过程而是一个土颗粒和粒组在不排水条件下的重新组构过程。
用击实试验模拟现场土的压实,这是一种半经验方法。
由于土的现场填筑辗压和室内击实试验具有不同的工作条件,两者之间的关系是根据工程实践经验求得的,因此很多国家以及一个国家的不同部门就可能有其自用的击实试验方法及仪器。
图5。
1击实仪国内常用的击实试验仪器如图5.1,主1—击实筒;2—护筒;要包括击实筒和击锤两部分,仪器型号和试3—导筒;4—击锥;5—底板验方法不同,其尺寸参数各异。
05第五讲:单自由度系统动力响应数值求解(1)

第五讲:单自由度系统动力响应数值求解 第五讲:单自由度系统 动力响应数值求解
一、脉冲荷载作用下的动力响应
瞬时冲量:脉冲荷载在极短时间t ≈0内给 瞬时冲量:脉冲荷载在极短时间 予振动物体的冲量:
p (t)
I p0 D t
动量增值:t =0时,瞬时冲量I 作用于质 点上m,使其增加动量,记作:
p0
~ pi ,令 pi 为区间的开始 pi 1为区间的
常量分段插值
线性分段插值
线性分段插值
~ pi ( pi pi 1 ) 2
Dp p (t ) pi i t Dti
这里,
Dpi ( pi 1 pi )
第五讲:单自由度系统动力响应数值求解 第五讲:单自由度系统 动力响应数值求解
t
Fk d t - (t - tk ) e sin d (t - tk ) m d
v ( t ) e t ( A sin d t B cos d t ) p(t )h( t t )dt (b) 0
问题: Duhamel 积 分的使用条件?
第五讲:单自由度系统动力响应数值求解 第五讲:单自由度系统 动力响应数值求解
v p ( t ) p(t )h( t t )dt
0
t
F1 d t - (t - t1 sin d ( t - t 1 ) m d e )
则(a)式成为 式成为卷积积分 卷积积分: : 方程的通解:
F t d t e- ( t -t sin d ( t - t) ) md
h(t t ) u (t )
1 m
t t
1 sin[n (t t )] t t m n
0
结构试验第五章 土木工程结构动载试验[可修改版ppt]
![结构试验第五章 土木工程结构动载试验[可修改版ppt]](https://img.taocdn.com/s3/m/8a4dd8b87e21af45b307a8de.png)
五、结构动载试验
5.3 结构动力特性的试验测定
[振动荷载法,强迫振动法]
优点:对于较复杂的动力问题,可得到若干个固有 频率。
缺点:需专门的激振器。
五、结构动载试验
5.3 结构动力特性的试验测定
[脉动法、环境随机振动法] 脉动法通常用于测量整体建筑物的动力特性,这种方法不用
方形平板的各阶模态及其对应的频率
五、结构动载试验
5.3 结构动力特性的试验测定
[振动荷载法]
当采用偏心式激振器时,激振 力与其频率的平方成正比。当 偏心块旋转频率逐渐增大,其 激振力也随之增加,这样就破 坏了共振所引起被测物振动幅 值增大的“纯洁”性。解决的 方法是在绘制共振曲线时将其 纵坐标更改为A/ω2
五、结构动载试验
5.3 结构动力特性的试验测定
每个结构都有其自身的动力特性,它是结构物自身所固有 的一种属性。
它取决于结构的组成形式,如材料性质、刚度、质量大小 及其分布情况等。
它与外荷载无关,当结构确定后,其自振特性也就随之确 定下来。
结构自振特性主要包括:
自振频率;阻尼;振型
五、结构动载试验
一般通过试验测定结构的动力特性参数
自由由于振结动构法形式差异强很迫大振,动所法用的方法、仪器也不 同,因此试验结果会出现较大差异,可进行多次 反复试验人,工获激得振可法靠的试验环结境果随。机振动法
通常的做法,通过某种方法对结构激振,使结构 产生振动,依据仪器记录到的振动波形进行分析。
五、结构动载试验
共振曲线
五、结构动载试验
5.3 结构动力特性的试验测定
[振动荷载法]
带宽法、半功率法求结构的阻尼
共振曲线
第4 5 6章对周期性荷载的反应

h(t ) 称为单位脉冲反应函数,其中t表示体系动 式中, 力反应的时间,τ表示单位脉冲作用的时刻。
v(t ) p( )h(t )d
0
t
,t 0
(7)
式(7)称为卷积积分,利用这个积分,可以获得任意荷 载作用下无阻尼结构体系在整个时间域内的反应。
• 上式的初始条件是t=0时结构处于静止状态。 • 对于其它特定的初始条件,这个解还必须加上一个附加自由振动反应
p( t )
正弦波冲击
阶段I:承受谐振荷载,从静止 开始运动,包含瞬态反应和稳态 反应。
p0
t
t1
t
阶段II
0 t t1
v(t )
阶段I
p0 1 (t1 ) (sin t sin t ) v(t1 ) v 2 k 1
阶段II:自由振动,与阶段I最终时刻的位移和速度有关。
∵ ∴
2 T
vmax 2v st sin
t 1
2
当t1≧T/2时,t 一定可以达到! 当t1<T/2时,t 就达不到!
max(1 cos t ) 2 max(1 cos t ) 2
极值出现在t >t1时!
(t ) sint 当t < 时, v
t t t1 0
( t1 ) v v(t ) sin t v( t1 ) cos t
矩形脉冲
矩形脉冲荷载:
F (t)
0 p( t ) p0
t 0, t t1 0 t t1
F0 t 0 t1
短时间滞留在结构上的荷载;
由于作用时间短,一般不考虑阻尼; 0<t<t1时: t>t1时:
建筑结构试验简答

建筑结构试验简答文件管理序列号:[K8UY-K9IO69-O6M243-OL889-F88688]第5、6章复习要点1.试件设计时为什么要注意试件形状?当从整体结构中取出部分构件单独进行试验时,试件设计应注意什么?答:试件设计之所以要注意它的形状,主要是要在试验时形成和实际工作相一致的应力状态。
在从整体结构中取出部分构件单独进行试验时,必须注意其边界条件的模拟,使其能如实反映该部分结构构件的实际工作状况。
2.采用模型试验时,为了保证模型试验所研究的物理现象与实物试验的同一现象是相似的,必需考虑哪些问题?答:采用模型试验时,为了保证模型试验所研究的物理现象与实物试验的同一现象是相似的,下列问题必需考虑:试验材料如何选择;试验参数如何确定;试验中应该测量哪些量;如何处理试验结果以及可以推广到什么样的现象上去。
3.在进行结构模型设计时,确定相似条件的方法有哪两种?答:确定相似条件的方法有方程式分析法和量纲分析法两种。
4.什么是结构试验的加载制度?它包括哪些内容?为什么对于不同性质的试验要求制订不同的加载制度?答:结构试验加载制度是指结构试验进行期间控制荷载与加载时间的关系。
它包括加载速度的快慢、加载时间间歇的长短、分级荷载的大小和加载、卸载循环的次数等。
由于结构构件的承载能力和变形性质与其所受荷载作用的时间特征有关,因此,对于不同性质的试验,必须根据试验的要求制订不同的加载制度。
5.预载的目的是什么?答:预载的目的有以下几点:1)使试验各部位接触良好,进入正常工作状态,荷载与变形关系趋于稳定;2)检验全部试验装置的可靠性;3)检查全部观测仪表工作是否正常;4)检查现场组织工作和人员的工作情况,起演习作用。
6.对于受弯构件,选取测量应变的截面应依据哪些原则?答:对于受弯构件,需按如下原则选取测量应变的截面:1)弯矩最大处;2)剪力最大处;3)弯矩与剪力均较大处;4)截面面积突变处;5)抗弯控制截面(截面较弱且弯矩值较大处);6)抗剪控制截面(截面较弱且剪力值较大处)。
土木工程荷载复习

第一章荷载与作用何谓作用?施加在结构上的一组集中力或分部力,或引起结构外加变形或约束变形的原因,统称为结构上的作用。
什么是直接作用和间接作用?例子施加在结构上的集中力和分部力成为直接作用。
例如,各种土木工程结构的自重、土压力、水压力、风压力、积雪重。
房屋建筑中的楼面上人群和加剧等重量,路面和桥梁上的车辆重量引起结构外加变形或约束变形的原因成为间接作用。
例如,地基变形、混凝土收缩徐变,温度变化、焊接变形、地震作用等。
(不是以外家里的形式直接施加在就够上)第二章土木工程荷载的分类及代表值可变作用和偶然作用?例子可变作用,在设计基准期内量值随时间变化,且变化与平均值相比不可忽略。
例如:风荷载、雪荷载、温度变化、冰荷载、波浪荷载、水位变化的水压力,路桥结构上的车辆荷载、人群荷载、房屋建筑中的楼面活荷载、积灰荷载、厂房吊车荷载、港口的堆货荷载。
偶然作用,在设计基准期内不一定出现,而一旦出现,其量值可能很大且持续时间短。
例如:爆炸力、撞击力、龙卷风、罕遇地震、活在。
罕遇洪水。
什么是固定作用和自由作用?例子固定作用,在结构上具有固定分布的作用。
例如:结构自重、楼面均布活荷载、结构上固定的设备自重等。
自由作用,在结构上一定范围内可以任意分布的作用,其出现的位置及量值都有可能是随机的。
例如:桥梁结构上的车辆荷载、工业厂房中的吊车荷载。
什么是静态作用和动态作用?例子静态作用,对结构或构件不产生加速度,或者所产生的加速度可以忽略不计的荷载。
例如:结构的自重、房屋楼面活荷载等。
动态作用,使结构或构件产生的加速度不可忽略的荷载。
例如:地震、爆炸力、船舶撞击力、设备的震动、工业厂房中的吊车荷载、以一定的速度通过桥梁的汽车火车荷载、作用于高耸结构上的风荷载。
永久作用和可变作用各有哪些代表值?永久荷载只有一个代表值:标准值可变荷载一般有三个代表值:标准值、频遇值和准永久值。
第三章地震作用什么是震级和地震烈度?震级是表明地震本身强度的大小和释放出能量的多少的等级。
《结构动力学》教学日志知识资料b

第
24
次
总结复习
知识点串讲
年月日
学生考核成绩记录
序号
项目
出勤
作业
学号
姓名
/
/
/
/
/
/
/
/
/
/
成
绩
/
/
/
/
/
/
/
/
成
绩
1
5
杨金银
2
2
甄一帆
3
4
周叙霖
4
1
史宝红
5
2
李明聪
6
3
桑胜涛
7
4
崔亚歌
8
5
贾世宁
9
6
连娜
10
7
周文丽
11
8
熊治凯
12
9
薛涛
13
0
周翱翔
14
1
赵锦涛
15
2
田里
16
3
孙可锋
17
4
王浩
教研室主任主管教学院(部)长
年月日年月日
教学计划内容
授课实施记录
课内
课外作业、实验
第
1
次
第1章绪论和概述
1.1结构动力分析主要目的
1.2荷载的分类(持时和来源)
1.3动力问题的基本特性
重点:结构动力分析意义及基本概念。
难点:动力问题与静力问题区别与联系。
寻找1-2本国外结构动力学相关的教材,供学习参考。
(自愿上交)
年月日
第
2
次
第1章绪论和概述
1.4离散化主意
1.5运动方程的建立
结构动力学5

p(t )e
i j t
dt
p(t )e
k k 0
N 1
i j t k
t t
p(t )e
k k 0
N 1
i
2kj N
将离散化的谱值代入Fourier逆变换公式,并应用矩形积 分公式得:
1 u (t k ) 2 1 2
U ( )e
it k
p(τ)dτ的动力反应
:
du(t ) p( )d h(t ) , t
在任意时间t结构的反应, 等于t以前所有脉冲 作用下反应的和 :
u (t ) du
0
t
p( )h(t )d
0
t
5.1 时域分析方法—Duhamel积分 2、对任意荷载的反应
无阻尼体系动力反应的Duhamel积分公式 :
1 U ( ) i 2 nU ( ) n U ( ) P( ) m
2 2
U ( ) F u(t ) , P( ) F p(t )
5.2 频域分析方法—Fourier变换法
2U ( ) i 2 nU ( ) n U ( )
结构动力学
(2003春)
结构动力学
第五章
单自由度体系对任意荷载的反应
在实际工程中,很多动力荷载既不是简谐荷载,也 不是周期性荷载,而是随时间任意变化的荷载,需要 采用更通用的方法来研究任意荷载作用下体系的动力 反应问题。
本章介绍三种动力反应问题的分析方法: 时域分析方法—Duhamel积分法, 频域分析方法—Fourier变换法, 时域逐步积分法—中心差分法;Newmark—β法; Wilson—θ法。
第五章工程结构动载试验

3、高层建筑和高耸构筑物设计时要解决风荷载所引起 的振动问题。
4、桥梁设计与建设中需要考虑车辆运动对桥梁的振动 及危害问题。
5、海洋采油平台设计中需要解决海浪的冲击对海洋采 油平台等不利影响问题。
6、研究建筑物如何抵抗爆炸等所产生的瞬时冲击荷载 对结构的影响。
1)当
,
时
满足此条件的测振 仪称位移计。一般位移 计的体积较大也较重, 使用时对被测系统有一 定影响,特别对于一些 质量较小的振动体不太 适用。
2)当
,
时
满足此条件的
测振仪称加速度计 。
5.3.2 测振传感器
拾振器除应正确反映振动体的振动外,尚应不失真 地将位移、速度及加速度等振动参量转换为电量,以便 用量电器进行测量。
电磁式振动台操作方便;振动波形好,频率范围广, 但激振力较小,仅几百N至几十kN。
5.2.3 液压振动台
液压振动台有单向运动、双向运动和三向运动等几种 ,振动台多采用电液伺服系统推动。在各种结构模型(或 足尺)动力试验中,模拟地震振动台是最理想的结构抗震 设备。
振动台实验室位于中国建筑科学研究院 研发基地,建筑面积3300平米,实验室 内拥有全国最大的6m╳6m三向六自由度 大型高性能模拟地震振动台。
阻尼比 :
5.4.3 脉动法
工程结构脉动来自两个方面,一方面是地面脉动;另 一方面是大气变化即风和气压等引起的微幅振动。脉动能 够明显反映出结构的固有频率。从脉动信号中可识别出结 构物的固有频率、阻尼比、振型等多种模态参数。
测量脉动信号要使用低噪声、高灵敏度的拾振器和放 大器,并应配有记录仪器和信号分析仪。
1、磁电式速度传感器
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§5.6 冲击荷载反应的近似分析 应用如下的近似关系:
高等结构动力学
mv
或
t1
0
p(t )dt
(5-19)
(5-20)
1 t1 v p(t )dt m 0 加荷结束之后的反应为自由振动:
v( t )
其中
t t t1
v(t1 )
sin t v(t1 ) cos t
t1/T D 0.20 0.66 0.40 1.05 0.50 1.20 0.75 1.42 1.00 1.55 1.50 1.69 2.00 1.76
§5.5
震动或反应谱(1)
高等结构动力学
§5.5
震动或反应谱(1)
由上述表达式,在无阻尼单自由度结构里,给定的冲击荷 载形式所引起的最大反应仅依赖于脉冲的持续时间与结构的固 有周期的比值t1/T。对于各种冲击荷载形式,画出动力放大系数 作为t1/T的函数的曲线。
(t1 ) 0
v(t1 ) v
有如下的近似关系:
v( t )
t1 1 ( p(t )dt )sin t m 0
(5-21)
§5.6 冲击荷载反应的近似分析
高等结构动力学
例题 E5-2 作为应用这个近似公式的一个例子,讨论
图E5-2中的结构在所示冲击荷载下的反应.在此情况下, t kg / W 3.14弧度 / 秒,且 1 p(t )dt 10千磅 秒。 0 反应约为 10 (386) v( t ) sin t 2000 (3.14) 其中重力加速度取作 g 386英寸 / 秒2。
当sin t 1时最大反应为
结构工程师最关心的、在弹簧中所产生的最大弹性力是:
2 T 2秒 ,对于这样的短持 因为这个系统的振动周期为
max
0.614英寸
f s ,max kvmax 51.1(0.614) 3.14千磅
t1 续时间荷载( 0.15 ), T
§5.6 冲击荷载反应的近似分析
§5.4
三角形脉冲
高等结构动力学
§5.4
三角形脉冲
讨论冲击荷载为图5-5所示的随时间而减小的三角形脉冲荷载。
图5-5 三角形脉冲
§5.4
三角形脉冲
高等结构动力学
阶段Ⅰ 在这个阶段,荷载为p0(1-t/t1),不难证明,在此荷载下的特解为 (5-11*)
如果假定为零初始条件,可以算出在一般解中的自由振动常数,从而求得 (5-12*)
§5.3
矩形脉冲
高等结构动力学
对于这种矩形脉冲,显然,如果t1≥T/2的话,最大反应将总是在阶段Ⅰ出现, 此时的动力放大系数D为2。对于持续时间比较短的荷载,最大反应将在阶段 Ⅱ的自由振动期间出现,而反应幅值将由方程(2-37)给出如下:
(5-9*)
从该式可得 (5-10*) 因此当t1/T小于1/2时,动力放大系数是一个正弦函数,它随荷载脉冲长度比 t1/T而变化。
§5.3
矩形脉冲
高等结构动力学
阶段I 在阶段I期间突然施加的恒荷载,称为单阶荷载。单阶荷载的特解即 为它所引起的静挠度 (5-10)
从这个结果,一般解中的自由振动常数可由满足静止的初始条件来确定,从 而很容易得到一般解:
当0≤t≤t1时: (5-7*) 阶段Ⅱ 在此阶段内,自由振动再次由方程(5-2*)给出: 当t=t-t1≥0时: (5-8*)
放大系数与脉冲面积对荷载峰值的比成比例。 比较图5—6中短周期范围内的各条曲线,就可
max 是反应的更有效的尺度. 看出这一点.因此,
§5.6 冲击荷载反应的近似分析
高等结构动力学
用第(2)条结论的数学表示法计算持续时间短 的冲击荷载下最大反应,对于质量m的脉冲—冲量的 关系可写成
mv [ p(t ) kv(t )]dt
§5.6 冲击荷载反应的近似分析
高等结构动力学
§5.6 冲击荷载反应的近似分析
对图5—6所示的反应谱及其它形式荷载的谱的 研究,得出关于冲击荷载下结构反应的两个结论: (1)对于长持续时间荷载( t1/T>1),动力放大 系数主要依赖于荷载达到它的最大值的增加速度; 具有足够持续时间的单阶荷载所产生的动力放
正弦波脉冲
高等结构动力学
结构工程师更关心冲击荷载的最大反应,它比全部反应过程 更有意义; 出现反应峰值的时间,可由方程(5-1*)对时间t求导并令其等 于零来确定。于是:
得:
因此
(5-3*)
§5.2
正弦波脉冲
高等结构动力学
表达式仅在ωt≤π时才是正确的,这就是说,最大反应出现在 冲击荷载作用时间内。对于最有意义的荷载情况来说,此时荷 载频率趋近于自由振动频率,即ω→ω,最大反应发生的时间可 用方程(5-3*)求出,将n=1代入并在(5-3*)式中取负号: (5-4*) 最大反应幅值可将方程(5-4*)代入方程(5-1*)而得到。这个结 果仅在假定ωt≤π时才是正确的,也即只有当β<1或ω<ω的情况 下才是正确的。 当β>1(ω>ω)时,最大反应出现在自由振动阶段内(阶段 Ⅱ)。这一阶段的初位移和初速度可将ωt=π代入方程(5-1*)而 得到:
高等结构动力学
近似分析可以认为是非常可靠的。实际上,将运动方程 直接积分来求得的最大反应为0.604英寸,因此近似结果 的误差小于2 %。
图E5-2 近似冲击反应分析
§5.5
震动或反应谱
高等结构动力学
§5.5
震动或反应谱(2)
根据表5-1所示数据可作出图5-6中的一条曲线,其它曲线亦 可用相同的方法画出,分别对应于其它冲击荷载形式。这些曲 线称为冲击荷裁的位移反应谱或简称反应谱。 利用这些曲线可以在工程所需精度内,估计作用在简单结 构上的给定冲击荷载所产生的最大效应。
0
t1
(5-18)
v 荷载引起的速度的改变。t1值小时,在荷载
作用期间所引起的位移 (t1 ) 是属于 (t1 ) 2量级的,而速 度改变 v 是属于t1量级的.因此,既然冲量也是t1量 级的,故当t1趋近于零时弹性力项 kv(t ) 自表达式消失, 而对持续时间短的荷载,它的值很小,可以忽略.
讨论单自由度体系动力荷载的另一种特殊类型——冲击荷 载.如图6-1的例子所示,这种荷载由一个单独的主要脉冲组成, 一般来说它的持续时间很短。与承受周期性荷载或谐振荷载的结 构比较,在控制结构的最大反应中,阻尼就显得不太重要了。 在冲击荷载下,结构的最大反应将在很短的时间内达到。在 这之前,阻尼力还来不及从结构吸收较多的能量。鉴于此,仅 讨论冲击荷载下体系的无阻尼反应.
§5.5
震动或反应谱
高等结构动力学
图5-6 对于三种脉冲型式的位移反应谱(震动谱)
§5.5
震动或反应谱
高等结构动力学
这些反应谱也可用来求出结构对作用在它基底的加速度脉冲的反应。如果作 用于基底的加速度为 ,则它所引起的等效冲击荷载为 [参看方程 (2-17)]。若以 代表最大基底加速度,则最大等效冲击荷载为 。 此时动力放大系数为 (5-16)
其中 为质量的最大总加速度。这是根据在无阻尼体系里,质量与加速度乘 积的大小必然等于弹性恢复力 得到的。
§5.5
震动或反应谱
高等结构动力学
通常仅对反应的绝对值大小感兴趣.上式可以改写为
(5-17)
因此,像用来估计冲击荷载下的最大位移反应一样,图5-6的反应谱曲线,显 然也同样可以用来估计质量m在基底承受加速度脉冲时的最大加速度反应, 当用于这种目的时,此曲线通常称作震动谱。
§5.2
正弦波脉冲
高等结构动力学
(5-5*)
根据方程(2-37),这个自由振动运动的幅值为 (5-6*)
因此,这种情况下的放大系数为: 当β>1,t>t1时
§5.3
矩形脉冲
高等结构动力学
§5.3
矩形脉冲
讨论图5-4所示的矩形脉冲。反应再次分为加荷阶段和接着 发生的自由振动阶段。
图5-4 矩形脉冲
图5-1 任意冲击荷载
§5.1 冲击荷载的一般性质
高等结构动力学
冲击荷载的特点
1、持续时间很短,结构的最大反应将在很短的时间 内达到; 2、在控制结构的最大反应中,阻尼就显得不太重要 了。
§5.2
正弦波脉冲
高等结构动力学
§5.2
正弦波脉冲
对可用简单解析函数表达的冲击荷载来说,可以得到运动 方程的闭合解。 讨论一下图5-2所示的正弦波脉冲。 反应可分为两个阶段:第一阶段荷载作用期间内的反应,
§5.2
正弦波脉冲
高等结构动力学
冲击荷载产生的动力反应,依赖于荷载持续时间与结构振动 周期的比; 对t1/T=3/4的反应比R(t)=v(t)/(p0/k) 示于图5-3*。 P(t)/k曲线,其峰值等于1(与反应比具有相同的比例尺).
图5-3* 由正弦脉冲引起的反应比(t1=3/4T)
§5.2
阶段Ⅱ 计算阶段Ⅰ结束时(t=t1)的方程(5-12*)及其一阶导数的值,得 到
(5-13*)
再将上式代人方程(5-2*),则可获得阶段Ⅱ 的自由振动反应。
§5.4
三角形脉冲
高等结构动力学
这些反应函数的最大值,如在其他情况一样,可用在速度为零这个条件下的 时间值来计算。对于持续时间很短的加荷情况(t1/T<0.4),最大反应在阶 段Ⅱ的自由振动期间出现;否则,最大反应在加荷阶段内出现(阶段Ⅰ)。 不同加荷持续时间的动力放大系数D=vmax/(p0/k)的值,示于表5-1。 表5-1 三角形冲击荷载作用下的动力放大系数
大系数为2;而缓慢地逐渐增加的荷载,其动力放
大系数为1 。
§5.6 冲击荷载反应的近似分析
高等结构动力学
(2)对于持续时间短的荷载,例如t1/T <1/4,最 大位移幅值 max 主要依赖于作用冲量 I 0 p(t )dt 的 大小, 而脉冲荷载的形式对它影响不大。但是,动
