天津市十二区县重点高中高三毕业班联考(一)

合集下载

2023年天津市十二区重点学校高三毕业班联考(一)答案

2023年天津市十二区重点学校高三毕业班联考（一）数学参考答案一、选择题:每小题5分，满分45分二、填空题:每小题5分，共30分.（两空中对一个得3分，对两个得5分）10.5511.-27012.()4122=+-y x 13.792；14.2515.8384-=-<<-a a 或三、解答题：本大题5小题，共75分．解答应写出文字说明，证明过程或演算步骤．（1）解:因为,所以,…………2分所以,因为,所以,所以,…………4分又,所以;…………5分（2）在△ABC 中，由余弦定理及a=2，c=3，B=π3，有22227b a c accosB =+-=，故．…………8分由正弦定理，可得sinA =a<c ，故cosA =…………10分因此22sin A sinAcosA ==，212217cos A cos A =-=．…………12分所以，()222sin A B sin AcosB cos AsinB -=-=1127-=…………14分17.（本小题满分15分）（1）方法一分别取,AB CD 的中点,G H ，连接,,EG GH FH ，……………1分由题意可知：点E ､F 分别为线段PB ､CQ 的中点.所以//,//EG PA FH QD ，因为PA DQ ∥，所以//EG FH ，所以点,,,E G H F 四点共面，因为,G H 分别为,AB CD 的中点，所以//GH AD ，AD ⊂平面ADQP ，GH ⊄平面ADQP ，所以//GH 平面ADQP ，……………3分题号123456789答案C A C D B A B D D又因为//FH QD ，QD ⊂平面ADQP ，FH ⊄平面ADQP ，所以//FH 平面ADQP ，……………4分又因为FH GH H = ，,FH GH ⊂平面EGHF ，所以平面//EGHF 平面ADQP ，因为EF ⊂平面EGHF，所以//EF 平面ADQP .……………5分方法二因为ABCD 为正方形，且PA ⊥平面ABCD ，所以,,AP AB AD 两两互相垂直，建立如图所示空间直角坐标系，……………1分则(0,0,3)P ，，(0,3,1)Q ，，,……………3分（建系和对一个点的坐标就给1分，全对给2分，没有出现点的坐标扣1分）所以，，，易知平面PADQ 的一个法向量)0,0,1(=a ，所以，所以，……………4分又因为平面ADQP ,所以//EF 平面ADQP .……………5分（2）设平面PCQ 的法向量(,,)m x y z =，则·0·0PC m CQ m ⎧=⎪⎨=⎪⎩，即，令1x =，则，所以平面PCQ 的一个法向量为)3,2,1(=m ，……………6分易知平面CQD 的一个法向量(0,1,0)n =，设平面PCQ 与平面CQD 夹角为θ，则，所以平面PCQ 与平面CQD夹角余弦值为……………8分（设角和作答具备其一即可，均不写扣1分）(3)假设存在点M ，，[]0,1λ∈，设(),,M x y z ，所以， (9)分所以所以……………10分由（2）得平面PCQ 的一个法向量为)3,2,1(=m ，∴，……………12分得.即，……………13分∴或，……………14分∴或.……………15分18.（本小题满分15分）（1）由直角三角形面积关系得22241c b b bc +⨯⨯=，即a b bc ⨯⨯=241解得21=a c ...........................3分（2）由（1）得c b c a 3,2==，易得)3,0(),3,0(c B c A -，直线l 的方程为c kx y 3-=,因为直线l 不过右顶点)0,2(c ，所以23≠k ，..................4分⎪⎩⎪⎨⎧-==+ckx y c y c x 31342222，得038)43(22=-+kcx x k ，24338k kc x N+=∴..................6分从而)0,3(433334,4338(222kc P k c c k k kc N ，+-+..................8分直线AN 的斜率为k kcc k kc c k cc k 43383643383433334222-=-=+-+-................9分故直线AN 的方程为c x ky 343+-=..................10分令c x 2=，得)323,2(c kcc Q +-，.................11分直线PQ 的斜率2332432332323=-+-=-+-=ckc kc c k c c ck ck PQ.................12分),3,0(c A 左顶点D ()0,2c -，23=AD k ，即14222=+=b a AD ，21=a c 解得2,6,8222===c b a .................14分∴椭圆的标准方程为16822=+y x .................15分19.（本小题满分15分）【详解】（1）因21=-+n n a a ，∴数列{}n a 是公差为d=2等差数列，且864S =，∴18782642a ⨯+⨯=，解得1=1a ，∴12(1)21n a n n =+-=-；....................2分设等比数列{}n b 的公比为q （0q >），因为13b =，3218b b -=，∴23318q q -=，即260q q --=，解得2q =-（舍去）或3q =，∴1333n n n b -=⨯=..................4分nn 31)1)(2n (2n 2)2(2b a a 1a c ）得1）由（2（n 1n n 2n n ⋅+--+=-=++.................5分()()()()122111212132213213n n n n n n n n -⎡⎤+==-⎢⎥-+⋅-⋅+⋅⎢⎥⎣⎦，....................6分0112231111111111[()()()()]2133333535373(21)3(21)3n nn n -=-+-+-+⋅⋅⋅+-⨯⨯⨯⨯⨯⨯-⋅+⋅0111()213(21)3n n =-⨯+⋅1122(21)3nn =-+⋅，.........................8分（3）⎪⎪⎩⎪⎪⎨⎧⋅-+=+为奇数为偶数n a n n n ,)1(,b 1a d 21n 2n2n )d d d d ()d d d d (S 1-2n 5312n 6422n +++++++++=∴ ................................9分])1(a a [b 1a b 1a b 1a b 1a [1-2n 531332211a a n nn ⋅-++-+-+++++++++= )]3-n 4()1(13951[]3n 2363432[321⋅-++-+-+++++=n n .......................10分n n Q P +=)2(3n 232-n 2363432 P 31)1(3n2 363432P 1432321++++++=∴++++=n n n n n 1111432133n 213n 2311 3n 2311)311(32 3n 23232323232 P 32:)2()1(+++++-=--=---=-+++++=-n n n n n n n n nn n 323n 223)33n 21(23P 1⋅+-=+-=∴+...................12分nn n n k k k k k k k kk n n k n n k n n k n a n n a n 323n 22333n 231n 2(3735(3533[(21)d d d d (P 12),3-k 4()1(k 2),33k 231k 2(2112),3-k 4()1(k 2,3k 212,)1(k 2,b 1a ,)1(,b 1a d 121102n 64211221n 2n 2n ⋅+-=+-+++-+-=++++=∴⎪⎩⎪⎨⎧-=⋅-=+-+=⎪⎩⎪⎨⎧-=⋅-==⎪⎩⎪⎨⎧-=⋅-=+=⎪⎪⎩⎪⎪⎨⎧⋅-+=---+ 为奇数为偶数方法二①])1(13951[Q 1-2n a n nn ⋅-++-+-= 为偶数时，当，n nn n 22*4444)]34()74([)139(5)1(==+++=-+--+++-++-= ....13分②12)34(21*4)34(444n +-=---=--+++=n n n n Q n 为奇数时，当...14分⎩⎨⎧+-=∴为偶数，为奇数，n n n n 212Q n ⎪⎪⎩⎪⎪⎨⎧++-+-+-=+=∴++为偶数，为奇数，n n n n n n n n 233n 21(231233n 21(23Q P S 112n .................................15分20.（本小题满分16分）解：(Ⅰ)2sin 2)(--=x e x f x，求导x e x f xcos 2)('-=，切线的斜率112)0('=-==f k ,又0)0(=f ，所以切点为)0,0(，所以，切线方程为xy =……………4分(Ⅱ)(ⅰ)求导x ae x f x cos )('-=，①当1≥a 时，当⎪⎭⎫⎝⎛∈2,0πx 时，1>x ae ，()1,0cos ∈x ，∴0)('>x f ，则)(x f y =在⎪⎭⎫⎝⎛2,0π上单调递增，没有极值点，不合题意，舍去；……………6分②当10<<a 时，求二阶导0sin )(''>+=x ae x f x ，所以)('x f 在⎪⎭⎫⎝⎛2,0π上递增，又01)0('<-=a f ，02'2>=⎪⎭⎫⎝⎛ππae f ，所以)('x f 在⎪⎭⎫ ⎝⎛2,0π上有唯一零点1x ，………………8分当()1,0x x ∈时，0)('<x f ，函数)(x f 单调递减；当⎪⎭⎫⎝⎛∈2,1πx x 时，0)('>x f ，函数)(x f 单调递增，所以函数)(x f y =在区间⎪⎭⎫⎝⎛2,0π内有唯一极值点，符合题意，综上，a 的取值范围是)10(，………………9分(ⅱ)由(ⅰ)知10<<a ，当⎪⎭⎫⎢⎣⎡∈ππ,2x 时，0cos )('>-=x ae x f x ，…………10分当()1,0x x ∈时，0)('<x f ，函数)(x f 单调递减；当()π,1x x ∈时，0)('>x f ，函数)(x f 单调递增；所以()1,0x x ∈时，0)0()(=<f x f ，则0)(1<x f ，又因为()01)(>-=-=πππe a a ae f ，所以)(x f 在()π,1x 上有唯一零点0x ，即)(x f 在()π,0上有唯一零点0x …………………12分因为a x aex f x --=1212sin )2(1，由(ⅰ)知0)('1=x f ，所以1cos 1x ae x=，则1111111121cos cos sin 2cos 2sin )2(x x x e x x x x e a x aex f --=--=⎪⎭⎫ ⎝⎛∈--=2,0),1sin 2(cos 11111πx e x e x x x ，………………13分设x x e x e x h ---=sin 2)(，⎪⎭⎫⎝⎛∈2,0πx ，则x x e x e x h -+-=cos 2)('，∵2>+-x x e e ，2cos 2<x ，所以0cos 2)('>-+=-x e e x h x x)(x h 在⎪⎭⎫⎝⎛2,0π为单调递增，又0)0(=h ，所以0)(>x h ，又⎪⎭⎫ ⎝⎛∈2,0πx 时，0cos 1>x ，所以01sin 2(cos )2(11111>--=x x e x e x x f .所以0)()2(01=>x f x f .由前面讨论知ππ<<<<0111,2x x x x ，)(x f 在()π,1x 单调递增，所以102x x <.……………16分。

2024届天津市十二区县重点校高三下学期第一次模拟考试生物试题(解析版)

D、植物细胞培养：指在离体条件下对单个植物细胞或细胞团进行培养使其增殖的技术，原理为细胞增殖，D正确。
故选B。
7.下图表示某生物的1个初级精母细胞经过减数分裂形成4个精细胞的过程。该过程中，不会发生的是（）
A.DNA分子结构改变
B.核DNA数目增加
C.非等位基因的重新组合
D.染色单体消失
【答案】B
【解析】
【详解】A．RNA与合成有关的酶即RNA聚合酶，其在细胞质中的核糖体上合成，而后通过核孔进入细胞核，不存在膜流现象，A错误；
B．真核细胞中含有细胞膜、细胞器膜和核膜等多种生物膜，普遍存在“膜流”现象；而大肠杆菌属于原核细胞，只有细胞膜一种生物膜，不存在“膜流”现象，B错误；
C．乙酰胆碱属于神经递质，由囊泡运输，囊泡的膜和细胞膜融合，以胞吐的方式把神经递质运输到突触间隙，存在“膜流”现象，质壁分离和吞噬细胞摄取抗原不存在膜结构间的相互转移，不存在膜流现象，C错误；
C.乙酰胆碱释放、质壁分离和吞噬细胞摄取抗原都体现“膜流”现象
D.唾液淀粉酶的合成与分泌过程中，高尔基体作为“膜流”的枢纽
【答案】D
【解析】
【分析】分泌蛋白的合成与分泌过程：附着在内质网上的核糖体合成蛋白质→内质网进行粗加工→内质网“出芽”形成囊泡→高尔基体进行再加工形成成熟的蛋白质→高尔基体“出芽”形成囊泡→细胞膜。
阅读下列材料，回答下列小题：
乳酸菌在乳中生长发酵乳糖产生乳酸.其产酸力是乳酸菌的重要特性。研究表明产酸力与菌株的β-半乳糖苷酶的活性相关，该酶基因位于质粒上，乳糖代谢由质粒控制。通过诱变可以获得乳糖代谢障碍突变体。突变的部位和数量影响对乳糖的利用能力。研究人员以B-3为出发菌株采用紫外线或亚硝基胍进行诱变选育获得高产酸的乳酸菌。

2024届天津市十二区县重点学校一模模拟考试数学试卷(解析版)

2024年天津市十二区县重点学校高三毕业班联考（一）模拟考数学本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟.第Ⅰ卷1至3页，第Ⅱ卷4至6页.答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上，并在规定位置粘贴考试用条形码.答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效.考试结束后，将本试卷和答题卡一并交回.祝各位考生考试顺利！第Ⅰ卷注意事项：1．每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.2．本卷共9小题，每小题5分，共45分.一．选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合{}{}12,03A x x B x x =∈-≤<=∈≤<Z N ，则A B = （）A.{}1,0,1,2-B.{}0,1,2C.{}0,1 D.{}1,2【答案】C 【解析】【分析】化简集合，结合交集的概念即可得解.【详解】由题意{}{}{}{}121,0,1,030,1,2A x x B x x =∈-≤<=-=∈≤<=Z N ，所以{}0,1A B = .故选：C.2.“01x ≤≤”是“11x≥”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】对11x≥可得01x <≤，然后根据充分条件和必要条件的定义判断即可.【详解】由11x ≥，则110x -≥，即10xx -≥，即()100x x x ⎧-≥⎨≠⎩，解得得01x <≤，则01x ≤≤不能推出11x ≥，11x≥能推出01x ≤≤，则“01x ≤≤”是“11x≥”的必要不充分条件.故选：B.3.已知函数()32xf x x =+，若()23321log 2,2,log 3a f b f c f ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，则（）A.a b c <<B.a c b <<C.c b a <<D.c a b<<【答案】D 【解析】【分析】判断出函数的单调性，再结合指数函数以及对数函数的单调性得出233212log 2log 3>>，利用函数的单调性即可得答案.【详解】由于函数32,x y y x ==在R 上均为增函数，故()32xf x x =+在R 上单调递增，由于32023210log 21,2,log log 10321><<<==，故233212log 2log 3>>，故()23231log log 223f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭，即c a b <<，故选：D4.下列结论中，错误的是（）A.数据4，1，6，2，9，5，8的第60百分位数为6B.若随机变量()()21,,20.21N P ξσξ~≤-=，则()40.79P ξ≤=C.已知经验回归方程为 1.8y bx=+ ，且2,20x y ==，则9.1b = D.根据分类变量X 与Y 成对样本数据，计算得到29.632χ=，依据小概率值0.001α=的2χ独立性检验()0.00110.828x =，可判断X 与Y 有关联，此推断犯错误的概率不大于0.001【答案】D 【解析】【分析】A 选项，将数据排序后，根据百分位数的定义得到答案；B 选项，由正态分布的对称性得到答案；C 选项，将样本中心点代入回归方程，求出9.1b= ；D 选项，由29.63210.828χ=<得到D 错误.【详解】A 选项，数据4，1，6，2，9，5，8排序后得到1，2，4，5，6，8，9，00760 4.2⨯=，故选取第5个数据作为第60百分位数，即为6，A 正确；B 选项，因为()21,N ξσ，根据对称性可知()()420.21P P ξξ≥=≤-=，故()410.210.79P ξ≤=-=，B 正确；C 选项，已知经验回归方程为 1.8y bx =+ ，且2,20x y ==，则2 1.820b += ，解得9.1b= ，C 正确；D 选项，29.63210.828χ=<，故不能得到此结论，D 错误故选：D5.如图是()y f x =的大致图象，则()f x 的解析式可能为（）A.2()sin f x x x =- B.()|sin |f x x x =-C.()21xf x =- D.21()4f x x x =--【答案】A 【解析】【分析】数形结合和导数分析A 选项函数图像特征，根据(0)0f =，奇偶性，单调性，利用排除法选出正确答案.【详解】对于A 选项2()sin f x x x =-，研究2sin ,y x y x ==的图像可知2()sin f x x x =-与x 轴有两个交点,且一点为坐标原点,另一个点横坐标为正，其他函数都不具备这样的特点.另外因为2sin y x x =-时2cos ,2sin 0y x x y x '''=-=+>所以2cos ,y x x '=-为R 上的增函数，0π2|10,|π>0x x y y ==''=-<=所以2sin y x x =-在R 上在某一个值左侧为减函数，右侧为增函数，结合零点和绝对值对图像的影响可判断A 正确.根据(0)0f =排除D 选项，B 选项根据()()sin sin sin f x x x x x x x-=---=-+=-对于x ∈R 都成立可以判断B 为偶函数，与所给图像不符，所以B 不正确.C 选项根据当0x >时()21xf x =-，为()0,∞+上得增函数与所给图像不符，所以C 不正确.故选：A6.如图，实心正方体1111ABCD A B C D -的棱长为2，其中上、下底面的中心分别为,Q R ．若从该正方体中挖去两个圆锥，且其中一个圆锥以R 为顶点，以正方形1111D C B A 的内切圆为底面，另一个圆锥以Q 为顶点，以正方形ABCD 的内切圆为底面，则该正方体剩余部分的体积为（）A.5π848-B.7π848-C.25π824-D.7π86-【答案】D 【解析】【分析】计算出正方体体积、两圆锥的体积及其公共部分的体积即可得.【详解】两圆锥的体积都为221112ππ12π333V r h ==⨯⨯⨯=，则其公共部分为2211π2π1326V ⎛⎫=⨯⨯⨯⨯= ⎪⎝⎭，故该正方体剩余部分的体积为3124ππ7π2288366V V V =-⨯+=-+=-.故选：D .7.回文联是我国对联中的一种．用回文形式写成的对联，既可顺读，也可倒读．不仅意思不变，而且颇具趣味．相传，清代北京城里有一家饭馆叫“天然居”，曾有一副有名的回文联：“客上天然居，居然天上客；人过大佛寺，寺佛大过人．”在数学中也有这样一类顺读与倒读都是同一个数的自然数，称之为“回文数”．如44，585，2662等；那么用数字1，2，3，4，5，6可以组成4位“回文数”的个数为（）A.30B.36C.360D.1296【答案】B 【解析】【分析】依据回文数对称的特征，可知有两种情况：在6个数字中任取1个，在6个数字中任取2个排列，由分类计数原理可得结果.【详解】由题意知：组成4位“回文数”，由对称性可知，只需确定后两位数字即可.可分为以下两种情况：当后两位数字重复时，即由一个数组成回文数，在6个数字中任取1个，则有16C 种；当后两位数字不同时，在6个数字中任取2个，按不同顺序排列，有26A 种.综上，用数字1，2，3，4，5，6可以组成4位“回文数”的个数为：6261C 36A =+.故选：B.8.已知函数()()sin f x A x B ωϕ=++（其中0,0,πA ωϕ>><）的部分图象如图所示，有以下结论：①()11π6f x f ⎛⎫≤⎪⎝⎭②函数π6f x ⎛⎫+⎪⎝⎭为偶函数③()π26f x f x ⎛⎫+-=⎪⎝⎭④()f x 在4π11π,36⎡⎤⎢⎥⎣⎦上单调递增所有正确结论的序号是（）A.①②B.①③④C.③④D.①④【答案】B 【解析】【分析】借助图象可得()f x 解析式，结合正弦函数的单调性、最值、奇偶性等逐项判断即可得.【详解】由图可得2012A +==，2012B -==，且0ω>，则2πππ2π36T ω⎛⎫==⨯+= ⎪⎝⎭，即2ω=，π3π22π,32k k ϕ⨯+=+∈Z ，即5π2π,6k k ϕ=+∈Z ，又π<ϕ，故5π6ϕ=，即()5sin 2π16f x x ⎛⎫=++ ⎪⎝⎭，对①：11π5π27π9π2π4π66622⨯+===+，由π2x =时，函数sin y x =取最大值，故11π6f ⎛⎫⎪⎝⎭是函数()f x 的最大值，故①正确；对②：ππ57sin 2π1sin 2π16366f x x x ⎛⎫⎛⎫⎛⎫+=+++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故②错误；对③：ππ575sin 2π1sin 2π1sin 2π163666f x x x x ⎛⎫⎛⎫⎛⎫⎛⎫-=-++=-++=-++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，则()π55sin 2π1sin 2π12666f x f x x x ⎛⎫⎛⎫⎛⎫+-=++-++= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭，故③正确；对④：当4π11π,36x ⎡⎤∈⎢⎥⎣⎦时，5π7π9πππ2,4π,4π62222x ⎡⎤⎡⎤+∈=-+⎢⎥⎢⎥⎣⎦⎣⎦，由函数sin y x =在ππ4π,4π22⎡⎤-+⎢⎥⎣⎦上单调递增，故函数()f x 在4π11π,36⎡⎤⎢⎥⎣⎦上单调递增，故④正确.故选：B.9.过双曲线()2222:10,0x y C a b a b -=>>的左焦点F 作圆222x y a +=的切线，切点为A ，直线FA 交直线0bx ay -=于点B ．若3BA AF =，则双曲线C 的离心率为（）A.B.C.355D.263【答案】D 【解析】【分析】取右焦点2F ，连接AO 、2BF ，作2F M AB ⊥于点M ，由题意结合几何性质可得相应的边长及角度间的关系，借助余弦定理列出与a 、b 、c 有关齐次式，计算即可得.【详解】取右焦点2F ，连接AO 、2BF ，作2F M AB ⊥于点M ，由FA 为圆222x y a +=的切线，故FA AO ⊥，又2F M AB ⊥，O 为2FF 中点，故A 为MF 中点，又3BA AF =，故M 为FB 中点，AF b ===，则2FM BM b ==，222F M OA a ==，则22BF c ==，OB ==0bx ay -=为双曲线的渐近线，故有2tan b BOF a∠=，则2cos a BOF c ∠=，在2BOF 中，由余弦定理可得22222cos a BOF c ∠==，则222293a b c =+-，即224b c =-，即()()()222222284c b cb bc -+=-，化简得2285b c =，即222885c a c -=，故263c e a ===.故选：D.【点睛】关键点点睛：本题考查双曲线离心率的求法，关键点在于借助题目所给条件，从几何的角度构造辅助线，得到新的长度关系与角度关系，从而结合题意构造相应与a 、b 、c 有关齐次式，得到离心率.第Ⅱ卷二．填空题：本大题共6小题，每小题5分，共30分．试题中包含两个空的，答对1个的给3分，全部答对的给5分．10.i 是虚数单位，则()32ii ,1ia b a b -=+∈+R ，则a b +的值为________．【答案】2-【解析】【分析】根据复数的乘法法则化简得到()i 32i b a b a ++=--，求出2a b +=-.【详解】由题意得()()i 1i 32i a b ++=-，即2i i i 32i b b a a ++=-+，()i 32i b a b a ++=--，故32a b a b -=⎧⎨+=-⎩，故答案为：2-11.设nx x ⎛ ⎝的展开式的二项式系数和为64，则展开式中常数项为_________.【答案】15【解析】【详解】试题分析：由二项式系数的性质，可得264n =，解可得，6n =；6x x ⎛ ⎝的展开式为()()16621661C 1C rr r r r r r r T x x x ---+⎛=⋅⋅=-⋅⋅ ⎝，令1602r r --=，可得4r =，则展开式中常数项为15．故答案为：15.12.已知抛物线()220x py p =->的焦点为F ，以点F 为圆心的圆与直线230x y -+=相切于点()2,1A --，则p =__________.【答案】4【解析】【分析】由题意可得直线AF 与直线230x y -+=垂直，进而可得出答案.【详解】0,2p F ⎛⎫-⎪⎝⎭，因为以点F 为圆心的圆与直线230x y -+=相切于点()2,1A --，所以直线AF与直线230x y -+=垂直，则()()122102p---⨯=---，解得4p =.故答案为：4.13.天津相声文化是天津具有代表性的地域文化符号，天津话妙趣横生，天津相声精彩纷呈，是最具特色的旅游亮点之一.某位北京游客经常来天津听相声，每次从北京出发来天津乘坐高铁和大巴的概率分别为0.6和0.4，高铁和大巴准点到达的概率分别为0.9和0.8，则他准点到达天津的概率是_________（分数作答）.若他已准点抵达天津，则此次来天津乘坐高铁准点到达比乘坐大巴准点到达的概率高__________（分数作答）.【答案】①.4350②.1143【解析】【分析】根据互斥事件的概率公式，求得他准点到达天津的概率，再结合条件概率的计算公式，即可求解.【详解】设事件A 为他准点到达天津，事件B 为他乘坐高铁到达天津，事件C 为他乘坐大巴到达天津，若他乘坐高铁，且正点到达天津的概率为()0.60.90.54P AB =⨯=；若他乘坐大巴，且正点到达天津的概率为()0.40.80.32P AC =⨯=；则()430.540.320.8650P A =+==，且()()()()0.54270.3216(|),(|)0.86430.8643P AB P AC P B A P C A P A P A ======,所以乘坐高铁准点到达比乘坐大巴准点到达的概率高271611434343-=.故答案为：4350，114314.在ABC 中，2,1,60AC BC C ==∠=︒，则CA CB +=______；若点P 为ABC 所在平面内的动点，且满足73PC =，则PA PB ⋅ 的取值范围是______．【答案】①.②.537,99⎡⎤-⎢⎥⎣⎦【解析】【分析】借助模长与数量积的关系即可得CA CB +，取AB 中点D ，借助向量的线性运算可得22PA PB PC PC CD CA CB ⋅=+⋅+⋅，逐项计算即可得其取值范围.【详解】2222cos 14122172CA CB CA CB CA CB C ++=∠=⨯++⨯=⋅+⨯ ，故CA CB +=，()()()2PA PB PC CA PC CB PC PC CA CB CA CB⋅=+⋅+=+⋅++⋅ ()()2121132769PC CA CB PC CA CB⎛⎫=+⋅+=+⋅+ ⎪⨯⨯+ ⎪⎝⎭，取AB 中点D ，则()22cos ,PC CA CB PC CD PC CD PC CD ⋅+=⋅=，2C D ==，[]cos ,1,1PC CD ∈- ，故()7772cos ,cos ,,333PC CA CB PC CD CD PC CD ⎡⎤⋅+==-⎢⎥⎣⎦，故537,99PA PB ⎡⎤⋅∈-⎢⎥⎣⎦.；537,99⎡⎤-⎢⎥⎣⎦.15.若函数()22441,33441,33x ax a x f x x ax a x ⎧-++≥⎪⎪=⎨⎪+-+<⎪⎩恰有两个不同的零点,m n ，且m n <，则n 的取值范围为______．【答案】1,13⎛⎫- ⎪⎝⎭【解析】【分析】借助换元法，设43t x =-，可得()224441,03334441,0333t a t a t f x t a t a t ⎧⎛⎫⎛⎫+-+++≥⎪ ⎪ ⎪⎪⎝⎭⎝⎭=⎨⎛⎫⎛⎫⎪+++-+< ⎪ ⎪⎪⎝⎭⎝⎭⎩，令()0f x =可得258,093258,093t t t a t t t ⎧++≥⎪⎪=⎨⎪---<⎪⎩，再令()258,093258,093t t t g t t t t ⎧++≥⎪⎪=⎨⎪---<⎪⎩，借助对勾函数性质即可得()g t 的单调性及其值域，若()g t a =恰有两个不同的实数根1t 、2t ，可得122551333t t -<<-<<-，即可得n 的取值范围.【详解】设43t x =-，则43x t =+，则()224441,03334441,0333t a t a t f x t a t a t ⎧⎛⎫⎛⎫+-+++≥⎪ ⎪ ⎪⎪⎝⎭⎝⎭=⎨⎛⎫⎛⎫⎪+++-+< ⎪ ⎪⎪⎝⎭⎝⎭⎩，令()0f x =，显然4,03x t ≠≠,则有258,093258,093t t t a t t t ⎧++>⎪⎪=⎨⎪---<⎪⎩，令()258,093258,093t t t g t t t t ⎧++>⎪⎪=⎨⎪---<⎪⎩，由对勾函数性质可知，当0t >时，()g t 在50,3⎛⎫ ⎪⎝⎭上单调递减，在5,3∞⎛⎫+ ⎪⎝⎭上单调递增，当0t <时，()g t 在5,3∞⎛⎫-- ⎪⎝⎭上单调递减，在5,03⎛⎫- ⎪⎝⎭上单调递增，又552586533393g ⎛⎫=++= ⎪⎝⎭⨯，5525825333393g ⎛⎫⎛⎫-=----= ⎪ ⎪⎛⎫⎝⎭⎝⎭⨯- ⎪⎝⎭，若()g t a =恰有两个不同的实数根1t 、2t ，且12t t <，则2,63a ⎛⎫∈⎪⎝⎭，令258693t t ---=，解得253t =-或13t =-，故122551333t t -<<-<<-，即有25454133333m n -<-<-<-<-，故113n -<<.故答案为：1,13⎛⎫- ⎪⎝⎭.【点睛】关键点点睛：本题关键点在与使用换元法及参变分离的方式，得到258,093258,093t t t a t t t ⎧++≥⎪⎪=⎨⎪---<⎪⎩，再设出函数()258,093258,093t t t g t t t t ⎧++≥⎪⎪=⎨⎪---<⎪⎩，结合对勾函数的性质得到()g t 的性质，从而借助()g t 的性质研究()g t a =的解的个数，即可得到n 的取值范围.三．解答题：本大题共5小题，共75分．解答应写出文字说明，证明过程或演算步骤．16.在ABC 中，角,,A B C 所对的边分别为,,a b c ，已知ABC 的面积为315，12,cos 4b c A -==-．（1）求a 和sin C 的值；（2）求πcos 23C ⎛⎫+⎪⎝⎭的值．【答案】（1）8a =，15sin 8C =（2）1721564-【解析】【分析】（1）结合面积公式、余弦定理与正弦定理计算即可得；（2）借助二倍角及两角和的余弦公式计算即可得.【小问1详解】在ABC 中，由1cos 4A =-，故A 为钝角，sin 4A ==，ABC的面积为，可得1sin 2bc A =11524bc ⨯=，则24bc =，联立2b c -=，解得6,4b c ==，由22212cos 3616264644a b c bc A ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭，可得8a =，由正弦定理得sin sin a c A C =4sin 154C =，解得15sin 8C =；【小问2详解】sin 8C = 且C 为锐角，7cos 8C ∴==，217sin22sin cos ,cos212sin 3232C C C C C ∴=⋅=∴=-=，πππ171715317215cos 2cos2cos sin2sin 33332232264C C C -⎛⎫+=-=⨯-⨯=⎪⎝⎭．17.如图，//AD BC 且2AD BC =，,//AD CD EG AD ⊥且,//EG AD CD FG =且2,CD FG DG =⊥平面,2ABCD DA DC DG ===．（1）若M 为CF 的中点，N 为EG 的中点，求证：//MN 平面CDE ；（2）求平面EBC 与平面FBC 夹角的余弦值；（3）若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60︒，求线段DP 的长．【答案】（1）证明见解析（2）10（3）33【解析】【分析】（1）利用空间向量的方法证明线面平行；（2）根据二面角的定义得到GCF ∠为平面EBC 与平面FBC 的夹角或其补角，然后求余弦值；（3）根据线面角的定义得到OPB ∠为直线BP 与平面ADGE 所成角，然后根据60OPB ∠=︒求线段DP .【小问1详解】如图，以D 为原点，分别以,,DA DC DG 为,,x y z 轴建立空间直角坐标系，()0,2,0C ，()0,0,0D ，()2,0,2E ，()1,0,2N ，30,,12M ⎛⎫ ⎪⎝⎭，31,,12MN ⎛⎫=- ⎪⎝⎭，()0,2,0DC = ，()2,0,2DE = ，设平面CDE 的法向量为()111,,m x y z =，则11120220m DC y m DE x z ⎧⋅==⎪⎨⋅=+=⎪⎩ ，令11x =，则10y =，11z =-，所以()1,0,1m =- ，因为110MN m ⋅=-=uuu r u r，而MN ⊄平面CDE ，所以MN ∥平面CDE .【小问2详解】连接GC ，过点F 作FH DC ⊥于点H ，因为EG AD ∥，AD BC ∥，所以EG BC ∥，则,,,E G C B 共面，因为DG ⊥平面ABCD ，AD ⊂平面ABCD ，所以DG AD ⊥，因为AD CD ⊥，CD DG D =I ，,CD DG ⊂平面CDGF ，所以AD ⊥平面CDGF ，因为AD BC ∥，所以BC ⊥平面CDGF ，因为CF ⊂平面CDGF ，所以BC CF ⊥，因为平面EBC ⋂平面FBC BC =，GC ⊂平面EBC ，FC ⊂平面FBC ，所以GCF ∠为平面EBC 与平面FBC 的夹角或其补角，GC ==1CH =，1GF =，CF ==所以222310cos210GC CF GF GCF GC CF +-∠==⋅⋅，所以平面EBC 与平面FBC 夹角的余弦值为31010.【小问3详解】取AD 中点O ，连接OB ，OP ，因为O 为AD 中点，2AD BC =，AD BC ∥，AD CD ⊥，所以OB AD ⊥，因为DG ⊥平面ABCD ，OB ⊂平面ABCD ，所以OB DG ⊥，因为AD DG D = ，,AD DG ⊂平面ADGE ，所以OB ⊥平面ADGE ，所以OPB ∠为直线BP 与平面ADGE 所成角，1OD =，2OB =，60OPB ∠=︒，所以233OP =，33DP ==，所以线段DP 的长为33.18.已知椭圆()222210x y a b a b +=>>的右顶点为A ，下顶点为B ，椭圆的离心率为53，且AB =（1）求椭圆的方程；（2）已知点M 在椭圆上（M 异于椭圆的顶点），点P 满足6OP OA =（O 为坐标原点），直线BM 与以P 为圆心的圆相切于点Q ，且Q 为BM 中点，求直线BM 斜率．【答案】（1）22194x y +=（2）2或29.【解析】【分析】（1）根据题意列出关于,,a b c 的方程组，求出,,a b c ，从而可求出椭圆的方程；（2）根据题意设直线BM 为2y kx =-，代入椭圆方程化简求出点M 的横坐标，再由Q 为BM 中点，可表示出点Q 的坐标，由6OP OA =求出点P 的坐标，再由直线BM 与以P 为圆心的圆相切于点Q ，可得1PQ BM k k =-⋅可求出k 的值.【小问1详解】由题意得2223AB c e a a b c ⎧==⎪⎪==⎨⎪=+⎪⎩，解得2229,4,5a b c ===，所以椭圆的方程为22194x y +=；【小问2详解】因为椭圆的右顶点为A ，下顶点为B ，所以(3,0),(0,2)A B -，因为点M 在椭圆上（M 异于椭圆的顶点），所以直线BM 的斜率存在且不为零，所以设直线BM 为2y kx =-，由221942x y y kx ⎧+=⎪⎨⎪=-⎩，得22(49)360k x kx +-=，因为0B x =，所以23649M kx k =+，因为Q 为BM 中点，所以21849Q kx k =+，所以222188224949Q Q k y kx k k-=-=-=++，所以22188,4949k Q k k -⎛⎫ ⎪++⎝⎭，因为(3,0)A ，6OP OA =，所以1,02P ⎛⎫⎪⎝⎭，因为直线BM 与以P 为圆心的圆相切于点Q ，所以1PQ BM k k =-⋅，即2280491181492k k k k --+⋅=--+，整理得292040k k -+=，解得2k =或29k =，所以直线BM 斜率为2或29.【点睛】关键点点睛：此题考查椭圆方程的求法，考查直线与椭圆的位置关系，解题的关键是设出直线BM 的方程，代入椭圆方程可表示出M 的坐标，从而可表示出点Q 的坐标，再结合圆的知识列方程可求得结果，考查计算能力，属于中档题.19.记n S 是等差数列{}n a 的前n 项和，数列{}n b 是等比数列，且满足245,24a S ==，21531,1b a b S =-=+．（1）求数列{}n a 和{}n b 的通项公式；（2）设数列{}n c 满足()()()*1111,32n n n n c c c S n b n ++=+=-∈N ，（ⅰ）求{}n c 的前21n +项的和21n T +；（ⅱ）求()211n k kk k a bc +=+∑.【答案】（1）21n a n =+，12n n b -=（2）2+12121+1n n T n +=-；()()2+1221112+1412n n k k n k k n a b c n +=++++=∑【解析】【分析】（1）借助等差数列与等比数列基本量计算即可得；（2）借助并项求和法可得21n T +，借助分组求和法与错位相减法可得()211n k kk k a bc +=+∑.【小问1详解】设等差数列{}n a 的公差为d ，等比数列{}n b 的公比为q ，由题知：1154624a d a d +=⎧⎨+=⎩，解得132a d =⎧⎨=⎩，()31221n a n n ∴=+-⋅=+，32153212,116b a b S b q ∴=-==+==⋅，所以12,1q b ==，12n n b -∴=；【小问2详解】（ⅰ）()()112,22n n n n a a nb S n n ++===+，()()()12322nn n c c n n n +∴+⋅+=-⋅，()()213222222n n nn n n c c n n n n++-⋅+==-++，则()()()123211234522121n n n n T c c c c c c c c c c c +++=+++=+++++++ 2222+422+421622422**********+12221464n n n n n n n n +-=-+=+-+-++=-++ ；（ⅱ）()212121111n n n k kk k k k k k k a bc a b c +++===+=+∑∑∑，()1212k k k a b k -⋅=+，则()211202111212213252432n n n n k kk a a b a b a bn b ++=+⨯=+++=⨯++++⋅∑ ，则()211221132524232n n k kk a bn ++==⨯+⨯+++∑ ，故()121212213222222432n n k kn k a bn +=+-⋅=+⨯+⨯+⨯-+∑ ()()()221214123432141212n n n n n ++-=+-+⋅=--+-，故()111221412n k kk n a n b ++==++∑，又2+12121121+1n n k n k c T n ++===-∑，故()()()22+12+1211121221+1+14121412n n n k kk k n n a bc n n n n ++=++=-=+++++∑.【点睛】关键点点睛：本题考查数列的求和方法，关键点在于求取21n T +时，由题目所给1n n c c ++，通过并项，将12321n c c c c ++++ 分解为()()()12345221n n c c c c c c c ++++++++ .20.已知函数()()()2ln 1,sin f x a x x x x g x x =-++=．（1）当1a =时，求曲线()y f x =在点()()1,1f 处的切线方程；（2）当0,0a x =>时，若在()g x 的图象上有一点列()**11,1,2,3,,,,22i i i A g i n i n ⎛⎫⎛⎫=⋅⋅⋅∈∈ ⎪ ⎪⎝⎭⎝⎭N N ，若直线1i i A A +的斜率为()1,2,3,,i k i n =⋅⋅⋅，（ⅰ）求证：()()316g x f x x >-；（ⅱ）求证：119nii k n =>-∑．【答案】（1）210x y --=（2）（ⅰ）证明见解析；（ⅱ）证明见解析【解析】【分析】（1）借助导数的几何意义计算即可得；（2）（ⅰ）令()3sin 6x h x x x =-+，即证()0h x >在0x >时恒成立，借助导数，多次求导后即可得；（ⅱ）计算可得111112sin 2cos 122i i i i k +++⎛⎫=- ⎪⎝⎭，由（ⅰ）可得2cos 12x x >-，即可得12311cos 1022i i ++>->，借助放缩法可得1112211712sin 2cos 112262i i i i ++++⎛⎫->-⨯ ⎪⎝⎭，结合等比数列求和公式及放缩即可得证.【小问1详解】当1a =时，()2ln 1f x x x =+，()11f =，所以()2ln 2f x x =+'，曲线()y f x =在点()1,1处切线的斜率为()12f '=，所以切线方程为()121y x -=-，即210x y --=；【小问2详解】（ⅰ）要证()()316g x f x x >-，即证0x >时，3sin 6x x x >-，令()3sin 6x h x x x =-+，即证()0h x >在0x >时恒成立，因为()2cos 12x h x x =-+'，令()2cos 12x m x x =+-，则()sin m x x x =-+'，令()sin n x x x =-+，则()()1cos 0,n x x n x =-≥'在()0,∞+内单调递增，所以()sin000n x >-+=，即()()0,m x m x '>在()0,∞+内单调递增，所以()cos0010m x >+-=,即()()0,h x h x '>在()0,∞+内单调递增，所以()0sin0006h x >-+=，即得证；（ⅱ）*i ∈N 时，1111111122sin sin 1122222i i i i i i i ig g k ++++=⎛⎫⎛⎫- ⎪ ⎪⎛⎫⎝⎭⎝⎭=- ⎪⎝⎭-11111111111122sin cos sin 2sin 2cos 122222i i i i i i i +++++++⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭，由（ⅰ）知，()2cos 102x m x x =+->，即2cos 12x x >-，则12311cos 1022i i ++>->，所以111112311112sin2cos 12sin 2112222i i i i i i ++++++⎛⎫⎛⎫⎛⎫->-- ⎪ ⎪⎝⎭⎝⎭⎝⎭1112213322111112sin121222622i i i i i i i +++++++⎛⎫⎛⎫⎛⎫=->-- ⎪ ⎪⎪⋅⎝⎭⎝⎭⎝⎭2222224422117111711111622626262i i i i i +++++⎛⎫⎛⎫=--=-⨯+⨯>-⨯ ⎪⎪⋅⎝⎭⎝⎭，2246822111171111771111624162222661212414nn i n n i k n n n ++=-⋅⎛⎫⎛⎫>-++++=-⋅=-⨯-⨯ ⎪ ⎪⎝⎭⎝⎭-∑ 1771716172184721449n n n n n +=-+⨯>->-=-，即得证.【点睛】关键点点睛：本题最后一问关键点在于由（ⅰ）中得到2cos 12x x >-，从而得到12311cos 1022i i ++>->，从而借助放缩法，得到2271162i i k +>-⨯.。

2023届天津市十二区重点中学高三毕业班联考(一)数学试题含答案

2023年天津市十二区重点学校高三毕业班联考（一）数学试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分.考试时间120分钟.第Ⅰ卷选择题（共50分）注意事项：1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目填涂在答题卡规定位置上.2.第Ⅰ卷每小题选出答案后，用2B 铅笔在答题卡上对应的答案标号涂黑.参考公式：·如果事件A 、B 互斥，那么()()()P A B P A P B ⋃=+·柱体的体积公式V Sh =.其中S 表示柱体的底面积，h 表示柱体的高.一、选择题（在每小题四个选项中，只有一项是符合题目要求的，本大题共9小题，每小题5分，满分45分）1.设全集{}3,2,1,0,1,2,3U =---，集合{}3,2,2,3A =--，{}3,0,1,2B =-，则()U A B ⋂=ð（）A.∅B.{}1 C.{}0,1 D.{}0,1,22.设x ∈R ，则“2log 1x <”是“260x x +-<”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.函数()1cos f x x x x ⎛⎫=- ⎪⎝⎭在其定义域上的图像大致是（）A. B.C. D.4.某校1000名学生参加环保知识竞赛，随机抽取了20名学生的考试成绩（单位：分），成绩的频率分布直方图如图所示，则下列说法正确的是（）A.频率分布直方图中a 的值为0.004B.估计这20名学生考试成绩的第60百分位数为75C.估计这20名学生数学考试成绩的众数为80D.估计总体中成绩落在[)60,70内的学生人数为1505.已知()f x 是偶函数，且当0x >时，()f x 单调递减，设122a =-，0.812b -⎛⎫= ⎪⎝⎭，52log 2c =，则()f a ，()f b ，()f c 大小关系为（）A.()()()f c f b f a <<B.()()()f c f b f a >>C.()()()f c f a f b << D.()()()f c f a f b >>6.如图，几何体Ω为一个圆柱和圆锥的组合体，圆锥的底面和圆柱的一个底面重合，圆锥的顶点为A ，圆柱的上、下底面的圆心分别为B 、C，若该几何体Ω存在外接球（即圆锥的顶点与底面圆周在球面上，且圆柱的底面圆周也在球面上）.已知24BC AB ==，则该组合体的体积等于（）A.56πB.70π3C.48πD.64π7.由伦敦著名建筑事务所Steyn Studio 设计的南非双曲线大教堂惊讶世界，该建筑是数学与建筑完美结合造就的艺术品.若将如图所示的大教堂外形弧线的一段近似看成双曲线22214y x a -=（0a >）下支的一部分，以原点为圆心，双曲线虚半轴长为半径长的圆与双曲线的两条渐近线分別相交于A 、B 、C 、D 四点，四边形ABCD 的面积为2a ，则双曲线的方程为（）A.22194y x -= B.221124y x -= C.229124y x -= D.222194y x -=8.已知函数()2cos 2sin 2f x x x x =+-，以下说法中，正确的是（）①函数()f x 关于点π,012⎛⎫ ⎪⎝⎭对称；②函数()f x 在ππ,66⎡⎤-⎢⎥⎣⎦上单调递增；③当π2π,63x ⎛⎫∈ ⎪⎝⎭吋，()f x 的取值范围为()2,0-；④将函数()f x 的图象向右平移π12个单位长度，所得图象对应的解折式为()2sin21g x x =-.A.①②B.②③④C.①③D.②9.如图所示，梯形ABCD 中，AD BC ∥，点E 为AB 的中点，0BA BC ⋅=，4BD BA BD AD ⋅=⋅= ，若向量C E 在向量C B上的投影向提的模为4，设M 、N 分别为线段CD 、AD 上的动点，且CM CD λ= ，19AN AD λ=，则EM EN ⋅ 的取值范围是（）A.11,9⎡⎫+∞⎪⎢⎣⎭B.1113,99⎡⎤⎢⎥⎣⎦C.1361,99⎡⎤⎢⎥⎣⎦D.1161,99⎡⎤⎢⎥⎣⎦第非选择题（共105分）二、填空题（本大题共6小题，每小题5分，共30分.把答案填在答题卡中的相应横线上）10.设复数z 满足()34i 12i z +=-（i 为虚数单位），则z 的值为______.11.二项式323x x ⎛⎫- ⎪⎝⎭的展开式中含x 的系数为______.12.已知圆经过点()3,0和点()1,2-，圆心在直线210x y +-=上，则圆的方程为______.13.袋子中装有n 个白球，3个黑球，2个红球，已知若从袋中每次取出1球，取出后不放回，在第一次取到黑球的条件下，第二次也取到黑球的概率为13，则n 的值为______，若从中任取3个球，用X 表示取出3球中黑球的个数，则随机变量X 的数学期望()E X =______.14已知0a >，0b >，且1ab =，则111a b a b+++的最小值为______.15.定义函数()(){}()()()()()(),min ,.f x f x g x f x g x g x f x g x ⎧≤⎪=⎨>⎪⎩，设(){}2min11,38h x x xax a =--+--，若()0hx =㤷有3个不同的实数拫，则实数a 的取值范围是______.三、解答题（本大题5小题，共75分.解答应写出必要的文字说明，证明过程或演算步骤）16.（本小题满分14分）在ABC △中，内角A 、B 、C的对边分別为a 、b 、c ，已知2sin sin cos tan C A A B =+.（1）求角B 的大小；（2）设2a =，3c =，求b 和()sin 2A B -的值.17.（本小题满分15分）已知底面ABCD 是正方形，PA ⊥平面ABCD ，PA DQ ∥，33PA AD DQ ===，点E 、F 分别为线段PB 、C Q 的中点.（1）求证：E F ∥平面PADQ ；（2）求平面PCQ 与平面CDQ 夹角的余弦值；（3）线段PC 上是否存在点M ，使得直线A M 与平面PCQ 所成角的正弦值是7，若存在求出PMMC的值，若不存在，说明理由.18.（本小题满分15分）已知椭圆C ：22221x y a b+=（0a b >>）的右焦点为点F ，A 、B 分别为椭圆C 的上、下顶点，若椭圆中心到直线AF 的距离为其短轴长的14.（1）求椭圆的离心率；（2）过点B 且斜率为k （0k >）的直线l 交椭圆C 于另一点N （异于椭圆的右顶点），交x 轴于点P ，直线AN 与直线x a =相交于点Q ，过点A 且与P Q 平行的直线截椭圆所C 的标准方程.19.（本小题满分15分）已知数列{}n a 满足12n n a a +-=，其前8项的和为64；数列{}n b 是公比大于0的等比数列，13b =，3218b b -=.（1）求数列{}n a 和{}n b 的通项公式；（2）记211n nn n na c a ab ++-=，*n ∈N ，求数列{}n c 的前n 项和n T ；（3）记()12221,1,n n n n n a n a d n b +⎧-⋅⎪⎪+=⎨⎪⎪⎩为奇数为偶数，求221nn kk S d==∑.20.（本小题满分16）已知函数()sin x f x ae x a =--.（注： 2.718281e =⋅⋅⋅是自然对数的底数）.（1）当2a =时，求曲线()y f x =在点()()0,0f 处的切线方程；（2）当0a >时，函数()f x 在区间π0,2⎛⎫⎪⎝⎭内有唯一的极值点1x .（ⅰ）求实数a 的取值范围；（ⅱ）求证：()f x 在区间()0,π内有唯一的零点0x ，且012x x <.2023年天津市十二区重点学校高三毕业班联考（一）数学参考答案一、选择题：每小题5分，满分45分题号123456789答案CACDBABDD二、填空题：每小题5分，共30分.（两空中对一个得3分，对两个得5分）10.511.270-12.()2214x y -+=13.2；9714.5215.843a -<<-或8a =-三、解答题：本大题5小题，共75分.解答应写出文字说明，证明过程或演算步骤.16.（1）解：因为2sin sin cos tan C A A B =+，所以()sin sin sin cos cos sin sin 2sin sin cos cos cos cos cos B A B A B A B CC A A B B B B++=+⨯===…………2分所以2sin cos sin C B C =，因为()0,πC ∈，所以sin 0C >，所以1cos 2B =…………4分又()0,πB ∈，所以π3B =；…………5分（2）在ABC △中，由余弦定理及2a =，3c =，π3B =，有2222cos 7b a c ac B =+-=，故b .…………8分由正弦定理sin sin a bA B=，可得sin A =.因为a c <，故cos A =.…………10分因此sin22sin cos 7A A A ==，21cos22cos 17A A =-=.…………12分所以，()11sin 2sin2cos cos2sin 727214A B A B A B -=-=⨯-⨯=.…………14分17.（本小题满分15分）（1）方法一：分别取AB ，CD 的中点G ，H ，连接EG ，GH ，FH ，…………1分由题意可知：点E 、F 分别为线段PB 、C Q 的中点.所以EG PA ∥，FH QD ∥，因为PA DQ ∥，所以EG FH ∥，所以点E ，G ，H ，F 四点共面，因为G ，H 分别为AB ，CD 的中点，所以GH AD ∥，A D ⊂平面ADQP ，GH ⊄平面ADQP ，所以GH ∥平面ADQP ，…………3分又因为FH QD ∥，QD ⊂平面ADQP ，FH ⊄平面ADQP ，所以FH ∥平面ADQP ，…………4分又因为FH GH H ⋂=，FH ，GH ⊂平面EGHF ，所以平面EGHF ∥平面ADQP ，因为EF ⊂平面EGHF ，所以E F ∥平面ADQP .…………5分方法二：因为ABCD 为正方形，且PA ⊥平面ABCD ，所以AP ，AB ，AD 两两互相垂直，建立如图所示空间直角坐标系，…………1分则()0,0,3P ，()3,3,0C ，()0,3,1Q ，()3,0,0B ，33,0,22E ⎛⎫⎪⎝⎭，31,3,22F ⎛⎫⎪⎝⎭…………3分（建系和对一个点的坐标就给1分，全对给2分，没有出现点的坐标扣1分）所以()0,3,1EF =- ，()3,3,3PC =- ，()3,0,1CQ =-，易知平面PADQ 的一个法向量()1,0,0a =，所以0a E F ⋅= ，所以E F a ⊥，……………….4分又因为EF ⊄平面ADQP ，所以E F ∥平面ADQP .…………5分（2）设平面PCQ 的法向量(),,m x y z =，则00PC m CQ m ⎧⋅=⎪⎨⋅=⎪⎩，即333030x y z x z +-=⎧⎨-+=⎩，令1x =，则3z =，2y =，所以平面PCQ 的一个法向量为()1,2,3m =，…………6分易知平面CQD 的一个法向量()0,1,0n =，设平面PCQ 与平面CQD 夹角为θ，则14cos cos ,7m n θ==，所以平面PCQ 与平面CQD夹角余弦值为7…………8分（设角和作答具备其一即可，均不写扣1分）（3）假设存在点M ，PM PC λ=，[]0,1λ∈，设(),,M x y z ，所以()(),,33,3,3x y z λ-=-，………….9分所以()3,3,33M λλλ-所以()3,3,33AM λλλ=-…………10分由（2）得平面PCQ 的一个法向量为()1,2,3m =，427=12分得212810λλ-+=.即()()21610λλ--=，…………13分12λ∴=或16λ=，…………14分1PM MC ∴=或15PM MC =.…………15分18.（本小题满分15分）（1）由直角三角形面积关系得124bc b =⨯⨯，即124bc b a =⨯⨯解得12c a =…………3分（2）由（1）得2ac =，b ，易得()A ，()0,B，直线l 的方程为y kx =，因为直线l 不过右顶点()2,0c ，所以2k ≠，…………4分2222143x y c c y kx ⎧+=⎪⎨⎪=⎩，得()22340k x +-=，234N x k ∴=+…………6分从而222834333,3434kc k c c N k k ⎛⎫- ⎪ ⎪++⎝⎭，3,0c P k ⎫⎪⎪⎝⎭…………8分直线AN2243333344c k k -==-…………9分故直线AN的方程为34y x k=-+…………10分令2x c =，得32,2c Q c k ⎛⎫-⎪⎝⎭，…………11分直线P Q的斜率322PQ ck k k-=== (12)分()A ，左顶点()2,0Dc -，2AD k =，即22214AD a b =+=，12c a =解得28a =，26b =，22c =.…………14分∴椭圆的标准方程为22186x y +=…………15分19.（本小题满分15分）【详解】（1）因12n n a a +-=，∴数列{}n a 是公差为2d =等差数列，且864S =，18782642a ⨯∴+⨯=，解得11a =，()12121n a n n ∴=+-=-；…………2分设等比数列{}n b 的公比为q （0q >），因为13b =，3218b b -=，23318q q ∴-=，即260q q --=，解得2q =-（舍去）或3q =，1333n n n b -∴=⨯=…………4分（2）由（1）得()()()21222121213n n nn n n n a c a a b n n +++--==-+⋅…………5分()()()()122111212132213213n n n n n n n n -⎡⎤+=-⎢⎥-+⋅-+⎣⎦=…………6分()()0112231111111112133333535373213213n nn n ⎡⎛⎤⎛⎫⎛⎫⎛⎫⎢ ⎥-+-+-+⋅⋅⋅+- ⎪⎪ ⎪ ⨯⨯⨯⨯⨯⨯-⋅⎤+⋅⎢=⎝⎭⎝⎭⎝⎭⎥⎦⎝⎦⎣()0111213213n n ⎛⎫- ⎪ ⎪⨯+⋅⎝⎭=()1122213n n -+⋅=，…………8分（3）()22121,1,n nn n n a n b d a n ++⎧⎪⎪=⎨⎪⎪-⋅⎩ 为偶数为奇数()()2246213521n n n S d d d d d d d d -∴=+++⋅⋅⋅+++++⋅⋅⋅+…………9分()3121352112311111nn n n a a a a a a a a b b b b -⎡⎤++++⎡⎤=+++⋅⋅⋅++-+-+⋅⋅⋅+-⋅⎢⎥⎣⎦⎣⎦()()1232462159131433333n n n n ⎡⎤⎡⎤=+++⋅⋅⋅++-+-+⋅⋅⋅+-⋅-⎢⎥⎣⎦⎣⎦…………10分n nP Q =+12324623333n nnP =+++⋅⋅⋅+ （1）23411246222333333n nn n n P +-∴=+++⋅⋅⋅++（2）（1）－（2）：1234122222223333333n n n nP +=++++⋅⋅⋅+-1112112n 12n 2n 333111333313n n n n n +++⎛⎫- ⎪+⎝⎭=-=----1323323123223n n n n n P +++⎛⎫∴=-=- ⎪⋅⎝⎭…………12分方法二：()()22121211,21211,,,n k n kk n k n n a a n kb b n d n a n k a +-++⎧=⎪=⎨⎪⎪-=⎧⎪⎪=⎨⎪⎩⋅-⎩-⋅为偶数为奇数()()()()1121232,2,22333143,21143,21k k kk k k k k n k n k k n k k n k -⎧⎪⎨⎪++⎛⎫⎧-== ⎪⎪⎝⎭==⎨⎪-⋅-=--⋅-=-⎩⎩()2462011211355721233232333333223n n n nn n n n P d d d d -⎡++⎤+⎛⎫⎛⎫⎛⎫∴=+++⋅⋅⋅+=-+-+⋅⋅⋅+-=- ⎪ ⎪ ⎢⎥⋅⎝⎭⎝⎭⎝⎭⎣⎦①当n 为偶数时，()21159131nn n Q a -⎡⎤=-+-+⋅⋅⋅+-⋅⎣⎦()()()()1591347434444*22nn n n ⎡⎤=-++-++⋅⋅⋅+--+-=++⋅⋅⋅+==⎣⎦，…………13分②当n 为奇数时，()()1444434*43212n n Q n n n -=++⋅⋅⋅+--=--=-+…………14分21,2,n n n Q n n -+⎧∴=⎨⎩为奇数为偶数121323121,2332312,23n nn n n n n n S P Q n n n ++⎧+⎛⎫--+ ⎪⎪⎪⎝⎭∴=+=⎨+⎛⎫⎪-+ ⎪⎪⎝⎭⎩为奇数为偶数…………15分20.（本小题满分16分）解：（1）()2sin 2x f x e x =--，求导()2cos x f x e x =-'，切线的斜率()0211kf '==-=，又()00f =，所以切点为()0,0，所以，切线方程为y x =…………4分（2）（ⅰ）求导()cos x f x ae x =-'，①当1a ≥时，当π0,2x ⎛⎫∈ ⎪⎝⎭时，1xae >，()cos 0,1x ∈，()0f x ∴'>，则()y f x =在π0,2⎛⎫⎪⎝⎭上单调递增，没有极值点，不合题意，舍去；…………6分②当01a <<时，求二阶导()sin 0x f x ae x =+'>'，所以()f x '在π0,2⎛⎫⎪⎝⎭上递增，又()010f a =-<'，π2π02f ae ⎛⎫=> ⎪⎝⎭'，所以()f x '在π0,2⎛⎫ ⎪⎝⎭上有唯一零点1x ，…………8分当()10,x x ∈时，()0f x '<，函数()f x 单调递减；当1π,2x x ⎛⎫∈ ⎪⎝⎭时，()0f x '>，函数()f x 单调递增，所以函数()y f x =在区间π0,2⎛⎫⎪⎝⎭内有唯一极值点，符合题意，综上，a 的取值范围是()0,1.…………9分（ⅱ）由（ⅰ）知01a <<，当π,π2x ⎡⎫∈⎪⎢⎣⎭时，()cos 0xf x ae x =->'，…………10分当()10,x x ∈时，()0f x '<，函数()f x 单调递减；当()1,πx x ∈时，()0f x '>，函数()f x 单调递增；所以()10,x x ∈时，()()00f x f <=，则()10f x <，又因为()()πππ10f ae a a e =-=->，所以()f x 在()1,πx 上有唯一零点0x ，即()f x 在()0,π上有唯一零点0x .…………12分因为()12112sin2x f x ae x a =--，由（ⅰ）知()10f x '=，所以11cos x ae x =，则()1112111111cos 2sin2cos 2sin cos x x x x f x ae x a e x x x e =--=--11111cos 2sin x x x e x e ⎛⎫=-- ⎪⎝⎭，1π0,2x ⎛⎫∈ ⎪⎝⎭…………13分设()2sin x x h x e x e -=--，π0,2x ⎛⎫∈ ⎪⎝⎭，则()2cos x x h x e x e -'=-+，2x x e e -+> ，2cos 2x <，所以()2cos 0x x h x e e x -'=+->()h x 在π0,2⎛⎫ ⎪⎝⎭为单调递增，又()00h =，所以()0h x >，又π0,2x ⎛⎫∈ ⎪⎝⎭时，1cos 0x >，所以()1111112cos 2sin 0x x f x x e x e ⎛⎫=--> ⎪⎝⎭.所以()()1020f x f x >=.由前面讨论知112πx x <<，10πx x <<，()f x 在()1,πx 单调递增，所以012x x <.…………16分。

天津市十二重点高三毕业班联考(一)化学试题

理科综合能力测试分为物理、化学、生物三部分，共300分，考试用时150分钟。

本部分为化学试卷，本试卷分第I卷（选择题）和第Ⅱ卷两部分，共100分。

第Ⅰ卷1至2页，第Ⅱ卷3至6页。

答卷前，考生务必将自己的姓名、准考证号涂写在答题卡上。

答卷时，考生务必将卷Ⅰ答案涂写在答题卡上，卷II答在答题纸上，答在试卷上的无效。

第I卷注意事项：1．每小题选出答案后，把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再填涂其它答案标号。

2．本卷共6题，每题6分，共36分。

在每题列出的四个选项中，只有一项最符合题目要求。

以下数据可供解题时参考：相对原子质量：H—1 C—12 O—16 Al—27 Na—23 S—321．下列说法正确的是（）A．海水淡化的常用方法有蒸馏法、离子交换法和电解法B．钢铁在焊接前可以用NH4C1溶液的酸性清除表面的铁锈C．甲醛和苯酚通过加聚反应制得酚醛树脂D．在轮船外壳上焊接锌块或接直流电源正极，均可减缓船体的腐蚀速率【答案】B【解析】海水淡化的常用方法有蒸馏法、离子交换法，电解时分别在两极生产氧气和氢气，不能得到纯净的水，不用电解法，故A错误；NH4C1水解呈酸性，铁锈可溶于酸性溶液，故B正确；甲醛和苯酚生成酚醛树脂和水，是缩聚反应，故C错误；在轮船外壳上接直流电源负极减缓船体腐蚀，故D错误。

【点睛】可以用牺牲阳极的阴极保护、外接电流的阴极保护防止金属腐蚀。

2．下列有关说法正确的是（）A．实验室制氢气，为了加快反应速率，可向稀硫酸中滴加少量硝酸铜溶液B．可用勒夏特列原理解释2NO2(g)N2O4(g)体系加压后颜色变深C．N2(g)+ 3H2(g)2NH3(g) ΔH＜0可通过加压方式增大其平衡常数D．二氧化硫和乙烯两种气体分别通入Br2的CCl4溶液，能使溶液褪色的是乙烯气体【答案】D【解析】硝酸具有氧化性，加入硝酸铜不能放出氢气，故A错误；加压后2NO2(g)N2O4(g)反应正向移动，不能用勒夏特列原理解释2NO2(g)N2O4(g)体系加压后颜色变深，故B错误；平衡常数只与温度有关，温度不变平衡常数不变，故C错误；乙烯与Br2的CCl4溶液发生加成反应，二氧化硫与Br2的CCl4溶液不反应，故D正确。

天津市十二区县重点中高三毕业班联考(一)

20XX年中学测试中学试题试卷科目：年级：考点：监考老师：日期：20XX年高中测试高中试题试卷科目：年级：考点：监考老师：日期：天津市十二区县重点中学2021年高三毕业班联考（一）语文试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间150分钟。

第Ⅰ卷（选择题共42分）一、（12分，每小题3分）1．下列词语中加点的字，每对的读音完全相同的一组是（）A．强．求/牵强纤．．夫/纤．尘不染来日方长．/教学相长．B．宿．仇/宿．将度．量/置之度．外方兴未艾．/自怨自艾．C．应．届/应．允落．笔/失魂落．魄差．可告慰/差．强人意D．果脯．/胸脯钥．．匙/北门锁钥假．．以辞色/假．模假式2．下列词语中没有．．错别字的一组是（）A．陷井扫描焕发青春己所不欲，勿施于人B．安详暮霭相濡以沫万事俱备，只欠东风C．摒弃缉拿美仑美奂防民之口，甚于防川D．诡计晦涩不假思索机不可失，失不再来3．依次填入下列横线处的词句，最恰当的一组是（）①意境来自诗人的抱负。

作者正因为忧国伤时，所以仅用“”十字就更为开阔宏丽地描绘出洞庭湖的气象来。

②“一词多义”的现象在文言文中是常见的，推断词义时，须看上下文。

切不可断定。

③被媒体称为经贸之旅、和平之旅和缅怀之旅的连宋大陆之行，有利于和缓两岸的关系并促进两地的交流和发展，这是的。

A．气蒸云梦泽，波撼岳阳楼遽然无可辩驳B．吴楚东南坼，乾坤日夜浮贸然毋庸置疑C．气蒸云梦泽，波撼岳阳城贸然无可辩驳D．吴楚东南坼，乾坤日夜浮遽然毋庸置疑4．下列各句中没有．．语病且句意明确的一组是（）A．伊朗外交部长表示，国际原子能机构理事会如果在2月2日召开的紧急会议上将伊朗核问题提交职合国安理会，伊朗将于同月4日停止允许核查人员对其核设施进行突击检查。

B．在新课程改革背景下，不适当地拓展课堂教学的互动空间，“知识和能力”“过程和方法”“情感、态度和价值观”三维教学目标就无法实现。

C．在被问及抵澳后回避媒体的问题时，郭晶晶回答：“媒体对我的关注很多，好在还不至于影响我的生活和比赛造成太多影响。

天津市十二区县重点校2024届高三下学期第一次模拟考试物理含答案

2024年天津市十二区重点学校高三毕业班联考（一）物理试卷（答案在最后）考生注意：1．试卷满分100分，考试时间60分钟．2．本考试分设试卷和答题纸．试卷包括两部分，第一部分为选择题，第二部分为非选择题．3．答题前，务必在答题纸上填涂姓名、班级、考场座位号和准考证号，作答必须涂或写在答题纸上，在试卷上作答一律不得分．第一部分的作答必须涂在答题卡上相应的区域，第二部分的作答必须写在答题卡上与试卷题号对应的位置．第Ⅰ部分选择题共40分一、单项选择题（本题共5小题，每小题5分，共25分．每小题给出的四个选项中，只有一个选项是正确的）1．下列说法正确的是（）A ．贝克勒尔通过对天然放射现象的研究，发现原子中存在原子核B ．β射线与X 射线的本质相同，都是电磁波C ．原子核的比结合能越大，原子核越稳定D ．核聚变与核裂变相比，相同质量的核燃料，核聚变反应中产生的能量更多，所以现在的核电站主要采用核聚变发电2．2023年12月14日，我国在酒泉卫星发射中心用长征二号F 运载火箭成功发射一型可重复使用的试验航天器．据介绍，该航天器运行一段时间后将返回国内预定着陆场，其间将按计划开展可重复使用技术验证及空间科学实验，为和平利用太空提供技术支撑．该航天器在近地圆轨道运行时（）A ．由于航天器处于完全失重状态，宇航员无法使用弹簧臂力器锻炼身体B ．绕行速度小于静止轨道卫星的速度C ．运行周期为24hD ．若航天器的周期为7，引力常量为G ,则地球的平均密度约为23GT π3．取一条较长的软绳，用手握住一端拉平后连续周期性地向上、向下抖动，可以看到在绳上产生一列波，a 、b 、c 为绳上的质点，某时刻波刚好传播到质点c ,绳上形成的波形如图所示，下列说法正确的是（）A ．质点a 开始振动的方向向上B ．之后质点b 比质点a 先回到平衡位置C ．再过四分之一周期，质点c 加速度向下且达到最大值D ．再过半个周期，质点c 向右移动半个波长4．重型气垫船有强悍的运力，主要用于投送登陆部队．已知其质量为5510kg ⨯,最高时速32m/s ,装有额定功率9600kW 的发动机．假设气垫船在海面沿直线航行且所受阻力不变，下列说法正确的是（）A ．无法计算重型气垫船在海面航行过程中所受的阻力大小B ．若重型气垫船以额定功率启动，则加速度先增大后减小到零C ．重型气垫船在海面以额定功率航行，速度为19.2m/s 时，加速度为20.4m/sD ．重型气垫船在海面以额定功率匀速航行，若阻力突然增大到原来的1.5倍，则气垫船将做加速度增大的减速运动5．地铁靠站时列车车体和屏蔽门之间安装有光电传感器．如图甲所示，若光线被乘客阻挡，电流发生变化，工作电路立即报警．如图乙所示，光线发射器内大量处于3n =激发态的氢原子向低能级跃迁时，辐射出的光中只有a 、b 两种可以使该光电管阴极逸出光电子，图丙所示为a 、b 光单独照射光电管时产生的光电流I 与光电管两端电压U 的关系图线．下列说法正确的是（）甲乙丙A ．该光电管阴极材料的逸出功不能小于1.89eVB ．a 光的频率高于b 光的频率C ．经同一障碍物时，b 光比a 更容易发生明显衍射D ．若部分光线被遮挡，则放大器的电流将增大，从而引发报警二、多项选择题（本题共3小题，每小题5分，共15分．每小题给出的四个选项中都有多个选项是正确的，全部选对的得5分，选对但不全的得3分，有选错或不答的得0分）6．下列有关热学问题说法正确的是（）甲乙丙丁A ．图甲是理想气体分子速率的分布规律，气体在①状态下的分子平均动能小于②状态下的分子平均动能B ．图乙是分子势能p E 与分子间距r 的关系示意图，在1r r >时分子力表现为引力C ．图丙为压力锅示意图，在关火后打开压力阀开始放气的瞬间，锅内气体对外界做功，内能减少D ．图丁为一定质量的理想气体分别在12T T 、温度下发生的等温变化，由图可知12T T <7．心电图仪是将心肌收缩产生的脉动转化为电压脉冲的仪器，其输出部分可等效为一个不计内阻的交流电源，其电压1U 会随着心跳频率发生变化，如图所示，心电图仪与一理想变压器的原线圈相连接，扬声器（等效为一个定值电阻）与一滑动变阻器连接在副线圈两端．下列说法正确的是（）A ．保持电压1U 不变，向左滑动滑片P ，副线圈两端的电压2U 减小B ．保持电压1U 不变，向左滑动滑片P ,变压器的输入功率变大C ．保持滑片P 不动，当1U 变大时，扬声器的功率变大D ．保持滑片P 不动，当1U 变大时，扬声器两端的电压变小8．如图所示，竖直固定的光滑绝缘细杆上O 点套有一个电荷量为(0)q q ->，质量为m 的小环，整个装置处在固定于杆左侧电荷量为()0Q Q +>的点电荷产生的电场中，杆上a 、b 两点与Q +正好构成等边三角形，c 是ab 的中点．使小环从O 点无初速度释放，小环通过a 点的速率为v ,若己知ab Oa l ==,静电常量为k ,重力加速度为g ,规定O 点电势为零．则（）A ．小环下落过程中机械能守恒B ．小环下落过程中电势能先减小后增大C ．小环在从c 点到b 点的过程中，速度不断减小D ．b 点电势为212mv mglq-第Ⅱ部分非选择题共60分三、填空题（本题共1小题，每空2分，共12分）9．（1）某学习小组利用如图甲所示的装置测量当地的重力加速度．甲乙丙①某同学测定的g 的数值比当地公认值大，造成的原因可能是_____________A ．开始计时时，过早按下秒表B ．实验时误将49次全振动记为50次C ．测摆长时摆线拉得过紧D ．摆线上端悬点未固定，振动中出现松动，使摆线长度增加了②测量小球直径时游标卡尺如图乙所示，其读数为_____________cm③实验中，测出不同摆长l 对应的周期值T ,作出2T l -图像，如图所示，已知图线上A 、B 两点的坐标分别为()()1122,,x y x y 、，可求出g =_____________．（2）①关于多用电表的使用，下列说法中正确的是_____________A ．用多用电表的欧姆挡测导体的电阻时，如果两手同时分别接触两表笔的金属杆，则测量值偏小B ．测量阻值不同的电阻时，都必须重新进行欧姆调零C ．测量电阻时，如果红、黑表笔分别插在负、正插孔，则不会影响测量结果D ．用多用电表的欧姆挡测电阻时，若指针偏转角度很小，则应换倍率更小的挡进行测量②在正确测量小灯泡的电阻时，红表笔接触点的电势比黑表笔_____________（选填“高”或“低”）③若欧姆表使用一段时间后，电池电动势不变，内阻变大，但此表仍能调零，则用欧姆表测量电阻时，测量值_____________（填“偏大”“偏小”或“不变”）．四、计算题（本题共3小题，其中第10题14分，第11题16分，第12题18分，共48分．解答题应写出必要的文字说明和方程式，只写出最后答案的不能得分，有数值计算的题，答案中必须明确写出数值和单位）10．如图所示，水平粗糙轨道AB 长为L ,竖直面内半径为R 的四分之一光滑圆弧轨道BC 与轨道AB 相切于B 点，质量为m 的物块P 以初速度0v 从A 点向左运动，与静止于B 点质量为2m 的物块Q 发生碰撞，碰撞时间极短，碰后两物块粘在一起运动，恰能到达轨道最高点C ,已知重力加速度为g ,物块P 、Q 均可视为质点，求：（1）两物块碰后瞬间对轨道B 点的压力N F 的大小；（2）物块P 与水平轨道AB 间的动摩擦因数μ；（3）碰撞过程中物块P 对物块Q 做的功W 的大小．11．如图所示，平行金属板a 、b 水平放置，上极板接电源负极，下极板接电源正极，板长0.3m L =,极板间距0.3m d =,与极板右端相接的竖直虚线MN 右侧有范围足够大的匀强磁场，磁感应强度大小2110T B -=⨯,方向垂直纸面向外．在两极板左端正中间O 点水平向右发射一比荷8210C /kg qm=⨯、初速度50210m /s v =⨯的带正电粒子．不计粒子的重力，不考虑极板边缘电场的影响．（1）若两金属板间加适当电压，粒子恰好从上极板右边缘射出电场，求粒子在磁场中运动的时间0t （结果中的π无需代入数值）；（2）若两金属板间加适当电压，粒子经电场、磁场偏转后，恰好能从下极板右边缘再次回到电场中，求所加电压U 为多大？12．某公园的游乐场中引进了电磁弹射儿童车项目，可简化如图，宽度为L 的水平轨道中BE CH 、两段为绝缘材料制成，其余部分均为导体，且轨道各部分都足够长．ABCD 和EFGH 区域均存在竖直向下的匀强磁场B （B 未知），AD 处接有电容大小为C 的电容器，FG 处接有阻值为2R 的定值电阻．儿童车可简化为一根质量m ,电阻为R 的导体棒（与轨道始终保持垂直且接触良好），开始时导体棒静止于AD 处（如图），电容器两端电压为0U ，然后闭合开关S ,导体棒开始向右加速弹射．已知重力加速度为g ,不计一切摩擦和阻力．求：（1）开始时电容器所带的电荷量0q ；（2）若导体棒在ABCD 轨道上获得的最终速度为，求整个过程中定值电阻2R 上产生的总热量Q ；（3）当B 为多大时，导体棒在ABCD 轨道上获得的最终速度最大？其最大值m v 为多少？2024年天津市十二所重点学校高三第一次联考物理试卷答案一、选择题（每小题5分，共25分．每小题给出的四个选项中，只有一个选项是正确的）12345CDBCA二、选择题（每小题5分，共15分．每小题给出的四个选项中，都有多个选项是正确的．全部选对的得5分，选对但不全的得3分，有选错或不答的得0分）678CDBCBD9．（12分，每空2分，少选的得1分，多选或错选不得分）（1）①BC②1.20③()221214x x y y π--（2）①AC ②低③不变10．（1）碰撞后恰好能运动到最高点21(2)0(2)2m m gR m m v -+=-+2分碰后瞬间：2(2)(2)N vF m m g m m R-+=+'2分根据牛顿第三定律，压力与支持力等大反向：N N F F ='1分得：9N F mg=1分（2）P 从A 到B 的过程中22101122mgL mv mv μ-=-2分碰撞过程中：1(2)mv m m v=+2分得：20182v gRgLμ-=1分（3）碰撞过程中：2122W mv =⋅2分得：2W mgR=1分评分标准：本题14分．第一问6分；第二问5分；第三问3分．其他方法只要做对，按每问（或步骤）的分数打包给分．11．（1）恰好从上极板右边缘射出电场：2122d at =1分0L v t =1分y v at =1分tan y v v θ=1分得：tan 1θ=,即45θ=︒在磁场中，2R T vπ=1分2v qvB mR =1分0270360t T ︒︒=1分得：603104t sπ-=⨯1分（2）在磁场中，2111mv qv B R =1分12cos x R α∆=1分01cos v v α=1分2d x y ∆=+1分2112y a t =1分1qE ma =1分U E d=1分得：200V 3U =1分评分标准：本题16分．第一问8分；第二问8分．12．（1）0q C U =2分得：00q CU =1分（2）对导体棒在EFGH 轨道运动过程：212Q mv =总2分23Q Q =总1分得：213Q mv =1分（3）导体棒在ABCD 轨道运动过程：0m BILt mv =-3分q It ∆=1分0q q q ∆=-1分q C U=1分mU BLv =1分或q C U∆=∆1分0U U U∆=-1分得：02m CLU v m CBL B=+当且仅当2mCBL B=即1m B L C =2分其最大值为02m U C v m=2分评分标准：本题18分．第一问3分；第二问4分；第三问11分．其他方法只要做对，按每问（或步骤）的分数打包给分．。

天津市十二区重点学校2023届高三下学期毕业班联考(一)数学试题(1)

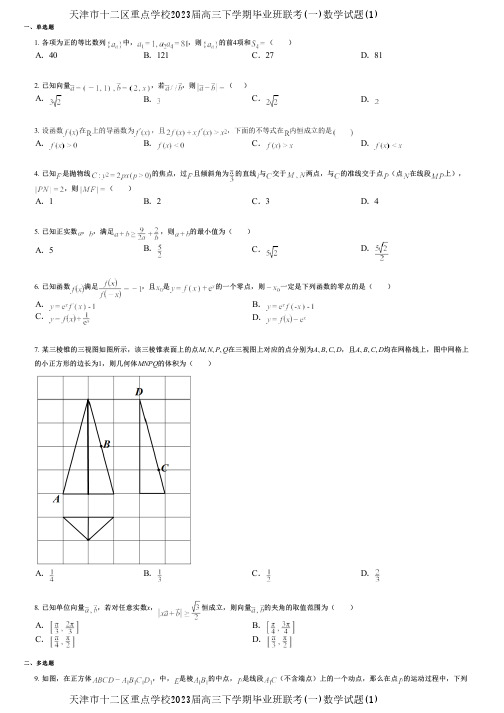
一、单选题二、多选题1.各项为正的等比数列中，，则的前4项和（）A ．40B ．121C ．27D ．812.已知向量，若，则（）A．B．C．D．3. 设函数在上的导函数为，且，下面的不等式在内恒成立的是A．B．C．D．4. 已知是抛物线的焦点，过且倾斜角为的直线与交于两点，与的准线交于点（点在线段上），，则（）A ．1B ．2C ．3D ．45. 已知正实数，，满足，则的最小值为（）A ．5B．C．D．6.已知函数满足，且是的一个零点，则一定是下列函数的零点的是（）A．B．C．D．7. 某三棱锥的三视图如图所示，该三棱锥表面上的点M ､N ､P ､Q 在三视图上对应的点分别为A ､B ､C ､D ，且A ､B ､C ､D 均在网格线上，图中网格上的小正方形的边长为1，则几何体MNPQ 的体积为（）A．B．C．D．8. 已知单位向量，若对任意实数x ，恒成立，则向量的夹角的取值范围为（）A．B．C．D．9. 如图，在正方体，中，是棱的中点，是线段（不含端点）上的一个动点，那么在点的运动过程中，下列天津市十二区重点学校2023届高三下学期毕业班联考(一)数学试题(1)天津市十二区重点学校2023届高三下学期毕业班联考(一)数学试题(1)三、填空题四、解答题说法中正确的有（）A ．存在某一位置，使得直线和直线相交B．存在某一位置，使得平面C ．点与点到平面的距离总相等D．三棱锥的体积不变10. 若，若恒成立，则的值不可以是（）A ．B ．1C．D．11. 对于函数，若存在两个常数，，使得，则称函数是“函数”，则下列函数能被称为“函数”的是（）A．B．C．D．12. 小明在一次面试活动中，10位评委给他的打分分别为：70，85，86，88，90，90，92，94，95，100．则下列说法正确的有（）A ．用简单随机抽样的方法从10个分数中随机去掉2个分数，则每个分数被去掉的概率都是B ．这10个分数的第60百分位数为91C ．这10个分数的平均数大于中位数D ．去掉一个最低分和一个最高分后，平均数会变大，而分数的方差会变小13. 北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步轨道卫星的轨道位于地球赤道所在平面，轨道高度为36000（轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为O ，半径r 为6400的球，其上点A的纬度是指与赤道平面所成角的度数．地球表面上能直接观测到的一颗地球静止同步轨道卫星点的纬度最大值为，该卫星信号覆盖地球表面的表面积（单位：），则S 与地球表面积之比为____________．14. 如图，F 1，F 2分别为椭圆的左、右焦点，点P 在椭圆上，△POF 2是面积为的正三角形，则b 2的值是________.15.在的展开式中，含项的系数为_______.16.已知抛物线上一点到焦点的距离为．(1)求抛物线的标准方程；(2)若点A，为抛物线位于轴上方不同的两点，直线，的斜率分别为，，且满足，求证：直线过定点．17. 全球变暖已经是近在眼前的国际性问题，冰川融化､极端气候的出现､生物多样性减少等等都会给人类的生存环境带来巨大灾难.某大学以对于全球变暖及其后果的看法为内容制作一份知识问卷，并邀请40名同学(男女各占一半)参与问卷的答题比赛，将同学随机分成20组，每组男女同学各一名，每名同学均回答同样的五个问题，答对一题得一分，答错或不答得零分，总分5分为满分.最后20组同学得分如下表：组别号12345678910男同学得分4554554455女同学得分3455545553组别号11121314151617181920男同学得分4444445543女同学得分5545435345（1）完成下列列联表，并判断是否有90%的把握认为“该次比赛是否得满分”与“性别”有关：男同学女同学总计该次比赛得满分该次比赛未得满分总计（2）随机变量表示每组男生分数与女生分数的差，求的分布列与数学期望.参考公式和数据：，.0.100.050.0102.7063.841 6.63518. 动车和BRT(快速公交）的出现，方便了人们的出行，并且带动了我国经济的巨大发展，根据统计，在2020年从甲市到乙市乘坐动车和BRT的人数众多，为了调查乘客对这两种出行方式的满意度，研究人员随机抽取了500名乘客进行调查，所得情况统计如下：满意程度30岁以下30-50岁50岁及50以上乘坐动车乘坐BRT乘坐动车乘坐BRT乘坐动车乘坐BRT满意5051001010020一般201540202025不满意5020102020（1）若从样本中任取1人，求抽取的乘客年龄在30岁及30岁以上的概率；（2）记满意为10分，一般为5分，不满意为0分，根据表中数据，计算样本中30~50岁乘坐动车乘客满意程度的平均分以及方差；（3）若从样本中30-50岁的满意程度一般的乘客中按照乘车类型用分层抽样的方法抽取6人，再从这6人中随机挑选3人咨询改进措施，求这3人中至少有2人乘坐BRT的概率．19. 已知函数.(1)求曲线在点处的切线方程；(2)设，证明：.20.盐水选种是古代劳动人民的智慧结晶，其原理是借助盐水估测种子的密度，进而判断其优良．现对一批某品种种子的密度（单位：）进行测定，测定结果整理成频率分布直方图如图所示，认为密度不小于的种子为优种，小于的为良种．自然情况下，优种和良种的萌发率分别为和．(1)估计这批种子密度的平均值；（同一组中的数据用该组区间的中点值为代表）(2)用频率估计概率，从这批种子（总数远大于）中选取粒在自然情况下种植，设萌发的种子数为，求随机变量的分布列和数学期望（各种子的萌发相互独立）．21. 已知函数．(1)画出f（x）的图象，并写出的解集；(2)令f（x）的最小值为T，正数a，b满足，证明：．。

2024届天津市十二区县重点校高三第一次模拟考试政治试题

2024年天津市十二区重点学校高三毕业班联考(一)政治试卷本部分为政治试卷，考试用时60分钟，共100分。

本试卷分第Ⅰ卷(选择题) 和第Ⅱ卷(非选择题)两部分，第Ⅰ卷1至 5页，第Ⅱ卷5至 8页。

答卷前，考生务必将自己的姓名、准考号涂写在答题卡上。

答卷时，考生务必将I卷答案涂在答题卡上，将Ⅱ卷答案写在答题卡上，答在试卷上的无效。

第Ⅰ卷注意事项：1. 每小题选出答案后，用铅笔把政治答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

2. 本卷共 15题，每题3分，共45分。

在每题列出的四个选项中，只有一项是最符合题目要求的。

一、单项选择题1. 2023年是中国改革开放45周年，中国将推进高水平对外开放，以高质量发展全面推进中国式现代化，为各国开放合作提供新机遇。

中国坚持推进对外开放是因为( )A. 开放必然带来进步，封闭必然落后B. 对外开放是决定当代中国命运的关键一招C. 中国发展离不开世界，世界发展离不开中国D. 对外开放是我国立足于世界民族之林的奋斗基点2. 习近平文化思想是新时代党领导文化建设实践经验的理论总结，既有文化理论观点上的创新和突破，又有文化工作布局上的部署要求，明体达用、体用贯通，明确了新时代文化建设的路线图。

习近平文化思想( )A. 是实现社会主义现代化的必由之路B. 为发展中国特色社会主义文化提供科学指南C. 成为中华民族团结奋斗的最大公约数和同心圆D. 是习近平新时代中国特色社会主义思想最为核心关键的部分政治试卷第 1 页共 8 页3. 中央经济工作会议提出：2024年财政赤字率不排除上调至3.8%或更高的可能性，发挥财政资金引导作用，缓缴中小微企业社保费，稳住市场主体，落实好结构性减税降费政策，重点支持科技创新和制造业发展。

以下措施传导正确的是( )A. 上调赤字率→稳定信贷增长→实体经济融资成本下降→推动制造业发展B. 缓缴中小微企业社保费→缓解企业用工压力→减少企业裁员→保障民生福祉C. 发挥财政资金引导→资金向重点支持领域倾斜→融资成本降低→促进提质增效D. 落实好结构性减税降费→货币流动性合理充裕→消费潜力回升→提高居民生活水平4. 某同学的爸爸在一家国有企业工作，每月有工资，年终有奖金。

(定稿)2024年天津市十二区重点学校高三毕业班联考(一)答案

2024年天津市十二区重点学校高三毕业班联考（一）数学参考答案一、选择题:每小题5分，满分45分10. }1{- 11. 189- 12. 72 13.51；32 14. b a 3431+ ；3134- 15. ）（），322,22322(----- 三、解答题：本大题5小题，共75分．解答应写出文字说明，证明过程或演算步骤．（16）（本小题满分14分）解析：（I ）由正弦定理得：(2sin )cos cos A C B B C =，…………1分显然则， …………3分又，故； …………4分∴由余弦定理可得，整理可得2233a b a -+=， …………5分又2a b +=，解得1a b ==， …………6分 ∴； …………8分（III ）由正弦定理得：，则1sin A ， …………9分∵b =，即，则B A >，故A 为锐角，∴cos A，…………10分∴，…………11分，…………12分∴. …………14分（17）（本小题满分15分）解析（I）【方法1】在三棱柱111ABC A B C-中，连接11AB A B E=，连接DE，由1//AC C P，D是棱1CC的中点，得D是AP的中点，由11ABB A为平行四边形，得E为线段1AB中点，于是1//DE PB，而DE⊂平面1BDA，1PB⊄平面1BDA，所以1//PB平面1BDA.【方法2】在三棱柱111ABC A B C-中，1A A⊥平面ABC，90BAC∠=︒，则直线11111,,A B AC A A两两垂直，以点1A为原点，直线11111,,A B AC A A分别为,,x y z轴建立空间直角坐标系，…………1分由21===AAACAB，得），（0,01A，），（0,021B，），（2,02B，），（1,2D，），（2,0A，），（2,2C，），（2,11M，），（0,4P…………2分设平面1BDA的法向量(,,)n x y z=，则），2,02(1=BA，），1,20(1=DA则⎪⎩⎪⎨⎧=+=⋅=+=⋅22211zyDAmzxBAn，令1=y，得），（2,12-=n，…………4分），（0,421-=PB 因为004221=+-⨯=⋅n PB ，所以n PB ⊥1 又因为⊄1PB 平面1BDA ，所以1//PB 平面1BDA . …………5分（II ）由（I ）平面1BDA 的法向量），（2,12-=n ，又），2,31(--=MP ，则52145314|432||||||cos |=⨯++-==><n MP n MP n MP ，…………9分所以直线MP 与平面1BDA 所成角的正弦值为52145 …………10分（III ）设平面1MPB 的一个法向量）（z y x m ,,=，），1,11(1-=M B ，），0,42(1-=P B ，则⎪⎩⎪⎨⎧=+-=⋅=++-=⋅0420211y x P B m z y x M B m 令1=z ，的），（1,24=m 设平面1MPB 与平面1BDA 夹角为θ，则63218321|228||||||cos |cos =⨯-+==><=n m n m n m ，θ， …………13分所以平面1MPB 与平面1BDA 夹角的余弦值63218. …………15分（18）（本小题满分15分）解（I ）：设椭圆的半焦距c ，由题意知⎪⎪⎪⎩⎪⎪⎪⎨⎧+===+222223221431c b a b c b a ，解得⎪⎩⎪⎨⎧==1422b a ，椭圆的方程1422=+y x …………5分（II ）分析得B A ,两点关于x 轴对称，由题意直线PA 斜率k 存在且不为0，并且纵截距不为0设直线()，，：00≠≠+=m k m kx y PA …………6分⎪⎭⎫⎝⎛-0,k m M …………7分 ⎪⎩⎪⎨⎧+==+m kx y y x 1422，化简得()044841222=-+++m kmx x k ， …………8分设()()2211,,,y x P y x A ⎪⎪⎪⎩⎪⎪⎪⎨⎧>∆+-=⋅+-=+041444182221221k m x x k km x x ， …………10分直线(),212122x x x x y y y y BP --+=-： …………11分,0=y 令()()()()12122112212212221212.y y y x y x y y x y y y x x x y y y x x x N ++=+++--=+-+-=()()()()mx x k x x m x kx m kx m kx m kx x m kx x 22212121121221++++=++++++=m k m k km k k km m k m k 42418418414422222-=+⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛+-=…………14分所以44=-⋅-=⋅kmm k ON OM . …………15分（19）（本小题满分15分）解析：（I ）1213++=n n n a a ,1=n 令3213=a a 则92=∴a ，,2=n 令5323=a a 则273=∴a ； …………2分由1213++=n n n a a ①，∴当2n ≥时，1213--=n n n a a ②，由÷①②得，当2n ≥时，119n n a a +-=， …………3分所以数列{}()*2N n a n ∈和数列{}()*21N n a n -∈是等比数列．因为,31=a 1213++=n n n a a ，所以,92=a所以12112393---=⋅=n n n a ，n n n a 212399=⋅=-，因此n n a 3=，从而()1322nn a n a -=>≥，所以数列{}n a 是“G 型数列”． …………6分（II ）（i ）因为数列{}n a 的各项均为正整数，且{}n a 为“G 型数列”，所以12n na a +>，所以12n n n a a a +>>，因此数列{}n a 递增．又1n nb a =+，所以110n n n n b b a a ++-=->，因此{}n b 递增，所以公比1q >．又{}n b 不是“G 型数列”，所以存在*0n ∈N ，使得0012n n b b +≤，所以2q ≤， …………8分又公比q 为正整数，所以2q =．又1112b a =+=，所以2nn b =，则12-=n n a ． …………10分（ii ）()()12121121212321232n n n n n nn n a a ++++=--=-⨯+>-⨯，因为()()21232422342n n n n n n n +-⨯=+->≥，所以()142n n n a a n +>≥，所以）（24111≥<+n a a n n n ， …………13分令∑=+=nk k k n a a S 111，当1n =时，113S =，当2n ≥时，231223341111111113444n n n n S a a a a a a a a +⎛⎫=+++⋅⋅⋅+<+++⋅⋅⋅+ ⎪⎝⎭21111111111154411331243121214n n --⎛⎫- ⎪⎛⎫⎝⎭=+=+-<+= ⎪⎝⎭- …………15分（其他答案酌情给分）（20）(本小题满分16分)解析：（I ）2)(x x e e x ch -+=，则2)('x x e e x ch --= …………1分所以2)2(22'--=e e ch 所以)(x ch y =在2=x 处的切线斜率为222--ee …………2分（II ）令x x a x e a x x G x sin 2cos )(2)1()(--+--=，则)sin 2)((cos 2sin )(2cos 2)1()('x e a x x x a x x e e a x x G x x x --=---++--= …………3分下面证明：对任意0>x ，0sin 2>-x e x 恒成立先证明：对任意0>x ，ex e x >.证明如下：设()e e xn x x =-，则()e e xn x '=-，当(),1x ∈-∞时，()0n x '<，函数单调递减，当()1,x ∈+∞时，()0n x '>，函数单调递增，故()()10n x n ≥=，故e e x x ≥， …………5分继续证明：对任意0>x ，x x sin >.证明如下：令()sin g x x x =-，则()1cos 0g x x '=-≥，因此()g x 在),0(+∞上单调递增；所以()()sin 00g x x x g =-≥=，故x x sin > …………7分当0a ≤时，对()0,x ∀∈+∞，都有0)('>x G ，函数)(x G 在()0,∞+上单调递增，则013)0()(≥--=>a G x G ，解得31-≤a ； …………8分当0a >时，对()0,x a ∀∈，都有0)('<x G ，对(),x a ∞∀∈+，都有0)('>x G ，函数()F x 在()0,a 上单调递减，在(),a +∞上单调递增，则对()0,x a ∀∈，都有013)0()(<--=<a G x G 成立，不符合题意，舍去. 综上所述，实数a 的取值范围是31-≤a . …………9分（III ）（ⅰ）2)(xx e e x sh --=，令x e e x x sh x F x x --=-=-2)()(，则012)('>-+=-x x e e x F 所以)(x F 在),0(+∞上单调递增，所以00)0()0()()(=-=>-=sh F x x sh x F 所以当0>x 时，x x sh >)(成立； …………10分（ⅱ）下面证明：当0>x 时，21cos 12x x ≥-成立，令2211cos )(x x x H +-=，则x x x H +-=sin )(' 由（II ）解答过程，对任意0>x ，x x sin >成立，所以0sin )('>+-=x x x H 所以)(x H 在),0(+∞上单调递增，所以0211cos )(2>+-=x x x H 所以当0>x 时，21cos 12x x ≥-成立 …………11分令1x n =，1n ≥且*N n ∈，可得211cos 12n n>-，即222112211cos111124412121n n n n n n ⎛⎫>-=->-=-- ⎪--+⎝⎭，由题意)()(2)2(x ch x sh x sh ⋅=，令1x n =，1n ≥且*N n ∈，可得)1()1(2)2(nch n sh n sh ⋅=，因为12)(>+=-xx e e x ch 所以)1(2)1()1(2)2(n sh n ch n sh n sh >⋅= …………12分由①当0>x 时，x x sh >)(，所以令1x n =，1n ≥且*N n ∈，可得nn sh 1)1(>所以nn sh n ch n sh n sh 2)1(2)1()1(2)2(>>⋅= …………13分由（II ）解答过程，对任意0>x ，x x sin >成立令1x n =，1n ≥且*N n ∈，可得)1sin(1n n > …………14分所以）nn n n n sh n ch n sh n sh 1tan()1cos(2)1sin(22)1(2)1()1(2)2(⋅=>>>⋅=又1n ≥且*N n ∈，所以101n<≤，所以)121121(1[2)1cos(2)1tan()2(+--->>n n n nn sh …………15分所以可得)121`121(1)5131(1)311(1[21tan )2(31tan )32(21tan )22(1tan )2(+---++--+-->++++n n n n sh sh sh sh 124212222+-=++-=n nn n n即可得12421tan )2(31tan )32(21tan )22(1tan )2(+->++++n n n nn sh sh sh sh ,(*N n ∈). …………16分。

天津市十二区县重点校2024届高三下学期第一次模拟考试数学含答案

2024年天津市十二区重点学校高三毕业班联考（一）数学试卷（答案在最后）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟。

答卷前，考生务必将自己的姓名、准考证号、考场/座位号填涂在答题卡规定位置上。

答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效。

考试结束后，将答题卡交回。

祝各位考生考试顺利！第Ⅰ卷注意事项：1．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号；2．本卷共9小题，每小题共5分，共45分。

参考公式：·如果事件A B 、互斥，那么()()()P A B P A P B =+ ·柱体的体积公式V Sh =，其中S 表示柱体的底面积，h 表示柱体的高。

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若复数z 满足()z 1-i =1+，则z =（）A ．1i-B ．1i+C ．22i-D ．22i+2．已知,a b ∈R ，则“b a >”是“22a b <”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．如图是函数()f x 的部分图象，则()f x 的解析式可能为（）A ．()sin522x xx f x -=-B ．()cos522x xx f x -=+C ．()cos522x xx f x -=-D ．()sin522x xx f x -=-4．已知函数()1x f x x e =-，若0.61212,log 29a f b f -⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，134c f ⎛⎫= ⎪⎝⎭，则,,a b c 的大小关系为（）A ．a b c<<B ．c b a<<C ．a c b<<D ．b c a<<5．已知等差数列{}n a 的前n 项和为n S ，且()*4224,21n n S S a a n N ==+∈，则5a =（）A ．6B ．9C ．11D ．146．下列说法正确的是（）A ．一组数据7,8,8,9,11,13,15,17,20,22的第80百分位数为17；B ．根据分类变量X 与Y 的成对样本数据，计算得到24.712χ=，根据小概率值0.05α=的独立性检验()0.05 3.841x =，可判断X 与Y 有关联，此推断犯错误的概率不大于0.05；C ．两个随机变量的线性相关性越强，相关系数的绝对值越接近于0；D ．若随机变量,ξη满足32ηξ=-，则()()32D D ηξ=-．7．如图是函数()()sin 0,0,22f x K x K ππωϕωϕ⎛⎫=+>>-<< ⎪⎝⎭的部分图象，A 是图象的一个最高点，D 是图象与y 轴的交点，,B C 是图象与x 轴的交点，且()0,1,D ABC -△的面积等于2π，则下列说法正确的是（）A ．函数()f x 的图象关于点,06π⎛⎫-⎪⎝⎭对称；B ．函数()f x 的最小正周期为2π；C ．函数()f x 的图象可由()2sin 2y x =的图象向右平移6π个单位长度得到；D ．函数()f x 的单调递增区间是,,63k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦。