高等结构动力学讲义
合集下载
高等结构动力学ppt

rk rk q1, q2 ,..., qn
(质点 k 的矢径)
稳定约束。所以有
n n drk rk dqi r i Vk k q dt dt i 1 qi i 1 qi
系统动能等于各质点动能之和
显然 mij m ji 是对称的。 则T是关于广义速度的二次型, 由于T>0,是正定二次型,则M正定对称的。
m
cij c ji 是对称的, 0
rk rk 1 n n m i q j k q 2 i 1 j 1 qi q j k 1 1 n n 1 T i q j q Cq cij q 2 i 1 j 1 2
iT M j 0
代入(3)式有
iT K j 0
当i j 时 令其为
(4)式恒成立,通常
iT Mi 0
Mi iT Mi ,
称为第 i 阶模态质量,同理
ki iT Ki ,
称为第 i 阶模态刚度,且有(由(3)式) :
Ki Mi
T i 2 T i i
7 l 13 31 12 EI
作用单位力后在 mi 上产生的位移,用 ij 表示。
.. .. .. y1 F1 m1 y1 11 F2 m2 y 2 12 F3 m3 y3 13
.. .. .. y2 F1 m1 y1 21 F2 m2 y 2 22 F3 m3 y3 23
对于 m 个质点的质点系, 共约束是 r 个, 那么广义 坐标系 n=3m-r 个,也就是有 n 个自由度数。
刚体在空间运动有六个 DOF
有限单元法将连续体离散成若干有限单元构成
高等结构动力学2

exp(ξωτ ) cos ω Dτdτ mω D ∫0 exp(ξωt ) 1 t exp(ξωτ ) ( ) B(t ) = p τ sin ω Dτdτ ∫ 0 mω D exp(ξωt ) 1
t
p (τ )
数值积分递推计算公式:v N = AN sin ω D t N − B N cos ω D t N 矩形公式: 曲边梯形:
AN = AN −1 exp( −ξω∆τ ) +
二次曲线: AN = AN −2 exp(−ξω∆τ )
+ ∆τ 3mω
∆τ y N −1 exp(−ξω∆τ ) mω D ∆τ [ y N −1 exp(−ξω∆τ ) + y N ] AN = AN −1 exp( −ξω∆τ ) + 2 mω D
FFT计算法则(续) ③ WNnm计算方法
(2 nm WN = WN
γ −1
nr −1 + 2γ − 2 nr − 2 +L+ n0 )( 2γ −1 mr −1 + 2γ − 2 mr − 2 +L+ m0 )
∵
a +b a b WN = WN WN
∴ W
nm N
=W
( 2γ −1 nr −1 + 2γ − 2 nr − 2 +L+ n0 )( 2γ −1 mr −1 ) N
1.1 无阻尼精确解(续)
广义卷积(General Convolution Integral):
v(t ) = p(τ )h(t − τ )dτ
0
∫
t
(t ≥ 0)
单位脉冲响应函数(Unit-Impulse Response Function):
t
p (τ )
数值积分递推计算公式:v N = AN sin ω D t N − B N cos ω D t N 矩形公式: 曲边梯形:
AN = AN −1 exp( −ξω∆τ ) +
二次曲线: AN = AN −2 exp(−ξω∆τ )
+ ∆τ 3mω
∆τ y N −1 exp(−ξω∆τ ) mω D ∆τ [ y N −1 exp(−ξω∆τ ) + y N ] AN = AN −1 exp( −ξω∆τ ) + 2 mω D
FFT计算法则(续) ③ WNnm计算方法
(2 nm WN = WN
γ −1
nr −1 + 2γ − 2 nr − 2 +L+ n0 )( 2γ −1 mr −1 + 2γ − 2 mr − 2 +L+ m0 )
∵
a +b a b WN = WN WN
∴ W
nm N
=W
( 2γ −1 nr −1 + 2γ − 2 nr − 2 +L+ n0 )( 2γ −1 mr −1 ) N
1.1 无阻尼精确解(续)
广义卷积(General Convolution Integral):
v(t ) = p(τ )h(t − τ )dτ
0
∫
t
(t ≥ 0)
单位脉冲响应函数(Unit-Impulse Response Function):
高等结构动力学

ED、FD和M — 地震谱密度水平,通常可以忽略
SC — 地基土对地震谱影响
ξ — 阻尼比
T — 周期
同济大学土木工程防灾国家重点实验室、桥梁工程系
3.1确定合适的地震输入(续) ¾响应谱简化 S = S (SC ,ξ , T )
结论:地震土越硬,卓越周期越小,带宽越小
同济大学土木工程防灾国家重点实验室、桥梁工程系
&& }+ [C ]{∆δ & }+ [K ]{∆δ } = {∆p(t )}+ {p T (t )} [M ss ]{∆δ vs ss vs ss vs
&& }− ([C ]{∆δ& }+ [C ]{∆δ& }) {∆p(t )} = −[M ss ]{∆δ ps ss ps sg g
&& (t )}− [C ]{∆δ& (t )}− {F (t )} {p (t )} = {p(t )}− [M ]{∆δ
概率性线性地震反应分析 各态平稳随机过程 自相关函数、功率谱密度、概率分布 概率性非线性地震反应分析
同济大学土木工程防灾国家重点实验室、桥梁工程系
小结
桥梁地震反应分析
实际地震波输入 确定合适的地震输入 模拟地震波输入 分步计算增量方程 建立系统的数学模型 静力平衡解耦方程 非线性地震时程分析 选择有效的求解方法 逐步积分法求解
同济大学土木工程防灾国家重点实验室、桥梁工程系
1. 桥梁抗震设计现状(续)
1.3 引起震害原因
¾地震问题 砂土液化、地基下沉、岸坡滑移或开裂 ¾结构问题 形式、构造或连接措施不当引起的落梁 ¾地震力分布问题 桥梁各支承点的地面运动不一致 ¾设计问题 墩柱本身抗震能力不足造成的破坏
SC — 地基土对地震谱影响
ξ — 阻尼比
T — 周期
同济大学土木工程防灾国家重点实验室、桥梁工程系
3.1确定合适的地震输入(续) ¾响应谱简化 S = S (SC ,ξ , T )
结论:地震土越硬,卓越周期越小,带宽越小
同济大学土木工程防灾国家重点实验室、桥梁工程系
&& }+ [C ]{∆δ & }+ [K ]{∆δ } = {∆p(t )}+ {p T (t )} [M ss ]{∆δ vs ss vs ss vs
&& }− ([C ]{∆δ& }+ [C ]{∆δ& }) {∆p(t )} = −[M ss ]{∆δ ps ss ps sg g
&& (t )}− [C ]{∆δ& (t )}− {F (t )} {p (t )} = {p(t )}− [M ]{∆δ
概率性线性地震反应分析 各态平稳随机过程 自相关函数、功率谱密度、概率分布 概率性非线性地震反应分析
同济大学土木工程防灾国家重点实验室、桥梁工程系
小结
桥梁地震反应分析
实际地震波输入 确定合适的地震输入 模拟地震波输入 分步计算增量方程 建立系统的数学模型 静力平衡解耦方程 非线性地震时程分析 选择有效的求解方法 逐步积分法求解
同济大学土木工程防灾国家重点实验室、桥梁工程系
1. 桥梁抗震设计现状(续)
1.3 引起震害原因
¾地震问题 砂土液化、地基下沉、岸坡滑移或开裂 ¾结构问题 形式、构造或连接措施不当引起的落梁 ¾地震力分布问题 桥梁各支承点的地面运动不一致 ¾设计问题 墩柱本身抗震能力不足造成的破坏
高等结构动力学

1
Input Loads System
output Response
3、结构系统的辨识和参数估计 动力学的拟问题
Input Loads
?
output Response
(1)已知input 和output,识别结构参数 (2)已知input满足一定假设,output可测,识别结构参数 (3)Health mornitoring:a、有无结构失效 b、损伤位置 c、损伤程度
3
Special topic I:Dynamic response 动态响应
4
5
6
7
不同方法计算whipping响应的比较
8
Springing analysis
激励频率
固有频率
9
In whipping and springing there are
10
11
12
通过分析结构能量传递途径,采用改变结构 参数实现抑制振动向目标区域传递
IMPULSIVE PRESSURE LOADING 26 AND RESPONSE ASSESSMENT(V.7)
Damaged structure due to Sloshing晃荡引起的结构损伤
Damaged corrugation
Impacted Area
27
IMPULSIVE PRESSURE LOADING 27 AND RESPONSE ASSESSMENT(V.7)
受脉冲压力载荷(砰击、晃荡、上浪等)作用的船体结构的设计总是一件棘手的 事情。到目前为止,脉冲载荷引起的结构损坏还是时有发生,表明船级社现 行的相关规范需要进一步改进。
When the duration of an impulsive pressure loading is much shorter than the natural period of the impacted structure, the impulse may represent the loading. However, if the duration is long enough as compared to the natural period, the amplitude of pressure may play an important role.
结构动力学课件PPT

地震作用
200 0 -200
t(sec)
0 5 10 15 20 25 30 35 40 45 50
结构在确定性荷载作用下的响应分析通 常称为结构振动分析。 结构在随机荷载作用下的响应分析, 被称为结构的随机振动分析。 本课程主要学习确定性荷载作用下的结 构振动分析。
§1-3 动力问题的基本特性
§2-5 广义单自由度体系:刚体集合
刚体的集合(弹性变形局限于局部弹性
元件中) 分布弹性(弹性变形在整个结构或某些 元件上连续形成) 只要可假定只有单一形式的位移,使得 结构按照单自由度体系运动,就可以按 照单自由度体系进行分析。
E2-1
A
x
x p( x,t ) = p a ( t )
1
令:
5l FE (t ) q(t ) 8
y FE (t )
FE(t) 定义为体系的等效动荷载或等效干扰力。其通用表达式
P FE (t )
含义:等效动荷载直接作用在质量自由度上产生的动位移与
实际动荷载产生的位移相等!
已经知道柔度和刚度k 之间的关系为: k 表达式成为:
简支梁: 比较: 刚架: 基本质量弹簧体系:
大型桥梁结构 的有限元模型
§1-5 运动方程的建立
定义
在结构动力分析中,描述体系质量运动规律的数学 方程,称为体系的运动微分方程,简称运动方程。 运动方程的解揭示了体系在各自由度方向的位移 随时间变化的规律。 建立运动方程是求解结构振动问题的重要基础。 常用方法:直接平衡法、虚功法、变分法。
(2-3)
刚度法: 取每一运动质量为隔离体,通过分析所受 的全部外力,建立质量各自由度的瞬时力平衡方 程,得到体系的运动方程。
高等结构动力学【教程】pdf格式

θx ,θy ,θz λ
u 位移向量
Λ
µ
υ ζ, ζ s , ζ a ρ
σ x ,σ y ,σ z , σ
2 2 σ2 x , σ B ( E ), σ D ( E )
V , Vx , V y , Vz
&, w && w, w We , Wi
τ τ xy
φ
& ,Y && , Y Ym , Y m m
D EI f gB , gD G h H ( n)
i I
薄板的弯曲刚度 梁的弯曲刚度 频率 非共振峰因子,共振峰值因子 地震风险分析中的几何系数;Lame 常数 震源深度 接受率
−1 修正的 Mercalli 烈度;冲量 P(t )dt ; 重要度系数(地震设计) 刚度,刚度矩阵,广义坐标下的刚度
8.移动荷载
1
1.2 振动的物理特性
发生在特定的频率范围。运动的车辆可以按照在其静止的重量上增加一个 冲压作用,实践表明这种做法对于一般高速公路和铁路桥设计是可行的, 但是在超高速移动的荷载作用下不一定行得通。机器设备的振动、爆炸和 打桩引起的振动必须借助于动力分析和实验解决。
在很多设计规范中找到,其他类型的荷载不那么常见,有关数据需要查阅 相关的研究文献。本课程的其中一个目标是讨论最重要的几种荷载的动力 特性,为进行相关的动力学分析和研究打下基础。
2.单自由度系统的振动
2.1 引言 2.2 运动方程 2.3 自由振动 2.4 阻尼 2.5 周期激励下的结构响应 2.6 任意激励下的结构响应 2.7 Duhamel 积分 2.8 支座运动 2.9 运动方程的直接积分法
5.地震作用及分析
5.1 引言 5.2 地震的特性 5.3 地震危险性 5.4 反应谱 5.5 地震作用的计算分析
同济大学高等结构动力学课件(全)

车辆振动作用 地震振动作用 风致振动作用
同济大学土木工程防灾国家重点实验室、 同济大学土木工程防灾国家重点实验室、桥梁工程系
主要内容
第一讲 单自由度系统自由振动 第二讲 单自由度系统强迫振动 第三讲 广义单自由度叠加方法 第四讲 广义单自由度分步方法 第五讲 多自由度系统动力问题 第六讲 特征值问题求解方法 第七讲 随机振动基础 第八讲 结构随机振动分析 第九讲 结构动力可靠性分析 第十讲 桥梁车辆振动作用 第十一讲 桥梁地震振动作用 第十二讲 桥梁风致振动作用
阻尼比计算:
2πξω vn = exp vn +1 ωD
Hale Waihona Puke 两边取对数: δ ≡ ln vn = 2πξ ≈ 2πξ = c
ξ≈
vn +1 1−ξ v n − v n +1
2mf
2πv n +1
ξ≈
vn − vn+m 2mπv n + m
振幅衰减值:振幅减小50%的振动次数
1. 1结构重力影响(续)
&&(t ) + cv &(t ) + k∆ st + kv (t ) = p (t ) + W mv
∵ k∆ st = W ∴ ∵ ∴
&&(t ) + cv &(t ) + kv (t ) = p (t ) mv
&&(t ) , v & (t ) &&(t ) = v ν &(t ) = v
A = 0,
B=− p0 β k 1 1 − β 2
无阻尼系统通解:
p v(t ) = 0 k 1 1 − β 2 (sin ω t − β sin ωt )
东南大学结构动力学课件

第十章结构动力学
(Dynamics)
§10-1 绪论 § 10-1 绪论 一.动荷载的定义
大小、方向和作用点随时间变化;在其作用下, 结构上的惯性力与外荷载相比不可忽视的荷载。 自重、缓慢变化的荷载,其惯性力与外荷载相 比很小,分析时仍视作静荷载。静荷载只与作用 位置有关,而动荷载是坐标和时间的函数。
第二类问题:参数(或称系统)识别 输入 (动力荷载) 结构 (系统) 输出 (动力反应)
第三类问题:荷载识别。 输入 (动力荷载) 结构 (系统) 输出 (动力反应)
第四类问题:控制问题 输入 (动力荷载) 结构 (系统) 控制系统 (装置、能量) 输出 (动力反应)
(二). 结构动力学的任务 讨论结构在动力荷载作用下反应的分析 方法。寻找结构固有动力特性、动力荷载和 结构反应三者间的相互关系,即结构在动力 荷载作用下的反应规律,为结构的动力可靠 性(安全、舒适)设计提供依据。 §10-2 结构动力分析中的动力自由度 一. 动力自由度的定义 确定体系中所有质量位置所需的独立坐标数, 称作体系的动力自由度。
q = qo = sin θt
∑M
&& mθ
B l
2
B
=0
2 3 2
3l
m A
B
m/3 C D
2 & & 4 + kθ B ⋅ l + 4 m ⋅ θ B l = ∫ x ⋅q0 ⋅ sin θt ⋅ dt
kyC
0
m
3
& &D y
其中 q0 sin θt ∫0
3l
2
2 3 l 9 q l x ⋅ dx = q0 2 sin θt ( ) 2 = 0 sin θt 2 8
(Dynamics)
§10-1 绪论 § 10-1 绪论 一.动荷载的定义
大小、方向和作用点随时间变化;在其作用下, 结构上的惯性力与外荷载相比不可忽视的荷载。 自重、缓慢变化的荷载,其惯性力与外荷载相 比很小,分析时仍视作静荷载。静荷载只与作用 位置有关,而动荷载是坐标和时间的函数。
第二类问题:参数(或称系统)识别 输入 (动力荷载) 结构 (系统) 输出 (动力反应)
第三类问题:荷载识别。 输入 (动力荷载) 结构 (系统) 输出 (动力反应)
第四类问题:控制问题 输入 (动力荷载) 结构 (系统) 控制系统 (装置、能量) 输出 (动力反应)
(二). 结构动力学的任务 讨论结构在动力荷载作用下反应的分析 方法。寻找结构固有动力特性、动力荷载和 结构反应三者间的相互关系,即结构在动力 荷载作用下的反应规律,为结构的动力可靠 性(安全、舒适)设计提供依据。 §10-2 结构动力分析中的动力自由度 一. 动力自由度的定义 确定体系中所有质量位置所需的独立坐标数, 称作体系的动力自由度。
q = qo = sin θt
∑M
&& mθ
B l
2
B
=0
2 3 2
3l
m A
B
m/3 C D
2 & & 4 + kθ B ⋅ l + 4 m ⋅ θ B l = ∫ x ⋅q0 ⋅ sin θt ⋅ dt
kyC
0
m
3
& &D y
其中 q0 sin θt ∫0
3l
2
2 3 l 9 q l x ⋅ dx = q0 2 sin θt ( ) 2 = 0 sin θt 2 8
第一章结构动力学概述1(长沙理工大学结构动力学)祥解PPT课件

结构动力学是研究动荷作用下结构动力反应规律的 学科。
1) 结构动力学的研究内容
当前结构动力学的研究内容可用下图表示
第一类问题:响应分析——正问题
输入 (动力荷载)
结构 (系统)
输出 (动力反应)
9
第二类问题:参数(或称系统)识别
输入 (动力荷载)
结构 (系统)
输出 (动力反应)
10
第三类问题:荷载识别。
结构动力学讲义
Tel.: Email:
1
教材 《结构动力学》
(杨茀康 人民交通出版社 张子明 清华大学出版社)
2
第一章、结构动力学概论
1.1 概述 1.2 基本概念 1.3 弹性系统的动力自由度 1.4 结构振动中的能量耗散-阻尼力 1.5结构运动方程的建立
3
1.1概述
首先请大家看中国唐山、日 本阪神地震及TOCOMA大桥 在风载下垮塌录像,希望能从 中体会到学习结构动力学的重 要性。更希望大家能学好结构 动力学!
m y(x)
广义坐标个数即 为自由度个数
m
结点位移个数即 为自由度个数
18
3. 自由度的确定
4)
1) 平面上的一个质点
• 理论计算法
对所设计的结构建立数学模型,通过计算机计算从理论 上验证设计是否满足动力性的要求。
• 试验量测法
用来检验数学模型的正确性,为理论计算提供确切数据。
• 试验与计算混合法
重要结构的动力研究常常需要将数值计算和试验结合起 来,一方面利用数值计算为结构试验提供依据,另一方 面,根据试验结果,不断修正模型以便数学模型能更好 地反映实际情况。
4
5
美国的TOCOMA大桥在风载下垮塌的案例
1940年7月1日,造型优美的塔科马钢铁大桥建成通车。大桥刚投入使用
1) 结构动力学的研究内容
当前结构动力学的研究内容可用下图表示
第一类问题:响应分析——正问题
输入 (动力荷载)
结构 (系统)
输出 (动力反应)
9
第二类问题:参数(或称系统)识别
输入 (动力荷载)
结构 (系统)
输出 (动力反应)
10
第三类问题:荷载识别。
结构动力学讲义
Tel.: Email:
1
教材 《结构动力学》
(杨茀康 人民交通出版社 张子明 清华大学出版社)
2
第一章、结构动力学概论
1.1 概述 1.2 基本概念 1.3 弹性系统的动力自由度 1.4 结构振动中的能量耗散-阻尼力 1.5结构运动方程的建立
3
1.1概述
首先请大家看中国唐山、日 本阪神地震及TOCOMA大桥 在风载下垮塌录像,希望能从 中体会到学习结构动力学的重 要性。更希望大家能学好结构 动力学!
m y(x)
广义坐标个数即 为自由度个数
m
结点位移个数即 为自由度个数
18
3. 自由度的确定
4)
1) 平面上的一个质点
• 理论计算法
对所设计的结构建立数学模型,通过计算机计算从理论 上验证设计是否满足动力性的要求。
• 试验量测法
用来检验数学模型的正确性,为理论计算提供确切数据。
• 试验与计算混合法
重要结构的动力研究常常需要将数值计算和试验结合起 来,一方面利用数值计算为结构试验提供依据,另一方 面,根据试验结果,不断修正模型以便数学模型能更好 地反映实际情况。
4
5
美国的TOCOMA大桥在风载下垮塌的案例
1940年7月1日,造型优美的塔科马钢铁大桥建成通车。大桥刚投入使用
高等结构力学 海大

dmy Fp t dt
1 2
F
i
pmi
i yi 0 yi mi y
i
1 4
设任一质量处的位移yi可用n个广义坐标(v1,v2vn)表示, 即
yi t yi v1 (t ), v2 (t )vn (t )
1 5
P
i j
F
i
pmi
yi U WR WP v j v j v j v j
i
v j
U WR WP v j 因此: Fpm yi i v v j v j i j j 惯性力在虚位移上所作虚功为
§1.5 体系振动运动方程建立的 基本原理
在通常情况下,把位移作为独立的几何参变数。为 了求出各种动力响应,应先建立动力位移方程。 描述动力位移方程的数学方程式称为结构的运动方 程。运动方程的解就提供了位移过程(位移随时间变化 规律),从而可求出其他各种所需的结构动力响应。 运动方程的建立,是结构动力学的核心问题。只有 运动方程建立正确,整个求解过程才有了可靠基础。建 立运动方程有几种常用的基本原理。分别介绍如下。 (1)达朗伯(D Alembert)原理 根据牛顿第二定律,任何质量为m物体的动量变化 率等于作用在这个物体上的力,即
a
b
d T m y y 因此 i i i i j dt v j
将(a) 和 (b)式代入(1-4)式,因为 vj(j=1,2,n)的任 意性,得 d y y i i i i i v j d T T WR W mi y yi U m y v j mi y i P d i j dt 0 v v j i j
高等结构动力学讲义

52
第 4 章 结构特征问题求解 4-4 矩阵变换法
53
第 4 章 结构特征问题求解 4-5 矢量正迭代法
54
第 4 章 结构特征问题求解 4-6 矢量逆迭代法
55
第 4 章 结构特征问题求解 4-6 矢量逆迭代法
56
第 4 章 结构特征问题求解 4-6 矢量逆迭代法
57
第 4 章 结构特征问题求解 4-6 矢量逆迭代法
20
第 2 章 离散体动力方程 2-1 动力分析中离散方法
直接法
21
第 2 章 离散体动力方程 2-1 动力分析中离散方法
差分法
22
第 2 章 离散体动力方程 2-1 动力分析中离散方法
加权残值法
23
第 2 章 离散体动力方程 2-1 动力分析中离散方法
24
第 2 章 离散体动力方程 2-1 动力分析中离散方法
41
第 3 章 有限元法 3-10 平面刚架振动
42
第 3 章 有限元法 3-10 平面刚架振动
43
第 3 章 有限元法 3-10 船舶板架振动
44
第 3 章 有限元法 3-10 船舶板架振动
45
第 3 章 有限元法 3-11 船体总振动
船体总振动
一维模型 二维模型 三维模型
46
34
第 3 章 有限元法 3-8 杆纵向振动
35
第 3 章 有限元法 3-8 杆纵向振动
36
第 3 章 有限元法 3-9 杆横向振动
37
第 3 章 有限元法 3-9 杆横向振动
38
第 3 章 有限元法 3-9 杆横向振动
39
第 3 章 有限元法 3-9 杆横向振动
高等结构动力学1-1

W=13
m
EI
自由度为1的体系称作单自由度体系; 自由度大于1的体系称作多(有限)自由度体系; 自由度无限多的体系为无限自由度体系。
W=2
§1.3 建立结构运动方程的一般方法
要了解和掌握结构动力反应的规律,必须首先建立描述结构 运动的(微分)方程。建立运动方法很多,择常用的简单介 绍如下: 1)直接平衡法 应用达朗泊尔原理,通过列瞬时“动平衡”方程来建立。 2) 虚功法 根据达朗泊尔原理和所假设的阻尼理论,在质量上考虑惯性 力、阻尼力的作用,则在任意瞬时质量应该处于“动平衡” 状态,因此根据虚位移原理,外力(动荷载、惯性力、阻尼 力)的总虚功应恒等于总虚变形功。也即通过列虚功方程象 1)一样来获得运动方程。由于是用虚功方程来建立平衡条件, 称虚功法。
§1.4 建立运动方程的基本步骤
直接平衡法列方程的一般步骤为: 1) 确定体系的自由度——质量独立位移数; 2) 建立坐标系,确定未知位移(坐标正向为正); 3) 根据阻尼理论确定质量所受的阻尼力; 列位移方程称柔度法 4) 根据达朗泊尔原理在质量上假想作用有惯性力 (注意:惯性力是实际的,但它不作用在质量上); 5) 将动力外荷、惯性力、阻尼力作为“外力”,按 位移计算公式求各质量沿自由度方向的位移,其结果 应该等于未知位移(满足协调),由此建立方程。
§1.4 建立振动微分方程举例
例-4试建立图示抗弯刚度为 EI 简支梁的 柔度法步骤: 1.在质量上沿位移正向加惯性力; 运动方程。(不计轴向变形)
2.求外力和惯性力引起的位移; 3.令该位移等于体系位移。
m P(t) l/2 l/2
解:图示结构只能产生竖向位移,显然这是单自由度 对称振动。设质量竖向位移为v,向下为正。 fd 将惯性力fI、阻尼力fd如图所示加于梁 fI 上,根据达朗贝尔原理和阻尼假定 l/2 l/2 f c v f m v P(t) I d 由位移计算可知,单位荷载下简支梁跨中竖向位移 3 l 为 因此在所示“外力”下,质量的位移为
哈工大高等结构动力学第四次课-PPT文档资料
§2.6 转子系统临界转速的概念
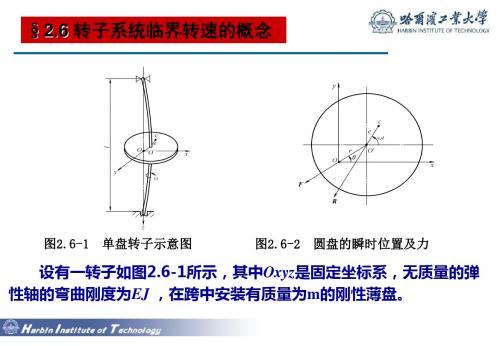
图2.6-1 单盘转子示意图
图2.6-2 圆盘的瞬时位置及力
设有一转子如图2.6-1所示,其中Oxyz是固定坐标系,无质量的弹 性轴的弯曲刚度为EJ ,在跨中安装有质量为m的刚性薄盘。
§2.6 转子系统临界转速的概念
由于材料、工艺等因素使圆盘的质心偏离轴线,偏心距为e 。当 转子以等角速度ω 自转时,偏心引起的离心惯性力将使轴弯曲,产生 动挠度,并随之带动圆盘公转。 设圆盘在瞬时t 的状态如图2.6-2所示,这时弹性轴因有动挠度 而对圆盘的作用力为 F ,它在坐标轴上的投影分别为
c Rx Fx m x c Ry Fy m y 由图2.6-4的几何关系知
(2-4)
xc x ecos t yc y esin t
对上式求两次导数,可得
(2-5)
图2.6-4
2 x x e cos t c 2 e y sin t c y
和 O'之间,即所谓圆盘的轻边飞出,这种现象称为自动定心,也 叫偏心转向。
§2.6 转子系统临界转速的概念
根据国际标准,临界转速定义为:系统共振时发生主响应的特征转 速,在这里就是使动挠度 取得极值的转速,r于是可利用条件 dr (2-13) 来确定临界转速,并以ωCr 表示。由(2-13)式得
2 2 2 e 2 2 dr n n n 0 3 d 2 2 22 2 2 2 n n 2
r
Fx kx F y ky
(2-1)
由材料力学可知,对于图2.6-3所示的模型
48 EJ k l3
(2-2)
图2.6-3
图2.6-1 单盘转子示意图
图2.6-2 圆盘的瞬时位置及力
设有一转子如图2.6-1所示,其中Oxyz是固定坐标系,无质量的弹 性轴的弯曲刚度为EJ ,在跨中安装有质量为m的刚性薄盘。
§2.6 转子系统临界转速的概念
由于材料、工艺等因素使圆盘的质心偏离轴线,偏心距为e 。当 转子以等角速度ω 自转时,偏心引起的离心惯性力将使轴弯曲,产生 动挠度,并随之带动圆盘公转。 设圆盘在瞬时t 的状态如图2.6-2所示,这时弹性轴因有动挠度 而对圆盘的作用力为 F ,它在坐标轴上的投影分别为
c Rx Fx m x c Ry Fy m y 由图2.6-4的几何关系知
(2-4)
xc x ecos t yc y esin t
对上式求两次导数,可得
(2-5)
图2.6-4
2 x x e cos t c 2 e y sin t c y
和 O'之间,即所谓圆盘的轻边飞出,这种现象称为自动定心,也 叫偏心转向。
§2.6 转子系统临界转速的概念
根据国际标准,临界转速定义为:系统共振时发生主响应的特征转 速,在这里就是使动挠度 取得极值的转速,r于是可利用条件 dr (2-13) 来确定临界转速,并以ωCr 表示。由(2-13)式得
2 2 2 e 2 2 dr n n n 0 3 d 2 2 22 2 2 2 n n 2
r
Fx kx F y ky
(2-1)
由材料力学可知,对于图2.6-3所示的模型
48 EJ k l3
(2-2)
图2.6-3
高等结构动力学4_连续体1_杆和梁

(2)弦的横向振动 (3)轴的扭转振动
2 2 y 1 2 y a0 2 p( x, t ) 2 t x
2 2 1 2 a p ( x, t ) 0 2 2 t x I p
虽然它们在运动表现形式上并不相同,但它们的运动微 分方程是类同的,都属于一维波动方程
假定振动过程中各横截面仍保持为平面
( x, t ) :杆上距离原点 x 处的截面在时
刻 t 的角位移 截面处扭矩 T
2 I p dx 2 t
达朗贝尔 惯性力偶
I p dx :微段绕轴线的转动惯量
连续系统的振动 / 一维波动方程
达朗贝尔原理: 2 T dx ) T pdx I p dx 2 (T
2 l 2l
( x) c1 sin
x
a0
c2 cos
x
a0
u ( x, t ) ( x )q (t )
连续系统的振动 / 杆的纵向振动
左端自由,右端固定 特征:固定端位移为零 自由端轴向力为零 边界条件 : u (l , t ) 0
0
x l
(l ) 0
c1 0
x
dx l
x
u ( x, t )
杆上距原点 x 处截面 在时刻 t 的纵向位移
横截面上的内力: F ES ES 达朗贝尔原理:
u x 2u F Sdx 2 ( F dx) F p( x, t )dx x t 2u u S 2 ( ES ) p( x, t ) x x t
连续系统的振动 / 杆的纵向振动
2 2u 2 u a0 2 x 2 t
u ( x , t ) ( x ) q (t )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 mm/s
2 mm/s
6 mm/s
3 mm/s
8 mm/s
4 mm/s
Note: The zone between upper and lower values reflects the shipboard vibration environment commonly experienced and accepted. Three different classification areas are presented: Classification A; Classification B; Classification C. For guidance, Classification A can be passenger cabins, Classification B crew accommodation areas, and Classification C working areas. 6
虚位移原理
11
第1章
单自由度系统
第 1-1 节 运动方程建立
哈密顿原理
12
第 1 章 单自由度系统 1-2 无阻尼系统自由振动
13
第 1 章 单自由度系统 1-2 无阻尼系统自由振动
固有频率计算——直接法
14
第 1 章 单自由度系统 1-2 无阻尼系统自由振动
固有频率计算——静伸长法
15
第 1 章 单自由度系统 1-2 无阻尼系统自由振动
第0章
绪论
结构系统的控制
主动控制
控制方法 被动控制 振源控制 控制方法 传播控制
7
第0章
绪论
结构动力优化设计
灵敏度分析
内容
8
第 1 章 单自由度系统 1-1 运动方程建立
系统振动时,确定任意时刻全部质量位移所需要的独立的几何参变量的 数目—结构系统的动力自由度。
描述结构系统动力位移的数学表达式—结构的运动方程。 运动方程的解—振动的位移历程。
34
第 3 章 有限元法 3-8 杆纵向振动
35
第 3 章 有限元法 3-8 杆纵向振动
36
第 3 章 有限元法 3-9 杆横向振动
37
第 3 章 有限元法 3-9 杆横向振动
38
第 3 章 有限元法 3-9 杆横向振动
39
第 3 章 有限元法 3-9 杆横向振动
40
第 3 章 有限元法 3-10 平面刚架振动
58
第 4 章 结构特征问题求解 4-6 矢量逆迭代法
作业2
用矢量逆迭代法求前三阶特征对
59
第 4 章 结构特征问题求解 4-7 结构特征问题求解 4-7 子空间迭代法
61
第 4 章 结构特征问题求解 4-7 子空间迭代法
62
第 5 章 结构动态响应分析 5-1 概述
69
第 5 章 结构动态响应分析 5-4 Houbolt法
70
第 5 章 结构动态响应分析 5-5 线加速度法
71
第 5 章 结构动态响应分析 5-6 Wilson-θ法
72
第 5 章 结构动态响应分析 5-6 Wilson-θ法
作业3 确定系统响应历程
x 2 0 1 6 2 x1 0 0 1 2 4 x 10 x2 2
27
第 2 章 离散体动力方程 2-2 瞬时最小势能原理
28
第 2 章 离散体动力方程 2-2 瞬时最小势能原理
29
第 2 章 离散体动力方程 2-2 瞬时最小势能原理
30
第 2 章 离散体动力方程 2-3 Hamilton原理
31
第 2 章 离散体动力方程 2-4 质量矩阵、阻尼矩阵
32
1
第0章
绪论
周期载荷
外载荷分析
随机性载荷 确定性载荷
瞬态载荷
低阶激励(周期载荷) 高阶激励(周期载荷) 轴频激励(周期载荷)
主机激励
螺旋桨激励
叶频激励(周期载荷) 倍叶频激励(周期载荷) 波击(周期载荷)
波浪激励
砰击(瞬态载荷) 拍击(瞬态载荷)
流体激励
涡击(周期载荷) 地震(瞬态载荷)
2
其他激励
加权残值法——配点法、子域法、最小二乘法、加辽金法
25
第 2 章 离散体动力方程 2-1 动力分析中离散方法
26
第 2 章 离散体动力方程 2-1 动力分析中离散方法
变分法
是研究泛函取极值的方法。从能量的观点出发,考察结构的变形和内力, 应用变分方法,得到所谓的能量变分原理。主要有瞬时最小势能原理和 Hamilton原理。 *有限元法 有限元法的基础:变分原理与计算机技术;它不同于加权残值法、李茨 法等,它不是在整个域内取试函数,而是在有限域内取试函数。 *关于P法、H法、P-H法
第0章
绪论
结构系统的动力响应
对给定的结构系统,求响应与激励的关系
线性系统(应力—应变关系服从胡克定律,可用叠加原理) 非线性系统(应力—应变关系不服从胡克定律,不可用叠加原理)
结构系统
包括:几何非线性、状态非线性、材料非线性
结构系统
无反馈系统(开环系统)
有反馈系统(闭环系统) 如:流固耦合系统 时变系统(与时间有关) 如:动态有限元 时不变系统(与时间无关) 保守系统(不考虑阻尼) 非保守系统(考虑阻尼)
80
第 6 章 动态子结构法 6-2 固定界面法
81
第 6 章 动态子结构法 6-2 固定界面法
82
第 6 章 动态子结构法 6-3 自由界面法
83
第 6 章 动态子结构法 6-3 自由界面法
84
第 6 章 动态子结构法 6-3 自由界面法
85
3
结构系统
结构系统
第0章
绪论
方法
有限单元方法 SAP ADINA NASTRAN MARC ANSYS ABAQUS SACS NAUTICUS 固有特性计算( 包括固有频率和振型) 响应计算
内容
4
第0章
绪论
系统辩识与参数识别
结构动力学的逆问题(反问题)
故障诊断
依靠现代实验手段,海底石油管道、平台桩腿等
63
第 5 章 结构动态响应分析 5-2 模态迭加法
64
第 5 章 结构动态响应分析 5-2 模态迭加法
65
第 5 章 结构动态响应分析 5-2 模态迭加法
66
第 5 章 结构动态响应分析 5-3 中心差分法
67
第 5 章 结构动态响应分析 5-3 中心差分法
68
第 5 章 结构动态响应分析 5-4 Houbolt法
第 3 章 有限元法 3-1 杆纵向振动质量矩阵
33
第 3 章 有限元法 3-1 杆纵向振动质量矩阵
3-2 梁单元的质量矩阵 (《船体振动学》P171) 3-3 平面问题中的三角形板单元质量矩阵 (《机床结构计算的有限元法》P152) 3-4 平面问题中的矩形板单元质量矩阵 (《机床结构计算的有限元法》P152) 3-5 板弯曲问题中的矩形板单元质量矩阵 (《机床结构计算的有限元法》P152) 3-6 板弯曲问题中的三角形板单元质量矩阵 (《机床结构计算的有限元法》P152) 3-7 平面问题和弯曲问题组合时矩形板单元质量矩阵 (《机床结构计算的有限元法》P152)
20
第 2 章 离散体动力方程 2-1 动力分析中离散方法
直接法
21
第 2 章 离散体动力方程 2-1 动力分析中离散方法
差分法
22
第 2 章 离散体动力方程 2-1 动力分析中离散方法
加权残值法
23
第 2 章 离散体动力方程 2-1 动力分析中离散方法
24
第 2 章 离散体动力方程 2-1 动力分析中离散方法
41
第 3 章 有限元法 3-10 平面刚架振动
42
第 3 章 有限元法 3-10 平面刚架振动
43
第 3 章 有限元法 3-10 船舶板架振动
44
第 3 章 有限元法 3-10 船舶板架振动
45
第 3 章 有限元法 3-11 船体总振动
船体总振动
一维模型 二维模型 三维模型
46
直接平衡法
运动方程建立 虚位移原理——作用在系统上的所有力在发生虚位移时所做的总功等 于零 哈密顿原理——在任何时间区段t1-t2内,动能和位能的变分加上所考 虑的非保守力所做功的变分必然等于零
9
第1章
单自由度系统
第 1-1 节 运动方程建立
直接平衡法
10
第1章
单自由度系统
第 1-1 节 运动方程建立
固有频率计算——能量法
16
第 1 章 单自由度系统 1-3 有阻尼系统自由振动
17
第 1 章 单自由度系统 1-4 简谐载荷作用动力响应
18
第 1 章 单自由度系统 1-5 基础简谐运动作用响应
19
第 2 章 离散体动力方程 2-1 动力分析中离散方法
离散方法
直接法 差分法 加权残值法 变分法
第 3 章 有限元法 3-11 船体总振动
作业1
设计一梁,求其固有频率 和振型。
47
第 4 章 结构特征问题求解 4-1 概述
48
第 4 章 结构特征问题求解 4-1 概述
49
第 4 章 结构特征问题求解 4-1 概述
50
第 4 章 结构特征问题求解 4-2 多项式迭代法
51
第 4 章 结构特征问题求解 4-3 Sturm序列法
73
第 5 章 结构动态响应分析 5-7 Newmark法
