用自然坐标表示平面曲线运动中的速度和加速度

合集下载

2013-01-2自然坐标系下的速度-加速度解析

2

0
dv v 2 a n＝a x i a y j a z k dt

瞬时曲率半径
大学物理
三、推广：一般平面曲线运动运动中的加速度
an
v
2

dv a dt

0
2
a
力学中利用加速度与曲率半径的关系求曲线轨迹上各点的曲率半径。
a

a
ds v v dt
ds v dt
1、瞬时速率
v
：
n
S+
反映了质点任一时刻沿轨道运动的快慢。
2、任何时刻质点的速度总沿轨道的切线方向，速度只有切线分量而无法向分量。

O

大学物理
二、自然坐标系下的加速度
由加速度的定义有
d v a dt
由于质点速度的方向一定沿着轨迹的切向，因此，自然坐标系中可将速度表示为：
2
＝1
大学物理
自然坐标系下加速度表达式：
2 dv v a n dt R
o
n
a
即圆周运动的加速度可分解为两个正交分量：
an a P
a dv dt
2 v an R
a 切向加速度，其大小表示质点速率变化的快慢 an 法向加速度，其大小反映质点速度方向变化的快慢
大学物理
Key: c
大学物理
三、推广：一般平面曲线运动中的加速度
质点的轨迹可以看成是由无穷多个圆组合而成。对圆周运动而言：曲率半径各点相同 R, 于是对曲线上任一点，研究该点的速度、加速度情况时，仅需要将 R 换成就得到一般曲线运动的加速度的正交分解式。

2-6自然坐标.曲线运动

(3) a n R 2 2 (6 )a a n at
2
(8 ) a
2 2 an at
9
例.一质点沿半径为R的圆周按规律 s
为正常数.求:
（1）t时刻的总加速度；
v ds dt
v0t
1 2
bt 运动，v
2
0
,b
v 0 bt
t 时刻切向加速度、法向加速度及加速度大小:
s v0t bt /2
2
v0 /2 b
2
它与圆周长之比即为圈数：
n
s 2R

v0
2
4Rb
12
[例题1] 汽车在半径为200m的圆弧形公路上刹车，刹车
开始阶段的运动学方程为 s 20 t 0 . 2 t 3 (单位：m，s). 求汽车在t=1s时的加速度.
[解] 加速度
a an en a tet
积分
d

2
d
dt R tg
得
1

1
0

t Rtg

0

2

t
dt R tg
6
0
三、任意曲线运动中的法向和切向加速度
质点的曲线轨迹可视作由无限多个圆组合而成
a a et an en
dv v a et en ——曲率圆半径 dt
m 1169 m 2 2
16
aτ b 2 dt dt 2 2 v (v0 bt ) a n R R
dv
d s
2
a
aτ an
2 2

§11-2研究点的运动的自然坐标法

υ=
ds = 2t − 4 dt
t=3=2×3-4=2（cm/s）
在第3s时 υ|
点的切向加速度为
dυ aτ = = 2(cm / s 2 ) dt
切向加速度为常数，即第3s时切向加速度为2cm/s² 第3s时点的法向加速度为
22 2 an = = = 0.8(cm / s ) R 5
υ2
aτ = lim ∆υ τ ∆t r = lim
当∆t→0时 ∆t→
r
r
r
r
υ1 − υ
∆t
r
r = lim
∆υ dv = ∆t dt
(11-9)
它的方向为∆t→0时∆Vτ的方向即为M点的切线方向aτ方向又叫切向加速度。当aτ和υ同号时，动点的运动方向和加速方向一致，动点作加速运动。当aτ和υ异号时，动点的运动方向和加速方向相反，动点作减速运动。
§11-2 用自然法研究点的平面曲线运动 11一、自然法 1、轨迹：动点运动时，所经过的路线称为动点的轨迹。动点作如图11-4所示曲线运动。在轨迹AB上任取一点O作为自然法的坐标原点，并在两侧规定出正负方向。动点M的位置，由弧长OM来表示。OM是一个代数量。图示OM为正。弧长OM称为动点的弧坐标或自然坐标。弧坐标的大小能唯一确定动点所在的位置。这种确定动点位置的方法称为自然法。弧长S显然是时间的函数。即 S=f(t) 这就是自然法所表达的运动方程。已知运动方程，就能确定动点在任意时刻所在的位置。二、位移和路程 1、位移：起始时刻和结束时刻动点所在位置之间的距离。 2、路程：是指动点在某一时间间隔内所经过的轨迹的长度。例如，如图11-4所示，在某一时间间隔内动点M从原点起，先沿负向运动到A点，（OA=S1）再从A移动到B点（OB=S）动点的始末位置是O、B，则点的位移为，而路程是弧长（）。

中国矿业大学(北京)《大学物理》课件第1章质点运动学

y 0.22 152 9.115 30 57m
r 66i 57 j
r
的大小
r的方向
r 662 (57)2 87m
arctan y arctan 57 41
x
66
（2）速度沿坐标轴 x、y 的投影为
vx
dx dt
d dt
(0.31t 2
7.2t
28)
0.62t 7.2
物体平动时可视为质点。物体上任一点的运动都可以代表物体的运动。
➢ 研究汽车突然刹车“前倾”或转弯涉及转动问题，汽车各部分运动情况不同，各
车轮受力差异很大，不能把汽车作质点处理。
质点是从客观实际中抽象出的理想模型，研究质点运动可以使问题简化而又不失客观真实性。
二、确定质点位置的方法
静止和运动是相对的地心学说被日心说取代，让人们明白，判断物体
求船的运动方程。
解取坐标系
v
依题意有
l0
l(t) l0 v t
h l(t)
坐标表示为
O
x
x(t) (l0 v t)2 h2
x(t)
说明
质点运动学的基本问题之一 , 是确定质点运动学方程。为正确写出质点运动学方程, 先要选定参考系、坐标系, 明确起始条件等, 找出质点坐标随时间变化的函数关系。
x 0.31t2 7.2t 28 y 0.22t 2 9.1t 30
试求 t =15s时小田鼠的（1）位矢;（2）速度; （3）加速度。
解（1）根据已知条件，小田鼠的位矢可写成
r
(0.31t
2
7.2t
28)i
(0.22t 2 9.1t 30) j
t = 15s 时

牛顿定律2

et et1 et 2

由速度大小的变化引起的，方向为切向单位矢量的方向，故被称为切向加速度，以 a 表示
t
由沿速度方向单位矢量的变化引起的
dv 所以切向加速度表示为： a t dt et
利用角量与线量的关系得：
dv dr d at et et r et r et dt dt dt
2、角速度：当t0时，平均角速度的极限值就是角速度
d lim t 0 t dt
即为圆运动的角速度，其单位为弧度每秒rads-1。
y
r
o
B A
x
3、速率与角速度的关系：在t时间内，质点从A点运动到B点，所经过的弧长为s=r，则当t0时，s/t的极限值为： y s lim r lim B t 0 t t 0 t 即
1- 3圆周运动(circular motion)
一平面极坐标设一质点在 Oxy 平面内
y
运动，某时刻它位于点 A .矢
径
为 . 于是质点在点 A 的位
置可由 A(r , ) 来确定 .
r
与
x
轴之间的夹角
以 ( r , ) 为坐标的参考系为平面极坐标系 . 它与直角坐标系之间的变换关系为
表示质点相对于S的速度等于质点相对于S`系的速度与S`系相对于S系的速度的矢量和，即质点在两个以恒定的速度做相对运动的参考系中的速度与参考系的关系，也即质点的速度变换公式，这也称为伽利略速度变换式。
习惯上，常把可视为静止的参考系 S作为基本参考系，质点相对于基本参考系S的速度 v 叫绝对速度，把相对于S系运动的参考系 S`作为运动参考系，质点相对于运动参考S`的速度 v' 叫做相对速度，而运动参考系S`相对于基本参考系S的速度 u 叫做牵连速度。由伽利略速度变换式得三者关系：

2013-01-2自然坐标系下的速度-加速度

a
a
0，an
a
an
0
为匀速率曲线运动（圆周运动）
dv dt
0
v2
n0
a an
a
a a a 2 an 2 dv dt2 v2 2
加速度总是指向曲线的凹侧
大学物理
自然坐标系中总加速度为：
a a an
改变速度大小
大小 a a 2 an2
加速度
方向 tan 1 an
下面三种情况分别代表那一类运动？
１. ，an＝0， a 0, 2. ＝常量，an 0，a＝0, 3. ＝常量，an 0，a 0,
１. 变速直线运动２. 匀速率圆周运动３. 变速率圆周运动
大学物理
讨论
质点沿固定的圆形轨道，若速率 v 均匀增加，at 、an、
a以及加速度与速度间的夹角中哪些量随时间变化？
v lim r
t0 t
ds
dt
vr ds v v v
dt
z
v
p s
s
r q
r(t)
r(t t)
o
y x
自然坐标系下的速度表达式
大学物理
讨论物理意义：
vr ds v v v
dt
ds v dt
1、瞬时速率 v：
反映了质点任一时刻沿轨道运动的快慢。
2、任何时刻质点的速度总沿轨道的切线方向，速度只有切线分量而无法向分量。
与切向加速度垂直
大学物理
例题
一质点沿半径为R的圆周按规律 s v0t b运t 2动/ 2，
v0、b 都是正的常量。求：
（1） t 时刻质点的总加速度的大小
（2） t 为何值时，总加速度的大小b

自然坐标圆周运动相对运动

《关于两门新科学的对话和数学证明对话集》一书，总结了他的科学思想以及在物理学和天文学方面的研究成果。
伽利略所取得的巨大成就，开创了近代物理学的新纪元。
自然坐标、圆周运动、角量描述、相对运动
3、绝对运动、牵连运动、相对运动
（1）位矢的关系
r
r'
质点P在相对作匀速直线运动
的两个坐标系中的移动 y y' u
自然坐标、圆周运动、角量描述、相对运动
2、相对运动
物体运动的轨迹依赖于观察者所处的参考系
自然坐标、圆周运动、角量描述、相对运动
伽利略（Galileo Galilei，1564—1642）
伽利略杰出的意大利物理学家和天文学家，实验物理学的先驱者。
他提出著名的相对性原理、惯性原理、抛体的运动定律、摆振动的等时性等。
2
1 x2g
y 2
v02
y
an
a
g
自然坐标、圆周运动、角量描述、相对运动
(2)
o v0
x
vx v0, vy gt
an
a
y
v
vx2 vy2
v02 g 2t 2
tan 1
gt v0
a
dv dt
g2t v02 g2t2
an g2 a 2
g
v0 g v02 g2t 2
与速度同向
与切向加速度垂直
总结：自然坐标
v v
a a an a ann
a
a
an
切向加速度
法向加速度
反映速度大小变化的快慢
反映速度方向变化的快慢程度
dv a dt
an
v2
aa
a 2 an 2

第2讲曲线运动的描述

a n g a
2 2
gv0 v ( gt )
2 0 2
O
x
代入数据，得
a
an
9 .8 2 5 302 (9.8 5) 2
9.8 30 302 (9.8 5) 2
an
8.36m s 2
a
g
y
5.12m s 2
例题2 质点在oxy平面内运动,其运动方程为
切向和法向加速度分别为:
dv d d 2 2 2 2 at ( vx vy ) ( 4 (4t ) ) 3.58m s dt dt dt
an a 2 at2 1.79m s 2
1.3 圆周运动及其描述
运动的线量描述：位置位移速度加速度（直角坐标系，自然坐标系）运动的角量描述：角位置角位移角速度角加速度 (用极坐标系描述圆周运动）
2 2 v vx v y vz2
tangential acceleration normal acceleration
切向加速度 a dv d s 2
dt
2
2
dt
法向加速度 an v
1 y R
y
O
3 2 2
, y y ( x)
R
2 a a a2 an
Δt 时间内转过的角度.
角位移的方向右手定则判定四指沿着质点运动方向弯曲，拇指指向为其正向.
有限大小的角位移Δθ不是矢量[不符合交换律]，无限小的角位移 d才是矢量. 先绕 x 轴转 π/ 2，再绕 y 轴转 π/ 2.
先绕 y 轴转 π/ 2，再绕 x 轴转 π/ 2.
最后的效果是不一样的.

理论力学1-3 自然坐标描述法

v2 an
16/19
x
例 1-3-4
l r
解
q r n
小结第1章新的概念：自然坐标、密切面、主法线、副法线灵活掌握基本公式

自然坐标中的速度自然坐标中的加速度（分量的意义）
v v r n l v r q v v d r l lv vA v l n dt
a — 质点速度大小的变化. an — 质点速度方向的变化. an 总是指向运动轨迹的曲率中心。
第1章
点的运动学
3/19
点的运动学
s
τ
P
s s(t )
s0
P
r
( s) v (t ) s
切向单位矢量
r
O
r
切向加速度
法向加速度
r r ( s ( t ))
4/19
讨论
6/13
v e ( e e )
2e 2sin t a 2
a e 2e 2e 2e
t π / 2
2 (ecos t ) 2 a
1
例 1-4-2 第1章点P以常速度v0沿曲线 = bcos3运动。求
e e
e e
e e e e e
第1章
点的运动学
3/13
点的运动学
e e
横向速度径向速度
2 )e ( )e ( (2
2

2 2v0 e 3b
10/13
例 1-4-3
a 2 2 d 1 ) 0 ( dt

1-5 质点的平面曲线运动

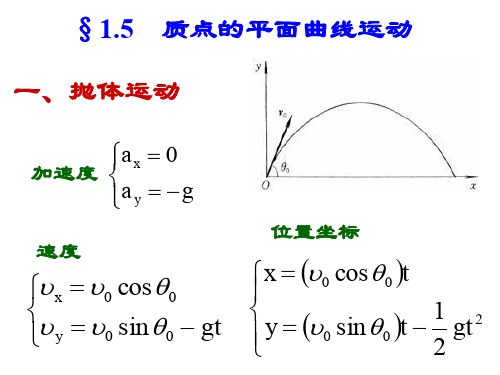
A.切向加速度一定改变，法向加速度也改变; B. 切向加速度可能不变，法向加速度一定改变; C. 切向加速度可能不变，法向加速度不变;
D. 切向加速度一定改变，法向加速度不变;
【例题2】下列那种说法是对的? A. 在圆周运动中，加速度的方向一定指向圆心； B. 匀速率圆周运动的速度和加速度都恒定不变； C. 物体作曲线运动时，速度方向一定在运动轨道的切线方向，法向分速度一定等于零，因此其法向加速度也一定等于零；
②匀变速圆周运动
常量
2
at R，an R
又
dω dt
d dt，
0 0
t 0
时,
，
可得：
0 t 1 2 θ θ 0 0 t t
2 2 2 0 2 ( 0 )
匀变速圆周运动
匀变速直线运动
sincossincosgt加速度速度位置坐标抛体运动轨迹方程忽略空气阻力时抛体运动的轨迹是抛物线1自然坐标系取轨迹上一固定点o为坐标原点规定两个随质点位置变化而改变方向的单位矢量一个是指向质点运动方向的切向单位矢量表示另一个是垂直于切向并指向轨迹凹侧的法向单位矢量可正可负因为质点运动的速度总是沿着轨道的切向所以在自然坐标系中速度矢量可表示为dtdsdsdtds第二项是速度方向变化所引起的加速度分量第一项表示由速度大小变化所引起的加速度分量大小等于速率对时间的变化率方向沿轨道切向为切向加速度加速度趋近于点a等腰oalimlim指向轨迹凹侧与法向单位矢量一致并且由速度方向变化所引起的加速度分量称为法向加速度dtdtdsdsdtdsds2圆周运动的角量描述角坐标匀速圆周运动4匀速圆周运动和匀变速圆周运动可得
dr dr ds (t )et (t ) dt ds dt

自-09工程-复试中国海洋大学工程学院复试考试大纲机械专业

机械工程综合考试性质本学科硕士研究生全国统一招生入学考试专业理论课程笔试。

作为选拔性考试，具有较高的信度、效度、必要的区分度和适当的难度。

考查目标重点考核学生对《工程图学》、《机械制造工程》、《互换性与测量技术》、《工程测试与信息处理》、《机电控制技术》、《液压与气压传动》等本科主干课程的基本概念和基本原理和基本技能的掌握,有关图表、计算公式的综合运用,以及对典型问题的计算和分析能力。

考试内容一、工程图学(一)理论考试部分1．机械制图国家标准的基本规定。

2．组合体的画图、读图及尺寸标注。

3．表示机件的图样画法,如视图，剖视，断面图，简化画法和其他规定画法。

4．零件图的阅读和绘制方法、机械零部件尺寸公差和形位公差基本理论、测量误差和测量数据处理方法、零件表面粗糙度、常用计量器具的工作原理。

5．装配图的绘制、读图及拆绘零件图。

(二）技能考试部分1．常用测绘仪器的基本操作能力。

2．机械零部件的几何参数测绘方法。

3．尺寸公差和形位公差的选择和标注方法。

4．表面粗糙度的选择和标注方法。

5．根据测绘数据，徒手绘制零件草图。

6．根据测绘数据，徒手绘制机械部件的装配示意图。

7．常用计算机绘图软件的操作能力：二维图纸的计算机绘制（AUTOCAD绘图软件）、使用三维建模软件（UG），完成指定零部件的零件建模和装配体建模。

二、机械制造工程(一）理论考试部分1．金属切削过程、切削用量选择2. 六点位原理、工件在机床夹具中的定位3. 机械加工精度基本概念4．影响机械加工精度的因素及其分析5. 机械加工表面质量及其分析6. 工艺规程设计基本概念、生产类型及其工艺特点7. 粗、精基准选择原则8. 加工余量及其计算、工艺尺寸链分析计算９. 先进制造技术概述(二）技能考试部分1．机械加工方法、金属切削机床、刀具选择２．零件加工工艺分析3．工件定位及其定位误差分析、定位方案分析4. 加工误差综合分析5. 工艺规程设计三、互换性与测量技术（一)理论考试部分1．互换性的基本概念，标准和标准化；优先数和优先数系。

自然坐标系中的速度、加速度

速度的矢量表示
总结词
速度的矢量表示包括大小和方向两个方面，通常用箭头表示方向，用绝对值表示大小。
VS
详细描述
矢量表示法是速度最常用的表示方法，它能够完整地描述速度的大小和方向。在自然坐标系中，速度的大小由箭头的长度表示，箭头的指向代表速度的方向。
速度的标量表示
总结词
速度的标量表示只考虑速度的大小，忽略方向，通常用绝对值表示。
特点
自然坐标系与质点运动的具体轨迹相关，可以直观地描述速度和加速度的方向和大小。
自然坐标系的应用
描述曲线运动
自然坐标系常用于描述质点在曲线上的运动，如行星绕太阳的椭圆轨道运动。
分析动力学
在分析力学中，自然坐标系用于描述质点的速度和加速度，进而研究其动力学行为。
自然坐标系与直角坐标系的区别与联系
02
03
健康管理
在健康管理中，个人的速度和加速度可以用来监测身体的运动状态，从而进行科学的健身计划和健康管理。
THANKS FOR WATCHING
感谢您的观看
定义法
根据加速度的定义式计算，即加速度等于速度的变化量除以时间的变化量。
公式法
根据加速度的公式计算，即加速度等于速度的导数或切向加速度。
02
速度在自然坐标系中的表示
速度的定义
总结词
速度是描述物体运动快慢的物理量，定义为物体在单位时间内通过的位移。
详细描述
速度是矢量，具有大小和方向，通常用符号"v"表示。在自然坐标系中，速度的大小等于物体在单位时间内通过的直线距离，方向则与物体位移的方向相同。
详细描述
匀速直线运动是指物体在直线轨道上以恒定速度进行的运动，其方程为 $s = v_0t$，其中 $s$ 是位移， $v_0$ 是初始速度，$t$ 是时间。

1.3 自然坐标系及运用

直线运动坐标 x 速度加速度
dx υ= dt dυ a= dt
圆周运动角坐标 θ 角速度角加速度
ω=
dθ dt dω β= dt
若a=恒量，则
υ − υ o = 2 a ∆x
1 2 ∆x = υo t + at 2 2 2
υ = υo + at
若β=恒量,则
ω = ωo + β t 1 2 ∆θ = ω o t + β t
当质点做圆周运动时，当质点做圆周运动时， ρ 为圆周运动的半径 R ；为常数，则切向加速度为零，如果 v 为常数，则切向加速度为零，合加速度方向指向圆心，称为向心加速度向心加速度；向指向圆心，称为向心加速度；
三．圆周运动在圆周运动中，线量与角量的关系为的关系为：在圆周运动中，线量与角量的关系为：
v dv dτˆ v dv d a= = (vτˆ) = τˆ + v dt dt dt dt
① 切向加速度
dv 表征速度大小变化率的物理量，沿切向 (τˆ)表征速度大小变化率 ( dt )的物理量， v
称切向加速度 aτ 。
d 2s v dv aτ = τˆ = 2 τˆ dt dt
② 法向加速度
v 为恒矢量， a为恒矢量，它一定作匀变
例1：一飞轮，从静止开始以恒角加速度2 rad ⋅ s ：一飞轮，从静止开始以恒角加速度转动，经过某一段时间后开始计时，转动，经过某一段时间后开始计时，在 5s 内飞轮转过75 问在开始计时以前，转过 rad，问在开始计时以前，飞轮转动了多长时间？ 1 2 匀角加速运动，解：匀角加速运动， θ = ω 0 t + β t 2 t = 5s β = 2rad/s 代入 θ = 75rad 75 = 5ω 0 + 25

第一次课-1.1 -1.2确定质点位置的方法

1.2 质点的位移、速度和加速度
一、位移（反映物体位置的变化）
r r (t t ) r (t )
P
s
位移位矢 r 在t 时间内的增量
说明
O

r (t )
r
P
r (t t )
Δr
(1) r是矢量， s 是标量，且大小一般不等 r s r 与Δr ( r)的区别 (2) 分清
x y z
2 2
2
方向
x cos r
y cos r
z cos r
3. 自然坐标法（用于运动轨迹已知的质点）
• O
s
P
说明自然坐标 s 是代数量 4. 运动学方程(函数) 直角坐标自然坐标位矢法
x x(t )
s f (t )

y y (t )
一、质点运动学的基本概念
质点：大小和形状可以忽略的物体
z
参照物
O
y
x
参照物：为了描述物体运动而被选作参考的物体或物体系
二、确定质点位置的常用方法
1. 直角坐标法 P(x, y, z) 2. 位矢法（质点位置由位置矢量描述）
z
r
参照物
y
O
x
位置矢量大小 r
r xi yj zk
v
三、加速度
1. 速度增量 v v (t t ) v (t )
v (t )
B
v (t t )
A

2 . 平均加速度
a v t
r (t )
r (t t )

大学物理第一章第二节圆周运动与一般平面曲线运动

2、角加速度
lim
t 0 t
d
dt
d 2
dt 2
方向？
四、圆周运动中线量和角量的关系 1、线速度与角速度 v R
角速度的方向:
按“右旋规则”确定角加速度的方向: 加速时与方向相同减速时与方向相反
y
R
o
x
2、切向加速度与角加速度 3、法向加速度与角速度
a R
an
v2 R
v
R 2
4、速度分量式
（1）可将抛体运动分解为沿x和y 两个方向的独立运动。
立进行的运动迭加而成。
※
抛体运动方程的矢量形式
v
(v0cos )i
(v0
sin
gt)
j
v0t
r
1
gt
2
2
v dr dt
r
t vdt
0
t 0
(vxi
vy
j )dt
(v0t
cos
)i
(v0t
sin
1 2
gt2 )
j
（2）也可将抛体运动分解为沿初速度方向的匀速直线运动和
t
a a
ax2
a
2 y
R 2
7
五、匀变速率圆周运动
常量，故 at r，an r 2
dω 常量，
dt
又
dω dt d dt，
如 t 0 时, 0 ， 0
可得：
0 t θ θ0 0t
1 2
t
2
2
2 0
2 (
0)
匀变速率圆周运动
0 t
θ
θ0
0t
1 2
t