材料力学习题及答案
材料力学习题及答案
材料力学习题及答案材料力学习题一一、计算题1.(12分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
三.填空题(23分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是__________;单元体只有形状改变而无体积改变的条件是__________________________。
2.(6分)杆件的基本变形一般有______、________、_________、________四种;而应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别用__________、_____________、______________来加以修正。
4.(5分)平面弯曲的定义为______________________________________。
5.(2分)低碳钢圆截面试件受扭时,沿____________截面破坏;铸铁圆截面试件受扭时,沿____________面破坏。
四、选择题(共2题,9分)2.(5分)图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:()材料力学习题二二、选择题:(每小题3分,共24分)1、危险截面是______所在的截面。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 导电性答案:D2. 根据胡克定律,当材料受到正应力时,其应变与应力成正比,比例系数称为:A. 杨氏模量B. 剪切模量C. 泊松比D. 屈服强度答案:A3. 在材料力学中,材料的屈服强度是指:A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料发生弹性变形的应力D. 材料发生脆性断裂的应力答案:A4. 材料的疲劳寿命与下列哪一项无关?A. 材料的疲劳极限B. 应力循环次数C. 材料的弹性模量D. 应力循环的幅度答案:C5. 在材料力学中,下列哪一项不是材料的力学性能指标?A. 硬度B. 韧性C. 密度D. 冲击韧性答案:C二、简答题(每题5分,共10分)6. 简述材料力学中弹性模量和剪切模量的区别。
答:弹性模量,也称为杨氏模量,是描述材料在受到正应力作用时,材料的纵向应变与应力成正比的比例系数。
剪切模量,也称为刚度模量,是描述材料在受到剪切应力作用时,材料的剪切应变与剪切应力成正比的比例系数。
7. 什么是材料的疲劳寿命,它与哪些因素有关?答:材料的疲劳寿命是指材料在反复加载和卸载过程中,从开始加载到发生疲劳断裂所需的循环次数。
它与材料的疲劳极限、应力循环的幅度、材料的微观结构和环境因素等有关。
三、计算题(每题15分,共30分)8. 一根直径为20mm的圆杆,材料的杨氏模量为200GPa,当受到100N的拉力时,求圆杆的伸长量。
答:首先计算圆杆的截面积A = π * (d/2)^2 = π * (0.02/2)^2m^2 = 3.14 * 0.01 m^2。
然后根据胡克定律ΔL = F * L / (A * E),其中 L 为杆长,假设 L = 1m,代入数值得ΔL = 100 * 1 / (3.14* 0.01 * 200 * 10^9) m = 7.96 * 10^-6 m。
材料力学考试题及答案

材料力学考试题及答案一、选择题(每题2分,共10分)1. 材料力学中,下列哪项不是应力的分类?A. 正应力B. 剪应力C. 拉应力D. 扭应力答案:C2. 材料力学中,下列哪项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 硬度答案:D3. 在拉伸试验中,下列哪项是正确的?A. 弹性模量是应力与应变的比值B. 屈服强度是材料开始发生塑性变形的应力C. 抗拉强度是材料在拉伸过程中的最大应力D. 所有选项都是正确的答案:D4. 根据胡克定律,下列哪项描述是错误的?A. 弹性范围内,应力与应变成正比B. 弹性模量是比例极限C. 应力是单位面积上的力D. 应变是单位长度的变形量答案:B5. 材料力学中,下列哪项不是材料的失效形式?A. 屈服B. 断裂C. 疲劳D. 腐蚀答案:D二、填空题(每空1分,共10分)1. 材料在受到拉伸力作用时,其内部产生的应力称为________。
答案:正应力2. 材料在受到剪切力作用时,其内部产生的应力称为________。
答案:剪应力3. 材料力学中,材料在外力作用下发生形变,当外力去除后,材料能够恢复原状的性质称为________。
答案:弹性4. 材料力学中,材料在外力作用下发生形变,当外力去除后,材料不能恢复原状的性质称为________。
答案:塑性5. 材料力学中,材料在外力作用下发生形变,当外力去除后,材料部分恢复原状的性质称为________。
答案:韧性三、简答题(每题5分,共20分)1. 简述材料力学中应力和应变的关系。
答案:材料力学中,应力和应变的关系可以通过胡克定律来描述,即在弹性范围内,应力与应变成正比,比例系数即为弹性模量。
2. 描述材料力学中材料的屈服现象。
答案:材料力学中,屈服现象指的是材料在受到外力作用时,从弹性变形过渡到塑性变形的临界点,此时材料的应力不再随着应变的增加而增加。
3. 解释材料力学中的疲劳破坏。
答案:材料力学中的疲劳破坏是指材料在循环加载下,即使应力水平低于材料的静态强度极限,也会在经过一定循环次数后发生破坏的现象。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 塑性C. 硬度D. 韧性2. 材料在拉伸过程中,当应力达到屈服点后,材料将:A. 断裂B. 产生永久变形C. 恢复原状D. 保持不变3. 材料的弹性模量是指:A. 材料的密度B. 材料的硬度C. 材料的抗拉强度D. 材料在弹性范围内应力与应变的比值4. 根据材料力学的胡克定律,下列说法正确的是:A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变无关D. 应力与应变成线性关系5. 材料的疲劳寿命是指:A. 材料的总寿命B. 材料在循环加载下达到破坏的周期数C. 材料的断裂寿命D. 材料的磨损寿命6. 材料的屈服强度是指:A. 材料在弹性范围内的最大应力B. 材料在塑性变形开始时的应力C. 材料的抗拉强度D. 材料的极限强度7. 材料的断裂韧性是指:A. 材料的硬度B. 材料的抗拉强度C. 材料抵抗裂纹扩展的能力D. 材料的屈服强度8. 材料力学中的泊松比是指:A. 材料的弹性模量B. 材料的屈服强度C. 材料在拉伸时横向应变与纵向应变的比值D. 材料的断裂韧性9. 在材料力学中,下列哪一项是衡量材料脆性程度的指标?A. 弹性模量B. 屈服强度C. 断裂韧性D. 泊松比10. 材料在受力过程中,当应力超过其极限强度时,将:A. 发生弹性变形B. 发生塑性变形C. 发生断裂D. 恢复原状答案1. C2. B3. D4. A5. B6. B7. C8. C9. C10. C试题二、简答题(每题10分,共30分)1. 简述材料力学中材料的三种基本力学性质。
2. 解释什么是材料的疲劳现象,并简述其对工程结构的影响。
3. 描述材料在拉伸过程中的四个主要阶段。
答案1. 材料的三种基本力学性质包括弹性、塑性和韧性。
弹性指的是材料在受到外力作用时发生变形,当外力移除后能够恢复原状的性质。
塑性是指材料在达到一定应力水平后,即使外力移除也无法完全恢复原状的性质。
材料力学的试题及答案

材料力学的试题及答案一、选择题1. 材料力学中,下列哪个选项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 硬度答案:D2. 根据材料力学的理论,下列哪个选项是正确的?A. 材料在弹性范围内,应力与应变成正比B. 材料在塑性变形后可以完全恢复原状C. 材料的屈服强度总是高于其抗拉强度D. 材料的硬度与弹性模量无关答案:A二、填空题1. 材料力学中,应力是指_______与_______的比值。
答案:单位面积上的压力;受力面积2. 在材料力学中,材料的弹性模量E与_______成正比,与_______成反比。
答案:杨氏模量;泊松比三、简答题1. 简述材料力学中材料的三种基本变形类型。
答案:材料力学中材料的三种基本变形类型包括拉伸、压缩和剪切。
2. 描述材料的弹性模量和屈服强度的区别。
答案:弹性模量是指材料在弹性范围内应力与应变的比值,反映了材料的刚性;屈服强度是指材料开始发生永久变形时的应力值,反映了材料的韧性。
四、计算题1. 已知一材料的弹性模量E=200 GPa,杨氏模量E=210 GPa,泊松比ν=0.3,试计算该材料的剪切模量G。
答案:G = E / (2(1+ν)) = 200 / (2(1+0.3)) = 200 / 2.6 ≈ 76.92 GPa2. 某材料的抗拉强度为σt=300 MPa,若该材料承受的应力为σ=200 MPa,试判断材料是否发生永久变形。
答案:由于σ < σt,材料不会发生永久变形。
五、论述题1. 论述材料力学在工程设计中的重要性。
答案:材料力学是工程设计中的基础学科,它提供了对材料在力作用下行为的深入理解。
通过材料力学的分析,工程师可以预测材料在各种载荷下的响应,设计出既安全又经济的结构。
此外,材料力学还有助于新材料的开发和现有材料性能的优化。
2. 讨论材料的疲劳寿命与其力学性能之间的关系。
答案:材料的疲劳寿命与其力学性能密切相关。
材料的疲劳寿命是指在循环载荷作用下材料能够承受的循环次数。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,弹性模量E的单位是()。
A. N/mB. N·mC. PaD. m/N答案:C2. 材料力学中,材料的屈服强度通常用()表示。
A. σyB. σsC. σbD. E答案:A3. 根据胡克定律,当应力超过材料的弹性极限时,材料将()。
A. 保持弹性B. 发生塑性变形C. 发生断裂D. 无法预测答案:B4. 材料力学中,第一强度理论认为材料破坏的原因是()。
A. 最大正应力B. 最大剪应力C. 最大正应变D. 最大剪应变答案:A5. 下列哪种材料不属于脆性材料()。
A. 玻璃B. 铸铁C. 混凝土D. 铝答案:D6. 材料力学中,梁的弯曲应力公式为()。
A. σ = Mc/IB. σ = Mc/IbC. σ = Mc/ID. σ = Mc/Ib答案:C7. 在材料力学中,梁的剪应力公式为()。
A. τ = VQ/IB. τ = VQ/ItC. τ = VQ/ID. τ = VQ/It答案:B8. 材料力学中,梁的挠度公式为()。
A. δ = (5PL^3)/(384EI)B. δ = (5PL^3)/(384EI)C. δ = (PL^3)/(48EI)D. δ = (PL^3)/(48EI)答案:C9. 材料力学中,影响材料屈服强度的因素不包括()。
A. 材料的微观结构B. 加载速度C. 温度D. 材料的密度答案:D10. 材料力学中,影响材料疲劳强度的因素不包括()。
A. 应力集中B. 表面粗糙度C. 材料的硬度D. 材料的导热性答案:D二、填空题(每题2分,共20分)1. 材料力学中,材料在外力作用下,其形状和尺寸发生的变化称为______。
答案:变形2. 材料力学中,材料在外力作用下,其内部产生的相互作用力称为______。
答案:应力3. 材料力学中,材料在外力作用下,其内部产生的相对位移称为______。
答案:应变4. 材料力学中,材料在外力作用下,其内部产生的单位面积上的力称为______。
材料力学试题及答案

材料力学试题及答案一、选择题(每题5分,共25分)1. 下列哪个选项是材料力学的基本假设之一?A. 材料是各向同性的B. 材料是各向异性的C. 材料是均匀的D. 材料是线弹性的答案:A2. 在材料力学中,下列哪个公式表示杆件的正应力?A. σ = F/AB. τ = F/AC. σ = F/LD. τ = F/L答案:A3. 当材料受到轴向拉伸时,下列哪个选项是正确的?A. 拉伸变形越大,材料的强度越高B. 拉伸变形越小,材料的强度越高C. 拉伸变形与材料的强度无关D. 拉伸变形与材料的强度成正比答案:B4. 下列哪种材料在拉伸过程中容易发生断裂?A. 钢材B. 铸铁C. 铝合金D. 塑料答案:B5. 下列哪个选项表示材料的泊松比?A. μ = E/GB. μ = G/EC. μ = σ/εD. μ = ε/σ答案:C二、填空题(每题10分,共30分)6. 材料力学研究的是材料在______作用下的力学性能。
答案:外力7. 材料的强度分为______强度和______强度。
答案:屈服强度、断裂强度8. 材料在受到轴向拉伸时,横截面上的正应力公式为______。
答案:σ = F/A三、计算题(每题25分,共50分)9. 一根直径为10mm的圆钢杆,受到轴向拉伸力F=20kN 的作用,求杆件横截面上的正应力。
解:已知:d = 10mm,F = 20kNA = π(d/2)^2 = π(10/2)^2 = 78.5mm^2σ = F/A = 20kN / 78.5mm^2 = 255.8N/mm^2答案:杆件横截面上的正应力为255.8N/mm^2。
10. 一根长度为1m的杆件,受到轴向拉伸力F=10kN的作用,已知材料的弹性模量E=200GPa,泊松比μ=0.3,求杆件的伸长量。
解:已知:L = 1m,F = 10kN,E = 200GPa,μ = 0.3ε = F/(EA) = 10kN / (200GPa × π(10mm)^2) =0.025δ = εL = 0.025 × 1000mm = 25mm答案:杆件的伸长量为25mm。
《材料力学》习题册附答案

F12312练习 1 绪论及基本概念1-1 是非题(1) 材料力学是研究构件承载能力的一门学科。
( 是 )(2)可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
(是)(3) 构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。
( 是 ) (4) 应力是内力分布集度。
(是 )(5) 材料力学主要研究构件弹性范围内的小变形问题。
(是 ) (6) 若物体产生位移,则必定同时产生变形。
(非 ) (7) 各向同性假设认为,材料沿各个方向具有相同的变形。
(F ) (8) 均匀性假设认为,材料内部各点的力学性质是相同的。
(是)(9) 根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。
(非) (10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(非 )1-2 填空题(1) 根据材料的主要性质对材料作如下三个基本假设:连续性假设、均匀性假设 、各向同性假设 。
(2) 工程中的强度 ,是指构件抵抗破坏的能力; 刚度 ,是指构件抵抗变形的能力。
(3) 保证构件正常或安全工作的基本要求包括 强度 , 刚度 ,和 稳定性三个方面。
3(4) 图示构件中,杆 1 发生 拉伸 变形,杆 2 发生 压缩 变形,杆 3 发生 弯曲 变形。
(5) 认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为 连续性假设。
根据这一假设构件的应力,应变和位移就可以用坐标的 连续 函数来表示。
(6) 图示结构中,杆 1 发生 弯曲变形,构件 2发生 剪切 变形,杆件 3 发生 弯曲与轴向压缩组合。
变形。
(7) 解除外力后,能完全消失的变形称为 弹性变形,不能消失而残余的的那部分变形称为 塑性变形 。
(8) 根据 小变形 条件,可以认为构件的变形远 小于 其原始尺寸。
1-3选择题(1)材料力学中对构件的受力和变形等问题可用连续函数来描述;通过试件所测得的材料的力学性能,可用于构件内部的任何部位。
材料力学试题及答案

材料力学试题及答案一、选择题1. 材料力学中,下列哪个参数是用来描述材料在受力时抵抗变形的能力?A. 弹性模量B. 屈服强度C. 抗拉强度D. 断裂韧性答案:A2. 以下哪种材料在受力后能够完全恢复原状?A. 弹性体B. 塑性体C. 粘弹性体D. 脆性体答案:A3. 应力集中现象主要发生在哪种情况下?A. 材料表面存在缺陷B. 材料内部存在孔洞C. 材料受到均匀分布的载荷D. 材料受到单一集中载荷答案:D4. 根据胡克定律,当应力不超过比例极限时,应力与应变之间的关系是:A. 线性的B. 非线性的C. 指数的D. 对数的答案:A5. 材料的疲劳破坏是指在何种条件下发生的?A. 单次超负荷B. 长期重复载荷C. 瞬间高温D. 腐蚀环境答案:B二、填空题1. 在简单的拉伸和压缩实验中,应力(σ)是力(F)与横截面积(A)的比值,即σ=______。
答案:F/A2. 材料的韧性是指其在断裂前能够吸收的能量,通常通过______试验来测定。
答案:冲击3. 当材料在受力时发生塑性变形,且变形量随时间增加而增加,这种现象称为______。
答案:蠕变4. 剪切应力τ是剪切力(V)与剪切面积(A)的比值,即τ=______。
答案:V/A5. 材料的泊松比是指在单轴拉伸时,横向应变与纵向应变的比值,通常用希腊字母______表示。
答案:ν三、简答题1. 请简述材料弹性模量的定义及其物理意义。
答:弹性模量,又称杨氏模量,是指材料在弹性范围内抵抗形变的能力的量度。
它定义为应力与相应应变的比值。
物理意义上,弹性模量越大,表示材料在受力时越不易发生形变,即材料越硬。
2. 描述材料的屈服现象,并解释屈服强度的重要性。
答:屈服现象是指材料在受到外力作用时,由弹性状态过渡到塑性状态的过程。
在这个过程中,材料首先经历弹性变形,当应力达到某个特定值时,即使应力不再增加,材料也会继续发生显著的塑性变形。
屈服强度是衡量材料开始屈服的应力值,它对于工程设计和材料选择具有重要意义,因为它决定了结构在载荷作用下的安全性和可靠性。
材料力学精选练习题及答案

材料力学精选练习题及答案
材料力学,是力学中的一个重要分支,它主要研究物质的力学
性质和形变行为。
在工程实践中,材料力学的知识和技能非常重要,不仅是理论基础,更是工程设计和制造中必不可少的一部分。
以下是材料力学的一些精选练习题及答案,供大家参考和学习。
1、弹性力学
题目:一个长为L,横截面积为A的钢杆,弹性模量为E,要
求它在受到一定的拉力F后产生的伸长量为δ,求钢杆所受的应力和应变。
解答:应力σ=F/A,应变ε=δ/L,弹性模量E=σ/ε,所以σ=F/A,ε=F/(AE),将δ带入ε可得σ=F(L/AE),ε=F/(AE)。
2、塑性力学
题目:在压缩试验中,一块铜板被加压后,其长度由原来的L
缩短至L',试求其应变。
解答:应变ε=(L-L')/L。
3、断裂力学
题目:一个半径为a的圆柱体被沿着一直径破裂,试求其破裂力F。
解答:破裂力F=πa^2σ_max。
4、疲劳力学
题目:在疲劳试验中,一个试件经过n个周期后发生失效,试求其循环应力幅值σ_a和平均应力σ_m。
解答:循环应力幅值σ_a和平均应力σ_m可根据试件的应力-应变曲线以及可能失效的总循环数和n计算得出。
5、复合材料力学
题目:一个由纤维和基材组成的复合材料,在受到一定的横向压力后,试求其纵向伸长量。
解答:通过复合材料的材料性质和几何体积参数可以计算出纵向伸长量。
以上是一些基本的材料力学练习题,希望对大家有所帮助。
在学习过程中,还需要不断积累和练习,才能真正掌握材料力学的知识和技能,为工程实践提供有力的支持和保障。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 塑性C. 脆性D. 磁性答案:D2. 根据胡克定律,弹簧的伸长量与所受力的关系是:A. 正比B. 反比C. 无关D. 非线性关系答案:A3. 材料的屈服强度是指:A. 材料开始发生永久变形的应力B. 材料发生断裂的应力C. 材料开始发生弹性变形的应力D. 材料达到最大应力点的应力答案:A4. 材料力学中,应力的定义为:A. 材料单位面积上承受的力B. 材料单位长度上承受的力C. 材料单位体积上承受的力D. 材料单位质量上承受的力答案:A5. 材料的泊松比是描述材料在受力时的:A. 弹性变形能力B. 塑性变形能力C. 横向变形与纵向变形的关系D. 断裂韧性答案:C6. 材料的疲劳寿命与下列哪个因素无关?A. 应力水平B. 材料的疲劳极限C. 温度D. 材料的弹性模量答案:D7. 在材料力学中,剪切应力与正应力的区别在于:A. 作用方向B. 作用面积C. 材料的破坏形式D. 材料的应力-应变曲线答案:A8. 材料的硬度通常通过什么测试来测量?A. 拉伸测试B. 压缩测试C. 冲击测试D. 硬度测试答案:D9. 材料的屈服现象通常发生在:A. 弹性阶段B. 塑性阶段C. 断裂阶段D. 疲劳阶段答案:B10. 材料的疲劳破坏通常发生在:A. 材料表面B. 材料内部C. 材料的接合处D. 材料的任何位置答案:A二、简答题(每题10分,共30分)1. 简述材料力学中材料的弹性模量和剪切模量的区别。
答:弹性模量是描述材料在单轴拉伸或压缩时,应力与应变比值的物理量,反映了材料抵抗变形的能力。
剪切模量则是描述材料在剪切状态下,剪切应力与剪切应变的比值,反映了材料抵抗剪切变形的能力。
2. 解释什么是材料的疲劳破坏,并简述其形成过程。
答:材料的疲劳破坏是指在反复加载和卸载的过程中,即使应力水平低于材料的屈服强度,材料也会逐渐发生损伤并最终导致断裂。
材料力学练习题与答案-全

材料力学练习题与答案-全1.当T三Tp时,剪切虎克定律及剪应力互等定理。
A、虎克定律成立,互等定理不成立B、虎克定律不成立,互等定理成立(正确答案)C、均不成立D、二者均成立2.木榫接头,当受F力作用时,接头的剪切面积和挤压面积分别是A、ab,lcB、cb,lbC、lb,cb(正确答案)D、lc,ab3.在下列四种材料中,()不可以应用各向同性假设。
A、铸钢B、玻璃C、松木(正确答案)D、铸铁4.一细长压杆当轴向压力P达到临界压力Pcr时受到微小干扰后发生失稳而处于微弯平衡状态,此时若解除压力P,则压杆的微弯变形。
A、有所缓和B、完全消失(正确答案)C、保持不变D、继续增大;5.矩形截面偏心受压杆件发生变形。
A、轴向压缩、平面弯曲B、轴向压缩、平面弯曲、扭转C、轴向压缩、斜弯曲(正确答案)D、轴向压缩、斜弯曲、扭转6.当杆件处于弯扭组合变形时,对于横截面的中性轴有这样的结论,正确的是:A、一定存在(正确答案)B、不一定存在C、一定不存在7.梁在某一段内作用有向下的分布载荷时,在该段内它的弯矩图为。
A、上凸曲线;(正确答案)B、下凸曲线;C、带有拐点的曲线;D、斜直线8.图示结构中,AB为钢材,BC为铝,在P力作用下()A、AB段轴力大B、BC段轴力大C、轴力一样大(正确答案)D、无法判断9.圆截面的悬臂梁在自由端受集中力的作用,若梁的长度增大一倍,其他条件不变,最大挠度是原来的倍。
图片2.pngA、2B、16C、8(正确答案)D、410.托架由横梁与杆组成。
若将杆由位于梁的下方改为位于梁的上方,其他条件不变,则此托架的承载力。
A、提高(正确答案)B、降低C、不变D、不确定11.单位长度的扭转角e与()无关A、杆的长度(正确答案)B、扭矩C、材料性质D、截面几何性质12.矩形截面拉弯组合变形时,对于横截面的中性轴有以下的结论。
正确的是:。
A、过形心B、过形心且与ZC轴有一夹角;C、不过形心,与ZC轴平行;(正确答案)D、不过形心,与ZC轴有一夹角。
材料力学习题大全及答案
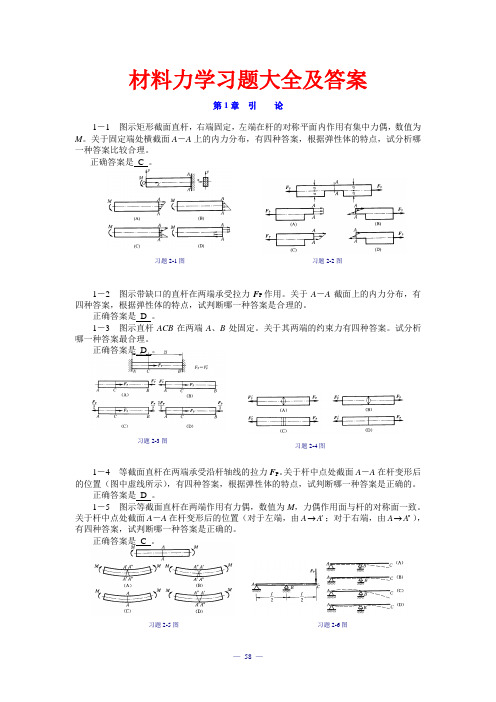
习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A )d d Q x F d M(B )d d Q x F (C )d d Q x F (D )d d Q xF 2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
材料力学考试题及答案

材料力学考试题及答案一、单项选择题(每题2分,共20分)1. 材料力学中,下列哪一项是正确的应力定义?A. 应力是物体内部单位面积上的内力B. 应力是物体内部单位体积上的内力C. 应力是物体内部单位长度上的内力D. 应力是物体内部单位质量上的内力答案:A2. 材料力学中,下列哪一项是正确的应变定义?A. 应变是物体长度的变化量与原始长度的比值B. 应变是物体长度的变化量与当前长度的比值C. 应变是物体体积的变化量与原始体积的比值D. 应变是物体体积的变化量与当前体积的比值答案:A3. 在拉伸试验中,若材料的屈服强度为300MPa,抗拉强度为400MPa,则该材料属于:A. 脆性材料B. 塑性材料C. 弹性材料D. 韧性材料答案:B4. 材料力学中,下列哪一项是正确的弹性模量定义?A. 弹性模量是材料在弹性阶段内应力与应变的比值B. 弹性模量是材料在塑性阶段内应力与应变的比值C. 弹性模量是材料在断裂阶段内应力与应变的比值D. 弹性模量是材料在任何阶段内应力与应变的比值答案:A5. 材料力学中,下列哪一项是正确的泊松比定义?A. 泊松比是材料在受力时横向应变与纵向应变的比值B. 泊松比是材料在受力时纵向应变与横向应变的比值C. 泊松比是材料在受力时体积应变与纵向应变的比值D. 泊松比是材料在受力时体积应变与横向应变的比值答案:A6. 在材料力学中,下列哪一项是正确的剪切应力定义?A. 剪切应力是材料内部单位面积上的剪切力B. 剪切应力是材料内部单位长度上的剪切力C. 剪切应力是材料内部单位体积上的剪切力D. 剪切应力是材料内部单位质量上的剪切力答案:A7. 材料力学中,下列哪一项是正确的扭矩定义?A. 扭矩是力与力臂的乘积B. 扭矩是力与力臂的比值C. 扭矩是力与力臂的商D. 扭矩是力与力臂的差值答案:A8. 在材料力学中,下列哪一项是正确的弯矩定义?A. 弯矩是力与力臂的乘积B. 弯矩是力与力臂的比值C. 弯矩是力与力臂的商D. 弯矩是力与力臂的差值答案:A9. 材料力学中,下列哪一项是正确的截面模量定义?A. 截面模量是截面面积与截面惯性矩的比值B. 截面模量是截面面积与截面惯性矩的乘积C. 截面模量是截面惯性矩与截面面积的比值D. 截面模量是截面惯性矩与截面面积的乘积答案:C10. 在材料力学中,下列哪一项是正确的应力集中定义?A. 应力集中是材料内部应力分布不均匀的现象B. 应力集中是材料内部应力分布均匀的现象C. 应力集中是材料内部应变分布不均匀的现象D. 应力集中是材料内部应变分布均匀的现象答案:A二、填空题(每题2分,共20分)11. 材料力学中,材料的弹性极限是指材料在______阶段的最大应力。
材料力学考试试题及答案

材料力学考试试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性能?A. 弹性B. 塑性C. 韧性D. 硬度2. 材料在拉伸过程中,若应力超过屈服点后继续增加,材料将进入:A. 弹性阶段B. 塑性阶段C. 断裂阶段D. 疲劳阶段3. 材料的弹性模量E表示的是:A. 材料的硬度B. 材料的韧性C. 材料的弹性程度D. 材料的屈服强度4. 根据材料力学理论,下列哪一项不是材料的疲劳破坏特点?A. 疲劳破坏是局部的B. 疲劳破坏是突然的C. 疲劳破坏是可预测的D. 疲劳破坏是累积的5. 在材料力学中,下列哪一项不是材料的失效模式?A. 屈服B. 断裂C. 腐蚀D. 疲劳6. 材料的屈服强度和抗拉强度之间的关系是:A. 屈服强度总是大于抗拉强度B. 屈服强度总是小于抗拉强度C. 屈服强度等于抗拉强度D. 两者之间没有固定关系7. 材料的疲劳寿命与下列哪一项无关?A. 应力水平B. 材料的微观结构C. 环境温度D. 材料的密度8. 材料的冲击韧性通常用下列哪一项来表示?A. 抗拉强度B. 屈服强度C. 硬度D. 冲击吸收能量9. 材料的疲劳寿命与加载频率的关系是:A. 正相关B. 负相关C. 无关D. 先正相关后负相关10. 在材料力学中,下列哪一项不是材料的应力-应变曲线的特点?A. 弹性阶段B. 屈服阶段C. 塑性阶段D. 线性阶段二、简答题(每题10分,共20分)1. 请简述材料的弹性模量和屈服强度的区别和联系。
2. 材料的疲劳破坏与静载下的破坏有何不同?三、计算题(每题15分,共30分)1. 已知一材料的弹性模量E=200 GPa,泊松比ν=0.3。
若材料受到拉伸力F=10 kN,试计算材料的应变ε和应力σ。
2. 某材料的疲劳寿命S-N曲线已知,当应力水平为σ=200 MPa时,疲劳寿命N=1000次。
若应力水平降低到150 MPa,根据Basis Goodman关系,计算新的疲劳寿命。
材料力学试题带答案解析

材料力学试题带答案解析一、填空题(每题5分,共25分)1. 材料力学的任务是研究材料在外力作用下的________、________和________。
答案:变形、破坏、强度解析:材料力学主要研究材料在外力作用下的力学行为,包括变形、破坏和强度等三个方面。
变形是指材料在力的作用下发生的形状和尺寸的改变;破坏是指材料在力的作用下失去承载能力;强度是指材料抵抗破坏的能力。
2. 材料的屈服强度是指材料在受到________作用时,能够承受的最大________。
答案:拉伸、应力解析:屈服强度是指材料在受到拉伸作用时,能够承受的最大应力。
当材料受到的应力超过屈服强度时,材料将发生塑性变形。
3. 在弹性范围内,胡克定律的表达式为________。
答案:σ = Eε解析:胡克定律是描述材料在弹性范围内应力与应变关系的定律。
其中,σ表示应力,E表示弹性模量,ε表示应变。
在弹性范围内,应力与应变呈线性关系。
4. 材料的弹性模量越大,表示材料的________越大。
答案:刚度解析:弹性模量是衡量材料刚度的重要指标,弹性模量越大,表示材料在受到外力作用时,抵抗变形的能力越强,即刚度越大。
5. 材料的泊松比是指材料在受到________作用时,横向应变与纵向应变的比值。
答案:拉伸解析:泊松比是描述材料在受到拉伸或压缩作用时,横向应变与纵向应变比值的系数。
当材料受到拉伸作用时,横向应变与纵向应变呈反比关系。
二、选择题(每题5分,共25分)1. 下列哪种材料具有较大的屈服强度?()A. 钢材B. 铝材C. 木材D. 塑料答案:A解析:钢材是一种具有较高屈服强度的材料,相比铝材、木材和塑料,其屈服强度更大。
2. 下列哪种情况下,材料的泊松比最小?()A. 拉伸B. 压缩C. 剪切D. 扭转答案:B解析:泊松比是描述材料在受到拉伸或压缩作用时,横向应变与纵向应变比值的系数。
在压缩情况下,材料的泊松比最小。
3. 下列哪个参数可以表示材料的抗剪强度?()A. 屈服强度B. 抗压强度C. 抗拉强度D. 剪切模量答案:D解析:剪切模量是描述材料在受到剪力作用时,抵抗变形的能力的参数,可以表示材料的抗剪强度。
材料力学考试题及答案

材料力学考试题及答案一、选择题(每题2分,共10分)1. 材料力学中,下列哪一项不是材料的基本力学性能?A. 弹性B. 塑性C. 韧性D. 密度答案:D2. 根据胡克定律,当应力和应变成正比时,下列哪一项是正确的?A. 应力和应变成正比B. 应力和应变成反比C. 应力和应变无关D. 应力和应变的关系是线性的答案:A3. 材料在受到外力作用时,如果外力消失后,材料不能恢复到原来的形状,这种现象称为:A. 弹性变形B. 塑性变形C. 蠕变D. 断裂答案:B4. 在材料力学中,下列哪一项不是常见的应力状态?A. 单轴应力状态B. 双轴应力状态C. 三轴应力状态D. 四轴应力状态答案:D5. 材料的屈服强度是指:A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料发生蠕变的应力D. 材料发生疲劳的应力答案:A二、填空题(每题2分,共10分)1. 材料力学中,______是指材料在受到外力作用后,能够恢复到原来形状的能力。
答案:弹性2. 当材料受到拉伸时,其横截面面积会______。
答案:减小3. 材料力学中的______是指材料在外力作用下抵抗变形的能力。
答案:强度4. 在材料力学中,______是指材料在受到外力作用后,不能恢复到原来形状的变形。
答案:塑性变形5. 材料的______是指材料在受到外力作用时,单位面积上的力。
答案:应力三、简答题(每题5分,共20分)1. 简述材料力学中弹性模量的定义及其物理意义。
答案:弹性模量,也称为杨氏模量,是描述材料弹性特性的物理量,定义为材料在弹性范围内,应力与应变的比值。
它表示材料抵抗形变的能力,弹性模量越大,材料的弹性越好。
2. 什么是材料的疲劳?请简述其产生的原因。
答案:材料的疲劳是指在循环载荷作用下,材料在远低于其屈服强度的应力水平下发生断裂的现象。
产生疲劳的原因主要是循环应力超过材料的疲劳极限,导致材料内部缺陷逐渐扩展,最终导致断裂。
3. 请解释材料力学中的泊松比,并说明其对材料性能的影响。
材料力学练习题与答案

材料力学练习题与答案1.灰铸铁的硬度测定方法是()A.布氏硬度(正确答案)B.洛氏硬度C.维氏硬度2.下列物质属于晶体的是()A.松香B.水晶(正确答案)C.石蜡3.冷塑性变形的金属晶粒重新结晶为均匀的等轴晶粒需进行的热处理是( )A.去应力退火B.完全退火C.再结晶退火(正确答案)4.下列情况属于相变过程的是()A.液态金属的结晶(正确答案)B.晶粒长大C.冷变形金属的再结晶5.在铁碳合金的基本组成相中,属于金属化合物是()A.铁素体B.渗碳体(正确答案)C.奥氏体6.调质是()A.淬火+低温回火B.淬火+中温回火C.淬火+高温回火(正确答案)7.下列关于合金元素在钢中的作用论述错误的是()A.合金元素的加入使铁素体产生固溶强化B.合金元素的加入使奥氏体相区的大小发生改变C.除钴外,合金元素的加入使C曲线左移(正确答案)8.阻止石墨化的元素有()A.硅B.磷C.硫(正确答案)9.属于软基体上分布硬质点的轴承合金有()A.锡基巴氏合金(正确答案)B.铝基轴承合金C.珠光体灰铸铁10.碳以片状石墨形式存在的铸铁是()A.灰铸铁(正确答案)B.白口铸铁C.球墨铸铁11. 截面上的全应力的方向( )A、平行于截面(正确答案)B、垂直于截面C、可以与截面任意夹角D、与截面无关12. 脆性材料的延伸率( )A、小于5%(正确答案)B、小于等于5%C、大于5%D、大于等于5%13.危险截面是()所在的截面。
A、最大面积B、最小面积C、最大应力(正确答案)D、最大内力14. 描述构件上一截面变形前后的夹角叫()A、线位移B、转角(正确答案)C、线应变D、角应变15. 塑性材料的名义屈服应力使用()A、σS表示(正确答案)B、σb表示C、σp表示D、σ0.2表示16. 描述构件上一截面变形前后的夹角叫()A、线位移B、转角(正确答案)C、线应变D、角应变17.塑性材料的名义屈服应力使用()A、σS表示(正确答案)B、σb表示C、σp表示D、σ0.2表示18. 构件在外力作用下()的能力称为稳定性。
材料力学的试题及答案

材料力学的试题及答案一、选择题(每题2分,共20分)1. 材料力学研究的对象是什么?A. 材料的化学性质B. 材料的力学性质C. 材料的热学性质D. 材料的电学性质2. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 韧性C. 硬度D. 塑性3. 材料力学中,应力的定义是什么?A. 力与面积的比值B. 力与体积的比值C. 力与长度的比值D. 面积与力的比值4. 材料力学中,下列哪一项不是材料的基本变形形式?A. 拉伸B. 压缩C. 扭转D. 膨胀5. 材料力学中,弹性模量表示什么?A. 材料的硬度B. 材料的韧性C. 材料的弹性D. 材料的塑性二、简答题(每题10分,共30分)6. 简述材料力学中材料的三种基本力学性质。
7. 解释材料力学中的应力-应变曲线,并说明其各阶段的意义。
8. 什么是材料的屈服强度,它在工程设计中的重要性是什么?三、计算题(每题25分,共50分)9. 一根直径为20mm,长度为200mm的圆杆,在两端受到100kN的拉伸力。
如果材料的弹性模量为200GPa,求圆杆的伸长量。
10. 一个直径为50mm,长为100mm的空心圆筒,内径为40mm,受到一个扭矩为500N·m。
如果材料的剪切模量为80GPa,求圆筒的最大剪切应力。
答案一、选择题1. B. 材料的力学性质2. C. 硬度3. A. 力与面积的比值4. D. 膨胀5. C. 材料的弹性二、简答题6. 材料力学中材料的三种基本力学性质包括弹性、塑性和韧性。
弹性是指材料在受到外力作用后能恢复原状的能力;塑性是指材料在达到一定应力后,即使撤去外力也不会完全恢复原状的性质;韧性是指材料在断裂前能吸收和分散能量的能力。
7. 应力-应变曲线是描述材料在受力过程中应力与应变之间关系的曲线。
它通常包括弹性阶段、屈服阶段、强化阶段和颈缩阶段。
弹性阶段表示材料在受力后能够完全恢复原状;屈服阶段是材料开始产生永久变形的点;强化阶段是材料在屈服后继续承受更大的应力而不断裂;颈缩阶段是材料接近断裂前发生的局部变细现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
资料力学-学习指导及习题谜底之迟辟智美创作第一章绪论1-1 图示圆截面杆,两端接受一对方向相反、力偶矩矢量沿轴线且年夜小均为M的力偶作用.试问在杆件的任一横截面m-m上存在何种内力分量,并确定其年夜小.解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其年夜小即是M.1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ.解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零.试问杆件横截面上存在何种内力分量,并确定其年夜小.图中之C点为截面形心.解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×××103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示.试求棱边AB与AD的平均正应变及A 点处直角BAD的切应变.解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最年夜值.解:(a) F N AB=F,F N BC=0,F N,max=F=F(b) F N AB=F,F N BC=-F,F N,max(c) F N AB=-2 kN, F N2BC=1 kN,F N CD=3 kN,F N=3 kN,max(d) F N AB=1 kN,F N BC=-1 kN,F N=1 kN,max2-2 图示阶梯形截面杆AC,接受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm.如欲使BC与AB段的正应力相同,试求BC段的直径.解:因BC与AB段的正应力相同,故2-3 图示轴向受拉等截面杆,横截面面积A=500 mm2,载荷F=50 kN.试求图示斜截面m-m上的正应力与切应力,以及杆内的最年夜正应力与最年夜切应力.解:2-4(2-11)图示桁架,由圆截面杆1与杆2组成,并在节点A接受载荷F=80kN作用.杆1、杆2的直径分别为d1=30mm和d2=20mm,两杆的资料相同,屈服极限σ=320MPa,平安因数n s.试校核桁架的强度.s解:由A点的平衡方程可求得1、2两杆的轴力分别为由此可见,桁架满足强度条件.2-5(2-14)图示桁架,接受载荷F作用.试计算该载荷的许用值[F].设各杆的横截面面积均为A,许用应力均为[σ].解:由C点的平衡条件由B点的平衡条件1杆轴力为最年夜,由其强度条件2-6(2-17)图示圆截面杆件,接受轴向拉力F作用.设拉杆的直径为d,端部墩头的直径为D,高度为h,试从强度方面考虑,建立三者间的合理比值.已知许用应力[σ]=120MPa,许用切应力[τ]=90MPa,许用挤压应力[σbs]=240MPa.解:由正应力强度条件由切应力强度条件由挤压强度条件式(1):式(3)得式(1):式(2)得故D:h:d::12-7(2-18)图示摇臂,接受载荷F1与F2作用.试确定轴销B的直径d.已知载荷F1=50kN,F2,许用切应力[τ]=100MPa,许用挤压应力[σ]=240MPa.bs解:摇臂ABC受F1、F2及B点支座反力F B三力作用,根据三力平衡汇交定理知F B的方向如图(b)所示.由平衡条件由切应力强度条件由挤压强度条件故轴销B的直径第三章轴向拉压变形3-1 图示硬铝试样,厚度δ=2mm,试验段板宽b=20mm,标距l=70mm.在轴向拉F=6kN的作用下,测得试验段伸长Δl,板宽缩短Δb.试计算硬铝的弹性模量E与泊松比μ.解:由胡克定律3-2(3-5) 图示桁架,在节点A处接受载荷F作用.从试验中测得杆1与杆2的纵向正应变分别为ε1×10-4与ε2×10-4.试确定载荷F及其方位角θ之值.已知杆1与杆2的横截面面积A1=A2=200mm2,弹性模量E1=E2=200GPa.解:杆1与杆2的轴力(拉力)分别为由A点的平衡条件(1)2+(2)2并开根,便得式(1):式(2)得3-3(3-6) 图示变宽度平板,接受轴向载荷F作用.试计算板的轴向变形.已知板的厚度为δ,长为l,左、右真个宽度分别为b1与b2,弹性模量为E.解:3-4(3-11) 图示刚性横梁AB,由钢丝绳并经无摩擦滑轮所支持.设钢丝绳的轴向刚度(即发生单位轴向变形所需之力)为k,试求当载荷F作用时端点B的铅垂位移.解:设钢丝绳的拉力为T,则由横梁AB的平衡条件钢丝绳伸长量由图(b)可以看出,C点铅垂位移为Δl/3,D点铅垂位移为2Δl/3,则B点铅垂位移为Δl,即 3-5(3-12) 试计算图示桁架节点A的水平与铅垂位移.设各杆各截面的拉压刚度均为EA.解:(a) 各杆轴力及伸长(缩短量)分别为因为3杆不变形,故A点水平位移为零,铅垂位移即是B点铅垂位移加2杆的伸长量,即(b)点的水平与铅垂位移分别为(注意AC杆轴力虽然为零,但对A位移有约束)3-6(3-14) 图a所示桁架,资料的应力-应变关系可用方程σn=Bε暗示(图b),其中n和B为由实验测定的已知常数.试求节点C的铅垂位移.设各杆的横截面面积均为A.(a) (b)解:2根杆的轴力都为2根杆的伸长量都为则节点C的铅垂位移3-7(3-16) 图示结构,梁BD为刚体,杆1、杆2与杆3的横截面面积与资料均相同.在梁的中点C接受集中载荷F作用.试计算该点的水平与铅垂位移.已知载荷F=20kN,各杆的横截面面积均为A=100mm2,弹性模量E=200GPa,梁长l=1000mm.解:各杆轴力及变形分别为梁BD作刚体平动,其上B、C、D三点位移相等3-8(3-17) 图示桁架,在节点B和C作用一对年夜小相等、方向相反的载荷F.设各杆各截面的拉压刚度均为EA,试计算节点B和C间的相对位移ΔB/C.解:根据能量守恒定律,有3-9(3-21) 由铝镁合金杆与钢质套管组成一复合杆,杆、管各载面的刚度分别为E1A1与E2A2.复合杆接受轴向载荷F作用,试计算铝镁合金杆与钢管横载面上的正应力以及杆的轴向变形.解:设杆、管接受的压力分别为F N1、F N2,则F N1+F N2=F (1)变形协调条件为杆、管伸长量相同,即联立求解方程(1)、(2),得杆、管横截面上的正应力分别为杆的轴向变形3-10(3-23) 图示结构,杆1与杆2的弹性模量均为E,横截面面积均为A,梁BC为刚体,载荷F=20kN,许用拉应力[σt]=160MPa,许用压应力[σc]=110MPa.试确定各杆的横截面面积.解:设杆1所受压力为F N1,杆2所受拉力为F N2,则由梁BC的平衡条件得变形协调条件为杆1缩短量即是杆2伸长量,即联立求解方程(1)、(2)得因为杆1、杆2的轴力相等,而许用压应力小于许用拉应力,故由杆1的压应力强度条件得3-11(3-25) 图示桁架,杆1、杆2与杆3分别用铸铁、铜和钢制成,许用应力分别为[σ1]=40MPa,[σ2]=60MPa,[σ3]=120MPa,弹性模量分别为E1=160GPa,E2=100GPa,E3=200GPa.若载荷F=160kN,A1=A2=2A3,试确定各杆的横截面面积.解:设杆1、杆2、杆3的轴力分别为F N1(压)、F N2(拉)、F N3(拉),则由C点的平衡条件杆1、杆2的变形图如图(b)所示,变形协调条件为C点的垂直位移即是杆3的伸长,即联立求解式(1)、(2)、(3)得由三杆的强度条件注意到条件 A1=A2=2A3,取A1=A2=2A3=2448mm2.3-12(3-30) 图示组合杆,由直径为30mm的钢杆套以外径为50mm、内径为30mm的铜管组成,二者由两个直径为10mm的铆钉连接在一起.铆接后,温度升高40°,试计算铆钉剪切面上的切应力.钢与铜的弹性模量分别为E s=200GPa与E c=100GPa,线膨胀系数分别为αl s×10-6℃-1与αl c=16×10-6℃-1.解:钢杆受拉、铜管受压,其轴力相等,设为F N,变形协调条件为钢杆和铜管的伸长量相等,即铆钉剪切面上的切应力3-13(3-32) 图示桁架,三杆的横截面面积、弹性模量与许用应力均相同,并分别为A、E与[σ],试确定该桁架的许用载荷[F].为了提高许用载荷之值,现将杆3的设计长度l酿成l+Δ.试问当Δ为何值时许用载荷最年夜,其值[F max]为何.解:静力平衡条件为变形协调条件为联立求解式(1)、(2)、(3)得杆3的轴力比杆1、杆2年夜,由杆3的强度条件若将杆3的设计长度l酿成l+Δ,要使许用载荷最年夜,只有三杆的应力都到达[σ],此时变形协调条件为第四章扭转4-1(4-3) 图示空心圆截面轴,外径D=40mm,内径d=20mm,扭矩T=1kN•m.试计算横截面上的最年夜、最小扭转切应力,以及A点处(ρA=15mm)的扭转切应力.解:因为τ与ρ成正比,所以4-2(4-10) 实心圆轴与空心圆轴通过牙嵌离合器连接.已知轴的转速n=100 r/min,传递功率P=10 kW,许用切应力[τ]=80MPa,d1/d2.试确定实心轴的直径d,空心轴的内、外径d1和d2.解:扭矩由实心轴的切应力强度条件由空心轴的切应力强度条件4-3(4-12) 某传动轴,转速n=300 r/min,轮1为主动轮,输入功率P1=50kW,轮2、轮3与轮4为从动轮,输出功率分别为P2=10kW,P3=P4=20kW.(1) 试求轴内的最年夜扭矩;(2) 若将轮1与轮3的位置对换,试分析对轴的受力是否有利.解:(1) 轮1、2、3、4作用在轴上扭力矩分别为轴内的最年夜扭矩若将轮1与轮3的位置对换,则最年夜扭矩酿成最年夜扭矩变小,固然对轴的受力有利.4-4(4-21) 图示两端固定的圆截面轴,接受扭力矩作用.试求支反力偶矩.设扭转刚度为已知常数.解:(a) 由对称性可看出,M A=M B,再由平衡可看出M A=M B=M(b)显然M A=M B,变形协调条件为解得(c)(d)由静力平衡方程得变形协调条件为联立求解式(1)、(2)得4-5(4-25) 图示组合轴,由套管与芯轴并借两端刚性平板牢固地连接在一起.设作用在刚性平板上的扭力矩为M=2kN·m,套管与芯轴的切变模量分别为G1=40GPa与G2=80GPa.试求套管与芯轴的扭矩及最年夜扭转切应力.解:设套管与芯轴的扭矩分别为T1、T2,则T1+T2 =M=2kN·m (1)变形协调条件为套管与芯轴的扭转角相等,即联立求解式(1)、(2),得套管与芯轴的最年夜扭转切应力分别为4-6(4-28) 将截面尺寸分别为φ100mm×90mm 与φ90mm×80mm的两钢管相套合,并在内管两端施加扭力矩M0=2kN·m后,将其两端与外管相焊接.试问在去失落扭力矩M0后,内、外管横截面上的最年夜扭转切应力.解:去失落扭力矩M0后,两钢管相互扭,其扭矩相等,设为T,设施加M0后内管扭转角为φ0.去失落M0后,内管带动外管回退扭转角φ1(此即外管扭转角),剩下的扭转角(φ0-φ1)即为内管扭转角,变形协调条件为内、外管横截面上的最年夜扭转切应力分别为4-7(4-29) 图示二轴,用突缘与螺栓相连接,各螺栓的资料、直径相同,并均匀地排列在直径为D=100mm的圆周上,突缘的厚度为δ=10mm,轴所接受的扭力矩为M=5.0 kN·m,螺栓的许用切应力[τ]=100MPa,许用挤压应力 [σbs]=300MPa.试确定螺栓的直径d.解:设每个螺栓接受的剪力为F S,则由切应力强度条件由挤压强度条件故螺栓的直径第五章弯曲应力1(5-1)、平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox坐标取向如图所示.试分析下列平衡微分方程中哪一个是正确的.解:B正确.平衡微分方程中的正负号由该梁Ox坐标取向及分布载荷q(x)的方向决定.截面弯矩和剪力的方向是不随坐标变动的,我们在处置这类问题时都按正方向画出.可是剪力和弯矩的增量面和坐标轴的取向有关,这样在对梁的微段列平衡方程式时就有所分歧,参考下图.当Ox坐标取向相反,向右时,相应(b),A是正确的.但无论A、B弯矩的二阶导数在q向上时,均为正,反之,为负.2(5-2)、对接受均布载荷q的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种谜底中哪一种是毛病的.解:A是毛病的.梁截面上的弯矩的正负号,与梁的坐标系无关,该梁上的弯矩为正,因此A是毛病的.弯矩曲线和一般曲线的凸凹相同,和y轴的方向有关,弯矩二阶导数为正时,曲线开口向着y轴的正向.q(x)向下时,无论x轴的方向如何,弯矩二阶导数均为负,曲线开口向着y轴的负向,因此B、C、D都是正确的.3(5-3)、应用平衡微分方程画出下列各梁的剪力图和弯矩图,并确定|F Q|max和|M|max.(本题和下题内力图中,内力年夜小只标注相应的系数.)解:4(5-4)、试作下列刚架的弯矩图,并确定|M|max.解:5(5-5)、静定梁接受平面载荷,但无集中力偶作用,其剪力图如图所示.若已知A端弯矩M(0)=0,试确定梁上的载荷(包括支座反力)及梁的弯矩图.解:6(5-6)、已知静定梁的剪力图和弯矩图,试确定梁上的载荷(包括支座反力).解:7(5-7)、静定梁接受平面载荷,但无集中力偶作用,其剪力图如图所示.若已知E端弯矩为零.请:(1)在Ox坐标中写出弯矩的表达式;(2)试确定梁上的载荷及梁的弯矩图.解:8(5-10) 在图示梁上,作用有集度为m=m(x)的分布力偶.试建立力偶矩集度、剪力及弯矩间的微分关系.解:用坐标分别为x与x+d x的横截面,从梁中切取一微段,如图(b).平衡方程为9(5-11) 对图示杆件,试建立载荷集度(轴向载荷集度q或扭力矩集度m)与相应内力(轴力或扭矩)间的微分关系.解:(a) 用坐标分别为x与x+d x的横截面,从杆中切取一微段,如图(c).平衡方程为(b) 用坐标分别为x与x+d x的横截面,从杆中切取一微段,如图(d).平衡方程为10(5-18) 直径为d的金属丝,环绕在直径为D的轮缘上.试求金属丝内的最年夜正应变与最年夜正应力.已知资料的弹性模量为E.解:11(5-23) 图示直径为d的圆木,现需从中切取一矩形截面梁.试问:(1) 如欲使所切矩形梁的弯曲强度最高,h和b应分别为何值;(2) 如欲使所切矩形梁的弯曲刚度最高,h和b应分别为何值;解:(1) 欲使梁的弯曲强度最高,只要抗弯截面系数取极年夜值,为此令(2) 欲使梁的弯曲刚度最高,只要惯性矩取极年夜值,为此令12(5-24) 图示简支梁,由№18工字钢制成,在外载荷作用下,测得横截面A底边的纵向正应变ε×10-4,试计算梁内的最年夜弯曲正应力.已知钢的弹性模量E=200GPa,a=1m.解:梁的剪力图及弯矩图如图所示,从弯矩图可见:13(5-32) 图示槽形截面铸铁梁,F=10kN,M e=70kN·m,许用拉应力[σt]=35MPa,许用压应力[σc]=120MPa.试校核梁的强度. 解:先求形心坐标,将图示截面看成一年夜矩形减去一小矩形惯性矩弯矩图如图所示,C 截面的左、右截面为危险截面. 在 C 左截面,其最年夜拉、压应力分别为夜拉、压应力分别为在 C 右截面,其最年 故14(5-35) 图示简支梁,由四块尺寸相同的木板胶接而成,试校核其强度. 已 知 载 荷 F=4kN , 梁 跨 度 l=400mm , 截 面 宽 度 b=50mm , 高 度 h=80mm,木板的许用应力[σ]=7MPa,胶缝的许用切应力[τ]=5MPa.解:从内力图可见木板的最年夜正应力由剪应力互等定理知:胶缝的最年夜切应力即是横截面上的最年夜切 应力 可见,该梁满足强度条件.15(5-41) 图示简支梁,接受偏斜的集中载荷 F 作用,试计算梁内的最年 夜弯曲正应力.已知 F=10kN,l=1m,b=90mm,h=180mm.解: 16(5-42) 图示悬臂梁,接受载荷 F1 与 F2 作用,已知 F1=800N,F2,l=1m,许用应力[σ]=160MPa.试分别按下列要求确定截面尺寸: (1) 截面为矩形,h=2b; (2) 截面为圆形.解:(1) 危险截面位于固定端(2)17(5-45) 一铸铁梁,其截面如图所示,已知许用压应力为许用拉应力 的 4 倍,即[σc]=4 [σt].试从强度方面考虑,宽度 b 为何值最佳. 解: 又因 y1+y2=400 mm,故 y1=80 mm,y2=320 mm.将截面对形心轴 z 取静 矩,得18(5-54) 图示直径为 d 的圆截面铸铁杆,接受偏心距为 e 的载荷 F 作用. 试证明:当 e≤d/8 时,横截面上不存在拉应力,即截面核心为 R=d/8 的圆形区域. 解: 19(5-55) 图示杆件,同时接受横向力与偏心压力作用,试确定 F 的许用 值.已知许用拉应力[σt]=30MPa,许用压应力[σc]=90MPa. 解:故 F 的许用值为.第 七 章 应力、应变状态分析7-1(7-1b) 已知应力状态如图所示(应力单位为 ),试用解析法计算 图中指定截面的正应力与切应力.解: 与 截面的应力分别为:;;;MPa7-2(7-2b)已知应力状态如图所示(应力单位为 ),试用解析法计算 图中指定截面的正应力与切应力.解: 与 截面的应力分别为:;;;7-3(7-2d)已知应力状态如图所示(应力单位为 ),试用图解法计算 图中指定截面的正应力与切应力.解:如图,得: 指定截面的正应力 切应力7-4(7-7) 已知某点 A 处截面 AB 与 AC 的应力如图所示(应力单位为 ),试用图解法求主应力的年夜小及所在截面的方位.解:由图,根据比例尺,可以获得:,,最年夜切应力.7-5(7态如图 向应力 力、最10c)已知应力状 所示,试画三 圆,并求主应 年夜正应力与解:对图示应力状态, 是主应力状态,其它两个主应力由 、 、 确定.在 平面内,由坐标( , )与( , )分别确定 和 点,以 为直径画 圆与 轴相交于 和 .再以 及 为直径作圆,即得三向应力圆.由上面的作图可知,主应力为,,,7-6(7-12)已知应力状态如图所示(应力单位为 ),试求主应力的年 夜小.解: 与 截面的应力分别为:;;;在 截面上没有切应力,所以是主应力之一.;;;7-7(7-13)已知构件概况某点处的正应变,,切应变,试求该概况处 方位的正应变 与最年夜应变 及其所在方位.解:得:7-8(7-20)图示矩形截面杆,接受轴向载荷 F 作用,试计算线段 AB 的正 应变.设截面尺寸 b 和 h 与资料的弹性常数 E 和μ均为已知.解:,,,AB 的正应酿成7-9(7-21)在构件概况某点 O 处,沿 , 与 方位,粘贴三个应变片,测得该三方位的正应变分别为,与,该概况处于平面应力状态,试求该点处的应力 , 与 .已知资料的弹性模量,泊松比解:显然,,并令,于是得切应变:7-10(7-6)图示受力板件,试证明 A 点处各截面的正应力与切应力均为零.证明:若在尖点 A 处沿自由鸿沟取三角形单位体如图所示,设单位体 、 面上的应力分量为 、 和 、 ,自由鸿沟上的应力分量为 ,则有由于、,因此,必有 、 、.这时,代表 A 点应力状态的应力圆缩为 坐标的原点,所以 A 点为零应力状态.7-11(7-15)构件概况某点 处,沿 , , 与 方位粘贴四个应变片,并测得相应正应变依次为,,与,试判断上述测试结果是否可靠.解:很明显,,得:又得:根据实验数据计算获得的两个 结果纷歧致,所以,上述丈量结果不 成靠.第 八 章应力状态与强度理论 1、 (8-4)试比力图示正方形棱柱体在下列两中情况下的相当应力 , 弹性常数 E 和μ均为已知. (a) 棱柱体轴向受压; (b) 棱柱体在刚性方模中轴向受压.解:对图(a)中的情况,应力状态如图(c) 对图(b)中的情况,应力状态如图(d)所以,,2、 (8-6)图示钢质拐轴,接受集中载荷 F 作用.试根据第三强度理论确 定轴 AB 的直径.已知载荷 F=1kN,许用应力[σ]=160Mpa. 解:扭矩弯矩 由 得:所以,3、 (8-10)图示齿轮传动轴,用钢制成.在齿轮Ⅰ上,作用有径向力、切向力;在齿轮Ⅱ上,作用有切向力、径向力.若许用应力[σ]=100Mpa,试根据第四强度理论确定轴径.解:计算简图如图所示,作 、 、 图.从图中可以看出,危险截面为 B 截面.其内力分量为: 由第四强度理论 得:4、8-4 圆截面轴的危险面上受有弯矩My、扭矩Mx 和轴力FNx 作 用,关于危险点的应力状态有下列四种.试判断哪一种是正确的. 请选择正确谜底. (图中微元上平行于纸平面的面对应着轴的横截面) 答:B5、 (8-13)图示圆截面钢杆,接受载荷 , 与扭力矩 作用.试根据第三强度理论校核杆的强度.已知载荷N,,扭力矩,许用应力[σ]=160Mpa.解:弯矩满足强度条件.6、 (8-25)图示铸铁构件,中段为一内径 D=200mm、壁厚δ=10mm 的圆筒,圆筒内的压力p=1Mpa,两真个轴向压力F=300kN,资料的泊松比μ,许用拉应力[σt]=30Mpa.试校核圆筒部份的强度.解:,,由第二强度理论:满足强度条件.7、(8-27)图薄壁圆筒,同时接受内压p与扭力矩M作用,由实验测得筒壁沿轴向及与轴线成方位的正应变分别为和.试求内压p与扭力矩M之值.筒的内径为D、壁厚δ、资料的弹性模量E与泊松比μ均为已知.解:,,,很显然,8、(8-22)图示油管,内径D=11mm,壁厚δ,内压p,许用应力[σ]=100Mpa.试校核油管的强度.解:,,由第三强度理论,满足强度条件.9、(8-11)图示圆截面杆,直径为d,接受轴向力F与扭矩M作用,杆用塑性资料制成,许用应力为[σ].试画出危险点处微体的应力状态图,并根据第四强度理论建立杆的强度条件.解:危险点的应力状态如图所示.,由第四强度理论,,可以获得杆的强度条件:10、(8-17)图示圆截面圆环,缺口处接受一对相距极近的载荷作用.已知圆环轴线的半径为,截面的直径为,资料的许用应力为,试根据第三强度理论确定的许用值.解:危险截面在A或B截面A:,,截面B:,由第三强度理论可见,危险截面为A截面.,得:即的许用值为:11、(8-16)图示等截面刚架,接受载荷与作用,且.试根据第三强度理论确定的许用值.已知许用应力为,截面为正方形,边长为,且.解:危险截面在A截面或C、D截面,C截面与D截面的应力状态一样. C截面:由第三强度理论,得:A截面:由第三强度理论,得:比力两个结果,可得:的许用值:12、(8-25)球形薄壁容器,其内径为,壁厚为,接受压强为p之内压.试证明壁内任一点处的主应力为,.证明:取球坐标,对球闭各点,以球心为原点.,,由于结构和受力均对称于球心,故球壁各点的应力状态相同.且由于球壁很薄.,对球壁上的任一点,取通过该点的直径平面(如图),由平衡条件对球壁内的任一点,因此,球壁内的任一点的应力状态为:,证毕.。
