(完整word版)人工智能习题答案搜索推理技术.docx
人工智能课后习题答案(清华大学出版社)

3
1
8
4
7
6
5
仙1(5)
K(5)
J(7)
2
3
1
8
4
7
6
5
1
2
3
8
4
7
6
5
1
2
3
8
4
7
6
5
F
L(5)
1
2
3
7
8
4
6
5
1
2
3
8
4
7
6
5
2
3
1
8
4
7
6
5
1
2
3
8
4
7
6
5
J(5)
A
I(5)
G(5)此
2
3
1
8
4
7
6
5
1
3
7
8
4
6
5
〔2)(0(釘肯i
九•上A•一
、丄:丿
上d
0丿11丿
第3章
3.18
(1)证明:待归结的命题公式为
(此文档为Word格式,下载后可以任意编辑修改!)
试卷装订封面
学年第学期
课程名称:
课程代码
学生系别
专业
班级
任课教师
阅卷教师
考试方式
开卷□闭卷V
考试日期
考试时间
阅卷日期
装订教师
装订日期
缺卷学生姓名及原因:
无
附:课程考试试卷分析表、期末考核成绩登记表
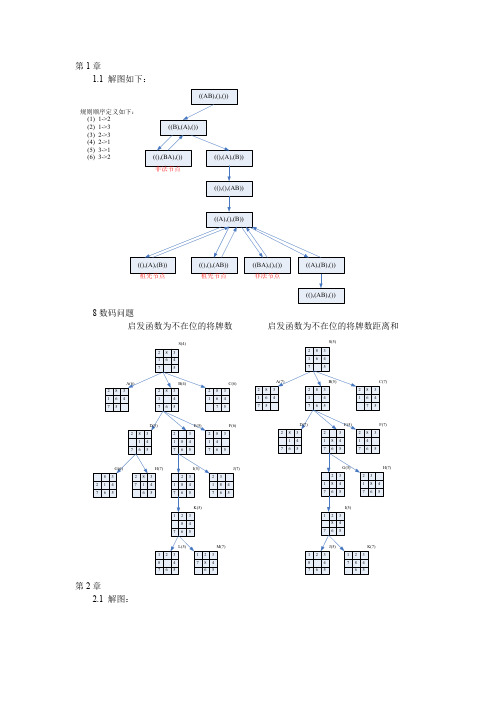
1.1解图如下:
规则顺序定义如下:
(1) 1->2
(完整word版)人工智能课后练习题

上海大学《人工智能》网络课课后习题答案1。
1育才新工科-人工智能简介1【判断题】《人工智能》课程为理工类通选课,本课程给予学生的主要是思想而不是知识。
对1.2图灵是谁?1【单选题】图灵曾协助军方破解()的著名密码系统Enigma。
A、英国B、美国C、德国D、日本2【判断题】电影《模仿游戏》是纪念图灵诞生90周年而拍摄的电影。
X3【判断题】图灵使用博弈论的方法破解了Enigma。
对1.3为什么图灵很灵?1【单选题】1937年,图灵在发表的论文()中,首次提出图灵机的概念。
A、《左右周期性的等价》B、《论可计算数及其在判定问题中的应用》C、《可计算性与λ可定义性》D、《论高斯误差函数》2【单选题】1950年,图灵在他的论文()中,提出了关于机器思维的问题.A、《论数字计算在决断难题中的应用》B、《论可计算数及其在判定问题中的应用》C、《可计算性与λ可定义性》D、《计算和智能》3【判断题】存在一种人类认为的可计算系统与图灵计算不等价。
X4【判断题】图灵测试是指测试者与被测试者(一个人和一台机器)隔开的情况下,通过一些装置(如键盘)向被测试者随意提问。
如果测试者不能确定出被测试者是人还是机器,那么这台机器就通过了测试,并被认为具有人类智能。
对1.4为什么图灵不灵?1【单选题】以下叙述不正确的是()。
A、图灵测试混淆了智能和人类的关系B、机器智能的机制必须与人类智能相同C、机器智能可以完全在特定的领域中超越人类智能D、机器智能可以有人类智能的创造力2【单选题】在政府报告中,()的报告使用“机器智能”这个词汇。
A、中国B、英国C、德国D、美国3【多选题】机器智能可以有自己的“人格"体现主要表现在().A、模型间的对抗—智能进化的方式B、机器智能的协作-机器智能的社会组织C、机器智能是社会的实际生产者D、机器智能可以有人类智能的创造力4【判断题】图灵测试存在的潜台词是机器智能的极限可以超越人的智能,机器智能可以不与人的智能可比拟.X1.5人类智能与机器智能如何共融及未来1【单选题】以下关于未来人类智能与机器智能共融的二元世界叙述不正确的是()。
人工智能确定性推理部分参考答案

人工智能确定性推理部分参考答案(共8页)-本页仅作为预览文档封面,使用时请删除本页-确定性推理部分参考答案1 判断下列公式是否为可合一,若可合一,则求出其最一般合一。
(1) P(a, b), P(x, y)(2) P(f(x), b), P(y, z)(3) P(f(x), y), P(y, f(b))(4) P(f(y), y, x), P(x, f(a), f(b))(5) P(x, y), P(y, x)解:(1) 可合一,其最一般和一为:σ={a/x, b/y}。
(2) 可合一,其最一般和一为:σ={y/f(x), b/z}。
(3) 可合一,其最一般和一为:σ={ f(b)/y, b/x}。
(4) 不可合一。
(5) 可合一,其最一般和一为:σ={ y/x}。
2 把下列谓词公式化成子句集:(1)(∀x)(∀y)(P(x, y)∧Q(x, y))(2)(∀x)(∀y)(P(x, y)→Q(x, y))(3)(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y)))(4)(∀x) (∀y) (∃z)(P(x, y)→Q(x, y)∨R(x, z))解:(1) 由于(∀x)(∀y)(P(x, y)∧Q(x, y))已经是Skolem标准型,且P(x, y)∧Q(x, y)已经是合取范式,所以可直接消去全称量词、合取词,得{ P(x, y), Q(x, y)}再进行变元换名得子句集:S={ P(x, y), Q(u, v)}(2) 对谓词公式(∀x)(∀y)(P(x, y)→Q(x, y)),先消去连接词“→”得:(∀x)(∀y)(¬P(x, y)∨Q(x, y))此公式已为Skolem标准型。
再消去全称量词得子句集:S={¬P(x, y)∨Q(x, y)}(3) 对谓词公式(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y))),先消去连接词“→”得:(∀x)(∃y)(P(x, y)∨(¬Q(x, y)∨R(x, y)))此公式已为前束范式。
人工智能复习参考(带答案).doc

复习参考题一、填空I•构成产生式系统的基本元素有综合数据库、规则库、控制系统,控制策略按执行规则的方式分类,分为止向、逆向、双向三类。
2•归结过程中控制策略的作用是给出控制策略,以使仅对选择合适的子句间方可做归结,避免多余的、不必要的归结式出现或者说,少做些归结仍能导出空子句。
常见的控制策略有线性归结策略、支持集策略、单元归结、输入归结。
3.公式G和公式的子句集并不等值,但它们在不可满足的意义下是一致的。
4.与或图的启发式搜索算法(A0*算法)的两个过程分别是图生成过程即扩展节点和计算耗散值的过程。
5.人工智能的研究途径主要有两种不同的观点,一种观点称为符号主义,认为人类智能基木单元是符号。
另一种观点称为连接主义(仿牛主义),认为职能的基本单元是神经元。
6.集合{P(a, x, f (g(y))? P(z, f (z) ,f(u)))的mgu (最一般合一置换)为{z/a, f(x)/x, u/g(y)}o7•语义网络是对知识的有向图表示方法,一个最简单的语义网络是一个形如节点1、弧、节点2的三元组,语义网络可以描述事物间多种复杂的语义关系、常用ISA、AKO弧表示节点间具有类屈的分类关系。
语义网络下的推理是通过继承和匹配实现的。
8.当前人工智能研究的热点之一就是机器学习。
常见的机器学习方法可分为连接学习、归纳学习、分析学习和遗传算法与分类器系统等。
一个机器学习系统应有环境、知识库、学习环节和执行环节四个基本部分组成。
9•常用的知识表示法有逻辑表示法、产牛式规则表示法、语义网络表示法、框架理论表示法、过程表示法等。
10.有两个A*算法A1和A2,若A1比A2有较多的启发信息,贝9hl(n)>h2(n)oII.关于A算法与A*算法,若规定h(n)M0,并J1定义启发函数:P|c(n)=g*(n)+h*(n) 表示初始状态S。
经点n到Fl标状态Sg最优路径的费用。
其屮g*(n)为So到n的最小费用,h*(n)为到Sg的实际最小费用。
人工智能技术导论(第三版)习题.docx

三大块: 一、搜索1.什么是搜索?有哪两大类搜索方法?两者的区别是什么?2.什么是状态空间?用状态空间表示问题时,什么是问题的解?什么是最优解,最优解唯一吗?3.在状态空间的搜索过程中,Open表和Closed表的作用与区别是什么?4.广度优先搜索与深度优先搜索有何区别?什么时候使用广度?什么时候使用深度?5. 下列问题应使用什么优先策略?1.国际象棋程序2.医疗诊断程序3.寻找使机器人从A点到B点的路径规划程序4.一个决定从原料到最终产品的生产步骤地最优次序的程序5.用于判断两个命题演算表达式是否等同的程序6.分析深度和广度的优缺点。
7.什么是与树?什么是或树?什么是与/或树?什么是可解节点?什么是解树?8.何为估价函数?在估价函数中,g(n)和h(n)各起什么作用?9.移动将牌游戏:B B W W EB表示黑色将牌,W表示白色将牌,E表示空格,走法为:(1)任意一个将牌可移入邻近的空格,其代价规定为1(2)任何一个将牌可相隔…个其他的将牌跳入空格,其代价为跳过奖牌的数H加1。
游戏要达到的目标是把所有的W移到B的左边,请定义一个启发式函数h(n),并给出用这个启发式函数产生的搜索树。
10.与或树如下图所示,请分别用与或树的广度和深度搜索求出解树。
二、确定性推理(一阶谓词)1.什么是置换?什么是合一?什么是二元归结式?2.什么是子句集?如何将谓词公式转化为子句集?3.把下列谓词公式转化为子句集。
1.(Vx)(Vy)(P(x,y)A2U,y))2.(Vx)(3y)(P(x, y) v (g(x, y) T R(x, y)))4.对下列各题分别证明G是否为Fl, F2,……Fn 的逻辑结论1.F1: (Vx)(P(x) t (Vy)(Q(y) t 7(九刃))F2: (3x)(P(x) A (Vy)(/?(y) L(x, y)))G:(色)(R(x) t2.F:(V X)(P(X)A((2(«)V2O)G: (%)(P(x)人Q(x))5.设有如下一段知识张、王、李都属于高山协会,该协会的每个成员不是滑雪运动员就是登山运动员,登山运动员不喜欢雨, 而且任一个不喜欢雪的运动员不是滑雪运动员,王讨厌李所喜欢的一切东西,而喜欢张所讨厌的一切东西, 张喜欢雨和雪。
(完整word版)人工智能课后习题答案(清华大学出版社)
第1章 1.1 解图如下:(1) 1->2(2) 1->3(3) 2->3(6) 3->2(5) 3->1(4) 2->1 8数码问题 启发函数为不在位的将牌数启发函数为不在位的将牌数距离和S(4)S(5)第2章 2.1 解图:第3章 3.18(1)证明:待归结的命题公式为()P Q P ∧→,合取范式为:P Q P ∧∧,求取子句集为{,,}S P Q P =,对子句集中的子句进行归结可得:① P ② Q③P ④ ①③归结 由上可得原公式成立。
(2)证明:待归结的命题公式为())(()())P Q R P Q P R →→∧→→→(,合取范式为:()()P Q R P Q P R ∨∨∧∨∧∧,求取子句集为{,,,}S P Q R P Q P R =∨∨∨,对子句集中的子句进行归结可得:① P Q R ∨∨ ② P Q ∨③ P ④R ⑤ Q②③归结⑥ P R ∨ ①④归结⑦ R ③⑥归结 ⑧ ④⑦归结 由上可得原公式成立。
(3)证明:待归结的命题公式为()(())Q P Q P Q →∧→→,合取范式为:()()Q P Q P Q ∨∧∨∧,求取子句集为{,,}S Q P Q P Q =∨∨,对子句集中的子句进行归结可得:① Q P ∨ ② Q③ Q P ∨④ P ①②归结 ⑤ P ②③归结 ⑥ ④⑤归结 由上可得原公式成立。
3.19 答案(1) {/,/,/}mgu a x b y b z = (2) {(())/,()/}mgu g f v x f v u = (3) 不可合一(4) {/,/,/}=mgu b x b y b z3.23 证明R1:所有不贫穷且聪明的人都快乐:(()()())∀∧→x Poor x Smart x Happy x R2:那些看书的人是聪明的:(()())∀→x read x Smart xR3:李明能看书且不贫穷:()()∧read Li Poor LiR4:快乐的人过着激动人心的生活:(()())∀→x Happy x Exciting x 结论李明过着激动人心的生活的否定:()Exciting Li将上述谓词公式转化为子句集并进行归结如下:由R1可得子句:①()()()Poor x Smart x Happy x∨∨由R2可得子句:②()()read y Smart y∨由R3可得子句:③()read Li④()Poor Li由R4可得子句:⑤()()∨Happy z Exciting z有结论的否定可得子句:⑥()Exciting Li根据以上6条子句,归结如下:⑦()Happy Li⑤⑥Li/z⑧()()∨⑦①Li/xPoor Li Smart Li⑨()Smart Li⑧④⑩()read Li⑨②Li/y⑩③⑪第4章4.9 答案4.11 答案第5章 5.9 答案 解:把该网络看成两个部分,首先求取(1|12)P T S S ∧。
(完整word版)人工智能 第7章 参考答案

第7章机器学习参考答案7-6 设训练例子集如下表所示:序号属性分类x1x21 T T +2 T T +3 T F -4 F F +5 F T _6 F T _请用ID3算法完成其学习过程。
解:设根节点为S,尽管它包含了所有的训练例子,但却没有包含任何分类信息,因此具有最大的信息熵。
即:H(S)= - (P(+)log2 P(+) + P(-)log2 P(-))式中P(+)=3/6,P(-)=3/6分别是决策方案为“+”或“-”时的概率。
因此有H(S)= - ((3/6)log2(3/6) + (3/6)log2(3/6))=1按照ID3算法,需要选择一个能使S的期望熵为最小的一个属性对根节点进行扩展,因此我们需要先计算S关于每个属性的条件熵:H(S|x i)= ( |S T| / |S|)* H(S T) + ( |S F| / |S|)* H(S F)其中,T和F为属性x i的属性值,S T和S F分别为x i=T或x i=F时的例子集,|S|、| S T|和|S F|分别为例子集S、S T和S F的大小。
下面先计算S关于属性x1的条件熵:在本题中,当x1=T时,有:S T={1,2,3}当x1=F时,有:S F={4,5,6}其中,S T和S F中的数字均为例子集S中的各个例子的序号,且有|S|=6,| S T |=| S F |=3。
由S T可知,其决策方案为“+”或“-”的概率分别是:P ST(+)=2/3P ST (-)=1/3因此有:H(S T)= - (P ST (+)log2 P ST (+) + P ST (-)log2 P ST (- ))= - ((2/3)log2(2/3) + (1/3)log2(1/3))=0.9183再由S F可知,其决策方案为“+”或“-”的概率分别是:P SF (+)=1/3P SF (-)=2/3则有:H (S F)= - (P SF (+)log2 P SF (+) + P SF (-)log2 P SF (- ))= - ((1/3)log2(1/3)+ (2/3)log2(2/3))=0.9183将H(S T)和H (S F)代入条件熵公式,有:H(S|x1)=(|S T|/|S|)H(S T)+ (|S F|/|S|)H(S F)=(3/6)﹡0.9183 + (3/6)﹡0.9183=0.9183下面再计算S关于属性x2的条件熵:在本题中,当x2=T时,有:S T={1,2,5,6}当x2=F时,有:S F={3,4}其中,S T和S F中的数字均为例子集S中的各个例子的序号,且有|S|=6,| S T |=4,| S F |=2。
人工智能习题作业推理I习题答案

5. 非单调推理的特点是:
(D)
A 在整个推理过程中,只采用正向推理,而不用反向推理
B 在整个推理过程中,只采用反向推理,而不用正向推理
C 在整个推理过程中,已知为真的命题数目随时间而严格减少
D 在整个推理过程中,已知为真的命题数目并不一定随时间而严格增加
6. 已知规则“如果张三是 25 岁,则李四很可能是 20 岁”,请选出下列表达式
D 启用规则不一定是触发规则
16. 假设有四条规则:
R1: IF 他在家 THEN 他做饭
R2: IF 他在家且他妻子也在家 THEN 他妻子做饭
R3: IF 他在家且他儿子也在家 THEN 他做饭
R4: IF 他在家且他儿子和妻子也在家 THEN 他妻子做饭
请问:当数据库为{他在家, 他妻子在家}时,哪些规则有冲突? ( A )
论 启动方法 从一个事件启动
解答 由询问关于目标状态的一个问题而
透明程序 推理方向 优点 缺点
不能解释其推理过程 由底向上推理 算法简单,容易实现 盲目搜索,可能会求解许多
启动 可解释其推理过程 由顶向下推理 搜索目的性强,推理效率高 目标的选择具有盲目性,可能会求
与总目标无关的子目标,每 解许多假的目标;当可能的结论数
D. (AGE HIS-FARTHER 25)
8. 公式(▽x){[(彐 y)(▽z)P(x,y,z)]=>(▽u)Q(x,u)},在消去蕴涵符号后,得到:
(C)
A ~(▽x){[(彐 y)(▽z)P(x,y,z)] ∧(▽u)Q(x,u)}
B (▽x){~[(彐 y)(▽z)P(x,y,z)] ∧(▽u)Q(x,u)}
C (▽x){~[(彐 y)(▽z)P(x,y,z)] ∨(▽u)Q(x,u)}
(完整word版)人工智能导论课参考答案第2章

第2章知识表示方法部分参考答案2.8设有如下语句,请用相应的谓词公式分别把他们表示出来:(1)有的人喜欢梅花,有的人喜欢菊花,有的人既喜欢梅花又喜欢菊花。
解:定义谓词P(x):x是人L(x,y):x喜欢y其中,y的个体域是{梅花,菊花}。
将知识用谓词表示为:(∃x )(P(x)→L(x, 梅花)∨L(x, 菊花)∨L(x, 梅花)∧L(x, 菊花))(2) 有人每天下午都去打篮球。
解:定义谓词P(x):x是人B(x):x打篮球A(y):y是下午将知识用谓词表示为:(∃x )(∀y) (A(y)→B(x)∧P(x))(3)新型计算机速度又快,存储容量又大。
解:定义谓词NC(x):x是新型计算机F(x):x速度快B(x):x容量大将知识用谓词表示为:(∀x) (NC(x)→F(x)∧B(x))(4) 不是每个计算机系的学生都喜欢在计算机上编程序。
解:定义谓词S(x):x是计算机系学生L(x, pragramming):x喜欢编程序U(x,computer):x使用计算机将知识用谓词表示为:¬(∀x) (S(x)→L(x, pragramming)∧U(x,computer))(5)凡是喜欢编程序的人都喜欢计算机。
解:定义谓词P(x):x是人L(x, y):x喜欢y将知识用谓词表示为:(∀x) (P(x)∧L(x,pragramming)→L(x, computer))2.9 用谓词表示法求解机器人摞积木问题。
设机器人有一只机械手,要处理的世界有一张桌子,桌上可堆放若干相同的方积木块。
机械手有4个操作积木的典型动作:从桌上拣起一块积木;将手中的积木放到桌之上;在积木上再摞上一块积木;从积木上面拣起一块积木。
积木世界的布局如下图所示。
解:(1) 先定义描述状态的谓词CLEAR(x):积木x 上面是空的。
ON(x, y):积木x 在积木y 的上面。
ONTABLE(x):积木x 在桌子上。
HOLDING(x):机械手抓住x 。
《人工智能》课后习题答案

《人工智能》课后习题答案第一章绪论1.1答:人工智能确实是让机器完成那些假如由人来做则需要智能的情况的科学。
人工智能是相关于人的自然智能而言,即用人工的方法和技术,研制智能机器或智能系统来仿照延伸和扩展人的智能,实现智能行为和“机器思维”,解决需要人类专家才能处理的问题。
1.2答:“智能”一词源于拉丁“Legere”,意思是收集、聚拢,智能通常用来表示从中进行选择、明白得和感受。
所谓自然智能确实是人类和一些动物所具有的智力和行为能力。
智力是针对具体情形的,依照不同的情形有不同的含义。
“智力”是指学会某种技能的能力,而不是指技能本身。
1.3答:专家系统是一个智能的运算机程序,他运用知识和推理步骤来解决只有专家才能解决的复杂问题。
即任何解题能力达到了同领域人类专家水平的运算机程序度能够称为专家系统。
1.4答:自然语言处理—语言翻译系统,金山词霸系列机器人—足球机器人模式识别—Microsoft Cartoon Maker博弈—围棋和跳棋第二章知识表达技术2.1解答:(1)状态空间(State Space)是利用状态变量和操作符号,表示系统或问题的有关知识的符号体系,状态空间是一个四元组(S,O,S0,G):S—状态集合;O—操作算子集合;S0—初始状态,S0⊂S;G—目的状态,G⊂S,(G可若干具体状态,也可满足某些性质的路径信息描述)从S0结点到G结点的路径被称为求解路径。
状态空间一解是一有限操作算子序列,它使初始状态转换为目标状态:O1 O2 O3 OkS0→−−−S1→−−−S2→−−−……→−−−G其中O1,…,Ok即为状态空间的一个解(解往往不是唯独的)(2)谓词逻辑是命题逻辑的扩充和进展,它将原子命题分解成客体和谓词两个部分。
与命题逻辑中命题公式相对应,谓词逻辑中也有谓词(命题函数)公式、原子谓词公式、复合谓词公式等概念。
一阶谓词逻辑是谓词逻辑中最直观的一种逻辑。
(3)语义网络是一种采纳网络形式表示人类知识的方法。
(完整word版)人工智能考试必备之简答题2

1、简述问题归约的主要组成部分.答问题归约主要由三部分组成: 一个初始问题描述;一套把问题变换为子问题的操作符;一套本原问题描述。
2、简述宽度优先搜索算法。
答:(1) 把起始节点放到OPEN表中(如果该起始节点为目标节点,则求得一个解答)。
(2)如果OPEN是个空表,则没有解,失败退出;否则继续. (3) 把第一个节点(节点n)从OPEN表移出,并把它放入CLOSED扩展节点表中。
(4) 扩展节点n。
如果没有后继节点,则转向上述第(2)步. (5) 把n的所有后继节点放到OPEN表的末端,提供从这些后继节点回到n的指针(6) 如果n的任一个后继节点是个目标节点,则找到一个解答,成功退出;否则转向第(2)步.3、计算智能的含义是什么?它涉及哪些研究分支?答:计算智能是一种智力方式的低层认知,它取决于制造者提供的数值数据,而不依赖于知识。
它与人工智能的主要区别在于它不含知识精品。
计算智能涉及神经计算、模糊计算、进化计算和人工生命等领域.4、简述智能和智能机器的含义.答:人的智能是人类理解和学习事物的能力,或者说,智能是思考和理解的能力而不是本能做事的能力。
智能是一种应用知识处理环境的能力或由目标准则衡量的抽象思考能力。
能够在各类环境中自主地或交互地执行各种拟人任务(anthropomorphic tasks) 的机器。
智能机器是一种能够呈现出人类智能行为的机器,而这种智能行为是人类用大脑考虑问题或者创造思想。
5、简述一个完整的符号系统具有的基本功能.(1)输入符号(input)(2)输出符号(output) (3)存储符号(store) (4)复制符号(copy) (5)建立符号结构:通过找出各符号间的关系,在符号系统中形成符号结构;(6)条件性迁移(conditional tramsfer):根据已有符号,继续完成活动过程.6、简述从反演树求取对某个问题的答案的过程?(1)把由目标公式的否定产生的每个子句添加到目标公式否定之否定的子句中去。
(完整版)人工智能习题解答

人工智能第1部分绪论1-1.什么是人工智能?试从学科和能力两方面加以说明。
答:从学科方面定义:人工智能是计算机科学中涉及研究、设计和应用智能机器的一个分支。
它的近期目标在于研究用机器来模拟和执行人脑的某些智力功能,并开发相关理论和技术从能力方面定义:人工智能是智能机器所执行的通常与人类智能有关的智能行为,如判断、推理、证明、识别、感知、理解、通信、设计、思考、规划、学习和问题求解等思维活动。
1-2.在人工智能的发展过程中,有哪些思想和思潮起了重要作用?答:1)数理逻辑和关于计算本质的新思想,提供了形式推理概念与即将发明的计算机之间的联系;2)1956年第一次人工智能研讨会召开,标志着人工智能学科的诞生;3)控制论思想把神经系统的工作原理与信息理论、控制理论、逻辑以及计算联系起来,影响了许多早期人工智能工作者,并成为他们的指导思想;4)计算机的发明与发展;5)专家系统与知识工程;6)机器学习、计算智能、人工神经网络和行为主义研究,推动人工智能研究的近一步发展。
1-3.为什么能够用机器(计算机)模仿人的智能?答:物理符号系统的假设:任何一个系统,如果它能够表现出智能,那么它就必定能执行输入符号、输出符号、存储符号、复制符号、建立符号结构、条件迁移6种功能。
反之,任何系统如果具有这6种功能,那么它就能够表现出智能(人类所具有的智能)。
物理符号系统的假设伴随有3个推论。
推论一:既然人具有智能,那么他(她)就一定是各物理符号系统;推论二:既然计算机是一个物理符号系统,它就一定能够表现出智能;推论三:既然人是一个物理符号系统,计算机也是一个物理符号系统,那么我们就能够用计算机来模拟人的活动。
1-4.人工智能的主要研究内容和应用领域是什么?其中,哪些是新的研究热点?答:研究和应用领域:问题求解(下棋程序),逻辑推理与定理证明(四色定理证明),自然语言理解,自动程序设计,专家系统,机器学习,神经网络,机器人学(星际探索机器人),模式识别(手写识别,汽车牌照识别,指纹识别),机器视觉(机器装配,卫星图像处理),智能控制,智能检索,智能调度与指挥(汽车运输高度,列车编组指挥),系统与语言工具。
(完整word版)人工智能课后答案

第一章课后习题1、对N=5、k≤3时,求解传教士和野人问题的产生式系统各组成部分进行描述(给出综合数据库、规则集合的形式化描述,给出初始状态和目标条件的描述),并画出状态空间图。
2、对量水问题给出产生式系统描述,并画出状态空间图.有两个无刻度标志的水壶,分别可装5升和2升的水.设另有一水缸,可用来向水壶灌水或倒出水,两个水壶之间,水也可以相互倾灌.已知5升壶为满壶,2升壶为空壶,问如何通过倒水或灌水操作,使能在2升的壶中量出一升的水来.3、对梵塔问题给出产生式系统描述,并讨论N为任意时状态空间的规模。
相传古代某处一庙宇中,有三根立柱,柱子上可套放直径不等的N个圆盘,开始时所有圆盘都放在第一根柱子上,且小盘处在大盘之上,即从下向上直径是递减的。
和尚们的任务是把所有圆盘一次一个地搬到另一个柱子上去(不许暂搁地上等),且小盘只许在大盘之上。
问和尚们如何搬法最后能完成将所有的盘子都移到第三根柱子上(其余两根柱子,有一根可作过渡盘子使用)。
求N=2时,求解该问题的产生式系统描述,给出其状态空间图。
讨论N为任意时,状态空间的规模。
4、对猴子摘香蕉问题,给出产生式系统描述。
一个房间里,天花板上挂有一串香蕉,有一只猴子可在房间里任意活动(到处走动,推移箱子,攀登箱子等)。
设房间里还有一只可被猴子移动的箱子,且猴子登上箱子时才能摘到香蕉,问猴子在某一状态下(设猴子位置为a,箱子位置为b,香蕉位置为c),如何行动可摘取到香蕉.5、对三枚钱币问题给出产生式系统描述及状态空间图。
设有三枚钱币,其排列处在"正、正、反"状态,现允许每次可翻动其中任意一个钱币,问只许操作三次的情况下,如何翻动钱币使其变成"正、正、正”或”反、反、反”状态。
6、说明怎样才能用一个产生式系统把十进制数转换为二进制数,并通过转换141.125这个数为二进制数,阐明其运行过程。
7、设可交换产生式系统的一条规则R可应用于综合数据库D来生成出D',试证明若R存在逆,则可应用于D’的规则集等同于可应用于D的规则集。
(完整版)人工智能(部分习题答案及解析)

1.什么是人类智能?它有哪些特征或特点?定义:人类所具有的智力和行为能力。
特点:主要体现为感知能力、记忆与思维能力、归纳与演绎能力、学习能力以及行为能力。
2.人工智能是何时、何地、怎样诞生的?解:人工智能于1956年夏季在美国Dartmouth大学诞生。
此时此地举办的关于用机器模拟人类智能问题的研讨会,第一次使用“人工智能”这一术语,标志着人工智能学科的诞生。
3.什么是人工智能?它的研究目标是?定义:用机器模拟人类智能。
研究目标:用计算机模仿人脑思维活动,解决复杂问题;从实用的观点来看,以知识为对象,研究知识的获取、知识的表示方法和知识的使用。
4.人工智能的发展经历了哪几个阶段?解:第一阶段:孕育期(1956年以前);第二阶段:人工智能基础技术的研究和形成(1956~1970年);第三阶段:发展和实用化阶段(1971~1980年);第四阶段:知识工程和专家系统(1980年至今)。
5.人工智能研究的基本内容有哪些?解:知识的获取、表示和使用。
6.人工智能有哪些主要研究领域?解:问题求解、专家系统、机器学习、模式识别、自动定论证明、自动程序设计、自然语言理解、机器人学、人工神经网络和智能检索等。
7.人工智能有哪几个主要学派?各自的特点是什么?主要学派:符号主义和联结主义。
特点:符号主义认为人类智能的基本单元是符号,认识过程就是符号表示下的符号计算,从而思维就是符号计算;联结主义认为人类智能的基本单元是神经元,认识过程是由神经元构成的网络的信息传递,这种传递是并行分布进行的。
8.人工智能的近期发展趋势有哪些?解:专家系统、机器人学、人工神经网络和智能检索。
9.什么是以符号处理为核心的方法?它有什么特征?解:通过符号处理来模拟人类求解问题的心理过程。
特征:基于数学逻辑对知识进行表示和推理。
11.什么是以网络连接为主的连接机制方法?它有什么特征?解:用硬件模拟人类神经网络,实现人类智能在机器上的模拟。
特征:研究神经网络。
(完整word版)人工智能 第6章 参考答案

第6章不确定性推理部分参考答案6.8 设有如下一组推理规则:r1: IF E1THEN E2 (0.6)r2: IF E2AND E3THEN E4 (0.7)r3: IF E4THEN H (0.8)r4: IF E5THEN H (0.9)且已知CF(E1)=0.5, CF(E3)=0.6, CF(E5)=0.7。
求CF(H)=?解:(1) 先由r1求CF(E2)CF(E2)=0.6 × max{0,CF(E1)}=0.6 × max{0,0.5}=0.3(2) 再由r2求CF(E4)CF(E4)=0.7 × max{0, min{CF(E2 ), CF(E3 )}}=0.7 × max{0, min{0.3, 0.6}}=0.21(3) 再由r3求CF1(H)CF1(H)= 0.8 × max{0,CF(E4)}=0.8 × max{0, 0.21)}=0.168(4) 再由r4求CF2(H)CF2(H)= 0.9 ×max{0,CF(E5)}=0.9 ×max{0, 0.7)}=0.63(5) 最后对CF1(H )和CF2(H)进行合成,求出CF(H)CF(H)= CF1(H)+CF2(H)+ CF1(H) × CF2(H)=0.6926.10 设有如下推理规则r1: IF E1THEN (2, 0.00001) H1r2: IF E2THEN (100, 0.0001) H1r3: IF E3THEN (200, 0.001) H2r4: IF H1THEN (50, 0.1) H2且已知P(E1)= P(E2)= P(H3)=0.6, P(H1)=0.091, P(H2)=0.01, 又由用户告知:P(E1| S1)=0.84, P(E2|S2)=0.68, P(E3|S3)=0.36请用主观Bayes方法求P(H2|S1, S2, S3)=?解:(1) 由r1计算O(H1| S1)先把H1的先验概率更新为在E1下的后验概率P(H1| E1)P(H1| E1)=(LS1× P(H1)) / ((LS1-1) × P(H1)+1)=(2 × 0.091) / ((2 -1) × 0.091 +1)=0.16682由于P(E1|S1)=0.84 > P(E1),使用P(H | S)公式的后半部分,得到在当前观察S1下的后验概率P(H1| S1)和后验几率O(H1| S1)P(H1| S1) = P(H1) + ((P(H1| E1) – P(H1)) / (1 - P(E1))) × (P(E1| S1) – P(E1))= 0.091 + (0.16682 –0.091) / (1 – 0.6)) × (0.84 – 0.6)=0.091 + 0.18955 × 0.24 = 0.136492O(H1| S1) = P(H1| S1) / (1 - P(H1| S1))= 0.15807(2) 由r2计算O(H1| S2)先把H1的先验概率更新为在E2下的后验概率P(H1| E2)P(H1| E2)=(LS2×P(H1)) / ((LS2-1) × P(H1)+1)=(100 × 0.091) / ((100 -1) × 0.091 +1)=0.90918由于P(E2|S2)=0.68 > P(E2),使用P(H | S)公式的后半部分,得到在当前观察S2下的后验概率P(H1| S2)和后验几率O(H1| S2)P(H1| S2) = P(H1) + ((P(H1| E2) – P(H1)) / (1 - P(E2))) × (P(E2| S2) – P(E2))= 0.091 + (0.90918 –0.091) / (1 – 0.6)) × (0.68 – 0.6)=0.25464O(H1| S2) = P(H1| S2) / (1 - P(H1| S2))=0.34163(3) 计算O(H1| S1,S2)和P(H1| S1,S2)先将H1的先验概率转换为先验几率O(H1) = P(H1) / (1 - P(H1)) = 0.091/(1-0.091)=0.10011再根据合成公式计算H1的后验几率O(H1| S1,S2)= (O(H1| S1) / O(H1)) × (O(H1| S2) / O(H1)) × O(H1)= (0.15807 / 0.10011) × (0.34163) / 0.10011) × 0.10011= 0.53942再将该后验几率转换为后验概率P(H1| S1,S2) = O(H1| S1,S2) / (1+ O(H1| S1,S2))= 0.35040(4) 由r3计算O(H2| S3)先把H2的先验概率更新为在E3下的后验概率P(H2| E3)P(H2| E3)=(LS3× P(H2)) / ((LS3-1) × P(H2)+1)=(200 × 0.01) / ((200 -1) × 0.01 +1)=0.09569由于P(E3|S3)=0.36 < P(E3),使用P(H | S)公式的前半部分,得到在当前观察S3下的后验概率P(H2| S3)和后验几率O(H2| S3)P(H2| S3) = P(H2 | ¬ E3) + (P(H2) – P(H2| ¬E3)) / P(E3)) × P(E3| S3)由当E3肯定不存在时有P(H2 | ¬ E3) = LN3× P(H2) / ((LN3-1) × P(H2) +1)= 0.001 × 0.01 / ((0.001 - 1) × 0.01 + 1)= 0.00001因此有P(H2| S3) = P(H2 | ¬ E3) + (P(H2) – P(H2| ¬E3)) / P(E3)) × P(E3| S3)=0.00001+((0.01-0.00001) / 0.6) × 0.36=0.00600O(H2| S3) = P(H2| S3) / (1 - P(H2| S3))=0.00604(5) 由r4计算O(H2| H1)先把H2的先验概率更新为在H1下的后验概率P(H2| H1)P(H2| H1)=(LS4× P(H2)) / ((LS4-1) × P(H2)+1)=(50 × 0.01) / ((50 -1) × 0.01 +1)=0.33557由于P(H1| S1,S2)=0.35040 > P(H1),使用P(H | S)公式的后半部分,得到在当前观察S1,S2下H2的后验概率P(H2| S1,S2)和后验几率O(H2| S1,S2)P(H2| S1,S2) = P(H2) + ((P(H2| H1) – P(H2)) / (1 - P(H1))) × (P(H1| S1,S2) – P(H1))= 0.01 + (0.33557 –0.01) / (1 – 0.091)) × (0.35040 – 0.091)=0.10291O(H2| S1,S2) = P(H2| S1, S2) / (1 - P(H2| S1, S2))=0.10291/ (1 - 0.10291) = 0.11472(6) 计算O(H2| S1,S2,S3)和P(H2| S1,S2,S3)先将H2的先验概率转换为先验几率O(H2) = P(H2) / (1 - P(H2) )= 0.01 / (1-0.01)=0.01010再根据合成公式计算H1的后验几率O(H2| S1,S2,S3)= (O(H2| S1,S2) / O(H2)) × (O(H2| S3) / O(H2)) ×O(H2)= (0.11472 / 0.01010) × (0.00604) / 0.01010) × 0.01010=0.06832再将该后验几率转换为后验概率P(H2| S1,S2,S3) = O(H1| S1,S2,S3) / (1+ O(H1| S1,S2,S3))= 0.06832 / (1+ 0.06832) = 0.06395可见,H2原来的概率是0.01,经过上述推理后得到的后验概率是0.06395,它相当于先验概率的6倍多。
(完整word版)人工智能习题答案搜索推理技术

(5) 若n为一目标节点,则有解并成功退出。此解是追踪图G中沿着指针从n到S这条路径而得到的(指针将在第7步中设置)
(6) 扩展节点n,生成不是n的祖先的那些后继节点的集合M。将M添入图G中。
(4)如果节点i为目标节点,则求得一个解。
(5)扩展节点i。如果没有后继节点,则转向第(2)步。
(6)对于节点i的每个后继节点j,计算g(j)=g(i)+c(i,j),并把所有后继节点j放进OPEN表。提供回到节点i的指针。
(7)转向第(2)步。
3-3化为子句形有哪些步骤?请结合例子说明之。
任一谓词演算公式可以化成一个子句集。其变换过程由下列九个步骤组成:
(3)把第一个节点(节点n)从OPEN表移到CLOSED表。
(4)如果节点n的深度等于最大深度,则转向(2)。
(5)扩展节点n,产生其全部后裔,并把它们放入OPEN表的前头。如果没有后裔,则转向(2)。
(6)如果后继节点中有任一个为目标节点,则求得一个解,成功退出;否则,转向(2)。
等代价搜索方法以g(i)的递增顺序扩展其节点,其算法如下:
图3.33迷宫一例
第一步
SAB
第二步
BH
BC
第三步
HG
CF
最终路径为SABCF
3-7用有界深度优先搜索方法求解图3.34所示八数码难题。
2
8
1
2
3
1
6
3
8
4
7
5
4
7
6
5
SoSg
图3-34八数码难题
人工智能习题答案.doc

(此文档为Word格式,下载后可以任意编辑修改!)试卷装订封面学年第学期课程名称:课程代码学生系别专业班级任课教师阅卷教师考试办法开卷□闭卷∨考试日期考试时刻阅卷日期装订教师装订日期缺卷学生名字及原因:无附:课程考试试卷剖析表、期末考核成绩登记表第一章绪论1-1. 什么是人工智能?试从学科和才能两方面加以阐明。
从学科视点来看:人工智能是核算机科学中触及研讨、规划和使用智能机器的一个分支。
它的近期首要方针在于研讨用机器来仿照和履行人脑的某些智能功用,并开发相关理论和技术。
从才能视点来看:人工智能是智能机器所履行的一般与人类智能有关的功用,如判别、推理、证明、辨认、感知、了解、规划、考虑、规划、学习和问题求解等思想活动1-2. 在人工智能的开展进程中,有哪些思想和思潮起了重要作用?操控论之父维纳 1940 年建议核算机五准则。
他开端考虑核算机如何能像大脑相同作业。
系统地创建了操控论,依据这一理论,一个机械体系完全能进行运算和回忆。
帕梅拉·麦考达克(Pamela McCorduck) 在她的著名的人工智能历史研究《机器思维》(Machine Who Think,1979) 中曾经指出:在复杂的机械装置与智能之间存在着长期的联系。
闻名的英国科学家图灵被称为人工智能之父 ,图灵不只发明了一个简略的通用的非数字核算模型,并且直接证明了核算机可能以某种被了解为智能的办法作业。
提出了闻名的图灵测验。
数理逻辑从 19 世纪末起就获迅速开展;到 20 世纪 30 时代开端用于描绘智能行为。
核算机呈现后,又在核算机上完成了逻辑演绎体系。
1943 年由生理学家麦卡洛克(McCulloch) 和数理逻辑学家皮茨(Pitts)创立的脑模型,即MP 模型。
60-70 年代,联结主义,尤其是对以感知机(perceptron)为代表的脑模型的研究曾出现过热潮,操控论思想早在 40-50 时代就成为时代思潮的重要部分,影响了前期的人工智能作业者。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-2试举例比较各种搜索方法的效率。
宽度优先搜索
(1)把起始节点放到OPEN表中(如果该起始节点为一目标节点,则求得一个解答)。
(2)如果OPEN是个空表,则没有解,失败退出;否则继续。
(3)
把第一个节点(节点n)从OPEN表移出,并把它放入
CLOSED扩展节点表中。
更换变量符号的名称,使一个变量符号不出现在一个以上的子句中
3-4如何通过消解反演求取问题的答案?
给出一个公式集S和目标公式L,通过反证或反演来求证目标公式L,其证明步骤如下:
(1)否定L,得~L;
(2)把~L添加到S中去;
(3)把新产生的集合{~L,S}化成子句集;
(4)应用消解原理,力图推导出一个表示矛盾的空子句NIL。
择一个目标节点作为节点i(要是有目标节点的话);否则,就从中选一个作为节点i。
把节点i从OPEN表移至扩展节点表CLOSED中。
(4)如果节点i为目标节点,则求得一个解。
(5)
扩展节点i。如果没有后继节点,则转向第
(2)步。
(6)
对于节点i的每个后继节点j,计算g(j)
=g(i)+c(i,j),并把所有后继节点
(2)。
等代价搜索方法以g(i)的递增顺序扩展其节点,其算法如下:
(1)把起始节点S放到未扩展节点表OPEN中。如果此起始节点为一目标节点,则求得一个解;否则令g(S) =0。
(2)如果OPEN是个空表,则没有解而失败退出。
(3)从OPEN表中选择一个节点i,使其g(i)为最小。如果有几个节点都合格,那么就要选
(4)选择OPEN表上的第一个节点,把它从OPEN表移出并放进CLOSED表中。称此节点为节点n,它是CLOSED表中节点的编号
(5)若n为一目标节点, 则有解并成功退出。 此解是追踪图G中沿着指针从n到S这条路径而得到的(指针将在第7步中设置)
(6)扩展节点n,生成不是n的祖先的那些后继节点的集合M。将M添入图G中。
3-7用有界深度优先搜索方法求解图3.34所示八数码难题。
2
8
1
2
3
1
6
3
8
4
7
5
4
7
6
5
So
Sg
图3-34八数码难题
按顺时针方向(上、右、下、左)试探,尝试移动空格,将最大深度定为5
S0(So)
2
8
1
6
3
7
5
4
S1
2
8
3
1
6
7
5
4
S2
2
8
3
1
6
4
7
(4)
扩展节点n。如果没有后继节点,则转向上述第(2)
步。
(5)
把n的所有后继节点放到OPEN表的末端 ,并提供从这些后继节点回到
n的指针。
(6)
如果n的任一个后继节点是个目标节点,则找到一个解答,成功退出;否则转向第
(2)
步。
有界深度优先搜索
(1)把起始节点S放到未扩展节点OPEN表中。如果此节点为一目标节点,则得到一个解。
j放进OPEN
表。提供回到节点i的指针。
(7)
转向第(2)步。
3-3化为子句形有哪些步骤?请结合例子说明之。
任一谓词演算公式可以化成一个子句集。其变换过程由下列九个步骤组成:
(1)消去蕴涵符号
将蕴涵符号化为析取和否定符号
(2)减少否定符号的辖域
每个否定符号最多只用到一个谓词符号上,并反复应用狄·摩根定律
(8)按某一任意方式或按某个探试值,重排OPEN表。
(9) GO LOOP。
重排OPEN表意味着,在第(6)步中,将优先扩展哪个节点,不同的排序标准对应着不同的
搜索策。
重排的原则当视具体需求而定,不同的原则对应着不同的搜索策略,如果想尽快地找到一个
解,则应当将最有可能达到目标节点的那些节点排在OPEN表的前面部分,如果想找到代
(5)只有按规则(1)~(4)求得的公式,才是合式公式等价关系有:
否定之否定
蕴含与与或形式的等价
狄.摩根定律分配律
交换律
结合律
逆否律
否定跨越量词
全称量词同与或连词
量词中的哑元
3-6用宽度优先搜索求图3.33所示迷宫的出路。
图3.33迷宫一例
第一步
SAB
第二步
BH B C
第三步
HG C F
最终路径为SABCF
前缀=全称量词串
母式=无量词公式
(6)把母式化为合取范式
反复应用分配律, 将母式写成许多合取项的合取的形式,而每一个合取项是一些谓词公式和
(或)谓词公式的否定的析取
(7)消去全称量词
消去前缀,即消去明显出现的全称量词
(8)消去连词符号(合取)
用{合取项1,合取项2}替换明显出现的合取符号
(9)更换变量名称
(2)如果OPEN为一空表,则失败退出。
(3)把第一个节点(节点n)从OPEN表移到CLOSED表。
(4)
如果节点n的深度等于最大深度,则转向(2)。
(5)
扩展节点n,产生其全部后裔,并把它们放入
OPEN表的 前头。如果没有后裔,则转向
(2)。
(6)
如果后继节点中有任一个为目标节点,则求得一个解,成功退出;否则,转向
第三章搜索推理技术
3-1什么是图搜索过程?其中,重排OPEN表意味着什么,重排的原则是什么?
图搜索的一般过程如下:
(1)建立一个搜索图G(初始只含有起始节点S),把S放到未扩展节点表中(OPEN表)中。
(2)建立一个已扩展节点表(CLOSED表),其初始为空表。
(3)LOOP:若OPEN表是空表,则失败退出。
3-5什么叫合适公式?合适公式有哪些等价关系?
合式公式的递归定义为:
(1)原子谓词公式是合式公式
(2)若A为合式公式,则A的否定也是合式公式
(3)
若A、B都是合式公式,则
A AND B, AOR B, AB, A
>B也都是合式公式
(4)
若A是合式公式,x为A
中的自由变元,则(ANY x)A
和(EXT x)A都是合式公式
(3)对变量标准化
对哑元改名以保证每个量词有其自己唯一的哑元
(4)消去存在量词
引入Skolem函数,消去存在量词
如果要消去的存在量词不在任何一个全称量词的辖域内,那么我们就用不含变量的Skolem
函数即常量。
(5)化为前束形
把所有全称量词移到公式的左边,并使每个量词的辖域包括这个量词后面公式的整个部分。前束形= (前缀) (母式)
(7)对那些未曾在G中出现过的(既未曾在OPEN表上或CLOSED表上出现过的)M成员设置一
个通向n的指针,并将它们加进OPEN表。
对已经在OPEN或CLOSED表上的每个M成员,确定是否需要更改通到n的指针方向。
对已在CLOSED表上的每个M成员,确定是否需要更改图G中通向它的每个后裔节点的
指针方向。
