高频电子线路(第二章 选频网络)-2讲解
高频电子线路ppt讲义2选频网络解析
高频电子线路中常用的选频网络有：
振荡电路（由L、C 组成） 单振荡回路
耦合振荡回路
选频网络
各种滤波器
LC集中滤波器
石英晶体滤波器 陶瓷滤波器 声表面波滤波器
功能：选频、阻抗变换
2.1.1 基本原理 2.1.2 串联振荡回路的谐振曲线和通频带 2.1.3 串联振荡回路的相位特性曲线
由电感线圈和电容器组成的单个振荡电路，称为 单振荡回路。
但是，近代无线电技术中，普遍遇到数字信号与图像信号的传输问题 ，在这种情况下，相位特性失真要严重影响通信质量。
.
N ()
I() I(0 )
1
j Q(
1
0 ) N ()e j ()
0
arctanQ
0
0
arctan
由右图可见，Q值愈 大，相频特性曲线在谐振 频率ω0附近的变化愈陡峭 。但是，线性度变差，或 者说，线性范围变窄。
选频特性曲线
若信号源内阻比较大应该选择怎样的谐振回路?
并联谐振回路
LC
Is
损
耗 电
R
阻
同样，要研究并联振荡回路的选频特性， 可以考察其阻抗随频率变化的规律。
回路的总阻抗
Z
R
jL
1
jC
R
jL
1
jC
R
jL
1 jC
R
jL
1 C
L
R
C
jL
1
C
CR L
1
jC
1
L
通常，损耗电阻R在工作频段内满足：R L 或 高Q
，谐振曲线愈尖锐，对外加电压的选频作 用愈显著，回路的选择性就愈好。
因此，要衡量电路偏离谐振的程度，必须包含Q和失谐量的综合效果。
Chapter 2 选频网络2
Q2 Q1
' 1 1 2 '2
(f)
0 (f0)
Q1> Q2
C. 如何计算通频带？ I 1 1 由定义可知： 2 Io 2 1
可以算出： 1
N(f )
N(f)=
1 2
I I0
Q2 Q1
' 1 1 2 '2
而 Q
2
o
0 2Q 0
VS VC 0 I 0 j jVS Q j0C R 1
v Lo v Co Vs Q
可见谐振时，电感L和电容C上的电压均为输入信号电 压的Q倍（通常Q值较大）。因此，必须预先注意回路元件 的耐压问题。故串联谐振也称为电压谐振。
复习、特性阻抗和品质因数 （1）特性阻抗 (characteristic impedance) 谐振时的感抗或容抗
(f)
0 (f0)
所以通频带公式2 07 2 1
LC集中滤波器 石英晶体滤波器 陶瓷滤波器 声表面波滤波器 单振荡回路
串联谐振回路
3.谐振的概念（共振、共鸣）
以单谐振回路为例，电路具有如下的特 征：在某一个特定的频率工作时，回路阻抗 值具有最小值(串联回路)或最大值(并联回 路)，亦即回路电流或电压达到最大，而当偏 离这一频率时，电流或电压下降得很快，回 路的这种特性就称之为谐振，这个特定的频 率称之为谐振频率。
1 1 Z S r jL r j (L ) jC C
（2 — 1）
0
1 LC
（2 — 2）
若在串联振荡回路两端加一恒压信号 ,U 则发生串联谐振 时因阻抗最小, 流过电路的电流最大, 称为谐振电流, 其值为
高频电子线路第二章精品PPT课件
2.2.3.1、石英晶体滤波器
一、石英晶体的物理特性
1、石英晶体的结构
图2.2.3.1（a）表示自然结晶
体，图（b）表示晶体的横断。
为了便于研究，人们根据石英晶
体的物理特性，在石英晶体内画
出三种几何对称轴，连接两个角
锥顶点的一根轴Z，称为光轴； 在图（b）中沿对角线的三条X 轴，称为电轴；与电轴相垂直的
当 JT 作滤波器使用时，f f p fq 决定了滤波器的通 带宽度。
2.2.3.1
晶体谐振器与一般振荡回路比较，有以下几个明显 的特点：
• ① 晶体的谐振频率 f p和 fq非常稳定。这是因为
Lq、Cq、rq 由晶体尺寸决定，由于晶体的物理特性
它们受外界因素（如温度、震动等）的影响小。
•② 有非常高的品质因数。而普通LC振荡回路的 Q 值只能到几百。
当 fs 偏离f0 ，强度减小 （原因是各 A0振幅不变，但相位变化）。
表面声波滤波器的幅频特性为具有 sin x x 的函数形式， 式中x n f f0 ，（f f f0 ）。
2.2.3.3
目前表面声波滤波器的中心频率可在10MHz～ 1GHz之间，相对带宽0.5为00 50 00 ，插入损耗最低仅几个dB，
沿弹性体表面传递的声波，有n节换能器，（n+1） 个电极或 N n个2 周期段。指间距b、指宽a决定声波波 长。
换能器频率 f0 d ， 传播速度。
周期段长（波长）：0 M 2(a b)
当外加信号频率 fs 时f0 ， 各节所发出的表面波同相迭加，振幅最大， 总振幅 As nA0
（A0 为每节所激发声波强度振幅）。
矩形系数可达1.2。 图2.2.3.8所示为一接有声表面波滤波器的预中放电
高频电子线路最新版课后习题解答第二章 选频网络与阻抗变换习题解答
第二章 选频网络与阻抗变换网络思考题与习题2.1选频网络的通频带指归一化频率特性由１下降到 0.707 时的两边界频率之间的宽度。
理想选频网络矩形系数1.0k ＝ 1 。
2.2 所谓谐振是指ＬＣ串联回路或并联回路的固有频率0f 等于 信号源的工作频率f 。
当工作频率f ＜0f 时，并联回路呈 感 性；当工作频率f ＞0f 并联回路呈 容 性；当工作频率f ＝0f 时，并联谐振回路的阻抗呈 纯阻 性且最 大 。
2.3 若0f 为串联回路的固有频率。
当信号源的工作频率f＜0f 时，串联回路呈 容 性；当工作频率f ＞0f 串联回路呈 感 性；当工作频率f ＝0f 时，串联谐振回路的阻抗呈 纯阻 性且最 小 。
2.4 串、并联谐振回路的Ｑ值定义为2π谐振时回路总储能谐振时回路一周内的耗能。
Ｑ值越大，意味着回路损耗小 ，谐振曲线越 陡 ，通频带宽越 窄 。
当考虑ＬＣ谐振回路的内阻和负载后，回路品质因数 下降 。
2.5 设r 为LC 并联谐振回路中电感L 的损耗电阻，则该谐振回路谐振电阻为reo L R C =，品质因数为ro o L Q ω= ,谐振频率为o ω谐振时流过电感或电容支路的电流为信号源电流的o Q 倍。
2.6 设r 为ＬＣ串联谐振回路中电感Ｌ的损耗电阻，则回路的品质因数为ro o L Q ω=，谐振频率为o ω=o Q 倍。
2.7 已知LC 串联谐振回路的C =100pF ，0f =1.5MHz ，谐振时的电阻5r =Ω，试求：L 和0Q 。
解：由0f =得22025330253301.5100L f C ==⨯112.6H μ=66002 1.510112.6105LQ r ωπ-⨯⨯⨯⨯==212≈2.8 在图2.T.1所示电路中，信号源频率f 0=1MHz ，信号源电压振幅s V =0.1mV ，回路空载Q值为100，r 是回路损耗电阻。
将1、2两端短路，电容C 调至100pF 时回路谐振。
高频电子线路知识点整理
高频电子线路重点第二章 选频网络一 . 基本见解所谓选频（滤波） ，就是 选出 需要的频率重量和 滤除不需要的频率重量。
电抗 (X)=容抗（1 )+感抗 (wL)阻抗 =电阻 (R)+j 电抗 ( L1 )CC阻抗的模把阻抗看作虚数求模二．串通谐振电路111.谐振时，（电抗）XL0 ，电容、电感消失了，相角等于0，谐振频率：CLC小 =R ，电流最大，此时 |Z| 最2.当 w<w 0 时，电流超前电压，相角小于 0，X<0 阻抗是容性；当 w>w 0 时，电压超前电流，相角大于0，X>0 阻抗是感性；QL13.回路的质量因素数 R 0CR （除 R ），增大回路电阻，质量因数下降，谐振时，电感和电容两端的电位差大小等于外加电压的Q 倍，相位相反4.回路电流与谐振时回路电流之比1 1N ( )e j ( ) (幅频 )，质量因数越高 ，谐振时的电流越大，比值j Q()越大， 曲线越尖 ，选频作用越明显， 选择性越好5.失谐△ w=w （再加电压的频率） -w （回路谐振频率） ，当 w 和 w 很周边时， 2ξ =X/R=Q ×2△ w/w 是广义失谐，回路电流与谐振时回路电流之比N ( )1 121 ，1226.当外加电压不变， w=w =w 时，其值为 1/ √ 2， w-w 为通频带， w ， w 为界线频率 / 半功率点 ，广义失谐为± 1 LR 7. 2，质量因数越高，选择性越好，通频带越窄0 7Q 2 f0 7f 0 通频带相对值2 f1 8.通频带绝对值Qf 0Q+ V s–9.相位特点Carctan Q0 arctanQ 越大，相位曲线在 w 0 处越陡峭10.能量关系电抗元件电感和电容不用耗外加电动势的能量，耗资能量的只有耗费 电阻 。
回路总瞬时储能w w L w C 1 CQ 2V sm 2 sin 2 t1C Q 2 V sm 2 cos 2 t 1 CQ 2 V sm 22222回路一个周期的耗费w R2π1 Vsm 12π 1CQV sm 21CQ 2 V sm 22 R 021回路储能w L wC2Q，表示回路或线圈中的耗费。
魏俊平 高频电子线路 第2章 高频小信号选频放大器
R. S
Us
L rC
解：1. 计算不考虑 RS、 RL时的回路固
RL
有特性：f0、Q、RP、BW0.7
f0
2
1 LC
(
2
1
)Hz 465kHz
586 106 200 1012
586 106
Q
LC r
200 1012 12
143
RP
L Cr
(
586 106 200 1012
Is'U
' o
IsU12
I's
I sU 12 U 'o
U 12 U 13
Is
1 n1
Is
1mA 5
0.2 mA
Uo
U13 n2
U
' o
n2
I
' s
Re
0.2 30.6 V
n2
10
0.612 V
思考讨论题
1. LC并联谐振回路有何基本特性?说明Q对 回路特性的影响。
2.1 LC谐振回路
2.1.3抽头谐振回路 2.电容分压式
【例2-3、2-4】
第2章 高频电路基础
例 2-3 如图， 抽头回路由电流源激励，忽略回路本 身的固有损耗，试求回路两端电压 u1(t) 的表示式及 回路带宽。
29
例2.4 下图中，线圈匝数 N12 = 10 匝， N13 = 50 匝，N45 = 5 匝，L13= 8.4 mH, C = 51 pF, Q =100, Is = 1 mA , Rs =10 kW, RL= 2.5 kW, 求有载品质因数Qe、通频带BW0.7、谐振输出电压Uo。
高频电子线路 第二章 选频网络
Chapter 2 选频网络§2.1 概述 §2.2 串联谐振回路12.1 概述一.选频的基本概念 二.选频网络的分类振荡回路（由L、C组成）单振荡回路 耦合振荡回路各种滤波器LC集中滤波器 石英晶体滤波器 陶瓷滤波器 声表面波滤波器2三.选频网络的的元器件选频网络中的元件主要是电阻（器）、电容（器） 和电感（器）, 它们都属于无源的线性元件。
1.电阻器一个电阻R的高频等效电路如图所示，其中CR为分布电容， LR为引线电感，R为电阻。
CR LR R电阻的高频等效电路32. 电感线圈的高频特性电感＋损耗电阻r＋分布电容（忽略）L r 1 L r 2电感线圈的串联等效电路 在两种形式中，电 感值近似不变，串 联电阻与并联电阻 的乘积等于感抗的 平方。
1’ LP R 2’电感线圈并联等效电路43. 电容器的高频特征R C Cpr电容器的串、并联等效电路两种形式中电容值近似不变，串联电阻 和并联电阻的乘积等于容抗的平方。
52.2 串联谐振回路串联谐振回路是指电感、电容、信号源三 者串联形成的电路。
6一. 谐振及谐振条件我们称当ω = ω0 时发生了串联谐振,谐振角频率ω0为:1 LCω0 =当回路谐振时的感抗或容抗，称之为特性阻抗， 用ρ表示。
X L0 = X C01 = ω0 L = = L =ρ C ω0C7二. 谐振特性回路阻抗的模|Zs|和幅角随φ变化的曲线分别如图所示 |Zs| φπ/ 2 r O ω0 O -π / 2 ω ω0 ω因此串联谐振时，电感L和电容C上的电压达到最大值且 为输入信号电压的Q倍，故串联谐振也称为电压谐振。
8三. 幅值特性谐振电流:发生串联谐振时因阻抗最小，流过电路的电流最 大，称为谐振电流，其值为.Vs I0 = R非谐振点处电流称为失谐处电流 I9谐振曲线:串联谐振回路中电流幅值与外加电动势频率之间 的关系曲线称为谐振曲线。
可用|N(f)|表示谐振曲线的函数。
高频电子线路张肃文第五版一二章总结
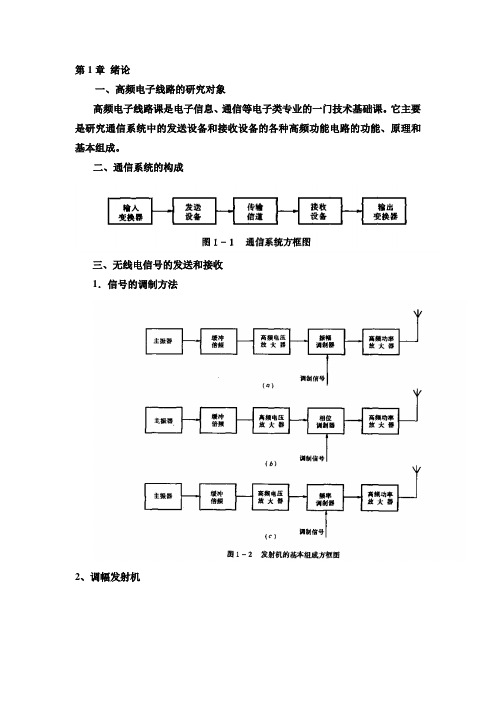
l．为什么在无线电通信中要便用“载波”发射，其作用是什么？
答：由于需要传送的信息转变成电信号后，其占有的频率成分基本上是低频范围。将这些低频范围的电信号直接发肘出去，有两个下可克服的缺点，一是选择性，相互干扰，下能实现多路通信。二是电信号频率低，天线发射无线尺寸太大。为此采用对载波进行调制的发送方式就能较好地解决这两个缺点，选用高频载频作为运载信息的信号，由于频率高，天线尺寸小。另外，不同的电台采用不同的载频，就很容易实现多路通信。
2 a图只要L1C1或L2C2之一为并联则为并联，二者为容性则为串联；
B图L1C1与L2C2只能呈现感性才能谐振，为并联谐振；
C图L1C1与L2C2只能呈现感性才能谐振，为串联谐振。
3注意利用 但不要使用
4根据 的比值选取合适的电容器。
2画出无线通信收发信机的原理框图，并说出各部分的功用。
答：
上图是一个语音无线电广播通信系统的基本组成框图，它由发射部分、接收部分以及无线信道三大部分组成。发射部分由话筒、音频放大器、调制器、变频器（不一定必须）、功率放大器和发射天线组成。
低频音频信号经放大后，首先进行调制后变成一个高频已调波，然后可通过变频，达到所需的发射频率，经高频功率放大后，由天线发射出去。接收设备由接收天线、高频小信号放大器、混频器、中频放大器、解调器、音频放大器、扬声器等组成。由天线接收来的信号，经放大后，再经过混频器，变成一中频已调波，然后检波，恢复出原来的信息，经低频功放放大后，驱动扬声器。
1．接入系数
电感抽头接入法、电容抽头部分接入法
2．电压源、电流源、电阻、电容、电感的折合
四、耦合回路
1．耦合系数
2．反射阻抗与等效阻抗
3．耦合回路的频率特性
高频电子线路课件第二章
p
有载参数的计算： 有载参数的计算： （1）谐振回路的总电导 ∑＝g s＋g p＋g L ）谐振回路的总电导G 其中g 其中 s＝1 / R s，g p＝1 / R p，g L＝1 / R L （2）谐振回路的品质因数 ） 谐振回路的空载品质因数 空载品质因数Q 谐振回路的空载品质因数 0值为 Q 0＝R p / (ω 0L) ＝1 / (ω 0L g p) ω ω 谐振回路的有载品质因数 谐振回路的有载品质因数QL值为 有载品质因数 Q L＝1 / (ω 0L G∑)＝1/ [ω 0L(g s＋g p＋g L)] ω ＝ / ω 所以 Q L＝Q 0/（1+ R p / R s + R p / R L）
1 ω0 = LC
称为RLC并联电路的谐振角频率 。 并联电路的谐振角频率 称为 并联电路的 则： Y=GP=RC/L=1/RP 谐振时，并联谐振回路： 谐振时，并联谐振回路： 1）容纳与感纳抵消（和为零）， ）容纳与感纳抵消（和为零）， 等效为一个纯电导G 纯电阻R 等效为一个纯电导 P （纯电阻 P）。 RP称为并联谐振阻抗（电阻）。 称为并联谐振阻抗（电阻）。 并联谐振阻抗 GP称为并联谐振导纳（电导）。 称为并联谐振导纳（电导）。 并联谐振导纳 ——— 回路可能达到的最小导纳 最大阻抗）。 （最大阻抗）。 2）工作频率低于谐振频率， ）工作频率低于谐振频率， 电路呈感性，反之，电路呈容性。 电路呈感性，反之，电路呈容性。
2-1
串联谐振含义：阻抗在特定频率上具有最小值 串联谐振含义：阻抗在特定频率上具有最小值， 在特定频率上具有最小 在其余频率点阻抗迅速增大。 在其余频率点阻抗迅速增大。
& V & I= = Z & V r + j (ωL − 1 ) ωC & V = r + jX
高频电子线路第二版第2章高频基础电路
特性好的电阻，即需要根
据电路工作频率的高低选
500Ω金属膜电阻
用不同类型的电阻。
2020/5/11
电阻器是电子线路中最常用的无源元件之一。在 电子电路中，一个或多个电阻可构成降压或分压电路 用于有源器件的直流偏置，也可作为直流或电子电路 的负载电阻完成某些特定功能。
电阻的主要类型： 高密度碳介质合成的碳膜电阻； 鎳或其它材料的线绕电阻； 温度穏定材料的金属膜电阻； 铝或铍基材料薄膜片的表面贴装（SMD）电阻
之比
p VL V L
2020/5/11
根据定义，将电压比V L /V L 变换为变压器的线圈圈数 比(或容抗、感抗比), 则令p为
则变换关系为
RL
1 p2
RL
gL p2gL
X L
1 p2
XL
CL p2CL
2020/5/11
Ig pIg
U g
1 p
U
g
例1：
例2：
p N2 N1
2
RL
1 p2
将L2+ M和RL并联支路等效为串联支路,在 QL2 1条件下
,
(L2 M)
X不变R L , 为SQ 1 L 2 2R L R ,L 2 而/ 0 (L 1 2 M )2R L0 2 (L 2 R LM )2
2020/5/11
再将RLS与L1+L2+2M串联支路等效为并联支路, 在串 联支路的 Q 1条件下,等效后的电感值不变仍为 L1+L2+2M, 而电阻为
工作频率进入射频频段宜选用片式多层陶瓷电 容器、片式塑封交流瓷介电容器和片式有机薄膜电 容器。但电容器的电容值不一定是理想值。
射频电路中经常需要旁路、电源去耦滤波和射 频接地等辅助电路，通常可以利用电容器具有自谐 振频率的特点来实现。
详细版高频电子线路(第五版)_第二章_选频网络.ppt
Z
L RC
1
1 j
j(L
R
L
1
)
R CR
R pL 1 pL R pRC
p
1 R2 LC L2
特性阻抗:
p
L
1
pC
L C
品质因数: Q
R
课件
谐振时的阻抗特性：
并联谐振时，回路呈纯电阻性， 且阻抗为最大值；
p,呈现感性
p,呈现容性
因此回路谐振时：
电纳B 0，回路导纳Y GP为最小值。 电压V0 IS / GP相应达到最大值且, 与IS同相
0
当
时
0
失谐
特性阻抗
π2 o
π 2
0
< 0，X < 0，回路呈容性 > 0，X > 0，回路呈感性
课件
VL0
I0
j0 L
VS R
j0L
j
0 L
R
VS
VC0 I0
1 VS
j0C R
1
j0C
j
1
0CR
VS
品质因数
Q
0L
R
1
0CR
1 R
L C
+ Vs
L
I
C
-
R
VL0
0
Vs
I0
所以: VL0 jQVs VC0 jQVs VC0
L RC
1
1 j
j(L
R
L
ห้องสมุดไป่ตู้
1
)
C
R CR
一般 L>> R,代入上式 ：
Z
RC
1
j(C
1
高频电子线路第二讲PPT课件
①用于对小信号进行放大功能的高频小功率管，对这一 类晶体管的要求是大增益、小噪声。目前，双极型小信号 放大晶体管的工作频率可以达到几千兆赫兹，噪声系数仅 为几个分贝。
②用于高频功率放大功能的高频功率放大管，对这一类 晶体管的要求是大增益、大功率输出。
小信号放大用的场效应管，工作频率也能达到同样高的 频率，噪声系数可以更小。
第二章 高频电子线路基础
第一节 引言
各种无线电设备主要由一些处理高频信号的功能电路， 如高频小信号放大器、高频功率放大器、振荡器、调制器 及相应的解调器组成。这些内容将在各个章节里分别讨论。 但是各个功能电路之间也有一些共性，这就是所使用的无 源元件、有源器件及其组件等绝大多数是相同的。这些元 器件是构成高频电路的基础。因此，本章首先予以讨论。 考虑到电子噪声存在于各种电子线路之中，它对通信中系 统中所传输的有用信号会形成干扰。所以，了解电子噪声 的产生根源，对从源头上抑制它或消弱它的影响，提高系 统性能非常有帮助。
1.串联谐振回路 凡是由电感L、电容C及电阻r与信号源串联组成的 电路，称为串联谐振回路。串联谐振回路的示意图如 图2-4所示。
L
ui
C
i r
图2-4 串联谐振回路
图中，电阻r通常包括电感线圈和电容器的损耗电 阻以及可能接入回路的外加电阻。如果在该电路电感 线圈或电容器中已经储有能量，则在回路电阻r很小的 前提下，电路中即使没有外加电动势，也可以产生振 荡。所以又称串联谐振回路为串联振荡电路。
数Q，即
Q 0 L 1 r 0rC
(2-10)
并联谐振时阻抗最大，回路呈现纯电阻性质，谐
振电阻R0为
R0
L rC
Q0 L
1 Q
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1
Ci
5 pF
Ri
5k
C1
Rp
20 pF L
0.8H
C2
4200ppFF
2
RO
5k
CO
20 pF
所以更精确的方法是： 方法二，先将 CO与C2合并。看成一个电容 C2
C2 CO C2 40 pF
这样 12两端总电容 C
Ci
C1 C1
C2 C
5
20 40 20 40
下呈容性
p
,
Zbc
c
所以在
下可将其看作一个电容
p
C
L1
C’
C
Zbc
p L1 2
r
为了简化这
pL1 2
些表达式， 提出了接入
所以 Zbc Z ac
r
p (L1 L2 ) 2
( L1 )2 L1 L2
系数p的概 念
r
§2.3.2 抽头式电路的阻抗变换
（R1
1
R2）(pC)2
这时，如果R1，R2都不大的情况下，
可以认为R1，R2都集中在电感之路。
且Q p
=
pL
R1 +R2
,
这一概念在实际中很
有用。
第二章 选频网络
•高频电子技术•
§2.3.2 抽头式电路的阻抗变换
为什么会存在“抽头式”电路?
– 1、减小信号源内阻和负载对回路的影响； – 2、可调抽头还可以实现阻抗匹配功能。
•高频电子技术•
2、抽头系数（接入系数）p的严格定义
抽头式电路中，抽头所夹的那个元件的阻抗， 与它所在的那个支路的整个阻抗之比，称为抽 头系数或接入系数，通常记为p
例如：a
L2
b
L1
c
p ZL1 p L1
L1
ZL1串L2 p (L1 L2 ) L1 L2
C
带入上页, 可得 Zbc p2 Z ac
习题详解：习题2.5
解：Q0
1
0C0 R
1
6
2 3.141.510
100 1012
5
212
L0
1
02C0
1 (2 3.141.5106 )2 1001012
113H
谐振时回路电流：I0
Vsm R
1mV 5
0.2mA
VL0m VC0m Q0Vsm =212mV
§2.3.2 抽头式电路的阻抗变换
•高频电子技术•
5、抽头式电路中电流源的等效变换
a
L2
bC
IS
L1
c a
根据前面的电压关系的 结论 Vbc p
p Vbc IS Zbc
Vac
Vac I S Zac
再根据前面的阻抗关系 的结论 Zbc p2
带入上式得 p Vbc IS p2 Zac Vac I S
Qp
1
pC
Qp2r
电抗部分(在图中为L)等效后不变
上图中的r其实就是Rs ; 图中RP ,它约为Q2倍的Rs (即r) 可见RP和r是有很大差别的,验证了我们学过的知识
•高频电子技术•
3.并联谐振回路其他形式
并联电路的广义形式：
•高频电子技术•
Zp
(p L)2
R1 R2
或Z p
等效
导纳直接相加，计算得以简化！
§2.3.1 串、并联阻抗等效变换
1、并联等效成串联
•高频电子技术•
注：图中电抗带颜色，纯电阻不带颜色
A
A
XS
XP
RP
等效
B
RS
B
根据等效的要求 ,两个电路从 AB两点看去,阻抗应该相等
显然串联电路的阻抗为 RS jX S
而并联电路的阻抗为
RP ( jX P ) RP jX P
习题详解：习题2.9（3.9四版）
1
Ci
Ri
5 pF 5k
C1
Rp
20 pF L
0.8H
C2
20 pF
2
RO
5k
CO
20 pF
Rp是L的内阻等效到 1、2 两端的电阻，所以题面 没画出来。 方法一：将 CO看成从C1C2抽头出来的元件，等效 到12两端。
但是别忘记一个前提：接入的电容要远远小于电路中的原有电容
1MHz CX 200 pF
1 25
253106 100 1012
63.6（）
0.1V
1
C2 200 pF
可知图中“？”处是一 个电阻RX
且RX R总 R 63.6 15.9 47.（7 ）
Z X由RX 47.7和CX 200 pF串联而成
0
L
1
0C1
0.1V
1
L
1
02C1
(2
1 106 )2 1001012
C1 100 pF
25（3 H）
又
V C1
Q0 V S
Q0
V C1
VS
10 100 0.1
而
1 Q0 R
L
1
R
C
Q0
L 1 C 100
253106 100 1012
a
效前后的阻抗相等来证明的。
等 效
Ci
b
L2 C
L1
由于推导比较繁琐且大纲不要 求，故略去推导过程，但结论 希望同学们记住，第三章有用。
c
抽头等效关系总结 •高频电子技术•
(bc为抽头,ac为总的回路的两个端点) (代 ’ 的变量为去掉抽头后的等效值)
阻抗的关系 Zbc p2
电压的关系 Vbc p
学习这一节的目的在于 为学习“高频小信号放大器”打好基础
第二章 选频网络
•高频电子技术•
§2.3.1 串、并联阻抗等效变换
什么是“等效”？
– 所谓等效就是指电路工作在某一频率时，不管其内 部的电路形式如何，从外部看去其阻抗是相等的。
为什么要进行等效变换？
– 主要是为了使电路的分析更加方便。例如：
解题注意：
1.注意脚标：L0 , C0
2.求Q0最好用Q0
1
0C0
R
，因为0
,C0
,
R都是给定的。
Q0
L0 C0
1 R
,
L0是通过0
,C0求出，误差大。
.
.
3.V
L0
,V
C0
是矢量；VL 0 m
,
VC
是标量。
0m
习题详解：习题2.6
LR
+ 1MHz
1 解：先看第一次谐振1，1端短路。
X
P
1
1
XP RP
2
代入
XP
倒数
代入
请同学们回忆 一下并联谐振 回路中的Q值:
Q
Rp
pL
Rp pC
恰好可以表示为 Rp XP
§2.3.1 串、并联阻抗等效变换
•高频电子技术•
1、并联等效成串联（结论）
得到
RS
RP 1 Q2
Q2 XS 1 Q2 XP
由于高频电路中 ,通常Q 1,所以
1
Z X RX j0CX
由于Q公式有好几个,所以解法也 有很多种,但结果应当是一样的。
47.7
j
2
1 10 6 200 10 12
(47.7
j796（) ）
第二章 选频网络
•高频电子技术•
§2.3 串、并联电路及抽头式电路的等效变换
本节主要内容： – §2.3.1 串、并联阻抗等效变换 – §2.3.2 抽头式电路的等效变换
X P2
RP 2
X
2 P
RP
j
RP 2
RP 2
X
2 P
XP
§2.3.1 串、并联阻抗等效变换
•高频电子技术•
1、并联等效成串联（续）
令并联电路阻抗等于串联电路阻抗(等效定义),有
RS
X P2
RP 2
X
2 P
RP
1
RP XP
2
RP 1
XS
RP 2
RP 2
X
2 P
•高频电子技术•
1、为什么通过抽头可调节谐振阻抗？
a
L2
b
Zbc
L1
C
c
? Zbc = Zac
Zac
p (L1 L2 ) 2
r
注意：电感、电容串并联时 值的大小的计算！
§2.3.2 抽头式电路的阻抗变换
引入抽头时阻抗的变化
•高频电子技术•
b
由于L2与C串联后这个支路 ,
L2
在谐振频率
Z ac
Vac
抽头处看进去的阻抗和电压都比较小
电阻去抽头
Ri
1 p2
Ri
变大
电流源去抽头
IS pIS
变小
电容去抽头
Ci p2Ci
变小
习题：
•高频电子技术•
教材P85（四版）习题3.9 教材P55（五版）习题2.9 注意：
– 请同学们在Ci的两端再并联一个电阻Rp(其值可以 通过Qp求出)；