100以内平方数表
100以内整数的平方及其规律

平方数的规律及100以内的整数平方表规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n 型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2 + 2ab (a-b)2=a2 + b2 -2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b 例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744 用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212 ,另外一些特殊结构的数字应该牢记,如882=7744, 112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).1-20的平方数221-40的平方数341-60的平方数461-80的平方数581-100的平方数。
平方数的规律及100以内的平方表

平方数的规律及100之内的整数平方表112=121122=144132=169142=196152=225 162=256172=289182=324192=361202=400 212=441222=484232=529242=576252=625 262=676272=729282=784292=841302=900 312=961322=1024332=1089342=1156352=1225 2222236=129637=136938=144439=152140=1600 412=1681422=1764432=1849442=1936452=2025 462=2116472=2209482=2304492=2401502=2500 512=2601522=2704532=2809542=2916552=3025 562=3136572=3249582=3364592=3481602=3600 612=3721622=3844632=3969642=4096652=4225 662=4356672=4489682=4624692=4761702=4900 712=5041722=5184732=5329742=5476752=5625 2222276=577677=592978=608479=624180=6400 812=6561822=6724832=6889842=7056852=7225 862=7396872=7569882=7744892=7921902=8100 912=8281922=8464932=8649942=8836952=9025 962=9216972=9409982=9604992=98011002=10000规律:(1)完整平方数的个位数字只好是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字同样.(3)(2)奇数的平方的个位数字是奇数,十位数字是偶数.(4)假如完整平方数的十位数字是奇数,则它的个位数字必定是6;反之,假如完整平方数的个位数字是6,则它的十位数字必定是奇数.(5)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(6)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.完整平方数的形式必以下两种之一:3n,3n+1.不可以被5整除的数的平方5n±1型,能被5整除的数的平方5n型.平方数的形式拥有以下形式16n,16n+1,16n+4,16n+9.完整平方数的各位数字之和的个位数字只好是0,1,3,4,6,7,9.(没有2,5,8)假如数p能整除a,但p的平方不可以整除a,a不是完整平方数.在两个相的整数的平方数之的全部整数都不是完整平方数.(12)一个正整数n是完整平方数的充足必需条件是n有奇数个因数(包含1和n).一个数假如是另一个整数的完整立方(即一个整数的三次方,或整数乘以它自己乘以它自己)那么我就称个数完整立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000,等. 假如正整数x,y, z 足不定方程x2+y2=z2,就称x,y,z一勾股数.x,y必然是一个奇数另一个偶数,不行能同奇数或同偶数.z 和z2必然都是奇数.五常的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841技巧:(a+b)2=a2+ b2+ 2ab(a-b)2=a2+b2-2ab ||||||a ×ab×b2×a×b a×ab×b2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=16988 2=(90-2)2=902+22-2×90×2=8100+4-360=7744用:①算能力,使算更快更正确;②估某数的平方根所的范,在判断某个大的数n能否是数能够小其可能因子的范,只要3到之的全部数能否是n的因子即可,超的都不用了.比如,判断2431能否22因此49<<50,2+4+3+1=10不可以被3整数,因49=2401<2431<2500=50,除,2341的个位既非0又非5,故只要7到47之的全部数可否整除2431即可,而53,59,61,67⋯⋯等更大的数都不用了,上2431=1117.③增添数字的熟习程度,比方162=256=28,322=1024=210,642=4096=212,此外一些特别构造的数字应当切记,如882=7744, 2211=121,22=484,(121和484从左到右与从右到左看是同样的) 2222212=144,21=441,13=169,31=961,(a左右颠倒后a也左右颠倒).。
平方数的规律及以内的平方表
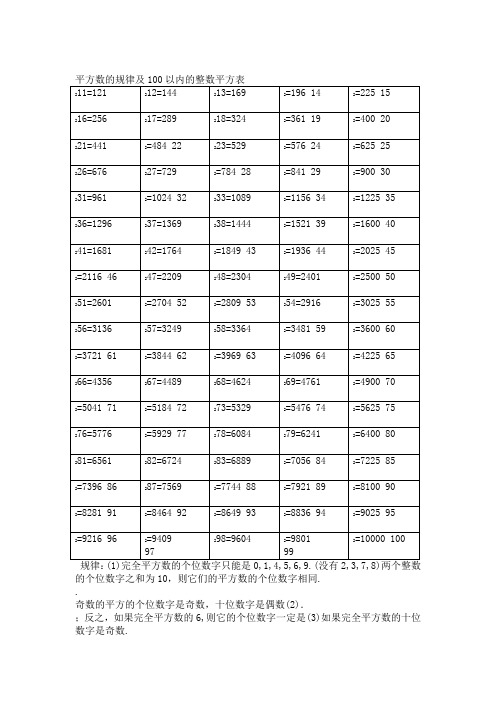
的个位数字之和为10,则它们的平方数的个位数字相同..奇数的平方的个位数字是奇数,十位数字是偶数(2).;反之,如果完全平方数的6,则它的个位数字一定是(3)如果完全平方数的十位数字是奇数.,则它的十位数字一定是奇数个位数字是61. 4的倍数加4偶数的平方是的倍数;奇数的平方是(4). 8n+4型;偶数的平方为8n或(5)奇数的平方是8n+1型:3n,3n+1.(6)完全平方数的形式必为下列两种之一. 5n型,能被5整除的数的平方为不能被5整除的数的平方为5n±1型(7)16n,16n+1,16n+4,16n+9.(8)平方数的形式具有下列形式2,5,8) 0,1,3,4,6,7,9.(没有(9)完全平方数的各位数字之和的个位数字只能是. a不是完全平方数的平方不能整除a,则(10)如果质数p能整除a,但p.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数n). 和(包括1是完全平方数的充分必要条件是(12)一个正整数nn有奇数个因数或整数乘以它本身乘以它,一个数如果是另一个整数的完全立方(即一个整数的三次方如,方数叫数,也做立们就称这个数为完全立方么本身),那我.等0,1,8,27,64,125,216,343,512,729,1000222.为一组勾股数+y就称=zx,y,z如果正整数x,y,z满足不定方程x,2必定都是奇数. 和zx,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z五组常见的勾股数:222222222222222+21+15;5=29+12=17=13;720+24;=25;38+4=59+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:222222-2ab -b)(a+b)+b=a=a+b+2ab(a||||||a×ab×b2×a×ba×ab×b2×a×b2222+2×10×3=100+9+60=169=10例:13 =(10+3)+32222-2×90×2=90=8100+4+2-88360=7744 =(90-2)用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,22整3不能被49<<50,2+4+3+1=10所以,=2401<2431<2500=5049是否为质数,因为2431判定除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117. 28210, 16=256=2=1024=2,32③增加对数字的熟悉程度,比如2122=7744, 另外一些特殊结构的数字应该牢记,如=4096=288,6422=484,(121和484从左到右与从右到左看是一样的11=121,22)22222).也左右颠倒a左右颠倒后=961,(a=169,31=441,13=144,2112.。
(完整word版)平方数的规律及100以内的平方表

精心整理平方数的规律及100以内的整数平方表(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.精心整理精心整理(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2=a2+b2+2ab(a-b)2=a2+b2-2ab||||||a×ab×b2×a×ba×ab×b2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).精心整理。
100以内平方表

规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2 + 2ab (a-b)2=a2 + b2 -2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到√n之间的所有质数是不是n的因子即可,超过√n的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<√2431<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=11×13×17.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212 ,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。
以内平方表正式版

以内平方表正式版规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2+2ab(a-b)2=a2+b2 -2ab|| | || |a×ab×b2×a×ba×ab×b2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。
100以内平方数速记

上文中主要对一些有趣的完全平方数进行了介绍,这篇是将所有的100以内完全平方数全部列举,并介绍一些速记方法。
我把它们分为20位一组,共4组,希望大家能每天记住一组,这样会记得快一些,大家加油!第一组:21~30 71~8020以内的平方如果还不熟记的话着实不应该啊!这两组呢,细心同学会发现21~30是以25为中心,71~80以75为中心,所以它们可以说是对联:22222222 30900 80640021441 84129 715041 62417922484 78428 ========222222222 725184 60847823529 72927 735329 59297724576 67626 745476 5=========22277676 25625 755625=== 末位5的平方可以用“头同尾合十”来算,观察这两副对联的每一行,末2位全部一样!所以,41、84、29、76这4个数大家一定要熟记!末2位解决掉之后,说说百位和千位。
20~30百位较小,死记不难。
71~80规律不明显,有两种记法:①规律很明显吧,不过21~29平方要特别熟记啊!② 73、74的千位为5,百位和它们本身个位一样,2765776=是符合一个数平方后末两位与它本身相同的,比较重要,应熟记;2786084=,上文提过,先把这4个记住。
其余71、72首位仍为5,百位比它们个位小1;77、79直接死记吧!第二组:41~50 51~60上一组比较难记,下面来一组比较轻松的。
先记51~60,这一组可用尾同头合十来算!22222222512601 55126 101522704 55227 204532809 55328 309542916 55429 416=⨯+===⨯+===⨯+===⨯+==22553025 55530 525=⨯+==后面的几个规律留给大家自己来找吧!22222222715041 21441 50446725184 22484 51447735329 23529 53548796241 29841 62854==-===-===-===-=对于41~50,其实和上述差不多,只不过用减法。
平方数的规律及100以内的平方表(最新编写)
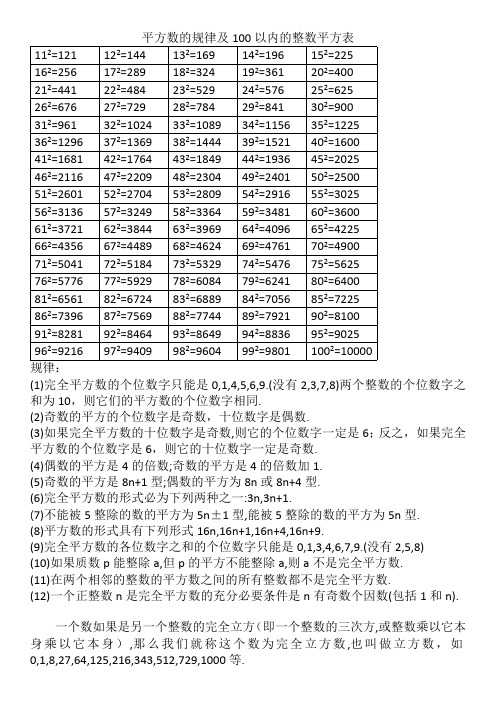
平方数的规律及100以内的整数平方表112=121122=144132=169142=196152=225162=256172=289182=324192=361202=400212=441222=484232=529242=576252=625262=676272=729282=784292=841302=900312=961322=1024332=1089342=1156352=1225362=1296372=1369382=1444392=1521402=1600412=1681422=1764432=1849442=1936452=2025462=2116472=2209482=2304492=2401502=2500512=2601522=2704532=2809542=2916552=3025562=3136572=3249582=3364592=3481602=3600612=3721622=3844632=3969642=4096652=4225662=4356672=4489682=4624692=4761702=4900712=5041722=5184732=5329742=5476752=5625762=5776772=5929782=6084792=6241802=6400812=6561822=6724832=6889842=7056852=7225862=7396872=7569882=7744892=7921902=8100912=8281922=8464932=8649942=8836952=9025962=9216972=9409982=9604992=98011002=10000规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2 + 2ab (a-b)2=a2 + b2 -2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,n超过的都不必检查了.例如,判定2431是否为质数,因为n2431492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.×13×③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212 ,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。
平方数的规律及以内的平方表

数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8).不是完全平方数a则a,的平方不能整除p但a,能整除p如果质数(10)..在两个相邻的整数的平方数之间的所有整数都不是完全平方数(11)n).和(包括1一个正整数n是完全平方数的充分必要条件是n有奇数个因数(12)或整数乘以它本身乘以它,一个数如果是另一个整数的完全立方(即一个整数的三次方也叫做立方数,如,本身),那么我们就称这个数为完全立方数.等0,1,8,27,64,125,216,343,512,729,1000222.为一组勾股数+y就称=zx,y,z如果正整数x,y,z满足不定方程x ,2必定都是奇数. 和zx,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z五组常见的勾股数:222222222222222 +21 ;+4=58 ;5;+12+15=1320 ;7=17+24=253=299+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:22222 2 -2ab =a + b b + 2ab (a(a+b)-= ab) +| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b2222+2×10×3=100+9+60=169 13=10=(10+3)+3例:2222-2×90×2=8100+4=90-88+2=(90-2)360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的都不必检查之间的所有质数是不是n到,只需检查3的因子即可,超过的筛选范围22,所以=2401<2431<2500=50是否为质数,因为了.例如,判定243149<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非49<5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.28210,=1024=2=256=2 ,3216③增加对数字的熟悉程度,比如2122=7744, 另外一些特殊结构的数字应该牢记,如=4096=288 ,6422=484,(121和484从左到右与从右到左看是一样的11=121,22)22222).也左右颠倒a左右颠倒后=961,(a=169,31=441,13=144,2112.。
100以内平方表

规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2 + 2ab (a-b)2=a2 + b2 -2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212 ,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。
(2021年整理)100以内平方数表

但是任然希望(100以内平方数表)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为100以内平方数表的全部内容。
数表
规律:
(1)完全平
方数的个位
数字只能是
0,1,4,5,6,
9.(没有2,3,
7,8)两个整
数的个位数
字之和为10,
则它们的平
方数的个位
数字相同.
(2)偶数的
平方是4的
倍数;奇数的平方是4的倍数加1。
(3)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.
(4)完全平方数的形式必为下列两种之一:3n,3n+1.
112=121。
