随机过程的模拟与数字特征
第五章 随机过程及数字特征

∫
+∞
−∞
x1 x 2 p( x1 , t1 ; x 2 , t 2 )dx1dx 2
=∫
+∞
−∞
∫
+∞
−∞
x1 x 2 p( x1 , x 2 ,τ )dx1dx 2
随机变量相关,集合平均数字特征与时间t有关. 随机变量相关,集合平均数字特征与时间t有关. 相关
5-3.2 时间平均
1.均值
µ xk = lim
5-3.1 集合平均
1.均值
+∞ 1 n 2 2 2 2.方差 σ x ( t ) = ∑ [ x k ( t ) − µ x ( t )] = ∫− ∞ [ x − µ x ( t )] p( x , t )dx n k =1
+∞ 1 n µ x ( t ) = ∑ x k ( t ) = ∫ x ( t ) p( x , t )dx −∞ n k =1
方差constdxdxdx542各态历经随机过程对于一个平稳随机过程其集合平均的数字特征不随时间发生变化而且与任意样本时间平均的数字特征相等这类随机过程称为各态历经随机过程
第五章 随机过程及数字特征
工程中随机振动的物理量是随时间变化的,如力, 工程中随机振动的物理量是随时间变化的,如力, 位移,速度,加速度. 位移,速度,加速度. 用随机变量虽然能表述随机振动的取值问题和数 字特征,但不能反映物理量取值随时间的变化, 字特征,但不能反映物理量取值随时间的变化,因此 需要用随机过程描述随机振动. 需要用随机过程描述随机振动.
2 x 2
+∞
∫
T
0
[ x ( t ) − µ x ]2 dt
3.自相关函数
Rx (τ ) = ∫ 1 = lim T →∞ T
随机过程知识点汇总

随机过程知识点汇总随机过程是指一组随机变量{X(t)},其中t属于某个集合T,每个随机变量X(t)都与一个时刻t相关联。
2.随机过程的分类随机过程可以分为离散时间随机过程和连续时间随机过程。
离散时间随机过程是指在离散的时间点上取值的随机过程,例如随机游走。
连续时间随机过程是指在连续的时间区间上取值的随机过程,例如XXX运动。
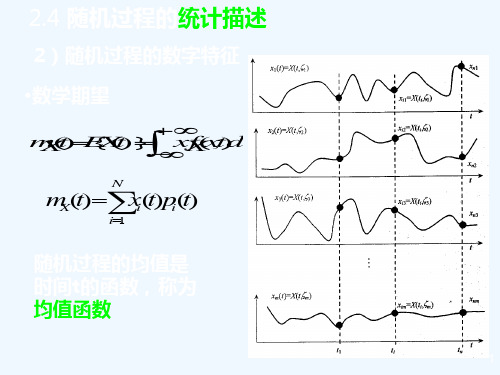
3.随机过程的数字特征随机过程的数字特征包括均值函数和自相关函数。
均值函数E[X(t)]描述了随机过程在不同时刻的平均取值。
自相关函数R(t1,t2)描述了随机过程在不同时刻的相关程度。
4.平稳随机过程平稳随机过程是指其均值函数和自相关函数都不随时间变化而变化的随机过程。
弱平稳随机过程的自相关函数只与时间差有关,而不依赖于具体的时间点。
强平稳随机过程的概率分布在时间上是不变的。
5.高斯随机过程高斯随机过程是指其任意有限个随机变量的线性组合都服从正态分布的随机过程。
高斯随机过程的均值函数和自相关函数可以唯一确定该过程。
6.马尔可夫随机过程马尔可夫随机过程是指其在给定当前状态下,未来状态的条件概率分布只依赖于当前状态,而与过去状态无关的随机过程。
马尔可夫性质可以用转移概率矩阵描述,并且可以用马尔可夫链来建模。
7.泊松过程泊松过程是指在一个时间段内随机事件发生的次数服从泊松分布的随机过程。
泊松过程的重要性质是独立增量和平稳增量。
8.随机过程的应用随机过程在金融学、信号处理、通信工程、控制理论等领域有广泛的应用。
例如,布朗运动被广泛应用于金融学中的期权定价,马尔可夫链被应用于自然语言处理中的语言模型。
t)|^2]协方差函数BZs,t)E[(ZsmZs))(ZtmZt))],其中Zs和Zt是Z在时刻s和t的取值。
复随机过程是由实部和虚部构成的随机过程,其均值和方差函数分别由实部和虚部的均值和方差函数计算得到。
协方差函数和相关函数也可以类似地计算得到。
复随机过程在通信系统中有广泛的应用,例如调制解调、信道编解码等。
随机过程的数字特征及概率意义。

随机过程的数字特征及概率意义。
1、随机过程的概念
随机变量的特点:在每次试验的结果中,以一定的概率取某些实现未知、但为确定的“数值”。
在实际问题中,我们需要研究在试验过程中随着时间而变化的随机变量,即随时间的改变而随机变化的过程。
随机过程:随参数(比如时间)改变而随机变化的过程称为随机过程,把这个参数称为时间。
在一次试验中,随机过程取一个样本向量或样本数列或样本函数,但究竟取哪一个则带有随机性。
但在大量的观察中,样本的出现是有统计规律性的。
2、随机过程的分类
(1)连续型随机过程:T是连续集,且对于任意的tet,X(t)是连续型随机变量,也就是时间和状态皆为连续的情况。
(2)离散型随机过程:T是连续集,且对于任意的tet,X(t)是离散型随机变量。
(3)连续型随机序列:T是离散集,且对于任意的tet,X(t)是连续型随机变量,它对应于时间离散、状态连续的情况,实际上,它可以用队连续性随机变量进行顺序等时间间隔采样得到。
(4)离散型随机序列:随机数字序列,随机过程的时间和状态都是离散的,为了适应数字化的需求,对连续型随机过程进行等时间间隔采样,派兵将采样值量化、分层,即得到这种连三随机过程,由以
上可知,最基本的是连续型随机过程,其他三类只是对它做离散处理而得。
随机过程的统计特性—数字特征

Q RX (t1 , t2 ) =
k1 , k2 ∈ ε X
∑
∑k ⋅k
1
2
⋅ P{ X (t1 ) = k1 , X (t2 ) = k2 }
一次结果中,决不会发生t1时刻的状态在ζ3上取值,而到t2时 刻的状态在ζ4上取值。k1,k2不在一条样本上,此情况发生的概率 为0。即P{X(t1)=k1,X(t2)=k2} =0。 由于一次试验结果只有一 个样本出现,若此次样本ζ3出现,则t1时刻的状态必在ζ3上取值, 且t2时刻的状态必还在ζ3上取值。 k1,k2必在一条样本上,此情况 发生的概率为1/4。 P{X(t1)=k1,X(t2)=k2} = 1/4。 ←样本ζi发生的概率。
∫
∞
−∞
x ⋅ f X ( x, t )d χ = mX (t )
mx(t) 描述了X(t)所有样本函数在各个时刻摆动的中心--即 在各个时刻摆动的中心 X(t)在各个时刻的状态(随机变量)的数学期望。
X (t ) 0
t1
m X (t1 )
m X (t i )
t m X (t )
ti
二、随机过程X(t)的均方值和方差 同理,把过程X (t)中的t视为固定时, X(t)为时刻t的状态(随机 变量)。其二阶原点矩:
例1、设随机过程X(t)=U·t,U在(0,1)上均匀分布,求E[X(t)], D[X(t)],Rx(t1,t2),Cx (t1,t2)。
⎧1, Q fU (u ) = ⎨ ⎩0,
解:
0 ≤ u ≤1 其它
∞ 1
t ∴ E[ X (t )] = E[U ⋅ t ] = t ⋅ E[U ] = t ⋅ ∫ ufU (u )du = t ⋅ ∫ udu = 0 -∞ 2 2 RX (t1 , t2 ) = E[ X (t1 ) X (t2 )] = E[U ⋅ t1 ⋅ U ⋅ t2 ] = t1 ⋅ t2 ⋅ E[U ] t1 ⋅ t2 = t1 ⋅ t2 ⋅ ∫ u ⋅ fU (u )du = t1 ⋅ t2 ⋅ ∫ u du = −∞ 0 3 t1 ⋅ t2 t1 t2 t1 ⋅ t2 − ⋅ = C X (t1 , t2 ) = RX (t1 , t2 ) − m(t1 ) ⋅ m(t2 ) = 2 2 12 3 2 t D[ X (t )] = C X (t , t ) = 12
随机过程及其统计描述ppt课件.ppt

任意时刻下,观测目的是X取什么值;全程的情况下, 观测目的是X(t)的函数形式.
7
12.1 随机过程的概念
随机相位正弦波
随机过程举例
考虑: X (t) a cos(t ), t (,)
式中 a,是正常数,是 (0, 2 ) 上服从均匀分布的随机变量。
当 在(0, 2 ) 内随机的取一个值 i ,可得样本函数:
2
0 cos(t1 ) cos(t2 ) f ( )d
a2
2
2
0 cos(t1 ) cos(t2 )d
a2
4
2
0 {cos[(t1 t2 ) 2 ] cos(t1 t2 )}d
a2 2
cos (t1
t2 )
方差函数
2 X
(t)
RX
(t , t )
2 X
(t)
a2 2
18
12.2 随机过程的统计描述
随机过程举例
抛掷一枚硬币的试验,样本空间是S={H,T}, 现借此定义随机过程:
cos t,
X (t) t,
当出现H, 当出现T,
t (, )
可将此随机过程改写为
X (t) Y cost (1Y )t ,
其中
Y
1, 0,
出现H 出现T
,
t (, )
X对Y和t的依赖,决定了X是一个随机过程. 确定了 Y之后,即可确定任意时刻和全程的观测结果.
集平均(统计平均)
X (t)是随机过程的所有样本函数在时刻 t 的函数值的平均值,通常称
这种平均为集平均或统计平均。
12
12.2 随机过程的统计描述
(二) 随机过程的数字特征
均方值函数
Ψ
随机信号分析实验报告(基于MATLAB语言)

随机信号分析实验报告——基于MATLAB语言姓名:_班级:_学号:专业:目录实验一随机序列的产生及数字特征估计 (2)实验目的 (2)实验原理 (2)实验内容及实验结果 (3)实验小结 (6)实验二随机过程的模拟与数字特征 (7)实验目的 (7)实验原理 (7)实验内容及实验结果 (8)实验小结 (11)实验三随机过程通过线性系统的分析 (12)实验目的 (12)实验原理 (12)实验内容及实验结果 (13)实验小结 (17)实验四窄带随机过程的产生及其性能测试 (18)实验目的 (18)实验原理 (18)实验内容及实验结果 (18)实验小结 (23)实验总结 (23)实验一随机序列的产生及数字特征估计实验目的1.学习和掌握随机数的产生方法。
2.实现随机序列的数字特征估计。
实验原理1.随机数的产生随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进行随机信号仿真分析时,需要模拟产生各种分布的随机数。
在计算机仿真时,通常利用数学方法产生随机数,这种随机数称为伪随机数。
伪随机数是按照一定的计算公式产生的,这个公式称为随机数发生器。
伪随机数本质上不是随机的,而且存在周期性,但是如果计算公式选择适当,所产生的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使用。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布, U(0,1)。
即实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数,通常采用的方法为线性同余法,公式如下:,序列为产生的(0,1)均匀分布随机数。
定理1.1若随机变量X 具有连续分布函数,而R 为(0,1)均匀分布随机变量,则有2.MATLAB中产生随机序列的函数(1)(0,1)均匀分布的随机序列函数:rand用法:x = rand(m,n)功能:产生m×n 的均匀分布随机数矩阵。
(2)正态分布的随机序列函数:randn用法:x = randn(m,n)功能:产生m×n 的标准正态分布随机数矩阵。
随机过程的数字特征

第三节 随机过程的数字特征定义6.3.1 设随机过程}),({T t t ∈ξ的一维分布函数为,我们称);(x t F ());()]([x t dF x t E t ∫+∞∞−==ξµξ()()∫+∞∞−−==);(][)]([22x t dF t x t D t ξξµξσ分别为随机过程}),({T t t ∈ξ的均值函数和方差函数。
对离散型的随机过程,其均值函数和方差函数分别为:()()∑===ni i i t p x t E t 1)]([ξµξ()()()()t p t x t t E t D t i ni i 2122][])([)]([ξξξµµξξσ∑=−=−==其中:()n i x t P t p i i ,,1},)({"===ξ对连续型的随机过程,其均值函数和相关函数分别为:()dx x t xf t E t ∫+∞∞−==);()]([ξµξ()()()∫+∞∞−−=−==dx x t f t x t t E t D t );(][])([)]([222ξξξµµξξσ均值函数和方差函数刻画了随机过程在不同时刻的统计特性,均值函数表示{)(t ξ}在各个不同时刻取值的摆动中心。
方差函数表示{)(t ξ}在各个不同时刻取值的关于()t ξµ的平均偏离程度。
但不能描述在不同时刻之间的相互关系,因此我们必须引入自相关函数和自协方差函数概念。
定义6.3.2 设随机过程}T t ),t ({∈ξ的二维分布函数为,我们称其自相关函数和自协方差函数分别为:),;,(2121x x t t F)x ,x ;t,t (dF x x )]t ()t ([E )t ,t (R 2121212121∫∫+∞∞−+∞∞−==ξξξ T t t ∈21,()[][])t ()t (t )t (E )t ,t (C 221121ξξξµξµξ−−=且:)t ()t ()t ,t (R )t ,t (C 212121ξξξξµµ−=若令,则t t t ==21()t t t R t t C 2),(),(ξξξµ−==D ξ(t )=2ξσ由此可以看出:均值函数()t ξµ和相关函数是最基本的数字特征,协方差函数和方差函数可以由它们确定。
随机过程的基本知识

• 解:X2 (t) =E(X(t)X(t))=E{AAcos(t)cos(t)}=cos^2(t)E(A^2) • =cos^2(t)(1x1+2x2+3x3)/3= 14 cos2 (t)
3
2 X
(t
)
E{[
X
(t
)
E(
X
(t))]2}
E{[
A
cos(t)
cos(t)E(
A)]2}
E{[ Acos(t) 2 cos(t)]2} E{cos2 (t)( A2 4A 4)}
• 特点2:随时间t的变化,X(t)在延续变化。
例3:股票的价格
• 记t时刻股票的价格为Y(t),则{Y(t),t>0}是一个随机 过程。
•图
• 特点1:给定时刻t,股票价格Y(t)不可预测,可以 认为是随机变量。
• 特点2:股票价格Y(t)随时间t的变化在不断变化。
例4 排队问题
• 记X(t)表示[0,t)小时内通过柜台的人数,则 {X(t),t>0}是一个随机过程。
所以
C 11tt11t22
1 t1t2
1
t
2 2
故( X (t1), X (t2 ))服从以(0,0) 为均值向量,C为协方差矩阵 的二维正态分布
例2:设随机过程X(t)=A cos(t), t实数,其中A是随
机变量,其分布律为:P{A=1}=P{A=2}=P{A=3}=1/3
求(1)X(t)的一维分布函数
是连续型,称该过程为连续型随机过程。 • 例:热噪声电压X(t)服从(a,b)上均匀分布 • 2、离散型 当X(t)是离散型,如排队问题
是离散型随机过程,t时刻通过的人数X(t)只 能取可数个值。据研究,X(t)服从泊松分布。
02第二讲随机过程概念及数字特征精品PPT课件

'
dt
'
E
1 T
T
2 T
2
T
2 T
2
(t)
(t
'
)e
j
(t t '
)dtdt
'
1 T
T
2 T
2
T
2 T
R(t
t ' )e
j(tt' )dtdt '
2
E[ FT () 2 ] 1
2
R(0)R()Fra bibliotek0二、功率谱密度
付氏变换(能量谱密度)F () f (t)e jtdt 沟通了确定信号时域和频
域的关系,随机过程在频率域中要讨论功率谱密度 ,主要原因有二 :
1. 对于随机过程来说,它由许许多多个样本函数来构成, 所以无法求其付氏 变换,可以说,随机过程不存在付氏变换。 2. 随机过程属于功率信号而不属于能量信号,所以讨论功率谱密度。
自相关遍历
R( )
遍历过程即指宽遍历过程.
四、严遍历过程或窄义遍历过程
的所有统计平均特性和其样函数所有相应的时间平 均特性以概率为一相等 1.遍历过程必定是平稳过程,但平稳过程不一定是遍历过程。
2.若 是平稳高斯过程, 且
;
:
则 是遍历过程
3.对于遍历过程,只要根据其一个样函数,便可得到其数字特征。
x1x2
10 x1 100
x2
dx1dx2
5
5 x2
5 5
x1
10
x1 100
x2
dx1dx2
5
5 x2
320500dx2
0
CX (t1,t2 ) E{[ X (t1) E[ X (t1)]][X (t1) E[ X (t1)]]} E[ X (t1) X (t1)] 0
2.2.12.2随机过程的数字特征

E ei(u1Xt1 un Xtn )
称为随机过程Xt , t T的有限维特征函数.
7
离散型随机过程
当时间参数集T取离散值n1, , nk , 时, 这种随机过程称为离散时间随机过程 . 此时,Xt是一串随机变量Xn1 , , Xnk , 所构成的序列,称为时间序列 .
方差函数
t T,随机过程 Xt , t T的一维分布函数
为 Ft x ,密度函数为 ft x ,则
2 Xt
Var X t
E X t
EX
t
2
2
x Xt dFt x
E Xt2 EXt 2 .
称为随机过程Xt , t T的方差函数.
3方差函数Fra bibliotek特殊地,
若E
当t1 t2 t,cX t1 , t2 2Xt .
5
自相关函数
t1 , t2 T,
RX t1, t2 E X X t1 t2
称为随机过程Xt , t T的自相关函数.
当t1 t2 t,RX t1 , t2 E X t 2 .
6
特征函数
t1 , , tn T,n 1
1 e 2t1 1 e 2 t2 t1 1 e 2t1 1 e 2 t2 t1
2
2
1 e 2 t2 t1
2
2
2
12
例子
P X X t1 t2 1
P Xt1 1, Xt2 1
0 t1 t2
Xt1 1, Xt2 1
P Xt1 1, Xt2 1 P Xt1 1, Xt2 1
X t
1, 若随机点在
1,
若随机点在
0, t 内发生偶数次
随机实验报告

随机信号实验报告课程:随机信号实验题目:随机过程的模拟与特征估计学院:四川大学电子信息学院学生名称:实验目的:1.学会利用MATLAB模拟产生各类随即序列。
2.熟悉和掌握随机信号数字特征估计的基本方法。
实验内容:1.模拟产生各种随即序列,并画出信号和波形。
(1)白噪声<高斯分布,正弦分布)。
(2)随相正弦波。
(3)白噪声中的多个正弦分布。
(4)二元随机信号。
(5)自然信号:语音,图形<选做)。
2.随机信号数字特征的估计(1)估计上诉随机信号的均值,方差,自相关函数,功率谱密度,概率密度。
(2)各估计量性能分析<选做)实验仪器:PC机一台MATLAB软件实验原理:随机变量常用到的数字特征是数字期望值、方差、自相关函数等。
相应地,随机过程常用到的数字特征是数字期望值、方差、相关函数等。
它们是由随机变量的数字特征推广而来,但是一般不再是确定的数值,而是确定的时间函数。
b5E2RGbCAP均值:mx(t>=E[X(t>]=;式中,p(x,t>是X<t)的一维概率密度。
mx(t>是随机过程X<t)的所有样本函数在时刻t的函数值的均值。
在matlab中用mea(>函数求均值。
p1EanqFDPw方差:<t)=D[X(t>]=E[];<t)是t 的确定函数,它描述了随机过程诸样本函数围绕数学期望mx(t>的分散程度。
若X<t)表示噪声电压,则方差<t)则表示瞬时交流功率的统计平均值。
在matlab中用var(>函数求均值。
DXDiTa9E3d自相关函数:Rx(t1,t2>=E[X(t1>X(t2>];自相关函数就是用来描述随机过程任意两个不同时刻状态之间相关性的重要数字特征。
在matlab中用xcorr<)来求自相关函数。
RTCrpUDGiT在matlab中可用函数rand、randn、normr、random即可生成满足各种需要的近似的独立随机序列。
北理工随机信号分析实验报告
本科实验报告实验名称:随机信号分析实验实验一 随机序列的产生及数字特征估计一、实验目的1、学习和掌握随机数的产生方法。
2、实现随机序列的数字特征估计。
二、实验原理1、随机数的产生随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进行随机信号仿真分析时,需要模拟产生各种分布的随机数。
在计算机仿真时,通常利用数学方法产生随机数,这种随机数称为伪随机数。
伪随机数是按照一定的计算公式产生的,这个公式称为随机数发生器。
伪随机数本质上不是随机的,而且存在周期性,但是如果计算公式选择适当,所产生的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使用。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布,即 U(0,1)。
实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数,通常采用的方法为线性同余法,公式如下:)(m od ,110N ky y y n n -=N y x n n /=序列{}n x 为产生的(0,1)均匀分布随机数。
下面给出了上式的3组常用参数: 1、10N 10,k 7==,周期7510≈⨯;2、(IBM 随机数发生器)3116N 2,k 23,==+周期8510≈⨯; 3、(ran0)315N 21,k 7,=-=周期9210≈⨯;由均匀分布随机数,可以利用反函数构造出任意分布的随机数。
定理 1.1 若随机变量 X 具有连续分布函数F X (x),而R 为(0,1)均匀分布随机变量,则有)(1R F X x -=由这一定理可知,分布函数为F X (x)的随机数可以由(0,1)均匀分布随机数按上式进行变换得到。
2、MATLAB 中产生随机序列的函数(1)(0,1)均匀分布的随机序列 函数:rand 用法:x = rand(m,n)功能:产生m ×n 的均匀分布随机数矩阵。
(2)正态分布的随机序列 函数:randn 用法:x = randn(m,n)功能:产生m ×n 的标准正态分布随机数矩阵。
第三讲 随机过程的数字特征和特征函数
3
•方 差
X 2(t) E {X ( [t) m X (t)2 } ]E{X2(t) }m X 2(t)
•均值与方差的物理意义:
x(t ) -----单位电阻上的电压 x 2 (t )/1-----消耗在单位电阻上的瞬时功率
[ x(t)m ]2x/(1t-)----消耗在单位电阻上的瞬时交流功率 E{[ x(t)m]2x/(1t)}-----消耗在单位电阻上的瞬交流功率的 统计平均值
•N维随机矢量的自相关
RX E[XXT]
E[X12] RX r21
rn1
r1 2 E[X22]
rn2
r1n
r2n
E[Xn2]
rij E[XiXj]
•N维随机矢量的协方差
D XE[X ( E)X X ( E)X T]
D[X1]
R X(tY 1 ,t2) m x(t1 )m Y(t2)
中心化互 相关函数
t1
t2
描述两个随机过程任意两个时刻之间的统计关联性
14
•两个随机过程的独立,不相关和正交
C X ( t1 ,Y t2 ) R X ( t1 Y ,t2 ) m x ( t1 ) m Y ( t2 )
CXY(t1,t2)0 R X(Y t1,t2)m x(t1)m Y(t2)
•均值和自相关函数是随机过程最基本的特征
10
例 随机相位信号 X(t)Acos( 0t )自相关函数和方差
m X ( t ) E { X ( t ) } E { A c0 o t ) s } A ( 0 2 c0 o t ) s 2 1 d ( 0
•自相关系数
第三讲随机过程的数字特征和特征函数讲解

第三讲随机过程的数字特征和特征函数讲解在概率论和统计学中,随机过程是指一组随机变量的集合,这些随机变量依赖于一个参数(通常是时间)。
随机过程的数字特征和特征函数是描述随机过程的重要概念。
1.数字特征:随机过程的数字特征是对其统计特性的度量,通常用于描述随机过程的平均值、方差、协方差等。
随机过程的数字特征可以通过计算随机变量的数学期望、方差等得到。
2.特征函数:特征函数是随机过程的一种表示方式,它是对随机过程的全面描述。
特征函数是随机变量的复数值函数,它对于每个时间点都定义了一个复数值,用来表示该时间点的随机变量的概率分布。
特征函数可以通过随机变量的概率密度函数计算得到。
特征函数的性质:-对称性:如果随机过程的数字特征对称,那么它的特征函数也对称。
-唯一性:特征函数能够唯一地表示一个随机过程的概率分布。
-独立性:随机过程的特征函数在不同时间点上是相互独立的。
-连续性:特征函数是连续函数,可以通过连续函数逼近定理来证明。
特征函数的应用:-用于推导随机过程的数字特征:通过特征函数可以推导出随机过程的数字特征,例如平均值、方差。
-用于计算随机过程的概率分布:通过特征函数可以计算随机过程的概率分布,例如计算随机过程在其中一时间点的概率。
-用于分析和处理随机过程的相关问题:通过特征函数可以进行随机过程的变换、滤波等操作,从而实现对随机过程的分析和处理。
总之,随机过程的数字特征和特征函数是描述随机过程的重要工具,它们可以用来分析和处理随机过程相关的问题,推导随机过程的数字特征,并计算随机过程的概率分布。
通信原理简答题答案1(个人整理)

通信原理简答题答案1(个人整理)通信原理第六版课后思考题第1章绪论1、何谓数字信号何谓模拟信号两者的根本区别是什么答:数字信号:电信号的参量仅可能取有限个值;模拟信号:电信号的参量取值连续;两者的根本区别在于电信号的参量取值是有限个值还是连续的。
2、画出模拟通信系统的一般模型。
3、何谓数字通信数字通信有哪些优缺点答:数字通信即通过数字信号传输的通信,相对模拟通信,有以下特点:1)传输的信号是离散式的或数字的;2)强调已调参数与基带信号之间的一一对应;3)抗干扰能力强,因为信号可以再生,从而消除噪声积累;4)传输差错可以控制;5)便于使用现代数字信号处理技术对数字信号进行处理;6)便于加密,可靠性高;7)便于实现各种信息的综合传输3、画出数字通信系统的一般模型。
答:4、按调制方式,通信系统如何分类答:分为基带传输和频带传输5、按传输信号的特征,通信系统如何分类答:按信道中传输的是模拟信号还是数字信号,可以分为模拟通信系统和数字通信系统6、按传输信号的复用方式,通信系统如何分类答:频分复用(FDM),时分复用(TDM),码分复用(CDM)7、通信系统的主要性能指标是什么第3章随机过程1、随机过程的数字特征主要有哪些它们分别表征随机过程的哪些特征答:均值:表示随机过程的n个样本函数曲线的摆动中心。
方差:表示随机过程在时刻t相对于均值a(t)的偏离程度。
相关函数:表示随机过程在任意两个时刻上获得的随机变量之间的关联程度。
2、何谓严平稳何谓广义平稳它们之间的关系如何答:严平稳:随机过程(t)的任意有限维分布函数与时间起点无关。
广义平稳:1)均值与t无关,为常数a。
2)自相关函数只与时间间隔=-有关。
严平稳随机过程一定是广义平稳的,反之则不一定成立。
4、平稳过程的自相关函数有哪些性质它与功率谱的关系如何答:自相关函数性质:(1)R(0)=E[]——的平均功率。
(2)R()=R(-)——的偶函数。
(3)——R()的上界。
随机过程的模拟与特征估计

[Px,f]=pwelch(x,window,noverlap,Nfft,Fs, 'onesided'); % 估计功率 谱密度 f=[-fliplr(f') (f(2:end))']; [-Fs/2, Fs/2] Py=[-fliplr(Px') (Px(2:end))']; % 对称的功率谱 plot(f,10*log10(Py), 'b'); grid on; 估计出来的功率谱密度为: % 构造一个对称的频率,范围是
w(n)为均值为 0,方差为 4 的高斯白噪声序列。 (1)模拟产生 X(n)序列的 500 观测样本函数,绘出波形图。 (2)用观测点估计信号的均值和方差。 (3)估计该过程的自相关函数和功率谱密度,并画出图形。
【分析】给定 AR 过程,可以用递推公式得出最终的输出序列。 或者按照一个白噪声通过线性系统的方式得到, 这个系统的传递 函数为: ,
随机过程的模拟与特征估计
1.实验目的 (1)了解随机过程特征估计的基本概念和方法 (2)学会运用 Matlab 软件产生各种随机过程,对随机过程的特 征进行估计 (3)通过实验了解不同估计方法所估计出来的结果差异 2.实验原理 (1)高斯白噪声的产生: N=1000;x=randn(N,1) 高斯:概率分布 (2)均值估计: 1 = N
(3)估计该过程的自相关函数和功率谱密度,并画出图形。 %估计的自相关函数序列 Mlag=20; % 定义最大自相关长度
Rx=xcorr(x,Mlag,'coeff'); m=-Mlag:Mlag; stem(m,Rx,'r.'); grid on; 最终的值为
实际的功率谱密度可以用类似于上面的方法进行估计: 用以下语句实现: window=hamming(20); noverlap=10; Nfft=512; Fs=1000; % 采用 hanmming 窗,长度为 20 % 重叠的点数 % 做 FFT 的点数 % 采样频率,为 1000Hz
随机过程的部分描述——数字特征

随机过程的部分描述——数字特征摘要: 虽然用随机过程的维分布函数或维概率密度函数能够完善地描述随机过程的统计特性。
但在实际工作中,有时不易或不需要求解出维分布函数或维概率密度函数,而用随机过程的数字特征即能刻画随机过程的重要特征,又...虽然用随机过程的维分布函数或维概率密度函数能够完善地描述随机过程的统计特性。
但在实际工作中,有时不易或不需要求解出维分布函数或维概率密度函数,而用随机过程的数字特征即能刻画随机过程的重要特征,又便于进行运算和实际测量,从而更简捷地解决实际工程问题。
随机过程的数字特征包括数学期望、方差和相关函数等。
一、数学期望(均值或统计平均)定义:并记为,是一时间函数,它表示随机过程各个时刻的数学期望随时间的变化情况,其本质就是随机过程所有样本函数的统计平均函数。
图3.2.1 画出了随机过程的个样本函数和它的数学期望。
图3.2.1 随机过程的数学期望和方差二、方差定义:由此可得也常记作,它表示随机过程在时刻对于均值的偏离程度,见图3.2.1。
称为随机过程均方差。
当均值时,方差为三、自协方差函数和自相关函数数学期望和方差描述了随机过程在各个孤立时刻的特征,但没有反映随机过程不同时刻之间的内在联系。
自协方差函数和自相关函数就是用来衡量随机过程在任意两个时刻上获得的随机变量的统计相关特性的。
1.自协方差函数定义其中,与为两个任意时刻;与为在和上所得到的数学期望;为二维概率密度函数。
2.自相关函数定义二者关系:上面的和是衡量同一个随机过程的相关程度的。
四、互协方差和互相关函数如果把自相关函数的概念引伸到两个或多个随机过程中,可以得互协方差或互相关函数。
设和分别表示两个随机过程,则1.互协方差函数定义 2.互相关函数定义由以上分析可见,随机过程的统计特性一般都与时刻有关。
就相关函数而言,它的相关程度与选择时刻及有关。
如果,可令,则自相关函数可以表示为,这说明,相关函数依赖于起始时刻及时间间隔,即相关函数是和的函数。
北京理工大学随机信号分析实验报告汇总

北京理⼯⼤学随机信号分析实验报告汇总本科实验报告实验名称:随机信号分析实验实验⼀随机序列的产⽣及数字特征估计⼀、实验⽬的1、学习和掌握随机数的产⽣⽅法。
2、实现随机序列的数字特征估计。
⼆、实验原理1、随机数的产⽣随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进⾏随机信号仿真分析时,需要模拟产⽣各种分布的随机数。
在计算机仿真时,通常利⽤数学⽅法产⽣随机数,这种随机数称为伪随机数。
伪随机数是按照⼀定的计算公式产⽣的,这个公式称为随机数发⽣器。
伪随机数本质上不是随机的,⽽且存在周期性,但是如果计算公式选择适当,所产⽣的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使⽤。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布,即 U(0,1)。
实际应⽤中有许多现成的随机数发⽣器可以⽤于产⽣(0,1)均匀分布随机数,通常采⽤的⽅法为线性同余法,公式如下:)(mod ,110N ky y y n n -=N y x n n /=序列{}n x 为产⽣的(0,1)均匀分布随机数。
下⾯给出了上式的3组常⽤参数: 1、10N 10,k 7==,周期7510≈?;2、(IBM 随机数发⽣器)3116N 2,k 23,==+周期8510≈?; 3、(ran0)315N 21,k 7,=-=周期9210≈?;由均匀分布随机数,可以利⽤反函数构造出任意分布的随机数。
定理 1.1 若随机变量 X 具有连续分布函数F X (x),⽽R 为(0,1)均匀分布随机变量,则有)(1R F X x -=由这⼀定理可知,分布函数为F X (x)的随机数可以由(0,1)均匀分布随机数按上式进⾏变换得到。
2、MATLAB 中产⽣随机序列的函数(1)(0,1)均匀分布的随机序列函数:rand ⽤法:x = rand(m,n)功能:产⽣m ×n 的均匀分布随机数矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二随机过程的模拟与数字特征
一、实验目的
1. 学习利用MATLAB模拟产生随机过程的方法。
2. 熟悉和掌握特征估计的基本方法及其MATLAB实现。
二、实验原理
1. 正态分布白噪声序列的产生
MATLAB提供了许多产生各种分布白噪声序列的函数,其中产生正态分布白噪声序列
的函数为randn。
函数:randn
用法:x = randn(m,n)
功能:产生 m Xn的标准正态分布随机数矩阵。
如果要产生服从 N ( ,「)分布的随机序列,则可以由标准正态随机序列产生。
如果X ~ N(0,1),则—■- N (,)。
2. 相关函数估计
MATLAB提供了函数 xcorr用于自相关函数的估计。
函数:xcorr
用法:c= xcorr (x,y)
c= xcorr (x)
c= xcorr (x,y ,'opiti on') c= xcorr (x, ,'opiti on')
功能:xcorr(x,y)计算X (n )与Y (n)的互相关,xcorr(x)计算X (n )的自相关。
option选项可以设定为:
'biased'有偏估计。
'un biased'无偏估计。
'coeff m = 0时的相关函数值归一化为1。
'none'不做归一化处理。
3. 功率谱估计
对于平稳随机序列X (n),如果它的相关函数满足
(2.1)
那么它的功率谱定义为自相关函数R X (m)的傅里叶变换:
(2.2)
功率谱表示随机信号频域的统计特性,有着重要的物理意义。
我们实际所能得到的随机
信号的长度总是有限的,用有限长度的信号所得的功率谱只是真实功率谱的估计,称为谱估计或谱分析。
功率谱估计的方法有很多种,这里我们介绍基于傅里叶分析的两种通用谱估计方法。
(1 )自相关法
■
先求自相关函数的估计「X (m),然后对自相关函数做傅里叶变换
N-L
R
fw) = 乂鞋(耐占皿
x
(2.3)
其中N表示用于估计样本序列的样本个数。
(2 )周期图法
先对样本序列x(n)做傅里叶变换
(2.4)
其中0 n| N-1,则功率谱估计为
s(u>) =
A
(2.5)
MATLAB函数periodogram 实现了周期图法的功率谱估计。
函数:periodogram
用法:[Pxx,w] = periodogram(x)
[Pxx,w] = periodogram(x,wi ndow)
[Pxx,w] = periodogram(x,wi ndow, nft)
[Pxx,f] = periodogram(x,wi ndow, nfft,fs)
periodogram(...)
功能:实现周期图法的功率谱估计。
其中:
Pxx为输出的功率谱估计值;
f为频率向量;
w为归一化的频率向量;
window代表窗函数,这种用法种对数据进行了加窗,对数据加窗是为了减少功率谱估计中因为数据截断产生的截断误差,表 2.1列出了产生常用窗函数的 MATLAB函数
矩形窗boxcar BlackDLan 窗blackinan
三角窗triang Chebyshev 窗chebft'in
[tanning 窗hann Bartlett 窗bartlett
Ehming 窗hamming Kaiser 窗kaiser nfft设定FFT算法的长度;
fs表示米样频率;
如果不指定输出参数(最后一种用法) ,则直接会出功率谱估计的波形。
三、实验内容
1.按如下模型产生一组随机序列
x(n)=0.8x(n-1)晋|囲(n)
其中黴(n)是均值为1,方差为4的正态分布白噪声序列。
估计过程的自相关函数和功率谱。
(1 )实验程序
m.文件如下:
#输入变量p表示x(n)里n的数值# fun ctio n f=fun c1(p) w=randn(1,p)*2+1;
#或 f=normrnd(1,2,1000,1)#
x=zeros(1,p);
for n = 2:1:p
x(n)=0.8*x(n-1)+ w(n); end figure(1) plot(x); c=xcorr(x);
plot(c);
figure(2);
title(' 'x(n) 的自相关函数 ');
figure(3);
periodogram(x);
title('x(n) 的功率谱 ');
end
(2)实验过程及结果:
在 command 命令栏里输入:
fun
c1(5000)
得到三个图的结果:
X 何的自相关函数
50 【
O D
-d l E e t r t *p p 」、
8p ) A o u a D 4 5 3 5
2 a 2
□
Q
o n
2000 3000 4000 5000 6000 7000 8000 9000 10000
磁门)的功率谱
o
40
0.2 0.3 04 0.5 0.S 0.7 0.8 0.9 1
Narmalized Frequency (心 rad/sample)
40
30
20 o
o 1 20
30
1—
2.设信号为
x(n)=引"(2两皿)十 Z 工n) -F 细(n) n=0,1 , I , N-1
其中fi =0 .05 , f2 =0 .12为正态分布白噪声序列,试在N =256和N= 1024点时,分别产生随机序列x(n),画出x(n)的波形并估计x(n)的相关函数和功率谱。
(1)实验程序:
写出m.文件
#输入变量p表示x(n)里n的数值# function f=fun c2(p)
f1 = 0.05;
f2 = 0.12;
w=ra ndn (1,p);
x = zeros(1,p);
for n=0:1:p-1
x(n+1) = sin (2*pi*f1* n) + 2*cos(2*pi*f2* n) + w(n+1);
end
figure(1);
plot(x);
title(' N=p 时x(n)的波形');
c = xcorr (x);
figure(2);
subplot(1,2,1);
plot(c);
title(' N=p时x(n)的相关函数'); subplot(1,2,2);
periodogram(x);
end
(2)实验过程及结果
在 command 命令栏里输入:
Func2(256)
得到三个图的结果:
M=256吋爛)的波形
50
200 250
z :
nn
5Q 100
3 2
1000
2256时K (n )的相关函数
8Q0
6QD
0.5 1
Normalized Frequency (xu rad/sample)
Periodogram Power Spectral Density Estimate
20
20
l
30
-
400
200
-200 ■400
200 400 EOO
〔
2C J E n 5s *P B
」
*g p ) A u ua nh (L
n -
ra
o
-40
在comma nd 命令栏里输入:。
