实验报告七-常微分方程初值问题的数值解法
常微分方程初值问题的数值解法

贵州师范大学数学与计算机科学学院学生实验报告课程名称: 数值分析 班级: 实验日期: 年 月 日 学 号: 姓名: 指导教师: 实验成绩: 一、实验名称实验六: 常微分方程初值问题数值解法 二、实验目的及要求1. 让学生掌握用Euler 法, Runge-Kutta 法求解常微分方程初值问题.2. 培养Matlab 编程与上机调试能力. 三、实验环境每人一台计算机,要求安装Windows XP 操作系统,Microsoft office2003、MATLAB6.5(或7.0). 四、实验内容1. 取步长h=0.1,0.05,0.01, ,用Euler 法及经典4阶Runge-Kutta 法求解初值问题⎩⎨⎧=≤≤++-=1)0()10(2222'y t t t y y 要求:1) 画出准确解(准确解22t e y t +=-)的曲线,近似解折线;2) 把节点0.1和0.5上的精确解与近似解比较,观察误差变化情况.2. 用 Euler 法,隐式Euler 法和经典4阶R-K 法取不同步长解初值问题⎪⎩⎪⎨⎧=∈-=21)0(],1,0[,50'y x y y 并画出曲线观察稳定性. 注:题1必须写实验报告五、算法描述及实验步骤Euler 法:输入 000),(,,,),,(y a x x h b a y x f = 输出 Euler 解y步1 ),,2,1(;m n h n a x hab m n =⨯+=-⇐步2 对1,,2,1,0-=m n 执行),(1n n n n y x f h y y ⨯+⇐+ 步3 输出T m y y y y ),,,(21 = 经典4阶R-K 法:输入 000),(,,,),,(y a x x h b a y x f = 输出 4阶R-K 解y 步1 ),,2,1(;m n h n a x hab m n =⨯+=-⇐步2 对1,,2,1,0-=m n 执行),(1n n y x f K ⇐,)5.0,(15.02hK y x f K n n +⇐+, )5.0,(25.03hK y x f K n n +⇐+,),(314hK y x f K n n +⇐+ )22(643211K K K K hy y n n ++++⇐+ 步3 输出T m y y y y ),,,(21 =六、调试过程及实验结果>> shiyan6Y1 =0.8000 0.6620 0.5776 0.5401 0.5441 0.5853 0.6602 0.7662 0.9009 1.0627 Y2 =0.8287 0.7103 0.6388 0.6093 0.6179 0.6612 0.7366 0.8419 0.9753 1.1353e1 =0.0287e2 =4.2469e-006 e1 =0.0738e2 =1.1609e-005注:至于h=0.05、0.01的情况将程序中的h值作相应的改动即可得。
常微分方程初值问题的数值解法

1 1 2 1 , 2 p 2
这里有 3 个未知 数, 2 个方程。
存在无穷多个解。所有满足上式的格式统称为2阶龙格 - 库 塔格式。注意到,p 1, 1 2 1 就是改进的欧拉法。
Step 1: 将 K2 在 ( xi , yi ) 点作 Taylor 展开
K 2 f ( xi ph, yi phK1 ) f ( xi , yi ) phf x ( xi , yi ) phK1 f y ( xi , yi ) O( h2 )
y( xi ) phy( xi ) O(h2 )
d f ( x, y) dx 首先希望能确定系数 1、2、p,使得到的算法格式有 2阶 dy 精度,即在 yi y( xi ) 的前提假设下,使得 f x ( x, y) f y ( x, y) dx Ri y( xi 1 ) yi 1 O(h3 ) f x ( x, y) f y ( x, y) f ( x, y) y( x )
y( x0 ) y0 yk 1 yk h f ( xk , yk 1 )
, k 0,1,...
隐式欧拉法的求解: 利用迭代的思路进行.
yi 1 yi hf ( xi , yi 1 )
变换为
y
( k 1) i 1
yi hf ( xi , y )
y i 1 K1 K2
1 1 y i h K 1 K 2 2 2 f ( xi , yi ) f ( xi h, yi hK 1 )
步长一定是一个h 吗?
§2 Runge-Kutta Method
常微分方程初值问题数值解法

常微分方程初值问题的数值解法在自然科学、工程技术、经济和医学等领域中,常常会遇到一阶常微分方程初值问题:(,),,(),y f x y a x b y a y '=≤≤⎧⎨=⎩ (1) 此处f 为,x y 的已知函数,0y 是给定的初始值。
本章讨论该问题的数值解法,要求f 在区域{(,)|,}G x y a x b y =≤≤<∞内连续,并对y 满足Lipschitz 条件,从而初值问题(1)有唯一的连续可微解()y y x =,且它是适定的。
1 几个简单的数值积分法1.1 Euler 方法(1)向前Euler 公式(显式Euler 公式)10(,),0,1,2,,(),n n n n y y hf x y n y y a +=+=⎧⎨=⎩(2) 其中h 为步长。
由此便可由初值0y 逐步算出一阶常微分方程初值问题(1)的解()y y x =在节点12,,x x 处的近似值12,,y y 。
该公式的局部截断误差为2()O h ,是一阶方法。
(2)向后Euler 公式(隐式Euler 公式)1110(,),0,1,2,,(),n n n n y y hf x y n y y a +++=+=⎧⎨=⎩(3) 这是一个隐格式,也是一阶方法。
这类隐格式的计算比显格式困难,一般采用迭代法求解。
首先用向前Euler 公式提供迭代初值,然后迭代计算:(0)1(1)()111(,),(,),0,1,2,n n n n k k n n n n y y hf x y y y hf x y k +++++⎧=+⎨=+=⎩ (4)1.2 梯形方法1110[(,)(,)],2(),(0,1,2,)n n n n n n h y y f x y f x y y y a n +++⎧=++⎪⎨⎪=⎩= (5) 这也是一个隐格式,是二阶方法。
一般也采用迭代法求解。
迭代公式如下:(0)1(1)()111(,),[(,)(,)],0,1,2,2n n n n k k n n n n n n y y hf x y h y y f x y f x y k +++++⎧=+⎪⎨=++=⎪⎩ (6)1.3 改进的Euler 方法11110(,),[(,)(,)],0,1,2,,2(),n n n n n n n n n n y y hf x y h y y f x y f x y n y y a ++++⎧=+⎪⎪=++=⎨⎪=⎪⎩(7) 为了便于上机编程计算,(7)可改写为110(,),(,),0,1,2,,1(),2(),p n n n cn n p n p c y y hf x y y y hf x y n y y y y y a ++=+⎧⎪=+⎪⎪=⎨=+⎪⎪=⎪⎩(8) 该格式是显式,也是二阶方法。
常微分方程的数值解法实验报告

常微分方程的数值解法专业班级:信息软件 姓名:吴中原 学号:120108010002 一、实验目的1、熟悉各种初值问题的算法,编出算法程序;2、明确各种算法的精度与所选步长有密切关系;通过计算更加了解各种 算法的优越性。
二、实验题目1、根据初值问题数值算法,分别选择二个初值问题编程计算;2、试分别取不同步长,考察某节点j x处数值解的误差变化情况; 3、试用不同算法求解某初值问题,结果有何异常; 4、分析各个算法的优缺点。
三、实验原理与理论基础(一) 欧拉法算法设计对常微分方程初始问题(6-1)(6-2)用数值方法求解时,我们总是认为(6-1)、(6-2)的解存在且唯一。
欧拉法是解初值问题的最简单的数值方法。
从(6-2)式由于y (x 0) = y 0已给定,因而可以算出),()('000y x f x y =。
设x 1 = h 充分小,则近似地有:),()(')()(00001y x f x y hx y x y =≈-(6-3)记 ,n ,,i x y y i i 10 )(== 从而我们可以取),(0001y x hf y y ==作为)(1x y 的近似值。
利用1y 及f (x 1, y 1)又可以算出)(2x y 的近似值:),(1112y x hf y y +=一般地,在任意点()h n x n 11+=+处)(x y 的近似值由下式给出),(1n n n n y x hf y y +=+(6-4)这就是欧拉法的计算公式,h 称为步长。
⎪⎩⎪⎨⎧==)( ),(d d 00y x y y x f x y(二)四阶龙格-库塔法算法设计:欧拉公式可以改写为:()111,i i i i y y k k hf x y +=+⎧⎪⎨=⎪⎩,它每一步计算(),f x y 的值一次,截断误差为()2o h 。
改进的欧拉公式可以改写为:()()()11212112,,i i i i i i y y k k k hf x y k hf x h y k +⎧=++⎪⎪=⎨⎪=++⎪⎩,它每一步要计算(),f x y 的值两次,截断误差为()3o h 。
数值计算实验报告-欧拉法常微分方程

数学与计算科学学院实验报告实验项目名称欧拉法解常微分方程所属课程名称数值计算实验类型验证型实验日期2012-6- 4班级隧道1002班学号201008020233姓名李彬彬成绩一、实验概述:【实验目的】 通过运用相关的数值计算软件,解决最基本的常微分方程的数值计算,并且能够熟练的运用这种方法。
【实验原理】 欧拉法1.对常微分方程初始问题(9.2))((9.1)),(00⎪⎩⎪⎨⎧==y x y y x f dxdy用数值方法求解时,我们总是认为(9.1)、(9.2)的解存在且唯一。
欧拉法是解初值问题的最简单的数值方法。
从(9.2)式由于y (x 0) = y 0已给定,因而可以算出),()('000y x f x y =设x 1 = h 充分小,则近似地有:),()(')()(00001y x f x y hx y x y =≈-(9.3)记 ,n ,,i x y y i i 10 )(== 从而我们可以取),(0001y x hf y y ==作为y (x 1)的近似值。
利用y 1及f (x 1, y 1)又可以算出y (x 2)的近似值:),(1112y x hf y y +=一般地,在任意点x n +1 = (n + 1)h 处y (x )的近似值由下式给出),(1n n n n y x hf y y +=+(9.4)这就是欧拉法的计算公式,h 称为步长。
不难看出,近似解的误差首先是由差商近似代替微商(见(9.3))引起的,这种近似代替所产生的误差称为截断误差。
还有一种误差称为舍入误差,这种误差是由于利用(9.4)进行计算时数值舍入引起的。
【实验环境】Windows XP 环境下运行 NumericalAnalyse 软件二、实验内容:【实验方案】在区间[0,1]上以h=0.1为步长,分别用欧拉法与预估-校正法求初值问题y’=y-2x/y且 y|x=0 =1的数值解。
将上述方程输入到软件NumericalAnalyse中步骤如图选择常微分方程的数值解法。
7 常微分方程初值问题的数值解法

h
2
y
( p)
(xn )
h
p
p! (8.7)
y
( p1)
( n )
( p 1 )!
其中
y , f ( x, y) ,, ' ' , ' ' y f x ( x, y) f x ( x, y) y f x f y f ( p) y
,
y ( n )
,
2! y ( n )
,,
( x n1 x n ) 或 (8 .2 )
2
y ( x n ) h f ( x n , y ( x n )) yn1 yn h f ( x n , yn )
h
2
2
( n 0 , 1, 2 , )
(8 .2 ) 叫 E u ler 显 格 式 , 可 循 环 求 解 。 方 法 二 、 数 值 微 分 法 — — 实 质 还 是 T a ylo r 展 开 法 ( 略 )
p1
).
定理 8 . 1
设 f ( x , y ) 关于第 2 个变元满足 Lipschitz 条件 | f ( x 1 , y 1 ) f ( x 2 , y 2 ) | L | y 1 , y 2 | 且 Euler 显格式的局部截断误差 | n | e
(ba )
满足 | R n | 1 ]h
' '
[ ]
(8 .9 )
p! 假 设 y n= y ( x n ), 则 ( 8 .7) 和 ( 8 .9) 得 局 部 截 断 误 差 为 Rn1 y ( x n1 ) yn1 h
p1
方法三 将方程
微分方程数值解实验报告

微分方程数值解实验报告实验目的:掌握微分方程数值解的基本方法,能够利用计算机编程求解微分方程。
实验原理:微分方程是自然科学与工程技术中常见的数学模型,它描述了变量之间的关系及其随时间、空间的变化规律。
解微分方程是研究和应用微分方程的基础,但有很多微分方程无法找到解析解,只能通过数值方法进行求解。
本实验采用欧拉方法和改进的欧拉方法求解微分方程的初值问题:$$\begin{cases}\frac{dy}{dt}=f(t,y)\\y(t_0)=y_0\end{cases}$$其中,$f(t,y)$是给定的函数,$y(t_0)=y_0$是已知的初值条件。
欧拉方法是最基本的数值解法,其步骤如下:1.给定$t_0$和$y_0$2.计算$t_{i+1}=t_i+h$,其中$h$是步长3. 计算$y_{i+1}=y_i+hf(t_i,y_i)$4.重复步骤2、3直到达到终止条件改进的欧拉方法是对欧拉方法进行改进,通过利用函数$y(t)$在$t+\frac{1}{2}h$处的斜率来更准确地估计$y_{i+1}$,其步骤如下:1.给定$t_0$和$y_0$2.计算$t_{i+1}=t_i+h$,其中$h$是步长3. 计算$y_*=y_i+\frac{1}{2}hf(t_i,y_i)$4. 计算$y_{i+1}=y_i+hf(t_i+\frac{1}{2}h,y_*)$5.重复步骤2、3、4直到达到终止条件实验步骤:1.编写程序实现欧拉方法和改进的欧拉方法2.给定微分方程和初值条件3.设置步长和终止条件4.利用欧拉方法和改进的欧拉方法求解微分方程5.比较不同步长下的数值解与解析解的误差6.绘制误差-步长曲线,分析数值解的精度和收敛性实验结果:以一阶常微分方程$y'=3ty+t$为例,给定初值$y(0)=1$,取步长$h=0.1$进行数值求解。
利用欧拉方法求解微分方程得到的数值解如下:\begin{array}{cccc}t & y_{\text{exact}} & y_{\text{Euler}} & \text{误差} \\ \hline0.0&1.000&1.000&0.000\\0.1&1.035&1.030&0.005\\0.2&1.104&1.108&0.004\\0.3&1.212&1.217&0.005\\0.4&1.360&1.364&0.004\\0.5&1.554&1.559&0.005\\0.6&1.805&1.810&0.005\\0.7&2.131&2.136&0.005\\0.8&2.554&2.560&0.006\\0.9&3.102&3.107&0.006\\1.0&3.807&3.812&0.005\\\end{array}利用改进的欧拉方法求解微分方程得到的数值解如下:\begin{array}{cccc}t & y_{\text{exact}} & y_{\text{Improved Euler}} & \text{误差} \\\hline0.0&1.000&1.000&0.000\\0.1&1.035&1.035&0.000\\0.2&1.104&1.103&0.001\\0.3&1.212&1.211&0.001\\0.4&1.360&1.358&0.002\\0.5&1.554&1.552&0.002\\0.6&1.805&1.802&0.003\\0.7&2.131&2.126&0.005\\0.8&2.554&2.545&0.009\\0.9&3.102&3.086&0.015\\1.0&3.807&3.774&0.032\\\end{array}误差-步长曲线如下:实验结论:通过对比欧拉方法和改进的欧拉方法的数值解与解析解的误差,可以发现改进的欧拉方法具有更高的精度和收敛性。
实验报告七常微分方程初值问题的数值解法

实验报告七常微分方程初值问题的数值解法浙江大学城市学院实验报告课程名称数值计算方法实验项目名称常微分方程初值问题得数值解法实验成绩指导老师(签名) 日期2015/12/16一、实验目得与要求1.用Matlab软件掌握求微分方程数值解得欧拉方法与龙格-库塔方法;2.通过实例学习用微分方程模型解决简化得实际问题。
二、实验内容与原理编程题2-1要求写出Matlab源程序(m文件),并有适当得注释语句;分析应用题2-2,2-3,2-4,2-5要求将问题得分析过程、Matlab源程序与运行结果与结果得解释、算法得分析写在实验报告上。
2-1编程编写用向前欧拉公式与改进欧拉公式求微分方程数值解得Matlab程序,问题如下:在区间内个等距点处,逼近下列初值问题得解,并对程序得每一句添上注释语句。
Euler法 y=euler(a,b,n,y0,f,f1,b1)改进Euler法y=eulerpro(a,b,n,y0,f,f1,b1)2-2分析应用题假设等分区间数,用欧拉法与改进欧拉法在区间内求解初值问题并作出解得曲线图形,同时将方程得解析解也画在同一张图上,并作比较,分析这两种方法得精度。
2-3分析应用题用以下三种不同得方法求下述微分方程得数值解,取画出解得图形,与精确值比较并进行分析。
1)欧拉法;2)改进欧拉法;3)龙格-库塔方法;2-4分析应用题考虑一个涉及到社会上与众不同得人得繁衍问题模型。
假设在时刻(单位为年),社会上有人口人,又假设所有与众不同得人与别得与众不同得人结婚后所生后代也就是与众不同得人。
而固定比例为得所有其她得后代也就是与众不同得人。
如果对所有人来说出生率假定为常数,又如果普通得人与与众不同得人得婚配就是任意得,则此问题可以用微分方程表示为:其中变量表示在时刻社会上与众不同得人得比例,表示在时刻人口中与众不同得人得数量。
1)假定与,当步长为年时,求从到解得近似值,并作出近似解得曲线图形。
2)精确求出微分方程得解,并将您当时在分题(b)中得到得结果与此时得精确值进行比较。
第5次实验报告(常微分方程初值问题的数值解法)

班级: 学号: 姓名: 成绩:实验5 常微分方程初值问题的数值解法实验1实验目的1)熟悉欧拉法、改进欧拉法和龙格-库塔法的原理。
2)根据以上方法,编程求解常微分方程初值问题。
2 实验内容(1)编写程序,用以上各种方法求解教材P232例7-1、习题6、11的初值问题。
(2) 使用系统自带的函数dsolve 和ode45求例7-1的符号解析解和数值解。
3实验原理求解微分方程初值问题00(,)()y f x y y x y '=⎧⎨=⎩ (1) 欧拉法(显式):10(,)n n n n n y y hf x y x x nh +=+⎧⎨=+⎩(2) 改进欧拉法(0)1(0)111(,)(,)(,)2n n n n n n n n n n y y hf x y h y y f x y f x y ++++⎧=+⎪⎨⎡⎤=++⎪⎣⎦⎩ (3) 经典龙格-库塔法(四阶)11234121324300(22)6(,)(,)22(,)22(,)()i i i i i i i i i i h y y K K K K K f x y h h K f x y K h h K f x y K K f x h y hK y y x +⎧=++++⎪⎪=⎪⎪=++⎪⎨⎪=++⎪⎪⎪=++⎪=⎪⎩4实验步骤1)建立函数文件,根据各公式编写程序;2)上机调试程序,运行程序进行计算,记录计算结果;3)分析各公式计算结果,比较各公式的优缺点。
5 程序设计欧拉法改进欧拉法function Euler1(x0,y0,h,n)%(x0,y0):方程的初值%h:步长%n:计算的步数for i=1:nx=x0+h;yp=y0+h*f(x0,y0);yc=y0+h*f(x,yp);y=(yp+yc)/2;x %在屏幕显示每一步的x值y %在屏幕显示每一步计算的方程的数值解 x0=x;y0=y;end经典龙格-库塔法1)函数function f=f(x,y) f=y-2*x/y;end6总结注:若要更改matlab计算的数值类型,可以通过在matlab中设置实现:File -> Preferences ->Array Editor窗口中,Format 下方将Default array format设置为:long解微分方程的MATLAB命令MATLAB中主要用dsolve求微分方程的符号解析解,ode45求数值解。
数值分析常微分方程初值问题的数值解

2、分别取步长 ,用显式欧拉法和隐式欧拉法求解初值问题
由结果分析算法的稳定性。(解析解为 )
解:当取步长 ,计算得到以下结果
准确值
显示欧拉法
隐式欧拉法
0
100.0000
100
0.5
0.0000
5776.5
0.0004
当取步长为 ,计算结果如下:
准确值
显示欧拉法
隐式欧拉法
0.0
100
100
100
0.01
60.6531
50
66.6667
0.02
36.7879
25
44.4445
0.03
22.3130
12.5
29.6296
0.04
13.5335
6.25
19.7531
0.05
8.2085
0.025
28.6505
23.7305
32.768
0.03
22.3130
17.79797
26.2144
由结果可知,当 时,显式欧拉法不太稳定,而隐式欧拉法发散;
当 时,显式欧拉法和隐式欧拉法都是稳定的。
3、选择某常微分方程初值问题的数值方法计算 的近似值,并保证有四位有效数字。
, ,
t
0.1
0.2
0.3
0.15
0.0553
-337.5
2.3324
0.2
0.0045506.20.66640.250.0004
-759.4
0.1904
0.3
常微分方程初值问题的数值解法

常微分方程初值问题数值解法初值问题:即满足初值条件的常微分方程的解y′=f(x,y),x∈[x0,b]y(x0)=y0.定理1(利普希茨条件)若存在正数L,使得对任意,y1,y2,有|f(x,y1)−f(x,y2)|≤L|(y1−y2)|定理2(解存在性)①若函数f在方区域x∈[a,b],y∈R连续,②函数f关于y 满足利普希茨条件,则对任意x∈[a,b],常微分方程存在唯一的连续可微数值解.两类问题:①单步法---计算下一个点的值yn+1只需要用到前面一个点的值yn②多步法---计算下一个点的值yn+1需要用到前面l个点的值yl1、欧拉法---下一个点的计算值等于前一个点的计算值加上步长乘以前一个点的函数值•具体过程一些批注:显式欧拉方程指下一步要计算的值,不在迭代方程中;隐式欧拉方程指下一步要计算的值,在迭代方程中。
怎么计算隐式欧拉方程----要借助显示欧拉迭代计算---一般用迭代法-----迭代---将微分方程在区间[xn,xn+1]进行积分,然后函数f进行近似,即可得到迭代方程-----迭代方程收敛性?由函数关于y满足利普希茨条件,可以推出迭代公式收敛。
•局部截断误差:假设前n步误差为0,我们计算第n+1步的误差,将次误差称为局部截断误差,且局部误差为O(hp+1)•p阶精度:由理论证明:若局部误差阶的时间复杂度为O(hp+1),则整体误差阶为O(hp)我们称公式精度为p。
•显示欧拉法与隐式欧拉法•梯形方法----将显式欧拉迭代方程与隐式欧拉迭代方程做一下加权平均,构造的计算公式.•改进的欧拉方法---思想:因为梯形公式是隐式公式,将显式欧拉公式对下一步的计算值进行预估,用梯形公式对下一步的计算值进行校正.2、龙格-库塔方法思想:根据Lagrange中值定理,下一次的计算值可以用前一次的计算值加上h乘以前一个点的斜率;而这个斜率用该区间上的多个点的斜率的算数平均来逼近。
注意:怎么计算任意斜率Ki?第i个点的斜率Ki有微分方程可以算出f′=f(xn,yn)所以要算的f(xn,yn)值,由欧拉法即可算出, yn+1=yn+hf′•2阶-龙格-库塔方法----类似改进的欧拉法根据Lagrange中值定理,下一次的计算值可以用前一次的计算值加上h乘以斜率;而这个斜率用区间上的端点和中点的斜率的算数平均来逼近。
第七次实验
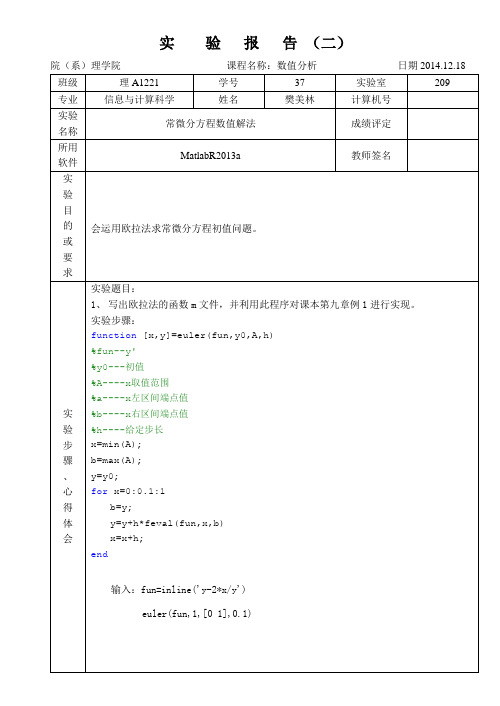
function[x,y]=euler(fun,y0,A,h)
%fun--y'
%y0---初值
%A----x取值范围
%a----x左区间端点值
%b----x右区间端点值
%h----给定步长
x=min(A);
b=max(A);
y=y+h*feval(fun,x,b)
x=x+h;
end
输入:fun=inline('y-2*x/y')
euler(fun,1,[01],0.1)
得到:
x =0.1000y =1.1000
x =0.2000 y =1.1918
x =0.3000 y =1.2774
x =0.4000 y =1.3582
x =0.5000 y =1.4351
实验报告(二)
院(系)理学院课程名称:数值分析日期2014.12.18
班级
理A1221
学号
37
实验室
209
专业
信息与计算科学
姓名
樊美林
计算机号
实验
名称
常微分方程数值解法
成绩评定
所用
软件
MatlabR2013a
教师签名
实
验
目
的
或
要
求
会运用欧拉法求常微分方程初值问题。
实
验
步
骤
、
心
得
体
会
实验题目:
1、写出欧拉法的函数m文件,并利用此程序对课本第九章例1进行实现。
x =0.6000 y =1.5090
x =0.7000 y =1.5803
x =0.8000 y =1.6498
常微分方程初值问题的数值解法

就得到初值问题(7.1),(7.2)的解y(t )的解析表达式。然而
在实际问题和科学研究中所遇到的微分方程往往很复
杂,很多情况下不可能求出它的解析解。有时侯即使
能求出解析解,也会由于很难从解析解中计算函数y(t )
的值而不实用。
例如,容易求出初值问题
y' 1 y cos t,0 t T
注意:这是“折
线法”而非“切
yN
线法”除第一个
点是曲线切线外,
其他点不是切线
而是折线(如右 图所示)。
y2 yy10
t0 a t1 t2
tN b x
§7.2.1 显式单步法的一般形式 显式单步法的一般形式是
yn1 yn h (tn , yn , h), n 0,1, , M 1 (7.2.4)
普希兹)条件。常数L称为函数f 在D0中的Lipschitz常数。
例1 函数f (t, y) t y 在区域D0 (t, y) | 1 t 2, 3 y 4
关于y满足Lipschitz条件,相应的Lipschitz常数可取为L 2
3 存在性定理 定理1 设函数f (t, y)在凸集D R2中有定义,若存在常数
(7.4)
若k 2,则数值解法(7.3)统称为多步法,或具体称 为k步法。
显示法、隐式法与截断误差 若在差分方程(7.3)中,ynk能表示为tn , yn, yn1, , ynk-1, h 的显函数,即
ynk G(tn , yn , yn1, , ynk-1, h), n 0,1, , M - k (7.5)
y0 yn1
Hale Waihona Puke y(t0 yn)
第7章-常微分方程初值问题的数值解法

由 点 斜 式 写 出 切 线 方 程 :
dy yy0(xx0)dx(x0,y0) y0(xx0)f(x0,y0)
等 步 长 为 h , 则 x x 0 h , 可 由 切 线 算 出 y 1
y1y0hf(x0,y0)
2021/4/9
10
其 中 , y n 1 是 当 y n y (x n )(精 确 解 )时 由 E u le r法 求 出 的 值 , 即 y n 无 误 差 。
将 y (x n 1 )在 x n 点 T a y lo r展 开 :
y (x n 1 ) y (x n h ) y (x n ) h f(x n ,y (x n )) (h 2 x2 n y ()xn1)
ax0 x1 x2 xn b 在节点上用离散化方法将连续型微分方程 转化成离散型代数方程即差分方程来求解。
具 体 作 法 : 利 用 y(x0)求 出 y(x1)的 近 似 值 y1, 再 由
y1求 出 y2,, 直 到 求 出 yn为 止 。 该 算 法 称 为 步 进
式 或 递 推 式 算 法 。
积 分 用 梯 形 公 式 , 且 令 : yn1y(xn1),yny(xn) 则 得 : yn1ynh 2(f(xn,yn)f(xn1,yn1))
R n 1 y (x n 1 ) y n 1 1 h 2 3y () x n x n 1
与Euler法结合,形成迭代算法,对n0, 1, 2,
yn(0)1ynhf(xn,yn) (75)
y 2021/4/9
(k1) n1
ynh2(f(xn,yn)f(xn1,yn(k1))k0,1,2,
12
2. Euler方法的截断误差
常微分方程数值解实验报告

常微分方程数值解实验报告学院:数学与信息科学专业:信息与计算科学:思义学号:201216524 课程:常微分方程数值解实验一:常微分方程的数值解法1、分别用Euler 法、改进的Euler 法(预报校正格式)和S —K 法求解初值问题。
(h=0.1)并与真解作比较。
⎩⎨⎧=++-=10(1y')y x y 1.1实验代码:%欧拉法function [x,y]=naeuler(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值围,y0是初值,h 是步长 x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1y(n+1)=y(n)+h*feval(dyfun,x(n),y(n)); end%改进的欧拉法function [x,m,y]=naeuler2(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值围,y0是初值,h 是步长。
%返回值x 为x 取值,m 为预报解,y 为校正解 x=xspan(1):h:xspan(2); y(1)=y0;m=zeros(length(x)-1,1); for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n)); y(n+1)=y(n)+h*k1; m(n)=y(n+1);k2=feval(dyfun,x(n+1),y(n+1));y(n+1)=y(n)+h*(k1+k2)/2;end%四阶S—K法function [x,y]=rk(dyfun,xspan,y0,h)%dyfun是常微分方程,xspan是x的取值围,y0是初值,h是步长。
x=xspan(1):h:xspan(2);y(1)=y0;for n=1:length(x)-1k1=feval(dyfun,x(n),y(n));k2=feval(dyfun,x(n)+h/2,y(n)+(h*k1)/2);k3=feval(dyfun,x(n)+h/2,y(n)+(h*k2)/2);k4=feval(dyfun,x(n)+h,y(n)+h*k3);y(n+1)=y(n)+(h/6)*(k1+2*k2+2*k3+k4);end%主程序x=[0:0.1:1];y=exp(-x)+x;dyfun=inline('-y+x+1');[x1,y1]=naeuler(dyfun,[0,1],1,0.1);[x2,m,y2]=naeuler2(dyfun,[0,1],1,0.1);[x3,y3]=rk(dyfun,[0,1],1,0.1);plot(x,y,'r',x1,y1,'+',x2,y2,'*',x3,y3,'o');xlabel('x');ylabel('y');legend('y为真解','y1为欧拉解','y2为改进欧拉解','y3为S—K解','Location','NorthWest');1.2实验结果:x 真解y 欧拉解y1 预报值m 校正值y2 S—K解y30.0 1.0000 1.0000 1.0000 1.00000.1 1.0048 1.0000 1.0000 1.0050 1.00480.2 1.0187 1.0100 1.0145 1.0190 1.01870.3 1.0408 1.0290 1.0371 1.0412 1.04080.4 1.0703 1.0561 1.0671 1.0708 1.07030.5 1.1065 1.0905 1.1037 1.1071 1.10650.6 1.1488 1.1314 1.1464 1.1494 1.14880.7 1.1966 1.1783 1.1945 1.1972 1.19660.8 1.2493 1.2305 1.2475 1.2500 1.24930.9 1.3066 1.2874 1.3050 1.3072 1.30661.0 1.3679 1.3487 1.3665 1.3685 1.36792、选取一种理论上收敛但是不稳定的算法对问题1进行计算,并与真解作比较。
常微分方程初值问题的数值解法

1
1、基本概念: 基本概念:
•一阶常微分方程初值问题是: 一阶常微分方程初值问题是: 一阶常微分方程初值问题是 y ′ =f(x,y) (1.1) y(x0)=y0 (1.2) 其中f是已知的xy平面上某个区域D上连续函数,式(1.1)是微分 方程,有无穷多解,式(1.2)是确定解的初始条件。 如一元函数y(x)对一切a≤x≤b 满足 (1) (x,y(x))∈D (2) y(x0)=y0 (3) y′存在,且y′(x)=f(x,y(x)) 则称y(x)是初值问题(1.1)、(1.2)在[a,b]上的解。 定义1.1 如果存在正常数L>0,使得对一切x∈[a,b]及y1 、y2 ∈[c,d] 有 |f(x,y1)-f(x,y2)|≤ L|y1- y2| (1.3) 则称f(x,y)满足对y的lipschitz(李普希滋)条件,其中L称为 lipschitz常数。
~ = y + hf ( x , y ) y k +1 k k k y k +1
2011-12-12
h y = y k + ( f ( x k , y k ) + f ( x k +1 , ~k +1 )) 2
12
Euler公式的几何意义 公式的几何意义
Y=y(x)
a
b
2011-12-12
13
例题:用Euler的数值解(取步长h=0.1计算到y3):
2011-12-12 4
求初值问题,是给出它的解在某些节点数值的近似值,这称为 数值离散方法,若要求出在[a,b} 上的离散解,引入点列{xK} , 其中 xk= xk-1 + hk-1 ,k=1,2,3….. xk称为节点, hk 称为步长。 通常,步长h不变,取为等距步长 hk =h= (b-a)/N ,N为等份 区间[a,b]分割数,节点变为等距节点,此时有 kh, xk= xk-1 + h= x0 + kh 记式(1.1),(1.2)的准确解y(x)在节点xk 之值为y(xk) ,而 记y(xk)的近似值为yk ,又记fk=f(xk , yk ),
常微分方程初值问题解法

8
4 后退的欧拉方法
(5)
9
(6)
(6)式称为后退的欧拉方法,它是隐式的, 欧拉公式(2)是显式的,
10
(7)
11
12
后退的欧拉方法的局部截断误差:
13
5 梯形方法
(8)
(8)式称为梯形方法.
14
梯形方法的局部截断误差:
15
6. 改进欧拉法及局部截断误差
(1)改进的欧拉公式:
预测步
~ yn 1 yn hf xn , yn
33
提高Runge-Kutta方法的精度的方法
提高积分方法的精度,我们最熟悉的(不一定是最好的)措施是
Richardson 外推法
我们用一个例子予以说明如下 的近似解: Euler法 yn 1 yn hyn y ( h ) ( x) y ( x) c1h c2 h 2 h 将步长减半为 时,有 2 h ( ) 1 1 y 2 ( x) y ( x) c1h c2 h 2 2 4
h) p 1 Yn( (1 1 ch
d
(h) n 1
因此可以从两次计算当中估计出每一步的截断误差,有了这个误差估计之后, 通过与控制误差限比较,就可以控制步长. 注意这个方法增加了计算量.
35
1 1 2 p
) (h (h) 2 Y Y n 1 ; n 1
30
yx 例 求解初值问题ODE : dy dx
易知其精确解为:y 2 2 x x 2 e x
2
,
y (0) 1.
步长都取为 h 0.1 分别用二阶、四阶 R K方法求解:
x
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
常微分方程初值问题的数值解法

常微分方程初值问题的数值解法在实际应用中,对于某些微分方程,我们并不能直接给出其解析解,需要通过数值方法来求得其近似解,以便更好地理解和掌握现象的本质。
常微分方程初值问题(IVP)即为一种最常见的微分方程求解问题,其求解方法有多种,本文将对常微分方程初值问题的数值解法进行较为详细的介绍。
一、欧拉法欧拉法是最基本的一种数值解法,它采用泰勒级数展开并截断低阶项,从而获得一个差分方程近似求解。
具体来讲,设 t 为独立变量,y(t) 为函数 y 关于 t 的函数,方程为:$$y'(t) = f(t, y(t)), \qquad y(t_0) = y_0$$其中 f(t,y(t)) 为已知的函数,y(t_0) 为已知的初值。
将函数 y(t) 进行泰勒级数展开:$$y(t+h) = y(t) + hf(t, y(t)) + O(h^2)$$其中 h 表示步长,O(h^2) 表示其他高阶项。
为了使误差较小,一般取步长 h 尽可能小,于是我们可以用欧拉公式表示数值解:$$y_{n+1} = y_n + hf(t_n, y_n), \qquad y_0 = y(t_0)$$欧拉法的优点是容易理解和实现,但是由于截取低阶项且使用的单步法,所以误差较大,精度较低,在具体应用时需要慎重考虑。
二、龙格-库塔法龙格-库塔法(Runge-Kutta method)是一种多步法,比欧拉法更加精确。
龙格-库塔法的主要思想是使用不同的插值多项式来计算近似解,并且将时间步长分解,每次计算需要多次求解。
以下简要介绍二阶和四阶龙格-库塔法。
二阶龙格-库塔法将时间步长 h 分解成两步 h/2,得到近似解表达式:$$\begin{aligned} k_1 &= hf(t_n, y_n)\\ k_2 &= hf(t_n+h/2,y_n+k_1/2)\\ y_{n+1} &= y_n+k_2+O(h^3)\\ \end{aligned}$$四阶龙格-库塔法四阶龙格-库塔法是龙格-库塔法中应用最为广泛的一种方法,其需要计算的中间值较多,但是具有更高的精度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告七-常微分方程初值问题的数值解法浙江大学城市学院实验报告课程名称数值计算方法实验项目名称常微分方程初值问题的数值解法实验成绩指导老师(签名)日期2015/12/16一. 实验目的和要求1.用Matlab软件掌握求微分方程数值解的欧拉方法和龙格-库塔方法;2.通过实例学习用微分方程模型解决简化的实际问题。
二. 实验内容和原理编程题2-1要求写出Matlab源程序(m文件),并有适当的注释语句;分析应用题2-2,2-3,2-4,2-5要求将问题的分析过程、Matlab源程序和运行结果和结果的解释、算法的分析写在实验报告上。
2-1编程编写用向前欧拉公式和改进欧拉公式求微分方程数值解的Matlab程序,问题如下:在区间[],a b 内(1)N +个等距点处,逼近下列初值问题的解,并对程序的每一句添上注释语句。
0(,)()y f x y a x b y a y '=≤≤= Euler 法 y=euler(a,b,n,y0,f,f1,b1) 改进Euler 法 y=eulerpro(a,b,n,y0,f,f1,b1)2-2 分析应用题假设等分区间数100n =,用欧拉法和改进欧拉法在区间[0,10]t ∈内求解初值问题()()20(0)10y t y t y '=-⎧⎨=⎩并作出解的曲线图形,同时将方程的解析解也画在同一张图上,并作比较,分析这两种方法的精度。
2-3 分析应用题用以下三种不同的方法求下述微分方程的数值解,取10h =201(0)1y y xx y '=+≤≤⎧⎨=⎩画出解的图形,与精确值比较并进行分析。
1)欧拉法; 2)改进欧拉法; 3)龙格-库塔方法;2-4 分析应用题考虑一个涉及到社会上与众不同的人的繁衍问题模型。
假设在时刻t (单位为年),社会上有人口()x t 人,又假设所有与众不同的人与别的与众不同的人结婚后所生后代也是与众不同的人。
而固定比例为r 的所有其他的后代也是与众不同的人。
如果对所有人来说出生率假定为常数b ,又如果普通的人和与众不同的人的婚配是任意的,则此问题可以用微分方程表示为:()(1())dp t rb p t dt =- 其中变量()()()i p t x t x t =表示在时刻t 社会上与众不同的人的比例,()ix t 表示在时刻t 人口中与众不同的人的数量。
1)假定(0)0.01,0.02p b ==和0.1r =,当步长为1h =年时,求从0t =到50t =解()p t 的近似值,并作出近似解的曲线图形。
2)精确求出微分方程的解()p t ,并将你当50t =时在分题(b)中得到的结果与此时的精确值进行比较。
【MATLAB 相关函数】求微分方程的解析解及其数值的代入dsolve(‘egn1’, ‘egn2’,L ‘x ’)subs (expr, {x,y,…}, {x1,y1,…} )其中‘egn i ’表示第i 个方程,‘x ’表示微分方程中的自变量,默认时自变量为t 。
subs 命令中的expr 、x 、y 为符合型表达式,x 、y 分别用数值x1、x2代入。
>> syms x y z>> subs('x+y+z',{x,y,z},{1,2,3})ans =6 >> syms x>> subs('x^2',x,2)ans =4>> s=dsolve(‘12Dy y ∧=+’, ‘(0)1y =’, ‘x ’) ans =tan(14)x pi -*>> syms x>> subs(s,x,2)ans =-0.3721⏹右端函数(,)f x y的自动生成f= inline(‘expr’, ’var1’, ‘var2’,……)其中’expr’表示函数的表达式,’var1’, ‘var2’表示函数表达式中的变量,运行该函数,生成一个新的函数表达式为 f (var1, var2, ……)。
>> f=inline('x+3*y','x','y')f =Inline function:f(x,y) = x+3*y>> f(2,3)ans =11⏹4,5阶龙格-库塔方法求解微分方程数值解[t,x]=ode45(f,ts,x0,opti ons)其中f是由待解方程写成的m文件名;x0为函数的初值;t,x分别为输出的自变量和函数值(列向量),t的步长是程序根据误差限自动选定的。
若ts=[t0,t1,t2,…,tf],则输出在自变量指定值,等步长时用ts=t0:k:tf,输出在等分点;options用于设定误差限(可以缺省,缺省时设定为相对误差310-,绝对误差610-),程序为:options=odeset(‘reltol’,rt,’abstol ’,at),这里rt,at分别为设定的相对误差和绝对误差。
常用选项见下表。
选项名功能可选值省缺值AbsTol 设定绝对误差正数16e-RelTol 设定相对误差正数13e-InitialStep 设定初始步长正数自动MaxStep 设定步长上界正数10tspan1,2,3,4,5 5 MaxOrder 设定ode15s的最高阶数Stats 显示计算成本on,off off统计BDF 设定ode15s是on,off off否用反向差分例:解微分方程204(0)1t y y t y y ⎧'=-<<⎪⎨⎪=⎩在命令窗口执行>> odefun = inline (‘2*y t y -’, ‘t ’, ‘y ’); >> [],45(,[0,4],1)t y ode odefun =; >> [],t y ans =0 1.0000 0.0502 1.0490 0.1005 1.0959 0.1507 1.1408 ……3.8507 2.9503 3.9005 2.9672 3.9502 2.98394.0000 3.0006>> plot(t ,y ,‘o-’,) %解函数图形表示>> 45(,[0,4],1)ode odefun %不用输出变量,则直接输出图形>> [],45(,0:4,1)t y ode odefun =;[],t y ans =0 1.0000 1.0000 1.7321 2.0000 2.2361 3.0000 2.6458 4.0000 3.0006三. 操作方法与实验步骤(包括实验数据记录和处理)2-1 编程编写用向前欧拉公式和改进欧拉公式求微分方程数值解的Matlab 程序,问题如下: 在区间[],a b 内(1)N +个等距点处,逼近下列初值问题的解,并对程序的每一句添上注释语句。
0(,)()y f x y a x b y a y '=≤≤= Euler 法 y=euler(a,b,n,y0,f,f1,b1) 改进Euler 法 y=eulerpro(a,b,n,y0,f,f1,b1)Euler 法y=euler(a,b,n,y0,f,f1,b1) y=zeros(1,n+1); y(1)=y0; h=(b-a)/n; x=a:h:b;for i=1:n;y(i+1)=y(i)+h*f(x(i),y(i)); endplot(x,y)hold on% 求微分方程的精确解x1=linspace(a,b,100);'精确解为's=dsolve(f1,b1,'x')syms xy1=zeros(1,100);fori=1:100y1(i)=subs(s,x,x1(i));endplot(x1,y1,'r')title('红色代表精确解')改进Euler法y=eulerpro(a,b,n,y0,f,f1,b1) % 求微分方程的数值解y=zeros(1,n+1);y(1)=y0;h=(b-a)/n;x=a:h:b;fori=1:n;T1=f(x(i),y(i));T2=f(x(i+1),y(i)+h*T1);y(i+1)=y(i)+(h/2)*(T1+T2); endplot(x,y)hold on% 求微分方程的精确解x1=linspace(a,b,100); '精确解为' s=dsolve(f1,b1,'x') syms xy1=zeros(1,100); for i=1:100y1(i)=subs(s,x,x1(i)); endplot(x1,y1,'r')title('红色代表精确解')2-2分析应用题假设等分区间数100n =,用欧拉法和改进欧拉法在区间[0,10]t ∈内求解初值问题()()20(0)10y t y t y '=-⎧⎨=⎩并作出解的曲线图形,同时将方程的解析解也画在同一张图上,并作比较,分析这两种方法的精度。
(1)向前欧拉法>>euler(0,10,100,10,inline('y-20','x','y'),'Dy=y-20',' y(0)=10')ans =精确解为s =20 - 10*exp(x)ans =1.0e+005 *Columns 1 through 80.0001 0.0001 0.0001 0.0001 0.0001 0.0000 0.00000.0000Columns 9 through 16-0.0000 -0.0000 -0.0001 -0.0001 -0.0001 -0.0001 -0.0002-0.0002Columns 17 through 24-0.0003 -0.0003 -0.0004 -0.0004 -0.0005 -0.0005 -0.0006-0.0007Columns 25 through 32-0.0008 -0.0009 -0.0010 -0.0011 -0.0012 -0.0014 -0.0015-0.0017Columns 33 through 40-0.0019 -0.0021 -0.0024 -0.0026 -0.0029 -0.0032 -0.0035-0.0039Columns 41 through 48-0.0043 -0.0048 -0.0053 -0.0058 -0.0064 -0.0071 -0.0078-0.0086Columns 49 through 56-0.0095 -0.0105 -0.0115 -0.0127 -0.0140 -0.0154 -0.0170-0.0187Columns 57 through 64-0.0206 -0.0227 -0.0250 -0.0275 -0.0302 -0.0333 -0.0366-0.0403Columns 65 through 72-0.0444 -0.0488 -0.0537 -0.0591 -0.0651 -0.0716 -0.0788-0.0867Columns 73 through 80-0.0954 -0.1049 -0.1154 -0.1270 -0.1397 -0.1537 -0.1691-0.1860Columns 81 through 88-0.2046 -0.2251 -0.2477 -0.2724 -0.2997 -0.3297 -0.3627-0.3990Columns 89 through 96-0.4389 -0.4828 -0.5311 -0.5842 -0.6427 -0.7070 -0.7777-0.8555Columns 97 through 101-0.9410 -1.0352 -1.1387 -1.2526 -1.3779(2)改进欧拉法>>eulerpro(0,10,100,10,inline('y-20','x','y'),'Dy=y-2 0','y(0)=10')ans =精确解为s =20 - 10*exp(x)ans =1.0e+005 *Columns 1 through 80.0001 0.0001 0.0001 0.0001 0.0001 0.0000 0.0000 -0.0000Columns 9 through 16-0.0000 -0.0000 -0.0001 -0.0001 -0.0001 -0.0002 -0.0002 -0.0002Columns 17 through 24-0.0003 -0.0003 -0.0004 -0.0005 -0.0005 -0.0006 -0.0007 -0.0008Columns 25 through 32-0.0009 -0.0010 -0.0011 -0.0013 -0.0014 -0.0016 -0.0018 -0.0020Columns 33 through 40-0.0022 -0.0025 -0.0028 -0.0031 -0.0034 -0.0038 -0.0042 -0.0047Columns 41 through 48-0.0052 -0.0058 -0.0064 -0.0071 -0.0079 -0.0087 -0.0097 -0.0107Columns 49 through 56-0.0119 -0.0131 -0.0145 -0.0161 -0.0178 -0.0197 -0.0218 -0.0241Columns 57 through 64-0.0266 -0.0294 -0.0325 -0.0360 -0.0398 -0.0440 -0.0486 -0.0537Columns 65 through 72-0.0594 -0.0656 -0.0726 -0.0802-0.0886 -0.0980 -0.1083 -0.1197Columns 73 through 80-0.1323 -0.1462 -0.1615 -0.1785 -0.1973 -0.2180 -0.2409 -0.2663Columns 81 through 88-0.2942 -0.3251 -0.3593 -0.3971 -0.4388 -0.4849 -0.5358 -0.5921Columns 89 through 96-0.6543 -0.7230 -0.7989 -0.8828 -0.9755 -1.0780 -1.1912 -1.3163Columns 97 through 101-1.4545 -1.6073 -1.7760 -1.9626 -2.1686改进欧拉法的精度比向前欧拉法更高。
