初中数学老师直言:刷完这50道经典几何难题,数学稳稳130+!
初中数学经典几何难题及答案
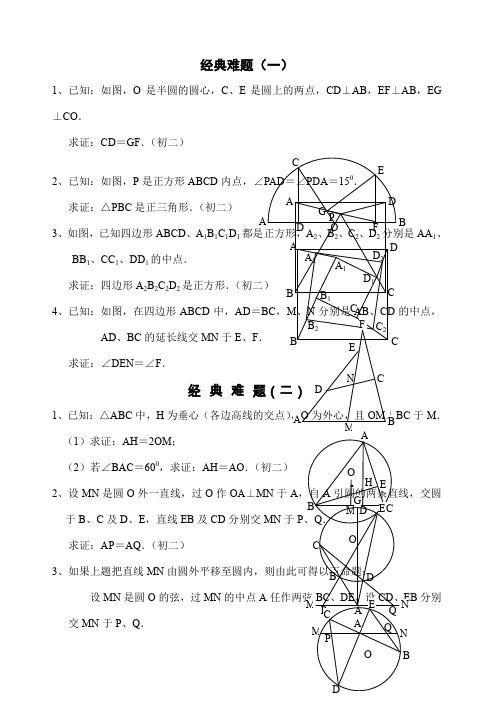
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . AP C DB A FGCE B O D D 2 C 2B 2 A 2 D 1C 1 B 1CBDA A 1A NF E C DM B · AD H EM CB O·GA ODB E CQ P NM ·O Q P B DE CN M · APC GFB Q A DE求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二) 经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二) 3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四) 1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF相交于P ,且DAF DE CB E DACBFF E P C BA O DB F AE C PAPC B PADC B CBDAAE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数. 经典难题(一)1.如下图做GH ⊥AB,连接EO 。
初中数学经典几何难题及答案
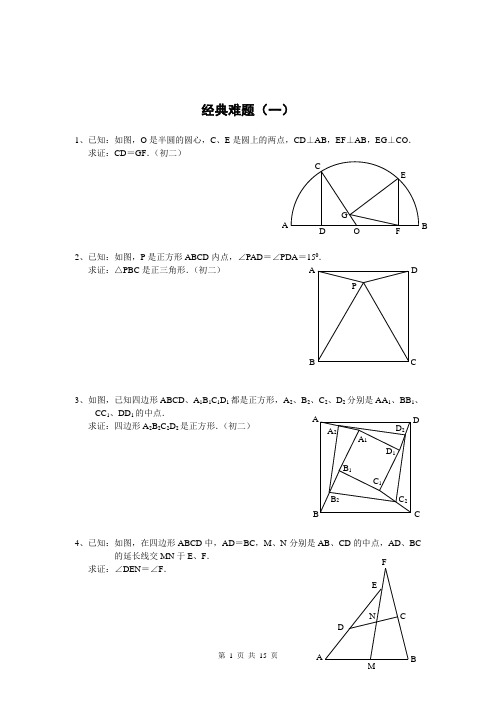
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDA A CBPD1.如下图做GH⊥AB,连接EO。
初中数学经典几何难题及答案

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 N FE CDP CG FB QA DE1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DE C N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F F EP C B A O D BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)AP C B P A D CB C B DAF PD E C B A1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDA A CBPD1.如下图做GH⊥AB,连接EO。
初中数学经典几何难题及答案
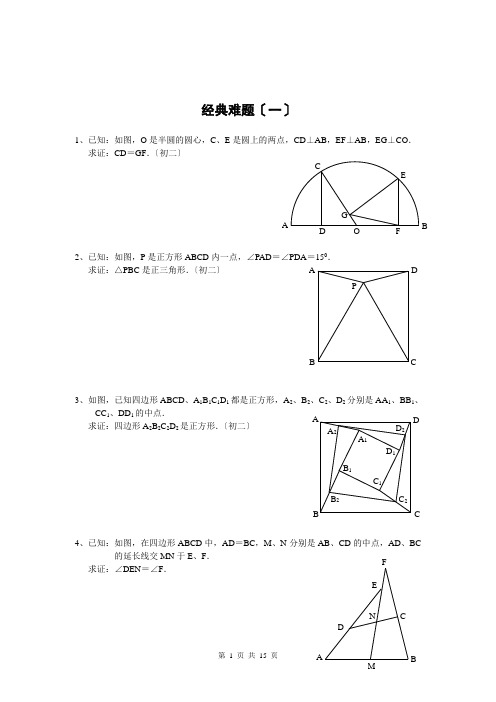
经典难题〔一〕1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .〔初二〕2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.〔初二〕3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.〔初二〕4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F1、已知:△ABC 中,H 为垂心〔各边高线的交点〕,O〔1〕求证:AH =2OM ; 〔2〕假设∠BAC =600,求证:AH =AO .〔初二〕2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .〔初二〕3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .〔初二〕4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .〔初二〕2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .〔初二〕3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .〔初二〕4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .〔初三〕1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.〔初二〕2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .〔初二〕3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .〔初二〕1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDA A CBPD⊥AB,连接EO。
初中数学经典几何难题及答案
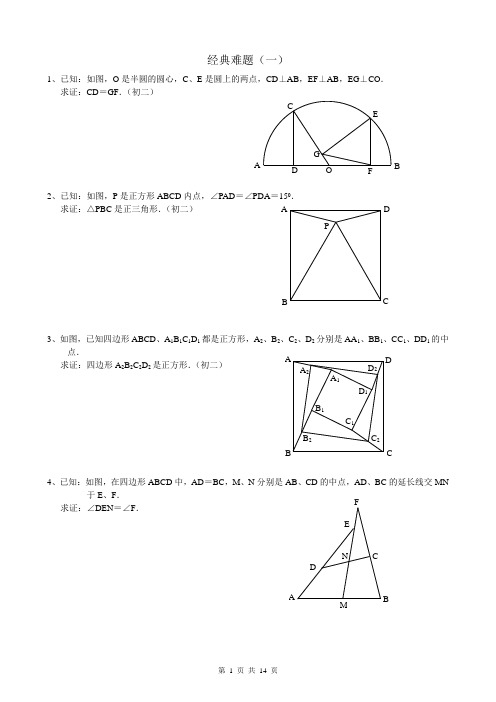
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 AN FE CDMBPCG FBQAD E1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· AD HE M C B O · GAO D B EC Q P NM · O Q PB DEC N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F F E PC B A OD BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)AP C B P A D CB C B DAF PD E C B A经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDA A CBPD经典难题(一)1.如下图做GH ⊥AB,连接EO 。
八上数学几何压轴题30道

八上数学几何压轴题30道当提到数学几何的压轴题,我们通常指的是那些考察学生对几何知识和解题能力的较难题目。
以下是30道八年级数学几何的压轴题示例:1. 计算一个正方形的对角线长度。
2. 证明三角形内角和为180度。
3. 判断一个四边形是否为平行四边形,并解释你的答案。
4. 计算一个圆的周长和面积。
5. 证明垂直平分线定理。
6. 证明等腰三角形的性质。
7. 计算一个梯形的面积。
8. 证明两条平行线被一条横截线所切割,对应角相等。
9. 计算一个正五边形的内角和外角。
10. 证明直角三角形的斜边长度与直角边长度的关系。
11. 解释相似三角形的性质。
12. 计算一个圆锥的体积。
13. 证明圆的直径与周长的关系。
14. 解释正交投影的原理。
15. 证明圆的切线与半径的垂直关系。
16. 计算一个正多边形的内角和外角。
17. 证明平行线的性质。
18. 解释三视图的绘制方法。
19. 计算一个球的表面积和体积。
20. 证明圆柱的体积公式。
21. 解释平行四边形的性质。
22. 计算一个椎体的体积。
23. 证明同位角与内错角的关系。
24. 解释棱台的性质。
25. 计算一个多面体的表面积和体积。
26. 证明圆锥的侧面积公式。
27. 解释圆的切线定理。
28. 计算一个圆环的面积。
29. 证明立体图形的展开图与表面积的关系。
30. 解释圆锥的性质。
以上是30道八年级数学几何的压轴题示例,这些题目涵盖了几何知识的各个方面,旨在考察学生的几何分析和解决问题的能力。
希望这些题目能够帮助你更好地理解数学几何的知识。
初中数学几何难题

初中数学几何难题
以下是一些初中数学几何的难题:
1. 在平面直角坐标系内,点A(1, 3)、B(4, 4)、C(6, 1)分别
是三角形ABC的顶点,求三角形ABC的面积。
2. 平行四边形ABCD中,对角线AC与BD相交于点O,已知AO
= 2cm,BO = 3cm,CO = 4cm,求DO的长度。
3. 在平面直角坐标系上,直线y = 2x + 1与直线y = -x + 5
相交于点A和B,点C(2, 5),求三角形ABC的周长。
4. 已知凸四边形ABCD的边长分别为AB = 8cm,BC = 6cm,CD = 8cm,DA = 4cm,求该四边形的面积。
5. 在平面直角坐标系内,已知四边形ABCD的坐标分别为A(-1, -1),B(1, -1),C(1, 1),D(-1, 1),求该四边形的面积。
这些题目在初中数学中属于难度较高的几何题目,需要一定的
几何知识和解题技巧来解答。
初中数学经典几何难题20例及答案

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)第1题图第2题图2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)第3题图第4题图4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)ANFE CDMB D 2C 2B 2A 2D 1C 1B 1C BDAA 1APC DBAFGCEB O D第1题图第2题图2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)第3题图第4题图4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)PCGFBQ ADE· OQPBDEC NM· A·GA O DBECQPNM·AD HEM C BO第1题图第2题图2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)第3题图第4题图4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)第1题图第2题图2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)PADCBAPC BO D BF AECPFE PCBAE DA CBFAFDECBD3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)第3题图第4题图4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.第1题图第2题图2、P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.第3题图第4题图4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300, ∠EBA =200,求∠BED 的度数.EDCBAAC BPDAC BPDA PCBFPDE CBACBDA经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF 。
初中数学经典几何难题及答案

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)A P C DBA F GCE BO D D 2 C 2 B 2 A 2D 1 C 1 B 1 C B DA A 1 A N F E C DMB· A D H E M C B O· GO DB ECP C GF BQ AD E3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)· O Q PBDE CN M · A D AF D E C B ED A C B FFEP C B AOD B FA E CPA P2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五) 1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.PA D CBC BD AF PDE CB A APCBA C BPD ED AAC BPD经典难题(一)1.如下图做GH ⊥AB,连接EO 。
初中数学经典几何难题与答案解析
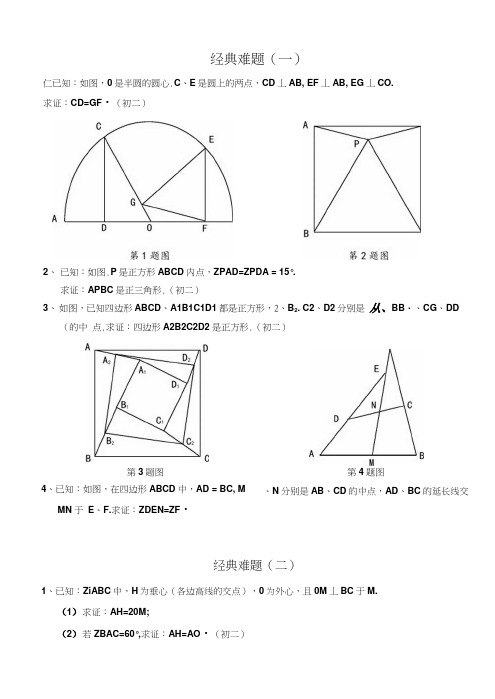
经典难题(一)仁已知:如图,0是半圆的圆心.C 、E 是圆上的两点,CD 丄AB, EF 丄AB, EG 丄CO. 求证:CD=GF ・(初二)求证:APBC 是正三角形.(初二)3、 如图,已知四边形ABCD 、A1B1C1D1都是正方形,2、B 2. C2、D2分别是 从、BB ・、CG 、DD(的中 点.求证:四边形A2B2C2D2是正方形.(初二)第3题图4、已知:如图,在四边形ABCD 中,AD = BC, MMN 于 E 、F.求证:ZDEN=ZF ・经典难题(二)1、已知:ZiABC 中,H 为垂心(各边高线的交点),0为外心,且0M 丄BC 于M.(1) 求证:AH=20M;(2) 若ZBAC=60°,求证:AH=AO ・(初二)第4题图、N 分别是AB 、CD 的中点,AD 、BC 的延长线交2、 已知:如图.P 是正方形ABCD 内点,ZPAD=ZPDA = 15°.2、设MN 是圆0外一直线.过0作0A 丄MN 于A,自A 引圆的两条直线,交圆于B 、C 及D 、E,直线EB 及CD 分别交MN 于P 、Q.求证:AP=AQ ・(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆0的弦,过MN 的中点A 任作两弦BC. DE,设CD 、EB 分别交MN 于P 、Q. 求证:AP=AQ ・(初二)求证:点P 到边AB 的距离等于AB 的一半・(初二)经典难题(三)1、如图,四边形ABCD 为正方形,DE/7AC, AE=AC, AE 与CD 相交于F. 求证:CE=CF ・(初二)第4题图在AABC 的外侧作正方形ACDE 和正方形CBFG,点PAGA第2题图是EF 的中点.3、设P 是正方形ABCD-边BC 上的任一点,PF 丄AP, CF 平分ZDCE. 求证:PA=PF ・(初二)第3题图 第4题图4、如图,PC 切圆0于C, AC 为圆的直径,PEF 为國的割线,AE 、AF 与直线P0相交于B 、D.求证:AB=DC, BC=AD ・(初三)经典难题(四)1.已知:ZiABC 是正三角形,P 是三角形内一点,PA=3, PB=4, PC=5.求:ZAPB 的慶数.(初二)求证:AE=AF ・(初二)2、 设P 是平行四边形ABCD 内部的一点,且ZPBA=ZPDA ・求证:ZPAB=ZPCB.(初二)3、 设ABCD 为圆内接凸四边形,求证:AB • CD+AD • BC=AC • BD.(初三)2、P 是边长为1的正方形ABCD 内的一点,求PA + PB+PC 的最小值. A4、平行四边形ABCD 中,设E 、F 分别是BC.AE = CF ・ 求证:ZDPA=ZDPC ・(初二)经典难题(五)1 >设 P 是边长为1的正△ ABC 内任一点,L = PA + PB + PC ,求证:WLV2.3、P为正方形ABCD内的一点,并且PA=a, PB = 2a, PC = 3a,求正方形的边长.经典难题(一)1、已知:如图,0是半圆的圆心,C、E是圆上的两点,CD丄AB, EF丄AB, EG丄CO.求证:CD=GFo (初二)证一:连接0E。
初中数学经典几何难题及答案

又∠EFC=∠DFA=450+300=750. 可证:CE=CF。
2.连接BD作CH⊥DE,可得四边形CGDH是正方形。
由AC=CE=2GC=2CH, 可得∠CEH=300,所以∠CAE=∠CEA=∠AED=150, 又∠FAE=900+450+150=1500, 从而可知道∠F=150,从而得出AE=AF。
得到BE=CF , FG=GE 。
推出 : △FGE为等边三角形 ,可得∠AFE=800 ,
既得:∠DFG=400
①
又BD=BC=BG ,既得∠BGD=800 ,既得∠DGF=400
②
推得:DF=DG ,得到:△DFE≌△DGE ,
从而推得:∠FED=∠BED=300 。
3.在BD取一点E,使∠BCE=∠ACD,既得△BEC∽△ADC,可得:
=,即AD•BC=BE•AC,
①
又∠ACB=∠DCE,可得△ABC∽△DEC,既得
=,即AB•CD=DE•AC,
②
由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证。
4.过D作AQ⊥AE ,AG⊥CF ,由==,可得:
D2分别是AA1、BB1、CC1、DD1的中点. D2 C2 B2 A2 D1 C1 B1 C B D A A1
求证:四边形A2B2C2D2是正方形.(初二)
4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中 点,AD、BC的延长线交MN于E、F.
A N F E C D M B 求证:∠DEN=∠F.
· G A O D B E C Q P
N M
求证:AP=AQ.(初二)
数学几何题精选50道及答案

数学几何题精选50道及答案**几何数学题1**:题目:在直角三角形ABC中,角A=90°,AB=5cm,BC=12cm。
求AC的长度。
**几何数学题2**:题目:在平行四边形WXYZ中,角W=80°,角X=100°。
求角Y和角Z的度数。
**几何数学题3**:题目:在正五边形PQRST中,每个内角的度数是多少?**几何数学题4**:题目:已知三角形DEF中,角D=60°,角E=45°。
求角F的度数。
**几何数学题5**:题目:在直角三角形LMN中,角L=90°,角M=60°。
若LN=8cm,求MN的长度。
**几何数学题6**:题目:已知平行四边形UVWX中,UV=7cm,WX=5cm,且角U=120°。
求VX的长度。
**几何数学题7**:题目:在等腰三角形PQR中,角P=80°。
求角Q和角R的度数。
**几何数学题8**:题目:在梯形STUV中,ST和UV是平行边,ST=9cm,UV=12cm,SV=5cm。
求TU的长度。
**几何数学题9**:题目:在正方形ABCD中,边长为15cm。
求对角线AC的长度。
**几何数学题10**:题目:在菱形EFGH中,角E=50°。
求角F、角G和角H的度数。
**几何数学题11**:题目:在直角三角形XYZ中,角X=90°,YZ=15cm,XZ=9cm。
求角Y和角Z的度数。
**几何数学题12**:题目:在平行四边形IJKL中,角I=130°,角K=70°。
求角J和角L的度数。
**几何数学题13**:题目:在正七边形ABCDEFGH中,每个内角的度数是多少?**几何数学题14**:题目:已知三角形PQS中,角P=40°,角Q=60°。
求角S的度数。
**几何数学题15**:题目:在直角三角形RST中,角R=90°,角S=45°。
老教授:30道几何经典题(含解析),孩子吃透,小升初直上98

老教授:30道几何经典题(含解析),孩子吃透,小升初直上
98
几何知识的教学是运用实物、图形等直观教具、学具,让学生通过观察、分析、比较来发现几何形体的特征,掌握有关的知识。
重视直观教学,加强动手操作,发展学生的空间观念,是几何教学的重要规律。
很多的同学在学习的过程中会遇到很多的难题,尤其到了三、四年级,开始接触一些简单的几何知识,运用公式,还要添加辅助线之类的,会让孩子们一时间觉得无从下手,频频丢分!
几何作为数学学习中的重难点题型,不仅仅是小学数学学习的重点,到了初中也是占了相当大的比重,其重点知识内容是循序渐进的,学生要想学好几何这部分的内容,必然要学会从整体都局部透彻的掌握。
鉴于很多家长向我反映孩子这方面的知识掌握的不够牢固,所以老师今天整理了小学数学中最常见的30个几何题型,建议家长们可以为孩子收藏起来,这对于孩子学习数学会有很大的帮助
您好,我专注于中小学教育,致力于提高孩子记忆力!
由于微信后台不能发送电子版文档,如果您需要更多高效的学习
方法、学习资料、快速记忆法、试卷练习题等、
或者是孩子学习上有任何问题,如注意力不集中、记忆力差、严重偏科等,。
(完整版)初中数学经典几何难题及答案.doc

经典难题(一)1、已知:如图,O 是半圆的圆心, C、E 是圆上的两点, CD ⊥ AB , EF⊥ AB ,EG⊥ CO.求证: CD = GF.(初二)CEAGO F BD2、已知:如图, P 是正方形 ABCD 内一点,∠ PAD=∠ PDA = 150.求证:△ PBC 是正三角形.(初二) A DPB C3、如图,已知四边形ABCD 、 A 1B 1C1D1都是正方形, A2、 B 2、C2、 D2分别是 AA 1、 BB 1、CC1、 DD 1的中点.求证:四边形 A 2B 2C2 D2是正方形.(初二)A DA 2 D2A 1D1B 1C1B2 C2B C4、已知:如图,在四边形ABCD 中, AD = BC , M 、N 分别是 AB 、CD 的中点, AD 、 BC的延长线交MN 于 E、 F.F 求证:∠ DEN =∠ F.EN CD经典难题(二)1、已知:△ ABC 中, H 为垂心(各边高线的交点), O 为外心,且 OM ⊥ BC 于 M .( 1)求证: AH = 2OM ; A ( 2)若∠ BAC =600,求证: AH = AO .(初二)O·H EB M D C2、设 MN 是圆 O 外一直线,过O 作 OA ⊥ MN 于 A ,自 A 引圆的两条直线,交圆于B 、 C及 D、 E,直线 EB 及 CD 分别交 MN 于 P、 Q.G求证: AP = AQ .(初二) EC O·B DMP AN Q3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设 MN 是圆 O 的弦,过 MN 的中点 A 任作两弦 BC 、DE ,设 CD 、 EB 分别交 MN于 P、Q.C E求证: AP= AQ .(初二)A M Q·P N·O BD4、如图,分别以△ ABC 的 AC 和 BC 为一边,在△ ABC 的外侧作正方形ACDE 和正方形CBFG ,点 P 是 EF 的中点.D求证:点 P 到边 AB 的距离等于AB 的一半.(初二)GECP FA QB经典难题(三)1、如图,四边形ABCD 为正方形, DE ∥ AC ,AE = AC , AE 与 CD 相交于 F.求证: CE= CF.(初二)DAF EB C2、如图,四边形ABCD 为正方形, DE ∥ AC ,且 CE= CA ,直线 EC 交 DA 延长线于 F.求证: AE =AF .(初二)A DFB CE3、设 P 是正方形 ABCD 一边 BC 上的任一点, PF⊥AP ,CF 平分∠ DCE.求证: PA= PF.(初二)A DFBP C E4、如图, PC 切圆 O 于 C, AC 为圆的直径, PEF 为圆的割线, AE 、AF 与直线 PO 相交于B 、 D.求证: AB = DC ,BC= AD .(初三)AB O DPEFC经典难题(四)1、已知:△ ABC 是正三角形,P 是三角形内一点,PA=3, PB= 4,PC= 5.求:∠ APB 的度数.(初二)APB C2、设 P 是平行四边形ABCD 内部的一点,且∠PBA =∠ PDA .求证:∠ PAB =∠ PCB .(初二)A DPB C3、设 ABCD 为圆内接凸四边形,求证:AB · CD + AD · BC= AC · BD .(初三)ADB C4、平行四边形ABCD 中,设 E、 F 分别是 BC、 AB 上的一点, AE 与 CF 相交于 P,且 AE =CF.求证:∠ DPA=∠ DPC .(初二)A DFPB E C经典难题(五)1 、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤ L <2.APB C2、已知: P 是边长为 1 的正方形ABCD 内的一点,求PA+ PB+ PC 的最小值.A DPCB3、 P 为正方形ABCD 内的一点,并且PA= a, PB= 2a, PC= 3a,求正方形的边长.A DC B4、如图,△ ABC 中,∠ ABC =∠ ACB = 800,D 、E 分别是 AB 、 AC 上的点,∠ DCA = 300, ∠ EBA = 200,求∠ BED 的度数.AED经 典 难 题(一)BC1.如下图做 GH ⊥ AB, 连接 EO 。
