第1章 金属的晶体结构 ppt课件[1]
合集下载
第一章-金属的晶体结构(共118张PPT)可修改全文

(3) 不需最小整数化; (4) 〔1 1 1〕
B面:
(1) 该面与z轴平行,因此x=1,y=2, z=∞; (2) 1/x=1,1/y=1/2,1/z=0; (3) 最小整数化1/x=2,1/y=1,1/z=0; (4) 〔2 1 0〕
C面:
(1) 该面过原点,必须沿y轴进行移动,因此x= ∞ ,y=-1,z=∞ (2) 1/x=0,1/y=-1,1/z=0; (3) 不需最小整数化;(4) 〔0 1 0〕
晶胞在三维空间的重复构成点阵
〔4〕晶格常数
在晶胞中建立三维坐标体系, 描述出晶胞的形状与大小
晶胞参数- 晶格常数:a、b、c 棱间夹角:α、β、γ
2 晶系与布拉菲点阵
依据点阵参数 的不同特点划分为七种晶系
(1) 三斜晶系
α≠β≠γ≠90° a≠ b≠ c
复杂单胞 底心单斜
(2) 单斜晶系
α=γ=90°≠β a≠ b≠ c
3 原子半径: r 2 a
4 配位数= 12
4
5 致密度= nv/V=(4×3πr3/4)/a3=0.74
γ-Fe(912~1394℃)、Cu、Ni、Al、Ag 等
——塑性较高
面心立方晶胞中原子半径与晶 格常数的关系
a
r 2a 4
(三)密排六方结构〔 h.c.p〕 〔 了解〕
金属:Zn、Mg、Be、α-Ti、α-Co等
具有光泽:吸收了能量从被激发态回到基态时所 产生的幅射;
良好的塑性:在固态金属中,电子云好似是 一种流动的万能胶,把所有的正离子都结合 在一起,所以金属键并不挑选结合对象,也 无方向性。当一块金属的两局部发生相对位 移时,金属正离子始终“浸泡〞在电子云中, 因而仍保持着金属键结合。这样金属便能经 受较大的变形而不断裂。
B面:
(1) 该面与z轴平行,因此x=1,y=2, z=∞; (2) 1/x=1,1/y=1/2,1/z=0; (3) 最小整数化1/x=2,1/y=1,1/z=0; (4) 〔2 1 0〕
C面:
(1) 该面过原点,必须沿y轴进行移动,因此x= ∞ ,y=-1,z=∞ (2) 1/x=0,1/y=-1,1/z=0; (3) 不需最小整数化;(4) 〔0 1 0〕
晶胞在三维空间的重复构成点阵
〔4〕晶格常数
在晶胞中建立三维坐标体系, 描述出晶胞的形状与大小
晶胞参数- 晶格常数:a、b、c 棱间夹角:α、β、γ
2 晶系与布拉菲点阵
依据点阵参数 的不同特点划分为七种晶系
(1) 三斜晶系
α≠β≠γ≠90° a≠ b≠ c
复杂单胞 底心单斜
(2) 单斜晶系
α=γ=90°≠β a≠ b≠ c
3 原子半径: r 2 a
4 配位数= 12
4
5 致密度= nv/V=(4×3πr3/4)/a3=0.74
γ-Fe(912~1394℃)、Cu、Ni、Al、Ag 等
——塑性较高
面心立方晶胞中原子半径与晶 格常数的关系
a
r 2a 4
(三)密排六方结构〔 h.c.p〕 〔 了解〕
金属:Zn、Mg、Be、α-Ti、α-Co等
具有光泽:吸收了能量从被激发态回到基态时所 产生的幅射;
良好的塑性:在固态金属中,电子云好似是 一种流动的万能胶,把所有的正离子都结合 在一起,所以金属键并不挑选结合对象,也 无方向性。当一块金属的两局部发生相对位 移时,金属正离子始终“浸泡〞在电子云中, 因而仍保持着金属键结合。这样金属便能经 受较大的变形而不断裂。
金属间化合物的晶体结构ppt课件.pptx
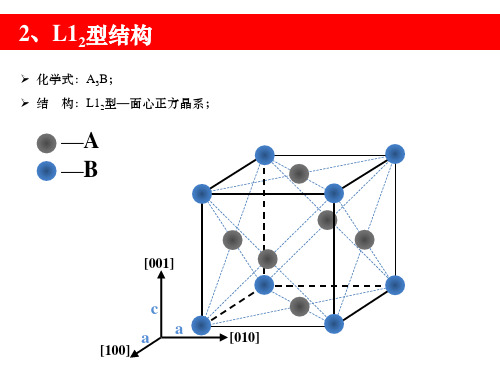
2、L12型结构
➢ 化学式:A3B; ➢ 结 构:L12型—面心正方晶系;
—A —B
[001]
c aa
[100]
[010]
3、L10型结构
➢ 化学式:AB; ➢ 结 构:L10型—面心正方晶系; ➢ 特点:[001]方向上是由仅含A原子组成的原子面与仅含B原子的原子面交替重叠
堆垛而成,所以[100]、[010]方向上的点阵常数与[001]方向的不一样,把[001]视 为c轴,其他两轴为a轴;
—A —B
[001]
c aa
[100]
[010]
4、DO22型结构
➢ 化学式:A3B; ➢ 结 构:DO22型—面心正方晶系;
—A —B
5、体心立方结 构
6、B2型结构
➢ 化学式:AB; ➢ 结 构:B2型—体心正方晶系;
—A —B
7、DO3型结构
➢ 化学式: A3B ; ➢ 结 构:DO3型—体心正方晶系;
—A —B
8、L21型结构
➢ 化学式: A2BC; ➢ 结 构:L21型—体心正方晶系;
—A —B —C
9、C11b型结构
➢ 化学式: AB2; ➢ 结 构:C11b型—体心正方晶系;
—A —B
10、hcp型结构
10、hcp型结构
11、DO19型结 构
➢ 化学式: A3B ;
—A —B
11、DO19型结 构
—A —B
12、Cu3Ti型结构
➢ 化学式: A3B ;
—A —B
12、 Cu3Ti型结构
—A —B
➢ 化学式:A3B; ➢ 结 构:L12型—面心正方晶系;
—A —B
[001]
c aa
[100]
[010]
3、L10型结构
➢ 化学式:AB; ➢ 结 构:L10型—面心正方晶系; ➢ 特点:[001]方向上是由仅含A原子组成的原子面与仅含B原子的原子面交替重叠
堆垛而成,所以[100]、[010]方向上的点阵常数与[001]方向的不一样,把[001]视 为c轴,其他两轴为a轴;
—A —B
[001]
c aa
[100]
[010]
4、DO22型结构
➢ 化学式:A3B; ➢ 结 构:DO22型—面心正方晶系;
—A —B
5、体心立方结 构
6、B2型结构
➢ 化学式:AB; ➢ 结 构:B2型—体心正方晶系;
—A —B
7、DO3型结构
➢ 化学式: A3B ; ➢ 结 构:DO3型—体心正方晶系;
—A —B
8、L21型结构
➢ 化学式: A2BC; ➢ 结 构:L21型—体心正方晶系;
—A —B —C
9、C11b型结构
➢ 化学式: AB2; ➢ 结 构:C11b型—体心正方晶系;
—A —B
10、hcp型结构
10、hcp型结构
11、DO19型结 构
➢ 化学式: A3B ;
—A —B
11、DO19型结 构
—A —B
12、Cu3Ti型结构
➢ 化学式: A3B ;
—A —B
12、 Cu3Ti型结构
—A —B
第一章金属的晶体结构

图2-6密排六方晶胞
第三节 晶体学概念
• • • • • • • 1.3.1 晶胞中的原子数 体心立方: 面心立方: 密排六方: 1.3.2 原子半径 1.3.3 配位数和致密度 配位数:指晶体结构中与任一个原子最近邻且等距离的原 子数目。 • 体心立方晶体8个,面心立方12个,密排六方12个,所以 面心立方和密排六方致密度高 • 致密度分别为0.68、0.74、0.74
图2-5
面心立方晶胞
• (3)密排六方晶胞(close packed lattice hexagonal):密排六方晶体的晶胞如图1.6所示。 • 它是由六个呈长方形的侧面和两个呈正六边形的 底面所组成的一个六方柱体。因此,需要用两个 晶格常数表示,一个是正六边形的边长a,另—个 是柱体的高c。在密排六方晶胞的每个角上和上、 下底面的小心都有一个原子,另外在中间还有三 个原子。因此,密排六方晶格的晶胞中所含的原 子数为:6×1/6×2+2×1/2+3=6个。 • 具有密排六方晶体结构的金属有Mg、Zn、Be、 Cd、α-Ti、α-Co等。
A、B组元组成的固溶体也可表示为A(B), 其中A为溶剂, B为 溶质。例如铜锌合金中锌溶入铜中形成的固溶体一般用α表 示, 亦可表示为Cu(Zn)。
• 固溶体特性:1固溶体成分可以在一定范围内变化, 在相图上表现为一个区域。2固溶体必须保持溶剂 组元的点阵类型。3纯金属结构有哪些类型,固溶 体也应有哪些类型,即固溶体本身没有独立的点 阵类型。4组元的原子尺寸不同会引起的点阵畸变, 原子尺寸相差越大,引起的畸变也越大。
• 1.3.4晶体中原子的排列方式(略) • 1.3.5 晶体结构中的间隙 • 三种典型晶体结构的四面体间隙、八面体间 隙(图1-13,1-14,1-15) • 间隙半径与原子半径之比rB/rA=?(见表1-2) • 可见面心立方结构八面体间隙比体心立方结 构四面体间隙还大,因此溶碳量大的分类 • 1.按溶剂分类 • (1)一次固溶体:以纯金属组元作为溶剂的 固溶体称为一次固溶体,也叫边际固溶体。 • (2)二次固溶体:以化合物为溶剂的固溶体 称二次固溶体,或叫中间固溶体。如电子 化合物、间隙相。 • 有的化合物和化合物之间,也可以相互溶 解而组成固溶体,如Fe3C和Mn3C,TiC和 TiN等。
机械工程材料 第1章 金属的晶体结构

常见的化学键
离子键 共价键 分子键 金属键
化学键的特性决定材料的组织结构和性能
第一节 材料的化学键
1.金属键
金属正离子和自由电子之间的相互吸引力而使金属原子结合的方式。
金属特性:导电、导热性,塑性,强度,金属光泽。
金属键模型
正离子与自由电子之间的吸引力
第一节 材料的化学键
2. 结合力和结合能
双原子作用模型
第四节 合金的相结构
(2) 按固溶度 有限固溶体、无限固溶体
(3) 按相对分布 有序固溶体、无序固溶体
无序分布
偏聚分布
短程有序分布
第四节 合金的相结构
2、固溶体的性能
溶入溶质原子形成固溶体而使金属强度、硬度升高而塑性、 韧性下降的现象。——固溶强化 溶质原子含量↑,σb、HB↑,ψ、αk↓ 固溶强化效果:间隙固溶体>置换固溶体。
可影响合金相的类型。
第四节 合金的相结构
1、固溶体——固态下组元间相互溶解而形成的相。 溶剂:原子分数多者,其晶格保持不变的组元。 溶质:原子分数少者。
溶剂
溶质
特点:所形成的固相晶体结构仍然保持溶剂晶格类型
第四节 合金的相结构
固溶体的分类:(1) 按溶质原子在晶格中的位置
置换固溶体 、间隙固溶体
x
第二节 材料晶体结构的概念
4、晶格特征参数
晶格常数:描述晶胞几何形状与大小的参数。如立方晶胞: 三棱边a、b、c; 三棱边夹角α、β、γ
晶胞所占原子数: 指一个晶胞所占的原子总数
配位数: 指晶体结构中与任何一个原子最近领且等距离的原子数目
致密度: 晶胞中原子所占体积与晶胞体积之比
其中配位数和致密度可衡量晶胞中原子排列的紧密程度
第一章 纯金属的晶体结构

பைடு நூலகம்
四、晶体的各向异性及同素异构转变
• • • • 晶体的伪各向同性 2、晶体的同素异构转变 同素异构体 重结晶过程 规律:有一定的转变温度;转变时需要过冷 (或过热);有结晶潜热产生;转变过程也 是由形核及核长大来完成的。
铁的同素异构转变
• Fe
§1—4 金属的实际晶体结构 二、金属实际晶体结构
点缺陷是一种热力学平衡缺陷
• 从热力学中己知,一个过程是否能够自发进行,取 决于体系的吉布斯自由能的变化。 • ΔG<0。 • ΔG=ΔU+PΔV—TΔS。在固态的条件下,体积的变 化ΔV常常可以忽略不计,因此可以近似地认为: ΔG=ΔU—TΔS=ΔF • 假设在一个有N个原子的理想晶体中,引入n个空位 内能将增加nUv。
螺型位错
混合型位错
• 刃型位错和 螺型位错混 合而成的
钼中的六角位错网络
柏氏向量
• 在切应力作用下,位错线很容易沿滑移面运动。一根位错 线扫过滑移面,滑移面两边的原子就相对移动一个原子间 距。大量位错扫过滑移面,就造成晶体的宏观切变。 • 柏氏向量的方向就是原子移动的方向,也就是晶体滑移的 方向。柏氏向量的大小就是原子移动的距离。它总是由一 个平衡位置指向另一个平衡位置,而不能是任意的方向和 大小。 • 每一根位错线都有自己的柏氏向量。
体心立方
晶体中的原子数 2 原子半径 : 3a / 4 原子体积: 3 a
3
16
配位数: 8 致密度:0.68 八面体间隙半径: 0.067a,6个 四面体间隙半径:0.126a,12个
体心立方间隙
体心立方
4.晶胞中四面体空隙
5 3
1
2
6
4
代表四面体空隙,位置在6个面的如图所示位 置。个数=6×4×1/2=12
四、晶体的各向异性及同素异构转变
• • • • 晶体的伪各向同性 2、晶体的同素异构转变 同素异构体 重结晶过程 规律:有一定的转变温度;转变时需要过冷 (或过热);有结晶潜热产生;转变过程也 是由形核及核长大来完成的。
铁的同素异构转变
• Fe
§1—4 金属的实际晶体结构 二、金属实际晶体结构
点缺陷是一种热力学平衡缺陷
• 从热力学中己知,一个过程是否能够自发进行,取 决于体系的吉布斯自由能的变化。 • ΔG<0。 • ΔG=ΔU+PΔV—TΔS。在固态的条件下,体积的变 化ΔV常常可以忽略不计,因此可以近似地认为: ΔG=ΔU—TΔS=ΔF • 假设在一个有N个原子的理想晶体中,引入n个空位 内能将增加nUv。
螺型位错
混合型位错
• 刃型位错和 螺型位错混 合而成的
钼中的六角位错网络
柏氏向量
• 在切应力作用下,位错线很容易沿滑移面运动。一根位错 线扫过滑移面,滑移面两边的原子就相对移动一个原子间 距。大量位错扫过滑移面,就造成晶体的宏观切变。 • 柏氏向量的方向就是原子移动的方向,也就是晶体滑移的 方向。柏氏向量的大小就是原子移动的距离。它总是由一 个平衡位置指向另一个平衡位置,而不能是任意的方向和 大小。 • 每一根位错线都有自己的柏氏向量。
体心立方
晶体中的原子数 2 原子半径 : 3a / 4 原子体积: 3 a
3
16
配位数: 8 致密度:0.68 八面体间隙半径: 0.067a,6个 四面体间隙半径:0.126a,12个
体心立方间隙
体心立方
4.晶胞中四面体空隙
5 3
1
2
6
4
代表四面体空隙,位置在6个面的如图所示位 置。个数=6×4×1/2=12
第1章_金属的晶体结构

(3)原子半径 atomic radius (4)致密度 atomic packing factor (APF)---0.68 (5)空隙半径 gap radius (6)配位数 coordination number—最近邻等距离原子数,体心
立方晶格的配位数为8。配位数越大, 原子排列紧密程度就越大。
面心立方晶胞原子排列
FCC –Page2/4
❖ 面心立方晶胞特征:
(1)晶格常数 a=b=c, α=β=γ=90° (2)晶胞原子数 (个)
➢
FCC –Page3/4
(3)原子半径
r原子
2a 4
or
a 2r原子 2
(4)致密度 0.74 (74%) (5)配位数 12
FCC –Page4/4
❖ 金属的晶格常数一般为:
1×10-10 m~7×10-10 m。
❖ 不同元素组成的金属晶体因晶格形式及晶格常数不同, 其物理、化学和力学性能也不同。
❖ 金属的晶体结构可用X射线(X-ray)结构分析技术进行测定。
1.2 金属的晶体结构 –3 三种典型的晶体结构
❖ 体心立方晶格(胞) Body-Centered Cubic (B.C.C.晶格) ❖ 面心立方晶格(胞) Face-Centered Cubic (F.C.C.晶格) ❖ 密排六方晶格(胞) Hexagonal Close-Packed (H.C.P.晶格)
ቤተ መጻሕፍቲ ባይዱ
1.1 金属简介
❖ 学习目标: ➢ 根据金属键的本质,解释固态金属的一些特性—导
电性、正的电阻温度系数、传热性及延展性等) ➢ 利用双原子作用模型,分析两个原子间的相互作用
(P3的图1-2)
1.2 金属的晶体结构 –1 晶体的特性
立方晶格的配位数为8。配位数越大, 原子排列紧密程度就越大。
面心立方晶胞原子排列
FCC –Page2/4
❖ 面心立方晶胞特征:
(1)晶格常数 a=b=c, α=β=γ=90° (2)晶胞原子数 (个)
➢
FCC –Page3/4
(3)原子半径
r原子
2a 4
or
a 2r原子 2
(4)致密度 0.74 (74%) (5)配位数 12
FCC –Page4/4
❖ 金属的晶格常数一般为:
1×10-10 m~7×10-10 m。
❖ 不同元素组成的金属晶体因晶格形式及晶格常数不同, 其物理、化学和力学性能也不同。
❖ 金属的晶体结构可用X射线(X-ray)结构分析技术进行测定。
1.2 金属的晶体结构 –3 三种典型的晶体结构
❖ 体心立方晶格(胞) Body-Centered Cubic (B.C.C.晶格) ❖ 面心立方晶格(胞) Face-Centered Cubic (F.C.C.晶格) ❖ 密排六方晶格(胞) Hexagonal Close-Packed (H.C.P.晶格)
ቤተ መጻሕፍቲ ባይዱ
1.1 金属简介
❖ 学习目标: ➢ 根据金属键的本质,解释固态金属的一些特性—导
电性、正的电阻温度系数、传热性及延展性等) ➢ 利用双原子作用模型,分析两个原子间的相互作用
(P3的图1-2)
1.2 金属的晶体结构 –1 晶体的特性
金属键金属晶体ppt课件.ppt

熔点/℃
Na 3s1 186 108.4 97.5
Mg 3s2 160 146.4 650
Al 3s23p1 143.1 326.4
660
Cr 3d54s1 124.9 397.5 1900
金属的熔点、硬度与金属键的强弱有关,金属键的强弱 又可以用原子化热来衡量。
原子化热是指1mol金属固体完全气化成相互远离的 气态原子时吸收的能量。
⑷金属晶体结构具有金属光泽和颜色
• 由于自由电子可吸收所有频率的光,然 后很快释放出各种频率的光,因此绝大 多数金属具有银白色或钢灰色光泽。而 某些金属(如铜、金、铯、铅等)由于 较易吸收某些频率的光而呈现较为特殊 的颜色。
• 当金属成粉末状时,金属晶体的晶面取
向杂乱、晶格排列不规则,吸收可见光
后辐射不出去,所以成黑色。
a
ρ= m = 4 M/NA V 2 2 d3
解此类题的关键! 37
已知铜晶胞是面心立方晶胞,该晶胞的边长为 3.6210-10m,每一个铜原子的质量为1.0551025kg ,试回答下列问题:
(1)一个晶胞中“实际”拥有的铜原子数是多少?
(2)该晶胞的体积是多大?
(3)利用以上结果计算金属铜的密度。
2. 晶胞中微粒数个晶胞共享,处于体心的 金属原子全部属于该晶胞。 微粒数为:8×1/8 + 1 = 2 (2)面心立方:
在立方体顶点的微粒为8个晶胞共有,在面心的为2 个晶胞共有。 微粒数为:8×1/8 + 6×1/2 = 4 (3)六方棱柱:
在六方体顶点的微粒为6个晶胞共有,在面心的为2 个棱柱共有,在体内的微粒全属于该棱柱。 微粒数为:12×1/6 + 2×1/2 + 3 = 6
(1)欲计算一个晶胞的体积,除假定金原子是钢 性小球外,还应假定 各面对角线上。的三个球两两相切
Na 3s1 186 108.4 97.5
Mg 3s2 160 146.4 650
Al 3s23p1 143.1 326.4
660
Cr 3d54s1 124.9 397.5 1900
金属的熔点、硬度与金属键的强弱有关,金属键的强弱 又可以用原子化热来衡量。
原子化热是指1mol金属固体完全气化成相互远离的 气态原子时吸收的能量。
⑷金属晶体结构具有金属光泽和颜色
• 由于自由电子可吸收所有频率的光,然 后很快释放出各种频率的光,因此绝大 多数金属具有银白色或钢灰色光泽。而 某些金属(如铜、金、铯、铅等)由于 较易吸收某些频率的光而呈现较为特殊 的颜色。
• 当金属成粉末状时,金属晶体的晶面取
向杂乱、晶格排列不规则,吸收可见光
后辐射不出去,所以成黑色。
a
ρ= m = 4 M/NA V 2 2 d3
解此类题的关键! 37
已知铜晶胞是面心立方晶胞,该晶胞的边长为 3.6210-10m,每一个铜原子的质量为1.0551025kg ,试回答下列问题:
(1)一个晶胞中“实际”拥有的铜原子数是多少?
(2)该晶胞的体积是多大?
(3)利用以上结果计算金属铜的密度。
2. 晶胞中微粒数个晶胞共享,处于体心的 金属原子全部属于该晶胞。 微粒数为:8×1/8 + 1 = 2 (2)面心立方:
在立方体顶点的微粒为8个晶胞共有,在面心的为2 个晶胞共有。 微粒数为:8×1/8 + 6×1/2 = 4 (3)六方棱柱:
在六方体顶点的微粒为6个晶胞共有,在面心的为2 个棱柱共有,在体内的微粒全属于该棱柱。 微粒数为:12×1/6 + 2×1/2 + 3 = 6
(1)欲计算一个晶胞的体积,除假定金原子是钢 性小球外,还应假定 各面对角线上。的三个球两两相切
固体物理学精品PPT课件

பைடு நூலகம்
4.最小内能性
由同一种化学成分构成的物质,在不同的条件下 可以呈现不同的物相,其相应的结合能或系统的内 能也必不相同。
但是,在相同的热力学条件下,在具有相同化学 成分物质的各种物态——气体、液体、非晶体、晶 体中,以晶体的内能最小,这个结论称为晶体的最 小内能性。
对于固体物质,由于晶体内能比非晶体内能小, 所以非晶体具有自发地向晶体转变的趋势;反之, 晶体不可能自发地转变为其它的物态形式。
在单晶体内部,原子都是规则地排列的。
* 多晶体( Multiple Crystal )
由许多小单晶(晶粒)构成的晶体,称为多晶体。 多晶体仅在各晶粒内原子才有序排列,不同晶粒内 的原子排列是不同的。
晶面的大小和形状受晶体生长条件的影响,它们 不是晶体品种的特征因素。
例如,岩盐(氯化钠)晶体的外形可以是立方体 或八面体,也可能是立方和八面的混合体,如图所 示。
有些晶体的解理性不明显,例如,金属晶体等。
晶体解理性在某些加工工艺中具有重要的意义, 例如,在划分晶体管管芯时,利用半导体晶体的解 理性可使管芯具有平整的边缘和防止无规则的断裂 发生,以保证成品率。
3.晶面角守恒定律
发育良好的单晶体,外形上最显著的特征是晶面 有规则地配置。一个理想完整的晶体,相应的晶面 具有相同的面积。晶体外形上的这种规则性,是晶 体内部分子或原子之间有序排列的反映。
晶格振动是晶体的特性之一。
§1.2 晶体的周期性
一、空间点阵学说 1.空间点阵
为了描述晶体结构的周期性,布拉菲在1848年提 出空间点阵学说,从而奠定了晶体结构几何理论的 基础。
按照空间点阵学说,晶体内部结构是由一些相同 的点子在空间规则地作周期性无限分布所构成的系 统,这些点子的总体称为点阵。
4.最小内能性
由同一种化学成分构成的物质,在不同的条件下 可以呈现不同的物相,其相应的结合能或系统的内 能也必不相同。
但是,在相同的热力学条件下,在具有相同化学 成分物质的各种物态——气体、液体、非晶体、晶 体中,以晶体的内能最小,这个结论称为晶体的最 小内能性。
对于固体物质,由于晶体内能比非晶体内能小, 所以非晶体具有自发地向晶体转变的趋势;反之, 晶体不可能自发地转变为其它的物态形式。
在单晶体内部,原子都是规则地排列的。
* 多晶体( Multiple Crystal )
由许多小单晶(晶粒)构成的晶体,称为多晶体。 多晶体仅在各晶粒内原子才有序排列,不同晶粒内 的原子排列是不同的。
晶面的大小和形状受晶体生长条件的影响,它们 不是晶体品种的特征因素。
例如,岩盐(氯化钠)晶体的外形可以是立方体 或八面体,也可能是立方和八面的混合体,如图所 示。
有些晶体的解理性不明显,例如,金属晶体等。
晶体解理性在某些加工工艺中具有重要的意义, 例如,在划分晶体管管芯时,利用半导体晶体的解 理性可使管芯具有平整的边缘和防止无规则的断裂 发生,以保证成品率。
3.晶面角守恒定律
发育良好的单晶体,外形上最显著的特征是晶面 有规则地配置。一个理想完整的晶体,相应的晶面 具有相同的面积。晶体外形上的这种规则性,是晶 体内部分子或原子之间有序排列的反映。
晶格振动是晶体的特性之一。
§1.2 晶体的周期性
一、空间点阵学说 1.空间点阵
为了描述晶体结构的周期性,布拉菲在1848年提 出空间点阵学说,从而奠定了晶体结构几何理论的 基础。
按照空间点阵学说,晶体内部结构是由一些相同 的点子在空间规则地作周期性无限分布所构成的系 统,这些点子的总体称为点阵。
金属的晶体结构

不管原子以哪种方式进行堆垛,在原子刚球之间都必然存在 间隙,这些间隙对金属的性能以及形成合金后的晶体结构都 有很重要的影响。分析间隙的数量、大小及位置对了解材料 的相结构、扩散、相变等问题都很重要。
间隙半径:间隙中所能容纳的最大圆球的半径。
体心立方晶格中的间隙
八面体间隙: 6个×0.067a
四面体间隙: 12个×0.126a
体心立方晶格(body-centred cubic)
体心立方金属有:-Fe、Cr、V、W、Mo 等30种 。体心立方晶胞Z Nhomakorabeac
a a 2r
a
bY
X
晶格常数:a=b=c; ===90
晶胞原子数: 2
1+8*1/8=2
原子半径:
致密度:0.68
致密度= Va/Vc,其中 Vc:晶胞体积a3 Va=nV1 =24r3/3 配位数:8 配位数越大,原子排列 越紧密。
四、金属晶体中的晶面和晶向
Z
c
b a
晶面─晶体点阵中,通 过阵点的任一平面,代 Y 表晶体的原子平面,称 为晶面。
第1章 金属的晶体结构
1.1 金属 1.2 金属的晶体结构 1.3 实际金属的晶体结构
本章重点与难点
• ①金属键;建立金属原子的结构模型 。 • ②建立晶格和晶胞的概念;最常见的晶体结构:
体心立方结构、面心立方结构、密排六方结构; 立方晶系的晶向指数和晶面指数。 • ③晶体中存在的缺陷:点缺陷、线缺陷(位错)、 面缺陷。
晶胞的棱边长度一般称为晶格常数或点阵常数,用a、b、 c表示。晶胞的棱间夹角叫轴间夹角。用α、β、γ表示。
2、七大晶系和十四种布拉菲点阵
依据空间点阵的基本特点划分为七大晶系:
间隙半径:间隙中所能容纳的最大圆球的半径。
体心立方晶格中的间隙
八面体间隙: 6个×0.067a
四面体间隙: 12个×0.126a
体心立方晶格(body-centred cubic)
体心立方金属有:-Fe、Cr、V、W、Mo 等30种 。体心立方晶胞Z Nhomakorabeac
a a 2r
a
bY
X
晶格常数:a=b=c; ===90
晶胞原子数: 2
1+8*1/8=2
原子半径:
致密度:0.68
致密度= Va/Vc,其中 Vc:晶胞体积a3 Va=nV1 =24r3/3 配位数:8 配位数越大,原子排列 越紧密。
四、金属晶体中的晶面和晶向
Z
c
b a
晶面─晶体点阵中,通 过阵点的任一平面,代 Y 表晶体的原子平面,称 为晶面。
第1章 金属的晶体结构
1.1 金属 1.2 金属的晶体结构 1.3 实际金属的晶体结构
本章重点与难点
• ①金属键;建立金属原子的结构模型 。 • ②建立晶格和晶胞的概念;最常见的晶体结构:
体心立方结构、面心立方结构、密排六方结构; 立方晶系的晶向指数和晶面指数。 • ③晶体中存在的缺陷:点缺陷、线缺陷(位错)、 面缺陷。
晶胞的棱边长度一般称为晶格常数或点阵常数,用a、b、 c表示。晶胞的棱间夹角叫轴间夹角。用α、β、γ表示。
2、七大晶系和十四种布拉菲点阵
依据空间点阵的基本特点划分为七大晶系:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢ 重点掌握金属材料的晶体结构、晶体缺陷和合金的结构,
2020/10/28
2
精品资料
1.1 金属简介
❖ 学习目标: ➢ 根据金属键的本质,解释固态金属的一些特性—导
电性、正的电阻温度系数、传热性及延展性等) ➢ 利用双原子作用模型,分析两个原子间的相互作用
(P3的图1-2)
2020/10/28
4
❖ 晶体结构:晶体中原子(离子或分子)规则排列的 方式。
❖ 晶格:通过金属原子(离子)的中心划出许多空间直线,由这些
直线形成的空间格架。(假想的格架)
❖ 晶格的结点:金属原子(或离子)平衡中心的位置。
2020/10/28
6
晶体
晶格
1.2 金属的晶体结构 –2 晶体结构与空间点阵(2)
❖ 晶胞unit cell :反映晶格特征的最小组成单元。
或 r原= 子 43a
a4r原子 3
2020/10/28
12
BCC –Page5/5
(5)间隙半径 若在晶胞空隙中放入刚性球, 则能放入球 的最大半径为空隙半径。
体心立方晶胞中有两种间隙:
四面体间隙半径为: r四=0.29r原子;八面体间隙半径为: r八=0.15r原子
2020/10/28
13
(2) 面心立方结构 (FCC晶格) –Page1/4
2020/10/28
或 r原= 子 43a
a4r原子 3
11
BCC –Page4/5
(4)致密度(APF) 晶胞中所包含的原子所占有的体 积与该晶胞体积之比 (也称密排系数)。 致密度越大, 原子排列紧密程度越大。
格)中有68%的体积被原子所占据, 其余 为空隙。式中:
立方晶格的配位数为8。配位数越大, 原子排列紧密程度就越大。
2020/10/28
10
BCC –Page3/5
(3)原子半径 晶胞中相距最近的两个原子之间距离的 一半, 或晶胞中原子密度最大的方向上相邻两原子之间 距离的一半称为原子半径(r原子)。 体心立方晶胞中原子相距最近的方向是体对角线, 所以 原子半径与晶格常数a之间的关系为:
晶胞在三维空间的重复排列构成晶格。 晶胞的基本特性反映晶体结构(晶格)的特点。
❖ 晶胞的几何特征:六个参数来描述
三条棱边长a、b、c(晶格常数) 三条棱边之间的夹角α、β、γ。
❖ 金属的晶格常数一般为:
1×10-10 m~7×10-10 m。
❖ 不同元素组成的金属晶体因晶格形式及晶格常数不同,
其物理、化学和力学性能也不同。
2
1
3
4
c6 7
5
8
2 1
3 4
c
6 5
7 8
体心立方晶胞原子排列
Eg2.020/钼10/2(8 Mo)、钨(W)、钒(V)、α-铁(α-Fe, <912 ℃) 9
BCC –Page2/5
❖ 体心立方晶胞特征:
(1)晶格常数 lattice constants a=b=c, α=β=γ=90°
(2)晶胞原子数 The number of the atoms belonging to one unit cell ---2个
(每个角上的原子在晶格中同时属于8个相邻的晶胞,因而每个
角上的原子属于一个晶胞仅为1/8, 而中心的那个原子则完全
属于这个晶胞。)
(3)原子半径 atomic radius
(4)致密度 atomic packing factor (APF)---0.68
(5)空隙半径 gap radius
(6)配位数 coordination number—最近邻等距离原子数,体心
1.2 金属的晶体结构 –1 晶体的特性
❖ 规则排列; ❖ 各向异性; ❖ 一定条件下晶态与非晶态可以互换。
2020/10/28
5
1.2 金属的晶体结构 –2 晶体结构与空间点阵(1)
材料性能取决于材料的化学成分和其内部的组织结构
Processing
Structure
Properties
Performance
(6)空隙半径
四面体空隙半径为: r四=0.225r原子 八面体空隙半径为: r八=0.414r原子
2020/10/28
17
(3)密排六方结构(HCP晶格)—Page1/2
❖ 原子排列:十二个金属原子分布在六方体的十二个角上, 在上下 底面的中心各分布一个原子, 上下底面之间均匀分布三个原子。
❖ 金属的晶体结构可用X射线(X-ray)结构分析技术进行测定。
2020/10/28
7
1.2 金属的晶体结构 –3 三种典型的晶体结构
❖ 体心立方晶格(胞) Body-Centered Cubic (B.C.C.晶格) ❖ 面心立方晶格(胞) Face-Centered Cubic (F.C.C.晶格) ❖ 密排六方晶格(胞) Hexagonal Close-Packed (H.C.P.晶格)
提示:
✓由于原子排列紧密程度不一样,当金属从面心立方晶格向体心 立方晶格转变时, 体积会发生变化。
✓钢在淬火时因相变而发生体积变化的原因。
✓不同晶体结构中原子排列的方式不同, 将会使它们的形变能 力不同。
2020/10/28
8
(1) 体心立方结构 (BCC晶格) –Page1/5
❖ 原子排列: 八个原子分别处于立方体的八个角上,一个原子 处于立方体的中心, 角上八个原子与中心原子紧靠一起。
❖ 面心立方晶胞特征:
(1)晶格常数 a=b=c, α=β=γ=90° (2)晶胞原子数 (个)
➢
2020/10/28
15
FCC –Page3/4
(3)原子半径 r原子
2 a or 4
a2r原子 2
(4)致密度 0.74 (74%)
(5)配位数 12
2020/10/28
16
FCC –Page4/4
金属学及热处理 材控101及102
2020/10/28
1
金属学及热处理--第一章
第一章 金属的晶体结构
❖ 内容提要: ➢ 本章介绍金属材料的结构与组织,包括
➢ 金属简介 (原子的结构特点、金属键的本质、结合力与结 合能)
➢ 纯金属的晶体结构 ➢ 晶体缺陷和合金的结构 ➢ 金属材料的组织。
❖ 学习目标:
❖ 原子排列:金属原子分布在立方体的八个角上和六个面的 中心。面中心的原子与该面四个角上的原子紧靠。
❖ 铝(Al)、铜(Cu)、镍(Ni)、金(Au)、银(Ag)、γ- 铁( γ-Fe, 912 ℃~1394 ℃)等具有这种晶格。
2020/10/28
14
面心立方晶胞原子排列
FCC –Page2/4
2020/10/28
2
精品资料
1.1 金属简介
❖ 学习目标: ➢ 根据金属键的本质,解释固态金属的一些特性—导
电性、正的电阻温度系数、传热性及延展性等) ➢ 利用双原子作用模型,分析两个原子间的相互作用
(P3的图1-2)
2020/10/28
4
❖ 晶体结构:晶体中原子(离子或分子)规则排列的 方式。
❖ 晶格:通过金属原子(离子)的中心划出许多空间直线,由这些
直线形成的空间格架。(假想的格架)
❖ 晶格的结点:金属原子(或离子)平衡中心的位置。
2020/10/28
6
晶体
晶格
1.2 金属的晶体结构 –2 晶体结构与空间点阵(2)
❖ 晶胞unit cell :反映晶格特征的最小组成单元。
或 r原= 子 43a
a4r原子 3
2020/10/28
12
BCC –Page5/5
(5)间隙半径 若在晶胞空隙中放入刚性球, 则能放入球 的最大半径为空隙半径。
体心立方晶胞中有两种间隙:
四面体间隙半径为: r四=0.29r原子;八面体间隙半径为: r八=0.15r原子
2020/10/28
13
(2) 面心立方结构 (FCC晶格) –Page1/4
2020/10/28
或 r原= 子 43a
a4r原子 3
11
BCC –Page4/5
(4)致密度(APF) 晶胞中所包含的原子所占有的体 积与该晶胞体积之比 (也称密排系数)。 致密度越大, 原子排列紧密程度越大。
格)中有68%的体积被原子所占据, 其余 为空隙。式中:
立方晶格的配位数为8。配位数越大, 原子排列紧密程度就越大。
2020/10/28
10
BCC –Page3/5
(3)原子半径 晶胞中相距最近的两个原子之间距离的 一半, 或晶胞中原子密度最大的方向上相邻两原子之间 距离的一半称为原子半径(r原子)。 体心立方晶胞中原子相距最近的方向是体对角线, 所以 原子半径与晶格常数a之间的关系为:
晶胞在三维空间的重复排列构成晶格。 晶胞的基本特性反映晶体结构(晶格)的特点。
❖ 晶胞的几何特征:六个参数来描述
三条棱边长a、b、c(晶格常数) 三条棱边之间的夹角α、β、γ。
❖ 金属的晶格常数一般为:
1×10-10 m~7×10-10 m。
❖ 不同元素组成的金属晶体因晶格形式及晶格常数不同,
其物理、化学和力学性能也不同。
2
1
3
4
c6 7
5
8
2 1
3 4
c
6 5
7 8
体心立方晶胞原子排列
Eg2.020/钼10/2(8 Mo)、钨(W)、钒(V)、α-铁(α-Fe, <912 ℃) 9
BCC –Page2/5
❖ 体心立方晶胞特征:
(1)晶格常数 lattice constants a=b=c, α=β=γ=90°
(2)晶胞原子数 The number of the atoms belonging to one unit cell ---2个
(每个角上的原子在晶格中同时属于8个相邻的晶胞,因而每个
角上的原子属于一个晶胞仅为1/8, 而中心的那个原子则完全
属于这个晶胞。)
(3)原子半径 atomic radius
(4)致密度 atomic packing factor (APF)---0.68
(5)空隙半径 gap radius
(6)配位数 coordination number—最近邻等距离原子数,体心
1.2 金属的晶体结构 –1 晶体的特性
❖ 规则排列; ❖ 各向异性; ❖ 一定条件下晶态与非晶态可以互换。
2020/10/28
5
1.2 金属的晶体结构 –2 晶体结构与空间点阵(1)
材料性能取决于材料的化学成分和其内部的组织结构
Processing
Structure
Properties
Performance
(6)空隙半径
四面体空隙半径为: r四=0.225r原子 八面体空隙半径为: r八=0.414r原子
2020/10/28
17
(3)密排六方结构(HCP晶格)—Page1/2
❖ 原子排列:十二个金属原子分布在六方体的十二个角上, 在上下 底面的中心各分布一个原子, 上下底面之间均匀分布三个原子。
❖ 金属的晶体结构可用X射线(X-ray)结构分析技术进行测定。
2020/10/28
7
1.2 金属的晶体结构 –3 三种典型的晶体结构
❖ 体心立方晶格(胞) Body-Centered Cubic (B.C.C.晶格) ❖ 面心立方晶格(胞) Face-Centered Cubic (F.C.C.晶格) ❖ 密排六方晶格(胞) Hexagonal Close-Packed (H.C.P.晶格)
提示:
✓由于原子排列紧密程度不一样,当金属从面心立方晶格向体心 立方晶格转变时, 体积会发生变化。
✓钢在淬火时因相变而发生体积变化的原因。
✓不同晶体结构中原子排列的方式不同, 将会使它们的形变能 力不同。
2020/10/28
8
(1) 体心立方结构 (BCC晶格) –Page1/5
❖ 原子排列: 八个原子分别处于立方体的八个角上,一个原子 处于立方体的中心, 角上八个原子与中心原子紧靠一起。
❖ 面心立方晶胞特征:
(1)晶格常数 a=b=c, α=β=γ=90° (2)晶胞原子数 (个)
➢
2020/10/28
15
FCC –Page3/4
(3)原子半径 r原子
2 a or 4
a2r原子 2
(4)致密度 0.74 (74%)
(5)配位数 12
2020/10/28
16
FCC –Page4/4
金属学及热处理 材控101及102
2020/10/28
1
金属学及热处理--第一章
第一章 金属的晶体结构
❖ 内容提要: ➢ 本章介绍金属材料的结构与组织,包括
➢ 金属简介 (原子的结构特点、金属键的本质、结合力与结 合能)
➢ 纯金属的晶体结构 ➢ 晶体缺陷和合金的结构 ➢ 金属材料的组织。
❖ 学习目标:
❖ 原子排列:金属原子分布在立方体的八个角上和六个面的 中心。面中心的原子与该面四个角上的原子紧靠。
❖ 铝(Al)、铜(Cu)、镍(Ni)、金(Au)、银(Ag)、γ- 铁( γ-Fe, 912 ℃~1394 ℃)等具有这种晶格。
2020/10/28
14
面心立方晶胞原子排列
FCC –Page2/4
