初二动点问题(非常经典)

合集下载

初二几何之动点问题知识讲解

初二几何之动点问题中考数学动点几何问题※动点求最值:两定一动型（“两个定点，一个动点”的条件下求最值。

例如上图中直线l 的同侧有两个定点A 、B,在直线l 上有一动点）例1、以正方形为载体如图，正方形ABCD 的面积为12，△ABE 是等边三角形，点E 在正方形内，在对角线AC 上有一动点P ，使PD+PE 的值最小，则其最小值是例2、以直角梯形为载体如图，在直角梯形中，AD ∥BC ，AB ⊥BC,AD=2，BC=DC=5，点P 在BC 上移动，当PA+PD 取得最小值时，△APD 中AP 边上的高为一定两动型（“一个定点”+“两个动点”）例3、以三角形为载体如图，在锐角△ABC 中，AB=4√2，∠BAC=45°，∠BAC 的平分线交BC 于点D,M 、N 分别是AD 、AB 上的动点，则BM+MN 的最小值是例4、以正方形、圆、角为载体正方形ABCD 的边长为2，E 为AB 的中点，P 是AC 上的一动点.连接BP ，EP ，则PB+PE 的最小值是例5、⊙O 的半径为2，点A 、B 、C 在⊙O 上，OA ⊥OB, ∠AOC=60°，P 是OB 上的一动点，PA+PC 的最小值是例6、如图，∠AOB=45°，P 是∠AOB 内一点，PO=10，Q 、R 分别是OA 、OB 上的动点，求△PQR 周长的最小值是 .例7：在△ABC 中，∠B=60°,BA=24CM,BC=16CM,(1)求△ABC 的面积；(2)现有动点P 从A 点出发，沿射线AB 向点B 方向运动，动点Q 从C 点出发，沿射线CB 也向点B 方向运动。

如果点P 的速度是4CM/秒，点Q 的速度是2CM/秒，它们同时出发，几秒钟后，△PBQ 的面积是△ABC 的面积的一半？ (3)在第（2）问题前提下，P,Q 两点之间的距离是多少？A例8：如图（3），在梯形中，厘米，厘米，的坡度动点从出发以2厘米/秒的速度沿方向向点运动，动点从点出发以3厘米/秒的速度沿方向向点运动，两个动点同时出发，当其中一个动点到达终点时，另一个动点也随之停止．设动点运动的时间为秒．（1）求边的长；（2）当为何值时，与相互平分；（3）连结设的面积为求与的函数关系式，求为何值时，有最大值？求最大值？※动点构成特殊图形例9、如图，在Rt ABC △中，9060ACB B ∠=∠=°，°，2BC =．点O 是AC 的中点，过点O 的直线l 从与AC 重合的位置开始，绕点O 作逆时针旋转，交AB 边于点D ．过点C 作CE AB ∥交直线l 于点E ，设直线l 的旋转角为α．（1）①当α= 度时，四边形EDBC 是等腰梯形，此时AD 的长为；②当α= 度时，四边形EDBC 是直角梯形，此时AD 的长为；（2）当90α=°时，判断四边形EDBC 是否为菱形，并说明理由．ABCD 906DC AB A AD ∠==∥，°，4DC =BC 34i =∶，P A AB B Q B B C D →→D t BC t PC BQ PQ ，PBQ △y ，y t t y 图精品文档B（备用例10、如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，，60B =︒∠. （1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①当点N 在线段AD 上时（如图2），PMN △的形状是否发生改变？若不变，求出PMN △的周长；若改变，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由.例11、数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=o ，且EF 交正方形外角DCG ∠的平分线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请A D EB FC 图4 ADE BF C 图5A D E B F C 图图A D E B F C P N M 图A D EB F CP N M （第25说明理由．例12、如图，在Rt △ABC 中，∠B =90°，BC，∠C =30°.点D 从点C 出发沿CA 方向以每秒2个单位长的速度向点A 匀速运动，同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D 、E 运动的时间是t 秒（t ＞0）.过点D 作DF ⊥BC 于点F ，连接DE 、EF .（1）求证：AE =DF ；（2）四边形AEFD 能够成为菱形吗？如果能，求出相应的t 值；如果不能，说明理由. （3）当t 为何值时，△DEF 为直角三角形？请说明理由.※利用函数与方程的思想和方法将所解决图形的性质（或所求图形面积）直接转化为函数或方程。

初二数学动点练习题

初二数学动点练习题1. 直线上的动点问题- 题目：在直线AB上，点C是动点，当点C沿着直线AB移动时，求证∠ACB是一个恒定的角度。

2. 圆上的动点问题- 题目：圆O的半径为5，点P是圆上的动点。

求证：无论点P在圆上如何移动，OP的长度始终为5。

3. 动点与线段的关系- 题目：线段AB的长度为10，点C是线段AB上的动点。

当点C从A向B移动时，求线段AC的长度与线段BC的长度之和是否恒定。

4. 动点与三角形的面积- 题目：三角形ABC的面积为30平方单位，点D是边AB上的动点。

求证：无论点D在AB上如何移动，三角形ACD的面积始终是三角形ABC面积的一半。

5. 动点与平行四边形的对角线- 题目：平行四边形ABCD中，点E是边AB上的动点，点F是边CD 上的动点，且EF始终是平行四边形的对角线。

求证：无论点E和点F如何移动，EF的长度始终等于AB和CD的长度之和。

6. 动点与圆的切线- 题目：圆O的半径为6，点P是圆O外的一点，点Q是圆O上的动点。

当点Q沿着圆O移动时，求证：点P到圆O的切线长度始终等于点P到点Q的距离。

7. 动点与相似三角形- 题目：三角形ABC与三角形DEF相似，点G是三角形ABC的动点，点H是三角形DEF的动点，且GH始终是三角形ABC和三角形DEF的对应边的平行线。

求证：无论点G和点H如何移动，三角形AGH与三角形DEF始终相似。

8. 动点与坐标系- 题目：在平面直角坐标系中，点A的坐标为(2,3)，点B的坐标为(5,6)。

点C是线段AB上的动点，其坐标为(x,y)。

求证：无论点C如何移动，x和y的和始终等于点A和点B坐标的和。

练习题答案提示：- 对于直线上的动点问题，可以利用角度的恒定性，结合直线的性质来证明。

- 对于圆上的动点问题，可以利用圆的半径性质来证明。

- 对于动点与线段的关系问题，可以利用线段长度的加法性质来证明。

- 对于动点与三角形的面积问题，可以利用三角形面积的计算公式来证明。

初二动点题经典例题

初二动点题经典例题篇一：标题：初二动点题经典例题正文:在初中数学中，动点问题是一个较为重要的知识点。

特别是在初二阶段，同学们需要掌握动点问题的基本概念、解题方法和技巧。

今天，我们将分享一些初二动点题的经典例题，希望能够帮助同学们更好地理解和掌握动点问题的解题方法。

例题 1: 已知圆心为 O、半径为 2 的圆与 x 轴正半轴交于 A，与 y 轴负半轴交于 B，点 C 在 x 轴正半轴上，点 D 在 y 轴正半轴上，CD⊥AB，问 CD 长度是否等于圆心角 AOB 的平分线弧长？解析：本题是一道圆与轴的交点问题。

根据圆的性质可知，圆心 O 是线段 AB 的中点，因此 CD 长度等于半径 2 的一半，即 CD=1。

此外，圆心角 AOB 的平分线弧长即为半径 2，因此 CD 长度等于圆心角 AOB 的平分线弧长。

拓展：在本题中，如果我们将 CD 的长度设为 x，则可以列出方程:x2 = 4(12 - x2)。

通过解方程，我们可以得到 x = 1，即 CD 的长度等于 1。

此外，在本题中，我们还利用了圆的性质，即圆心 O 是线段 AB 的中点，因此 CD 是线段 AB 的一半。

这种利用圆的性质求解动点问题的方法，在初中数学中是非常常见的。

例题 2: 已知点 P(x,y) 是圆 C:x2 + y2 = 4 圆上任意一点，圆 C 与 x 轴正半轴交于 A，与 y 轴负半轴交于 B，点 C 在 x 轴正半轴上，点 D 在 y 轴正半轴上，CD⊥AB，问 CD 长度是否等于圆 C 的半径？解析：本题是一道圆与轴的交点问题。

根据圆的性质可知，圆 C 的圆心 O 是线段 AB 的中点，因此 CD 长度等于半径 2 的一半，即 CD=1/2。

此外，圆 C 与x 轴正半轴交于 A，与 y 轴负半轴交于 B，因此 CD 的长度等于圆 C 所对的圆心角 AOB 的平分线弧长。

拓展：在本题中，如果我们将 CD 的长度设为 x，则可以列出方程:x2 = 4(12 - x2)。

初二动点问题

1、在矩形ABCD中，BC=16，DC=12，动点P从动点D出发，在线段DA上以每秒2的速度运动，动点Q从点C出发，在线段BC上以每秒1的速度向B运动，两点同时出发，当P运动到A时，点Q也随即停止运动，设运动时间为t
（1）设△BPQ的面积为S，求S与t的函数关系式
2.是否存在时刻t，使得PQ平分BD？若存在，求出t的值
3.当t为何值时，以BPQ三点为顶点的三角形是等腰三角形
2、如图，梯形ABCD中，AB‖CD，AB=24cm，DC=10cm，点P和Q同时分别从D、B出发，P由D向C运动，速度为每秒1cm，点Q由B向A运动，速度为每秒3cm，试求几秒后，P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形？。

初二动点题经典例题

初二动点题经典例题1. 一个匀速运动的点A，从时刻t1=0开始，以速度v1=20m/s向右匀速运行，另一个点B，从时刻t2=3s开始，以速度v2=30m/s向左匀速运动。

已知AB的距离为50m。

在何时和何处两点相遇？解析：假设两点在时刻t相遇，此时A和B的距离为50m，即20t=50-30(t-3)，解得t=4s，代入任意一个点的运动方程，得到相遇点的位置为A：80m处，B：-30m处。

2. 一个小球从山顶垂直落下，同时一架小飞机从山顶正东方向以恒定的速度飞行，计划以恰好与小球在同一位置。

假设小球到达地面时，小飞机飞行距离为5000m，小球落地时间为5s，小飞机速度为300m/s，请问小飞机飞行的距离和时间。

解析：小球落地时间为5s，根据重力加速度为9.8m/s^2，可以求出小球落地时的速度v=49m/s，所以小球垂直落下的高度为h=1/2×g×t^2=122.5m。

小飞机在水平方向的速度为300m/s，所以小飞机需要飞行的时间为122.5/300=0.408s，小飞机飞行的距离为0.408×300=122.4m。

3. 一个小球从高50米的平台上自由落下，同时在离这个平台250米的地面上有一个接力棒接球手张三，假设张三向上抛接球时的初速度为5m/s，小球和张三同时开始运动，请问小球和张三在哪个时刻相遇？解析：首先计算小球自由落体运动到地面的时间t1=sqrt(2h/g)=3.19s，再根据张三所在位置与小球落地位置的距离和张三抛球的速度，计算出张三抛球到小球落地位置所需的时间t2=25s，因此小球和张三的距离一开始是250+50=300m，小球下落的距离为1/2*g*t1^2=784.5m，因此当小球运动了t=t2-t1=21.81s时，它的位置离地面为300-784.5+1/2*g*t^2=-215.09m，可以得到张三和小球在21.81s时相遇。

初二数学动点问题练习(含答案)

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q分别从A，C同时出发，设移动时间为t秒。

当t= 时，四边形是平行四边形；6当t= 时，四边形是等腰梯形. 82、如图2，正方形ABCD的边长为4，点M在边DC上，且DM=1，N为对角线AC上任意一点，则DN+MN的最小值为 53、如图，在Rt ABC△中，9060ACB B∠=∠=°，°，2BC=．点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE AB∥交直线l于点E，设直线l的旋转角为α．（1）①当α=度时，四边形EDBC是等腰梯形，此时AD的长为；②当α=度时，四边形EDBC是直角梯形，此时AD的长为；（2）当90α=°时，判断四边形EDBC是否为菱形，并说明理由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC是菱形.∵∠α=∠ACB=900，∴BC//ED. ∵CE//AB, ∴四边形EDBC是平行四边形在Rt△ABC中，∠ACB=900，∠B=600,BC=2, ∴∠A=300.∴AB=4,AC∴AO=12AC.在Rt△AOD中，∠A=300，∴AD=2.∴BD=2. ∴BD=BC. 又∵四边形EDBC是平行四边形，∴四边形EDBC是菱形4、在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.（备用图）CBED图1NMA BCDEMN图2ACBEDNM图3(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE=AD ＋BE ； (2)当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明. 解：（1）① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB② ∵△ADC ≌△CEB ∴CE=AD ，CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ，CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时，DE=BE-AD(或AD=BE-DE ，BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ，又∵AC=BC ， ∴△ACD ≌△CBE ， ∴AD=CE ，CD=BE ， ∴DE=CD-CE=BE-AD.5、数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．解：（1）正确．证明：在AB 上取一点M ，使AM EC =，连接ME ． BM BE ∴=．45BME ∴∠=°，135AME ∴∠=°． CF 是外角平分线，45DCF ∴∠=°，135ECF ∴∠=°． AME ECF ∴∠=∠． 90AEB BAE ∠+∠=°，90AEB CEF ∠+∠=°， ∴BAE CEF ∠=∠． AME BCF ∴△≌△（ASA ）． AE EF ∴=．（2）正确．证明：在BA 的延长线上取一点N ．使AN CE =，连接NE ．BN BE ∴=． 45N PCE ∴∠=∠=°．四边形ABCD 是正方形， AD BE ∴∥． DAE BEA ∴∠=∠． NAE CEF ∴∠=∠．ANE ECF ∴△≌△（ASA ）． AE EF ∴=．6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动，设P 的运动时间为t. 求（1）△ PAB 为等腰三角形的t 值；（2）△ PAB 为直角三角形的t 值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△ PAB 为直角三角形的t 值AD FC G E B 图1 AD FG B 图3A D FC GE B 图2A D F C GB M A D FC G B N7、如图1，在等腰梯形ABCD中，AD BC∥，E是AB的中点，过点E作EF BC∥交CD于点F．46AB BC==，，60B=︒∠.求：（1）求点E到BC的距离；（2）点P为线段EF上的一个动点，过P作PM EF⊥交BC于点M，过M作MN AB∥交折线ADC 于点N，连结PN，设EP x=.①当点N在线段AD上时（如图2），P M N△的形状是否发生改变？若不变，求出PMN△的周长；若改变，请说明理由；②当点N在线段DC上时（如图3），是否存在点P，使PMN△为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由解（1）如图1，过点E作EG BC⊥于点G．∵E为AB的中点，∴122BE AB==．在Rt EBG△中，60B=︒∠，∴30BEG=︒∠．∴112BG BE EG====，A DEBFC图4（备用）A DEBFC图5（备用）A DEBFC图1 图2A DEBFCPNM图3A DEBFCPNM（第25题）即点E 到BC（2）①当点N 在线段AD 上运动时，PMN △的形状不发生改变． ∵PM EF EG EF ⊥⊥，， ∴PM EG ∥． ∵EF BC ∥， ∴EP GM =，PM EG == 同理4MN AB ==．如图2，过点P 作PH MN ⊥于H ，∵MN AB ∥，∴6030NMC B PMH ==︒=︒∠∠，∠．∴12PH PM == ∴3cos302MH PM =︒=．则35422NH MN MH =-=-=．在Rt PNH △中，PN === ∴PMN △的周长=4PM PN MN ++=．②当点N 在线段DC 上运动时，PMN △的形状发生改变，但MNC △恒为等边三角形．当PM PN =时，如图3，作PR MN ⊥于R ，则MR NR =．类似①，32MR =．∴23MN MR ==． ∵MNC △是等边三角形，∴3MC MN ==．此时，6132x EP GM BC BG MC ===--=--=．当MP MN =时，如图4，这时MC MN MP ===此时，615x EP GM ===-= 当NP NM =时，如图5，30NPM PMN ==︒∠∠．则120PMN =︒∠，又60MNC =︒∠， ∴180PNM MNC +=︒∠∠．因此点P 与F 重合，PMC △为直角三角形． ∴tan301MC PM =︒=．此时，6114x EP GM ===--=．综上所述，当2x =或4或(5-时，PMN △为等腰三角形．8、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点．(1）如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动图3A D E BFCPN M 图4A D EBF CP MN 图5A DEBF （P ） CM NGGRG图1A D EBF CG 图2A D EBFCPNMG H①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由； ②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒， ∴313BP CQ ==⨯=厘米， ∵10AB =厘米，点D 为AB 的中点， ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米， ∴835PC =-=厘米， ∴PC BD =．又∵AB AC =， ∴B C ∠=∠， ∴BPD CQP △≌△． ②∵P Qv v ≠， ∴BP CQ ≠，又∵BPD CQP △≌△，B C ∠=∠，则45BP PC CQ BD ====，，∴点P ，点Q 运动的时间433BP t ==秒， ∴515443Q CQ v t===厘米/秒。

(完整版)初二动点问题(含答案)

动态问题一、所谓“动点型问题”是指题设图形中存在一个或多个动点，它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键：动中求静.数学思想：分类思想数形结合思想转化思想类型：1。

利用图形想到三角形全等，相似及三角函数2.分析题目，了解有几个动点，动点的路程,速度(动点怎么动)3.结合图形和题目,得出已知或能间接求出的数据4。

分情况讨论,把每种可能情况列出来，不要漏5.动点一般在中考都是压轴题，步骤不重要，重要的是思路6。

动点类题目一般都有好几问，前一问大都是后一问的提示,就像几何探究类题一样，如果后面的题难了，可以反过去看看前面问题的结论二、例题：1、如图1,梯形ABCD中，AD∥ BC，∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q分别从A，C同时出发，设移动时间为t秒。

当t= 时,四边形是平行四边形；当t= 时,四边形是等腰梯形.2、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1，N为对角线AC上任意一点,则DN+MN的最小值为．的长为；的长为 ;4、在△ABC中，∠ACB=90°，AC=BC,直线MN经过点C，且AD⊥MN于D，BE⊥MN于E。

(1)当直线MN绕点C旋转到图1的位置时,求证：①△ADC≌△CEB；②DE=AD＋BE；（2)当直线MN绕点C旋转到图2的位置时,求证：DE=AD—BE；(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明.5、数学课上，张老师出示了问题:如图1，四边形ABCD是正方形，点E是边BCEFCF于点F，求证：AE=EF．AB的中点M,连接ME,则AM=EC在此基础上，同学们作了进一步的研究：(1）小颖提出：如图2，如果把“点E是边BC的中点"改为“点E是边BC上(除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由;（2）小华提出：如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确,请说明理由．ACBAED图1NMA BCDEMN图2ACBEDNM图36、如图，射线MB上，MB=9，A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB方向以1个单位/秒的速度移动，设P的运动时间为t.求（1）△ PAB为等腰三角形的t值；(2)△ PAB为直角三角形的t值；（3）若AB=5且∠ABM=45 °,其他条件不变，直接写出△ PAB为直角三角形的t值（1）如果点P在线段BC上以3cm/s的速度由B点向CCA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等，经过1②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时，能（2）若点Q以②中的运动速度从点C来的运动速度从点B边运动,求经过多长时间点P与点Q第一次哪条边上相遇?A DFC GEB图1A DFC GEB图3A DFC GEB图2。

八年级数学上学期之动点问题(精品)

八年级数学动点问题拔高练习1、如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC=60°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方。

〔1〕将图1中的三角板绕点O顺时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；〔2〕将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为_________秒〔直接写出结果〕；〔3〕将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由。

2、已知AB∥CD，直线l与AB、CD分别交于点E、F，点P是直线CD上的一个动点〔点P不与F重合〕，点M在EF上，且∠FMP=∠FPM，〔1〕如图1，当点P在射线FC上移动时，若∠AEF=60°，则∠FPM=_________；假设∠AEF=a，则∠FPM=_________；〔2〕如图2，当点P在射线FD上移动时，猜想∠FPM与∠AEF有怎样的数量关系？请你说明理由。

3、如图〔1〕直线GC ∥HD ，EF 交CG 、HD 于A 、B ，三条直线把EF 右侧的平面分成①、②、③三个区域，〔规定：直线上各点不属于任何区域〕．将一个透明的直角三角尺放置在该图中，使得30°角〔即∠P 〕的两边分别经过点A 、B ，当点P 落在某个区域时，连接PA 、PB ，得到∠PBD 、∠PAC 两个角．〔1〕如图〔1〕，当点P 落在第②区域时，求∠PAC+∠PBD 的度数；〔2〕如图〔2〕，当点P 落在第③区域时，∠PAC ﹣∠PBD=_________度〔3〕如图〔3〕，当点P 落在第①区域时，直接写出∠PAC 、∠PBD 之间的等量关系。

4、操作示例如图1，△ABC 中，AD 为BC 边上的中线，则S △ABD =S △ADC ．实践探究〔1〕在图2中，E 、F 分别为矩形ABCD 的边AD 、BC 的中点，则S 阴和S 矩形ABCD 之间满足的关系式为_________〔2〕在图3中，E 、F 分别为平行四边形ABCD 的边AD 、BC 的中点，则S 阴和S 平行四边形ABCD 之间满足的关系式为_________；〔3〕在图4中，E 、F 分别为任意四边形ABCD 的边AD 、BC 的中点，则S 阴和S 四边形ABCD 之间满足的关系式为_________；解决问题：〔4〕在图5中，E 、G 、F 、H 分别为任意四边形ABCD 的边AD 、AB 、BC 、CD 的中点，并且图中阴影部分的面积为20平方米，求图中四个小三角形的面积和，即S 1+S 2+S 3+S 4=_________。

完整版)八年级下册数学期末考试常见动点问题

完整版)八年级下册数学期末考试常见动点问题1、在梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm。

动点P从点A开始，沿AD边，以1厘米/秒的速度向点D运动；动点Q从点C开始，沿CB边，以3厘米/秒的速度向B点运动。

已知P、Q两点分别从A、C同时出发，当其中一点到达端点时，另一点也随之停止运动。

求：1）t为何值时，四边形PQCD是平行四边形？2）在某个时刻，四边形PQCD可能是菱形吗？为什么？3）t为何值时，四边形PQCD是直角梯形？4）t为何值时，四边形PQCD是等腰梯形？2、在矩形ABCD中，AB=20cm，BC=4cm，点P从A开始沿折线A—B—C—D以4cm/s的速度运动，点Q从C开始沿CD边1cm/s的速度移动。

如果点P、Q分别从A、C同时出发，当其中一点到达点D时，另一点也随之停止运动。

设运动时间为t(s)，求t为何值时，四边形APQD也为矩形？3、在等腰梯形ABCD中，AB∥DC，AD=BC=5cm，AB=12cm，CD=6cm，点P从A开始沿AB边向B以每秒3cm 的速度移动，点Q从C开始沿CD边向D以每秒1cm的速度移动。

如果点P、Q分别从A、C同时出发，当其中一点到达终点时运动停止。

设运动时间为t秒，求：1）证明当t=3时，四边形APQD是平行四边形；2）是否存在t使得PQ平分对角线BD？若存在，求出此时的t；若不存在，说明理由；3）若△DPQ是以PQ为腰的等腰三角形，求t的值。

4、在四边形ABCD中，AD∥BC，且AD>BC，BC=6cm，P、Q分别从A、C同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C向B运动。

几秒后四边形ABQP是平行四边形？5、已知：△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动。

初二动点问题(含标准答案)

初二动点问题（含答案）作者:日期: 2动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点，它们在线段、射线或弧线上运动的一类开放性题目•解决这类问题的关键是动中求静，灵活运用有关数学知识解决问题•关键：动中求静•数学思想：分类思想数形结合思想转化思想1、如图1,梯形ABCD 中，AD // BC,/ B=90 ° , AB=14cm,AD=18cm,BC=21cm,点P 从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P, Q分别从A , C同时出发，设移动时间为t秒。

当t= _____ 时，四边形是平行四边形；6当t= _____ 时，四边形是等腰梯形• 82、如图2,正方形ABCD的边长为4,点M在边DC上，且DM=1 , N为对角线AC上任意一点，则DN+MN的最小值为_________ 53、如图，在只也ABC中，ACB 90°, B 60°, BC 2•点°是AC的中点，过点°的直线l从与AC重合的位置开始，绕点°作逆时针旋转，交AB边于点D •过点C作2CE // AB 交直线I 于点E ，设直线I 的旋转角为(1)①当度时，四边形EDBC 是等腰梯形，此时AD 的长为②当度时，四边形EDBC 是直角梯形，此时 AD 的长为(2)当 90°时，判断四边形 EDBC 是否为菱形，并说明理由.解：(1 ［① 30, 1 :② 60, 1.5;(2)当/% =900时，四边形 EDBC 是菱形•v/a =/ACB=90°,「. BC//ED. T CE//AB,二四边形 EDBC 是平行四边形在 Rt △ABC 中，/ ACB=900,/ B=60°,BC=2, /./ A=30°.137AC3••• AB=4,AC=2 '3. ••• A°= 2 = 3 •在 Rt △ AOD 中，/ A=30,二 AD=2.B• BD=2. • BD=BC. 又•••四边形 EDBC 是平行四边形, •四边形EDBC 是菱形 4、C ,A(1) 当直线 MN 绕点C 旋转到图1的位置时，求证：①△ ADC ◎△ CEB •，②DE=AD + BE ;⑵当直线 MN 绕点C 旋转到图2的位置时，求证： DE=AD-BE ;⑶当直线MN 绕点C 旋转到图3的位置时，试问 DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明•解：(1 ［① •••/ ACD= / ACB=90 •••/ CAD+ / ACD=90 /-Z BCE+ / ACD=90•••/ CAD= Z BCE •/ AC=BCADC ◎△ CEB② •/△ ADC ◎△ CEB • CE=AD , CD=BE • DE=CE+CD=AD+BE(2) T Z ADC= Z CEB= Z ACB=90°ACD= Z CBE又 ■: AC=BCACD ◎△ CBE • CE=AD , CD=BE • DE=CE-CD=AD-BE(3) 当 MN 旋转至U 图 3 的位置时，DE=BE-AD(或 AD=BE-DE , BE=AD+DE 等)•/Z ADC= Z CEB= Z ACB=90° /Z ACD= Z CBE , 又 ■: AC=BC ,ACD ◎△ CBE ,• AD=CE , CD=BE ,• DE=CD-CE=BE-AD.5、数学课上，张老师出示了问题：如图1,四边形ABCD 是正方形，点E 是边BC 的中点. AEF 90°,且EF 交正方形外角 DCG 的平行线CF 于点F ,求证：AE=EF.经过思考，小明展示了一种正确的解题思路：取AB 的中点 M 连接 ME 则 AM =EC,易证△ AME ECF ，所以 AE EF .在此基础上，同学们作了进一步的研究：(1 )小颖提出：如图2,如果把“点E 是边BC 的中点”改为“点 E 是边BC 上(除B, C 外)的任意一点”，其它条件不变，那么结论“ AE=EF'仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；(3) 若AB=5且Z ABM=45 °，其他条件不变，直接写出△ PAB 为直角三角形的t 值(2)小华提出：如图3，点E 是BC 的延长线上(除C 点外)的任意一点，其他条件不变，结论“AE=EF' 仍然成立.你认为小华的观点正确吗？如果正确，写出证明过程；解：(1)正确. 证明：在 AB 上取一点M ，使AM45°DCFBM BE . BME QCF 是外角平分线，AMEQ AEBBAE(2)正确.证明：在BA 的延长线上取一点 NBN BE . N PCEQ 四边形ABCD 是正方形， ADAE BEA . NAE △ ANEECF (ASA ). AE EF .ECF . BAE 90°， CEF . AEB△6、如图，射线MB 上,MB=9,A 是射线 MB 方向以1个单位/秒的速度移动，设求(PAB 为等腰三角形的t 值;MB 外一点,AB=5且A 到射线 P 的运动时间为t.(2)△ PAB 为直角三角形的t 值; 如果不正确，请说明理由. MB 的距离为3,动点P 从图沿射线2 ＞过P 作PG 丄IVIN 于G VMN/7AB^NM=NP过N 作NR 丄MP^R 则有：RM=0.5FM= V宀忑 J ：Rt ANMRM^RM- y MN=」CMV3 再A — {5・X j ■亍:、x=43。

(完整版)初二数学动点问题归类复习(含例题、练习及答案)

初二数学动点问题归类复习（含例题、练习及答案）所谓“动点型问题”是指题设图形中存在一个或多个动点, 它们在线段、射线或弧线上运动的一类开放性题目. 解决这类问题的关键是动中求静, 灵活运用有关数学知识解决问题.关键: 动中求静. 数学思想：分类思想数形结合思想转化思想本文将初一至二学习过的有关知识，结合动点问题进行归类复习，希望对同学们能有所帮助。

一、等腰三角形类：因动点产生的等腰三角形问题例1：（2013 年上海市虹口区中考模拟第25 题）如图1，在Rt△ABC 中，∠ A＝90°，AB＝6，AC ＝8，点 D 为边BC 的中点，DE⊥BC 交边AC 于点E，点P 为射线AB 上的一动点，点Q 为边AC 上的一动点，且∠ PDQ ＝90°．（1）求ED 、EC 的长；（2）若BP＝2，求CQ 的长；（3）记线段PQ与线段DE的交点为F，若△ PDF 为等腰三角形，求BP的长．思路点拨1．第（2）题BP＝ 2 分两种情况．2．解第（2）题时，画准确的示意图有利于理解题意，观察线段之间的和差关系．3．第（3）题探求等腰三角形PDF 时，根据相似三角形的传递性，转化为探求等腰三角形CDQ ．解答：（1）在Rt△ ABC 中，AB＝6，AC＝8，所以BC＝10．3 15 25在Rt△CDE 中，CD ＝5，所以ED CD tan C 5 ，EC ．4 4 4（2）如图2，过点 D 作DM⊥AB，DN⊥AC，垂足分别为M、N，那么DM、DN 是△ABC 的两条中位线，DM＝4，DN＝3．由∠ PDQ ＝90°，∠ MDN ＝90°，可得∠ PDM ＝∠ QDN ．因此△ PDM∽△ QDN．①如图3，当BP＝2，P在BM 上时，PM＝1．3 3 3 19此时QN 3PM 3．所以CQ CN QN 4 3 19．4 4 4 4②如图4，当BP＝2，P在MB 的延长线上时，PM＝5．所以PMQNDM 4．所以QN 3PM ，PM 4QN．DN 3 4 3图2图33 15 15 31此时QN 3PM 15．所以CQ CN QN 4 15 31．4444（3）如图5，如图2，在Rt △PDQ 中，tan QPD QD DN3PD DM4在Rt△ ABC 中，tan C BA 3BA 3．所以∠ QPD＝∠ C．CA 4由∠ PDQ ＝90°，∠ CDE ＝90°，可得∠ PDF＝∠ CDQ．因此△ PDF∽△ CDQ．当△ PDF 是等腰三角形时，△ CDQ 也是等腰三角形．①如图5，当CQ＝CD＝5时，QN＝CQ－CN＝5－4＝1（如图 3 所示）．4 4 4 5此时PM QN ．所以BP BM PM 3 ．3 3 3 3②如图6，当QC＝QD 时，由CH cosC CH，可得CQ5425 CQ25825所以QN＝CN－CQ＝4257（如图 2 所示）．8847此时PM QN ．所以BP BM PM 3 7253666③不存在DP＝DF 的情况．这是因为∠ DFP≥∠ DQP >∠ DPQ （如图5，图6所示）．图5 图 6考点伸展：如图6，当△ CDQ 是等腰三角形时，根据等角的余角相等，可以得到△BDP 也是等腰三25角形，PB＝PD ．在△ BDP 中可以直接求解BP ．6二、直角三角形：因动点产生的直角三角形问题4 例2：（2008年河南省中考第23题）如图1，直线y x 4和x轴、y轴的交点分别为B、C，点3A 的坐标是（-2，0）．（1）试说明△ ABC 是等腰三角形；2）动点M从A出发沿x轴向点B运动，同时动点N从点B出发沿线段BC向点C运动，运动的速度均为每秒 1 个单位长度．当其中一个动点到达终点时，他们都停止运动．设M 运动t 秒时，△MON 的面积为S．① 求S与t 的函数关系式；②设点M 在线段OB 上运动时，是否存在S＝4的情形？若存在，求出对应的t 值；若不存在请说明理由；③在运动过程中，当△ MON 为直角三角形时，求t 的值．5思路点拨：1．第（ 1）题说明△ ABC 是等腰三角形，暗示了两个动点 M 、N 同时出发，同时到达终点． 2．不论 M 在 AO 上还是在 OB 上，用含有 t 的式子表示 OM 边上的高都是相同的，用含有 t 的式子表示 OM 要分类讨论．3．将 S ＝4 代入对应的函数解析式，解关于 t 的方程．4．分类讨论△ MON 为直角三角形，不存在∠ ONM ＝ 90°的可能．解答：4（ 1）直线 y3 x4 与 x 轴的交点为 B （3，0）、与 y 轴的交点 C （ 0，4）．3Rt △BOC 中， OB ＝ 3，OC ＝ 4，所以 BC ＝ 5．点 A 的坐标是（ -2，0），所以 BA ＝5．因此 BC ＝ BA ，所以△ ABC 是等腰三角形．（ 2）①如图 2，图 3，过点 N 作 NH ⊥AB ，垂足为 H ．44 在 Rt △BNH 中， BN ＝t ， sin B ，所以 NH t ． 55 如图 2，当 M 在 AO 上时， OM ＝2－t ，此时1 1 42 2 4 S OM NH (2 t) t t t ．定义域为 0< t ≤2．2 2 5 5 5如图 3，当 M 在 OB 上时， OM ＝t － 2，此时11 42 2 SOM NH (t 2) t t 2 2 25 5解得 t 1 2 11， t 2 2 11（舍去负值）因此，当点 M 在线段 OB 上运动时，存在 S ＝4 的情形，此时 t 2 11 ．3③ 如图 4，当∠ OMN ＝90°时，在 Rt △BNM 中， BN ＝ t ，BM 5 t ，cosB ，4．55 5 54t5t 325 所以．解得 t ．t 58如图 5，当∠ OMN ＝90°时， N 与 C 重合， t 5．不存在∠ ONM ＝90°的可能．考点伸在本题情景下，如果△ MON 的边与 AC 平行，求 t 的值．如图 6，当 ON//AC 时， t ＝如图 7，当 MN //AC 时， t ＝2.5．6，BA ＝3 5 ．分别以 OA 、OC 边所在直线为 x 轴、 y 轴建立如图 1 所示的平面直角坐标系．图1图2 思路点拨： 1．第（ 1）题和第（ 2）题蕴含了 OB 与 DF垂直的结论，为第（ 3）题讨论菱形提供了计算基础．2．讨论菱形要进行两次（两级）分类，先按照 DO 为边和对角线分类，再进行二级分类，图6三、平行四边形问题：因动点产生的平行四边形问题例 3：（ 2010年山西省中考第 26 题）在直角梯形 OABC 中，CB//OA ，∠ COA ＝90°， CB ＝3，OA（ 1）求点 B 的坐标；（2）已知 D 、E 分别为线段 OC 、OB 上的点，直线 DE 的解析式；（3）点 M 是（2）中直线 DE 上的一个动点，在 D 、M 、N 为顶点的四边形是菱形？若存在，请求OD ＝5，OE ＝2EB ，直线 DE 交 x 轴于点 F ．求 x 轴上方的平面内是否存在另一点 N ，使以 O 、 N 的坐标；若不存在，请说明理由．DO 与DM、DO 与DN 为邻边．解答：(1)如图2，作BH⊥x 轴，垂足为H，那么四边形BCOH 为矩形，OH＝CB＝3．在Rt△ ABH 中，AH ＝3，BA＝3 5，所以BH＝6．因此点 B 的坐标为(3,6)．22(2) 因为OE＝2EB，所以x E x B 2 ，y E y B 4 ，E(2,4)．33 b 5, 1设直线DE 的解析式为y＝kx＋b，代入D(0,5)，E(2,4)，得解得k ，b 5 ．所2k b 4. 21 以直线DE 的解析式为y x 5 ．21(3) 由y x 5，知直线DE 与x轴交于点F(10,0)，OF＝10，DF＝5 5 ．2①如图3，当DO 为菱形的对角线时，MN 与DO 互相垂直平分，点M 是DF 的中点．此时点M55 的坐标为(5, )，点N 的坐标为( －5, )．22②如图4，当DO、DN为菱形的邻边时，点N与点O关于点E对称，此时点N的坐标为(4,8)．③如图5，当DO、DM 为菱形的邻边时，NO ＝5，延长MN交x轴于P．考点伸展如果第( 3)题没有限定点N 在x 轴上方的平面内，那么菱形还有如图 6 的情形．由△ NPO ∽△ DOF ，得NP POOFNO，即NP PO 5．解得NP 5DF 5 10 5 5图3图5 图6DOPO四、相似三角形：因动点产生的相似三角形问题例4：（2013 年苏州中考28 题）如图，点O 为矩形ABCD 的对称中心，AB=10cm，BC=12cm，点E、F、G 分别从A、B、C 三点同时出发，沿矩形的边按逆时针方向匀速运动，点 E 的运动速度为1cm/s，点 F 的运动速度为3cm/s，点G 的运动速度为 1.5cm/s，当点 F 到达点 C （即点 F 与点 C 重合）时，三个点随之停止运动．在运动过程中，△ EBF 关于直线EF 的对称图形是△EB′F．设点E、F、G 运动的时间为t（单位：s）．（1）当t= s 时，四边形EBFB ′为正方形；（2）若以点E、B、F 为顶点的三角形与以点F，C，G 为顶点的三角形相似，求t 的值；（3）是否存在实数t，使得点B′与点O 重合？若存在，求出t的值；若不存在，请说明理由．相似，分两种情况，需要分类讨论，逐一分析计算；（3）本问为存在型问题．假设存在，则可以分别求出在不同条件下的t 值，它们互相矛盾，所以不存在．解答：（1）若四边形EBFB′为正方形，则BE=BF ，即：10﹣t=3t，解得t=2.5；（2）分两种情况，讨论如下：① 若△EBF∽△FCG ，则有，即，解得：t=2.8；② 若△EBF∽△GCF ，则有，即，解得：t=﹣14﹣2 （不合题意，舍去）或t=﹣14+2 ．∴当t=2.8 s或t=（﹣14+2 ）s时，以点E、B、F 为顶点的三角形与以点F，C，G 为顶点的三角形相似．（3）假设存在实数t，使得点B′与点O 重合．如图，过点O 作OM⊥BC 于点M，则在Rt△OFM 中，OF =BF =3t，FM = BC﹣BF=6﹣3t，OM=5，由勾股定理得：OM2+FM 2=OF2，即：52+（6﹣3t）2=（3t）2解得：t= ；过点O 作ON⊥AB 于点N，则在Rt△OEN 中，OE=BE=10﹣t，EN=BE﹣BN=10﹣t﹣5=5﹣t，ON=6，由勾股定理得：ON2+EN2=OE2，即：62+（5﹣t）2=（10﹣t）2解得：t=3.9．∵ ≠3.9，∴不存在实数t，使得点 B ′与点O 重合．考点伸本题为运动型综合题，考查了矩形性质、轴对称、相似三角形的判定性质、勾股定理、解方程等知识点．题目并不复杂，但需要仔细分析题意，认真作答．第（2）问中，需要分类讨论，避免漏解；第（3）问是存在型问题，可以先假设存在，然后通过推导出互相矛盾的结论，从而判定不存在．拓展练习：1、如图1，梯形ABCD 中，AD∥ BC，∠ B=90 °，AB=14cm,AD=18cm,BC=21cm, 点P从 A 开始沿AD 边以1cm/秒的速度移动，点Q 从 C 开始沿CB 向点 B 以 2 cm/秒的速度移动，如果P，Q 分别从A，C同时出发，设移动时间为t 秒。

初二动点问题(非常经典)

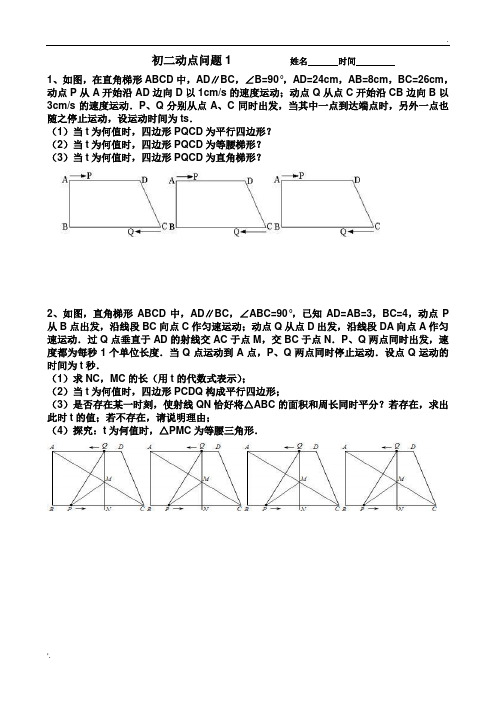
初二动点问题1 姓名时间1、如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从A开始沿AD边向D以1cm/s的速度运动；动点Q从点C开始沿CB边向B以3cm/s的速度运动．P、Q分别从点A、C同时出发，当其中一点到达端点时，另外一点也随之停止运动，设运动时间为ts．（1）当t为何值时，四边形PQCD为平行四边形？（2）当t为何值时，四边形PQCD为等腰梯形？（3）当t为何值时，四边形PQCD为直角梯形？2、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，已知AD=AB=3，BC=4，动点P 从B点出发，沿线段BC向点C作匀速运动；动点Q从点D出发，沿线段DA向点A作匀速运动．过Q点垂直于AD的射线交AC于点M，交BC于点N．P、Q两点同时出发，速度都为每秒1个单位长度．当Q点运动到A点，P、Q两点同时停止运动．设点Q运动的时间为t秒．（1）求NC，MC的长（用t的代数式表示）；（2）当t为何值时，四边形PCDQ构成平行四边形；（3）是否存在某一时刻，使射线QN恰好将△ABC的面积和周长同时平分？若存在，求出此时t的值；若不存在，请说明理由；（4）探究：t为何值时，△PMC为等腰三角形．3、如图，在直角梯形ABCD中，AD∥BC，∠C=90°，BC=16，DC=12，AD=21，动点P 从点D出发，沿射线DA的方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，P、Q分别从点D、C同时出发，当点Q运动到点B时，点P随之停止运动，设运动时间为t（s）．（1）设△BPQ的面积为S，求S与t之间的函数关系；（2）当t为何值时，以B、P、Q三点为顶点的三角形是等腰三角形？4、直线y=- 3/4x+6与坐标轴分别交于A、B两点，动点P、Q同时从O点出发，同时到达A点，运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O⇒B⇒A 运动．（1）直接写出A、B两点的坐标；（2）设点Q的运动时间为t（秒），△OPQ的面积为S，求出S与t之间的函数关系式；（3）当S= 48/5时，求出点P的坐标，并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标．5、如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于E．（1）试说明EO=FO；（2）当点O运动到何处时，四边形AECF是矩形并证明你的结论；（3）若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论．。

初二一次函数动点经典题型(全部题型)

一次函数动点问题例题如图，直线1l 的解析表达式为33y x =-+，且1l 与x 轴交于点D ，直线2l 经过点A B ，，直线1l ，2l 交于点C ．（1）求点D 的坐标；（2）求直线2l 的解析表达式；（3）求ADC △的面积；（4）在直线2l 上存在异于点C 的另一点P ，使得ADP △与ADC △的面积相等，请直接．．写出点P 的坐标．练习题如图,以等边△OAB 的边OB 所在直线为x 轴,点O 为坐标原点,使点A 在第一象限建立平面直角坐标系，其中△OAB 边长为6个单位，点P 从O 点出发沿折线OAB 向B 点以3单位/秒的速度向B 点运动,点Q 从O 点出发以2单位/秒的速度沿折线OBA 向A 点运动，两点同时出发，运动时间为t （单位：秒），当两点相遇时运动停止.① 点A 坐标为_____________，P 、Q 两点相遇时交点的坐标为________________; ② 当t =2时，S =△OPQ ____________;当t =3时，OPQ S =△____________;③ 设△OPQ 的面积为S ，试求S 关于t 的函数关系式;④ 当△OPQ 的面积最大时，试求在y 轴上能否找一点M ，使得以M 、P 、Q 为顶点的三角形是Rt △，若能找到请求出M 点的坐标，若不能找到请简单说明理由。

xyOAB xyOAB x yOAB例题如图，在Rt △AOB 中，∠AOB=90°，OA=3cm ，OB=4cm ，以点O 为坐标原点建立坐标系，设P 、Q 分别为AB 、OB 边上的动点它们同时分别从点A 、O 向B 点匀速运动，速度均为1cm/秒，设P 、Q 移动时间为t （0≤t ≤4）（1）过点P 做PM ⊥OA 于M ，求证：AM ：AO=PM ：BO=AP ：AB ，并求出P 点的坐标（用t 表示）（2）求△OPQ 面积S （cm 2），与运动时间t （秒）之间的函数关系式，当t 为何值时，S 有最大值？最大是多少？（3）当t 为何值时，△OPQ 为直角三角形？（4）证明无论t 为何值时，△OPQ 都不可能为正三角形。

初二数学动点问题经典例题

初二数学动点问题经典例题
在初二数学中，动点问题是一个非常经典的题型。

这类问题通常涉及到一个或多个物体在运动过程中的位置、速度和时间等概念。

通过解答这些问题，学生可以加深对运动学知识的理解，并培养逻辑思维和问题解决能力。

以下是一个典型的初二数学动点问题例题：
问题：小明从家出发，以每小时5公里的速度向东行驶。

同时，小李从距离小明家20公里的地方，以每小时8公里的速度向西行驶。

问多长时间后，他们会相遇？
解析：首先，我们可以设定问题的解答时间为t小时后。

在t小时后，小明已经行驶了5t公里，而小李则行驶了8t公里。

由于小明和小李是相向而行的，所以他们的距离可以表示为5t + 8t = 13t 公里。

根据题目中的信息，他们相遇的位置应该是离小明家20公里的地方。

因此，我们可以得到以下方程：
5t + 8t = 20
13t = 20
t ≈ 1.54
所以，他们会在约1.54小时后相遇。

这个例题展示了动点问题的基本解题步骤。

首先，我们需要设定解答时间，然后根据题目提供的信息推导出数学方程，最后通过求解方程得到答案。

除了这个例题，还可以进一步拓展动点问题。

例如，可以考虑多个物体的相对运动，或者考虑到加速度的影响等。

这些问题需要学生运用更多的运动学知识和计算方法来解答。

通过解答这些动点问题，学生可以锻炼数学思维和逻辑推理能力，同时也增强对运动学概念的理解。

这对于数学的学习和应用都具有重要的意义。

因此，在初二数学学习中，动点问题是一个非常有教育价值的题型。

初二数学动点问题练习(含答案)

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD中，AD∥ BC，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q分别从A，C同时出发，设移动时间为t秒。

当t= 时，四边形是平行四边形；6当t= 时，四边形是等腰梯形. 82、如图2，正方形ABCD的边长为4，点M在边DC上，且DM=1，N为对角线AC上任意一点，则DN+MN的最小值为 53、如图，在中，，．点是的中点，过点的直线从与重合的位置开始，绕点作逆时针旋转，交边于点．过点作交直线于点，设直线的旋转角为．（1）①当度时，四边形是等腰梯形，此时的长为；②当度时，四边形是直角梯形，此时的长为；（2）当时，判断四边形是否为菱形，并说明理由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC 是菱形.∵∠α=∠ACB=900，∴BC//ED. ∵CE//AB, ∴四边形EDBC 是平行四边形在Rt△ABC 中，∠ACB=900，∠B=600,BC=2, ∴∠A=300. ∴AB=4,AC=2. ∴AO== .在Rt△AOD 中，∠A=300，∴AD=2. ∴BD=2. ∴BD=BC. 又∵四边形EDBC 是平行四边形， ∴四边形EDBC 是菱形4、在△ABC 中，∠ACB=90°，AC=BC ，直线MN 经过点C ，且AD⊥MN 于D ，BE⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD ＋BE ；(2)当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ；CBAE D图1NM(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明.解：（1）① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90°∴∠BCE+∠ACD=90°∴∠CAD=∠BCE ∵AC=BC ∴△ADC≌△CEB② ∵△ADC≌△CEB ∴CE=AD，CD=BE ∴DE=CE+CD=AD+BE(2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC∴△ACD≌△CBE ∴CE=AD，CD=BE ∴DE=CE-CD=AD-BE(3) 当MN旋转到图3的位置时，DE=BE-AD(或AD=BE-DE，BE=AD+DE等)∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE，又∵AC=BC，∴△ACD≌△CBE，∴AD=CE，CD=BE，∴DE=CD-CE=BE-AD.5、数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E 是边BC的中点．，且EF交正方形外角的平行线CF于点F，求证：AE=EF．经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证，所以．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．解：（1）正确．证明：在上取一点，使，连接．．，．是外角平分线，，．．，，．（ASA）．．（2）正确．证明：在的延长线上取一点．使，连接．．．四边形是正方形，．．．（ASA）．．6、如图, 射线MB上,MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB方向以1个单位/秒的速度移动，设P的运动时间为t.求（1）△ PAB为等腰三角形的t值；（2）△ PAB为直角三角形的t值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△ PAB为直角三角形的t值7、如图1，在等腰梯形中，，是的中点，过点作交于点．，.求：（1）求点到的距离；（2）点为线段上的一个动点，过作交于点，过作交折线于点，连结，设.①当点在线段上时（如图2），的形状是否发生改变？若不变，求出的周长；若改变，请说明理由；②当点在线段上时（如图3），是否存在点，使为等腰三角形？若存在，请求出所有满足要求的的值；若不存在，请说明理由解（1）如图1，过点作于点 ∵为的中点， ∴ 在中， ∴ ∴ 即点到的距离为（2）①当点在线段上运动时，的形状不发生改变． ∵ ∴ ∵ ∴，同理如图2，过点作于，∵A D E BF C图4（备用）AD EBF C 图5（备用）A D E BFC图1 图2A D EBFC PNM图3A D E BF C PN M （第25题）∴ ∴ ∴ 则在中， ∴的周长=②当点在线段上运动时，的形状发生改变，但恒为等边三角形．当时，如图3，作于，则类似①， ∴ ∵是等边三角形，∴ 此时，当时，如图4，这时此时，当时，如图5，则又∴ 因此点与重合，为直角三角形． ∴ 此时，图3A D E BFCPN M 图4A D EBF CP MN 图5A DEBF （P ） CM NGGRG综上所述，当或4或时，为等腰三角形．8、如图，已知中，厘米，厘米，点为的中点．(1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等，经过1秒后，与是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使与全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿三边运动，求经过多长时间点P与点Q第一次在的哪条边上相遇？解：（1）①∵秒，∴厘米，∵厘米，点为的中点，∴厘米．又∵厘米，∴厘米，∴．又∵，∴，∴．②∵，∴，又∵，，则，∴点，点运动的时间秒，∴厘米/秒。