天线原理与设计(王建)4PDF版
天线原理与设计(王建)4PDF版

可得
Hϕ
=
j Im [e− jβ R1 4πρ
+ e− jβ R2
− 2 cos(β l)e− jβr ]
(2.21) (2.22) (2.23)
再由麦氏方程 ∇ × H = jωε0E ,可得
Eρ
=
jη0 I m 4πρ
[( z
ez + l)
R2
量法求辐射功率的表示相同,但其中的电磁场已经不同。
坡印亭矢量法中所用的电磁场是远区场,这里的积分面
在天线表面,式中的电磁场必须是近场。
式(2.26)中的电磁场矢量分别为 E = ρˆ Eρ + zˆEz和 H = ϕˆHϕ ,
则
E × H* = zˆEρ Hϕ* − ρˆ Ez Hϕ*
(2.27)
返回
=
Z0′2 Rr
(2.18)
链接
(6) 对称振子谐振长度的缩短现象
对称振子的谐振长度是其输入阻抗的虚部为零时的 长度。由前面图可见,Xin=0对应的电长度略小于0.25和 略小于0.5。这一现象称之为缩短效应。振子天线愈粗, 缩短愈多。所以,实际使用的半波振子全长是小于半个 波长的。产生缩短的原因大致有两点:
当ρ=a时,这三个近场分量就是振子圆柱表面的场。
2. 感应电动势法求辐射阻抗
假如我们把坡印亭矢量法中的大球面缩小,直到缩小
到天线的圆柱表面,通过这一封闭柱面的总功率表示为
Pr
=
1 2
�∫∫s E× H*ids
(2.26)
式中,s为圆柱表面,ds = nˆds ,nˆ 为圆柱表面的外法线单位 矢量,ds为积分面元。从形式上看,式(2.26)与坡印亭矢
⎪⎩β = ω L1C1
天线原理与设计(王建)8PDF版

4π | Fmax |2
(6.8)
2
W = ∫ dϕ ∫
0
2π
π
0
π⎛ Z F (θ ) sin Z ⎞ 0 sin θ dθ = 2π ∫ ⎜ ⋅ ⎟ sin θ dθ 2 0 Fmax ⎝ sin Z 0 Z ⎠
2
4π Z 0 2 β L (ξ +1) / 2 sin Z 2 4π = ( ) ∫ ( ) dZ = g (Z0 ) β L ( ξ − 1) / 2 β L sin Z 0 Z βL
δ =π /N
(6.16)
当N=10时,正是如图中 红线所示的端射阵方向图, 这个方向图就是10单元强方 向性端射阵的方向图。
6.3.3 强方向性端射阵的方向性系数
由式(6.12) D = β L / g ( Z 0 ) ,取 g ( Z 0 ) = g min = 0.871 ,可得 强方向性端射阵的方向性系数为
(6.3) (6.4) (6.5) (6.6) (6.7)
链接
δ L = Nd , ξ = 1 + βd 端射阵方向图最大值出现在θ=0处,因此令 Z 0 = Z |θ =0 = β L(1 − ξ ) / 2 sin( Z 0 ) Fmax = Z0
由方向性系数公式
4π D = 2π = π 2 W d ϕ F ( θ )sin θ d θ ∫ ∫
βL 2π Nd Nd L De = = ⋅ = 7.213 ≃ 1.8 × (4 ) = 1.8D g ( Z 0 ) λ 0.871 λ λ
(6.17)
式中,D=4L/λ为普通端射阵的方向性系数。
6.3.4 强方向性端射阵的波瓣宽度
1. 主瓣零点宽度2θ0 由前面式(6.3),即
天线原理与设计(王建)3PDF版(优选.)

+
I1 I0
e− jβ r1 ]
r1
作远场近似:对幅度 1/ r1 ≃ 1/ r0
对相位 r1 = r0 − rˆ0izˆd = r0 − d cosθ
(1.89)
并设
I1 / I0 = me− jα
(1.90)
式中,m为两单元电流幅度比,α为两单元电流之间的相
位差,若α>0,则I1滞后于I0;若α<0,则I1超前于I0 ; 若α=0 ,则I1与I0同相位。式(1.89)可写作
(1.93)
合成相差
ψ = β d cosθ − α
(1.94)
由式(1.92)可见,二元阵总场方向图由两部分相乘而 得,第一部分f0(θ,φ)为单元天线的方向图函数;第二部 分fa(θ,φ)称为阵因子,它与单元间距d、电流幅度比值m、 相位差α和空间方向角θ有关,与单元天线无关。因此 得方向图相乘原理:
(1.106)
阵因子为
N −1
N −1
∑ ∑ = E0
e = E jn( β d cosθ −α ) 0
e jnψ = E0 fa (ψ )
n=0
n=0
+ 2 + e jβd sinθ sinϕ ]
=
j 60I r
e− jβ r
− jβ d sinθ sinϕ
f0 (θ ,ϕ )[e 2
+ e ] jβ d sinθ sinϕ 2
2
=
j 60I r
e− jβ r
f0
(θ
,ϕ
)4
cos2
(
βd 2
sinθsinຫໍສະໝຸດ )=j 60I r
e− jβ r
天线原理与设计 讲义

( xˆJ x + yˆJ y + zˆJ z )e jβr′cosψ ds′ ( xˆM x + yˆM y + zˆMz )e jβ r′cosψ ds′
⎩
s
s
由直角坐标矢量到球坐标矢量的转换公式
⎡ ⎢ ⎢
Ar Aθ
⎤ ⎥ ⎥
=
⎡sinθ ⎢⎢cosθ
cosϕ cosϕ
⎣⎢ Aϕ ⎦⎥ ⎢⎣− sinϕ
求解口面天线的辐射场,须先求得开口面上的场分布,然后按惠更斯—菲涅 尔原理,把开口面分割成许多小面元。根据面元的辐射场,并在整个开口面 S 上 积分,最后可求得口面天线的辐射场。
要按照这个过程求解口面天线的辐射场,还有一个问题必须解决,因为我们 知道,要求解一个辐射系统的辐射场,是根据振荡源(电流源 J 和磁流源 M(Jm ) ) 来求解的,而不是直接由场来求场。根据等效原理,就可将口面天线口径面上的 电磁场等效为电、磁流。
以口径面 S 上的次级源分布代替实际源分布以后,封闭面内的场 E = H = 0 ,
但封闭面外的场不变,口径面 S 上的电磁场的切向分量 nˆ × Hs 和 nˆ × Es 也不变。 在新的分析系统中(见图 b),口径面 S 的内外侧,电磁场由 0 值跃变为 Hs 和 Es , 即发生了不连续,这种不连续只有在存在相应的面电流 Js 和面磁流 Ms 时才能发 生。因此证明了口径面 S 上的 Js 和 Ms 分别为:
⎩
s
∫∫ ⎧
⎪
Lθ
=
⎨
s
⎡⎣M x cosθ cosϕ + M y cosθ sinϕ ⎤⎦ e jβ ( xcosϕ + ysinϕ )sinθ dxdy
∫∫ ⎪Lϕ = ⎡⎣−M x sinϕ + M y cosϕ ⎤⎦ e jβ ( xcosϕ + ysinϕ )sinθ dxdy
天线原理与设计(王建)6PDF版

(1) 传输线模式
见图(b),由端口a-b或e-f向短路端看去的输入阻抗为
Zt = jZ0 tan(β l / 2)
(4.19)
式中,Z0是双线传输线的特性阻抗。b、e两点等电位, 则a-b两点的输入电流为
(2) 天线模式
U /2 It = Zt
(4.20)
见图(c),由于c、d两点同电位,g、h同
f0
f0
π
RA
(4.12)
由此式可见,对称振子的频带宽度与它的平均特性阻抗
Z'0有关。如果RA不变,那么Z'0愈小带宽就愈宽。由Z'0的
表示
Z0′
= 120[ln(
2l ρe
)
− 1]
(4.13)
可见,减小Z'0的有效途径是增大振子的截面半径。在中、 短波波段,广泛采用架设在地面上一定高度的水平对称
天线原理与设计
教师: 王建 电子工程学院二系
第四章 双极与单极天线
双极天线就是前面提到的对称振子天线,这种天线 从馈电输入端看去有两个臂。所谓单极天线,就是从输 入端看去只有一个臂的天线,如导电平板上的鞭天线, 垂直接地天线等。
4.1 近地水平与垂直半波天线
1、近地水平半波天线
近地水平半波振子天线广泛应用于短波(λ=10~100 米)通信中,其振子臂可由黄铜线、钢包线和多股软铜线 水平拉直构成,中间由高频绝缘子连接两臂,可由双线 传输线馈电,如下图所示。
链接
4.2 对称天线的频带宽度
天线的电气参量大多数都是频率的函数。当工作频 率偏离中心频率(设计频率)时,可能使方向图发生畸变, 增益下降,馈电传输线上驻波增大等。因此,工程上往 往要规定一个频率范围。在此频率范围内,天线的电特 性变化不影响工作,这个频率范围就是工作频带宽度。
天线设计原理

射电磁波的电场平行于圆柱振子长度方向,则其 E 面为 yz 平面,H 面为 xy 平面。
表 0-1 给出了这两个天线的 E 面和 H 面及其方向图函数表示。
表 0-1 图 0-3 所示的八木天线和角锥喇叭天线的 E 面和 H 面及其方向图函数表示
5
《天线原理与设计》讲稿
王建
(a) 极坐标幅度方向图
(a) 直角坐标幅度方向图
(c) 极坐标分贝方向图
(d) 直角坐标分贝方向图
图 0-2 七元八木天线xy平面(H面,θ=90o)内的二维场强幅度和分贝表示的归一化方向图
天线方向图一般呈花瓣状,称之为波瓣或波束。其中包含最大辐射方向的波
瓣称之为主瓣,其它的称为副瓣或旁瓣,并分为第一副瓣、第二副瓣等,与主瓣
■三维方向图
以图 0-1(a)所示的典型七元八木天线为例,其辐射电场幅度的球坐标三维方 向图和直角坐标三维方向图如图 0-1(b)(c)所示。它们是以天线上某点为中心,远 区某一距离为半径作球面,按球面上各点的电场强度模值与该点所在的方向角 (θ ,ϕ )而绘出的。三维场强方向图直观、形象地描述了天线辐射场在空间各个方 向上的幅度分布及波瓣情况。但是在描述方向图的某些重要特性细节如主瓣宽 度、副瓣电平等方面则显得不方便。因此,工程上大多采用二维方向图来描述天 线的辐射特性。
图数据并绘出方向图。大多线极化天线的远区辐射电磁场一般可表示为如下形式
Eθ
=
E0
e− jβr r
f (θ ,ϕ )
(0.1)
Hϕ
=
Eθ η0
(0.2)
4
《天线原理与设计》讲稿
天线原理与设计(王建)1PDF版

可见,天线方向图是在远区球面上的场强分布。
●归一化方向图
f (θ ,ϕ ) F (θ ,ϕ ) = f (θ m ,ϕ m )
(0.3)
式中,(θm ,φm)为天线最大辐射方向;
f (θm ,φm)为方向图函数的最大值。
由归一化方向图函数绘制出的方向图称为归 一化方向图。由式(0.1)和(0.2)可以看出,天线远 区辐射电场和磁场的方向图函数是相同的,因 此,由方向图函数和归一化方向图函数表示的方 向图统称为天线的辐射场方向图。
为便于分析和研究天线性能出发,天线可以分为如下 几大类:
(1~6)章 (1) 线天线(Wire Antennas) —— ——(1
(8~10章) (2) 口径天线(Aperture Antennas) —— ——(8
(3) 阵列天线(Array Antennas) —(1章部分,5章)
(4) 透镜天线(Lens Antennas) —(10章部分)
六十和七十年代是天线发展的鼎盛时期。这 个时期在天线理论方法方面以及各项技术的应用 方面都在突飞猛进的发展。
(1)在天线理论方法方面
■几何绕射理论 ■平面波谱展开法 ■时域有限差分法 ■天线近场测量理论 ■矩量法 ■有限元法 ■时域积分方程法 ■阵列分析与综合理论
这些理论方法为天线的工程设计奠定了坚实的基础, 随着计算机技术的发展大都形成了计算机仿真的电子自动 化设计软件。
■ HFSS软件 ■ CST软件 ■ FEKO软件
■ IE3D软件 ■ FIDELITY软件
(2)在天线技术应用方面
卫星通信技术发展推动了卫星天线和大型地面站天线 的发展,出现了大型平面阵、卡塞格仑天线及各种反射面 天线馈源。 雷达制导、搜索、跟踪、预警技术的应用推动了单脉 冲雷达天线、相控阵天线,多波束天线的发展。 半导体技术的发展使无线电技术向毫米波、亚毫米波 甚至更高频率发展,对天线提出了小型化、集成化、宽带 化等一系列要求,出现了有源天线、微带天线和印刷天线、 印制板开槽天线、表面波天线、共形阵列天线等。 微带天线和印刷天线由于其具有小型化、低剖面、便 于集成,成本低、天线图案千变万化,所以至今仍在发 展,其方向包括阵列、极化、宽带、高效率、双频和多频 谐振等。
天线原理与设计3.4.6 背射(返射)天线概述

背射天线是20世纪60年代初在引向天线基础上发展起来 的一种新型天线。
1. 背射天线(Back Fire Antenna) 在引向天线最末端的引向器后面再加一反射盘T,就构 成背射天线,如图3-4-22所示。
图3-4-22 背射天线
反射盘一般称为表面波反射器,它的直径大致与同一 增益的抛物面天线的直径相等; 反射盘与反射器之间的距离 应为λ/2的整数倍。如果在反射盘的边缘上再加一圈反射环 (边框),则可使增益再加大2 dB左右。一个设计良好的背射
8 dB的增益,其 增益可用下式大致估算:
G 60 L
(3-4-13)
2. 短背射天线(Short BacБайду номын сангаас Fire Antenna) 这种天线由一根有源振子(或开口波导、 小喇叭)和两个 反射盘组成,如图3-4-23所示。
图 3-4-23 短背射天线
天线原理与设计(王建)9PDF版

EsmW cos( β l cos θ ) − cos β l − jβ r H sθ = − j e π rη sin θ
(7.13)
缝隙天线产生的电场为 EsmW cos( β l cosθ ) − cos β l − jβ r Esϕ = − H sθη = j e (7.14) πr sin θ 式中,Esm是缝隙口面上电场腹点值,因是细缝(W<<λ), 在Esm处得电压V0= EsmW。 可见,理想缝隙的方向图与对偶的电振子的方向图 相同,只不过场的极化方向互换而已。 电振子电磁场为: Edθ 、Hdφ 缝隙电磁场为: Hsθ 、Esφ ■缝隙天线的方向图 )时,缝隙方向图如下图所示。 当为半波缝隙(2l=λ/2 /2)
天线原理与设计
教师: 王建
电子工程学院二系
第七章 开槽天线 (Slot Antennas)
开槽天线又叫缝隙天线。为了分析的方便,将用到 巴俾涅原理。利用巴俾涅原理在分析开槽(缝隙)天线时, 可将开槽天线用一互补的金属天线等效,若互补的金属 天线在空间的场能求得,则开槽天线的辐射场就能确 定,但要经过电磁对偶关系求得。因此,这章将先介绍 两个原理,一是电磁对偶原理,一是巴俾涅原理。
如果一个分析系统中既有电流 i e (伴随有电荷 ρ e ),也 有磁流 i m(或伴随有磁荷ρ m),则可分别求解由电流源产生 的场 Ee,He ( De = ε Ee,Be = µ He)和由磁流源产生的场 Em,Hm (D m = ε Em,B m = µ H m),则该系统的总场为
⎧E = E e + E m ⎨ ⎩H = H e + H m
⎧E d = E i + E sd ⎨ ⎩H d = H i + H sd
天线原理与设计2015
四分之一波长套筒巴伦
开路
短路
8
微带贴片天线基模辐射原理
两开路端的水平分量可以等效为无限大平面上同相激励的两个缝隙. 缝的电场方向与长边垂直,并沿长边W 均匀分布.
缝的宽度为L h,长度为w,两缝间距为l 2 .
微带天线的辐射可以等效为由两个缝隙所组成的二元阵列.
9
例
某天线只在半空间均匀辐射,求其方向性系数.
3
全向天线
根据天线的方向性,可以 将天线分成三类:
① 等向模式天线:理想的点源, 其在空间的辐射为各向同性, 辐射方向图为一个圆球,现实 中不存在,为了标定其它天线 的增益而设定。 ② 全向天线:在某一个平面内, 辐射方向图的截面是一个圆, 在其它截面非圆,具有一定的 指向性。 ③ 定向天线:辐射主要集中在某 个方向上。
5
时变电磁场中的唯一性定理
电磁场麦克斯韦方程组的定解需要利用边界条件才能确定. 对于一个有耗区域,区域中的场源加上边界上所有的电场切向分量, 或边界上的磁场切向分量,或部分边界上的电场切向分量和其余边界 上的磁场切向分量,惟一地确定该区域中的场.无耗媒质中的场可看 成有耗媒质中损耗非常小时的相应场.
)60 o的方向为 = m 60 o ,
即 150o 或30o , r2 2km处,有
r1 1 103 1 103 1 o H E0 sin 30 sin 30 0.663 A m . 3 2 r2 r2 2 120 2 10
o
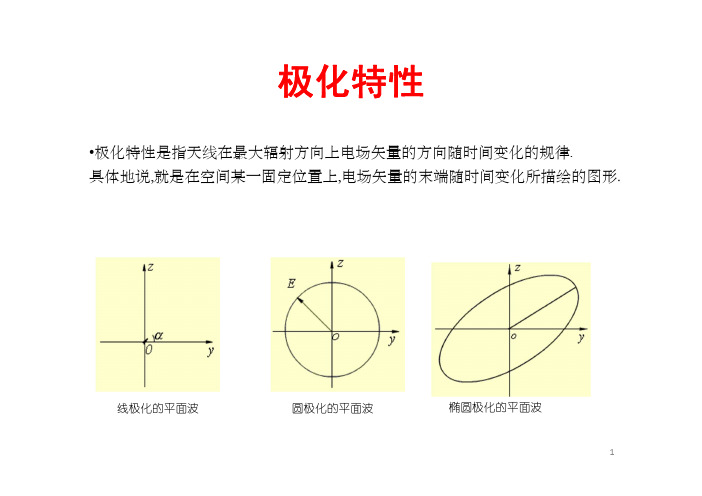
极化特性
•极化特性是指天线在最大辐射方向上电场矢量的方向随时间变化的规律. 具体地说,就是在空间某一固定位置上,电场矢量的末端随时间变化所描绘的图形.
线极化的平面波
第4章(183)

(4.1-3)
第 4 章 天线理论基础
图4.1-5 电磁辐射形成过程
第 4 章 天线理论基础
根据传输线知识, 终端开路的双导线上电压、 电流呈 驻波分布, 导线终端电流为零, 离开终端每半个波长为电 流节点, 两导线上电流方向相反,如图4.1-6(a)所示。 所有 的场在导线之间加强, 在其它地方减弱, 电磁场能量沿双 导线传播, 注意前提条件是导线之间的距离远小于波长, 没有电磁辐射产生。 如果导线向外弯曲, 弯曲段长度为1/4 波长,如图4.1-6(b)所示, 导线上电流分布近似为正弦分布, 因此就产生如图4.1-5所示的电磁辐射。
第 4 章 天线理论基础
图4.1-6 从开路传输线向振子天线的演化示意图
第 4 章 天线理论基础
4.1.3
1. 按工作性质分类, 有发射天线、 接收天线和收发 共用天线。 2. 按用途分类 按用途分类, 有通信天线、 广播天线、 电视天 线、 雷达天线、 导航天线、 测向天线等。
第 4 章 天线理论基础
E j H
(4.2-4b)
第 4 章 天线理论基础
B 0
D
(4.2-4c) (4.2-4d)
第 4 章 天线理论基础
电流连续方程的频域表达式为
B A
(4.2-5)
第 4 章 天线理论基础
已知天线电流密度J (或电荷密度ρ)分布, 由麦克斯韦 方程(4.2-4a)~(4.2-4d)直接求得空间电场E、 磁场H分布非常 困难。 为便于求解, 引入矢量位A和标量位φ,分析过程如 下:
第 4 章 天线理论基础
图4.3-1 电基本振子
第 4 章 天线理论基础
对空间任意点P(r, θ, φ), 根据(4.2-14)式, 电基本振 子在该点产生的矢量位
天线原理与设计

2021/4/1
31
第31页/共72页
电小天线的宽带技术
• 无论是电小偶极子天线还是电小环天线其带宽 都是非常窄的。要增加电小天线的带宽,可以 从以下几个方面考虑:
• 新原理天线; • 采用参差调谐的概念来展宽频带; • 采用电振子和磁振子互补的概念来扩展频带; • 加大阻尼,用牺牲效率的办法来换取一定频带的工
a
A
b
Ka Ab
6
2
3
KaV
6
2
3
V'
9 2
VS
VS
4 3
2
3
其中V=Ab为天线的体积;V’为有效体积;V’=Ka,bV;VS为弧度球的体积。
2021/4/1
9
第9页/共72页
集中参数分析法
(a)
(b)
(c)
(d) 线
(e)宽
(f)多线环
环
条环
• 扩展频带:降低整个天线系统的Q值。增大与负载之间
• 沿天线连续变化它的电阻是困难的,可以采用分段逼近的办法来代替。当 然,电阻将引起损耗,效率将下降。
2021/4/1
33
第33页/共72页
电阻加载示例
• 某国外机载多频 道天线,用 10W线绕电阻 与辐射片并联, 以扩展天线带宽, 天线效率不足万 分之一。
N
(2n 1)Qn (ka) Q n1
2N 2 4N
2021/4/1
29
第29页/共72页
传输线模型法
2021/4/1
• 天线是由传输线演变而来, 是特殊形式的传输线;
• 各种形式的电小天线具有相 似性;
• 电小偶极子天线可以等效为: 辐射电阻与无损耗开路传输 线串联;
王健阵列天线讲义4

§2.6 伍德沃德—劳森抽样法简称伍德沃德法。
这种方法是用于天线波束赋形的一种常用的方向图综合方法,它是对所需方向图在不同离散角度处进行抽样来实现预期方向图的。
与各方向抽样和联系的是谐波电流,谐波电流对应的场叫做构成函数。
综合方法分为连续的线源和离散的线阵分别讨论。
对于连续线源。
其构成函数为形式,对于离散线阵,其构成函数为形式。
各谐波电流激励系数等于所要求的方向图在对应抽样点上的幅度。
谐波电流的有限项之和为源的总激励。
构成函数的有限项之和则为综合的方向图,其中每一项代表一个电流谐波产生的场。
sin()/m m a u u m m sin()/(sin )m m a nu n u m a 伍德沃德方法中有关公式的处理类似于信号理论中的香农(Shannon)抽样定理。
该定理指出:“一个有限频带的函数,如果最高频率为()g t h f ,则函数可以用等间隔的抽样唯一地表示。
抽样间隔必须不大于()g t 1/(2)/2h h t f T Δ==,为对应于最高频率的周期”。
用类似的方法综合天线方向图时,其抽样间隔应取h T /L λ弧度,L 为源的长度。
2.6.1连续线源(1) 连续线源上的电流分布对于长为L 的连续线源,伍德沃德方法是令连续线源的总电流I (z )在线上用若干谐波电流()n I z 的有限和来表示:()(),/2/2N n n N I z I z L z L =−=−≤∑≤ (2.119)式中谐波电流为cos (),/2/2n jkz n n a I z e L z L Lθ−=−≤≤ (2.120) n θ代表所需方向图的抽样角度。
(2N 个偶数抽样)1,2,,n =±±± N N (2N +1个奇数抽样)0,1,2,,n =±±± (2) 谐波电流产生的场方向图由各谐波电流()n I z 产生的场方向图函数(即构成函数)为/2/2(cos cos )cos /2/2()()n L L jkz jkz n n n L L a S I z e dz e L θθθθ−−−==∫∫dzsin[(cos cos )]2(cos cos )2n n n kL a θθθθ−=− (2.121) 其最大值发生在n θθ=处。
天线原理与设计(王建)7PDF版

链接
■对端射阵
F (θ )
=
sin[N β d (1 − cosθ ) / 2] N sin[β d (1 − cosθ ) / 2]
|N >>1 ≈
sin[N β d (1 − cosθ ) / 2] N β d (1 − cosθ ) / 2
式中,θ为阵轴与射线之 间的夹角;α为相邻单元 之间的馈电相位差。
其最大值条件为 ψ |θ =θm = β d cosθm − α = 0
得 α = β d cosθm
可得
ψ = β d (cosθ − cosθm )
最大值为 fmax = N 归一化阵因子为 F (ψ ) = sin(Nψ / 2)
■对扫描阵,θm为最大扫描角。例如, 在侧向两边±30º内 扫描,应取θm=90º-30º=60º,得抑制栅瓣条件为d< 2λ/3 。
2、零点位置θ0n
零点指方向图两个波瓣之间的节点。令F(ψ)=0,可 得方向图的零点位置。除ψ=0外, 方向图零点可由sin(Nψ
/2)=0确定。有
Nψ / 2 = nπ , n = ±1, ±2,...
N sin(ψ / 2)
以上是第一章介绍过的内容。下面对均匀直线阵作 进一步介绍。
1、可见区与非可见区、最大值方向、栅瓣及其抑 制条件
(1) 可见区与非可见区
从数学上看,阵因子F(ψ)是在范围-∞<ψ<∞内的周期 函数, 实际上θ的变化范围为0≤θ≤π, 由ψ=βdcosθ-α 可得对应的实际范围为
设直线阵总长为L=Nd,若L>>λ,则
2λ 2ϕ0 = Nd
■对端射阵(θm=0)
由式(5.14)取n=-1,有
2ϕ0
天线原理与设计

天线原理与设计绪论0.1 天线在无线电工程中的作用天线已随处可见,它已与我们的日常生活密切相关。
例如,收听无线电广播的收音机需要天线,电视机需要天线,手机也需要天线。
在一些建筑物、汽车、轮船、飞机上等都可以看见各种形式的天线。
收音机、电视机使用的天线一般是接收天线,广播电视台的天线则为发射天线。
而手机天线则收发共用,但须经过移动通信基站天线转收和转发。
实际上,一切无线电设备(包括无线电通讯、广播、电视、雷达、导航等系统)都是利用无线电波来进行工作的,而从几MHz的超长波到四十多GHz的毫米波段电磁波的发射和接收都要通过天线来实现。
天线是这样一个部件,作发射时,它将电路中的高频电流或馈电传输线上的导行波有效地转换成某种极化的空间电磁波,向规定的方向发射出去;作接收时,则将来自空间特定方向的某种极化的电磁波有效地转换为电路中的高频电流或传输线上的导行波。
综上所述,天线的作用主要有四点:(1) 能量转换对于发射天线,天线应将电路中的高频电流能量或传输线上的导行波能量尽可能多地转换为空间的电磁波能量辐射出去。
对于接收天线,天线应将接收的电磁波能量最大限度地转换为电路中的高频电流能量输送到接收机。
这就要求天线与发射机源或与接收机负载尽可能好的匹配。
一副好的天线,就是一个好的能量转换器。
(2) 定向辐射或接收对于发射天线,辐射的电磁波能量应尽可能集中在指定的方向上,而在其它方向不辐射或辐射很弱。
对于接收天线,只接收来自指定方向上的的电磁波,在其它方向接收能力很弱或不接收。
例如,就雷达而言,它的任务是搜索和跟踪特定的目标。
如果雷达天线不具有尖锐的方向性,就无法辨别和测定目标的位置。
而且如果天线没有方向性,或方向性弱,则对发射天线来说,它所辐射的能量中只有一少部分到达指定方向,大部分能量浪费在不需要的方向上。
对接收天线来说,在接收到所需要信号的同时,还将接收到来自其它方向的干扰信号或噪声信号,致使所需信号完全淹没在干扰和噪声中。
天线原理与设计3.4.1 引向天线的工作原理

实际工作中,引向天线振子间的距离一般在0.1λ~0.4λ之 间,在这种条件下,振子“2”对振子“1”的电流相位差等 于多少才能使振子“2”成为引向器或反射器呢?下面作一 般性分析。 设I2=mI1ejα,间距d=0.1λ~0.4λ,则在M点E2对E1 的相位差Ψ=α+kd。根据d的范围, 36°≤kd≤144°。
图 3-4-7 (dr=d1=d2=…=0.15λ, 2a/λ=0.0025)
图 3-4-4 二元引向天线
考虑到天线阵的阻抗特性,振子“2”的电流由下式决 定:
式中
I2 Z21 me ja
I1
Z22
m
R221
X
2 21
R222Biblioteka X2 22
π arctan X 21 arctan X 22
R21
R22
(3-4-2) (3-4-3)
表3-4-1 电流比(2l1/λ=0.475)
图 3-4-5
(a) 2l1/λ=0.475, 2l2/λ=0.500; (b) 2l1/λ=0.475, 2l2/λ=0.450
3. 多元引向天线(Multiple Element Antenna) 为了得到足够的方向性,实际使用的引向天线大多数是 更多元数的,图3-4-6(a)就是一个六元引向天线,其中的有源
图 3-4-3 电流相位条件
由此可知,在d/λ≤0.4的前提下,振子“2”作为引向器
反射器:0 180
引向器:-180
0
(3-4-1)
2. 二元引向天线(Two Element Yagi Uda Antenna) 实用中为了使天线的结构简单、 牢固、 成本低,在引 向天线中广泛采用无源振子作为引向器或反射器,如图3-4-4 所示。由于一般只有一个有源振子,在引向天线中无源振子
天线原理与设计讲义.ppt

简言之:天线的功能主要有两点: (1)能量转换 (2)定向辐射或接收 无线电通讯线路中的辐射和接收天线示意:
发射系统等效电路:
天线等效电路中最主要的一个参数——辐射电阻Rr。 可以认为天线辐射的电磁波能量全部由Rr吸收。
发射天线空间辐射方向图。
●典型的空间三维方向图
●典型的二维方向图
各种各样的方向图是由各种各样的天线实现的。
■ IE3D软件 ■ FIDELITY软件
(2)在天线技术应用方面
卫星通信技术发展推动了卫星天线和大型地面站天 线的发展,出现了大型平面阵、卡塞格仑天线及各种反 射面天线馈源。
雷达制导、搜索、跟踪、预警技术的应用推动了单 脉冲雷达天线、相控阵天线,多波束天线的发展。
半导体技术的发展使无线电技术向毫米波、亚毫米 波甚至更高频率发展,对天线提出了小型化、集成化、 宽带化等一系列要求,出现了有源天线、微带天线和印 刷天线、印制板开槽天线、表面波天线、共形阵列天线 等。
另外,还有八木天线,对数周期天线、阵列天线。阵 列天线又有直线阵天线、平面阵天线、附在某些载体表 面的共形阵列天线等。
为便于分析和研究天线性能出发,天线可以分为如下 几大类:
(1) 线天线(Wire Antennas) ——(1~6)章
(2) 口径天线(Aperture Antennas) ——(8~10章)
(1)在天线理论方法方面
■几何绕射理论 ■平面波谱展开法 ■时域有限差分法 ■天线近场测量理论
■矩量法 ■有限元法 ■时域积分方程法 ■阵列分析与综合理论
这些理论方法为天线的工程设计奠定了坚实的基础,
随着计算机技术的发展大都形成了计算机仿真的电子自 动化设计软件。
■ HFSS软件 ■ CST软件 ■ FEKO软件
天线原理与设计讲义图文

第一章天线的方向图天线的方向图可以反映出天线的辐射特性,一般情况下天线的方向图表示天线辐射电磁波的功率或场强在空间各个方向的分布图形。
而相位、极化方向图只在特殊应用中使用。
对不同的用途,要求天线有不同的方向图。
这一章介绍几种简单的直线天线和简单阵列天线的方向图,以及地面对天线方向图的影响。
简单天线涉及元天线、单线行波天线、对称振子天线等。
简单阵列天线涉及由同类型天线组成的二元阵、三元阵和多元阵,对简单阵列将介绍方向图相乘原理。
线天线的分析基础是元天线。
一个有限尺寸的线天线可看作是无穷多个元天线的辐射场在空间某点的叠加。
因此这里首先讨论元天线。
1.1元天线1.1.1 元天线的辐射场元天线又称作基本振子或电流元,它是一个长为的无穷小直导线,其上电流为均匀分布dz I 。
如果建立如图1-1所示坐标系,由电磁场理论很容易求得其矢量位A 为j 0ˆ4r z e z Idz zA rβμπ−=A ˆ= (1.1图1-1 (a 基本振子及坐标系 (b 基本振子及场分量取向在求坐标系中,A 的表示为ˆˆr rAA A ˆθϕθϕ=++A ,利用球坐标中矢量各分量与直角坐标系中矢量各分量的关系矩阵sin cos sin sin cos cos cos cos sin sin sin cos 0r x y z A A A A A Aθϕθϕθϕθθϕθϕθϕϕ⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡=−⎡⎡⎡⎡⎡⎡⎡⎡⎡−⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡ (1.2 因,可得0x y A A == cos sin 0r z z A A A A A θϕθθ⎡=⎡=−⎡⎡=⎡ (1.3由00j +j ωωμε∇∇=−A E A i 和01μ=∇×H A ,可得基本振子的电磁场各分量为 j j 02j 021j sin (14j 11j sin [1]4j (j 1cos (12j 0r rr r r Idz H e r r Idz E e r r r Idz E e r r E H Hβϕβθβϕθβθπββηθπββηθπβ−−−⎡=+⎡⎡⎡=++⎡⎡⎡=+⎡⎡⎡===⎡(1.4 式中,E 为电场强度;H 为磁场强度;下标、r θ、ϕ表示球坐标系中的各分量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设有一段长为l,特性阻抗为Zc的有耗开路传输线如 下图(a)所示,由传输线理论可得其输入阻抗为
Zin = Zc coth(γ l)
= Zc coth[(α + jβ )l] (2.1)
式中,Zc =
R1 + jω L1 (2.2)
G1 + jωC1
γ = α + jβ
= (R1 + jω L1)(G + jωC1) (2.3a)
βl
(2.16)
当 (Rr / Z0′)2 ≪ sin2 βl 且l≤0.4λ 时,上式又可简化为
Zin
=
Rr sin2 β l
−
jZ0′
cot(β l)
(2.17)
由式(2.16)计算的对称振子输入电阻和电抗随l/λ变化的曲 线如下图所示,图中参变量为振子的平均特性阻抗Z'0 。
由此图可总结出对称振子天线输入阻抗的如下特点:
=
Z0′2 Rr
(2.18)
链接
(6) 对称振子谐振长度的缩短现象
对称振子的谐振长度是其输入阻抗的虚部为零时的 长度。由前面图可见,Xin=0对应的电长度略小于0.25和 略小于0.5。这一现象称之为缩短效应。振子天线愈粗, 缩短愈多。所以,实际使用的半波振子全长是小于半个 波长的。产生缩短的原因大致有两点:
⎪⎩β = ω L1C1
(2.4)
Zc
=
Z0(1 −
j
R1 2ω L1
)
=
Z0(1 −
jα β
)
(2.5)
Z0为传输线无耗时的特性阻抗
Z0 = L1 / C1
(2.7)
若已知Z0、R1和C1,由式(2.1)就可确定一段长为l的有耗 开路传输线的输入阻抗。显然这还不能用于对称振子天
线,因为双线传输线与对称天线存在如下显著的差别:
(3)当l≈λ/4时(半波振子),输入电抗为零,对称振子就如 一个串联谐振电路。此时Zin≈Rin= Rr=73Ω。 (4) 当λ/4<l<λ/2时,输入阻抗呈感性;
(5) 当l≈λ/2时(全波振子),振子相当于一个并联谐振电路,
输入电抗为零, 输入电阻为最大值, 此时由式(2.16)有
Zin
=
Rin
当振子半径很小时,封闭柱面的上下底面的积分可忽 略不计,只考虑圆柱侧面的积分。此时
ds = ρˆds = ρˆadϕdz
把式(2.27)代入(2.26), 并注意到近场各分量与坐标φ无关,
得
∫ ∫ Pr
=
1 −
2
2π
dϕ
0
l −l
Ez
(a,
z
)Hϕ*
(a,
z
)adz
∫ = − 1
2
l −l
Ez
(a,
z
)Hϕ*
(a,
z
)2π
adz
(2.28)
由安培环路定律 2π aHϕ (a, z) = I (z) ,则得
∫1
Pr = − 2
l −l
Ez
(a,
z)I
*
(
z)dz
(2.29)
式中,[-Ez(a,z)dz]表示振子dz小段上驱动电流流动的感应 电动势,故此法称之为“感应电动势法”。
链接
由
Pr
=
1 2
返回
(1) 传输线是非辐射系统,线上损耗为导体的欧姆损耗。 而对称振子天线是辐射系统,电流从输入端到末端,其 间的每一点都将产生能量的辐射,可用单位长度上的能 量损耗来表示传输线的分布电阻R1。
(2) 双线传输线的两线距离恒定,分布参数是均匀的。 而对称振子天线的两臂上对称点之间的距离是变化的, 见前面图(b),分布参数是非均匀的。
坡印亭矢量法是先求得天线的辐射功率Pr,然后由 Rr=2 Pr/ I2m 求得其辐射电阻。这个方法前面已经作了介 绍。这里主要讨论等值传输线法和感应电势法。
2.1 等值传输线法
坡印亭矢量法是由远区辐射场求得表示功率密度的 坡印亭矢量,然后在以天线中点为圆心,以远区距离为 半径的一个球面上积分求得辐射功率,最后求得辐射电 阻。该方法的缺点是:
− 2z cos(β l) e− jβr ] r
和
Ez
=
− jη0Im 4π
e− jβ R1 [
R1
+
e− jβ R2 R2
− 2 cos(β l) e− jβr ] r
(2.24) (2.25)
圆柱对称振子的近区电磁场只有三个分量Hφ、Eρ和 Ez,这三个场分量的最后一项在振子臂长l 恰好为λ/2的奇 数倍时为零。
返回1 返回
(1) 对称振子的平均特性阻抗Z'0愈小,输入阻抗Zin=Rin+ jXin随l/λ的变化就愈小,阻抗曲线就愈平缓,其频率特
性就愈好。实际中常采用加大振子直径的办法来降低特
性阻抗,以展宽工作频带。短波波段使用的笼形对称振
子(P67)就是基于这个原理。 (2) 当l<λ/4时,输入阻抗呈容性, 并有不大的输入电阻。
①以上计算是取β'=β, 但由于电流波沿振子边传输边辐 射有衰减, 使得相位常数变大β'>β , 波长缩短λ'<λ 。
②振子天线的“末端效应”。振子导体有一定直径,使振 子馈电端和两个末端的分布电容增大, 馈电端的效应使得附 加电容与天线输入阻抗一起并联在馈电传输线上,引起误差;两 个末端的效应使得末端电流不为零,这将使振子的等效 长度增大,造成谐振长度缩短,如下图所示。
但是,对称振子天线的输入阻抗仍然可用式(2.1)表 示,但必须修改参数Zc、α 和β。 1、修改特性阻抗Zc
在D>>ρ的情况下,无耗双线传输线的特性阻抗为
Z0 = 120 ln(D / ρ)
(2.7)
链接Biblioteka 式中D为两线间距,ρ为导线截面直径,见下图。而对称 振子两臂上的两个对称点之间的距离为D=2z,其特性阻 抗在0<z<l内是变化的。可用如下方法求对称振子的平均 特性阻抗
4、对称振子的输入阻抗Zin
由式(2.1)的输入阻抗公式 Zin = Zc′ coth[(α′ + jβ )l]
及
Zc′
=
Z0′(1 −
j α′) β
,并把虚、实部分开,得
Zin
=
Z0′(1 −
jα
′ )
coth[(
β
jβ
+ α′)l]
=
Z0′
{[sinh(2α′l) − α′ sin(2β l)]
|
Im
|2
Zr
∫ Z0′
=
1 l
l
2z
120ln( )dz
0
ρ
= 120[ln( 2l ) − 1] ρ
(2.8)
由此式可见,对称振子的
臂长l愈小, 或导线截面直 径ρ愈大, 则Z'0就小。把 式(2.5)中的Z0用Z'0替代, 得
Zc′
=
Z0′ (1−
j
α β
)
(2.9)
链接
2、修改衰减常数α
在不计G1的情况下,传输线的衰减常数α是由传输 线上单位长度的导体热损耗电阻R1产生的。对于对称振 子天线来说,不计导体热损耗,R1由单位长度的辐射电 阻R'1取代,并假设R'1沿天线是均匀的。这际上就是确定
■对称振子有一定直径,其馈电端和末端分布电容增 大,末端电流实际不为零,振子愈粗,末端效应愈显 著,这也将影响相位常数。
一般情况下,可由β'取代β。由于影响相位常数改变 的因素不止一个,要确定是较困难的。书上P33图2-8给 出了天线上电流传播的相位常数与自由空间相位常数的 比值ξ=β'/β随l/λ变化的曲线,参变量为d/λ,d为导线直 径。在大多数情况下β'与β接近,所以工程上一般取β' =β。
天线原理与设计
教师: 王建 电子工程学院二系
第二章 天线的阻抗
本章的主要目的是要求天线的输入阻抗,它是天线 的重要参数之一。因为知道天线的输入阻抗之后,就可 以选择合适的馈电传输线与之匹配。
要严格计算天线的输入阻抗是困难的,工程上常采 用一些近似方法。主要有三种方法,即
■ 坡印亭矢量法;
■ 等值传输线法; ■ 感应电势法。
量法求辐射功率的表示相同,但其中的电磁场已经不同。
坡印亭矢量法中所用的电磁场是远区场,这里的积分面
在天线表面,式中的电磁场必须是近场。
式(2.26)中的电磁场矢量分别为 E = ρˆ Eρ + zˆEz和 H = ϕˆHϕ ,
则
E × H* = zˆEρ Hϕ* − ρˆ Ez Hϕ*
(2.27)
返回
臂上,并代入I(z)=Imsin[β(l-|z|)] 后积分,得
R1′
=
l
[1
−
2Rr sin(2β
l
)
]
(2.13)
2βl
因此
α ′ = R1′ =
Rr
2Z0′
Z
0′l
[1
−
sin(2β 2βl
l
)
]
(2.14)
3、修改相位常数β
影响天线电流传播相位常数改变的原因有两点:
■电流波在天线上一边传输一边辐射,使得电流有衰 减,电流传播的相速减小,波长缩短,相位常数大于自 由空间相位常数。
(1) 只能计算天线的输入电阻,不能计算输入电抗。 (2) 由于假定天线上电流为正弦分布,使得天线输入端为 波节点时(如全波振子),不能求出输入电阻。
等值传输线法可以计算天线输入阻抗(包括虚、实部)。 该方法所得公式简便,便于工程应用。
