(完整版)专题8二次函数与圆组合压轴题
二次函数与圆结合的压轴题Word版

图6xy FE H N MPD C B AO二次函数和圆【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数ky x=(1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二次函数图象的解析式;(2) 若二次函数图象的顶点为D ,问当k 为何值时,四边形ADBP 为菱形.【例题2】(湖南省韶关市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
设M 是AB 的中点,P 是线段DE 上的动点. (1)求M 、D 两点的坐标;(2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标;(3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的面积.【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B.(1)求直线CB的解析式;(2)若抛物线y=ax2+b x+c的顶点在直线BC上,与x轴的交点恰为点E、F,求该抛物线的解析式;(3)试判断点C是否在抛物线上?(4)在抛物线上是否存在三个点,由它构成的三角形与△AOC相似?直接写出两组这样的点.【例题4】(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E.(1)求m的值及抛物线的解析式;(2)设∠DBC = α,∠CBE = β,求sin(α-β)的值;(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.【例题5】(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B .已知抛物线216y x bx c =++过点A 和B ,与y 轴交于点C .(1)求点C 的坐标,并画出抛物线的大致图象.(2)点Q (8,m )在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ +PB 的最小值.(3)CE 是过点C 的⊙M 的切线,点E 是切点,求OE 所在直线的解析式.【例题6】(山西省临汾市)26. 如图所示,在平面直角坐标系中,M 经过原点O ,且与x 轴、y 轴分别相交于(60)(08)A B --,,,两点.(1)请求出直线AB 的函数表达式;(2)若有一抛物线的对称轴平行于y 轴且经过点M ,顶点C 在M 上,开口向下,且经过点B ,求此抛物线的函数表达式;(3)设(2)中的抛物线交x 轴于D E ,两点,在抛物线上是否存在点P ,使得115PDE ABC S S =△△?若存在,请求出点P 的坐标;若不存在,请说明理由.【例题7】在△ABC 中,∠A =90°,AB =4,AC =3,M 是AB ∥BC交AC 于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形x(1)用含x 的代数式表示△MNP 的面积S ; (2)当x 为何值时,⊙O 与直线BC 相切?(3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少?【例题8】如图,点P 在y 轴上,半径为3的⊙P 分别交x 轴于A 、B 两点,AB=4,交y 轴负半轴于点C ,连接AP 并延长交⊙P 于点D ,过D 作⊙P 的切线分别交x 轴、y 轴于点F 、G ; (1)求直线FG 的解析式;(2)连接CD 交AB 于点E ,求PCD tan 的值;(3)设M 是劣弧BC 上的一个动点,连接DM 交x 轴于点N ,问:是否存在这样的一个常数k ,始终满足AN ·AB+DN ·DM=K ,如果存在,请求出K 的值,如果不存在,请说明理由;A B M N D OA B C M N P 图 1O AB M N 图 3O。
二次函数和圆综合(压轴题+例题+巩固+答案解析)

【例1】.如图,点()40M ,,以点M 为圆心、2为半径的圆与x 轴交于点A B ,.已知抛物216y x bx c =++过点A 和B ,与y 轴交于点C .⑴ 求点C 的坐标,并画出抛物线的大致图象.⑵ 点()8Q m ,在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ PB + 最小值. ⑶ CE 是过点C 的M ⊙的切线,点E 是切点,求OE 所在直线的解析式.【巩固】已知抛物线2y ax bx c =++与y 轴的交点为C ,顶点为M ,直线CM 的解析式2y x =-+并且线段CM 的长为(1)求抛物线的解析式。
(2)设抛物线与x 轴有两个交点A (X 1 ,0)、B (X 2 ,0),且点A 在B 的左侧,求线段AB 的长。
(3)若以AB 为直径作⊙N ,请你判断直线CM 与⊙N 的位置关系,并说明理由。
【例2】如图,在平面直角坐标系中,以点(04)C ,为圆心,半径为4的圆交y 轴正半轴于点A ,AB 是C ⊙的切线.动点P 从点A 开始沿AB 方向以每秒1个单位长度的速度运动,点Q 从O 点开始沿x 轴正方向以每秒4个单位长度的速度运动,且动点P 、Q 从点A 和点O 同时出发,设运动时间为t (秒).⑴当1t =时,得到1P 、1Q 两点,求经过A 、1P 、1Q 三点的抛物线解析式及对称轴l ;⑵当t 为何值时,直线PQ 与C ⊙相切?并写出此时点P 和点Q 的坐标;⑶在⑵的条件下,抛物线对称轴l 上存在一点N ,使NP NQ +最小,求出点N 的坐标并说明理由.提示:(1)先求出t=1时,AP 和OQ 的长,即可求得P 1,Q 1的坐标,然后用待定系数法即可得出抛物线的解析式.进而可求出对称轴l 的解析式.(2)当直线PQ 与圆C 相切时,连接CP ,CQ 则有Rt △CMP ∽Rt △QMC (M 为PG 与圆的切点),因此可设当t=a 秒时,PQ 与圆相切,然后用a 表示出AP ,OQ 的长即PM ,QM 的长(切线长定理).由此可求出a 的值.(3)本题的关键是确定N 的位置,先找出与P 点关于直线l 对称的点P ′的坐标,连接P ′Q ,那么P ′Q 与直线l 的交点即为所求的N 点,可先求出直线P ′Q 的解析式,进而可求出N 点的坐标.【巩固】已知二次函数图象的顶点在原点O ,对称轴为y 轴.一次函数1y kx =+的图象与 二次函数的图象交于A B ,两点(A 在B 的左侧),且A 点坐标为()44-,.平行于x 轴的直线l 过()01-,点.⑴ 求一次函数与二次函数的解析式;⑵ 判断以线段AB 为直径的圆与直线l 的位置关系,并给出证明;⑶ 把二次函数的图象向右平移2个单位,再向下平移t 个单位()0t >,二次函数的图象与x轴交于M N,,三点的圆的,两点,一次函数图象交y轴于F点.当t为何值时,过F M N面积最小?最小面积是多少?【例3】如图1,⊙O的半径为1,正方形ABCD顶点B坐标为(),,顶点D在⊙O上运动.50⑴当点D运动到与点A、O在同一条直线上时,试证明直线CD与⊙O相切;⑵当直线CD与⊙O相切时,求OD所在直线对应的函数关系式;⑶设点D的横坐标为x,正方形ABCD的面积为S,求S与x之间的函数关系式,并求出S 的最大值与最小值.【巩固】如图,已知点A 从()10,出发,以1个单位长度/秒的速度沿x 轴向正方向运动,以O A ,为顶点作菱形OABC ,使点B C ,在第一象限,且60AOC ∠=︒;以()03P ,为圆心,PC 为半径作圆.设点A 运动了t 秒,求: ⑴ 点C 的坐标(用含t 的代数式表示);⑵ 当点A 在运动过程中,所有使P 与菱形OABC 的边所在直线相切的t 的值.【例4】已知:如图,抛物线213y x m =+与x 轴交于A B ,两点,与y 轴交于C 点,90ACB ∠=︒⑴ 求m 的值及抛物线顶点坐标;⑵ 过A B C ,,的三点的M ⊙交y 轴于另一点D ,连结DM 并延长交M ⊙于点E ,过E 点的M ⊙的切线分别交x 轴、y 轴于点F G ,,求直线FG 的解析式;⑶ 在条件⑵下,设P 为CBD 上的动点(P 不与C D ,重合),连结PA 交y 轴于点H ,问是否存在一个常数k ,始终满足AH AP k ⋅=,如果存在,请写出求解过程;如果不存在,请说明理由.【巩固】如图,已知点A的坐标是(),,以AB为直径作O',90-,,点B的坐标是()10交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.⑴求抛物线的解析式;⑵点E是AC延长线上一点,BCE∠的平分线CD交O'于点D,连结BD,求直线BD的解析式;⑶在⑵的条件下,抛物线上是否存在点P,使得PDB CBD∠=∠?如果存在,请求出点P的坐标;如果不存在,请说明理由.DCEA yxBO O'课后作业:1.如图,直角坐标系中,已知两点()A,,点B在第一象限且OAB2000O,,()∆为正三角形,OAB∆的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.⑴求B C,两点的坐标;⑵求直线CD的函数解析式;⑶设E F,分别是线段AB AD,上的两个动点,且EF平分四边形ABCD的周长.试探究:AEF∆的最大面积?参考答案例1【巩固】例2分析:(1)先求出t=1时,AP和OQ的长,即可求得P1,Q1的坐标,然后用待定系数法即可得出抛物线的解析式.进而可求出对称轴l的解析式.(2)当直线PQ与圆C相切时,连接CP,CQ则有Rt△CMP∽Rt△QMC(M为PG与圆的切点),因此可设当t=a秒时,PQ与圆相切,然后用a表示出AP,OQ的长即PM,QM的长(切线长定理).由此可求出a的值.(3)本题的关键是确定N的位置,先找出与P点关于直线l对称的点P′的坐标,连接P′Q,那么P′Q与直线l的交点即为所求的N点,可先求出直线P′Q的解析式,进而可求出N点的坐标.【巩固】例3【巩固】例4【巩固】作业。
二次函数与圆结合的压轴题

图6xy FE H N MPD C B AO二次函数与圆【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数ky x=(1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二次函数图象的解析式;(2) 若二次函数图象的顶点为D,问当k 为何值时,四边形ADBP 为菱形.【例题2】(湖南省韶关市) 25、如图6,在平面直角坐标系中,四边形OABC 就是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
设M 就是AB 的中点,P 就是线段DE 上的动点、 (1)求M 、D 两点的坐标;(2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标;(3)过P 作PH ⊥BC,垂足为H,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的面积、【例题3】(甘肃省白银等7市新课程)28、 在直角坐标系中,⊙A 的半径为4,圆心A 的坐标为(2,0),⊙A 与x 轴交于E 、F 两点,与y 轴交于C 、D 两点,过点C 作⊙A 的切线BC ,交x 轴于点B . (1)求直线CB 的解析式;(2)若抛物线y =ax 2+b x +c 的顶点在直线BC 上,与x轴的交点恰为点E 、F ,求该抛物线的解析式; (3)试判断点C 就是否在抛物线上?(4) 在抛物线上就是否存在三个点,由它构成的三角形与△AOC 相似?直接写出两组这样的点.【例题4】(绵阳市)25、如图,已知抛物线y = ax 2 + bx -3与x 轴交于A 、B 两点,与y 轴交于C点,经过A 、B 、C 三点的圆的圆心M (1,m )恰好在此抛物线的对称轴上,⊙M 的半径为5.设⊙M 与y 轴交于D ,抛物线的顶点为E . (1)求m 的值及抛物线的解析式;(2)设∠DBC = α,∠CBE = β,求sin(α-β)的值;(3)探究坐标轴上就是否存在点P ,使得以P 、A 、C 为顶点的三角形与△BCE 相似?若存在,请指出点P 的位置,并直接写出点P 的坐标;若不存在,请说明理由.【例题5】(南充市)25、如图,点M (4,0),以点M 为圆心、2为半径的圆与x 轴交于点A 、B .已知抛物线216y x bx c =++过点A 与B ,与y 轴交于点C .(1)求点C 的坐标,并画出抛物线的大致图象.(2)点Q (8,m )在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ +PB 的最小值.(3)CE 就是过点C 的⊙M 的切线,点E 就是切点,求OE 所在直线的解析式.【例题6】(山西省临汾市)26、 如图所示,在平面直角坐标系中,M 经过原点O ,且与x 轴、y 轴分别相交于(60)(08)A B --,,,两点.(1)请求出直线AB 的函数表达式;(2)若有一抛物线的对称轴平行于y 轴且经过点M ,顶点C 在M 上,开口向下,且经过点B ,求此抛物线的函数表达式;(3)设(2)中的抛物线交x 轴于D E ,两点,在抛物线上就是否存在点P ,使得115PDE ABC S S =△△?若存在,请求出点P 的坐标;若不存在,请说明理由.【例题7】在△ABC 中,∠A =90°,AB =4,AC =3,M 就是AB 交AC于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形AMPN .令AM (1)用含x 的代数式表示△MNP 的面积S ; (2)当x 为何值时,⊙O 与直线BC 相切?(3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值就是多少?xB【例题8】如图,点P 在y 轴上,半径为3的⊙P 分别交x 轴于A 、B 两点,AB=4,交y 轴负半轴于点C,连接AP并延长交⊙P 于点D,过D 作⊙P 的切线分别交x 轴、y 轴于点F 、G; (1)求直线FG 的解析式;(2)连接CD 交AB 于点E,求PCD tan 的值;(3)设M 就是劣弧BC 上的一个动点,连接DM 交x 轴于点N,问:就是否存在这样的一个常数k,始终满足AN ·AB+DN ·DM=K,如果存在,请求出K 的值,如果不存在,请说明理由;ABMND OABMN 图 3O。
2023年九年级数学中考专题:二次函数与圆综合压轴题(含简单答案)

2023年九年级数学中考专题:二次函数与圆综合压轴题1.如图1,在平面直角坐标系中,O为坐标原点,已知抛物线与x轴交于,两点,与y轴交于点C.(1)求抛物线解析式;(2)如图2,M是抛物线顶点,的外接圆与x轴的另一交点为D,与y轴的另一交点为E.①求;②若点N是第一象限内抛物线上的一个动点,在射线上是否存在点P,使得与相似?如果存在,请求出点P的坐标;(3)点Q是拋物线对称轴上一动点,若为锐角,且,请直接写出点Q 纵坐标的取值范围.2.【概念学习】在平面直角坐标系中,对于已知的点和图形,给出如下定义:如果图形上存在一点,使得当时,,则称点为图形的一个“垂近点”.(1)【初步理解】若图形为线段,,,在点、、、中,是线段的“垂近点”的为________;(2)【知识应用】若图形为以坐标原点为圆心,2为半径的圆,直线与轴交于点、与轴交于点,如果线段上的点都是的“垂近点”,求的取值范围;(3)若图形为抛物线,以点为中心,半径为的四边形,轴,轴,如果正四边形上存在“垂近点”,直接写出的取值范围.3.在平面直角坐标系xOy中,已知抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y 轴交于C点,D为抛物线顶点.(1)连接AD,交y轴于点E,P是抛物线上的一个动点.①如图一,点P是第一象限的抛物线上的一点,连接PD交x轴于F,连接,若,求点P的坐标.②如图二,点P在第四象限的抛物线上,连接AP、BE交于点G,若,则w 有最大值还是最小值?w的最值是多少?(2)如图三,点P是第四象限抛物线上的一点,过A、B、P三点作圆N,过点作轴,垂足为I,交圆N于点M,点在运动过程中,线段是否变化?若有变化,求出MI的取值范围;若不变,求出其定值.(3)点Q是抛物线对称轴上一动点,连接OQ、AQ,设AOQ外接圆圆心为H,当的值最大时,请直接写出点H的坐标.4.如图1,在平面直角坐标系中,已知抛物线y=ax2+bx-4(a≠0)经过点A(-2,0)和点B(4,0).(1)求这条抛物线所对应的函数表达式;(2)点P为抛物线上第一象限内一点,若S△ABC=2S△PBC,求点P的坐标;(3)如图2,点D是第二象限内抛物线上一点,过点D作DF⊥x轴,垂足为F,△ABD 的外接圆与DF相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.5.如图,抛物线经过点,,直线AC的解析式为,且与y轴相交于点C,若点E是直线AB上的一个动点,过点E作轴交AC于点F.(1)求抛物线的解析式;(2)点H是y轴上一动点,连结EH,HF,当点E运动到什么位置时,四边形EAFH 是矩形?求出此时点E,H的坐标;(3)在(2)的前提下,以点E为圆心,EH长为半径作圆,点M为上以动点,求的最小值.6.已知二次函数的图象经过点A(2,0),B(,0),C(0,4),点为二次函数第二象限内抛物线上一动点,轴于点,交直线于点,以为直径的圆⊙M与交于点.(1)求这个二次函数的关系式;(2)当三角形周长最大时.求此时点点坐标及三角形的周长;(3)在(2)的条件下,点N为⊙M上一动点,连接BN,点Q为BN的中点,连接HQ,求HQ的取值范围.7.如图,在平面直角坐标系中,抛物线,y与轴交于A、B两点,与轴交于点C.(1)求点A、B、C的坐标;(2)如图1,连接BC,点D是抛物线上一点,若∠DCB=∠ABC,求点D的坐标;(3)如图2,若点P在以点O为圆心,OA长为半径作的圆上,连接BP、CP,请你直接写出CP+BP的最小值.8.如图,在平面直角坐标系中,半径为1的圆的圆心在坐标原点,且与两坐标轴分别交于、、、四点,点坐标为.抛物线与轴交于点,与直线交于点、,且、分别与圆相切于点和点.(1)求抛物线的解析式.(2)过点作圆的切线交的延长线于点,判断点是否在抛物线上,说明理由.(3)抛物线对称轴交轴于点,连接并延长交于点,求点的坐标.9.如图,在平面直角坐标系中,抛物线交y轴于点,交x轴于两点.(1)求此抛物线的解析式;(2)已知点P是抛物线上的一个动点,且位于A、C两点之间,问:当点P运动到什么位置时,的面积最大?并求出此时P点的坐标和的最大面积;(3)过点B作线段的垂线交抛物线于点D,如果以点C为圆心的圆与直线相切,请判断抛物线的对称轴l与有怎样的位置关系,并给出证明.10.如图,直线与x轴交于点B,与y轴交于点C,抛物线经过B、C两点,且与x轴交于另一点A.(1)求抛物线的解析式.(2)点P是线段BC下方的抛物线上的动点(不与点B、C重合),过P作PD∥y轴交BC 于点D,以PD为直径的圆交BC于另一点E,求DE的最大值及此时点P的坐标;(3)当(2)中的DE取最大值时,将△PDE绕点D旋转,当点P落在坐标轴上时,求点E的坐标.11.直角坐标系xOy中,有反比例函数上的一动点P,以点P为圆心的圆始终与y轴相切,设切点为A(1)如图1,⊙P运动到与x轴相切时,求OP2的值.(2)设圆P运动时与x轴相交,交点为B、C,如图2,当四边形ABCP是菱形时,①求出A、B、C三点的坐标.②设一抛物线过A、B、C三点,在该抛物线上是否存在点Q,使△QBP的面积是菱形ABCP 面积的?若存在,求出所有满足条件的Q点的坐标;若不存在,说明理由.12.已知:如图,在平面直角坐标系xOy中,以点P(2,)为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).(1)求经过A、B、C三点的抛物线的解析式;(2)在(1)中的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的.如果存在,请直接写出所有满足条件的M点的坐标;如果若不存在,请说明理由;(3)如果一个动点D自点P出发,先到达y轴上的某点,再到达x轴上某点,最后运动到(1)中抛物线的顶点Q处,求使点D运动的总路径最短的路径的长.13.已知,如图,二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),B(3,0),点E为二次函数第一象限内抛物线上一动点,EH⊥x轴于点H,交直线BC于点F,以EF为直径的圆⊙M与BC交于点R.(1)求这个二次函数关系式.(2)当△EFR周长最大时.①求此时点E点坐标及△EFR周长.②点P为⊙M上一动点,连接BP,点Q为BP的中点,连接HQ,求HQ的最大值.14.如图所示,对称轴为直线的抛物线与轴交于、两点,与轴交于点,点在抛物线对称轴上并且位于轴的下方,以点为圆心作过、两点的圆,恰好使得弧的长为周长的.(1)求该抛物线的解析式;(2)求的半径和圆心的坐标,并判断抛物线的顶点与的位置关系;(3)在抛物线上是否存在一点,使得?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.15.已知抛物线y=ax2+bx+5(a≠0)经过A(5,0),B(6,1)两点,且与y轴交于点C.(1)求抛物线y=ax2+bx+5(a≠0)的函数关系式;(2)如图1,连接AC,E为线段AC上一点且横坐标为1,⊙P是△OAE外接圆,求圆心P 点的坐标;(3)如图2,连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F;①点E在运动过程中四边形OEAF的面积是否为定值?如果是,请求出这个定值;如果不是,请说明理由;②求出当△AEF的面积取得最大值时,点E的坐标.16.如图1,已知圆O的圆心为原点,半径为2,与坐标轴交于A,C,D,E四点,B 为OD中点.(1)求过A,B,C三点的抛物线解析式;(2)如图2,连接BC,AC.点P在第一象限且为圆O上一动点,连接BP,交AC于点M,交OC于点N,当MC2=MN•MB时,求M点的坐标;(3)如图3,若抛物线与圆O的另外两个交点分别为H,F,请判断四边形CFEH的形状,并说明理由.17.已知一次函数:与轴交于点,与轴交于点.抛物线(、为常数)过定点,连接,点为线段上一动点.(1)求出点的坐标;(2)过作于点,于点,设点横坐标为,长度为,试求关于的函数解析式;(3)①当,时,该抛物线上存在唯一的点使,求此时抛物线的解析式;②过点作交线段于点,连接并延长交的外接圆于点,当点在上移动时,求的最大值.18.已知抛物线经过,,三个点.(1)求抛物线的解析式;(2)如图1,作的外接圆,为上方半圆上一点,当时,求的长;(3)如图2,直线与抛物线交于,两点,与轴交于点,作轴的平行线,分别与线段、抛物线交于,两点(点与点,不重合),点为射线上一点,当与相似时,求的最大面积.参考答案:1.(1)(2)①;②存在,或或或(3)或2.(1),;(2);(3)或时,正方形上存在抛物线的“垂近点”.3.(1)①,②w有最小值,w的最值是(2)不变,(3)或4.(1);(2);(3)为定值.5.(1);(2),;(3)6.(1);(2)F(,4),△EFD的周长为;(3).7.(1),,;(2),;(3)8.(1);(2)点在抛物线上;(3)9.(1);(2),;(3)相交,10.(1)y=x2﹣x﹣2;(2)m=2时,DE有最大值,此时P;(3),或E或11.(1)16;(2)①A(0,),B(2,0),C(6,0);②存在,满足条件的Q点有(0,),(14,),(8,)和(6,0).12.(1).(2)存在,点M的坐标为(0,),(3,0),(4,),(7,).(3).13.(1)y=﹣x2+2x+3;(2)①E(,),周长为+;②HQ的最大值大为:+.14.(1)(2)2,,点在上(3)存在,,,15.(1)抛物线解析式为y=x2﹣x+5(2)圆心P点的坐标为(,)(3)①四边形OEAF的面积是定值,这个定值为;②当△OEF的面积取得最小值时,E点坐标为(,)16.(1)y=﹣x2+x+2;(2)M(,);(3)四边形CFEH是矩形.17.(1);(2)();(3)①;②18.(1);(2);(3).。
二次函数与圆的综合压轴题

二次函数与圆的综合压轴题
一、题目描述
本题是一道综合性的数学题,涉及到二次函数和圆的相关知识。
具体要求如下:
给定一个二次函数 $y=ax^2+bx+c$ 和一个圆 $x^2+y^2=r^2$,其中 $a,b,c,r$ 均为已知常数,且 $a\neq0$。
请编写一个函数,判断该二次函数与圆是否有交点,并输出交点的坐标。
二、解题思路
1. 二次函数与圆的关系
首先,我们需要了解二次函数和圆之间的关系。
对于一个二次函数$y=ax^2+bx+c$ 和一个圆 $x^2+y^2=r^2$,它们之间可能存在以下三种情况:
(1)没有交点:当二次函数和圆分离时,它们没有交点。
(2)相切:当二次函数和圆相切时,它们只有一个交点。
(3)相交:当二次函数和圆相交时,它们有两个交点。
接下来,我们需要确定如何求出这些交点的坐标。
2. 求解交点坐标
对于一条直线和一个圆之间的交点坐标可以通过联立直线方程和圆方程求解。
但是对于一个二次函数而言,并不存在明确的直线方程。
因此,在本题中,我们可以通过以下步骤求解交点坐标:
(1)将二次函数和圆的方程联立,得到一个关于 $x$ 的二次方程。
(2)解出该二次方程的根,即为交点的横坐标。
(3)将横坐标代入二次函数或圆的方程中,求出相应的纵坐标。
最后,我们需要根据交点个数输出不同的结果。
如果没有交点,则输出“无交点”;如果有一个交点,则输出该交点坐标;如果有两个交点,则输出两个交点坐标。
三、代码实现
下面是本题的完整代码实现:。
二次函数与圆综合训练(含解析)

二次函数与圆综合提高(压轴题)1、如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE 翻折,与梯形BCED重叠的部分记作图形L.(1)求△ABC的面积;(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;∴MO=OE,∠MOE=120°,∴∠OME=30°,∴∠DME=90°,∴DE是直径,S⊙O=π×12=π.2、(2013•压轴题)如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(﹣4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.(1)求直线AB的函数解析式;(2)当点P在线段AB(不包括A,B两点)上时.①求证:∠BDE=∠ADP;②设DE=x,DF=y.请求出y关于x的函数解析式;(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.解:(1)设直线AB的函数解析式为y=kx+4,代入(4,0)得:4k+4=0,解得:k=﹣1,则直线AB的函数解析式为y=﹣x+4;(2)①由已知得:OB=OC,∠BOD=∠COD=90°,又∵OD=OD,∴△BOD≌△COD,∴∠BOD=∠CDO,∵∠CDO=∠ADP,∴∠BDE=∠ADP,②连结PE,∵∠ADP是△DPE的一个外角,∴∠ADP=∠DEP+∠DPE,∵∠BDE是△ABD的一个外角,∴∠BDE=∠ABD+∠OAB,∵∠ADP=∠BDE,∠DEP=∠ABD,∴∠DPE=∠OAB,∵OA=OB=4,∠AOB=90°,OD=43, ∴点D 的坐标为(0,﹣43), 直线CD 的解析式为:y=﹣13x ﹣43, 由得:,∴点P 的坐标为(8,﹣4),综上所述,点P 的坐标为(2,2)或(8,﹣4).3、抛物线y=x ²-bx-3b+3过A 、B 两点(点A 在点B 的左边),交y轴于点C ,且经过点(b -2,2b 2-5b -1).(1)求这条抛物线的解析式;(2)⊙M 过A 、B 、C 三点,交y 轴于另一点D ,求点M 的坐标;(3)连接AM 、DM ,将∠AMD 绕点M 顺时针旋转,两边MA 、MD 与x轴、y 轴分别交于点E 、F ,若△DMF 为等腰三角形,求点E 的坐标.解析:(1)把点(b -2,2b 2-5b -1)代入解析式,得2b 2-5b -1=(b -2)2+b (b -2)-3b +3, ……………1′解得b =2.∴抛物线的解析式为y =x 2+2x -3. ……………2′(2)由x 2+2x -3=0,得x =-3或x=1.∴A (-3,0)、B (1,0)、C (0,-3).抛物线的对称轴是直线x =-1,圆心M 在直线x =-1上. ……………3′∴设M (-1,n ),作MG ⊥x 轴于G ,MH ⊥y 轴于H ,连接MC 、MB .∴MH =1,BG =2. ……………4′∵MB =MC ,∴BG 2+MG 2=MH 2+CH 2,即4+n 2=1+(3+n )2,解得n=-1,∴点M (-1,-1) ……………5′(3)如图,由M (-1,-1),得MG =MH .∵MA =MD ,∴Rt △AMG ≌RtDMH ,∴∠1=∠2.由旋转可知∠3=∠4. ∴△AME ≌△DMF .若△DMF 为等腰三角形,则△AME 为等腰三角形. ……………6′设E (x ,0),△AME 为等腰三角形,分三种情况:①AE =AM =5,则x=5-3,∴E (5-3,0);②∵M 在AB 的垂直平分线上,∴MA =ME =MB ,∴E (1,0) ……………7′③点E 在AM 的垂直平分线上,则AE =ME .AE =x +3,ME 2=MG 2+EG 2=1+(-1-x )2,∴(x +3)2=1+(-1-x )2,解得x =47-,∴E (47-,0). ∴所求点E 的坐标为(5-3,0),(1,0),(47-,0) ……………8′4、(2013•压轴题)如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=.(1)求抛物线的解析式;(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA 面积的最大值;(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.:解:(1)如答图1所示,过点D作DE⊥x轴于点E,则DE=3,OE=2.∵tan∠DBA==,∴BE=6,∴OB=BE﹣OE=4,∴B(﹣4,0).∵点B(﹣4,0)、D(2,3)在抛物线y=ax2+bx﹣2(a≠0)上,∴,解得,∴抛物线的解析式为:y=x2+x﹣2.(2)抛物线的解析式为:y=x2+x﹣2,令x=0,得y=﹣2,∴C(0,﹣2),令y=0,得x=﹣4或1,∴A(1,0).设点M坐标为(m,n)(m<0,n<0),如答图1所示,过点M作MF⊥x轴于点F,则MF=﹣n,OF=﹣m,BF=4+m.S四边形BMCA=S△BMF+S梯形MFOC+S△AOC=BF•MF+(MF+OC)•OF+OA•OC=(4+m)×(﹣n)+(﹣n+2)×(﹣m)+×1×2=﹣2n﹣m+1∵点M(m,n)在抛物线y=x2+x﹣2上,∴n=m2+m﹣2,代入上式得:S四边形BMCA=﹣m2﹣4m+5=﹣(m+2)2+9,∴当m=﹣2时,四边形BMCA面积有最大值,最大值为9.(3)假设存在这样的⊙Q.如答图2所示,设直线x=﹣2与x轴交于点G,与直线AC交于点F.设直线AC的解析式为y=kx+b,将A(1,0)、C(0,﹣2)代入得:,解得:k=2,b=﹣2,∴直线AC解析式为:y=2x﹣2,令x=﹣2,得y=﹣6,∴F(﹣2,﹣6),GF=6.在Rt△AGF中,由勾股定理得:AF===3.设Q(﹣2,n),则在Rt△AGF中,由勾股定理得:OQ==.设⊙Q与直线AC相切于点E,则QE=OQ=.坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C.(1)求经过A、B、C三点的抛物线所对应的函数解析式;(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;∴MC与⊙P的位置关系是相切.6、(2013•压轴题)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=ax2+bx+c的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(﹣23,0),以0C为直径作半圆,圆心为D.(1)求二次函数的解析式;(2)求证:直线BE是⊙D的切线;(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C 不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.解答:解:(1)由题意,得A(0,2),B(2,2),E的坐标为(﹣23,0),则,解得,,∴该二次函数的解析式为:y=﹣98x2+94x+2;(2)如图,过点D作DG⊥BE于点G.由题意,得ED=+1=,EC=2+=,BC=2,∴BE==.∵∠BEC=∠DEG,∠EGD=∠ECB=90°,∴△EGD∽△ECB,∴=,∴DG=1.∵⊙D的半径是1,且DG⊥BE,∴BE是⊙D的切线;(3)由题意,得E(﹣23,0),B(2,2).设直线BE为y=kx+h(k≠0).则,解得,,∴直线BE为:y=34x+12.∵直线BE与抛物线的对称轴交点为P,对称轴直线为x=1,∴点P的纵坐标y=54,即P(1,54).∵MN∥BE, ∴∠MNC=∠BEC.∵∠C=∠C=90°,∴△MNC∽△BEC,∴=,∴=2t ,则CN=43t , ∴DN=t﹣1,∴S △PND =12DN•PD=5568t -. S △MNC =12CN•CM=23t 2. S 梯形PDCM =(12PD+CM )•CD=5182t +. ∵S=S △PND +S 梯形PDCM ﹣S △MNC =﹣+t (0<t <2).∵抛物线S=﹣+t (0<t <2)的开口方向向下,∴S 存在最大值.当t=1时,S 最大=23. 7、(2013•)已知:一元二次方程x +kx+k ﹣=0.(1)求证:不论k 为何实数时,此方程总有两个实数根;(2)设k <0,当二次函数y=x 2+kx+k ﹣的图象与x 轴的两个交点A 、B 间的距离为4时,求此二次函数的解析式;(3)在(2)的条件下,若抛物线的顶点为C ,过y 轴上一点M (0,m )作y 轴的垂线l ,当m 为何值时,直线l 与△ABC 的外接圆有公共点?(1)证明:∵△=k 2﹣4××(k ﹣)=k 2﹣2k+1=(k ﹣1)2≥0,∴关于x 的一元二次方程x 2+kx+k ﹣=0,不论k 为何实数时,此方程总有两个实数根;(2)令y=0,则x 2+kx+k ﹣=0.∵x A +x B =﹣2k ,x A •x B =2k ﹣1,∴|x A ﹣x B |===2|k ﹣1|=4,即|k ﹣1|=2,解得k=3(不合题意,舍去),或k=﹣1.∴此二次函数的解析式是y=x 2﹣x ﹣;(3)由(2)知,抛物线的解析式是y=x 2﹣x ﹣.易求A (﹣1,0),B (3,0),C (1,﹣2),∴AB=4,AC=2,BC=2.显然AC 2+BC 2=AB 2,得△ABC 是等腰直角三角形.AB 为斜边,∴外接圆的直径为AB=4,∴﹣2≤m≤2.8、(2013•压轴题)如图,已知抛物线y=ax +bx+c (a≠0)的顶点坐标为(4,﹣),且与y轴交于点C (0,2),与x 轴交于A ,B 两点(点A 在点B 的左边).(1)求抛物线的解析式及A ,B 两点的坐标;(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP 的最小值,若不存在,请说明理由;(3)在以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.解:(1)由题意,设抛物线的解析式为y=a(x﹣4)2﹣(a≠0)∵抛物线经过(0,2)∴a(0﹣4)2﹣=2解得:a=∴y=(x﹣4)2﹣即:y=x2﹣x+2当y=0时,x2﹣x+2=0解得:x=2或x=6∴A(2,0),B(6,0);(2)存在,如图2,由(1)知:抛物线的对称轴l为x=4,因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小∵B(6,0),C(0,2)∴OB=6,OC=2∴BC=2,∴AP+CP=BC=2∴AP+CP的最小值为2;(3)如图3,连接ME∵CE是⊙M的切线∴ME⊥CE,∠CEM=90°由题意,得OC=ME=2,∠ODC=∠MDE∵在△COD与△MED中∴△COD≌△MED(AAS),∴OD=DE,DC=DM设OD=x则CD=DM=OM﹣OD=4﹣x则RT△COD中,OD2+OC2=CD2,∴x2+22=(4﹣x)2∴x=∴D(,0)设直线CE的解析式为y=kx+b∵直线CE过C(0,2),D(,0)两点,则解得:∴直线CE的解析式为y=﹣+2;圆的圆心坐标为C (2,0),B 是第一象限圆弧上的一点,且BC ⊥AC ,抛物线c bx x y ++-=221经过C 、B 两点,与x 轴的另一交点为D 。
二次函数与圆结合的压轴题

图6x yFEH N MPDC BAO二次函数与圆【例题1】 (芜湖市) 已知圆P 得圆心在反比例函数图象上,并与x 轴相交于A 、B 两点. 且始终与y轴相切于定点C (0,1).(1) 求经过A 、B 、C 三点得二次函数图象得解析式;(2) 若二次函数图象得顶点为D,问当k 为何值时,四边形AD BP为菱形.【例题2】(湖南省韶关市)25、如图6,在平面直角坐标系中,四边形OABC 就是矩形,OA=4,A B=2,直线与坐标轴交于D 、E 。
设M 就是AB 得中点,P就是线段DE 上得动点、 (1)求M 、D 两点得坐标;(2)当P在什么位置时,PA=PB?求出此时P 点得坐标;(3)过P 作P H⊥BC,垂足为H,当以P M为直径得⊙F 与BC相切于点N 时,求梯形PM BH 得面积、【例题3】(甘肃省白银等7市新课程)28、 在直角坐标系中,⊙A 得半径为4,圆心A 得坐标为(2,0),⊙A 与x轴交于E 、F两点,与y轴交于C 、D两点,过点C 作⊙A得切线BC ,交x 轴于点B.(1)求直线CB 得解析式;(2)若抛物线y =ax 2+b x +c 得顶点在直线BC 上,与x轴得交点恰为点E 、F ,求该抛物线得解析式; (3)试判断点C 就是否在抛物线上?(4) 在抛物线上就是否存在三个点,由它构成得三角形与△AOC 相似?直接写出两组这样得点.【例题4】(绵阳市)25、如图,已知抛物线y = ax 2+ bx -3与x 轴交于A、B 两点,与y轴交于C 点,经过A 、B 、C三点得圆得圆心M (1,m )恰好在此抛物线得对称轴上,⊙M得半径为.设⊙M与y轴交于D ,抛物线得顶点为E . (1)求m 得值及抛物线得解析式;(2)设∠D BC = α,∠CBE = β,求si n(α-β)得值;(3)探究坐标轴上就是否存在点P ,使得以P 、A 、C为顶点得三角形与△BCE 相似?若存在,请指出点P得位置,并直接写出点P 得坐标;若不存在,请说明理由.【例题5】(南充市)25、如图,点M (4,0),以点M 为圆心、2为半径得圆与x 轴交于点A 、B .已知抛物线过点A与B,与y 轴交于点C .ﻫ(1)求点C 得坐标,并画出抛物线得大致图象. (2)点Q (8,m )在抛物线上,点P 为此抛物线对称轴上一个动点,求PQ+PB 得最小值.(3)CE 就是过点C得⊙M得切线,点E 就是切点,求OE 所在直线得解析式.ﻫ【例题6】(山西省临汾市)26、 如图所示,在平面直角坐标系中,经过原点,且与轴、轴分别相交于两点.(1)请求出直线得函数表达式;(2)若有一抛物线得对称轴平行于轴且经过点,顶点在上,开口向下,且经过点,求此抛物线得函数表达式; (3)设(2)中得抛物线交轴于两点,在抛物线上就是否存在点,使得?若存在,请求出点得坐标;若不存在,请说明理由.【例题7】在△AB C中,∠A =90°,AB =4,AC =3,M就是AB 上得动点(不与A ,B 重合),过M 点作MN ∥B C交AC 于点N .以M N为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM =x. (1)用含x 得代数式表示△MNP 得面积S;(2)当x 为何值时,⊙O 与直线BC 相切? (3)在动点M 得运动过程中,记△MNP 与梯形BCNM 重合得面积为y ,试求y 关于x得函数表达式,并求x 为何值时,y得值最大,最大值就是多少?【例题8】如图,点P 在y轴上,半径为3得⊙P 分别交x轴于A 、B 两点,AB=4,交y 轴负半轴于点连接AP 并延长交⊙P于点D ,过D 作⊙P 得切线分别交x 轴、y轴于点F、G; (1)求直线FG 得解析式;(2)连接CD 交AB 于点E,求得值;(3)设M 就是劣弧B C上得一个动点,连接DM 交x 轴于点N,AN ·AB+DN ·D M=K,如果存在,请求出K 得值,如果不存在,请说明理由;A MBxyODEA BC D E x y M OA B CM N D图 2 O A B CM N P 图 1 O A B C MN P图 3O。
圆与二次函数结合型压轴题专题(解析版)--2024年中考数学重难点

圆与二次函数结合型压轴题专题通用的解题思路:一、点在圆上的使用技巧:①没告诉半径,利用圆上的点到圆心的距离等于半径可以表示出半径的长度;②告诉半径,圆上的点到圆心的距离等于半径这个等量关系可以求出一个参数。
二、判断直线与圆的位置关系的标准流程:第一步,利用圆上的点到圆心的距离等于半径表示出半径r ,第二步,表示出圆心到直线的距离d ,第三步,比较半径r 和距离d 的大小:若半径r >距离d ,则直线与圆相交,若半径r =距离d ,则直线与圆相切,若半径r <距离d ,则直线与圆相离。
三、记直线l 被圆C 截得的弦长为|AB |的常用方法弦长公式:AB =2r 2-d 21(长沙中考)如图,抛物线y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)的对称轴为y 轴,且经过(0,0)和(a ,116)两点,点P 在该抛物线上运动,以点P 为圆心的⊙P 总经过定点A (0,2).(1)求a ,b ,c 的值;(2)求证:在点P 运动的过程中,⊙P 始终与x 轴相交;(3)设⊙P 与x 轴相交于M (x 1,0),N (x 2,0)(x 1<x 2)两点,当△AMN 为等腰三角形时,求圆心P 的纵坐标.【解答】解:(1)∵抛物线y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)的对称轴为y 轴,且经过(0,0)和(a ,116)两点,∴抛物线的一般式为:y =ax 2,∴116=a (a )2,解得:a =±14,∵图象开口向上,∴a =14,∴抛物线解析式为:y =14x 2,故a =14,b =c =0;(2)设P (x ,y ),⊙P 的半径r =x 2+y -2 2,又∵y =14x 2,则r =x 2+14x 2-2 2,化简得:r =116x 4+4>14x 2,∴点P 在运动过程中,⊙P 始终与x 轴相交;(3)设P (t ,14t 2),∵r 2-y 2=4,∴MH =NH =2,∴M (t -2,0),N (t +2,0),A (0,2),∵△AMN 为等腰三角形,∴AM =AN ,AM =MN ,AN =MN ,(t -2)2+(2-0)2=(t +2)2+(2-0)2,∴t =0,(t -2)2+(2-0)2=42,∴t =2±23,(t +2)2+(2-0)2=42,∴t =-2±23,①当t =0时,P 的纵坐标为0,②当t =2±23时,P Y =14(2±23)2=4±23,∴P 的纵坐标为4±23,③当t =-2±23时,P Y =14(2±23)2=4±23,∴P 的纵坐标为4±23,综上所述,P 的纵坐标为:0或4+23或4-23.2(岳麓区校级月考)如图,已知直线l :y =-1和抛物线L :y =ax 2+bx +c (a ≠0),抛物线L 的顶点为原点,且经过点A 2a ,14,直线y =kx +1与y 轴交于点F ,与抛物线L 交于点B (x 1,y 1),C (x 2,y 2),且x 1<x 2.(1)求抛物线L 的解析式;(2)点P 是抛物线L 上一动点.①以点P 为圆心,PF 为半径作⊙P ,试判断⊙P 与直线l 的位置关系,并说明理由;②若点Q (2,3),当|PQ -PF |的值最大时,求点P 的坐标;(3)求证:无论k 为何值,直线l 总是与以BC 为直径的圆相切.【解答】解:(1)抛物线的表达式为:y =ax 2,将点A 坐标代入上式得:14=a (2a )2,解得:a =14,故抛物线的表达式为:y =14x 2⋯①;(2)①点F (0,1),设:点P (m ,14m 2),则PF =m 2+14m 2-1 2=14m 2+1,而点P 到直线l 的距离为:14m 2+1,则⊙P 与直线l 的位置关系为相切;②当点P 、Q 、F 三点共线时,|PQ -PF |最大,将点FQ 的坐标代入一次函数表达式:y =kx +b 并解得:直线FQ 的函数表达式为:y =x +1⋯②,联立①②并解得:x =2±22,故点P 的坐标为:(2+22,3+22)或(2-22,3-22);(3)将抛物线的表达式与直线y =kx +1联立并整理得:x 2-4kx -4=0,则x 1+x 2=4k ,x 1x 2=-4,则y 1+y 2=k (x 1+x 2)+2=4k 2+2,则x 2-x 1=x 1+x 2 2-4x 1x 2=4,设直线BC 的倾斜角为α,则tan α=k ,则cosα=1k 2+1,则BC =x 2-x 1k 2+1=4(k 2+1),则12BC =2k 2+2,设BC 的中点为M (2k ,2k 2+1),则点M 到直线l 的距离为:2k 2+2,故直线l 总是与以BC 为直径的圆相切.3在平面直角坐标系xOy 中,已知二次函数y =14x 2+mx +n 的图象经过点A (2,0)和点B (1,-34),直线l 经过抛物线的顶点且与y 轴垂直,垂足为Q .(1)求该二次函数的表达式;(2)设抛物线上有一动点P 从点B 处出发沿抛物线向上运动,其纵坐标y 1随时间t (t ≥0)的变化规律为y 1=-34+2t .现以线段OP 为直径作⊙C .①当点P 在起始位置点B 处时,试判断直线l 与⊙C 的位置关系,并说明理由;在点P 运动的过程中,直线l 与⊙C 是否始终保持这种位置关系?请说明你的理由.②若在点P 开始运动的同时,直线l 也向上平行移动,且垂足Q 的纵坐标y 2随时间t 的变化规律为y 2=-1+3t ,则当t 在什么范围内变化时,直线l 与⊙C 相交?此时,若直线l 被⊙C 所截得的弦长为a ,试求a 2的最大值.【解答】解:(1)将点A (2,0)和点B (1,-34)分别代入y =14x 2+mx +n 中,得:14×4+2m +n =014+m +n =-34 ,解得:m =0n =-1 ,∴抛物线的解析式:y =14x 2-1;(2)①将P 点纵坐标代入(1)的解析式,得:14x 2-1=-34+2t ,x =8t +1,∴P (8t +1,-34+2t ),∴圆心C (8t +12,-38+t ),∴点C 到直线l 的距离:-38+t -(-1)=t +58;而OP 2=8t +1+(-34+2t )2,得OP =2t +54,半径OC =t +58;∴直线l 与⊙C 始终保持相切.②Ⅰ、由①可知,若直线l 与⊙C 相切,则:2t -58=t +58,t =54;∴当0<t <54时,直线l 与⊙C 相交;Ⅱ、∵0<t <54时,圆心C 到直线l 的距离为d =|2t -58|,又半径为r =t +58,∴a 2=4(r 2-d 2)=4[(t +58)2-|2t -58|2]=-12t 2+15t ,∴t =58时,a 的平方取得最大值为7516.4(长沙中考)如图半径分别为m ,n (0<m <n )的两圆⊙O 1和⊙O 2相交于P ,Q 两点,且点P (4,1),两圆同时与两坐标轴相切,⊙O 1与x 轴,y 轴分别切于点M ,点N ,⊙O 2与x 轴,y 轴分别切于点R ,点H .(1)求两圆的圆心O 1,O 2所在直线的解析式;(2)求两圆的圆心O 1,O 2之间的距离d ;(3)令四边形PO 1QO 2的面积为S 1,四边形RMO 1O 2的面积为S 2.试探究:是否存在一条经过P ,Q 两点、开口向下,且在x 轴上截得的线段长为s 1-s 2 2d 的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.【解答】解:(1)由题意可知O 1(m ,m ),O 2(n ,n ),设过点O 1,O 2的直线解析式为y =kx +b ,则有:mk +b =m nk +b =n (0<m <n ),解得k =1b =0 ,∴所求直线的解析式为:y =x .(2)由相交两圆的性质,可知P 、Q 点关于O 1O 2对称.∵P (4,1),直线O 1O 2解析式为y =x ,∴Q (1,4).如解答图1,连接O 1Q .∵Q (1,4),O 1(m ,m ),根据两点间距离公式得到:O 1Q =m -1 2+m -4 2=2m 2-10m +17,又O 1Q 为小圆半径,即QO 1=m ,∴2m 2-10m +17=m ,化简得:m 2-10m +17=0①如解答图1,连接O 2Q ,同理可得:n 2-10n +17=0②由①,②式可知,m 、n 是一元二次方程x 2-10x +17=0③的两个根,解③得:x =5±22,∵0<m <n ,∴m =5-22,n =5+22.∵O 1(m ,m ),O 2(n ,n ),∴d =O 1O 2=m -n 2+m -n 2=8.(3)假设存在这样的抛物线,其解析式为y =ax 2+bx +c ,因为开口向下,所以a <0.如解答图2,连接PQ .由相交两圆性质可知,PQ ⊥O 1O 2.∵P (4,1),Q (1,4),∴PQ =4-1 2+1-4 2=32,又O 1O 2=8,∴S 1=12PQ •O 1O 2=12×32×8=122;又S 2=12(O 2R +O 1M )•MR =12(n +m )(n -m )=202;∴s 1-s 2 2d =122-202 2×8=1,即抛物线在x 轴上截得的线段长为1.∵抛物线过点P (4,1),Q (1,4),∴16a +4b +c =1a +b +c =4 ,解得b =-5a +1 c =5+4a,∴抛物线解析式为:y =ax 2-(5a +1)x +5+4a ,令y =0,则有:ax 2-(5a +1)x +5+4a =0,设两根为x 1,x 2,则有:x 1+x 2=5a +1a ,x 1x 2=5+4a a,∵在x 轴上截得的线段长为1,即|x 1-x 2|=1,∴(x 1-x 2)2=1,∴(x 1+x 2)2-4x 1x 2=1,即(5a +1a )2-4(5+4a a )=1,化简得:8a 2-10a +1=0,解得a =5±178,可见a 的两个根均大于0,这与抛物线开口向下(即a <0)矛盾,∴不存在这样的抛物线.5(广益)如图1,已知一次函数y =-x +4与反比例函数y =3x相交于P ,Q 两点(P 在Q 的右侧).(1)求P ,Q 的坐标并写出△OPQ 的面积;(2)如图2,已知M (m ,m ),N (n ,n ),其中(0<m <n ),若分别以M ,N 为圆心的圆均与x 轴相切,切点分别为A ,B ,并且点P 既在⊙M 上又在⊙N 上.①求直线MN 的解析式;②求出线段MN 的长度d ;(3)在(2)的前提上,记四边形PMQN 的面积为S 1,四边形AMNB 的面积为S 2,已知抛物线y =ax 2+bx +c 满足两个条件:①经过点P 和点Q ,②该抛物线截x 轴得到的线段长度为s 1-s 2 d,请求出抛物线二次项系数a 的值.【解答】解:(1)由题意得:y =-x +4y =3x.解这个方程组得:x 1=1y 1=3 ,x 2=3y 2=1 .∵P 在Q的右侧,∴P (3,1),Q (1,3).设直线PQ 交x 轴于点C ,如图,则C (4,0).∴OC =4.过点Q 作QE ⊥OC 于E ,过点P 作PF ⊥OC 于F ,则QE =3,PF =1.∴S △OPQ =S △OQC -S △OPC =12×OC ×QE -12OC ×PF =6-2=4.(2)①∵M (m ,m ),N (n ,n ),∴直线MN 的解析式为:y =x .②∵以M ,N 为圆心的圆均与x 轴相切,切点分别为A ,B ,∴MA ⊥AB ,NB ⊥AB .过点P 作PE ⊥MA 于E ,PF ⊥NB 与,过点M 作MG ⊥NB 于G ,如图,则∠NMG =45°.∴MN =2MG .∵M (m ,m ),N (n ,n ),P (3,1),∴MA =m ,NB =n ,PE =3-m ,PM =3-m 2+m -1 2,ME =m -1,PF =n -3,NF =n -1.∵点P 既在⊙M 上又在⊙N 上,∴PM =MA ,PN =NB .∴PM 2=MA 2,PN 2=NB 2.∴(3-m )2+(m -1)2=m 2,(n -3)2+(n -1)2=n 2.整理得:m 2-8m +10=0,n 2-8n +10=0.∴m ,n (0<m <n )是方程x 2-8x +10=0的两个根.∴m +n =8,mn =10.∴(n -m )2=(m +n )2-4mn =24.∴n -m =26.∵MG =AB =n -m ,∴MG =26.∴MN =2MG =43,∴d =43.(3)抛物线y =ax 2+bx +c 满足经过点P 和点Q ,∴a +b +c =39a +3b +c =1.∴b =-1-4a c =3a +4 .∵S 1=12PQ ×MN =12×22×43=46,S 2=12MA +MB ⋅AB =12m +n ×n -m =12×8×26=86,∴s 1-s 2 d =4643=2.设抛物线y =ax 2+bx +c 与x 轴的交点为(x 1,0),(x 2,0),∴|x 1-x 2|=2.∴x 1-x 2 2=2.∴x 1+x 2 2-4x 1⋅x 2=2.∵x 1,x 2是方程ax 2+bx +c =0的两个根,∴x 1+x 2=-b a ,x 1⋅x 2=c a .∴-b a 2-4×c a =2.∴-1-4a a 2-4×3a +4a=2.整理得:2a 2-8a +1=0.解得:a =4±14.∴抛物线二次项系数a 的值为:4+14或4-14.6已知:如图,抛物线y =ax 2+bx +c (a ≠O )经过X 轴上的两点A (x 1,0)、B (x 2,0)和y 轴上的点C (0,-32),⊙P 的圆心P 在y 轴上,且经过B 、C 两点,若b =3a ,AB =23,(1)求抛物线的解析式;(2)设D 在抛物线上,且C ,D 两点关于抛物线的对称轴对称,问直线BD 是否经过圆心P ,并说明理由;(3)设直线BD 交⊙P 于另一点E ,求经过E 点的⊙P 的切线的解析式.【解答】解:(1)∵轴上的点C (0,-32),∴c =-32,又∵b =3a ,AB =23,令ax 2+3ax -32=0,|x 1-x 2|=23,解得:a =23,b =233;∴抛物线的解析式是:y =23x 2+233x -32.(4分)(2)D (-3,-32),直线B D 为:y =33x -12,连接BP ,设⊙P 的半径为R ,R 2=32 2+32-R 2,R =1,P (0,-12),点P 的坐标满足直线BD 的解析式y =33x -12.∴直线B D 经过圆心P .(3)过点E 作EF ⊥y 轴于F ,得△OPB ≌△FPE ,E (-32,-1),设经过E 点⊙P 的切线L 交y 轴于点Q .则∠P EQ =90°,EF ⊥PQ ,∴P E 2=P F •PQ ,∴PQ =2,Q (0,-2.5),∴切线L 为:y =-3x -2.5.7(青竹湖)定义:如果一条直线与一条曲线有且只有一个交点,且曲线位于直线的同旁,称之为直线与曲线相切,这条直线叫做曲线的切线,直线与曲线的唯一交点叫做切点.(1)如图,在平面直角坐标系中,点O 为坐标原点,以点A (0,-3)为圆心,5为半径作圆A ,交x 轴的负半轴于点B ,求过点B 的圆A 的切线的解析式;(2)若抛物线y =ax 2(a ≠0)与直线y =kx +b (k ≠0)相切于点(2,2),求直线的解析式;(3)若函数y =14x 2+(n -k -1)x +m +k -2的图象与直线y =-x 相切,且当-1≤n ≤2时,m 的最小值为k ,求k 的值.【解答】解:(1)如图1,连接AB ,记过点B 的⊙A 切线交y 轴于点E ,∴AB =5,∠ABE =90°,∵A (0,-3),∠AOB =90°,∴OA =3,∴OB =AB 2-OA 2=52-32=4,∴B (-4,0),∵∠OAB =∠BAE ,∠AOB =∠ABE =90°,∴△OAB ∽△BAE ,∴AB AE =OA BA ,∴AE =AB ⋅BA OA =253,∴OE =AE -OA =253-3=163,∴E (0,163),设直线BE 解析式为:y =kx +163,∴-4k +163=0,解得:k =43,∴过点B 的⊙A 的切线的解析式为y =43x +163,方法二:设直线BE 的解析式为y =k (x +4),∴E (0,4k ),∴AB =5,AE =4k +3,BE =42+4k 2,由勾股定理可得,AB 2+BE 2=AE 2,∴25+16+16k 2=16k 2+9+24k ,∴k =43,∴过点B 的⊙A 的切线的解析式为y =43x +163;(2)∵抛物线y =ax 2经过点(2,2),∴4a =2,解得:a =12,∴抛物线解析式:y =12x 2,∵直线y =kx +b 经过点(2,2),∴2k +b =2,可得:b =2-2k ,∴直线解析式为:y =kx +2-2k ,∵直线与抛物线相切,∴关于x 的方程12x 2=kx +2-2k 有两个相等的实数根,方程整理得:x 2-2kx +4k -4=0,∴△=(-2k )2-4(4k -4)=0,解得:k 1=k 2=2,∴直线解析式为y =2x -2,(3)∵函数y =14x 2+(n -k -1)x +m +k -2的图象与直线y =-x 相切,∴关于x 的方程14x 2+(n -k -1)x +m +k -2=-x 有两个相等的实数根,方程整理得:14x 2+(n -k )x +m +k -2=0,∴△=(n -k )2-4×14(m +k -2)=0,整理得:m =(n -k )2-k +2,可看作m 关于n 的二次函数,对应抛物线开口向上,对称轴为直线x =k ,∵当-1≤n ≤2时,m 的最小值为k ,①如图2,当k <-1时,在-1≤n ≤2时m 随n 的增大而增大,∴n =-1时,m 取得最小值k ,∴(-1-k )2-k +2=k ,方程无解,②如图3,当-1≤k ≤2时,n =k 时,m 取得最小值k ,∴-k +2=k ,解得:k =1,③如图4,当k >2时,在-1≤n ≤2时m 随n 的增大而减小,∴n =2时,m 取得最小值k ,∴(2-k )2-k +2=k ,解得:k 1=3+3,k 2=3-3(舍去),综上所述,k 的值为1或3+3.8(麓山国际)如图,经过定点A 的直线y =k (x -2)+1(k <0)交抛物线y =-x 2+4x 于B ,C 两点(点C 在点B 的右侧),D 为抛物线的顶点.(1)直接写出点A 的坐标;(2)如图(1),若△ACD 的面积是△ABD 面积的两倍,求k 的值;(3)如图(2),以AC 为直径作⊙E ,若⊙E 与直线y =t 所截的弦长恒为定值,求t 的值.【解答】解:(1)∵A 为直线y =k (x -2)+1上的定点,∴A 的坐标与k 无关,∴x -2=0,∴x =2,此时y =1,∴点A 的坐标为(2,1);(2)∵y =-x 2+4x =-(x -2)2+4,∴顶点D 的坐标为(2,4),∵点A 的坐标为(2,1),∴AD ⊥x 轴.如图(1),分别过点B ,C 作直线AD 的垂线,垂足分别为M ,N ,设B ,C 的横坐标分别为x 1,x 2,∵△ACD 的面积是△ABD 面积的两倍,∴CN =2BM ,∴x 2-2=2(2-x 1),∴2x 1+x 2=6.联立y =x 2+4x y =kx -2k +1 ,得x 2+(k -4)x -2k +1=0,①解得x 1=4-k -k 2+122,x 2=4-k +k 2+122,∴2×4-k -k 2+122+4-k +k 2+122=6,化简得:k 2+12=-3k ,解得k =-62.另解:接上解,由①得x 1+x 2=4-k ,又由2x 1+x 2=6,得x 1=2+k .∴(2+k )2+(k -4)(2+k )-2k +1=0,解得k =±62.∵k <0,∴k =-62;(3)如图(2),设⊙E 与直线y =t 交于点G ,H ,点C 的坐标为(a ,-a 2+4a ).∵E 是AC 的中点,∴将线段AE 沿AC 方向平移与EC 重合,∴x E -x A =x C -x E ,y E -y A =y C -y E ,∴x E =12(x A +x C ),y E =12(y A +y C ).∴E (1+a 2,-a 2+4a +12).分别过点E ,A 作x 轴,y 轴的平行线交于点F ,在Rt △AEF 中,由勾股定理得:EA 2=1+a 2-2 2+-a 2+4a +12-1 2=a 2-1 2+-a 2+4a +12-1 2,过点E作PE⊥GH,垂足为P,连接EH,∴GH=2PH,EP2=-a2+4a+12-t 2,又∵AE=EH,∴GH2=4PH2=4(EH2-EP2)=4(EA2-EP2)=4[a2-12+-a2+4a+12-12--a2+4a+12-t2]=4[a24-a+1+-a2+4a+12-12-(-a2+4a+1)+1--a2+4a+122+t(-a2+4a+1)-t2]=4[(54-t)a2+(4t-5)a+1+t-t2].∵GH的长为定值,∴5 4-t=0,且4t-5=0,∴t=54.9(长郡)如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A、B两点.(1)分别求A、B、C三点的坐标;(2)如图1,设经过A、B两点的抛物线解析式为y=14x-52+k,它的顶点为E,求证:直线EA与⊙M相切;(3)如图2,过点M作直线FG∥y轴,与圆分别交于F、G两点,点P为弧FB上任意一点(不与B、F重合),连接FP、AP,FN⊥BP的延长线于点N.请问AP-BPPN是否为定值,若为定值,请求出这个值,若不为定值,请说明理由.【解答】解:(1)如图1,连接CM、AM,连接ME交x轴于点D,则ME⊥x轴,∵⊙M与y轴相切于点C,点M的坐标是(5,4),∴CM⊥y轴,即C(0,4),⊙M的半径为5,∴AM=5,DM=4,∴AD=DB=AM2-DM2=52-42=3,∴OA=5-3=2,∴A(2,0),B(8,0);(2)证明:将A(2,0)代入y=14x-52+k中,可得k=-94,∴E(5,-94),∴DE=94,∴ME=DE+MD=94+4=254,则AE2=32+942=22516,MA2+AE2=52+22516=62516,ME2=254 2=62516,∴MA2+AE2=ME2,∴MA⊥AE,又∵MA为半径,∴直线EA与⊙M相切;(3)AP-BPPN为定值,理由如下:连接AF、BF,作FQ⊥AP于点Q,∵∠FPN为圆内接四边形ABPF的外角,∴∠FPN=∠FAB,又∵MF⊥AB,∴AF=BF,∴∠FAB=∠FBA=∠FPA,∴∠FPN=∠FPA,∵FQ⊥AP,FN⊥PN,∴FQ=FN,又∵FP=FP,∴Rt△FPQ≌Rt△FPN(HL),∴PQ=PN,又∵AF=BF,FQ=FN,∴Rt△AFQ≌Rt△BFN(HL),∴AQ=BN,∴AP-BPPN =AQ+PQ-BPPN=BP+PN+PQ-BPPN=2PNPN=2.10(长郡)如图1,抛物线y=14x2-2x与x轴交于O、A两点,点B为抛物线的顶点,连接OB.(1)求∠AOB的度数;(2)如图2,以点A为圆心,4为半径作⊙A,点M在⊙A上.连接OM、BM,①当△OBM是以OB为底的等腰三角形时,求点M的坐标;②如图3,取OM的中点N,连接BN,当点M在⊙A上运动时,求线段BN长度的取值范围.【解答】解:(1)令y=0,则14x2-2x=0,解得:x=0或8.∴A(8,0).∴OA=8.∵y=14x2-2x=14x-42-4,∴B(4,-4).过点B作BD⊥OA于点D,如图,则OD =4,BD =4,∴OD =BD ,∴∠AOB =∠OBD =45°;(2)①设⊙A 与x 轴交于点C ,则C (4,0).连接BC ,如图,∵B (4,-4),∴BC ⊥OA .∵CO =CB =4,∴△CBO 是以OB 为底的等腰三角形.∴点M 与点C 重合时,△MBO 是以OB 为底的等腰三角形.此时点M (4,0);过点A 作AM ⊥x 轴,交⊙A 于点M ,延长MA 交⊙A 于点E ,连接BE ,过点M 作MF ⊥y 轴于点F ,如图,则M (8,4),E (8,-4),F (0,4).∴MF =ME =8.∵B (4,-4),∴BE ∥x 轴.∴BE ⊥ME ,BE =4.∴∠BEM =∠MFO =90°,BE =OF =4.在△MOF 和△MBE 中,MF =ME∠MFO =∠BEM =90°OF =BE,∴△MOF ≌△MBE (SAS ).∴MO =MB .∴△MBO 是以OB 为底的等腰三角形.此时点M (8,4);综上,当△OBM 是以OB 为底的等腰三角形时,点M 的坐标为(4,0)或(8,4);②设⊙A 与x 轴交于点C ,则C (4,0).连接BC ,CN ,AM ,如图,AM=2.∵A(8,0),∴点C是OA的中点.∵N为OM的中点,∴CN是△OMA的中位线.∴CN=12当点M在⊙A上运动时,由三角形的三边的关系定理可知:BC-CN≤BN≤BC+CN.∵BC=4,∴4-2≤BN≤4+2.∴线段BN长度的取值范围为:2≤BN≤6.。
【2021中考专题】二次函数与圆综合压轴题

【2021中考专题】二次函数与圆综合压轴题★初中数学研学堂★★方法揭秘★解决函数与圆的综合问题的关键是找准函数与圆的结合点,弄清题目的本质,利用圆的基本性质和函数的性质、数形结合、方程思想、全等与相似,以便找到对应的解题途径.常见的考法有:1. 直线与圆的位置关系:平面直角坐标系中的直线与圆的位置关系问题关键是圆心到直线的距离等于半径的大小,常用的方法有:(1)利用圆心到直线的距离等于半径的大小这一数量关系列出关系式解决问题(2)利用勾股定理解决问题(3) 利用相似列出比例式解决问题2.函数与圆的新定义题目:利用已掌握的知识和方法理解新定义,化生为熟3.函数与圆的性质综合类问题:利用几何性质,结合图形,找到问题中的“不变”关键因素和“临界位置”.01★典例剖析★如图,抛物线y=ax2+9/4x+c经过点A(-1,0)和点C(0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y 轴,交抛物线于点P.(1)求该抛物线的解析式;(2)在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;(3)以M为圆心,MP为半径作⊙M,当⊙M与坐标轴相切时,求出⊙M的半径.010202典例剖析★在平面直角坐标系中,二次函数y=1/2x2+bx+c的图象与x轴交于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.(1)求二次函数的解析式;(2)如图甲,连接AC,PA,PC,若S△PAC=15/2,求点P的坐标;(3)如图乙,过A,B,P三点作⊙M,过点P作PE⊥x轴,垂足为D,交⊙M于点E.点P在运动过程中线段DE的长是否变化,若有变化,求出DE的取值范围;若不变,求DE的长.010203【二次函数压轴】相似三角形存在性问题的解题策略【二次函数压轴】5种解题策略带你玩转45°角【2021中考】一道综合性较强的以等边三角形为背景的几何压轴题【2021中考】一道相似压轴题解法微探【2021中考专题】二次函数压轴题之角的存在性【2021中考】分享一道相似三角形几何压轴题【2021中考】两道网研几何综合题解法探究【2021中考】一道网研几何综合题的解法探究倍半角、相似基本型破解几何压轴题【2021中考备考干货分享】最值系列之胡不归模型★公众号★。
初中数学二次函数与圆相结合的压轴题专题,中考数学二次函数与圆相结合的经典题型讲解及答案解析
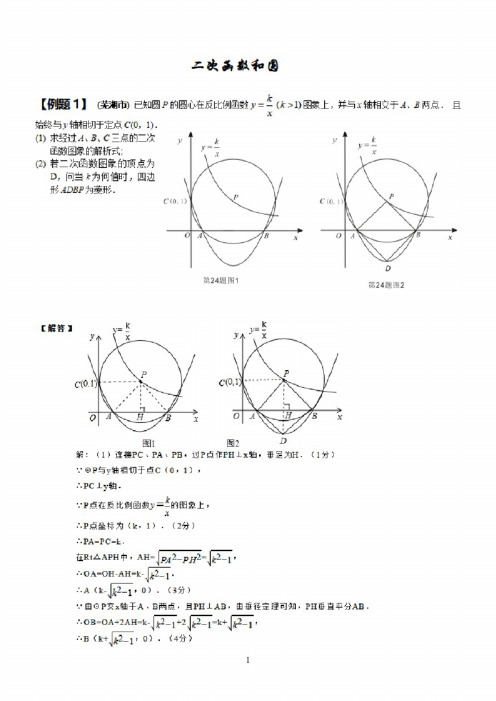
【仲烦1】(我市)已知圆P的圆心在反比例函数y=-(A:>1)上,并与工轴相交于X、3两点.且x始终与]轴相切于定点C(0,1).⑴求经过三点的二次匣1数图象的解析式;(2)若二次函教图象的顶点为D,问当上为何值时'四边形也站尹为菱形.【耕音】解:(1)连接PC、PAx PB,谊P点ffPHXx轴.垂足为H・(1分)与y轴相切于点C(0, 1),.-.PC±y^.•.•P点在反比例函数》二占的囹象上,X•.•P点坐标为(k,1).(2分)•.•PAU.在RtAAPH中,AH=厨2_尸於后一1,•'•A(k-90 ).(3分)•.•由。
P交x轴于A、B两点,且PHJLAB,由垂径击理可知,PH垂直平分AB.AOB=OA+2AH=k•••B3小2_1,0).《4分〉故过A、B两点的抛物线的对称轴为PH所在的直钱斛析式为x=k.可设该抛物线解析式为y=a<x-k)2+h.(5分)又二.抛物线过C(。
,1),B(k-^2_r0),[ak^-^h=1•3|—?昭得a=l,h=1-k^.(7分)•.•抛物线解析式为y=心)2+1上2.(B分)(2)由<1)知抛物线顶点D坐标为(k,l-k2>•・•DH-k2-l.若四边形ADBP为装形.则必有PH=DH.(10分)VPH=1,.•-k2-l=l.又">1,(11分)•・•当k取以时,PD与AB互相垂直平分,则四边形ADBP为菱形•(12分)3【百麒2]翎南省韶关市)25.如图6,在平面直角坐标系中旭边形OABC是矩形,。
虹4应=2,直线),=-":与坐标轴交于D、E。
设M是加的中点,P是线段DE上的动点.(1)求M、D两点的坐标;<2)当P在什么位置时,PA=PB?求出此时P点的坐标j<3)过P作PH1BC,垂足为H,当以PM为直径的OF与BC相切于点N时,求梯形PHBH的面积.图6【分析】(1)因为四边形OABC是逅形,0A=4,AB=2»直线>=r-?与坐标轴交于D、E,M是AB的中点2.所以令y=0,即司术出D的坐标,而AM-1.印以M(4,1);(2)因为PA=PB.断以P是AB的香直平分线和直线ED的交点,而AE的中垂线是y=l,断以P的纵坐标为1,令直线ED的解析式中的y=l,求出的x的值即为相应的P的横坐标;(3〉可设P(x,y>,连将PN、MN、NF,因为点P在y・x-:上,所以P《x,粮据蹦意可2得PNlMNi FN±BCi F是圈心,又因N是钱段HB的中点,HN-NB-—»PH-2-(-x*-)t2 2 2BM=1,利用直径对的圆周角是直甬可得到ZHPX-ZHNP=ZHNP-ZBNM=90°•所以ZHPN=ZB取ph ir£x+| NM,又因ZPHN-ZB-900-所以可得到R tAPNH<^RtANMB•所以—•A2=—^,这BM BN—4-x1—样牧可得到关于X的方程,解之即可求出X的值,而饬求面招的四边形是一个直角梯形,南以Spg=也皿滋或"医号)("6+应)=.21_色叵.2 2 24满答】俄;《1)M", 1),D《9,0);(2分)2(2)V PA=PB>•七点P在线段AB的中毒线上,•.•点P的纵坐标是I,3又•:点P在尸-X-—上,2・.•点P的坐标为(【,1)?(4分)(3)设P(x,y),连接PN、MN、NF,3点P lSy=・x+-上,匕3・'・P(x ,-w+—),2依题意知:PN«LMN>FN^BC,F是圆心,・'・N是线段HB的中点,HN=NB=±M,PH=2.2口,BM=1,<6分)22HPN-ZHNP=NHNP-ZBNM=90°,NHPN=ZBNN1,又ZPHN=ZB=90°5RtAPNH^RtANMBs:HN_PH•'两南,4-x x*.."F=二,-等」22,(8分)x?-12x+14=0»朋得;x-6-j22(^-*>^舍去),k=6-皿=些罕=空也艾竺=一*孕屈,(9分)2【例题31(||-4省白银等7市新课程)28.在直角坐标系中>0A的丰径为4,圆心A曜标为(2, 0),S与X轴交于E、尸两点,与),轴交于(7、D两点,过点(7作0X的切线时,交x轴于点3.(1)求直线C5的解析式:(2)若抛物线.件履7)日€的顶点在直线3C上,与x轴的交点恰为点E、已求该抛物线的解析式J(3)试判断点C是否在抛物线上?(4)在抛物线上是否存在三个点,由它构成的三角形与A4OC相似?直接与出两组这样的点•4[分析】(1>SHAC.根撮区]的李径求出AC. W1B点人的坐麻求出0A,燃后利用勾腹定理列式求出0C・从而得到点C的坐标,再求出ZCAO=60=.然后粮掘直有三甬形两锐角互余米出NB=30。
(完整版)中考数学压轴题二次函数与圆(最新整理)

第四讲:二次函数与圆综合中考要求例题精讲一、二次函数与圆综合【例1】已知:抛物线与轴相交于两点,2:(1)(2)M y x m x m =+-+-x 12(0)(0)A x B x ,,,且.12x x <(Ⅰ)若,且为正整数,求抛物线的解析式;120x x <m M (Ⅱ)若,求的取值范围;1211x x <>,m (Ⅲ)试判断是否存在,使经过点和点的圆与轴相切于点,若存在,求出m A B y (02)C ,的值;若不存在,试说明理由;2:(1)(2)M y x m x m =+-+-(Ⅳ)若直线过点,与(Ⅰ)中的抛物线相交于两点,且使,求直线的:l y kx b =+(07)F ,M P Q ,12PF FQ =l 解析式.【解析】(Ⅰ)解法一:由题意得,.1220x x m =-<解得,.2m <为正整数,∴.∴.m 1m =21y x =-解法二:由题意知,当时,.0x =20(1)0(2)0y m m =+-⨯+-<(以下同解法一)解法三:,22(1)4(2)(3)m m m ∆=---=- .12(1)(3)122m m x x x m --±-∴=∴=-=-,,又.∴.(以下同解法一.)122020x x x m <∴=-> ,2m <解法四:令,即,0y =2(1)(2)0x m x m +-+-=∴.(以下同解法三.)12(1)(2)012x x m x x m ++-==-=-,,(Ⅱ)解法一:.1212111010x x x x <>∴-<-> ,,,,即.1212()10x x x x -++<,1212(1)2x x m x x m +=--=- ,∴.解得:.(2)(1)10m m -+-+<1m <∴的取值范围是.m 1m <解法二:由题意知,当时,1x =. 1(1)(2)0y m m =+-+-<解得:.1m <∴的取值范围是.m 1m <解法三:由(Ⅰ)的解法三、四知,.1212x x m =-=-,∴1211x x <> ,,21m ->∴.∴的取值范围是.1m <m 1m<(Ⅲ)存在.解法一:因为过两点的圆与轴相切于点,所以两点在轴的同侧,A B ,y (02)C ,A B ,y ∴.120x x >由切割线定理知,,2OC OA OB =A即.∴,2122x x =124x x =∴∴.12 4.x x =2 4.6m m -=∴=解法二:连接.圆心所在直线, O B O C '',11222b m mx a --=-=-=设直线与轴交于点,圆心为,12mx -=x D O '则.122mO D OC O C OD -''====,,2132AB AB x x m BD =-==-= ,∴32m BD -=在中, .Rt O DB '△222O D DB O B ''+=即.解得 .22231222m m --⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭6m =(Ⅳ)设,则.1122()()P x y Q x y ,,,22112211y x y x =-=-,过分别向轴引垂线,垂足分别为. 则.P Q ,x 112(0)(0)P x Q x ,,,11PP FO QQ ∥∥所以由平行线分线段成比例定理知,.11PO PFOQ FQ=因此,,即.120102x x -=-212x x =-过分别向轴引垂线,垂足分别为,P Q ,y 2122(0)(0)P y Q y ,,,则.所以..22PP QQ ∥22FP P FQ Q △∽△22P F FPFQ FQ ∴=.. 127172y y -∴=-12212y y ∴-=22122211212(1) 1.2324 1.x x x x ∴--=-∴-=-,或.21142x x ∴=∴=,12x =-当时,点.直线过,12x =(23)P , l (23)(07)P F ,,,解得7032.k b k b =⨯+⎧∴⎨=⨯+⎩,72.b k =⎧⎨=-⎩,当时,点.直线过,12x =-(23)P -, l (23)(07)P F -,,, 解得703(2).k b k b =⨯+⎧∴⎨=⨯-+⎩,72.b k =⎧⎨=⎩,故所求直线的解析式为:,或.l 27y x =+27y x =-+【例2】已知抛物线与y 轴的交点为C ,顶点为M ,直线CM 的解析式2y ax bx c =++并且线段CM 的长为2y x =-+(1)求抛物线的解析式。
二次函数压轴题(与圆综合问题)

二次函数压轴题(与圆综合问题)【典例分析】例1 如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C 三点的圆与y轴的另一个交点为D.(1)如图1,已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4);①求此抛物线的函数解析式;②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;(2)如图2,若a=1,c=-4,求证:无论b取何值,点D的坐标均不改变.思路点拨(2)连接AD、BC,如图2.若a=1,c=-4,则抛物线的解析式为y=x2+bx-4,可得C(0,-4),OC=4.设点A(x1,0),B(x2,0),则OA=-x1,OB=x2,且x1、x2是方程x2+bx-4=0的两根,根据根与系数的关系可得OA•OB=4.由A、D、B、C四点共圆可得∠ADC=∠ABC,∠DAB=∠DCB,从而可得△ADO∽∽△CBO,根据相似三角形的性质可得OC•OD=OA•OB=4,从而可得OD=1,即可得到D(0,1),因而无论b 取何值,点D的坐标均不改变.满分解答(1)①∵抛物线y=ax2+bx+c过点A(-2,0),B(8,0),C(0,-4),∴42064804a b ca b cc-+=⎧⎪++=⎨⎪=-⎩,解得14324abc⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩.学#科网∴抛物线的解析式为y=14x2-32x-4;②过点M作ME∥y轴,交BD于点E,连接BC,如图1.∴D(0,4).设直线BD的解析式为y=mx+n.∵B(8,0),D(0,4),∴804m nn+=⎧⎨=⎩,学&科网解得124mn⎧=-⎪⎨⎪=⎩,(2)连接AD、BC,如图2.若a=1,c=-4,则抛物线的解析式为y=x2+bx-4,则C(0,-4),OC=4.设点A(x1,0),B(x2,0),则OA=-x1,OB=x2,且x1、x2是方程x2+bx-4=0的两根,∴OA•OB=-x1•x2=-(-4)=4.考点:圆的综合题例2已知抛物线经过A(3,0), B(4,1)两点,且与y轴交于点C.(1)求抛物线的函数关系式及点C的坐标;(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB 于点F,当△OEF的面积取得最小值时,求点E的坐标.思路点拨(1)用待定系数法求解;(2) 假设存在,分两种情况讨论(3)根据面积公式,列出二次函数,求函数的最值.满分解答(1)将A(3,0),B(4,1)代人得∴∴∴C(0,3) 学科@网②当∠ABP=90O时,过B作BP∥AC,BP交抛物线于点P. ∵A(3,0),C(0,3)∴直线AC的函数关系式为将直线AC向上平移2个单位与直线BP重合.则直线BP的函数关系式为由,得又B(4,1),∴P2(-1,6).综上所述,存在两点P1(0,3), P2(-1,6).(3)∵∠OAE=∠OAF=45O,而∠OEF=∠OAF=45O, ∠OFE=∠OAE=45O,∴∠OEF=∠OFE=45O,∴OE=OF,∠EOF=90O∵点E在线段AC上,∴设E∴=∴===∴当时,取最小值,此时,∴例3如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.(1)求D点的坐标和圆D的半径;(2)求sin∠ACB的值和经过C、A、B三点的抛物线对应的函数表达式;(3)设抛物线的顶点为F,证明直线AF与圆D相切.思路点拨(1)连接CD,过点D作DE⊥AB,垂足为E,连接AD.依据垂径定理可知AE=3,然后依据切线的性质可知CD⊥y轴,然后可证明四边形OCDE为矩形,则DE=4,然后依据勾股定理可求得AD的长,故此可求得⊙D的半径和点D的坐标;学科.网(2)先求得A(2,0)、B(8,0).设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入可求得a 的值.根据三角形面积公式得:S△ABC=BC×AC sin∠ACB=AB×CO,代入计算即可;(3)求得抛物线的顶点F的坐标,然后求得DF和AF的长,依据勾股定理的逆定理可证明△DAF为直角三角形,则∠DAF=90°,故此AF是⊙D的切线.满分解答(2)如图1所示:∵D(5,4),∴E(5,0),∴A(2,0)、B(8,0).设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入得:16a=4,解得:a,∴抛物线的解析式为y x 2x +4.∵S △ABC =BC ×AC sin ∠ACB =AB ×CO ,∴sin ∠ACB ==.例4如图,已知二次函数()22y x m 4m =--(m >0)的图象与x 轴交于A 、B 两点.(1)写出A 、B 两点的坐标(坐标用m 表示);(2)若二次函数图象的顶点P 在以AB 为直径的圆上,求二次函数的解析式; (3)设以AB 为直径的⊙M 与y 轴交于C 、D 两点,求CD 的长. 思路点拨(1)解关于x 的一元二次方程()22x m 4m 0--=,求出x 的值,即可得到A 、B 两点的坐标。
010——二次函数——压轴(与圆有关篇).docx

二次函数(与圆有关)如图,在平面直角坐标系屮,正方形ABCD 和正方形DEFG 的边长分别为2a, 2b,点A, D, G 在y 轴上,坐 标原点0为AD 的中点,抛物线y=mx 2ac, F 两点,连接FD 并延长交抛物线于点M.(3)判断以FM 为直径的圆与AB 所在直线的位置关系,并说明理由.a如图,二次函数y二ax'+bx+c的图象交x轴于A(・l, 0), B (2, 0),交y轴于C (0, -2),过A, C画直线.(1)求二次函数的解析式;(2)点P在x轴正半轴上,且PA二PC,求OP的长;(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.①若M在y轴右狈IJ,且厶CHMs/XAOC (点C与点A对应),求点M的坐标;(备用图)如图,抛物线y二■一x2+mx+n的图象经过点A (2, 3),对称轴为直线x=l, —次函数y二kx+b的图象经过 4 点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.(1)求抛物线的解析式;(2)若PA: PB=3: 1,求一次函数的解析式;(3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得OC同时与x轴和直线AP都相切,如果存在,请求出点C的坐标,如果不存在,请说明理由.(1) 求该二次函数的关系式;(2) 过y 轴上的一点M (0, m)作y 轴的垂线,若该垂线与AABC 的外接圆有公共点,求in 的取值范围;(3) 在该二次函数的图象上是否存在点D,使四边形ACBD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由。
1 7 如图,已知抛物线m: y二ax? - 6ax+c (a>0)的顶点A在x轴上,并过点B (0, 1),直线n: y二-2x+2与x 轴交于点D,与抛物线m的对称轴1交于点F,过B点的直线BE与直线n相交于点E (・7, 7).(1)求抛物线m的解析式;(2)P是1上的一个动点,若以B, E, P为顶点的三角形的周长最小,求点P的坐标;(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标; 若不存在,请说明理由.如图,在平面直角坐标系中,点0为坐标原点,直线/与抛物线y=n^nx相交于A (1, 3 ), 〃(4, 0) 两点.(1)求出抛物线的解析式;(2)在坐标轴上是否存在点〃,使得△/!少是以线段为斜边的直角三角形?若存在,求出点〃的坐标; 若不存在,说明理由;(3)点P是线段川〃上一动点,(点戶不与点彳、g重合),过点P作PM// OA,交第一象限内的抛物线于点MN 臥过点〃作MCLx轴于点Q,交AB于点N,若'BCN、側的面积S/^o、5\恥满足二2弘妙,求出——NC24. (2015荆州12分)如图,在平面直角坐标系中,O为原点,UABCD的边BC在兀轴上,D点在y 轴上,C 点坐标为(2, 0), BC=6, ZBCD=60。
2024年九年级中考数学专题复习:圆与二次函数的综合压轴题(含答案)
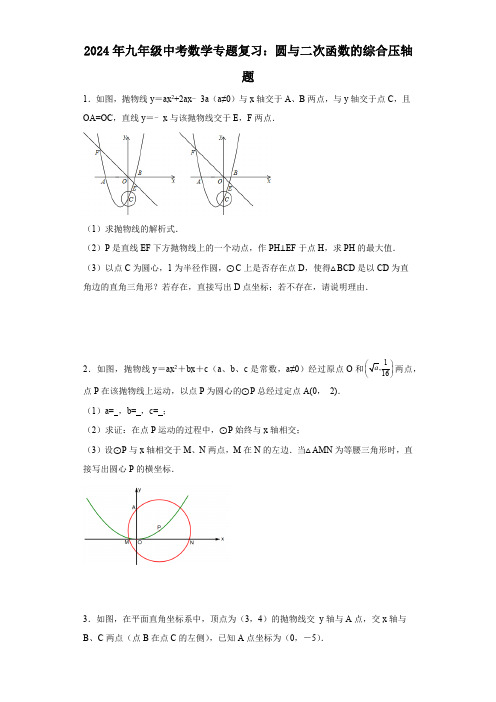
2024年九年级中考数学专题复习:圆与二次函数的综合压轴题(1)求抛物线的解析式.3.如图,在平面直角坐标系中,顶点为(B、C两点(点B在点C的左侧),已知(1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线与点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴与⊙C的位置关系,并给出证明.(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形.若存在,求点P的坐标;若不存在,请说明理由.4.如图所示:在平面直角坐标系中,圆M经过原点O且与X轴Y轴分别相交于A(-6,0),B(0,-8)两点(1)请写出直线AB的解析式(2)若有一抛物线的对称轴平行于Y轴且经过点M,顶点C在圆M上,开口向下且经过点B.求此抛物线的函数表达式(3)设(2)中的抛物线交X轴于D、E两点,在抛物线上是否存在点P,使得.若存在,请直接写出所有点P的坐标,若不存在,请说明理由5.如图,二次函数y=a +bx +c 的图象交x 轴于A 、B 两点,交y 轴于点C .且B (1,0),若将△BOC 绕点O 逆时针旋转90°,所得△DOE 的顶点E 恰好与点A 重合,且△ACD 的面积为3.(1)求这个二次函数的关系式.(2)设这个二次函数图象的顶点为M ,请在y 轴上找一点P ,使得△PAM 的周长最小,并求出点P 的坐标.(3)设这个函数图象的对称轴l 交x 轴于点N ,问:A 、M 、C 、D 、N 这5个点是否会在同一个圆上?若在同一个圆上,请求出这个圆的圆心坐标,并作简要说明;若不可能,请说明理由.6.如图,在直角坐标系中,以点A (,0 )为圆心,以2为半径的圆与x 轴相交于点B 、C ,与y 轴相交于点D 、E (1)若抛物线经过C 、D 两点,求抛物线的表达式,并判断点B 是否在该抛物线上(2)在(1)中的抛物线的对称轴上求一点P ,使得△PBD 的周长最小(3)设Q 为(1)中的抛物线对称轴上的一点,在抛物线上是否存在这样的点M ,使得四边形BCQM 是平行四边形,若存在,求出点M 的坐标;若不存在,说明理由2x7.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B 两点,开口向下的抛物线经过点A,B,且其顶点P在⊙C上.(1)求∠ACB的大小;(2)写出A,B两点的坐标;(3)试确定此抛物线的解析式;(4)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.8.如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);①求此抛物线的表达式与点D的坐标;②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.9.如图,在平面直角坐标系中,圆M经过原点O,且与x轴、y轴分别相交于A(-8,0),B(0,-6)两点.(1)求出直线AB的函数解析式;(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且(1)求该抛物线的函数关系式及顶点12.如图,已知在平面直角坐标系xOy 中,抛物线与x 轴交于点A (﹣1,0)和点B ,与y 轴相交于点C (0,3),抛物线的对称轴为直线.(1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标;(2)如果直线y=kx+b 经过C 、M 两点,且与x 轴交于点D ,点C 关于直线的对称点为N ,试证明四边形CDAN 是平行四边形;(3)点P 在直线上,且以点P 为圆心的圆经过A 、B 两点,并且与直线CD 相切,求点P 的坐标.13.在平面直角坐标系中,直线交轴于点,交轴于点,抛物线经过点,与直线交于点.(1)求抛物线的解析式;(2)如图,横坐标为的点在直线上方的抛物线上,过点作轴交2y ax 2x c =++l l l直线于点,以为直径的圆交直线于另一点.当点在轴上时,求的周长;将绕坐标平面内的某一点按顺时针方向旋转,得到,点的对应点分别是.若的两个顶点恰好落在抛物线上,请直接写出点2)(2)当△BOD为等边三角形时,求点B的坐标;(3)若以点B为圆心、r为半径作圆B,当圆B与两个坐标轴同时相切时,求点B的坐标.16.如图,已知抛物线y=ax2+bx﹣3(a≠0)经过点A(3,0),B(﹣1,0).(1)求该抛物线的解析式;(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.参考答案:)((3)-;(,)(,;最大值为;(3≤m≤.﹣x+x+1=;(,)或(﹣,)185。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题八二次函数压轴题一、核心讲练1.如图在平面直角坐标系中,直线y=-34x+3与x轴、y轴分别交于A、B两点,点P、Q同时从点A出发,运动时间为t秒.其中点P沿射线AB运动,速度为每秒4个单位长度,点Q沿射线AO运动,速度为每秒5个单位长度.以点Q为圆心,PQ长为半径作⊙Q.(1)求证:直线AB是⊙Q的切线;(2)过点A左侧x轴上的任意一点C(m,0),作直线AB的垂线CM,垂足为M.若CM与⊙Q相切于点D,求m与t的函数关系式(不需写出自变量的取值范围);(3)在(2)的条件下,是否存在点C,直线AB、CM、y轴与⊙Q同时相切?若存在,请直接写出此时点C的坐标;若不存在,请说明理由.2.如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-12x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.(1)求抛物线y=-x2+bx+c的表达式;(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求12AM+CM它的最小值.3.如图,已知二次函数y=49x2-4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为5,P为⊙C上一动点.(1)点B,C的坐标分别为B(),C();(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3)连接PB,若E为PB的中点,连接OE,则OE的最大值=.二、满分突破如图,y关于x的二次函数y=-33m(x+m)(x-3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(-3,0),连接ED.(m>0)(1)写出A、B、D三点的坐标;(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.专题八课堂小测1.下列实数中最大的数是()A.3B.0C.2D.-42.将180 000用科学记数法表示应为()A.18×104B.1.8×105C.1.8×106D.18×1053.一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为()A.40°B.45°C.50°D.10°4.为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,结果如下表:则关于“户外活动时间”这组数据的众数、中位数、平均数分别是()A.3、3、3B.6、2、3C.3、3、2D.3、2、35.下列根式是最简二次根式的是()A.13B.0.3C.3D.206.如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为()A.30°B.45°C.50°D.75°7.某书店推出一种优惠卡,每张卡售价20元,凭卡购书可享受8折优惠.小慧同学到该书店购书,她先买优惠卡再凭卡付款,结果节省了10元.若此次小慧同学不买卡直接购书,则她需付款多少元?()A.140元B.150元C.160元D.200元8.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为()A.x2-6=(10-x)2B.x2-62=(10-x)2C.x2+6=(10-x)2D.x2+62=(10-x)29.规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:①方程x2+2x﹣8=0是倍根方程;②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);④若点(m,n)在反比例函数y=4x的图象上,则关于x的方程mx2+5x+n=0是倍户外活动的时间(小时) 1 2 3 6 学生人数(人) 2 2 4 2根方程.上述结论中正确的有()A.①②B.③④C.②③D.②④10.若单项式-5x4y2m+n与2017x m-n y2是同类项,则m-7n的算术平方根是.11.若关于x的分式方程2+1kx=2的解为负数,则k的取值范围为.12.观察下列图形:它们是按一定规律排列的,依照此规律,第9个图形中共有个点.13.将直线y=x+b沿y轴向下平移3个单位长度,点A(-1,2)关于y轴的对称点落在平移后的直线上,则b的值为.14.如图,A、B、C是⊙O上的三点,且四边形OABC是菱形.若点D是圆上异于A、B、C的另一点,则∠ADC的度数是.15.如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=kx(x<0)的图象交AB于点N,S矩形OABC=32,DE:DO=12,则BN的长为.参考答案一、核心讲练例1. (1)连接QP .在Rt △AOB 中,OA =4,OB =3,∴AB =5,∵AP =4t ,AQ =5t ,∴=AP OA AQ AB =45,∵∠P AQ =∠BAO ,∴△P AQ ∽△BAO ,∴∠APQ =∠AOB =90°,∴QP ⊥AB ,∴AB 是⊙O 的切线. (2)①如图2中,当直线CM 在⊙O 的左侧与⊙Q 相切时,设切点为D ,则四边形PQDM 是正方形. 易知PQ =DQ =3t ,CQ =54•3t =154t ,∵OC +CQ +AQ =4,∴m +154t t +5t =4,∴m =4-354t . ②如图3中,当直线CM 在⊙O 的右侧与⊙Q 相切时,设切点为D ,则四边形PQDM 是正方形.∵OC +AQ -CQ =4,∴m +5t -154t =4,∴m =4-54t . (3)存在.理由如下:如图4中,当⊙Q 在y 则的右侧与y 轴相切时,3t +5t =4,t =12,由(2)可知,m =-38或278.如图5中,当⊙Q 在y 则的左侧与y 轴相切时,5t -3t =4,t =2,由(2)可知,m =-272或32. 综上所述,满足条件的点C 的坐标为(-38,0)或(278,0)或(-272,0)或(32,0).例2. (1) y =-x 2-2x +4;(2)直线AB 的解析式为y =2x +4,设E (m ,2m +4),∴G (m ,-m 2-2m +4),∵四边形GEOB 是平行四边形,∴EG =OB =4,∴-m 2-2m +4-2m -4=4,∴m =-2,∴G (-2,4).(3)①如图1,由(2)知,直线AB 的解析式为y =2x +4,∴设E (a ,2a +4),∵直线AC :y =-12x -6, ∴F (a ,-12a -6),设H (0,p ),∵以点A ,E ,F ,H 为顶点的四边形是矩形,∵直线AB 的解析式为y =2x +4,直线AC :y =-12x -6,∴AB ⊥AC ,∴EF 为对角线,∴12(-4+0)=12(a +a ),12(4+p )=12(2a +4-12a -6), ∴a =-2,P =-1,∴E (-2,0).H (0,-1);②如图2,由①知,E (-2,0),H (0,-1),A (-4,-4),∴EH =5,AE =25,设AE 交⊙E 于G ,取EG 的中点P ,∴PE =52,连接PC 交⊙E 于M ,连接EM ,∴EM =EH =5,∴PE ME =12,∵ME AE =12, ∴PE ME =ME AE =12,∵∠PEM =∠MEA ,∴△PEM ∽△MEA ,∴1=2PM ME AM AE ,∴PM =12AM ,∴12AM +CM的最小值=PC ,设点P (p ,2p +4),∵E (-2,0),∴PE 2=(p +2)2+(2p +4)2=5(p +2)2,∵PE =52,∴5(p +2)2=54, ∴p =-52或p =-32 (由于E (-2,0),所以舍去),∴P (-52,-1),∵C (0,-6),∴PC =552,即12AM +CM =552.例3.(1) 3,0;0,﹣4;(2)存在点P ,使得△PBC 为直角三角形,①当PB 与⊙相切时,△PBC 为直角三角形,如图(2)a ,连接BC ,∵OB =3.OC =4,∴BC =5,∵CP 2⊥BP 2,CP 2=5,∴BP 2=25,过P 2作P 2E ⊥x 轴于E ,P 2F ⊥y 轴于F ,则△CP 2F ∽△BP 2E , ∴2222=P F CP P E BP =12,设OC =P 2E =2x ,CP 2=OE =x ,∴BE =3﹣x ,CF =2x ﹣4,∴BE CF =324x x --=2,∴x =115,2x =225, ∴FP 2=115,EP 2=225,∴P 2(115,-225),过P 1作P 1G ⊥x 轴于G ,P 1H ⊥y 轴于H ,同理求得P 1(-1,-2), ②当BC ⊥PC 时,△PBC 为直角三角形,过P 4作P 4H ⊥y 轴于H ,则△BOC ∽△CHP 4,∴445==5P H P C CH OB OC BC =,∴CH =355,P 4H =455,∴P 4(455,-355-4);同理P 3(-455,355-4); 综上所述:点P 的坐标为:(-1,-2)或(115,-225)或(455,-355﹣4)或(-455,355-4); (3)如图(3),连接AP ,∵OB =OA ,BE =EP ,∴OE =12AP ,∴当AP 最大时,OE 的值最大,∵当P 在AC 的延长线上时,AP 的值最大,最大值=5+5,∴OE 的最大值为552+二、满分突破(1)A (-m ,0),B (3m ,0),D (0,3m ).(2) y =33mx +3m .将y =-m 33(x +m )(x -m )化为顶点式:y =-m 33(x ﹣m )2+334m .∴顶点M 的坐标为(m 334m ).代入y =33mx +3m 得:m 2=m ,∵m >0,∴m =1.所以,当m =1时,M 点在直线DE 上. 连接CD ,C 为AB 中点,C 点坐标为C (m ,0).∵OD =3,OC =1,∴CD =2,D 点在圆上,又∵OE =3,DE 2=OD 2+OE 2=12,EC 2=16,CD 2=4,∴CD 2+DE 2=EC 2.∴∠EDC =90°∴直线ED 与⊙C 相切.(3)当0<m≤3时,S △AED =21AE •OD =23m (3-m ),S =-23m 2+233m ;当m >3时,S △AED =21AE •OD =23m (m -3).即S =23m 2_ 233m . S 关于m 的函数图象的示意图如右:课堂小测1.A ;2.B ;3.D ;4.A ;5.C ;6.B ;7.B ;8.D ;9.C ;10.4;11. k <3且k ≠1;12.135;13.4;14.60°或120°;15.3;。
