2014-计算力学-10-非线性结构解析
工程力学中的应力和应变分布的计算方法

工程力学中的应力和应变分布的计算方法工程力学是工程领域中研究物体在作用力下产生的应力和应变的学科。
在工程设计和结构分析中,准确计算应力和应变分布是至关重要的,它们对于评估结构的安全性和可靠性具有重要意义。
本文将介绍工程力学中常用的应力和应变分布的计算方法。
一、应力的计算方法1. 线性结构的应力计算方法在线性结构中,应力可以通过应力=力/截面积的公式进行计算。
对于受压或受拉的杆件,应力等于施加在杆件上的力除以杆件的截面积。
对于弯曲杆件,应力的计算需要考虑弯矩和截面惯性矩的影响。
根据梁的弯矩公式,弯曲杆件上的应力等于弯矩乘以截面离轴距离除以截面惯性矩。
2. 非线性结构的应力计算方法对于非线性结构,如塑性材料或复合材料,应力的计算方法会更加复杂。
在这种情况下,常常需要使用数值模拟方法,如有限元分析,来计算应力分布。
有限元分析通过将结构划分为有限数量的小单元,并在每个小单元上进行应力计算,然后将结果汇总得到整个结构上的应力分布。
二、应变的计算方法1. 线性结构的应变计算方法在工程力学中,应变定义为物体长度或体积的变化与原始长度或体积之比。
对于受压或受拉的线性结构,应变计算可以通过应变=位移/原始长度的公式进行。
位移是杆件两端的距离差,原始长度是杆件未受力时的长度。
2. 非线性结构的应变计算方法对于非线性结构,应变的计算方法也会更加复杂。
类似于应力计算,可以使用有限元分析等数值模拟方法来计算非线性结构上的应变分布。
有限元分析可以考虑材料的非线性特性,如材料的应力-应变曲线,从而得到更精确的应变分布。
三、常见应力和应变分布形式1. 拉伸和压缩应力分布在拉伸和压缩加载下,线性材料的应力分布呈现均匀分布。
即在整个截面上应力大小相等。
但对于非线性材料,应力分布可能呈现不均匀分布,尤其是在接近临界点时。
2. 弯曲应力分布在弯曲结构中,线性材料的应力分布呈现最大值位于中性轴线处,随着距离中性轴线的增加而逐渐减小。
对于非线性材料,应力分布也会受到材料特性的影响,可能不呈现对称的形式。
非线性结构有限元分析概论

一、线性问题的基本方程
由复杂结构受力平衡问题的虚功方程有:
v T dv vuT qvdv suT qsds u0T R0
vmu
T
••
u dv
v
Du
T
•
u
dv
(10-1)
上式左端为内力的虚功,右端为外力的功。
由于: u N u Bu C
式中 u 为单元体内的位移; u为节点位移; N 形函数阵;
t t t
T
S t t t
dvt
W t t
(10-18)
返回
其中:
W tt o
tv
u
T
q tt tv
中推荐采用BFGS法。
程序对几何非线性的考虑可采用完全的拉格朗
日公式或改进的拉格朗日公式。在非线性动态分析
中采用隐式时间积分(Newmarli法和Wilson- 法) 或显式时间积分(中心差分法)的方法。隐式时间
积分通常用来分析结构的振动问题,显式时间积分
主要用来分析波传布现象。
返回
第一节 有限元基本方程
解此方程也用隐式时间积分,显式时间积分或振形迭加
法求解。
返回
二、非线性问题的基本方程
对于非线性问题通常不能用一步直接求解方案,必须分成
若干步加载,按各个阶段不同的非线性性质逐步求解,即增量求
解方案。
1.增量形式的平衡方程:
已知设:0,△t,2△t‥‥的位移和应力(各载荷步的)
要求出:t+△t步时的位移和应力。
ov oe T o
o e dv
ov
o
T
t o
SdvtW t o来自ovoe Tt o
S
dv
非线性动力系统的数值计算方法及稳定性分析

非线性动力系统的数值计算方法及稳定性分析非线性动力系统是一种非常常见的实际物理系统,例如电路、化学反应、天气系统等,它们的行为通常比线性系统更加复杂。
数值计算非线性动力系统的稳定性与动力学特性是一个非常重要的课题,对于研究和预测实际系统的行为有着非常重要的意义。
在本文中,我们将介绍几种常见的非线性动力系统的数值计算方法及它们的稳定性分析。
一、欧拉法欧拉法是动力系统数值计算中最基本的一种方法。
它的基本思路是将连续的时间离散化,将微分方程转化成差分方程,然后用迭代的方式求解。
欧拉法的迭代公式为:$$y_{n+1}=y_{n}+hf(y_n)$$其中,$h$为步长,$f(y_n)$是微分方程在$y_n$处的导数。
欧拉法是一种比较简单易懂的方法,但是它的稳定性较差,容易产生数值误差。
欧拉法对于初始值的依赖性很强,如果步长$h$选取过大,就会导致解的不稳定。
因此,在使用欧拉法进行数值计算时,我们需要根据实际问题来调整步长,以保证数值解的正确性。
二、龙格-库塔法龙格-库塔法是一种常见的数值积分方法,在动力系统数值计算中也常常被使用。
它的基本思路是利用微分方程的某些性质,选取合适的时间步长和权重,在数值上求得微分方程的积分近似解。
龙格-库塔法通常可以由一些权重系数和步长系数组成,如下:$$Y_{n+1}=Y_n+\frac{1}{6}(k_1+2k_2+2k_3+k_4)$$$$k_1=hf(Y_n)$$$$k_2=hf(Y_n+\frac{1}{2}k_1)$$$$k_3=hf(Y_n+\frac{1}{2}k_2)$$$$k_4=hf(Y_n+k_3)$$其中,$k_1,k_2,k_3,k_4$均为微分方程在相应位置处的导数。
龙格-库塔法比欧拉法更加稳定,适用于多数动力系统的数值计算。
但是,龙格-库塔法在计算一些比较长时间范围内的运动时,需要降低步长以保证解的精度。
同时,权重系数和步长系数也需要根据具体问题调整,才能得到更加准确的数值解。
非线性结构有限元分析

在程序中,对增量方程求解的平衡迭代采用修正 的牛顿迭代法或BFGS法。 1. 修正的牛顿迭代法。它与完全的牛顿法的不同在 于迭代过程中系数矩阵保持不变,因此不需要重新形 成和分解刚度阵,从而大大减少了计算量。但是这样 又带来了收敛速度慢和发散问题,对此程序中加入了 加速收敛和发散处理的措施。这些措施并不明显地增 加求解的时间,但却会对修正的牛顿迭代法的性能有 所改进。 2. BFGS法。又称矩阵修正迭代,是拟牛顿法的一 种。它实际上是完全的牛顿法与修正的牛顿法之间的 一种折中方法。因为它在迭代过程中,并不重新形成
0 t t t k xi N k0 xik, xi N kt xik, xi N kt t x( i 10-28) k 1 k 1 k 1 n n n
0 k t k t t k 其中: xi , xi , xi 为节点k,i方向上在0,t, t+△t时刻的
返回
取位移插值函数为: n
t
写成矩阵形式:
t i
ui N u
k 1
t k k i
;
ui N k uik
k 1
n
(10-26) (10-27)
u [N ] u
t k i
;
ui [ N ]uik
其中:Nk为插值函数,[N]为形函数矩阵; t k ui ,uik 为k点i方向上t时刻的位移和位移增量; n为单元节点数。 取坐标变换为:
v
v s
{R} [ N ]T qv dv [ N ]T qs ds {R0}
{u}
外载荷阵 (10-6) 为节点位移对时间的二 次导数;
为节点位移对时间的一 次导数。
{u}
工程力学中的非线性分析方法有哪些?

工程力学中的非线性分析方法有哪些?在工程力学领域,非线性问题的研究至关重要。
与线性问题相比,非线性问题更加复杂,需要采用专门的分析方法来准确描述和解决。
下面我们就来探讨一下工程力学中常见的非线性分析方法。
首先要提到的是有限元法。
这是一种非常强大且广泛应用的数值分析方法。
在处理非线性问题时,它能够有效地模拟材料的非线性行为,比如塑性、蠕变等。
通过将复杂的结构离散为有限个单元,并对每个单元进行分析,最终得到整个结构的响应。
对于几何非线性问题,如大变形、大转动等,有限元法能够通过更新坐标和刚度矩阵来准确捕捉结构的变化。
而对于材料非线性,如弹塑性问题,通过定义合适的本构关系,可以精确地模拟材料在不同应力状态下的行为。
再来看看边界元法。
它是另一种有效的数值方法,特别适用于处理无限域或半无限域问题。
在非线性分析中,边界元法可以结合迭代算法来求解非线性边界条件或非线性材料特性。
与有限元法相比,边界元法通常只需要对边界进行离散,从而降低了问题的维数,减少了计算量。
但在处理复杂的非线性问题时,其数学推导和编程实现可能会相对复杂。
还有一种方法是摄动法。
这是一种基于微扰理论的分析方法。
对于弱非线性问题,通过将非线性项视为对线性问题的小扰动,将问题的解表示为一个级数形式。
通过求解这个级数的各项,可以逐步逼近非线性问题的精确解。
摄动法在处理一些简单的非线性问题时非常有效,但对于强非线性问题,其精度可能会受到限制。
接下来是增量法。
在处理非线性问题时,将加载过程或变形过程分成一系列的小增量。
在每个增量步内,将问题近似为线性问题进行求解,然后逐步累加得到最终的结果。
这种方法适用于各种非线性问题,尤其是在考虑加载历史和路径相关性的情况下。
非线性有限差分法也是常用的手段之一。
它直接对控制方程进行离散,通过差分近似来表示导数项。
在处理非线性问题时,可以采用迭代的方式求解离散后的方程组。
这种方法对于简单的几何形状和边界条件的问题较为适用,但对于复杂的结构可能会面临网格划分和精度控制的挑战。
梁杆结构几何非线性有限元的数值实现方法

NUMERICAL IMPLEMENTATION OF GEOMETRICALLY NONLINEAR FINITE ELEMENT METHOD FOR BEAM STRUCTURES
CHEN Zheng-qing
(College of Civil Engineering, Hunan University, Changsha 410082, China)
= tσ ij + ∆∗T ij = ∆∗ Eij
(1) (2)
而它在 t+Δt 时刻柯西应变就等于其增量:
t + ∆t t Eij
式中, ∆ Eij 为:
∗
∆∗ Eij = ∆∗ε ij + ∆∗ηij 1 ∆∗ε ij = (∆ui ,j + ∆u j ,i ) 2 1 ∆∗ηij = ∆uk ,i ∆uk ,j 2
———————————————
收稿日期:2013-05-01;修改日期:2014-03-06 基金项目:国家自然科学基金项目(91215302) 作者简介: 陈政清(1947―), 男, 湖南湘潭人, 教授, 博士, 湖南大学风工程研究中心主任, 主要从事结构振动与控制研究(E-mail: zqchen@).
(3) (4) (5)
44
工
程
力
学
E G [ t kαβ ]{∆qα } = {t+ ∆t Pβ − tψ β } + t kαβ
仍然假定变形体的应变增量是小应变,应 力应变增量关系可以记为:
(14) (15) (16)
′ ∆∗ε kl ∆∗T ij = Cijki
功增量方程如下: ′ = A3 ′ − A4 ′ A1′ + A2 式中:
工程力学中的非线性分析技术有哪些?

工程力学中的非线性分析技术有哪些?在工程力学的广袤领域中,非线性分析技术扮演着至关重要的角色。
当我们面对复杂的工程结构和材料行为时,线性分析往往无法准确描述其真实的力学特性,这时非线性分析技术就成为了我们探索和理解的有力工具。
首先,让我们来谈谈几何非线性分析。
想象一下一根长长的钢梁,在受到巨大的载荷时会发生明显的弯曲和变形。
这种情况下,梁的几何形状的改变会对其力学性能产生显著影响。
几何非线性分析考虑了结构在大变形下的几何变化,不再将结构的变形视为微小量。
通过这种分析,可以更准确地预测结构的承载能力和稳定性。
材料非线性分析也是不可或缺的一部分。
材料在不同的应力和应变条件下,其力学性能可能会发生巨大的变化。
例如,金属材料在达到屈服点后会出现塑性变形,其应力应变关系不再是线性的。
而对于像橡胶这样的超弹性材料,其力学行为更是复杂多样。
材料非线性分析能够准确地模拟这些材料在各种工况下的力学响应,为工程设计提供可靠的依据。
接触非线性分析在很多实际工程问题中也十分常见。
当两个或多个物体相互接触时,接触区域的压力分布、摩擦力以及可能的分离和滑动等现象都需要精确的模拟。
比如在机械零件的装配中,零件之间的接触状态对整个系统的性能有着重要影响。
接触非线性分析能够考虑接触表面的几何形状、材料特性以及接触力的传递,从而有效地评估接触部位的可靠性和耐久性。
边界非线性分析则主要关注边界条件的非线性特征。
在某些情况下,结构的边界条件可能会随着载荷的变化而发生改变。
例如,在地基与建筑物的相互作用中,地基的支撑刚度可能会随着建筑物的沉降而变化。
边界非线性分析能够处理这种复杂的边界条件变化,为工程结构的分析提供更真实的模拟。
再来看看非线性动力学分析。
当结构受到动态载荷,如地震、风载或机器振动时,其响应可能表现出非线性的特征。
非线性动力学分析可以帮助我们研究结构在这些复杂动态载荷下的稳定性、振动频率和振幅等重要特性。
这对于设计抗震结构、航空航天飞行器以及其他动态系统至关重要。
ANSYS讲义非线性分析
• 力/力矩不平衡量 {R}
FORCE CONVERGENCE VALUE
• 最大的自由度增量 {u}
MAX DOF INC
• 力收敛判据
CRITERION
• 载荷步与子步数
LOAD STEP
1 SUBSTEP 14
第35页/共97页
输出文件的信息(续)
输出窗口包括(续) :
• 当前子步的迭代步数
EQUIL ITER 1 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= -0.1645E-01
FORCE CONVERGENCE VALUE = 10.35
CRITERION= 2.095
DISP CONVERGENCE VALUE = 0.2409E-01 CRITERION= 0.9406
第11页/共97页
概述
ANSYS 最常用的非线性功能
• 几何非线性
大应变,大位移与大转动
-- 结构稳定性 (前屈曲分析与后屈曲分析)
• 塑性
• 超弹性
• 接触非线性
第12页/共97页
非线性分析
第13页/共97页
主要内容
应理解非线性分析中所用到的基本术语:
1. Newton-Raphson法 2. 收敛 3. 载荷步,子步和平衡迭代 4. 自动时间步 5. 输出文件信息 6. 非线性求解过程 7. 高级求解控制 8. 重启动分析
1. 几何非线性
大应变,大位移,大旋转
2. 材料非线性
塑性,超弹性,粘弹性,蠕变
3. 状态改变非线性
接触,单元死活
第3页/共97页
几何非线性
如果一个结构承受大的变形,它改变的几何构形可导致非线性行 为。大位移、大应变和大旋转是几何非线性的例子。
计算固体计算力学 - 第二章 非线性方程组的解法

p
则称序列{an}至少p阶收敛。 收敛阶大的序列比收敛阶小的序列收敛的快。
15
计算固体计算力学
Newton法得到的序列{an}具有二阶收敛速度。 粗略的说,用Newton法迭代一次大约有效数位 增加一倍,例如, a0准确到一位,则迭代3次就 可以得到准确8位的近似解。这意味着Newton 法收敛很快,这是它的主要优点。 Newton法自校正的。也就是说,an+1仅依赖于 Ψ(an)及an,前面迭代产生的舍入误差不会一步步 传下去。
则-Ψ(an)=R-P(an)可代表失衡力矢量。 于是,收敛准则同前,取位移收敛准则或 失衡力收敛准则。
12
计算固体计算力学
算法:
(1)给定初始近似a0及计算精度α和β; (2)假定已经进行了n次迭代,已求出an及Ψ(an), 计算 K
a a an
n T
(3)解方程组KTnΔan=- Ψ(an),得Δan ; (4)求an+1=an+Δan及Ψ(an+1) ; (5)直至 Δan 满足收敛性; (6)结束。
13
计算固体计算力学
一个单变量的非线性方程,用Newton 法求解过程如图:
14
计算固体计算力学
讨论:迭代法的收敛速度问题 即研究迭代序列{an, n=0,1,…}收敛的快慢。 假定迭代序列{an}收敛于a*,且存在p≥1及常 数η>0,使当n≥ n0 下式成立
a
n 1
a a a
(a , ) ,a Δ a , Δ 0
引入切线矩阵且略去高阶小量后可改写为
Δa KT (a, )1 RΔ
33
计算固体计算力学
设荷载增量因子λ分别取如下值
桥梁结构非线性特性及求解方法概述

桥梁结构非线性特性及求解方法概述摘要:桥梁结构中普遍存在非线性问题。
由于某些材料的特殊特性、结构本身几何构造的特殊性以及结构施工过程中外界条件的改变,往往会体现出各类明显的非线性特征。
因此,要对桥梁结构进行精确而详细的分析,就要对其进行非线性问题的求解。
本文对桥梁结构的给累非线性以及解决方式进行了说明,为求解桥梁非线性问题提供一定的参考。
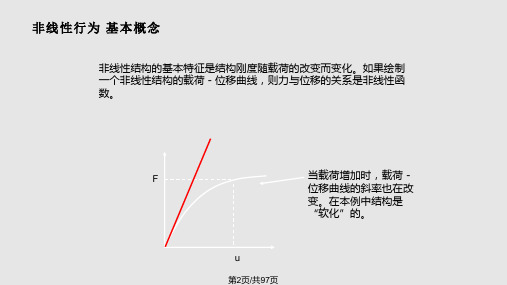
关键词:结构非线性;非线性求解Overview of Nonlinear Characteristics and Solution Method of Bridge Structure Abstract: There are generally some nonlinear phenomena in the bridge structure. Dueto the special characteristics of certain materials, the particularity of the geometric structure of the structure itself and the change of external conditions during the construction process, various types of obvious nonlinear characteristics are often manifested. Therefore, to conduct accurate and detailed analysis of the bridge structure, it is necessary to solve the nonlinear problem. This paper describes the nonlinearity and solution of the bridge structure, and provides a reference for solving nonlinear problems of bridges.Keywords: material nonlinearity; geometric nonlinearity; state nonlinearity1 非线性问题的定义和种类非线性结构的基本特征是结构刚度随着荷载的改变而变化,力与位移的关系是非线性函数。
非线性结构有限元分析课件

非线性结构有限元分析的步骤与流程
• 设定边界条件和载荷,如固定约束、压力 或力矩等。
非线性结构有限元分析的步骤与流程
01 步骤三:求解
02
选择合适的求解器,如Newton-Raphson迭代法或 直接积分法。
03 进行迭代计算,求解非线性结构的内力和变形。
非线性结构有限元分析的步骤与流程
01
步骤四:后处理
非线性有限元分析的基本概念
总结词
非线性有限元分析是一种数值分析方法,通过将复杂的结构或系统离散化为有限个小的单元,并建立 每个单元的数学模型,来模拟和分析结构的非线性行为。
详细描述
非线性有限元分析是一种基于离散化的数值分析方法,通过将复杂的结构或系统划分为有限个小的单 元(或称为有限元),并建立每个单元的数学模型,来模拟和分析结构的非线性行为。这种方法能够 考虑各种复杂的边界条件和材料特性,提供更精确的数值结果。
非线性有限元分析的常用方法
总结词
非线性有限元分析的常用方法包括迭代法、增量法、 降维法等。这些方法可以根据不同的非线性问题选择 使用,以达到更好的分析效果。
详细描述
在非线性有限元分析中,常用的方法包括迭代法、增量 法、降维法等。迭代法是通过不断迭代更新有限元的位 移和应力,逐步逼近真实解的方法;增量法是将总载荷 分成若干个小的增量,对每个增量进行迭代计算,最终 得到结构的总响应;降维法则是通过引入一些简化的假 设或模型,将高维的非线性问题降维处理,以简化计算 和提高计算效率。这些方法各有优缺点,应根据具体的 非线性问题选择使用。
03
02
弹性后效
材料在卸载后发生的变形延迟现象。
材料强化
材料在受力过程中发生的强度增加 现象。
04
10结构力学——结构的稳定计算

哈工大 土木工程学院
4 / 85
16
结构的稳定计算
第一类失稳的基本特征 结构失稳前后平衡状态所对应的变形性质发生改变,分支 点处平衡形式具有两重性,分支点处的荷载即为临界荷载, 称分支点失稳。 FP FP FP < FPcr时,杆件仅产生压 缩变形。轻微侧扰,杆件微 II 不稳定 弯;干扰撤消,状态复原 FPcr 0 (平衡路径唯一)。
Δ f
FP
FPcr
O
l
l
由极值点的失稳问题突然转化为受拉的强度问题
哈工大 土木工程学院
9 / 85
16
结构的稳定计算
稳定性分析有基于小变形的线性理论和基于大变 形的非线性理论。非线性理论考虑有限变形对平 衡的影响,分析结果与实验结果较吻合,但分析 过程复杂。不管是第一类稳定问题,还是第二类 稳定问题,它们都是一个变形问题,稳定计算都 必须根据其变形状态来进行,有时还要求研究超 过临界状态之后的后屈曲平衡状态。
• 第二类失稳属于几何非线性问题,而当结构变形达到 一定程度时通常伴有材料非线性的出现,因此计算比 较复杂,但却是精确解。
哈工大 土木工程学院
18 / 85
16
结构的稳定计算
分析结论
• 第一类失稳常可用物理概念清晰的解析式表达,计算 较简单,有利于对影响临界荷载的各种因素形成直观 的认识。但计算出的临界荷载偏大,不安全。 • 第一类失稳的临界荷载是第二类临界荷载的上限值, 对因缺陷引起的第二类失稳问题常可以将第一类失稳 的临界荷载乘以折减系数,或对其表达式进行适当修 改,以求其临界荷载值,这便于设计应用。
哈工大 土木工程学院
17 / 85
16
结构非线性分析

结构非线性分析理论1.结构设计方法结构设计方法从传统的容许应力设计法发展到了基于概率统计的极限状态设计法。
传统的容许应力设计法是基于线弹性理论,依照经验选取一定的安全系数,以构件危险截面某一点的计算应力不超过材料的容许应力为准则,目前在某些领域仍在使用。
安全系数,是一个单一的根据经验确定的数值,没有考虑不同结构之间的差异,不能保证不同结构具有同等的安全水平。
此外,容许应力设计法以弹性理论计算内力,对那些发展塑性变形能提高承载力的构件或结构(如受弯构件),比那些发展塑性变形不能提高承载力的构件或结构(如轴心受力构件)具有较大的安全储备。
概率极限状态设计法是采用数理统计方法按照一定概率确定荷载或材料的代表值,并给出结构的功能函数,用结构失效概率或可靠指标度量结构的可靠性。
《建筑结构可靠度设计统一标准》将极限状态分为两类:(1)承载能力极限状态,是指结构或结构构件达到最大承载能力或不适于继续承载的变形;(2)正常使用极限状态,是指结构或结构构件达到正常使用或耐久性能的某项规定限值。
结构按极限状态设计应符合下列要求:()0,21≥n X X X g (1.1)式((1.1)中g(X i )为结构功能函数,X i (i =1, 2……n)为基本变量,是指影响该结构功能的各种作用、材料性能、几何参数等。
目前我国结构设计规范基本都是采用以概率理论为基础的极限状态设计方法,用分项系数设计表达式进行计算。
美国的钢结构设计采用了两种设计方法:ASD(Allowable Stress Design)和LRFD(Load and Resistance Factor Design),即容许应力设计法和分项系数设计法,McCormac 指出LRFD 相比ASD ,并不一定节省材料,虽然在很多情况下可以取得这样的效果,而在不同荷载作用下能给结构提供等同的可靠性,对于活载和恒载,ASD 采用的安全系数是一样的,而LRFD 对恒载则采用了一个较小的荷载系数(恒载比活载能更准确的确定),也就是说如果恒载大于活载,LRFD 比ASD 节省材料。
桥梁结构非线性分析

桥梁结构非线性分析桥梁结构非线性分析是一种复杂的工程分析方法,用于研究桥梁在受载情况下的非线性力学行为。
传统的线性分析方法假设结构在整个加载过程中是刚性的,并且不考虑材料的非线性特性。
然而,在实际的桥梁结构中,存在许多导致结构非线性的因素,如几何非线性(大变形和位移)、材料非线性(应力-应变关系)和接触非线性(节点接触和摩擦)等。
因此,非线性分析能够更准确地预测桥梁结构的性能和破坏状态。
在桥梁结构的非线性分析中,通常采用有限元方法来建立结构的数值模型。
有限元方法将结构分割成许多小单元,每个单元具有一组节点和元素属性。
通过数学方程和边界条件,可以计算出每个节点的位移和应力情况,并进一步推导整个结构的非线性行为。
在进行桥梁结构的非线性分析时,需要考虑以下几个方面:1.几何非线性:在大变形和位移情况下,线性假设不再成立。
因此,在模型中需要考虑基于几何非线性进行的形变和应力计算。
这通常涉及到杆单元的应变能计算和弯曲挠度的计算。
2.材料非线性:材料的应力-应变关系在不同的载荷范围内具有非线性特性。
在分析中需要考虑这些非线性关系,并根据实际材料的力学特性进行建模。
常见的材料非线性模型包括弹塑性模型、本构方程和破坏准则等。
3.接触非线性:在桥梁结构中,节点之间的接触和摩擦会导致结构的非线性行为。
在分析中,需要考虑节点的接触状态,并利用适当的接触力模型来计算相应的接触力。
这通常涉及到利用接触法相和摩擦系数来描述节点之间的相互作用。
4.非线性分析方法:非线性分析中常用的方法包括弧长法、切线法和增量法等。
弧长法是一种迭代过程,用于解决材料和几何非线性问题。
切线法是一种通过计算切线刚度矩阵,在每个时间步骤中更新位移和力的方法。
增量法则是将分析过程分成若干个小步骤,并逐步增加应力和位移的方法。
总之,桥梁结构的非线性分析方法可以更准确地预测结构的性能和破坏状态。
在实际工程中,通过采用合适的非线性分析方法和模型,可以提高桥梁结构的设计和维护水平,确保桥梁的安全性和可靠性。
东南大学计算力学课件(研究生课程) 第9章 非线性简介

2014/12/4 6
9.1 概况
材料非线性(Nonlinear stress-strain behavior) 应力——应变关系是非线性的。 塑性屈服( y ) 非线性弹性(塑料、岩石、土壤等) 蠕变(高温环境变形随时间增大)
2014/12/4
8
状态非线性
9.1 概况
许多普通结构表现出一种与状态相关的非线性行为, 例如,一根钢索可能是松散的,也可能是绷紧的。螺栓孔 可能是接触的,也可能是不接触的, 冻土可能是冻结的,也 可能是融化的。这些系统的刚度由于系统状态的改变在
不同的值之间突然变化。状态改变也许和载荷直接有关
③ 每迭代一次需形成一次系数矩阵,并求解一次
线n 性 方K程n11组R。
2014/12/4
15
单自由度一维非线性问题
k
u
P
k k0 kN k0 常数 kN u的函数
2014/12/4 16
单自由度一维非线性问题
k0 kN u P
kN f(u)
给定P就可以得到u,根据弹簧性质 可以知道f(u)是已知函数
1 n 1
p
讨论:① 精度 e n n1 er
2014/12/4
误差的范数
容许值
14
非线性问题的一般处理方法
------ 直接迭代法
② 收敛性
R
R K R
R K
-p
-p
0 1 2 3
0
n1 n n2
下凹一般收敛
计算力学中的非线性分析研究

计算力学中的非线性分析研究计算力学是一门研究力学问题的学科,其主要研究对象是物体的运动规律以及力的作用情况。
在实际工程问题中,往往存在着非线性的情况,因此非线性分析在计算力学中具有重要的研究意义。
非线性分析的基本概念非线性分析即研究非线性问题的方法和技术。
与线性分析不同,非线性分析需要考虑物体的非线性力学特性,如材料的非线性行为、几何形状的非线性效应等。
在非线性分析中,常常会遇到以下几类问题:1. 材料非线性问题:材料的应力-应变关系不再遵循线性弹性模型,而是呈现出非线性行为的特征。
这涉及到材料的塑性、粘塑性、弹塑性等非线性性质的描述和分析。
2. 几何非线性问题:物体的几何形状发生变化时,会引起内部应力和应变的变化,从而对物体的力学行为产生显著影响。
几何非线性问题描述了物体在大变形情况下的力学响应。
3. 边界条件非线性问题:对于某些问题,边界条件的变化可能引起物体力学行为的非线性变化。
边界条件非线性问题研究的是如何在不同边界条件下对物体的力学问题进行分析。
非线性分析方法非线性分析方法主要包括两个方面:数值方法和解析方法。
数值方法是指通过建立数学模型,利用计算机进行数值计算求解。
其中,有限元法(FEM)是最常用的数值分析方法之一。
它将连续的物体划分为有限个单元,通过在每个单元内建立适当的形函数和节点,将强度计算问题转化为求解线性方程组的问题。
有限元法在非线性分析中有着广泛的应用。
解析方法是指利用数学分析手段求解非线性问题的方法。
在非线性分析中,解析方法常常用于线性化求解。
其基本思想是将非线性问题线性化,然后利用线性求解的方法求解近似解。
通常,线性化求解可以通过泰勒级数展开来实现。
非线性分析在工程中的应用非线性分析在工程领域中有着广泛的应用。
以下是一些应用场景的介绍:1. 结构力学分析:在工程中,材料的非线性行为、几何变形的影响以及边界条件变化等都会对结构的力学行为产生显著影响。
非线性分析可以用于评估结构的强度和稳定性,并对结构进行优化设计。
动力学中的非线性力学非线性力学系统的分析

动力学中的非线性力学非线性力学系统的分析非线性力学是研究非线性物体行为的学科领域,它与传统的线性力学相对应。
在动力学中,非线性力学系统的分析具有重要的理论和实际意义。
本文将从理论和实践两个方面,对动力学中的非线性力学系统进行分析。
一、理论分析非线性力学系统的理论分析是建立在非线性动力学的基础上的。
在非线性动力学中,系统的运动方程不是简单的线性关系,而是包含了非线性项的微分方程。
为了深入理解非线性力学系统的特性,我们需要使用一些数学工具和方法,如微分方程、相空间、稳定性理论等。
对于一维系统,我们可以通过相图来研究非线性系统的行为。
相图展现了系统在不同状态下的演化轨迹,并能够判断系统的稳定性和周期性。
对于多维系统,我们可以使用数学工具和计算机模拟来研究系统的稳定性和演化。
通过理论分析,我们可以揭示非线性力学系统的某些特性,如吸引子的存在与性质、周期解和混沌现象等。
这些理论研究对于我们理解自然和工程界的复杂现象具有重要意义。
二、实践分析在实践中,非线性力学系统的分析经常涉及到实验和数值计算。
实验是通过实际操作来观察和测量系统的行为,从而得到实际数据。
数值计算则是通过计算机模拟来解决非线性力学系统的微分方程,得到系统的行为。
实践分析非线性力学系统的过程中,需要注意以下几个方面:1. 实验设计:合理的实验设计能够获取准确的数据,并且能够反映系统的真实行为。
在实验设计中,需要考虑系统参数的选择、测量仪器的准确性和可靠性,以及外界干扰因素的控制等。
2. 数据处理:在获得实验数据后,需要进行数据处理和分析。
常用的数据处理方法有滤波、平均等统计方法,以及预处理方法如去趋势、去噪声等。
在数据处理过程中,需要根据具体问题选择合适的方法,以得到可靠的结果。
3. 数值计算:对于非线性力学系统,由于系统的运动方程通常是复杂的非线性微分方程,很难通过解析求解得到准确解。
因此,数值计算成为研究非线性力学的重要手段之一。
数值计算方法如欧拉法、Runge-Kutta法等可以用来模拟系统的行为。
非线性1:非线性结构分析报告

非线性结构分析非线性结构的定义在日常生活中,会经常遇到结构非线性。
例如,无论何时用钉书针钉书,金属钉书钉将永久地弯曲成一个不同的形状。
(看图1─1(a))如果你在一个木架上放置重物,随着时间的迁移它将越来越下垂。
(看图1─1(b))。
当在汽车或卡车上装货时,它的轮胎和下面路面间接触将随货物重量的啬而变化。
(看图1─1(c))如果将上面例子所载荷变形曲线画出来,你将发现它们都显示了非线性结构的基本特征--变化的结构刚性.图1─1 非线性结构行为的普通例子非线性行为的原因引起结构非线性的原因很多,它可以被分成三种主要类型:状态变化(包括接触)许多普通结构的表现出一种与状态相关的非线性行为,例如,一根只能拉伸的电缆可能是松散的,也可能是绷紧的。
轴承套可能是接触的,也可能是不接触的, 冻土可能是冻结的,也可能是融化的。
这些系统的刚度由于系统状态的改变在不同的值之间突然变化。
状态改变也许和载荷直接有关(如在电缆情况中),也可能由某种外部原因引起(如在冻土中的紊乱热力学条件)。
ANSYS程序中单元的激活与杀死选项用来给这种状态的变化建模。
接触是一种很普遍的非线性行为,接触是状态变化非线性类型形中一个特殊而重要的子集。
几何非线性如果结构经受大变形,它变化的几何形状可能会引起结构的非线性地响应。
一个例的垂向刚性)。
随着垂向载荷的增加,杆不断弯曲以致于动力臂明显地减少,导致杆端显示出在较高载荷下不断增长的刚性。
图1─2 钓鱼杆示范几何非线性材料非线性非线性的应力──应变关系是结构非线性名的常见原因。
许多因素可以影响材料的应力──应变性质,包括加载历史(如在弹─塑性响应状况下),环境状况(如温度),加载的时间总量(如在蠕变响应状况下)。
牛顿一拉森方法ANSYS程序的方程求解器计算一系列的联立线性方程来预测工程系统的响应。
然而,非线性结构的行为不能直接用这样一系列的线性方程表示。
需要一系列的带校正的线性近似来求解非线性问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简介
对增量方程求解的平衡迭代采用修正的牛顿迭代法或BFGS法。 1. 修正的牛顿迭代法。它与完全的牛顿法的不同在于迭代过程中系数矩 阵保持不变,因此不需要重新形成和分解刚度阵,从而大大减少了计算量。 但是这样又带来了收敛速度慢和发散问题,对此程序中加入了加速收敛和 发散处理的措施。这些措施并不明显地增加求解的时间,但却会对修正的 牛顿迭代法的性能有所改进。 2. BFGS法。又称矩阵修正迭代,是拟牛顿法的一种。它实际上是完全 的牛顿法与修正的牛顿法之间的一种折中方法。因为它在迭代过程中,并 不重新形成刚度阵,但也不保持不变,而是用某种方法对刚度阵(确切地 说是对它的逆)进行修改,从而求解。它在有限元分析遇到的许多问题中, 具有相当好的收敛性,尤其在复杂材料的非线性分析和动态分析中推荐采 用BFGS法。 程序对几何非线性的考虑可采用完全拉格朗日公式或改进拉格朗日公 式。在非线性动态分析中采用隐式时间积分(Newmarli法和Wilson- 法) 或显式时间积分(中心差分法)的方法。隐式时间积分通常用来分析结 构的振动问题,显式时间积分主要用来分析波传布现象。
简介
对于结构的几何非线性和材料非线性分析,可以归结为外 力与内力的平衡方程,它是关于节点位移的非线性方程;非线 性的稳态与瞬态温度场计算归结为热流平衡方程,它是关于节 点温度的非线性方程;因此非线性分析的有限元计算最终归结 为非线性方程求解。 非线性分析简而言之就是: 将系统的平衡方程式根据系统的非线性特性不断地进行修正, 然后求平衡方程的增量解。 如果是几何非线性,则在新的一步增量求解之前,坐标系进行 修正,然后去求解方程,并计算几何非线性对刚度阵和载荷阵 的修正。 若为材料非线性,则是将等效刚度阵和载荷阵不断地进行修正, 然后进行求解。
(10-11) (10-12) (10-13) (10-14) (10-15)
增量应力、应变之间的关系有:
o o o
S C
利用(10-11)-(10-15), o C为弹塑性关系矩阵。 注意到: t ot o ,方程(10-9)可改写成增量形式: 其中
一、在大位移问题中,尽管位移很大,结构的应变仍然不大,属于大位移 小应变问题,材料的应力- 应变关系仍是线性的,只是应变-位移关系是非 线性的。物体经历大的刚体位移和转动,固连于物体坐标系中的应变分量 仍假设为小量。 二、非线性效应由应变应力关系的非线性所引起,位移分量仍假设为小量, 应力-应变关系是非线性的,即材料非线性问题;最一般的情况是位移、转 动和应变都不再是小量,不但位移-应变是非线性的,而且应力-应变关系 也是非线性的,即双重非线性问题。
t t
[M ]
{u} [ D]
t t
{u} [ K ]t t {u} t t {R}
(10-8)
解此方程也用隐式时间积分,显式时间积分或振形迭加法求解。
有限元基本方程
二、非线性问题的基本方程 对非线性问题通常不能用一步直接求解方案,须分成若干步 加载,按各个阶段不同的非线性性质逐步求解,即增量求解方案。 1.增量形式的平衡方程: 已知设:0,△t,2△t‥‥的位移和应力(各载荷步的) 要求出:t+△t步时的位移和应力。
os
qs ds u t ot R
(10-10)
有限元基本方程
写成增量形式 :
S S S u u u e
t t o t o t o t t o t o o t t o t o o o o o
有限元基本方程
一、线性问题的基本方程 由复杂结构受力平衡问题的虚功方程有:
T R0 dv u q dv u q ds u v s 0 v v s T T T
m u u dv D u u dv
有限元基本方程
[ K ]u {R} [ M ]{u} [ D]{u}
其中:
(10-2)
[ K ] [ B]T [C ][B]dv
v
刚度矩阵 质量矩阵 阻尼矩阵
s
(10-3) (10-4) (10-5)
[ M ] [ N ]T m[ N ]dv
v
[ D] [ N ]T D[ N ]dv
①全拉格朗日(T· L)公式
以 t =0 时刻状态为度量基准,求 t +△t 时刻的值。 由虚功方程: 其中:
t t o
ov
t t o
T t t
t S dvt o W
T t t o(10-来自)W u ov
T t t o
qv dv u
T T v v
(10-1)
上式左端为内力的虚功,右端为外力的功。 由于:
u N u Bu C
式中
u 为单元体内的位移; u为节点位移; N 形函数阵;
C 弹性系数矩阵。
代入上式并整理后得线性问题有限元基本方程
非线性结构有限元分析
有限元基本方程
材料模式
非线性问题求解
简介
在工程结构的分析计算中,从本质上讲,所有力学问题都是非线性的, 线性假设只是实际问题的一种简化。对于固体或结构力学非线性问题来说, 有限元法是一种有效的数值方法。
通常把结构非线性问题分为两大类:几何非线性和材料非线性。这主要 包括:
v
v
{R} [ N ]T qv dv [ N ]T qs ds {R0}
{u}
(10-6) 外载荷阵 为节点位移对时间的二 次导数;
{u}
为节点位移对时间的一 次导数。
有限元基本方程
对于静力问题方程简化为:
[ K ]u {R}
(10-7)
对动力分析问题,在 t t 时的控制平衡方程为:
