第三章管路,孔口和管嘴的水力计算(3)
合集下载
《水力学》练习题1—6
水力学习题1一、单项选择题1.某流体的运动粘度v=3×10-6m2/s,密度ρ=800kg/m3,其动力粘度μ为( )A.3.75×10-9Pa·sB.2.4×10-3Pa·sC.2.4×105Pa·sD.2.4×109Pa·s2.图中相互之间可以列总流伯努利方程的断面是A.1-1断面和2-2断面B.2-2断面和3-3断面C.1-1断面和3-3断面D.3-3断面和4-4断面3.如图所示，孔板上各孔口的大小形状相同，则各孔口的出流量是( )A.Q A>Q BB.Q A=Q BC.Q A<Q BD.不能确定4.并联管道A、B，两管材料、直径相同，长度 B=2 A，两管的水头损失关系为( )A.hfB =hfAB.hfB =2hfAC.hfB =1.41hfAD.hfB =4hfA5.如图所示，水泵的扬程是( )A.z1B.z2C.z1+ z2D.z1+ z2+h w6.在已知通过流量Q、渠道底坡i、边坡系数m及粗糙系数n的条件下，计算梯形断面渠道尺寸的补充条件及设问不能是( )A.给定水深h，求底宽bB.给定宽深比β，求水深h与底宽bC.给定最大允许流速［v］max，求水底h与底宽bD.给定水力坡度J，求水深h与底宽b7.断面单位能量e随水深h的变化规律是( )A.e存在极大值B.e存在极小值C.e随h增加而单调增加D.e随h增加而单调减少8.下列各型水面曲线中，表现为上凸型的水面曲线是( )A.M3型B.C3型C.S3型D.H3型9.根据堰顶厚度与堰上水头的比值，堰可分为( )A.宽顶堰、实用堰和薄壁堰B.自由溢流堰、淹没溢流堰和侧收缩堰C.三角堰、梯形堰和矩形堰D.溢流堰、曲线型实用堰和折线型实用堰10.速度v、长度l、运动粘度v的无量纲组合是( )A.vlv2B.v lv2C.v lv22D.vlv二、填空题（不写解答过程，将正确的答案写在每小题的空格内。
工程流体力学-单元5
重 庆 能 源 职 业 学 院 教 案课程名称：流体力学 授课时间 2013 年 3 月授课教师：年 月日授课对象 系 别油气储运系本次课学时年级班次章节题目第三章 压力管路和孔口、管嘴的水力计算目的要求（含技能要求）掌握压力管路的分类、水力计算，掌握薄壁小孔出流的特征本节重点压力管路的水力计算及薄壁小孔出流 本节难点压力管路的水力计算及薄壁小孔出流 教学方法 理论教学与实例举例相结合。
教学用具 PPT 。
问题引入以实例引入。
如何突出重点 多次重复及字体区别。
难点与重点讲解方法 实例与课程内容相结合，加深印象。
内容与步骤简单长管的水力计算 复杂长管的水力计算 沿程均匀泄流管路 短管的水力计算定水头孔口和管嘴泄流 变水头泄流压力管路中的水击 本次课小 节课程小结 本章着重讨论运用流体运动的基本规律和水头损失的计算方法对实际工程管路进行水力计算，总结出实用的计算方法。
教后札记讨论、思考题、作业（含实训作业）1、何为管路特性曲线，有何用途？2、串并联管路各有何特点？在输油管上有哪些应用？3、分支管路应如何进行水力计算？重庆能源职业学院教案教学内容压力管路介绍压力管路在工程实际中的主要应用。
（10分钟）压力管路的分类（10分钟）长管的水力计算（20分钟）复杂管路的水力计算（50分钟）复杂管路的水力计算（60分钟）短管的水力计算（30分钟）孔口出流介绍孔口出流在工程实际中的主要应用和研究方法。
（10分钟）孔口出流的分类本节主要讨论孔口出流的一些基本概念：薄壁孔口、厚壁孔口、大孔口、小孔口、自由出流、淹没出流。
重点介绍薄壁孔口和厚壁孔口的主要技术特征。
（20分钟）薄壁小孔口自由出流分析推导薄壁小孔口自由出流时的各个特征参数计算公式。
（60分钟）水击现象日常生活中，快速开关阀门、停泵或突然断电一、水击的产生1、水击现象（水锤）在有压管路内，由于流速急剧变化，引起管内压强突然变化，并在整个管长范围传播的现象，称水击。
流体力学--第3章习题
4. 图示两根完全相同的长管道，只是安装高度 不同，两管道的流量关系为： C A.Q1<Q2； B.Q1>Q2； C.Q1=Q2； D.不定。
1-1断面、2-2断面的伯努利方程为
H1 H 2 h f
Q l hf 2 K
2
其中， K f (d , ) 称为流量模数
5. 两水池水位差为H，用两根等径等长、沿程阻 力系数均相同的管道连接，按长管考虑，则： B A.Q1>Q2； B.Q1=Q2； C.Q1<Q2； D.Q2=0。
3. 圆管层流，实测管轴线上流速为4m／s，则断面平 均流速为： C A. 4m／s B. 3.2m／s C. 2m／s D. 1m／s
二、计算题
1. ρ=0.85g/cm3、v=0.18cm2/s的油在管径为100mm的 管中以 v =6.35cm/s的速度作层流运动， 求（1）管中心处的最大流速； （2）在离管中心r=20mm处的流速； （3）沿程阻力系数λ ； （4）管壁切应力τ0及每1000km管长的水头损失。
hf H
L
h
解：管路输送功率为：
2 N Qh Q H 3
∴ 输送流量
3N 3 1000 1000 Q 1.2 m 3 s 2H 2 1000 9.81 127.4
沿程水头损失
H l v2 l 1 4Q hf 2 3 d 2g d 2 g d
等式右边 2 log(
3.7d
2.15 Re
) 7
可认为等式两边相等，解得λ=0.02。 气流的压强损失
l v p gh f 540Pa d 2
2
管路的水力计算
一、选择题
流体力学孔口管嘴出流与管路水力计算
流体力学孔口管嘴出流与管路水力计算流体力学是研究流体运动和力学性质的物理学科。
在水力学中，孔口管嘴出流和管路水力计算是流体力学的一个重要应用。
1.孔口管嘴出流孔口管嘴出流是指在一定压力差下，流体从孔口或管嘴中流出的现象。
它是一种自由射流，不受管道限制，流速和流量可以自由变化。
对于理想流体来说，根据贝努利定律和连续性方程，可以得出孔口管嘴出流速度的计算公式：v = √(2gh)其中，v为出流速度，g为重力加速度，h为液面距离孔口或管嘴的高度差。
可以看出，出流速度与液面高度差成正比，与重力加速度的平方根成正比。
对于真实流体来说，考虑到粘性和摩擦等因素，出流速度会稍有减小。
此时，可以使用液体流量系数进行修正。
液体流量系数是指实际流量与理论流量之比，一般使用实验数据来确定。
根据实验结果，可以通过乘以液体流量系数来修正出流速度的计算。
管路水力计算是指在给定管道材料、管径和流体性质的条件下，计算流体在管路中的流动状态、压力损失以及流量等参数。
管路水力计算是实际工程中常见的问题，它可以帮助我们了解管道的输送性能和节能问题。
管道中的流体运动受到多个因素的影响，包括管道长度、管道粗糙度、流速、流量等。
在水力学计算中，一般常用的公式有达西公式和罗斯诺-魏谢巴赫公式。
达西公式可以用来计算管道中流体的摩阻损失，它的计算公式为：ΔP=λ(L/D)(v^2/2g)其中，ΔP为管道中的压力损失，L为管道长度，D为管道直径，v为流速，g为重力加速度，λ为摩阻系数，也称为达西摩阻系数。
罗斯诺-魏谢巴赫公式则可以用来计算管路中流体的水力损失，它的计算公式为：ΔP=ρ(h_f+h_m)其中，ΔP为管路中的总压力损失，ρ为流体密度，h_f为摩阻压力损失，也称为莫阿P（Moody）摩阻，h_m为各种表面或局部的附加压力损失。
除了达西公式和罗斯诺-魏谢巴赫公式，还有一些经验公式和图表可以用来计算管路的压力损失和流量。
这些公式和图表都是根据实验数据和经验总结得出的，可以帮助工程师在实际应用中进行快速计算。
孔口,管嘴出流和有压管路
相同点
流量计算公式的形式以及流量系数的数值均相同
不同点
两者的作用水头在计量时有所不同，自由出流时是指上游水 池液面至下游出口中心的高度，而淹没出流时则指得是上下 游水位差。
出口位置处的总水头线和测压管水头线的画法不同
短管水力计算的内容
四类问题 已知水头H、管径d，计算通过流量Q；
校核输水 能力
已知流量Q、管径d，计算作用水头H，以确定水箱、水塔水位 标高或水泵扬程H值；
经济流速——在选用时应使得给水的总成本（包括铺设水管的 建筑费、泵站建筑费、水塔建筑费及抽水经常运转费之总和） 最小的流速。
一般的中、小直径的管路大致为：
——当直径 d=100-400mm，经济流速 v =0.6~1.0m/s ——当直径 d400mm，经济流速 v =1.0~1.4m/s
3
2g
(H下3 2
H
32 上
)
b为宽 d为高
如果用孔口中心高度H作为孔口作用水头，将孔口断面 各点的压强水头视为相等，按小孔口计算的流量为
Q bd 2gH
大孔口的流量系数
孔口形状和水流收缩情况
全部不完善收缩 底部无收缩，侧向收缩较大 底部无收缩，侧向收缩较小 底部无收缩，侧向收缩极小
流量系数
圆柱形短管内形成收缩,然后又逐渐扩大
H 0 0v02 0 0 v 2 v 2 ,
2g
2g 2g
H0
1
vB2
2g
流速
vB
1
1
2gH0 2gH0
对锐缘进口的管嘴，ζ=0.5， 1 0.82
1 0.5
流量
Q vB A A 2gH0 n A 2gH0
流量计算公式的形式以及流量系数的数值均相同
不同点
两者的作用水头在计量时有所不同，自由出流时是指上游水 池液面至下游出口中心的高度，而淹没出流时则指得是上下 游水位差。
出口位置处的总水头线和测压管水头线的画法不同
短管水力计算的内容
四类问题 已知水头H、管径d，计算通过流量Q；
校核输水 能力
已知流量Q、管径d，计算作用水头H，以确定水箱、水塔水位 标高或水泵扬程H值；
经济流速——在选用时应使得给水的总成本（包括铺设水管的 建筑费、泵站建筑费、水塔建筑费及抽水经常运转费之总和） 最小的流速。
一般的中、小直径的管路大致为：
——当直径 d=100-400mm，经济流速 v =0.6~1.0m/s ——当直径 d400mm，经济流速 v =1.0~1.4m/s
3
2g
(H下3 2
H
32 上
)
b为宽 d为高
如果用孔口中心高度H作为孔口作用水头，将孔口断面 各点的压强水头视为相等，按小孔口计算的流量为
Q bd 2gH
大孔口的流量系数
孔口形状和水流收缩情况
全部不完善收缩 底部无收缩，侧向收缩较大 底部无收缩，侧向收缩较小 底部无收缩，侧向收缩极小
流量系数
圆柱形短管内形成收缩,然后又逐渐扩大
H 0 0v02 0 0 v 2 v 2 ,
2g
2g 2g
H0
1
vB2
2g
流速
vB
1
1
2gH0 2gH0
对锐缘进口的管嘴，ζ=0.5， 1 0.82
1 0.5
流量
Q vB A A 2gH0 n A 2gH0
流体力学——管路、空口和管嘴的水里计算
vd
,
现
d=0.01m,
v =0.2m/s, 1.308 10 6 m 2 s 代 入 后 有
Re 流动为层流同理可求 d m 时 Re 流动为湍流
4-10（新书后题 4-10) 从相对压强 pm=5.49×10
p 2 p1
由连续方程
5
d2
h
hf
2 ， v1d12 v2 d 2
将 v1 v 2 (
2 2
d2 4 ) 代入， d1
则，
2 v2 [(
d2 2 ) 1] gh d1
所以， Q v 2
d 22
4
d 22
4
(
gh d2 2 ) 1 d1
4
0.48 2
9.81 0.01 0.0327m 3 / s 4 1
4
解: 润滑油的运动粘度 / 1.1529 10 , 园管损失为 1.765m, 园管沿程损失 hf 可
4
以用达西公式表示 ： h f
64lv 2 vd l v2 , 对层流 , 64 / Re , 有 Re , 但 Re , 2 gdh f d 2g
2 5.49 10 5 18 1000(7.5 0.024 ) 0.012 5.024 m s
v
4-11（新书后题 4-11) 长管输送液体只计沿程损失，当 H，L 一定，沿程损失为 H/3 时管路 输送功率为最大，已知 H=127.4m, L=500m, 管路末端可用水头 h=2H/3，管路末端可用功率 为 1000Kw, λ=0.024,求管路的输送流量与管路直径。
l v2 , 对 层 流 , 64 / Re , 有 d 2g
管路、孔口和管嘴的水力计算
在工程实际的一般问题中，只需研究各运动参 数的时均值，可使问题大大简化。
第二节 管路的水力计算
一、流动阻力及能量损失的两种形式 二、圆管的层流运动 三、沿程阻力系数 四、局部阻力系数 五、管路的水力计算
第三节 圆管中的层流流动
不可压缩流体在一半径为R的水平放置等截面圆 管中作定常层流运动，现在分析这一流动的有 关力学特征。
工程中也可取2000，即
层流： Re 2320 湍流： Re 2320
当过流断面是非圆断面时，
Re vR
或
Re vde
R是水力半径， de 是水力直径， de 4R
用R计算的临界雷诺数 Rec 580
层流： Re 580
湍流： Re 580
例1. 一等径圆管内径d=100mm，流通运动粘 度ν=1.306×10-6m2/s的水，求管中保持层流流 态的最大流量。
p
gh f
l
d
v 2
2
540Pa
第五节 局部水头损失
当水流流过流程中的阀门、弯头、扩散段、收缩段等 局部障碍时，具有粘性的水流将在这些障碍处脱离固 体表面产生耗能严重的旋涡，这是产生局部损失的主 要原因，另外，旋涡随主流下移也将引起下游一定范 围内水流机械能减少。
流动处于湍流水力光滑区
0.3164 Re0.25
0.0348
沿程水头损失
hf
l
d
v2 2g
1000 1.212 0.0348
0.2 19.6
12.99m油柱
例3. 有一镀锌铁管，l=40m，d=0.2m， △=0.15mm， 输送干空气，其密度ρ=1.2kg/m3，运动粘度ν=15.7× 10-6m2/s，测得风量Q=1700m3/h，气流的沿程损失为多 少？
第二节 管路的水力计算
一、流动阻力及能量损失的两种形式 二、圆管的层流运动 三、沿程阻力系数 四、局部阻力系数 五、管路的水力计算
第三节 圆管中的层流流动
不可压缩流体在一半径为R的水平放置等截面圆 管中作定常层流运动，现在分析这一流动的有 关力学特征。
工程中也可取2000，即
层流： Re 2320 湍流： Re 2320
当过流断面是非圆断面时，
Re vR
或
Re vde
R是水力半径， de 是水力直径， de 4R
用R计算的临界雷诺数 Rec 580
层流： Re 580
湍流： Re 580
例1. 一等径圆管内径d=100mm，流通运动粘 度ν=1.306×10-6m2/s的水，求管中保持层流流 态的最大流量。
p
gh f
l
d
v 2
2
540Pa
第五节 局部水头损失
当水流流过流程中的阀门、弯头、扩散段、收缩段等 局部障碍时，具有粘性的水流将在这些障碍处脱离固 体表面产生耗能严重的旋涡，这是产生局部损失的主 要原因，另外，旋涡随主流下移也将引起下游一定范 围内水流机械能减少。
流动处于湍流水力光滑区
0.3164 Re0.25
0.0348
沿程水头损失
hf
l
d
v2 2g
1000 1.212 0.0348
0.2 19.6
12.99m油柱
例3. 有一镀锌铁管，l=40m，d=0.2m， △=0.15mm， 输送干空气，其密度ρ=1.2kg/m3，运动粘度ν=15.7× 10-6m2/s，测得风量Q=1700m3/h，气流的沿程损失为多 少？
管路孔口和管嘴的水力计算
再列干管与支管2之间的能量方程，用同样的方法求干管
流量q与支管2流量q2之间的关系，此时有：
40
v22 2g
h 2
8q22
g 2d24
h 2
d
1 50m
1
h 2
l
d
v2 2g
2l2
d2
v22 2g
三
v22 2g
l
d
8q2
g 2d 4
2l2
d2
三
8q22
g 2d24
e
q, l, d
q1,l1, d1 2
l
d
8q2
g 2d 4
1
1l1
d1
三
8q12
g 2d14
由此式得：
q1
30 1
l
d
1l1
d1
8q2
g 2d
三
4
g 2d14
8
30
150 0.8
9.8
8q2 3.142
0.84
9.8
3.142
0.64
8
1
200 0.6
1
1.5
9
q1
30 37.82q2 1.6 213.331
c
（C）式给出了干管流量q与支管1流量q1之间的关系。
再来计算一次近似的1, 2和 ,为此先计算近似
的Re, Re1 和Re2
12
Re
4q
d
4 3.77 3.14106 0.8
6 106
Re1
4q1
d1
4 2.233 3.14106 0.6
4.72 106
Re 2
4q2
第三章 管路,孔口和管嘴的水力计算(3)
C
D
C
vc
3～4D
v
15
三、变水头孔口出流
变水头出流是非定常问题， 变水头出流是非定常问题，但在水位随时间变化的速 率较小的情况下，如果把整个水头变化范围分为若干等份， 率较小的情况下，如果把整个水头变化范围分为若干等份， 则在每一等份可近似看作定常，通常称这种为准定常流。 则在每一等份可近似看作定常，通常称这种为准定常流。 如图所示， 如图所示，容器内自由表面积为 Ω ，在dt时段内水 时段内水 头的增量为dH， 头的增量为 ，则dt时段 时段 内孔口的泄水量为： 内孔口的泄水量为：
2ΩH t= µA 2gH
（3-52） ）
表明非定常流的 泄水时间等于相 同水头下定常泄 放同样体积所需 时间的两倍。 时间的两倍。
17
H+
O
2 α0v0
αv
2 0 0
1
H
2g
1
H0 C D
2g
= H0为 口 总 头 孔 的 水 ;
2
Байду номын сангаас
vc 令 ω =ζ h 2g
ζ为 口 局 阻 系 孔 的 部 力 数
O
v0
A
AC C
5
vc
将其代入能量方程可得： 将其代入能量方程可得：
2 vc ∴H0 = (1+ζ ) 2g 1 ∴vc = 2gH0 = ϕ 2gH0 1+ζ
l1
l1 < 3a l2 > 3b
不 完 善 完善收缩 收 l2 缩
无收缩
4
以孔口中心的水平面为基准面，列断面 与收缩断 以孔口中心的水平面为基准面，列断面1-1与收缩断 之间的能量方程: 面C-C之间的能量方程 之间的能量方程
孔口、管嘴和管道的流动计算方法(ppt 74页)
S1S2 S82gld5
h2 hh1 A点连续性方程
q1q2 Q 解得 q12.79 L/s q21.2L 1/s
（2）当h是多少时，由低位油箱流出的q2=0？ 令q2=0，解得h=1.27m
（3）当h>1.27m时会出现什么情况？
会出现高位油箱向低位油箱倒灌的现象
（4）当z为多高，高位油箱泄空后空气不会进入泵 内，且又可使低位油箱可泄空？
H0——作用水头
H0
1
vB2
2g
流速
1
vB 1
2gH 0 2gH 0
对锐缘进口的管嘴，ζ=0.5， 1 0.82
10.5
流量 Q vBAA2g0 H A2g0 H
0.82
真空的抽吸作用，流量增加
2.管嘴正常使用条件 防止气蚀 列C-C、B-B断面能量方程
g
0.75H0
允许真空值 H0的极限值
hv7m
H00.7759.3m
——管嘴正常使用条件之一
l3~4d ——管嘴正常使用条件之二
3.管嘴的种类 （a）圆柱外伸管嘴； （b）圆柱内伸管嘴 ； （c）外伸收缩型管嘴 ； （d）外伸扩张型管嘴 ； （e）流线型外伸管嘴
类型
特点
ζφε μ
1→突扩ζ=1，H0→H
H l v2
d 2g
v2
4Q
d
2
2
代入，得
8 l
H
d
2d4g
Q2
SH——管路阻抗 S2/m5
HSHQ2
8 l
p
d
2d4
Q2
Sp kg/m7
p SpQ2 类比电路：S→R H(p)→U Q2→I
h2 hh1 A点连续性方程
q1q2 Q 解得 q12.79 L/s q21.2L 1/s
（2）当h是多少时，由低位油箱流出的q2=0？ 令q2=0，解得h=1.27m
（3）当h>1.27m时会出现什么情况？
会出现高位油箱向低位油箱倒灌的现象
（4）当z为多高，高位油箱泄空后空气不会进入泵 内，且又可使低位油箱可泄空？
H0——作用水头
H0
1
vB2
2g
流速
1
vB 1
2gH 0 2gH 0
对锐缘进口的管嘴，ζ=0.5， 1 0.82
10.5
流量 Q vBAA2g0 H A2g0 H
0.82
真空的抽吸作用，流量增加
2.管嘴正常使用条件 防止气蚀 列C-C、B-B断面能量方程
g
0.75H0
允许真空值 H0的极限值
hv7m
H00.7759.3m
——管嘴正常使用条件之一
l3~4d ——管嘴正常使用条件之二
3.管嘴的种类 （a）圆柱外伸管嘴； （b）圆柱内伸管嘴 ； （c）外伸收缩型管嘴 ； （d）外伸扩张型管嘴 ； （e）流线型外伸管嘴
类型
特点
ζφε μ
1→突扩ζ=1，H0→H
H l v2
d 2g
v2
4Q
d
2
2
代入，得
8 l
H
d
2d4g
Q2
SH——管路阻抗 S2/m5
HSHQ2
8 l
p
d
2d4
Q2
Sp kg/m7
p SpQ2 类比电路：S→R H(p)→U Q2→I
管嘴的水力计算
要保证水泵的真空值不超过规定的允许值，就必须按水泵最大允 许真空值（一般不超过6－7m）计算水泵允许安装高度H允。
以等截面容器为例，设容器截面积为w，无补给水，初始水头为 H1，终止水头为H2，要求泄流时间为T。
设某一时刻水头为H，在dt时段 内水位变化值为dH，体积变化 值为wdt，应等于dt时段内从孔 口流出的液体体积。
Qdt A 2gHdt Wdt
T dt H2 w dh H1 A 2g h
教学基本要求
1、了解有压管流的基本特点。掌握孔口、管嘴的水力 计算；
2、掌握短管（水泵、虹吸管）的水力计算方法； 3、了解复杂管道的特点和计算方法，重点掌握串联管
道和并联管道的水力计算。 4、了解有压管道中的水击现象和水击传播过程。
孔口出流：在贮水池、水箱等容器侧壁上开一孔口，水经孔口流 出的水力现象。
管嘴出流：在孔口上连接长度为3－4倍孔径的短管，水流经此短管 并在出口断面满管流出的水力现象。 有压管流：流体沿管道满管流动的水力现象。
Ｈ
Ｈ
Ｈ
相同点：有压流动。
不同点： 孔口出流只有局部损失； 管嘴出流虽有沿程损失，但与局部损失相比很小，可以忽略。 有压管流沿流动方向有一定的边界长度，水头损失包括沿程损 失和局部损失。
vc
1
c 0
2gH0
2 gH 0
1 c 0
ψ称为孔口的流速系数，一般取αc=1
流量 Q Ac 2gH0 A 2gH0 A 2gH0 μ称为孔口流量系数。
实验测得孔口流速系数：φ= 0.97～0.98
孔口的局部阻力系数： 0
1
2
1
1 0.9 72
通常可用自由出流与淹没出流计算公式解决以下三类问题： 已知流量Q，管径d，管长L等，求水头H（或Z）； 已知水头H（或Z），管径d，管长L等，求流量Q； 已知流量Q，水头H，管长L等，求管径d。
第三章 管路,孔口和管嘴的水力计算(1)
l v2 hf = λ L 达 L 西公式 d 2g 其 ：hf ： 程水头损 ； 中 沿 失
λ ：沿程阻力系数；
沿程阻力系数和管道内表面的粗糙度有关， 沿程阻力系数和管道内表面的粗糙度有关，是一个无量纲 由实验确定。 数，由实验确定。 11
2、局部阻力与局部损失 、
粘性流体流经各种局部障碍装置如阀门、弯头、 粘性流体流经各种局部障碍装置如阀门、弯头、 变截面管等时， 变截面管等时，由于过流断面在局部地区发生急剧变 从而引起速度的大小和方向也发生急剧变化， 化，从而引起速度的大小和方向也发生急剧变化，质 局部阻力。 点间进行动量交换而产生的阻力称为局部阻力 点间进行动量交换而产生的阻力称为局部阻力。流体 为克服局部阻力而损失掉的机械能称为局部损失 局部损失。 为克服局部阻力而损失掉的机械能称为局部损失。
紊流
lg vc lg vc ′
lg v
14
对于紊流： 对于紊流：
lg hf = lg k2 + tanθ lg v
lg hf
m=1.75-2.0
∴hf = k2v
= lg k2 + mlg v
m
m=1
其中: m =1.75 ~ 2
表示紊流沿程水头损失与流速的 1.75~2次方成正比。可见沿程水头 次方成正比。 次方成正比 损失与流动形态密切相关，因此， 损失与流动形态密切相关，因此， 欲确定损失，必先判定流态。 欲确定损失，必先判定流态。
2
一、雷诺实验： 雷诺实验：
3
1、层流状态：所有流 、层流状态： 体质点做定向有规则的 运动。 运动。
(a)
2、过渡状态：颜色水 、过渡状态： 开始抖动， 开始抖动，直线形状遭 到破坏。 到破坏。
第三章 管路孔口和管嘴的水力计算(3N)PPT课件
H l 30030m, 10 10
qK HK 30K 1,
l
300 10
K g 2d 5 8
由于 取决 R和 e于壁面 ,但状 流况 量,无 不法 知R确 道 e,定 时
故须采,先 用假 试 0设 算 .0,2 则 法 :有
K 9.83.1420.85 14.1 80.2
2
qK11.1 4 14.4m 63/s
h
l
d
8q2
g2d4
0 .01 1 0 8 .35 59 .0 8 8 3 .1 0 .2 2 4 20 .3 4 1.9 8 m
所以泵的扬程为： H 1 1 0 .9 8 2.9 m 8
所以泵的功率为：
P oH il 9 q. 2 4 2 2 .9 8 1 0 .2 5 .3 K 3 W
三
g2d24
8
代入已知数据得：
q2
4037.82q2 3.36602
f
12
根据流动的连续性有： qq1q2
g
将（C）与(f)代入(g)得：
q
1 3.6 0 32.7 8 1.32 3q 32 1
4 03.7 82q2 3.36610
h
采用逐次逼近法求解，假设 12 0 .0 2 ,q 1 m 3/s
q1.73 3 15.4(8m3/s) 10
4
例题5：
如图所示：带泵管路用 来将油液从低位油箱打 入高位
油箱，两油箱均为敞口 ，自由液面差为 10 m, 钢管管路 总长 l 150 m,直径 d 30 cm,
油的重度 9221 .4 N m3 , 粘 度 10 6 m2 s 。试问：
当想保证管路中有
凝土管，
孔口、管嘴出流和有压管流
H0
2v2 2
2g
hw
1 v l d
由此得到管道的流量为
2 gH o
A Q l d
2 gH o
由该式 看出，管道的流量取决于H0、A和Hw。A由管径
的大小决定，Hw按第四章水头损失计算方法求得。
若
1 1.0 代入式 v l d
hw h f h j
1
pa
该式说明短管水流在 自由出流的情况下， 其作用水头H0 一部分 消耗于水流的沿程水 1 头损失和局部水头损 失，另一部分转化为 管道2-2断面的流速水头。
v1
H HP v 2 H
v2
闸门
2
对于等直径管 ， 管中流速为常数v， 所以v2=v，代入上式 ，取α2=α，得
1)短管自由出流
液体经短管流动流入大气后，流束四周受到大气压的 作用，称这种流动为短管自由出流，图示为一短管自由出流。
液流从水箱 进入管径为d， 装有一个阀门并 带有两个弯头的 管路，管路总长 度为 l。
1 pa
v1
1
H HP v 2 H
v2
闸门
2
取出口中心高程的水平面为基准面 0-0，断面1-1 取在 管道入口上游水流满足渐变流条件处，2-2断面则取在管流 出口处，对断面1-1至断面2-2 的水流建立能量方程：
可见， 同一短管在自由出流和淹没出流的情况下，
其流量计算公式的形式及μc的数值均相同，但作用水头
H0 的计量基准不同，淹没出流时作用水头是以下游水面 为基准 ，自由出流时是以通过管道出口断面中心点的水
平面为基准。
3)、短管的水力计算问题
短管的水力计算包括以下几类问题： ①已知作用水头、断面尺寸和局部阻碍的组成，计算 管道输水能力，求流量； ② 已知管线的布置和必需输送的流量（设计 流量）， 求所需水头（例如：设计水箱、 水塔的水位标高H、水泵 的扬程H等）； ③ 已知管线布置，设计流量及作用水头，求管径d； ④ 分析计算沿管道各过水断面的压强。
孔口、管嘴和管道的流动计算方法(ppt 74页)
Qi 0 b.由控制线确定水力坡度 J H hc
l l' 39
l’——局部损失折算成沿程损失的长度，称为局 阻的当量长度（手册可查）
c.由各管段J相等条件，计算各管段管径和损失
J
1 di
1 2g
4Qi
d
2 i
2
1
di
8Qi2 2 gJ
5
→标准化
hi
l l' di
vi2 2g
d.校核 hi hc H
v2 2g
20
1→突扩ζ=1，H0→H
H l v2
d 2g
v2
4Q
d
2
2
代入，得
8 l
H
d
2d 4g
Q2
SH——管路阻抗 S2/m5
H SHQ2
21
8 l
p
d
2d 4
Q2
Sp kg/m7
p SpQ2 类比电路：S→R H(p)→U Q2→I
非圆管
pa pC
g
0.75H0
允许真空值 H0的极限值
hv 7m
H 0
7 0.75
9.3m
——管嘴正常使用条件之一
l 3 ~ 4d
——管嘴正常使用条件之二
15
3.管嘴的种类 （a）圆柱外伸管嘴； （b）圆柱内伸管嘴 ； （c）外伸收缩型管嘴 ； （d）外伸扩张型管嘴 ； （e）流线型外伸管嘴
16
dh
2S
t
A 2g
h1 h2
10
容器放空：h2=0
2S t
h1
2Sh1
2V
A 2g A 2gh1 Qmax
V——放空容器的体积 Qmax——开始出流时最大流量
l l' 39
l’——局部损失折算成沿程损失的长度，称为局 阻的当量长度（手册可查）
c.由各管段J相等条件，计算各管段管径和损失
J
1 di
1 2g
4Qi
d
2 i
2
1
di
8Qi2 2 gJ
5
→标准化
hi
l l' di
vi2 2g
d.校核 hi hc H
v2 2g
20
1→突扩ζ=1，H0→H
H l v2
d 2g
v2
4Q
d
2
2
代入，得
8 l
H
d
2d 4g
Q2
SH——管路阻抗 S2/m5
H SHQ2
21
8 l
p
d
2d 4
Q2
Sp kg/m7
p SpQ2 类比电路：S→R H(p)→U Q2→I
非圆管
pa pC
g
0.75H0
允许真空值 H0的极限值
hv 7m
H 0
7 0.75
9.3m
——管嘴正常使用条件之一
l 3 ~ 4d
——管嘴正常使用条件之二
15
3.管嘴的种类 （a）圆柱外伸管嘴； （b）圆柱内伸管嘴 ； （c）外伸收缩型管嘴 ； （d）外伸扩张型管嘴 ； （e）流线型外伸管嘴
16
dh
2S
t
A 2g
h1 h2
10
容器放空：h2=0
2S t
h1
2Sh1
2V
A 2g A 2gh1 Qmax
V——放空容器的体积 Qmax——开始出流时最大流量
孔口管嘴出流、有压管路基本概念
α V
2 01 01
2g
= H2 + 0 +
α 02V02
2g
2
+ hw
l V2 hw = (∑ λ + ∑ ζ ) d 2g
1 V= l λ +∑ ζ ∑ d 2 gH
Q = AV = c A 2 gH
Fluid Mechanics 流 体 力 学
例1:用虹吸管自钻井输水至集水池.如图所示,虹吸管长 l=lAB+lBC=30+40=70m,d=200mm.钻井至集水池间的恒定水位高差 H=1.60m.又已知λ=0.03,管路进口120弯头90°弯头及出口处的 局部阻力系数分别为ζ1=0.5,ζ2=0.2,ζ3=0.5,ζ4=1.0. 试求:(1)流经虹吸管的流量; (2)如虹吸管顶部B点的安装高度hB=4.5m ,校核其真空度.
Fluid Mechanics 流 体 力 学
第三节 管嘴出流
一,圆柱形外管嘴出流 当圆孔壁厚δ等于3 4d时 或者在孔口处外接一段长l= 当圆孔壁厚δ等于3～4d时,或者在孔口处外接一段长l= 3～ 的圆管时,此时的出流称为圆柱形外管嘴出流, 4d 的圆管时,此时的出流称为圆柱形外管嘴出流,外接短管称 为管嘴. 为管嘴. 通过收缩断面形心引基准线0 列出A 通过收缩断面形心引基准线0-0,列出A-A及 a v 两断面的能量方程. B-B两断面的能量方程. p 2g
vc2 he = hm = ξ1 , 2g
H0
H C
0
d
0 C
2 2 vc pA pC α A vA 移项整理得: 移项整理得:αc + ξ1 ) = (Z A ZC ) + ( + γ 2g 2g
孔口、管嘴和管道的流动计算方法
vB2
2g
流速
1
vB 1
2gH 0 2gH 0
对锐缘进口的管嘴，ζ=0.5， 1 0.82
10.5
流量 Q vBAA2g0 H A2g0 H
0.82
真空的抽吸作用，流量增加
2.管嘴正常使用条件 防止气蚀 列C-C、B-B断面能量方程
pgC 2vC g2 pgB 2vB g2 hw
hw
l d
pagpCzCz11 l1ldl121 CHhv7~8m
d 12
最大安装高度
1l1
hmaxzCz1hv
d
l1l2
1C Hhv
d 1不计，损失线性下降，总水
头线与测压管水头线重合
单位长阻抗——比阻a
aH
SH L
28d5g
s2/m6
HLaHQ2
H 0z1z2H
收缩断面流速
1
vC 11
2gH 0 2gH 0
孔口流量
QvCACvCACA2gH 0
与自由出流一致
气体： 作用压力
p0p1p2
v1 2v2 2 2
（略去高差）
流速 v 2 p0
流量 Q A 2 p0
p0 0 排气
p0 0 吸气
应用：孔板流量计
H 0z1z2p1 gp2v1 22 gv2 2 g p
伸管嘴 流量大
0.04 0.98 1 0.98
4.例：水箱中用一带薄壁孔口的板隔开，孔口及两出 流管嘴直径均为d=100mm，为保证水位不变，流入水 箱左边的流量Q=80L/s，求两管嘴出流的流量q1、q2
解：设孔口的流量为q
qA2gh 1h2
对管嘴
q1 1A 2gh1
第三章 管路,孔口和管嘴的水力计算(3)
6
m
3
,粘
阀
m
2
2
2
s
。试问：
当想保证管路中有 qv 0.2 m
3
泵
1 1
10m
s
的流量时，
泵的功率应为多大？
解：
P 泵的功率应等于：
oil Hq
式中：H----泵的扬程；q----管路流量（不记泵内部泄漏） 管路需用扬程为： 2 2 p2 v2 p1 v1 z1 h H z2 2g 2g
式中：
h 1 d
8q1
2
2 4
g d1
2
h 1
2
a 三 v12来自50m1
1
l v
2
1l1 v1
d1
q1 , l1 , d1 2
q, l , d
2
20m
2g
2g
2g
1l1 8q1 l 8q 2 4 d 三 g 2 d 4 d g d 1 1
根据各管段流量计算雷诺数，以求相应的阻力系数：
0l0
d0
8q0
2
2 4
g d 0
1l1
d1
8q1
2
2 4
g d1
3l3
d3
8q3
2
2 4
b
g d3
将(b)代入(a)得：
2 8q3 0l0 8q0 1l1 8q1 3l3 HT 1 2 4 2 4 2 4 d0 g d0 d1 g d1 d3 g d3 2 2
这几个系数与零次近似值相差较大，故还须作下一次近 似，由 q, q1, q2 , , 1和2 的一次近似值计算它们的 二次近似值。 反复进行三次近似计算，最后结果为：
m
3
,粘
阀
m
2
2
2
s
。试问：
当想保证管路中有 qv 0.2 m
3
泵
1 1
10m
s
的流量时，
泵的功率应为多大？
解：
P 泵的功率应等于：
oil Hq
式中：H----泵的扬程；q----管路流量（不记泵内部泄漏） 管路需用扬程为： 2 2 p2 v2 p1 v1 z1 h H z2 2g 2g
式中：
h 1 d
8q1
2
2 4
g d1
2
h 1
2
a 三 v12来自50m1
1
l v
2
1l1 v1
d1
q1 , l1 , d1 2
q, l , d
2
20m
2g
2g
2g
1l1 8q1 l 8q 2 4 d 三 g 2 d 4 d g d 1 1
根据各管段流量计算雷诺数，以求相应的阻力系数：
0l0
d0
8q0
2
2 4
g d 0
1l1
d1
8q1
2
2 4
g d1
3l3
d3
8q3
2
2 4
b
g d3
将(b)代入(a)得：
2 8q3 0l0 8q0 1l1 8q1 3l3 HT 1 2 4 2 4 2 4 d0 g d0 d1 g d1 d3 g d3 2 2
这几个系数与零次近似值相差较大，故还须作下一次近 似，由 q, q1, q2 , , 1和2 的一次近似值计算它们的 二次近似值。 反复进行三次近似计算，最后结果为：
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1
Ac A2
vc2 2g
vc2 2g
h h1c hc2 1
vc2 2g
将h表达式代入能量方程,并注意到v0 v2 0
z 1 vc2
2g
vc
1
1
2gz 2gz （3-47）
式中 为淹没出流的速度系数，与自由出流流速
系数 的表达式相同
9
淹没出流的流量为：
q vc Ac A 2gz A 2gz
v0
v C
D A AC
c
C
5
O
将其代入能量方程可得：
H0
1
vc2
2g
vc
1
1
2gH0 2gH0 （3-44）
1 为流速系数，与有关,由实验确定， 1
对完善收缩的小孔口,一般取 0.97。
孔口自由出流的流量为：Q vc Ac
vc 2gH0 ; Ac A
6
所以有： Q A 2gH0 A 2gH0 （3-45）
Ⅰ
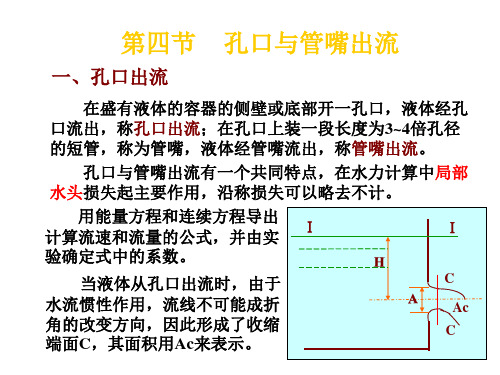
验确定式中的系数。
当液体从孔口出流时，由于
C
水流惯性作用，流线不可能成折
Ac
角的改变方向，因此形成了收缩
端面C，其面积用Ac来表示。
C
1
1、孔口出流的分类
小孔口出流：D/H ＞10为小孔口
大孔口出流：D/H＜10为大孔口，
D/H 为孔口直径与水头的比值。
恒定出流、非恒定出：
自由出流、淹没出流：在大气中的出流为自由出流；
并且：
式中 是流量系数，其值常由实验确定。
对于完善收缩的圆形小孔口， 0.64, 0.97
0.97 0.64 0.62
对于其它情况，可查经验公式。对于大孔口的自由 出流的流速及流量仍可采用公式（3-44）和（3-45）计 算，只是相应的水头应近似取为孔口形心处的值，具体 的流量系数也与小孔口出流不同，大孔口的流量系数值 见表3-7。
其中：为淹没出流的流量系数，与自由出流的 流量系数表达式相同。可取 。
10
4. 厚壁孔口出流
厚壁孔口出流与薄
壁孔口出流的差别在于收
缩系数和边壁性质有关，
注意到收缩系数定义中的
A
A为孔口外侧面积，容易 看出孔边修圆后，收缩减
Ac
Ac
小，收缩系数和流量系数
都增大。
11
二、管嘴出流
如下图所示，常见的管嘴有五种形式：
在水面下的出流为淹没出流。
薄壁出流、厚壁出流：薄壁出流确切地讲就是锐缘孔口出
流，流体与孔壁只有周线上接触，孔壁厚度不影响射流形
态，否则就是厚壁出流，如孔边修圆的情况，此时孔壁参与
了出流的收缩，但收缩断面还是在流出孔口后形成。如果壁
厚达到3～4D，孔口就可以称为管嘴，收缩断面将会在管嘴内
形成，而后再扩展成满流流出管嘴。管嘴出流的能量损失只
考虑局部损失，如果管嘴再长，以致必须考虑沿程损失时就
是短管了。
2
2、薄壁孔口出流
液体从孔口以射流状态流出，流线不能在孔口处急剧改 变方向，而会在流出孔口后在孔口附近形成收缩断面，此断 面可视为处在渐变流段中，其上压强均匀。
收缩断面面积Ac与孔口 面积A的比 值用ε表示，即：
Ac
A
ε称为收缩系数，它是无量纲 数，由实验确定。
a bc
d
e
a为圆柱形外管嘴；b为圆柱形内管嘴；c为圆锥形收缩管嘴； d为圆锥形扩张管嘴；e为流线形管嘴。
12
管嘴出流的流速和流量公式与孔口出流的形式类似： 自由出流时：
v 2gH0 ;q A 2gH0 淹没出流时：v 2gH0 ; q A 2gH0 各种管嘴的, , 值见表3 8
第四节 孔口与管嘴出流
一、孔口出流
在盛有液体的容器的侧壁或底部开一孔口，液体经孔 口流出，称孔口出流；在孔口上装一段长度为3~4倍孔径 的短管，称为管嘴，液体经管嘴流出，称管嘴出流。
孔口与管嘴出流有一个共同特点，在水力计算中局部 水头损失起主要作用，沿称损失可以略去不计。
用能量方程和连续方程导出
计算流速和流量的公式，并由实 Ⅰ
13
圆柱形外伸管嘴出流的局部损失由两部分组成，即孔口的局 部水头损失及收缩断面后扩展产生的局部损失，水头损失大于 孔口出流。但是管嘴出流为满流，收缩系数为1，因此流量系 数仍比孔口大，其出流公式为
v n 2gH0
Q n A 2gH0 n A 2gH0
C
D
vc v
C 3～4D
14
管嘴出流流量系数的加大也可以从管嘴收缩断面处存在的真 空来解释，由于收缩断面在管嘴内，压强要比孔口出流时的零 压低，必然会提高吸出流量的能力。
7
3、孔口的淹没出流
孔口淹没出流时，作用于孔口任一点的上、下游的水头 差相等，因此，对淹没出流而言,孔口无大小之 分。
对断面1-1和2-2列能量方程：
z 0v02
2g
2v22
2g
h
h
vc2 2g
为断面1至断面C 和断面C至断面2
的能量损失之和。
h1c
vc2 2g
1
v1
2
C
v2
C
1
28
hc2
O
0v02
2g
H
H0
v0
v C
D A
AC
c
C
O
3
如果沿孔口的所有周界上液体都有收缩，称为全部收 缩，反之称为部分收缩。
全部收缩又分为完善收缩和不完善收缩。视孔口边缘 与容器边壁距离与孔口尺寸之比的大小而定，大于3则可 认为完全收缩。完善收缩时，
ε的范围是0.63-0.64。
l1 3a l2 3b
a l1
b
不
完
完善收缩
善 收
l2
缩
无收缩
4
以孔口中心的水平面为基准面，列断面1-1与收缩断
面C-C之间的能量方程:
H
0v02
2g
0 cvc2
2g
h
式中：收缩断面的平均流速;
h为水头损失。 1
O
0v02 2g
1
H
0v02
2g
H0为孔口的总水头;
H
H0
令h
vc 2 2g
为孔口的局部阻力系数
C
D
vc
v
C 3～4D
15
三、变水头孔口出流
变水头出流是非定常问题，但在水位随时间变化的速
率较小的情况下，如果把整个水头变化范围分为若干等份， 则在每一等份可近似看作定常，通常称这种为准定常流。
如图所示，容器内自由表面积为 ，在dt时段内水
头的增量为dH，则dt时段
内孔口的泄水量为：
Q
qdt dH
并取H0 H ,则 :
H1 H H2
0
dH
0
A 2gH dt dH
16
即：
dt dH
A 2g H
式（3-52）
t
t dt
H2 dH
0
A 2g H1 H
2 A 2g
H1 H2
（3-51）
当H1 H , H2 0时,上式可写为:
t 2H
A 2gH
（3-52）
表明非定常流的 泄水时间等于相 同水头下定常泄 放同样体积所需
时间的两倍。
17