原子物理学第六章超精细结构
原子物理学,褚圣麟第六章

2
1 1 1 1 ( 1) 1(1 1) ( 1) 2 2 2 2 2 g1 1 1 1 3 2 ( 1) 2 2
第 六 章 在 磁 场 中 的 原 子
M
M2 g 2
3 2 6 5
1 2 3 5
1 2
3 2
M
2
3 2
,
1 2
3 5
6 5
M1
h
c
3 .4
第 六 章 在 磁 场 中 的 原 子
1. 可测原子的基态的 g 值. 2. 原子处在磁场为单峰, 固体出现多个共振峰.
3. 波谱精细结构用于研究分子、固体、液体结构.
4. 超精细结构: 用于测量原子核的角动量量子数. 晶体顺磁共振吸收曲线
2l 1 个
超精细结构
(一个峰裂成几个挨近的峰)
PJ
洛伦兹单位
L
eB 4 π mc
d
dP
第 六 章 在 磁 场 中 的 原 子
附加能量
2
E Mg B B
15 g 1 4 3
例 求 P3 2 在磁场中能级的分裂。
L 1, s 1 2 , J 3 2
2 3 4 4 5 3 2
M
3 2
2π
第 2. 原子受磁场作用的附加能量 六 e 章 E J B cos g PJ B cos 2m 在 B h 磁 J PJ cos M , 2π 场 中 M J , J 1, , J . 的 原 附加能量 E Mg B B 子 光谱项差 eh B T E hc Mg MgL 4 π m hc
《原子物理学》(褚圣麟)第六章_磁场中的原子

E eB Mg MgL 光谱项差: T hc 4mc
e 1 洛仑兹单位: L B 0.47 cm B 4mc
第6章 在磁场中的原子
结 论
E Mg B B
1.原子在磁场中所获得的附加能量与B成正比;
2.因为M取(2J+1)个可能值,因此无磁场时的原子
的一个能级,在磁场中分为(2J+1)个子能级。
1 2
,
第6章 在磁场中的原子 原子 Su, Cd, Hg,, Pb
史特恩-盖拉赫实验结果
g — — Mg 0 相片图样
基态
1
S0 P0 S1 / 2 P1/ 2 P2 P1 P0
Su,
Pb
3 2 2 3
0
H, Li, Na, K
Cu, Ag,, Au Tl
2
1
1 3
2/3 3/2
3 3, ,0 2
1 dB L 2 1 dB L 2 S ( ) z ( ) Mg B 2m dZ v 2m dZ v
M J , J 1, J
原子态为2s+1Lj的原子将分裂为2j+1束。 如实验中使用基态氢原子、银原子,基态原态 所以进入非均匀磁场中要分裂为两束。
2
S1 / 2 , M
PJ
E J B J B cos
B
J
e E g p J B cos 2m
h p J cos M M 2
磁量子数: M J , J 1, J 共(2J+1)个
第6章 在磁场中的原子
e E Mg B Mg B B 2m
e L g B B, 2me
J e g g 2me PJ
原子物理学第六章PPT课件

下几节中分别讨论: 一方面是要说明产生这些现象的缘由, 另一方面也要说明怎样通过这些现象又可以
窥见原子的结构。 这些问题有共同性,可以统一在一套理论中。 因此下面先进行磁场对原子起作用的一般讨论。
然后分别进入具体问题 。
2021/3/12
6
§6.1 原子的磁矩
2021/3/12
7
引子:原子磁性问题的关键是原子的磁矩。
2021/3/12
3
1896年开始,塞曼逐步发现,当光源放在足 够强的磁场中时,所发出的光谱线都分裂成几条, 条数随能级的类别而不同,而分裂后的谱线成分 是偏振的。后人称这现象为塞曼效应。这现象反 映原子结构的情况,到现在仍用来研究有关原子 的问题。
1944年扎弗伊斯基发现了磁共振现象,随后数 年中发展了这方面的试验。基本内容是,在稳定 的磁场中放置要研究的材料样品,在加交变磁场, 如果后者的频率合适,样品会从交变场吸收能量。 这类实验在科学上有重要的应用。它的基础也是 原子的磁性问题。
第六章 在磁场中的原子
S
N
2021/3/12
1
§6.1 原子的磁矩 §6.2 外磁场对原子的作用 §6.3 史特恩—盖拉赫实验的结果 §6.4 顺磁共振 §6.5 塞曼效应 §6.6 抗磁性、顺磁性和铁磁性
2021/3/12
2
第六章 在磁场中的原子 本章综合讨论原子处在磁场中所发生的 一些现象和有关理论。
电子的轨道磁矩
在第二章中讨论到原子中的电子,由于轨道运动, 具有轨道磁矩,它的数值是(标量式)
方向同
pl
l
e 2m
pl
相反。(矢量式)
l
e 2m
pl
(1)
用量子力学的pl 值,即
氢原子的超精细结构 ppt课件

2021/8/10
氢原子的超精细结构
原子光谱研究的数量级
• 在研究原子光谱的初始阶段,我们只把原子核看成有一定 质量的点电荷,得到原子光谱的粗结构;在考虑自旋作用 后,得到了光谱的精细结构;当谈到原子核的自旋、磁矩 和电四极矩时,将得到光谱的超精细结构。
• 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭
• “不怕太阳晒,也不怕那风雨狂,只怕先生骂我 笨,没有学问无颜见爹娘 ……”
• “太阳当空照,花儿对我笑,小鸟说早早早……”
氢原子的精细结构
• 氢原子能谱的特点:
1、P、D、F等能级一分为二,S能级不分裂
E E 2、对氢原子而言,因其无极化和贯穿,同n不同l的 rel 和 l, s
时,原子核处
• 式中第一项是电子轨道运动在核处产生的磁场, 是电子轨 道运动速度, 是以原子核为远点的电子的坐标;第二项是 电子的自旋磁矩 在核出产生的磁场。最终将 改写为:
2021/8/10
氢原子的超精细结构
磁偶极超精细相互作用
• 此时,磁偶极相互作用能量(哈密顿量)是:
2021/8/10
氢原子的超精细结构
2021/8/10
氢原子的超精细结构
核磁矩
• 类似于原子磁矩的表示式,核磁矩和核自旋角动量I成正比。
μ I = g Iμ NI
• 显然,在磁场中,核自旋磁矩与磁场相互作用所产生的附 加能量为
U = - μ I • B = - g I μ N BmI
• 因为m I有2I+1个值,所以有2I+1个不同的附加能量,于是 就发生赛曼能级分裂,一条核能级在磁场中就分裂为2I+1 条,相邻两条分裂能级间的能量差为
原子物理学4-6章的知识要点(自己整理的,仅作参考)

总量子数: L S , L S 1,, L S J
对于具有两个价电子的 原子,当 给定, L
2 S 1
LJ
状态 0时J L。有一个可能的角动量 (单态) S 状态 1时J L 1, L, L 1。有三个可能的角动量 (三重态)
结论:具有两个价电子的原子都有单态和三重态的能级结构.
h h 0 (m2 g2 m1g1 )B B
当体系自旋为0时, g2 g1 1
h h 0 ( m 2 m1 ) B B
反常塞曼效应
钠是单原子体系,其主线系相当于 np→3s的跃迁 纳原子分裂谱线的能量:
h h ( m 2 g 2 m1 g1 ) B B 分裂谱线的频率: ( m 2 g 2 m1 g1 ) L eB 拉摩频率: L 14B(T )GHz h 4me 分裂谱线的波数: (m2 g2 m1 g1 ) L L E 1 L 46.7 B(T )m , 46.7 B SI c B B
sz B
朗德(Lande)因子(g因子)
定义一个g因子,使得对于任意角动量量子数j 所对 应的磁矩及其在z方向的投影均可表为:
j j ( j 1)g j B jz m j g j B
g是反映微观粒子内部 运动的一个重要物理量. (至今仍是一个假设)
3 s( s 1) l ( l 1) s 0, l 0 g g l 1 gj 2 2 j ( j 1) s 0, l 0 g g s 2
主量子数 角量子数
n, n 1, 2,3, 4,......
四、超精细结构

四、超精细结构用分辨率很高的光谱学方法研究原子光谱时,可以发现许多原子光谱线由多条线构成,呈现出非常精细的结构,大约比精细结构小3个数量级,称之为超精细结构。
最早解释超精细结构的是泡利,1926年,泡利提出了核自旋和核磁矩的假定。
许多核具有自旋,伴随之具有磁矩。
核磁矩与电子之间的相互作用造成能级分裂。
核磁矩很小,能级的分裂也很小。
许多核还有电四极矩,核电四极矩与电子在核处所产生的电场梯度相互作用引起能量的微小改变,叠加在磁矩引起的超精细结构上,使分裂偏离朗德间隔定则。
能级的超精细结构造成光谱线的超精细结构。
[7]在量子力学中,超精细结构与精细结构的形成机理具有相似性,都是通过磁矩耦合来实现的。
然而,形态场假说却否定了上述观点,因为在复式原子模型中,核外电子只存在自旋磁矩,不存在轨道磁矩;电子的自旋磁场方向是固定的,与原子核的磁场方向保持一致,二者共同构成了原子的磁场。
在核磁场与电子磁场之间,不发生磁矩多重耦合作用,因而不会引起原子能级的分裂。
那么,原子谱线的超精细结构是如何形成的呢?复式原子模型认为,超精细结构与原子磁轴的摆动有关,属于原子谱线的一种偏振位移行为。
电磁波具有偏振属性,每一条谱线都是偏振光在观测轴上投影。
与塞曼效应相对照,在没有磁场的环境中,发光原子的磁轴取向是自由的,相对观测轴的倾角各异,每条谱线的偏振位移值不尽相同,由此构成了谱线的超精细结构。
参照图示,设α为原子磁轴方向OP与观测轴OX的夹角,d0为原子磁轴垂直于观测轴OX时偏振光的位移值(极大值)。
光的偏振方向为电子轨道的切线方向,与光的传播方向相垂直,简单进行换算,得谱线偏振位移值为:d=d0 sinα;谱线的超精细结构与精细结构的区别在于,谱线的超精细结构是一种谱线偏振位移行为,与电磁波频率没有关系;而谱线精细结构则是原子能级的精细结构所致,电磁波频率发生了变化。
还有一种情形,有一种核子数为奇数的原子核产生的谱线分裂现象,由于谱线裂距比正常的精细结构裂距小几个数量级,因此被称为超精细结构。
原子物理学第章原子的精细结构

原子物理学第章:原子的精细结构原子是构成物质的基本单位,它由带正电荷的核心和围绕核心运动的带负电荷的电子组成。
在经典物理学中,原子被认为是静止的,但是量子力学的发展揭示了原子的精细结构,例如电子云和量子态等。
本文将讨论原子的精细结构,以及描述这些结构的理论。
原子的基本结构原子核是由带正电荷的质子和中性的中子组成的。
这些粒子组成的核心决定了原子的一些基本特性,包括原子质量和化学性质。
核外的电子以轨道形式围绕着核心运动,这些轨道在经典物理学中被描述为电子在核心周围的椭圆轨道。
但是,在量子力学中,这些轨道被描述为存在于不同能级的电子云。
原子的精细结构在原子的基本结构之上,原子的精细结构描述了电子在其轨道中产生的细微变化,而非在不同能级之间转移。
原子的精细结构可以通过使用量子力学的原理进行处理。
这些原理中最重要的是狄拉克方程。
狄拉克方程提供了描述原子核和电子之间相互作用的框架。
该方程考虑了相对论效应,在公式中使用了四个分量而不是三个分量来表示电子的波函数。
这个方程也解释了为什么电子在原子中可以处于更高的能态而不精确遵守电子云模型。
量子力学也提供了描述原子精细结构的其他理论,例如斯坦纳-帕仑季定理和塞曼效应。
斯坦纳-帕仑季定理揭示了原子能级之间的相互作用,而塞曼效应则描述了原子光谱线的结构。
精细结构的应用原子的精细结构不仅仅是一种理论,它也具有实际应用。
例如,光电子能谱被用于测量单个电子在原子中的能量分布,这可以用于识别物质的组成。
原子钟是另一个应用,精确测量铯原子的精细结构,提供了高精度的时间标准。
原子的精细结构是量子力学中的一个重要概念。
它描述了在原子核和电子之间相互作用的微小变化,对于实际应用而言具有重要意义。
虽然还有许多未解决的问题,但是研究原子的精细结构继续引领着物理学、化学和其他领域的发展。
原子物理学课程学习资料

《原子物理学》课程学习资料(2011年5月许迈昌编写)一、教学目的:本课程是应用物理学的一门专业基础课,属普通物理课程,其任务使学生掌握原子的组成成份,理解组成原子的电子、原子核之间的相互作用及电子的运动规律,理解原子的量子理论,理解电子的量子角动量和量子磁矩,理解磁场对原子磁矩的作用,理解原子能级结构,理解原子辐射规律和原子光谱.理解原子核的组成以及核衰变、核反应等现象.了解原子物理的实验方法及具体应用,提高学生科学研究的素质. 二、课程内容要求第一章 原子的位形:卢瑟福模型理解电子和原子核的电量、质量和大小量级,使学生掌握原子线度及组成成份,掌握原子的卢瑟福有核模型,理解α粒子散射的实验和理论.瞄准距离21201cot ,224Z Z e a b a Eθπε==第二章 原子的量子态:玻尔模型理解黑体辐射、光电效应规律,使学生理解微观领域物理量的量子化规律,逐步理解微观领域的研究方法,理解原子核对核外电子的基本作用——库仑场,理解玻尔原子量子能级(假说)与原子光谱(实验测量)的关系.光量子的能量与动量,/E h p h c νν==,类氢离子光谱波数242222230211111(),,()(4)21e A A e e Ae m E R R Z R R m c m n n ch hc hc m παλπε∞=-===='+。
第三章 量子力学导论:理解波粒二象性,/,E h h p p mv νλ===、不确定关系/2,/2x x p E t ∆∆≥∆∆≥ 、波函数、概率密度2P ψ=、态叠加原理,薛定谔方程等概念与规律.使学生了解研究微观领域的基础——量子力学的基本概念和基本理论,掌握原子的角动量量子规则. 第四章 原子的精细结构:电子的自旋理解原子磁矩、电子自旋的概念,使学生掌握微观领域独有的自旋运动,理解自旋与轨道相互作用,理解关于原子角动量的矢量模式,理解原子角动量的耦合方式,理解原子磁矩与原子角动量的关系,理解磁场对原子磁矩的作用,理解原子光谱精细结构产生的原因,理解塞曼效应与原子角动量的关系.222ˆˆ31()ˆ22J SL g J-=+,,j z j j B m g μμ=-,0,1,2,,j m j=±±± ,类氢原子L-S 耦合43()2(1)Z U E n l l α∆=+,2211()4e eB m g m g m ννπ'=+-,帕刑-巴拉克效应(2)2s L ee BU m m m =+ , 第五章 多电子原子:泡利原理理解氦光谱和能级、角动量耦合、泡利原理、周期表、多电子组态和原子能态、洪特定则的内容.掌握两个角动量耦合的一般法则,理解两个价电子原子的光谱和能级,理解泡利原理,了解元素周期表、原子壳层理论,了解多电子组态和原子能态的关系,了解用ML 投影方法给出原子基态.第六章X射线:理解X射线产生的机制,了解X射线的吸收,了解吸收限、掌握康普顿散射.第七章原子核物理学概论:认识核的基本特性,掌握结合能、核自旋、核磁矩等概念,了解核力、核结构模型,了解核衰变的统计规律、α衰变、β衰变、了解γ衰变.参考书目1 韦斯科夫.二十世纪物理学.科学出版社,19792 费米夫人.原子在我家中.科学出版社,19793 王福山.近代物理学史研究(一)(1983),(二)(1986).复旦大学出版社.二、部分习题(一)论述题1.夫朗克—赫兹实验的原理和结论。
原子物理学(原子的精细结构电子自旋)

旋极化材料。
自旋电子学
利用电子自旋的特性,开发新型 自旋电子学器件,如自旋晶体管
和自旋存储器等。
磁性材料研究
通过研究电子自旋的磁学性质, 有助于深入了解磁性材料的微观
结构和物理性质。
05 原子物理学的发展前景与 挑战
原子物理学与其他学科的交叉研究
原子核位于原子的中 心,电子围绕原子核 运动。
原子的电子排布
电子在原子核外的不同能级轨道 上运动,离原子核越远的轨道,
其能量越高。
电子按照一定的规律填充在不同 的能级轨道上,形成电子排布。
电子排布决定了原子的化学性质 和电子状态,是研究原子结构的
重要内容。
原子的能级与光谱
原子的能级是指原子内部电子 运动的能量状态,不同的能级 具有不同的能量。
原子物理学在新能源与技术中的应用
太阳能电池技术
01
原子物理学在太阳能电池技术中的应用,通过优化材料结构和
提高光电转换效率,为可再生能源的发展提供支持。
核聚变能源
02
通过原子物理学对核聚变反应过程的研究,实现可控核聚变能
源的开发,为未来能源供应提供可持续的解决方案。
磁约束核聚变装置
03
利用原子物理学的原理和技术,设计和建造磁约束核聚变装置,
当原子从一个能级跃迁到另一 个能级时,会吸收或释放一定 频率的光子,形成光谱。
光谱分析是研究原子能级结构 和性质的重要手段,可以用于 元素分析和化学分析等。
02 原子核的结构与性质
原子核的组成
01
02
03
质子和中子
原子核由质子和中子组成, 质子带正电荷,中子不带 电。
锂原子的超精细结构的理论计算

1s22p
3/2-
-7.3809179796
-200.845083461
根据表一可以看出,1s22s组态能级没有发生 精细分裂,1s22p组态能级分裂为两条,这与 理论结果完全一致。为了能直观的了解和表 示出锂(Li)的精细结构能级,在此作出了它 的1s22p组态的能级的精细结构图,如图二(1) F 所示。 2
1 WM 1 ( J , J ) AJ C 2
( F I 1)( F 1) J 2 1 3( K 1)( K 2 F )( K 2 I )( K 2 J 1) 2 I (2 I 1) J ( J 1) WE 2 ( J , J 2) BJ , J 2
J=3/2
0 3 1
1
J=1/2
1 2
(1)
(2)
图二、锂(Li)的1s22p组态的精细结构 能级和超精细能级分裂图
2.锂(Li)的超精细结构常量A因数和B因 数分析
表 二 和 表 三 分 别 表 示 出 了 锂 ( Li) 的 1s22s组态和1s22p组态的超精细结构常量A 因数和B因数。
表二、锂(Li)的1s22s组态的超精细结构 常量A因数和B因数
对于1s22s组态,将计算结果与实验结果 和其他理论结果[8]比较(表四所示),发现相 差比较大。
表四、锂(Li)的1s22s组态的磁偶极系数A因 数对比
a u t h o r A
1 / 2
( M H z )
theory Guan et al. 401.352
Tong et al.
This work
原子核的电四极矩 一般认为,大多数原子核的形状是偏离与 球形不大的轴对称椭球。原子核所产生电势
原子物理学研究中的精细结构常数

原子物理学研究中的精细结构常数在原子物理学研究中,精细结构常数是一个非常重要的物理常数。
精细结构常数可以用来描述原子的能量构造和电子的角动量等物理性质,它的精确测量对于精确地计算原子能级和精细结构有着重要的意义。
一、精细结构常数的定义与计算精细结构常数的定义是:$\alpha=\frac{1}{137}$,它是精密电子学的基本量纲之一。
在量子力学理论中,精细结构常数是相对论修正量的体现。
相对论导致了电子的较重一侧所发生的光子引力,已知该引力被合适的比率描述。
在经典情况下,$e^2/\hbar c$是该比率应有的值,而在相对论情况下,包括对于反常磁矩的描述,在自然单位下$\alpha$是该比率的量纲。
\begin{equation}\alpha=\frac{e^2}{\hbar c}\approx\frac{1}{137}\end{equation}在精细结构理论中,可以利用相对论量子力学的方法来计算能级的精细结构。
相对论量子力学中,电子的质量是动能的一种表现形式,因此在量子力学理论中,应该反映出质量的贡献。
当我们考虑电子的运动时,需要将其角动量和质量结合考虑,具体来说,就是需要用到相对论动量$\vec{p}$和自旋$\vec{s}$的合成量,即电子的相对论矢量算符$\vec{\alpha}$和$\vec{\beta}$。
\begin{equation}\vec{\alpha}=\frac{\vec{p}c^2}{E+mc^2},\vec{\beta}=\frac{\vec{p}}{mc},\alpha_i\beta_j+\alpha_j\beta_i=2\delta_{ij}\end{equation}相对论矢量算符$\vec{\alpha}$和$\vec{\beta}$之间的对易关系是:\begin{equation}[\alpha_i,\alpha_j]_+=2\delta_{ij},[\beta_i,\beta_j]_+=2\delta_{ij},[ \alpha_i,\beta_j]_-=0\end{equation}利用相对论量子力学的方法计算能级精细结构时,可以用到多种方法,例如时间依赖扰动方法、空间扰动方法、自能修正方法等等。
原子物理学课件--第六章

–即核子只与最近邻核子作用
• 极短程内存在排斥力
–小于0.8fm:斥力 –0.8fm ~ 2fm:吸引力 –大于10fm:核力消失
• 核力与电荷无关(1)
–质子和质子之间,中子和中子之间,质子和 中子之间的核力相同
6.3.1.基本性质(3)
• 核力与电荷无关(2)
Fpp Fnn Fnp Vpp Vnn Vnp
6.1.3.原子核的自旋和磁矩(2)
• 核自旋 原子核磁矩
I
gI
e 2mp
I
gI
he 2mp
i i 1 gI
i i 1N
核磁子
核g因子
只能由实验测得 数值有正有负
• 核磁矩z分量 I,z gI mI N
• 原子磁矩>核磁矩原子总磁矩忽略核磁矩
J gJ
ii 1B,
–维象模型 • 不从第一性原理,依靠一定的实验事实基础 上建立起来的模型
6.4.2.费米气体模型(1)
• 费米气体模型
–核子为费米子,自旋为1/2,核子之间无互作 用
–约束:泡利不相容原理。
6.4.3.壳层模型(1)
• 原子核的性质随着质子数或中子数的增 加显示出周期性的变化。
– 存在幻数核, 即当原子核内的质子数或中子 数为2, 8, 20, 28, 50, 82和126时核特别稳定。 原子核内部存在着某种壳层结构。
(10MHz数量级)磁场,
– 当磁场满足h =E时,原子核会表现出对该高
频磁场能量的强烈吸收,由低能级向相邻的高 能级跃迁,这种现象称为核磁共振。
6.1.3.原子核的自旋和磁矩(5)
• 原子核的电四极矩(1)
原子物理学六章X射线PPT课件

靶材由用途 决定
X射线可用高速电子流轰击阳极靶A而获得,或由Z>10的原 子内壳层跃迁而产生.
高速电子流与靶相撞时,电子因受阻失去动能,中约1%转变为X 射线,大部分转变为热能。
5
第5页/共49页
《原子物理学》第六章 X射线
X射线管的结构
封闭式X射线管实质上是一个大 的真空二极管
X射线管的阴极
105 ~ 107 mmHg
A
+
17
《原子物理学》第六章 X射线
X射线衍射与散射光束线和实验站
18
第18页/共49页
《原子物理学》第六章 X射线
劳厄实验(1912)
X射线源 d ~ 0.1 nm
~ 0.1 nm 晶片光栅
晶 体 的 三 维 光 栅
劳厄斑
Lane.德 (1879-1960 年)
19
第19页/共49页
《原子物理学》第六章 X射线
对劳厄斑的解释
1913年布喇格父 子建立了布喇格公 式.不但能解释劳厄 斑点,而且能用于对 晶体结构的研究。
当能量很高的X射线射到晶体各层面 的原子时,原子中的电子将发生强迫 振荡,从而向周围发射同频率的电磁 波,即产生了电磁波的散射, 而每个 原子则是散射的子波波源.劳厄斑正 是散射的电磁波的叠加.
X射线的波长数量级为Å,要分辩X射线的光栅也要在Å的数量级才行。 晶体有规范的原子排列,且原子间距也在Å的数量级。是天然的三维光栅。
劳厄想到了这一点,但普朗克对他的想法不予支持。后来去找正在攻读 博士的索末菲,经两次实验后终于成功进行了X射线的衍射实验。
铅板
K-
p
晶片
X射线衍射实验演示
第17页/共49页
原子物理学(杨福家)总结

原子物理学四、五、六、七、八章总结第四章1、定性解释电子自旋定性解释电子自旋和和轨道运动相互作用的物理机制。
原子内价电子的自旋磁矩与电子轨道运动所产生的磁场间的相互作用,是磁相互作用。
电子自旋对轨道磁场有两个取向,导致了能级的双重分裂,这就是碱金属原子能级双重结构的由来这种作用能通常比电子与电子之间的静电库仑能小(在LS 耦合的情况下),因此是产生原子能级精细结构即多重分裂(包括双重分裂)的原因。
2、原子态55D 4的自旋和轨道角的自旋和轨道角动量动量动量量子数是多少?总角量子数是多少?总角量子数是多少?总角动量动量动量在空间有几在空间有几个取向,如何实验证实?自旋量子数:s=2轨道量子数:l=2角动量量子数:J=4总角动量在空间有9个取向。
由于J J J m J −−=,,1,⋯,共12+J 个数值,相应地就有12+J 个分立的2z 数值,即在感光片上就有12+J 个黑条,它代表了12+J 个空间取向。
所以,从感光黑条的数目,就可以求出总角动量在空间有几个取向。
3、写出碱金属原子的能级公式,说明各写出碱金属原子的能级公式,说明各量量含义含义。
22jl njl n Rhc Z E ∆−−=其中,Z:原子序数,R:里德堡常数,h:普朗克常量,c:光速,n:主量子数,jl ∆:量子数亏损。
4、朗德间隔定则德间隔定则::在三重态中,一对相邻的能级之间的间隔与两个J 值中较大的那个成正比。
5、同科电子:n 和l 二量子数相同的电子。
6、Stark 效应效应::原子能级在外加电场中的移位和分裂。
7、塞曼效应效应::一条谱线在外磁场作用下一分为三,彼此间间隔相等,且间隔值为B B µ。
反常塞曼效应:光谱线在磁场中分裂的数目可以不是三个,间隔也不尽相同。
8、帕邢帕邢--巴克效应:在磁场非常强的情况下,反常塞曼效应会重新表现为正常塞曼效应,即谱线的多重分裂会重新表现为三重分裂,这是帕邢和巴克分别于1912和1913年发现的,故名帕邢-巴克效应。
原子物理学课件第6章

M 1 M2 M1 1 M1 M2
多一个, P光子 右旋圆偏振光
x
圆偏振光
Ex Ey
Ax cost Ay cos(t
2
)
y
从垂直磁场方向观察(假设为x轴)
Ey
Ay
cos(t
),线偏振光
2
z
k
M 0 :
光子的角动量垂直B方向 从B方向观察:无光谱
2
2J+1 = 2 EB E0 MgBB
S 1 , L 0, J 1
2
2
S2 1 2
11
M , g 2
22
E0 B B 1
2BB
2 1
E0 B B 2
E MgB B 1 2B B B B
2
设 : B 0时, E E0
2 3
23
1 1
1 3
,
1 3
2
5 3 ,1 L
~ ~0
共六条
L
1 3
5 3
L L
g2
=
4/3
M2g 2
2,
2 3
g1 = 2 M1g 1 1
M2 M2g2
2 P3 E2
2
0
E2
E2
E2
E2
222233BBBBBBBB13312222
BB
2 E2 2BB
M1g1 1 0 1
~ 1,1,1 0,0,0 1,1,1L
P1 1
E1
M 1 0 1
1 E1 B B 0 E1 1 E1 B B
原子物理学课件 (6)
3 2P
EL, S, B =(ML+2MS)BB
的值有五种组合。 下能级: 32S1/2 退化为: 3 2S S=1/2, MS =1/2, -1/2; L=0, ML= 0. 共产生3条谱线!
EL, S, B 的值有两种组合。
5.3.6 有超精细结构时的塞曼能级分裂
回顾:在第三章中介绍, 原子中电子的轨道角动量 和自旋角动量 的耦合
------ 帕邢-贝克效 应
32 P / 2 32 S1/ 2 ); 仍以Na双线 :589.6 nm 线( 1
32 P / 2 32 S1/ 2 ). 589.0 nm 线( 3
强磁场中,
直接与强外场
耦合,
无耦合,无
上能级 : 32P1/2 和 32P3/2
退化为:
S=1/2, MS =1/2, -1/2; L=1, ML =1, 0, -1 .
角动量定律:
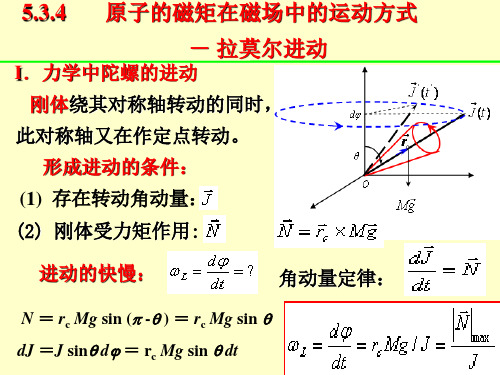
II.拉莫尔进动
原子的角动量(磁矩)在磁场中满足: (1) 存在角动量: (2) 受力矩作用: 所以,原子的角动量(磁矩)在磁场中进动:拉莫尔进动
(旋磁比)= J / J 由: 有:
III,角动量在磁场中的运动
A,弱外磁场中,
>>
的运动
------弱磁场中(正常和反常) 塞曼效应的磁能级分裂公式 守恒量和本征值 “一 一 对应” 对应的量子数为好量子数。 非守恒量; 2, L2, S2 Jz : 守恒量; 好量子数?? J
情况2: 在外磁场中,如果属强场,按角动量矢量模型
其中,
所以, 其中,
Why?
所以:
Ej,I, B =mj gj B B + a mjmI
例如:碱金属原子的基态 2S1/2, 对 I=1/2 (核自旋量子数) 因为,
原子物理6第六章解析
第 六
4)X射线是不可见光,它能使某些物质发出
章 可见光的荧光;
:
X 5)X射线本质上是一种电磁波,同此它具有
射 线
反射、折射、衍射、偏振等性质。
首页
上一页
下一页
第二节:X射线的产生机制
返回
连续谱
实验表明,X射线由两部分构成,一部分
第 波长连续变化,称为连续谱;
六 章
另一部分波长是分立的,与靶材料有关,成为
荧光屏仍然发光,
X射线的
发现
而且这种射线能使黑纸包住的照相底片感光,
不被电磁场偏转。
X射线的
经过一个多月的研究,他未能搞清这种射线 产生
的本质,
第
六 因此赋予它一个神秘的名字
章 :
--X射线(伦琴射线)。
X
1895年12月28日,伦琴向德国物理学医学
射 线
会递交了第一篇关于X射线的论文,《论新的射
线》,并公布了他夫人的X射线手骨照片。
:
在评价这一故事时所说的那样,“科学家的‘灵
X
射 线
感’对科学家的发现‘非常重要’;这种灵感必
源于他的丰富的实践和经验。”
首页
上一页
下一页
第一节:X射线的发现
X射线的 发现
如图,在真空管 (106 108 mmHg) 两阴极和阳
极之间加高压,阳极选用不同的重金属材料
第 六
制成,电子打在阳极上便可得到X射线,其
的I~λ曲线。由图可见 决定的。
与靶min无关。是由管压V 连续谱
连续谱产生的微观机制
标识谱
通过上面对连续谱特征的分析可知:连续谱不应
该是原子光谱,而应该是电子在靶上减速而产生的。
rb原子超精细结构旋波近似

rb原子超精细结构旋波近似
标题:RB原子超精细结构旋波近似
RB原子的超精细结构旋波近似是原子物理学中一种重要的近似方法,通过对RB原子的超精细结构进行研究,可以更好地理解原子的内部结构和相互作用。
本文将以人类的视角,以生动的描述和流畅的叙述,探讨RB原子超精细结构旋波近似的原理和应用。
第一部分:RB原子的超精细结构
RB原子是由一个正电子和一个负电子组成的简单原子,它们之间通过电磁相互作用相互吸引。
RB原子的超精细结构是指在原子的基本结构基础上,考虑了电子自旋、核自旋和电子与核之间的相互作用后的更精确描述。
第二部分:旋波近似的原理
旋波近似是一种常用的求解RB原子超精细结构的方法。
它基于电子和核自旋的相互作用,将原子系统的哈密顿量进行展开,并利用旋波近似将高阶项忽略,从而简化求解过程。
这种近似方法在计算上更加可行,并能够得到较为准确的结果。
第三部分:旋波近似的应用
旋波近似在原子物理学中有着广泛的应用。
通过对RB原子超精细结构的研究,可以揭示出原子中微观粒子之间的相互作用规律,从而为其他领域的研究提供理论基础。
此外,旋波近似还可以用于设
计和优化原子钟、磁共振成像等精密测量仪器,进一步推动科学技术的发展。
结论:RB原子超精细结构旋波近似是一种重要的研究方法,通过对RB原子的超精细结构进行描述,可以更好地理解原子的内部结构和相互作用。
旋波近似的原理和应用使得我们能够更好地探索原子世界的奥秘,并为相关领域的研究和应用提供了便利。
通过深入研究RB原子超精细结构旋波近似,我们能够更好地认识到原子物理学的重要性和广泛应用的前景。
在原子物理学中巧用精细结构常数

在原子物理学中巧用精细结构常数
王宏
【期刊名称】《遵义师范学院学报》
【年(卷),期】2010(012)003
【摘要】量纲分析法是研究较为复杂的自然现象中各物理量之间的关系及内在规律性的有效工具,在量纲分析法的基础上,作者探讨了精细结构常数在原子物理学中的应用.
【总页数】2页(P71-72)
【作者】王宏
【作者单位】遵义师范学院,物理系,贵州,遵义,563002
【正文语种】中文
【中图分类】O562
【相关文献】
1.原子物理学中的组合常数应用 [J], 彭双艳
2.组合常数方法在原子物理学中的应用 [J], 高丽丽;宋文福;何训
3.Co2+离子在CsMgCl3晶体中的g因子和超精细结构常数研究 [J], 董会宁;邬劭轶
4.钫原子磁偶极超精细结构常数及其同位素的磁偶极矩的理论计算 [J], 娄冰琼; 李芳; 王沛妍; 王黎明; 唐永波
5.氘化锂中Rh^(2+){A}中心g因子和超精细结构常数的理论研究 [J], 张华明;邬劭轶;鲁广铎;张志红;魏丽华
因版权原因,仅展示原文概要,查看原文内容请购买。
