最新高中物理必修2第五章曲线运动知识点总结
高中物理必修二第五章曲线轨迹知识点总结

高中物理必修二第五章曲线轨迹知识点总
结
第五章曲线轨迹是高中物理必修二的重要章节,是进一步理解力学与数学知识的基础,本文总结了该章节的重点内容。
1. 曲线的切线和法线
- 任意一点的切线方向是该点速度方向
- 切线方向发生改变,速度大小不变,产生加速度
- 切线方向不变,速度大小改变,产生切向加速度
- 法线方向是切线方向的逆时针旋转90度
2. 一段曲线的长度
- 一段曲线的长度可以近似看作许多小线段的长度之和
- 当小线段长度趋近于0时,该总长度即为曲线长度
3. 曲率和半径
- 曲率指曲线在某一点的弯曲程度
- 曲率越大,曲线弯曲程度越大
- 半径是曲率的倒数,其值越小,曲率越大
4. 圆的运动学方程
- 圆的运动学方程:x²+y²=r²
- 圆的运动可用向量表示:r(t)=<xcosωt,ysinωt>
- 圆的速度大小和方向是一定的
- 圆的加速度大小不变,方向沿切线方向
- 圆的轨迹是一段不断变化曲率的运动轨迹
以上就是第五章曲线轨迹的重点知识点总结。
了解了这些知识,可以更好地理解曲线运动的规律和特点,为高中物理学习打好基础。
度高一必修2物理曲线运动知识点

度高一必修2物理曲线运动知识点
高中物理是高中文科(自然迷信)基础科目之一,小编预备了高一必修2物理曲线运动知识点,详细请看以下内容。
一、知识点
(一)曲线运动的条件:合外力与运动方向不在一条直线上
(二)曲线运动的研讨方法:运动的分解与分解(平行四边形定那么、三角形法那么)
(三)曲线运动的分类:合力的性质(匀变速:平抛运动、非匀变速曲线:匀速圆周运动)
(四)匀速圆周运动
1受力剖析,所受合力的特点:向心力大小、方向
2向心减速度、线速度、角速度的定义(文字、定义式)
3向心力的公式(多角度的:线速度、角速度、周期、频率、转)
(五)平抛运动
1受力剖析,只受重力
2速度,水平、竖直方向分速度的表达式;位移,水平、竖直方向位移的表达式
3速度与水平方向的夹角、位移与水平方向的夹角
(五)离心运动的定义、条件
二、调查内容、要求及方式
1曲线运动性质的判别:明白曲线运动的条件、牛二定律(选
择题)
2匀速圆周运动中的静态变化:熟练掌握匀速圆周运动各物理量之间的关系式(选择、填空)
3匀速圆周运动中物理量的计算:受力剖析、向心减速度的几种表示方式、合力提供向心力(计算题)
3运动的分解与分解:分运动与和运动的等时性、等效性(选择、填空)
4平抛运动相关:平抛运动中速度、位移、夹角的计算,分运动与和运动的等时性、等效性(选择、填空、计算)
5离心运动:临界条件、最大静摩擦力、匀速圆周运动相关计算(选择、计算)
高中是人生中的关键阶段,大家一定要好好掌握高中,编辑教员为大家整理的高一必修2物理曲线运动知识点,希望大家喜欢。
高中物理必修二知识点总结归纳

高中物理必修二知识点总结归纳第五章 曲线运动1.曲线运动的特征(1)曲线运动的轨迹是曲线。
(2)由于运动的速度方向总沿轨迹的切线方向,又由于曲线运动的轨迹是曲线,所以曲线运动的速度方向时刻变化。
即使其速度大小保持恒定,由于其方向不断变化,所以说:曲线运动一定是变速运动。
(3)由于曲线运动的速度一定是变化的,至少其方向总是不断变化的,所以,做曲线运动的物体的中速度必不为零,所受到的合外力必不为零,必定有加速度。
(注意:合外力为零只有两种状态:静止和匀速直线运动。
)曲线运动速度方向一定变化,曲线运动一定是变速运动,反之,变速运动不一定是曲线运动。
2.物体做曲线运动的条件(1)从动力学角度看:物体所受合外力方向跟它的速度方向不在同一条直线上。
(2)从运动学角度看:物体的加速度方向跟它的速度方向不在同一条直线上。
3.匀变速运动:加速度(大小和方向)不变的运动。
也可以说是:合外力不变的运动。
4.曲线运动的合力、轨迹、速度之间的关系(1)轨迹特点:轨迹在速度方向和合力方向之间,且向合力方向一侧弯曲。
(2)合力的效果:合力沿切线方向的分力F2改变速度的大小,沿径向的分力F1改变速度的方向。
①当合力方向与速度方向的夹角为锐角时,物体的速率将增大。
②当合力方向与速度方向的夹角为钝角时,物体的速率将减小。
③当合力方向与速度方向垂直时,物体的速率不变。
(举例:匀速圆周运动)绳拉物体合运动:实际的运动。
对应的是合速度。
方法:把合速度分解为沿绳方向和垂直于绳方向。
小船渡河例1:一艘小船在200m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是5m/s,求:(1)欲使船渡河时间最短,船应该怎样渡河?最短时间是多少?船经过的位移多大?(2)欲使航行位移最短,船应该怎样渡河?最短位移是多少?渡河时间多长?船渡河时间:主要看小船垂直于河岸的分速度,如果小船垂直于河岸没有分速度,则不能渡河。
(此时=0°,即船头的方向应该垂直于河岸)解:(1)结论:欲使船渡河时间最短,船头的方向应该垂直于河岸。
高中物理必修2 第五章 曲线运动 知识点汇总

3. 圆周运动 a) 线速度
v
s t
匀速圆周运动的线速度的大小处处相等, 但是方向时刻在变化, 所以这里的匀速指 的是速率。 b) 角速度
t 2r 2 , r
角速度的单位为:弧度每秒,rad/s。 弧度是弧长与半径的比值,为角度的国际单位。360°周角的弧度是: 所以平角弧度= π,直角弧度=π/2 。 转速 n = 转每秒,转每分。 周期 T。 c) 线速度与角速度的关系
微信公众号:初高中物理老师,关注后可以进行具体问题的答疑。
2. 平抛运动 a) 抛体运动:以一定的速度将物体抛出,如果物体只受重力的作用,这时的运动叫做 抛体运动;抛体运动开始时的速度叫做初速度。如果初速度是沿水平方向的,这 个运动叫做平抛运动。 b) 平抛运动的速度: i. 速度的大小
vx v0 v y gt
2
向心力
v2 Fn m m 2 r ,向心力是根据力的作用效果命名的,可以是 r
重力、弹力或者摩擦力,也可以这些力的分力或者合力。 c) 变速圆周运动 除了受到向心力以外,还受到跟圆周相切的力,Ft,产生圆周运动切线方向的加速 度。 5. 线运动 知识点汇总
1. 曲线运动 a) 曲线运动的描述:位移和速度,其定义与直线运动一样。这两个量是矢量,所以包 括了方向和大小。由于是曲线运动所以这两量的方向是时刻在变化的; b) c) 曲线运动速度的方向:质点在某一点的速度方向沿着曲线在这一点的切线方向; 曲线运动,由于速度的方向总在发生改变,也就说明有加速度,所以曲线运动是变 速运动; d) 由于位移和速度是矢量, 可以用分解在两个互相垂直的方向上的分矢量来表示。 (类 似于力的正交分解) e) 当物体所受合力方向与它的速度方向不在同一直线上时,物体做曲线运动。
【高中物理】高中物理必修二第五章知识点:曲线运动

【高中物理】高中物理必修二第五章知识点:曲线运动
高中物理是高中学习的重要学科,整理了高中物理知识点,供广大高中生学习参考,希望有所帮助!
>>>
高中物理
必修二各章知识点汇总<<
高中英语
;<
第五章曲线运动
一、知识点
(一)曲线运动的条件:再分外力与运动方向无此一条直线上
(二)曲线运动的研究方法:运动的合成与分解(平行四边形定则、三角形法则)
(三)曲线运动的分类:合力的性质(坯变速箱:元显恭甩运动、非匀变速箱曲线:匀速圆周运动)
(四)匀速圆周运动
1受力分析,所受到合力的特点:向心力大小、方向
2向心加速度、线速度、角速度的定义(文字、定义式)
3向心力的公式(多角度的:线速度、角速度、周期、频率、转回)
(五)平抛运动
1受力分析,只受到重力
2速度,水平、竖直方向分速度的表达式;位移,水平、竖直方向位移的表达式
3速度与水平方向的夹角、加速度与水平方向的夹角
(五)离心运动的定义、条件
二、实地考察内容、建议及方式
1曲线运动性质的判断:明确曲线运动的条件、牛二定律(选择题)
2匀速圆周运动中的动态变化:熟练掌握匀速圆周运动各物理量之间的关系式(挑选、填空题)
3匀速圆周运动中物理量的计算:受力分析、向心加速度的几种表示方式、合力提供向心力(计算题)
3运动的制备与水解:分后运动与和运动的等时性、耦合性(挑选、填空题)
4平抛运动相关:平抛运动中速度、位移、夹角的计算,分运动与和运动的等时性、等效性(选择、填空、计算)
5Vergt运动:临界条件、最小静摩擦力、匀速圆周运动有关排序(挑选、排序)。
人教版物理必修二第五章曲线运动知识总结

物体做曲线运动轨迹分析1.合外力方向与轨迹的关系物体做曲线运动的轨迹一定夹在合外力方向与速度方向之间,速度方向与轨迹相切,合外力方向指向曲线的“凹”侧。
2.速率变化情况判断①当合外力方向与速度方向的夹角为锐角时,物体的速率增大;②当合外力方向与速度方向的夹角为钝角时,物体的速率减小;③当合外力方向与速度方向垂直时,物体的速率不变。
物体做曲线运动的条件1.曲线运动(1)速度的方向:质点在某一点的速度方向,沿曲线在这一点的切线方向。
(2)运动的性质:做曲线运动的物体,速度的方向时刻在改变,所以曲线运动一定是变速运动。
(3)曲线运动的条件:物体所受合外力的方向跟它的速度方向不在同一条直线上或它的加速度方向与速度方向不在同一条直线上。
2.物体做曲线运动的条件①因为速度时刻在变,所以一定存在加速度;②物体受到的合外力与初速度不共线。
运动的合成与分解1.基本概念(1)合运动与分运动:一个物体的实际运动往往参与几个运动,这几个运动叫做实际运动的分运动,这个实际运动叫做这几个分运动的合运动;(4)运动的分解:已知合运动求分运动的过程;(5)运算法则:运动的合成与分解包括位移、速度和加速度的合成与分解,遵循平行四边形定则。
2.合运动性质的判断(1)判断方法:若加速度与初速度的方向在同一直线上,则为直线运动,否则为曲线运动;(2)几种常见的情况a.两个匀速直线运动的合运动仍然是匀速直线运动;b.一个匀速直线运动与一个匀变速直线运动的合运动仍然是匀变速运动,当二者共线时为匀变速直线运动,不共线时为匀变速曲线运动。
3.两个直线运动的合运动性质的判断根据合加速度方向与合初速度方向判定合运动是直线运动还是曲线运动,具体分一个匀速直线运动、一个匀变速直线运动 匀变速曲线运动 两个初速度为零的匀加速直线运动匀加速直线运动 两个初速度不为零的匀变速直线运动如果v 合与a 合共线,为匀变速直线运动 如果v 合与a 合不共线,为匀变速曲线运动小船渡河问题 1.模型条件(1)物体同时参与两个匀速直线运动。
最新人教版高中物理必修2第五章变速圆周运动和一般曲线运动

1.变速圆周运动 总结:切向分力改变速度的大
பைடு நூலகம்
F
Fn O
小,法向分力改变速度的方向。
2.一般的曲线运动
处理方法:把曲线分割成许多短的小段,
每一 段都看作一小段圆弧,对圆弧采用圆 周运动的方法分析。
变速圆周运动和一般曲线运动
变速圆周运动:速度大 小也发生变化的圆周运动
再见!
物体所受的合力不指向 圆心,分解为两个力Ft、Fn (如图)
这两个分力的作用效果是什么? Ft改变速度的大小, Fn改变速度的方向
变速圆周运动和一般曲线运动
一般曲线运动:运 动轨迹既不是直线也不 是圆周的曲线运动。
研究方法:曲线上各个地方弯曲的程 度不一样,可以分割成很多极短的小段, 每一段都可以看作是一小段圆弧,就可以 采取圆周运动的方法处理了。
最新人教版高中物理必修2第五章《曲线运动》本章小结

整合提升知识网络⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧========∆∆==∆∆=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧=====⎩⎨⎧222222220200/4/:/4/::/2/:/2/::/tan 2/:,,:::T r m r m r m v F T r r r v a r v T t T r t l v v v gt y t v x gt v v v y y x πωπωωπϕωπθ向心力向心加速度线速度和角速度的关系角速度线速度动的物理量描述圆周运变速曲线运动运动性质周运动匀速圆运动规律匀变速曲线运动运动性质平抛运动曲线运动两种特殊的等时性独立性等效性合运动与分运动的关系运动的合成与分解研究方法度不在同一条直线上物体所受的合外力与速产生条件曲线运动动运线曲 重点突破一、运动的合成与分解【例1】小船在200 m 宽的河中横渡,水流速度为3 m /s ,船在静水中的航速是5 m /s ,求:(1)当小船的船头始终正对岸行驶时,它将在何时、何处到达河对岸? (2)要使小船到达河的正对岸,应如何行驶?多长时间能到达对岸? 解答:(1)因为小船垂直河岸的速度即为小船在静水中的行驶速度,且在这一方向上,小船做匀速运动,故渡河时间t=5200=船v d s=40 s ,小船沿河流方向的位移s=v 水t=3×40 m=120 m ,即在正对岸下游120 m 处靠岸.(2)要使小船垂直到达对岸,小船的合速度应垂直河岸,其速度的图示如图6-1所示,由图可知v 合=22水船v v - =4 m /s ,因而这种情况下船的渡河时间t′=4200=船v d s=50 s.这时船行驶方向与岸的上游的夹角为θ,则cosθ=53=船水v v =0.6,所以θ=53°,即船的航向与岸的上游所成角度为53°.图6-1类题演练 1在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去,水流速度为v 1,摩托艇在静水中的航速为v 2,战士救人的地点A 离岸边最近处O 的距离为d.战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O 点的距离为( ) A.21222v v dv - B.0 C.21v dv D.12v dv解析:要最短时间将人送到岸上,应驾驶摩托艇垂直河岸行驶,最短时间t=2v d,摩托艇登陆点偏离O 点是因为摩托艇随河水向下游漂流的结果,所以离O 点的距离s=v 1t=21v dv . 答案:C 类题演练 2如图6-2所示,水平面上有一物体,人通过定滑轮用绳子拉它,在图示位置时,若人的速度为5 m/s ,则物体的瞬时速度为_____________m/s.图6-2解析:把绳子末端的速度分解后有:v 1cos60°=v 2cos30° 所以v 1=35360cos 30cos 22==︒︒v v m/s.答案:35二、平抛运动【例2】一艘敌舰正以v 1=12 m /s 的速度逃跑,执行追击任务的飞机,在距水面高度h=320 m 的水平线上以速度v 2=105 m/s 同向飞行.为击中敌舰,应“提前”投弹.如空气阻力可以不计,重力加速度g 取10 m /s 2,飞机投弹时,沿水平方向它与敌舰之间的距离应为多大?如投弹后飞机仍以原速度飞行,在炸弹击中敌舰时,飞机与敌舰的位置有何关系?解析:投下的炸弹竖直方向上做自由落体运动,水平方向上以飞机的速度v 2做匀速运动,炸弹在空中飞行的时间为 t=1032022⨯=g h s=8 s 在8 s 时间内,炸弹沿水平方向飞行的距离s 2=v 2t ,敌舰在同一方向上运动的距离s 1=v 1t ,由图6-3可以看出,飞机投弹时水平方向上“提前”距离应为:图6-3s=v 2t-v 1t=105×8 m-12×8 m=744 m.在t=8 s 时间内,炸弹与飞机沿水平方向的运动情况相同,都以速度v 2做匀速运动,水平方向上运动的距离都是s 2=v 2t=840 m.所以,炸弹击中敌舰时,飞机恰好从敌舰的正上方飞过.答案:744 m ;飞机在敌舰正上方 类题演练 3如图6-4所示,排球场总长为18 m ,设球网高度为2 m ,运动员站在离网3 m 的线上(图中虚线所示)正对网前跳起将球水平击出(空气阻力不计).图6-4(1)设击球点在3 m 线正上方高度为2.5 m 处,试问击球的速度在什么范围内才能使球既不触网也不越界.(2)若击球点在3 m 线正上方的高度小于某个值,那么无论水平击球的速度是多大,球不是触网就是越界,试求这个高度(g 取10 m /s 2). 解析:(1)作出如图所示的平面图,若刚好不触网,设球的速度为v 1,则水平位移为3 m 的过程中:水平方向有:s=v 0t ,即3 m=v 1t ① 竖直方向有:y=221gt , 即2.5 m-2 m=221gt ② 由①②两式得:v 1=103m/s同理可得刚好不越界的速度v 2=212m/s 故速度范围为:s m v s m /212/103<<.(2)设发球高度为H 时,发出的球刚好越过球网落在边界线上,则刚好不触网时有:s=v 0t ,即3m=v 0t ③ H-h=221gt ,即H-2m=221gt ④ 同理,当球落在界线上时有:12 m=v 0t′ ⑤ H=221gt ⑥ 解③④⑤⑥得H=2.13 m即当击球高度小于2.13 m 时,无论球的水平速度多大,则球不是触网就是越界. 答案:(1)s m v s m /212/103<< (2)2.13 m类题演练 4如图6-5所示,从高为H 的A 点平抛一物体,其水平射程为2s ;在A 点正上方高为2H 的B 点同方向平抛另一物体,其水平射程为s,“两物体在空中的运行轨道在同一竖直面内,且都从同一个屏M 的顶端擦过,求屏M 的高度.图6-5解析:由h=221gt 和x=v 0t 得t A =g H 2,s A =2s=v A gH 2 t B =g H 4,s B =s=v B gH 4 因为A 、B 均刚好擦过M 点,则在M 前的运动中 t A ′=g h H )(2-,s A ′=v A g h H )(2- t B ′=g h H )2(2-,s B ′=v B gh H )2(2-其中s A ′=s A ′,由以上各式解得h=H 76. 答案:H 76 三、圆周运动 1.向心力的计算【例3】如图6-6所示,已知绳长为L 1=20 cm ,水平杆L 2=0.1 m ,小球质量m=0.3 kg ,整个装置可绕竖直轴转动,问:(1)要使绳子与竖直方向成45°角,试求该装置必须以多大的角速度转动才行? (2)此时绳子的张力是多大?图6-6思路分析:小球绕杆做圆周运动,其轨道平面在水平面内,轨道半径r=L 2+Lsin45°,绳的拉力与重力的合力提供小球做圆周运动的向心力.解析:对小球受力分析如图6-7所示,设绳对小球拉力为F ,重力为mg ,则绳的拉力与重力的合力提供小球做圆周运动的向心力.图6-7对小球利用牛顿第二定律可得: mgtan45°=mω2r r=L 2+Lsin45°联立以上两式,将数值代入可得 ω=6.4 rad /s F=︒45cos mg=4.24 N.答案:(1)6.4 rad/s (2)4.24 N 类题演练 5 如图6-8所示,圆锥摆的摆长为L 、摆角为α,质量为m 的摆球在水平面内做匀速圆周运动,则( )图6-8A.摆线的拉力为αcos mgB.摆球的向心加速度为gcosαC.其运动周期为g L π2 D.其运动周期为gL απcos 2 解析:小球受力分析如图所示,则Fsinα=r Tm 224π=maFcosα=mg r=Lsinα联立上面三式解得: F=αcos mg,a=gtanα, T=gL απcos 2 故A 、D 正确. 答案:AD2.水平面内圆周运动的临界计算【例4】如图6-9所示,一个光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,母线与轴线之间的夹角为θ=30°,一条长为L 的绳(质量不计),一端固定在圆锥体的顶点O 处,另一端拴着一个质量为m 的小物体(物体可看作质点),物体以速率v 绕圆锥体的轴线做水平匀速圆周运动.图6-9(1)当v=gL 61时,求绳对物体的拉力; (2)当v=gL 23时,求绳对物体的拉力. 解析:水平方向:F T sin θ-F N cosθ=θsin 2L v m ①竖直方向:F T cosθ+F N sinθ=mg ② 联立①②两式解得:F N =mgsinθ-θsin 2L v m由上可看出当θ、L 、m 一定时,线速度v 越大,支持力F N 越小,当v 满足一定条件,设v=v 0时,能使F N =0,此时锥面与物体间恰好无相互作用,即mgsinθ-θθsin cos 2L v m =0 v=θθcos sin 2gL将θ=30°代入上式得v 0=63gL. (1)当0161v gL v <=时,物体在锥面上运动,联立①②两式解得 F T1=mgcosθ+mg mg L v m 612321+==1.03mg.(2)当0223v gL v >=时,物体己离开锥面,但仍绕轴线做水平面内的匀速圆周运动,设此时绳与轴线间的夹角为α(α>θ),物体仅受重力和拉力作用,这时F T2s inα=αsin 22L v m ③F T2cosα=mg ④ 联立③④两式解得cosα=21, 所以α=60°F T2=mgcosα+23212+=mg L v mmg=2mg. 答案:(1)1.03mg (2)2mg类题演练 6有一水平放置的圆盘,上面放有一劲度系数为k 的弹簧,如图6-10所示,弹簧的一端固定于轴O 上,另一端挂一质量为m 的物体A.物体与盘面间的动摩擦因数为μ,开始时弹簧未发生形变,长度为R ,求:图6-10(1)盘的转速n 0为多大时,物体A 开始滑动? (2)当转速达到2n 0时,弹簧的伸长量Δx 是多少? 解析:(1)圆盘开始转动时,A 所受静摩擦力提供向心力,则有 μmg≥mω02R ① 又因为ω0=2πn 0 ② 由①②两式得Rgn μπ210≤即当Rgn μπ210=时物体A 开始滑动.(2)转速增加到2n 0时,有μmg+kΔx=mω12r ③ ω1=2π×2n 0 ④r=R+Δx ⑤ 整理得Δx=mgRkR mgRμμ43-.答案:(1)R gμπ21 (2)mgRkR mgRμμ43-3.离心运动 【例5】如图6-11所示是离心试验器的原理图,可以用离心试验器来研究超负荷对人体的影响,测试人的抗荷能力.离心试验器转动时,被测者做匀速圆周运动,现观察到图中的直线AB (即垂直于座位的直线)与水平杆成30°角,被测者对座位的压力是他所受重力的多少倍?图6-11 解析:被测试者做匀速圆周运动所需要的向心力由他所受重力和座位对他的支持力的合力提供,受力如图6-12所示.图6-12在竖直方向受力平衡,有 F N sin30°=mg ①在水平方向,由牛顿第二定律得F N cos30°=mrω2 ②由①式可得:F N =︒30sin mg=2mg即被测试者所受座位的压力是其重力的2倍. 答案:2倍 类题演练 7如图6-13所示,已知m A =2m B =3m C ,它们距轴的关系是r A =r C =B r 21,三物体与转盘表面的动摩擦因数相同,当转盘的转速逐渐增加时( )图6-13A.物体A 先滑动B.物体B 先滑动C.物体C 先滑动D.B 与C 同时开始滑动解析:摩擦力提供物体随盘转动的向心力,物体滑动时有:μmg≤mω2r ,即μg≤ω2r ,故r 越大越易滑动. 答案:B四、圆周运动与其他知识的综合问题 1.圆周运动与机械能守恒相结合【例6】一质量为m 的金属小球用L 长的细线拴起,固定在一点O ,然后将线拉至水平,在悬点O 的正下方某处P 钉一光滑钉子,如图6-14所示,为使悬线从水平释放碰钉后小球仍做圆周运动,则OP 的最小距离是多少?(g 取10 m /s 2)图6-14解析:要使悬线碰钉后小球做圆周运动,即能使小球到达以P 点为圆心的圆周的最高点M ,而刚能达到最高点M 的条件是:到M 点小球所需向心力刚好由自身重力mg 提供,此时悬线拉力为零,即有mg=Rv m2高,其中R 为以P 点为圆心的圆周的半径,v min 为小球到达M点的最小速度,而根据机械能守恒定律,有mg(L-2R)=221高mv 联立解得R=L 52,即为小球以P 点为圆心的最小半径,所以OP=L-R=L 53为OP 间的最小距离.故OP 段的最小距离是L 53. 答案:L 53 2.圆周运动与动能定理相结合【例7】如图6-15所示,小球原来能在光滑的水平面上做匀速圆周运动,若剪断B 、C 之间的细绳,当A 球重新达到稳定状态后,则A 球的( )图6-15A.运动半径变大B.速率变大C.角速度变大D.周期变大 解析:A 球原来做匀速圆周运动,绳的拉力提供向心力,而绳的拉力等于B 、C 的重力之和;当B 、C 间绳断后,绳的拉力变小,此时拉力不足以提供向心力,A 球将做离心运动,故半径变大,A 球向外运动过程中要克服绳的拉力做功,动能变小,故速率变小,而周期T=vrπ2,r 变大,v 变小,故T 变大. 答案:AD3.圆周运动的周期性【例8】如图6-16所示,竖直圆筒内壁光滑,半径为R ,顶部有入口A ,在A 的正下方h 处有出口B ,一质量为m 的小球从入口A 沿圆筒壁切线方向水平射入圆筒,要使球从B 处飞出,小球进入入口A 处的速度v 0应满足什么条件?在运动过程中,球对筒的压力是多大?图6-16思路分析:该题是圆周运动与自由落体运动相结合的题目,小球在竖直方向上只受重力,做自由落体运动,小球在水平方向筒壁的弹力提供小球做圆周运动的向心力. 解析:设小球下落时间为t ,则h=221gt ,t=gh 2,要保证小球从B 点射出,该段时间内小球转n 圈,则t=ghv nR 220=∙π,故v 0=h g nR 22π(n=1,2,3,…),小球做圆周运动需要的向心力F=nRmg n R v m 22202π=(n=1,2,3,…),由牛顿第三定律可知球对筒壁的压力为F′=nRm gn 222π(n=1,2,3,…),可化简得F′=2π2nRmg (n=1,2,3,…).答案:见解析 4.其他综合题【例9】不久前在张家界市国际特技表演赛上,一飞行员做半径为50 m 的特技表演.设飞行员质量为60 kg ,飞机做竖直平面上的圆周运动,在最高点时他对座椅的压力与重力相同.他关掉发动机做圆周运动,在最低点时:(1)他对座位的压力是多大?(2)在圆周运动的过程中他曾有眼睛“黑视”的情况发生,“黑视”在何处最严重?(不考虑空气阻力,g 取10 m/s 2) 解析:(1)在最高点的向心力为2mg ,速度为v 1 2mg=Rv m 21,v 1=501022⨯⨯=gR m/s=1010 m/s. 在最低点:2121mv +mgh=2221mv v 2=gh v 221+,h=2Rv 2=501041000421⨯⨯+=+gR v m/s=3010 m/s这时压力F N =mg+F 向=mg+Rv m 22=4 200 N. (2)由于超重,血压降低,脑部缺血造成“黑视”,在最低点时最严重.答案:见解析。
【高中物理】高中物理必修二第五章知识点:曲线运动

【高中物理】高中物理必修二第五章知识点:曲线运动
高中物理是高中学习的重要学科,整理了高中物理知识点,供广大高中生学习参考,希望有所帮助!
>>>
高中物理
必修两章中的知识点摘要<<
高中英语
;<
第五章曲线运动
一、知识点
(一)曲线运动的条件:合外力与运动方向不在一条直线上
(二)曲线运动的研究方法:运动的合成与分解(平行四边形规则、三角形规则)
(三)曲线运动的分类:合力的性质(匀变速:平抛运动、非匀变速曲线:匀速圆周运动)
(四)匀速圆周运动
1受力分析,所受合力的特点:向心力大小、方向
2向心加速度、线速度和角速度的定义(文本和定义)
3向心力的公式(多角度的:线速度、角速度、周期、频率、转)
(五)水平投掷动作
1受力分析,只受重力
2.速度,水平方向和垂直方向的分速度表达式;位移,水平和垂直位移的表达式
3速度与水平方向的夹角、位移与水平方向的夹角
(五)离心运动的定义和条件
二、考察内容、要求及方式
1.判断曲线运动的性质:澄清曲线运动的条件和牛耳定律(多项选择题)
2匀速圆周运动中的动态变化:熟练掌握匀速圆周运动各物理量之间的关系式(选择、填空)
3匀速圆周运动中物理量的计算:力分析、向心加速度的几种表达式和合力提供的向心力(计算问题)
3运动的合成与分解:分运动与和运动的等时性、等效性(选择、填空)
4、水平投掷运动的相关性:水平投掷运动中速度、位移和夹角的计算,包括运动和运动的等时性和等价性(选择、填空和计算)
5离心运动:临界条件、最大静摩擦力、匀速圆周运动相关计算(选择、计算)。
高中物理必修二知识点总结(人教版)
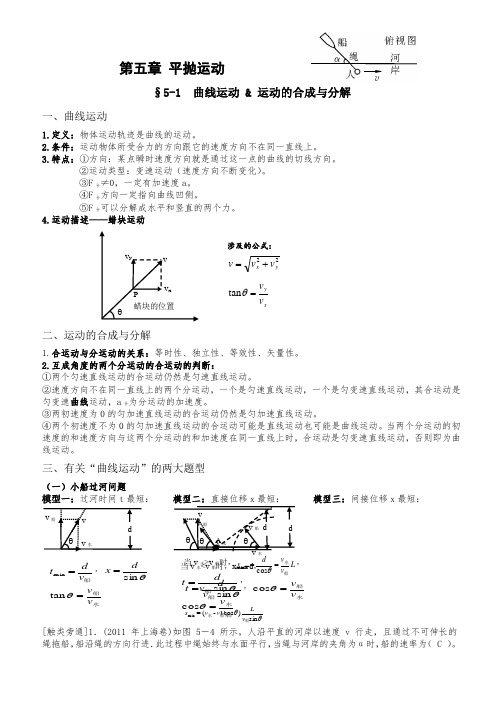
P蜡块的位置v v xv y 涉及的公式:22y x v v v += xy v v =θtan θv v 水 v 船 θ 船v d t =m in ,θsin d x = 水船v v=θtand第五章 平抛运动§5-1 曲线运动 & 运动的合成与分解一、曲线运动1.定义:物体运动轨迹是曲线的运动。
2.条件:运动物体所受合力的方向跟它的速度方向不在同一直线上。
3.特点:①方向:某点瞬时速度方向就是通过这一点的曲线的切线方向。
②运动类型:变速运动(速度方向不断变化)。
③F 合≠0,一定有加速度a 。
④F 合方向一定指向曲线凹侧。
⑤F 合可以分解成水平和竖直的两个力。
4.运动描述——蜡块运动二、运动的合成与分解1.合运动与分运动的关系:等时性、独立性、等效性、矢量性。
2.互成角度的两个分运动的合运动的判断:①两个匀速直线运动的合运动仍然是匀速直线运动。
②速度方向不在同一直线上的两个分运动,一个是匀速直线运动,一个是匀变速直线运动,其合运动是匀变速曲线运动,a 合为分运动的加速度。
③两初速度为0的匀加速直线运动的合运动仍然是匀加速直线运动。
④两个初速度不为0的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。
当两个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时,合运动是匀变速直线运动,否则即为曲线运动。
三、有关“曲线运动”的两大题型(一)小船过河问题模型一:过河时间t 最短: 模型二:直接位移x 最短: 模型三:间接位移x 最短:[触类旁通]1.(2011 年上海卷)如图 5-4 所示,人沿平直的河岸以速度 v 行走,且通过不可伸长的绳拖船,船沿绳的方向行进.此过程中绳始终与水面平行,当绳与河岸的夹角为α时,船的速率为( C )。
d v v 水v θ 当v 水<v 船时,x min =d , θsin 船v d t =, 船水v v =θcos A v 水v 船 θ 当v 水>v 船时,L v v d x 船水==θcos min , θsin 船v d t =,水船v v =θcos θθsin )cos -(min 船船水v L v v s = θ v 船 dαsin .v A αsin .vB αcos .vC αcos .v D解析:依题意,船沿着绳子的方向前进,即船的速度总是沿着绳子的,根据绳子两端连接的物体在绳子方向上的投影速度相同,可知人的速度 v 在绳子方向上的分量等于船速,故 v 船=v cos α,C 正确. 2.(2011 年江苏卷)如图 5-5 所示,甲、乙两同学从河中O 点出发,分别沿直线游到 A 点和 B 点后,立即沿原路线返回到 O 点,OA 、OB 分别与水流方向平行和垂直,且 OA =OB.若水流速度不变,两人在静水中游速相等,则他们所用时间 t 甲、t 乙的大小关系为(C)A .t 甲<t 乙B .t 甲=t 乙C .t 甲>t 乙D .无法确定解析:设游速为v ,水速为v 0,OA =OB =l ,则t 甲=l v +v 0+l v -v 0;乙沿OB运动,乙的速度矢量图如图4所示,合速度必须沿OB 方向,则t 乙=2·l v 2-v 2,联立解得t 甲>t 乙,C 正确. (二)绳杆问题(连带运动问题)1、实质:合运动的识别与合运动的分解。
高中物理必修二知识点总结:第五章曲线运动

高中物理必修二知识点总结:第五章曲线运动(人教版)这一章是在前边几章的学习基础之上,研究一种更为复杂的运动方式:曲线运动。
这也是运动学中更为重要的一部分内容,本章的重难点就在于抛体运动、圆周运动。
考试的要求:Ⅰ、对所学知识要知道其含义,并能在有关的问题中识别并直接运用,相当于课程标准中的“了解”和“认识”。
Ⅱ、能够理解所学知识的确切含义以及和其他知识的联系,能够解释,在实际问题的分析、综合、推理、和判断等过程中加以运用,相当于课程标准的“理解”,“应用”。
要求Ⅱ:曲线运动、抛体运动、圆周运动。
知识构建:新知归纳:一、曲线运动●曲线运动1、定义:物体的运动轨迹不是直线的运动称为曲线运动。
2.物体做曲线运动的条件(1)当物体所受合力的方向跟它的速度方向不在同一直线上时,这个合力总能产生一个改变速度方向的效果,物体就一定做曲线运动。
(2)当物体做曲线运动时,它的合力所产生的加速度的方向与速度方向也不在同一直线上。
(3)物体的运动状态是由其受力条件及初始运动状态共同确定的.2、曲线运动的特点:质点在某一点的速度方向,就是通过该点的曲线的切线方向.质点的速度方向时刻在改变,所以曲线运动一定是变速运动。
物体运动的性质由加速度决定(加速度为零时物体静止或做匀速运动;加速度恒定时物体做匀变速运动;加速度变化时物体做变加速运动)。
3、曲线运动的速度方向(1)在曲线运动中,运动质点在某一点的瞬时速度方向,就是通过这一点的曲线切线的方向。
(2)曲线运动的速度方向时刻改变,无论速度的大小变或不变,运动的速度总是变化的,故曲线运动是一种变速运动。
4、曲线运动的轨迹:作曲线运动的物体,其轨迹向合外力所指向的一方弯曲,若已知物体的运动轨迹,可判断出物体所受合外力的大致方向,如平抛运动的轨迹向下弯曲,圆周运动的轨迹总是向圆心弯曲等。
●曲线运动常见的类型:(1)a=0:匀速直线运动或静止。
(2)a恒定:性质为匀变速运动,分为:①v、a同向,匀加速直线运动;②v、a反向,匀减速直线运动;③v、a 成角度,匀变速曲线运动(轨迹在v、a之间,和速度v的方向相切,方向逐渐向a的方向接近,但不可能达到。
高一物理人教版必修二第五章曲线运动概念总结

第五章 曲线运动一、曲线运动:质点的运动轨迹是曲线的运动;1、曲线运动中速度的方向是时刻改变的,质点在某一点(或某一时刻)的速度的方向是在曲线的这一点的切线方向.2、物体做直线运动的条件:物体所受合外力为零或所受合外力方向和物体的运动方向在同一直线上.物体做曲线运动的条件:质点所受合外力的方向与其运动方向不在同一条直线上;且轨迹向其受力方向偏折,运动轨迹在v 、a 之间,和速度v 的方向相切,方向逐渐向a 的方向接近,但不可能达到。
[注意]1)当物体做曲线运动时,它的合力所产生的加速度的方向与速度方向也不在同一直线上;2)物体的运动状态是由其受力条件及初始运动状态共同确定的;①物体运动的性质由加速度决定(加速度为零时物体静止或做匀速运动;加速度恒定时物体做匀变速运动;加速度变化时物体做变加速运动)。
②物体运动的轨迹(直线还是曲线)由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动;速度和加速度方向成角度时物体做曲线运动), 3、曲线运动的特点:1)曲线运动一定是变速运动;质点的路程总大于位移大小,其平均速率大小大于平均速度大小;质点作曲线运动时,受到合外力和相应的速度一定不为零;2)曲线运动的轨迹是一条曲线,其轨迹轨迹始终夹在合外力方向(加速度方向)与速度方向之间,而且向合外力的方向弯曲,即合外力(加速度)指向轨迹凹侧。
3)曲线运动中物体所受合外力沿切线方向的分力使物体速度的大小发生变化,沿法线方向的分力使物体的速度方向发生变化。
[注意]:①做曲线运动的物体所受合外力是变化的.(×)[此力不一定变化]②两个分运动是匀速直线运动,则合运动是匀速直线运动或静止. ③已知两个分运动都是匀加(互成一定角度,不共线)则合运动是:a .合合与v a 共线是匀加直线运动; b.合合与v a 不共线是匀变曲线运动. ④一个分运动是匀速,另一个是匀加(初速度为零),则合运动:a .合合与v a 共线⎪⎩⎪⎨⎧-=+=atv v atv v 00合合反向,同向, b.合合与v a 不共线:匀变速曲线运动. 4、曲线运动一定是变速运动;5、曲线运动的加速度(合外力)与其速度方向不在同一条直线上;6、力的作用:(1)力的方向与运动方向一致时,力只能改变速度的大小,不能改变速度的方向,物体只能做直线运动; (2)力的方向与运动方向垂直时,力只能改变速度的方向,不能改变速度的大小。
(完整)高中物理必修二第五章曲线运动知识点总结,推荐文档

船一、曲线运动曲线运动知识点总结(MYX )1、所有物体的运动从轨迹的不同可以分为两大类:直线运动和曲线运动。
2、曲线运动的产生条件:合外力方向与速度方向不共线(≠0°,≠180°)性质:变速运动 3、曲线运动的速度方向:某点的瞬时速度方向就是轨迹上该点的切线方向。
4、曲线运动一定收到合外力,“拐弯必受力,”合外力方向:指向轨迹的凹侧。
若合外力方向与速度方向夹角为 θ,特点:当 0°<θ<90°,速度增大;当 0°<θ<180°,速度增大; θ=90°,速度大小不变。
5、曲线运动加速度:与合外力同向,切向加速度改变速度大小;径向加速度改变速度方向。
6、关于运动的合成与分解(1) 合运动与分运动定义:如果物体同时参与了几个运动,那么物体实际发生的运动就叫做那几个运动的合运动。
那几个运动叫做这个实际运动的分运动.特征:① 等时性;② 独立性;③ 等效性;④ 同一性。
(2) 运动的合成与分解的几种情况: ①两个任意角度的匀速直线运动的合运动为匀速直线运动。
②一个匀速直线运动和一个匀变速直线运动的合运动为匀变速运动,当二者共线时轨迹为直线,不共线时轨迹为曲线。
③两个匀变速直线运动合成时,当合速度与合加速度共线时,合运动为匀变速直线运动;当合速度与合加速度不共线时,合运动为曲线运动。
二、小船过河问题1、渡河时间最少:无论船速与水速谁大谁小,均是船头与河岸垂直,渡河时间t min沿v 合 的方向。
2、位移最小:d =,合速度方向v 船v 水 ①若v > v ,船头偏向上游,使得合速度垂直于河岸,船头偏上上游的角度为cos= ,最小位移船水船为l min= d 。
②若v 船水< v ,则无论船的航向如何,总是被水冲向下游,则当船速与合速度垂直时渡河位移最小,船v 船d v 水 头偏向上游的角度为cos =,过河最小位移为l min =v 水cos= d v 。
高中学习物理必修2第五章节曲线运动知识点计划
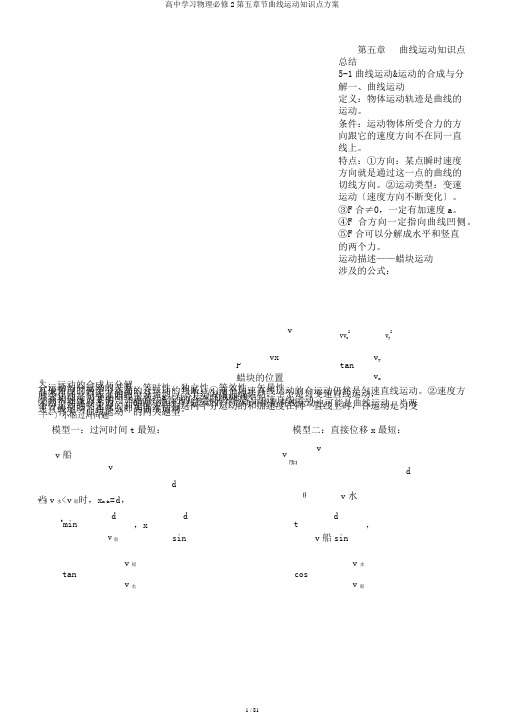
第五章 曲线运动知识点总结5-1曲线运动&运动的合成与分解一、曲线运动定义:物体运动轨迹是曲线的运动。
条件:运动物体所受合力的方向跟它的速度方向不在同一直线上。
特点:①方向:某点瞬时速度方向就是通过这一点的曲线的切线方向。
②运动类型:变速运动〔速度方向不断变化〕。
③F 合≠0,一定有加速度a 。
④F 合方向一定指向曲线凹侧。
⑤F 合可以分解成水平和竖直的两个力。
运动描述——蜡块运动 涉及的公式:vvv x 2v y 2vxv yP tan蜡块的位置v x θ二、运动的合成与分解合运动与分运动的关系:等时性、独立性、等效性、矢量性。
互成角度的两个分运动的合运动的判断:①两个匀速直线运动的合运动仍然是匀速直线运动。
②速度方向不在同一直线上的两个分运动,一个是匀速直线运动,一个是匀变速直线运动, 其合运动是匀变速曲线运动,a 合为分运动的加速度。
③两初速度为0的匀加速直线运动的合运动仍然是匀加速直线运动。
④两个初速度不为 0的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。
当两 个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时,合运动是匀变 速直线运动,否那么即为曲线运动。
三、有关“曲线运动〞的两大题型 〔一〕小船过河问题模型一:过河时间t 最短: 模型二:直接位移x 最短:v 船vvv船ddθv 水 v 水 当v 水<v 船时,x min =d ,tmind d td,v 船,xv 船sinsintanv 船cosv 水v 水v 船模型三:间接位移x最短:v船v船dθAθv水当v水>v船时,x min dcostd,cos v船sinsmin(v水-v船cos)Lv船sinv水L,v船v船v水〔二〕绳杆问题(连带运动问题)1、实质:合运动的识别与合运动的分解。
2、关键:①物体的实际运动是合速度,分速度的方向要按实际运动效果确定;②沿绳〔或杆〕方向的分速度大小相等。
高一物理必修二第五章:曲线运动知识框架
曲线运动知识框架图
曲
线
运
动
一.无支撑物物体在竖直平面内做圆周运动
例1:质量为
要满足什么条件
例2:假设上题中的小球在最高点时速度大小为
例3:
动,那么小球在最高点的最小速度是多少
小球对轨道内壁的压力大小是多少?
二.有支撑物物体在竖直面内做圆周运动
例1:质量为1kg 的小球固定在长为0.4m的轻质木杆的一端,小球绕木杆的另一端在竖直面内做圆周运动,当小球运动到最高点时,小球与杆之间无弹力作用,求小球的速度大小是多少? (g=10m/s2)
例2:假设上题中小球在最高点的速度大小是6m/s时,求小球与杆的弹力的大小与方向? (g=10m/s2)
例3:假设上题中小球在最高点的速度大小是1m/s时,求小球与杆的弹力的大小和方向? (g=10m/s2)
例4: 假如把上题中的小球放在竖直面内半径为的光滑圆管轨道中,使小球做圆周运动,当它运动到圆管的最高点时,它与圆管的上壁和下壁均无挤压,求此时小球的速度大小是多少? (g=10m/s2)
例5:上题中的小球运动到最高点时速度为12m/s,求小球与管壁产生弹力的大小与方向? (g=10m/s2)
例6:上题中的小球运动到最高点时速度为2m/s,求小球与管壁产生弹力的大小与方
向? (g=10m/s2)
第 1 页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品 文档 欢迎 下载船v d t =m in ,θsin dx =水船v v =θtan第五章 曲线运动知识点总结§5-1 曲线运动 & 运动的合成与分解 一、曲线运动1.定义:物体运动轨迹是曲线的运动。
2.条件:运动物体所受合力的方向跟它的速度方向不在同一直线上。
3.特点:①方向:某点瞬时速度方向就是通过这一点的曲线的切线方向。
②运动类型:变速运动(速度方向不断变化)。
③F 合≠0,一定有加速度a 。
④F 合方向一定指向曲线凹侧。
⑤F 合可以分解成水平和竖直的两个力。
4.运动描述——蜡块运动二、运动的合成与分解1.合运动与分运动的关系:等时性、独立性、等效性、矢量性。
2.互成角度的两个分运动的合运动的判断:①两个匀速直线运动的合运动仍然是匀速直线运动。
②速度方向不在同一直线上的两个分运动,一个是匀速直线运动,一个是匀变速直线运动,其合运动是匀变速曲线运动,a 合为分运动的加速度。
③两初速度为0的匀加速直线运动的合运动仍然是匀加速直线运动。
④两个初速度不为0的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。
当两个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时,合运动是匀变速直线运动,否则即为曲线运动。
三、有关“曲线运动”的两大题型(一)小船过河问题模型一:过河时间t 最短: 模型二:直接位移x 最短:当v 水<v 船时,x min =d ,θsin 船v dt =,船水v v =θcos精品 文档 欢迎 下载α模型三:间接位移x 最短:(二)绳杆问题(连带运动问题)1、实质:合运动的识别与合运动的分解。
2、关键:①物体的实际运动是合速度,分速度的方向要按实际运动效果确定;②沿绳(或杆)方向的分速度大小相等。
模型四:如图甲,绳子一头连着物体B ,一头拉小船A ,这时船的运动方向不沿绳子。
甲 乙处理方法:如图乙,把小船的速度v A 沿绳方向和垂直于绳的方向分解为v 1和v 2,v 1就是拉绳的速度,v A 就是小船的实际速度。
§5-2 平抛运动 & 类平抛运动 一、抛体运动1.定义:以一定的速度将物体抛出,在空气阻力可以忽略的情况下,物体只受重力的作用,它的运动即为抛体运动。
2.条件:①物体具有初速度;②运动过程中只受G 。
二、平抛运动1.定义:如果物体运动的初速度是沿水平方向的,这个运动就叫做平抛运动。
2.条件:①物体具有水平方向的加速度;②运动过程中只受G 。
3.处理方法:平抛运动可以看作两个分运动的合运动:一个是水平方向的匀速直线运动,一个是竖直方向的自由落体运动。
4.规律:Av 水v 船 θ 当v 水>v 船时,L v v dx 船水==θcos min , θsin 船v dt =,水船v v =θcosθθsin )cos -(min 船船水v Lv v s =θv 船 d精品 文档 欢迎 下载5.应用结论——影响做平抛运动的物体的飞行时间、射程及落地速度的因素a 、飞行时间:ght 2=,t 与物体下落高度h 有关,与初速度v 0无关。
b 、水平射程:,200ghv t v x ==由v 0和h 共同决定。
c 、落地速度:gh v v v v y 220220+=+=,v 由v 0和v y 共同决定。
三、平抛运动及类平抛运动常见问题“斜面问题:§5-3 圆周运动 & 向心力 & 生活中常见圆周运动 一、匀速圆周运动1.定义:物体的运动轨迹是圆的运动叫做圆周运动,物体运动的线速度大小不变的圆周运动即为匀速圆周 运动。
2.特点:①轨迹是圆;②线速度、加速度均大小不变,方向不断改变,故属于加速度改变的(1)位移:222200011,,()(),tan .222gt x v t y gt s v t gt v α===+= (2)速度:0v v x=,gt v y =,22)(gt v v +=,0tan v gt=θ (3)推论:①从抛出点开始,任意时刻速度偏向角θ的正切值等于 位移偏向角α的正切值的两倍。
证明如下:0tan gt v θ=,20012tan .2gtgt v t v α== tan θ=2tan α ②从抛出点开始,任意时刻速度的反向延长线对应的水平位移的交点为此水平位移的中点,即.2tan xy=θ如果物体落在斜面上,则位移偏向角与斜面倾斜角相等。
处理方法:1.沿水平方向的匀速运动和竖直方向的自由落体运动;2.沿斜面方向的匀加速运动和垂直斜面方向的竖直上抛运动。
考点一:物体从A 运动到B 的时间:根据gv t gt y t v x θtan 221,020=⇒== 考点二:B 点的速度v B 及其与v 0的夹角α: )tan 2arctan(,tan 41)(20220θαθ=+=+=v gt v v考点三:A 、B 之间的距离s :θθθcos tan 2cos 20g v x s ==精品 文档 欢迎 下载.2,2222R vT n T R v nR R T R v πππωππω====−−→−===变形变速曲线运动,匀速圆周运动的角速度恒定;③匀速圆周运动发生条件是质点受到大小不变、方向始终与速度方向垂直的合外力;④匀速圆周运动的运动状态周而复始地出现,匀速圆周运动具有周期性。
3.描述圆周运动的物理量:(1)线速度v 是描述质点沿圆周运动快慢的物理量,是矢量;其方向沿轨迹切线,国际单位制中单位符号是m/s ,匀速圆周运动中,v 的大小不变,方向却一直在变;(2)角速度ω是描述质点绕圆心转动快慢的物理量,是矢量;国际单位符号是rad /s ; (3)周期T 是质点沿圆周运动一周所用时间,在国际单位制中单位符号是s ;(4)频率f 是质点在单位时间内完成一个完整圆周运动的次数,在国际单位制中单位符号是Hz ;(5)转速n 是质点在单位时间内转过的圈数,单位符号为r/s ,以及r/min . 4.各运动参量之间的转换关系:5.三种常见的转动装置及其特点:模型一:共轴传动 模型二:皮带传动模型三:齿轮传动B A B A BA T T r R v v ===,,ωωr R T T R r v v A B A B B A ===,,ωωABB A B A n n r r T T v v ωω====2121,rv一定ω一定.)2(22222rnrTvrrvanππωω=⎪⎭⎫⎝⎛====二、向心加速度1.定义:任何做匀速圆周运动的物体的加速度都指向圆心,这个加速度叫向心加速度。
注:并不是任何情况下,向心加速度的方向都是指向圆心。
当物体做变速圆周运动时,向心加速度的一个分加速度指向圆心。
2.方向:在匀速圆周运动中,始终指向圆心,始终与线速度的方向垂直。
向心加速度只改变线速度的方向而非大小。
3.意义:描述圆周运动速度方向方向改变快慢的物理量。
4.公式:5.三、向心力1.定义:做圆周运动的物体所受到的沿着半径指向圆心的合力,叫做向心力。
2.方向:总是指向圆心。
3.公式:.)2(22222rnmrTmmvrmrvmFnππωω=⎪⎭⎫⎝⎛====4.几个注意点:①向心力的方向总是指向圆心,它的方向时刻在变化,虽然它的大小不变,但是向心力也是变力。
②在受力分析时,只分析性质力,而不分析效果力,因此在受力分析是,不要加上向心力。
③描述做匀速圆周运动的物体时,不能说该物体受向心力,而是说该物体受到什么力,这几个力的合力充当或提供向心力。
四、变速圆周运动的处理方法1.特点:线速度、向心力、向心加速度的大小和方向均变化。
2.动力学方程:合外力沿法线方向的分力提供向心力:rmrvmFn22ω==。
合外力沿切线方向的分力产生切线加速度:FT=mωaT。
3.离心运动:(1)当物体实际受到的沿半径方向的合力满足F供=F需=mω2r时,物体做圆周运动;当F供<F 需=mω2r时,物体做离心运动。
(2)离心运动并不是受“离心力”的作用产生的运动,而是惯性的表现,是F供<F需的结果;离心运动也不是沿半径方向向外远离圆心的运动。
(3)精品文档欢迎下载精品 文档 欢迎 下载用细绳拴一小球在竖直平面内转动绳对球只有拉力①若F =0,则mg =mv2R ,v =gR②若F ≠0,则v>gR小球固定在轻杆的一端在竖直平面内转动杆对球可以是拉力也可以是支持力①若F =0,则mg =mv 2R,v =gR②若F 向下,则mg +F =m v 2R ,v>gR③若F 向上,则mg -F =mv 2R或mg -F =0,则0≤v<gR小球在竖直细管内转动管对球的弹力F N 可以向上也可以向下依据mg =mv 20R判断,若v =v 0,F N =0;若v<v 0,F N 向上;若v>v 0,F N 向下球壳外的小球在最高点时弹力F N 的方向向上①如果刚好能通过球壳的最高点A ,则v A =0,F N =mg②如果到达某点后离开球壳面,该点处小球受到壳面的弹力F N =0,之后改做斜抛运动,若在最高点离开则为平抛运动(一)解题步骤:①明确研究对象; ②定圆心找半径;③对研究对象进行受力分析; ④对外力进行正交分解;⑤列方程:将与和物体在同一圆周运动平面上的力或其分力代数运算后,另得数等于向心力;⑥解方程并对结果进行必要的讨论。
(二)典型模型:I 、圆周运动中的动力学问题谈一谈:圆周运动问题属于一般的动力学问题,无非是由物体的受力情况确定物体的运动情况,或者由物体的运动情况求解物体的受力情况。
解题思路就是,以加速度为纽带,运用那个牛顿第二定律和运动学公式列方程,求解并讨论。
模型一:火车转弯问题:NF 合 mg hLa 、 涉及公式:Lh mgmg F =≈=θθsin mgtan 合① Rv m F 20=合②,由①②得:LRghv =0。
b 、分析:设转弯时火车的行驶速度为v ,则:(1)若v>v 0,外轨道对火车轮缘有挤压作用; (2)若v<v 0,内轨道对火车轮缘有挤压作用。
精品 文档 欢迎 下载模型二:汽车过拱桥问题:II 、圆周运动的临界问题A.常见竖直平面内圆周运动的最高点的临界问题谈一谈:竖直平面内的圆周运动是典型的变速圆周运动。
对于物体在竖直平面内做变速圆周运动的问题,中学物理只研究问题通过最高点和最低点的情况,并且经常出现有关最高点的临界问题。
模型三:轻绳约束、单轨约束条件下,小球过圆周最高点:模型四:轻杆约束、双轨约束条件下,小球过圆周最高点:a 、涉及公式:R v m F mg N 2=-,所以当mg Rv m mg F N <-=2,此时汽车处于失重状态,而且v 越大越明显,因此汽车过拱桥时不宜告诉行驶。
