六年级数学下册《正比例》知识点
人教版六年级数学下册第四单元《正比例和反比例》(复习课件)

汽车所行路程与相应耗油量是两种相关联的量,耗油量
随着所行路程的变化而变化。所行路程增加,耗油量随
着增加;所行路程减少,耗油量随着减少。
4.已知y与x成正比例关系,在下表的空格中填写合
适的数。(选题源于教材P49第4题)
5
15
8
3
12.5
25
50
5.同一时间、同一地点测得3棵树的树高及其影长如
下表。(选题源于教材P50第5题)
长劲鹿:0.8×18=14.4(千米)
答:斑马18分钟跑了21.6千米,
长颈鹿跑了14.4千米。
下面的图象表示斑马和长颈鹿的奔跑情况。
(3)从图象上看,斑马跑得快还是长颈鹿跑得快?
从图像上看,10分钟时,斑马跑了
12千米,长劲鹿跑了8千米。
答:斑马跑得快。
判断下面各题中的两种量是否成反比例关系,并说明理由。
面积与所需地砖数量如下表。
所需地砖数量与每块地砖的面积是否成反比例?
为什么?(选题源于教材P51第8题)
成反比例关系。
因为所需地砖数量与每块地砖的面积的乘
积等于教室的面积,而教室的面积一定,
所以所需地砖数量与每块地砖的面积成反
比例关系。
2.食品加工厂准备把一批新酿的醋装瓶运往商店。
所装瓶数与每瓶容量是否成反比例关系?为什么?
有x、y、z三个相关联的量,并有xy=z。
(1)当z一定时,x与y成
比例关系。
反
xy=z
(一定) 即xy的积一定,则xy成反比例。
正
(2)当x一定时,z与y成
比例关系。
z
=x
xy=z
则zy成正比例。
y (一定),
正 比例关系。
北师版六年级下册数学第4单元 正比例与反比例 正比例

易错点: y
x
=k(一定),y和x成正比例。
作业
请完成《典中点》的“应用提升练”和“思维 拓展练”习题,具体内容见习题课件。
第2课时正比例
探究点2 判断两个量是否成正比例的方法
圆的面积与半径成正比例吗?
3
圆的面积
3.14
半径
1
12.56 2
28.26 3
圆的面积与半径的比值不相等。
圆的面积与半径不成正比例。
第四单元正比例与反比例
正比例(建议两课时完成)
BS六年级下册
1 课堂探究点
(1)正比例的意义 (2)判断两个量是否成正比例的方法
2 课时流程
探索 新知
课堂 小结
当堂 检测
课后 作业
探究点1 正比例的意义
下面是正方形周长与边长、面积与边长之间的变化情况,
把表格填写完整,并说说你分别发现了什么。
边长/cm
160 数量/kg 15 18 16 20 总价/元 120 144 128 160
数量,总价。
比值是8,比值表示单价。 成正比例关系。
归纳总结:
像这样,路程和时间两个量,时间变化, 所行驶的路程也随着变化,而且路程与时 间的比值(也就是速度)一定,我们就说 路程和时间成正比例。
小试牛刀(教材P42练一练) 1. 学校科学小组在同一时间、同一地点进行观察实验,测 2. 得竹竿的高与竿影的长如下表。
乐乐和爸爸的年龄变化情况如下,把表填写完整。 乐乐的年龄/岁 6 7 8 9 10 11 爸爸的年龄/岁 32 33 34 35 36 37
他们的年龄成正比例吗?为什么?
乐乐的年龄与爸爸年龄的比值不是一个确定的值, 所以,他们的年龄不成正比例。
六年级下册正比例和反比例数学知识点

六年级下册正比例和反比例数学知识点一、变化的量生活中存在着大量互相依存的变量,一种量变化,另一种量也随着变化。
二、正比例1. 正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果用字母x和y表示两种相关联的量,用字母k表示它们的比值(一定),正比例关系可以表示为:y/x=k(一定)。
2. 应用正比例的意义判断两种量是否成正比例:有些相关联的量,虽然也是一种量随着另一种量的变化而变化,但它们相对应的数的比值不一定,就不成正比例,如被减数与差,正方形的面积与边长等。
三、画一画正比例的图像是一条直线。
四、反比例1. 反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的乘积,反比例的关系式可以表示为:xy=k(一定)。
2. 判断两个量是不是成反比例:要先想这两个量是不是相关联的量;再运用数量关系式进行判断,看这两个量的积是否一定;最后作出结论。
五、观察与探究当两个变量成反比例关系时,所绘成的图像是一条光滑曲线。
六、图形的放缩一幅图放大或缩小,只有按照相同的比来画,画的图才像。
七、比例尺1. 比例尺:图上距离与实际距离的比,叫做这幅图的比例尺。
图上距离=实际距离比例尺实际距离=图上距离比例尺2. 比例尺的分类:比例尺根据实际距离是缩小还是扩大,分为缩小比例尺和放大比例尺。
根据表现形式的不同,比例尺还可分为线段比例尺和数值比例尺。
3. 比例尺的应用:(1)、已知比例尺和图上距离,求实际距离课本、报刊杂志中的成语、名言警句等俯首皆是,但学生写作文运用到文章中的甚少,即使运用也很难做到恰如其分。
为什么?还是没有彻底“记死”的缘故。
要解决这个问题,方法很简单,每天花3-5分钟左右的时间记一条成语、一则名言警句即可。
西师大版六年级下册数学《比例》正比例和反比例说课教学课件复习

(一)比例尺的概念
在绘制比较精细的零 件图时,经常需要把 零件的尺寸按一定的 比放大,你知道这幅 零件图纸的比例尺 2:1表示什么吗?
比例尺2:1表示图上 距离是实际距离的2 倍。实际距离是图
1
上距离的 2 。
为了计算方便,一般把比例尺写成前项或后项是1的形式!
(二)计算一幅图的比例尺
北京到天津的实际距离是120 km,在一幅地图 上量得两地的图上距离是2.4cm。这幅地图的比例尺是 多少?
3 ︰1
2
=
︰4
42 3 9
比例的基本性质
在一个比例中,两个外项的积 等于两个内项的积,叫做比例的基 本性质。
议一议:
3 =9
2
6
1.8 = 0.6
1.5
0.5
综练习
1.猜猜我是谁。 5 ︰ 4=10 ︰?
2 ︰1 55
3 =?︰ 8
拓展练习
用下面的数能组成比例吗? 3 5 6 10
如果a×2=b×5,那么 a:b=( 5):( 2)
不管哪种情况,都需要确定图上距离和实际距离 的比。这就是比例的知识在实际生活中的一种应用。 今天,我们就来学习这方面的知识。
推进新课
1.比例尺的意义。
因为在绘制地图和其它平面图 时,经常要用到图上距离与实 际距离的比,我们就把它起个 名字,叫做比例尺。
图上距离:实际距离=比例尺
有时图上距离与实际距离的比也可以写成分数形式。
观察上面两个比,你发现了 什么?
2︰3=6︰9
表示两个比相等的式子叫做比例
3︰2=9︰6 内项
外项
在一个比例中,两端的两项叫做
比例的外项,中间的两项叫做比
例的内项。
人教版六年级数学下册讲义-正比例和反比例(含答案)

正比例和反比例的课堂讲义教材导入:1.两种相关联的量:一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
总价和数量是成正比例的量,总价与数量成正比例关系。
2.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
高度和底面积是成反比例的量,高度与底面积成反比例关系。
(一)正比例的意义例1 一列火车行驶的时间和所行的路程如下表:填空:1、表中有和两种量,当时间是1小时,路程是当时间是2小时,路程是,这说明时间这种量变化了,路程这种量也。
2、观察表格:我们从左往右观察,时间扩大2倍,对应的路程也倍,时间扩大3倍,对应的路程也倍……从右往左观察,时间缩小8倍,对应的路程也;时间缩小7倍,对应的路程也……通过观察,我们发现路程是随着的变化而变化的。
时间扩大路程也扩大,时间缩小路程也。
它们扩大、缩小的规律是。
3、比值60,实际上是火车的:将这些式子所表示的意义写成一个关系式:路程=速度(—定)。
时间4、小结:通过刚才的观察和分析.我们知道路程和时间是两种 的量。
(两种相关联的量。
)路程和时间这两种量的变化规律是 。
(路程和时间的比的比值(速度)总是一定的。
)【规律方法】理解成正比例的意义。
判断两种量是不是成正比例,分三步:一看它们是不是相关联的两种量;二是看一种量变化,另一种量是不是也随着变化;满足了前面两个条件,再看它们的比值是否一定。
不要省去任何一步。
如果用字母x和y分别表示两种相关联的量,用k表示它们的比值,正比例关系可以用这样的式子来表示:xy= K (一定)。
【变式训练1】【难度分级】 A1、下面各题中哪两种量成正比例?为什么? ①笔记本单价一定,数量和总价。
②汽车行驶速度一定,行驶的路程和时间。
③工作效率一定,工作时间和工作总量。
六年级数学下册正比例和反比例知识点

六年级数学下册正比例和反比例知识点一、内容概要正比例和反比例是六年级数学下册的重要知识点,简单来说正比例表示两个量成正比关系,当一个量增加时,另一个量也会增加,反之亦然。
好比速度和时间是常见的正比例例子,当速度加快时,需要的时间就会减少。
反比例则是当两个量中的其中一个增加时,另一个会减少。
像是你在爬山过程中体力消耗与海拔高度的关系,海拔越高体力消耗越大,反之越省力就是反比例的例子。
掌握这些知识可以帮助我们更好地理解生活中的各种现象,接下来我们将详细解析这两个概念的应用和解题方法。
1. 回顾数学基础知识,为学习正比例和反比例做铺垫亲爱的小朋友们,转眼间我们已经进入了六年级的数学之旅,那么今天我们来一起回顾一下前面学过的数学知识,为接下来要学习的正比例和反比例知识点做好铺垫吧!数学的世界总是充满了神奇的奥秘,让我们一步步走进这个奇妙的世界。
我们知道数学是生活中的一把钥匙,它能帮助我们解决很多有趣的问题。
在学习正比例和反比例之前,我们要先打好基础。
回顾一下我们之前学过的关于数量和数量之间的关系的知识,比如当我们买文具时,文具的数量和总价之间就有一种特殊的关系。
买一支笔和买十支笔的价格是不一样的,这就是数量和价格之间的关系。
这就是我们接下来要学习的正比例和反比例的基础,你们准备好了吗?接下来我们要更深入地去探索这种关系的奥秘!2. 简述正比例和反比例的概念及其在实际生活中的应用反比例呢?它与正比例相反,当一个量变大时,另一个量就会变小。
比如说你在调节电视机的音量和亮度时,通常音量越大,电视屏幕的亮度就越低,因为电视的音量和亮度就是一对反比例关系。
再如开车的时候,车速越慢反而里程消耗越多;一个钟表转得越慢它行走的总圈数就越大等生活中都可以发现反比例的例子。
明白正比例和反比例的概念后,我们就可以更好地理解和解决生活中的很多问题啦!二、正比例知识点我们知道生活中有很多事物之间是有关系的,比如你吃的零食越多,肚子就越容易饱。
人教版六年级下册数学单元知识点归纳——第四单元 比例

4 比 例一、比例的意义表示两个比相等的式子叫做比例。
二、比例的基本性质1.组成比例的四个数,叫做比例的项,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
2.比例的基本性质:在比例里....,.两个外项的积等于两.........个内项的积。
......可以用字母表示比例的基本性质,如果a ∶b=c ∶d ,那么ad=bc 。
3.运用比例的意义和比例的基本性质可以判断两个比是否可以组成比例,也可以解比例。
三、解比例1.求比例中的未知项........,.叫做解比例。
......2.解比例的依据:比例的基本性质.......。
3.解比例的方法:利用比例的基本性质将比例转化..............为外项之积与内项之积相等的等式...............,.再通过解方程求出........未知项的值。
......四、正比例1.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
2.如果用字母y 和x 表示两种相关联的量,用k 表示它们的比值(一定),正比例关系可以表示为=k ..。
3.正比例的图象......:如果把成正比例关系的两个量中相对应的数都看作是一个数对,在方格纸上把写这些数对相对应的点连起来,形成一条射线..;反之,该射线上的每一个点对应的就是正比例关系中两个相关联的量的一组具体值。
五、反比例提示:组成比例的两个比既可以写成带比号的形式,也可以写成分数的形式,但读法相同。
例如:2.4×40=1.6×60提示:如果4个不同的数能组成比例,那么这4个数一共能组成8个不同的比例。
提示:应用比例的基本性质不是解比例唯一的方法,也可以用求比值的方法或其他方法解比例。
总结:判断两种量是否成正比例的方法:先找变量(两种相关联的量),再看定量(两种量是比值一定,还是乘积一定),最后作出判断。
2021年北师大版数学六下第四单元《正比例和反比例》章节知识点、达标训练附解析
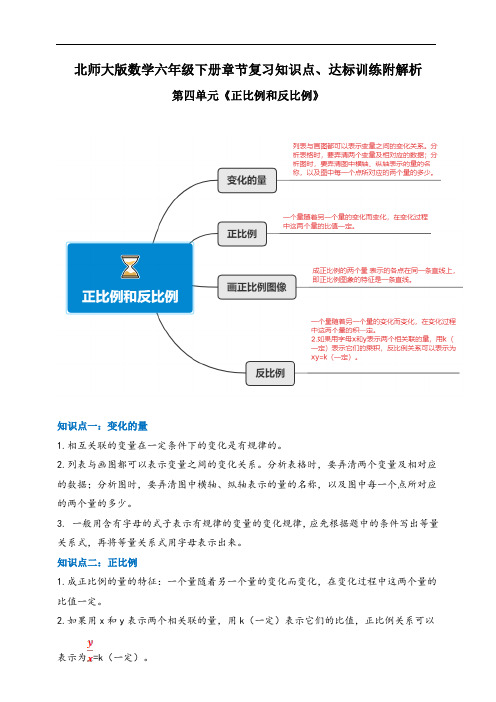
北师大版数学六年级下册章节复习知识点、达标训练附解析第四单元《正比例和反比例》知识点一:变化的量1.相互关联的变量在一定条件下的变化是有规律的。
2.列表与画图都可以表示变量之间的变化关系。
分析表格时,要弄清两个变量及相对应的数据;分析图时,要弄清图中横轴、纵轴表示的量的名称,以及图中每一个点所对应的两个量的多少。
3. 一般用含有字母的式子表示有规律的变量的变化规律,应先根据题中的条件写出等量关系式,再将等量关系式用字母表示出来。
知识点二:正比例1.成正比例的量的特征:一个量随着另一个量的变化而变化,在变化过程中这两个量的比值一定。
2.如果用x和y表示两个相关联的量,用k(一定)表示它们的比值,正比例关系可以表示为=k(一定)。
3.判断两个量是否成正比例的方法(1)首先,要确定这两个量是不是相关联的量(其中一个量是否随着另一个量的变化而变化);(2)其次,要根据两个变量之间的数值对应关系,计算出两个变量每一对数值的比值;(3)最后,根据比值是否一定来判断这两个变量是否成正比例。
知识点三:正比例图像1.成正比例的两个量表示的各点在同一条直线上,即正比例图象的特征是一条直线。
2.从正比例图象中可以得出任意一点所表示的意义。
3. 观察正比例图象时,要先明确横轴、纵轴表示的意义,从图象中可以直观地看出两个量的变化情况,不需要计算,由一个量的值可以直接找到与它对应的另一个量的值。
知识点四:反比例1.成反比例的量的特征:一个量随着另一个量的变化而变化,在变化过程中这两个量的积一定。
2.如果用字母x和y表示两个相关联的量,用k(一定)表示它们的乘积,反比例关系可以表示为xy=k(一定)。
3.判断两个量是否成反比例的方法(1)首先,要确定这两个量是不是相关联的量(其中一个量是否随着另一个量的变化而变化);(2)其次,要根据两个变量之间的数值对应关系,计算出两个变量每一对数值的积;(3)最后,根据积是否一定来判断这两个变量是否成反比例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学下册《正比例》知识点
知识点
正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果用字母x和y表示两种相关联的量,用字母表示它们的比值,正比例关系可以表示为:y/x=。
应用正比例的意义判断两种量是否成正比例:有些相关联的量,虽然也是一种量随着另一种量的变化而变化,但它们相对应的数的比值不一定,就不成正比例,如被减数与差,正方形的面积与边长等。
练习题
工程队修一条水渠,原计划每天修360米,30天修完。
修10天后,每天多修40米,再修多少天就能完成任务?
农场挖一条水渠,头5天挖了180米,照这样速度,又用了16天挖完这条水渠。
这条水渠全长多少米?
40千克小麦能磨面粉32千克,照这样计算,7吨小麦能磨面粉多少千克?
机床厂4天能生产小机床32台,照这样计算,要生产120台小机床需几天?
测量小组把一米长的竹竿直立在地面上,测得它的影子
长度是1.6米,同时测得电线杆的影子长度是4米,求电线杆高多少米?
要测量一棵树的高度,量得树的影子长度是8.4米,同时用一根2米长的标杆直立在地面上,量得影子长度是1.2米,这棵树高是多少米?
一辆汽车从甲地开往乙地,甲乙两地相距405千米,头4小时行驶了180千米,剩下的路程还要行多少小时?
某印刷厂计划三月份印刷课本XX0本,结果上旬就印刷7000本,照这样速度,三月份可以多印刷多少本?
用5辆同样汽车运粮食一次能运22.5吨,照这样计算,要把36吨粮食一次运完,需要增加多少辆这样的汽车?
0、服装厂生产制服,前3个月生产0.48万套,照这样计算,今年可以生产制服多少万套?。
