2.2.2-3习题课---文本资料
【公开课课件】选修二 2-3 第二章 2.2.2 事件的相互独立性课件(共15张PPT)

小结:
( 互斥事件)
求
分类 P(A+B)= P(A) + P (B)
较
正向
复
杂
事
分步P(A·B)= P来自A) ·P (B)( 互独事件)
件
概 率
反向
对立事件的概率
0.6 (1 0.6) (1 0.6) 0.6
0.24 0.24 0.48
答:其中恰由1人击中目标的概率为0.48.
例题: 甲、乙二人各进行1次射击比赛,如
果2人击中目标的概率都是0.6,求: (3)至少有一人击中目标的概率.
解法1:两人各射击一次至少有一人击中目标的概率是
P P( A • B) [P( A • B) P( A • B)] 0.36 0.48 0.84
时发生,根据相互独立事件的概率的乘法公式,得到
P(A•B)=P(A) •P(B)=0.6×0.6=0.36
答:两人都击中目标的概率是0.36
例题: 甲、乙二人各进行1次射击比赛,如
果2人击中目标的概率都是0.6,求: (2) 其中恰有1人击中目标的概率?
解:“二人各射击1次,恰有1人击中目标”包括两种
1 P(A B) A、B中至多有一个发生的概率
中国有句古话“三个臭皮匠,赛过 一个诸葛亮”。今天我们就从数学的角度 来对这个问题进行一下探讨,三个臭皮匠 真的能顶上一个诸葛亮吗?
如果对于某一个问题,诸葛亮能 解决问题的概率是90%,而甲皮匠解 决问题的概率是50%,乙皮匠解决问 题的概率是50%,丙皮匠解决问题的 概率是60%,那么需要多少个皮匠才 能赛过一个诸葛亮呢?
解法2:两人都未击中的概率是 P(A • B) P(A) • P(B)
第二章2.2.2事件的相互独立性习题课

[学业水平训练]1.(2014·福州八县市高二期末联考)抛掷3枚质地均匀的硬币,A ={既有正面向上又有反面向上},B ={至多有一个反面向上},则A 与B 关系是( )A .互斥事件B .对立事件C .相互独立事件D .不相互独立事件解析:选C.由已知,有P (A )=1-28=34,P (B )=1-48=12,P (AB )=38,满足P (AB )=P (A )P (B ),则事件A 与事件B 相互独立,故选C.2.甲、乙两人独立地解同一问题,甲解出这个问题的概率是14,乙解出这个问题的概率是12,那么其中至少有1人解出这个问题的概率是( ) A.34 B.18 C.78 D.58解析:选D.设至少有1人解出这个问题的概率是P ,则由题意知,(1-14)(1-12)=1-P ,∴P =58.3.如图所示,在两个圆盘中,指针落在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是( )A.49B.29C.23D.13解析:选A.左边转盘指针落在奇数区域的概率为46=23,右边转盘指针落在奇数区域的概率为23,∴两个指针同时落在奇数区域的概率为23×23=49.4.(2014·九江检测)某大街在甲、乙、丙三处设有红、绿灯,汽车在这三处因遇绿灯而通行的概率分别为13、12、23,则汽车在这三处因遇红灯而停车一次的概率为( )A.19B.16C.13D.718解析:选D.设汽车分别在甲、乙、丙三处通行为事件A 、B 、C ,则P (A )=13,P (B )=12,P (C )=23,停车一次即为事件A BC +A B C +A B C 的发生,故概率为P =(1-13)×12×23+13×(1-12)×23+13×12×(1-23)=718.5.(2014·东莞调研)从甲袋中摸出一个红球的概率是13,从乙袋中摸出一个红球的概率是12,从两袋各摸出一个球,则23等于( ) A .2个球不都是红球的概率 B .2个球都是红球的概率 C .至少有1个红球的概率D .2个球中恰有1个红球的概率解析:选C.分别记从甲、乙袋中摸出一个红球为事件A 、B ,则P (A )=13,P (B )=12,由于A 、B 相互独立,所以1-P (A )P (B )=1-23×12=23.根据互斥事件可知C 正确.6.(2014·铜陵质检)在甲盒内的200个螺杆中有160个是A 型,在乙盒内的240个螺母中有180个是A 型.若从甲、乙两盒内各取一个,则能配成A 型螺栓的概率为________.解析:从甲盒内取一个A 型螺杆记为事件M ,从乙盒内取一个A 型螺母记为事件N ,因事件M 、N 相互独立,则能配成A 型螺栓(即一个A 型螺杆与一个A 型螺母)的概率为P (MN )=P (M )P (N )=160200×180240=35.答案:357.已知P (A )=0.3,P (B )=0.5,当事件A ,B 相互独立时,P (A ∪B )=________,P (A |B )=________.解析:因为A 、B 相互独立,所以P (A ∪B )=P (A )+P (B )-P (A )·P (B )=0.3+0.5-0.3×0.5=0.65,P (A |B )=P (A )=0.3. 答案:0.65 0.38.如图所示,荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍.假设现在青蛙在A 叶上,则跳三次之后停在A 叶上的概率是________.解析:由已知逆时针跳一次的概率为23,顺时针跳一次的概率为13.则逆时针跳三次停在A上的概率为P 1=23×23×23=827,顺时针跳三次停在A 上的概率为P 2=13×13×13=127.所以跳三次之后停在A 上的概率为P =P 1+P 2=827+127=13.答案:139.某班甲、乙、丙三名同学竞选班委,甲当选的概率为45,乙当选的概率为35,丙当选的概率为710.(1)求恰有一名同学当选的概率; (2)求至多两人当选的概率.解:设甲、乙、丙当选的事件分别为A ,B ,C ,则有P (A )=45,P (B )=35,P (C )=710.(1)因为事件A ,B ,C 相互独立,恰有一名同学当选的概率为 P (A B C )+P (A B C )+P (A B C )=P (A )P (B )P (C )+P (A )P (B )P (C )+P (A )P (B )·P (C )=45×25×310+15×35×310+15×25×710=47250.(2)至多有两人当选的概率为1-P (ABC )=1-P (A )P (B )P (C )=1-45×35×710=83125.10.(2014·石家庄高二检测)某公司招聘员工,指定三门考试课程,有两种考试方案: 方案一:考三门课程至少有两门及格为考试通过;方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.假设某应聘者对三门指定课程考试及格的概率分别为0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.(1)求该应聘者用方案一通过的概率; (2)求该应聘者用方案二通过的概率.解:记“应聘者对三门考试及格的事件”分别为A ,B ,C . P (A )=0.5,P (B )=0.6,P (C )=0.9. (1)该应聘者用方案一通过的概率是P 1=P (A B C )+P (A BC )+P (A B C )+P (ABC )=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9=0.03+0.27+0.18+0.27=0.75.(2)应聘者用方案二通过的概率P 2=13P (AB )+13P (BC )+13P (AC )=13(0.5×0.6+0.6×0.9+0.5×0.9) =13×1.29=0.43. [高考水平训练]1.设两个独立事件A 和B 都不发生的概率为19,A 发生B 不发生的概率与B 发生A 不发生的概率相同,则事件A 发生的概率P (A )是( )A.29B.118C.13D.23解析:选D.由题意,P (A )·P (B )=19,P (A )·P (B )=P (A )·P (B ).设P (A )=x ,P (B )=y , 则⎩⎪⎨⎪⎧ (1-x )(1-y )=19,(1-x )y =x (1-y ).即⎩⎪⎨⎪⎧1-x -y +xy =19,x =y ,∴x 2-2x +1=19,∴x -1=-13,或x -1=13(舍去),∴x =23,故选D.2.同学甲参加某科普知识竞赛,需回答三个问题,竞赛规则规定:答对第一、二、三个问题分别得100分、100分、200分,答错或不答均得零分.假设同学甲答对第一、二、三个问题的概率分别为0.8,0.6,0.5,且各题答对与否相互之间没有影响,则同学甲得分不低于300分的概率是________.解析:设“同学甲答对第i 个题”为事件A i (i =1,2,3),则P (A 1)=0.8,P (A 2)=0.6,P (A 3)=0.5,且A 1,A 2,A 3相互独立,同学甲得分不低于300分对应于事件A 1A 2A 3∪A 1A -2A 3∪A-1A 2A 3发生,故所求概率为P =P (A 1A 2A 3∪A 1A -2A 3∪A -1A 2A 3) =P (A 1A 2A 3)+P (A 1A -2A 3)+P (A -1A 2A 3) =P (A 1)P (A 2)P (A 3)+P (A 1)P (A -2)·P (A 3)+P (A -1)P (A 2)P (A 3)=0.8×0.6×0.5+0.8×0.4×0.5+0.2×0.6×0.5=0.46. 答案:0.463.李浩的棋艺不如张岚,李浩每局赢张岚的概率只有0.45.假设他们下棋时各局的输赢是独立的.(1)计算他们的3局棋中李浩至少赢1局的概率; (2)计算他们的6局棋中李浩至少赢1局的概率.解:(1)用A 1,A 2,A 3分别表示第1,第2,第3局李浩输.则A =A 1∩A 2∩A 3表示李浩连输3局.其对立事件A 表示3局中李浩至少赢1局.因为事件A 1,A 2,A 3相互独立,并且P (A 1)=P (A 2)=P (A 3)=1-0.45=0.55, 所以P (A )=P (A 1)P (A 2)P (A 3)=0.553≈0.166 4. 于是P (A )=1-P (A )=0.833 6.说明3局棋中李浩至少赢1局的概率还是很大的.(2)用A 1,A 2,…,A 6分别表示第1,第2,…,第6局李浩输,则B =A 1∩A 2∩…∩A 6表示李浩连输6局,其对立事件B 表示6局中李浩至少赢1局.因为事件A 1,A 2,…,A 6相互独立,并且P (A 1)=P (A 2)=…=P (A 6)=1-0.45=0.55, 所以P (B )=P (A 1)P (A 2)·…·P (A 6)=0.556≈0.027 7.于是P (B )=1-P (B )=0.972 3. 说明6局棋中李浩至少赢1局的概率大于0.97.4.甲、乙2个人独立地破译一个密码,他们能译出密码的概率分别为13和14,求:(1)2个人都译不出密码的概率; (2)至多1个人译出密码的概率; (3)至少1个人译出密码的概率.解:记“甲独立地译出密码”为事件A ,“乙独立地译出密码”为事件B ,A ,B 为相互独立事件,且P (A )=13,P (B )=14.(1)2个人都译不出密码的概率为P (A B )=P (A )·P (B )=[1-P (A )]·[1-P (B )]=⎝⎛⎭⎫1-13⎝⎛⎭⎫1-14=12. (2)“至多1个人译出密码”的对立事件为“有2个人译出密码”,所以至多1个人译出密码的概率为1-P (AB )=1-P (A )P (B )=1-13×14=1112.。
2021秋九上2、2一元二次方程的解法3用配方法解二次项系数不是1的一元二次方程习题湘教版

9.用配方法解方程3x2+x=1,应在方程两边同时( C )
A.先除以 3,再加上16 C.先除以 3,再加上316
B.先乘13,再减去16 D.先乘13,再减去316
10.用配方法解下列方程时,配方有错误的是( B )
A.x2-2x-99=0化为(x-1)2=100
B.x2+8x+9=0化为(x+4)2=25 C.2t2-7t-4=0 化为t-742=8116 D.3x2-4x-2=0 化为x-232=190
第2章 一元二次方程
2.2 一元二次方程的解法
第3课时 用配方法解二次项系数不是1的 一元二次方程
新知笔记 1 2 ≥0
提示:点击 进入习题
1B 2B 3A 4A 5B
答案显示
6C 7 -6 8 见习题 9C 10 B
11 D 12 B 13 见习题 14 见习题 15 见习题
答案显示
16 见习题
11.
下列对于配方法叙述错误的是( D )
A.二次项系数为1,一次项系数是偶数的一元二次方程都
适合用配方法求解
B.一次项系数是0的一元二次方程都不适合用配方法求解
C.用配方法解二次项系数不是1的一元二次方程时,第一
步可以在方程两边同时除以二次项系数
D.用配方法解二次项系数不是1的一元二次方程时,第一
A.4(x-1)2=1
B.4(x-1)2=5
C.4(x-1)2=3
D.4(x-1)2=-3
2.用配方法解一元二次方程-3x2+4x+1=0的第一步是 把方程的两边同时除以( B )
A.3 B.-3 C.13 D.-13
3.【2020·聊城】用配方法解一元二次方程2x2-3x-1=0
时,配方正确的是( A )
高中数学精讲优练课型第二章基本初等函数(I)2.2.2对数函数及其性质第2课时习题课对数函数及其性质

第七页,共44页。
(4)(分类讨论(tǎolùn)法)当a>1时,函数y=logax在定义域上是增函数, 则有logaπ>loga3.14; 当0<a<1时,函数y=logax在定义域上是减函数, 则有logaπ<loga3.14. 综上所述,当a>1时,logaπ>loga3.14; 当0<a<1时,logaπ<loga3.14.
1 当f(x)=2log x=12 4时,解得x= ,2
故该函数的定义1 域为
1
2
4
[1 , 1]. 42
第十六页,共44页。
2.(变换条件(tiáojiàn))若将本题中的函数“f(x)=2log x”改为 1
“f(x)=
+3log2x-1”,其他条件(tiáojià2n)不变,又如何求其值
域呢?
角度2:与对数函数有关的奇偶性问题
【典例】讨论(tǎolùn)函数f(x)=log3(
+x)的奇偶性.
【解题探究】本例函数f(x)=log3( x2 +1x)的定义域是什么?
提示:因为 域为R.
>x≥-x,所以
x2 1
+xx>2 0对1 任意实数都成立,故函数的定义 x2 1
第三十页,共44页。
【解析( jiě xī)】因为 >|x|≥-x,
2log
2 2
x
第十七页,共44页。
【解析】令t=log2x,则f(t)=2t2+3t-1, 因为2≤x≤4,所以(suǒyǐ)t=log2x在[2,4]上为增函数. 当x=2时,t取得最小值1,当x=4时,t取得最大值2, 故1≤t≤2. 又f(t)=2t2+3t-1在[1,2]上为增函数, 故当t=1时,f(t)取得最小值4, 当t=2时,f(t)取得最大值13, 所以(suǒyǐ)函数f(x)的值域为[4,13].
2.2.3 习题课

乘 法 分 配 律
例2、102×43 =(100+2) ×43 =100×43+2×43 =4300+86 =4386 你来练一练 101×99
202×35 89×99 45×199
例3、25×88 =25×(80+8) 乘法分配律 =25×80+25×8 =2000+200 =2200 把88分成4×22 方法二:25×88 乘法结合律 =25×4×22 =100×22 =2200
(3)78×20+22×20=( 78 + 22 )×20
〇
例1、943×67+943×33 =943×(67+33) =943×100 =94300 练、35×103-35×3 =35×(103-3) =35×100 =3500
〇
〇
〇
〇 〇 〇 〇
457×55+457×45 130×29-30×29
找出相同的因数:
516+5 24
3624+19 24+ 4524
=(36+19+45)×24
12927+129 72+ 129
=129×(27+72+1)
〇
〇
=5×(16+24)
〇
〇 〇
〇
〇
〇
例2、102×43 =(100+2) ×43
=100×43+2×43 =4300+86 表示100个43 =4386 加上2个43就是
你来练一练 25×32 =25×4×8
28×250 =250×4×7
56×125 8×25×4×125 =7×(8×125) =(8×125)×(4×25)
应用乘法规律简算 1、例:943×67+943×33 =943×(67+33) 直接应用乘法分配律 练:457×55+457×45
2-2-2-3 对数函数的图像与性质(第3课时 习题课) 课件(人教A版必修1)

课 时 作 业
第 4页
第一章
1.2
习题课
新课标A版 ·数学 ·必修1
课 时 学 案
第 5页
第一章
1.2
习题课
新课标A版 ·数学 ·必修1
例1
设
x -1 2e ,x<2 f(x)= 2 log3x -1,x≥2,
求 f[f(2)]的值.
解析
f(2)=log33=1,f[f(2)]=f(1)=2. 2
答案
第 9页
第一章
1.2
习题课
新课标A版 ·数学 ·必修1
例5
已知函数 y=log2(x2-2ax+a)的值域为 R,求实数 a.
解析
要使 y=x2-2ax+a 能取到(0,+∞)所有值,∴Δ=
4a2-4a≥0⇒a≥1 或 a≤0. 答案 (-∞,0]∪[1,+∞)
第10页
第一章
1.2
习题课
新课标A版 ·数学 ·必修1
课时作业(二十九)
第11页
第一章
1.2
习题课
新课标A版 ·数学 ·必修1
第二章
基本初等函数(Ⅰ)
第 1页
第一章
1.2
习题课
新课标A版 ·数学 ·必修1
2.2 对数函数
第 2页
第一章
1.2
习题课
新课标A版 ·数学 ·必修1
2.2.2 对数函数的图像与性质(第3课时 习题课)第 3页Fra bibliotek第一章
1.2
习题课
新课标A版 ·数学 ·必修1
课 时 学 案
定义域:0<a<1 时,(1,+∞),
a>1 时,(-∞,1). 值域:0<a<1 时,(1,+∞),a>1 时,(-∞,1).
2017年高中数学第二章随机变量及其分布2.2.2事件的相互独立性习题课件新人教A版选修2_3

解:记“甲射击 1 次,击中目标”为事件 A,“乙射击 1 次, 击中目标”为事件 B,则 A 与 B,A 与 B,A 与 B ,A 与 B 为相互 独立事件,
(1)2 人都射中目标的概率为: P(AB)=P(A)·P(B)=0.8×0.9=0.72.
(2)“2 人各射击 1 次,恰有 1 人射中目标”包括两种情况: 一种是甲射中、乙未射中(事件 A B 发生),另一种是甲未射中、乙 射中(事件 A B 发生).根据题意,事件 A B 与 A B 互斥,根据互斥 事件的概率加法公式和相互独立事件的概率乘法公式,所求的概 率为:
(2)D= C ,P(D)=1-P(C)=1-0.8=0.2, P(E)=0.8×0.2×0.8+0.8×0.8×0.2+0.2×0.8×0.8=0.384.
11.某项选拔共有四轮考核,每轮设有一个问题,能正确回 答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回 答第一、二、三、四轮问题的概率分别为45、35、25、15,且各轮问 题能否正确回答互不影响:
(3)分别抛掷 2 枚相同的硬币,事件 M:“第 1 枚为正面”,
事件 N:“两枚结果相同”.
这 3 个问题中,M,N 是相互独立事件的有( )
A.3 个
B.2 个
C.1 个
D.0 个
解析:(1)中,M,N 是互斥事件;(2)中,P(M)=35,P(N)=12.
即事件 M 的结果对事件 N 的结果有影响,所以 M,N 不是相互
P(A B )+P( A B)=P(A)·P( B )+P( A )·P(B) =0.8×(1-0.9)+(1-0.8)×0.9 =0.08+0.18=0.26.
(3)“2 人至少有 1 人射中”包括“2 人都中”和“2 人有 1 人 射中”2 种情况,其概率为
2.2.3杂化轨道理论教学设计2024-2025学年高二上学期化学人教版(2019)选择性必修2
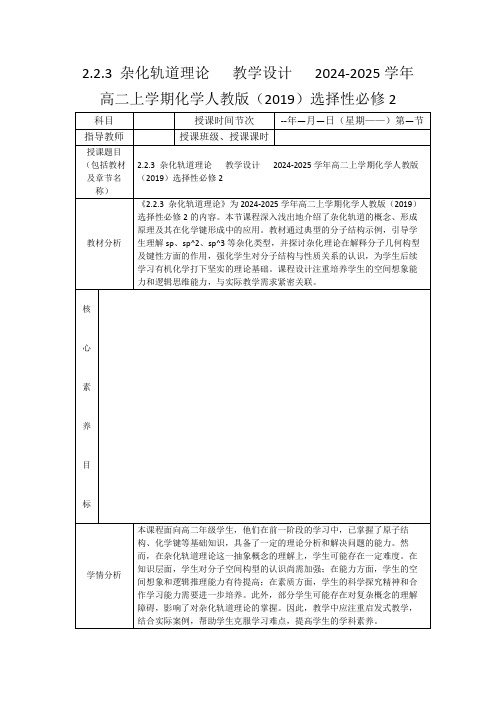
3.加强课后辅导,针对学生在杂化轨道理论方面存在的问题,进行有针对性的指导,提高教学效果。
板书设计
1.标题:2.2.3杂化轨道理论
-杂化轨道定义
-杂化类型:sp、sp^2、sp^3
-杂化轨道与分子结构
-杂化轨道与分子性质
核心素养目标
学情分析
本课程面向高二年级学生,他们在前一阶段的学习中,已掌握了原子结构、化学键等基础知识,概念的理解上,学生可能存在一定难度。在知识层面,学生对分子空间构型的认识尚需加强;在能力方面,学生的空间想象和逻辑推理能力有待提高;在素质方面,学生的科学探究精神和合作学习能力需要进一步培养。此外,部分学生可能存在对复杂概念的理解障碍,影响了对杂化轨道理论的掌握。因此,教学中应注重启发式教学,结合实际案例,帮助学生克服学习难点,提高学生的学科素养。
3.应用题:给出2-3个分子的结构,要求学生判断其杂化类型,并解释其分子性质。
4.实践题:分组讨论,每组选择一个有机分子,分析其杂化类型,并在课堂上展示分析过程和结果。
5.快速问答:教师随机提问,学生快速回答,问题涉及课程内容的重点和难点。
总用时:45分钟
在教学过程中,注意关注学生的学习反馈,及时调整教学方法和节奏,确保学生能够理解和掌握杂化轨道理论。同时,注重培养学生的学科素养,提高他们的解决问题的能力。
学生学习效果
1.理解杂化轨道的概念,掌握sp、sp^2、sp^3等杂化类型及其形成原理。
2.应用杂化轨道理论解释分子几何构型及键性,分析分子的结构与性质关系。
板书设计以简洁明了为原则,通过关键词和核心概念突出课程重点,结合直观的分子模型简图和杂化轨道示意图,帮助学生更好地理解抽象的理论知识,增强课堂学习的趣味性和艺术性。
2020新课标改编版第2章 2.2.3 椭圆习题课 _11-15

好文档分创建
3
又 0<x0<a,∴x0=a2a-b2b2,
且 0<a2a-b2b2<a,而 b2=a2-c2,
∴0<a2-c2 c2<1.∴0<e12-1<1.∴
2 2 <e<1.
求离心率的取值范围,关键是根据题设条件得到关于 a,c 的不等关系,或者得到 a,c 的取值范围.
好文档分创建
4
【变式与拓展】
则
e=
5 3.
好文档分创建5ຫໍສະໝຸດ 它想,自已和山猫一样辛辛苦苦忙一年,花的时间精力比山猫还多,可是市场上鱼的价格比桃子的高出几倍,山猫一年中也比自己多赚了许多钱,这不是明罢着种桃树吃亏了?精明的猴子决定明年不 种桃树也改了去养鱼,于是请人掘走所有桃树并在果园里挖了个鱼塘,大小规格和山猫的一样。“这真是鸟类的骄傲,歌声无与伦比!”“别看羽毛漆黑,貌不出众,歌声却出类拔萃!”比赛大厅沸腾了 ,乌鸦也陶醉了。这下农夫可大吃一惊,说道:
好文档分创建
2
题型2 求椭圆离心率的取值
例2:设椭圆上存在一点 P,它到椭圆中心和长轴一个端点
的连线互相垂直,求椭圆离心率的取值范围. 自主解答:设椭圆方程为ax22+by22=1(a>b>0), A 为右顶点(a,0),P 为(x0,y0), ∵PO⊥PA,∴xy00·x0y-0 a=-1, 即 y20=ax0-x20.又ax202+by022=1, ∴(a2-b2)x20-a3x0+a2b2=0, (x0-a)[(a2-b2)x0-ab2]=0.
软件下载
“啊呀,我真是自作自受,自讨苦吃啦。
“前倨后恭”这句成语就是从这个故事来的。”虎大王寻思片刻说:“那你是动物王国的二头领了。, 大象饿了,就用象牙挖根子吃
高一数学必修4课件:2-2-3向量数乘运算及其几何意义

→ → 1→ PN ,则选项A,C,D不正确,很明显MP = 2 MN ,则选项B正 确.
第二章
2.2
2.2.3
成才之路 ·数学 ·人教A版 · 必修4
4.向量的线性运算
加、减、数乘 向量的________________运算统称为向量的线性运算,
对于任意向量a,b以及任意实数λ,μ1,μ2,恒有λ(μ1a± 2b)= μ λμ1a± 2b. λμ
第二章
2.2
2.2.3
成才之路 ·数学 ·人教A版 · 必修4
已知非零向量a,b满足a=4b,则( A.|a|=|b| C.a与b的方向相同 B.4|a|=|b|
)
D.a与b的方向相反
[答案] C
第二章
2.2
2.2.3
成才之路 ·数学 ·人教A版 · 必修4
[解析]
∵a=4b,4>0,∴|a|=4|b|.
第二章
2.2
2.2.3
成才之路 ·数学 ·人教A版 · 必修4
定义 长度 方 向 λ>0 λ=0 λ<0
向量 一般地,实数λ与向量a的积是一个____,
这种运算叫做向量的数乘,记作λa |λa|=|λ|a λa的方向与a的方向______ 相同 λa=0 λa的方向与a的方向_____ 相反
第二章
第二章 平面向量
成才之路 ·数学 ·人教A版 · 必修4
课前自主预习 随堂应用练习 思路方法技巧 课后强化作业 探索延拓创新
第二章
2.2
2.2.3
成才之路 ·数学 ·人教A版 · 必修4
课前自主预习
第二章
2.2
2.2.3
成才之路 ·数学 ·人教A版 · 必修4
2018-2019学年高中数学人教A版必修一:2.2.2 对数函数及其性质 第二课时 对数函数的图象及性质的应用

眼皮蹦跳跳专业文档眼皮蹦跳跳专业文
2019/8/14
档
14
即时训练2-1:(1)(2017·北京高一月考)已知f(x)=log3x,f(a)>f(2),那么a的取值范 围是( )
(A){a|a>2} (B){a|1<a<2}
(C){a|a> 1 } (D){a| 1 <a<1}
2
2
(2)函数 y= log1 3x 4 1 的定义域是
2
3
2
32
答案:(1)A (2)( 4 , 3 ]
32
眼皮蹦跳跳专业文档眼皮蹦跳跳专业文
2019/8/14
档
15
题型三 对数型复合函数的单调性
【例 3】 (2018·唐山高一期末)函数 f(x)= log1 (x2-2x-3)的单调递增区间是( )
(A)(-∞,-1)
(B)(-∞,1)
2
(C)(1,+∞)
眼皮蹦跳跳专业文档眼皮蹦跳跳专业文
2019/8/14
档
22
即时训练4-1:已知f(x)=loga(1-x)+loga(x+3)(a>0且a≠1). (1)求函数f(x)的定义域、值域; (2)若函数f(x)有最小值为-2,求a的值.
解:(1)因为
1 x 0, x 3 0,
所以
定义域为{x|-3<x<1}.
眼皮蹦跳跳专业文档眼皮蹦跳跳专业文
2019/8/14
档
2
新知探求 课堂探究
眼皮蹦跳跳专业文档眼皮蹦跳跳专业文
2019/8/14
档
3
新知探求·素养养成
自我检测
2.2.3杂化轨道理论教学设计2023-2024学年高二化学人教版(2019)选择性必修2

1.教材:确保每位学生都有本节课所需的教材或学习资料。教材应包括本节课的相关内容,如杂化轨道的定义、类型以及应用等。
2.辅助材料:准备与教学内容相关的图片、图表、视频等多媒体资源。这些资源可以帮助学生更直观地理解杂化轨道的概念和应用。例如,可以准备一些分子的结构图、杂化轨道的示意图等。
3.实验器材:如果涉及实验,确保实验器材的完整性和安全性。例如,如果本节课涉及到有机化合物的制备或性质实验,需要准备相应的试剂、仪器设备等,并确保实验器材的质量和安全。
4.教室布置:根据教学需要,布置教室环境,如分组讨论区、实验操作台等。为了促进学生之间的交流和合作,可以将教室布置成小组讨论的形式,设置一些讨论区和实验操作台,方便学生进行小组讨论和实验操作。
5.教学工具:准备投影仪、计算机、白板等教学工具,以便教师进行讲解和展示。同时,确保每个学生都能清晰地看到多媒体资源和教师的讲解。
4.练习题:提供一些练习题,让学生巩固所学内容,并能运用杂化轨道理论解决实际问题。
核心素养目标
本节课的核心素养目标包括:
1.理解能力:通过讲解和练习,使学生能够理解杂化轨道的定义、类型和应用,并能够运用杂化轨道理论分析有机化合物的结构。
2.科学思维:培养学生运用科学思维方法,分析问题、解决问题的能力。通过让学生分析不同杂化轨道的类型和应用,培养学生的逻辑思维和批判性思维。
1.知识层次:大部分学生对于基本的化学概念和原理有一定的掌握,但对于较为复杂的杂化轨道理论可能还存在一定的困难。因此,在教学过程中,教师需要循序渐进,从基本概念入手,逐步引导学生理解杂化轨道的定义和应用。
2.能力层次:学生在之前的化学学习中,已经具备了一定的观察、实验和思维能力。但针对杂化轨道这一抽象的概念,学生可能还存在一定的理解障碍。因此,在教学过程中,教师需要注重培养学生的抽象思维能力,通过讲解、举例和练习等方式,帮助学生理解和掌握杂化轨道理论。
2.2整式的加减(第三课时)教学设计2023-2024学年人教版数学七年级上册

其次,我会收集学生的课后作业和练习题,以评估他们在实际应用整式加减知识方面的能力。通过分析学生的作业,我可以了解他们在合并同类项、简化整式以及解决实际问题时可能遇到的困难和错误。
3. 实例分析:结合实际问题,运用整式的加减方法解决问题,提高学生运用数学知识解决实际问题的能力。
4. 练习题:完成教材中的练习题,巩固整式的加减运算方法,提高计算速度和准确性。
二、核心素养目标
1. 培养学生运用数学语言表达和逻辑思维能力,通过整式的加减运算,提高学生对数学符号的理解和运用能力。
2. 培养学生的观察能力和抽象思维能力,使学生能够从具体问题中抽象出数学模型,并用所学知识解决问题。
2. 教学软件:运用数学软件辅助教学,让学生通过实际操作,加深对整式加减运算的理解。
3. 实物教具:使用实物教具,如代数棒等,让学生在动手操作中直观地感受整式的合并过程。
五、教学实施过程
1. 课前自主探索
- 教师活动:
发布预习任务:通过学校在线学习平台,发布关于整式加减预习的PPT和视频资料,明确预习目标和要求。
3. 培养学生的运算能力和问题解决能力,掌握整式的加减法则,并能熟练运用于解决实际生活中的数学问题。
4. 培养学生的合作意识和团队精神,通过小组讨论和合作完成练习题,提高学生沟通交流和协作解决问题的能力。
三、学习者分析
1. 学生已经掌握了整式的概念、同类项的定义以及简单的整式加减运算。他们能够识别同类项并进行初步的合并运算。
2.2.2《杂化轨道理论》教学设计2023-2024学年高二化学人教版(2019)选择性必修2

5.教师评价与反馈:
-针对学生在课堂上的表现,给予及时的鼓励和纠正,帮助学生建立正确的概念和理解。
-对小组讨论成果进行点评,指出各组的优点和不足,提供改进建议,促进学生的团队协作和批判性思维。
-根据随堂测试结果,分析学生的知识盲点和误区,进行针对性的讲解和复习。
①杂化轨道的定义
②杂化轨道的形成原因2.杂化轨道的类与分子几何构型① sp杂化
② sp^2杂化
③ sp^3杂化
3.杂化轨道的应用
①解释分子结构
②预测分子性质
③指导化学反应
板书设计:
一、杂化轨道理论
1.定义与形成原因
2.类型与分子几何构型
3.应用
板书重点突出杂化轨道的定义、形成原因、类型及其在分子结构解释和性质预测中的应用。条理清晰,简洁明了,有助于学生理解和记忆。
3.计算题:计算乙炔分子中碳原子的杂化类型和分子几何构型。
解答:乙炔分子中,碳原子形成一个σ键和两个π键,不含有孤对电子。根据杂化轨道理论,碳原子采用sp杂化,形成直线型几何构型。
4.计算题:计算氨分子中氮原子的杂化类型和分子几何构型。
解答:氨分子中,氮原子形成三个σ键和一个孤对电子。根据杂化轨道理论,氮原子采用sp^3杂化,形成三角锥形几何构型。
过程:
各组代表依次上台展示讨论成果,包括主题的现状、挑战及解决方案。
其他学生和教师对展示内容进行提问和点评,促进互动交流。
教师总结各组的亮点和不足,并提出进一步的建议和改进方向。
6.课堂小结(5分钟)
目标:回顾本节课的主要内容,强调杂化轨道的重要性和意义。
过程:
济南版生物七年级上册2.2.2 脊椎动物的主要类群--鱼类 课件

犬齿,适于撕裂肉食
脑干
发达的神经系统:由脑、脊髓和它们所发 出的神经组成。 (尤其大脑发达)
能对外界刺激作出反应, 适应较复杂的生活环境
哺乳动物特点总结:
1.体表: 被毛 2.体内: 有膈 3.呼吸: 肺 4.牙齿: 分化—门齿、臼齿、犬齿 5.生殖发育: 胎生 、 哺乳 6.神经: 发达—脑、脊髓、神经,
海狮
【习题5】
兔能够对外界环境的变化作出反应,主要因 为( B)
A.具有较大的耳朵 B.具有发达的大脑和神经 C.视觉敏锐 D.嗅觉发达
点拨:家兔具有发达的神经系统,尤其 大脑发达,能对外界环境变化迅速做出 反应,适应复杂的陆地生活
脊椎动物比较
生活 环境
体表 特征
呼吸 体温 器官
生殖 方式
鱼类 水中
意图。下列说法正确的是( D ) A.②和③都能进行气体交换 B.气体进入体内的途径是①→②→③ C.①是气管、②是肺、③是气囊 D.家鸽的呼吸方式是双重呼吸
例6下列哪项不是家鸽与飞行生活相适应的特点( D ) A.体表被覆羽毛 B.前肢变成翼 C.体内有气囊 D.直肠发达
例7 生活在水里,用鳃呼吸,体表被有鳞片的动物是( B )
鸟类
鱼类 节肢动物
软体动物
环环节节动动物物
扁扁形形动动物物
单单单细细细胞胞胞动动动物物物
被子植物
裸子植物
苔藓植物
线性动物
蕨类植物
腔肠动物
藻类植物
脊椎动物 无脊椎动物
爬行类
鸟类
被子植物
鱼类
裸子植物
节肢动物
软体动物
环环节节动动物物
苔藓植物
线性动物
扁扁形形动动物物
单单单细细细胞胞胞动动动物物物
2022秋七年级数学上册 第2章 整式加减2.2 整式加减第3课时整式加减——降幂(升幂)排列习题课

13、生气是拿别人做错的事来惩罚自 己。2022/2/282022/2/282022/2/282022/2/282/28/2022
14、抱最大的希望,作最大的努力。2022年2月28日 星期一 2022/2/282022/2/282022/2/28
15、一个人炫耀什么,说明他内心缺 少什么 。。2022年2月 2022/2/282022/2/282022/2/282/28/2022
4.下列式子中,按字母m的升幂排列,并且次
数为1的项的系数为-1的二次三项式是( D )
A.-m+m2+6
B.3+m+4m2
C.2n2-mn-5m2n5 D.-3-m+2m2
5.把多项式9m2+7m+3m3-1按m的降幂排 列后,第3项是( B )
A.9m2 B.7m C.+3m3 D.-1
6.将多项式a3-5ab2-7b3+6a2b按某一字母的 升(降)幂排列正确的是( B )
第2章 整式加减
2.2 整式加减 第3课时 整式加减——降幂(升幂)
排列
提示:点击 进入习题
1B 2D 3A 4D 5B
答案显示
6B 7 升幂;a;降幂 8 见习题 9 2或3或4 10 见习题
提示:点击 进入习题
11 见习题 12 见习题
答案显示
1.多项式x5y2+2x4y3-3x2y2-4xy是( B ) A.按x的升幂排列的 B.按x的降幂排列的 C.按y的升幂排列的 D.按y的降幂排列的
16、业余生活要有意义,不要越轨。2022/2/282022/2/28Februar y 28, 2022
17、一个人即使已登上顶峰,也仍要 自强不 息。2022/2/282022/2/282022/2/282022/2/28
系统函数的零极点分布决定时域特性

目录1.引言 (2)2.虚拟仪器开发软件Labview入门 (3)2.1 Labview简介 (3)2.2 利用Labview编程完成习题设计 (3)3.利用LabVIEW实现系统函数的零极点分布决定时域特性的设计 (20)3.1系统函数的零极点分布决定时域特性的基本原理 (20)3.2系统函数的零极点分布决定时域特性的编程设计及实现 (22)3.3运行结果及分析 (23)4. 总结 (25)5.参考文献 (25)1.引言冲激响应h(t)与系统函数H(s) 从时域和变换域两方面表征了同一系统的本性。
在s 域分析中,借助系统函数在s平面零点与极点分布的研究,可以简明、直观地给出系统响应的许多规律。
系统的时域、频域特性集中地以其系统函数的零、极点分布表现出来。
主要优点:可以预言系统的时域特性;便于划分系统的各个分量(自由/强迫,瞬态/稳态);可以用来说明系统的正弦稳态特性。
2.虚拟仪器开发软件Labview入门2.1 Labview简介LabVIEW是一种程序开发环境,由美国国家仪器(NI)公司研制开发的,类似于C 和BASIC开发环境,但是LabVIEW与其他计算机语言的显著区别是:其他计算机语言都是采用基于文本的语言产生代码,而LabVIEW使用的是图形化编辑语言G编写程序,产生的程序是框图的形式。
LabVIEW(Laboratory Virtual Instrument Engineering Workbench)是一种用图标代替文本行创建应用程序的图形化编程语言。
传统文本编程语言根据语句和指令的先后顺序决定程序执行顺序,LabVIEW 则采用数据流编程方式,程序框图中节点之间的数据流向决定VI及函数的执行顺序。
VI指虚拟仪器,是LabVIEW]的程序模块。
LabVIEW 提供很多外观与传统仪器(如示波器、万用表)类似的控件,可用来方便地创建用户界面。
用户界面在LabVIEW中被称为前面板。
使用图标和连线,可以通过编程对前面板上的对象进行控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2.2-3 习题课
一、抽样方法中的图表问题: 例1、某单位200名职工的年龄分布情况如下图,现要 从中抽取40名职工样本,用系统抽样法,将全体职工 随机按1~200编号,并按编号顺序平均分40组(1~5号, 6~10号,…,196~200号)。若第五组抽出的号码为 22,则第8组抽取的号码是 。若用分层抽样 法,则40岁以下年龄段应抽取 人。
50岁以上
20% 50% 30%
40岁以下
40~50岁
二、用样本估计总体中的图表问题:
例2、某工厂对一些产品进行了抽样检测,下图是根据抽样后 的产品净重(单位:g)数据绘制的频率分布直方图,其中产 品净重的范围是[96,106],样本数据分组为[96,98),[98,100),
[100,102),[102,104),[104,106]。已知样本中产品净重小于 100g的个数是36,则样本净重大于或等于104g的产品个数是
频率/组距 0.150 0.125 0.100 0.075 0.050 o 产品净重/g
(
)
A.90
C.60
B.75
D.45
例3、随机抽取某中学甲、乙两班各10名同学,测量他们的身 高(单位:cm),获得身高数据的茎叶图如下图所示:
甲班 2 18 0 0 1 0 17 8 8 3 2 16 8 15 1 03689 258 9 乙班
27.0 23.9 41.6 33.1 40.6 18.8 13.7 28.9 13.2 14.5 27.0 34.8 28.9 3.2 50.1 5.6 8.7 15.2 7.1 5.2 16.5 13.8 19.2 11.2 15.7 10.0 5.6 1.5 33.8 9.2
请由这些数字计算平均数、中位数、标准差,并对它们的含 义进行解释。
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差。
例4、某校甲乙两个班各有5名编号为1,2,3,4,5的学生 进行投篮练习,每人投10次,投中的次数如下表: 学生 甲班乙班1号 66
2号 7
7
3号 7
6
4号 8
7 。
5号 7
9
则以上两组数据的方差中较小的一个 S 2 =
例5、已知40个数据中前20个数据的平均数和方差 分别为60、20,后20个数据的平均数和方差分别 为80、40,求这40个数据的平均数和方差。
练习:
(1)农场种植的甲乙两种水稻,在面积相等的两块稻田中连续6年的年 平均产量如下(单位:500kg)
品种 甲 乙 第1年 900 890 第2年 920 960 第3年 900 950 第4年 850 850 第5年 910 860 第6年 920 890
那种水稻的产量比较稳定? (2)下列数据是30个不同国家中每100000名男性患某种疾 病的死亡率:
