大学物理质点运动学圆周运动
大学物理简程 张三慧主编第1章 质点运动学

at
a
R
an
o
a rc ta n
an at
14
1.7
y
相对运动
y
E
V
S:小球
V:马车
B
rS E A0 rV E
A
E:地面
rS V
o
o
x
rS E rS V rV E v S E v S V vV E
a lim
v t
t 0
lim
vn t
t 0
lim
vt t
t 0
an at
12
切向加速度:
vt v (t t ) v (t ) v
a t lim v t dv dt d ( R ) dt R d dt
v B A y v B y v A y v B sin 30 v A 600 km / h
v BA v B A x v B A y 9 1 7 km / h
2 2
v AB v A v B
23
0
16
dv dt
dv dt
du dt
若两个参考系相对做匀速直线运动,即 a r 则
a a
矢量合成的平行四边形法则:
A
A
B
C
B
C
矢量合成的三角形法则:
A A
C
B
C
B
17
矢量的分解:
A B B
y
A
第1章 质点运动学
质点运动学

ω 2 − ω02 = 2βθ
6
例:一质点圆运动,半径 r 运动方程为 θ =-t2+4t, 求:质点的 v (t ) a (t ) 解:θ = −t 2 + 4t
rad
ω = −2t + 4
β = −2
rad/s
rad/s 2
∴ v = rω = r (−2t + 4) aτ = r β = −2r
d2r v2 =a= 2 dt r
d2r =0 2 dt
19
5. 质点的运动方程: x =x(t) y =y(t) 在求质点速度和加速度时,有人采用如下方法:
dr 先从 r = x + y 求出 r = r (t ) ,再由 v = dt d2r 和 a = 2 求出质点的 v 和 a 的大小。此法错在何处? dt
一矢量等于二矢量之和,作矢量图
vPK vK′K
vPK′
利用三角形知识求解
上式再对t求导,可得:aPK = aPK′ + aK′K
加速度的变换定理
求相对运动问题的一般方法: 1. 确定研究对象 3. 分析 vPK P
2. 确定定参考系 K,动参考系 K/
vPK ′ vK ′K 的大小、方向
4. 依据 v PK = v PK ′ + v K ′K 画矢量图,从已知边、角,求未知 边、角(解三角形),问题得到解决。
2 v 2 − v0 = 2a( x − x0 )
ω 2 − ω02 = 2β (θ − θ 0 )
例:质点作匀角加速圆运动,t =0 时 θ0 , ω0 ,β =恒量 求:θ ( t )=? ω ( t )=? ω (θ )=? 解: 从 β→ ω→ θ 积分法
大学物理第1章质点运动学的描述
t0
0 2 4
t 2s 4
2
t 2s
x/m
6
-6 -4 -2
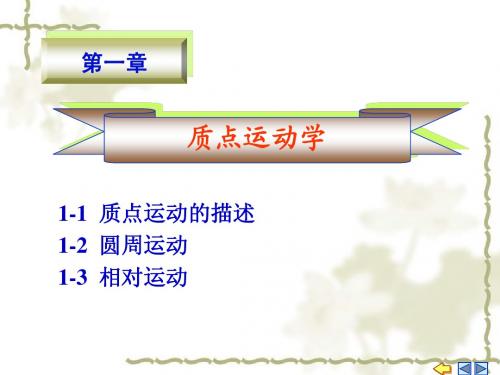
例3 如图所示, A、B 两物体由一长为 l 的刚性 细杆相连, A、B 两物体可在光滑轨道上滑行.如物体 A以恒定的速率 v 向左滑行, 当 60 时, 物体B的 速率为多少? 解 建立坐标系如图, 物体A 的速度
1. 5 arctan 56.3 1
(2) 运动方程
x(t ) (1m s )t 2m
y(t ) ( m s )t 2m
1 4 2 2
1
由运动方程消去参数
1 -1 2 y ( m ) x x 3m 4
轨迹图
t 4s
6
t 可得轨迹方程为
y/m
三、位置变化的快慢——速度
速度是描写质点位置变化快慢和方向的物理量,是矢量。
速率是描写质点运动路程随时间变化快慢的物理量,是标量。 1 平均速度 在t 时间内, 质点从点 A 运动到点 B, 其位移为
B
y
r r (t t) r (t)
r (t t)
s r
质点是经过科学抽象而形成的理想化的物理模 型 . 目的是为了突出研究对象的主要性质 , 暂不考 虑一些次要的因素 .
二、位置矢量、运动方程、位移
1 位置矢量
确定质点P某一时刻在 坐标系里的位置的物理量称 . 位置矢量, 简称位矢 r
y
y j
r xi yj zk
j k 式中 i 、 、 分别为x、y、z
xA xB xB x A
yB y A
o
x
经过时间间隔 t 后, 质点位置矢量发生变化, 由 始点 A 指向终点 B 的有向线段 AB 称为点 A 到 B 的 位移矢量 r . 位移矢量也简称位移.
大学物理第一章 质点运动学-习题及答案

第一章 质点运动学1-1 一质点在平面上运动,已知质点位置矢量的表示式为j i r 22bt at += (其中b a ,为常量) 则该质点作(A )匀速直线运动 (B )变速直线运动(C )抛物线运动 (D )一般曲线运动 [B]解:由j i rv bt at t 22d d +==知 v 随t 变化,质点作变速运动。
又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。
故该质点作变速直线运动。
1-2 质点作曲线运动,r 表示位置矢量,s 表示路程,t a 表示切向加速度,下列表达式中,① a t v =d ② v t r =d ③ v t s =d d ④ t a t =d d v (A )只有(1)、(4)是对的。
(B )只有(2)、(4)是对的。
(C )只有(2)是对的。
(D )只有(3)是对的。
[D]解:由定义:t vt a d d d d ≠=v ; t r t s t v d d d d d d ≠==r ; t t v a d d d d v ≠=τ只有③正确。
1-3 在相对地面静止的坐标系内,A 、B 二船都以21s m -⋅的速率匀速行驶,A 船沿x 轴正向,B 船沿y 轴正向。
今在A 船上设置与静止坐标系方向相同的坐标系(x ,y 方向单位矢用j i ,表示),那么在A 船上的坐标系中,B 船的速度(以1s m -⋅为单位)为(A )j i 22+ (B )j i 22+-(C )j i 22-- (D )j i 22- [B]解:由i v 2=对地A ,j v 2=对地B 可得 A B A B 地对对地对v v v +=⎰对地对地A B v v -=i j 22-=j i 22+-= (1s m -⋅)1-4 一质点沿x 方向运动,其加速度随时间变化关系为)SI (23t a +=如果初始时质点的速度0v 为51s m -⋅,则当t 为3s 时,质点的速度1s m 23-⋅=v解:⎰+=tta v v 00d13s m 23d )23(5-⋅=++=⎰tt1-5 一质点的运动方程为SI)(62t t x -=,则在t 由0至4s 的时间间隔内,质点的位移大小为 8m ,在t 由0到4s 的时间间隔内质点走过的路程为 10m 。
大学物理科学出版社第四版第一章质点运动学

第一章 质点运动学一、 基本要求1.掌握位矢、位移、速度、加速度,角速度和角加速度等描述质点运动和运动变化的物理量。
2. 能借助于直角坐标计算质点在平面内运动时的速度、加速度。
3.能计算质点作圆周运动时的角速度和角加速度,切向加速度和法向加速度。
4.理解伽利略坐标,速度变换。
二、 基本内容1.位置矢量(位矢)位置矢量表示质点任意时刻在空间的位置,用从坐标原点向质点所在点所引的一条有向线段r 表示。
r 的端点表示任意时刻质点的空间位置。
r同时表示任意时刻质点离坐标原点的距离及质点位置相对坐标系的方位。
位矢是描述质点运动状态的物理量之一。
注意:(1)瞬时性:质点运动时,其位矢是随时间变化的,即()t r r=;(2)相对性:用r描述质点位置时,对同一质点在同一时刻的位置,在不同坐标系中r 可以是不相同的。
它表示了r的相对性,也反映了运动描述的相对性;(3)矢量性:r为矢量,它有大小,有方向,服从几何加法。
在直角坐标系Oxyz 中k z j y i x r++= 222z y x r r ++==r z r y r x ===γβαcos ,cos ,cos质点运动时, ()t r r= (运动方程矢量式)()()()⎪⎩⎪⎨⎧===t z z t y y t x x (运动方程标量式)。
2.位移()(),j y i x t r t t r r ∆+∆=-∆+=∆ r∆的模()()22y x r ∆+∆=∆ 。
注意:(1)r∆与r ∆:前者表示质点位置变化,是矢量,同时反映位置变化的大小和方位;后者是标量,反映质点位置离开坐标原点的距离的变化。
(2)r∆与s ∆:s ∆表示t —t t ∆+时间内质点通过的路程,是标量,只有质点沿直线运动时两者大小相同或0→∆t 时,s r ∆=∆。
3. 速度dtrd v =是描述位置矢量随时间的变化。
在直角坐标系中k v j v i v k dtdz j dt dy i dt dx dt r d v z y x++=++==222222z y x v v v dt dz dt dy dt dx v v ++=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛==v的方向:在直线运动中,v>0表示沿坐标轴正向运动,v <0表示沿坐标轴负向运动。
大学物理第一章 质点运动学-习题及答案

第一章 质点运动学1-1 一质点在平面上运动,已知质点位置矢量的表示式为j i r 22bt at += (其中b a ,为常量) 则该质点作(A )匀速直线运动 (B )变速直线运动(C )抛物线运动 (D )一般曲线运动 [B]解:由j i rv bt at t 22d d +==知 v 随t 变化,质点作变速运动。
又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。
故该质点作变速直线运动。
1-2 质点作曲线运动,r 表示位置矢量,s 表示路程,t a 表示切向加速度,下列表达式中,① a t v =d ② v t r =d ③ v t s =d d ④ t a t =d d v (A )只有(1)、(4)是对的。
(B )只有(2)、(4)是对的。
(C )只有(2)是对的。
(D )只有(3)是对的。
[D]解:由定义:t vt a d d d d ≠=v ; t r t s t v d d d d d d ≠==r ; t t v a d d d d v ≠=τ只有③正确。
1-3 在相对地面静止的坐标系内,A 、B 二船都以21s m -⋅的速率匀速行驶,A 船沿x 轴正向,B 船沿y 轴正向。
今在A 船上设置与静止坐标系方向相同的坐标系(x ,y 方向单位矢用j i ,表示),那么在A 船上的坐标系中,B 船的速度(以1s m -⋅为单位)为(A )j i 22+ (B )j i 22+-(C )j i 22-- (D )j i 22- [B]解:由i v 2=对地A ,j v 2=对地B 可得 A B A B 地对对地对v v v +=⎰对地对地A B v v -=i j 22-=j i 22+-= (1s m -⋅)1-4 一质点沿x 方向运动,其加速度随时间变化关系为)SI (23t a +=如果初始时质点的速度0v 为51s m -⋅,则当t 为3s 时,质点的速度1s m 23-⋅=v解:⎰+=tta v v 00d13s m 23d )23(5-⋅=++=⎰tt1-5 一质点的运动方程为SI)(62t t x -=,则在t 由0至4s 的时间间隔内,质点的位移大小为 8m ,在t 由0到4s 的时间间隔内质点走过的路程为 10m 。
大学物理知识点总结

Br ∆A rB ryr ∆第一章质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r 称为位矢 位矢r xi yj =+,大小 2r r x y ==+运动方程()r r t =运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆△,2r x =∆+△路程是△t 时间内质点运动轨迹长度s ∆是标量。
明确r ∆、r ∆、s ∆的含义(∆≠∆≠∆r r s ) 2. 速度(描述物体运动快慢和方向的物理量)平均速度xyr x y i j ij t t t瞬时速度(速度) t 0r drv limt dt∆→∆==∆(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x +=+==,2222yx v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛== ds dr dt dt= 速度的大小称速率。
3. 加速度(是描述速度变化快慢的物理量)平均加速度va t ∆=∆ 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆△ a 方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x二.抛体运动运动方程矢量式为 2012r v t gt =+分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量:线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。
大学物理圆周运动及其描述质点运动学的基本问题
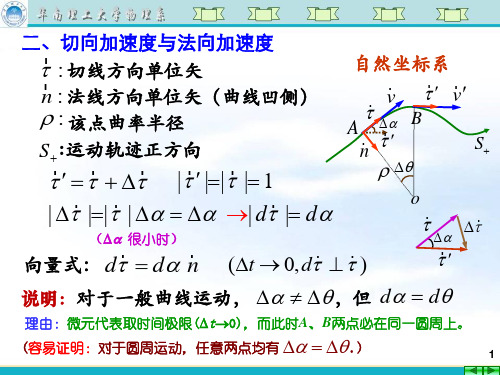
解:设 t = 0 时质点位于 s = 0 的P点处。
①
a
dv dt
d 2s dt 2
k
an
v2 R
(v0
kt)2 R
a
aτ2 an2
(v0 kt)2 (kR)2 R
12
② 令 a = k ,即 a
解得 t v0 / k
(v0 kt)2 (kR)2 k R
③ 当a = k 时,t = v0 /k ,由此可求得质点历经的路
ar与vr方向的夹角:
arctan an
a
讨论
0 ,
2
a 0,
v
90o, a 0, v const
,
2
a 0,
v
r
a
S
r an
r
ar
r a
ar
3
例:半径为R的滑轮可绕中心轴转动。绕于滑轮上的无形
变细绳其下端挂一重物。已知重物按 h = (1/2)a1t2 的规律 下降,求轮沿上任一点 P 的加速度(设绳与轮之间无相
v | x | t
(t 0)
y
v0
l1
而 x l v v0
(三角形任意两边之差小于第三边)
h l2 v
l x
船速大于绳速
o
x2 x1
x
15
§1-5 质点运动学中的两类基本问题
第一类:
已知 rr rr (t), 求vr , ar , 用微分。
rr 微分 vr 微分 ar
第二类:
已知 ar 及初始条件 vr0、rr0, 求vr、rr,用积分。
1 2
at 2
2 02 2 ( 0 ) v2 v02 2a(s s0 )
大学物理12圆周运动

基本参考系
S'系(O' x' y' z')
运动参考系
u是S’系相对S系
运动的速度
1-3 相对运动
yy'
P P'
*
oo'
xx'
t0
y
o
P
y'
D
r
P'
uQ
r'
xx'
ut o' t t
第一章 质点运动学
22
物理学
第五版
位移关系
r r'D 或 r r'ut
速度变换
r r' u t t v v'u
理解伽利略速度变换式, 并会用它求简 单的质点相对运动问题.
第一章 质点运动学
2
物理学
第五版
质点运动的自然坐标描述
自然坐标系 —— 坐标原点固接 于质点, 坐标轴沿质点运动轨道
1-2 圆周ev运t 动 evt B
的切向和法向的坐标系,叫做自
然坐标系。切向以质点前进方向 A
为 侧正方,向记 为做 正,ev记t ,做法ev向n以。曲线凹
y
A
r
二 圆周运动的角速度
❖ 角坐标 (t)
o
❖角位移
y
xx
B
❖ 角速度
lim
d
t0 t dt
r A
o
x
单位:rad·s-1
第一章 质点运动学
4
物理学
第五版
1-2 圆周运动
❖ 速率 v lim Δs r lim Δθ
Δt0 Δt
Δt0 Δt
大学物理上部分试题及答案 .

第一章 质点运动学一、填空题1. 一质点作半径为R 的匀速圆周运动,在此过程中质点的切向加速度的方向 改变 ,法向加速度的大小 不变 。
(填“改变”或“不变”)2. 一质点作半径为 0.1 m 的圆周运动,其角位移随时间t 的变化规律是= 2 + 4t 2 (SI)。
在t =2 s 时,它的法向加速度大小a n =_______25.6_______m/s 2;切向加速度大小a t =________0.8______ m/s 2。
3. 一质点在OXY 平面内运动,其运动方程为22,192x t y t ==-,则质点在任意时刻的速度表达式为 j t i42-=ν ;加速度表达式为j a 4-=。
4、沿半径为R 的圆周运动,运动学方程为 212t θ=+ (SI) ,则t时刻质点的法向加速度大小为a n =( 16 R t 2 ) ;角加速度β=( 4 rad /s 2 )(1 分).5. 一质点作半径为 0.1 m 的圆周运动,其角位置的运动学方程为:2214πt +=θ,则其切向加速度大小为t a =______0.1______2m s -⋅, 第1秒末法向加速度的大小为n a =______0.1______2m s -⋅.6.一小球沿斜面向上作直线运动,其运动方程为:245t t s -+=,则小球运动到最高点的时刻是t =___2___s .7、一质点在OXY 平面内运动,其运动方程为22,192x t y t ==-,则质点在任意时刻的速度表达式为( j t i42-=ν );加速度表达式为( j a 4-= )。
8. 一质点沿半径R=0.4 m 作圆周运动,其角位置θ=2+3t 2,在t=2s 时,它的法向加速度n a =( 57.6 )2/s m ,切向加速度t a =( 2.4 ) 2/s m 。
9、已知质点的运动方程为j t i t r )2(22-+=,式中r 的单位为m ,t 的单位为s 。
大学物理知识点总结

大学物理知识点总结 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIANBr ∆A rB ryr ∆第一章质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r 称为位矢 位矢r xi yj =+,大小 2r r x y ==+运动方程 ()r r t =运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆△,2r x =∆+△路程是△t 时间内质点运动轨迹长度s ∆是标量。
明确r ∆、r ∆、s ∆的含义(∆≠∆≠∆r r s )2. 速度(描述物体运动快慢和方向的物理量)平均速度xyr x y i j ij t t t瞬时速度(速度) t 0r drv limt dt∆→∆==∆(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x +=+==,2222yx v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛== ds dr dt dt= 速度的大小称速率。
3. 加速度(是描述速度变化快慢的物理量)平均加速度va t ∆=∆ 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆△ a 方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x二.抛体运动运动方程矢量式为 2012r v t gt =+分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量:线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。
大学物理质点运动学总结

大学物理质点运动学总结一、引言在大学物理课程中,运动学是物理学的基础,它研究物体的运动状态和运动规律。
其中,质点运动学是运动学的一部分,主要研究质点的运动性质和运动规律。
下面将对大学物理质点运动学进行总结。
二、质点的运动描述1. 位置和位移质点在运动过程中,位置可以用空间直角坐标系或极坐标系来描述。
而位移是指物体从初始位置到最终位置的变化量,它是个矢量量,具有大小和方向。
2. 速度与速度的计算方法速度是指单位时间内位移的变化量,可以用瞬时速度和平均速度来描述。
瞬时速度是指某一瞬间的速度,可以通过求导位移对时间的导数得到。
平均速度是指物体在一段时间内总位移与总时间的比值。
3. 加速度与加速度的计算方法加速度是指单位时间内速度的变化量,也是个矢量量。
可以用瞬时加速度和平均加速度来描述。
瞬时加速度是指某一瞬间的加速度,可以通过求导速度对时间的导数得到。
平均加速度是指物体在一段时间内总速度变化与总时间的比值。
三、常见的运动规律1. 一维运动规律一维运动规律描述了在一条直线上运动的物体的运动规律。
其中最重要的是匀速直线运动规律和匀加速直线运动规律。
匀速直线运动规律指出,当物体在匀速直线运动时,其位移与时间成正比。
匀加速直线运动规律指出,在匀加速直线运动中,物体的位移与时间的关系是二次函数。
2. 斜抛运动规律斜抛运动是指物体沿着一个初速度方向在空中做抛体运动的一种情况。
在斜抛运动中,物体的水平速度保持恒定,垂直速度受到重力的作用而发生改变。
斜抛运动的水平运动和垂直运动可以分开来考虑,通过合成两个运动,可以得出物体的轨迹和运动规律。
3. 圆周运动规律圆周运动是指物体在半径相同的圆内以恒定速度做匀速圆周运动的一种情况。
在圆周运动中,质点的速度方向始终垂直于半径的方向,因此质点在圆周上的运动轨迹是一个圆。
圆周运动的相关公式可以由质点完成单位时间所走过的弧长与所需的时间的比值来推导。
四、运动学的应用1. 自由落体问题自由落体是指物体在无空气阻力情况下,在重力作用下自由垂直下落的一种运动。
一质点沿半径为r的圆周运动,运动学方程为

一质点沿半径为r的圆周运动,运动学方
程为
运动学是研究物体运动的一门科学,它是力学的重要组成部分,是研究物体运动规律的重要手段。
一质点沿半径为r的
圆周运动的运动学方程是:x=rcosα,y=rsinα,v=rω,a=rα,
其中,x,y分别为一质点在圆周上的横纵坐标,v为一质点在
圆周上的速度,a为一质点在圆周上的加速度,r为圆周半径,α为一质点在圆周上的角度,ω为一质点在圆周上的角速度。
一质点沿半径为r的圆周运动是一种特殊的直线运动,它
是一种定向运动,运动方向不断改变,运动的轨迹是一个圆周。
运动的过程中,一质点的位置不断变化,但是它的瞬时速度一直保持定值,而加速度一直保持为零,这就是直线运动的最大的特点。
一质点沿半径为r的圆周运动的运动学方程,是我们研究
物体运动规律的重要依据。
它可以帮助我们准确计算物体在圆周上的运动轨迹,这对我们研究物体运动规律,研究物理学和力学问题具有重要意义。
此外,一质点沿半径为r的圆周运动的运动学方程,也可
以帮助我们研究复杂的物理系统,比如:人体的运动、机器人的运动、木块的旋转等。
这些复杂的物理系统,都可以用一质点沿半径为r的圆周运动的运动学方程来描述,这样就可以更
准确地研究这些复杂的物理系统。
总之,一质点沿半径为r的圆周运动的运动学方程,是我
们研究物体运动规律的重要依据,它可以帮助我们准确计算物体在圆周上的运动轨迹,也可以帮助我们研究复杂的物理系统,已达到更准确的研究结果。
大学物理课后答案第1章质点运动学习题解答

,解得
(2) , ,
1-13质点M作平面曲线运动,自O点出发经图示轨迹运动到C点。图中,OA段为直线,AB、BC段分别为不同半径的两个1/4圆周。设 时,M在 点,已知运动方程为 (SI),求 s时刻,质点M的切向加速度和法向加速度的大小。
解: 时 此时质点在大圆上
…
时
1-14一质点沿半径为 的圆周按 的规律运动,其中 和 都是常数。求:(1)质点在 时刻的加速度;(2) 为何值时,加速度在数值上等于 ;(3)当加速度大小为 时质点已沿圆周运行了几圈
解:
,
&
1-8一艘正在沿直线行驶的快艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即 ,式中 为正常数。试证明快艇在关闭发动机后又行驶 距离时的速度为 ,式中 是发动机关闭瞬时的速度。
解:
,
1-9一飞轮的转速在5s内由900rev/min均匀地减到800rev/min。求:(1)飞轮的角加速度;(2)在此5s内飞轮的总转数;(3)再经几秒飞轮将停止转动。
解: ,即
~
1-5一质点在 平面内运动,运动方程为 (SI)。(1)求质点运动的轨道方程并画出运动轨道;(2)计算1s末和2s末质点的瞬时速度和瞬时加速度;(3)在什么时刻质点的位置矢量与其速度矢量恰好垂直这时,它们的 、 分量各为多少(4)在什么时刻质点离原点最近算出这一距离。
解: , ,
(1) ,
消t,得轨道方程: ,
其曲线为开口向下的抛物线,如右图。
(2) ,
,
(3) ,
*
解得: ,
时, , , ,
时, , , ,
以上物理量均为国际单位。
(4)
令 ,解得
1-6一物体沿 轴运动,其加速度和位置的关系满足 (SI)。物体在 处的速度为10 m/s,求物体的速度和位置的关系。
大学物理上-知识点

1、 质点运动量的描述(1) 位置矢量r:运动方程: k t z j t y i t x t r )()()()(++=;模为 222z y x r ++=位移矢量:)()(t r t t r r -∆+=∆;注意:一般r r ∆≠∆(2) 速度:x y z dr v v i v j v k dt ==++,分量式:x y z v ,v ,v dx dy dzdt dt dt===; 速度的大小:222x y z dr ds v v v v v dt dt==++=≡,v 为速率。
速度方向沿曲线切线指向运动的前方。
平均速度:x y z r v v i v j v k t ∆==++∆,分量式:,,x y z x y zv v v t t t∆∆∆===∆∆∆ (3) 加速度:22x y z dv d r a a i a j a k dt dt===++,加速度大小:222xy z a a a a =++ 分量式:222222,,y x z x y z dv dv dv d x d y d za a a dt dt dt dt dt dt ======; 自然坐标系:t e v v =,n n t t e a e a a+=,t dv a dt =(有正负!),2n v a ρ=,此处v 为速率,ρ为曲率半径。
2、 圆周运动:角位置θ,角速度d dt θω=,角加速度:d dtωα=; 角量与线量的关系:θR s =,R v ω=,t dv a R dt α==,22n va R Rω==3、 抛体运动:0000200000cos 1sin 2x x x x y y y y a v v v x v ta g v v gt v gt y v t gt θθ=→==→=⎧⎪⎨=-→=-=-→=-⎪⎩其中0θ为起抛角。
22t n a a g += 4、 相对运动速度变换: AB AC CB v v v =+ 或表示为 AB AC BC v v v =- 加速度变换:AB AC CB a a a =+ 或 AB AC BC a a a =-(注意:这是矢量加法,用平行四边形作图或分解为分量计算;注意下标的规律。
(完整版)大学物理质点运动学习题及答案(2)

第1章质点运动学习题及答案1.|∆r |与∆r 有无不同?d r d v dr dv 和有无不同?和有无不同?其不同在哪里?试举例说明.d t d t dt dt解:|∆r |与∆r 不同.|∆r |表示质点运动位移的大小,而∆r 则表示质点运动时其径向长度的增量;d r d r dr dr 和不同.表示质点运动速度的大小,而则表示质点运动速度的径向分d t d t dt dt量;d v d v dv dv 和不同.表示质点运动加速度的大小,而则表示质点运动加速度的切向分量.d t d t dt dt2.质点沿直线运动,其位置矢量是否一定方向不变?质点位置矢量方向不变,质点是否一定做直线运动?解:质点沿直线运动,其位置矢量方向可以改变;质点位置矢量方向不变,质点一定做直线运动.3.匀速圆周运动的速度和加速度是否都恒定不变?圆周运动的加速度是否总是指向圆心,为什么?解:由于匀速圆周运动的速度和加速度的方向总是随时间发生变化的,因此,其速度和加速度不是恒定不变的;只有匀速圆周运动的加速度总是指向圆心,故一般来讲,圆周运动的加速度不一定指向圆心.4.一物体做直线运动,运动方程为x =6t -2t ,式中各量均采用国际单位制,求:(1)第二秒内的平均速度(2)第三秒末的速度;(3)第一秒末的加速度;(4)物体运动的类型。
23x(t )=6t 2-2t 3解:由于:v(t )=dx =12t -6t 2dtdv a(t )==12-12t dtx (2)-x (1)=4(ms -1)2-12-1所以:(1)第二秒内的平均速度:v =(2)第三秒末的速度:v (3)=12⨯3-6⨯3=-18(ms )(3)第一秒末的加速度:a (1)=12-12⨯1=0(ms )(4)物体运动的类型为变速直线运动。
-2=10t i +5t j ,式中的r ,t 分别以m,s 为单位,试求;5.一质点运动方程的表达式为r (t )(1)质点的速度和加速度;(2)质点的轨迹方程。
大学物理第一章 质点运动学

a 常量,v v0 at,
•匀变速直线运动:
1 2 x x0 v0t at 2 2 2 v v0 2a( x x0 )
注意:以上各式仅适用于匀加速情形。
t t
要求 v( y ),可由
dv dv dy dv a v dt dy dt dy
有
积分得
v
dv kv v dy
2
dv kdy v
y dv v ky v0 v k 0 dy ln v0 ky, v v0e
1-3 曲线运动
一.运动的分解
如图,A、B为在同一高度的两个小球。在同一 时刻,使A球自由落体,B球沿水平方向射出,虽然 两球的轨道不同,但是两球总是在同一时刻落地。 说明,B球的运动可分解为在水平方向作匀速直线运 动,在竖直方向作自由落体运动。
其大小注意a aa a2 x 2 y2 z
dv dv a a dt dt
•描述质点运动的状态参量的特性 状态参量包括
r , v, a
应注意它们的
(1)矢量性。注意矢量和标量的区别。
(2)瞬时性。注意瞬时量和过程量的区别。 (3)相对性。对不同参照系有不同的描述。
1 gx y xtg 2 2 2 v0 cos 19.6 2 50tg 50tg 19.6(1 tg ) 2 cos
两边一起定积分得
dv dv adt kv dt kdt 2 v
2
v
v0
t dv k dt 2 0 v
v0 v(t ) kv0t 1
03运动学圆周运动 (自然坐标系、角速度、角加速度、切向加速度、法向加速度)

这时加速度可以表示为 a aτ t an n
6
由于τ与n相互垂直,加速度a的大小与aτ 、an的 关系为 2 2
a a an
例1、半径R=0.5米的飞轮绕中心轴转动, 其运动函数 为θ=t3+3t(SI)求t=2秒时,轮缘上一点的角速度角加速 度以及切向加速度、法向加速度。 解:ω=3t2+3
dr d d v R sin i R cos j R d ( sin i cos j ) dt dt dt dt
Y
V
r
d R [cos( )i sin( ) j ] dt 2 2
X
括号中的项是与r垂直的单位矢量
d lim t 0 t dt
2
平均角加速度 t
t 0
瞬时角加速度 lim d
t dt
(SI)单位:rad/s2 角速度与角加速度都是矢量,角速度的方向由右手定 则确定。(规定用右手螺旋定则来判定:四指方向为 绕向,大拇指方向为角速度方向!! ) α与ω同向。质点作加速圆周运动。
an=gcos γ =gV x/V=9.13m/s2
aτ=gcosβ=gVy/V=3.53m/s2
ρ=V2/an=25.03m
11
5 质点运动学小结: 1、描述运动的物理量 :t、Δt、r、Δr、v、a 、 s dv dr 加速度: a 2、定义:速度 v dt dt 对一维的情况:v=dx/dt a=dv/dt 3、质点运动学的两类问题: 1)已知运动方程,求速度、加速度。 解法:用求导数的方法解决。 2)已知速度(或加速度)及初始条件求运动方程。
△τ=1× △ θ 当△t→0时, dτ=1× d θ、方向指向曲率中 心(即法向)。 d d n dt dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v
v v(t t )
v v n ( t )
θ
2.切向加速度 a
Chapter 1. 质点运动学 主编 v v a a lim lim t 0 t t 0 t
P. 16 / 21 .
讨论
对于作曲线运动的物体,以下几种说法中哪一 种是正确的: (A)切向加速度必不为零; (B)法向加速度必不为零(拐点处除外); (C)由于速度沿切线方向,法向分速度必为零, 因此法向加速度必为零; (D)若物体作匀速率运动,其总加速度必为零;
(E)若物体的加速度 变速率运动 .
P. 5 / 21 .
匀变速圆周运动 特征:角加速度 = 常数
设: t 0 时, 0 , 0
2 ( 0 )
2 2 0
d
dt d dt
d dt
0
t
t0
0 t
2 1 0 0t t 2
0 t t 1 0 0
.rad/s 2 2 2 an r 10 m/s 2 at r 10 .m/s
a at2 an2 10 2 1
an 加速度与速度方向夹角 arc(tan ) 72 21 at
Chapter 1. 质点运动学 主编:杨茂田 §1. 3 圆周运动
P. 2 / 21 .
圆周运动的角量描述
(一)在极坐标系中可用一组角量描述:
☻角位置:极角 θ (rad)
☻角位置变化:角位移 △θ ( rad ) ☻角位置变化快慢:角速度 ω
(rad/s)
s
r o
P
ω lim dθ t 0 t dt ds v ω 代入 ds rdθ rdt r
即
v r
Chapter 1. 质点运动学 主编:杨茂田 §1. 3 圆周运动
P. 3 / 21 .
☻角速度变化快慢: 角加速度 (rad/s2)
2 d d lim t 0 t dt dt 2
s
P
☻角位置变动快慢:角速度 ω
(rad/s)
ω lim dθ t 0 t dt ds v ω 代入 ds rdθ rdt r
4.一般曲线运动的 a n 与 a
Chapter 1. 质点运动学 主编:杨茂田§1. 3 圆周运动
P. 15 / 21 .
作辅助园:半径r =曲率半径 v2 ˆn an e
dv ˆ a e dt
C a an a
Chapter 1. 质点运动学 主编:杨茂田§1. 3 圆周运动
o
P
(t )
☻ a an a
2 2 2 dv v dv a a a ( ) ( ) 大小: dt (对曲线运动) r dt 2 n 2
方向: arctg (
an ) a
Chapter 1. 质点运动学 主编:杨茂田§1. 3 圆周运动
a
an
o
v
v v(t t )
v v n ( t )
θ
2.切向加速度 a
Chapter 1. 质点运动学 主编:杨茂田§1. 3 圆周运动
P. 12 / 21 .
v v a a lim lim t 0 t t 0 t
P. 10 / 21 .
(1)式两边同除△t : lim v lim vn lim v t 0 t t 0 t t 0 t
v(t t )
v (t ) ae ˆ
P P
a an a 1.法向加速度 a n
a
P
v v(t t ) v(t ) v
d ( r ) d dv a r r dt dt dt
2 n 2
a
an
o
(t )
☻ a an a
2 2 2 dv v dv a a a ( ) ( ) 大小: dt (对曲线运动) r dt
a
P
v v(t t ) v(t ) v 1.法向加速度 a n v n v n an an lim lim t 0 t t 0 t lim v v d v t 0 t dt 2 2 v an v r r
切向加速度 法向加速度
a
ˆ e n θ r an
ω( t )
o
v n v n an an lim lim t 0 t t 0 t lim v v d v t 0 t dt
2 v an v r r 2
P. 14 / 21 .
☻ an 由 v 方向变化引起,指向圆心; a a由 v 大小变化引起, 当 v 0 时, a 与 v 同方向,否则相反。 a an
o
P
(t )
v2 ˆ n r 2 e ˆn an e r dv ˆ r e ˆ a e dt
Chapter 1. 质点运动学 主编:杨茂田 §1. 3 圆周运动
P. 1 / 21 .
一 平面极坐标
在平面上取定一点O,称为极点。从O出发引一条 射线Ox,称为极轴。平面上任一点P的位置就可以用 线段OP的长度ρ以及从Ox到OP的角度θ来确定,有序 数对(ρ,θ)就称为P点的极坐标,记为P(ρ,θ); ρ称为P点的极径,θ称为P点的极角。
(1 )
o
v :为速度增量在切线方向分量
v v(t t ) v(t ) v
vn :为速度增量在法线方向分量
v
vn v(t ) θ vθ
v v(t t )
v v n ( t )
θ
Chapter 1. 质点运动学 主编:杨茂田§1. 3 圆周运动
P. 9 / 21 .
(1)式两边同除△t : lim v lim vn lim v t 0 t t 0 t t 0 t
v(t t )
ˆ e
v( t )
ˆ n θ r e
P
ω( t )
分解: v vn v
方向: arctg (
an ) a
Chapter 1. 质点运动学 主编:杨茂田§1. 3 圆周运动
P. 13 / 21 .
☻ an 由 v 方向变化引起,指向圆心; a a由 v 大小变化引起, 当 v 0 时, a 与 v 同方向,否则相反。 a an
en
Chapter 1. 质点运动学 主编:杨茂田 §1. 3 圆周运动
P. 8 / 21 .
切向与法向加速度
质点作圆周运动。建立自然
v(t t )
ˆ e
v( t )
坐标系如图所示。
ˆ n θ r e
(1 )
P
ω( t )
分解: v vn v
o
v :为速度增量在切线方向分量
v v(t t ) v(t ) v
vn :为速度增量在法线方向分量
v
vn v(t ) θ vθ
v v(t t )
v v n ( t )
θ
Chapter 1. 质点运动学 主编:杨茂田 §1. 3 圆周运动
为恒矢量,它一定作匀 a
Chapter 1. 质点运动学 主编:杨茂田§1. 3 圆周运动
P. 17 / 21 .
例题1
一质点做半径为r=10m的圆周运动,角加速度 2 为 .rad/s ,若质点由静止开始运动,求质点 在第一秒末的角速度,法向加速度和切向加速度, 总加速度的大小和方向?
即
r r o
v r
Chapter 1. 质点运动学 主编:杨茂田 §1. 3 圆周运动
P. 4 / 21 .
☻角速度变动快慢: 角加速度 (rad/s2)
2 d d lim t 0 t dt dt 2
Chapter 1. 质点运动学 主编:杨茂田 §1. 3 圆周运动
0dt t )dt d t(
0 0
t
Chapter 1. 质点运动学 主编:杨茂田 §1. 3 圆周运动
P. 6 / 21 .
(二)、自然坐标系
直角坐标系中:
dv dvy ˆ dvz ˆ dv x ˆ ˆ a i j k ax ˆ i ay ˆ j azk dt dt dt dt
如何直观反映加速度 a 是怎样随着速度的大小和方
向变化而变化
Chapter 1. 质点运动学 主编:杨茂田 §1. 3 圆周运动
P. 7 / 21 .
二
自然坐标
在运动质点轨道上任取 一点为坐标系原点,在 该点处沿轨道的切线和 法线方向建立两个互相 垂直的坐标系
A
et
et en
切线方向指向质点前进方向 法线方向指向轨迹曲线凹侧
