Kernel Method 核回归 核方法
kernel密度法

kernel密度法(原创版)目录1.介绍 Kernel 密度估计法2.Kernel 密度法的原理3.Kernel 密度法的应用4.Kernel 密度法的优缺点正文一、介绍 Kernel 密度估计法Kernel 密度估计法是一种常用的非参数统计方法,用于估计连续型随机变量的概率密度函数。
该方法通过核函数将数据映射到高维空间,在高维空间中计算密度,再将密度映射回原空间。
Kernel 密度估计法具有较强的理论性质和实用性。
二、Kernel 密度法的原理Kernel 密度法的基本思想是利用核函数将原始数据映射到高维空间,然后使用高维空间中的数据计算密度。
核函数的选择和带宽的确定是Kernel 密度估计法的关键。
1.核函数:核函数是一种对称的函数,将原始数据映射到高维空间。
常用的核函数有高斯核、线性核、多项式核等。
2.带宽:带宽是核函数中的重要参数,决定了核函数的形状。
带宽越小,核函数越尖锐,估计的密度函数越接近真实密度函数;带宽越大,核函数越平缓,估计的密度函数越平滑。
三、Kernel 密度法的应用Kernel 密度法广泛应用于数据分析、信号处理、模式识别等领域,具有重要的实际意义。
1.数据分析:Kernel 密度法可以用于分析数据的分布特征,如均值、方差等。
2.信号处理:Kernel 密度法可以用于信号的滤波、去噪等。
3.模式识别:Kernel 密度法可以用于图像识别、语音识别等领域。
四、Kernel 密度法的优缺点1.优点:Kernel 密度法具有较强的理论性质,可以估计任意形状的密度函数;同时,Kernel 密度法具有较好的鲁棒性,能够处理含有异常值的数据。
kernel密度法

核密度估计(Kernel Density Estimation,简称KDE)是一种非参数统计方法,用于估计一个概率密度函数。
它常用于对数据集进行平滑处理,以更好地理解数据的分布特征。
核密度估计的基本思想是,对每个数据点放置一个核(通常是一个概率密度函数,如正态分布),然后通过对所有核进行求和来估计整体的概率密度函数。
核的宽度通常由一个参数(带宽)控制,带宽的选择会影响估计结果的平滑程度。
数学上,给定数据集 \(\{x_1, x_2, ..., x_n\}\),核密度估计的公式为:
\[ \hat{f}(x) = \frac{1}{n} \sum_{i=1}^{n}
K\left(\frac{x - x_i}{h}\right) \]
其中,\(K\) 是核函数,\(h\) 是带宽。
常用的核函数包括正态分布(也称为高斯核)和Epanechnikov 核。
带宽的选择对估计结果影响较大,选择合适的带宽是核密度估计中的一个重要问题。
核密度估计广泛应用于数据分析、可视化和模型评估等领域,它可以帮助揭示数据的分布情况,识别潜在的模式和趋势。
AI术语

人工智能专业重要词汇表1、A开头的词汇:Artificial General Intelligence/AGI通用人工智能Artificial Intelligence/AI人工智能Association analysis关联分析Attention mechanism注意力机制Attribute conditional independence assumption属性条件独立性假设Attribute space属性空间Attribute value属性值Autoencoder自编码器Automatic speech recognition自动语音识别Automatic summarization自动摘要Average gradient平均梯度Average-Pooling平均池化Accumulated error backpropagation累积误差逆传播Activation Function激活函数Adaptive Resonance Theory/ART自适应谐振理论Addictive model加性学习Adversarial Networks对抗网络Affine Layer仿射层Affinity matrix亲和矩阵Agent代理/ 智能体Algorithm算法Alpha-beta pruningα-β剪枝Anomaly detection异常检测Approximation近似Area Under ROC Curve/AUC R oc 曲线下面积2、B开头的词汇Backpropagation Through Time通过时间的反向传播Backpropagation/BP反向传播Base learner基学习器Base learning algorithm基学习算法Batch Normalization/BN批量归一化Bayes decision rule贝叶斯判定准则Bayes Model Averaging/BMA贝叶斯模型平均Bayes optimal classifier贝叶斯最优分类器Bayesian decision theory贝叶斯决策论Bayesian network贝叶斯网络Between-class scatter matrix类间散度矩阵Bias偏置/ 偏差Bias-variance decomposition偏差-方差分解Bias-Variance Dilemma偏差–方差困境Bi-directional Long-Short Term Memory/Bi-LSTM双向长短期记忆Binary classification二分类Binomial test二项检验Bi-partition二分法Boltzmann machine玻尔兹曼机Bootstrap sampling自助采样法/可重复采样/有放回采样Bootstrapping自助法Break-Event Point/BEP平衡点3、C开头的词汇Calibration校准Cascade-Correlation级联相关Categorical attribute离散属性Class-conditional probability类条件概率Classification and regression tree/CART分类与回归树Classifier分类器Class-imbalance类别不平衡Closed -form闭式Cluster簇/类/集群Cluster analysis聚类分析Clustering聚类Clustering ensemble聚类集成Co-adapting共适应Coding matrix编码矩阵COLT国际学习理论会议Committee-based learning基于委员会的学习Competitive learning竞争型学习Component learner组件学习器Comprehensibility可解释性Computation Cost计算成本Computational Linguistics计算语言学Computer vision计算机视觉Concept drift概念漂移Concept Learning System /CLS概念学习系统Conditional entropy条件熵Conditional mutual information条件互信息Conditional Probability Table/CPT条件概率表Conditional random field/CRF条件随机场Conditional risk条件风险Confidence置信度Confusion matrix混淆矩阵Connection weight连接权Connectionism连结主义Consistency一致性/相合性Contingency table列联表Continuous attribute连续属性Convergence收敛Conversational agent会话智能体Convex quadratic programming凸二次规划Convexity凸性Convolutional neural network/CNN卷积神经网络Co-occurrence同现Correlation coefficient相关系数Cosine similarity余弦相似度Cost curve成本曲线Cost Function成本函数Cost matrix成本矩阵Cost-sensitive成本敏感Cross entropy交叉熵Cross validation交叉验证Crowdsourcing众包Curse of dimensionality维数灾难Cut point截断点Cutting plane algorithm割平面法4、D开头的词汇Data mining数据挖掘Data set数据集Decision Boundary决策边界Decision stump决策树桩Decision tree决策树/判定树Deduction演绎Deep Belief Network深度信念网络Deep Convolutional Generative Adversarial Network/DCGAN深度卷积生成对抗网络Deep learning深度学习Deep neural network/DNN深度神经网络Deep Q-Learning深度Q 学习Deep Q-Network深度Q 网络Density estimation密度估计Density-based clustering密度聚类Differentiable neural computer可微分神经计算机Dimensionality reduction algorithm降维算法Directed edge有向边Disagreement measure不合度量Discriminative model判别模型Discriminator判别器Distance measure距离度量Distance metric learning距离度量学习Distribution分布Divergence散度Diversity measure多样性度量/差异性度量Domain adaption领域自适应Downsampling下采样D-separation (Directed separation)有向分离Dual problem对偶问题Dummy node哑结点Dynamic Fusion动态融合Dynamic programming动态规划5、E开头的词汇Eigenvalue decomposition特征值分解Embedding嵌入Emotional analysis情绪分析Empirical conditional entropy经验条件熵Empirical entropy经验熵Empirical error经验误差Empirical risk经验风险End-to-End端到端Energy-based model基于能量的模型Ensemble learning集成学习Ensemble pruning集成修剪Error Correcting Output Codes/ECOC纠错输出码Error rate错误率Error-ambiguity decomposition误差-分歧分解Euclidean distance欧氏距离Evolutionary computation演化计算Expectation-Maximization期望最大化Expected loss期望损失Exploding Gradient Problem梯度爆炸问题Exponential loss function指数损失函数Extreme Learning Machine/ELM超限学习机6、F开头的词汇Factorization因子分解False negative假负类False positive假正类False Positive Rate/FPR假正例率Feature engineering特征工程Feature selection特征选择Feature vector特征向量Featured Learning特征学习Feedforward Neural Networks/FNN前馈神经网络Fine-tuning微调Flipping output翻转法Fluctuation震荡Forward stagewise algorithm前向分步算法Frequentist频率主义学派Full-rank matrix满秩矩阵Functional neuron功能神经元7、G开头的词汇Gain ratio增益率Game theory博弈论Gaussian kernel function高斯核函数Gaussian Mixture Model高斯混合模型General Problem Solving通用问题求解Generalization泛化Generalization error泛化误差Generalization error bound泛化误差上界Generalized Lagrange function广义拉格朗日函数Generalized linear model广义线性模型Generalized Rayleigh quotient广义瑞利商Generative Adversarial Networks/GAN生成对抗网络Generative Model生成模型Generator生成器Genetic Algorithm/GA遗传算法Gibbs sampling吉布斯采样Gini index基尼指数Global minimum全局最小Global Optimization全局优化Gradient boosting梯度提升Gradient Descent梯度下降Graph theory图论Ground-truth真相/真实8、H开头的词汇Hard margin硬间隔Hard voting硬投票Harmonic mean调和平均Hesse matrix海塞矩阵Hidden dynamic model隐动态模型Hidden layer隐藏层Hidden Markov Model/HMM隐马尔可夫模型Hierarchical clustering层次聚类Hilbert space希尔伯特空间Hinge loss function合页损失函数Hold-out留出法Homogeneous同质Hybrid computing混合计算Hyperparameter超参数Hypothesis假设Hypothesis test假设验证9、I开头的词汇ICML国际机器学习会议Improved iterative scaling/IIS改进的迭代尺度法Incremental learning增量学习Independent and identically distributed/i.i.d.独立同分布Independent Component Analysis/ICA独立成分分析Indicator function指示函数Individual learner个体学习器Induction归纳Inductive bias归纳偏好Inductive learning归纳学习Inductive Logic Programming/ILP归纳逻辑程序设计Information entropy信息熵Information gain信息增益Input layer输入层Insensitive loss不敏感损失Inter-cluster similarity簇间相似度International Conference for Machine Learning/ICML国际机器学习大会Intra-cluster similarity簇内相似度Intrinsic value固有值Isometric Mapping/Isomap等度量映射Isotonic regression等分回归Iterative Dichotomiser迭代二分器10、K开头的词汇Kernel method核方法Kernel trick核技巧Kernelized Linear Discriminant Analysis/KLDA核线性判别分析K-fold cross validation k 折交叉验证/k 倍交叉验证K-Means Clustering K –均值聚类K-Nearest Neighbours Algorithm/KNN K近邻算法Knowledge base知识库Knowledge Representation知识表征11、L开头的词汇Label space标记空间Lagrange duality拉格朗日对偶性Lagrange multiplier拉格朗日乘子Laplace smoothing拉普拉斯平滑Laplacian correction拉普拉斯修正Latent Dirichlet Allocation隐狄利克雷分布Latent semantic analysis潜在语义分析Latent variable隐变量Lazy learning懒惰学习Learner学习器Learning by analogy类比学习Learning rate学习率Learning Vector Quantization/LVQ学习向量量化Least squares regression tree最小二乘回归树Leave-One-Out/LOO留一法linear chain conditional random field线性链条件随机场Linear Discriminant Analysis/LDA线性判别分析Linear model线性模型Linear Regression线性回归Link function联系函数Local Markov property局部马尔可夫性Local minimum局部最小Log likelihood对数似然Log odds/logit对数几率Logistic Regression Logistic 回归Log-likelihood对数似然Log-linear regression对数线性回归Long-Short Term Memory/LSTM长短期记忆Loss function损失函数12、M开头的词汇Machine translation/MT机器翻译Macron-P宏查准率Macron-R宏查全率Majority voting绝对多数投票法Manifold assumption流形假设Manifold learning流形学习Margin theory间隔理论Marginal distribution边际分布Marginal independence边际独立性Marginalization边际化Markov Chain Monte Carlo/MCMC马尔可夫链蒙特卡罗方法Markov Random Field马尔可夫随机场Maximal clique最大团Maximum Likelihood Estimation/MLE极大似然估计/极大似然法Maximum margin最大间隔Maximum weighted spanning tree最大带权生成树Max-Pooling最大池化Mean squared error均方误差Meta-learner元学习器Metric learning度量学习Micro-P微查准率Micro-R微查全率Minimal Description Length/MDL最小描述长度Minimax game极小极大博弈Misclassification cost误分类成本Mixture of experts混合专家Momentum动量Moral graph道德图/端正图Multi-class classification多分类Multi-document summarization多文档摘要Multi-layer feedforward neural networks多层前馈神经网络Multilayer Perceptron/MLP多层感知器Multimodal learning多模态学习Multiple Dimensional Scaling多维缩放Multiple linear regression多元线性回归Multi-response Linear Regression /MLR多响应线性回归Mutual information互信息13、N开头的词汇Naive bayes朴素贝叶斯Naive Bayes Classifier朴素贝叶斯分类器Named entity recognition命名实体识别Nash equilibrium纳什均衡Natural language generation/NLG自然语言生成Natural language processing自然语言处理Negative class负类Negative correlation负相关法Negative Log Likelihood负对数似然Neighbourhood Component Analysis/NCA近邻成分分析Neural Machine Translation神经机器翻译Neural Turing Machine神经图灵机Newton method牛顿法NIPS国际神经信息处理系统会议No Free Lunch Theorem/NFL没有免费的午餐定理Noise-contrastive estimation噪音对比估计Nominal attribute列名属性Non-convex optimization非凸优化Nonlinear model非线性模型Non-metric distance非度量距离Non-negative matrix factorization非负矩阵分解Non-ordinal attribute无序属性Non-Saturating Game非饱和博弈Norm范数Normalization归一化Nuclear norm核范数Numerical attribute数值属性14、O开头的词汇Objective function目标函数Oblique decision tree斜决策树Occam’s razor奥卡姆剃刀Odds几率Off-Policy离策略One shot learning一次性学习One-Dependent Estimator/ODE独依赖估计On-Policy在策略Ordinal attribute有序属性Out-of-bag estimate包外估计Output layer输出层Output smearing输出调制法Overfitting过拟合/过配Oversampling过采样15、P开头的词汇Paired t-test成对t 检验Pairwise成对型Pairwise Markov property成对马尔可夫性Parameter参数Parameter estimation参数估计Parameter tuning调参Parse tree解析树Particle Swarm Optimization/PSO粒子群优化算法Part-of-speech tagging词性标注Perceptron感知机Performance measure性能度量Plug and Play Generative Network即插即用生成网络Plurality voting相对多数投票法Polarity detection极性检测Polynomial kernel function多项式核函数Pooling池化Positive class正类Positive definite matrix正定矩阵Post-hoc test后续检验Post-pruning后剪枝potential function势函数Precision查准率/准确率Prepruning预剪枝Principal component analysis/PCA主成分分析Principle of multiple explanations多释原则Prior先验Probability Graphical Model概率图模型Proximal Gradient Descent/PGD近端梯度下降Pruning剪枝Pseudo-label伪标记16、Q开头的词汇Quantized Neural Network量子化神经网络Quantum computer量子计算机Quantum Computing量子计算Quasi Newton method拟牛顿法17、R开头的词汇Radial Basis Function/RBF径向基函数Random Forest Algorithm随机森林算法Random walk随机漫步Recall查全率/召回率Receiver Operating Characteristic/ROC受试者工作特征Rectified Linear Unit/ReLU线性修正单元Recurrent Neural Network循环神经网络Recursive neural network递归神经网络Reference model参考模型Regression回归Regularization正则化Reinforcement learning/RL强化学习Representation learning表征学习Representer theorem表示定理reproducing kernel Hilbert space/RKHS再生核希尔伯特空间Re-sampling重采样法Rescaling再缩放Residual Mapping残差映射Residual Network残差网络Restricted Boltzmann Machine/RBM受限玻尔兹曼机Restricted Isometry Property/RIP限定等距性Re-weighting重赋权法Robustness稳健性/鲁棒性Root node根结点Rule Engine规则引擎Rule learning规则学习18、S开头的词汇Saddle point鞍点Sample space样本空间Sampling采样Score function评分函数Self-Driving自动驾驶Self-Organizing Map/SOM自组织映射Semi-naive Bayes classifiers半朴素贝叶斯分类器Semi-Supervised Learning半监督学习semi-Supervised Support Vector Machine半监督支持向量机Sentiment analysis情感分析Separating hyperplane分离超平面Sigmoid function Sigmoid 函数Similarity measure相似度度量Simulated annealing模拟退火Simultaneous localization and mapping同步定位与地图构建Singular Value Decomposition奇异值分解Slack variables松弛变量Smoothing平滑Soft margin软间隔Soft margin maximization软间隔最大化Soft voting软投票Sparse representation稀疏表征Sparsity稀疏性Specialization特化Spectral Clustering谱聚类Speech Recognition语音识别Splitting variable切分变量Squashing function挤压函数Stability-plasticity dilemma可塑性-稳定性困境Statistical learning统计学习Status feature function状态特征函Stochastic gradient descent随机梯度下降Stratified sampling分层采样Structural risk结构风险Structural risk minimization/SRM结构风险最小化Subspace子空间Supervised learning监督学习/有导师学习support vector expansion支持向量展式Support Vector Machine/SVM支持向量机Surrogat loss替代损失Surrogate function替代函数Symbolic learning符号学习Symbolism符号主义Synset同义词集19、T开头的词汇T-Distribution Stochastic Neighbour Embedding/t-SNE T–分布随机近邻嵌入Tensor张量Tensor Processing Units/TPU张量处理单元The least square method最小二乘法Threshold阈值Threshold logic unit阈值逻辑单元Threshold-moving阈值移动Time Step时间步骤Tokenization标记化Training error训练误差Training instance训练示例/训练例Transductive learning直推学习Transfer learning迁移学习Treebank树库Tria-by-error试错法True negative真负类True positive真正类True Positive Rate/TPR真正例率Turing Machine图灵机Twice-learning二次学习20、U开头的词汇Underfitting欠拟合/欠配Undersampling欠采样Understandability可理解性Unequal cost非均等代价Unit-step function单位阶跃函数Univariate decision tree单变量决策树Unsupervised learning无监督学习/无导师学习Unsupervised layer-wise training无监督逐层训练Upsampling上采样21、V开头的词汇Vanishing Gradient Problem梯度消失问题Variational inference变分推断VC Theory VC维理论Version space版本空间Viterbi algorithm维特比算法Von Neumann architecture冯·诺伊曼架构22、W开头的词汇Wasserstein GAN/WGAN Wasserstein生成对抗网络Weak learner弱学习器Weight权重Weight sharing权共享Weighted voting加权投票法Within-class scatter matrix类内散度矩阵Word embedding词嵌入Word sense disambiguation词义消歧23、Z开头的词汇Zero-data learning零数据学习Zero-shot learning零次学习。
核密度估计和非参数回归

核密度估计和⾮参数回归你可能听说过核密度估计(KDE:kernel density estimation)或⾮参数回归(non-parametric regression)。
你甚⾄可能在不知不觉的情况下使⽤它。
⽐如在Python中使⽤seaborn或plotly时,distplot就是这样,在默认情况下都会使⽤核密度估计器。
但是这些⼤概是什么意思呢?也许你处理了⼀个回归问题,却发现线性回归不能很好地⼯作,因为特性和标签之间的依赖似乎是⾮线性的。
在这⾥,核回归(kernel regression)可能是⼀种解决⽅案。
在这篇⽂章中,我们通过⽰例,并试图对内核估计背后的理论有⼀个直观的理解。
此外,我们还看到了这些概念在Python中的实现。
核回归图1:全球⾕歌搜索“chocolate”;x轴:时间,y轴:搜索百分⽐让我们从⼀个例⼦开始。
假设你是⼀个数据科学家,在⼀家糖果⼯⼚的巧克⼒部门⼯作。
你可能想要预测巧克⼒的需求基于它的历史需求,作为第⼀步,想要分析趋势。
2004-2020年的巧克⼒需求可能类似于图1中的数据。
显然,这是有季节性的,冬天的需求会增加,但是由于你对趋势感兴趣,你决定摆脱这些波动。
为此,你可以计算窗⼝为b个⽉的移动平均线,也就是说,对于每⼀个时刻t,你计算从t-b到t+b的时间段内需求的平均值。
更正式地说,如果我们有⼀段时间内观察到的数据X(1),…,X(n),即⼀个时间序列,窗⼝为b的移动平均值可以定义为从下图(图2)中可以看出,移动平均值是原始数据的平滑版本,平滑程度取决于带宽。
带宽越⼤,函数越平滑。
图2:窗⼝带宽为6、24和42的移动平均;x轴:时间,y轴:搜索百分⽐带宽的选择⾄关重要,但不清楚如何选择带宽。
如果带宽太⼩,我们可能⽆法摆脱季节性波动。
如果带宽太⼤,我们可能⽆法捕捉到趋势。
例如,如果我们选择带宽b = 0,则具有原始数据及其季节性。
相反,如果b = n,我们仅获得所有观测值的平均值,⽽看不到任何趋势。
Kernel Method 核回归 核方法

15
i =1
局部线性回归
ˆ E ( r ( x0 ) ) = ∑wi ( x0 ) r ( xi )
n
r ( xi ) ≈ r ( x0 ) + r′ ( x0 )( xi − x0 ) +
r′′( x0 ) 2 xi − x0 ) ( 2
局部线性回归通过自动修改核,将偏差降至一阶
≈ r ( x0 ) ∑wi ( x0 ) + r′ ( x0 ) ∑( xi − x0 ) wi ( x0 )
r′′ ( x0 ) 2 + ∑( xi − x0 ) wi ( x0 ) 2 i=1
局部线性回归:在每一个将要被预测的点x 处解一个单独的加权最小二乘问题,找到使 下述表达式最小的 β ( x)
∑K ( x, x ) y − x β ( x)
i =1 h i i i
n
2
13
局部线性回归
Y = sin ( X ) + ε , X ~ Uniform[0,1] , ε ~ N ( 0,1 3)
G =φ ( X) (φ ( X) ) , Gij = φ ( xi ) ,φ ( x j ) = K( xi , x j )
T
利用核函数计算内积
27
另一种对偶表示推导方式
线性岭回归最小化:
p p n 2 yi − r ( xi ) ) + λ∑β j2 , r ( xi ) = ∑xij β j ∑( j =1 j=1 i=1
= ∫∫ Kh ( x, u) yf ( y | u) f ( u) dydu
非参数回归分析方法与应用

非参数回归分析方法与应用回归分析是统计学中一种常用的数据分析方法,用于研究自变量与因变量之间的关系。
传统的回归分析方法通常基于参数模型,假设自变量与因变量之间存在线性关系,并通过估计参数来建立模型。
然而,在实际应用中,很多情况下自变量与因变量之间的关系并不是线性的,此时非参数回归分析方法就能够提供更为灵活的建模方式。
非参数回归分析方法不对模型做出具体的函数形式假设,而是利用样本数据自身的信息来估计回归函数。
其中,最为常用的非参数回归方法包括核回归和局部线性回归。
核回归是一种基于核函数的非参数回归方法。
核函数在样本点周围形成一个权重函数,用于估计回归函数的值。
通过调整核函数的带宽,可以控制权重函数的宽窄,从而影响回归函数的平滑程度。
核回归方法具有较好的非线性拟合能力,适用于处理复杂的数据关系。
局部线性回归是一种将线性回归与核回归相结合的方法。
它在核回归的基础上,对回归函数进行局部线性逼近,以提高模型的拟合精度。
局部线性回归方法通过引入权重矩阵,将样本点附近的数据赋予更高的权重,从而实现对回归函数的局部逼近。
这种方法不仅能够拟合非线性关系,还能够在局部范围内进行线性逼近,具有较好的平滑性和拟合精度。
非参数回归分析方法在实际应用中具有广泛的应用价值。
首先,它能够处理非线性关系,适用于各种类型的数据。
例如,在金融领域,非参数回归方法可以用于建立股票价格与影响因素之间的关系模型,帮助投资者进行投资决策。
其次,非参数回归方法不对数据的分布做出假设,对异常值和离群点具有较好的鲁棒性。
这在处理实际数据时非常有用,可以减少异常值对模型的影响。
此外,非参数回归方法还能够处理高维数据,通过引入降维技术,可以对多个自变量进行建模。
然而,非参数回归分析方法也存在一些限制。
首先,由于不对回归函数做出具体的形式假设,模型的拟合过程相对复杂,计算量较大。
其次,非参数回归方法对样本数据的要求较高,需要大量的样本数据才能获得可靠的估计结果。
本书介绍了核方法Kernel记得上高等数理统计
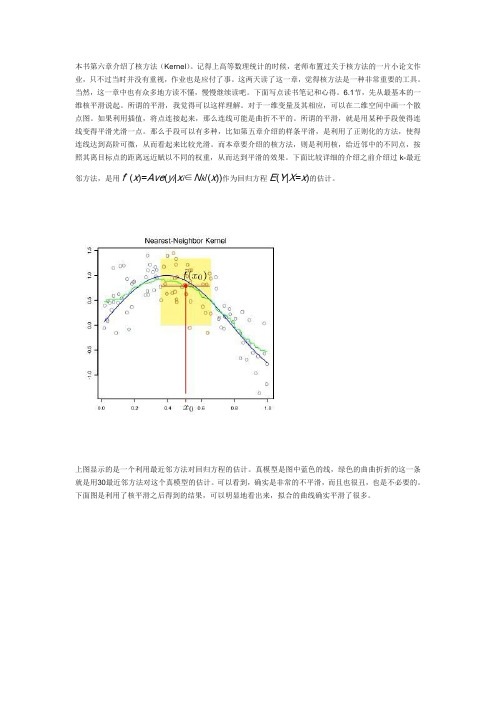
本书第六章介绍了核方法(Kernel)。
记得上高等数理统计的时候,老师布置过关于核方法的一片小论文作业,只不过当时并没有重视,作业也是应付了事。
这两天读了这一章,觉得核方法是一种非常重要的工具。
当然,这一章中也有众多地方读不懂,慢慢继续读吧。
下面写点读书笔记和心得。
6.1节,先从最基本的一维核平滑说起。
所谓的平滑,我觉得可以这样理解。
对于一维变量及其相应,可以在二维空间中画一个散点图。
如果利用插值,将点连接起来,那么连线可能是曲折不平的。
所谓的平滑,就是用某种手段使得连线变得平滑光滑一点。
那么手段可以有多种,比如第五章介绍的样条平滑,是利用了正则化的方法,使得连线达到高阶可微,从而看起来比较光滑。
而本章要介绍的核方法,则是利用核,给近邻中的不同点,按照其离目标点的距离远近赋以不同的权重,从而达到平滑的效果。
下面比较详细的介绍之前介绍过k-最近邻方法,是用fˆ(x)=Ave(y i|x i∈N k/(x))作为回归方程E(Y|X=x)的估计。
上图显示的是一个利用最近邻方法对回归方程的估计。
真模型是图中蓝色的线,绿色的曲曲折折的这一条就是用30最近邻方法对这个真模型的估计。
可以看到,确实是非常的不平滑,而且也很丑,也是不必要的。
下面图是利用了核平滑之后得到的结果,可以明显地看出来,拟合的曲线确实平滑了很多。
上面仅仅是一个核平滑的例子。
下面给出一维核平滑的一些具体的公式fˆ(x0)=∑Ni=1Kλ(x0,xi)yi∑Ni=1Kλ(x0,xi)这个就是利用核平滑对x0点的真实值的估计,可以看出,这其实是一个加权平均,相比起最近邻方法,这里的特殊的地方就是权重Kλ(x0,x)。
这个权重就称为核。
核函数有很多种,常用的包括Epanechnikov quadratic 核:Kλ(x0,x)=D(x−x0λ) with D(t)=34(1−t2),|t|<1这个图就是D(t)的图像,可以看出,随着离目标点的距离越来越远,所附加的权重也是平滑的越来越小。
非参数估计的累积概率分布转换为标准正态分布的方法

非参数估计的累积概率分布转换为标准正态分布的方法1. 引言1.1 什么是非参数估计非参数估计是一种统计学方法,它不依赖于任何特定的参数假设。
在传统的参数估计中,人们通常会假设数据服从某种特定的分布,然后通过拟合该分布的参数来进行估计。
但是在实际应用中,我们经常会遇到数据分布未知或者非常复杂的情况,这时参数估计就显得力不从心。
非参数估计的出现正是为了解决这个问题。
在非参数估计中,我们不对数据的分布形状进行任何假设,而是直接利用观测数据本身来推断总体分布的特征。
这种方法的优势在于可以更灵活地适应各种复杂情况,不受参数假设的限制。
非参数估计也更加稳健,对异常值的影响更小。
非参数估计是一种强大的统计工具,适用于各种不同类型的数据分析问题。
通过不依赖于参数假设,非参数估计能够更好地适应现实世界中复杂多变的情况,提高数据分析的准确性和可靠性。
在进行数据分析时,我们可以根据具体情况选择参数估计或非参数估计方法,以取得更好的分析效果。
1.2 什么是累积概率分布累积概率分布是描述连续型随机变量取值范围的一种数学概念。
在统计学和概率论中,累积概率分布函数是一个用来表示随机变量取值在一个给定点之前的概率的函数。
它可以帮助我们理解某个事件发生的概率,在统计数据分析中起着非常重要的作用。
累积概率分布函数通常用大写字母F表示,对于一个随机变量X,其累积概率分布函数可以表示为F(x)=P(X≤x)。
这个函数描述了随机变量X小于或等于给定值x的概率。
在实际应用中,累积概率分布函数可以帮助我们计算出在某个值之前的概率,或者通过其反函数计算出给定概率对应的值。
通过分析累积概率分布函数,我们可以了解到随机变量的分布特征,对数据的概率分布进行推断和预测。
在数据分析和统计建模中,了解和掌握累积概率分布函数是非常重要的,可以帮助我们进行有效的数据处理和推断。
了解累积概率分布函数的概念和性质对于数据分析和统计推断是至关重要的。
1.3 为什么要将累积概率分布转换为标准正态分布将累积概率分布转换为标准正态分布的一个主要原因是为了更方便地进行数据分析和统计推断。
krpa流程参数使用

2023 krpa流程参数使用CATALOGUE目录•KRPA 流程介绍•KRPA 流程参数•KRPA 流程参数使用示例•KRPA 流程参数使用注意事项•KRPA 流程参数使用常见问题及解决方案01 KRPA 流程介绍KRPA(Kernel Ridge Preservation Assistance)是一种基于核方法(Kernel Method)的Ridge Preservation Assistance工具,用于保护和增强图像或谱图数据的结构信息。
目的KRPA旨在解决在核方法应用过程中存在的数据结构信息丢失问题,通过使用KRPA,能够有效地保护和增强数据中的结构信息,提高核方法的性能。
定义KRPA 是什么VSKRPA 的应用场景图像识别在图像识别任务中,KRPA可以用于保护和增强图像中的结构信息,从而提高识别模型的性能。
谱图分析在谱图分析任务中,KRPA可以用于保护和增强谱图中的结构信息,从而提高分析的准确性和稳定性。
KRPA 的工作原理01KRPA基于核方法理论,通过建立输入数据与高斯核函数之间的映射关系,将输入空间映射到一个高维特征空间;02在高维特征空间中,使用线性回归方法学习数据的结构信息,并使用所学习到的结构信息来指导训练核方法模型;03KRPA的训练过程可以看作是一个监督学习问题,其中输入数据是特征向量,输出数据是目标变量,使用结构风险最小化原则来优化模型参数。
02 KRPA 流程参数这是KRPA流程的输入参数之一,它是一个列表,包含需要进行后续处理的原始数据。
这些数据可以是文本、图像或其他类型的数据。
input_data这是指明输入数据格式的参数,例如CSV、TXT、JSON等。
根据不同的数据格式,KRPA流程会采用不同的解析策略。
input_formatoutput_file这是KRPA流程的输出文件路径,它是一个字符串类型。
通常情况下,KRPA流程将处理结果写入到指定的输出文件中。
高斯过程回归 matlab

高斯过程回归 matlab高斯过程回归(Gaussian Process Regression,GPR)是一种非参数的回归方法,适用于样本量较少、噪声较大、无法用简单的函数拟合的数据集。
它通过概率的方法建立了输入与输出之间的映射关系,可以用于非线性回归、插值、分类等问题。
本文将介绍如何使用Matlab实现高斯过程回归。
1. 准备工作首先需要安装Matlab的统计和机器学习工具箱。
可以使用命令`ver`检查是否安装了这两个工具箱。
如果没有安装,可以在Matlab中的“Add-Ons”功能中安装。
接下来,我们需要准备一个数据集。
在本文中,我们将使用Matlab自带的“makima”函数生成一个带噪声的数据集,代码如下:```matlab x = -1:0.1:1; y = makima(x,cos(10*x)) + 0.1*randn(size(x)); plot(x,y,'o') ```这个代码将在图像中生成一个带噪声的数据点集。
2. 建立模型在建立模型之前,我们需要确定数据点之间的协方差,通常使用高斯核函数(Gaussian kernel)进行计算。
高斯核函数的公式如下:$$K(x_i, x_j) = \sigma_f^2 exp\left(-\frac{\| x_i - x_j \|^2}{2l^2}\right)$$其中$\sigma_f$表示信号强度,$l$表示长度尺度。
协方差以$\sigma_f^2$为中心,随着数据点$x_i$和$x_j$之间的距离变远而迅速衰减。
我们需要估计这两个参数的值。
在Matlab中,可以使用`fitrgp`函数创建高斯过程回归的模型。
代码如下:```matlab gpr_model =fitrgp(x',y','KernelFunction','ARDSquaredExponentia l','Sigma',1,'BasisFunction','constant','FitMethod' ,'exact') ```这个代码将建立一个高斯过程回归的模型,并将其存储在`gpr_model`变量中。
kernal密度估计

kernal密度估计引言在统计学中,核密度估计(Kernel Density Estimation,简称KDE)是一种用来估计概率密度函数的非参数方法。
它通过将每个数据点周围的小核函数进行平滑处理,从而得到连续的概率密度估计结果。
这种方法广泛应用于数据分析、模式识别和机器学习等领域。
核密度估计原理核密度估计的基本原理是通过将核函数(Kernel Function)与每个数据点结合,对每个点周围的区域进行插值求和,从而得到密度的估计值。
核函数是一个非负函数,且在整个定义域上的积分为1。
常用的核函数有高斯核、均匀核和三角核等。
核密度估计的公式如下:f̂(x)=1n∑Kni=1(x−x iℎ)其中,f̂(x)表示在点x处的密度估计值,n表示样本容量,x i表示第i个数据点,K表示核函数,ℎ表示带宽(Bandwidth)。
带宽ℎ的选择对于核密度估计的结果起到重要的影响。
如果带宽选择过小,估计值会过于精细,可能会产生过拟合现象;如果带宽选择过大,估计值会过于平滑,可能会产生欠拟合现象。
通常可以通过交叉验证或规则调整的方法来选择合适的带宽。
KDE的优点和缺点核密度估计方法具有以下优点: - 非参数方法:核密度估计方法不对数据的分布进行假设,可以适用于各种类型和形状的数据。
- 无需指定参数:与参数估计方法相比,核密度估计方法可以避免对参数的先验设定,更加灵活。
- 连续性:通过核函数的平滑处理,得到的密度估计结果是连续的,可以提供更细致的信息。
然而,核密度估计方法也存在一些缺点: - 计算复杂度高:核密度估计方法对于大规模数据集的计算复杂度较高,特别是在高维情况下。
- 带宽选择问题:选择合适的带宽对于核密度估计结果的准确性和稳定性非常重要,但是没有明确的标准或方法可以确定最佳带宽。
KDE的应用核密度估计方法在各个领域都有广泛的应用,下面介绍一些常见的应用场景。
数据分析与可视化核密度估计方法可以用于对数据的分布进行分析和可视化。
高斯过程回归高斯核函数

高斯过程回归高斯核函数引言高斯过程回归(Gaussian Process Regression ,简称GPR )是一种用于建立回归模型的方法,其核心思想是利用高斯过程(Gaussian Process )对目标函数进行建模。
而高斯核函数(Gaussian Kernel )是GPR 中最常用的核函数之一,它在捕捉数据之间的相关性方面表现出色。
本文将详细介绍高斯过程回归以及高斯核函数的原理和应用。
高斯过程回归1. 什么是高斯过程回归高斯过程回归是一种非参数模型,它假设数据集中的每个数据点都服从一个高斯分布,同时假设数据之间的相关性可以用一个协方差函数表示。
在高斯过程回归中,我们通过训练数据集来估计目标函数在整个输入空间上的分布。
与传统的参数化回归模型不同,高斯过程回归可以灵活地适应不同的数据分布和非线性关系。
2. 高斯过程回归的原理高斯过程回归的核心是对目标函数进行建模。
假设我们有一个训练数据集D ={(x i ,y i )}i=1n ,其中x i 表示输入变量,y i 表示对应的输出变量。
我们希望通过训练数据集来预测任意一个测试点x ∗的输出y ∗。
高斯过程回归假设目标函数服从一个高斯过程,即对于任意的x i ,y i 都服从一个高斯分布:y i ∼N (m (x i ),k(x i ,x j ))其中m (x i )表示均值函数,k(x i ,x j )表示协方差函数。
常用的协方差函数有线性核、高斯核、多项式核等。
3. 高斯核函数高斯核函数是高斯过程回归中最常用的核函数之一。
高斯核函数的定义如下:k(x i,x j)=exp(−∥x i−x j∥22l2)其中l表示核函数的长度尺度,决定了相邻点之间的相似性。
当l较大时,高斯核的值变化较为平滑,反之则变化较为陡峭。
4. 高斯过程回归的预测在高斯过程回归中,我们通过训练数据集估计均值函数m(x)和协方差函数k(x i,x j)的参数。
然后,对于任意一个测试点x∗,我们可以根据训练数据集得到的均值函数和协方差函数来预测其对应的输出y∗。
kernel密度法

Kernel密度法1. 引言Kernel密度法是一种非参数的概率密度估计方法,它通过对数据进行平滑处理,来估计数据的概率密度函数。
在统计学和机器学习领域中,Kernel密度法被广泛应用于数据分析、模式识别、异常检测等任务中。
本文将介绍Kernel密度法的原理、应用场景、算法实现和优缺点等方面的内容,以帮助读者更好地理解和应用这一方法。
2. 原理Kernel密度法的基本思想是将每个数据点周围的一定范围内的数据点都视为与该数据点具有相似的特征,然后通过对这些相似数据点的贡献进行加权平均,得到该数据点处的概率密度估计值。
具体而言,假设我们有一组n个样本数据X={x1,x2,...,x n},我们希望估计数据x 处的概率密度。
对于每个样本x i,我们定义一个核函数K(⋅),表示样本x i处的贡献权重。
常用的核函数有高斯核函数、Epanechnikov核函数等。
Kernel密度法的估计函数可以表示为:f̂(x)=1n∑1ℎni=1K(x−x iℎ)其中,ℎ是一个正数,称为带宽参数。
带宽参数决定了核函数的宽度,它的选择对估计结果有重要影响。
通常可以使用交叉验证等方法来选择最优的带宽参数。
3. 应用场景Kernel密度法广泛应用于以下几个领域:3.1 数据分析在数据分析中,我们经常需要对数据进行概率密度估计。
Kernel密度法可以帮助我们估计数据的概率密度函数,从而更好地理解数据的分布情况。
例如,在金融领域中,我们可以使用Kernel密度法来估计股票价格的概率密度函数,以便进行风险分析和投资决策。
3.2 模式识别在模式识别中,我们需要对样本数据进行分类或聚类。
Kernel密度法可以用于计算样本数据的概率密度,从而帮助我们判断样本的类别或聚类情况。
例如,在图像识别中,我们可以使用Kernel密度法来估计不同类别图像的概率密度,然后基于最大概率原则进行分类。
3.3 异常检测在异常检测中,我们希望找出与正常数据有较大差异的异常数据。
核相关滤波算法 -回复

核相关滤波算法-回复核相关滤波算法(Kernel Correlation Filter)是一种广泛应用于目标跟踪领域的算法。
它通过利用离散傅里叶变换和最小二乘回归分析,实现对目标在图像中的准确跟踪。
本文将详细介绍核相关滤波算法的原理、流程以及在目标跟踪中的应用。
1. 算法原理核相关滤波算法的核心思想是利用训练集数据来学习目标的表示方式,然后在测试图像中通过寻找最相似的表示来实现目标跟踪。
其原理可以概括为以下几个步骤:1.1 训练阶段在训练阶段,首先从目标的初始帧中选取一个有代表性的图像块作为模板,然后通过离散傅里叶变换(DFT)将图像块转换到频域。
接着,计算目标表示的傅里叶系数,将其存储为滤波模板。
该滤波模板可以被认为是目标的特征描述,包含了目标的形状和外观信息。
1.2 测试阶段在测试阶段,首先对测试图像中的每个候选图像块执行和训练阶段相同的傅里叶变换操作,将其转换到频域。
然后,将该频域图像块与滤波模板进行相关运算,得到一个响应图。
响应图的峰值对应于图像中目标的最佳匹配位置。
1.3 响应图的处理为了提高算法的准确性和鲁棒性,响应图常常需要经过进一步的处理。
典型的处理方法包括峰值削弱(peak suppression)和泛化(regularization)。
峰值削弱通过抑制响应图中的非峰值部分,使得只有最相关的目标位置保留下来。
泛化则通过引入先验约束,减少对于特定目标的过拟合。
2. 算法流程核相关滤波算法可以总结为以下几个主要步骤:2.1 初始化选择目标初始帧,并从中选取一个图像块作为滤波模板。
2.2 傅里叶变换对滤波模板和测试图像的所有候选图像块执行离散傅里叶变换,将其转换到频域。
2.3 相关运算将频域图像块与滤波模板进行相关运算,得到响应图。
2.4 响应图处理对响应图进行峰值削弱和泛化处理,得到最终跟踪结果。
2.5 目标定位在最终处理后的响应图中,确定最大峰值对应的图像坐标,即目标的位置。
3. 目标跟踪应用核相关滤波算法在目标跟踪领域有着广泛的应用。
核函数的实现和应用

核函数的实现和应用核函数是一种优秀的机器学习算法,它可以将高维度数据通过非线性变换映射到低维度的子空间中,用来进行分类或回归。
简单来说,核函数就是一种基于向量内积的函数,可以应用于支持向量机(SVM)等机器学习算法中,使得分类器的性能更加优秀。
一、核函数的实现核函数的实现通常有两种方法:一种是通过数值计算来实现,这种方法适用于简单的核函数,例如径向基函数(RBF)核函数;另一种是通过显式地定义核函数来实现,这种方法适用于复杂的核函数,例如多项式核函数。
1. 数值计算法对于径向基函数核函数,其公式如下:K(x_i, x_j) = exp(-||x_i-x_j||^2/2sigma^2 )其中,x_i和x_j分别表示训练集中的两个样本,sigma为高斯核的带宽参数。
该公式可以通过数值计算来实现,具体步骤如下:(1)计算训练集样本之间的欧几里得距离。
(2)将欧几里得距离除以2sigma^2 。
(3)将结果取负值并进行指数运算。
(4)最终得到核函数的值。
2. 定义核函数法对于复杂的核函数,可以显式地将核函数定义出来,并直接应用到机器学习算法中。
例如,多项式核函数的定义如下:K(x_i, x_j) = (x_i^Tx_j + c)^d其中,c和d分别为常数,x_i和x_j分别表示训练集中的两个样本。
这种方法的优点是可以更容易地定义出多种复杂的核函数,缺点是实现时需要考虑到纬度的规模。
二、核函数的应用核函数在机器学习中有着广泛的应用,下面将具体介绍一些核函数在SVM等机器学习算法中的应用。
1. 线性核函数线性核函数是SVM最简单的核函数之一,其公式如下:K(x_i, x_j) = x_i^Tx_j这种核函数的主要优点是计算速度快、参数较少,且在数据集线性可分的情况下具有好的分类性能。
2. 多项式核函数K(x_i, x_j) = (x_i^Tx_j + c)^d其中,c和d分别为常数。
该核函数的优点在于其能够表达出非线性的分类决策边界,但是需要注意的是,该核函数容易产生过拟合现象。
fitrgp函数

fitrgp函数摘要:一、fitrgp 函数的定义与背景二、fitrgp 函数的参数及其作用三、fitrgp 函数的返回值及其意义四、fitrgp 函数在实际问题中的应用与案例五、总结与展望正文:fitrgp 函数是R 语言中一个用于拟合高斯过程回归模型的函数,高斯过程回归是一种基于核函数的回归方法,可以用于处理非线性问题。
通过fitrgp 函数,我们可以方便地构建高斯过程回归模型并对数据进行拟合。
一、fitrgp 函数的定义与背景fitrgp 函数是R 语言中的一个内置函数,用于拟合高斯过程回归模型(Gaussian Process Regression, GPR)。
高斯过程回归是一种基于核函数的回归方法,可以用于处理非线性问题。
在R 语言中,fitrgp 函数是gpr 包中的一个重要函数,通过这个函数,我们可以方便地构建高斯过程回归模型并对数据进行拟合。
二、fitrgp 函数的参数及其作用fitrgp 函数需要指定以下参数:1.x:输入数据,即自变量(input data, x)。
2.y:输出数据,即因变量(output data, y)。
3.kernel:核函数,用于定义高斯过程的核函数(kernel function)。
4.alpha:回归系数的最小二乘值(minimum squared value of the regression coefficients, alpha)。
5.optimize:优化方法,用于指定优化算法(optimization method)。
6.trace:是否返回优化过程的轨迹(return the optimization trajectory)。
三、fitrgp 函数的返回值及其意义fitrgp 函数的返回值主要包括以下几个部分:1.fit:拟合后的高斯过程回归模型。
2.sigma:模型中的噪声标准差(noise standard deviation)。
3.alpha:模型中的回归系数(regression coefficients)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
边界上的局部线性回归: 将偏差降至一阶
14
核回归:局部线性回归
则估计为:
rˆ x xˆ x
xT XT W x X 1 XT W x y
n
wi x yi
i 1
其中W(x)是一个 n n的对角矩阵且第i个对角元素是Kh x, xi
估认计为在是y等i上价是核线性的,因为权重项 wi(x)不涉及yi ,可被
xi , x j
p
得到解:
点积 xij xkj xiT xk
j 1
Q y 1 1 G 0 2 G I1 y
2 2
相应的回归方程为:
j
1
2
n
i xij
i 1
rˆ x x, yT G I 1 z, where z x, xi
31
核化岭回归
将点积 Gij xi , x j 换成核函数 Kij K xi , x j
22
对偶表示
一种对偶表示为:
XT X I p XT y
XT X I XT y 1 XT y XT X
1XT y X XT
1 y X
y X y XXT
XXT y
G In 1 y
其中 G XXT
需O(n3)运算
23
xij
j
i
29
Wolfe对偶问题
将
j
1
2
n
i xij
i 1
和
i
1 2
i代入拉格朗日函数
原目标函数
L ,, 转化为
n
p
i2
2 j
i 1
j 1
n
i 1
i
yi
p
j1
xij
j
i
Q
1 4
n i 1
i2
1
4
pnn
ik xij xkj
j1 i1 k 1
n
i yi
i1
y h2
K
y
yi h2
dy
1 n
n i1 Kh1 x, xi
sh2 yi K sds
K(x)dx 1, xK(x)dx 0
1 n
n i 1
Kh1
x, xi
yi
4
核回归:Nadaraya-Watson
证明(续)
r
x
f
x, y f x
ydy
rˆ
gˆh
x
g
x
h2 2
g
''
x
x2K
2
x dx
同理,
gˆh
x
1 nh
2
x其中 i 2 x
8
核回归:Nadaraya-Watson
最后,得到估计的风险为
R
r,
rˆn
1 4
h4
x2K 2 xdx
4
r
x
2r x
f x f x
dx
2K2 nhf
x x
dx
dx
最佳带宽以 n1 5的速率减少,在这种选择下风险以 n4 5
的速率减少,这是最佳收敛速率(同核密度估计)
9
核回归:Nadaraya-Watson
实际应用中,利用交叉验证对求最佳带宽h。 交叉验证对风险的估计为
Jˆ
h
n
Yi
rˆi
xi
2
i 1
实际上不必每次留下一个计算单独估计,可以
写成以下形式
Jˆ
h
n
Yi
rˆ
xi
2
i 1
1
2
1
K 0
n j 1
K
xi
p
xij
j 1
1
2
n
k xkj
k 1
1 2
i
1
4
n
i2
i1
1
4
n i1
n
ik
k 1
p
xij xkj
j1
n
i yi
i1
30
最优解
写成矩阵形式为:
Q
n
i yi
i1
1 4
n
i2
i1
1
4
n i1
n
ik
k 1
p
xij xkj
j1
Q
T
y
1 T
4
1
4
T G ,
where
Gij
j 1
xij
j
i
28
Wolfe对偶问题
转化为其对偶问题: Q min L, , ,
对L求偏导并置为0,得到
L
j
n
2 j i xij 0
i1
j
1
2
n
i xij
i 1
L
i
2i i 0
i
1 2
i
L , ,
n
i2
i 1
p
2 j
j 1
n
i
i 1
yi
p j 1
射: : 和一个学习方法,使得
F的维数比X高 , 因此模型更丰富
算法只需要计算点积
存在一个核函数,使得
x , x K x, x
点积核
在算法中任何出现项 x, x 的地方,用K x, x 代替
亦称为原方法的核化(kernelizing the original method).
35
什么样的函数可以作为核函数?
对偶岭回归
为了预测一个新的点
n
f (x) , x i xi , x
i 1
其中 z xi , x
XT, G In 1 y
yT G I1 z
此时只需计算Gram矩阵G
G XXT , Gij xi , x j
岭回归只需计算数据点的内积
24
特征空间中的线性回归
基本思想:
x0
n
n
由于 wi x0 1, xi x0 wi x0 0
i1
偏差 为
i 1
rˆ x0
r x0
r x0
2
n i 1
xi
x0 2
wi
x0
16
局部线性回归
边界上的局部等价核 (绿色点)
内部区域的局部等价核 (绿色点)
17
局部多项式回归
局部多项式回归:用d次多项式回归代替线性回归
K n
i1 h
x, xi
yi
K n
j1 h
x, xj
3
核回归:Nadaraya-Watson
证明:fˆ
x,
y
1 n
n i 1
Kh1
x, xi Kh2
y,
yi
yfˆ x, ydy 1 n
n i1
Kh1 x, xi yKh2 y, yi dy
1 n
n i1 Kh1 x, xi
可以考虑任意阶的多项式,但有一个偏差和方差的折中 通常认为:超过线性的话,会增大方差,但对偏差的减
少不大,因为局部线性回归能处理大多数的边界偏差,
18
可变宽度核
可变宽度核:如使每一个训练点的带宽与它的第k个 近邻的距离成反比
在实际应用中很好用,虽然尚未有理论支持怎样选择参数 不会改变收敛速度,但在有限样本时表现更好
36
半正定核的性质
对称
K(x, x)
(x), (x)
(x), (x) K(x, x)
rˆ x wi x yi i 1
其中
wi x
Kh x, xi
n
Kh x, xj
j 1
6
核回归:Nadaraya-Watson
将核回归估计写成如下形式:rˆ x
其中
gˆh
x
1 n
n i 1
Kh
x,
xi
yi
,fˆh
gˆh x
1 n
n i 1
Kh
x, xi
yi
n
yi r xi 2
p
2 j
,
r xi
p
xij j
i1
j1
j1
等价于
min
j
满足约束
n i 1
i2
p j 1
2 j
p
i yi r xi yi xij j
j1
则拉格朗日函数为
L , ,
n
i2
i 1
p
2 j
j 1
n
i 1
i
yi
p
注意:上述这些扩展(包括局部线性/局部多项式) 都可应用到核密度估计中
19
核方法
为什么要用核方法?
得到更丰富的模型,但仍然采用同样的方法
如岭回归方法核岭回归
内容
Kernel trick 再生Hilbert空间
20
线性模型
线性模型:
方便、应用广泛 有很强的理论保证 但还是有局限性
Mercer’s 定理给出了连续对称函数k可作为核函数 的充要条件:半正定
半正定核:
对称:k x, x k x, x
且对任意训练样本点 x1, , xn 和任意 1, , n R
满足
K i j ij 0, Kij k xi , x j
i, j
K被称为Gram矩阵或核矩阵。
矩阵形式:
TK 0
权重为核函数的值,邻域由核函数的宽度控制
2
核回归:Nadaraya-Watson
回忆一下回归方程的定义:
r x Y | X x yf y | x dy
yf f
x, y dy x, y dy
