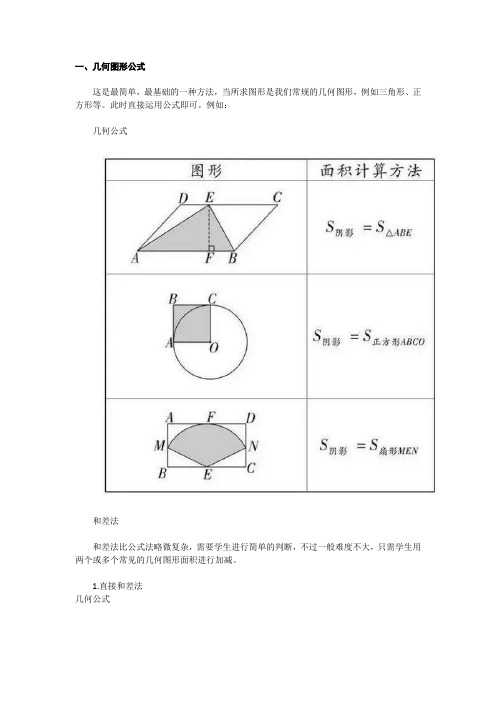
初中几何图形知识点归纳doc资料
数学几何图形初中知识点总结

数学几何图形初中知识点总结数学几何是初中数学中的重要分支,涉及到平面几何和立体几何两个方面。
通过学习几何,学生可以培养逻辑思维能力和空间想象能力,并且为高中阶段的学习打下坚实的基础。
下面我将从初中数学几何的基本概念、图形的性质和常见的几何推理等方面,对几个重要的知识点进行总结。
一、图形的基本概念在几何学中,图形是指由点和线组成的可见形状。
初中数学中常见的图形包括:点、线段、直线、射线、角、多边形等。
1. 点:没有大小和形状,用大写字母表示,如A、B、C。
2. 线段:由两个点A和B确定,有起点和终点,并且有固定的长度。
用线段AB表示。
3. 直线:无限延伸的线段,没有起点和终点。
用小写字母表示,如l、m、n。
4. 射线:由一个起点和一个方向确定的直线。
用起点和任一点的字母表示,如射线AB。
5. 角:由两条射线共同起点构成的图形。
常用度(°)表示,如∠ABC。
6. 多边形:由若干条线段组成的封闭图形。
常见的多边形有三角形、四边形、五边形等。
二、图形的性质和关系了解图形的性质和关系对于几何学的学习非常重要,它们帮助我们判定图形的种类,以及解决各种几何问题。
1. 三角形的性质:(1)三角形的内角和为180°。
(2)等边三角形的三条边都相等,内角都是60°。
(3)等腰三角形的两条边相等,两个底角也相等。
(4)直角三角形的一个角是90°。
2. 四边形的性质:(1)矩形的对角线相等,且相交于中点。
(2)平行四边形的对边分别平行且相等。
(3)菱形的对角线互相垂直,且互相平分。
(4)正方形是矩形和菱形的特例,四条边相等且四个角都是90°。
3. 圆的性质:(1)圆是由平面上与一个点距离相等的所有点组成的图形。
(2)圆心到圆上任意一点的距离称为半径。
(3)圆上任意两点之间的距离称为弧,弧上的距离等于半径的长度。
(4)直径是通过圆心的两个点,并且等于半径的两倍。
三、常见的几何推理通过推理,可以从已知条件中得出推论,解决各种几何问题。
初中几何图形知识点整理

初中几何图形知识点整理好的,以下是为您整理的初中几何图形知识点:在我们的初中数学世界里,几何图形就像是一个个神秘的小城堡,等着我们去探索和发现其中的秘密。
今天咱们就一起来揭开它们的面纱!先来说说点、线、面、体吧。
点动成线,线动成面,面动成体,这就像是一场神奇的魔法。
就拿咱们平时写字的笔来说,笔尖在纸上移动,留下的痕迹就是线;把一张纸折起来,这张纸就从一个平面变成了一个立体的形状。
三角形可是几何图形中的“常客”。
三角形按角分,可以分为锐角三角形、直角三角形和钝角三角形。
这就好比我们选水果,有酸酸甜甜的锐角三角形“水果”,有“方方正正”的直角三角形“水果”,还有“有点钝角”的钝角三角形“水果”。
按边分呢,又有等边三角形、等腰三角形和一般三角形。
等边三角形那三条边就像三个好兄弟,长度都一样,团结得很;等腰三角形呢,就有两条边像双胞胎似的长度相等。
三角形的内角和是 180 度,这可是个铁打的定律。
记得有一次我和同学一起做手工,我们用硬纸板剪了一个三角形,然后好奇地量了量每个角的度数,加起来果然是 180 度,当时可把我们高兴坏了。
再来说说四边形。
平行四边形的两组对边分别平行且相等,就像两个小朋友手拉手,走得又平又稳。
矩形呢,不仅对边平行相等,还有四个角都是直角,就像一个站得笔直的士兵。
菱形不仅对边平行,四条边还都相等,如同一个精致的小菱形宝石。
而正方形,那更是集各种优点于一身,不仅对边平行、四条边相等,四个角还都是直角,简直就是四边形中的“全能冠军”。
还有多边形。
多边形的内角和公式是(n 2)×180 度,外角和永远是 360 度。
想象一下,我们在操场上画一个多边形,然后沿着边走一圈,不管这个多边形有几条边,转一圈回来,角度的总和总是360 度,是不是很神奇?圆也是初中几何中重要的一员。
圆的周长公式是 C =2πr,面积公式是 S =πr² 。
记得有一次我去买蛋糕,看到蛋糕师傅在做圆形的蛋糕,我就在想,这个蛋糕的周长和面积该怎么算呢?在学习几何图形的过程中,我们不仅要记住这些知识点,更要学会运用它们来解决实际问题。
初中几何的图形知识点总结

初中几何的图形知识点总结几何图形是初中数学重要的内容之一,它是我们日常生活中经常接触到的一种数学形式。
几何图形的知识对学生的数学学习和生活实际应用都有着很重要的作用。
以下是初中几何图形知识点的总结:一、平面几何基础知识:1. 点、线、面的基本概念:点是最基本的几何图形,它没有长、宽、高,只有位置。
线是由无数个点组成的,是没有宽度的。
面是有无限多个点和线组成的,是有长度和宽度的。
2. 直线和线段的区别:直线是由无数个点组成的,方向不受限制。
线段是直线的一部分,有两个端点,有长度。
3. 射线和角的概念:射线是一条有一个起点且无穷延伸的直线,角是由两条有公共端点的射线组成的。
4. 多边形的概念:多边形是有限个线段组成的闭合图形,其中的线段都是直线。
这些线段的交点称为顶点。
5. 圆的概念:圆是平面上和一个定点的距离相等的所有点的集合。
6. 三角形的分类:三角形根据边长和角度的大小可以分为等边三角形、等腰三角形、直角三角形、钝角三角形和锐角三角形等。
7. 四边形的分类:四边形根据对边的对应边等长情况和对角线的长度关系,可以分为平行四边形、菱形、矩形、正方形和梯形等。
8. 梯形和平行四边形的性质:梯形有一组对边平行,这种梯形为平行四边形。
9. 直角三角形和勾股定理:直角三角形的两条直角边的平方和等于斜边的平方。
这被称为勾股定理。
二、立体几何基础知识:1. 立体几何的基本概念:立体几何是空间几何的一个重要分支,它研究的对象是有长度、宽度和高度的物体。
常见的立体图形有立方体、长方体、正方体和棱锥等。
2. 立体图形的表面积和体积:立体图形的表面积是指其所有的外表面的总和,而体积是指其内部所包含的所有空间。
3. 平面图形展开成立体图形:平面图形可以通过展开成一个立体图形,根据已知的平面图形可以构造出立体图形的表面积和体积。
4. 立体图形的三视图:立体图形通常可以通过正视图、俯视图和侧视图来全面地展现其形状和大小。
三、几何变换:1. 平移、旋转、翻转、对称变换的概念和性质:几何变换是指将原来的图形按照一定的规则进行改变的过程,其中包括平移、旋转、翻转和对称变换等。
初中几何基本图形归纳(基本图形+常考图形)

初中几何基本图形归纳(基本图形+常考图形)初中几何常见基本图形1.基本图形及结论A、B、C、D分别为四边形的顶点,AC=BD,AD=BC,∠AOC=∠BOD,∠AOD=∠BOC。
2.直角三角形在直角三角形ABC中,∠C=90°,OA为斜边的中线,OD⊥XXX。
3.等腰三角形在等腰三角形ABC中,AB=AC,AD为角A的平分线,BD=CD。
4.三角形的面积公式在三角形ABC中,AB2=BD×BC,AC2=CD×BC。
5.三角形内角和公式在三角形ABC中,∠A+∠B+∠C=180°。
6.平行四边形在平行四边形ABCD中,∠A+∠B=∠C+∠D,AC平分∠BAD。
7.直角三角形的斜边中线在直角三角形ABC中,BD为斜边AC的中线,∠B=∠D。
8.直角三角形的高线在直角三角形ABC中,PA⊥AB,PB⊥AC,PC⊥BC,且PA=PB+PC,∠P=∠A/2.9.直角三角形的内心在直角三角形ABC中,∠P=∠A/2,PD为角A的平分线,AD=BD=AC=DC。
10.直角三角形的外心在直角三角形ABC中,∠P=90°-∠A/2,以AB的中点O为圆心,AB为半径作圆,交AC于点P,则P为三角形ABC的外心。
11.等腰三角形的中线在等腰三角形ABC中,AB=CB,BD为角B的平分线,且BC∥AD。
12.等边三角形在等边三角形ABC中,AB=AC=BC。
13.等角三角形在等角三角形ABC中,∠A=∠B=∠C。
14.三角形的相似在三角形ABC和DEF中,如果∠A=∠D,∠B=∠E,∠C=∠F,则称三角形ABC与DEF相似。
15.圆的基本性质在圆O中,AB为直径,则∠C=90°,且AC=BC=OD。
16.圆的切线在圆O中,以点A为圆心,AB为半径作圆,则CD为圆O的切线。
17.圆的割线在圆O中,以点A为圆心,AC为半径作圆,则BD为圆O的割线。
18.圆的弦在圆O中,AB为圆O的弦,R为圆O的半径,则弦长公式为AB2=BD×BC,且弦AB平分∠AOB。
初中数学中的几何平面图形知识点归纳

初中数学中的几何平面图形知识点归纳几何平面图形是初中数学中的重要内容之一,它涉及到许多重要的知识点。
在本文中,我们将对初中数学中常见的几何平面图形进行归纳总结,以便更好地理解和记忆。
1. 点、线、面在几何平面图形中,最基本的元素是点、线、面。
点是几何图形的最小单位,不具备长度、宽度和高度等属性。
线由两个点组成,表示两点之间的最短路径。
面是由多条线段所围成的区域,有有界和无界两种概念。
2. 线段、射线、直线线段是两个端点之间的线段,有特定的长度。
射线是一条有一个端点的线段,可以延伸到无穷远。
直线是无所不在的线,具有无限延伸的特性。
3. 角度和三角形角度是由两条射线所围成的空间,通常以“°”表示。
我们常见到的钝角(大于90°),直角(等于90°)和锐角(小于90°)。
三角形是由三条线段组成的图形,其内部的三个角的和等于180°。
我们常见的三角形有等边三角形、等腰三角形和直角三角形等。
4. 四边形四边形是由四条线段组成的图形,有矩形、正方形、平行四边形、梯形和菱形等不同类型。
矩形的对边相等且相互平行,正方形是一种特殊的矩形,其边长相等。
平行四边形的对边相等且相互平行,梯形是只有一对对边平行的四边形,菱形的四条边相等。
5. 圆、弧、扇形圆是由半径为r的一组点组成的集合,其内任意两点的距离都等于r。
弧是由圆上两点之间的一段弧线组成,可以看作圆上的线段。
扇形是以圆心为中心,由弧和两条半径组成的图形。
6. 相交和平行线在几何平面图形中,两条线段交于一点时称为相交,交点称为交点。
如果两条线段永远不会相交,则称为平行线。
7. 相似和全等图形相似图形是指形状相似但大小不同的图形,它们之间的对应角度相等,对应边的比例相等。
全等图形是指形状和大小完全相同的图形。
8. 线段的中点和垂直平分线线段的中点是指将线段等分为两等分的点,位于线段的正中央。
垂直平分线是指将一条线段垂直平分为两段,并将其两端延长至无穷远的直线。
初中数学几何的相关知识点总结
=(2sinαcos^2(α)+cos^2(α)sinα-sin^3(α))/(cos^3(α)-cosαsin^2(α)-2sin^2(α)cosα)
上下同除以cos^3(α),得:
tan3α=(3tanα-tan^3(α))/(1-3tan^2(α))
截一个几何体:用一个平面去截一个图形,截出的面叫做截面。
视图:主视图,左视图,俯视图。
多边形:他们是由一些不在同一条直线上的线段依次首尾相连组成的封闭图形。
弧、扇形:①由一条弧和经过这条弧的端点的两条半径所组成的图形叫扇形。②圆可以分割成若干个扇形。
2、角
线:①线段有两个端点。②将线段向一个方向无限延长就形成了射线。射线只有一个端点。③将线段的两端无限延长就形成了直线。直线没有端点。④经过两点有且只有一条直线。
公理:①公认的真命题叫做公理。②其他真命题的正确性都通过推理的方法证实,经过证明的真命题称为定理。③同位角相等,两直线平行,反之亦然;SAS、ASA、SSS,反之亦然;同旁内角互补,两直线平行,反之亦然;内错角相等,两直线平行,反之亦然;三角形三个内角的和等于180度;三角形的一个外交等于和他不相邻的两个内角的和;三角心的一个外角大于任何一个和他不相邻的内角。④由一个公理或定理直接推出的定理,叫做这个公理或定理的推论。
三、图形的认识
1、点,线,面
点,线,面:①图形是由点,线,面构成的。②面与面相交得线,线与线相交得点。③点动成线,线动成面,面动成体。
展开与折叠:①在棱柱中,任何相邻的两个面的交线叫做棱,侧棱是相邻两个侧面的交线,棱柱的所有侧棱长相等,棱柱的上下底面的形状相同,侧面的形状都是长方体。②N棱柱就是底面图形有N条边的棱柱。
初中几何知识点大全

1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12 两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理(SSS) 有三边对应相等的两个三角形全等26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^247勾股定理的逆定理如果三角形的三边长a、b、c有关系222a b c+=,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理 三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的一半2a b L +=,S Lh = 83 (1)比例的基本性质 如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d84 (2)合比性质 如果a /b=c /d,那么(a±b)/b=(c±d)/d85 (3)等比性质 如果a /b=c /d=…=m /n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a /b86 平行线分线段成比例定理 三条平行线截两条直线,所得的对应线段成比例87 推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理 如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例 90 定理 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似 91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA )92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS )94 判定定理3 三边对应成比例,两三角形相似(SSS )95 定理 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆。
初三数学几何知识点归纳

初三数学几何知识点归纳一、三角形1. 三角形的基本概念- 三角形由不在同一直线上的三条线段首尾顺次相接所组成。
- 三角形的三边关系:三角形任意两边之和大于第三边,任意两边之差小于第三边。
例如,若三角形三边为a、b、c,则a + b>c,a - b<c。
2. 三角形的分类- 按角分类:- 锐角三角形:三个角都是锐角的三角形。
- 直角三角形:有一个角是直角的三角形,直角三角形中斜边最长,两直角边的平方和等于斜边的平方(勾股定理a^2+b^2=c^2,其中c为斜边,a、b为两直角边)。
- 钝角三角形:有一个角是钝角的三角形。
- 按边分类:- 不等边三角形:三边都不相等的三角形。
- 等腰三角形:有两边相等的三角形,相等的两边叫做腰,另一边叫做底边;两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
等腰三角形两底角相等(等边对等角),等腰三角形三线合一(底边上的高、底边上的中线、顶角平分线互相重合)。
- 等边三角形:三边都相等的三角形,等边三角形三个角都是60^∘,等边三角形是特殊的等腰三角形。
3. 三角形的内角和与外角- 三角形内角和定理:三角形三个内角的和等于180^∘。
- 三角形的外角:三角形的一边与另一边的延长线组成的角。
三角形的一个外角等于与它不相邻的两个内角的和;三角形的一个外角大于任何一个与它不相邻的内角。
二、四边形1. 平行四边形- 定义:两组对边分别平行的四边形叫做平行四边形。
- 性质:- 平行四边形的对边平行且相等。
- 平行四边形的对角相等,邻角互补。
- 平行四边形的对角线互相平分。
- 判定:- 两组对边分别平行的四边形是平行四边形。
- 两组对边分别相等的四边形是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
- 两组对角分别相等的四边形是平行四边形。
- 对角线互相平分的四边形是平行四边形。
2. 矩形- 定义:有一个角是直角的平行四边形叫做矩形。
- 性质:- 矩形具有平行四边形的所有性质。
(完整版)人教版七年级数学第四章《几何图形初步》知识点汇总

第四章《几何图形初步》知识点汇总01、几何图形①几何图形的定义:我们把实物中抽象出来的各种图形叫做几何图形。
②几何图形分为图形和图形。
③平面图形:图形所表示的各个部分都在内的图形,如直线、三角形等。
④立体图形:图形所表示的各个部分同一平面内的图形,如圆柱体。
02、常见的立体图形①柱体:A棱柱: B 圆柱②椎体:A棱锥 B圆锥球体等03、立体图形的三视图:从不同方向观察几何体,从正面、上面、左面三个不同方向看一个物体,然后描出三张所看到的图(分别叫做______、______、_______),这样就可以把立体图形转化为平面图形。
①会观察小正方体堆积图形画出三视图②会根据三视图知道堆积的小正方体的个数04、立体图形的展开图①圆柱的平面展开图是。
②圆锥的平面展开图是。
③n棱柱的侧面展开图是 n个形,n棱柱有个底面,都是,n棱柱的平面展开图是。
④n 棱锥的侧面展开图是 n个形,n棱锥有个底面,是,n棱锥的平面展开图是。
⑤正方体的展开图共分四类:①掌握在正方体展开图中找相对面的方法②会根据展开图中的图案判断是哪个图形的展开图05、点、线、面、体几何图形的组成:由___、___、___组成。
_____是构成图形的基本元素点动成_____、____动成____、____动成____。
06、直线:①点与直线的位置关系:第一种关系:点在直线____,或者说直线______点;第二种关系:点在直线____,或者说直线_________点。
②直线公理:经过两点有且只有一条直线(简称:______________);07、直线与直线的位置关系①同一平面内,两条直线的位置关系分为:_____与_____②当两条不同的直线________时,我们就称这两条直线相交,这个_______叫做它们的_____。
08、射线:①表示方法:端点字母必须写在前②判断两条射线是同一条射线的方法:_________________09、线段①基本性质:___________________②两点之间的距离__________________③线段的中点10、比较线段大小的方法:_______法和______法11会作图:作一条线段等于已知线段知道延长(反向延长)射线和线段的作图语言12、角:①由一点引出两条射线形成的图形叫做角。
几何全部知识点归纳总结

几何全部知识点归纳总结一、基本概念几何学中的基本概念主要包括点、线、平面和角等。
1. 点:几何学中的最基本概念,没有长度、面积和体积,只有位置。
用大写字母标记,如A、B、C等。
2. 线:由一组相互平行的点构成,没有宽度和高度。
用小写字母标记,如l、m、n等。
3. 线段:两个端点确定的有限长度的线段是线段,用AB表示。
4. 射线:一个端点,一个方向组成的直线叫做射线5. 平面:由一组在同一平面上的点集合构成,没有厚度,用大写字母表示平面。
6. 角:由两条线段或两条射线的公共端点组成的图形,分为凸角和凹角,用∠ABC(顶点为B)表示。
7. 多边形:平面图形的一种,是由多条线段所围成的区域,如三角形、四边形、五边形等。
8. 圆:一个平面上所有到一个固定点距离相等的点的集合构成的图形,其中的这个固定点叫做圆心。
二、性质和定理几何学中有许多重要的性质和定理,它们是几何学理论体系的基础。
1. 点、线、面的性质:(1)直线上的任意两点可以确定一条唯一的直线。
(2)通过三点不在一条直线上的平面是唯一的。
2. 角的性质:(1)对顶角相等。
(2)邻补角相等。
(3)垂直角互为邻补角。
3. 三角形的性质和定理:(1)三角形内角和为180度。
(2)等腰三角形的底角相等。
(3)直角三角形中,斜边的平方等于两腰的平方和。
(4)全等三角形的对应边和对应角相等。
4. 四边形的性质和定理:(1)相邻角互补、对角互补。
(2)平行四边形的对边相等、对角相等。
(3)梯形的对边平行。
5. 圆的性质和定理:(1)圆的内切角等于圆周角的一半。
(2)相交弦的乘积等于相交弦的乘积。
(3)圆的切线垂直于半径。
三、常见图形几何学中有许多常见的图形,包括三角形、四边形、圆等。
1. 三角形三角形是一个有三个边和三个角的多边形,是几何学中研究最多的图形之一。
根据边的长度和角的大小,可以将三角形分为等边三角形、等腰三角形、直角三角形、普通三角形等。
2. 四边形四边形是一个有四个边和四个角的多边形,根据边和角的性质不同,可以分为平行四边形、梯形、矩形、正方形、菱形等。
初中数学几何图形知识点

初中数学几何图形知识点(学习版)编制人:__________________审核人:__________________审批人:__________________编制学校:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的教育资料,如语文资料、数学资料、英语资料、物理资料、化学资料、地理资料、政治资料、历史资料、艺术资料、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides various types of educational materials for everyone, such as language materials, mathematics materials, English materials, physical materials, chemical materials, geographic materials, political materials, historical materials, art materials, other materials, etc. Please pay attention to the data format and writing method!初中数学几何图形知识点1、点,线,面点,线,面:①图形是由点,线,面构成的。
初中几何图形知识点梳理

初中几何图形知识点梳理几何学是数学的一个重要分支,研究平面和空间中的图形及其性质和变换。
在初中阶段,几何图形作为数学的重要内容之一,学生需要掌握一些基本的几何概念、图形的性质和计算方法。
下面,我将对初中几何图形的知识点进行梳理,帮助学生更好地理解和掌握这些内容。
一、点、线、面及其关系1. 点:几何图形的基本要素,没有长度、面积和体积,只有位置;2. 直线:由无数个点依次排列而成,没有宽度,可以延伸到无穷远;3. 射线:起点是一个固定点,从起点开始向某个方向无限延伸;4. 线段:由两个点确定的有限部分;5. 平面:由无数平行线的集合构成,没有边界,可以延伸到无穷远。
二、分类与性质1. 点的分类:原点、顶点、中点等;2. 线的分类:直线、曲线、射线等;3. 角的分类:锐角、直角、钝角、平角等;4. 三角形:三边和三个角确定,根据边长和角度分为等边三角形、等腰三角形、直角三角形等;5. 矩形:四条边都相等,相对的边两两平行;6. 正方形:四条边和四个角都相等,边两两平行;7. 平行四边形:对边平行且相等;8. 梯形:有两对平行边;9. 圆:由一个点到平面上任意一点的距离都相等;10. 圆的性质:半径、直径、圆心、弦、弧等概念。
三、计算方法1. 计算周长:根据图形的边长求和;2. 计算面积:根据图形的性质和给定的数据,利用相应的公式计算;- 三角形的面积计算:S=底边乘以高的一半;- 矩形的面积计算:S=长乘以宽;- 正方形的面积计算:S=边长的平方;- 圆的面积计算:S=3.14乘以半径的平方;3. 计算体积:根据图形的性质和给定的数据,利用相应的公式计算;- 直角三角形的体积计算:V=底面积乘以高的一半;- 矩形的体积计算:V=长乘以宽乘以高;- 正方体的体积计算:V=边长的立方;- 圆柱的体积计算:V=3.14乘以半径的平方乘以高。
四、平面几何推理1. 用图推理:根据已知条件给出结论,应用图形性质进行推理;2. 用反证法证明:通过否定已知条件的情况,推出一个矛盾的结论,从而证明原命题的正确性;3. 用反向推理证明:从结论出发,反向推导出符合条件的各种情形,判断结论是否正确。
word完整版初中几何图形知识点归纳推荐文档

初中几何图形知识点归纳三角形知识点、概念总结1. 三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2. 三角形的分类(1)三角形按逆分董如下(不尊三荊形.底和膜不等的等腰三角形三轴形 寻腰壬莆开丸等边三角黔3. 三角形的三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边。
4. 高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高。
5. 中线:在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线。
6. 角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
7.三角形技角分棗如下:,直荊三角形|(視擀三角形 钝惭三甬瞩 料三甬形8. 三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性。
9. 三角形内角和定理:三角形三个内角的和等于180推论1直角三角形的两个锐角互余推论2三角形的一个外角等于和它不相邻的两个内角和推论3三角形的一个外角大于任何一个和它不相邻的内角;三角形的内角和是外角和的一半10. 三角形的外角:三角形的一条边与另一条边延长线的夹角,叫做三角形的外角。
11. 三角形外角的性质(1)顶点是三角形的一个顶点,一边是三角形的一边,另一边是三角形的一边的延长线;(2 )三角形的一个外角等于与它不相邻的两个内角和;(3)三角形的一个外角大于与它不相邻的任一内角;(4)三角形的外角和是360 °。
四边形(含多边形)知识点、概念总结一、平行四边形的定义、性质及判定1. 两组对边平行的四边形是平行四边形。
2. 性质:(1)平行四边形的对边相等且平行(2)平行四边形的对角相等,邻角互补(3)平行四边形的对角线互相平分3. 判定:(1)两组对边分别平行的四边形是平行四边形(2)两组对边分别相等的四边形是平行四边形(3)一组对边平行且相等的四边形是平行四边形(4)两组对角分别相等的四边形是平行四边形(5)对角线互相平分的四边形是平行四边形4. 对称性:平行四边形是中心对称图形二、矩形的定义、性质及判定1. 定义:有一个角是直角的平行四边形叫做矩形2. 性质:矩形的四个角都是直角,矩形的对角线相等3. 判定:(1)有一个角是直角的平行四边形叫做矩形(2)有三个角是直角的四边形是矩形(3)两条对角线相等的平行四边形是矩形4. 对称性:矩形是轴对称图形也是中心对称图形。
七年级数学几何图形初步认识知识点

第二章 几何图形的初步认识2.1从生活中认识几何图形知识点:一、认识几何图形几何图形二、几何图形的构成1、面与面相交成___,线与线相交成___。
2、点动成___,___动成面,面动成___。
3、___、___、___是构成几何图形的基本要素,体是由___围成的。
4、面有___面和___面,线有___线和___线。
引申探讨:n 棱柱有几个顶点、几条棱、几个面2.2 点和线知识点:1、点的表示: A B 用一个大写的字母,例如:点A、点B2、线段的表示:方法一 :用表示端点的两个大写字母(没有次序). 例如:线段AB、线段BA.方法二:用一个小写字母.例如线段a.3、射线的表示:用表示端点的大写字母和其余任一点的字母(表示端点的大写字母必须写在前). 例如:射线AB4、直线的表示:方法一 :用表示任两点的两个大写字母(没有次序). 例如:直线AB、直线BA.方法二:用一个小写字母.例如直线a.5、线段、射线、直线的比较:6、直线的性质:经过两点有一条直线,并且只有一条直线(简记为:两点确定一条直线)7、点与直线的位置关系:点在直线上(直线经过点);点在直线外(直线不经过点)引申探讨:1、一条直线上有n个点,会有几条线段?2、握手问题、票价问题、车票问题。
2.3线段的长短知识点:1、线段长短的比较方法:(两种)(1)度量法:是从数量的角度来比较(2)叠合法:是从图形的角度来比较另外了解估测法:依据已有的经验来判断2、线段的画法:3、线段的性质:两点之间的所有连线中,线段最短。
(简记为:两点之间,线段最短。
)引申探讨:蚂蚁爬行问题2.4 线段的和与差知识点:一、线段的和与差的概念及作图方法二、线段的和与差的计算三、线段的中点几何图形初步一、本节学习指导本节知识点比较简单,都是基础,当看书应该就能理解。
二、知识要点1、几何图形从实物中抽象出来的各种图形,包括立体图形和平面图形。
立体图形:有些几何图形的各个部分不都在同一平面内,它们是立体图形。
初中几何基本图形归纳

初中几何基本图形归纳初中几何常见基本图形1 1 1213141516①AC平分/BAD②AB=CB③BC //ADAA H MMWAAD=BD=AC=DC“二推二”㊉㊉7㊉㊉DE=BC/2D、DE//BCB CA DEF= (AD+BC ) /2E、EF // BC //ADAC:BC:AB= 1^/3: 2“二推一”1718192021CD为中线IAP平分Z BACPB=PC①AB=AC !②BD=CD !③AD 丄BC !④N1=N2 !1E、F、G、HC为中点CA型X型DE //BC假A型DC假子母型四边形EFGH为平行四边形AD AEBD CDAD AEBD CDAD AE DEAB AC BCAD AE DEAB AC BCAD AE DEAB AC BC2AC =AD •BBC:AC:AB= 1:1^22231① 过圆心 推三垂直于弦 ® 7®®®'亘②I I②II23平分弦平分弦所对的优弧 平分弦所对的劣弧24___ CA ©AB 为直径V/ C=90°蝶型25ABOCAD PA 规型26AO *P27282930ABCBC PC2 2 2=d +(a/2) d+h=RPD PBPA PD ADPC PB BCPB PD BDPC PA ACPB PA=PD PCAB BC ACBD AB AD 2AB 2=BD BCAC/ A= / DCE / A+ / DCB=180■①i过圆心 d a“二推一”i ②过切点 a:③ 垂直于切线a㊉㊉7®PA=PB / APO=/ BPO32 ◎一/1=/ P / 2=/CA B33 01、02、A三点共线34 c© —0l 丄02 AC=BC几何基本图形1、如图,正三角形ABCxx AE=CD AD BE交于F:AEB^A AD②/ BFD=600AEF^A ABE2、如图,正三角形ABCxx F是^ABCxx心,正三角形边长为a:①AF: DF AD=2 1 : 3 ②xx半径DF= ③外接圆半径AF=3、如图Rt△ ABCxx / C=90Q / B=30Q AC=a D 是AC上的点:①xx半径为②外接圆半径为4、如图Rt△ ABCxx / C=90Q AB=AC=a D是AC上的点:①当D是AC中点时,BD长为; ②当BD是角平分线时,BD长为。
初中数学(几何)知识点总结

初中数学(几何)知识点总结图形的初步认识考点一、直线、射线和线段1、几何图形:从实物中抽象出来的各种图形,包括立体图形和平面图形。
立体图形:有些几何图形的各个部分不都在同一平面内,它们是立体图形。
平面图形:有些几何图形的各个部分都在同一平面内,它们是平面图形。
2、点、线、面、体(1)几何图形的组成点:线和线相交的地方是点,它是几何图形中最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
(2)点动成线,线动成面,面动成体。
3、直线的概念:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。
4、射线的概念:直线上一点和它一旁的部分叫做射线。
这个点叫做射线的端点。
5、线段的概念:直线上两个点和它们之间的部分叫做线段。
这两个点叫做线段的端点。
6、点、直线、射线和线段的表示在几何里,我们常用字母表示图形。
一个点可以用一个大写字母表示。
一条直线可以用一个小写字母表示。
一条射线可以用端点和射线上另一点来表示。
一条线段可用它的端点的两个大写字母来表示。
注意:(1)表示点、直线、射线、线段时,都要在字母前面注明点、直线、射线、线段。
(2)直线和射线无长度,线段有长度。
(3)直线无端点,射线有一个端点,线段有两个端点。
(4)点和直线的位置关系有线面两种:①点在直线上,或者说直线经过这个点。
②点在直线外,或者说直线不经过这个点。
7、直线的性质(1)直线公理:经过两个点有一条直线,并且只有一条直线。
它可以简单地说成:过两点有且只有一条直线。
(2)过一点的直线有无数条。
(3)直线是是向两方面无限延伸的,无端点,不可度量,不能比较大小。
(4)直线上有无穷多个点。
(5)两条不同的直线至多有一个公共点。
8、线段的性质(1)线段公理:所有连接两点的线中,线段最短。
也可简单说成:两点之间线段最短。
(2)连接两点的线段的长度,叫做这两点的距离。
(3)线段的中点到两端点的距离相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中几何图形知识点归纳
三角形知识点、概念总结
1. 三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2. 三角形的分类
3. 三角形的三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边。
4. 高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高。
5. 中线:在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线。
6. 角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
7. 高线、中线、角平分线的意义和做法
8. 三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性。
9. 三角形内角和定理:三角形三个内角的和等于180°
推论1 直角三角形的两个锐角互余
推论2 三角形的一个外角等于和它不相邻的两个内角和
推论3 三角形的一个外角大于任何一个和它不相邻的内角;三角形的内角和是外角和的一半
10. 三角形的外角:三角形的一条边与另一条边延长线的夹角,叫做三角形的外角。
11. 三角形外角的性质
(1)顶点是三角形的一个顶点,一边是三角形的一边,另一边是三角形的一边的延长线;
(2)三角形的一个外角等于与它不相邻的两个内角和;
(3)三角形的一个外角大于与它不相邻的任一内角;
(4)三角形的外角和是360°。
四边形(含多边形)知识点、概念总结
一、平行四边形的定义、性质及判定
1. 两组对边平行的四边形是平行四边形。
2. 性质:
(1)平行四边形的对边相等且平行
(2)平行四边形的对角相等,邻角互补
(3)平行四边形的对角线互相平分
3. 判定:
(1)两组对边分别平行的四边形是平行四边形
(2)两组对边分别相等的四边形是平行四边形
(3)一组对边平行且相等的四边形是平行四边形
(4)两组对角分别相等的四边形是平行四边形
(5)对角线互相平分的四边形是平行四边形
4. 对称性:平行四边形是中心对称图形
二、矩形的定义、性质及判定
1. 定义:有一个角是直角的平行四边形叫做矩形
2. 性质:矩形的四个角都是直角,矩形的对角线相等
3. 判定:
(1)有一个角是直角的平行四边形叫做矩形
(2)有三个角是直角的四边形是矩形
(3)两条对角线相等的平行四边形是矩形
4. 对称性:矩形是轴对称图形也是中心对称图形。
三、菱形的定义、性质及判定
1. 定义:有一组邻边相等的平行四边形叫做菱形
(1)菱形的四条边都相等
(2)菱形的对角线互相垂直,并且每一条对角线平分一组对角
(3)菱形被两条对角线分成四个全等的直角三角形
(4)菱形的面积等于两条对角线长的积的一半
2. s菱=争6(n、6分别为对角线长)
3. 判定:
(1)有一组邻边相等的平行四边形叫做菱形
(2)四条边都相等的四边形是菱形
(3)对角线互相垂直的平行四边形是菱形
4. 对称性:菱形是轴对称图形也是中心对称图形
四、正方形定义、性质及判定
1. 定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形
2. 性质:
(1)正方形四个角都是直角,四条边都相等
(2)正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角
(3)正方形的一条对角线把正方形分成两个全等的等腰直角三角形
(4)正方形的对角线与边的夹角是45°
(5)正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形
3. 判定:
(1)先判定一个四边形是矩形,再判定出有一组邻边相等
(2)先判定一个四边形是菱形,再判定出有一个角是直角
4. 对称性:正方形是轴对称图形也是中心对称图形
五、梯形的定义、等腰梯形的性质及判定
1. 定义:一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯
形.一腰垂直于底的梯形是直角梯形
2. 等腰梯形的性质:等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等
3. 等腰梯形的判定:两腰相等的梯形是等腰梯形;同一底上的两个角相等的梯形是等腰梯形;两条对角线相等的梯形是等腰梯形
4. 对称性:等腰梯形是轴对称图形
六、三角形的中位线平行于三角形的第三边并等于第三边的一半;梯形的中位线平行于梯形的两底并等于两底和的一半。
七、线段的重心是线段的中点;平行四边形的重心是两对角线的交点;三角形的重心是三条中线的交点。
八、依次连接任意一个四边形各边中点所得的四边形叫中点四边形。
九、多边形
1. 多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。
2. 多边形的内角:多边形相邻两边组成的角叫做它的内角。
3. 多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。
4. 多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
5. 多边形的分类:分为凸多边形及凹多边形,凸多边形又可称为平面多边形,凹多边形又称空间多边形。
多边形还可以分为正多边形和非正多边形。
正多边形各边相等且各内角相等。
6. 正多边形:在平面内,各个角都相等,各条边都相等的多边形叫做正多边形。
7. 平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面。
8. 公式与性质
多边形内角和公式:n边形的内角和等于(n-2)·180°
9. 多边形外角和定理:
(1)n边形外角和等于n·180°-(n-2)·180°=360°
(2)边形的每个内角与它相邻的外角是邻补角,所以n边形内角和加外角和等于n·180°
10. 多边形对角线的条数:
(1)从n边形的一个顶点出发可以引(n-3)条对角线,把多边形分词(n-2)个三角形
(2)n边形共有n(n-3)/2条对角线。
