(完整)高中数学三年最全思维导图
合集下载
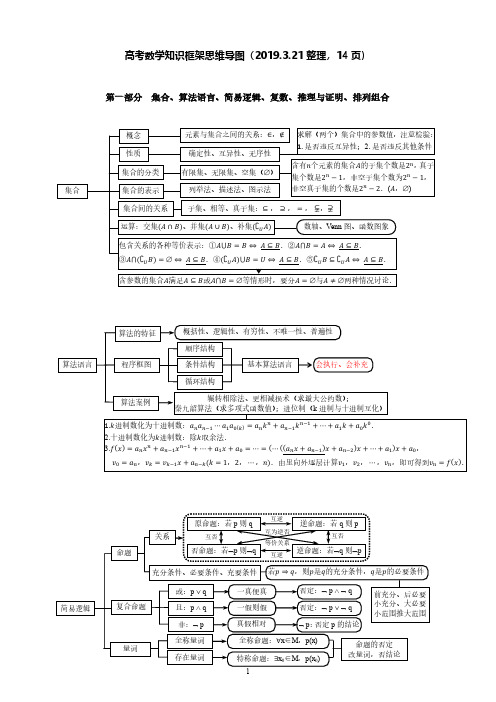
高中数学知识框架思维导图(整理版)

基本初等函数 指数函数、对数函数、幂函数、三角函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用 分段探究,整体考察 复合函数的单调性:同增异减 赋值法、典型的函数模型 零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换:������ = ������(������) → ������ = ������(������ ± ������),������ = ������(������) → ������ = ������(������) ± ������,������, ������ > 0 函数图象 及其变换 对称变换:������ = ������(������) → ������ = −������(������),������ = ������(������) → ������ = ������(−������),������ = ������(������) → ������ = −������(−������) 翻折变换:������ = ������(������) → ������ = |������(������)|,������ = ������(������) → ������ = ������(|������|) 伸缩变换:������ = ������(������) → ������ = ������������(������),������ = ������(������) → ������ = ������(������������)
������
第二部分
角的概念
三角函数与平面向量
弧长公式������ = ������������、扇形面积公式������ = ������������
2 1 π 2
高中数学知识框架思维导图
i.
①(1 ± i)2 = ±2i;
②1+i = i;1−i = −i;
1−i
1+i
③������ + ������i = i(������ − ������i),
如3+4i = i(4−3i) = i;
4−3i 4−� = ������ + ������i、复平面内点 Z(������, ������)、向量���⃗⃗���⃗⃗���⃗��� = (������, ������)的一一对应关系; 复数模的几何意义:|������| = |������ + ������i| = √������2 + ������2 = |���⃗⃗���⃗⃗���⃗���|
2.对数的运算性质(������>0,且������ ≠1,������>0,������>0):①log������(������ ∙ ������) = log������������ + log������������;
简易逻辑
命题
关系
原命题:若 p 则 q
互否
否命题:若p 则q
互逆
互为逆否 等价关系
互逆
逆命题:若 q 则 p
互否
逆命题:若q 则p
充分条件、必要条件、充要条件 若������ ⇒ ������,则������是������的充分条件,������是������的必要条件
复合命题 量词
或:p q 且:p q 非: p 全称量词 存在量词
2
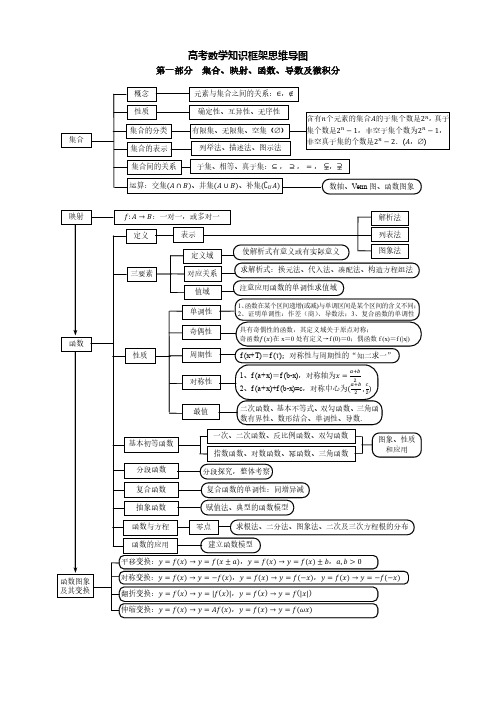
映射
函数
函数图象 及其变换
第二部分 函数、导数及微积分
������: ������ → ������:一对一,或多对一
高中数学知识框架思维导图(整理版)
柯西不等式
第四部分
位置关系
截距
解析几何
斜率公式、倾斜角的变化与斜率的变化: = tan , =
倾斜角和斜率
重合
A1B2-A2B1=0,C1B2-C2B1=0
平行
A1B2-A2B1=0,C1B2-C2B1≠0
相交
A1B2-A2B1≠0
垂直
直线的方程
z 的几何意义:
过可行域内一点(, )
向直线 = , = 作
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
对称性
y=Asin(x+)+b
化简、求值、
证明(恒等变形)
)
值域
图象
对称轴(正切函数除外)经过函数图象
的最高(或低)点且垂直 x 轴的直线,
对称中心是正余弦函数图象的零点,正
切函数的对称中心为( ,0)(k∈Z).
最值
2
①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1
2+1 −1
高中数学思维导图(新课标)

c 0 c 为常数
'
f x 与 f x 0 的区别
vt S , at vt
'
0 0
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
导 数
导数概念
运动的平均速度 曲线的割线的斜率
'
0
k f
'
'
x
0
' '
; x
n
nx 1 x
定
映
A中元素在B中都有唯一的象;可一对一 (一一映射),也可多对一,但不可一对多 定义 函数的概念 表示 定义域
列表法 解析法 图象法 使解析式有意义及实际意义
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
射
三要素
区间 单调性 奇偶性 周期性 对称性
对应关系 值域
常用换元法求解析式 观察法、判别式法、分离常数法、单调性法、最值法、 重要不等式、三角法、图象法、线性规划等
函数的 基本性质
函 数
函数常见的
最值
几种变换
基本初等函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用
平移变换、对称变换 翻折变换、伸缩变换
三角函数 单调性:同增异减 赋值法,典型的函数 零点 建立函数模型 求根法、二分法、图象法;一元二次方程根的分布 退出 上一页
函数的平均变化率
函数的瞬时变化率 运动的瞬时速度 曲线的切线的斜率
第一部分 第二部分 第三部分 第四部分 第五部分 第六部分
集合与简易逻辑 映射、函数、导数、定积分与微积分 三角函数与平面向量 数列 不等式 立体几何与空间向量
'
f x 与 f x 0 的区别
vt S , at vt
'
0 0
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
导 数
导数概念
运动的平均速度 曲线的割线的斜率
'
0
k f
'
'
x
0
' '
; x
n
nx 1 x
定
映
A中元素在B中都有唯一的象;可一对一 (一一映射),也可多对一,但不可一对多 定义 函数的概念 表示 定义域
列表法 解析法 图象法 使解析式有意义及实际意义
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
射
三要素
区间 单调性 奇偶性 周期性 对称性
对应关系 值域
常用换元法求解析式 观察法、判别式法、分离常数法、单调性法、最值法、 重要不等式、三角法、图象法、线性规划等
函数的 基本性质
函 数
函数常见的
最值
几种变换
基本初等函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用
平移变换、对称变换 翻折变换、伸缩变换
三角函数 单调性:同增异减 赋值法,典型的函数 零点 建立函数模型 求根法、二分法、图象法;一元二次方程根的分布 退出 上一页
函数的平均变化率
函数的瞬时变化率 运动的瞬时速度 曲线的切线的斜率
第一部分 第二部分 第三部分 第四部分 第五部分 第六部分
集合与简易逻辑 映射、函数、导数、定积分与微积分 三角函数与平面向量 数列 不等式 立体几何与空间向量
高中数学知识框架思维导图(整理版)

2 : 2 + 2 + 2 = 0.
点斜式:y-y0=k(x-x0)
注意:截距可正、
可负,也可为 0.
2 −1
注意各种形式的转化和运用范围.
x y
截距式: + =1
a b
两直线的交点
距离
一般式:Ax+By+C=0
两点间的距离公式|1 2 | = √(1 − 2 )2 + (1 − 2 )2 .
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1ቤተ መጻሕፍቲ ባይዱ
2+1 −1
− (+2)2 )
= (−1) (
1
2−1
+
错位相加法: = ( + )−1 → = ( + ) −
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
与 的关系
1 ,
= 1,
= {
− −1 , ≥ 2.
构造等差数列
an+1 p an
= · +1 转为③
qn q qn-1
⑤an + 1=pan+qn
点斜式:y-y0=k(x-x0)
注意:截距可正、
可负,也可为 0.
2 −1
注意各种形式的转化和运用范围.
x y
截距式: + =1
a b
两直线的交点
距离
一般式:Ax+By+C=0
两点间的距离公式|1 2 | = √(1 − 2 )2 + (1 − 2 )2 .
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1ቤተ መጻሕፍቲ ባይዱ
2+1 −1
− (+2)2 )
= (−1) (
1
2−1
+
错位相加法: = ( + )−1 → = ( + ) −
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
与 的关系
1 ,
= 1,
= {
− −1 , ≥ 2.
构造等差数列
an+1 p an
= · +1 转为③
qn q qn-1
⑤an + 1=pan+qn
