习题5.4 各地区建筑业总产值和建筑业企业利润总额案例分析

合集下载

建筑企业法律案例分析题(3篇)

第1篇一、案例背景某建筑企业（以下简称“A企业”）成立于2005年，主要从事房屋建筑工程施工。

近年来，A企业在市场竞争中不断发展壮大，承接了多个大型工程项目。

2019年，A企业与某房地产开发公司（以下简称“B公司”）签订了一份《建设工程施工合同》，约定由A企业承建B公司开发的某住宅小区项目。

合同总价款为2亿元，工期为两年。

合同中还约定了付款方式、违约责任等条款。

在施工过程中，A企业严格按照合同约定进行施工，但B公司因资金问题，未能按时支付工程进度款。

A企业多次催促B公司支付，但B公司以各种理由推脱。

在工程接近尾声时，B公司突然宣布破产，导致A企业陷入困境。

二、法律问题1. A企业能否要求B公司支付剩余工程款？2. B公司破产，A企业如何维护自身合法权益？3. A企业能否对B公司的破产财产提起破产债权申报？三、案例分析（一）A企业能否要求B公司支付剩余工程款根据《中华人民共和国合同法》第八条的规定：“依法成立的合同，对当事人具有法律约束力。

当事人应当按照约定履行自己的义务，不得擅自变更或者解除合同。

”本案中，A企业与B公司签订的《建设工程施工合同》是双方真实意思表示，且符合法律规定，因此该合同对双方具有法律约束力。

根据《中华人民共和国合同法》第一百零七条的规定：“当事人一方不履行合同义务或者履行合同义务不符合约定的，应当承担继续履行、采取补救措施或者赔偿损失等违约责任。

”本案中，B公司未能按时支付工程进度款，已构成违约。

根据合同约定，B公司应承担违约责任，A企业有权要求B公司支付剩余工程款。

（二）B公司破产，A企业如何维护自身合法权益1. 申报破产债权：根据《中华人民共和国企业破产法》第四十八条的规定：“债权人申报债权，应当向管理人提交债权证明和有关证据。

”A企业应在规定时间内向B公司破产管理人申报债权，并提供相关证据，如合同、发票、付款凭证等。

2. 参加债权人会议：根据《中华人民共和国企业破产法》第五十二条的规定：“债权人有权参加债权人会议，对破产财产的分配方案等事项发表意见。

建筑工程法律案例分析题(3篇)

第1篇一、案情简介甲公司是一家从事建筑工程施工的企业，乙公司是一家房地产开发企业。

2010年，甲公司通过投标获得了乙公司开发的某住宅小区的建筑工程施工项目。

双方签订了一份施工合同，约定甲公司负责该住宅小区的土建、安装、装饰装修等工程的施工，工期为2年。

合同中还约定，甲公司需在工程竣工验收合格后支付乙公司一定的工程款，并在工程竣工后一年内办理产权证。

在施工过程中，甲公司按照合同约定完成了施工任务，并于2012年完成了竣工验收。

然而，在办理产权证的过程中，甲公司发现乙公司提供的土地使用权证存在瑕疵，导致无法办理产权证。

甲公司多次与乙公司协商，要求乙公司承担相应的责任，但乙公司以各种理由推脱。

无奈之下，甲公司向法院提起诉讼，要求乙公司承担违约责任。

二、争议焦点1. 乙公司是否应当承担违约责任？2. 乙公司应当承担何种违约责任？三、案例分析1. 乙公司是否应当承担违约责任？根据《中华人民共和国合同法》第107条规定：“当事人一方不履行合同义务或者履行合同义务不符合约定的，应当承担违约责任。

”在本案中，乙公司提供的土地使用权证存在瑕疵，导致甲公司无法办理产权证，属于乙公司未能履行合同义务的行为。

因此，乙公司应当承担违约责任。

2. 乙公司应当承担何种违约责任？根据《中华人民共和国合同法》第114条规定：“当事人一方不履行合同义务或者履行合同义务不符合约定的，应当承担以下违约责任：（一）继续履行；（二）采取补救措施；（三）赔偿损失。

”在本案中，乙公司提供的土地使用权证存在瑕疵，导致甲公司无法办理产权证，给甲公司造成了经济损失。

因此，乙公司应当承担以下违约责任：（1）继续履行：乙公司应当尽快解决土地使用权证的问题，协助甲公司办理产权证。

（2）赔偿损失：乙公司应当赔偿甲公司因无法办理产权证而遭受的经济损失。

四、判决结果法院经审理认为，乙公司提供的土地使用权证存在瑕疵，导致甲公司无法办理产权证，属于乙公司未能履行合同义务的行为。

建筑企业法律案例分析题(3篇)

第1篇一、案例背景某建筑公司（以下简称“甲公司”）是一家具有国家一级资质的建筑施工企业。

2019年，甲公司与某房地产开发公司（以下简称“乙公司”）签订了一份建筑工程施工合同，约定由甲公司承建乙公司开发的某住宅小区项目。

合同金额为1亿元人民币，工期为24个月。

合同中还约定，若因甲方原因导致工期延误，每延误一天，甲方应向乙方支付合同金额的1‰作为违约金。

2020年3月，由于甲公司施工过程中管理不善，导致项目进度严重滞后。

至2021年1月，项目工期延误已达10个月。

乙公司多次与甲公司协商，要求其加快施工进度，但甲公司以各种理由推脱，拒不履行合同约定的违约责任。

乙公司遂向法院提起诉讼，要求甲公司支付违约金1000万元，并赔偿因其工期延误造成的损失。

二、案件争议焦点1. 甲公司是否应承担工期延误的违约责任？2. 乙公司要求甲公司支付的违约金是否过高？三、法律分析1. 关于工期延误的违约责任根据《中华人民共和国合同法》第一百零七条规定：“当事人一方不履行合同义务或者履行合同义务不符合约定的，应当承担继续履行、采取补救措施或者赔偿损失等违约责任。

”本案中，甲公司作为合同约定的施工方，未能按照合同约定的时间完成工程，已构成违约。

根据合同约定，甲公司应承担工期延误的违约责任。

2. 关于违约金是否过高的问题根据《中华人民共和国合同法》第一百一十四条规定：“当事人可以约定一方违约时应当根据违约情况向对方支付一定数额的违约金，也可以约定因违约产生的损失赔偿额的计算方法。

约定的违约金低于造成的损失的，当事人可以请求人民法院或者仲裁机构予以增加；约定的违约金过分高于造成的损失的，当事人可以请求人民法院或者仲裁机构予以适当减少。

”本案中，乙公司要求甲公司支付的违约金为合同金额的1‰，即1000万元。

根据合同约定，甲公司因工期延误给乙公司造成的损失可能远远超过1000万元，因此，乙公司要求支付的违约金并不过高。

四、法院判决经审理，法院认为甲公司未能按照合同约定的时间完成工程，构成违约，应承担工期延误的违约责任。

第五章-异方差性(作业任务)

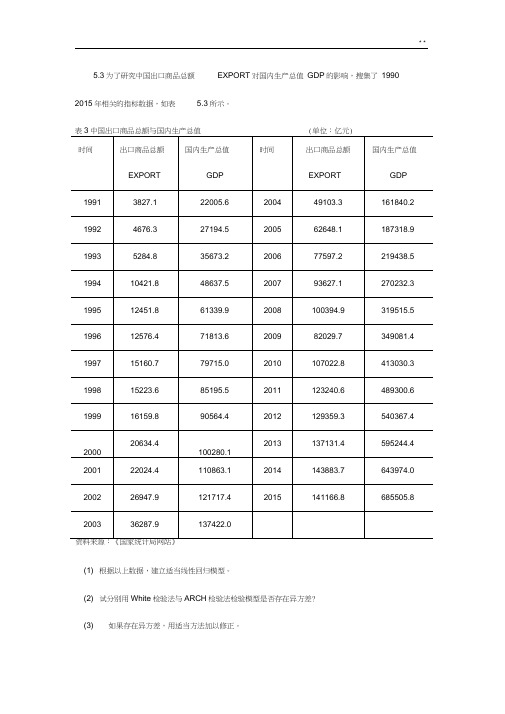
5.3为了研究中国出口商品总额EXPORT对国内生产总值GDP的影响，搜集了1990 2015年相关的指标数据，如表 5.3所示。

(1) 根据以上数据，建立适当线性回归模型。

(2) 试分别用White检验法与ARCH检验法检验模型是否存在异方差?(3) 如果存在异方差，用适当方法加以修正。

解：（1）Dependent Variable: YMethod: Least SquaresDate: 04/18/20 Time: 15:38Sample: 1991 2015Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C -673.0863 15354.24 -0.0438370.965 4X 4.061131 0.201677 20.136840.000 0R-squared 0.946323 Mean dependent var234690. 8Adjusted R-squared 0.943990 S.D. dependent var210356. 7S.E. of regression 49784.06 Akaike info criterion 24.5454Sum squared resid 5.70E+10 Schwarz criterion 24.64291 Log likelihood -304.8174 Hannan-Quinn criter. 24.57244F-statistic 405.4924 Durbin-Watson stat 0.366228Prob(F-statistic) 0.000000模型回归的结果：AY 673.0863 4.0611X it ( 0.0438 )(20.1368)R20.9463, n 25(2) white:该模型存在异方差Heteroskedasticity Test: WhiteF-statistic 4.493068 Prob. F(2,22) 0.0231Obs*R-squared 7.250127 Prob. Chi-Square(2) 0.0266 Scaled explained SS 8.361541 Prob. Chi-Square(2) 0.0153Test Equation:Dependent Variable: RESIDEMethod: Least SquaresDate: 04/18/20 Time: 17:45Sample: 1991 2015Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C -1.00E+09 1.43E+09 -0.7003780.491 0XA2 -0.455420 0.420966 -1.081847 0.2910 X 102226.2 60664.19 1.685117 0.1061R-squared 0.290005 Mean dependent var2.28E+0 9Adjusted R-squared 0.225460 S.D. dependent var 3.84E+09S.E. of regression 3.38E+09 Akaike info criterion 46.83295Sum squared resid 2.51E+20 Schwarz criterion 46.97922 Log likelihood -582.4119 Hannan-Quinn criter. 46.87352F-statistic 4.493068 Durbin-Watson stat 0.749886Prob(F-statistic) 0.023110ARCH检验：该模型存在异方差Test Equation:Dependent Variable: RESID A2Method: Least SquaresDate: 04/18/20 Time: 19:55Sample (adjusted): 1992 2015Included observations: 24 after adjustmentsVariableCoefficient Std. Error t-Statistic Prob. C8.66E+08 6.92E+08 1.251684 0.2238RESID A 2(-1) 0.817146 0.1889444.3248020.0003 R-squared0.459511 Mean dependent var 2.37E+09 Adjusted R-squared 0.434944 S.D. dependent var 3.90E+09S.E. of regression 2.93E+09 Akaike info criterion 46.51293 Sum squared resid 1.89E+20 Schwarz criterion 46.61110 Log likelihood -556.1552 Hannan-Quinn criter. 46.53898 F-statistic 18.70391Durbin-Watson stat0.888067Prob(F-statistic)0.000273(3)修正：加权最小二乘法修正却 WF Woricflil-ri UTLECi id tl e^cJ\ i « T t"l t-|<p-r f T 护i ■"i-i ■「■ H 1 < ~HV Prbll 1 T ffM r« 11 BHR 7 F r F -K * J *■ J —厂ilTHL 日芦£臼电*电引 OdiJ 1 0*左(■ 20 3>5r^lucilifl -MI^I TGR 1 Z7Q I S w= — T ,皿”=E Ba^-oa 山口 fE=-UH a P -OE = -口曰 3.2 1 且-口9 I B 之与尸-口口 ti .3-Z2E-DO 出q,峙尸・C 旦( 4.3-1 E-O^3 0 3IE 09 N.HMU O-QI 立o 右匚> - nO4 TDE--W Z.&15^=- DC1 hi-tiE - "IIIJ i. um r ci Q SJ ^F -iii i 旦日二-①口Dependent Variable: Y Method: Least Squares Date: 04/18/20 Time: 20:46 Sample: 1991 2015Included observations: 25 Weighting series: W2Weight type: Inverse variance (average scaling)VariableCoefficientStd. Errort-StatisticProb.C 10781.17 2188.706 4.925821 0.0001 X3.9316060.19200420.476670.0000Weighted StatisticsR-squared0.947998 Mean dependent var 51703.40 Adjusted R-squared 0.945737 S.D. dependent var 11816.72 S.E. of regression 8420.515 Akaike info criterion 20.99135 Sum squared resid1.63E+09Schwarz criterion21.08886「工 P U 『匕 7 日nQ r U J-4m y Q M-n!R-0 Kc D 」a 口 9m 日0: B 吝口 oaooom 口「1 ;「m =2 Q 工H rKLog likelihood -260.3919 Hannan-Quinn criter. 21.01839F-statistic 419.2938 Durbin-Watson stat 0.539863 Prob(F-statistic) 0.000000 Weighted mean dep. 39406.30 Unweighted StatisticsR-squared 0.944994 Mean dependent var234690. 8Adjusted R-squared 0.942602 S.D. dependent var 210356.7S.E. of regression 50396.82 Sum squared resid 5.84E+1修正后进行white检验:Heteroskedasticity Test: WhiteF-statistic 0.261901 Prob. F(2,22) 0.7720 Obs*R-squared 0.581387 Prob. Chi-Square(2) 0.7477 Scaled explained SS 0.211737 Prob. Chi-Square(2) 0.8995Test Equation:Dependent Variable: WGT_RESID A2Method: Least SquaresDate: 04/18/20 Time: 20:41Sample: 1991 2015Included observations: 25Collinear test regressors dropped from specificationVariable Coefficient Std. Error t-Statistic Prob.C 71441488 22046212 3.2405340.003 8X*WGTA2 -2711.961 5055.773 -0.536409 0.5971 WGTA2 13536351 20714871 0.653461 0.5202R-squared 0.023255 Mean dependent var 65232673 Adjusted R-squared -0.065539 S.D. dependent var 61762160 S.E. of regression 63753972 Akaike info criterion 38.89113Sum squared resid 8.94E+16 Schwarz criterion 39.03739 Log likelihood -483.1391 Hannan-Quinn criter. 38.9317F-statistic 0.261901 Durbin-Watson stat 0.898907Prob(F-statistic) 0.771953修正后的模型为AY 10781.17 3.931606X it (4.925821)(20.47667)R20.9480, n 255.4 表5.4的数据是2011年各地区建筑业总产值（X）和建筑业企业利润总额（Y）。

建筑公司法律案例分析题(3篇)

第1篇一、案情简介某建筑公司（以下简称“甲公司”）成立于2000年，是一家专业从事建筑工程施工的企业。

2018年，甲公司承接了一项由乙房地产开发公司（以下简称“乙公司”）投资的住宅小区建设项目。

合同约定，甲公司负责该小区的土建施工，总工期为两年，合同总价为人民币1亿元。

在施工过程中，由于甲公司管理不善，导致工程进度严重滞后，实际工期超过了合同约定的期限。

此外，甲公司在施工过程中还发生了多起安全事故，造成人员伤亡和财产损失。

乙公司多次与甲公司协商，要求其加快工程进度、整改安全隐患，但甲公司均以各种理由推脱。

2020年，乙公司向当地人民法院提起诉讼，要求甲公司承担违约责任，赔偿因其违约行为造成的经济损失和合理费用。

在诉讼过程中，甲公司提出以下抗辩：1. 工期延误是由于不可抗力因素导致的，甲公司不应承担违约责任。

2. 发生的安全事故是由于乙公司提供的施工图纸存在缺陷导致的，甲公司不应承担安全事故责任。

3. 甲公司已经按照合同约定完成了工程量，不应承担未完成工程量的违约责任。

二、法律问题1. 甲公司是否应承担工期延误的违约责任？2. 甲公司是否应承担安全事故的责任？3. 甲公司是否应承担未完成工程量的违约责任？三、案例分析（一）工期延误的违约责任根据《中华人民共和国合同法》第一百零七条规定：“当事人一方不履行合同义务或者履行合同义务不符合约定的，应当承担违约责任。

”在本案中，甲公司未按照合同约定的工期完成工程，构成违约。

关于工期延误的原因，甲公司主张是由于不可抗力因素导致的。

根据《中华人民共和国合同法》第一百一十七条规定：“不可抗力是指不能预见、不能避免并不能克服的客观情况。

”在本案中，甲公司未能提供充分的证据证明其工期延误是由于不可抗力因素导致的。

因此，法院判定甲公司应承担工期延误的违约责任。

（二）安全事故的责任根据《中华人民共和国安全生产法》第四十三条规定：“生产经营单位应当建立健全安全生产责任制，加强安全生产管理，防止和减少生产安全事故。

各地区建筑业总产值对建筑业企业利润总额的影响

计量经济学期末实验报告实验名称：各地区建筑业总产值对建筑业企业利润总额的影响姓名：学号：班级：指导教师：时间：一、研究的背景近年来，由于房地产事业的快速发展，同时也带动了建筑业的总产值业的飞速增长，为了研究各地区建筑业总产值和建筑业企业利润总额之间的关系，预测未来的增长趋势，需建立计量经济学模型。

二、指标选取和数据搜集从《中国统计年鉴》可以收集到以下数据：表1.各地区建筑业总产值和建筑业企业利润总额（单位：万元）三、实验过程（一）模型设定为了分析各地建筑业企业利润总额与建筑业总产值的关系，选择2007年“建筑业企业利润总额”为被解释变量（用Y表示），选择2007年“建筑业总产值”为解释变量（用X）表示。

为分析建筑业企业利润总额（Y）和建筑业总产值(X)的关系，作如下散点图：表2.建筑业企业利润总额与建筑业总产值的散点图从散点图可以看出建筑业企业利润总额（Y）与建筑业总产值（X）大体呈现为线性关系，为分析建筑业企业利润总额随建筑业总产值变动的数量规律性，可以建立如下简单的线性回归模型:其中，、为模型参数；为随机扰动项。

（二）参数估计利用软件，生成Y、X的数据，并采用这些数据对模型进行回归，结果如表3所示:表3.回归结果可用规范的形式将参数估计和结果写为（36196.79）（0.001553）t =（－0.800980）（20.82325）R2=0.937312 433.6076 31（三）模型检验1.经济意义检验所估计的参数，，这说明建筑业总产值入每增加1万元，平均来说可导致建筑业企业利润总额增加万元。

这与理论分析和经验判断一致。

2统计意义检验（1）拟合优度：由表3中的数据可以得到R2=0.937312，这说明模型对样本的拟合很好。

（2）方程显著性（F检验）：由表3知，F检验的p值<0.05，说明回归方程是显著的。

（3）参数显著性（t检验）：针对H0：=0和H：=0，由表3知，估计的回归系数的标准误差和t值分别为：（）=36196.79，t（）=－0.800980；的标准误差和t值分别为：()= 0.001553，t（）=20.82325。

建筑项目利润分析总结范文

建筑项目利润分析总结范文一、项目概况。

咱这个建筑项目啊，就像是一场大冒险。

从一块空地开始，要建起一座能遮风挡雨、让人安心居住或者工作的大楼，那可是相当不容易。

项目包括了基础建设、主体结构搭建、内外装修等一系列复杂的工程，就像搭积木，不过这积木可是超级巨大又复杂的那种。

二、收入情况。

1. 合同收入。

最初谈项目的时候，那合同上的金额就像是一个诱人的大蛋糕。

经过一轮又一轮的谈判，终于确定了一个看起来很美的数字。

这可是项目收入的主要来源，就像基本工资一样，心里踏实不少。

不过呢，这钱也不是那么好拿的，后面的活儿得干得漂亮才行。

2. 变更收入。

在项目进行过程中，就像走在路上突然发现了一些岔路口。

甲方有时候会提出一些变更要求，这就像游戏里突然开启了新的支线任务。

有些变更会给咱带来额外的收入，比如说增加了一些功能区域或者改变了某些建筑材料的规格。

这些变更收入就像是奖金，给总收入添砖加瓦。

三、成本分析。

1. 材料成本。

材料可是建筑的“肉和骨头”啊。

从钢筋水泥到砖块木材，每一样都得花钱买。

这些材料的价格就像调皮的小精灵，一会儿涨一会儿跌。

有时候刚订了一批材料，结果市场价格就降了，那感觉就像吃了个闷亏。

而且还得考虑运输成本、仓储成本啥的，就像给这些小精灵们盖房子住，也是一笔不小的开销。

2. 人工成本。

咱的建筑工人可是项目的主力军，就像一群勤劳的小蜜蜂。

他们的工资、福利啥的加起来也是个大数目。

而且人工成本还得根据工程进度来安排，有时候赶工期，就得加班加点，这加班费就像额外的蜂蜜，得给小蜜蜂们准备好。

要是工人的技术水平参差不齐，还可能影响工程质量，那就像蜂蜜里掺了沙子，得不偿失啊。

3. 设备成本。

那些大型的建筑设备，像塔吊、挖掘机之类的，就像超级英雄的装备。

租这些设备或者买下来都要花不少钱。

设备还得保养维修，就像给超级英雄做体检和治疗，要是设备出了故障，那可就像超级英雄突然“掉链子”，耽误工期不说，还得花更多的钱去修。

四、利润计算与分析。

第五章练习题及参考解答

第五章练习题及参考解答5.1 设消费函数为i i i i u X X Y +++=33221βββ式中，i Y 为消费支出；i X 2为个人可支配收入；i X 3为个人的流动资产；i u 为随机误差项，并且222)(,0)(i i i X u Var u E σ==（其中2σ为常数）。

试回答以下问题：(1)选用适当的变换修正异方差，要求写出变换过程；(2)写出修正异方差后的参数估计量的表达式。

【练习题5.1参考解答】（1）因为22()i i f X X =，所以取221i iW X =，用2i W 乘给定模型两端，得 312322221i i iii i i Y X u X X X X βββ=+++ 上述模型的随机误差项的方差为一固定常数，即22221()()i i i iu Var Var u X X σ==（2）根据加权最小二乘法，可得修正异方差后的参数估计式为***12233ˆˆˆY X X βββ=-- ()()()()()()()***2****22232322322*2*2**2223223ˆi i ii i i i i i i i i i i i i i i W y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑()()()()()()()***2****23222222332*2*2**2223223ˆii i i i i i i i i i i ii ii i iW y x W x W y x W x x WxWxWx xβ-=-∑∑∑∑∑∑∑其中22232***23222,,i ii ii i iiiW X W X W Y XXYWWW ===∑∑∑∑∑∑******222333i i i i i x X X x X X y Y Y =-=-=-5.2 对于第三章练习题3.3家庭书刊消费与家庭收入及户主受教育年数关系的分析，进一步作以下分析:1）判断模型123i i i i Y X T u βββ=+++是否存在异方差性。

计量经济学

计量经济学1横截⾯数据是指（） [单选题] *A.同⾯时点上相同统计单位相同统计指标组成的数据B.同⾯时点上相同统计单位不同统计指标组成的数据C.同⾯时点上不同统计单位相同统计指标组成的数据(正确答案)D.同⾯时点上不同统计单位不同统计指标组成的数据2.下⾯属于横截⾯数据的是（） [单选题] *A.某年某地区20个乡镇⾯业产值的合计数B.某年某地区20个乡镇各镇的⾯业产值(正确答案)C.1991−2003年各年某地区20个乡镇企业各镇的⾯业产值D.1991−2003年各年某地区20个乡镇企业的平均⾯业产值3.计量经济模型是指（） [单选题] *A.投⾯产出模型B.数学规划模型C.模糊数学模型D.包含随机扰动项的经济数学模型(正确答案)4.计量经济学是下列哪⾯学科的分⾯学科（） [单选题] *A.数学B.经济学(正确答案)C.统计学D.数理统计学5.同⾯统计指标同⾯统计单位按时间顺序记录形成的数据列是（） [单选题] *A.时期数据(正确答案)B.横截⾯数据C.时间序列数据D.混合数据6.经济计量分析⾯作的基本步骤是（） [单选题] *A.确定模型导向→确定变量及⾯程式→检验模型→估计模型B.个体设计→总体估计→估计模型→应⾯模型C.设定模型→估计参数→收集样本资料→应⾯模型D.设定理论模型→收集样本资料→估计模型参数→检验模型(正确答案)7.相关系数r的取值范围是（） [单选题] *A.r≥1B.r≤-1C.0≤r≤1D.−1≤r≤1(正确答案)8.如果X和Y在统计上独⾯，则相关系数等于（） [单选题] *A.1B.0(正确答案)C.-1D.∞9.相关关系是指（） [单选题] *A.变量间不确定性关系(正确答案)B.变量间的⾯独⾯关系C.变量间的函数关系D.变量间的因果关系10.经计算，变量x与y之间相关系数为-0.75，则⾯者之间存在（） [单选题] *A.中度负相关B.⾯度负相关C.中度线性负相关(正确答案)D.低度负相关11.反映由模型中解释变量所解释的那部分离差大小的是（） [单选题] *A.残差平方和B.总体平方和C.回归平方和(正确答案)D.离差和12进行一元线性回归分析时的两个变量（） [单选题] *A.都是随机变量B.都不是随机变量C.随机的或非随机都可以D.一个是随机变量，一个不是随机变量(正确答案)13.产量(X，台)与单位产品成本(Y，元/台)之间的回归方程为Image，这说明（）[单选题] *A.产量每增加一台，单位产品成本增加356元B.产量每增加一台，单位产品成本平均减少1.5元(正确答案)C.产量每增加一台，单位产品成本平均增加356元D.产量每增加一台，单位产品成本减少1.5元14.设Y表示实际观测值，Image表示OLS估计回归值，则下列哪项成立（） [单选题] *A.ImageB.Image(正确答案)C.ImageD.Image15.参数Image的估计量Image具备有效性是指（） [单选题] *A.ImageB.ImageC.Image(正确答案)D.Image16.已知某一直线回归方程的判定系数为0.64，则解释变量与被解释变量间的线性相关系数为（） [单选题] *A.0.4B.0.8(正确答案)C.0.32D.0.6417.判定系数R2的取值范围是（） [单选题] *A.R2≥1B.R2≤-1C.0≤R2≤1(正确答案)D.－1≤R2≤118.相关系数r的取值范围是（） [单选题] *A.r≥1B.r≤-1C.0≤r≤1D.－1≤r≤1(正确答案)19一元线性回归模型Image经典假设不包括（） [单选题] *A.Image～N(0，1)(正确答案)B.Image(常数)C.ImageD.Image20.用一组有30个观测值的样本估计模型Image，在0.05的显著性水平下对Image的显著性作t检验，则Image显著地不等于零的条件是其统计量t大于（） [单选题] *A.t0.05(30)B.t0.025(30)C.t0.05(29)D.t0.025(28)(正确答案)21.以带“^”表示估计值，u表示随机误差项，e表示残差，如果y与x为线性相关关系，则下列哪些是正确的（） [单选题] *A.ImageB.ImageC.Image(正确答案)D.Image22.假设线性回归模型满足全部基本假设，则其参数估计量具备的条件不包括（）[单选题] *A.可靠性(正确答案)B.有效性C.无偏性D.线性23.下列方法中哪一个是回归分析中估计回归参数的方法主要有（） [单选题] *A.相关系数法B.方差分析法C.最小二乘估计法(正确答案)D.因子分析法24.用一组有20个观测值的样本估计模型Image，在0.05的显著性水平下对Image的显著性作t检验，则Image显著地不等于零的条件是其统计量t大于（） [单选题] *A.t0.025(18)(正确答案)B.t0.05(19)C.t0.05(19)D.t0.025(20)25.在总体回归直线Image中，Image表示（） [单选题] *A.当X增加一个单位时，Y增加Image个单位B.当Y增加一个单位时，X增加Image个单位C.当X增加一个单位时，Y平均增加Image个单位(正确答案)D.当Y增加一个单位时，X平均增加Image个单位26.用OLS估计经典线性模型Image，则样本回归直线通过点（） [单选题] *A.ImageB.ImageC.ImageD.Image(正确答案)27.二元线性回归模型中,普通最小二乘法估计参数的准则是使（） [单选题] *A.ImageB.Image(正确答案)C.ImageD.Image28.用一组有30 个观测值的样本估计模型后，在0.05的显著性水平下对的显著性作t检验，则显著地不等于零的条件是其统计量大于等于（） [单选题] *A.(27)(正确答案)B.(28)C.(1，28)D.(30)29.参双对数模型中，参数的含义是（） [单选题] *A.X的绝对量发生一定变动时，引起因变量Y的相对变化率B.Y关于X的边际变化C.X的相对变化，引起Y的期望值绝对量变化D.Y关于X的弹性(正确答案)30.当变量之间的相关系数大于多少时，我们认为变量之间存在严重多重共线性（） [单选题] *A.0.5B.0.6C.0.7D.0.8(正确答案)31.方差膨胀因子大于多少时，认为变量间存在严重多重共线性（） [单选题] *A.9B.10(正确答案)C.11D.1232.在二元线性回归模型中，表示（） [单选题] *A.当X1不变时，X2每变动一个单位Y的平均变动B.当X2不变时，X1每变动一个单位Y的平均变动(正确答案)C.当X1和X2都保持不变时，Y的平均变动D.当X1和X2都变动一个单位时，Y的平均变动33.模型中引入实际上与解释变量有关的变量，会导致参数的OLS估计量方差（）[单选题] *A.不变B.增大(正确答案)C.减小D.有偏34.存在严重的多重共线性时，参数估计量的值（） [单选题] *A.变大B.变小C.无穷大D.无法估计(正确答案)35.在线性回归模型中，若解释变量和的观测值成比例，即有，其中k为非零常数，则表明模型中存在（） [单选题] *A.方差非齐性B.多重共线性(正确答案)C.序列相关D.设定误差36.当模型中的解释变量存在完全多重共线性时，参数估计量的方差为（） [单选题] *A.0B.1C.最小D.∞(正确答案)37.在由n=30的一组样本估计的包含3个解释变量的线性回归模型中，计算得可决系数为0.8500，则调整后的可决系数为（） [单选题] *A.0.8327(正确答案)B.0.8603C.0.8655D.0.868938.在二元线性回归模型中，表示（） [单选题] *A.当X1不变时，X2每变动一个单位Y的平均变动B.当X2不变时，X1每变动一个单位Y的平均变动(正确答案)C.当X1和X2都保持不变时，Y的平均变动D.当X1和X2都变动一个单位时，Y的平均变动39.在模型的经济意义检验中，不包括检验下面的哪一项（） [单选题] *A.参数估计量的显著性(正确答案)B.参数估计量的大小C.参数估计量的符号D.参数估计量的相互关系40.一元线性回归模型的经典假设不包括（） [单选题] *A.～N(0，1)(正确答案)B.(常数)CD.41.用一组有40个观测值的样本估计模型，在0.05的显著性水平下对的显著性作t 检验，则显著地不等于零的条件是其统计量t大于（） [单选题] *A.t0.025(38)(正确答案)B.t0.05(39)C.t0.05(39)D.t0.025(40)42.判定系数R2=0.8，说明回归直线能解释被解释变量总变差的（） [单选题] *A.89%B.80%(正确答案)C.64%D.20%43.以下关于相关关系显著性检验论述正确的有（） [单选题] *A.构建的检验统计量为Z统计量B.构建的检验统计量为F统计量C.原假设是想推翻的假设，即不相关、相关系数为零(正确答案)D.原假设是想论证的假设，即变量间相关关系显著44.经计算，变量x与y之间相关系数为-0.75，则⾯者之间存在（） [单选题] *A.中度负相关(正确答案)B.⾯度负相关C.高度负线性相关D.低度负相关45.下列方法中哪一个是回归分析中估计回归参数的方法主要有（） [单选题] *A.相关系数法B.方差分析法C.最小二乘估计法(正确答案)D.因子分析法46.下面属于横截面数据的是（） [单选题] *A.1991－2014年各年西安市10个区的地区生产产值B.2014年西安市10个区的地区生产产值(正确答案)C.2014年西安市10个区的地区生产产值的平均数D.2014年西安市10个区的地区生产产值的合计数47.相关系数r的取值范围是（） [单选题] *A.r≥1B.r≤-1C.0≤r≤1D.－1≤r≤1(正确答案)48.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数，从而提高估计精度，即（） [单选题] *A.重视大误差的作用，轻视小误差的作用B.重视小误差和大误差的作用C.重视小误差的作用，轻视大误差的作用(正确答案)D.轻视小误差和大误差的作用49.Y的平均值的区间预测较点预测更为科学。

计量经济学第三章案例分析

习题5.4一、模型设定假定各地区建筑业总产值和建筑业企业利润总额之间满足线性约束，则理论模型设定为表1各地区建筑业总产值（X ）和建筑业企业利润总额(Y)i i i X Y μββ++=21二、参数估计估计结果为=2.368138+0.034980t=(0.261691) (19.94530)=0.932055 F=397.8152iY ˆiX 2R三、检验模型的异方差（一）goldfeld-quandt检验由图得到残差平方和21i=5739.944，残差平方和22i=23084.48 ,根据goldfeld-quandt检验，F统计量为F===4.0217在α=0.05下,式中α分子、分母的自由度均为10，查F分母表得临界值F0.05（10,10）=2.98，因为F=4.0217>F0.05(10,10)=2.98,所以拒绝原假设，表明模型确实存在异方差（二）White检验根据White检验中辅助函数的构造，则辅助函数为经估计出现White 检验结果，见图从图可以看出，n =20.15100,由White 检验知，查分布表，得临界值(2)=5.9915,同时X 和的t 检验也显著。

比较计算的统计量与临界值，因为n =20.15100>(2)=5.9915，所以拒绝原假设，不拒绝备择假设，表明模型存在异方差。

四、异方差性的修正在运用WLS 法估计中，可以分别选中各种权数做比较，从中则较为理想的权数。

经估计检验用权数1/X t 2的效果最好。

下图为估计结果tt t tv x x +∂+∂+∂=22102σ2R 2χ205.0χ2X 2R 205.0χ可以看出，运用加权最小二乘法消除了预防差性后，参数的t 检验均显著，F 检验也显著，即估计结果为t=(8.303693) (6.569011)=0.976392 DW=1.816022 F=43.15191五．结论这说明个地区建筑业总产值每增加1元，平均来说将增加0.018026元建筑业企业利润总额，而不是引子中得出的需要增加0.37627元建筑业企业利润总额。

庞皓计量经济学第三版课后习题及答案顶配

庞皓计量经济学第三版课后习题及答案顶配庞皓计量经济学第三版课后习题及答案顶配 Last revised by LE LE in 2021第⼆章练习题及参考解答表中是1992年亚洲各国⼈均寿命（Y）、按购买⼒平价计算的⼈均GDP（X1）、成⼈识字率（X2）、⼀岁⼉童疫苗接种率（X3）的数据（1）分别分析各国⼈均寿命与⼈均GDP、成⼈识字率、⼀岁⼉童疫苗接种率的数量关系。

（2）对所建⽴的回归模型进⾏检验。

【练习题参考解答】（1）分别设定简单线性回归模型，分析各国⼈均寿命与⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率的数量关系:1)⼈均寿命与⼈均 GDP 关系Y i 1 2 X1i u i估计检验结果:2)⼈均寿命与成⼈识字率关系3)⼈均寿命与⼀岁⼉童疫苗接种率关系（2）对所建⽴的多个回归模型进⾏检验由⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率分别对⼈均寿命回归结果的参数 t 检验值均明确⼤于其临界值,⽽且从对应的P 值看,均⼩于 ,所以⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率分别对⼈均寿命都有显着影响.（3）分析对⽐各个简单线性回归模型⼈均寿命与⼈均 GDP 回归的可决系数为⼈均寿命与成⼈识字率回归的可决系数为⼈均寿命与⼀岁⼉童疫苗接种率的可决系数为相对说来,⼈均寿命由成⼈识字率作出解释的⽐重更⼤⼀些为了研究浙江省财政预算收⼊与全省⽣产总值的关系,由浙江省统计年鉴得到以下数据:的显着性,⽤规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果 2011 年，全省⽣产总值为 32000 亿元，⽐上年增长 %,利⽤计量经济模型对浙江省 2011 年的财政预算收⼊做出点预测和区间预测(3)建⽴浙江省财政预算收⼊对数与全省⽣产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学⽣独⽴完成由12对观测值估计得消费函数为：（1）消费⽀出C的点预测值；（2）在95%的置信概率下消费⽀出C平均值的预测区间。

财务案例分析综合练习题及答案

财务案例分析综合练习题及答案在企业的运营和管理中，财务决策和财务状况的分析至关重要。

以下将通过一些具体的案例来进行财务分析，并给出相应的答案和解析。

案例一：某公司 2021 年的销售额为 500 万元，销售成本为 300 万元，销售及管理费用为 50 万元，利息费用为 10 万元，所得税税率为 25%。

计算该公司 2021 年的净利润。

答案：首先，计算毛利＝销售额销售成本＝ 500 300 ＝ 200 万元。

然后，计算营业利润＝毛利销售及管理费用＝ 200 50 ＝ 150 万元。

接着，计算利润总额＝营业利润利息费用＝ 150 10 ＝ 140 万元。

最后，净利润＝利润总额 ×（1 所得税税率）＝ 140 ×（1 25%）＝ 105万元。

解析：这个案例主要考查了基本的利润计算方法。

净利润是企业最终的盈利成果，通过逐步扣除各项成本和费用，并考虑所得税的影响，得出净利润的数值。

案例二：＿____公司 2020 年初的资产总额为 800 万元，负债总额为 300 万元，所有者权益为 500 万元。

2020 年该公司实现净利润 100 万元，提取盈余公积 10 万元，向股东分配现金股利 30 万元。

计算 2020 年末该公司的资产总额、负债总额和所有者权益。

答案：资产＝负债＋所有者权益。

年初负债总额为 300 万元，所有者权益为 500 万元，资产总额为 800 万元。

2020 年实现净利润 100 万元，所有者权益增加 100 万元。

提取盈余公积 10 万元，所有者权益内部一增一减，总额不变。

向股东分配现金股利 30 万元，所有者权益减少 30 万元。

所以年末所有者权益＝ 500 ＋ 100 30 10 ＝ 560 万元。

由于没有其他影响资产和负债的事项，资产总额＝负债总额＋所有者权益＝ 300 ＋ 560 ＝ 860 万元，负债总额不变仍为 300 万元。

解析：这个案例重点在于理解资产、负债和所有者权益之间的平衡关系，以及净利润对所有者权益的影响，以及利润分配对所有者权益内部结构的调整。

建筑财务利润分析报告(3篇)

第1篇一、前言随着我国经济的快速发展，建筑行业作为国民经济的重要支柱产业，近年来呈现出蓬勃发展的态势。

为了更好地了解建筑企业的经营状况，提高企业的盈利能力，本报告对某建筑企业的财务利润进行了全面分析。

二、企业概况某建筑企业成立于20XX年，主要从事房屋建筑、基础设施建设、装饰装修等业务。

经过多年的发展，企业规模不断扩大，业务范围逐步拓展，已成为我国建筑行业的一颗璀璨明珠。

三、财务数据概述为了便于分析，以下是对某建筑企业近三年的财务数据概述：1. 营业收入：20XX年1.2亿元，20XX年1.5亿元，20XX年1.8亿元。

2. 净利润：20XX年0.2亿元，20XX年0.3亿元，20XX年0.4亿元。

3. 资产总额：20XX年3亿元，20XX年4亿元，20XX年5亿元。

4. 负债总额：20XX年2亿元，20XX年3亿元，20XX年4亿元。

四、财务利润分析1. 营业收入分析从上述数据可以看出，某建筑企业近三年的营业收入呈现出逐年增长的趋势。

这主要得益于我国经济的快速发展以及企业业务的不断拓展。

然而，需要注意的是，虽然营业收入逐年增长，但增速有所放缓。

这可能与企业面临的市场竞争加剧、原材料价格上涨等因素有关。

2. 净利润分析与营业收入相比，某建筑企业的净利润增长速度更快。

这表明企业在提高收入的同时，也注重了成本控制和利润提升。

从数据来看，净利润的增长主要得益于以下两个方面：（1）毛利率提升：通过优化采购渠道、加强内部管理，企业毛利率逐年提高，从而带动了净利润的增长。

（2）费用控制：企业加强费用控制，尤其是管理费用和销售费用，使得费用占收入的比例逐年下降，从而提高了净利润。

3. 资产负债分析从资产负债数据来看，某建筑企业的资产总额和负债总额均呈逐年增长趋势。

这表明企业在扩大业务规模的同时，也在加大投资力度。

然而，需要注意的是，资产负债率逐年上升，企业面临一定的财务风险。

为降低财务风险，企业应加强资产负债管理，优化资本结构。

建筑业企业盈利能力的分析与比较

竞争对手分析法
竞争对手的业务结构分析
了解竞争对手的业务范围、市场份额、客户群体和产品类型等，评估竞争对手在市场中的地位和竞争优势。
竞争对手的战略规划分析
了解竞争对手的战略规划、发展目标和市场定位等，评估竞争对手未来的发展动向和可能对行业产生的影响。
竞争对手的财务状况分析
了解竞争对手的资产规模、负债状况、盈利能力和现金流状况等财务指标，评估竞争对手的实力和经营稳定性。
研究目的
本研究采用文献资料法、案例分析法和数据分析法等多种研究方法，对建筑业企业的盈利能力进行深入分析。
研究方法
CHAPTER
02
建筑业企业盈利能力概述
盈利能力是指企业获取利润的能力。对于建筑业企业而言，盈利能力意味着它们在提供建筑服务或销售建筑材料过程中，能够获得并维持盈利的能力。
建筑业企业的盈利能力通常通过收入、成本、税金等财务数据进行计算和分析。
通过分析建筑业企业的资产负债表，可以了解该企业的资产和负债状况，评估企业的偿债能力和经营稳定性。
利润表分析
利润表反映了建筑业企业的盈利情况，通过对利润表的分析，可以了解企业的盈利能力、成本结构和营业额等信息。
现金流量表分析
现金流量表反映了建筑业企业的现金流入和流出情况，通过对现金流量表的分析，可以了解企业的现金产生能力、资金运用效率和财务风险等。
政策法规
政府对建筑业的政策法规，如产业政策、环保政策、税收政策等，对建筑业企业的盈利能力产生影响。
经济状况
宏观经济状况，如经济增长率、物价水平、就业率等，以及微观经济状况，如行业发展趋势、市场竞争状况等，都对建筑业企业的盈利能力产生影响。
CHAPTER
04
建筑业企业盈利能力的分析方法

庞皓计量经济学(第二版)第五、六章习题参考解答

试解答以下问题：(1)选用适当的变换修正异方差，要求写出变换过程；(2)写出修正异方差后的参数估计量的表达式。

练习题5.1参考解答：（1）因为22()i i f X X =，所以取221i iW X =，用2i W 乘给定模型两端，得 312322221i i iii i i Y X u X X X X βββ=+++ 上述模型的随机误差项的方差为一固定常数，即22221()()i i i iu Var Var u X X σ==（2）根据加权最小二乘法，可得修正异方差后的参数估计式为***12233ˆˆˆY X X βββ=--()()()()()()()***2****22232322322*2*2**2223223ˆii i i i i i i i i i i i i i i i i W y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑()()()()()()()***2****23222222332*2*2**2223223ˆii i i i i i i i i i i i i i i i i W y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑其中22232***23222,,i ii ii iiiiW X W X W Y XXYWWW===∑∑∑∑∑∑******222333i i i i i x X X x X X y Y Y =-=-=-5.2 下表是消费Y 与收入X 的数据，试根据所给数据资料完成以下问题：（1）估计回归模型u X Y ++=21ββ中的未知参数1β和2β，并写出样本回归模型的书写格式；（2）试用Goldfeld-Quandt 法和White 法检验模型的异方差性；（3）选用合适的方法修正异方差。

关于2007年各地区建筑业总产值和建筑企业利润总额的计量分析

Unweighted Statistics
R-squared
0.889534
Mean dependent var
503587.9
Adjusted R-squared
0.885725
S.D. dependent var
560014.2
S.E. of regression
189310.2
Sum squared resid
Dependent Variable: RESID^2
Method: Least Squares
Date: 10/24/12 Time: 15:40
Sample: 1 31
Included observations: 31
Variable
Coefficient
Std. Error
t-Statistic
C
7315.971
42602.33
0.171727
0.8668
X
0.023235
0.007770
2.990359
0.0123
R-squared
0.448407
Mean dependent var
116525.3
Adjusted R-squared
0.398262
S.D. dependent var
101961.9
Durbin-Watson stat
2.139515
Prob(F-statistic)
0.000000
估计结果为 -28992.91+0.032345X（2）
36196.790.001553
t (-0.800980) (20.82325)
0.937312F=433.6076

第五章练习题及参考解答(第四版)

第五章练习题参考解答5.1 设消费函数为i i i i u X X Y +++=33221βββ式中，i Y 为消费支出；i X 2为个人可支配收入；i X 3为个人的流动资产；i u 为随机误差项，并且222)(,0)(i i i X u Var u E σ==（其中2σ为常数）。

试回答以下问题：(1)选用适当的变换修正异方差，要求写出变换过程；(2)写出修正异方差后的参数估计量的表达式。

【练习题5.1参考解答】（1）设f(X 2i )=X 2i 2，则异方差Var (μi )=σ2X 2i 2=σ2f(X 2i )，回归方程两端同时除以√f(X 2i )得：Y f(X 2i )=βf(X 2i )=βX f(X 2i )+βX f(X 2i )μf(X 2i )令Y i ∗=i 2i )X 2i ∗=2i )X 3i ∗=3i2i )υi =i2i )则上式变为：Y i ∗=β2+β1X 2i ∗+β3X 3i ∗+υi因此Var (υi )=σ2X 2i2f(X 2i )=σ2通过变换原模型的异方差得到修正。

（2）令w i =1f(X 2i)则修正后的残差平方和∑w i e i 2=∑w i (Y i −β̂1−β̂2X 2i −β̂3X 3i )2 方程两边求导并令导数为零，可得参数估计量的表达式如下：β̂1=∑w i (Y i −β̂1−β̂2X 2i −β̂3X 3i )∑w iβ̂2=∑w i (Y i −β̂1−β̂3X 3i )X 2i ∑w i X 2i2 β̂3=∑w i (Y i −β̂1−β̂3X 3i )X 3i ∑w i X 3i2 5.2 对于第三章练习题3.3家庭书刊消费与家庭收入及户主受教育年数关系的分析，进一步作以下分析:1）判断模型123i i i i Y X T u βββ=+++是否存在异方差性。

2。

如果模型存在异方差性，应怎样去估计其参数？3）对比分析的结果，你对第三章练习题3.3的结论有什么评价? 【练习题5.2参考解答】（1）作回归 123i i i i Y X T u βββ=+++，:用White 法检验异方差性从上表以看出， nR 2=12.0569，由White 检验知，在α=0.05下，查χ2分布表,得临界值χ0.052(2)=5.9915，同时2X 的t 检验值也显著。

习题5.4 各地区建筑业总产值和建筑业企业利润总额案例分析

习题5.4 各地区建筑业总产值和建筑业企业利润总额案例分析13应用统计班 132097101姬紫朝习题5.4 各地区建筑业总产值和建筑业企业利润总额案例分析一、模型设定：为分析比较各地区建筑业总产值和建筑业企业利润总额的关系，建立各地区建筑业总产值和建筑业企业利润总额的回归模型。

假设各地区建筑业总产值和建筑业企业利润总额之间满足线性约束，则理论模型设定为：Y i =β1+β2Xi+μi式中，Yi 表示建筑业企业利润总额；Xi建筑业总产值。

由《国家统计网站》得到表5.4.1所示的数据。

表5.4.1各地区建筑业总产值（X）和建筑业企业利润总额(Y)二、参数估计：利用EViews软件，生成Y、X的数据，采用OLS方法估计参数，得到回归结果如图5.4.2图5.4.2 回归结果估计结果为Yˆi=2.368138+0.034980X it =(0.261691) (19.94530)R²=0.932055， F=397.8152三、检验模型异方差：由于地区建筑业总产值不同，对建筑业企业利润总额有不同的影响，这种差异使得模型很容易产生异方差，从而影响模型的估计和运用。

为此，需对模型是否存在异方差进行检验。

（一）White检验利用EViews软件进行White检验，构造辅助函数为：σ2t=α0+α1X t+α2X²t+υt检验结果如图5.4.3所示。

图5.4.3 White 检验结果从图5.4.3可以看出，nR ²=19.95415，由White 检验知，在α=0.05下，查χ²分布表，得临界值χ²0.05（2）=5.9915,同时X 和X ²的t 检验值也显著。

比较计算的χ²统计量与临界值，因为nR ²=19.95415>χ²0.05（2）=5.9915,所以拒接原假设，不拒绝备择假设，表明存在异方差。

四、异方差性的修正（一）加权最小二乘法利用EViews 软件进行加权最小二乘法选用权数ω=x1消除模型中的异方差性，得到图4.5.4的加权最小二乘结果。