弯曲内力习题及答案

合集下载

弯曲内力习题与答案

弯曲力1. 长l的梁用绳向上吊起，如图所示。

钢绳绑扎处离梁端部的距离为x。

梁由自重引起的最大弯矩|M|max为最小时的x值为：(A) /2l；(B) /6l；(C…) 1)/2l。

l；(D) 1)/22. 多跨静定梁的两种受载情况如图(a)、(b)所示。

下列结论中哪个是正确的？(A) 两者的剪力图相同，弯矩图也相同；(B) 两者的剪力图相同，弯矩图不同；(C) 两者的剪力图不同，弯矩图相同；(D….) 两者的剪力图不同，弯矩图也不同。

3. 图示(a)、(b)两根梁，它们的(A) 剪力图、弯矩图都相同；(B…) 剪力图相同，弯矩图不同；(C) 剪力图不同，弯矩图相同；(D) 剪力图、弯矩图都不同。

4. 图示梁，当力偶M e的位置改变时，有下列结论：(A) 剪力图、弯矩图都改变；(B…) 剪力图不变，只弯矩图改变；(C) 弯矩图不变，只剪力图改变；(D) 剪力图、弯矩图都不变。

5. 图示梁C截面弯矩M C = ；为使M C =0，则M e= ；为使全梁不出现正弯矩，则M e≥。

6. 图示梁，已知F、l、a。

使梁的最大弯矩为最小时，梁端重量P= 。

7. 图示梁受分布力偶作用，其值沿轴线按线性规律分布，则B端支反力为，弯矩图为次曲线，|M |max 发生在处。

8. 图示梁，m (x )为沿梁长每单位长度上的力偶矩值，m (x )、q (x )、F S (x )和M (x )之间的微分关系为：S d ();d F x x = d ()d M x x = 。

9. 外伸梁受载如图，欲使AB 中点的弯矩等于零时，需在B 端加多大的集中力偶矩（将大小和方向标在图上）。

10. 简支梁受载如图，欲使A 截面弯矩等于零时，则=e21e /M M 。

1-10题答案：1. C 2. D 3. B 4. B 5. 28e2M ql -；42ql ；22ql 6. ⎪⎭⎫⎝⎛-a l a F 24 7. m 0/2；二；l /28. q (x )；F S (x )+ m (x ) 9. 10. 1/211-60题. 作图示梁的剪力图和弯矩图。

02-弯曲内力-习题课

第5章弯曲内力5-1 选择题答： CmaxMS max F 如将图示的力F 平移到梁AD 的C 截面上，则梁上的与。

FCBDAaaaA. 前者不变，后者改变B. 两者都改变C. 前者改变，后者不变D. 两者都不变， 3A F F =23D F F =S max 23F F =max 24233B M M F a Fa ==⋅=max 22233C F M M a Fa==⋅=因为平移后支反力不变，，不变。

，平移后，但平移前5-2 选择题答： D图示平面刚架ABC ，A 端固定，在其平面内施加图示集中力F ，其m-m 截面上的内力分量不为零。

A. B. C. D. M S F NF 、、 M NF、 M S F 、 S F NF、 F CBAmm力F 作用线过m-m 截面形心，弯矩M 为零。

5-3 选择题答： C图示简支梁上作用均布载荷q 和集中力偶M 0，当M 0在梁上任意移动时，梁的。

A. M 、F S 图都变化B. M 、F S 图都不变化C. M 图改变、F S 图不变D. F S 图改变、M 图不变当M 0在梁上任意移动时，支反力不会改变，q 也不变， F S 只与横向外力有关，所以F S 图不变。

M 0位置不同，M 图发生突变的截面改变了。

BqAM 05-4 选择题设梁的剪力图如图所示，则梁的。

答：B33(kN)F S 5ABCA. AB 段有均布载荷，BC 段没有B. BC 段有均布载荷，AB 段没有C. 两段均有均布载荷D. 两段均无均布载荷S F =常数Sd ==0d F q xSd =0d F q x<AB 段，， BC 段为斜直线，5-5 选择题右端固定的悬臂梁长为4 m ，其 M 图如图所示，则在x =2m 处。

答：AA. 既有集中力，又有集中力偶B. 只有集中力C. 既无集中力，也无集中力偶D. 只有集中力偶M (kN·m)332m2m该处M 有突变，说明有集中力偶；两边M 图斜率不同，说明F S 不同，是集中力作用引起的。

弯曲内力例题(0509)

max
和
M max 及其所
P
y
m=Pa
1、列出梁的剪力方程和弯矩方程
AB段:
A
x
x a
B a
C
x
FQ ( x) 0
(0 x a )
M ( x) m Pa (0 x a)
材料力学
弯曲内力/剪力方程和弯矩方程剪力图和弯矩图 BC段: m=Pa P
FQ ( x) P
( a x 2a )
弯矩立柱弯矩图为抛物线，左侧受压，1、2截面的弯矩值为
M1 0,
qa2/2
3
qa/2
4
2M4 0
qa/2
1
FAy
材料力学
M
FAx
1 2 1 2 M 2 qa a qa qa , 2 2 1 2 M 3 qa , M 4 0 2
作弯矩图。
弯曲内力/平面刚架内力图
x 3.1m
1 M E F 3.1 FAy 2.1 q 2.12 2
(-)
材料力学
1.41kN.m (+)
-3kN.m
(-)
-2.2kN.m
1.41kN.m M D左 2.2kN.m
q
P qa q
qa qa
a
FQ
a
a 2qa qa
M
qa 2 qa / 2
材料力学
弯曲内力/剪力和弯矩
M1 2qa
A
2
q
M 2 2qa2
B
C
a a 4a
FAy
FBy
取左段梁为研究对象:
取右段梁为研究对象:
FQc FAy q 2a qa

05第五章材料力学习题解答(弯曲内力)

a
a
(i)
解：(a) (1) 求约束反力
qa
2qa qa
C
A
B
q
a
a
a
a
(j)
MA
A x
2P
C
M0=Pa
B
RA
∑Y = 0 RA − 2P = 0
RA = 2P
∑ M A = 0 M A − 2Pa + M0 = 0
(2) 列剪力方程和弯矩方程
M A = Pa
Q(x)
⎧= ⎨⎩=
RA RA
= −
2P 2P
q
M2
C
a
求内力
P=qa
B
Q2 = P + qa = 2qa
M2
=
−P
×
a
−
qa
×
a 2
+
M
=
−
1 2
qa 2
(b) (1)求约束反力
P=200N
1
23
A
1C
DB
RA 200
23
200 200
RD
∑ MD = 0 RA × 400 − P × 200 = 0
RA = 100N
(2) 截开 1-1 截面，取左段，加内力
=
x 0
∈ (0,a) x ∈(a,
2a]
上海理工大学力学教研室
3
M
(x)
⎧= ⎨⎩ =
RA RA
× ×
x x
+ +
MA MA
= −
2Px − Pa 2P × (x − a)
=
Pa
(3) 画 Q 图和 M 图

第5章-弯曲内力例题详解

剪力弯矩最大值: 剪力弯矩最大值
FS max = qa
M max
4. 讨论
作用处，在 Me 作用处，左右横截面上的剪力相同，上的剪力相同，弯矩值突变
单辉祖,材料力学教程
M 右 − M左 = Me
5
例 5-4 载荷可沿梁移动，求梁的最大剪力与最大弯矩载荷可沿梁移动，解：1. FS 与 M 图：
3. 画剪力与弯矩图剪力图:
FS1 = bF l FS2 = − aF l
弯矩图: 弯矩图
M1 =
bF x1 l
M2 =
aF x2 l Fab = l
最大值: 最大值
FS,max
bF = （b > a 时） l
M max
4. 讨论
作用处, 在 F 作用处左右横截面上的弯矩相,
∑M
A
= 0,
∑F
y
=0
FAx = qa, FCy = FAy = qa/2
2. 建立内力方程 BC 段：
qa FS1 = − , 2
qa M1 = x1 2
AB 段：
FS2 = qx 2 ,
qa q 2 M 2 = a − x2 2 2 qa FN2 = 2
单辉祖,材料力学教程
14
3. 画内力图
FSA+ = − FAy = −2F
单辉祖,材料力学教程
M A+ = M e − FAy ⋅ ∆ = Fl
M D− = F ⋅0=0 =
1
FSD− = F
例题
例 5-2 建立剪力与弯矩方程，画剪力与弯矩图建立剪力与弯矩方程，
FAy = bF l FBy = aF l
解：1. 支反力计算： 2. 建立剪力与弯矩方程

材料力学弯曲变形答案

第一章绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。

( ) 1.2 内力只作用在杆件截面的形心处。

( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。

( ) 1.4 确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。

( ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。

( ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。

( ) 1.7 同一截面上正应力ζ与切应力η必相互垂直。

( ) 1.8 同一截面上各点的正应力ζ必定大小相等，方向相同。

( ) 1.9 同一截面上各点的切应力η必相互平行。

( ) 1.10 应变分为正应变ε和切应变γ。

( ) 1.11 应变为无量纲量。

( ) 1.12 若物体各部分均无变形，则物体内各点的应变均为零。

( ) 1.13 若物体内各点的应变均为零，则物体无位移。

( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。

( )1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。

( )1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。

( )二、填空题1.1 材料力学主要研究受力后发生的，以及由此产生的。

1.2 拉伸或压缩的受力特征是，变形特征是。

1.3 剪切的受力特征是，变形特征是。

1.4 扭转的受力特征是，变形特征是。

B题1.15图题1.16图1.5 弯曲的受力特征是，变形特征是。

1.6 组合受力与变形是指。

1.7 构件的承载能力包括，和三个方面。

1.8 所谓，是指材料或构件抵抗破坏的能力。

所谓，是指构件抵抗变形的能力。

所谓，是指材料或构件保持其原有平衡形式的能力。

1.9 根据固体材料的性能作如下三个基本假设，，。

材料力学课后习题答案5章

(b)
保留有限量，略去一阶和二阶微量后，得
足标 C 系指梁微段右端面的形心，对题图(b)亦同。根据题图 b，由
∑F
略去微量 qdx 后，得
y
=0 ，FS左 + qdx − FS右 = 0
FS右 = FS左
仍据题图 b，由
(c)
∑M
C
=0 ，M 右 − M e − qdx(
dx ) − FS左 dx − M 左 = 0 2
11l 处有 FS2 = 0 ， M 2 有极大值，其值为 24 121 2 M 2 max = M max = ql 1152
(d)解：1．建立剪力、弯矩方程
8
图 5-9d 坐标如图 5-9d(1)所示，由截面法易得剪力、弯矩方程分别为
q( x1 ) ⋅ x1 qx 2 =− 1 2 l ql FS2 = − + qx2 4 qx 3 M1 = − 1 3l q 2 ql l M 2 = x2 − ⋅ ( + x2 ) 2 4 6 FS1 = −
2 q0l q 0 x2 FS = − + 4 l q x3 ql M = 0 x2 − 0 2 4 3l
l (0 ≤ x2 ≤ ) 2 l (0 ≤ x2 ≤ ) 2
(e) (f)
3．画剪力、弯矩图依据式(c)和(e)可绘剪力图，如图 5-9b(2)所示；依据式(d)和(f)可绘弯矩图，如图 5-9b(3) 所示。 (c)解：1．求支反力
=0 ，FS左 + F + qdx − FS右 = 0
保留有限量，略去微量 qdx 后，得
FS右 − FS左 = F
为了更一般地反映 F 作用处剪力的突变情况（把向下的 F 也包括在内），可将上式改写为

测试题-弯曲内力(答案)

班级：学号：姓名：《工程力学》弯曲内力测试题一、判断题（每小题2分，共20分）1、根据剪力图和弯矩图，可以初步判断梁的危险截面位置。

（√）2、梁的内力图通常与横截面面积有关。

（×）3、将梁上的集中力平移，不会改变梁的内力分布。

（×）4、梁端铰支座处无集中力偶作用，该端铰支座处的弯矩必为零。

（√）5、分布载荷q（x）向上为负，向下为正。

（×）6、简支梁的支座上作用集中力偶M，当跨长l改变时，梁内最大剪力发生改变，而最大弯矩不改变。

（√）7、剪力图上斜直线部分一定有分布载荷作用。

（√）8、在集中力作用的截面处，剪力图有突变，弯矩图连续但不光滑。

（√）9、梁在集中力偶作用截面处，弯矩图有突变，剪力图无变化。

（√）10、在梁的某一段上，若无载荷q作用，则该段梁上的剪力为常数。

（√）二、单项选择题（每小题2分，共20分）1、如图所示，火车轮轴产生的是（D ）。

A．拉伸或压缩变形B．剪切变形C．扭转变形D．弯曲变形2、梁在集中力偶作用的截面处，它的内力图为（C ）。

A. 剪力图有突变，弯矩图无变化B. 剪力图有突变，弯矩图有转折C. 弯矩图有突变，剪力图无变化D. 弯矩图有突变，剪力图有转折3、在下图四种情况中，截面上弯矩为正，剪力为负的是（B ）。

4、梁在某一段内作用有向下的分布力时，则在该段内，弯矩图是一条（A ）。

A. 上凸曲线B. 下凸曲线C. 带有拐点的曲线；D. 斜直线5、梁受力如图，在B截面处（D ）A. 剪力图有突变，弯矩图连续光滑B. 剪力图有尖角，弯矩图连续光滑C. 剪力图、弯矩图都有尖角D. 剪力图有突变，弯矩图有尖角6、图示梁，当力偶M e的位置改变时，有（B ）A. 剪力图、弯矩图都改变B. 剪力图不变，只弯矩图改变C. 弯矩图不变，只剪力图改变D. 剪力图、弯矩图都不变F qCBAFM eaqa a7、若梁的受力情况对于梁的中央截面为反对称（如图），则下列结论中正确的是（D ）A. 剪力图和弯矩图均为反对称，中央截面上剪力为零B. 剪力图和弯矩图均为对称，中央截面上弯矩为零C. 剪力图反对称，弯矩图对称，中央截面上剪力为零D. 剪力图对称，弯矩图反对称，中央截面上弯矩为零8、多跨静定梁的两种受载情况分别如图所示，力F靠近铰链，以下结论正确的是（C ）A. 两者的剪力图和弯矩图完全相同B. 两者的剪力图相同，弯矩图不同C. 两者的剪力图不同，弯矩图相同D. 两者的剪力图和弯矩图均不相同9、多跨静定梁的两种受载情况如图所示，下列结论中正确的是（D ）A. 两者的剪力图和弯矩图完全相同B. 两者的剪力图相同，弯矩图不同C. 两者的剪力图不同，弯矩图相同D. 两者的剪力图和弯矩图均不相同10、若梁的剪力图和弯矩图分别如图所示，则该图表明（C ）A. AB段有均布载荷，BC段无载荷；B. AB 段无载荷，B截面处有向上的集中力，BC段有向下的均布载荷；C. AB 段无载荷，B截面处有向下的集中力，BC段有向下的均布载荷；D. AB 段无载荷，B截面处有顺时针的集中力偶，BC段有向下的均布载荷。

材料力学答案4弯曲内力

A
C
B 出剪力图和弯矩图。
x1
x2
解：1．确定约束力
FAy
l
FBy
M /l
M A＝0， MB＝0
Fs:

Ma / l
M:

FAy＝M / l FBy＝ -M / l
2．写出剪力和弯矩方程
AC FS x1＝M / l 0 x1 a
M x1＝Mx1 / l 0 x1 a
剪力图和弯矩图
例1
1kN.m
A
C D B 解法2：1．确定约束力
FAY
Fs（ kN） 0.89
1.5m
1.5m
2kN
1.5m
FBY
1.11
（+）
FAy＝0.89 kN FFy＝1.11 kN
（-）
2．确定控制面为A、C 、D、B两侧截面。
3．从A截面左侧开始画
剪力图。
19
剪力图和弯矩图
例1
x 5．确定控制面上的弯矩值，并将其标在
M－x中。
22
剪力图和弯矩图
例2
q
D 解法2：1．确定约束力
A
B
FAy
9qa/4
4a
a qa FBy
FAy＝
9 4
qa
,
FBy＝
3 4
qa
Fs （+）
（-） qa
7qa/4
2．确定控制面，即A 、B、D两侧截面。
3．从A截面左测开始画
剪力图。
23
剪力图和弯矩图

Mb / l
CB FS x2 ＝M / l 0 x2 b
M x2 ＝ Mx2 / l 0 x2 b

弯曲内力习题课

x MA
FAy
F’Dy
q
x
FDy
FBy
FDy qa / 2 FBy 3qa / 2
FAy qa / 2 M A qa2 / 2
Fs
15KN
O
（-）
1.5m 20KN
M
+
2.5m
（-）
x
25KN
O
（-）
8.75KN•m 20KN•m
x
40KN•m
Fs
qa 3qa 4 3qa 4
O
(+)
(+)
M B＝0， M A＝0
∴ FAy＝8/9 kN , FBy＝10/9 kN
2．确定控制面在集中力、集中力偶以及支座的两侧截面均为控制
面。即A、C、D、E、F、B截面。
1KN.m
A
CD E F B
3．建立坐标系
8/9 kN=FAY
FS (KN)
O
1.5m
2kN
1.5m
1.5m
10/9
(+)
(-)
8/9
FBY 建立FS－x和M－x坐标系
＝10/9 kN
4．应用截面法确定控制 x 面上的剪力和弯矩值，并
将其标在 FS － x 和 M － x
坐标系中。再根据微分关
M (KN.m)
系连图线。
O (-)
(-)
x
1/3
4/3
5/3
试画出图示外伸梁的剪力图和弯矩图。
P1 =2kN q =1kN/m
一梁段上载荷图、剪力图、弯矩图三图的形状关系
q图
FS图
水平直线
斜直线
M图斜直线

材料力学精选试题及答案-弯曲变形、内力和应力

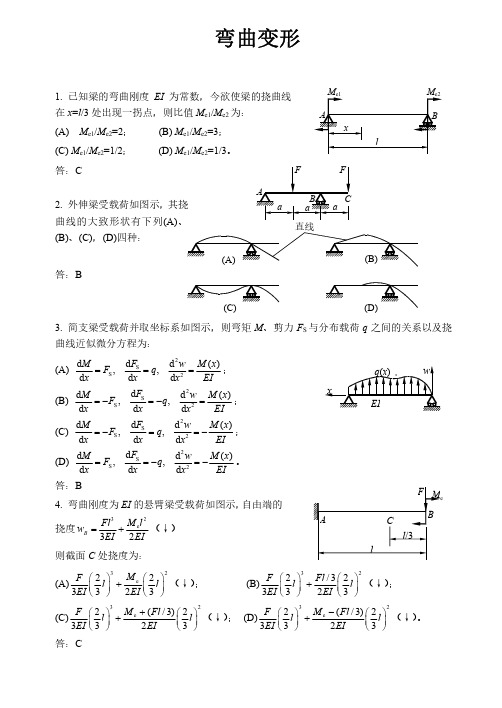
9. 试画出图示静定组合梁在集中力 F 作用下挠曲线的大致形状。答：
F
直线 F
2a
aaa
10. 画出图示各梁的挠曲线大致形状。
F
Me=Fl
A
B
l
l
C
D
l
(a)
答： M x
Me=Fl
A
B
l
l
(b)
M
F
C
D
l
x
Me 直线
Me 直线
(a)
(b)
11. 作图示外伸梁的弯矩图及其挠曲线的大致形状。 M
Fl/4
A a
B
C
aa
直线
答：B
(A)
(B)
(C)
(D)
3. 简支梁受载荷并取坐标系如图示，则弯矩 M、剪力 FS 与分布载荷 q 之间的关系以及挠曲线近似微分方程为：
(A)
dM dx
FS ,
dFS q, dx
d2w M (x) ； dx2 EI
(B)
dM dx
FS,
dFS q, dx
d2w M (x) ； dx2 EI
Δl
l
dx
w
0
EI
l
M (x) dx
w
0
EI
a 0
q 2
x2
dx
b 0
qa2 2
dx
w EI
b 0
qbx
q 2
x2
dx
0
得 a3 + 3a2b -2b3 = 0
a3 + a2b + 2a2b -2b3 = 0 a2 + 2ba -2b2 = 0

工程力学弯曲内力课后答案

工程力学弯曲内力课后答案【篇一：工程力学的习题详细解答第08(1)章】ass=txt>1-1、2-2截面无限接近于载荷作用解：(a) 以整个梁为研究对象，求得支反力： ra?rb?p2由截面法，分别以1-1截面左半部分、2-2截面右半部分为研究对象，求得：qppl1?2， m1?4q??ppl22， m2?4可见，集中力作用处，剪力有突变，突变值为p，弯矩不变。

(b) 以整个梁为研究对象，求得支反力： rmma??l，rb?l由截面法，分别以1-1截面左半部分、2-2截面右半部分为研究对象，求得： qmm1??l，m1??2qmm2??l，m2?2可见，集中力偶作用处，弯矩有突变，突变值为m，剪力不变。

6-1(a)(a1)(a2)(a3)解：1．求支反力，图(a)，?mc?0： ra?6?12?10?3?0，ra?7kn?y?0： ra?rb?10?0，rb?3kn2．列内力方程，图(a)和(a1)，q(x)???7kn 0?x?3??3kn 3?x?6m(x)???7x?12 kn?m0? x ?3?3(6?x) kn?m3? x ?63．作内力图，图(a2)，(a)。

(b)(b1)(b2)q(b3)m解：1．求支反力，图(b)，?m0： r1lb?a?l?2ql2?ql?2?0，ra?0?y?0： ra?rb?q?l?ql?0， rb?2ql 2．列内力方程，图(b)和(b1)， q(x)????qx 0?x?l?ql l?x?3l2m(x)????qx20?x?l??ql(3l2?x) l ?x?3l23．作内力图，图(b2)，(b3)。

6-2qm(b)6-3q (kn/m)为的等截面钢筋混矩的绝对值相等，应将起吊点a、b放在何处（即a??）？解：作梁的计算简图及其m图。

由m?max?m?max，即ql?l?q?l2qa22??2?a???2???2???2即a2?la?l24?0求得 a?2?12l?0.20l7。

2016工程力学（高教第3版）习题解答：第8章弯曲内力

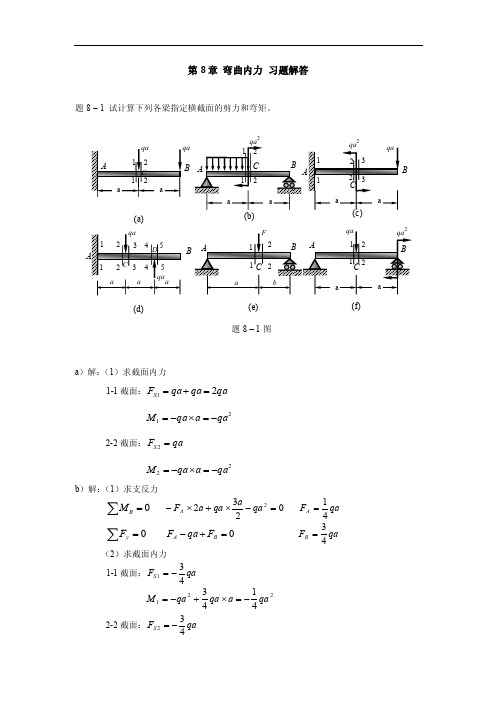
第8章弯曲内力习题解答题8 – 1 试计算下列各梁指定横截面的剪力和弯矩。

a ）解：（1）求截面内力1-1截面：qa qa qa F S 21=+= 21qa a qa M -=⨯-=2-2截面：qa F S =222qa a qa M -=⨯-= b ）解：（1）求支反力∑=0B M 02322=-⨯+⨯-qa a qa a F A qa F A 41= ∑=0y F 0=+-BA F qa F qa FB 43= （2）求截面内力1-1截面：qa F S 431-= 2214143qa a qa qa M -=⨯+-= 2-2截面：qa F S 432-=B B2(a)(d)(e) (f)题8 – 1图224343qa a qa M =⨯= c ）解：（1）求截面内力1-1截面：qa F S =12212qa a qa qa M -=⨯--=2-2截面：qa F S =2022=⨯-=a qa qa M3-3截面：qa F S =323qa a qa M -=⨯-= d ）解：（1）求截面内力1-1截面：01=-=qa qa F S212qa a qa a qa M -=⨯-⨯-=2-2截面：02=-=qa qa F S22qa a qa M =⨯=3-3截面：qa F S =323qa a qa M -=⨯-=4-4截面：qa F S -=404=M5-5截面：05=S F05=M e ）解：（1）求支反力∑=0B M ()0=-+⨯Fb b a F A b a FbF A +=∑=0y F 0=+-BA F F F ba Fa F B += （2）求截面内力1-1截面：ba Fbb a Fa F F S +=+-=1b a F a bb b a Fa b F M B +=⨯+=⨯=1 2-2截面：b a FaF F B S +-=-=2ba F a bb b a Fa b F M B +=⨯+=⨯=2 f ）（1）求支反力∑=0BM 022=-⨯+⨯-qa a qa a F A 0=A F∑=0yF0=+-B A F qa F qa F B =（2）求截面内力 1-1截面：01=S F01=M （取AC 段为研究对象）2-2截面：qa F S -=20222=⨯+-=⨯+-=a qa qa a F qa M B3-3截面：qa F S -=323qa M -=题8 – 2 试列出下列各梁的剪力及弯矩方程，作剪力图及弯矩图并求出maxSF 及maxM。

材料力学中国建筑工业出版社第四章弯曲内力答案

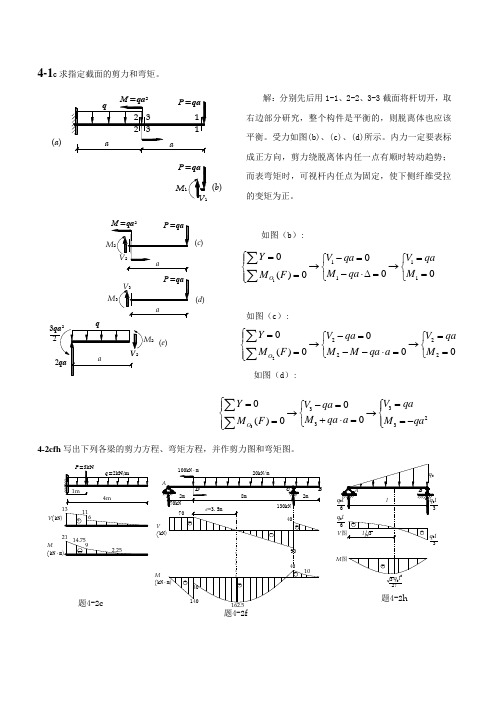
解：分别先后用1-1、2-2、3-3截面将杆切开，取右边部分研究，整个构件是平衡的，则脱离体也应该平衡。

受力如图(b)、(c)、(d)所示。

内力一定要表标成正方向，剪力绕脱离体内任一点有顺时转动趋势；而表弯矩时，可视杆内任点为固定，使下侧纤维受拉的变矩为正。

如图（b ）:如图（c ）:如图（d ）:4-1c 求指定截面的剪力和弯矩。

4-2cfh 写出下列各梁的剪力方程、弯矩方程，并作剪力图和弯矩图。

题4-2cV MkN ·题4-2f·题4-2h230q l 27(a )(b )M P 111110000()0O Y V qa V qa M qa M M F ⎧=-==⎧⎧⎪→→⎨⎨⎨-⋅∆===⎩⎩⎪⎩∑∑2(e )M (d )a(c )a333233000()0O Y V qa V qa M qa a M qa M F ⎧==-=⎧⎧⎪⎪→→⎨⎨⎨+⋅==-=⎪⎩⎩⎪⎩∑∑222220000()0O Y V qa V qa M M qa a M M F ⎧=-==⎧⎧⎪→→⎨⎨⎨--⋅===⎩⎩⎪⎩∑∑4-3dfgh 用微分关系作下列各梁的剪力图和弯矩图4kN ·m+题4-3d10.25MkN ·m)VkN)--1243.5-10.25-+322+-题4-3fM 图85Pl 83Pl 16Pl P/4-43.5--12MkN ·m)V kN)24++-26.257.57.5题4-3g5P/4+P=15kN+-24313.875313.875qaM 图V 图2qa +-2+-2+-qa2qa题4-3hMkN ·V kN)3.1254-6 起吊一根自重为q （N/m ）的等截面钢筋混凝土梁，问起吊点的合理位置x 应为多少（令梁在吊点处和中点处的最大正负弯矩的绝对值相等）MkN ·m)V kN)题4-6+2ql(l-2x)/4-q l /8qx/22qx/2qx ql/2-qx ql/2-qxqx--+--+q22qx/8qx/82题4-74-7天车梁上小车轮距为c ，起重量为P ，问小车走到什么位置时，梁弯矩最大？并求出最大弯矩。

弯曲时的内力和应力

第七章弯曲时的内力和应力※ 说明：本文档仅限练习。

与考试无任何联系。

如答案有误请自行修改。

如仍有疑问咨询相关教师。

Q群125207914一、填空题：1、梁产生弯曲变形时的受力特点，是梁在过轴线的平面内受到外力偶的作用或者受到和梁轴线相___________的外力的作用。

3、矩形截面梁弯曲时，其横截面上的剪力作用线必然________于外力并通过截面________。

5、梁弯曲时，任一横截面上的弯矩可通过该截面一侧（左侧或右侧）的外力确定，它等于该一侧所有外力对________力矩的代数和。

7、用截面法确定梁横截面上的剪力时，若截面右侧的外力合力向上，则剪力为______。

9、将一悬臂梁的自重简化为均布载荷，设其载荷集度为q，梁长为L，由此可知在距固定端L/2处的横截面上的剪力为_________，固定端处横截面上的弯矩为__________。

10、在梁的集中力偶左、右两侧无限接近的横截面上，剪力相等，而弯矩则发生_______，_________值等于梁上集中力偶的力偶矩。

11、剪力图和弯矩图是通过________和___________的函数图象表示的。

18、在梁的某一段内，若无分布载荷q（X）的作用，则剪力图是__________于X轴的直线。

19、在梁的弯矩图上，某一横截面上的弯矩有极值（极大值或极小值），该极值必发生在对应于剪力___________的横截面上。

21、梁在发生弯曲变形的同时伴有剪切变形,这种平面弯曲称为__________弯曲。

24、梁在弯曲时的中性轴，就是梁的___________与横截面的交线。

28、梁弯曲时,横截面中性轴上各点的正应力等于零,而距中性轴________处的各正应力为最大。

29、梁弯曲变形后，以中性层为界，靠__________边的一侧纵向纤维受压力作用,而靠__________边的一侧纵向纤维受拉应力作用。

31、等截面梁内的最大正应力总是出现在最大___________所在的横截面上。

弯曲的内力与强度计算习题

弯曲的内力与强度计算一、判断题1.如图1示截面上，弯矩M和剪力Q的符号是：M为正，Q为负。

（）图12.取不同的坐标系时，弯曲内力的符号情况是M不同，Q相同。

（）3、在集中力作用的截面处，Q图有突变，M连续但不光滑。

（）4、梁在集中力偶作用截面处，M图有突变，Q图无变化。

（）5.梁在某截面处，若剪力Q=0，则该截面的M值一定为零值。

（）6.在梁的某一段上，若无荷载作用，则该梁段上的剪力为常数。

（）7.梁的内力图通常与横截面面积有关。

（）8.应用理论力学中的外力定理，将梁的横向集中力左右平移时，梁的Q图，M图都不变。

（）9.将梁上集中力偶左右平移时，梁的Q图不变，M图变化。

（）10.图2所示简支梁跨中截面上的内力为M≠0，Q=0。

（）图 2 图 311.梁的剪力图如图3所示，则梁的BC段有均布荷载，AB段没有。

（）12.上题中，作用于B处的集中力大小为6KN，方向向上。

（）13.右端固定的悬臂梁，长为4m，M图如图示，则在x=2m处，既有集中力又有集中力偶。

（）图 4 图 514.上题中，作用在x=2m处的集中力偶大小为6KN·m，转向为顺时针。

（）15.图5所示梁中，AB跨间剪力为零。

（）16.中性轴是中性层与横截面的交线。

（）17.梁任意截面上的剪力，在数值上等于截面一侧所有外力的代数和。

（）18.弯矩图表示梁的各横截面上弯矩沿轴线变化的情况，是分析梁的危险截面的依据之一。

（）19.梁上某段无荷载作用，即q=0，此段剪力图为平行x的直线；弯矩图也为平行x轴的直线。

（）20.梁上某段有均布荷载作用，即q=常数，故剪力图为斜直线；弯矩图为二次抛物线。

（）21.极值弯矩一定是梁上最大的弯矩。

（）22.最大弯矩Mmax只可能发生在集中力F作用处，因此只需校核此截面强度是否满足梁的强度条件。

（）23.截面积相等，抗弯截面模量必相等，截面积不等，抗弯截面模量必不相等。

（）24.大多数梁都只进行弯曲正应力强度核算，而不作弯曲剪应力核算，这是因为它们横截面上只有正应力存在。

第四章弯曲内力习题及答案

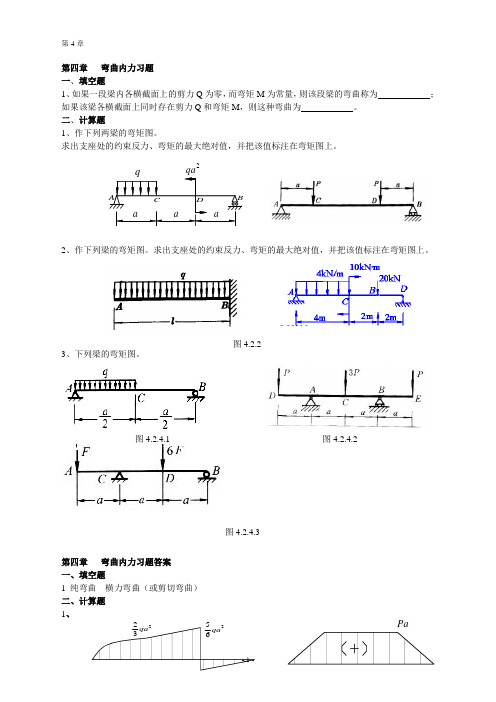
q 2qa a a a
A C
D
B
第四章弯曲内力习题
一、填空题
1、如果一段梁内各横截面上的剪力Q 为零，而弯矩M 为常量，则该段梁的弯曲称为；如果该梁各横截面上同时存在剪力Q 和弯矩M ，则这种弯曲为。

二、计算题
1、作下列两梁的弯矩图。

求出支座处的约束反力、弯矩的最大绝对值，并把该值标注在弯矩图上。

2、作下列梁的弯矩图。