树形结构数据表的设计
表结构模型

表结构模型表结构模型是关系型数据库中最基本的概念之一。
它描述了表的结构,并定义了表中各个字段的属性、类型、大小等信息。
表结构模型是关系型数据库管理系统的核心,它提供了强大的数据管理和查询功能,可以实现数据的高效存储和检索。
本文将介绍表结构模型的基本概念和常见的表结构类型。
一、表结构模型的基本概念表结构模型是关系型数据库中最基本的概念之一,它由表名、字段名、字段类型、大小、约束等多个元素构成。
其中,表名和字段名是唯一标识表结构模型的关键信息,它们的取名应该具有唯一性和描述性。
字段类型和大小用于限制数据的类型和长度,以保证数据的一致性。
约束是对表中数据的限制条件,包括主键、外键、唯一性约束等,它们用于保证数据的完整性和正确性。
二、表结构类型的分类根据表结构的不同特点和应用需求,表结构可以分为以下几种类型:1.扁平型结构扁平型结构是一种最简单的表结构,它由多个属性组成,没有分隔符分开属性,一个记录占用一行,每列都有唯一的列名和数据类型,不能存在重复的行和列。
扁平型结构通常用于存储简单的数据、公共信息和配置文件等。
2.关系型结构关系型结构是一种比较常见的表结构,它由多个属性组成,每个属性是唯一的,数据之间通过行和列的相对位置建立关系。
在关系型结构中,每个表都对应一个唯一的主键,用于唯一标识表中的每一行记录。
关系型结构通常用于存储结构化的数据,例如会员信息表、订单信息表、商品信息表等。
3.层次型结构层次型结构是一种具有树形结构的表结构,它由多个属性组成,每个属性都可以有多个子属性,形成一个父子关系。
在层次型结构中,根节点没有父节点,叶子节点没有子节点。
层次型结构通常用于存储具有明显层次关系的数据,例如组织架构表、目录结构表等。
4.网状型结构网状型结构是一种比较复杂的表结构,它由多个实体组成,每个实体都可以有多个父实体和子实体,形成一个网状结构。
在网状型结构中,一个实体可以对应多个父实体,一个实体也可以对应多个子实体。
文件目录结构的树形显示(数据结构课程设计,树、队列,C语言描述)

⽂件⽬录结构的树形显⽰(数据结构课程设计,树、队列,C语⾔描述)⼀、要解决的问题给出某⼀个操作系统下⽬录和⽂件信息,输⼊的数据第⼀⾏为根⽬录节点。
若是⽬录节点,那么它的孩⼦节点将在第⼆⾏中被列出,同时⽤⼀对圆括号“()”界定。
同样,如果这些孩⼦节点中某⼀个也是⽬录的话,那么这个⽬录所包含的内容将在随后的⼀⾏中列出,由⼀对圆括号“()”界定。
⽬录的输⼊输⼊格式为:*name size,⽂件的输⼊输⼊格式为:name size。
Name为⼀串不超过10个字符组成,并且字符串中不能有‘(’,‘)’,‘[‘,’]’和’*’。
Size是该⽂件/⽬录的⼤⼩,⽂件的size输⼊值为该⽂件的⼤⼩,⽬录的size输⼊值都为1。
树结构最多10层,每⼀层最多2个⽂件/⽬录。
要求编程实现将其排列成⼀棵有⼀定缩进的树,输出要求:第d层的⽂件/⽬录名前⾯需要缩进8*d个空格,兄弟节点要在同⼀列上。
并计算每⼀个⽬录⼤⼩,⽬录⼤⼩为所包含的所有⼦⽬录和⽂件⼤⼩以及⾃⾝⼤⼩的总和。
例如输⼊:*/usr 1(*mark 1 *alex 1)(hw.c 3 *course 1) (hw.c 5)(aa.txt 12)输出|_*/usr[24]|_*mark[17]| |_hw.c[3]| |_*course[13]| |_aa.txt[12]|_*alex[6]|_hw.c[3]⼆、算法基本思想描述:采⽤孩⼦兄弟双亲链表的数据存储结构建⽴⼆叉树,再先序遍历该⼆叉树输出所有节点。
输出时,通过parent节点的第⼀个孩⼦是否有兄弟节点控制缩进输出” | ”或” ”;⽬录的⼤⼩为该⽬录左⼦树(以其第⼀个孩⼦为根的树)所有节点的size和加上它本⾝⼤⼩。
三、设计1. 数据结构的设计和说明在⼀开始设计要采⽤的数据结构时,虽然课题只要求“树结构最多10层(树的深度),每⼀层最多2个⽂件/⽬录”,考虑到问题的实际意义,我决定把它优化消除这⼀限制,于是采⽤孩⼦兄弟的数据结构,后来由于缩进输出的需要⼜增加了parent域。
03、1数据结构第一部分--线性表-树与二叉树

数据结构(一)目录第1章序论 (1)1.1 什么是数据? (1)1.2 什么是数据元素? (1)1.3 什么是数据结构及种类? (1)1.4 数据的逻辑结构 (1)1.5 数据的物理结构 (1)1.6 算法和算法分析 (1)1.7 算法的五个特性 (1)1.8 算法设计的要求 (2)1.9 算法效率的度量 (2)第2章线性表 (3)2.1 线性表举例 (3)2.2 线性表的存储 (4)2.3 线性表-栈 (4)2.4 队列 (4)2.5 双端队列 (6)第3章树和二叉树 (6)3.1 树 (6)3.1.1 树的基本概念 (6)3.1.2 树的常用存储结构 (6)3.1.3 树的遍历 (7)3.2 二叉树 (7)3.2.1 二叉树的基本概念 (7)3.2.2 二叉树与树的区别 (7)3.2.3 树及森林转到二叉树 (7)3.2.4 二叉树的性质 (8)3.2.5 满二叉树 (8)3.2.6 完全二叉树 (8)3.2.7 完全二叉树的性质 (9)3.2.8 二叉树的四种遍历 (9)3.2.9 二叉排序树 (10)3.2.10 平衡二叉树 (11)3.2.11 m阶B-树 (11)3.2.12 最优二叉树 (11)3.2.13 二叉树的存储结构 (12)3.3 广义表 (13)3.4 矩阵的压缩存储 (14)3.4.1 特殊矩阵 (14)3.4.2 压缩存储 (14)第4章历年真题讲解 (15)4.1 2009年上半年 (15)4.2 2009年下半年 (15)4.3 2010年上半年 (15)4.4 2011年上半年 (16)4.5 2011年下半年 (16)4.6 2012年上半年 (17)4.7 2012年下半年 (17)4.8 2013年上半年 (18)4.9 2013年下半年 (18)4.10 2014年上半年 (18)4.11 2014年下半年 (19)4.12 2015年上半年 (19)4.13 2015年下半年 (19)4.14 2016年上半年 (20)第1章序论什么是数据?所有能输入到计算机中并能够被计算机程序处理的符号的总称,它是计算机程序加工的原料。
[TREE]采用左右值编码来存储无限分级树形结构的数据库表设计
![[TREE]采用左右值编码来存储无限分级树形结构的数据库表设计](https://img.taocdn.com/s3/m/2ad4bd136edb6f1aff001fe2.png)
采用左右值编码来存储无限分级树形结构的数据库表设计之前我介绍过一种按位数编码保存树形结构数据的表设计方法,详情见:浅谈数据库设计技巧(上)该设计方案的优点是:只用一条查询语句即可得到某个根节点及其所有子孙节点的先序遍历。
由于消除了递归,在数据记录量较大时,可以大大提高列表效率。
但是,这种编码方案由于层信息位数的限制,限制了每层能所允许的最大子节点数量及最大层数。
同时,在添加新节点的时候必须先计算新节点的位置是否超过最大限制。
上面的设计方案必须预先设定类别树的最大层数以及最大子节点数,不是无限分级,在某些场合并不能采用,那么还有更完美的解决方案吗?通过google的搜索,我又探索到一种全新的无递归查询,无限分级的编码方案——左右值。
原文的程序代码是用php写的,但是通过仔细阅读其数据库表设计说明及相关的sql语句,我彻底弄懂了这种巧妙的设计思路,并在这种设计中新增了删除节点,同层平移的需求(原文只提供了列表及插入子节点的sql语句)。
下面我力图用比较简短的文字,少量图表,及相关核心sql语句来描述这种设计方案:首先,我们弄一棵树作为例子:商品|---食品| |---肉类| | |--猪肉| |---蔬菜类| |--白菜|---电器|--电视机|--电冰箱select count(*) from tree where lft <= 2 and rgt >= 11为了方便列表,我们可以为tree表建立一个视图,添加一个层数列,该类别的层数可以写一个自定义函数来计算。
该函数如下:CREATE FUNCTION dbo.CountLayer(@type_id int)RETURNS intASbegindeclare@result intset@result=0declare@lft intdeclare@rgt intif exists (select1from tree where type_id=@type_id)beginselect@lft=lft,@rgt=rgt from tree where type_id=@type_idselect@result=count(*) from tree where lft <=@lft and rgt >=@rgtendreturn@resultendGO然后,我们建立如下视图:CREATE VIEW dbo.TreeViewASSELECT type_id, name, lft, rgt, dbo.CountLayer(type_id) AS layer FROM dbo.tree ORDE R BY lftGO()AS declare declare ifgo假定我们要在节点“肉类”下添加一个子节点“牛肉”,该树将变成:1商品18+2+--------------------------------------------+2食品11+2 12+2电器17+2+-----------------+ +-------------------------+3肉类6+2 7+2蔬菜类10+2 13+2电视机14+2 15+2电冰箱16+2 +-------------+4猪肉5 6牛肉78+2白菜9+2看完上图相应节点左右值的变化后,相信大家都知道该如何写相应的sql脚本吧?下面我给出相对完整的插入子节点的存储过程:CREATE PROCEDURE[dbo].[AddSubNodeByNode](@type_id int,@name varchar(50))ASdeclare@rgt intif exists (select1from tree where type_id=@type_id)beginSET XACT_ABORT ONBEGIN TRANSACTIONselect@rgt=rgt from tree where type_id=@type_idupdate tree set rgt=rgt+2where rgt>=@rgtupdate tree set lft=lft+2where lft>=@rgtinsert into tree (name,lft,rgt) values (@name,@rgt,@rgt+1)COMMIT TRANSACTIONSET XACT_ABORT OFFend然后,我们删除节点“电视机”,再来看看该树会变成什么情况:1商品20-2+-----------------------------------+2食品13 14电器19-2+-----------------+3肉类8 9蔬菜类12 17-2电冰箱18-2+----------+4猪肉5 6牛肉7 10白菜11相应的存储过程如下:CREATE PROCEDURE[dbo].[DelNode]@type_id intASdeclare@lft intdeclare@rgt intif exists (select1from tree where type_id=@type_id)beginSET XACT_ABORT ONBEGIN TRANSACTIONselect@lft=lft,@rgt=rgt from tree where type_id=@type_iddelete from tree where lft>=@lft and rgt<=@rgtupdate tree set lft=lft-(@rgt-@lft+1) where lft>@lftupdate tree set rgt=rgt-(@rgt-@lft+1) where rgt>@rgtCOMMIT TRANSACTIONSET XACT_ABORT OFFEnd注意:因为删除某个节点会同时删除该节点的所有子孙节点,而这些被删除的节点的个数为:(被删节点的右值-被删节点的左值+1)/2,而任何一个节点同时具有唯一的左值和唯一的右值,故删除作废节点后,其他相应节点的左、右值需要调整的幅度应为:减少(被删节点的右值-被删节点的左值+1)。
数据结构设计的实际案例分析

数据结构设计的实际案例分析数据结构是计算机科学中非常重要的一个概念,它是指数据元素之间的关系,以及数据元素本身的存储结构。
在计算机程序设计中,合理的数据结构设计可以提高程序的效率和性能,同时也能够更好地组织和管理数据。
本文将通过实际案例分析,探讨数据结构设计在实际应用中的重要性和作用。
### 1. 电商平台订单管理系统假设我们要设计一个电商平台的订单管理系统,该系统需要支持用户下单、支付、发货、退款等功能。
在这个案例中,我们可以使用树形数据结构来管理订单信息。
具体来说,我们可以使用二叉搜索树来存储订单信息,其中每个节点表示一个订单,节点的左子树存储比该订单金额小的订单,右子树存储比该订单金额大的订单。
这样设计可以快速地查找订单信息,提高系统的响应速度。
此外,我们还可以使用哈希表来存储订单号和订单信息的映射关系,这样可以通过订单号快速定位到对应的订单信息。
同时,使用队列来管理订单的处理顺序,保证订单按照先后顺序进行处理,避免出现混乱的情况。
### 2. 社交网络好友关系管理另一个实际案例是设计一个社交网络的好友关系管理系统。
在这个系统中,我们需要存储用户之间的好友关系,以及好友之间的互动信息。
为了高效地管理好友关系,我们可以使用图这种数据结构来表示用户之间的关系。
具体来说,我们可以使用邻接表来存储用户的好友列表,其中每个用户对应一个顶点,顶点之间的边表示好友关系。
这样设计可以快速地查找用户的好友列表,推荐新的好友,以及分析用户之间的社交关系。
此外,我们还可以使用栈来管理用户之间的消息通知,保证消息按照先后顺序进行处理。
同时,使用优先队列来实现消息推送功能,根据用户的偏好和行为习惯,将重要的消息优先推送给用户,提高用户体验。
### 3. 医院挂号排队系统最后一个案例是设计一个医院的挂号排队系统。
在这个系统中,我们需要管理患者的挂号信息,医生的排班信息,以及患者的就诊顺序。
为了高效地管理挂号信息和排队顺序,我们可以使用队列这种数据结构来实现。
《数据结构与算法设计》第5章 树

5.2.2 二叉树的性质
➢ 满二叉树和完全二叉树
满二叉树是指深度为h且节点数取得最大值2h-1的二叉树。 如果一棵深度为h的二叉树,除第h层外,其他每层的节点数 都达到最大,且最后一层的节点自左而右连续分布,这样的二 叉树称为完全二叉树。
5.2.2 二叉树的性质
5.2.2 二叉树的性质
性质6 对含有n个节点的完全二叉树自上而下、同一层从左往右 对节点编号0,1,2,…,n-1,则节点之间存在以下关系: (1)若i=0,则节点i是根节点,无双亲;若i>0,则其双亲节 点的编号为i/2-1; (2)若2×i +1≤n,则i的左孩子编号为2×i+1; (3)若2×i+2≤n,则i的右孩子编号为2×i+2; (4)若i>1且为偶数,则节点i是其双亲的右孩子,且有编号为 i-1的左兄弟; (5)若i<n-1且为奇数,则节点i是其双亲的左孩子,且有编号 为i+1的右兄弟。
5.3.3 二叉树的二叉链表类模板定义
//根据二叉树的先序遍历序列和中序遍历序列创建以r为根的二叉树
void CreateBinaryTree(BTNode<DataType> * &r, DataType pre[], DataType
in[], int preStart, int preEnd, int inStart, int inEnd); int Height(BTNode<DataType> *r); //求以r为根的二叉树高度 //求以r为根的二叉树中叶子节点数目
5.1.2 树的术语
(9)节点的层次:从根节点开始,根为第一层,根的孩子为 第二层,根的孩子的孩子为第三层,依次类推,树中任一节 点所在的层次是其双亲节点所在的层次数加1。 (10)堂兄弟:双亲在同一层的节点互为堂兄弟。
树形结构的菜单表设计与查询

树形结构的菜单表设计与查询开发中经常会遇到树形结构的场景,⽐如:导航菜单、组织机构等等,但凡是有这种⽗⼦层级结构的都是如此,⼀级类⽬、⼆级类⽬、三级类⽬。
对于这种树形结构的表要如何设计呢?接下来⼀起探讨⼀下⾸先,想⼀个问题,⽤⾮关系型数据库存储可不可以?答案是肯定可以的,⽐如⽤mongoDB,直接将整棵树存成json。
但是,这样不利于按条件查询,当然也取决于具体的需求,抛开需求谈设计都是耍流氓。
在菜单这个场景下,⼀般还是⽤关系型数据库存储,可以将最终的查询结构缓存起来。
常⽤的⽅法有四种:每⼀条记录存parent_id每⼀条记录存整个tree path经过的node枚举每⼀条记录存 nleft 和 nright维护⼀个表,所有的tree path作为记录进⾏保存第⼀种:每条记录存储parent_id这种⽅式简单明了,但是想要查询某个节点的所有⽗级和⼦级的时候⽐较困难,势必需要⽤到递归,在mysql⾥⾯就得写存储过程,太⿇烦了。
当然,如果只有两级的话就⽐较简单了,⾃连接就搞定了,例如:第四种:单独⽤⼀种表保存节点之间的关系CREATE TABLE `city` (`id` int(11) NOT NULL AUTO_INCREMENT,`name` varchar(16),PRIMARY KEY (`id`) USING BTREE) ENGINE = InnoDB AUTO_INCREMENT =1CHARACTER SET= utf8mb4;CREATE TABLE `city_tree_path_info` (`id` int(11) NOT NULL AUTO_INCREMENT,`city_id` int(11) NOT NULL,`ancestor_id` int(11) NOT NULL COMMENT '祖先ID',`level` tinyint(4) NOT NULL COMMENT '层级',PRIMARY KEY (`id`) USING BTREE) ENGINE = InnoDB AUTO_INCREMENT =1CHARACTER SET= utf8mb4;上⾯这个例⼦中,city表代表城市,city_tree_path_info代表城市之间的层级关系,ancestor_id表⽰⽗级和祖⽗级ID,level是当前记录相对于ancestor_id⽽⾔的层级。
查询树状结构的数据显示形式

查询树状结构的数据显示形式全文共四篇示例,供读者参考第一篇示例:树状结构在数据显示和存储中经常被使用,它具有清晰的层次关系和易于理解的特点。
在实际应用中,我们经常需要查询树状结构的数据,以便找到所需的信息或进行统计分析。
本文将探讨查询树状结构数据的显示形式,以及如何有效地展示和处理这种数据。
树状结构通常是一种分层的数据结构,由根节点和若干子节点组成。
每个节点可以有多个子节点,但只能有一个父节点。
在实际应用中,树状结构常常用于表示组织结构、分类体系、文件目录等具有层级关系的数据。
在一个公司的组织结构中,总经理是根节点,部门经理是子节点,员工是子节点的子节点,依次类推。
1. 展开-折叠式显示:在展开-折叠式显示中,树状结构以层次化的方式展示出来,用户可以通过点击节点旁边的“+”或“-”符号来展开或折叠子节点。
这种显示形式适合于较大的树状结构,可以让用户快速定位到所需的节点。
2. 标签式显示:在标签式显示中,每个节点都被赋予一个标签或名称,用户可以通过输入标签或名称来查找特定节点。
这种显示形式适合于用户知道节点名称但不知道节点位置的情况。
3. 缩略图式显示:在缩略图式显示中,树状结构被以图形的方式展示出来,节点之间的层次关系可以通过不同的形状或颜色来表示。
这种显示形式适合于更直观地展示树状结构的关系。
在查询树状结构数据时,除了显示形式之外,还需要考虑如何高效地进行查询和分析。
以下是几点建议:1. 使用递归算法:由于树状结构的特点是递归性的,因此在查询和处理树状结构数据时,通常会用到递归算法。
递归算法可以简化代码逻辑,提高效率。
2. 添加索引优化性能:如果树状结构数据较大,可以考虑添加索引以提高查询性能。
通过为树状结构的某些字段建立索引,可以加快查询速度。
3. 避免循环依赖:在设计树状结构数据时,应避免出现循环依赖的情况,避免造成递归查询死循环的问题。
4. 使用缓存减少数据库查询:对于频繁查询的树状结构数据,可以考虑使用缓存技术,减少对数据库的访问次数,提高查询效率。
打印树形结构
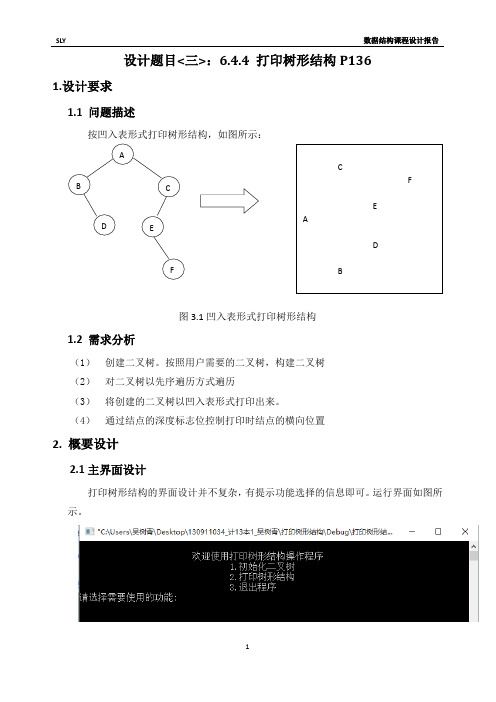
typedef struct Node//定义二叉树结点 {
char data; struct Node *lchild;//左孩子指针 struct Node *rchild;//右孩子指针 int depth;//结点深度,用于打印控制横向的位置 }Node,*BiTree;
}
} (3).界面模块
void view()//界面显示
{ printf("\n\t\t\t 欢迎使用打印树形结构操作程序\n"); printf("\t\t\t\t1.初始化二叉树\n"); printf("\t\t\t\t2.打印树形结构\n"); printf("\t\t\t\t3.退出程序\n"); printf("请选择需要使用的功能:");
3
exitApplication()
SLY
4.2 系统主要子程序详细设计
(1)主函数模块设计 主函数。调用函数并逐步功能实现和打印。
void main() {
int n; int loop=1; BiTree T; view(); scanf("%d",&n);//接收一个数值,判断执行什么操作 while(loop) {
和结点深度标志域(depth)。结点示意图如下:
lchild
data
depth
rchild
2.3 系统功能设计
图 3.3 结点示意图
本程序设计了 4 个功能子菜单,其描述如下: ① 二叉树的初始化。由函数 CreatTree()实现。该功能按照自上而下从左往右 的顺序输入二叉树结点,构造二叉树。 ② 打印树形结构。由函数 prev()实现。该函数实现二叉树的先序遍历,并同 时格式化输出结点的数据信息。 ③ 退出操作。由 exit(0)函数实现。 ④ 主界面显示
excel树形结构表格

excel树形结构表格
Excel树形结构表格是一种用于展示层次结构数据的表格格式。
在Excel中,可以使用数据透视表、条件格式和公式等功能来创建树形结构表格。
以下是创建Excel树形结构表格的步骤:
1. 准备数据:首先需要将层次结构数据整理成表格形式,每个节点作为一行,节点之间的关系用父子关系表示。
例如,以下是一个组织结构的数据:
```
部门ID 部门名称上级部门ID
1 总部-1
2 人事部1
3 财务部1
4 市场部1
5 技术部1
6 研发部4
7 销售部4
8 行政部2
```
2. 创建数据透视表:选中包含数据的单元格区域,然后点击“插入”选项卡中的“数据透视表”按钮,选择“新的工作表”,然后点击“确定”。
3. 设置数据透视表字段:在数据透视表字段列表中,将“部门名称”拖动到“行”区域,将“上级部门ID”拖动到“列”区域。
这样,数据透视表会自动显示层次结构。
4. 调整数据透视表样式:选中数据透视表中的所有单元格,然后点击“设计”选项卡中的“套用样式”,选择一个合适的样式。
此外,还可以使用条件格式来突出显示不同级别的节点。
5. 添加展开/折叠功能:在数据透视表的任意单元格上右键单击,选择“显示字段列表”,然后取消勾选“上级部门ID”字段。
接下来,在数据透视表的任意单元格上右键单击,选择“显示详细信息”,然后勾选“上级部门ID”字段。
这样,就实现了展开/折叠功能。
通过以上步骤,就可以在Excel中创建一个树形结构表格。
需要注意的是,这种方法适用于较小的数据集,如果数据集较大,建议使用专门的树形结构控件或插件。
树形结构数据库表设计

树形结构数据库表设计转载:逻辑数据库设计 - 单纯的树(递归关系数据)相信有过开发经验的朋友都曾碰到过这样⼀个需求。
假设你正在为⼀个新闻⽹站开发⼀个评论功能,读者可以评论原⽂甚⾄相互回复。
这个需求并不简单,相互回复会导致⽆限多的分⽀,⽆限多的祖先-后代关系。
这是⼀种典型的递归关系数据。
对于这个问题,以下给出⼏个解决⽅案,各位客观可斟酌后选择。
⼀、邻接表:依赖⽗节点 邻接表的⽅案如下(仅仅说明问题): CREATE TABLE Comments( CommentId int PK, ParentId int, --记录⽗节点 ArticleId int, CommentBody nvarchar(500), FOREIGN KEY (ParentId) REFERENCES Comments(CommentId) --⾃连接,主键外键都在⾃⼰表内 FOREIGN KEY (ArticleId) REFERENCES Articles(ArticleId) ) 由于偷懒,所以采⽤了书本中的图了,Bugs就是Articles: 这种设计⽅式就叫做邻接表。
这可能是存储分层结构数据中最普通的⽅案了。
下⾯给出⼀些数据来显⽰⼀下评论表中的分层结构数据。
⽰例表: 图⽚说明存储结构:邻接表的优缺分析 邻接表的优缺分析 对于以上邻接表,很多程序员已经将其当成默认的解决⽅案了,但即便是这样,但它在从前还是有存在的问题的。
分析1:查询⼀个节点的所有后代(求⼦树)怎么查呢? 我们先看看以前查询两层的数据的SQL语句: SELECT c1.*,c2.* FROM Comments c1 LEFT OUTER JOIN Comments2 c2 ON c2.ParentId = mentId 显然,每需要查多⼀层,就需要联结多⼀次表。
SQL查询的联结次数是有限的,因此不能⽆限深的获取所有的后代。
⽽且,这种这样联结,执⾏Count()这样的聚合函数也相当困难。
多叉树结合JavaScript树形控件实现无限级树形菜单(一种构建多级有序树形结构JSON(或XML)数据源的方法)

多叉树结合JavaScript树形控件实现无限级树形菜单(一种构建多级有序树形结构JSON(或XML)数据源的方法)一、问题研究的背景和意义在Web应用程序开发领域,基于AJAX技术的JavaScript树形控件已经被广泛使用,它用来在Html页面上展现具有层次结构的数据项。
目前市场上常见的JavaScript框架及组件库中均包含自己的树形控件,例如JQuery、Dojo、Yahoo UI、Ext JS等,还有一些独立的树形控件,例如dhtmlxtree等,这些树形控件完美的解决了层次数据的展示问题。
展示离不开数据,树形控件主要利用AJAX技术从服务器端获取数据源,数据源的格式主要包括JSON、XML等,而这些层次数据一般都存储在数据库中。
“无限级树形菜单”,顾名思义,没有级别的限制,它的数据通常来自数据库中的无限级层次数据,这种数据的存储表通常包括id和parentId这两个字段,以此来表示数据之间的层次关系。
现在问题来了,既然树形控件的数据源采用JSON或XML等格式的字符串来组织层次数据,而层次数据又存储在数据库的表中,那么如何建立起树形控件与层次数据之间的关系,换句话说,如何将数据库中的层次数据转换成对应的层次结构的JSON或XML格式的字符串,返回给客户端的JavaScript 树形控件?这就是我们要解决的关键技术问题。
本文将以目前市场上比较火热的Ext JS框架为例,讲述实现无限级树形菜单的方法,该方法同样适用于其它类似的JS树形控件。
Ext JS框架是富客户端开发中出类拔萃的框架之一。
在Ext的UI控件中,树形控件无疑是最为常用的控件之一,它用来实现树形结构的菜单。
TreeNode用来实现静态的树形菜单,AsyncTreeNode用来实现动态的异步加载树形菜单,后者最为常用,它通过接收服务器端返回来的JSON格式的数据,动态生成树形菜单节点。
动态生成树有两种思路:一种是一次性生成全部树节点,另一种是逐级加载树节点(利用AJAX,每次点击节点时查询下一级节点)。
el-table树形表格嵌套表单

一、概述随着互联网和信息技术的快速发展,各种数据可视化的需求也越来越迫切。
在管理系统中,表格是一种常见的数据展示方式,而树形表格和嵌套表单则是表格的一种特殊形式。
本文将重点介绍el-table树形表格嵌套表单的设计和实现。
二、el-table树形表格的概念1. el-table树形表格是基于Element UI框架的一种数据展示形式,它可以将数据以树形结构的方式进行展示,方便用户查看和操作数据。
2. el-table树形表格通常用于展示具有层级关系的数据,比如组织架构、文件目录树等。
3. el-table树形表格的特点是可以展开和折叠子节点,并且可以在展开子节点的同时加载子节点的数据。
三、el-table树形表格的基本用法1. 在使用el-table树形表格之前,首先需要引入Element UI框架,并按照其文档进行配置。
2. el-table树形表格的基本用法包括定义表格的列和数据,并在列配置中使用tree属性来表示该列数据的层级关系。
3. 在el-table组件中使用expand-event属性来配置展开子节点的事件,并使用load属性来配置加载子节点数据的事件。
四、el-table树形表格嵌套表单的设计思路1. el-table树形表格是一种展示数据的方式,而嵌套表单是一种用于编辑数据的方式,将两者结合可以实现对树形结构数据的展示和编辑。
2. el-table树形表格嵌套表单的设计思路是在树形表格的每一行数据后面添加一个展开按钮,点击展开按钮可以显示该行数据对应的表单,从而实现对该行数据的编辑。
3. 嵌套表单可以使用Element UI框架提供的form组件来进行设计,在form组件中使用ref属性来获取表单的引用,方便在展开按钮点击事件中进行表单的显示和隐藏操作。
五、el-table树形表格嵌套表单的实现步骤1. 在el-table树形表格的列配置中添加一个操作列,用于显示展开按钮,并在click事件中编写展开按钮的点击逻辑。
antdesign a-tree blocknode用法-概述说明以及解释

antdesign a-tree blocknode用法-概述说明以及解释1.引言1.1 概述在撰写本文时,我们将重点关注antdesign中的a-tree组件以及其子组件blocknode的用法。
该组件是一种用于展示树形结构数据的UI组件,可以适用于各种需求场景。
在本文中,我们将首先对antdesign进行简介,然后介绍a-tree组件的基本特点和使用方法。
接着,我们将重点解析blocknode这个子组件的用法,包括其在树形结构中的作用和基本使用。
本文将提供详细的示例代码和演示结果,以帮助读者快速上手。
本文的目的在于全面介绍antdesign中a-tree组件以及blocknode 的用法,帮助读者理解它们的基本功能和应用场景。
通过学习本文,读者将能够熟练地使用a-tree组件和blocknode子组件,并能够根据自己的需求进行二次开发和定制化。
在下一节中,我们将对antdesign进行简单介绍,为读者提供一个整体的了解。
1.2 文章结构文章结构部分的内容应该包括对整篇文章的整体安排和组织方式的解释。
该部分可以包括以下内容:1. 文章的章节划分:介绍文章各个章节的名称和序号,以及每个章节所涵盖的内容。
2. 章节之间的逻辑关系:说明各个章节之间的逻辑关系,以便读者能够理解文章的结构和思路。
3. 文章的主题和主旨:概括性地解释文章的主题和主旨,让读者知道整篇文章的核心内容和目的。
4. 段落的组织方式:说明整个文章的段落结构,包括段落的标题和段落之间的链接关系。
5. 重点和亮点部分的安排:指出文章中的重点和亮点部分,并解释为什么这些部分是关键和独特的。
例如,在这篇文章中,可以写道:本文将按照以下结构进行组织:首先,在引言部分,我们会介绍该文章的概述、结构和目的。
然后,在正文部分,我们会先简要介绍一下antdesign的背景和特点,接着详细介绍a-tree组件的功能和用法。
其中,我们会重点探讨blocknode的用法,包括其功能和相关代码示例。
数据结构课程设计_二叉树操作

数据结构课程设计_⼆叉树操作数据结构课程设计题⽬:⼆叉树的操作学⽣姓名:学号:系部名称:计算机科学与技术系专业班级:指导教师:课程设计任务书第⼀章程序要求1)完成⼆叉树的基本操作。
2)建⽴以⼆叉链表为存储结构的⼆叉树;3)实现⼆叉树的先序、中序和后序遍历;4)求⼆叉树的结点总数、叶⼦结点个数及⼆叉树的深度。
第⼆章算法分析建⽴以⼆叉链表为存储结构的⼆叉树,在次⼆叉树上进⾏操作;1先序遍历⼆叉树的操作定义为:若⼆叉树唯恐则为空操作;否则(1)访问根节点;(2)先序遍历做字数和;(3)先序遍历有⼦树;2中序遍历⼆叉树的操作定义为:若⼆叉树为空,则空操作;否则(1)中序遍历做⼦树;(2)访问根节点;(3)中序遍历有⼦树;3后续遍历⼆叉树的操作定义为:若⼆叉树为空则为空操作;否则(1)后序遍历左⼦树;(2)后序遍历右⼦树;(3)访问根节点;⼆叉树的结点总数、叶⼦结点个数及⼆叉树的深度。
第三章⼆叉树的基本操作和算法实现⼆叉树是⼀种重要的⾮线性数据结构,是另⼀种树形结构,它的特点是每个节点之多有两棵⼦树(即⼆叉树中不存在度⼤于2的结点),并且⼆叉树的结点有左右之分,其次序不能随便颠倒。
1.1⼆叉树创建⼆叉树的很多操作都是基于遍历实现的。
⼆叉树的遍历是采⽤某种策略使得采⽤树形结构组织的若⼲年借点对应于⼀个线性序列。
⼆叉树的遍历策略有四种:先序遍历中续遍历后续遍历和层次遍历。
基本要求1 从键盘接受输⼊数据(先序),以⼆叉链表作为存储结构,建⽴⼆叉树。
2 输出⼆叉树。
3 对⼆叉树进⾏遍历(先序,中序,后序和层次遍历)4 将⼆叉树的遍历打印出来。
⼀.问题描述⼆叉树的很多操作都是基于遍历实现的。
⼆叉树的遍历是采⽤某种策略使得采⽤树型结构组织的若⼲结点对应于⼀个线性序列。
⼆叉树的遍历策略有四种:先序遍历、中序遍历、后序遍历和层次遍历。
⼆.基本要求1.从键盘接受输⼊数据(先序),以⼆叉链表作为存储结构,建⽴⼆叉树。
2.输出⼆叉树。
指标树形结构

指标树形结构指标树形结构是一种展示指标层级关系的方式,通常用于展示企业或组织的业务指标体系。
这种结构可以帮助人们更好地理解和管理业务数据,以便做出更好的决策。
一、指标树形结构的概述指标树形结构是一种以树形方式展示指标及其子指标层级关系的工具。
它通常由一个顶层指标(或根节点)和若干个子指标(或子节点)组成。
每个指标都可以分解为更具体的子指标,这些子指标通常与父指标相关联,并进一步描述父指标的含义和目标。
二、指标树形结构的作用1. 层级化管理:通过将指标分解为子指标,可以更容易地管理和跟踪每个层级的数据,从而提高数据透明度和可操作性。
2. 业务理解:指标树形结构可以帮助企业员工更好地理解业务目标和指标体系,从而更好地实现业务目标。
3. 决策支持:通过将指标按照层级关系进行组织,可以更容易地分析数据并发现数据背后的趋势和规律,从而为决策提供支持。
4. 沟通协作:指标树形结构可以促进不同部门之间的沟通协作,因为所有相关人员都可以使用相同的指标体系来交流和评估业务情况。
三、如何构建指标树形结构1. 确定顶层指标:首先需要确定顶层指标,通常是业务目标或战略目标的概括性描述。
2. 分解子指标:针对每个顶层指标,需要将其分解为若干个子指标。
这些子指标应该能够更具体地描述父指标的含义和目标。
3. 层级关系设计:在设计指标树形结构时,需要注意每个层级之间的关系。
应该将相关性强、逻辑关系紧密的指标放在同一层级,以便更好地组织和管理数据。
4. 数据源确认:在构建指标树形结构之前,需要确认每个指标的数据来源。
这有助于确保数据的准确性和可靠性,并为后续的数据分析和决策提供支持。
5. 系统实施:根据设计和确认的指标树形结构,可以将其实现到相应的系统中。
这有助于提高数据管理和分析的效率和准确性。
四、常见的指标树形结构形式1. 年度/季度/月度指标分解:将年度/季度/月度总目标分解为各个部门的子目标,形成树形结构。
2. 客户/产品/渠道等维度分解:针对不同维度(如客户、产品、渠道等)分别进行分解,形成相应的树形结构。
office文档树形结构

office文档树形结构
要在Microsoft Office文档中创建树形结构,您可以采用以下方法:
在“绘图”工具栏上,点击“插入组织结构图或其他图示”,然后在出现的“图示库”中选择“用于显示层次关系”的一种。
点击“确定”后,您将看到一个层次结构图。
此时,您可以在这些方框中输入相关的内容。
若要在某个结构下增加分支,先选中该结构,然后在“组织结构图”工具栏上点击“插入形状”,选择是插入同事、下属还是助手。
如果您对默认的效果不满意,可以在“组织结构图”工具栏上选择“自动套用格式”,这里给出了除“默认”外的16种效果,总有一款可以满足您的需求。
在“版式”中,除了标准样式外,还提供了两边悬挂、左悬挂、右悬挂等供您选择。
值得注意的是,用绘图工具制作的树形结构图整体是一副图片,所以您可以在Word中像操作图片一样对它进行操作。
以上方法仅供参考,如果您遇到问题,可以查阅软件的使用说明或者请教专业人士。
2024版《数据结构图》ppt课件

良好的数据结构可以带来更高的运 行或存储效率,是算法设计的基础, 对程序设计的成败起到关键作用。
常见数据结构类型介绍
线性数据结构
如数组、链表、栈、队 列等,数据元素之间存
在一对一的关系。
树形数据结构
如二叉树、多叉树、森 林等,数据元素之间存
在一对多的关系。
图形数据结构
由顶点和边组成,数据 元素之间存在多对多的
队列定义、特点及应用场景
队列的特点 只能在队尾进行插入操作,队头进行删除操作。
队列是一种双端开口的线性结构。
队列定义、特点及应用场景
应用场景 操作系统的任务调度。 缓冲区的实现,如打印机缓冲区。
队列定义、特点及应用场景
广度优先搜索(BFS)。
消息队列和事件驱动模型。
串定义、基本操作及实现方法
最短路径问题 求解图中两个顶点之间的最短路径,即路径上边 的权值之和最小。
3
算法介绍 Prim算法、Kruskal算法、Dijkstra算法、Floyd 算法等。
拓扑排序和关键路径问题探讨
拓扑排序
对有向无环图(DAG)进行排序, 使得对每一条有向边(u,v),均有
u在v之前。
关键路径问题
求解有向无环图中从源点到汇点 的最长路径,即关键路径,它决
遍历二叉树和线索二叉树
遍历二叉树
先序遍历、中序遍历和后序遍历。遍历算 法可以采用递归或非递归方式实现。
VS
线索二叉树
利用二叉链表中的空指针来存放其前驱结 点和后继结点的信息,使得在遍历二叉树 时可以利用这些线索得到前驱和后继结点, 从而方便地遍历二叉树。
树、森林与二叉树转换技巧
树转换为二叉树
加线、去线、层次调整。将树中的每个结点的所有孩子结点用线连接起来,再去掉与原结点相连的线,最后 将整棵树的层次进行调整,使得每个结点的左子树为其第一个孩子,右子树为其兄弟结点。
quasar 树形折叠表格

quasar 树形折叠表格Quasar 是一个基于 Vue.js 的前端框架,它提供了丰富的组件和工具,可以帮助开发者快速构建现代化的 Web 应用程序。
其中,Quasar 也提供了表格组件,但是并没有直接提供树形折叠表格的组件。
如果你需要在 Quasar 中实现树形折叠表格,你可以考虑以下几种方法:1. 自定义组件,你可以自己编写一个树形折叠表格的组件,利用 Quasar 提供的表格组件和树形结构的数据来实现。
你可以使用Quasar 的表格组件来展示数据,并通过自定义的逻辑来实现树形结构和折叠展开功能。
2. 使用第三方组件库,Quasar 是基于 Vue.js 的,你可以考虑使用其他的 Vue.js 组件库,例如 Element UI、Ant Design Vue 等,它们提供了树形表格的组件,可以直接在 Quasar 中使用。
3. 扩展 Quasar 表格组件,如果你对 Quasar 的表格组件比较熟悉,你可以尝试扩展 Quasar 的表格组件,添加树形折叠功能。
你可以查阅 Quasar 的文档,了解如何扩展组件,并根据需要进行修改和添加。
需要注意的是,无论采用哪种方法,你都需要考虑到以下几个方面:数据结构,树形折叠表格需要树形结构的数据,你需要根据实际需求来组织和处理数据。
展开折叠功能,你需要实现树形结构的展开和折叠功能,可以通过监听事件或者添加按钮来控制展开和折叠。
样式设计,你可以根据需求自定义树形折叠表格的样式,使其符合项目的整体风格。
总之,虽然 Quasar 没有直接提供树形折叠表格的组件,但你可以通过自定义组件、使用第三方组件库或者扩展 Quasar 的表格组件来实现这个功能。
希望这些信息对你有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
树形结构的数据库表Schema设计程序设计过程中,我们常常用树形结构来表征某些数据的关联关系,如企业上下级部门、栏目结构、商品分类等等,通常而言,这些树状结构需要借助于数据库完成持久化。
然而目前的各种基于关系的数据库,都是以二维表的形式记录存储数据信息,因此是不能直接将Tree 存入DBMS,设计合适的Schema及其对应的CRUD算法是实现关系型数据库中存储树形结构的关键。
理想中树形结构应该具备如下特征:数据存储冗余度小、直观性强;检索遍历过程简单高效;节点增删改查CRUD操作高效。
无意中在网上搜索到一种很巧妙的设计,原文是英文,看过后感觉有点意思,于是便整理了一下。
本文将介绍两种树形结构的Schema设计方案:一种是直观而简单的设计思路,另一种是基于左右值编码的改进方案。
一、基本数据本文列举了一个食品族谱的例子进行讲解,通过类别、颜色和品种组织食品,树形结构图如下:二、继承关系驱动的Schema设计对树形结构最直观的分析莫过于节点之间的继承关系上,通过显示地描述某一节点的父节点,从而能够建立二维的关系表,则这种方案的Tree表结构通常设计为:{Node_id,Parent_id},上述数据可以描述为如下图所示:这种方案的优点很明显:设计和实现自然而然,非常直观和方便。
缺点当然也是非常的突出:由于直接地记录了节点之间的继承关系,因此对Tree的任何CRUD操作都将是低效的,这主要归根于频繁的“递归”操作,递归过程不断地访问数据库,每次数据库IO都会有时间开销。
当然,这种方案并非没有用武之地,在Tree规模相对较小的情况下,我们可以借助于缓存机制来做优化,将Tree的信息载入内存进行处理,避免直接对数据库IO操作的性能开销。
三、基于左右值编码的Schema设计在基于数据库的一般应用中,查询的需求总要大于删除和修改。
为了避免对于树形结构查询时的“递归”过程,基于Tree的前序遍历设计一种全新的无递归查询、无限分组的左右值编码方案,来保存该树的数据。
第一次看见这种表结构,相信大部分人都不清楚左值(Lft)和右值(Rgt)是如何计算出来的,而且这种表设计似乎并没有保存父子节点的继承关系。
但当你用手指指着表中的数字从1数到18,你应该会发现点什么吧。
对,你手指移动的顺序就是对这棵树进行前序遍历的顺序,如下图所示。
当我们从根节点Food左侧开始,标记为1,并沿前序遍历的方向,依次在遍历的路径上标注数字,最后我们回到了根节点Food,并在右边写上了18。
第一次看见这种表结构,相信大部分人都不清楚左值(Lft)和右值(Rgt)是如何计算出来的,而且这种表设计似乎并没有保存父子节点的继承关系。
但当你用手指指着表中的数字从1数到18,你应该会发现点什么吧。
对,你手指移动的顺序就是对这棵树进行前序遍历的顺序,如下图所示。
当我们从根节点Food左侧开始,标记为1,并沿前序遍历的方向,依次在遍历的路径上标注数字,最后我们回到了根节点Food,并在右边写上了18。
依据此设计,我们可以推断出所有左值大于2,并且右值小于11的节点都是Fruit的后续节点,整棵树的结构通过左值和右值存储了下来。
然而,这还不够,我们的目的是能够对树进行CRUD操作,即需要构造出与之配套的相关算法。
四、树形结构CRUD算法(1)获取某节点的子孙节点只需要一条SQL语句,即可返回该节点子孙节点的前序遍历列表,以Fruit为例:SELECT* FROM Tree WHERE Lft BETWEEN 2 AND 11 ORDER BY Lft ASC。
查询结果如下所示:那么某个节点到底有多少的子孙节点呢?通过该节点的左、右值我们可以将其子孙节点圈进来,则子孙总数= (右值–左值– 1) / 2,以Fruit为例,其子孙总数为:(11 –2 – 1) / 2 = 4。
同时,为了更为直观地展现树形结构,我们需要知道节点在树中所处的层次,通过左、右值的SQL查询即可实现,以Fruit为例:SELECTCOUNT(*) FROM Tree WHERE Lft <= 2 AND Rgt >=11。
为了方便描述,我们可以为Tree建立一个视图,添加一个层次数列,该列数值可以写一个自定义函数来计算,函数定义如下:[sql]view plaincopy1CREATE FUNCTION dbo.CountLayer2(3 @node_id int4)5RETURNS int6AS7begin8declare @result int9set @result = 010declare @lft int11declare @rgt int12 if exists(select Node_id from Tree where Node_id = @node_id)13begin14select @lft = Lft, @rgt = Rgt from Tree where node_id = @node_id15select @result = count(*) from Tree where Lft <= @lft and Rgt >= @rgt 16end17return @result18end19GO基于层次计算函数,我们创建一个视图,添加了新的记录节点层次的数列:[sql]view plaincopy20CREATE VIEW dbo.TreeView21AS22SELECT Node_id, Name, Lft, Rgt, dbo.CountLayer(Node_id) AS Layer FROM dbo.Tree ORDER BY Lft23GO创建存储过程,用于计算给定节点的所有子孙节点及相应的层次:[sql]view plaincopy24CREATE PROCEDURE [dbo].[GetChildrenNodeList]25(26 @node_id int27)28AS29declare @lft int30declare @rgt int31if exists(select Node_id from Tree where node_id = @node_id)32begin33select @lft = Lft, @rgt = Rgt from Tree where Node_id = @node_id 34select * from TreeView where Lft between @lft and @rgt order by Lft ASC 35end36GO现在,我们使用上面的存储过程来计算节点Fruit所有子孙节点及对应层次,查询结果如下:从上面的实现中,我们可以看出采用左右值编码的设计方案,在进行树的查询遍历时,只需要进行2次数据库查询,消除了递归,再加上查询条件都是数字的比较,查询的效率是极高的,随着树规模的不断扩大,基于左右值编码的设计方案将比传统的递归方案查询效率提高更多。
当然,前面我们只给出了一个简单的获取节点子孙的算法,真正地使用这棵树我们需要实现插入、删除同层平移节点等功能。
(2)获取某节点的族谱路径假定我们要获得某节点的族谱路径,则根据左、右值分析只需要一条SQL语句即可完成,以Fruit为例:SELECT* FROM Tree WHERE Lft < 2 AND Rgt > 11 ORDER BY Lft ASC ,相对完整的存储过程:[sql]view plaincopy37CREATE PROCEDURE [dbo].[GetParentNodePath]38(39 @node_id int40)41AS42declare @lft int43declare @rgt int44if exists(select Node_id from Tree where Node_id = @node_id)45begin46select @lft = Lft, @rgt = Rgt from Tree where Node_id = @node_id 47select * from TreeView where Lft < @lft and Rgt > @rgt order by Lft ASC 48end49GO(3)为某节点添加子孙节点假定我们要在节点“Red”下添加一个新的子节点“Apple”,该树将变成如下图所示,其中红色节点为新增节点。
仔细观察图中节点左右值变化,相信大家都应该能够推断出如何写SQL脚本了吧。
我们可以给出相对完整的插入子节点的存储过程:[sql]view plaincopy50CREATE PROCEDURE [dbo].[AddSubNode]51(52 @node_id int,53 @node_name varchar(50)54)55AS56declare @rgt int57if exists(select Node_id from Tree where Node_id = @node_id)58begin59SET XACT_ABORT ON60BEGIN TRANSCTION61select @rgt = Rgt from Tree where Node_id = @node_id62update Tree set Rgt = Rgt + 2 where Rgt >= @rgt63update Tree set Lft = Lft + 2 where Lft >= @rgt64insert into Tree(Name, Lft, Rgt) values(@node_name, @rgt, @rgt + 1) 65COMMIT TRANSACTION66SET XACT_ABORT OFF67end68GO(4)删除某节点如果我们想要删除某个节点,会同时删除该节点的所有子孙节点,而这些被删除的节点的个数为:(被删除节点的右值–被删除节点的左值+ 1) / 2,而剩下的节点左、右值在大于被删除节点左、右值的情况下会进行调整。
来看看树会发生什么变化,以Beef为例,删除效果如下图所示。
则我们可以构造出相应的存储过程:[sql]view plaincopy69CREATE PROCEDURE [dbo].[DelNode]70(71 @node_id int72)73AS74declare @lft int75declare @rgt int76if exists(select Node_id from Tree where Node_id = @node_id)77begin78SET XACT_ABORT ON79BEGIN TRANSCTION80select @lft = Lft, @rgt = Rgt from Tree where Node_id = @node_id 81delete from Tree where Lft >= @lft and Rgt <= @rgt82update Tree set Lft = Lft – (@rgt - @lft + 1) where Lft > @lft 83update Tree set Rgt = Rgt – (@rgt - @lft + 1) where Rgt > @rgt 84COMMIT TRANSACTION85SET XACT_ABORT OFF86end87GO五、总结我们可以对这种通过左右值编码实现无限分组的树形结构Schema设计方案做一个总结:(1)优点:在消除了递归操作的前提下实现了无限分组,而且查询条件是基于整形数字的比较,效率很高。
